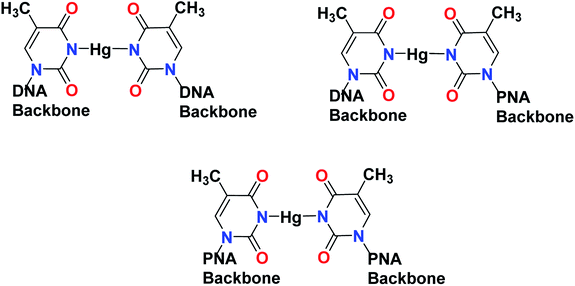
Open Access Article
Open Access ArticleRole of the backbone of nucleic acids in the stability of Hg2+-mediated canonical base pairs and thymine–thymine mispair: a DFT study†
Surjit Bhai ab and
Bishwajit Ganguly
ab and
Bishwajit Ganguly *a
*a
aComputation and Simulation Unit (Analytical and Environmental Science Division and Centralized Instrument Facility), CSIR-Central Salt and Marine Chemicals Research Institute, Bhavnagar, Gujarat, India-364 002. E-mail: gang_12@rediffmail.com; ganguly@csmcri.res.in; surjitbhai94@gmail.com; Fax: +91-278-2567562; Tel: +91-278-2567760, ext. 6770
bAcademy of Scientific and Innovative Research (AcSIR), Ghaziabad 201002, Uttar Pradesh, India
First published on 10th November 2020
Abstract
Metal-mediated base pairs have attracted attention in nucleic acid research and molecular devices. Herein, we report a systematic computational study on Hg2+-mediated base pairs with canonical and TT mispair dimers. The computed results revealed that the model DTTD (thymine–thymine with DNA backbone) mispair is more energetically favored than the canonical base pairs. The DTTTTD mispair dimer is more energetically stable by ∼36.0 kcal mol−1 than the corresponding canonical DATGCD base pairs. The Hg⋯Hg metallophilic interaction was observed with the DTTTTD mispair and not the canonical base pairs. The DATGCD (adenine: thymine, guanine: cytosine) base pairs were significantly perturbed upon interaction with the mercury ion; however, the TTTT mispairs were aligned upon interaction with the Hg2+ ion. The DTTTTD mispair adopts a B-type conformation with proper alignment of its nucleobases along the axis. The MESP calculations showed a larger Vmin value for the interacting nitrogen centers of the thymine nucleobase, supporting its stronger binding with the Hg2+ ion compared to the other nucleobases. The role of the backbone is crucial in nucleic acids to determine many useful properties, and PNAs have been exploited extensively in the literature. Thus, this study was further extended to metal-mediated PNA-containing dimer mispairs such as DTTTTP (thymine–thymine dimer model with hybrid DNA and PNA backbone) and PTTTTP (thymine–thymine dimer model with PNA backbone). The calculated results showed that the PTTTTP PNA mispair is thermodynamically more stable than the canonical dimers. The enthalpy calculated for DTTTTD and PTTTTP at the B3LYP-D3/6-31G* level of theory showed that PTTTTP is ∼3.0 kcal mol−1 more stable than DTTTTD. The metallophilic interaction of Hg2+ ions in the PTTTTP mispair was not observed; however, the metal ions interact with the nitrogen of the thymine bases, presumably enhancing the stability of this mispair by strong electrostatic interactions. These interactions arise due to the P-type conformations of PNAs, which lack metallophilic interactions between the metal ions and can adopt a wider and more unwounded helix. The interaction of the mispair dimers with the explicit water molecules also showed a similar stability trend to that observed with the implicit solvation model. The metallophilic interaction (Hg⋯Hg) was found to be conserved in DTTTTD. The AIM analysis performed for these dimers revealed that the interactions are primarily electrostatic in nature. The UV-vis absorption spectra of the mispair systems calculated at the B3LYP-D3/6-31G* level of theory using the TD-DFT method in the aqueous phase suggested that the absorption maximum is located at a longer wavelength in the case of PTTTTP compared to the corresponding DTTTTD and can be a signature to identify the formation of metal-mediated nucleic acid systems.
Introduction
The interactions of nucleic acids such as deoxyribonucleic acids (DNA) and peptide nucleic acids (PNA) with metal ions have attracted attention in biological processes and their potential applications in nanotechnology.1–9 The derivatives of DNA have been applied in medicine, synthetic organic chemistry, materials science, and biotechnology.10–16 Different applications of DNA and its derivatives can be attained due to the robustness, high rigidity, and hybridization properties of its double helix. Previously, the introduction of non-natural base pairs into DNA has been implemented to expand the genetic alphabet.17–20 Numerous reports are available concerning artificial nucleobases, which allow site-specific functionalization with selected metal ions.21 In metal-mediated base pairs, the hydrogen bonding in the Watson–Crick model, adenine–thymine (AT), and guanine–cytosine (GC) are replaced by metal ions. Functionalized DNA can be achieved by inserting metal ions between the base pairs.2 Metal-mediated base pairs with artificial nucleosides have been extensively studied in the field of nanotechnology.9 Metal-containing double helices are known to exhibit enhanced physical and chemical properties as well as electrical and magnetic properties.21,22 The natural nucleobases are replaced by ligands with high affinity for metal ions.3,5 These modifications lead to coordinate bonds to the metal ions rather than hydrogen bonding between the nucleobases and metal ions.In an earlier report, Tanaka and Shionoya explored the benefits of artificial nucleosides in metal-mediated base pairs and their applications in DNA.1 Similarly, Meggers et al. investigated Cu2+-mediated artificial base pairs containing pyridine-2,6-dicarboxylate (Dipic) and pyridine (Py) nucleobases as a complementary base pair.23 The melting temperature transition profile confirmed that the Dipic:Py artificial base pair with the mediating Cu2+ ion has potential applications in materials.23 The crystal structure of artificial nucleic acids with a Cu2+-mediated double helix was also observed, which led to the Z-conformation.24 Another ligand, hydroxypyridone, with consecutive mediating Cu2+ ions was also incorporated in the middle of the DNA duplex, which were ferromagnetically coupled to each other.25 Theoretical studies have been performed to study the ferromagnetic behavior of Cu2+ and Mn2+ together with the modified DNA helix.26 Tanaka et al. incorporated heterogeneous metal ions, i.e., Cu2+ and Hg2+, using artificial base pairs (hydroxypyridone, salen, and pyrimidine) and natural bases (thymine).27 Experimental and computational studies have also been performed to examine purine-modified pyridine base pairs with Ni2+ metal ions selectively captured in the double helix, which were found to be more stable than the A:T and G:C base pairs.28
The synthetic nucleotide peptide nucleic acid (PNA) has also attracted attention due to the interaction of metal ions in its backbone and nitrogenous nucleobases.6,29–34 PNA is an analog of DNA, which contains a pseudo peptide linkage with N-(2-aminoethyl)-glycine (Aeg).35 PNA has the advantage of binding strongly to complementary nucleic acids such as DNA and RNA.35 Furthermore, the neutral backbone of PNA shows greater chemical stability than the negatively charged phosphate backbone of DNA.36 Several artificial nucleobases such as bipyridine have also been designed to incorporate metal ions into the PNA duplexes.6,37
Mercury is known to be highly toxic to human health and has a severe effect on the environment. Mercury ions (Hg2+) denature the DNA duplex structure at the molecular level. Miyake et al. concluded that the thymine–thymine (TT) pyrimidine mispair selectively captures Hg2+ ions.38 The selective capture of Hg2+ by the TT mispair shifted its thermally induced transition profiles to a higher temperature.38 The mercury-mediated TT-mispair structure was investigated using 15N NMR spectroscopy.39 Experimental reports are available regarding the thermodynamic properties between the TT single mispair as well as consecutive TT mispairs with Hg2+ ions and the charge transfer process in oligonucleotides containing the T–Hg2+–T complex.40–42 Further, the nature of the mercury atom in the T–Hg2+–T complex was also examined by Raman spectroscopy.43 Computational studies showed the charge transfer efficiency in these complexes, which gives information regarding the hole-transfer process.44 The computational results shed light on the mechanistic pathway for the deprotonation of the imino group of thymine and water-assisted tautomerization and formation of T–Hg2+–T complexes.45 However, the computational reports primarily focused on the T–Hg2+–T mispair and their electronic properties. Herein, we report a systematic computational study on the binding affinity of the Hg2+ ion with canonical and thymine–thymine mispairs to examine the comparative stability of the latter case. The literature revealed that the hybrid nucleic acid duplexes enhance the stability; however, there are no reports on the stability of mercury ions with these duplexes.35 It should be mentioned that DNAs and PNAs prefer to adopt B-type and P-type conformations, respectively.46,47 The Hg2+-mediated TT mispair preserves the B-conformation of the helix in the case of DNA with metallophilic interactions. Thus, it is interesting to examine the Hg2+-mediated interactions with PNA duplexes of the P-conformation and the nature of binding under the similar conditions compared to natural DNA duplexes. Therefore, this study was also performed with hybrid and PNA duplexes to examine their stability with Hg2+ ions similar to that in natural nucleic acids. The computed results revealed the overall binding affinity of natural and artificial nucleic acids to mercury ions and provided insight to achieve even better binding affinity with mercury ions than the reported results. This study also highlighted the influence of the backbones of the nucleic acids to attain a higher binding affinity of PNA mispairs with Hg2+ ions (Scheme 1).
Computational methods
All geometries of canonical and mispair were fully optimized at the B3LYP-D3/6-31G* level of theory in the aqueous phase using the polarized continuum solvation (PCM) model.48,49 Gas phase calculations were also performed for single canonical and mispair systems of DNA and PNA. The basis set superposition error (BSSE) was performed at the same level of theory. Confirmation of the minimum optimized geometries was carried out by analysis of the positive vibrational frequencies. We employed the effective core potential such as LANL2DZ for the mediating mercury ion (Hg2+) in the canonical and mispair systems.50 The binding energies were calculated using eqn (A).| Binding energy (ΔE) = Ecomplex − (EDNA/PNA + EHg2+) | (A) |
The recent benchmark studies performed for larger complexes have shown the importance of London dispersion-corrected density functional theory DFT-D3 to provide accurate interaction energies.54–56 The thermodynamics of supramolecular complexes including neutral molecules and positively charged molecules by ab initio quantum chemical methods have shown the secondary effects such as solvation and change in entropy in the supramolecular interactions.56 The binding energies are considered as the driving force for binding criteria; however, in the presence of solution, the role of enthalpy–entropy compensation is crucial to deduce the correct predictions. The results reported for the complexation study of the nucleic acids are based on the binding (ΔE), enthalpic and free energies calculated in the solvent medium.56
Results and discussion
The standard crystal structures of DNA and PNA duplex were obtained from the Protein Data Bank (https://www.rcsb.org) PDB IDs: 1BNA, 1NR8, and 1PUP CSD site to model the study.46,57 The crystal structure of mercury-mediated thymine residues (TT mispair) in DNA was obtained from PDB ID: 4L24.58 The mercury-mediated AT and GC base pairs were developed using AT and GC duplex crystal structures for calculations, respectively.Initially, we optimized the single canonical and mispair systems of DNA and PNA using the B3LYP-D3/6-31G* level of theory in the gas phase (Fig. S1 and S2,† respectively). The interaction of Hg2+ with the corresponding base pair was corrected with basis set superposition error (Table S1†). Watson Crick hydrogen bonding was observed in the case of the canonical systems DATD and DGCD (Fig. S1 and S2,† respectively). The distance between N–Hg2+ in DATD and DGCD was found to be 2.14 Å and 2.22 Å, and 2.25 Å and 2.34 Å, respectively. The metal-mediated single base pairs also showed hydrogen bonding interactions in DATD and DGCD, which were found to have lengths of 2.02 Å and 1.95 Å, respectively. The Hg2+ ion-mediated mispair DTTD was optimized in an orthogonal fashion and the distance between the N–Hg2+ in the T–Hg2+–T complex was found to be 2.17 Å and 2.18 Å, respectively (Fig. S1 and S2†). The orthogonal geometry of DTTD shows an angle of 85.5° between the base pairs in the T–Hg2+–T complex in the gas phase. The perturbation was also observed in the mispair of the mercury-mediated PNA–PNA (T–Hg2+–T) complex with an angle of 34° between the base pairs (Fig. S1 and S2†). The canonical base pairs in PNA also showed hydrogen bonding in a Watson Crick manner with the Hg2+-mediated base pairs. The hydrogen bonding distance in the case of PATP was PGCP is 2.01 Å and 1.93 Å (Fig. S1 and S2†), respectively. The distance between N–Hg2+ in PATP and PGCP was found to be 2.16 Å and 2.23 Å, and 2.25 Å and 2.36 Å (Fig. S1 and S2†), respectively.
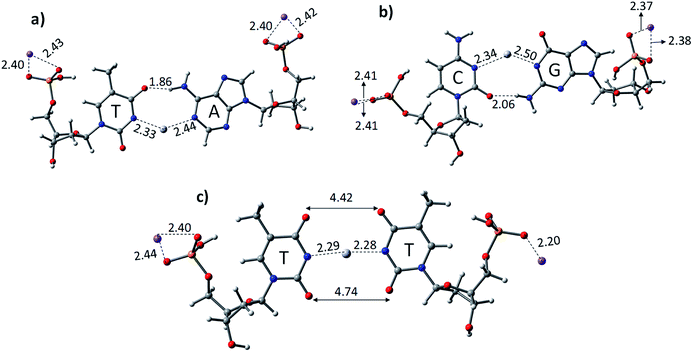
The experimental reports on the 1H proton NMR measurements and single crystal X-ray analysis of the Hg2+-mediated DNA–DNA duplex revealed that the base pairs should attain linearity, while complexation with the metal ion and the base pair stacking interactions are preserved.59 The crucial role of solvent in the mercury-mediated DNA–DNA duplex was also studied and reported in the literature with model systems.59–61 The computational studies showed that the stacking interactions of the metal-mediated base pairs can be achieved in solvent systems.60 Therefore, we examined all the structures of canonical AT, GC, and TT mispair (DNA and PNA) with Hg2+, which were optimized at the B3LYP-D3/6-31G* level of theory in the aqueous phase using the polarized continuum solvation (PCM) model (Fig. 1 and 3).48,62 The thermodynamic stability of the canonical AT, GC, and TT mispairs was investigated with single base pairs and a mercury ion. The calculated results show that the AT and GC base pairs deviate from linearity upon binding with the Hg2+ metal ion (Fig. 1). A deviation in the binding of the canonical base pairs, the Watson–Crick hydrogen-bonding pattern, was observed. Hydrogen bonding was observed in the case of AT base pairs with a distance of 1.86 Å, whereas in the case of the GC base pairs, the H-bonding distance is 2.06 Å between base pairs (Fig. 1). The Hg2+ ion-mediated TT mispair binds linearly and forms a T–Hg2+–T complex. The distance between Hg–N in the T–Hg2+–T complex was found to be 2.28 Å, which is consistent with earlier computational reports.60,61 Miyake et al. reported that the T–Hg2+–T pair is more stable than canonical (AT and GC) base pairs, and no notable effect was seen for other transition and alkaline earth metal ions.38 The stability of the T–Hg2+–T complex in the DNA duplex was confirmed by melting curves and circular dichroism (CD) studies.38
Further, the mechanistic pathway of T–Hg2+–T was examined by proton NMR, where the dissociation of the imino protons of the thymine residues occurs when the complexation of Hg2+ occurs.38 The crystal structure of the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex of 1-methylthymine
1 complex of 1-methylthymine![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Hg2+ of T–Hg2+–T was also reported.63 Previous computational results proposed a binding mechanism of T–Hg2+–T complex involving two main steps: (1) the substitution of the imino proton with the mercury ion by abstracting the imino proton from the thymine base by the hydroxo ligand and (2) tautomerization of the thymine base leads to the release of the imino proton and formation of a completely dehydrated T–Hg2+–T complex and oxonium ion.45 The calculated results performed for the TT mispairs in this study showed their stronger binding and stability compared to canonical base pairs when mediated with Hg2+ (Table 1). The nitrogen of thymine in the base pairs (N–Hg2+–N) is linear and the oxygen in the thymine residue shows a distance of 4.42 Å, which is in good agreement with the earlier reports.61,63 The calculated binding energies using the B3LYP-D3/6-31G* level of theory for DTTD, DATD, and DGCD are −69.4, −54.2, and −52.3 kcal mol−1, respectively. The calculated gas phase and aqueous phase results suggest that the latter approach is in good agreement with the experimentally observed mercury-mediated DNA–DNA duplex, where base pair stacking interactions can be achieved.
Hg2+ of T–Hg2+–T was also reported.63 Previous computational results proposed a binding mechanism of T–Hg2+–T complex involving two main steps: (1) the substitution of the imino proton with the mercury ion by abstracting the imino proton from the thymine base by the hydroxo ligand and (2) tautomerization of the thymine base leads to the release of the imino proton and formation of a completely dehydrated T–Hg2+–T complex and oxonium ion.45 The calculated results performed for the TT mispairs in this study showed their stronger binding and stability compared to canonical base pairs when mediated with Hg2+ (Table 1). The nitrogen of thymine in the base pairs (N–Hg2+–N) is linear and the oxygen in the thymine residue shows a distance of 4.42 Å, which is in good agreement with the earlier reports.61,63 The calculated binding energies using the B3LYP-D3/6-31G* level of theory for DTTD, DATD, and DGCD are −69.4, −54.2, and −52.3 kcal mol−1, respectively. The calculated gas phase and aqueous phase results suggest that the latter approach is in good agreement with the experimentally observed mercury-mediated DNA–DNA duplex, where base pair stacking interactions can be achieved.
| Hg2+-mediated system | B3LYP-D3/6-31G* ΔE (kcal mol−1) | B3LYP-D3/6-31G* ΔH (kcal mol−1) |
|---|---|---|
| DATD | −54.2 | −48.0 |
| DGCD | −52.3 | −46.4 |
| DTTD | −69.4 | −61.9 |
| PATP | −51.5 | −45.8 |
| PGCP | −51.7 | −46.3 |
| PTTP | −80.7 | −75.1 |
| DATGCD | −120.8 | −108.5 |
| DTTTTD | −156.4 | −144.8 |
| DTTTTP | −155.2 | −146.0 |
| PTTTTP | −156.6 | −147.9 |
We further examined the molecular electrostatic potential (MESP) of the deprotonated individual nucleotide (A, T, G and, C) of DNA, as shown in Fig. 2. The MESP generated for the deprotonated nucleotides of DNA were computed at the B3LYP-D3/6-31G* level of theory in the aqueous phase. In deoxyadenosine monophosphate (dAMP), the negative potential was maximum at the phosphate backbone (−102.8 kcal mol−1), whereas in deoxycytidine monophosphate (dCMP), it was at the nitrogenous bases (Vmin = −122.0 kcal mol−1). In the case of deoxyguanosine monophosphate (dGMP) and deoxythymidine monophosphate (dTMP), the negative potential showed the maximum value at the deprotonated nitrogenous bases (−227.9 and −228.9 kcal mol−1, respectively). Thus, the MESP values suggest that the mispair DTTD can bind more strongly with the Hg2+ ion compared to the canonical base pairs, which is consistent with the binding stability obtained using DFT calculations (Fig. 2 and Table 1).
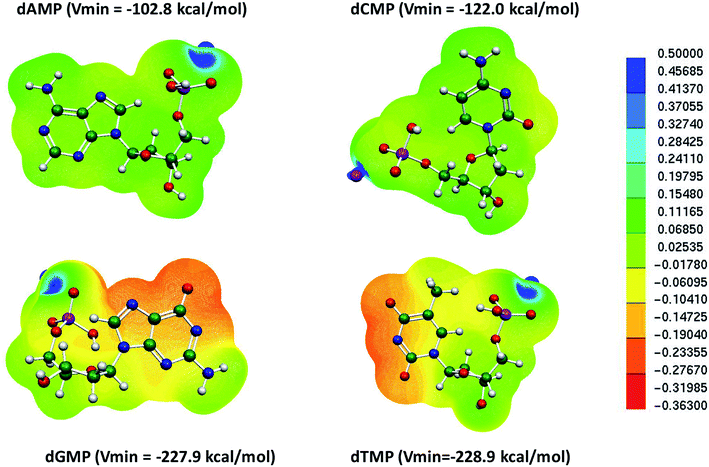 | ||
| Fig. 2 MESP of individual deprotonated nucleotides in DNA nucleotides calculated at the B3LYP-D3/6-31G* level of theory in the aqueous phase. | ||
Recently, we reported the role of the backbones on the binding stability of nucleic acids with metal ions.29 Peptide nucleic acid (PNA) containing neutral backbones with metal ions has attracted interest for designing bio-nanomaterials and biosensors.6,31,64–67 PNA is also known to mimic the behavior of DNA, in which the deoxyribose sugar and phosphate backbone are replaced by the N-(2-amino-ethyl)glycine unit attached through the methylene carbonyl linkage.35,67 PNA as an artificial backbone obeys Watson–Crick base pairing with the complementary nucleic acids.35 The neutral PNA backbone plays an important role in complexation with Mg2+, Zn2+, and Cu2+ metal ions.29 The binding of alkali and transition metal ions to PNA has been investigated extensively.6,29,31,65,67 The coordination property of metal ions and the hybridization property of PNA can extend the applications of PNA in the field of nanomaterials and biosensors. However, the binding of the mercury ion (Hg2+) to the PNA nucleotides is rare in the literature. Therefore, it is interesting to examine the binding affinity of PNA mispairs with Hg2+ and their stability against DNA nucleotides.
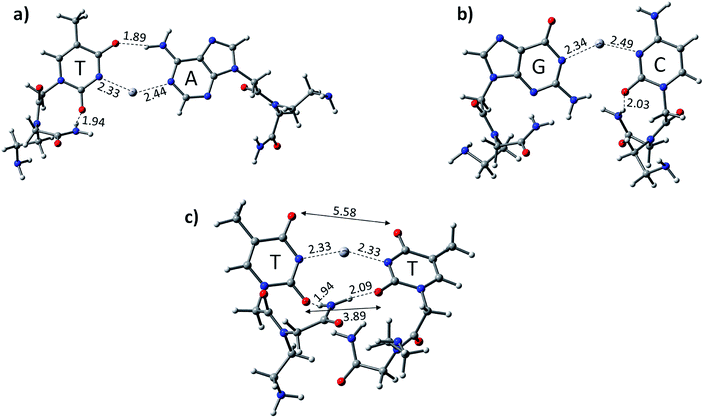
We optimized the PNA geometries with a mercury ion at the same level of theory in the aqueous phase employing the PCM solvation model (Fig. 3). For the calculations, the PDB of PNAs were obtained from the Protein Data Bank (https://www.rcsb.org) PDB ID: 1PUP CSD site.47 The distance of Hg2+–N in –N–Hg2+–N– in the canonical base pairs (AT and GC) was found to be 2.33 Å and 2.44 Å in AT and 2.34 Å and 2.49 Å in the GC base pairs, respectively (Fig. 3). The PNA showed an additional hydrogen bonding from the backbone to the pyrimidine nucleobase, i.e., cytosine and thymine (Fig. 3). The additional hydrogen bonding of the PNA was observed due to its flexible backbone with a distance of 1.94 Å and 2.03 Å in the PATP and PGCP base pairs, respectively (Fig. 3). The angles of the –N–Hg2+–N– canonical base pairs in PNA PATP and PGCP are 135.2° and 140.5°, respectively. In the TT mispair of PNA, the angle of N–Hg2+–N is 154.6° and the Hg2+ ion is equidistant from the nitrogen atoms (2.33 Å). The distance between the two oxygen atoms in thymine was found to be 3.9 Å and 5.6 Å, respectively. The additional hydrogen bonding from the PNA backbone to the thymine nucleobases in PTTP is 1.94 Å.
The calculated results reveal that the TT mispair containing the PNA backbone has a higher binding affinity towards the Hg2+ ion than canonical AT and GC base pairs. The calculated binding energies of PTTP, PATP, and PGCP at the B3LYP-D3/6-31G* level of theory are −80.7, −51.5, and −51.7 kcal mol−1, respectively (Table 1). The PTTP mispair is energetically favoured compared to the DTTD mispair and all the single canonical base pairs (Table 1). The calculated enthalpy at the same level of theory also follows a similar trend to that of the other mispair and canonical base pairs (Table 1).
Similarly, the MESP of the deprotonated PNA nucleotides was also computed at the same level of theory in the aqueous phase (Fig. 4). The negative potential of the guanine-containing PNA backbone (P–Gua = −213.0 kcal mol−1) was found to be higher than that of the other nucleotides in the case of PNA. Importantly, the Vmin resides on the oxygen of the pyrimidine ring of P–Gua. The thymine-containing PNA (P–Thy) has the maximum negative potential of the nitrogenous base in the imine region (Fig. 4). The binding affinity of the single DNA and PNA base-pairs with the Hg2+ ion calculated at the same level of theory revealed that the canonical and TT mispair of DNA interact strongly with the metal ion compared to the corresponding PNA case, and the MESPs of the nucleobases corroborate this finding (Table 1 and Fig. 2, 4).
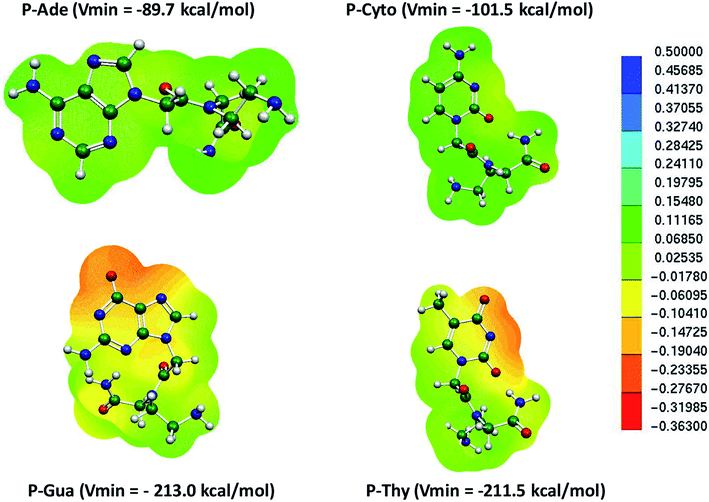 | ||
| Fig. 4 MESP of individual deprotonated PNA nucleotides calculated at the B3LYP-D3/6-31G* level of theory in the aqueous phase. | ||
The formation of the T–Hg2+–T complex results in the stabilization of the duplexes, which depends on the T–Hg2+–T dimers.4 The metallophilic interaction (Hg⋯Hg) and stacking of the base pairs in the DNA duplexes are crucial for their stability.59,61 The calculated results for the T–Hg2+–T mispair were found to be in agreement with the experimental results and suggest that a similar trend can exist in the dimer form.41 Therefore, we examined the duplex stability by modelling using more realistic TT dimer systems with two mercury ions in the DNA and PNA systems. We extended the study of Hg2+ mediation with the canonical base pair (ATGC) and (TTTT) dimer mispairs. The geometries were fully optimized at the B3LYP-D3/6-31G* level of theory in the aqueous phase (Fig. 5).
Yamaguchi et al. investigated the three-dimensional (3D) structure of a DNA duplex including dimer TT mispair with Hg2+ using NMR spectroscopy.59 The 3D structure of T–Hg2+–T adopts the standard B-form of the duplex, obeying the Watson–Crick base pairs.59 The mercury ions were found to be completely aligned through the DNA helical axis and shielded from the bulk water.59 The ΔS, ΔH, and ΔG were also calculated via ONIOM calculations.59 There is no direct evidence of water molecules assisting the stabilization of the TT mispair with the Hg2+ ion. Nonetheless, we performed the study in the aqueous phase using the PCM solvation model.
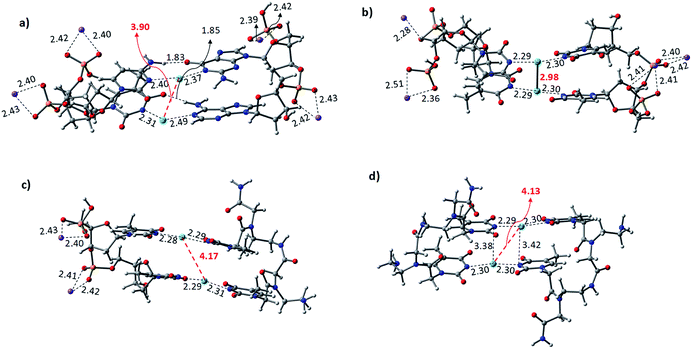
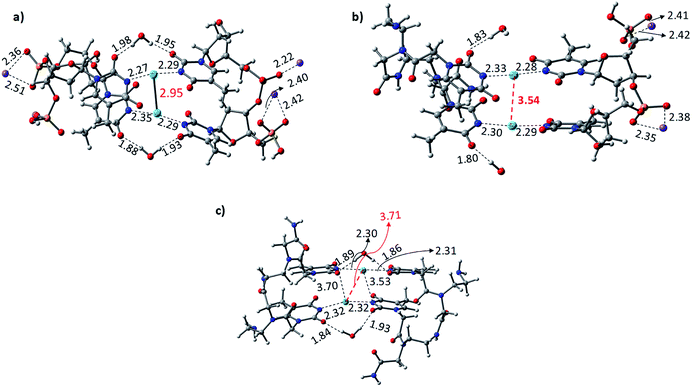
The Hg2+-mediated canonical ATGC base pairs were largely perturbed during the geometry optimization of this duplex model. The distance from the imine region (N3 of the thymine) and the metallophilic interaction to the mercury ion is shown in Fig. 5. Experimental reports suggest a decrease in the viscosity of DNA and the chain shifting mechanism in denatured DNA upon the addition of mercury ions.68,69 This is well corroborated with our results in the case of the canonical base pairs (DATGCD) upon mediation with mercury ions. The calculated results reveal that the canonical ATGC base pairs are perturbed significantly upon the addition of mercury ions, in agreement with the observed results that the duplex model is not stable and loses its DNA structural property. In contrast, the calculated results show the metallophilic (Hg⋯Hg) interaction in the case of the T–Hg2+–T dimer (DTTTTD), which is in good agreement with the literature.58 Therefore, according to the calculations, these dimer complexes, DTTTTD, can form the stable helix B form, which is difficult to achieve in DATGCD due to the large perturbations in the duplex model geometries.
The binding energies (ΔE) and change in enthalpies (ΔH) of all the canonical and mispair Hg2+-mediated systems of DNA and PNA base pairs calculated at the B3LYP-D3/6-31G* level of theory in the aqueous phase are shown in Table 1. The binding energy of the TTTT mispairs of DNA and PNA are energetically favored compared to the canonical (ATGC) base pairs in DNA. These results are in good agreement with the interaction of the single base pairs of DNA and PNA with the Hg2+ ion (Table 1). The geometry of the canonical DATGCD system in DNA is largely perturbed when binding to two mercury ions. The metallophilic interaction between the two consecutive Hg2+ ions was found to be 3.90 Å (Fig. 5). Interestingly, the DTTTTD dimer system with the DNA backbone showed relatively smaller perturbation and the thymine base pairs are completely aligned with the Hg2+ ions. The metallophilic interactions between the two consecutive mercury ions are found to be 2.98 Å, equidistant (∼2.30 Å) with the thymine base pairs (Fig. 5). This is well corroborated with the available X-ray structure of the T–Hg2+–T dimer systems.58 Hybrid duplexes such as PNA–DNA duplexes generally have higher thermal stabilities than their DNA counterpart and show unique ionic strength effects due to the presence of a neutral backbone.70 These unique properties of the hybrid duplex give insight into their applications in antisense and antigene drugs.35,71
The Hg2+-mediated hybrid DNA and PNA mispair system (PTTTTD) has not been explored in the literature. In the case of the hybrid DNA and PNA mispair system (PTTTTD), the interaction of the base pairs with Hg2+ perturbs the geometry significantly, i.e., the inter-base pair distance increases, and consequently less metallophilic interactions between the two Hg2+ ions are observed (Fig. 5). The calculations performed with the PTTTTP flexible PNA backbones also showed the large displacement in the base pairs, which results in the non-alignment of the mercury ions in the base pair structure. The calculated binding energies showed that the PTTTTP mispair is energetically favored compared to the DTTTTD and DTTTTP mispairs and canonical DATGCD base pair (Table 1). The calculated enthalpic (ΔH) results at the B3LYP-D3/6-31G* level of theory also showed similar a stability trend for the DTTTTD and DTTTTP mispairs. The free energies computed at the same level of theory also showed the energetically favored TT mispair in both DNA and PNA (Table S2†). In the case of the ATGC base pairs and TTTT dimer systems, the TTTT mispair showed higher stability compared to the canonical base pair (ATGC), as shown in Table 1. Interestingly, the PNA backbone-containing mispair (PTTTTP) showed higher stability compared to the hybrid PNA–DNA (DTTTTP) and DNA–DNA (DTTTTD) duplex model systems. The computed binding stability between the single T–Hg2+–T monomer and T–Hg2+–T dimer signifies that higher stability can be achieved with the T–Hg2+–T dimer-containing PNA backbone (PTTTTP), as shown in Table 1. The enthalpy (ΔH) calculated at the B3LYP-D3/6-31G* level of theory for the dimer base pairs in the DNA duplex model (DATGCD and DTTTTD) were found to be −108.5 and −144.8 kcal mol−1, whereas, in the case of the hybrid DTTTTP and PTTTTP, the stability of these duplex models was −146.0 and −147.9 kcal mol−1, respectively. The electronic energies (ΔE) calculated for DTTTTD and DTTTTP showed a slightly better energetic preference in the latter case; however, the free energy data showed the preference in the former case (Table S2†). It is known that the nucleobases play an important role in the architecture of nucleic acid duplexes such as DNA–DNA, DNA–PNA, and PNA–PNA, which show a variation in the arrangement of the base-pairs.47,72,73 The DNA–DNA duplexes are well known to have a B-type helix conformation with stacked base pairs perpendicular to the helix axis. The hybrid DNA–PNA duplex also adopts a B-type helix conformation, where the base pairs are nearly perpendicular to the helix axis.73 However, a shallow and wide helix in the case of PNA–PNA has been reported, which adopts a unique P-form conformation, clearly distinguishing between the A and B forms of the helix.47 The P-form conformation in the PNA–PNA duplex has a large cavity along the helix axis. However, the nucleobases in the PNA–PNA duplex resembles an A-like stacking conformation. This unique conformation is governed by the overlap in the base pair stacking.47 The calculated results suggest that this nucleobase architecture is found to be preserved in the models studied for the metal-mediated mispairs. In the case of the T–Hg2+–T dimer mispairs, it is more interesting to define the helix conformation and the role of the nucleobases. The DTTTTD dimer adopts a B-type conformation with well-stacked base pairs perpendicular to the helix axis. The hybrid DTTTTP adopts a B-type conformation with small perturbation in the nucleobases. However, the strand displacement in the PTTTTP dimer preserves the P-type conformation (Fig. S3†). Overall, the structural variation in the Hg2+-mediated mispairs can be observed compared to the canonical DNA–DNA, DNA–PNA and PNA–PNA duplexes. The X-displacement, rise, and tilt in the nucleobase were preserved a similar conformation in the Hg2+-mediated mispair compared to the canonical unmodified duplexes. According to our calculations, the helix parameter such as X-displacement was clearly observed by the structural analysis, which varied in the entire duplex model studied here (Fig. S3†). The PTTTTP mispair causes nucleobase fluctuations such as X-displacement from the helix axis, leading to a wider and more unwounded helix than the standard B-form of DNA duplexes (Fig. S3†).
The role of explicit water molecules in the formation of a thymine–Hg2+–thymine metal-mediated DNA base pair has been reported.44 The water molecules participate in the coordination of the mercury ion with the T–Hg2+–T base pair and exhibit an interaction with both the metal ion and the base. The Hg2+ ion usually prefers the coordination of four, and the trans-aqua cluster of the mercury ion in four-coordination with the T–Hg2+–T base pair was also observed. We examined the role of explicit water molecules with the stability of T–Hg2+–T dimer mispair systems (DTTTTD, DTTTTP, and PTTTTP). The Hg2+ ions are generally tri-coordinated in the dimers with base pairs and metallophilic (Hg⋯Hg) interaction, and hence the fourth coordination was engaged with an explicit water molecule (Fig. 6). The water complexed geometries were fully optimized for two explicit water molecules in T–Hg2+–T for the dimer mispair systems (DTTTTD, DTTTTP, and PTTTTP) at the B3LYP-D3/6-31G* level of theory in the implicit solvent system. The calculated results suggest that the water molecules are hydrogen-bonded with the thymine base pair in DTTTTD and the metallophilic Hg⋯Hg interaction is maintained, as observed without the explicit water molecules (Fig. 5). The interaction of the explicit water molecules with DTTTTP and PTTTTP reveals that the metallophilic Hg⋯Hg interaction is slightly larger compared to the corresponding geometries without water molecules. The electronic, enthalpic and free energies calculated for the three systems showed the very similar stability of these dimers, as observed without the interaction with explicit water molecules in the implicit solvent model (Table 1 and Fig. S2, S3†).
We performed atom in molecules (AIM) analysis at the B3LYP-D3/6-31G* level of theory to reveal the binding behavior of the Hg2+ ion with T–Hg2+–T complex in DNA and PNA. The critical points (CPs) were generated to reveal the binding behavior of Hg2+ to the studied complexes, as shown in Tables 2 and 3. The behavior of the Hg2+ ion in the canonical base pairs and mispair complex T–Hg2+–T in DNA and PNA can be characterized using other topological parameters in AIM such as gradient (Laplacian) of the electron density ∇2r, the total energy H(r), potential energy V(r), and Lagrangian kinetic energies G(r). The existence of a non-covalent interaction, i.e., (3, −1), critical point indicates the bonding behavior of the Hg2+ ion and its complex with DNA and PNA canonical base pairs and mispairs. The interaction is considered to be shared when |V(r)| > G(r) and H(r) is a negative value, whereas the interaction is considered to be a closed shell when |V(r)| < G(r) and H(r) is a positive value. The larger the value of the potential energy density V(r), the more negative the total energy densities H(r), the bonded interaction is considered to be more shared, and hence the stabilization would be greater at that geometry.74 The interaction would be a closed shell when the ratio of |V(r)|/G(r) < 1, but when the ratio is |V(r)|/G(r) > 2, a covalent nature will occur for these interactions. The intermediate situation will occur when the ratio falls between a value of 1 and 2.75
| DNA & PNA complexes with Hg2+ | Critical-points (CP) | Density of all electrons | Laplacian of electron density (∇2r) | Total energy density H(r) | Potential energy density V(r) | Lagrangian kinetic energy G(r) | |V(r)|/G(r) |
|---|---|---|---|---|---|---|---|
| DATD | CP-95 | 0.04822 | 0.19051 | −0.00345 | −0.04899 | 0.04553 | 0.92 |
| CP-102 | 0.06182 | 0.24317 | −0.00801 | −0.06804 | 0.06003 | 1.00 | |
| CP-140 | 0.03109 | 0.09995 | −0.00041 | −0.02582 | 0.02540 | 1.01 | |
| DGCD | CP-78 | 0.01906 | 0.06423 | 0.00020 | −0.01485 | 0.01506 | 0.98 |
| CP-91 | 0.04209 | 0.16351 | −0.00192 | −0.04047 | 0.03854 | 1.05 | |
| CP-93 | 0.06024 | 0.23683 | −0.00755 | −0.06607 | 0.05852 | 1.12 | |
| CP-144 | 0.01954 | 0.06385 | −0.00001 | −0.01599 | 0.01597 | 1.00 | |
| DTTD | CP-105 | 0.06791 | 0.26349 | −0.01040 | −0.07606 | 0.06566 | 1.15 |
| CP-112 | 0.06680 | 0.25869 | −0.00994 | −0.07428 | 0.06433 | 1.15 | |
| CP-142 | 0.01977 | 0.07601 | 0.00162 | −0.01575 | 0.01738 | 0.90 | |
| CP-158 | 0.02019 | 0.07683 | 0.00152 | −0.01615 | 0.01768 | 0.91 | |
| PATP | CP-124 | 0.04823 | 0.19076 | −0.00345 | −0.04901 | 0.04556 | 1.07 |
| CP-127 | 0.06125 | 0.24300 | −0.00776 | −0.06759 | 0.05982 | 1.12 | |
| CP-158 | 0.02874 | 0.09236 | −0.00034 | −0.02378 | 0.02343 | 1.01 | |
| PGCP | CP-85 | 0.05982 | 0.23382 | −0.00732 | −0.06494 | 0.05762 | 1.12 |
| CP-89 | 0.04261 | 0.16607 | −0.00205 | −0.04122 | 0.03916 | 1.05 | |
| CP-107 | 0.01358 | 0.05666 | 0.00281 | −0.00852 | 0.01134 | 0.75 | |
| CP-126 | 0.02079 | 0.06799 | −0.00018 | −0.01737 | 0.01718 | 1.01 | |
| CP-146 | 0.00597 | 0.02448 | 0.00111 | −0.00389 | 0.00500 | 0.77 | |
| CP-166 | 0.00978 | 0.03457 | 0.00117 | −0.00628 | 0.00746 | 0.84 | |
| PTTP | CP-87 | 0.06114 | 0.23957 | −0.00774 | −0.06669 | 0.05894 | 1.13 |
| CP-91 | 0.06050 | 0.23662 | −0.00750 | −0.06564 | 0.05813 | 1.12 | |
| CP-110 | 0.02706 | 0.08558 | −0.00075 | −0.02291 | 0.02215 | 1.03 | |
| CP-112 | 0.01290 | 0.04613 | 0.00095 | −0.00961 | 0.01057 | 0.96 | |
| CP-114 | 0.02625 | 0.08276 | −0.00073 | −0.02216 | 0.02142 | 1.04 | |
| CP-137 | 0.01214 | 0.04356 | 0.00097 | −0.00894 | 0.00991 | 0.89 | |
| CP-158 | 0.01257 | 0.04420 | 0.00063 | −0.00977 | 0.01041 | 0.93 | |
| CP-177 | 0.01298 | 0.04536 | 0.00060 | −0.01013 | 0.01073 | 0.94 |
| DNA and PNA complexes with Hg2+ | Critical points | Density of all electrons | Laplacian of electron density (∇2r) | Total energy density H(r) | Potential energy density V(r) | Lagrangian kinetic energy G(r) | |V(r)|/G(r) |
|---|---|---|---|---|---|---|---|
| DATGCD | CP-193 | 0.04258 | 0.16492 | −0.00205 | −0.04098 | 0.03893 | 1.05 |
| CP-233 | 0.06434 | 0.25514 | −0.00898 | −0.07227 | 0.06328 | 1.14 | |
| CP-246 | 0.05602 | 0.21314 | −0.00601 | −0.05824 | 0.05223 | 1.11 | |
| CP-248 | 0.05196 | 0.20745 | −0.00462 | −0.05469 | 0.05007 | 1.08 | |
| CP-211 | 0.00568 | 0.02040 | 0.00093 | −0.00311 | 0.00404 | 0.77 | |
| CP-220 | 0.00485 | 0.02067 | 0.00069 | −0.00378 | 0.00447 | 0.84 | |
| CP-256 | 0.00436 | 0.01389 | 0.00044 | −0.00258 | 0.00302 | 0.85 | |
| CP-167 | 0.01890 | 0.05901 | −0.00035 | −0.01546 | 0.01510 | 1.02 | |
| CP-325 | 0.00392 | 0.01082 | 0.00046 | −0.00178 | 0.00224 | 1.25 | |
| CP-318 | 0.03207 | 0.10872 | 0.00007 | −0.02703 | 0.02710 | 0.99 | |
| CP-276 | 0.03122 | 0.10155 | −0.00030 | −0.02600 | 0.02569 | 1.01 | |
| DTTTTD | CP-234 (Hg–Hg) | 0.01577 | 0.08644 | 0.00255 | −0.01485 | 0.01740 | 0.85 |
| CP-208 (N–Hg) | 0.06731 | 0.25994 | −0.01017 | −0.07498 | 0.06481 | 1.15 | |
| CP-239 (N–Hg) | 0.06604 | 0.25571 | 0.00962 | −0.07315 | 0.06352 | 1.10 | |
| CP-253 (N–Hg) | 0.06718 | 0.26157 | −0.01011 | −0.07524 | 0.06513 | 1.15 | |
| CP-237 (N–Hg) | 0.06599 | 0.25390 | −0.00963 | −0.07279 | 0.06316 | 1.15 | |
| CP-195 | 0.00500 | 0.01933 | 0.00101 | −0.00271 | 0.00372 | 0.66 | |
| CP-241 | 0.00454 | 0.01469 | 0.00045 | −0.00275 | 0.00321 | 0.66 | |
| CP-190 | 0.00463 | 0.01766 | 0.00094 | −0.00252 | 0.00346 | 0.66 | |
| CP-254 | 0.00377 | 0.01185 | 0.00044 | −0.00207 | 0.00251 | 1.00 | |
| CP-201 | 0.00679 | 0.02151 | 0.00110 | −0.00317 | 0.00427 | 0.75 | |
| DTTTTP | CP-175 (N–Hg) | 0.06813 | 0.26470 | −0.01050 | −0.07651 | 0.06600 | 1.15 |
| CP-180 (N–Hg) | 0.06758 | 0.02622 | −0.01025 | −0.07554 | 0.06529 | 1.15 | |
| CP-235 (N–Hg) | 0.29080 | −0.01087 | −0.30250 | −0.03332 | 0.03069 | 1.08 | |
| CP-237 (N–Hg) | 0.06716 | 0.26124 | −0.01012 | −0.07519 | 0.06506 | 1.15 | |
| CP-208 | 0.00473 | 0.01693 | 0.00081 | −0.00252 | 0.00334 | 0.75 | |
| CP-205 | 0.00603 | 0.02115 | 0.00088 | −0.00339 | 0.00427 | 0.82 | |
| CP-197 | 0.00453 | 0.01284 | 0.00045 | −0.00229 | 0.00275 | 0.84 | |
| CP-162 | 0.00914 | 0.03121 | 0.00085 | −0.00609 | 0.00694 | 1.00 | |
| CP-239 | 0.00575 | 0.01844 | 0.00071 | −0.00317 | 0.00389 | 0.81 | |
| CP-256 | 0.02008 | 0.06815 | 0.00047 | −0.01608 | 0.01655 | 0.97 | |
| PTTTTP | CP-180 (N–Hg) | 0.06599 | 0.25483 | −0.00967 | −0.07307 | 0.06340 | 1.15 |
| CP-185 (N–Hg) | 0.06621 | 0.25651 | −0.00972 | −0.07351 | 0.06378 | 1.15 | |
| CP-274 (N–Hg) | 0.06673 | 0.25862 | −0.00993 | −0.07431 | 0.06437 | 1.15 | |
| CP-283 (N–Hg) | 0.06556 | 0.25368 | −0.00945 | −0.07243 | 0.06298 | 1.16 | |
| CP-225 | 0.00616 | 0.02163 | 0.00089 | −0.00348 | 0.00438 | 0.79 | |
| CP-230 | 0.00579 | 0.02036 | 0.00087 | −0.00323 | 0.00410 | 0.78 | |
| CP-213 | 0.00297 | 0.00962 | 0.00046 | −0.00146 | 0.00193 | 0.75 | |
| CP-246 | 0.00425 | 0.01219 | 0.00045 | −0.00214 | 0.00259 | 0.82 | |
| CP-240 | 0.01010 | 0.03376 | 0.00076 | −0.00691 | 0.00767 | 0.90 |
The AIM analysis suggests that the N–Hg2+–N interaction is electrostatic in nature. The |V(r)|/G(r) ratio of DTTD and PTTP falls under the intermediate situations. In DTTD, the critical points generated such as CP-105, CP-112, CP-142, and CP-158 are closed-shell interactions, whereas in the case of the PNA base pairs, the critical points of the backbone interactions are also observed besides the imino regions. The critical points of the imino region in the PTTP mispair (CP-87 and CP-91) and some backbone interactions such as CP-110 and CP-112, and CP-114, CP-137, CP-158, and CP-177, respectively, are electrostatic in nature (Table 2). The CPs of the backbone interactions in the canonical base pairs PATP and PGCP also show close shell interaction (Table 2).
The AIM analyses of the canonical and mispair dimers were performed at the same level of theory in the aqueous phase (Table 3). The critical points were generated in the imino regions and other backbone interactions of the ATGC, DTTTTD, hybrid DTTTTP, and PTTTTP duplex model studied here (Table 3). The metallophilic interactions between the consecutive mercury Hg⋯Hg was observed in the case of DTTTTD (CP-234) (Table 3). The Hg⋯Hg metallophilic interaction is missing in the case of the PTTTTP mispair due to the displacement in the thymine nucleobases. The adopted P-conformations with the mercury ion-mediated PTTTTP mispair experience interactions between the nitrogen of the base-pair and Hg2+, which contribute effectively to stabilizing these mispair nucleobases.
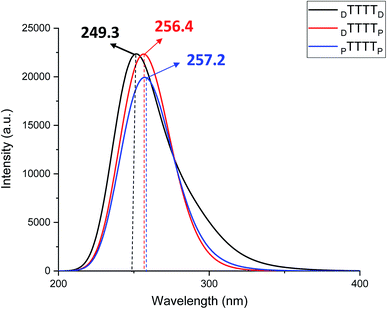
These metal-mediated complexes can be characterized via UV-vis spectroscopy.46 The UV-vis absorption spectra of T–Hg2+–T complexes have been reported for the binding of Hg2+ to thymine nucleobases.46 Experimental and computational reports on the UV-vis absorption spectrum of TT dimers with Hg2+ are available, which appears at 260 nm with the successive addition of mercury ions.38,61,76 The mercury-mediated formation of TT dimers in DNA duplexes causes a decrease in the optical density with an increase in the Hg2+ ion concentration in the different model systems. We examined the UV-vis absorption spectra using time-dependent density functional theory (TD-DFT) calculations in the aqueous phase (Fig. 7). The experimental UV-vis absorption spectra reported for DNA duplexes with Hg2+ ions appear at ∼260.0 nm.4 The changes in the UV-vis absorption spectrum of the DNA–DNA, hybrid DNA–PNA, and PNA–PNA duplex systems were examined with the molecular orbitals of the respective transitions. Four molecular orbitals for the duplexes, namely, the HOMO, LUMO, LUMO+1, and LUMO+2, were mainly involved in the principal excitation, as shown in Fig. 8. The metallophilic interaction can be seen in the case of DTTTTD; however, in the hybrid duplex DTTTTP, the metallophilic interaction is not prominent, whereas in the case of PTTTTP, due to the strand displacement in the PNA–PNA duplex, the metal orbitals do not overlap to form effective interactions (Fig. 8).
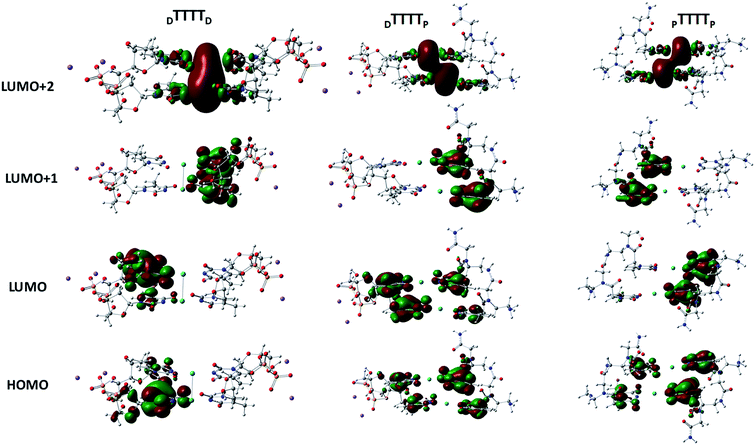 | ||
| Fig. 8 Molecular orbitals involved in the principal excitations, namely HOMO, LUMO, LUMO+1, and LUMO+2, of DTTTTD, DTTTTP, and PTTTTP. | ||
Conclusion
In this work, we examined the stability of mercury ion-mediated canonical (AT and GC base pair) and TT mispairs mediated with Hg2+ ion using monomer and dimer models computationally. The B3LYP-D3/6-31G* calculated results suggest that the DTTD mispair is energetically more stable by ∼17.0 kcal mol−1 compared to the canonical DNA (DATD and DGCD) base pairs. The B-conformation was preserved for the DTTD mispair compared to the corresponding DATD and DGCD base pairs. The influence of the backbones on the metal-mediated base pairs was examined using PNA. The PTTP mispair also showed remarkable stability (∼30.0 kcal mol−1) compared to the canonical PNA (PATP and PGCP) base pairs. The T–Hg2+–T geometry was found to be more aligned compared to the canonical base pairs. The MESP analysis revealed that the maximum negative potential is at the nitrogen centers of thymine (Vmin = −228.9 kcal mol−1), and hence contributes effectively to its binding with the Hg2+ ion. The experimental reports revealed that the metallophilic interactions contribute to stabilize the thymine–thymine mispair with mercury ions. Therefore, we studied the dimer systems (ATGC and TTTT) in DNA and with PNA nucleic acids. The calculated electronic energy results (ΔE) indicated that the DTTTTD mispair (∼36.0 kcal mol−1) is more energetically stable than the canonical DATGCD base pairs. The calculated enthalpy (ΔH) also followed similar trends to that of the single and dimer model systems. The metallophilic interaction (Hg⋯Hg) that appeared in DTTTTD leads to more stability than the canonical base pairs. The proper alignment of the nucleobases along the axis can be seen in the DTTTTD mispair, which adopts a B-type conformation. The metallophilic interaction was not observed in the case of the PTTTTP mispair; however, the Hg2+ ion interacts with the nitrogen of the thymine bases, which was revealed by the AIM analysis. The role of explicit water molecules was also examined with the DTTTTD, DTTTTP, and PTTTTP mispair systems. The calculated results revealed that the explicit water molecules conserve the metallophilic (Hg⋯Hg) interaction in DTTTTD and the relative energetic trends of the mispair dimer systems are similar to that of the implicit solvent systems. The AIM analysis demonstrated that the stabilizing interactions are electrostatic in nature. The P-type conformation was largely preserved with PTTTTP, which led to a wider helix in the Hg2+-mediated systems. The UV-vis absorption spectra calculated using TD-DFT at the B3LYP-D3/6-31G* level of theory in the aqueous phase suggested that the absorption maxima can be shifted to longer wavelengths for the PTTTTP mispair (∼257.2 nm) than the other mispairs. Thus, the calculated results reveal that the T–Hg2+–T complex is a key structure with PNAs and can lead to the development of potential applications of metal-mediated base pairs in nanotechnology.Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. B. and B. G thanks DBT, New Delhi (Grant no. BT/PR12730/BID/7/523/2015), and DST for financial support. S. B. is thankful to the Academy of Scientific and Innovative Research (AcSIR), Ghaziabad 201002, Uttar Pradesh, India for his PhD registration. The CSIR-CSMCRI registration number is 83/2020. We thank the anonymous reviewers for their constructive comments/suggestions that have helped us to improved our manuscript.References
- K. Tanaka, A. Tengeiji, T. Kato, N. Toyama and M. Shionoya, Science, 2003, 299, 1212–1213 CrossRef CAS.
- H. A. Wagenknecht, Angew. Chem., Int. Ed., 2003, 42, 3204–3206 CrossRef CAS.
- M. Shionoya and K. Tanaka, Curr. Opin. Chem. Biol., 2004, 8, 592–597 CrossRef CAS.
- Y. Miyake, H. Togashi, M. Tashiro, H. Yamaguchi, S. Oda, M. Kudo, Y. Tanaka, Y. Kondo, R. Sawa, T. Fujimoto, T. Machinami and A. Ono, J. Am. Chem. Soc., 2006, 128, 2172–2173 CrossRef CAS.
- G. H. Clever, C. Kaul and T. Carell, Angew. Chem., Int. Ed., 2007, 46, 6226–6236 CrossRef CAS.
- R. M. Franzini, R. M. Watson, G. K. Patra, R. M. Breece, D. L. Tierney, M. P. Hendrich and C. Achim, Inorg. Chem., 2006, 45, 9798–9811 CrossRef CAS.
- J. Liu, Z. Cao and Y. Lu, Chem. Rev., 2009, 109, 1948–1998 CrossRef CAS.
- S. Johannsen, N. Megger, D. Böhme, R. K. O. Sigel and J. Müller, Nat. Chem., 2010, 2, 229–234 CrossRef CAS.
- G. H. Clever and M. Shionoya, Coord. Chem. Rev., 2010, 254, 2391–2402 CrossRef CAS.
- X. Li and D. R. Liu, Angew. Chem., Int. Ed., 2004, 43, 4848–4870 CrossRef CAS.
- C. Potera, Nat. Biotechnol., 2007, 25, 497–499 CrossRef CAS.
- Y. Lu and J. Liu, Curr. Opin. Biotechnol., 2006, 17, 580–588 CrossRef CAS.
- C. M. Niemeyer, Angew. Chem., Int. Ed., 2001, 40, 4128–4158 CrossRef CAS.
- U. Feldkamp and C. M. Niemeyer, Angew. Chem., Int. Ed., 2006, 45, 1856–1876 CrossRef CAS.
- N. C. Seeman, Nature, 2003, 421, 427–431 CrossRef.
- E. T. Kool, Acc. Chem. Res., 2002, 35, 936–943 CrossRef CAS.
- I. Hirao, Curr. Opin. Chem. Biol., 2006, 10, 622–627 CrossRef CAS.
- S. A. Benner, Acc. Chem. Res., 2004, 37, 784–797 CrossRef CAS.
- S. R. Lynch, H. Liu, J. Gao and E. T. Kool, J. Am. Chem. Soc., 2006, 128, 14704–14711 CrossRef CAS.
- A. H. F. Lee and E. T. Kool, J. Am. Chem. Soc., 2005, 127, 3332–3338 CrossRef CAS.
- T. Carell, C. Behrens and J. Gierlich, Org. Biomol. Chem., 2003, 1, 2221–2228 RSC.
- K. M. Stewart and L. W. McLaughlin, J. Am. Chem. Soc., 2004, 126, 2050–2057 CrossRef CAS.
- E. Meggers, P. L. Holland, W. B. Tolman, F. E. Romesberg and P. G. Schultz, J. Am. Chem. Soc., 2000, 122, 10714–10715 CrossRef CAS.
- S. Atwell, E. Meggers, G. Spraggon and P. G. Schultz, J. Am. Chem. Soc., 2001, 123, 12364–12367 CrossRef CAS.
- K. Tanaka, A. Tengeiji, T. Kato, N. Toyama and M. Shionoya, Science, 2003, 299, 1212–1213 CrossRef CAS.
- S. S. Mallajosyula and S. K. Pati, Phys. Rev. Lett., 2007, 98, 1–4 CrossRef.
- K. Tanaka, G. H. Clever, Y. Takezawa, Y. Yamada, C. Kaul, M. Shionoya and T. Carell, Nat. Nanotechnol., 2006, 1, 190–194 CrossRef CAS.
- C. Switzer, S. Sinha, P. H. Kim and B. D. Heuberger, Angew. Chem., Int. Ed., 2005, 44, 1529–1532 CrossRef CAS.
- S. Bhai and B. Ganguly, J. Mol. Graphics Modell., 2019, 93, 107445 CrossRef CAS.
- D. L. Popescu, T. J. Parolin and C. Achim, J. Am. Chem. Soc., 2003, 125, 6354–6355 CrossRef CAS.
- R. M. Watson, Y. A. Skorik, G. K. Patra and C. Achim, J. Am. Chem. Soc., 2005, 127, 14628–14639 CrossRef CAS.
- A. Küsel, J. Zhang, M. A. Gil, A. C. Stückl, W. Meyer-Klaucke, F. Meyer and U. Diederichsen, Eur. J. Inorg. Chem., 2005, 2005, 4317–4324 CrossRef.
- B. P. Gilmartin, K. Ohr, R. L. McLaughlin, R. Koerner and M. E. Williams, J. Am. Chem. Soc., 2005, 127, 9546–9555 CrossRef CAS.
- K. Ohr, R. L. McLaughlin and M. E. Williams, Inorg. Chem., 2007, 46, 965–974 CrossRef CAS.
- M. Egholm, O. Buchardt, L. Christensen, C. Behrens, S. M. Freier, D. A. Driver, R. H. Berg, S. K. Kim, B. Norden and P. E. Nielsen, Nature, 1993, 365, 566–568 CrossRef CAS.
- P. E. Nielsen, M. Egholm, R. H. Berg and O. Buchardt, Science, 1991, 254, 1497–1500 CrossRef CAS.
- H. Shimada, T. Sakurai, Y. Kitamura, H. Matsuura and T. Ihara, Dalton Trans., 2013, 42, 16006–16013 RSC.
- Y. Miyake, H. Togashi, M. Tashiro, H. Yamaguchi, S. Oda, M. Kudo, Y. Tanaka, Y. Kondo, R. Sawa, T. Fujimoto, T. Machinami and A. Ono, J. Am. Chem. Soc., 2006, 128, 2172–2173 CrossRef CAS.
- Y. Tanaka, S. Oda, H. Yamaguchi, Y. Kondo, C. Kojima and A. Ono, J. Am. Chem. Soc., 2007, 129, 244–245 CrossRef CAS.
- H. Yamaguchi, J. Šebera, J. Kondo, S. Oda, T. Komuro, T. Kawamura, T. Dairaku, Y. Kondo, I. Okamoto, A. Ono, J. V. Burda, C. Kojima, V. Sychrovský and Y. Tanaka, Nucleic Acids Res., 2014, 42, 4094–4099 CrossRef CAS.
- H. Torigoe, A. Ono and T. Kozasa, Chem.–Eur. J., 2010, 16, 13218–13225 CrossRef CAS.
- I. Kratochvílová, M. Golan, M. Vala, M. Špérová, M. Weiter, O. Páv, J. Šebera, I. Rosenberg, V. Sychrovský, Y. Tanaka and F. M. Bickelhaupt, J. Phys. Chem. B, 2014, 118, 5374–5381 CrossRef.
- T. Uchiyama, T. Miura, H. Takeuchi, T. Dairaku, T. Komuro, T. Kawamura, Y. Kondo, L. Benda, V. Sychrovský, P. Bouř, I. Okamoto, A. Ono and Y. Tanaka, Nucleic Acids Res., 2012, 40, 5766–5774 CrossRef CAS.
- A. A. Voityuk, J. Phys. Chem. B, 2006, 110, 21010–21013 CrossRef CAS.
- J. Šebera, J. Burda, M. Straka, A. Ono, C. Kojima, Y. Tanaka and V. Sychrovský, Chem.–Eur. J., 2013, 19, 9884–9894 CrossRef.
- H. R. Drew, R. M. Wing, T. Takano, C. Broka, S. Tanaka, K. Itakura and R. E. Dickerson, Proc. Natl. Acad. Sci. U. S. A., 1981, 78, 2179–2183 CrossRef CAS.
- H. Rasmussen, S. J. Kastrup, J. N. Nielsen, J. M. Nielsen and P. E. Nielsen, Nat. Struct. Biol., 1997, 4, 98–101 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- J. S. Binkley, J. A. Pople and W. J. Hehre, J. Am. Chem. Soc., 1980, 102, 939–947 CrossRef CAS.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270–283 CrossRef CAS.
- R. F. W. Bader, Chem. Rev., 1991, 91, 893–928 CrossRef CAS.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS.
- M. A. R. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, H. J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, J. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, M. I. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, J. T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, Jr, J. A. Montgomery, V. N. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, J. C. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. E. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, R. E. S. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. L. M. O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, S. K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, D. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and J. Fox, Gaussian 09 (revision B.1), Gaussian, Inc., Wallingford, CT Search PubMed.
- P. L. Silvestrelli, J. Phys. Chem. A, 2009, 113, 5224–5234 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- S. Grimme, Chem.–Eur. J., 2012, 18, 9955–9964 CrossRef CAS.
- V. Menchise, G. De Simone, T. Tedeschi, R. Corradini, S. Sforza, R. Marchelli, D. Capasso, M. Saviano and C. Pedone, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 12021–12026 CrossRef CAS.
- J. Kondo, T. Yamada, C. Hirose, I. Okamoto, Y. Tanaka and A. Ono, Angew. Chem., Int. Ed., 2014, 53, 2385–2388 CrossRef CAS.
- H. Yamaguchi, J. Šebera, J. Kondo, S. Oda, T. Komuro, T. Kawamura, T. Dairaku, Y. Kondo, I. Okamoto, A. Ono, J. V. Burda, C. Kojima, V. Sychrovský and Y. Tanaka, Nucleic Acids Res., 2014, 42, 4094–4099 CrossRef CAS.
- L. Benda, M. Straka, V. Sychrovský, P. Bouř and Y. Tanaka, J. Phys. Chem. A, 2012, 116, 8313–8320 CrossRef CAS.
- H. Miyachi, T. Matsui, Y. Shigeta and K. Hirao, Phys. Chem. Chem. Phys., 2010, 12, 909–917 RSC.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093 CrossRef CAS.
- L. D. Kosturko, C. Folzer and R. F. Stewart, Biochemistry, 1974, 13, 3949–3952 CrossRef CAS.
- P. E. Nielsen, Curr. Opin. Struct. Biol., 1999, 9, 353–357 CrossRef CAS.
- A. Mokhir, R. Stiebing and R. Kraemer, Bioorg. Med. Chem. Lett., 2003, 13, 1399–1401 CrossRef CAS.
- N. C. Seeman, Trends Biochem. Sci., 2005, 30, 119–125 CrossRef CAS.
- L. Gao, C. Li, X. Li and H. B. Kraatz, Chem. Commun., 2010, 46, 6344–6346 RSC.
- T. Yamane and N. Davidson, J. Am. Chem. Soc., 1961, 83, 2599–2607 CrossRef CAS.
- S. Katz, Biochim. Biophys. Acta, Spec. Sect. Nucleic Acids Relat. Subj., 1963, 68, 240–253 CAS.
- S. Tomac, M. Sarkar, T. Ratilainen, P. Wittung, P. E. Nielsen, B. Norden and A. Graslund, J. Am. Chem. Soc., 1996, 118, 5544–5552 CrossRef CAS.
- J. C. Hanvey, N. J. Peffer, J. E. Bisi, S. A. Thomson, R. Cadilla, J. A. Josey, D. J. Ricca, C. F. Hassman, M. A. Bonham, K. G. Au, S. G. Carter, D. A. Bruckenstein, A. L. Boyd, S. A. Noble and L. E. Babiss, Science, 1992, 258, 1481–1485 CrossRef CAS.
- G. Barone, C. Fonseca Guerra and F. M. Bickelhaupt, ChemistryOpen, 2013, 2, 186–193 CrossRef CAS.
- M. Leijon, A. Gräslund, P. E. Nielsen, O. Buchardt, S. M. Kristensen, M. Eriksson and B. Nordén, Biochemistry, 1994, 33, 9820–9825 CrossRef CAS.
- D. Cremer and E. Kraka, Angew. Chem., Int. Ed. Engl., 1984, 23, 627–628 CrossRef.
- E. Espinosa, I. Alkorta, J. Elguero and E. Molins, J. Chem. Phys., 2002, 117, 5529–5542 CrossRef CAS.
- A. Kamal, Z. She, R. Sharma and H. B. Kraatz, Electrochim. Acta, 2017, 243, 44–52 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: The optimized geometries of the canonical base pairs and mispair of DNA and PNA mediated with Hg2+ at the B3LYP-D3/6-31G* level of theory in the gaseous phase, comparison between the helix orientation of the Hg2+-mediated mispairs, helix parameters, stacking in DNA–DNA, DNA–PNA and PNA–PNA duplexes, and schematic view of the helix parameters. Cartesian coordinates are given for all geometries. See DOI: 10.1039/d0ra07526d |
| This journal is © The Royal Society of Chemistry 2020 |