Open Access Article
Open Access ArticleCoordinating capillary infiltration with anodic oxidation: a multi-functional strategy for electrochemical fabrication of graphene†
Pu Duan‡
abc,
Siwei Yang‡abc,
Peng He*abc,
Penglei Zhangabc,
Xiaoming Xieabc and
Guqiao Ding *abc
*abc
aState Key Laboratory of Functional Materials for Informatics, Shanghai Institute of Microsystem and Information Technology, Chinese Academy of Sciences, Shanghai 200050, P. R. China. E-mail: hepeng@mail.sim.ac.cn
bCAS Center for Excellence in Superconducting Electronics (CENSE), Shanghai, 200050, P. R. China. E-mail: gqding@mail.sim.ac.cn
cCollege of Materials Science and Opto-Electronic Technology, University of Chinese Academy of Sciences, Beijing 100049, P. R. China
First published on 7th December 2020
Abstract
Electrochemical exfoliation of graphite stands out as a promising alternative to the existing methods for scalable graphene fabrication. However, factors governing the electrochemical process and the underlying mechanism are complex and how to effectively control the exfoliation process is far from completely clear despite many attempts in previous works. Herein, for the first time, capillary infiltration, anodic oxidation and their dependence on temperature were found to be critical in determining the electrolyte infiltration and the anodic oxidation process. On this basis, we achieved tuning of sheet dimensions (both thickness and lateral size) and surface chemistry of graphene by facilely controlling the temperature (5–95 °C). Four kinds of graphene materials featuring small size, porosity, water dispersibility and large size can be selectively fabricated in the same electrolyte system at different temperatures. Especially, low-temperature exfoliation results in high yields (99.5%) of small-sized graphene, which is a new breakthrough for electrochemical methods. The finding and associated mechanism of temperature's influence on both capillary infiltration and anodic oxidation not only deepen our understanding of the electrochemical exfoliation, but also make electrochemistry a versatile technique for graphene fabrication.
Introduction
Graphene is a unique 2D carbon exhibiting excellence in mechanical properties,1 optical transmittance,2 thermal and electronic transport abilities.3 Scalable and low-cost production of graphene is a pressing requirement to realize its large-scale applications and commercialization.4,5 Various methods such as mechanical exfoliation,6 chemical vapor deposition (CVD),7 oxidative exfoliation8 and liquid exfoliation9 have been developed to prepare graphene. Nevertheless, these methods still face challenges in increasing the cost-effectiveness and/or environment acceptance though some of them have been scaled up. For instance, CVD can grow high-quality graphene in film form but suffers from complex process at high temperature and high costs.10 Oxidative exfoliation like the Hummer's method can yield graphene oxide (GO) in large quantity with low costs. However, the oxidation process is generally accompanied by high pollution risk and results in hard-to-repair structural defects in the products.11In recent years, electrochemical exfoliation has attracted great attentions due to its safety, environmental friendliness and cost-effectiveness.12–14 In this method, graphite often serves as the electrode(s) and exfoliated under an electric potential in a specific electrolyte. The whole exfoliation are considered to mainly include intercalation of the charged species and bubbling expansion of the graphite electrode(s). Besides, the graphite precursor may also participate in some electrochemical reactions as reactant, which changes the surface chemistry of the products.15 Many factors that may affect these processes have been investigated in an attempt to make clear the underlying mechanism and better tune the parameters of the resulting graphene. Among these factors, the applied potential and electrolyte are the most studied and also the most effective factors to control the crystalline quality of the products.16,17 For example, graphene materials produced by negative potentials generally possess better quality than that by positive potentials due to the anodic oxidation under positive potentials.18 Electrolytes including chemicals such as (2,2,6,6-tetramethylpiperidin-1-yl)oxyl (TEMPO) and hydrogen peroxide (H2O2) are necessary for high-quality graphene fabrication under positive potentials that because these chemicals can capture the in situ generated free radicals and inhibit the anodic oxidation reactions.19,20 To the contrary, intercalation in concentrated sulfuric acid and then exfoliation in aqueous sulfuric acid solution enable preparation of defective GO.13 Despite of these progress, the existing understandings are far from enough to make electrochemical exfoliation a powerful technique for graphene preparation in terms of the efficiency, lateral size, quality and the properties. For instance, electrochemically derived graphene sheets generally have wide size distributions spanning sub-micron to several microns and moderate yields in the 7–75% range.12,21 Better controllability is necessary to develop more desirable electrochemical methods. The difficulty lies in fully considering the interacting processes involved in the electrochemical exfoliation and all possible factors influencing these processes.
Herein, for the first time, we demonstrated temperature as a critical factor determining the dimensions (lateral size and thickness) and structural defects (porosity and surface chemistry) of the electrochemically derived graphene. Temperature variations were found to affect not only the anodic oxidation process but also the electrolyte infiltration of graphite surface, a physical process that is important for the intercalation but never reported before. Intercalation and bubble exfoliation should be based on the surface infiltration of graphite particles by the electrolyte. In other words, the electrolyte must reach the graphite surfaces and edges prior to the intercalation and subsequent exfoliation. Capillary infiltration supplied power for surface infiltration.22–25 In the range of 5–95 °C, low temperature was revealed to favor the capillary infiltration by electrolyte due to the temperature-sensitive surface tension of the electrolyte. Whereas high temperature was confirmed to deepen the anodic oxidation due to the changes in thermodynamic parameters of the radical involved reactions. Based on this mechanism, dimensions and structure defects of the graphene can be controlled by facile temperature modulation. Four kinds of products including small-sized graphene, porous graphene, water-dispersible graphene and large-sized graphene are selectively fabricated in one electrolyte system, enabling electrochemistry a multi-functional strategy for graphene preparation.
Experimental section
Chemical and materials
Graphite foil was purchased from Qingdao Huatai Graphite Co., Ltd. (Qingdao, China). Ammonium sulfate ((NH4)2SO4, ≥98.5%), ammonia solution (NH3·H2O, 28.0–30.0%), (2,2,6,6-tetramethylpiperidin-1-yl)oxyl (TEMPO, 98%) and calcium hydroxide (Ca(OH)2, ≥95.0%) were purchased from Aladdin Co., Ltd. (Shanghai, China). All chemicals were used as received without further purification. The deionized water (DI water, resistivity ∼18.2 MΩ cm at 25 °C) used throughout all experiments was made by the Millipore Water Purification System.Electrochemical fabrication of graphene
Graphite foil (10 × 40 × 1 mm) and Pt foil (10 × 40 × 0.1 mm) were used as the working electrode and counter electrode in the electrochemical system. The electrolyte was prepared by dissolving 1.32 g (NH4)2SO4 and 3.3 mL NH3·H2O (28–30%) in 100 mL deionized water. The distance between the graphite and the Pt electrode remained ∼2 cm throughout the electrochemical process. Electrochemical exfoliation was carried out by applying a positive voltage (+10 V) on the graphite electrode. After complete exfoliation, the products obtained at different temperatures (5, 15, 25, 35, 45, 55, 65, 75, 85 and 95 °C) were collected by vacuum filtration and repeatedly washed by deionized water and complete desiccation to get the powder. Finally, the powder was bath-sonicated into DMF or DI water to get dispersion for further characterization.The yield of graphene is calculated as shown in eqn (1):
| Yield = Mgraphene/Mprecursor | (1) |
Characterization
Transmission electron microscopy (TEM, Hitachi Tokyo Japan) with an accelerating voltage of 80 kV was used to measure the thickness of products. Scanning electron microscopy (SEM, TESCAN MIRA3) was used to image the morphology of samples. Raman spectroscopy techniques with an excitation laser of 532 nm and a laser spot size of 1 μm was conducted by Rise, WITec, Germany. The laser power on the sample was kept lower than 1 mW to avoid damage and heat induced effects in Raman spectroscopy analyses. Atomic force microscopy (AFM, Oxford Instruments, Cypher S) was carried out under ambient condition. X-ray photoelectron spectroscopy (XPS) was conducted by SPECS Surface Nano Analysis GmbH, Germany. Malvern Zetasizer Nano-ZS90 was used to measure the zeta potential of graphene dispersion. Two laser beams at 780 nm were irradiated to measure the electrophoretic mobility of graphene particles using the principles of dynamic light scattering. The Zetasizer analyzer calculates the value of the zeta potential from electrophoretic mobility using the Smoluchowski equation: ξ = μη/ε, where ξ is the zeta potential, μ is the electrophoretic mobility, η is the viscosity of the solution, and ε is the dielectric constant of the solvent. Force tensiometer (Sigma 700 tensiometer) is used to determine the surface tension of electrolyte at different temperatures. The conductance of the films was characterized by four point probe method using MCP-T370. Measurements were taken in five different spots of the same sample, and the conductivity was averaged.Result and discussion
Capillary infiltration of the anode and its dependence on temperature
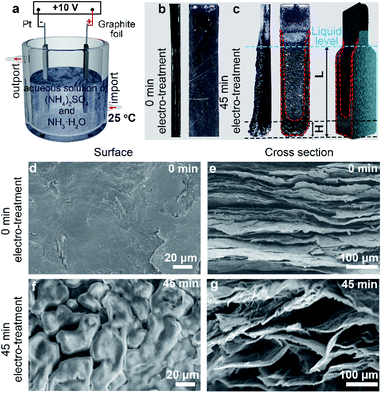
As shown in Fig. 1a, graphite foil and Pt foil were respectively employed as anode and cathode (with a distance of 2 cm). Specially, the mixed aqueous solution of (NH4)2SO4 (0.1 M) and NH3·H2O (0.5 M) was employed as electrolyte. Aqueous solution of (NH4)2SO4 is a commonly used electrolyte to electrochemically intercalate and exfoliate the graphite under positive potentials.12 Specifically, SO42− possesses a similar dimension (0.46 nm) to the interlayer spacing of graphite (0.34 nm) and thus tends to intercalate into the gallery of graphite. Moreover, SO42− can be reduced to produce SO2 in the interlayers of graphite gas under a relatively low reduction potential (+0.20 V), leading to high exfoliation efficiency compared with other anions.9 However, the electrochemical exfoliation in pure (NH4)2SO4 solution is too fast (generally several seconds) to be well controlled. Therefore, we chose (NH4)2SO4 but introduced NH3·H2O to slow down the electrochemical process, which we think may help to probe the mechanism and increase the controllability. Comparative studies show that the electrochemical exfoliation time was elongated from 99 min in aqueous solution of (NH4)2SO4 to 190 min in the mixed aqueous electrolyte of (NH4)2SO4 and NH3·H2O (Fig. S1†). After 45 min of bias voltage application (+10 V) at 25 °C, obvious expansion took place on the graphite foil at both bottom and edge areas (Fig. 1b and c). In addition to volume change, the expansion area shows deeper color than the unexpanded area and obvious electrolyte infiltration of the graphite foil. The color difference can be used to quantify the infiltration. As labeled in Fig. 1c the characteristic size of the totally infiltrated bottom was defined as infiltration depth (H) and the total size of anode under liquid level was defined as effective exfoliation length (L). It can be observed that the bottom area undergone faster infiltration (larger H) and expansion than the edge areas.Interestingly, the infiltration and expansion were also observed above the liquid level (Fig. 1c). This finding indicates the presence of capillary infiltration and good wettability of the electrolyte to graphite at room temperature. Further structure characterization and experiments suggested that capillary force drives the electrolyte infiltration. Typical SEM images (Fig. 1d and e) revealed that the starting electrode has a smooth surface (Fig. 1d) and a relatively dense cross section (Fig. 1e). This microstructure explains the facts that the graphite foil does not show any infiltration when immersed in the electrolyte. After 45 min of electrochemical treatment, a porous network was clearly identified (Fig. 1f) on the surface of the infiltrated area. Simultaneously, numerous pores of approximately 50–100 μm in size appeared on the cross section. This structure evolution can be ascribed to the continuous gas evolution during electrochemical treatment.12,13 Considering the size distribution of the in situ formed pores, we think the electrolyte infiltration of the graphite anode is induced mainly by capillary force.26 This induction can be confirmed by freeze-drying the infiltrated anodes and then probe their behavior when re-submerged in electrolyte. Results (Fig. S2†) shows that the freeze-dried anode restored to the infiltration state before drying when only the anode tip was allowed to contact the electrolyte solution surface. So capillary force should be responsible for the infiltration of the anode during electrochemical exfoliation since the anode undergone neglectable structure change during freeze-drying.
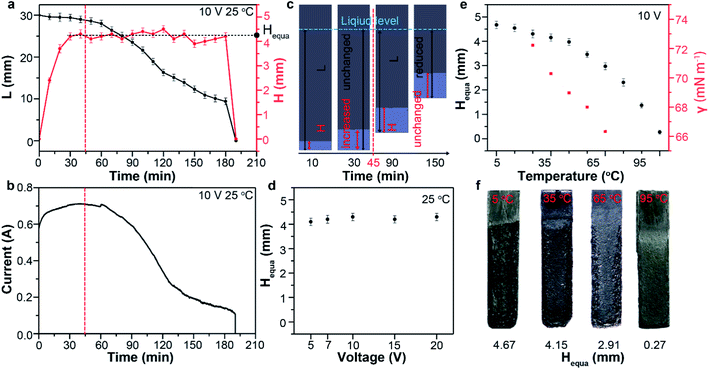
The capillary infiltration process (reflected by H–t curve in Fig. 2a) is closely related to the exfoliation process (reflected by L–t curve in Fig. 2a and I–t curve in Fig. 2b) during the electrochemical treatment at 25 °C. In the first 45 min, the almost unchanged L value indicate a very slow exfoliation at the beginning (Fig. S3†), which is consistent with the observation. Whereas I and H show evident increase in this period. This suggest a process dominated by gradual increase of contact area between graphite and electrolyte (the effective electrolysis area) as a results of the electrolyte infiltration into the anode. Only after the pre-infiltration process, the exfoliation started in the infiltrated bottom area. In the next 150 min, lots of products were observed to detach from the anode bottom (Fig. S3†), leading to the gradual decrease of L to 0 mm. Consequently, I decreased gradually over time with the similar trend of change to L. During this period, however, H undergone a long fluctuation period around 4.30 mm before the rapid decrease to 0 mm. This indicated the limit of the capillary infiltration subjected by the surface tension of electrolyte and a maximum of H remain about 4.3 mm during the electrochemical exfoliation. There must be a dynamic equilibrium between the infiltration and exfoliation: when L reduced as a result of detached products from the anode, the electrolyte would infiltrated forward and reached the limit again (about 4.30 mm). We defined H in the dynamic equilibrium as the equilibrium infiltration depth (denoted by Hequa, Fig. 2a). During this dynamic equilibrium, the bottom area below the Hequa level of graphite anode was infiltrated completely by the electrolyte and exfoliation was found to take place mainly in this area. So, larger Hequa corresponded to better electrolyte infiltration state and potentially better exfoliation of the graphite anode.
Previous reports demonstrated that the electrochemical exfoliation starting by intercalation of charged species into graphite interlayers upon the application of electric potentials.12,13 Then, the intercalants were electrochemically oxidized and produce gaseous species such as CO2, CO and O2 with bubble evolution.27,28 Finally, these bubbles expand and exert large force in graphite galleries, separating weakly bonded graphene layers from one another.29 However, a fact neglected by previous reports is that intercalation and bubble exfoliation should be based on the surface infiltration of graphite particles by the electrolyte. In other words, the electrolyte must reach the graphite surfaces and edges prior to the intercalation and subsequent exfoliation. It is not difficult to understand that good infiltration of the electrode would promote the electrochemical exfoliation. In most cases and our study, the graphite electrodes are composed of densely and randomly stacked graphite flakes. So, good infiltration of every flakes before electrochemical exfoliation is expected to increase the yield of graphene. We think that the electrolyte infiltration is a neglected process should be given priority when further optimizing the electrochemical exfoliation. To confirm this, it is critical to control the capillary infiltration process.
Theoretically, the infiltration capability of liquids driven by capillary force is determined by the capillary structure and surface tension. This can be described by equation 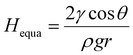 , where the capillary structure is represented by the capillary tube size (r) and Heuqa reflexes the infiltration capability. For a porous structure, r is the effective pore radius, γ is the surface tension of electrolyte, θ is the contact angle between graphite and electrolyte, ρ is the density of electrolyte and g refers to the acceleration of gravity.30,31 The capillary structure is in situ formed during the electrochemical treatment as discussed above. So, surface tension would be a variable with better controllability than the capillary structure to modulate the infiltration capability in this case.32,33 In an electrochemical system, the surface tension of the electrolyte can be altered by the voltages applied on the electrodes, which is known as the electric capillary effect.34,35 However, we found that Heuqa at different voltages shows no obvious change (Fig. 2d) below 20 V at 25 °C. The Heuqa was 4.14, 4.32, 4.31, 4.26 and 4.40 mm at 5, 7, 10, 15 and 20 V, respectively. This may be ascribed to the much higher biases than the electrode potential because electric capillary effect are reported to take place generally in the bias range around the electrode potential. Then we turned to temperature, another parameter that may change the surface tension. As shown in Fig. 2e and f, both surface tension and Heuqa show significant negative correlation with temperature in the 5–95 °C range. The Heuqa values at 5, 15, 25, 35, 45, 55, 65, 75, 85 and 95 °C were 4.67, 4.54, 4.30, 4.15, 3.97, 3.46, 2.91, 2.31, 1.37 and 0.27 mm, respectively. This confirmed that Heuqa was strongly related to temperature. Temperature as a factor to affect the resulting products of electrochemical exfoliation is also expected through capillary infiltration modulation.
, where the capillary structure is represented by the capillary tube size (r) and Heuqa reflexes the infiltration capability. For a porous structure, r is the effective pore radius, γ is the surface tension of electrolyte, θ is the contact angle between graphite and electrolyte, ρ is the density of electrolyte and g refers to the acceleration of gravity.30,31 The capillary structure is in situ formed during the electrochemical treatment as discussed above. So, surface tension would be a variable with better controllability than the capillary structure to modulate the infiltration capability in this case.32,33 In an electrochemical system, the surface tension of the electrolyte can be altered by the voltages applied on the electrodes, which is known as the electric capillary effect.34,35 However, we found that Heuqa at different voltages shows no obvious change (Fig. 2d) below 20 V at 25 °C. The Heuqa was 4.14, 4.32, 4.31, 4.26 and 4.40 mm at 5, 7, 10, 15 and 20 V, respectively. This may be ascribed to the much higher biases than the electrode potential because electric capillary effect are reported to take place generally in the bias range around the electrode potential. Then we turned to temperature, another parameter that may change the surface tension. As shown in Fig. 2e and f, both surface tension and Heuqa show significant negative correlation with temperature in the 5–95 °C range. The Heuqa values at 5, 15, 25, 35, 45, 55, 65, 75, 85 and 95 °C were 4.67, 4.54, 4.30, 4.15, 3.97, 3.46, 2.91, 2.31, 1.37 and 0.27 mm, respectively. This confirmed that Heuqa was strongly related to temperature. Temperature as a factor to affect the resulting products of electrochemical exfoliation is also expected through capillary infiltration modulation.
Anodic oxidation and its dependence on temperature
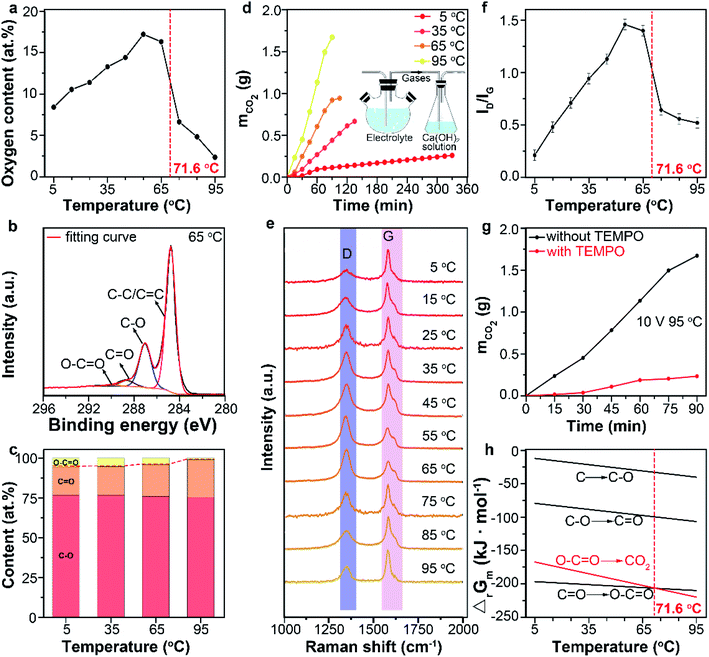
Graphite as the anode tends to be electrochemically oxidized and change the surface chemistry of the products by participating the anodic oxidation reactions. No previous work reported the influence of temperature on anodic oxidation. But it should be considered when temperature is used to modulate the intercalation and exfoliation processes. Combustion elemental analysis (Fig. 3a) was conducted to analyze the oxygen content of products prepared at different temperatures. The oxygen content of products increased as the temperature raised from 5 to 65 °C but decreased rapidly as the temperature raised from 65 to 95 °C. Fig. 3b shows the typical high-resolution C 1s spectrum of product obtained at 65 °C. The XPS spectra were calibrated to the position of the C–C peaks of 284.5 ± 0.2 eV. The four peaks at 290.4 eV, 288.8 eV, 286.8 eV and 284.7 eV can be assigned to O–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, C
O, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, C–O groups and C
O, C–O groups and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C/C–C bond, respectively.36 The deconvolution analysis of the C 1s XPS spectra revealed that the content of C–O group barely changed (75.8 at% ± 0.7 at%) when the temperature raised (Fig. 3c) from 5 to 95 °C (Fig. S4†). However, obvious content change from 17.8 at% to 23.5 at% for C
C/C–C bond, respectively.36 The deconvolution analysis of the C 1s XPS spectra revealed that the content of C–O group barely changed (75.8 at% ± 0.7 at%) when the temperature raised (Fig. 3c) from 5 to 95 °C (Fig. S4†). However, obvious content change from 17.8 at% to 23.5 at% for C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and from 5.5 at% to 1.1 at% for O–C
O and from 5.5 at% to 1.1 at% for O–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O was detected (Fig. 3c). Importantly, the content of O–C
O was detected (Fig. 3c). Importantly, the content of O–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group decreased tardily from 5.5 at% to 4.0 at% when the temperature raised from 5 to 65 °C but decreased evidently from 4.0 at% to 1.1 at% when the temperature raised from 65 to 95 °C (Fig. 3c). This indicated more significant oxidation at elevated temperature range (between 65 and 95 °C).
O group decreased tardily from 5.5 at% to 4.0 at% when the temperature raised from 5 to 65 °C but decreased evidently from 4.0 at% to 1.1 at% when the temperature raised from 65 to 95 °C (Fig. 3c). This indicated more significant oxidation at elevated temperature range (between 65 and 95 °C).
In addition to the oxygen-containing functional groups, CO2 is also a product of the anodic oxidation that should not be neglected especially in deep oxidation of graphite.12 The amount of CO2 can be measured by collecting the released gas with Ca(OH)2 solution and weighing the mass change (Fig. 3d inset). As shown in Fig. 3d, higher temperatures lead to a larger production rates of CO2, which indicated fast and deep oxidation process of graphite into CO2 at high temperatures.37–40 Combining the XPS results, it can be induced that more oxygen-containing functional groups were further oxidized to CO2 at high temperature, causing the decreasing oxygen content of products at high temperature. The above results also suggest that the products of anodic oxidation are dominated by oxygen-containing functional groups in 5–65 °C range and by CO2 in 65–95 °C range.
Raman data gave the similar results. Peaks centering at 1580 cm−1 and 1350 cm−1 in Raman spectra of graphene can be assigned to the G and D bands, respectively. The G band corresponds to the vibration of sp2 bonded carbon atoms in a two-dimensional hexagonal lattice, whereas the D band is resulted either from the vibration of carbon atoms with dangling bonds in crystal lattice plane terminations of disordered graphite, or from the defects in graphene sheets.41–44 The relative peak intensity of D band to G band, ID/IG, is considered as a crucial index of the defect concentration on the graphene. In our study, the ID/IG values of the products were 0.21, 0.48, 0.71, 0.94, 1.13, 1.46, 1.40, 0.64, 0.55 and 0.51 when the reaction temperatures were 5, 15, 25, 35, 45, 55, 65, 75, 85 and 95 °C, respectively (Fig. 3e and f). The obvious decrease of ID/IG at temperature higher than 65 °C revealed the decrease of structure defect, which can be ascribed to the further oxidation of oxygen-containing functional groups (C–O, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, O–C
O, O–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) into CO2 at high temperatures.
O) into CO2 at high temperatures.
Thermodynamics of the oxidation reactions was analyzed to explain the influence of temperature. In dilute or moderately concentrated salt aqueous solutions, water splitting takes place at potentials around 1.23 V and generates mainly oxygen gas at the anode. Nevertheless, the high anodic over potential (e.g., 10 V) discharges water into active intermediates including hydroxyl radicals (˙OH) at the anode following the reaction below.14,19,45
| H2O → H+ + e− + ˙OH |
To confirm this, we introduced (2,2,6,6-tetramethylpiperidin-1-yl)oxyl (TEMPO) as a free radical trapping agent to suppress the formation of ˙OH in the electrolyte solution. The mass of CO2 decreased obviously by almost 7 times with the presence of TEMPO (Fig. 3e). The results illustrated the ˙OH was the main oxidant in the electrochemical process. The pathway that ˙OH oxidize the graphite electrode into oxygen-containing functional groups and further into CO2 can be described by reaction (2)–(5).11,12
| C + ˙OH → C–OH | (2) |
C–OH + ˙OH → C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O + H2O O + H2O
| (3) |
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O + ˙OH → HO–C O + ˙OH → HO–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O
| (4) |
HO–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O + ˙OH → CO2 + H2O O + ˙OH → CO2 + H2O
| (5) |
The Gibbs free energy (ΔrGm) of reaction (2)–(5) at different temperatures was calculated (Fig. 3f). Above 71.6 °C, reaction (5) is more thermodynamically favorable than reaction (2)–(4), due to its large negative change of the Gibbs free energy.46 Thus, oxygen-containing functional groups were more likely to be further oxidized into CO2 at this temperature range. This well explained the dramatical decrease of oxygen content when the temperature raised from 65 to 95 °C.
Temperature enabling fabrication of different graphene materials by coordinating capillary infiltration with anodic oxidation
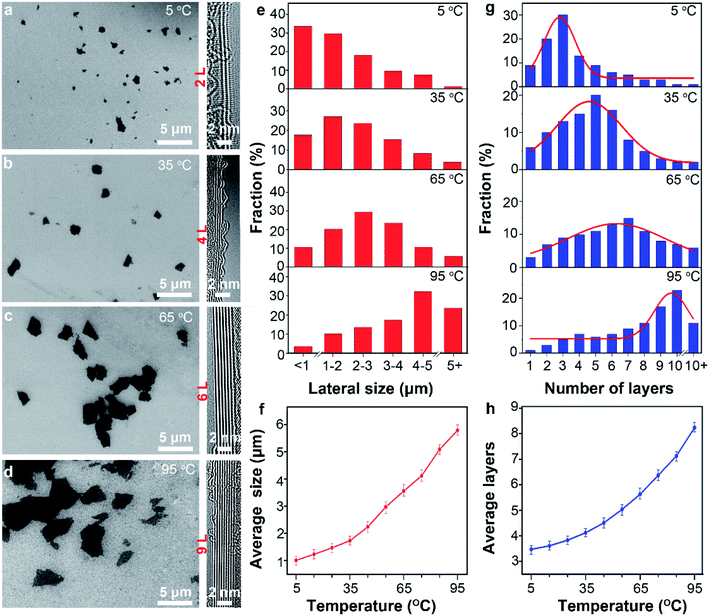
As discussed above, temperature change simultaneously affect two process, namely the capillary infiltration of electrolyte and the anodic oxidation of graphite. The latter leads to the change of surface chemistry. However, the influence of the temperature-sensitive capillary infiltration is not clear. Considering the significance of infiltration for exfoliation, parameters of the product including lateral size and thickness as well as the yield are possibly to be affected by temperature.Typical SEM images (Fig. 4a–d) present the lateral sizes of the different products prepared at different temperatures. The average lateral sizes increased from 1.01 ± 0.15 to 5.79 ± 0.25 as the temperature raised from 5 to 95 °C (Fig. 4e, f and S5†). Similarly, TEM data (Fig. S6 and S7†) from more than 50 sheets shows that the thickness of the products increased monotonously from 3.5 ± 0.2 to 8.2 ± 0.3 as the temperature increase from 5 to 95 °C (Fig. 4g and h). Remarkably, at 5 °C, more than 75% sheets in the products were not thicker than 3 atomic layers. At 35, 65 and 95 °C, the thickness distributed mainly in 4–6 layers (53%), 5–7 layers (48%) and 9–12 layers (51%), respectively. The typical AFM images (Fig. S9†) shows the irregular shape of the graphene sheets obtained at different temperature, which is consistent with TEM results. Further, Gaussian fitting curves (Fig. S10†) suggested smaller FWHM value and more uniform thickness distribution of graphene sheets at 5 °C.
These results indicate that graphene with smaller lateral size and lower thickness can be obtained at lower temperature. However, previous reports demonstrated that strong anodic oxidation at high temperature favor small size and low thickness.47 The obvious contradictions suggested that the capillary infiltration plays an important role at low temperature in decreasing the lateral size and thickness of graphene. As discussed above, large surface tension of electrolyte enabled good infiltration of the electrode to promote the intercalation of anions into graphite layers. Therefore, more adequate intercalation and exfoliation would result in low thickness and small lateral size after subsequent ultrasonication. In contrast, poor infiltration at high temperature as indicated by the Hequa causes inadequate intercalation and exfoliation of the graphitic particles. Thus, the products prepared at higher temperature possess larger lateral size and higher thickness.
Results in Fig. 3 and 4 jointly demonstrated that tuning surface chemistry and sheet dimension (thickness and lateral size) can be achieved via capillary infiltration, anodic oxidation and their dependence on temperature. Therefore, graphene with specific characters can be obtained in the proposed electrolyte system at different temperatures.
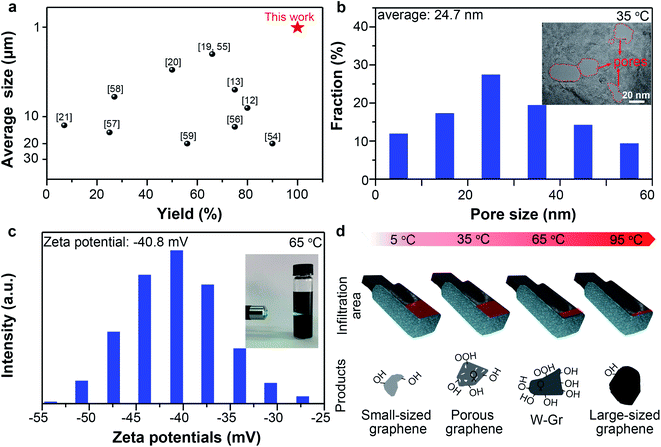
At 5 °C, small-sized graphene (average lateral size: 1.01 μm) can be prepared with remarkably high yields (99.5%) compared with previously reported works (Fig. 5a). Small-sized graphene is preferred by most printing techniques because of the possible nozzle block by large graphene.48 It should be noted that the electrochemically derived graphene sheets generally have wide size distributions (1.5–50 μm) and moderate yields in the 7–75% range (Fig. 5a).
At 35 °C, porous graphene was prepared with yields of about 69.5%. Graphene with a porous structure is useful due to its open ions channels at nano scale on the basal planes and edge activity.49 High-resolution TEM (HRTEM) image shows many pores penetrated through the thicknesses of the graphene layers with diameters ranging from 5 to 60 nm (Fig. 5b inset). Statistic data from HRTEM images (Fig. S11†) of porous graphene sheets indicated that the pores have an average diameter of 24.7 nm with a pore density50 of 10.6 μm−2 (Fig. 5b). The generation of pores can be ascribed to the anodic oxidation. The strong oxidative ˙OH radicals attack the carbon atoms of the graphene layers to form COX, thereby leaving pores on the surface of graphene.51 Pores can also be observed in the graphene obtained at 65 °C (Fig. S12†) but with a much lower density (3.1 μm−2). The increased thickness as temperature increased should be responsible for the decrease of the penetrated pores because we found many unpenetrated pores on the sheet prepared at 65 °C.
Besides, we realized successful fabrication of water-dispersible graphene (W-Gr) with 28.3% yields at 65 °C. Dispersion of W-Gr with a concentration of ∼0.78 g L−1 maintained stable for up to 3 weeks without apparent agglomeration (Fig. S13†). Distinct Tyndall effect (Fig. 5c inset) intuitively showed that the laser can clearly pass through above W-Gr aqueous solution, indicating the uniform dispersing state of W-Gr in water. Dispersing of graphene in water with good stability is desirable in numerous fields due to its good processability, acceptable electric conductivity and environmental friendly usages.52 A high zeta potential of −40.8 mV (Fig. 5c) reveals the origin of this stability from the repulsive interactions of negatively charged surface. So the stability can be ascribed to the grafted oxygen-containing groups, which tend to ionize in aqueous system to produce negatively charged surface.52 As shown in Fig. S14,† the WCA (water contact angle) of graphene film obtained at 5, 35, 65, 95 °C were 67.2°, 59.8°, 58.8°, 74.2°. At 65 °C, the WCA of graphene was lower than other temperatures, indicating the better hydrophilicity than others. This results agrees well with the results that graphene prepared at 65 °C has the best dispersibility in water. Surface oxygen-containing groups provide polar centers to attract water molecules and enhance the surface hydrophilicity, thus lowering the WCA values.53 Simultaneously, oxygen-containing group on graphene surface provides the electrostatic repulsions required to stabilize the graphene colloidal dispersions in water. Our results have demonstrated that the oxygen content of graphene prepared at 65 °C was higher than that of graphene obtained at other temperatures. So, it is not strange to obtain graphene with good water dispersibility at 65 °C. Moreover, large-sized graphene (5.79 μm on average) with low oxygen-content (∼2.36 at%) was prepared at 95 °C. However, the yields were only about 11.5%, highlighting the importance of adequate infiltration for deep exfoliation.
Fig. 5d summarized the graphene related materials prepared at different temperatures. We also evaluated the processability and electrical conductivity of these products. Free-standing graphene films can be assembled from all the four kinds of graphene materials by vacuum filtration and subsequent drying. Fig. S15† shows that the electrical conductivities of these graphene films are 3.2 × 104, 2.5 × 104, 1.4 × 104 and 2.7 × 104 S m−1 when the preparation temperature were 5, 35, 65 and 95 °C, respectively. But for graphene with perfect structure, the electrical conductivity decreases as the thickness of graphene increased because of the stacking of graphene sheet.60 Our results contradicting with the literature highlights the influence of defect and oxygen contents on the electrical conductivity. Defect and high oxygen content weaken the electronic transmission and increase the resistivity.61,62 As shown in Fig. S16,† the thickness of graphene prepared at 95 °C is higher, but it possesses lower defect (smaller ID/IG) and oxygen contents compared to 35 and 65 °C, leading to better electrical conductivity of the sample prepared at 95 °C than at 35 and 65 °C. Notably, the graphene film prepared at 5 °C have excellent electrical conductivity of 3.2 × 104 S m−1. This value is higher than that of the films assembled from other electrochemical exfoliated graphene and reduced graphene oxide but lower than that of CVD-graphene films owing to the presence of defects in our electrochemically derived graphene (Table S1 and Fig. S17†). So the electrical conductivity results is consistent with the XPS and Raman analysis and reflex the negative effect of surface functionalization on crystal structure of graphene.
Conclusions
In summary, we demonstrated that temperature plays a crucial role in determining the electrolyte infiltration and the anodic oxidation process by influencing capillary infiltration and anodic oxidation. Hence, tuning of sheet dimension (lateral size and thickness) and surface chemistry of graphene was achieved by facile temperature modulation. Small-sized graphene with remarkable high yields (99.5%), porous graphene with an average pore size of 24.7 nm, W-Gr with excellent dispersibility in water and large-sized graphene with fewer structural defects can be respectively prepared at 5, 35, 65 and 95 °C. These products fabricated in one electrolyte system prove a multi-functional strategy for electrochemical preparation of graphene. Our finding of temperature as the main factor to coordinate capillary infiltration and anodic oxidation provides deeper understanding of electrochemical exfoliation and a new strategy for large-scale preparation of various graphene-related materials.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grants 51802337, 11774368 and 11804353) and Science and Technology Commission of Shanghai Municipality (Grants 18511110600).Notes and references
- C. Lee, X. Wei, J. W. Kysar and J. Hone, Science, 2008, 321, 385–388 CrossRef CAS
.
- S. Bae, H. Kim, Y. Lee, X. Xu, J. S. Park, Y. Zheng, J. Balakrishnan, T. Lei, H. Ri Kim, Y. Il Song, Y. J. Kim, K. S. Kim, B. Özyilmaz, J. H. Ahn, B. H. Hong and S. Iijima, Nat. Nanotechnol., 2010, 5, 574–578 CrossRef CAS
.
- N. M. Gabor, J. C. W. Song, Q. Ma, N. L. Nair, T. Taychatanapat, K. Watanabe, T. Taniguchi, L. S. Levitov and P. Jarillo-Herrero, Science, 2011, 334, 648–652 CrossRef CAS
.
- Z. S. Wu, G. Zhou, L. C. Yin, W. Ren, F. Li and H. M. Cheng, Nano Energy, 2012, 1, 107–131 CrossRef CAS
.
- Y. Jiang, Z. Xu, T. Huang, Y. Liu, F. Guo, J. Xi, W. Gao and C. Gao, Adv. Funct. Mater., 2018, 28, 1–8 Search PubMed
.
- K. S. Novoselov, V. I. Fal’Ko, L. Colombo, P. R. Gellert, M. G. Schwab and K. Kim, Nature, 2012, 490, 192–200 CrossRef CAS
.
- L. Shi, K. Chen, R. Du, A. Bachmatiuk, M. H. Rümmeli, K. Xie, Y. Huang, Y. Zhang and Z. Liu, J. Am. Chem. Soc., 2016, 138, 6360–6363 CrossRef CAS
.
- S. Kim, S. K. Kim, P. Sun, N. Oh and P. V Braun, Nano Lett., 2017, 17, 6893–6899 CrossRef CAS
.
- Y. Hernandez, V. Nicolosi, M. Lotya, F. M. Blighe, Z. Sun, S. De, I. T. McGovern, B. Holland, M. Byrne, Y. K. Gun’Ko, J. J. Boland, P. Niraj, G. Duesberg, S. Krishnamurthy, R. Goodhue, J. Hutchison, V. Scardaci, A. C. Ferrari and J. N. Coleman, Nat. Nanotechnol., 2008, 3, 563–568 CrossRef CAS
.
- W. Ren and H. M. Cheng, Nat. Nanotechnol., 2014, 9, 726–730 CrossRef CAS
.
- J. Cao, P. He, M. A. Mohammed, X. Zhao, R. J. Young, B. Derby, I. A. Kinloch and R. A. W. Dryfe, J. Am. Chem. Soc., 2017, 139, 17446–17456 CrossRef CAS
.
- K. Parvez, Z. S. Wu, R. Li, X. Liu, R. Graf, X. Feng and K. Müllen, J. Am. Chem. Soc., 2014, 136, 6083–6091 CrossRef CAS
.
- K. Parvez, R. Li, S. R. Puniredd, Y. Hernandez, F. Hinkel, S. Wang, X. Feng and K. Müllen, ACS Nano, 2013, 7, 3598–3606 CrossRef CAS
.
- S. Pei, Q. Wei, K. Huang, H. M. Cheng and W. Ren, Nat. Commun., 2018, 9, 145 CrossRef
.
- C. T. J. Low, F. C. Walsh, M. H. Chakrabarti, M. A. Hashim and M. A. Hussain, Carbon, 2013, 54, 1–21 CrossRef CAS
.
- D. Chen, F. Wang, Y. Li, W. W. Wang, T. X. Huang, J. F. Li, K. S. Novoselov, Z. Q. Tian and D. Zhan, Chem. Commun., 2019, 55, 3379–3382 RSC
.
- N. Liu, F. Luo, H. Wu, Y. Liu, C. Zhang and J. Chen, Adv. Funct. Mater., 2008, 18, 1518–1525 CrossRef CAS
.
- A. M. Abdelkader, I. A. Kinloch and R. A. W. Dryfe, ACS Appl. Mater. Interfaces, 2014, 6, 1632–1639 CrossRef CAS
.
- S. Yang, S. Brüller, Z. S. Wu, Z. Liu, K. Parvez, R. Dong, F. Richard, P. Samorì, X. Feng and K. Müllen, J. Am. Chem. Soc., 2015, 137, 13927–13932 CrossRef CAS
.
- S. Tian, P. He, L. Chen, H. Wang, G. Ding and X. Xie, Chem. Mater., 2017, 29, 6214–6219 CrossRef CAS
.
- C. Y. Su, A. Y. Lu, Y. Xu, F. R. Chen, A. N. Khlobystov and L. J. Li, ACS Nano, 2011, 5, 2332–2339 CrossRef CAS
.
- Z. Juang, C. Wu, C. Lo, W. Chen, C. Huang, J. Hwang, F. Chen, K. Leou and C. Tsai, Carbon, 2009, 47, 2026–2031 CrossRef CAS
.
- H. Fu, P. Varadhan, M. Tsai, W. Li, Q. Ding, C. Lin, M. Bonifazi, A. Fratalocchi, S. Jin and J. He, Nano Energy, 2020, 70, 104478 CrossRef CAS
.
- C. Wu, J. Zhang, X. Tong, P. Yu, J. Xu, J. Wu, Z. M. Wang, J. Lou and Y. Chueh, Small, 2019, 15, 1900578 CrossRef
.
- A. Manikandan, L. Lee, Y. C. Wang, C.-W. Chen, Y. Z. Chen, H. Medina, J. Y. Tseng, Z. M. Wang and Y. L. Chueh, J. Mater. Chem. A, 2017, 5, 13320–13328 RSC
.
- A. Soucemarianadin, R. Lenormand, E. Touboul and G. Daccord, Phys. Rev. A, 1987, 36, 1855–1859 CrossRef
.
- F. Beck, J. Jiang and H. Krohn, J. Electroanal. Chem., 1995, 389, 161–165 CrossRef
.
- F. Beck, H. Junge and H. Krohn, Electrochim. Acta, 1981, 26, 799–809 CrossRef CAS
.
- C. A. Goss, J. C. Brumfield, E. A. Irene and R. W. Murray, Anal. Chem., 1993, 65, 1378–1389 CrossRef CAS
.
- S. Kumar, A. Kumar, A. Shukla, A. K. Gupta and R. Devi, J. Eur. Ceram. Soc., 2009, 29, 2643–2650 CrossRef CAS
.
- M. Lago and M. Araujo, Phys. A, 2001, 289, 1–17 CrossRef CAS
.
- E. Aumann, L. M. Hildemann and A. Tabazadeh, Atmos. Environ., 2010, 44, 329–337 CrossRef CAS
.
- G. J. Gittens, J. Colloid Interface Sci., 1969, 30, 406–412 CrossRef CAS
.
- Y. Zhang and Y. Xu, Adv. Funct. Mater., 2019, 29, 1902171 CrossRef
.
- C. Y. Yang, C. L. Wu, Y. H. Lin, L. H. Tsai, Y. C. Chi, J. H. Chang, C. I. Wu, H. K. Tsai, D. P. Tsai and G. R. Lin, Opt. Mater. Express, 2013, 3, 1893–1905 CrossRef
.
- H. Tang, P. He, T. Huang, Z. Cao, P. Zhang, G. Wang, X. Wang, G. Ding and X. Xie, Carbon, 2019, 143, 559–563 CrossRef CAS
.
- S. F. Leung, H. C. Fu, M. Zhang, A. H. Hassan, T. Jiang, K. N. Salama, Z. L. Wang and J. H. He, Energy Environ. Sci., 2020, 13, 1300–1308 RSC
.
- M. Hadadian, J. H. Smått and J.-P. Correa-Baena, Energy Environ. Sci., 2020, 13, 1377–1407 RSC
.
- H. Lu, Z. Huang, M. S. Martinez, J. C. Johnson, J. M. Luther and M. C. Beard, Energy Environ. Sci., 2020, 13, 1347–1376 RSC
.
- T. Sudayama, K. Uehara, T. Mukai, D. Asakura, X.-M. Shi, A. Tsuchimoto, B. Mortemard de Boisse, T. Shimada, E. Watanabe, Y. Harada, M. Nakayama, M. Okubo and A. Yamada, Energy Environ. Sci., 2020, 13, 1492–1500 RSC
.
- G. D. Yuan, W. J. Zhang, Y. Yang, Y. B. Tang, Y. Q. Li, J. X. Wang, X. M. Meng, Z. B. He, C. M. L. Wu, I. Bello, C. S. Lee and S. T. Lee, Chem. Phys. Lett., 2009, 467, 361–364 CrossRef CAS
.
- A. Dato, V. Radmilovic, Z. Lee, J. Phillips and M. Frenklach, Nano Lett., 2008, 8, 2012–2016 CrossRef CAS
.
- H. Gao, L. Song, W. Guo, L. Huang, D. Yang, F. Wang, Y. Zuo, X. Fan, Z. Liu, W. Gao, R. Vajtai, K. Hackenberg and P. M. Ajayan, Carbon, 2012, 50, 4476–4482 CrossRef CAS
.
- C. W. Huang, C. H. Hsu, P. L. Kuo, C. T. Hsieh and H. Teng, Carbon, 2011, 49, 895–903 CrossRef CAS
.
- J. M. Munuera, J. I. Paredes, M. Enterría, A. Pagán, S. Villar-Rodil, M. F. R. Pereira, J. I. Martins, J. L. Figueiredo, J. L. Cenis, A. Martínez-Alonso and J. M. D. Tascón, ACS Appl. Mater. Interfaces, 2017, 9, 24085–24099 CrossRef CAS
.
- Y. Marcus, J. Chem. Soc., Faraday Trans., 1991, 87, 2995–2999 RSC
.
- M. He, X. Guo, J. Huang, H. Shen, Q. Zeng and L. Wang, Carbon, 2018, 140, 508–520 CrossRef CAS
.
- Z. Liu, Z. S. Wu, S. Yang, R. Dong, X. Feng and K. Müllen, Adv. Mater., 2016, 28, 2217–2222 CrossRef CAS
.
- M. Kotal, H. Kim, S. Roy and I. K. Oh, J. Mater. Chem. A, 2017, 5, 17253–17266 RSC
.
- X. Han, M. R. Funk, F. Shen, Y. C. Chen, Y. Li, C. J. Campbell, J. Dai, X. Yang, J. W. Kim, Y. Liao, J. W. Connell, V. Barone, Z. Chen, Y. Lin and L. Hu, ACS Nano, 2014, 8, 8255–8265 CrossRef CAS
.
- A. K. Lu, H. Y. Li and Y. Yu, J. Mater. Chem. A, 2019, 7, 7852–7858 RSC
.
- H. S. Wang, S. Y. Tian, S. W. Yang, G. Wang, X. F. You, L. X. Xu, Q. T. Li, P. He, G. Q. Ding, Z. Liu and X. M. Xie, Green Chem., 2018, 20, 1306–1315 RSC
.
- A. Ashraf, Y. Wu, M. C. Wang, N. R. Aluru, S. A. Dastgheib and S. W. Nam, Langmuir, 2014, 30, 12827–12836 CrossRef CAS
.
- L. Wu, W. Li, P. Li, S. Liao, S. Qiu, M. Chen, Y. Guo, Q. Li, C. Zhu and L. Liu, Small, 2014, 10, 1421–1429 CrossRef CAS
.
- S. Yang, A. G. Ricciardulli, S. Liu, R. Dong, M. R. Lohe, A. Becker, M. A. Squillaci, P. Samorì, K. Müllen and X. Feng, Angew. Chem., Int. Ed., 2017, 56, 6669–6675 CrossRef CAS
.
- Z. Y. Xia, G. Giambastiani, C. Christodoulou, M. V Nardi, N. Koch, E. Treossi, V. Bellani, S. Pezzini, F. Corticelli, V. Morandi, A. Zanelli and V. Palermo, Chempluschem, 2014, 79, 439–446 CrossRef CAS
.
- X. Huang, S. Li, Z. Qi, W. Zhang, W. Ye and Y. Fang, Nanotechnology, 2015, 26, 105602 CrossRef
.
- C. H. Chen, S. W. Yang, M. C. Chuang, W. Y. Woon and C. Y. Su, Nanoscale, 2015, 7, 15362–15373 RSC
.
- J. Liu, C. K. Poh, D. Zhan, L. Lai, S. H. Lim, L. Wang, X. Liu, N. Gopal Sahoo, C. Li, Z. Shen and J. Lin, Nano Energy, 2013, 2, 377–386 CrossRef CAS
.
- P. N. Nirmalraj, T. Lutz, S. Kumar, G. S. Duesberg and J. J. Boland, Nano Lett., 2011, 16–22 CrossRef CAS
.
- S. F. Pei, J. P. Zhao, J. H. Du, W. C. Ren and H. M. Cheng, Carbon, 2010, 48, 15 Search PubMed
.
- H. A. Becerril, J. Mao, Z. F. Liu, R. M. Stoltenberg, Z. N. Bao and Y. S. Chen, ACS Nano, 2008, 2, 463 CrossRef CAS
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra07531k |
| ‡ P. Duan and S. Yang contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2020 |