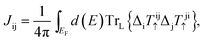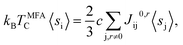DOI:
10.1039/D0RA07543D
(Paper)
RSC Adv., 2020,
10, 44633-44640
Pressure dependent half-metallic ferromagnetism in inverse Heusler alloy Fe2CoAl: a DFT+U calculations
Received
2nd September 2020
, Accepted 5th November 2020
First published on 17th December 2020
Abstract
We report the electronic and magnetic properties along with the Curie temperature (TC) of the inverse full Heusler alloy (HA) Fe2CoAl obtained by using the first-principles computational method. Our calculations suggests that Fe2CoAl is a magnetic metal when treated within PBE-GGA under the applied compressive pressures. However, the implementation of electron–electron (U) (i.e., GGA+U) with varying compressive pressure (P) drastically changes the profile of the electronic structure. The application of GGA+U along with pressure induces ferromagnetic half-metallicity with an integer value of total magnetic moment ∼4.0 μB per unit cell. The integer value is in accordance with the Slater–Pauling's rule. Here, we demonstrate the variation of semiconducting gap in the spin down channel. The band gap increases from 0.0 eV to 0.72 eV when increasing the pressure from 0 to 30 GPa. Beyond 30 GPa, the electronic band gap decreases, and it is completely diminished at 60 GPa, exhibiting metallic behaviour. The analysis of the computed results shows that the treatment of electron–electron interactions within GGA+U and the application of compressive pressure in Fe2CoAl enables d–d orbital hybridization giving rise to a half-metal ferromagnet. The TC calculated from mean field approximation (MFA) decreases up to 30 GPa and then increases linearly up to 60 GPa.
1 Introduction
The discovery of the prototype Heusler alloy Cu2MnAl in 1903 (ref. 1) initiated new research interest due to its ferromagnetic behaviour despite having all non-magnetic constituents.1,2 Heusler alloys have been studied for 120 years, but the application of these materials in spintronics has only been considered for 30–40 years.3–12 Half-metal ferromagnetism (HMF) is the top priority among all the explored properties of Heusler alloys.13–20 HMF occurs when magnetic materials exhibit metallic behavior in one of the spin channels whereas the other spin channel is semiconducting. Rigorous research has been performed in order to understand the underlying mechanism of unusual ferromagnetic behaviour in terms of atomistic scale interactions. Several theories and models have been proposed for the integration of these exotic properties in new technological applications in spintronics.21 Spintronics is a branch of science which deals with the charge and spin of an electron. High capacity storage devices, magnetic RAM, spin-injection, spin-valves, spin-filters, GMR, TMR, and many more potential electron spin-based components are foreseen.22–25 To improve the storage capacity of memory devices, the manipulation of spin degrees of freedom is crucial. Fabrication of practical devices with enhanced efficiency is another challenging task. Some of the Heusler alloys with high spin polarization and high Curie temperature21,26 are promising and may complement this goal. Although the practical application of HMF in spintronic devices is in the preliminary stage, lab work is still in progress. Heusler alloys with 3d-orbitals are very sensitive to externally applied fields (temperature, pressure, electric and magnetic fields), and as a result their electronic and magnetic properties can be tuned very readily. The d–d orbital hybridization between the transition metals is reported to be responsible for some of their outstanding electronic and magnetic properties, including the high value of spin polarization at the Fermi level (EF).18 They exhibit low Gilbert damping, high Curie temperature, high spin polarization, etc.27–37 In addition, Heusler alloys are also explored as potential thermoelectric materials38 due to the presence of non-toxic components and their large range of working temperatures as compared to other thermoelectric materials.39–42 Currently, numerous theoretical and experimental research investigations are in progress to study the electronic and magnetic properties of Heusler alloys via structural modifications under applied strain and hydrostatic pressure. Under applied hydrostatic pressure, the bond lengths vary due to the displacement of atoms from their mean positions and changes electronic charge densities which have a direct impact on the electronic and magnetic properties.43,44 Ram et al. have reported significant changes in the band structure of Co2XY (X = Cr, Mn and Y = Al, Ga) type direct full-Heusler alloys under applied pressure.45 Rasul et al.46 have studied the quaternary Heusler alloys ScNiCrX (X = Al, Ga) using a first-principles approach and reported the robustness of the half-metallicity up to 6 GPa and 16 GPa for ScNiCrAl and ScNiCrGa, respectively. Amudhavalli et al.47 studied Fe-based ferromagnetic quaternary Heusler alloys and reported a pressure induced structural phase transition at 151.6 GPa, 33.7 GPa, 76.4 GPa, 85.3 GPa, 87.7 GPa and 96.5 GPa for CoFeTiSi, CoFeTiGe, CoFeTiAs, NiFeTiSi, NiFeTiGe and NiFeTiAs, respectively. The same group,48 performing similar kinds of studies, have reported a half-metal to metal phase transition for Co2TiAl, Co2TiGa and Co2TiIn under applied external pressures of 76.5 GPa, 73.1 GPa and 63.9 GPa, respectively. Rambabu et al. studied the variation of the Curie temperature (TC) under applied pressure and reported enhanced TC at high compressive pressures.49 There are reports on the variation of TC of various Heusler alloys (such as Ni–Mn based alloys) under applied pressure.50–52 Dannenberg et al.53 reported the structural dependence of TC of Fe2CoGa: ∼780 K for L21 and ∼770 K for L10, respectively. Some more promising results for TCs for Fe-based full-Heusler alloys54 under ambient conditions are: 925 K (Fe2CoGe), 750 K (Fe2NiGe), 845 K (Fe2NiGa), 798 K (Fe2CuGa), and 875 K (Fe2CuAl). In our previous work55 only Co2FeAl exhibited half-metallicity with the implementation of DFT+U whereas Fe2CoAl was metallic. However, there is a pseudo bandgap above the Fermi energy in the spin-down channel of Fe2CoAl within DFT+U. Thus we were encouraged to implement external pressure to observe the location of the bandgap. Interestingly, we have observed a projection of the bandgap in the Fermi level in the spin-down channel, giving rise to half-metallicity. Therefore, we have applied pressure, which shortens the bond lengths and facilitates d–d hybridization, which may give the desired results. In this paper, we have also tried to explore the electronic and magnetic properties along with the TC under compressive pressure using the first-principles approach. We report the sensitiveness of the electronic and magnetic properties under lattice strain due to applied pressure.
2 Computational details
In terms of their chemical compositions, Heusler alloys are classified as binary (X3Z), ternary (X2YZ or XYZ), and quaternary (AXYZ) compounds, where A, X and Y are transition metals and Z is a p-block element. Binary HAs only have two distinguishable elements in the unit cell. In general, ternary HAs are of two types viz. full (X2YZ) and half (XYZ) HAs. The stoichiometric atomic ratios of full (X2YZ) and half (XYZ) ternary HAs are 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, respectively. On the other hand, quaternary HAs have an equiatomic stoichiometric ratio of 1
1, respectively. On the other hand, quaternary HAs have an equiatomic stoichiometric ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Herein, we focus on ternary full-HAs. Ternary full-HAs crystallize in two ordered phases: Cu2MnAl-type with space group Fm
1. Herein, we focus on ternary full-HAs. Ternary full-HAs crystallize in two ordered phases: Cu2MnAl-type with space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (225)35,56 and Hg2CuTi-type with the F
m (225)35,56 and Hg2CuTi-type with the F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m (216) space group.57,58 The former is referred to as regular/direct (L21) and the latter is inverse/indirect with XA-structure. The atomic Wyckoff positions for both the XA-phase and the L21-phase of Fe2CoAl are tabulated in Table 1. In the case of ternary inverse full-HAs the electronegativity of the X-atom is less than that of the Y-atom (X = Fe and Y = Co). Thus, our Fe2CoAl system is an inverse full-HA with the electronegativity of the Fe-atom being less than that of the Co-atom. The primitive and conventional unit cells of Fe2CoAl with XA-structure are shown in Fig. 1. To study the electronic and magnetic properties of the inverse full-Heusler alloy Fe2CoAl, we have performed first-principles Density Functional Theory (DFT) calculations.59,60 All electron–electron interactions were considered according to the generalized gradient approximation (GGA) within the Perdew–Burke–Ernzerhof (PBE) parametrization.61 We are aware that GGA is inadequate for treating strongly correlated d-electrons to derive accurate electronic structures. On the other hand, the successful obtainment of accurate electronic properties by using GGA+U has already been reported for many Heusler alloys.62–67 Therefore, we have applied a screened Coulomb interaction along with the conventional GGA (GGA+U or DFT+U) in order to deal with strongly correlated 3d electrons.68 We have adopted U parameters of 3.82 eV for Fe and 3.89 eV for Co according to our previous work.55,69 For computation, we have used the all electron orbital based full potential linearized augmented plane wave (FP-LAPW) basis set formalism as implemented in the WIEN2K package.70 The non-spherical cut off value of angular momentum within the muffin tin (MT) sphere is lmax = 10. RMT × Kmax = 7 where Kmax is the maximum value of the reciprocal lattice vector in the plane wave expansion and RMT is the smallest muffin tin (MT) radius. To model the electronic structure, the first Brillouin zone (BZ) was integrated by taking a 10 × 10 × 10 k-mesh grid within the Monkhorst package. The self-consistency convergence criterion was set to be 0.0001 Ry. The ferromagnetic–antiferromagnetic exchange energy Jij is a key parameter in determining the Curie temperature (TC). A code based on the single-site coherent potential approximation within the Green’s function approach called spin-polarized relativistic Korringa–Kohn–Rostoker (SPR-KKR)71,72 was used for the calculation of TC.
3m (216) space group.57,58 The former is referred to as regular/direct (L21) and the latter is inverse/indirect with XA-structure. The atomic Wyckoff positions for both the XA-phase and the L21-phase of Fe2CoAl are tabulated in Table 1. In the case of ternary inverse full-HAs the electronegativity of the X-atom is less than that of the Y-atom (X = Fe and Y = Co). Thus, our Fe2CoAl system is an inverse full-HA with the electronegativity of the Fe-atom being less than that of the Co-atom. The primitive and conventional unit cells of Fe2CoAl with XA-structure are shown in Fig. 1. To study the electronic and magnetic properties of the inverse full-Heusler alloy Fe2CoAl, we have performed first-principles Density Functional Theory (DFT) calculations.59,60 All electron–electron interactions were considered according to the generalized gradient approximation (GGA) within the Perdew–Burke–Ernzerhof (PBE) parametrization.61 We are aware that GGA is inadequate for treating strongly correlated d-electrons to derive accurate electronic structures. On the other hand, the successful obtainment of accurate electronic properties by using GGA+U has already been reported for many Heusler alloys.62–67 Therefore, we have applied a screened Coulomb interaction along with the conventional GGA (GGA+U or DFT+U) in order to deal with strongly correlated 3d electrons.68 We have adopted U parameters of 3.82 eV for Fe and 3.89 eV for Co according to our previous work.55,69 For computation, we have used the all electron orbital based full potential linearized augmented plane wave (FP-LAPW) basis set formalism as implemented in the WIEN2K package.70 The non-spherical cut off value of angular momentum within the muffin tin (MT) sphere is lmax = 10. RMT × Kmax = 7 where Kmax is the maximum value of the reciprocal lattice vector in the plane wave expansion and RMT is the smallest muffin tin (MT) radius. To model the electronic structure, the first Brillouin zone (BZ) was integrated by taking a 10 × 10 × 10 k-mesh grid within the Monkhorst package. The self-consistency convergence criterion was set to be 0.0001 Ry. The ferromagnetic–antiferromagnetic exchange energy Jij is a key parameter in determining the Curie temperature (TC). A code based on the single-site coherent potential approximation within the Green’s function approach called spin-polarized relativistic Korringa–Kohn–Rostoker (SPR-KKR)71,72 was used for the calculation of TC.
Table 1 Wyckoff positions of the Fe2-based inverse full-Heusler alloy Fe2CoAl
| Positions |
x |
y |
z |
| Inverse |
| Fe1 |
0.75 |
0.75 |
0.75 |
| Fe2 |
0.50 |
0.50 |
0.50 |
| Co |
0.25 |
0.25 |
0.25 |
| Al |
0.00 |
0.00 |
0.00 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| Direct |
| Fe1 |
0.25 |
0.25 |
0.25 |
| Fe2 |
0.75 |
0.75 |
0.75 |
| Co |
0.50 |
0.50 |
0.50 |
| Al |
0.00 |
0.00 |
0.00 |
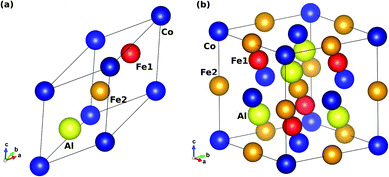 |
| | Fig. 1 (a) Primitive and (b) conventional unit cell of the inverse Heusler alloy Fe2CoAl with space group F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m. Balls in red, orange, blue and yellow in the represents Fe1, Fe2, Co and Al respectively. 3m. Balls in red, orange, blue and yellow in the represents Fe1, Fe2, Co and Al respectively. | |
3 Results and discussion
3.1 Structural properties
Our first-principles calculations start with the optimization of both the L21 (direct) and XA (inverse) structures with different magnetic configurations. The initial magnetic configurations set for our calculations are ferromagnetic FM (Fe1↑, Fe2↑, Co↑), antiferromagnetic AFM1 (Fe1↑, Fe2↓, Co↑), and AFM2 (Fe1↑, Fe2↑, Co↓) (see Table 2). The variations in total energy versus the lattice constant a (Å) for both the direct and inverse phases with the FM, AFM1 and AFM2 magnetic configurations are shown in Fig. 2a and b. The XA-structure (inverse) with the FM configuration is energetically favourable with the minimum energy as shown by the blue line and the diamonds [see Fig. 2b]. The ground state energy and pressure as a function of volume are also presented in Fig. 2c and d. The calculated lattice constant is 5.73 Å and is consistent with previously reported values of 5.70 Å,73 5.71 Å,74 5.766 ± 0.05 Å,75 and 5.732 Å.76 This result also agrees well with the results for several other analogous Fe-based inverse Heusler alloys whose lattice parameters vary from 5.5 to 6.2 Å.35,54,55,77–84 Further, the cohesive energy has been calculated from eqn (1). The cohesive energy results are presented in Fig. 7c and confirm the ground state stability of each system under different applied pressures.| |
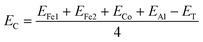 | (1) |
Here in eqn (1), EFe1, EFe2, ECo, EAl and ET are the individual energies of Fe1, Fe2, Co, and Al, and the total energy of the system, respectively. n = 4 denotes the total number of atoms in the unit cell.
Table 2 Magnetic configuration (MC) of the individual atoms Fe1, Fe2, Co, and Al, and total ground state energy ET in Ry
| MC |
Fe1 |
Fe2 |
Co |
Al |
ET |
| Inverse |
| FM |
↑ |
↑ |
↑ |
N |
−1074.852 |
| AFM1 |
↑ |
↓ |
↑ |
N |
−1074.829 |
| AFM2 |
↑ |
↑ |
↓ |
N |
−1074.8509 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| Direct |
| FM |
↑ |
↑ |
↑ |
N |
−1074.818 |
| AFM1 |
↑ |
↓ |
↑ |
N |
−1074.792 |
| AFM2 |
↑ |
↑ |
↓ |
N |
−1074.758 |
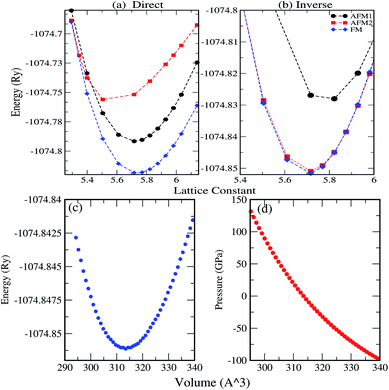 |
| | Fig. 2 Variation of total energy as a function of lattice constant a (Å): (a) direct phase, (b) inverse phase (AMF1, AFM2 and FM configurations are represented by black, red and blue lines, respectively), (c) ground state energy as a function of volume in Å3 for FM and (d) pressure in GPa as a function of volume in Å3. | |
3.2 Electronic and magnetic properties
We have investigated the electronic properties of Fe2CoAl by calculating the total density of states (TDOS) and energy bands at different pressures using GGA+U [cf. Fig. 3–5]. We have already reported the inadequacy of GGA in deriving the electronic properties in our previous work.55 On the other hand, GGA+U has predicted a band gap in the spin down channel but this is well above the Fermi level (EF). We have observed the presence of some band edges at the EF, mostly originating from Fe1-d (t2g), Fe2-d (eg, t2g) and Co-d (eg, t2g) [cf. Fig. 4a–d]. However, the Fe1-d (eg) state is hardly seen in the picture as it lies far below the EF in the spin up channel [cf. Fig. 4a]. Hence, we have proceeded with our calculations by using GGA+U along with the application of compressive pressure. Interestingly, on the application of compressive pressure (5 GPa), the EF is pushed upward within the band gap [Fig. 3a and b]. The half-metallic band gap is attributed to the d–d hybridization between Fe2-d and Co-d followed by Fe1-d states to give bonding–antibonding states as in the case of other full-Heusler alloys.15–19,26 The bonding states at the top of the valence band form the valence band maximum (VBM) and the lowest antibonding states in the conduction region form the conduction band minimum (CBM). On the other hand, the spin up channel is still conducting. This hybrid characteristic of being semiconducting in the spin down channel and conducting in the spin up channel results in peculiar half-metal ferromagnetic (HMF) behaviour. We have also noticed widening of the band gap with increasing compressive pressure, as this facilitates hybridization due to shortening of the bond lengths. The energy band gap increases from 0.0 eV to 0.72 eV on increasing the pressure from 0 to 30 GPa [cf. Fig. 7d]. This result can also be confirmed by the energy band structure which exhibits the indirect nature of the band gap as measured along the L–X symmetry and denoted by the green circles [cf. Fig. 5]. In Fig. 3 and 4, we observe a large band gap of ∼0.72 eV at 30 GPa with the EF pinned exactly in the middle of the band gap, providing more evidence of half-metallicity. A further increase in applied pressure (say beyond 30 GPa) decreases the band gap with drifting of the upper band edge (CBM) towards lower energy (specifically towards the EF). This can be seen in Fig. 3b and 4a–d in which the Fe1-d state has moved towards higher energy in the conduction band, taking part less in the d–d hybridization, and the coupled Fe2-d–Co-d bands are pushed towards lower energy (i.e. towards the EF) in the spin down region. It looks like the EF shifts from the lower to the upper edge of the half-metallic band gap in the spin down channel on increasing the pressure, a typical feature of band flip. At 60 GPa the CBM (upper edge of the band gap) appears at the EF, thus diminishing the half-metallic behaviour and increasing the metallicity. The robustness of the half-metallicty is measured in terms of spin polarization at the EF. The degree of spin polarization in the vicinity of the EF can be analyzed by P = [N↑(EF) − N↓(EF)]/[N↑(EF) + N↓(EF)], where N↑(EF) and N↓(EF) are the numbers of states at EF for the spin up and spin down channels, respectively. Our GGA+U calculation with pressure has significantly improved the spin polarization by more than 45%. At 5 GPa we estimated ∼98% spin polarization. On varying the pressure, 5 < P < 60 GPa, we have achieved perfect half-metallic behaviour in our Fe2CoAl system. The projection of EF inside the band gap in the spin down channel and the finite value of the electron density around EF in the spin up channel at 5 < P < 60 GPa results in 100% spin polarization. To analyse the nature of the bonding between the atoms we have calculated the valence electron charge density (e Å−3) and the results at 30 GPa are presented in Fig. 6. The analysis of the charge density shows the presence of metallic bonding between the atoms and no sign of covalent bonds.
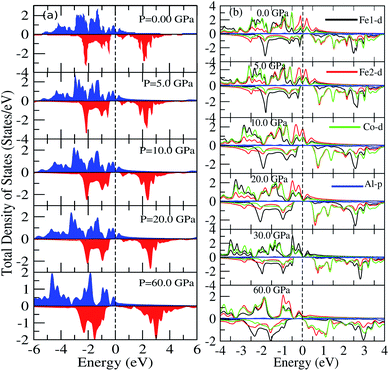 |
| | Fig. 3 (a) Total DOS calculated using GGA+U, (b) partial DOS of Fe1-d, Fe2-d, Co-d and Al-p calculated with GGA+U at different pressures. | |
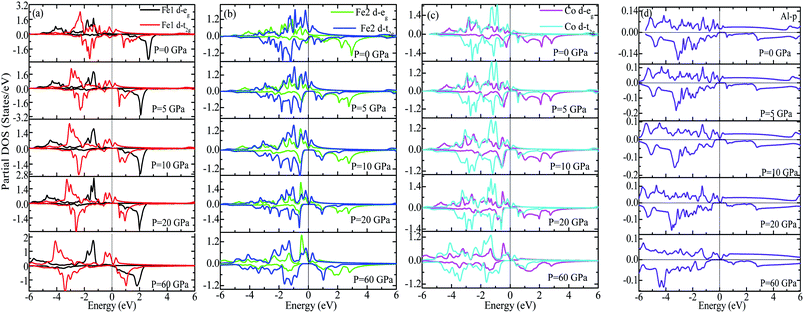 |
| | Fig. 4 (a) Partial DOS of Fe1 (d-eg, d-t2g), (b) partial DOS of Fe2 (d-eg, d-t2g), (c) partial DOS of Co (d-eg, d-t2g) and (d) partial DOS of Al-p at different pressures. | |
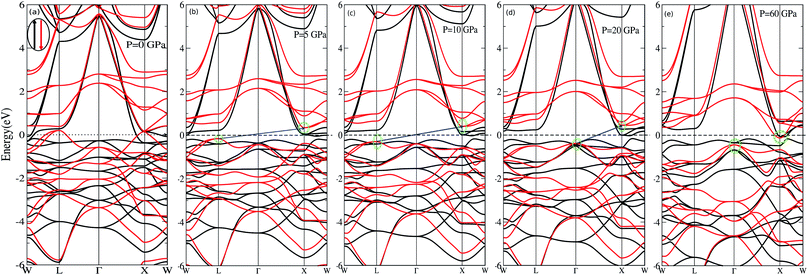 |
| | Fig. 5 Band energies of Fe2CoAl calculated with GGA+U at (a) P = 0 GPa, (b) P = 5 GPa, (c) P = 10 GPa, (d) P = 20 GPa and (e) P = 60 GPa. | |
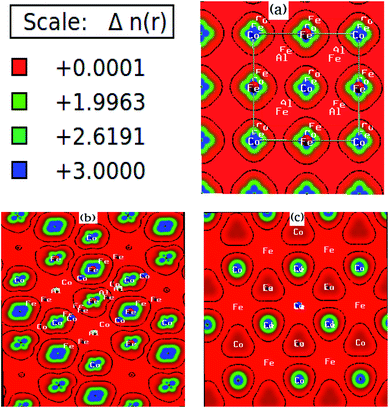 |
| | Fig. 6 Electron density (e Å−3) of Fe2CoAl along the (a) 001, (b) 011 and (c) 111 directions. | |
As reported elsewhere, the magnetic properties of perfect half-metallic ferromagnet (HMF) Heusler alloys (HAs) can be predicted from the total number of valence electrons present in the unit cell.15–18,26 The total magnetic moment can be derived from the Slater–Pauling (SP) rule18 as given by Mt = (Zt − 24) μB, where Mt is the total magnetic moment and Zt is the total number of valence electrons. The total number of valence electrons in our Fe2CoAl system is 2 × 8 + 9 + 3 = 28. So the expected value of the total magnetic moment is Mt = 4.0 μB which results in the half-metallicity. The total magnetic moment obtained from GGA sharply deviates from the Slater–Pauling rule. However, on treating the system within GGA+U and applying pressures (0–70 GPa), the total magnetic moment Mt varies around 4.0 μB. The highest Mt = 4.440 μB and the lowest Mt = 3.981 μB, calculated at 0 GPa and 70 GPa, respectively [Table 3]. The Mt values at 0 and 70 GPa do not comply with the SP rule. Also, at 60 GPa Mt = 3.988 μB and ΔμB = ∼0.012 or ∼0.3%. At applied pressures of 5 < P < 60 GPa, the Mt value is ∼4 μB. Thus, we can claim that the Mt values are in accordance with the SP rule18 at 5 < P < 60 GPa. We also present the variation of the partial magnetic moments calculated with GGA and GGA+U under different pressures in Fig. 7a and their numerical values are tabulated in Table 3.
Table 3 Total and partial magnetic moments (in μB) calculated with GGA+U along with the Curie temperature TC (in K)
| P (GPa) |
MTot |
MFe1 |
MFe2 |
MCo |
TcalC |
TMFAC |
| 0.0 |
4.440 |
2.126 |
1.011 |
1.109 |
826.640 |
1164.30 |
| 5.0 |
4.030 |
2.158 |
0.989 |
1.075 |
752.430 |
1134.90 |
| 10.0 |
3.999 |
2.171 |
0.990 |
1.051 |
746.819 |
1130.60 |
| 20.0 |
3.990 |
2.165 |
1.010 |
1.018 |
745.190 |
1127.20 |
| 30.0 |
4.000 |
2.155 |
1.016 |
0.995 |
747.000 |
1124.20 |
| 40.0 |
3.996 |
2.152 |
1.009 |
0.979 |
744.828 |
1146.30 |
| 50.0 |
4.009 |
2.137 |
1.025 |
0.978 |
748.629 |
1173.50 |
| 60.0 |
3.988 |
2.121 |
1.028 |
0.964 |
746.276 |
1190.40 |
| 70.0 |
3.981 |
2.105 |
1.024 |
0.957 |
743.561 |
1187.00 |
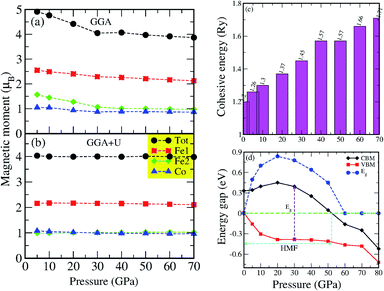 |
| | Fig. 7 (a and b) Total and partial magnetic moments calculated with the FPLAPW method using WIEN2K, variation of (c) cohesive energy and (d) energy band gap as a function of pressure. | |
In order to further understand the magnetic interactions and magnetic properties, we have calculated the magnetic exchange energy by modeling the pair exchange interaction parameter Jij. The Jij parameter is computed using the Heisenberg model.17 The exchange coupling interactions are mapped between the atoms sitting at the i and j sites separated by some distance as in eqn (2)
| |
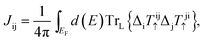 | (2) |
where Δ
i =
ti↑−1 −
tj↓−1,
t↑↓−1 is the atomic
t-matrix of the magnetic impurities at site i for the spin up/down state,
Tij↑↓ is the scattering path operator between the i and j sites for the spin up/down state, and Tr
L is the trace over the orbital variables of the scattering matrices. The calculated exchange parameters
Jij for a central Fe1 atom interacting with all other atoms (Al–Fe1, Fe1–Fe1, Fe2–Fe1 and Co–Fe1) as a function of
Rij/
a at different pressures are shown in
Fig. 8a–d. The estimated
Jij is a key parameter for obtaining the Curie temperature (
TC) in the mean-field approximation (MFA) as given in
eqn (3):
| |
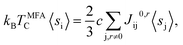 | (3) |
where
kB is the Boltzmann constant,
c is the concentration of the impurities, and 〈
sj〉 is the average j component of the unit vector
srj along the direction of magnetization. The
Jij below
Rij/
a = ∼1 (below 1) shows a finite stable value. Meanwhile, the
Jij values above
Rij/
a = ∼1 (above 1) either remain close to 0 meV or fluctuate around 0 meV [
cf. Fig. 8a–d]. The variation of the total
Jij along with the calculated
TMFAC as a function of
Rij/
a under different pressures are shown in
Fig. 9a and b. We can see that on increasing the pressure up to 30 GPa the
Jij parameter decreases systematically. This leads to a decrease in
TMFAC. As shown in
Fig. 8c the
Jij value is governed by a strong interaction between Fe1 and Fe2. The lowest calculated value of
TMFAC = 1124.20 K at 30 GPa is mainly attributed to the low value of
Jij due to the short range (
Rij/
a < ∼1) interaction between Fe1 and Fe2 [see inset (blue line) in
Fig. 8c]. For the Al–Fe1, Fe1–Fe1 and Co–Fe1 interactions, the
Jij values are intermediate at 30 GPa [
cf. Fig. 8a–d]. On increasing the pressure beyond 30 GPa there occurs a linear increase in
TMFAC, which reaches a maximum at 60 GPa. Our results for
TMFAC contradict with the results of Rambabu
et al. for Co
2CrX (X = Al, Ga, In) below 30 GPa, whereas at high pressure,
i.e., above 30 GPa they follow a similar trend.
49 The calculated
TC values obtained from the mean field approximation are tabulated in
Table 3. The other method to estimate the
TC in relation to the total magnetic moment (
Mt) of HMF-HAs is given by
eqn (4).
19,26| | |
TcalC = 23 + 181 × Mt
| (4) |
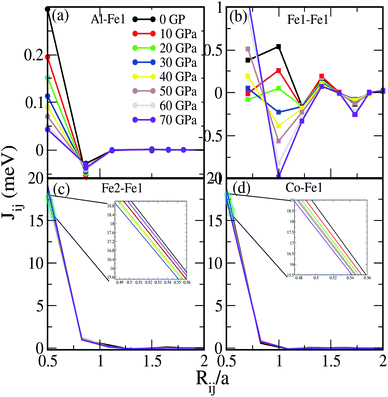 |
| | Fig. 8 Exchange interaction Jij (meV) between (a) Al and Fe1, (b) Fe1 and Fe1, (c) Fe2 and Fe1 and (d) Co and Fe1 at different pressures. | |
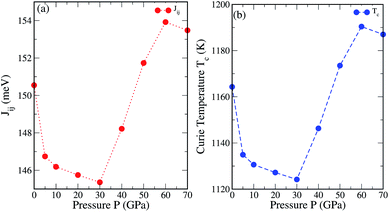 |
| | Fig. 9 (a) Exchange interaction Jij (meV) and (b) Curie temperature TMFAC (K) as a function of pressure. | |
As we have already discussed the inefficiency of GGA in deriving the half-metallicity, estimating TC by taking the Mt obtained from GGA is not justifiable. Therefore, we have taken the Mt values calculated with GGA+U and substituted in eqn (4) to obtain the TcalC. The estimated values of TcalC are presented in Table 3. The TcalC values vary from 826.640 K to 743.561 K on varying the pressure from 0 to 70 GPa. These results are in good agreement with the TCs of other analogous Fe-based inverse full-HAs.54 We have noted that the TC obtained from eqn (4) appears to be independent of interaction strength as the variation of the total magnetic moment (Mt) is very small. Referring to Table 3, the TC values calculated with the MFA (eqn (3)) look much higher as compared to those calculated with eqn (4). The large values of TMFAC may arise due to inability to include the magnetic percolation effect within the mean field approximation.55
4 Conclusion
In summary, we have studied the structural, electronic and magnetic properties of the inverse HA Fe2CoAl along with the TC values obtained from GGA and GGA+U under applied pressures. We have shown that the strong correlation mainly comes from the Fe-3d and Co-d states, and the inclusion of electron–electron interactions within GGA as the GGA+U formalism is essential to describe the electronic properties. The implementation of GGA+U along with compressive pressure (5 < P < 60 GPa) leads to half-metallic behavior with the opening of a spin minority band gap. The predicted integer value of the total magnetic moment in the inverse full-Heusler alloy Fe2CoAl, ∼4.0 μB at 30 GPa, is in accordance with the Slater–Pauling rule, which supports the half-metallicity. The TC calculated from eqn (4) is 747 K at 30 GPa, in good agreement with the results of other Fe-based inverse full-HAs. However, the results from MFA are overestimated.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
D. P. R. acknowledges the Department of Science and Technology New Delhi, Govt of India vide Lett. No. INT/RUS/RFBR/P-264. I. V. M. acknowledges the Russian Foundation for Basic Research (RFBR), Russia, RFBR-17-57-45024. M. P. G. thanks the Alexander von Humboldt Foundation for the equipment subsidy grants. D. P. R. extends condolences to the family of Prof. G. M. Mikhailov, an Indo-Russian project collaborator.
Notes and references
- F. Heusler, W. Starck and E. Haupt, Verh. Dtsch. Phys. Ges., 1903, 5, 220–223 Search PubMed.
- O. Heusler, Ann. Phys., 1934, 411(2), 155 Search PubMed.
- D. C. Price, J. Phys. F: Met. Phys., 1978, 8, 933 Search PubMed.
- J. Kubler, A. R. Williams and C. B. Sommers, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 28, 1745 Search PubMed.
- J. L. Moran-Lapeza, R. Rodriguez-Albab and F. Aguilera-Granja, J. Magn. Magn. Mater., 1994, 131, 417 Search PubMed.
- E. Sasioglu, L. M. Sandratskii, P. Bruno and I. Galanakis, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 184415 Search PubMed.
- J. Thoene, S. Chadov, G. Fecher, C. Felser and J. Kubler, J. Phys. D: Appl. Phys., 2009, 42, 084013 Search PubMed.
- S. Trudel, O. Gaier, J. Hamrle and B. Hillebrands, J. Phys. D: Appl. Phys., 2010, 43, 193001 Search PubMed.
- D. P. Rai, J. Hashemifar and M. Jamal, et al., Indian J. Phys., 2010, 84, 717–721 Search PubMed.
- D. P. Rai, Sandeep and M. P. Ghimire, et al., Bull. Mater. Sci., 2011, 34, 1219–1222 Search PubMed.
- S. Roy, N. Khan, R. Singha, A. Pariari and P. Mandal, Phys. Rev. B, 2019, 99, 214414 Search PubMed.
- I. V. Malikov, L. A. Fomin, V. A. Berezin, A. V. Chernykh, D. P. Rai and G. M. Mikhailov, Ferroelectrics, 2019, 541(1), 79–92 Search PubMed.
- R. A. de Groot, F. M. Mueller, P. G. van Engen and K. H. J. Buschow, Phys. Rev. Lett., 1983, 50, 2024 Search PubMed.
- K. H. J. Buschow and P. G. van Engen, J. Magn. Magn. Mater., 1981, 25, 90–96 Search PubMed.
- H. Kandpal, G. Fecher, C. Felser and G. Schonhense, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 094422 Search PubMed.
- C. Felser, L. Wollmann, S. Chadov, G. Fecher and S. Parkin, APL Mater., 2015, 3, 041518 Search PubMed.
- A. Liechtenstein, M. Katsnelson, V. Antropov and V. Gubanov, J. Magn. Magn. Mater., 1987, 67(1), 65–74 Search PubMed.
- I. Galanakis, E. Sasıoglu and K. Ozdogan, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 064408 Search PubMed.
- X. Q. Chen, R. Podloucky and P. Rogl, J. Appl. Phys., 2006, 100, 113901 Search PubMed.
- A. Bansil, S. Kaprzyk and J. Tobola, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 13396 Search PubMed.
- A. Fert, Thin Solid Films, 2008, 517, 2 Search PubMed.
- L. Xingxing and Y. Jinlong, Natl. Sci. Rev., 2016, 3, 365 Search PubMed.
- I. Galankis, K. Ozdogan and E. Sasioglu, AIP Adv., 2016, 6, 055606 Search PubMed.
- A. Planes, L. Manosa and M. Acet, J. Phys.: Condens. Matter, 2009, 21, 233201 Search PubMed.
- P. Entel, V. D. Buchelnikov, V. V. Khovailo, A. T. Zayak, W. A. Adeagbo, M. E. Gruner, H. C. Herper and E. F. Wassermann, J. Phys. D: Appl. Phys., 2006, 39, 865 Search PubMed.
- S. Wurmehl, G. H. Fecher, H. C. Kandpal, V. Ksenofontov, C. Felser and H.-J. Lin, Appl. Phys. Lett., 2006, 88(3), 032503 Search PubMed.
- L. Bainsla and K. Suresh, Appl. Phys. Lett., 2016, 3, 031101 Search PubMed.
- X. Wang, Z. Cheng, J. Wang, X. Wang and G. Liu, J. Mater. Chem. C, 2016, 4, 7176–7192 Search PubMed.
- T. Graf, C. Felser and S. Parkin, Prog. Solid State Chem., 2011, 39, 1–50 Search PubMed.
- S. Sanvito, C. Oses, J. Xue, A. Tiwari, M. Zic, T. Archer, P. Tozman, M. Venkatesan, M. Coey and S. Curtarolo, Sci. Adv., 2017, 3(4), e1602241 Search PubMed.
- D. Bensaid, T. Hellal, M. Ameri, Y. Azzaz, B. Doumi, Y. Al-Douri, B. Abderrahim and F. Benzoudji, J. Supercond. Novel Magn., 2016, 29, 1843–1850 Search PubMed.
- I. Yahiaoui, A. Lazreg, Z. Dridi, Y. Al-Douri and B. Bouhafs, J. Supercond. Novel Magn., 2017, 30, 421–424 Search PubMed.
- F. Semari, F. Dahmane, N. Baki, Y. Al-Douri, S. Akbudak, G. Ugur, S. Ugur, A. Bouhemadou, R. Khenata and C. H. Voon, Chin. J. Phys., 2018, 56, 567–573 Search PubMed.
- F. Khelfaoui, M. Ameri, D. Bensaid, I. Ameri and Y. Al-Douri, J. Supercond. Novel Magn., 2018, 31, 3183–3192 Search PubMed.
- D. P. Rai, Sandeep, A. Shankar, R. Khenata, A. H. Reshak, C. E. Ekuma, R. K. Thapa and S.-H. Ke, AIP Adv., 2017, 7(4), 045118 Search PubMed.
- D. Wu, Z. Zhe, L. Li, Z. Zhang, H. Zhao, J. Wang, B. Ma and Q. Jin, Sci. Rep., 2015, 5, 12352 Search PubMed.
- L. D. M. Shaughnessy, R. Snow and C. Y. Fong, Phys. Rev. A: At., Mol., Opt. Phys., 2011, 2011, 140805 Search PubMed.
- O. Appel and Y. Gelbstein, J. Electron. Mater., 2014, 43(6), 1976–1982 Search PubMed.
- Y. Gelbstein, J. Electron. Mater., 2011, 40(5), 533–536 Search PubMed.
- Y. Gelbstein, J. Davidow, E. Leshem, O. Pinshow and S. Moisa, Phys. Status Solidi B, 2014, 251(7), 1431–1437 Search PubMed.
- G. M. Guttmann, D. Dadon and Y. Gelbstein, J. Appl. Phys., 2015, 118, 065102 Search PubMed.
- G. Komisarchik, D. Fuks and Y. Gelbstein, J. Appl. Phys., 2016, 120(5), 055104 Search PubMed.
- T. Ouahrani, Eur. Phys. J. B, 2013, 86, 369 Search PubMed.
- M. Marques, G. J. Ackland, L. F. Lundegaard, G. Stinton, R. J. Nelmes, M. I. McMahon and C. J. Garcia, Phys. Rev. Lett., 2009, 103, 115501 Search PubMed.
- S. Ram, M. R. Chauhan, K. Agarwal and V. Kanchana, Philos. Mag. Lett., 2011, 91, 545 Search PubMed.
- M. N. Rasul, A. Javed, M. A. Khan and A. Hussain, Mater. Chem. Phys., 2019, 222, 321–332 Search PubMed.
- A. Amudhavalli, R. Rajeswarapalanichamy and K. Iyakutti, J. Magn. Magn. Mater., 2017, 441, 21–38 Search PubMed.
- A. Amudhavalli, R. Rajeswarapalanichamy and K. Iyakutti, Phase Transitions, 2019, 92, 875–887 Search PubMed.
- P. Rambabu, B. Anuroopa, M. Manivel Raja and V. Kanchana, Solid State Sci., 2020, 105, 106257 Search PubMed.
- E. Sasioglu, L. M. Sandratskii and P. Bruno, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 214412 Search PubMed.
- B. Hamri, B. Abbar, A. Hamri, O. Baraka, A. Hallouche and A. Zaoui, Comput. Condens. Matter, 2015, 3, 14 Search PubMed.
- X. P. Wei, Y. D. Chu, X. W. Sun, J. B. Deng and Y. Z. Xing, J. Supercond. Novel Magn., 2014, 27, 1099 Search PubMed.
- A. Dannenberg, M. Siewert, M. E. Gruner, M. Wuttig and P. Entel, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 214421 Search PubMed.
- T. Gasi, V. Ksenofontov, J. Kiss, S. Chadov, A. K. Nayak, M. Nicklas, J. Winterlik, M. Schwall, P. Klaer, P. Adler and C. Felser, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 064411 Search PubMed.
- L. Siakeng, G. M. Mikhailov and D. P. Rai, J. Mater. Chem. C, 2018, 6, 10341–10349 Search PubMed.
- D. P. Rai, C. E. Ekuma, A. Boochani, S. Solaymani and R. K. Thapa, J. Appl. Phys., 2018, 123, 161509 Search PubMed.
- Y. Feng, B. Wu, H. Yuan, A. Kuang and H. Chen, J. Alloys Compd., 2013, 557, 202–208 Search PubMed.
- A. Ahmad, A. K. Das and S. K. Srivastava, Eur. Phys. J. B, 2020, 93, 96 Search PubMed.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 Search PubMed.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 Search PubMed.
- L. Mikaeilzadeh, A. Tavana and F. Khoeini, Sci. Rep., 2019, 9, 20075 Search PubMed.
- B. Fadila, M. Ameri, D. Bensaid, M. Noureddine, I. Ameri, S. Mesbah and Y. Al-Douri, J. Magn. Magn. Mater., 2018, 448, 208–220 Search PubMed.
- X. H. Kang and J. M. Zhang, J. Phys. Chem. Solids, 2017, 105, 9–15 Search PubMed.
- S. A. Khandy, I. Islam and D. C. Gupta, et al., Sci. Rep., 2019, 9, 1475 Search PubMed.
- K. Nawa and Y. Miura, RSC Adv., 2019, 9, 30462–30478 Search PubMed.
- C. Zhang, H. Huang, C. Wu, Z. Zhu, Z. He and G. Liu, Front. Phys., 2020, 8, 232 Search PubMed.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 Search PubMed.
- D. P. Rai, A. Shankar, Sandeep, L. R. Singh, M. Jamal, S. J. Hashemifar, M. P. Ghimire and R. K. Thapa, Arm. J. Phys., 2012, 5, 105–110 Search PubMed.
- P. Blaha, K. Schwarz, G. Madsen, D. Kvasnicka, J. Luitz, F. Laskowski, F. Tran and L. D. Marks, WIEN2K, An Augmented Plane Wave+Local Orbitals Program for Calculating Crystal Structure, ed. K. Schwarz, Technical University, Wien, Austria, 2018 Search PubMed.
- H. Ebert and J. Minar, Rep. Prog. Phys., 2011, 74(9), 096501 Search PubMed.
- H. Ebert, Fully Relativistic Band Structure Calculations for Magnetic Solids - Formalism and Application, Springer Berlin Heidelberg, Berlin, Heidelberg, 2000, vol. 535, pp. 191–246 Search PubMed.
- Y. I. Matsushita, et al., J. Phys. D: Appl. Phys., 2017, 50, 095002 Search PubMed.
- M. Gilleben, et al., J. Comput. Chem., 2010, 31, 612–619 Search PubMed.
- E. S. Popiel, W. Zarek and M. Tuszynski, Nucleonika, 2004, 49, S49–S52 Search PubMed.
- V. Jain, et al., AIP Conf. Proc., 2013, 1536, 935–936 Search PubMed.
- S. Ghosh and S. Ghosh, Phys. Scr., 2019, 256, 1900039 Search PubMed.
- M. Meinert, M. P. Geisler, J. Schmalhorst, U. Heinzmann, E. Arenholz, W. Hetaba, M. Stöger-Pollach, A. Hütten and G. Reiss, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 085127 Search PubMed.
- K. Endo, H. Matsuda and K. Itoh, J. Phys. Soc. Jpn., 1995, 64, 2329–2332 Search PubMed.
- H. Luo, Z. Zhu, L. Ma, S. Xu, H. Liu, J. Qu, Y. Li and G. Wu, J. Phys. D: Appl. Phys., 2007, 40(22), 7121–7127 Search PubMed.
- N. Arıkan, A. İyigör, A. Candan, Ş. Uğur, Z. Charifi, H. Baaziz and G. Uğur, J. Mater. Sci., 2014, 49(12), 4180–4190 Search PubMed.
- M. Friak, A. Slavik, I. Mihalikova, D. Holec, M. Vsianska, M. Sob, M. Palm and J. Neugebauer, Materials, 2018, 11(9), 1732 Search PubMed.
- F. Dahmane, Y. Mogulkoc, B. Doumi, A. Tadjer, R. Khenata, S. B. Omran, D. P. Rai, G. Murtaza and D. Varshney, J. Magn. Magn. Mater., 2016, 407, 167–174 Search PubMed.
- F. Aguilera-Granja and R. H. Aguilera-del-Toro, Mater. Res. Express, 2019, 6, 106118 Search PubMed.
|
| This journal is © The Royal Society of Chemistry 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Lalrinkimaab,
Lalhriatzualaa,
L. A. Fomin
*a,
Lalrinkimaab,
Lalhriatzualaa,
L. A. Fomin c,
I. V. Malikovc,
Adlane Sayede
c,
I. V. Malikovc,
Adlane Sayede d,
Madhav Prasad Ghimire
d,
Madhav Prasad Ghimire *e,
R. K. Thapab and
Lalthakimi Zadeng
*e,
R. K. Thapab and
Lalthakimi Zadeng b
b
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, respectively. On the other hand, quaternary HAs have an equiatomic stoichiometric ratio of 1
1, respectively. On the other hand, quaternary HAs have an equiatomic stoichiometric ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Herein, we focus on ternary full-HAs. Ternary full-HAs crystallize in two ordered phases: Cu2MnAl-type with space group Fm
1. Herein, we focus on ternary full-HAs. Ternary full-HAs crystallize in two ordered phases: Cu2MnAl-type with space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (225)35,56 and Hg2CuTi-type with the F
m (225)35,56 and Hg2CuTi-type with the F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m (216) space group.57,58 The former is referred to as regular/direct (L21) and the latter is inverse/indirect with XA-structure. The atomic Wyckoff positions for both the XA-phase and the L21-phase of Fe2CoAl are tabulated in Table 1. In the case of ternary inverse full-HAs the electronegativity of the X-atom is less than that of the Y-atom (X = Fe and Y = Co). Thus, our Fe2CoAl system is an inverse full-HA with the electronegativity of the Fe-atom being less than that of the Co-atom. The primitive and conventional unit cells of Fe2CoAl with XA-structure are shown in Fig. 1. To study the electronic and magnetic properties of the inverse full-Heusler alloy Fe2CoAl, we have performed first-principles Density Functional Theory (DFT) calculations.59,60 All electron–electron interactions were considered according to the generalized gradient approximation (GGA) within the Perdew–Burke–Ernzerhof (PBE) parametrization.61 We are aware that GGA is inadequate for treating strongly correlated d-electrons to derive accurate electronic structures. On the other hand, the successful obtainment of accurate electronic properties by using GGA+U has already been reported for many Heusler alloys.62–67 Therefore, we have applied a screened Coulomb interaction along with the conventional GGA (GGA+U or DFT+U) in order to deal with strongly correlated 3d electrons.68 We have adopted U parameters of 3.82 eV for Fe and 3.89 eV for Co according to our previous work.55,69 For computation, we have used the all electron orbital based full potential linearized augmented plane wave (FP-LAPW) basis set formalism as implemented in the WIEN2K package.70 The non-spherical cut off value of angular momentum within the muffin tin (MT) sphere is lmax = 10. RMT × Kmax = 7 where Kmax is the maximum value of the reciprocal lattice vector in the plane wave expansion and RMT is the smallest muffin tin (MT) radius. To model the electronic structure, the first Brillouin zone (BZ) was integrated by taking a 10 × 10 × 10 k-mesh grid within the Monkhorst package. The self-consistency convergence criterion was set to be 0.0001 Ry. The ferromagnetic–antiferromagnetic exchange energy Jij is a key parameter in determining the Curie temperature (TC). A code based on the single-site coherent potential approximation within the Green’s function approach called spin-polarized relativistic Korringa–Kohn–Rostoker (SPR-KKR)71,72 was used for the calculation of TC.
3m (216) space group.57,58 The former is referred to as regular/direct (L21) and the latter is inverse/indirect with XA-structure. The atomic Wyckoff positions for both the XA-phase and the L21-phase of Fe2CoAl are tabulated in Table 1. In the case of ternary inverse full-HAs the electronegativity of the X-atom is less than that of the Y-atom (X = Fe and Y = Co). Thus, our Fe2CoAl system is an inverse full-HA with the electronegativity of the Fe-atom being less than that of the Co-atom. The primitive and conventional unit cells of Fe2CoAl with XA-structure are shown in Fig. 1. To study the electronic and magnetic properties of the inverse full-Heusler alloy Fe2CoAl, we have performed first-principles Density Functional Theory (DFT) calculations.59,60 All electron–electron interactions were considered according to the generalized gradient approximation (GGA) within the Perdew–Burke–Ernzerhof (PBE) parametrization.61 We are aware that GGA is inadequate for treating strongly correlated d-electrons to derive accurate electronic structures. On the other hand, the successful obtainment of accurate electronic properties by using GGA+U has already been reported for many Heusler alloys.62–67 Therefore, we have applied a screened Coulomb interaction along with the conventional GGA (GGA+U or DFT+U) in order to deal with strongly correlated 3d electrons.68 We have adopted U parameters of 3.82 eV for Fe and 3.89 eV for Co according to our previous work.55,69 For computation, we have used the all electron orbital based full potential linearized augmented plane wave (FP-LAPW) basis set formalism as implemented in the WIEN2K package.70 The non-spherical cut off value of angular momentum within the muffin tin (MT) sphere is lmax = 10. RMT × Kmax = 7 where Kmax is the maximum value of the reciprocal lattice vector in the plane wave expansion and RMT is the smallest muffin tin (MT) radius. To model the electronic structure, the first Brillouin zone (BZ) was integrated by taking a 10 × 10 × 10 k-mesh grid within the Monkhorst package. The self-consistency convergence criterion was set to be 0.0001 Ry. The ferromagnetic–antiferromagnetic exchange energy Jij is a key parameter in determining the Curie temperature (TC). A code based on the single-site coherent potential approximation within the Green’s function approach called spin-polarized relativistic Korringa–Kohn–Rostoker (SPR-KKR)71,72 was used for the calculation of TC.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
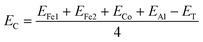
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)