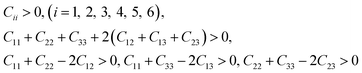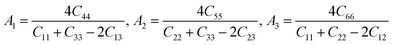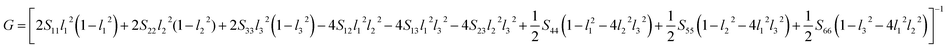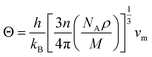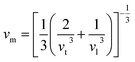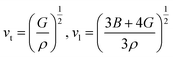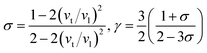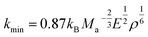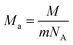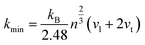DOI:
10.1039/D0RA07633C
(Paper)
RSC Adv., 2020,
10, 37142-37152
Ab initio study of elastic anisotropies and thermal conductivities of rhenium diborides in different crystal structures
Received
6th September 2020
, Accepted 2nd October 2020
First published on 7th October 2020
Abstract
The phase stabilities, elastic anisotropies, and thermal conductivities of ReB2 diborides under ambient conditions have been investigated by using density functional theory calculations. It was found that P63/mmc (hP6-ReB2), Pmmn (oP6-ReB2), R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (hR3-ReB2), R
m (hR3-ReB2), R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (hR6-ReB2), and C2/m (mC12-ReB2) of ReB2 are both mechanically and dynamically stable, and the order of phase stability is hP6 > oP6 > hR3 > hR6 > mC12. Moreover, the calculated Vickers hardness showed that hP6-ReB2, oP6-ReB2, hR3-ReB2, and mC12-ReB2 were potential hard materials, while hR6-ReB2 could not be used as a candidate hard material. In addition, the elastic-dependent anisotropy properties of ReB2 in different crystal structures were also investigated. The results show that the anisotropic order of the Young's modulus and shear modulus of ReB2 is hR6 > mC12 > oP6 > hP6 > hR3, while that of the bulk modulus is mC12 > hR3 > hP6 > oP6 > hR6. Finally, by means of Clarke's and Cahill's models, the minimum thermal conductivities of ReB2 in different crystal structures were further evaluated, and the order of them is hR3 > hP6 > mC12 > oP6 > hR6. Moreover, the results show that all these ReB2 diborides exhibit relatively low thermal conductivities and are suitable for thermal insulation materials.
m (hR6-ReB2), and C2/m (mC12-ReB2) of ReB2 are both mechanically and dynamically stable, and the order of phase stability is hP6 > oP6 > hR3 > hR6 > mC12. Moreover, the calculated Vickers hardness showed that hP6-ReB2, oP6-ReB2, hR3-ReB2, and mC12-ReB2 were potential hard materials, while hR6-ReB2 could not be used as a candidate hard material. In addition, the elastic-dependent anisotropy properties of ReB2 in different crystal structures were also investigated. The results show that the anisotropic order of the Young's modulus and shear modulus of ReB2 is hR6 > mC12 > oP6 > hP6 > hR3, while that of the bulk modulus is mC12 > hR3 > hP6 > oP6 > hR6. Finally, by means of Clarke's and Cahill's models, the minimum thermal conductivities of ReB2 in different crystal structures were further evaluated, and the order of them is hR3 > hP6 > mC12 > oP6 > hR6. Moreover, the results show that all these ReB2 diborides exhibit relatively low thermal conductivities and are suitable for thermal insulation materials.
1 Introduction
Rhenium borides have attracted great attention in recent years1–7 because of their excellent properties such as chemical inertness, high hardness, wear resistance, and electronic conductivity. So far, four binary phases in the system Re–B have been synthesized under environmental conditions, which are Re3B with orthorhombic phase (Cmcm), ReB3 with hexagonal phase (P63/mmc), Re7B3 with hexagonal phase (P63mc), and ReB2 with hexagonal phase (P63/mmc).8–10 Besides, a new monoclinic phase (C2/m) of Re3B was further synthesized under elevated pressure–temperature conditions.11 Meanwhile, other rhenium borides not studied in experiments, such as Re2B, ReB, Re2B3, Re3B7, Re2B5 and ReB4, were also reported theoretically.6,12–15 Among them, ReB2 has attracted the most attention due to its interesting properties and ability to be synthesized through a variety of techniques at atmospheric pressure.1,2,16–18
Due to the superior mechanical properties, ReB2 diborides is a potential hard compound for diverse applications. Therefore, their structural and inner physical properties have been frequently studied theoretically.7,15,19–21 In 2007, Wang et al.19 studied the structural, elastic, and electronic properties of ReB2 by using first-principles calculations. It is found that ReB2 are both elastically stable with the hexagonal phase P63/mmc (hP6-ReB2) and orthorhombic phase Pmmn (oP6-ReB2) under environmental conditions, and the former was more stable than the latter. Moreover, their study showed that ReB2 is potentially superhard material on the basis of its large bulk moduli and large shear to bulk modulus ratios. Meanwhile, Zhao et al.15 studied the phase stability of ReB2 under pressure by using density functional theory and found that hP6-ReB2 is the most stable phase up to 100 GPa. Later, Zhong et al.20 investigated the lattice parameters, total energies and mechanical stability of ReB2 in eight possible crystal structures by performed first-principles calculations. The eight potential ReB2 structures were based on the known transition metal and light element compounds. They found that the ReB2-type (hP6-ReB2) will transition to MoB2-type (hR6-ReB2) of ReB2 at about 272 GPa. Furthermore, Maździarz et al.7 investigated the structural and inner physical properties of ReB2 polymorphs by using density functional theory calculations, which found that P63/mmc (hP6-ReB2), Pmmn (oP6-ReB2) and R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (hR3-ReB2) are both mechanically and dynamically stable at ambient conditions. However, due to previous studies only using some known structures in transition-metal diborides to study the structures stability of ReB2 at ambient conditions and high pressure, the results obtained were not comprehensive. Therefore, we employed the particle swarm optimization (PSO) algorithm to investigate the crystal structure of ReB2 under different pressures,21 and found that hP6-ReB2, oP6-ReB2, hR3-ReB2, hR6-ReB2, and monoclinic phase C2/m (mC12-ReB2) both had relatively low enthalpy at zero pressure, indicating that these phases might be metastable structures of ReB2 at ambient conditions.
m (hR3-ReB2) are both mechanically and dynamically stable at ambient conditions. However, due to previous studies only using some known structures in transition-metal diborides to study the structures stability of ReB2 at ambient conditions and high pressure, the results obtained were not comprehensive. Therefore, we employed the particle swarm optimization (PSO) algorithm to investigate the crystal structure of ReB2 under different pressures,21 and found that hP6-ReB2, oP6-ReB2, hR3-ReB2, hR6-ReB2, and monoclinic phase C2/m (mC12-ReB2) both had relatively low enthalpy at zero pressure, indicating that these phases might be metastable structures of ReB2 at ambient conditions.
As mentioned above, five structures in hP6, oP6, hR3, hR6, and mC12 of ReB2 have been reported at ambient conditions. However, so far, their inner physical properties have not been systematically investigated. Since elastic anisotropy is an important factor affecting the mechanical stability of materials, and thermal conductivity is of great significance for its high temperature application. Therefore, in order to acquire a thorough comprehension about the ReB2 diborides at ambient conditions, we revisit their inner physical properties, especially the elastic anisotropies and thermal conductivity by using first-principles calculations within the density functional theory (DFT) in this work. Our research results are expected to provide beneficial guidance for the experimental and theoretical work of ReB2 diborides in the future.
2 Theoretical method and computation details
Ab initio calculations in the framework of density functional theory (DFT) were carried out with the CASTEP code22,23 with a Perdew–Burke–Ernzerhof (PBE)24 exchange–correlation functional form of the generalized gradient approximation (GGA). The ultrasoft pseudopotential was employed to describe the electron–ion interactions with 5s25p65d56s2 and 2s22p1 treated as valence electrons for Re and B atoms, respectively. The kinetic energy cutoff for the plane-wave basis set was 600 eV, and the Monkhorst–Pack k-point meshes were 16 × 16 × 6 for conventional cells of hP6-ReB2, 8 × 13 × 9 for conventional cells of oP6-ReB2, 16 × 16 × 16 for conventional cells of hR3-ReB2, 16 × 16 × 16 for conventional cells of hR6-ReB2, and 4 × 12 × 17 for conventional cells of mC12-ReB2, respectively. The tolerances for the geometry optimisation are 5 × 10−6 eV per atom for energy and 0.01 eV Å−1 for force. For phonon calculations, the finite displacement method25 was employed within the CASTEP code. The supercell of all ReB2 diborides defined by cutoff radius of 5.0 Å. Moreover, the force calculations were conducted with 10 × 10 × 4, 5 × 9 × 6, 10 × 10 × 10, 11 × 11 × 11, and 3 × 9 × 5 k-meshes for hP6-ReB2, oP6-ReB2, hR3-ReB2, hR6-ReB2, and mC12-ReB2 supercells, respectively. The above calculation parameters were carefully checked to ensure absolute convergence of the total energy.
3 Results and discussion
3.1 Crystal structures and phase stability
The different crystal structures of ReB2 are presented in Fig. 1. Our calculations start with the structural optimization by minimizing the total energy to obtain their equilibrium lattice constants. The calculated ground state results, along with the available experimental3,10 and theoretical data,6,7,20,26,27 are given in Table 1. As shown, our calculated lattice parameters a and c of hP6-ReB2 are within 0.24% and 0.16% of the experimental data of ref. 10, respectively. Moreover, the lattice parameters of other ReB2 structures are also consistent with the previous theoretical data within an acceptable error of ∼1%. This assessment validated the reliability of our calculation method and demonstrated that our parameter setting is accurate enough to be used in subsequent studies.
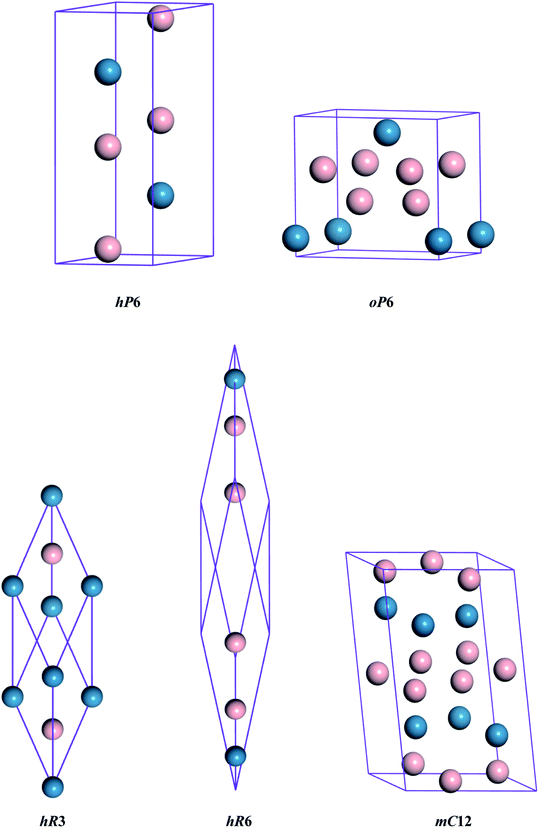 |
| | Fig. 1 Crystal structures of ReB2. The blue and pink spheres represent the Re and B atoms, respectively. | |
Table 1 Calculated lattice parameters, cell volume V0 and formation enthalpies ΔH of ReB2 in different crystal structures, together with the available experimental (exp.) and theoretical (cal.) data
| Space group |
Pearson symbol |
Lattice parameters (Å) |
V0 (Å3) |
ΔH (eV per atom) |
Ref. |
| a |
b |
c |
| P63/mmc |
hP6 |
2.907 |
2.907 |
7.490 |
54.843 |
−1.25 |
This work |
| 2.894 |
2.894 |
7.416 |
53.790 |
−1.34 |
Cal.6 |
| 2.899 |
2.899 |
7.435 |
54.114 |
Cal.7 |
| 2.900 |
2.900 |
7.478 |
54.464 |
Exp.10 |
| 2.897 |
2.897 |
7.472 |
54.308 |
Exp.3 |
| Pmmn |
oP6 |
4.619 |
2.899 |
4.122 |
55.205 |
−1.04 |
This work |
| 4.600 |
2.892 |
4.094 |
54.463 |
Cal.7 |
| 4.582 |
2.869 |
4.077 |
53.595 |
Cal.26 |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
hR3 |
4.112 |
4.112 |
4.112 |
27.580 |
−1.03 |
This work |
| 4.082 |
4.082 |
4.082 |
26.676 |
Cal.7 |
| 4.126 |
4.126 |
4.126 |
28.110 |
Cal.27 |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
hR6 |
7.244 |
7.244 |
7.244 |
53.724 |
−0.35 |
This work |
| 7.251 |
7.251 |
7.251 |
54.359 |
Cal.27 |
| 7.173 |
7.173 |
7.173 |
52.083 |
Cal.20 |
| C2/m |
mC12 |
7.850 |
2.889 |
4.903 |
110.005 |
−0.28 |
This work |
In order to evaluate the relative stability of different ReB2 structures, the dynamic stability is first checked. The calculated phonon dispersion curves of them at 0 GPa are shown in Fig. 2. As shown, all five ReB2 diborides have no imaginary phonon frequency, indicating that they are dynamically stable under environmental pressure. In addition, the formation enthalpies are further evaluated using α phase of boron and cubic phase (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) of rhenium as the reference structures by the equation: ΔH = H (ReB2) − H (Re) − 2H (B). As shown in Table 1, the obtained formation enthalpies of hP6-ReB2, oP6-ReB2, hR3-ReB2, hR6-ReB2, and mC12-ReB2 are all negative. Among them, hP6-ReB2 possesses the smallest formation enthalpy (−1.25 eV f.u.−1) and is the most energetically stable ReB2, which is consistent with the previous experimental1,10 and theoretical7,15,26,28 results. After it, the formation enthalpy of oP6-ReB2, hR3-ReB2, and hR6-ReB2 are −1.04, −1.03, and −0.35 eV f.u.−1, respectively. Meanwhile, mC12-ReB2 shows the largest formation enthalpy (−0.28 eV f.u.−1), indicating that its stability is the weakest. Therefore, the phase stability order of ReB2 should be hP6 > oP6 > hR3 > hR6 > mC12.
m) of rhenium as the reference structures by the equation: ΔH = H (ReB2) − H (Re) − 2H (B). As shown in Table 1, the obtained formation enthalpies of hP6-ReB2, oP6-ReB2, hR3-ReB2, hR6-ReB2, and mC12-ReB2 are all negative. Among them, hP6-ReB2 possesses the smallest formation enthalpy (−1.25 eV f.u.−1) and is the most energetically stable ReB2, which is consistent with the previous experimental1,10 and theoretical7,15,26,28 results. After it, the formation enthalpy of oP6-ReB2, hR3-ReB2, and hR6-ReB2 are −1.04, −1.03, and −0.35 eV f.u.−1, respectively. Meanwhile, mC12-ReB2 shows the largest formation enthalpy (−0.28 eV f.u.−1), indicating that its stability is the weakest. Therefore, the phase stability order of ReB2 should be hP6 > oP6 > hR3 > hR6 > mC12.
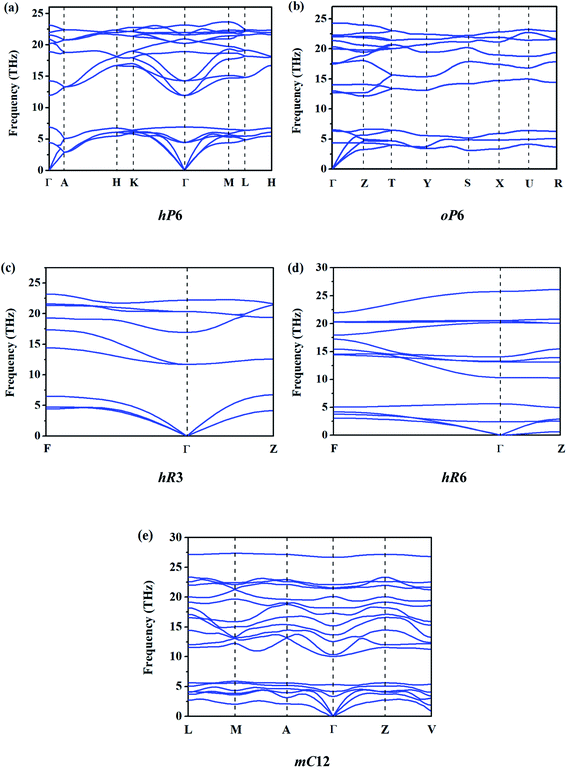 |
| | Fig. 2 Calculated phonon dispersion curves of ReB2 in different crystal structures. | |
3.2 Mechanical properties
3.2.1 Elastic constants and Vickers hardness. Since the elastic constants can be used to judge the mechanical stiffness and stability of materials, we further studied the elastic properties of ReB2 in different crystal structures by using the strain–stress method. The calculated elastic constants, along with the available theoretical data,7,19,20,26,29 are given in Table 2. It is obvious that our obtained elastic constants of different ReB2 structures are in agreement with the other theoretical results. Moreover, for hexagonal structure of hP6-ReB2, its mechanical stability criteria is:| |
|
C44 > 0, C11 − |C12| > 0, (C11 + C12)C33 − 2C132 > 0
| (1) |
Table 2 Calculated elastic constants Cij (in GPa) and Vickers hardness HV (in GPa) of ReB2 in different crystal structures, together with the available theoretical data
| Phase |
C11 |
C12 |
C13 |
C22 |
C23 |
C33 |
C44 |
C55 |
C66 |
HV |
Ref. |
| hP6-ReB2 |
629 |
161 |
124 |
|
|
1011 |
266 |
|
234 |
38.3 |
This work |
| 671 |
147 |
137 |
|
|
1040 |
274 |
|
262 |
40.6 |
Cal.7 |
| 668 |
137 |
147 |
|
|
1063 |
273 |
|
266 |
|
Cal.29 |
| 643 |
159 |
129 |
|
|
1035 |
263 |
|
244 |
|
Cal.19 |
| oP6-ReB2 |
598 |
188 |
162 |
618 |
101 |
895 |
206 |
307 |
255 |
35.5 |
This work |
| 569 |
226 |
173 |
585 |
108 |
923 |
211 |
333 |
248 |
33.3 |
Cal.7 |
| 595 |
208 |
173 |
606 |
100 |
931 |
221 |
331 |
282 |
29.3 |
Cal.26 |
| hR3-ReB2 |
635 |
144 |
164 |
|
|
950 |
285 |
|
245 |
39.3 |
This work |
| 649 |
138 |
147 |
|
|
997 |
298 |
|
256 |
41.7 |
Cal.7 |
| hR6-ReB2 |
599 |
173 |
226 |
|
|
612 |
69 |
|
213 |
6.7 |
This work |
| 630 |
160 |
214 |
|
|
668 |
81 |
|
235 |
|
Cal.20 |
| mC12-ReB2 |
955 |
130 |
149 |
629 |
108 |
608 |
207 |
263 |
280 |
38.5 |
This work |
The mechanical stability criteria for orthorhombic phase of oP6-ReB2 is:
| |
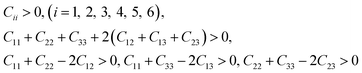 | (2) |
For rhombohedral crystals of hR3-ReB2 and hR6-ReB2, their mechanical stability can be judged from:
| |
|
C11 − |C12| > 0, (C11 + C12)C33 − 2C132 > 0, (C11 − C12)C44 − 2C142 > 0
| (3) |
For monoclinic phase of mC12-ReB2, the mechanical stability criteria is:
| |
 | (4) |
As shown in Table 2, our calculated elastic constants of these ReB2 structures all satisfy the corresponding criteria of mechanical stability, indicating that they are mechanically stable. In addition, we can found that the C33 values of hP6-ReB2, oP6-ReB2, hR3-ReB2, and hR6-ReB2 are both greater than C11 and C22, indicating that their c axis is stiffer than a and b axis. As for mC12-ReB2, it is very in-compressible along the a axis because its C11 is much bigger than C22 and C33.
Furthermore, it is worth noting that our calculated C33 of hP6-ReB2, oP6-ReB2, and hR3-ReB2 are 1011, 895, and 950 GPa, respectively. This is comparable to the C11 value (∼1079 GPa) of diamond,30 suggesting that these ReB2 diborides may also be potential hard materials. To evaluate the hardness of ReB2 in different crystal structures, the empirical model proposed by Chen et al.31 is employed in present work. This model has been successfully applied to a wide range of material systems32–35 and it can be expressed as
| |
|
HV = 2(k2G)0.585 − 3; k = G/B
| (5) |
where G and B is the shear modulus and bulk modulus respectively, which can be deduced from the Voigt–Reuss–Hill approximation36 by the elastic constants Cij. The calculated Vickers hardness HV, along with the available theoretical data,7,26 are also given in Table 2. As shown, our calculated Vickers hardness of hP6-ReB2, oP6-ReB2, hR3-ReB2, hR6-ReB2, and mC12-ReB2 is 38.3, 35.5, 39.3, 8.5, and 38.5 GPa, respectively, which is consistent with the other theoretical results. Moreover, our results showed that hP6-ReB2, oP6-ReB2, hR3-ReB2, and mC12-ReB2 are both potential hard materials, where hR6-ReB2 can not be used as candidate hard materials. From the above, the hardness order of ReB2 is hR3 > mC12 > hP6 > oP6 > hR6.
3.2.2 Anisotropic properties. As shown in Table 2, there is a relationship of C11 = C22 ≠ C33 for hP6-ReB2, hR3-ReB2, and hR6-ReB2, while that for oP6-ReB2 and mC12-ReB2 is C11 ≠ C22 ≠ C33, indicating that the elastic constants of these ReB2 diborides are anisotropic. Since the anisotropy of elastic constants will result in different mechanical properties of materials in different directions, it is of great significance to fully describe such anisotropic behavior for understanding the mechanical properties of materials. To do so, we can use the elastic anisotropic index (AU),37 as well as the percentages of compression anisotropy (Acomp) and shear anisotropy (Ashear),38 to describe the elastic anisotropy of solid. For elastic isotropic crystals, the values of AU, Acomp and Ashear are equal to zero. Other values suggest the elastic anisotropy degree of the crystal. In Table 3, the calculated anisotropy indices AU, Acomp, and Ashear of ReB2 in different crystal structures are listed. As shown, our calculated AU of hP6-ReB2 is 0.23, which is consistent with the theoretical assessment of 0.27 in ref. 39. Moreover, the results show that hR6-ReB2 (AU ∼ 3.33) has the highest elastic anisotropy and hR3-ReB2 (AU ∼ 0.20) possesses the lowest elastic anisotropy. Thus, the order of elastic anisotropy of ReB2 should be hR6 > mC12 > oP6 > hP6 > hR3. This order can also be reflected by Ashear values. In addition, the calculated maximum value (∼2.25%) and minimum value (∼0.13%) of Acomp belongs to mC12-ReB2 and hR6-ReB2, respectively, which means that mC12-ReB2 has the highest compression anisotropy, while hR6-ReB2 has the lowest compression anisotropy. Therefore, the order of compression anisotropy of ReB2 is mC12 > hR3 > hP6 > oP6 > hR6.
Table 3 Calculated elastic anisotropic indexes (AU, Acomp, Ashear, A1, A2 and A3) of ReB2 in different crystal structures, together with the available theoretical data
| Phase |
AU |
Acomp (%) |
Ashear (%) |
A1 |
A2 |
A3 |
Ref. |
| hP6-ReB2 |
0.23 |
1.69 |
1.93 |
0.76 |
0.76 |
1.00 |
This work |
| 0.27 |
|
|
0.74 |
0.74 |
1.00 |
Cal.39 |
| oP6-ReB2 |
0.25 |
0.88 |
2.28 |
0.70 |
0.94 |
1.21 |
This work |
| hR3-ReB2 |
0.20 |
1.78 |
1.62 |
0.91 |
0.91 |
1.00 |
This work |
| hR6-ReB2 |
3.33 |
0.13 |
24.99 |
0.36 |
0.36 |
1.00 |
This work |
| mC12-ReB2 |
0.27 |
2.25 |
2.17 |
0.65 |
1.03 |
0.85 |
This work |
Besides, the elastic anisotropy can also be weighted by shear anisotropic factors. The anisotropic factor A1 in the (100) plane between [011] and [010] directions, A2 in the (010) plane between [101] and [001] directions, and A3 in the (001) plane between [110] and [010] directions can be expressed as40
| |
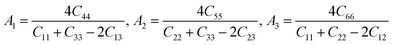 | (6) |
For isotropic crystals, the shear anisotropy factors A1, A2, and A3 are always equal to 1. A deviation indicates the anisotropy of the crystal. The calculated A1, A2, and A3 of different ReB2 structures are also presented in Table 3. As shown, our calculated A1, A2, and A3 of hP6-ReB2 are 0.76, 0.76, and 1.00, respectively, which are in good agreement with the other theoretical values.39 Moreover, the calculated A1 and A2 of hR6-ReB2 deviate more significantly from 1, indicating that it shows the highest shear anisotropy in the (100) and (010) planes. Further, it can be seen that the calculated A3 of hP6-ReB2, hR3-ReB2, and hR6-ReB2 is equal to 1, which means that these three ReB2 structures are both shear isotropy in the (001) plane. Meanwhile, the absolute value of (A3 − 1) for oP6-ReB2 is larger than that for mC12-ReB2, suggesting that oP6-ReB2 has higher shear anisotropy in the (001) plane.
Another better method to study the mechanical anisotropy of materials is to use the directional bulk modulus B, Young's modulus E, and shear modulus G. These three direction-dependent quantities can be expressed as41,42
| |
|
B = [(S11 + S12 + S13)l12 + (S12 + S22 + S23)l22 + (S13 + S23 + S33)l32]−1
| (7) |
| |
|
E = (l14S11 + 2l12l22S12 + 2l12l32S13 + l24S22 + 2l22l32S23 + l34S33 + l22l32S44 + l12l32S55 + l12l22S66)−1
| (8) |
| |
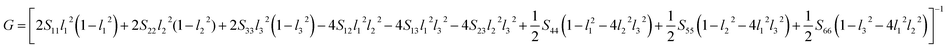 | (9) |
The above three formulas can be used for any crystal system, where l1, l2, and l3 are the direction cosines, and Sij are the elements in the compliance tensor. The directional bulk modulus, Young's modulus, and shear modulus of ReB2 in different crystal structures are plotted in Fig. 3–5, respectively. As shown in Fig. 3, the bulk modulus of different ReB2 structures in three-dimensional diagrams are not spherical, indicating that their bulk modulus are all anisotropic. According to the deviation degree from the sphere, we can know that mC12-ReB2 and hR6-ReB2 exhibit the largest and least anisotropic of bulk modulus, respectively, which is consistent with our above analysis on Acomp. As for Young's modulus (see Fig. 4) and shear modulus (see Fig. 5), the hR6-ReB2 shows the most remarkable anisotropic nature, followed by mC12-ReB2, oP6-ReB2, and hP6-ReB2, and the last for hR3-ReB2. Therefore, the anisotropic order of Young's modulus and shear modulus of ReB2 is hR6 > mC12 > oP6 > hP6 > hR3, which is in good agreement with the results of AU and Ashear.
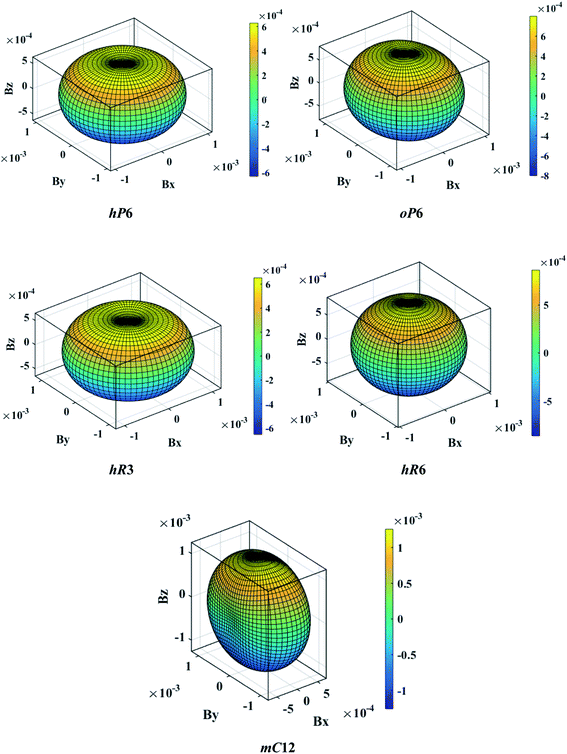 |
| | Fig. 3 The direction-dependent bulk modulus of ReB2 in different crystal structures. | |
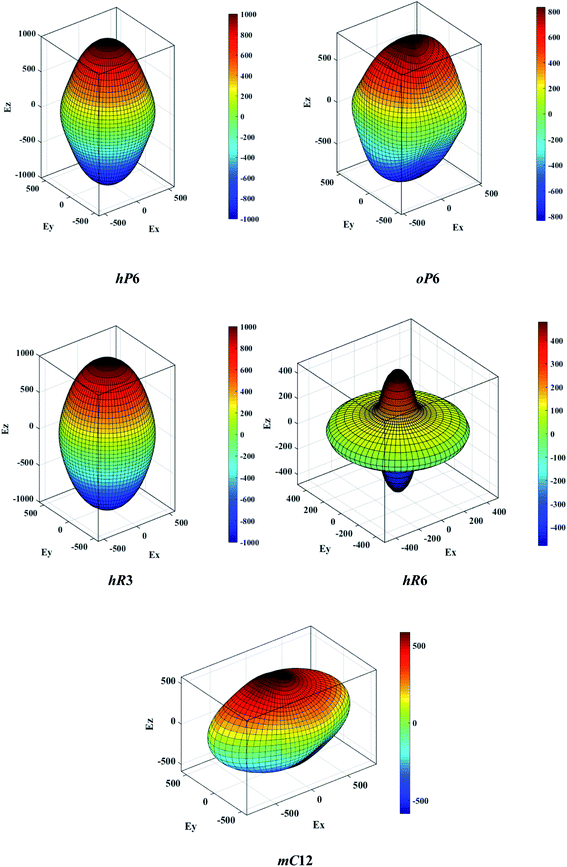 |
| | Fig. 4 The direction-dependent Young's modulus of ReB2 in different crystal structures. | |
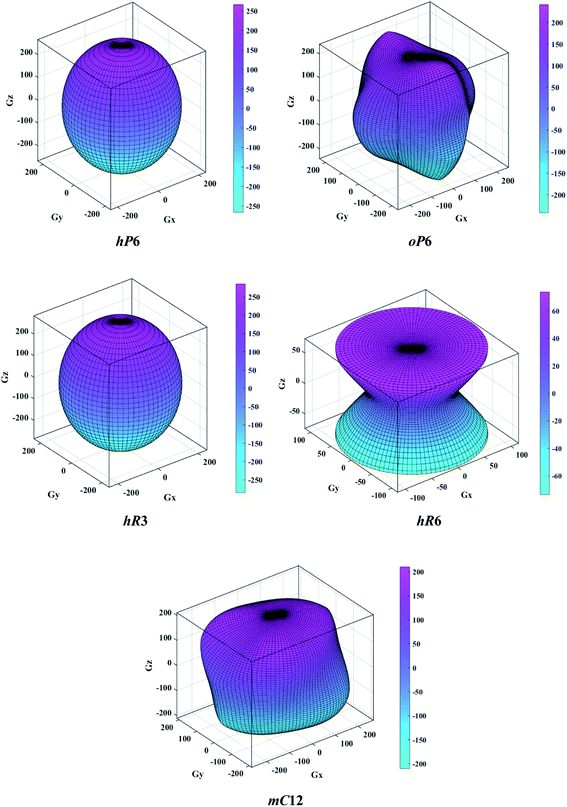 |
| | Fig. 5 The direction-dependent shear modulus of ReB2 in different crystal structures. | |
3.3 Debye temperatures and thermal conductivities
Debye temperature is an important fundamental parameter that is closely related to the specific heat and melting temperature of solid, and it can be deduced from the following formula43| |
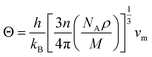 | (10) |
where h is the Planck constant, kB is the Boltzmann constant, NA is the Avogadro number, n is the number of atoms per formula unit, M is the molecular mass per formula unit, ρ is the density, vm is the average sound velocity and it can be obtained from| |
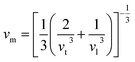 | (11) |
According to Navier's equations,44 the transverse sound velocity vt and longitudinal sound velocity vl can be estimated by
| |
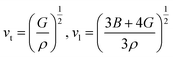 | (12) |
Then, Poisson ratio σ and Grüneisen parameter γ can be calculated as follows:45,46
| |
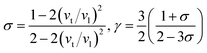 | (13) |
The calculated sound velocities vt, vl and vm, Debye temperature Θ, Poisson's ratio σ, and Grüneisen parameter γ of different ReB2 structures are given in Table 4. As shown, hR3-ReB2 have the largest average sound velocity vm and Debye temperature Θ, followed by hP6-ReB2, mC12-ReB2, and oP6-ReB2, and the smallest for hR6-ReB2. Usually, a higher Debye temperature implies a larger thermal conductivity. Therefore, hR3-ReB2 should has the highest thermal conductivity, while hR6-ReB2 possesses the lowest thermal conductivity. Moreover, it is well known that the higher the Debye temperature, the greater the microhardness of the material. Therefore, the order of microhardness of ReB2 should be hR3 > hP6 > mC12 > oP6 > hR6. In addition, Poisson's ratio σ can be used as a criterion for ductility/brittleness. As shown in Table 4, our calculated Poisson's ratios of hP6-ReB2, oP6-ReB2, hR3-ReB2, and mC12-ReB2 are both less than 0.26, which means that they are brittle in nature. Meanwhile, the σ value of hR6-ReB2 is larger than the critical value, implying its ductile nature. Furthermore, it is known that a large Grüneisen parameter usually reflects a strong crystal anharmonicity. Therefore, the order of crystal anharmonicity of ReB2 should be hR6 > oP6 > hR3 > hP6 > mC12.
Table 4 The density ρ, transverse sound velocity vt, longitudinal sound velocity vl, average sound velocity vm, Debye temperature Θ, Poisson's ratio σ, and Grüneisen parameter γ of ReB2 in different crystal structures
| Phase |
ρ (g cm−3) |
vt (km s−1) |
vl (km s−1) |
vm (km s−1) |
Θ (K) |
σ |
γ |
| hP6-ReB2 |
12.58 |
3.29 |
5.28 |
3.62 |
515.78 |
0.182 |
1.22 |
| oP6-ReB2 |
12.50 |
3.21 |
5.20 |
3.55 |
503.72 |
0.191 |
1.25 |
| hR3-ReB2 |
12.51 |
3.33 |
5.34 |
3.66 |
520.80 |
0.185 |
1.23 |
| hR6-ReB2 |
12.85 |
2.26 |
4.48 |
2.55 |
363.70 |
0.342 |
2.07 |
| mC12-ReB2 |
12.55 |
3.25 |
5.19 |
3.58 |
508.72 |
0.178 |
1.20 |
In addition, the minimum thermal conductivities of these ReB2 diborides are further studied in present work, which is of great significance for their high-temperature application. Two theoretical models proposed by Clarke47,48 and Cahill49 are used to estimate the minimum thermal conductivities of ReB2 in different crystal structures. The Clarke's model follows Debye approach, assuming that the free path of phonon is equal to the interatomic spacing, which can be expressed as:
| |
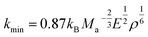 | (14) |
| |
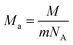 | (15) |
where
kB is the Boltzmann's constant,
Ma is the average mass per atom in the unit cell,
E is the Young's modulus,
ρ is the density,
M is the molar mass,
m is the total number of atoms per unit cell, and
NA is the Avogadro's number. Meanwhile, the Cahill's model is mainly based on the Einstein's model, and it can be expressed as:
| |
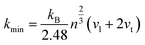 | (16) |
where
n is the density of the number of atoms per unit volume,
vl and
vt are the longitudinal and transverse sound velocities, respectively. The calculated minimum thermal conductivities of the different ReB
2 structures are given in
Table 5. As shown, the calculated value of
kClarkemin is always slightly less than that of
kCahillmin at a given pressure, which is mainly because Clarke's model does not consider the contributions of optical phonon modes to thermal conductivity. Moreover, it is evident that hR3-ReB
2 had the highest minimum thermal conductivities form both Clarke's and Cahill's model, followed by hP6-ReB
2, mC12-ReB
2, and oP6-ReB
2, while hR6-ReB
2 possessed the lowest minimum thermal conductivities. Therefore, the order of minimum thermal conductivities of ReB
2 is hR3 > hP6 > mC12 > oP6 > hR6, which is in agreement with the results of Debye temperature. Furthermore, our calculations show that these five ReB
2 diborides exhibit relatively low thermal conductivities and are suitable for thermal insulation materials.
Table 5 Calculated minimum thermal conductivities kmin (W m−1 K−1) of ReB2 in different crystal structures
| Phase |
Clarke model |
Cahill model |
| Ma(10−25) |
kmin |
n(1029) |
kmin |
| hP6-ReB2 |
1.150 |
1.389 |
1.094 |
1.509 |
| oP6-ReB2 |
1.150 |
1.357 |
1.087 |
1.475 |
| hR3-ReB2 |
1.150 |
1.480 |
1.088 |
1.521 |
| hR6-ReB2 |
1.150 |
1.027 |
1.117 |
1.162 |
| mC12-ReB2 |
1.150 |
1.367 |
1.091 |
1.484 |
4 Conclusions
In conclusion, we have systemically investigated the phase stabilities, elastic anisotropies, and thermal conductivities of ReB2 in five crystal structures by first-principles calculations. Our calculated lattice parameters a, c and cell volume V0 are consistent well with other available experimental and theoretical data. The calculation of elastic constants and phonon dispersion curves shows that these five ReB2 structures are both mechanically and dynamically stable at ambient conditions. According to the calculated formation enthalpies, the order of phase stability of ReB2 is hP6 > oP6 > hR3 > hR6 > mC12. Moreover, our calculation shows that the hardnesses of hP6-ReB2, oP6-ReB2, hR3-ReB2, and mC12-ReB2 are 38.3, 35.5, 39.3, and 38.5 GPa, respectively, indicating that they are potential hard materials. In addition, all the five ReB2 structures exhibit elastic anisotropy, and the anisotropic order of Young's modulus and shear modulus should be hR6 > mC12 > oP6 > hP6 > hR3, while that of bulk modulus is mC12 > hR3 > hP6 > oP6 > hR6. Finally, the minimum thermal conductivities of the five ReB2 structures are further evaluated, and the order of them is hR3 > hP6 > mC12 > oP6 > hR6. Moreover, the results show that these five ReB2 diborides all exhibit relatively low thermal conductivities and are suitable for thermal insulation materials.
Conflicts of interest
There are no conflicts of interest to declare.
Acknowledgements
This work was supported by the National Natural Science Foundation of China under Grant No. 11904282 and 11747110, and the Doctoral Scientific Research Foundation of Xi'an University of Science and Technology under Grant No. 2018QDJ029, and the Science and Technology Tackling Project of the Education Department of Henan Province under Grant No. 172102210072.
References
- H. Y. Chung, M. B. Weinberger, J. B. Levine, A. Kavner, J. M. Yang, S. H. Tolbert and R. B. Kaner, Science, 2007, 316, 436–439 CrossRef CAS.
- N. Dubrovinskaia, L. Dubrovinsky and V. L. Solozhenko, Science, 2007, 318, 1550 CrossRef.
- J. B. Levine, S. L. Nguyen, H. I. Rasool, J. A. Wright, S. E. Brown and R. B. Kaner, J. Am. Chem. Soc., 2008, 130, 16953–16958 CrossRef CAS.
- C. S. Lue, Y. F. Tao and T. H. Su, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 033107 CrossRef.
- X. Q. Chen, C. L. Fu, M. Krcmar and G. S. Painter, Phys. Rev. Lett., 2008, 100, 196403 CrossRef.
- H. Y. Gou, Z. B. Wang, J. W. Zhang, S. T. Yan and F. M. Gao, Inorg. Chem., 2009, 48, 581–587 CrossRef CAS.
- M. Maździarz and T. Mościcki, J. Alloys Compd., 2016, 657, 878–888 CrossRef.
- B. Aronsson, E. Stenberg and J. Aselius, Acta Chem. Scand., 1960, 14, 733–741 CrossRef CAS.
- B. Aronsson, M. Backman and S. Rundqvist, Acta Chem. Scand., 1960, 14, 1001 CrossRef CAS.
- S. J. La Placa and B. Post, Acta Crystallogr., 1962, 15, 97–99 CrossRef CAS.
- A. Tyutyunnik, T. Dyachkova, Y. Zaynulin and S. Gromilov, J. Struct. Chem., 2014, 55, 84–88 CrossRef CAS.
- M. Wang, Y. Li, T. Cui, Y. Ma and G. Zou, Appl. Phys. Lett., 2008, 93, 101905 CrossRef.
- G. Soto, M. G. Moreno-Armenta and A. Reyes-Serrato, Comput. Mater. Sci., 2008, 44, 628–634 CrossRef CAS.
- E. J. Zhao, J. P. Wang, J. Meng and Z. J. Wu, J. Solid State Chem., 2009, 182, 960–965 CrossRef CAS.
- E. Zhao, J. P. Wang, J. Meng and Z. J. Wu, J. Comput. Chem., 2010, 31, 1904–1910 CAS.
- S. Otani, T. Aizawa and Y. Ishizawa, J. Alloys Compd., 1997, 252, 19–21 CrossRef.
- M. Frotscher, M. Holzel and B. Albert, Z. Anorg. Allg. Chem., 2010, 636, 1783–1786 CrossRef CAS.
- S. Guo, J. Eur. Ceram. Soc., 2014, 34, 4443–4449 CrossRef CAS.
- Y. X. Wang, Appl. Phys. Lett., 2007, 91, 101904 CrossRef.
- M. M. Zhong, X. Y. Kuang, Z. H. Wang, P. Shao, L. P. Ding and X. F. Huang, J. Alloys Compd., 2013, 581, 206–212 CrossRef CAS.
- Y. X. Wang, Z. X. Yan, W. Liu and G. L. Zhou, J. Appl. Phys., 2019, 126, 135901 CrossRef.
- M. C. Payne, M. P. Teter, D. C. Allen, T. A. Arias and J. D. Joannopoulos, Rev. Mod. Phys., 1992, 64, 1045 CrossRef CAS.
- V. Milman, B. Winkler, J. A. White, C. J. Packard, M. C. Payne, E. V. Akhmatskaya and R. H. Nobes, Int. J. Quant. Chem., 2000, 77, 895–910 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- K. Parlinski, Z. Q. Li and Y. Kawazoe, Phys. Rev. Lett., 1997, 78, 4063 CrossRef CAS.
- M. M. Zhong, X. Y. Kuang, Z. H. Wang, P. Shao, L. P. Ding and X. F. Huang, J. Phys. Chem. C, 2013, 117, 10643–10652 CrossRef CAS.
- R. F. Zhang, D. Legut, R. Niewa, A. S. Argon and S. Veprek, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 104104 CrossRef.
- Y. C. Liang and B. Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 132101 CrossRef.
- X. F. Hao, Y. H. Xu, Z. J. Wu, D. F. Zhou, X. J. Liu, X. Q. Cao and J. Meng, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 224112 CrossRef.
- H. J. McSkimin, P. Andreatch and P. Glynn, J. Appl. Phys., 1972, 43, 985–987 CrossRef CAS.
- X. Chen, H. Niu, D. Li and Y. Li, Intermetallics, 2011, 19, 1275–1281 CrossRef CAS.
- A. Misra and W. Y. Ching, Sci. Rep., 2013, 3, 1488 CrossRef.
- X. Chen, H. Niu, C. Franchini, D. Li and Y. Li, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 121405 CrossRef.
- Y. Liang, Y. Gou, X. Yuan, Z. Zhong and W. Zhang, Chem. Phys. Lett., 2013, 580, 48–52 CrossRef CAS.
- H. Y. Zhang, F. Xi, Z. Y. Zeng, X. R. Chen and L. C. Cai, J. Phys. Chem. C, 2017, 121, 7397–7403 CrossRef CAS.
- G. V. Sin’ko and N. A. Smirnov, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 214108 CrossRef.
- S. I. Ranganathan and M. Ostoja-Starzewski, Phys. Rev. Lett., 2008, 101, 055504 CrossRef.
- F. W. Vahldiek and S. A. Mersol, Anisotropy in Single-Crystal Refractory Compound, Springer, US, 1968 Search PubMed.
- M. Marín-Suárez, M. E. Vélez, J. David and M. Arroyave-Franco, Comput. Mater. Sci., 2016, 122, 240–248 CrossRef.
- P. Ravindran, L. Fast, P. A. Korzhavyi, B. Johansson, J. Wills and O. Eriksson, J. Appl. Phys., 1998, 84, 4891–4904 CrossRef CAS.
- J. F. Nye, Physical Properties of Crystals: Their Representation by Tensors and Matrices, Clarendon Press, Oxford, 1985 Search PubMed.
- R. F. S. Hearmon and A. A. Maradudin, Phys. Today, 1961, 14, 48 CrossRef.
- O. L. Anderson, J. Phys. Chem. Solids, 1963, 24, 909–917 CrossRef CAS.
- K. B. Panda and K. S. Ravi Chandran, Comput. Mater. Sci., 2006, 35, 134–150 CrossRef CAS.
- Y. L. Pei, J. Q. He, J. F. Li, F. Li, Q. J. Liu, W. Pan, C. Barreteau, D. Berardan, N. Dragoe and L. D. Zhao, NPG Asia Mater., 2013, 5, 47 CrossRef.
- Y. Xiao, C. Chang, Y. L. Pei, D. Wu, K. L. Peng, X. Y. Zhou, S. K. Gong, J. Q. He, Y. S. Zhang, Z. Zeng and L. D. Zhao, Phys. Rev. B, 2016, 94, 125203 CrossRef.
- D. R. Clarke, Surf. Coating. Technol., 2003, 163, 67–74 CrossRef.
- D. R. Clarke and C. G. Levi, Annu. Rev. Mater. Res., 2003, 33, 383–417 CrossRef CAS.
- D. G. Cahill, S. K. Watson and R. O. Pohl, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6131 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Ying Y. Liua,
Zheng X. Yana,
W. Liua and
Jian B. Gub
*a,
Ying Y. Liua,
Zheng X. Yana,
W. Liua and
Jian B. Gub
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (hR3-ReB2), R
m (hR3-ReB2), R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (hR6-ReB2), and C2/m (mC12-ReB2) of ReB2 are both mechanically and dynamically stable, and the order of phase stability is hP6 > oP6 > hR3 > hR6 > mC12. Moreover, the calculated Vickers hardness showed that hP6-ReB2, oP6-ReB2, hR3-ReB2, and mC12-ReB2 were potential hard materials, while hR6-ReB2 could not be used as a candidate hard material. In addition, the elastic-dependent anisotropy properties of ReB2 in different crystal structures were also investigated. The results show that the anisotropic order of the Young's modulus and shear modulus of ReB2 is hR6 > mC12 > oP6 > hP6 > hR3, while that of the bulk modulus is mC12 > hR3 > hP6 > oP6 > hR6. Finally, by means of Clarke's and Cahill's models, the minimum thermal conductivities of ReB2 in different crystal structures were further evaluated, and the order of them is hR3 > hP6 > mC12 > oP6 > hR6. Moreover, the results show that all these ReB2 diborides exhibit relatively low thermal conductivities and are suitable for thermal insulation materials.
m (hR6-ReB2), and C2/m (mC12-ReB2) of ReB2 are both mechanically and dynamically stable, and the order of phase stability is hP6 > oP6 > hR3 > hR6 > mC12. Moreover, the calculated Vickers hardness showed that hP6-ReB2, oP6-ReB2, hR3-ReB2, and mC12-ReB2 were potential hard materials, while hR6-ReB2 could not be used as a candidate hard material. In addition, the elastic-dependent anisotropy properties of ReB2 in different crystal structures were also investigated. The results show that the anisotropic order of the Young's modulus and shear modulus of ReB2 is hR6 > mC12 > oP6 > hP6 > hR3, while that of the bulk modulus is mC12 > hR3 > hP6 > oP6 > hR6. Finally, by means of Clarke's and Cahill's models, the minimum thermal conductivities of ReB2 in different crystal structures were further evaluated, and the order of them is hR3 > hP6 > mC12 > oP6 > hR6. Moreover, the results show that all these ReB2 diborides exhibit relatively low thermal conductivities and are suitable for thermal insulation materials.![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (hR3-ReB2) are both mechanically and dynamically stable at ambient conditions. However, due to previous studies only using some known structures in transition-metal diborides to study the structures stability of ReB2 at ambient conditions and high pressure, the results obtained were not comprehensive. Therefore, we employed the particle swarm optimization (PSO) algorithm to investigate the crystal structure of ReB2 under different pressures,21 and found that hP6-ReB2, oP6-ReB2, hR3-ReB2, hR6-ReB2, and monoclinic phase C2/m (mC12-ReB2) both had relatively low enthalpy at zero pressure, indicating that these phases might be metastable structures of ReB2 at ambient conditions.
m (hR3-ReB2) are both mechanically and dynamically stable at ambient conditions. However, due to previous studies only using some known structures in transition-metal diborides to study the structures stability of ReB2 at ambient conditions and high pressure, the results obtained were not comprehensive. Therefore, we employed the particle swarm optimization (PSO) algorithm to investigate the crystal structure of ReB2 under different pressures,21 and found that hP6-ReB2, oP6-ReB2, hR3-ReB2, hR6-ReB2, and monoclinic phase C2/m (mC12-ReB2) both had relatively low enthalpy at zero pressure, indicating that these phases might be metastable structures of ReB2 at ambient conditions.
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m
m![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m
m![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) of rhenium as the reference structures by the equation: ΔH = H (ReB2) − H (Re) − 2H (B). As shown in Table 1, the obtained formation enthalpies of hP6-ReB2, oP6-ReB2, hR3-ReB2, hR6-ReB2, and mC12-ReB2 are all negative. Among them, hP6-ReB2 possesses the smallest formation enthalpy (−1.25 eV f.u.−1) and is the most energetically stable ReB2, which is consistent with the previous experimental1,10 and theoretical7,15,26,28 results. After it, the formation enthalpy of oP6-ReB2, hR3-ReB2, and hR6-ReB2 are −1.04, −1.03, and −0.35 eV f.u.−1, respectively. Meanwhile, mC12-ReB2 shows the largest formation enthalpy (−0.28 eV f.u.−1), indicating that its stability is the weakest. Therefore, the phase stability order of ReB2 should be hP6 > oP6 > hR3 > hR6 > mC12.
m) of rhenium as the reference structures by the equation: ΔH = H (ReB2) − H (Re) − 2H (B). As shown in Table 1, the obtained formation enthalpies of hP6-ReB2, oP6-ReB2, hR3-ReB2, hR6-ReB2, and mC12-ReB2 are all negative. Among them, hP6-ReB2 possesses the smallest formation enthalpy (−1.25 eV f.u.−1) and is the most energetically stable ReB2, which is consistent with the previous experimental1,10 and theoretical7,15,26,28 results. After it, the formation enthalpy of oP6-ReB2, hR3-ReB2, and hR6-ReB2 are −1.04, −1.03, and −0.35 eV f.u.−1, respectively. Meanwhile, mC12-ReB2 shows the largest formation enthalpy (−0.28 eV f.u.−1), indicating that its stability is the weakest. Therefore, the phase stability order of ReB2 should be hP6 > oP6 > hR3 > hR6 > mC12.