Structural configuration and tetragonal phase stability in the equiatomic quaternary Heusler compound TiZnMnSi

Abstract

Heusler materials have aroused great scientific research interest during recent years due to their special electronic and magnetic properties. Especially for the equiatomic quaternary Heusler compounds, they exhibit very high composition flexibility and structure tunability. In this work, we have carried out a systematic study on the structural configuration and tetragonal stability for the Heusler compound TiZnMnSi by first-principles calculations. Results reveal the type-A structure with ferromagnetic state possesses the lowest total energy and thus should be the ground state configuration. Based on the equilibrium lattice constant, the electronic band structures and magnetic moments have been computed. The tetragonal phase transformation is then investigated by using the total energy variation under different tetragonal strains, and the stability analysis of the mechanical and dynamic properties indicates that TiZnMnSi exhibits a strong tendency for the tetragonal phase. These findings could provide reference data for relative experiments as well as a very helpful theoretical reference for this fascinating class of materials.

---

Introduction

During recent years, scientific research in the field of materials science and condensed matter physics has achieved great progress due to the fast improvement in material processing technologies and equipment, including the vast computing power increase. Among the wide ranges and various purposes of material applications, magnetic metal or half-metal materials have become of high interest recently, especially for the development of magnetic random-access memory and magnetic shape memory technologies.^1–3 The search for novel smart magnetic materials has indeed increased tremendously and they have become essential for a new generation of intelligent materials.

The family of Heusler materials stand out as one of the most promising candidates due to their excellent electronic and magnetic characteristics,^4–31 such as, high Curie temperature, compatible crystal structure and tuneable properties. Initially, Heusler compounds have two typical classes:^31–47 half-Heusler with generic chemical formula XYZ and full-Heusler with formula X₂YZ, where X and Y represent the transition metal elements and Z is from the main group elements. Despite the different stoichiometric ratios in these two Heusler kinds, there are always three elements in both of them and thus they can be regarded as ternary compounds. Until recently, quaternary Heusler alloys start to show up and they can be simply obtained by replacing one X in the full Heusler materials by a different forth element X′. Thus, the quaternary Heusler with formula XX′YZ has stoichiometric ratio of 1 : 1 : 1 : 1 and thus the name of equiatomic quaternary Heusler (EQH) is derived.^22,48–57 Both experimental investigations and theoretical calculations have gradually began, e.g., Bainsla et al. have prepared the equiatomic quaternary CoFeCrAl Heusler alloy with arc melting technique and found that it exhibits Y-type structure with only a very small amount of anti-site disorder and it has half metallicity with high spin polarization;⁵² Paudel et al. have theoretically studied the structural, magnetic, electronic and elastic properties for the LiMgPdSb-type EQH alloys CoFeZrZ (Z = Ge, Sb, and Si) and examined their half metallic behaviour under different values of Hubbard correlation parameter U by using GGA+U method;⁵³ Rani et al. have combined a theoretical and experimental study on the half metallic behaviour of EQH alloys CoRuMnGe and CoRuVZ (Z = Al, Ga);⁵⁴ Wang et al. and Hao et al. have designed new EQH compounds ZrRhTiIn and TiZrRuZ⁴⁹ (Z = Al, Ga, In) from first principle computations;⁵⁵ several other works focused on the rare-earth-element based EQH materials, like ScFeCrT (T = Si, Ge), LuCoCrZ (Z = Si, Ge), YCoCrZ (Z = Si, Al, Ge, Ga), MCoVZ (M = Lu, Y; Z = Si, Ge) and they show better prospect for spintronic applications;^51,58,59 and Gao et al. conducted a high-throughput screening for spin gapless semiconductors (SGSs) in EQH compounds after Bainsla et al. reported the SGS signature in EQH CoFeMnSi.^48,56,60 Compared with the ternary Heusler materials, the EQH compounds bring out several special advantages, like high composition flexibility and better property tunability. Consequently, more research attention and effort are continuously dedicated in the development of EQH materials.

Among the vast varieties of Heusler materials, Ti-based and Mn-based Heusler compounds have attracted a lot of research interest because of the presence of magnetism and possible phase transformation, which can be particularly interesting for the development of magnetic-tunnel-junction memory material and ferromagnetic shape memory material. In this work, a systematic theoretical investigation has been detailed on the equiatomic quaternary Heusler compound TiZnMnSi, which is composed of the very common elements. Its ground state structural configuration and magnetic ordering have been determined and the corresponding equilibrium lattice constant is derived. The calculated electronic band structures reveal the metallic nature in this compound. More importantly, the possible tetragonal phase transformation is further examined from different perspectives. Results clearly indicate that the tetragonal phase can indeed reduce the total energy and the minimum tetragonal energy point is found at c/a equal to 1.33. At last, we have also cross-evaluated the mechanical and dynamic stabilities for the tetragonal and cubic phases. This comprehensive study can serve as a useful guidance for the future experimental research of the quaternary Heusler compound TiZnMnSi and also promote some relative studies in other similar quaternary Heusler compounds.

Computational methodology

The EQH compound TiZnMnSi has been theoretically explored with first principles calculations under the framework of density functional theory,⁶¹ as implemented in the Cambridge Serial Total Energy Package code.⁶² The pseudo potential plane wave method has been applied and the Perdew–Burke–Ernzerhof functional with generalized gradient approximation has been selected for the electronic exchange energy.^63,64 The valence electron configurations for Ti (3d²4s²), Mn (3d⁵4s²), Zn (3d¹⁰4s²) and Si (3s²3p²) have been chosen, respectively. A plane wave cutoff energy of 500 eV has been set and two different Monkhorst–Pack grids of 12 × 12 × 12 and 12 × 12 × 15 k sampling points in the first Brillouin zone have been used for the cubic and tetragonal structures, respectively. The self-consistent converge for energy and stress were set as 1 × 10⁻⁶ eV and 1 × 10⁻² eV Å⁻¹.

Results and discussions

Crystal structure

In general, EQH compounds normally exhibit LiMgPdSn crystal structure,^{52,56,65–68} also known as Y-type structure, in which the four equal stoichiometric elements form four interpenetrating face centred cubic sublattices as defined by the four Wyckoff positions of A(0,0,0), B(1/4,1/4,1/4), C(1/2,1/2,1/2), and D(3/4,3/4,3/4). According to the general site occupation rule in Heusler compounds,^{49,50,69–72} the main group element always enters to the D site, leaving the other three positions for the transition metal elements. Since there are three transition metal elements in the EQH compound TiZnMnSi and it has not been synthesized in experiments, we have considered all the possible atomic configurations for the three transition metal atoms and they can be reduced to the three independent structures, in which the four Wyckoff sites ABCD are sequentially occupied by TiZnMnSi, TiMnZnSi and MnTiZnSi, and they are respectively defined as type-A, B and C structures for simple purpose in current work. The corresponding crystal structures are shown in Fig. 1 and the different atomic occupations are highlighted by the diagonal colour line along the cubic cell.

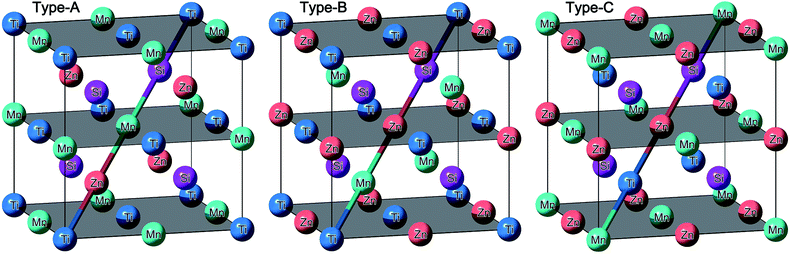Fig. 1 The crystal structure of the EQH compound TiZnMnSi in different atomic configurations.

In order to determine the ground state atomic orderings, we have calculated the total energies at different lattice constants for the three structural types and the obtained results are reported in Fig. 2. Since the magnetism is a major feature for Heusler compounds and many studies have found that Mn element can carry large magnetic moment in Mn-based Heusler materials, we thus further considered two possible magnetic configurations for each structure type, the ferromagnetic (FM) state and the nonmagnetic (NM) state. As displayed in Fig. 2, we can clearly see that the ferromagnetic state shows lower total energy than the nonmagnetic counterpart for all three structural configurations. It is observed for each configuration the total energies for both FM and NM states converge to the same values with lattice decrease and this is related to the electron delocalization at smaller lattice constants. With a polynomial fit of the total energy versus the lattice constant for each structural state, we can derive the equilibrium lattice constant. The obtained values are summarized in Table 1. The lowest total energy is found for type-A structure under ferromagnetic arrangement, which indicates that it should be energetically preferred as the ground state configuration.

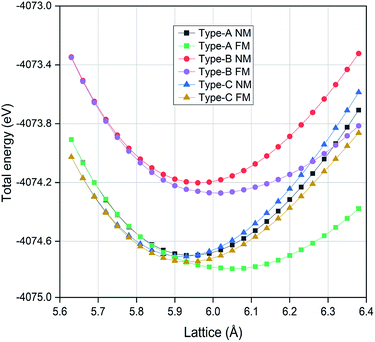Fig. 2 The calculated total energies for the EQH compound TiZnMnSi in different atomic configurations and magnetic orders.

Table 1 The calculated equilibrium lattice constant (Å), total and partial magnetic moments (μ_B) for the EQH compound TiZnMnSi in different atomic configurations and magnetic states

Structural type	Magnetic state	Lattice	MTotal	MTi	MZn	MMn	MSi
Type-A	NM	5.943
	FM	6.055	2.21	−0.87	−0.08	3.24	−0.08
Type-B	NM	5.962
	FM	6.011	1.26	−1.10	−0.03	2.44	−0.02
Type-C	NM	5.918
	FM	5.934	0.90	−0.32	−0.06	1.29	−0.01

---

Electronic and magnetic properties

Based on the determined ground state structural configuration and equilibrium lattice constant, we have further examined the electronic and magnetic properties for the EQH compound TiZnMnSi. The calculated spin polarized electronic band structures are displayed in Fig. 3, with the Fermi energy level shifted to 0 eV. Since only the bands nearby the Fermi level play major role, we have set the energy range from −3 eV to 3 eV. We can observe that there are multiple bands overlap with the Fermi level in both spin-up and spin-down channels, meaning that TiZnMnSi has metallic behaviour in both spin directions at the ground state.

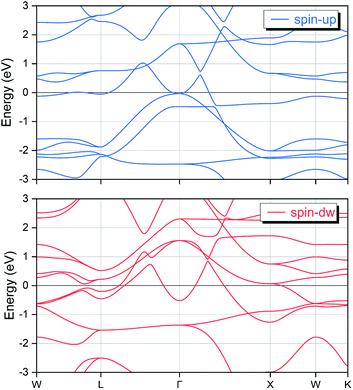Fig. 3 The calculated spin-polarized electronic band structures for the EQH compound TiZnMnSi at the equilibrium lattice constant.

To better understand the spin polarization and magnetic origination, we have also calculated the magnetic moments and densities of states. The obtained values for the total and atom-resolved magnetic moments are also listed in Table 1. Except the ground state type-A structure, we have also provided the results for other structures. It can be clearly seen that the total magnetic moment for the EQH compound TiZnMnSi is 2.21 μ_B and it is mainly originated from the Mn and Ti atoms. This magnetic contribution behaviour can also be accessed with the total and partial densities of states, as shown in Fig. 4. Similar as the electronic band structures, we have only displayed the vicinity energy range around the Fermi energy level, which has been highlighted by the vertical black line in the middle. It is found that the total density of state is majorly contributed from the same two atoms Ti and Mn in both spin-up and spin-down directions, as revealed by their relatively large shaded areas of red and green colours, respectively. Whereas, the densities of states for Zn and Si are very small as their colour filled areas are very narrow compared with Ti and Mn. From Fig. 4, we can also check the spin splitting effect and the correlation states for different atoms between the two spin directions. For Ti atom, its density distributions exhibit two high peak areas around 0 to 3 eV; there is a slight horizontal energy shift between the two spin channels, which results into small spin splitting effect. This splitting behaviour even becomes much more prominent for Mn atom with a strongly asymmetric density distribution between the two spins, a high peak at −2 eV in spin-up direction and another high peak at 1 eV in spin-down direction. These spin splitting effects in Ti and Mn can also be reflected from their large magnetic moments, as discussed above. Besides, we also notice that the density distributions for Ti and Mn atoms show very large separation in the spin-up direction yet an almost complete overlap in the spin-down direction, indicating their strong correlation state in the spin-down direction. Considering the Fermi energy level, the high peak density of Mn atom in the spin-up direction corresponds to the bonding state while the other peak in the spin-down direction resemble the antibonding state.

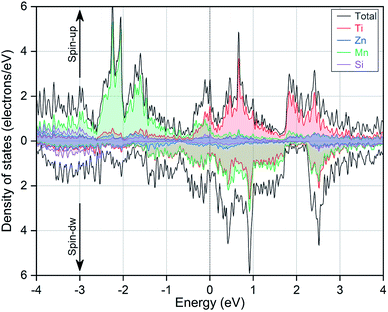Fig. 4 The calculated total and partial densities of states in both spin directions for the EQH compound TiZnMnSi at the ground state.

Tetragonal phase transformation

In the family of Heusler materials, tetragonal phase often exists and many previous studies have confirmed this from both experimental characterization and theoretical calculation, such as, Faleev et al. have comprehensively examined 286 full Heusler alloys and found 62% have tetragonal ground states at zero temperature;² Wu et al. have investigated a series of palladium based Heusler alloys Pd₂YZ (Y = Co, Fe, Mn; Z = B, Al, Ga, In, Tl, Si, Ge, Sn, Pb, P, As, Sb) and discovered that most of them show potential tetragonal distortion;⁷¹ Han et al. have studied all-d-metal Heusler alloys X_2−xMn_1+xV (X = Pd, Ni, Pt, Ag, Au, Ir, Co; x = 1, 0) and determined all the Mn-poor alloys prefer to have a tetragonal phase instead of a cubic one;⁵⁰ Liu et al. and Faleev et al. have both observed the tetragonal structure in several Mn-based full Heusler compounds from experimental characterizations.^8,73,74

Compared with the cubic structure, tetragonal phase in Heusler compounds can be even more useful for the potential applications in spintronic fields. In particular, the perpendicular magnetic anisotropy in the tetragonally distorted Heusler materials can be critical to the development of magnetic-tunnel-junction (MTJ) memory elements for the spin-transfer torque magnetic random-access memory technology.² In order to assess the possible tetragonal phase transformation in the EQH compound TiZnMnSi, we have introduced the tetragonal strains by simply varying the c/a ratio while keeping the unit cell volume constant at the cubic structure. Different structures can be obtained at different tetragonal strains: stretched or compressed cubic structure along c axis when c/a is larger smaller than 1.

First, we can explore the tetragonal phase stability in the EQH compound TiZnMnSi by calculating the total energy variation at different tetragonal strains. The obtained results are shown in Fig. 5 with the energy difference normalized according to the cubic equilibrium lattice system at c/a equal to 1. We can immediately find that both tetragonal strains in compressing and stretching sides can further reduce the total energy, indicating the tetragonal phase can possibly exist from energetic point of view. The maximum energy decrease has been calculated and displayed for both tetragonal sides and it is seen that the tetragonal strain in stretching side exhibits much larger energy reduction about 0.21 eV at c/a of 1.33 than that of 0.04 eV in the compressing side at c/a of 0.85. Based on the previous studies, the occurrence of a stable tetragonal phase in Heusler compounds requires the transformation energy larger than 0.1 eV. Thus, the possible tetragonal phase is expected in the stretching tetragonal strain side at c/a of 1.33 for the EQH compound TiZnMnSi. As known, the electronic properties of solid materials are strongly related with their structures. To investigate this phase transformation effect, we have computed the electronic band structures of TiZnMnSi in tetragonal phase and the obtained results are shown in Fig. 6. Note the same energy range as the cubic band structure is used yet different high symmetric points are selected for the k paths. We can see the band structures for the tetragonal phase are completely different from those of the cubic phase, see Fig. 3. However, the metallic feature is maintained for both spin directions as there are multiple bands overlapping with the Fermi energy level.

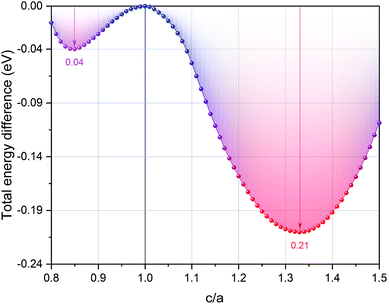Fig. 5 The calculated total energy difference for the EQH compound TiZnMnSi under different tetragonal strains. The energy value is normalized with respect to the cubic structure.

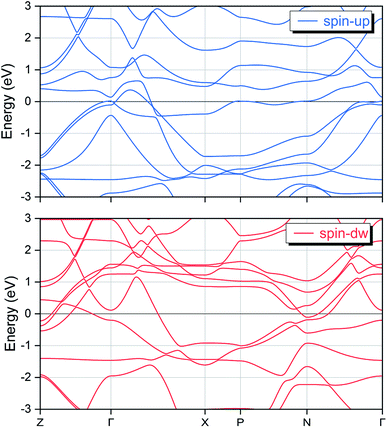Fig. 6 The calculated spin-polarized electronic band structures for the EQH compound TiZnMnSi in tetragonal phase.

As suggested in previous studies,^2,50,71 the presence of the tetragonal phase in Heusler alloys is related with the peak-and-valley structure of their densities of states around the Fermi energy level. Thus, we have computed the total density of states for the tetragonal phase and compared it with the cubic one, as plotted in Fig. 7. We can see that the Fermi level, as marked by the vertical black dashed line in the middle, is located exactly at the middle of two peaks in both spin directions for the cubic structure; whereas, it smoothly shifts into much shallower valley positions in the tetragonal structure. The precise values of the densities of states at the Fermi level for both cubic and tetragonal structures are also labelled in the right axis. The high peak value in the cubic structure can cause high total energy of the system and thus leads to poor structural stabilities, which results into the tetragonal phase transformation in the EQH compound TiZnMnSi.

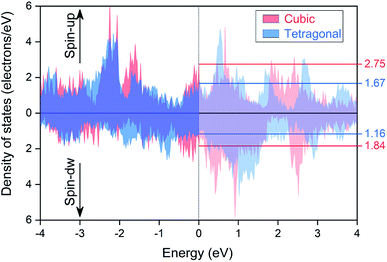Fig. 7 The calculated total densities of states for the EQH compound TiZnMnSi under both cubic and tetragonal phases.

Except the total energy variation, we can also evaluate the tetragonal phase stability with the mechanical and dynamic properties. We have computed the phonon dispersion spectra for both cubic and tetragonal phases with the finite displacement method and the results are displayed in Fig. 8. A strong phonon softening behaviour is present in the cubic structure as highlighted by the two red-colour curves with very large imaginary frequencies. In contrary, the phonon curve for the tetragonal phase exhibits no soft frequency, highlighting its dynamic stability.

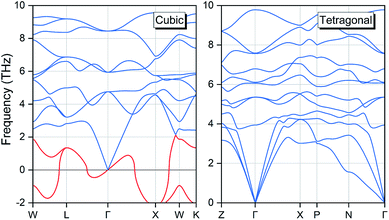Fig. 8 The calculated phonon dispersion spectra for the EQH compound TiZnMnSi in both cubic and tetragonal phases.

Besides, we have also examined the mechanical properties for the EQH compound TiZnMnSi by employing the stress strain method.^75,76 There are three independent elastic constants for the cubic structure, C₁₁ C₁₂ and C₄₄, and six constants for the tetragonal one, C₁₁, C₁₂, C₁₃, C₃₃, C₄₄ and C₆₆. Their derived values are all summarized in Table 2. According to the generalized Born–Huang elastic criteria,⁷⁷ the mechanical stabilities for cubic and tetragonal structures should satisfy the following two conditions, respectively. Based on the derived elastic constants in Table 2, we can directly verify that the EQH compound TiZnMnSi is mechanically stable in tetragonal phase. Combining the dynamic and mechanical stabilities together, we can see that the EQH compound TiZnMnSi exhibits highly probable tetragonal phase transformation. Furthermore, we have also computed the directional dependent mechanical Young's modulus and shear modulus for the EQH compound TiZnMnSi under the stable tetragonal phase with the ELATE program,⁷⁸ as shown in Fig. 9. A very strong mechanical anisotropy can be clearly observed with the very large directional variation for both moduli. The maximum values for the Young's modulus and shear modulus are found along the [111] and [001] directions, respectively.

C₁₁ − C₁₂ > 0, C₁₁ + 2C₁₂ > 0, C₄₄ > 0 (1)

C₁₁ > |C₁₂|, 2C₁₃² < C₃₃(C₁₁ + C₁₂), C₄₄ > 0, C₆₆ > 0 (2)

Table 2 The calculated elastic constants (C_ij) in GPa for the EQH compound TiZnMnSi in both cubic and tetragonal structures

Phase	C11	C12	C13	C33	C44	C66
Cubic	89.45	118.28			18.56
Tetragonal	127.37	125.40	90.67	145.23	67.00	53.66

---

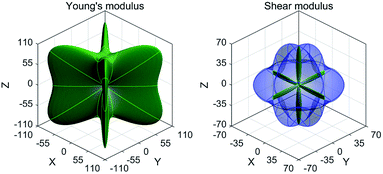Fig. 9 The calculated directional dependent Young's modulus and shear modulus for the EQH compound TiZnMnSi under the tetragonal phase.

Conclusions

In current study, we have performed a detailed theoretical investigation on the equiatomic quaternary Heusler compound TiZnMnSi by first principles calculations based on density functional theory. Among the three independent structural configurations and the two magnetic states considered, type-A atomic ordering under ferromagnetic arrangement has been determined to be the energetically preferable ground state. On the basis of obtained equilibrium lattice constant, we have calculated its electronic and magnetic properties for TiZnMnSi. Spin polarized band structures exhibit metallic feature with multiple bands crossing the Fermi energy level. The total magnetic moment of 2.21 μ_B is mainly contributed by Mn and Ti atoms, whose spin splitting effects are quite strong, especially for Mn atom, as revealed from their partial densities of states. Afterwards, we have focused on the possible tetragonal phase transformation and examined the total energy difference under different tetragonal strains. Obtained results clearly indicate the tetragonal phase can further reduce the total energy of the system and the minimum energy point is located at the tetragonal strain c/a equal to 1.33. The origin of the tetragonal phase has been analysed with the peak-and-valley structure of the total densities of states for the cubic and tetragonal structure. In the last, the tetragonal phase is further verified with its mechanical and dynamic stabilities. This systematic work can provide a very helpful reference for the further investigation of the quaternary Heusler compound TiZnMnSi and even inspire other related researches.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by National Natural Science Foundation of China (No. 61904153). R. Khenata acknowledges the financial Support of the General Direction of Scientific Research and Technological Development (DGRSDT).

References

1. R. A. de Groot, F. M. Mueller, P. G. v. Engen and K. H. J. Buschow, Phys. Rev. Lett., 1983, 50, 2024–2027.
2. S. V. Faleev, Y. Ferrante, J. Jeong, M. G. Samant, B. Jones and S. S. P. Parkin, Phys. Rev. Appl., 2017, 7, 034022.
3. H. van Leuken and R. A. de Groot, Phys. Rev. Lett., 1995, 74, 1171–1173.
4. S. Anand, M. Wood, Y. Xia, C. Wolverton and G. J. Snyder, Joule, 2019, 3, 1226–1238.
5. A. Hutten, J. Schmalhorst, A. Thomas, S. Kammerer, M. Sacher, D. Ebke, N. N. Liu, X. Kou and G. Reiss, J. Alloys Compd., 2006, 423, 148–152.
6. X. T. Wang, Z. X. Cheng, J. L. Wang, X. L. Wang and G. D. Liu, J. Mater. Chem. C, 2016, 4, 7176–7192.
7. K. Manna, Y. Sun, L. Muechler, J. Kubler and C. Felser, Nat. Rev. Mater., 2018, 3, 244–256.
8. S. V. Faleev, Y. Ferrante, J. Jeong, M. G. Samant, B. Jones and S. S. P. Parkin, Phys. Rev. Mater., 2017, 1, 024402.
9. T. Graf, C. Felser and S. S. P. Parkin, Prog. Solid State Chem., 2011, 39, 1–50.
10. A. K. Nayak, K. G. Suresh and A. K. Nigam, Acta Mater., 2011, 59, 3304–3312.
11. X. D. Xu, Z. X. Chen, Y. Sakuraba, A. Perumal, K. Masuda, L. S. R. Kumara, H. Tajiri, T. Nakatani, J. Wang, W. Zhou, Y. Miura, T. Ohkubo and K. Hono, Acta Mater., 2019, 176, 33–42.
12. I. Galanakis and E. Şaşıoğlu, Appl. Phys. Lett., 2011, 99, 052509.
13. S. Skaftouros, K. Ozdogan, E. Sasioglu and I. Galanakis, Appl. Phys. Lett., 2013, 102, 022402.
14. Y. Feng, X. R. Chen, T. Zhou, H. K. Yuan and H. Chen, Appl. Surf. Sci., 2015, 346, 1–10.
15. L. Hao, J. You, R. Khenata, Y. Wang, X. Wang and T. Yang, Crystals, 2019, 9, 422.
16. X. Tan, J. You, P.-F. Liu and Y. Wang, Crystals, 2019, 9, 678.
17. T. Yang, J. T. Cao and X. T. Wang, Crystals, 2018, 8, 429.
18. A. Dehghan and S. Davatolhagh, J. Alloys Compd., 2019, 772, 132–139.
19. Enamullah and S. C. Lee, J. Alloys Compd., 2018, 765, 1055–1060.
20. H. Kara, M. U. Kahaly and K. Ozdogan, J. Alloys Compd., 2018, 735, 950–958.
21. T. Yang, L. Y. Hao, R. Khenata and X. T. Wang, Materials, 2018, 11, 2091.
22. Y. Han, Y. Wu, T. Li, R. Khenata, T. Yang and X. Wang, Materials, 2018, 11, 797.
23. J. You, J. Cao, R. Khenata, X. Wang, X. Shen and T. Yang, Materials, 2019, 12, 3117.
24. P. D. Patel, S. M. Shinde, S. D. Gupta and P. K. Jha, Mater. Res. Express, 2019, 6, 076307.
25. T. Fichtner, C. Wang, A. A. Levin, G. Kreiner, C. S. Mejia, S. Fabbrici, F. Albertini and C. Felser, Metals, 2015, 5, 484–503.
26. S. Chadov, X. Qi, J. Kubler, G. H. Fecher, C. Felser and S. C. Zhang, Nat. Mater., 2010, 9, 541–545.
27. I. Shigeta, T. Kubota, Y. Sakuraba, S. Kimura, S. Awaji, K. Takanashi and M. Hiroi, Phys. B, 2018, 536, 310–313.
28. X.-P. Wei, X.-R. Hu, S.-B. Chu, G.-Y. Mao, L.-B. Hu, T. Lei and J.-B. Deng, Phys. B, 2011, 406, 1139–1142.
29. X. Chen, Y. Huang and H. Chen, RSC Adv., 2017, 7, 44647–44654.
30. X. Chen, Y. Huang, J. Liu, H. Yuan and H. Chen, RSC Adv., 2019, 9, 3847–3855.
31. X. Wang, Z. Cheng, J. Wang, L. Wang, Z. Yu, C. Fang, J. Yang and G. Liu, RSC Adv., 2016, 6, 57041–57047.
32. I. Galanakis and P. Mavropoulos, J. Phys.: Condens. Matter, 2007, 19, 315213.
33. R. Y. Umetsu, M. Tsujikawa, K. Saito, K. Ono, T. Ishigaki, R. Kainuma and M. Shirai, J. Phys.: Condens. Matter, 2019, 31, 065801.
34. G. Y. Gao, L. Hu, K. L. Yao, B. Luo and N. Liu, J. Alloys Compd., 2013, 551, 539–543.
35. L. Wang and Y. J. Jin, J. Magn. Magn. Mater., 2015, 385, 55–59.
36. X. T. Wang, Z. X. Cheng, R. Khenata, H. Rozale, J. L. Wang, L. Y. Wang, R. K. Guo and G. D. Liu, J. Magn. Magn. Mater., 2017, 423, 285–290.
37. X. T. Wang, T. T. Lin, H. Rozale, X. F. Dai and G. D. Liu, J. Magn. Magn. Mater., 2016, 402, 190–195.
38. T. Yang, J. You, L. Hao, R. Khenata, Z.-Y. Wang and X. Wang, J. Magn. Magn. Mater., 2020, 498, 166188.
39. Q. Zeng, J. Shen, H. Zhang, J. Chen, B. Ding, X. Xi, E. Liu, W. Wang and G. Wu, J. Phys.: Condens. Matter, 2019, 31, 425401.
40. S. J. Hashemifar, P. Kratzer and M. Scheffler, Phys. Rev. Lett., 2005, 94, 096402.
41. S. Ouardi, G. H. Fecher, C. Felser and J. Kubler, Phys. Rev. Lett., 2013, 110, 100401.
42. S. Andrieu, A. Neggache, T. Hauet, T. Devolder, A. Hallal, M. Chshiev, A. M. Bataille, P. Le Fevre and F. Bertran, Phys. Rev. B, 2016, 93, 094417.
43. S. Chadov, S.-C. Wu, C. Felser and I. Galanakis, Phys. Rev. B, 2017, 96, 024435.
44. Y. Han, Z. Chen, M. Kuang, Z. Liu, X. Wang and X. Wang, Results Phys., 2019, 12, 435–446.
45. T. Yang, L. Hao, R. Khenata and X. Wang, R. Soc. Open Sci., 2019, 6, 191007.
46. X. Wang, H. Khachai, R. Khenata, H. Yuan, L. Wang, W. Wang, A. Bouhemadou, L. Hao, X. Dai, R. Guo, G. Liu and Z. Cheng, Sci. Rep., 2017, 7, 16183.
47. Z. H. Liu, A. Burigu, Y. J. Zhang, H. M. Jafri, X. Q. Ma, E. K. Liu, W. H. Wang and G. H. Wu, Scr. Mater., 2018, 143, 122–125.
48. L. Bainsla and K. G. Suresh, Appl. Phys. Rev., 2016, 3, 031101.
49. L. Hao, M. Tan, R. Khenata, X. Wang and T. Yang, Chin. J. Phys., 2019, 62, 54–64.
50. Y. Han, M. Wu, Y. Feng, Z. Cheng, T. Lin, T. Yang, R. Khenata and X. Wang, IUCrJ, 2019, 6, 465–472.
51. X. Wang, Z. Cheng, G. Liu, X. Dai, R. Khenata, L. Wang and A. Bouhemadou, IUCrJ, 2017, 4, 758–768.
52. L. Bainsla, A. I. Mallick, A. A. Coelho, A. K. Nigam, B. S. D. C. S. Varaprasad, Y. K. Takahashi, A. Alam, K. G. Suresh and K. Hono, J. Magn. Magn. Mater., 2015, 394, 82–86.
53. R. Paudel and J. C. Zhu, J. Magn. Magn. Mater., 2018, 453, 10–16.
54. D. Rani, L. Bainsla, K. G. Suresh and A. Alam, J. Magn. Magn. Mater., 2019, 492, 165662.
55. J. X. Wang, Z. B. Chen and Y. C. Gao, J. Phys. Chem. Solids, 2018, 116, 72–78.
56. L. Bainsla, A. I. Mallick, M. M. Raja, A. K. Nigam, B. S. D. C. S. Varaprasad, Y. K. Takahashi, A. Alam, K. G. Suresh and K. Hono, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 104408.
57. Y. Han, M. Wu, M. Kuang, T. Yang, X. Chen and X. Wang, Results Phys., 2018, 11, 1134–1141.
58. L. Zhang, X. Wang and Z. Cheng, J. Alloys Compd., 2017, 718, 63–74.
59. M. N. Rasool, A. Hussain, A. Javed and M. A. Khan, J. Magn. Magn. Mater., 2017, 426, 421–428.
60. Q. Gao, I. Opahle and H. Zhang, Phys. Rev. Mater., 2019, 3, 024410.
61. M. C. Payne, M. P. Teter, D. C. Allan, T. A. Arias and J. D. Joannopoulos, Rev. Mod. Phys., 1992, 64, 1045–1097.
62. M. D. Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, J. Phys.: Condens. Matter, 2002, 14, 2717–2744.
63. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
64. D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895.
65. G. Z. Xu, E. K. Liu, Y. Du, G. J. Li, G. D. Liu, W. H. Wang and G. H. Wu, EPL, 2013, 102, 17007.
66. K. Özdoğan, E. Şaşıoğlu and I. Galanakis, J. Appl. Phys., 2013, 113, 193903.
67. L. Bainsla, A. I. Mallick, M. M. Raja, A. A. Coelho, A. K. Nigam, D. D. Johnson, A. Alam and K. G. Suresh, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 045201.
68. X. D. Yang, X. L. Wu, B. Wu, Y. Peng, P. Li and H. S. Huang, Mater. Sci. Eng., B, 2016, 209, 45–50.
69. H. Luo, Z. Zhu, L. Ma, S. Xu, X. Zhu, C. Jiang, H. Xu and G. Wu, J. Phys. D: Appl. Phys., 2008, 41, 055010.
70. Y. Ma, Z. Ni, H. Luo, H. Liu, F. Meng, E. Liu, W. Wang and G. Wu, Intermetallics, 2017, 81, 1–8.
71. M. Wu, Y. Han, A. Bouhemadou, Z. Cheng, R. Khenata, M. Kuang, X. Wang, T. Yang, H. Yuan and X. Wang, IUCrJ, 2019, 6, 218–225.
72. J. G. Tan, Z. H. Liu, Y. J. Zhang, G. T. Li, H. G. Zhang, G. D. Liu and X. Q. Ma, Results Phys., 2019, 12, 1182–1189.
73. Z. H. Liu, Z. J. Tang, J. G. Tan, Y. J. Zhang, Z. G. Wu, X. T. Wang, G. D. Liu and X. Q. Ma, IUCrJ, 2018, 5, 794–800.
74. C. Felser, V. Alijani, J. Winterlik, S. Chadov and A. K. Nayak, IEEE Trans. Magn., 2013, 49, 682–685.
75. J. Wang, J. Li, S. Yip, S. Phillpot and D. Wolf, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 12627–12635.
76. S. Yip, J. Li, M. J. Tang and J. G. Wang, Mater. Sci. Eng., A, 2001, 317, 236–240.
77. F. Mouhat and F. X. Coudert, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 224104.
78. R. Gaillac, P. Pullumbi and F. X. Coudert, J. Phys.: Condens. Matter, 2016, 28, 275201.

---

Footnote

† Authors contributed equally.

---