DOI:
10.1039/D0RA07873E
(Paper)
RSC Adv., 2020,
10, 41588-41599
Removal of atrazine from aqueous solutions onto a magnetite/chitosan/activated carbon composite in a fixed-bed column system: optimization using response surface methodology
Received
14th September 2020
, Accepted 2nd November 2020
First published on 13th November 2020
Abstract
In this study, a magnetite/chitosan/activated carbon (MCHAC) composite is proposed as an efficient adsorbent for the removal of atrazine from aqueous solutions. The prepared composite was characterized using Fourier-transform infrared (FTIR) and X-ray diffraction (XRD) methods. Response surface methodology (RSM) coupled with composite central design (CCD) were used to optimize the effects of the four independent variables, pH, initial concentration of atrazine (C0), bed depth (H), and flow rate (Q), which influence the adsorption process. The experimental results modeled using response surface methodology (RSM) coupled with central composite design (CCD) (RSM–CCD) indicated a quadratic relationship with p < 0.0001 for adsorption capacity at saturation (qs) and fraction of bed utilization (FBU). The results of the experiments performed under the optimized conditions, pH = 5.07, C0 = 137.86 mg L−1, H = 2.99 cm and Q = 1.038 mL min−1, showed a qs value of 62.32 mg g−1 and FBU of 72.26%, with a deviation value of less than 0.05 from the predicted qs and FBU values. The obtained breakthrough curves were fitted with four mathematical models, Thomas, Bohart–Adams, Yan and Yoon–Nelson, in order to determine the limiting step of the mass transfer of the atrazine adsorption onto the composite. A desorption study of the composite revealed the high reuse potential for MCHAC, thus, the prepared material could be used as a low-cost and efficient adsorbent for the decontamination of polluted wastewater.
1. Introduction
Benin Republic is one of the top cotton producers in West Africa, with more than 600![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 tons of cotton produced each year. To achieve this performance, large quantities of chemical fertilizers, pesticides and herbicides are imported each year and used for cotton farming. This practice has led to pollution of the aquatic environment by the residues of phytosanitary products.1 Atrazine is one of the triazine herbicides that are very selective and widely used for weed control in cotton and cereal crops. Atrazine is persistent, non-biodegradable and its residues may accumulate in seeds, sediments, fishery products and may contaminate surface water and groundwater. Moreover, atrazine is also classified as a hazardous compound due to the negative impact it has on the aquatic environment and human health.2,3 Thus, several methods such as photodegradation,4 electrocatalytic processes,5 oxidation processes,6 membrane techniques,7 biological treatments8 and adsorption9,10 are used for the removal of atrazine from polluted water. Among these methods, adsorption processes have become very attractive techniques because of their simplicity and low cost.11,12
000 tons of cotton produced each year. To achieve this performance, large quantities of chemical fertilizers, pesticides and herbicides are imported each year and used for cotton farming. This practice has led to pollution of the aquatic environment by the residues of phytosanitary products.1 Atrazine is one of the triazine herbicides that are very selective and widely used for weed control in cotton and cereal crops. Atrazine is persistent, non-biodegradable and its residues may accumulate in seeds, sediments, fishery products and may contaminate surface water and groundwater. Moreover, atrazine is also classified as a hazardous compound due to the negative impact it has on the aquatic environment and human health.2,3 Thus, several methods such as photodegradation,4 electrocatalytic processes,5 oxidation processes,6 membrane techniques,7 biological treatments8 and adsorption9,10 are used for the removal of atrazine from polluted water. Among these methods, adsorption processes have become very attractive techniques because of their simplicity and low cost.11,12
Activated carbon, chitosan and their composites have mainly been used as adsorbents for organic pollutants and heavy metals in wastewater.13–16 However, after the adsorption process, the separation of the adsorbent-loaded pollutants from the reaction medium by filtration is very difficult. Thus, in order to solve the problem, research has been focused on the development of new materials for this purpose, including magnetic nanoparticles.17,18 Magnetite (Fe3O4) is a non-toxic material, both to human health and the environment. The use of magnetic-based adsorbents in wastewater treatment has received wide attention because magnetic nanoparticles are endowed with surface charges and can be easily separated from the reaction matrix using a magnet.19 Thus, magnetic nanoparticles have been combined with other materials such as graphene oxide,9,20,21 activated carbon17,22,23 and chitosan24 for the removal of heavy metals, dyes and pesticide residues from water. However, activated carbon and chitosan mainly used for their development are of commercial origin, meaning that they contribute towards an increase in the cost of water treatment. Thus, this study focuses on the preparation of a new and low-cost, magnetite/chitosan/activated carbon (MCHAC) composite material that could improve the removal of pesticide residues from aqueous solutions and also be easily separable from the reaction matrix after the adsorption process is complete. The composite was prepared via the coprecipitation of a FeSO4 and FeCl3 mixture, using activated carbon (AC) prepared from peanut shells, and chitosan (CH) extracted from local crab shells. The prepared composite was characterized using Fourier-transform infrared (FTIR) spectroscopy, X-ray diffraction and N2 adsorption/desorption measurements. Then, the adsorption potential of MCHAC was investigated on atrazine under a fixed bed column system. The dynamics of the adsorption process were optimized by response surface methodology (RSM) coupled with central composite design (CCD) and the modeling of the breakthrough curves was performed using mathematical models.
2. Experimental
2.1. Preparation of the magnetite/chitosan/activated carbon (MCHAC)
The CH and AC used for the development of the MCHAC were produced from crab and peanut shells respectively. The activated carbon was prepared via chemical activation using H3PO4 (85%, Sigma-Aldrich) of peanut shells collected from the women's cooperative in Natitingou town (Benin) with an impregnation ratio (weight of H3PO4/weight of peanut shells) of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The chitosan was produced by the deacetylation of chitin extracted from local crab shells collected from markets in Porto-Novo town (Benin). The preparation process and the characteristics of the CH and AC were described in detail in previous work.13
1. The chitosan was produced by the deacetylation of chitin extracted from local crab shells collected from markets in Porto-Novo town (Benin). The preparation process and the characteristics of the CH and AC were described in detail in previous work.13
The MCHAC composite was prepared according to the coprecipitation method reported by Danalioglu et al.25 and Qu et al.26 According to the method, a mixture of 0.175 mol of FeSO4· 7H2O (98.50%, Klincent Mumbai) and 0.350 mol of FeCl3 (97%, Klincent Mumbai) with n(Fe2+)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n(Fe3+) = 1
n(Fe3+) = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 was dissolved in 100 mL of distilled water under stirring at 300 rpm for 2 h. Then, a solution of 2.5% (w/v) of chitosan was prepared by dissolving 5.0 g of chitosan in 250 mL of a 5% acetic acid solution under stirring for 6 h. After preparing, the chitosan solution was added to a solution of a mixture of (Fe2+/Fe3+). After 6 h of stirring at 300 rpm, 10 g of activated carbon was introduced into the system. The obtained suspension was shaken for 6 h and then, 10 mL of 8 M NH4OH (28%, Sigma-Aldrich) solution was added dropwise. The measured pH of the resulting mixture was in the range of 11–12. Then, the suspension was stirred using a helix agitator at 100 rpm under hydrothermal treatment at 80 °C for 3 h. The formed precipitate was collected using a magnet and then washed several times with distilled water and finally using 250 mL of absolute ethanol (96%, Sigma-Aldrich). The obtained MCHAC composite was oven dried at 60 °C for 12 h, and then crushed and sieved (0.1 mm to 0.2 mm). The schematic process of the preparation of the MCHAC composite is shown in Fig. 1.
2 was dissolved in 100 mL of distilled water under stirring at 300 rpm for 2 h. Then, a solution of 2.5% (w/v) of chitosan was prepared by dissolving 5.0 g of chitosan in 250 mL of a 5% acetic acid solution under stirring for 6 h. After preparing, the chitosan solution was added to a solution of a mixture of (Fe2+/Fe3+). After 6 h of stirring at 300 rpm, 10 g of activated carbon was introduced into the system. The obtained suspension was shaken for 6 h and then, 10 mL of 8 M NH4OH (28%, Sigma-Aldrich) solution was added dropwise. The measured pH of the resulting mixture was in the range of 11–12. Then, the suspension was stirred using a helix agitator at 100 rpm under hydrothermal treatment at 80 °C for 3 h. The formed precipitate was collected using a magnet and then washed several times with distilled water and finally using 250 mL of absolute ethanol (96%, Sigma-Aldrich). The obtained MCHAC composite was oven dried at 60 °C for 12 h, and then crushed and sieved (0.1 mm to 0.2 mm). The schematic process of the preparation of the MCHAC composite is shown in Fig. 1.
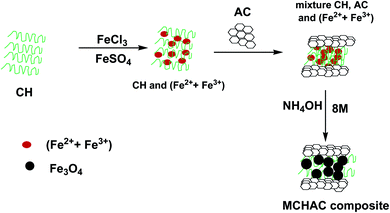 |
| | Fig. 1 Schematic overview of the preparation of MCHAC. | |
2.2. Atrazine solution
A stock solution of 500 mg L−1 of atrazine was prepared by dissolving 312.5 mg of atrazine (80%, Boachen Chemical Industry) in 500 mL of methanol (96%, Sigma-Aldrich). Atrazine solutions with concentrations ranging from 10 to 200 mg L−1 were prepared by diluting the stock solution with distilled water. The absorbance spectrum of the atrazine solution at 10 mg L−1 was recorded using a UV-Vis VWR 1600 spectrophotometer in order to determine the maximum absorption wavelength, which was determined to be 221 nm. After this, the calibration curve of atrazine solution (1–20 mg L−1) was plotted and used to quantify the atrazine concentration in all of the experiments.
2.3. Characterization of the MCHAC composite
The MCHAC composite was characterized using different analytical methods. The point of zero-charge of the composite was determined according to the previously reported study by Marin et al.27 FTIR spectroscopy was used to characterize the surface functional groups of MCHAC with a PerkinElmer 100 Series spectrometer. The X-ray diffraction of MCHAC was carried out using an analytical Empyrean X-ray diffractometer. The pore analysis of the composite was carried out using N2 adsorption and desorption measurements at 77 K with a Micromeritics 2010 analyzer.
2.4. Fixed-bed column adsorption study
2.4.1. Fixed-bed experiments. The experiments were performed in glass columns with an internal diameter of 1.4 cm and a length of 50 cm. A fixed amount of glass wool was inserted at the bottom of the column to serve as the support material for the adsorbent. The atrazine solution of desired concentration was pumped into the column at a constant flow rate set to 1 mL min−1 using a peristaltic pump. The pH of the inlet atrazine solution was adjusted with HCl 0.1 M and NaOH 0.1 M. All tests were conducted at a room temperature of 30 °C. The volumes of the effluents of atrazine were collected at regular time intervals at the bottom of the column. The residual concentration of atrazine in the effluent samples was quantified using a UV-Vis VWR 1600 spectrophotometer at a wavelength of 221 nm. The pH (5 to 9), bed depth H (1 to 3 cm), flow rate Q (1 to 3 mL min−1) and initial concentration of atrazine solution C0 (40 to 200 mg L−1) were investigated in terms of the effect they have on the adsorption process. Breakthrough curves were obtained by continuous monitoring of the process. For this purpose, the breakthrough time (tb), breakthrough concentration (Cb), saturation time (ts), saturation concentration (Cs), adsorption capacity at the saturation time (qs), and the fraction of bed utilization (FBU) can be expressed as follows:28| |
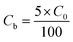 | (1) |
| |
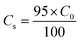 | (2) |
| |
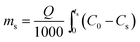 | (3) |
| |
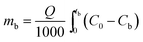 | (4) |
| |
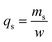 | (5) |
| |
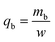 | (6) |
| |
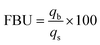 | (7) |
where tb and ts (min) are the times taken to reach 5% and 95% of C0 respectively, where C0 (mg L−1) is the initial concentration of atrazine solution, mb and ms (mg) are the weights of atrazine at breakthrough and saturation, respectively, w (g) is the weight of the composite bed in the column.
2.4.2. RSM-CCD optimization. RSM coupled with CCD was used to evaluate the individual as well as the combined effect of the independent variables that influence the adsorption of atrazine onto the MCHAC composite. Four independent variables, the C0 (initial concentration of atrazine), pH of the atrazine solution, H (bed depth of the composite in the column), and Q (flow rate of the solution) were included in the RSM-CCD measurements. The experimental ranges of the four parameters were selected after the preliminary experiments. Their values with units and symbols are given in Table 1. In this study, the Design Expert version 11 software was used to model the adsorption capacity at equilibrium (qs) and the FBU. The results obtained for twenty-four experiments as well as the responses predicted by the Design Expert software and using RSM-CCD are summarized in Table 2.
Table 1 Characteristics of the experimental variables
| Variables |
Symbol |
Values |
| Min. |
Max. |
| pH |
A |
5 |
9 |
| C0 (mg L−1) |
B |
42.17 |
187.98 |
| H (cm) |
C |
1 |
3 |
| Q (mL min−1) |
D |
1 |
3 |
Table 2 Experimental data and predicted responses
| Run |
Factor 1: A, pH |
Factor 2: B, C0 (mg L−1) |
Factor 3: C, H (cm) |
Factor 4: D, Q (mL min−1) |
Response 1, qs (mg g−1) |
Predicted 1, (mg g−1) |
Response 2, FBU (%) |
Predicted 2, (%) |
| 1 |
5 |
50.58 |
1 |
1 |
14.85 |
12.54 |
29.75 |
31.99 |
| 2 |
5 |
94.49 |
1 |
1 |
31.50 |
31.17 |
17.70 |
13.80 |
| 3 |
5 |
187.98 |
1 |
1 |
53.38 |
53.41 |
7.72 |
6.76 |
| 4 |
9 |
96.88 |
1 |
1 |
16.28 |
17.56 |
28.06 |
25.10 |
| 5 |
9 |
183.26 |
1 |
1 |
23.33 |
23.01 |
14.56 |
16.00 |
| 6 |
9 |
47.65 |
2 |
1 |
12.50 |
12.32 |
49.60 |
47.52 |
| 7 |
5 |
47.65 |
1 |
1 |
19.30 |
17.79 |
19.84 |
19.48 |
| 8 |
5 |
42.17 |
2 |
1 |
30.90 |
28.89 |
43.79 |
47.00 |
| 9 |
5 |
92.75 |
2 |
1 |
39.63 |
42.11 |
45.19 |
44.82 |
| 10 |
9 |
94.89 |
2 |
1 |
14.31 |
16.25 |
40.24 |
44.19 |
| 11 |
9 |
183.26 |
2 |
1 |
19.92 |
19.50 |
44.50 |
41.92 |
| 12 |
7 |
47.65 |
1 |
1 |
5.81 |
9.50 |
25.92 |
28.68 |
| 13 |
5 |
47.65 |
3 |
1 |
38.49 |
41.22 |
67.71 |
65.02 |
| 14 |
7 |
94.15 |
1 |
1 |
16.86 |
18.72 |
22.34 |
22.36 |
| 15 |
7 |
183.26 |
1 |
1 |
34.43 |
32.24 |
12.47 |
14.20 |
| 16 |
5 |
94.49 |
3 |
1 |
55.48 |
52.08 |
70.09 |
66.85 |
| 17 |
7 |
42.17 |
2 |
1 |
16.75 |
14.85 |
55.83 |
50.21 |
| 18 |
7 |
94.89 |
2 |
1 |
29.07 |
23.96 |
52.59 |
47.19 |
| 19 |
7 |
183.26 |
2 |
1 |
31.98 |
34.97 |
45.64 |
46.20 |
| 20 |
7 |
50.03 |
3 |
1 |
18.81 |
20.85 |
58.63 |
62.08 |
| 21 |
7 |
94.89 |
3 |
1 |
28.64 |
27.27 |
60.74 |
63.23 |
| 22 |
5 |
96.68 |
2 |
2 |
42.77 |
43.06 |
42.01 |
44.72 |
| 23 |
5 |
93.60 |
2 |
2 |
41.54 |
42.31 |
41.24 |
44.79 |
| 24 |
5 |
96.68 |
2 |
3 |
41.91 |
43.06 |
42.65 |
44.72 |
The quadratic polynomial model that links the responses qs and FBU as a function of independent parameters was established using the following relationship:
| |
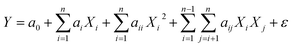 | (E1) |
where
Y is the predicted response;
a0,
ai,
aii and
aij are the constant, linear, quadratic and interaction values of regression coefficients, respectively;
Xi and
Xj are the coded variables;
i and
j are the coded independent parameters; and
ε and
n are the residual term and the number of variables, respectively.
29
2.4.3. Modeling of the breakthrough curves. The shape of the breakthrough curves is an essential characteristic for the description of the adsorption dynamics. In order to model the breakthrough curves well, four mathematical models, Thomas,30 Bohart–Adams,31 Yoon–Nelson32 and Yan,33 were tested. The equations of these models can be expressed as follows:Thomas:
| |
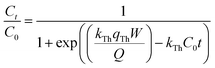 | (8) |
Bohart–Adams:
| |
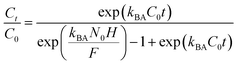 | (9) |
Yoon–Nelson:
| |
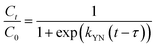 | (10) |
Yan:
| |
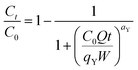 | (11) |
where
kTh (mL min
−1 mg
−1) and
qTh (mg g
−1) are the kinetic rate and the adsorption capacity of the Thomas model,
kBA (mL min
−1 mg
−1) is the kinetic rate of the Bohart–Adams model,
N0 (mg L
−1) is the saturation concentration,
F (cm min
−1) is the linear rate of the solution (
F =
Q/
A),
A (cm
2) is the section area of the column
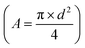 d
d (cm) is the internal diameter of the column,
qY (mg g
−1) and
aY (mL min
−1 mg
−1) are the adsorption capacity and the rate constant of the Yan model, respectively,
kYN (min
−1) is the rate constant of the Yoon–Nelson model and
τ (min) is the time taken to reach 50% of
C0.
2.5. Desorption and regeneration study
Column regeneration tests were performed by eluting the saturated bed with desorbing agents such as 0.10 M NaOH and 0.10 M HCl at a constant flow rate of 2 mL min−1 until a residual concentration of atrazine was less than 5% of C0. The regenerated bed was then rinsed several times with distilled water at 2 mL min−1 for 1 h and then reused for the next adsorption/desorption cycle three times.
2.6. Statistical analysis
The reliability of the fitting of the experimental data to the models was checked using the values of the coefficient of determination (R2), the sum of the square errors (SSE) and the Chi-squared test (χ2). A high R2 value and low values for SSE and χ2 reveal a good fit between the experimental and calculated data. R2, SSE and χ2 are expressed using the following relationships:34| |
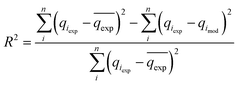 | (12) |
| |
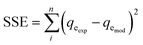 | (13) |
| |
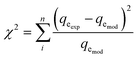 | (14) |
where qeexp and qemod (mg g−1) are the experimental and calculated adsorption capacities from the model equation.
3. Results and discussion
3.1. Characteristics of MCHAC
The FTIR spectrum of the MCHAC composite is shown in Fig. 2A. The spectrum reveals a broad band near 3430 cm−1, characterizing the stretching vibration of O–H from the composite structure.21 The peaks observed at 2918 and 2858 cm−1 were assigned to the stretching vibration of C–H bonds from chitosan and activated carbon,35,36 respectively. The band at 1635 cm−1 can be attributed to the vibration stretching of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O in carbonyl groups.25,37 The bands at 1352, 1165 and 1071 cm−1 can be assigned to the vibration stretching of C–N and the C–O–C bridge in chitosan.38 In addition, the peak at 916 cm−1 may be attributed to the O–H bending vibration.23 Finally, the intense band at 584 cm−1 was characteristic of the magnetic phase and was assigned to the stretching vibration of Fe–O bonds in the composite.35,39 These observations suggested that magnetite, chitosan and activated carbon were successful combined in the MCHAC composite.
O in carbonyl groups.25,37 The bands at 1352, 1165 and 1071 cm−1 can be assigned to the vibration stretching of C–N and the C–O–C bridge in chitosan.38 In addition, the peak at 916 cm−1 may be attributed to the O–H bending vibration.23 Finally, the intense band at 584 cm−1 was characteristic of the magnetic phase and was assigned to the stretching vibration of Fe–O bonds in the composite.35,39 These observations suggested that magnetite, chitosan and activated carbon were successful combined in the MCHAC composite.
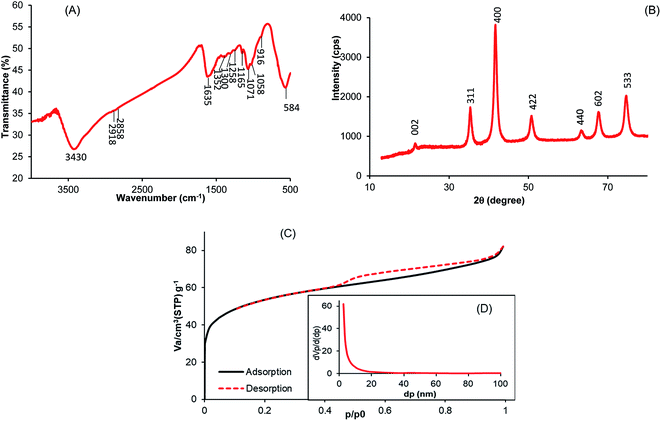 |
| | Fig. 2 (A) IRFT spectrum of MCHAC; (B) XRD pattern of MCHAC; (C) N2 adsorption/desorption onto MCHAC; (D) pore distribution of MCHAC. | |
Fig. 2B shows the X-ray diffraction pattern of MCHAC, revealing that the composite has a crystalline structure with six characteristic peaks at 2θ = 35.43°, 41.70°, 50.94°, 63.70°, 67.53° and 74.84°, which can be attributed to the (311), (400), (422), (440), (602) and (533) planes of Fe3O4 (JCPDS no. 96-591-0064), respectively,24,27,38,40 indicating the presence of magnetite in MCHAC. In addition, the diffraction peak with low intensity observed at 2θ = 21.51° may be assigned to the (002) plane of the cellulose I structure in chitosan (JCPDS no. 03-0226).13,15 The results also reveal that the peaks for activated carbon do not appear in the pattern of MCHAC because of the amorphous structure of the carbonaceous material.17,36
The plot of the N2 physisorption of MCHAC at 77 K shown in Fig. 2C reveals a type IV isotherm with a H3 hysteresis loop at relatively high pressure, suggesting that it has a mesoporous structure. The textural parameters determined from Fig. 2D are 189.50 m2 g−1, 0.1263 cm3 g−1 and 2.66 nm for the specific surface area, the total volume of pores and the mean pore diameter, respectively, confirming the mesoporous structure of MCHAC. The results in Table 3 show that the specific surface area of MCHAC was found to be less than the 458.22 m2 g−1 measured for AC and greater than the 100 m2 g−1 determined for Fe3O4. This suggests that the pores of the AC particles are clogged with magnetite nanoparticles and chitosan particles. Furthermore, the specific surface area of MCHAC was also found to be less than the 204 m2 g−1 observed by Danalioglu et al.25 for an AC/CH/Fe3O4 composite and higher than the 162.99 m2 g−1 and 123.83 m2 g−1 values reported by Tang and Karaer et al.35,41 for multi-walled carbon nanotubes (MWCNTs) and CTN/AC-Fe3O4 composites, respectively. Therefore, the high specific surface area of MCHAC suggests that it has better potential for adsorption.
Table 3 Textural parameters of AC, CH, Fe3O4 and MCHAC
| |
Specific surface area (m2 g−1) |
Total volume of pore (cm3 g−1) |
Mean diameter of pore (nm) |
| AC |
458.22 |
0.230 |
2.42 |
| CH |
0.14 |
0.0293 |
831.29 |
| Fe3O4 |
100 |
0.297 |
11.86 |
| MCHAC |
189.50 |
0.126 |
2.66 |
3.2. Fixed bed column study
3.2.1. Statistical analysis and model fitting. The results of the analysis of variance (ANOVA) are shown in Tables 4 and 5. The results reveals an F-value of 47.53 and P-value of <0.0001 for qs (Table 4), and an F-value of 54.45 and P-value of <0.0001 for the FBU (Table 5), indicating a good fit of the models to the experimental data. In addition, the significance that the coefficients have on the adsorption process was explored using the P-value (Tables 4 and 5). In the case of the adsorption capacity qs, the P-value was <0.05 for pH, concentration, bed depth and interactions between pH × concentration, pH × bed depth and pH × pH, which suggests that these factors significantly influence the adsorption process. However, the interaction between concentration × bed depth (P-value = 0.2612 > 0.05) insignificantly affects the process. Moreover, only pH × bed depth and concentration × bed depth interactions significantly affect the FBU. In addition, the adjusted values of R2 0.9529 for qs and 0.9587 for FBU are high and on the same magnitude as the predicted values of 0.9122 and 0.9225, respectively. The difference between the adjusted and the predicted values of R2 is less than 0.05, which also implies good agreement between the experimental responses and those predicted. The high values of the ratios of 22.696 and 25.123 also confirm the applicability of the model in optimizing the adsorption process.
Table 4 ANOVA factors for qs
| Source |
Sum of squares |
df |
Mean square |
F value |
P value |
| Model |
3939.47 |
10 |
393.95 |
47.53 |
<0.0001 |
| A-pH |
76.41 |
1 |
76.41 |
9.22 |
0.0096 |
| B-concentration |
297.04 |
1 |
297.04 |
35.84 |
<0.0001 |
| C-bed depth |
121.94 |
1 |
121.94 |
14.71 |
0.0021 |
| D-flow rate |
3.61 |
1 |
3.61 |
0.4359 |
0.5206 |
| AB |
232.50 |
1 |
232.50 |
28.05 |
0.0001 |
| AC |
176.62 |
1 |
176.62 |
21.31 |
0.0005 |
| AD |
0.000 |
0 |
|
|
|
| BC |
11.44 |
1 |
11.44 |
1.38 |
0.2612 |
| CD |
0.000 |
0 |
|
|
|
| A2 |
138.07 |
1 |
138.07 |
16.66 |
0.0013 |
| B2 |
13.01 |
1 |
13.01 |
1.57 |
0.2324 |
| C2 |
6.23 |
1 |
0.7516 |
0.4017 |
|
| Residual |
107.75 |
13 |
8.29 |
|
|
| Cor. total |
4047.22 |
23 |
|
|
|
| Std dev. |
2.88 |
R2 |
0.9734 |
Rpred2 |
0.9122 |
| Mean |
28.28 |
Radj2 |
0.9529 |
Adeq Precision |
22.6957 |
| CV |
10.18 |
|
|
|
|
Table 5 ANOVA factors for the FBU
| Source |
Sum of squares |
df |
Mean square |
F value |
P value |
| Model |
6981.44 |
10 |
698.14 |
54.45 |
<0.0001 |
| A-pH |
15.25 |
1 |
15.25 |
1.19 |
0.2953 |
| B-concentration |
12.03 |
1 |
12.03 |
0.9384 |
0.3504 |
| C-bed depth |
1950.53 |
1 |
1950.53 |
152.13 |
<0.0001 |
| D-flow rate |
34.50 |
1 |
34.50 |
2.69 |
0.1249 |
| AB |
8.80 |
1 |
8.80 |
0.6865 |
0.4223 |
| AC |
189.17 |
1 |
189.17 |
14.75 |
0.0020 |
| AD |
0.000 |
0 |
|
|
|
| BC |
91.21 |
1 |
91.21 |
7.11 |
0.0194 |
| CD |
0.000 |
0 |
|
|
|
| A2 |
26.58 |
1 |
26.58 |
2.07 |
0.1736 |
| B2 |
1.28 |
1 |
1.28 |
0.0999 |
0.7570 |
| C2 |
117.05 |
1 |
117.05 |
9.13 |
0.0098 |
| Residual |
166.68 |
13 |
12.82 |
|
|
| Cor. total |
7148.11 |
23 |
|
|
|
| Std dev. |
3.58 |
R2 |
0.9767 |
Rpred2 |
0.9225 |
| Mean |
39.12 |
Radj2 |
0.9587 |
Adeq Précision |
25.1229 |
| CV |
9.15 |
|
|
|
|
To better understand the model's suitability to the experimental results, graphs of the normal probability as a function of the residual values were plotted and the results shown in Fig. 3 reveal that the residual values are near to the normality line, thus, the residual values obtained are normal.
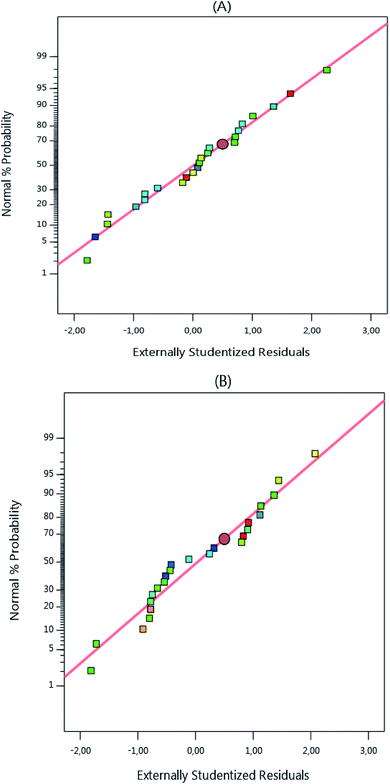 |
| | Fig. 3 Normal probability plots of the atrazine columns. | |
Finally, the reliability of the fit of the quadratic model to the response values was investigated through the regression analysis of eqn (E1). The relationships between the variations of the qs and FBU responses, and the independent variables are given by the following equations:
| | |
qs = 29.00620 − 15.58284 × A + 0.600098 × B + 34.48823 × C − 1.07454 × D – 0.044301 × A × B − 3.20734 × A × C − 0.027631 × B × C + 1.39113 × A2 − 0.000406 × B2 − 1.33206 × C2
| (E2) |
| | |
FBU = 44.36 − 1.60 × A − 1.95 × B + 22.39 × C − 3.32 × D − 1.41 × A × B − 6.64 × A × C + 6.40 × B × C − 2.44 × A2 + 0.8584 × B2 − 5.77 × C2
| (E3) |
3.2.2. Response surface and contour plots. The effects of the four independent variables on the adsorption process were investigated through the surface curves displayed in Fig. 4 and 5. It can be observed from Fig. 4 that qs increases upon increasing the initial concentration C0 of atrazine and the bed depth H, confirming that C0 and H have a positive effect on qs. The results also reveal that qs decreases with an increase in the pH and the flow rate Q. The decrease in the qs values with an increase in the pH may be justified by the progressive appearance of the negative loads on the adsorbent surface, which result in a low interaction between the adsorbent surface and the atrazine molecules, and a decrease in adsorption capacity. Indeed, the point of zero-charge (pHzpc) of MCHAC was found to be 6.8. In addition, atrazine is a weak base with a pKa value of 1.7.42 Increasing the pH led to progressive deprotonation of the functional groups from the composite surface, and also suggested that the atrazine molecules were in the neutral form.43 Moreover, an increase in the Q value led to an increase in the number of atrazine molecules ready to be adsorbed on the surface of adsorbent, which resulted in a decrease in the resistance to mass transfer through the adsorbent bed and reduced the residence time of adsorbate in the column to allow the diffusion of atrazine molecules into the pores of the adsorbent.
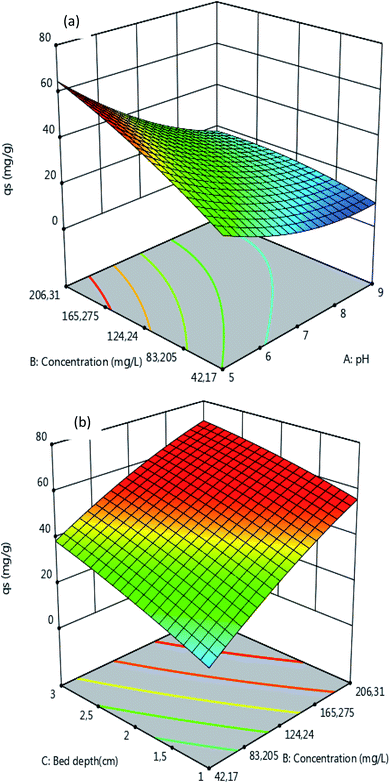 |
| | Fig. 4 Response surfaces of qs as function of the (a) initial concentration and pH (H = 2 cm, Q = 2 mL min−1) and (b) bed depth and initial concentration (pH = 5, Q = 2 mL min−1). | |
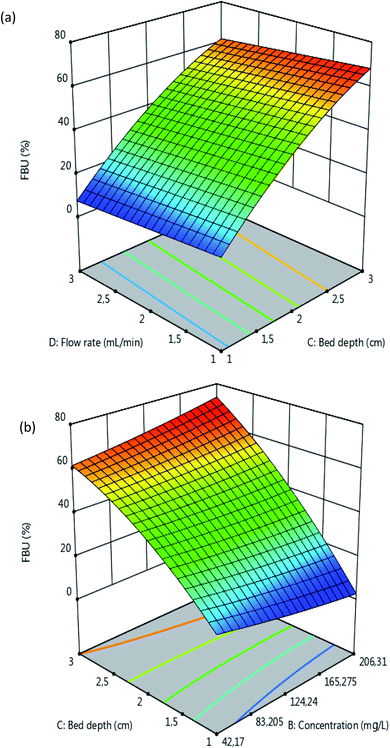 |
| | Fig. 5 Response surfaces of the FBU as a function of the (a) flow rate and bed depth (pH = 5, C0 = 100 mg L−1) and (b) bed depth and initial concentration (pH = 5, Q = 2 mL min−1). | |
The results in Fig. 5 reveal that the FBU values increase with an increase in the bed depth and a decrease in the flow rate. It can also be seen that the FBU values increase with an increase in C0 and the bed depth. These observations can be explained by the fact that at the beginning of the adsorption process with a low concentration of atrazine there is great availability of adsorbent surface for the adsorption to take place. Moreover, the increase in the bed depth led to the increase in the specific surface area of adsorbent, which provided more active sites available for adsorption and justified the increase in the FBU values. In addition, the increase in the values of FBU with increasing in concentration of atrazine may be explained by the higher concentration gradient which occurred at a high initial concentration of atrazine, which then resulted in faster mass transfer through the bed depth of MCHAC.44
Furthermore, to optimize the experimental variables involved in the adsorption of atrazine, eqn (E2) and (E3) were used. The optimization parameters obtained are pH = 5.07, C0 = 137.86 mg L−1, H = 2.99 cm and Q = 1.038 mL min−1, and the maximum response values qs = 59.82 mg g−1 and FBU = 70.64% are displayed in Fig. 6. The experiments were carried out three times with similar conditions such as the optimized conditions, pH = 5.0, C0 = 140 mg L−1, H = 3 cm and Q = 1 mL min−1, to give qs = 62.32 ± 1.32 mg g−1 and FBU = 72.26 ± 2.04%, with deviation values of 0.042 for qs and 0.045 for FBU of less than 0.05, suggesting good similarity between the observed responses and the results predicted by the model.
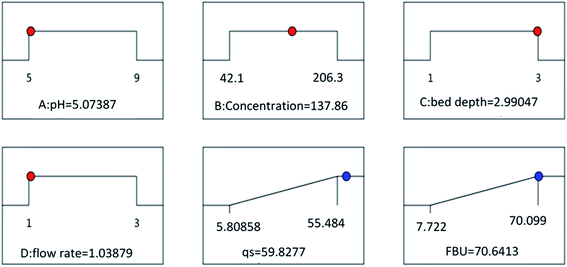 |
| | Fig. 6 Optimization of the conditions. | |
3.2.3. Effects of the parameters on the breakthrough curves.
3.2.3.1 Effects of the solution pH and the initial concentration of atrazine. The effects of pH and of initial concentration were studied at pH 5, 7 and 9 and atrazine concentrations of 42.17, 92.75 and 187.98 mg L−1. The results obtained at fixed values of a bed depth of H = 2 cm and flow rate of Q = 1 mL min−1 are shown in Fig. 7A, B and Table 6. The results depict a decrease in breakthrough time tb, saturation time ts, adsorption capacity at breakthrough qb, adsorption capacity at saturation qs and FBU, suggesting that increasing the pH results in a decrease in the adsorption efficiency of atrazine. In addition, it was revealed from Fig. 7B that tb and ts sharply decrease from 390 to 163 min and from 1620 to 620 min, respectively, with an increase in the atrazine concentration from 42.17 to 187.98 mg L−1 (Table 6). Finally, gradual increases in qb, qs and FBU were also observed upon increasing the atrazine concentration. Similar results were reported by Homem, and Wernke et al.,44,45 in their studies on the adsorption of atrazine and diuron in a fixed-bed column.
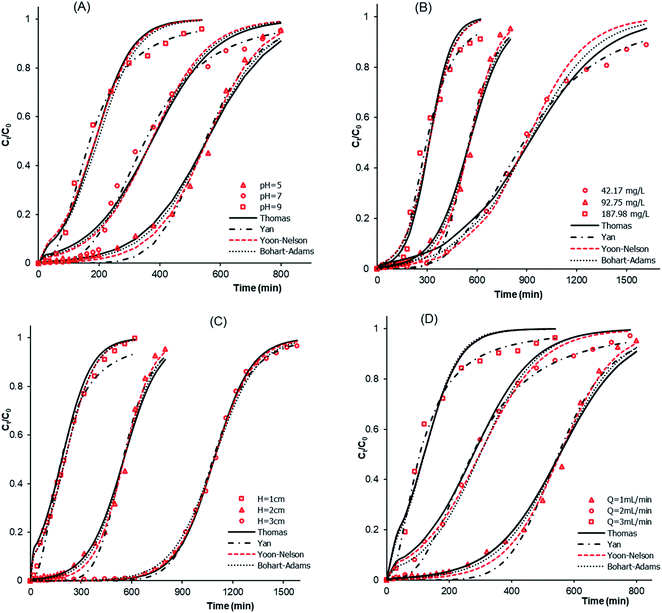 |
| | Fig. 7 Breakthrough curves and modeling showing the effects of the (A) pH of atrazine solution (C0 = 92.75 mg L−1, Q = 1 mL min−1, H = 2 cm), (B) initial concentration of atrazine (pH = 5, Q = 1 mL min−1, H = 2 cm), (C) bed height (pH = 5, C0 = 92.75 mg L−1, Q = 1 mL min−1), and (D) flow rate (pH = 5, C0 = 92.75 mg L−1, H = 2 cm). | |
Table 6 Effects of the parameters on the breakthrough curves
| Parameters |
Atrazine solution pH |
Initial concentration, C0 (mg L−1) |
Bed depth, H (cm) |
Flow rate, Q (mL min−1) |
| |
5 |
7 |
9 |
42.17 |
92.75 |
187.98 |
1 |
2 |
3 |
1 |
2 |
3 |
| tb (min) |
238 |
197 |
75 |
390 |
238 |
163 |
37 |
238 |
750 |
238 |
77 |
30 |
| ts (min) |
800 |
800 |
540 |
1620 |
800 |
620 |
505 |
800 |
1510 |
800 |
730 |
508 |
| qb (mg g−1) |
17.909 |
15.292 |
5.758 |
13.522 |
17.909 |
25.082 |
5.612 |
17.909 |
38.894 |
17.945 |
17.967 |
17.875 |
| qs (mg g−1) |
39.632 |
29.074 |
14.309 |
30.900 |
39.632 |
47.049 |
31.704 |
39.632 |
55.484 |
39.630 |
42.77 |
41.910 |
| FBU (%) |
45.188 |
52.596 |
40.244 |
43.793 |
45.188 |
53.309 |
17.70 |
45.188 |
70.099 |
45.188 |
42.01 |
42.65 |
3.2.3.2. Effects of the bed depth and the flow rate. The effects that the bed depth and flow rate have on the adsorption process were investigated with H values of 1, 2 and 3 cm and Q in the range of 1–3 mL min−1. The results obtained for pH = 5 and C0 = 92.75 mg L−1 are shown in Fig. 7C and D. The results from Fig. 7C show that the tb, ts, qb, qs and FBU values increase with an increase in the bed depth. An increase in the bed depth values led to an increase in the number of available sites on the adsorbent surface, which resulted in significant mass transfer through the adsorbent bed and thus, justified the increase in qb and qs. The increase in tb and ts may be justified by the great resistance to transfer caused by an increase in the bed depth. Lonappan, and Batra et al.,28,46 observed the same trend during the adsorption of diclofenac and bisphenol A in a fixed-bed column. The results presented in Fig. 7D indicate that, tb and ts decrease with an increase in the flow rate. This trend is due to the resistance to mass transfer through the adsorbent bed. In addition, the increase in qs from 39.63 to 41.91 mg g−1 with an increase in the flow rate from 1 to 3 mL min−1 may be due to the decrease in mass transfer resistance. This behavior is in accordance with that noted by Hethnawi et al.47 during the adsorption process of metformin.
3.2.4. Dynamic modeling of breakthrough curves. To better describe the dynamic behavior of the adsorption process, the Thomas, Yan, Yoon–Nelson and Bohart–Adams mathematical models were used to fit the breakthrough curves. The results of the fitting and the calculated parameters are displayed in Fig. 7 and Table 7. All of the breakthrough curves are asymmetrical S-shaped curves, suggesting that the breakthrough curves are composed of two parts corresponding to two different mechanisms of the adsorption process.48 The results of the fitting reveal that the Thomas model is a good fit to the experimental data. Moreover, the adsorption capacity qTh values calculated using the Thomas model are slightly higher than the experimental qs values. In addition, the values of the Thomas parameter kTh increased with an increase in pH and Q values and then decreased with an increase in H and C0. This observation implies that the adsorption mechanism is not controlled by the mass transfer at the interface of the adsorbent.49 Furthermore, the Yan model showed a better fit to the experimental results because the R2 values are close to 1 and the SSE values are too low. In addition, the adsorption capacity qY values calculated according to the Yan equation are close to the qs values. Moreover, the values of the time τ taken to reach 50% of C0 calculated according to the Yoon–Nelson model increased with an increase in the bed depth and decreased with increases in pH, C0 and flow rate (Table 7). Finally, the Bohart–Adams model reveals the highest R2 values and lowest SSE values. This observation also shows that the Bohart–Adams model is a good fit to the experimental results. Therefore, surface diffusion was determined as the rate-limiting step of the adsorption process.50 The values of the maximum volumetric capacity N0 increased with an increase in the bed depth and C0, and then decreased with an increase in flow rate and pH. The results of this study suggest that all of the models tested can be used to describe the adsorption dynamics of the adsorption of atrazine onto MCHAC.
Table 7 Model parameters
| |
Parameters |
Bed depth H (cm) |
Initial concentration C0 (mg L−1) |
Atrazine solution pH |
Flow rate Q (mL min−1) |
| |
|
1 |
2 |
3 |
42.17 |
92.75 |
187.98 |
5 |
7 |
9 |
1 |
2 |
3 |
| |
qsexp (mg g−1) |
31.699 |
39.632 |
55.485 |
30.900 |
39.632 |
47.050 |
39.632 |
29.074 |
14.309 |
39.632 |
42.77 |
41.91 |
| Thomas |
kTh (mL min−1 mg−1) |
0.122 |
0.101 |
0.096 |
0.101 |
0.101 |
0.081 |
0.101 |
0.101 |
0.173 |
0.101 |
0.104 |
0.184 |
| qTh (mg g−1) |
29.470 |
42.844 |
57.137 |
32.375 |
42.844 |
49.032 |
42.844 |
29.545 |
14.728 |
42.844 |
46.948 |
29.951 |
| R2 |
0.997 |
0.995 |
0.997 |
0.995 |
0.995 |
0.986 |
0.995 |
0.992 |
0.990 |
0.995 |
0.997 |
0.982 |
| SSE |
0.040 |
0.026 |
0.050 |
0.028 |
0.026 |
0.169 |
0.026 |
0.070 |
0.047 |
0.026 |
0.024 |
0.068 |
| Yan |
aY (mL min−1 mg−1) |
2.203 |
6.641 |
9.436 |
3.730 |
6.641 |
3.647 |
6.641 |
3.489 |
2.585 |
6.641 |
2.770 |
2.022 |
| qY (mg g−1) |
29.061 |
42.500 |
56.756 |
31.177 |
42.500 |
46.430 |
42.500 |
27.763 |
13.333 |
42.500 |
44.151 |
25.767 |
| R2 |
0.994 |
0.995 |
0.999 |
0.999 |
0.995 |
0.996 |
0.995 |
0.998 |
0.999 |
0.995 |
0.998 |
0.997 |
| SSE |
0.030 |
0.033 |
0.007 |
0.005 |
0.033 |
0.020 |
0.033 |
0.017 |
0.005 |
0.033 |
0.0077 |
0.009 |
| Yoon–Nelson |
kYN (min−1) |
0.011 |
0.012 |
0.009 |
0.006 |
0.012 |
0.013 |
0.012 |
0.011 |
0.015 |
0.012 |
0.010 |
0.018 |
| τ (min) |
206.202 |
555.475 |
1088.380 |
896.104 |
555.475 |
312.988 |
555.475 |
371.752 |
186.249 |
555.475 |
297.562 |
119.778 |
| R2 |
0.996 |
0.997 |
1.000 |
0.996 |
0.997 |
0.989 |
0.997 |
0.992 |
0.990 |
0.997 |
0.996 |
0.983 |
| SSE |
0.017 |
0.014 |
0.005 |
0.053 |
0.014 |
0.065 |
0.014 |
0.069 |
0.046 |
0.014 |
0.023 |
0.067 |
| Bohart–Adams |
kBA (mL min−1 mg−1) |
0.123 |
0.110 |
0.084 |
0.117 |
0.110 |
0.073 |
0.110 |
0.108 |
0.163 |
0.110 |
0.114 |
0.194 |
| No (mg L−1) |
15.820 |
20.200 |
26.917 |
15.222 |
20.200 |
23.074 |
20.200 |
13.970 |
7.378 |
20.200 |
22.951 |
14.359 |
| R2 |
0.996 |
0.997 |
0.994 |
0.996 |
0.997 |
0.989 |
0.997 |
0.992 |
0.987 |
0.997 |
0.996 |
0.984 |
| SSE |
0.018 |
0.018 |
0.008 |
0.035 |
0.018 |
0.065 |
0.018 |
0.070 |
0.050 |
0.018 |
0.026 |
0.068 |
3.2.5. Desorption and regeneration study. The study of the adsorption and desorption of MCHAC was performed in order to determine the applicability and cost-effectiveness of the composite for use in water treatment applications. The columns were regenerated over three cycles using 0.1 M NaOH and 0.1 M HCl solutions as desorbing agents and the breakthrough curves of the regeneration process are displayed in Fig. 8. The results reveal the same trend with slight changes, suggesting that the composite can be regenerated over the three cycles tested. Furthermore, the results in Table 8 indicate a decrease in the saturation time ts from 730 to 610 min with HCl and from 730 to 675 min with NaOH. In addition, a slight increase in the qs and FBU values was noted during the process. The qs values increased from 42.77 to 43.54 mg g−1 with HCl and from 42.77 to 45.99 mg g−1 with NaOH. The higher desorption efficiency of the composite with HCl and NaOH suggests the existence of a high affinity between the desorbing agents and the adsorbed atrazine molecules. In addition, the desorption results shown in Fig. 8B and D reveal a decrease in the contact time of the desorption with HCl (Fig. 8B) and an increase in the contact time of the desorption with NaOH (Fig. 8D). These observations suggest that the use of HCl solution as a column eluent could lead to a partial dissolution of the composite material during the desorption process. However, a significant difference is not observed between the weight of the composite material before and after the three adsorption/desorption cycles attempted, hence, the prepared composite has good recovery efficiency and its use for the treatment of contaminated wastewater would contribute to a significant reduction in the cost of the process. These results are in accordance with those reported by Homem et al.45 and Ali et al.,51 who studied the efficiency of atrazine desorption from Moringa oleifera seed husks and an iron nano-composite material.
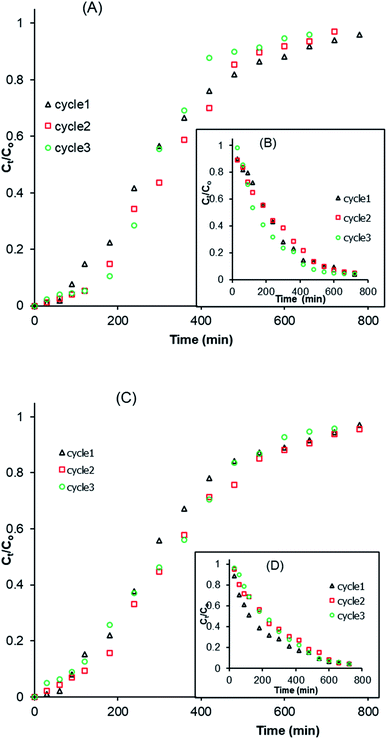 |
| | Fig. 8 Breakthrough curves of the adsorption/desorption of atrazine in a fixed-bed column by MCHAC over three cycles: (A and B) HCl; (C and D) NaOH; (A and C) adsorption; (B and D) desorption (C0 = 96.68 mg L−1, Q = 2 mL min−1, H = 2 cm). | |
Table 8 Fixed-bed column adsorption process parameters for three adsorption/desorption cycles
| |
Parameters |
Desorbing agents |
| HCl |
NaOH |
| Cycle 1 |
ts (min) |
730.00 |
730.00 |
| qs (mg g−1) |
42.77 |
42.77 |
| FBU (%) |
42.01 |
42.01 |
| Cycle 2 |
ts (min) |
685.00 |
760.00 |
| qs (mg g−1) |
49.64 |
51.79 |
| FBU (%) |
44.97 |
42.29 |
| Cycle 3 |
ts (min) |
610.00 |
675.00 |
| qs (mg g−1) |
43.54 |
45.99 |
| FBU (%) |
45.77 |
43.67 |
4. Conclusion
A magnetite/chitosan/activated carbon composite was successfully prepared for the removal of the herbicide atrazine from aqueous solutions in a fixed-bed column system. The characteristics of MCHAC were measured using FTIR spectroscopy, XRD and BET analysis. The results reveal that the prepared material has a crystalline structure, mesoporous surface and a high specific surface area of 189.50 m2 g−1. The results from the RSM-CCD study reveal a value of P < 0.0001 for qs and the FBU. The results also reveal that the MCHAC composite has good adsorption potential for atrazine in aqueous solution with a qs value of 62.32 mg g−1 and an FBU value of 72.26%, obtained under the optimal conditions of pH = 5.07, an initial concentration of atrazine of C0 = 137.86 mg L−1, bed depth H = 2.99 cm and flow rate Q = 1.038 mL min−1. The study of the breakthrough curves modeling suggested that the Bohart–Adams model gave the best fit to the experimental results, with the highest values of R2 and lowest values of SSE. Accordingly, internal and external diffusion of atrazine molecules in the pores of the composite material was found to be the rate-limiting step of the mechanism of the adsorption process. After three cycles of adsorption/desorption, the breakthrough curves revealed the same trend. Overall, the magnetite/chitosan/activated carbon composite shows high adsorption of atrazine from aqueous medium, and high potential for its reusability after three cycles, and can thus be used as a low-cost and efficient adsorbent for atrazine and the removal of other pollutants from contaminated wastewater.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The authors gratefully acknowledge the administration authorities of “Ecole Normale Supérieure” (ENS) of Natitingou, Benin for research funding.
References
- M. A. N. Gbaguidi, H. H. Soclo, Y. M. Issa, B. Fayomi, R. Dognon, A. Agagbe, C. Bonou, A. Youssao, L. F. Dovonou and A. Sanni, Int. J. Biol. Chem. Sci., 2011, 5, 1476–1490 Search PubMed.
- S. A. Abdulelah, K. G. Crile, A. Almouseli, S. Awali, A. Y. Tutwiler, E. A. Tien, V. J. Manzo, M. N. Hadeed and R. M. Belanger, Chemosphere, 2020, 239, 124786 CrossRef CAS.
- C. Sun, Y. Xu, N. Hu, J. Ma, S. Sun, W. Cao, G. Klobucar, G. Hu and Y. Zhao, Chemosphere, 2020, 244, 125514 CrossRef CAS.
- H. Atarodi and H. Faghihian, J. Photochem. Photobiol., A, 2019, 382, 111892 CrossRef CAS.
- S. Komtchou, N. Delegan, A. Dirany, P. Drogui, D. Robert and M. A. El Khakani, Catal. Today, 2020, 340, 323–333 CrossRef CAS.
- Y. Hong, J. Peng, X. Zhao, Y. Yan, B. Lai and G. Yao, Chem. Eng. J., 2019, 370, 354–363 CAS.
- P. N. Chandra and K. Usha, Mater. Today: Proc., 2020 DOI:10.1016/j.matpr.2020.05.263.
- I. A. Saleh, N. Zouari and M. A. Al-Ghouti, Environ. Technol. Innov., 2020, 19, 101026 CrossRef.
- P. K. Boruah, B. Sharma, N. Hussain and M. R. Das, Chemosphere, 2017, 168, 1058–1067 CrossRef CAS.
- A. D. N'Diaye, C. Boudokhane, M. Kankou and H. Dhaouadi, Chem. Ecol., 2019, 35(7), 678–692 CrossRef.
- A. Mojiri, J. L. Zhou, B. Robinson, A. Ohashi, N. Ozaki, T. Kindaichi, H. Farraji and M. Vakili, Chemosphere, 2020, 253, 126646 CrossRef CAS.
- Z. Anfar, H. A. Ahsaine, M. Zbair, A. Amedlous, A. A. El Fakir, A. Jada and N. El Alem, Crit. Rev. Environ. Sci. Technol., 2019, 50(10), 1043–1084 CrossRef.
- J. K. Fatombi, E. A. Idohou, S. A. Osseni, I. Agani, D. Neumeyer, M. Verelst, R. Mauricot and T. Aminou, Fibers Polym., 2019, 20, 1820–1832 CrossRef CAS.
- J. K. Fatombi, I. Agani, S. A. Osseni, E. A. Idohou, D. Neumeyer, M. Verelst, R. Mauricot and T. Aminou, Desalin. Water Treat., 2020, 189, 250–263 CrossRef CAS.
- E. A. Idohou, J. K. Fatombi, S. A. Osseni, I. Agani, D. Neumeyer, M. Verelst, R. Mauricot and T. Aminou, Surf. Interfaces, 2020, 21, 100741 CrossRef.
- Z. Anfar, A. Amedlous, A. A. El Fakir, H. A. Ahsaine, M. Zbair, S. Lhanafi, R. El Haouti, A. Jada and N. El Alem, ACS Omega, 2019, 4, 9434–9445 CrossRef CAS.
- Z. Anfar, A. Amedlous, A. A. El Fakir, M. Zbair, H. A. Ahsaine, A. Jada and N. El Alem, Chemosphere, 2019, 236, 124351 CrossRef CAS.
- L. Spessato, A. L. Cazetta, S. Melo, O. Pezoti, J. Tami, A. Ronix, J. M. Fonseca, A. F. Martins, T. L. Silva and V. C. Almeida, J. Mol. Liq., 2020, 300, 112282 CrossRef CAS.
- F. Mashkoor and A. Nasar, J. Magn. Magn. Mater., 2020, 500, 166408 CrossRef CAS.
- R. Xing, J. He, P. Hao and W. Zhou, Colloids Surf., A, 2020, 589, 124466 CrossRef.
- M. A. Andrade, T. R. T. Santos, M. F. Silva, M. F. Vieira, R. Bergamasco and S. Hamoudi, Sep. Sci. Technol., 2018, 54(16), 2653–2670 CrossRef.
- M. Y. Badi, A. Azari, H. Pasalari, A. Esrafili and M. Farzadkia, J. Mol. Liq., 2018, 261, 146–154 CrossRef.
- C. S. Castro, M. C. Guerreiro, M. Gonc, L. O. A. Oliveira and A. S. Anastacio, J. Hazard. Mater., 2009, 164, 609–614 CrossRef CAS.
- H. Rasoulzadeh, M. H. Dehghani, A. S. Mohammadi, R. R. Karri, R. Nabizadeh, S. Nazmara, K. H. Kim and J. N. Sahu, J. Mol. Liq., 2020, 297, 111893 CrossRef CAS.
- S. T. Danalioglu, S. S. Bayazit, O. K. Kuyumcu and M. A. Salam, J. Mol. Liq., 2017, 240, 589–596 CrossRef CAS.
- S. Qu, J. Wang, J. Kong, P. Yang and G. Chen, Talanta, 2007, 71, 1096–1102 CrossRef CAS.
- P. Marin, R. Bergamasco, A. N. Modenes, P. R. Paraiso and S. Hamoudi, Process Saf. Environ. Prot., 2019, 123, 59–71 CrossRef CAS.
- L. Lonappan, T. Rouissi, Y. Liu, S. K. Brar and R. Y. Surampalli, J. Environ. Chem. Eng., 2019, 7, 102894 CrossRef CAS.
- H. Mahdizadeh and M. Malakootian, Process Saf. Environ. Prot., 2019, 123, 299–308 CrossRef CAS.
- C. H. J. Thomas, J. Am. Chem. Soc., 1944, 66(2), 1664–1666 CrossRef.
- G. S. Bohart and E. Q. Adams, J. Franklin Inst., 1920, 189(5), 669 CrossRef.
- Y. H. Yoon and J. H. Nelson, Am. Ind. Hyg. Assoc. J., 1984, 45(8), 509–516 CrossRef CAS.
- G. Yan, T. Viraraghavan and M. Chen, J. Franklin Inst., 2001, 19(1), 25–43 CAS.
- K. Y. Foo and B. H. Hameed, Adv. Colloid Interface Sci., 2009, 149, 19–27 CrossRef.
- H. Karaer and I. Kaya, Microporous Mesoporous Mater., 2016, 232, 26–38 CrossRef CAS.
- F. C. Cavusoglu, S. Akan, E. A. Ari, E. Cetinkaya, E. Colak, G. N. Dastan, S. Deniz, D. Erdem, M. Koksal, S. Korkmaz, N. Onsekiz, B. Orucoglu, D. Ozkaya, H. B. Uslu, C. Unal, O. Yildiz, S. O. Aydinoglu and S. S. Bayazit, Korean J. Chem. Eng., 2019, 36(11), 1915–1921 CrossRef CAS.
- I. Agani, J. K. Fatombi, N. Topanou, E. A. Idohou and T. Aminou, Am. J. Appl. Chem., 2020, 8(3), 82–88 CrossRef.
- T. Ahamad, M. Naushad and M. Alshahrani, Int. J. Biol. Macromol., 2020, 147, 258–267 CrossRef CAS.
- Z. Weijiang, Z. Yace, G. Yuvaraja and X. Jiao, Int. J. Biol. Macromol., 2017, 105, 422–430 CrossRef.
- M. Malakootian, A. Nasiri and H. Mahdizadeh, Water Sci. Technol., 2018, 78(10), 2158–2170 CrossRef CAS.
- W. W. Tang, G. M. Zeng, J. L. Gong, Y. Liu, X. Y. Wang, Y. Y. Liu, Z. F. Liu, L. Chen, X. R. Zhang and D. Z. Tu, Chem. Eng. J., 2012, 211–212, 470–478 CrossRef CAS.
- L. F. Cusioli, C. O. Bezerra, H. B. Quesada, A. T. A. Baptista, L. Nishi, M. F. Vieira and R. Bergamasco, Environ. Technol., 2019 DOI:10.1080/09593330.2019.1653381.
- M. Shirmardi, N. Alavi, E. C. Lima, A. Takdastan, A. H. Mahvi and A. A. Babaei, Process Saf. Environ. Prot., 2016, 103, 23–35 CrossRef CAS.
- G. Wernke, M. R. F. Klen, M. F. Vieira, P. Y. R. Suzaki, H. K. S. de Souza, Q. L. Shimabuku and R. Bergamasco, Environ. Technol., 2018, 41(5), 638–648 CrossRef.
- N. C. Homem, A. M. S. Vieira, R. Bergamasco and M. F. Vieira, Can. J. Chem. Eng., 2018, 9999, 1–11 Search PubMed.
- S. Batra, D. Datta, S. N. Beesabathuni, N. Kanjolia and S. Saha, Process Saf. Environ. Prot., 2019, 122, 232–246 CrossRef CAS.
- A. Hethnawi, M. Alnajjar, A. D. Manasrah, A. Hassan, G. Vitale, R. Jeong and N. N. Nassar, Colloids Surf., A, 2020, 597, 124814 CrossRef CAS.
- N. Blagojev, D. Kukic, V. Vasic, M. Sciban, J. Prodanovic and O. Bera, J. Hazard. Mater., 2019, 363, 366–375 CrossRef CAS.
- J. Lopez-Cervantes, D. I. Sanchez-Machado, R. G. Sanchez-Duarte and M. A. Correa-Murrieta, Adsorpt. Sci. Technol., 2018, 36(1–2), 215–232 CrossRef CAS.
- P. Liao, Z. Zhan, J. Dai, X. Wu, W. Zhang, K. Wang and S. Yuan, Chem. Eng. J., 2013, 228, 496–505 CrossRef CAS.
- I. Ali, Z. A. Al-Othman and A. Al-Warthan, Int. J. Environ. Sci. Technol., 2016, 13, 733–742 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ab,
Sèmiyou A. Osseni
*ab,
Sèmiyou A. Osseni a,
Esta A. Idohoua,
David Neumeyer
a,
Esta A. Idohoua,
David Neumeyer c,
Marc Verelstc,
Robert Mauricotc and
Taofiki Aminoub
c,
Marc Verelstc,
Robert Mauricotc and
Taofiki Aminoub
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 tons of cotton produced each year. To achieve this performance, large quantities of chemical fertilizers, pesticides and herbicides are imported each year and used for cotton farming. This practice has led to pollution of the aquatic environment by the residues of phytosanitary products.1 Atrazine is one of the triazine herbicides that are very selective and widely used for weed control in cotton and cereal crops. Atrazine is persistent, non-biodegradable and its residues may accumulate in seeds, sediments, fishery products and may contaminate surface water and groundwater. Moreover, atrazine is also classified as a hazardous compound due to the negative impact it has on the aquatic environment and human health.2,3 Thus, several methods such as photodegradation,4 electrocatalytic processes,5 oxidation processes,6 membrane techniques,7 biological treatments8 and adsorption9,10 are used for the removal of atrazine from polluted water. Among these methods, adsorption processes have become very attractive techniques because of their simplicity and low cost.11,12
000 tons of cotton produced each year. To achieve this performance, large quantities of chemical fertilizers, pesticides and herbicides are imported each year and used for cotton farming. This practice has led to pollution of the aquatic environment by the residues of phytosanitary products.1 Atrazine is one of the triazine herbicides that are very selective and widely used for weed control in cotton and cereal crops. Atrazine is persistent, non-biodegradable and its residues may accumulate in seeds, sediments, fishery products and may contaminate surface water and groundwater. Moreover, atrazine is also classified as a hazardous compound due to the negative impact it has on the aquatic environment and human health.2,3 Thus, several methods such as photodegradation,4 electrocatalytic processes,5 oxidation processes,6 membrane techniques,7 biological treatments8 and adsorption9,10 are used for the removal of atrazine from polluted water. Among these methods, adsorption processes have become very attractive techniques because of their simplicity and low cost.11,12
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The chitosan was produced by the deacetylation of chitin extracted from local crab shells collected from markets in Porto-Novo town (Benin). The preparation process and the characteristics of the CH and AC were described in detail in previous work.13
1. The chitosan was produced by the deacetylation of chitin extracted from local crab shells collected from markets in Porto-Novo town (Benin). The preparation process and the characteristics of the CH and AC were described in detail in previous work.13
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n(Fe3+) = 1
n(Fe3+) = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 was dissolved in 100 mL of distilled water under stirring at 300 rpm for 2 h. Then, a solution of 2.5% (w/v) of chitosan was prepared by dissolving 5.0 g of chitosan in 250 mL of a 5% acetic acid solution under stirring for 6 h. After preparing, the chitosan solution was added to a solution of a mixture of (Fe2+/Fe3+). After 6 h of stirring at 300 rpm, 10 g of activated carbon was introduced into the system. The obtained suspension was shaken for 6 h and then, 10 mL of 8 M NH4OH (28%, Sigma-Aldrich) solution was added dropwise. The measured pH of the resulting mixture was in the range of 11–12. Then, the suspension was stirred using a helix agitator at 100 rpm under hydrothermal treatment at 80 °C for 3 h. The formed precipitate was collected using a magnet and then washed several times with distilled water and finally using 250 mL of absolute ethanol (96%, Sigma-Aldrich). The obtained MCHAC composite was oven dried at 60 °C for 12 h, and then crushed and sieved (0.1 mm to 0.2 mm). The schematic process of the preparation of the MCHAC composite is shown in Fig. 1.
2 was dissolved in 100 mL of distilled water under stirring at 300 rpm for 2 h. Then, a solution of 2.5% (w/v) of chitosan was prepared by dissolving 5.0 g of chitosan in 250 mL of a 5% acetic acid solution under stirring for 6 h. After preparing, the chitosan solution was added to a solution of a mixture of (Fe2+/Fe3+). After 6 h of stirring at 300 rpm, 10 g of activated carbon was introduced into the system. The obtained suspension was shaken for 6 h and then, 10 mL of 8 M NH4OH (28%, Sigma-Aldrich) solution was added dropwise. The measured pH of the resulting mixture was in the range of 11–12. Then, the suspension was stirred using a helix agitator at 100 rpm under hydrothermal treatment at 80 °C for 3 h. The formed precipitate was collected using a magnet and then washed several times with distilled water and finally using 250 mL of absolute ethanol (96%, Sigma-Aldrich). The obtained MCHAC composite was oven dried at 60 °C for 12 h, and then crushed and sieved (0.1 mm to 0.2 mm). The schematic process of the preparation of the MCHAC composite is shown in Fig. 1.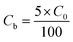
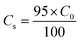
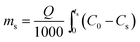
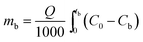
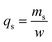
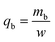
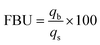
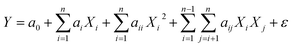
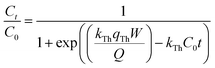
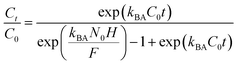
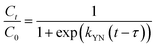
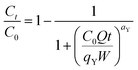
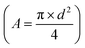 d (cm) is the internal diameter of the column, qY (mg g−1) and aY (mL min−1 mg−1) are the adsorption capacity and the rate constant of the Yan model, respectively, kYN (min−1) is the rate constant of the Yoon–Nelson model and τ (min) is the time taken to reach 50% of C0.
d (cm) is the internal diameter of the column, qY (mg g−1) and aY (mL min−1 mg−1) are the adsorption capacity and the rate constant of the Yan model, respectively, kYN (min−1) is the rate constant of the Yoon–Nelson model and τ (min) is the time taken to reach 50% of C0.
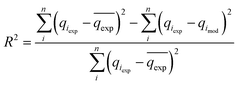
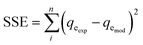

![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O in carbonyl groups.25,37 The bands at 1352, 1165 and 1071 cm−1 can be assigned to the vibration stretching of C–N and the C–O–C bridge in chitosan.38 In addition, the peak at 916 cm−1 may be attributed to the O–H bending vibration.23 Finally, the intense band at 584 cm−1 was characteristic of the magnetic phase and was assigned to the stretching vibration of Fe–O bonds in the composite.35,39 These observations suggested that magnetite, chitosan and activated carbon were successful combined in the MCHAC composite.
O in carbonyl groups.25,37 The bands at 1352, 1165 and 1071 cm−1 can be assigned to the vibration stretching of C–N and the C–O–C bridge in chitosan.38 In addition, the peak at 916 cm−1 may be attributed to the O–H bending vibration.23 Finally, the intense band at 584 cm−1 was characteristic of the magnetic phase and was assigned to the stretching vibration of Fe–O bonds in the composite.35,39 These observations suggested that magnetite, chitosan and activated carbon were successful combined in the MCHAC composite.








