Open Access Article
Open Access ArticleInteractions, electronic and optical properties of nanographene–peptide complexes: a theoretical study†
Ruby Srivastava *
*
CSIR-Centre for Cellular and Molecular Biology, Hyderabad, India. E-mail: amitruby1@gmail.com; ruby@ccmb.res.in.
First published on 21st October 2020
Abstract
We studied the interaction of planar phenylalanine (phe), tryptophan (try), tyrosine (tyr); amide asparagine (asn) and glutamine (gln); arginine (arg) side-chains, charged histidine (his-c) and charged lysine (lys-c) side-chains on a nanographene (g) surface by Density Functional theory (DFT) and Time Dependent Density Functional Theory (TDDFT). The occupied number of states by the system at each energy level and relative contribution of a particular atom/orbital has been studied by Density of States (DOS) and Partial Density of States (PDOS) respectively. Atom-in Molecules (AIM) analysis and non-covalent interaction (NCI) PLOT are used to study the interactions in these complexes. The absorption spectra and HOMO–LUMO (HL) gaps are quantitatively analysed to study the correlation between the optical properties of the studied complexes. The HL gap of peptides is larger than the HL gap of graphene–peptide complexes, indicating strong interactions. All the peptides interact from the above the nanographene surfaces. garg, glys-c, gtry and gtyr complexes have smaller bond distance as compared to gasn, ggln, ghis-c and gphe complexes. AIM analysis and (NCI) PLOT showed noncovalent interactions for these complexes. TDDFT calculations indicated the applicability of these complexes as biosensors.
1. Introduction
Graphene, a two-dimensional (2D) sp2-hybridized single atomic layer of carbon material, chemically bonded with hexagonal symmetry, has been used widely with many potential applications1,2 for nanobio-medicine and nanobio-sensing.3–6 Due to its optoelectronic, absorption, sensing and catalytic properties, graphene plays a key role in the development of photovoltaics, optical switches, actuators, photodetectors, photo-catalysts, photo modulators, photo-thermal therapy and bioimaging.1c Graphene has also been widely used as active or scaffold materials,7,8 electronic devices,9–11 energy storage systems,12,13 energy conversion devices,14,15 and bio/chemical sensors.16 It has been seen in recent years that a variety of short peptide probes have been identified as biomarkers for many diseases. The noncovalent graphene–peptide based biosensors are used with excellent diagnostic function, due to large 2D aromatic surface of graphene, immobilization of biomolecules and its π–π stacking interaction. Thus it is necessary to find out the specific adsorption configurations of biological molecules (proteins or peptides) to ensure the availability of one section of the biomolecule to be solvent exposed, and simultaneously, the strong binding of the other section of the biomolecule to the graphene surface. π–π interactions (or stacking) of the aromatic functionalities have been very important interactions between different peptide side chains, between side chain and backbone, and between peptide side chain and graphene surfaces.17–23 Usually graphene has a planar aromatic dominant structure and it binds with peptide side chains with aromatic or amide groups.17,22 Previous reports indicated strong binding affinity between a graphene surface and peptide side chains with planar groups.24–27 π–π interactions plays an important role in the adsorption behavior and peptide orientation preference on a graphene surface, so it is very important to study its interactions. It has been observed that enzyme immobilization on graphene or graphene oxide occurs due to weak interactions, which included hydrophobic, electrostatic, and π–π stacking interactions. Studies conducted for short-chain peptides bonded to graphene indicated that small peptides assemble prefer to the edge or planar surface of graphene via electrostatic or π–π interactions.28–31 As peptides has simple structures, it is usually easy to study graphene–peptide interactions. The conformational changes can also predicted by both experimental32 and theoretical means.33 In a previous study of graphene and carbon nanotubes interaction with phenylalanine (Phe), histidine (His), tyrosine (Tyr), and tryptophan (Trp) molecules, it was observed that the aromatic rings of these amino acids prefer parallel orientation with the plane of graphene and CNTs through π–π interactions.33 Based on the experimental studies,16 we have selected eight arginine (arg), asparagine (asn), glutamine (gln), cationic-histidine (his-c), cationic-lysine (lys-c), phenylalanine (phe), tryptophan (try), tyrosine (tyr) peptides and a nanographene (g) surface to study the electronic, optical properties and interaction of graphene–arginine (garg), graphene–asparagine (gasn), graphene–glutamine (ggln), graphene–cationic histidine (ghis-c), graphene–cationic lysine (glys-c), graphene–phenylalanine (gphe), graphene–tryptophan (gtry) and graphene–tyrosine (gtyr) complexes by DFT and TDDFT methods.2. Calculation method
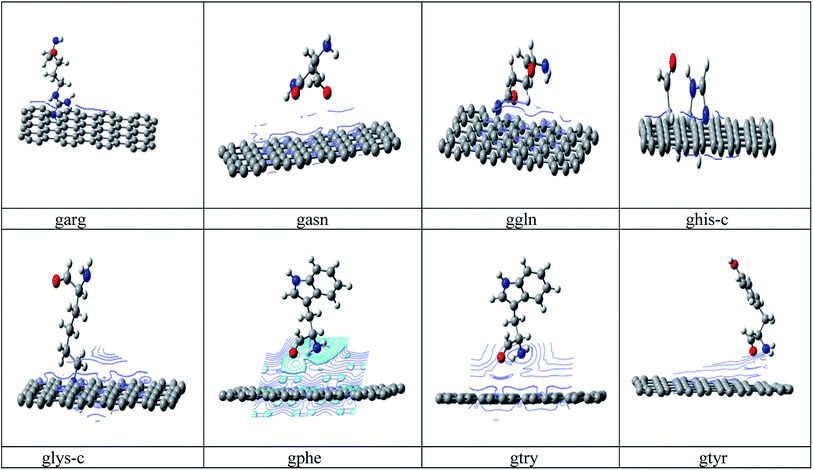
Conformational search has been carried out on all amino acids, (rotation about each single bond) by G09 (ref. 34) software using B3LYP35a/6-31G* method and based on lower energy conformations the final structure has been reoptimized using two different DFT methods. The energy values of the optimized peptide with three different approaches (a)B3LYP35a/6-31 G*, (b) M06 (ref. 35b)/6- 31G* and (c) B3LYP-D2 (ref. 35c)/6-31G* is given in ESI Table 1.† Finally the lowest energies obtained by B3LYP-D2/6-31G(d,p) method is used for all calculations. B3LYP-D2 functional is selected to include the dispersion correction energy term which is relatively simple function of interatomic distances and contain adjustable parameters to fit the conformational and interaction energies.Initial configuration of nanographene is built by Avogadro package36 with UFF force field. The nanographene sheet has a planar neutral singlet structure with 72 carbon atoms. To maintain the consistency of results, the structure of nanographene is reoptimized again with B3LYP-D2/6-31G* method. Vibrational frequency analysis has been carried out for all complexes to confirm the stability of these complexes and it was found that there is no negative frequency for the reported complexes. Various initial spatial (guessed) arrangements of amino acid residue above the nanographene has been made and optimized with B3LYP-D2/6-31G* method and finally the structures with lowest energy minima was reported in Fig. 1. Again vibrational frequency analysis has been carried out for the stability of these nanographene–peptide complexes and no negative frequency has been found for all the reported complexes.
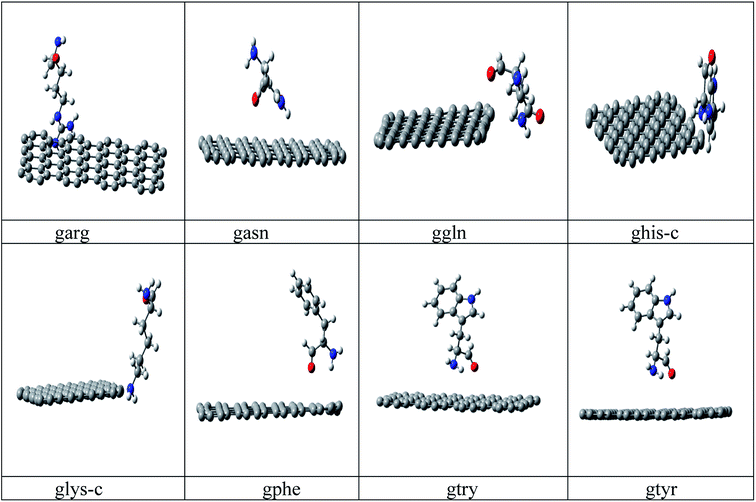 | ||
| Fig. 1 Optimized structures of the studied nanographene–peptide Complexes in aqueous medium by DFT method. | ||
Gaussview37 is used for visualization of structures and NCIPLOT figures. All the calculations have been carried out with self-consistent reaction field (SCRF) theory with polarizable continuum method (PCM).38 The dielectric constant was chosen as the standard value for water (ε = 78.39). TDDFT calculations are also carried out with the same level of B3LYP-D2/6-31G* method, as in terms of reliability also, state-specific dispersion correction is desired, in which the electron redistribution induced by electronic excitation should be reflected in the calculations.
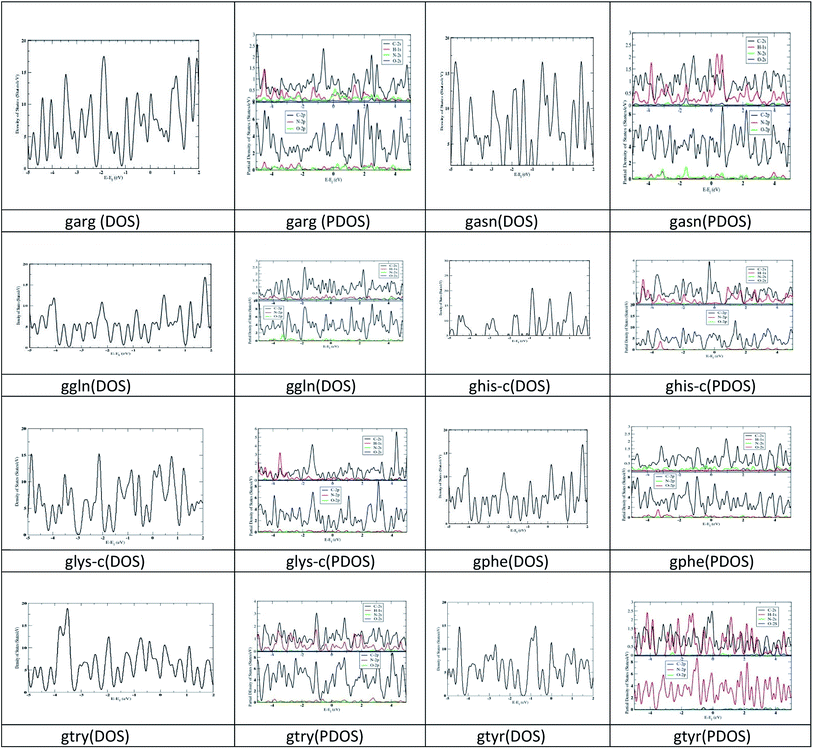
First-principles calculations are performed on the optimized geometries of complexes in solvent (water) using the density functional theory (DFT) approach implemented in SIESTA39 (Spanish Initiative for the Electronic Simulations with Thousands of Atoms) 4.1.b4 program package. In addition, the van der Waals density functional (vdW-DF) as proposed by Dion et al.40 is used to calculate the adsorption energies for these models. The exchange and correction terms are described using generalized gradient approximation (GGA) in the scheme of the Perdew–Burke–Ernzerhof (PBE) functional. Double-ς basis set plus polarization function41 is used for all the calculations. Lattice constant 1 Å, Monkhorst pack of 2 × 2 × 0.5 k-point mesh for Brillouin zone integration, cut-off 300 Ry and Gaussian smearing of 0.10 eV are used for the Density of States (DOS) and partial density of states (PDOS) calculations (Fig. 2).
The properties of bond critical points (BCPs) are performed by AIM analysis with AIM 2000 package.42,43 Two of its charge density-based topological descriptors, i.e. bond path (bp) and the presence of (3, −1) bond critical point (bcp) between interacting atomic basins have proved very useful in inferring the presence of a chemical bonding in these chemical systems, which has been used here for the calculations.
2.1. Atoms-in-molecules analysis
The Laplacian of electron density ∇2ρ(r) at the bond critical point is given by the local expression of virial theorem as,42
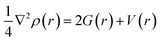 | (1) |
In which G(r) and V(r) are kinetic and potential energy densities respectively. A negative value of ∇2ρ(r) show excess potential energy at BCP, which is the condition of all shared electron covalent interactions. A positive ∇2ρ(r) value shows excess kinetic energy and indicates closed shell electrostatic interaction. It also predicts the depletion of electronic charge over the bond length. The electron density Hamiltonian H(r) is given by the following equation
| H(r) = G(r) + V(r) | (2) |
Koch and Popelier43 proposed both ∇2ρ(r) > 0 and H(r) > 0 for weak and medium bonds; ∇2ρ(r) > 0 and H(r) < 0 for strong hydrogen bonds and both ∇2ρ(r) < 0 and H(r) < 0 for very strong hydrogen bonds.
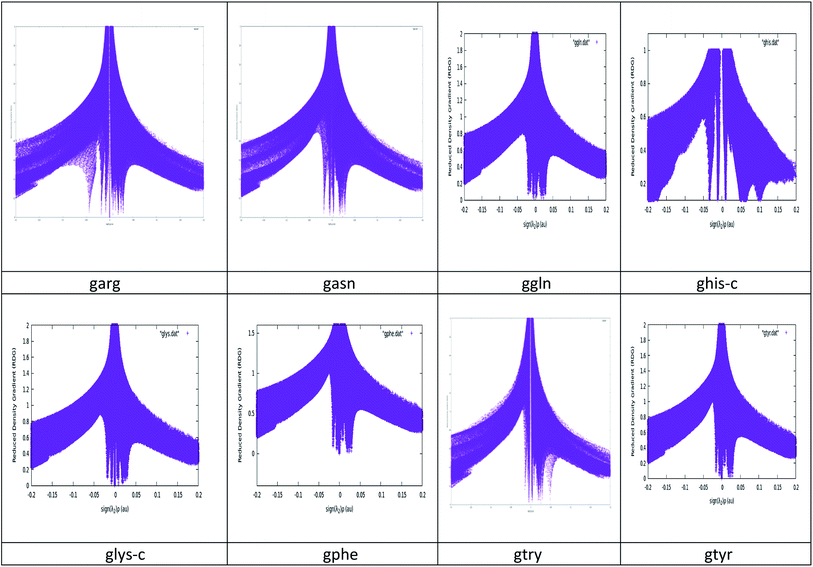
It has been observed in recent years that because of the precise criteria, AIM analysis sometimes failed to identify weakly bound and van der Waals interactions in chemical systems.44–48 So the Reduced Density Gradient-Non Covalent Interaction (RDG-NCI) approach is used to investigate the interactions for graphene–peptide complexes. The detail discussion regarding NCIPLOT49 is given in results section.
3. Results and discussion1
3.1. Optimized geometries of nanographene and peptides
The optimized geometry of nanographene and peptides (arg, asn, phe, gln, his-c, lys-c, try and tyr) are given in ESI Fig. 1.† The HL gap, dipole moment and polarizability of these complexes are given in ESI Table 1.† The polarizability of nanographene is larger (474.22) compared to the peptide molecules. The calculated polarizabilities by our method are slightly higher than the polarizability calculated in a previous study33 by MP2/6-31G* method, yet the polarizability trend remain same for try > tyr > phe > his peptides. The HL gap for nanographene (3.86 eV) is lower than the HL gap of peptide complexes. It has been observed in a previous study that the HL gap of graphene sheet varies as a function of its size and spatial variation of the electron density across the nano-graphene sheet.2c Peptide complexes asn, gln, phe and tyr have higher HL gaps. The trend of HL gap is gln > phe > asn > tyr > lys-c > his-c > try > arg. No correlation has been observed between polarizability and HL gap for the peptide complexes. The dipole moment of nanographene sheet and peptide complexes is between (0.001–5.421) debye. DOS and PDOS analysis has also been carried out for the studied structures. The DOS structures show larger band gap for asn, gln, phe and tyr and smaller band gap for nanographene and other peptides, which has been verified by the HL gap values with DFT calculations also. See ESI Fig. 2.† PDOS figures show that the HOMO, LUMO of these nanographene–peptide complexes are solely from π electrons. See ESI Fig. 3.†3.2. Adsorption energies and geometries
The adsorption energy of the studied complexes is calculated by the formula:| Ead = Eg–pep − Eg − Epep | (3) |
| Complexes | Bond distance (Å) | −Ead (eV) | Charge (C) | Charge (N/O) | Δq | |
|---|---|---|---|---|---|---|
| B3LYP-D2 | GGA (vdW) | |||||
| garg | 2.919 | 11.87 | 11.09 | 0.0644 | 0.0001 N | 0.0643 |
| gasn | 5.038 | 9.78 | 8.47 | 0.0563 | −0.4577 O | 0.4014 |
| ggln | 6.185 | 13.84 | 12.43 | 0.0633 | 0.0000 N | 0.0633 |
| ghis-c | 6.152 | 16.61 | 16.07 | 0.0142 | 0.0000 N | 0.0142 |
| glys-c | 3.824 | 21.16 | 20.88 | 0.1132 | −0.4402 O | 0.3270 |
| gphe | 5.543 | 13.70 | 12.97 | 0.0072 | −0.3309 O | 0.3237 |
| gtry | 4.727 | 13.83 | 13.68 | −0.1427 | −0.3287 O | 0.1860 |
| gtyr | 4.845 | 13.81 | 12.88 | 0.0598 | 0.0001 O | 0.0597 |
| Complexes | HL gap (eV) | Dipole moment (D) | Polarizability |
|---|---|---|---|
| garg | 3.06 | 7.66 | 536.56 |
| gasn | 3.83 | 2.42 | 514.22 |
| ggln | 3.83 | 2.87 | 548.09 |
| ghis-c | 3.06 | 7.84 | 415.42 |
| glys-c | 4.22 | 2.59 | 444.89 |
| gphe | 3.82 | 2.48 | 526.18 |
| gtry | 3.64 | 2.99 | 552.67 |
| gtyr | 3.84 | 3.04 | 537.31 |
As his-c and lys-c interact to the nanographene in cationic states, the charges on the interacted atom (N/O) is zero. The aromatic rings of the peptides prefer to orient perpendicularly to the plane of the nanographene, indicating weak π–π interactions. We have not found any correlation between the polarizability and the strength of the interaction in our studied complexes. It has been observed that all peptides interact from above the nanographene surfaces.
DOS graph also reflected larger band gap for glys-c, gtyr, gasn and ggln, complexes, while the band gap is small for the other complexes. The peaks are observed at both HOMO and LUMO level. PDOS analysis reflects the significant contribution from the p orbital contribution from carbon atom. The s orbital contribution from nitrogen and oxygen are less significant in these complexes.
3.3. AIM analysis and NCIPLOT analysis
The calculated electron density ρBCP, its Laplacian ∇2ρBCP, total electron energy density HBCP, and its components (the local kinetic energy density) GBCP, and the local potential energy density VBCP for grapheme–peptide complexes are reported in Table 3. The larger ρ value for these complexes indicated its strong interaction. The positive Laplacian HBCP indicates a dominant closed shell (electrostatic) interaction. Hydrogen bond has increased the strength of these complexes. The nature of interactions is determined by the balance between the GBCP and VBCP values. If the absolute ratio of these quantities is less than 0.5, it is a shared interaction. For 0.5 < −Gbcp/VBCP < 1 values, the interaction is partly covalent in nature and for −Gbcp/VBCP > 1, the interaction is noncovalent in nature. In our studied complexes, these interactions are noncovalent as the absolute values for −Gbcp/VBCP > 1.50| Complexes | ρBCP | ∇2ρBCP | GBCP | VBCP | HBCP | −GBCP/VBCP |
|---|---|---|---|---|---|---|
| garg | 0.18337 | 0.018567 | 0.267603 | −0.265170 | 0.511774 | 1.01 |
| gasn | 0.02707 | −0.03092 | 0.027812 | −0.003100 | 0.024705 | 8.95 |
| ggln | 0.25398 | 0.14260 | 0.352636 | −0.345242 | 0.547878 | 1.02 |
| ghis-c | 0.40865 | −1.80950 | 0.423888 | −0.414388 | 2.638276 | 1.02 |
| glys-c | 0.01937 | −0.01611 | 0.014526 | −0.001584 | 0.012941 | 9.17 |
| gphe | 0.00375 | −0.003490 | 0.002761 | −0.000733 | 0.002028 | 3.77 |
| gtry | 0.01165 | −0.010670 | 0.008512 | −0.002159 | 0.006352 | 3.94 |
| gtyr | 0.18173 | 0.027842 | 0.253700 | −0.251543 | 0.475244 | 1.01 |
NCI plots avoid complex algorithms and numerical pitfalls and offer valuable crystal bonding information, so the interactions have been studied by NCIPLOT graphs and isosurfaces. From NCIPLOT graphs, we plotted the reduced density gradient as a function of the density (mapped as isosurfaces) over the molecule of interest. The sign of the second Hessian eigen value times the electron density (sign (λ2)ρ) au help us to visualize the attractive/stabilizing (favourable) or repulsive (unfavourable) interactions. The second ingredient of the NCI index classifies the interactions as attractive or repulsive according to the sign of the second density Hessian eigen value (λ2). NCI plot also allows an assessment of host–guest assembly complementarities and the extent to which weak interactions stabilize a complex along with the qualitative information regarding the involved molecular regions in the interaction. Red–blue–green colour scheme defines the nature of interactions. RDG (s) and electron density (ρ) combination allowed a rough partition of real space into bonding regions: high-s low-ρ corresponds to non-interacting density tails, low-s high-ρ to covalent bonds, and low-s low-ρ to noncovalent interactions. The value of sign(λ2)ρ is color-mapped onto the s-isosurfaces. The favoured color scheme is a red-green-blue scale with red for ρ+cut (repulsive) and blue for ρ−cut (attractive). We obtained the purple color for the studied complexes which is more inclined towards blue region. The electron density alone clearly distinguishes between the hydrogen bonds (the peak at sign(λ2)ρ ≅ −0.05 and the rest of the intermolecular interactions, represented by the wide band around zero density. The three-dimensional plot identifies the bonding regions corresponding to each of these peaks. The hydrogen bonds appear as round, much localized, blue NCI domains. The localized, high-density NCI regions for hydrogen-bonds indicate a relatively strong, highly-directional, intermolecular interaction while the weak interactions extend over large regions of intermolecular contacts. A cut-off value of s close to zero, typically s < 0.5, is chosen in order to recover all the noncovalent interactions in the system, i.e. all the spikes of the 2D plots. The corresponding reduced density gradient isosurfaces give rise to closed domains in the molecular space which highlighted the spatial localization of the interactions within the system. See Fig. 3. The blue color of isosurface shows the existence of a strong electrostatic stabilizing contribution to the interaction. See Fig. 4. The hydrogen bonding interactions play a very important role in graphene–peptide complexes as the geometrical shape, stability and functionality of these functional materials depend on these noncovalent interactions.
 | ||
| Fig. 4 Isosurface Plots of the studied graphene–peptide complexes. Gaussview has been used to generate these surfaces with isovalue = 0.0001. | ||
3.4. Optical properties
In previous studies,51,52 the absorption spectra and HOMO–LUMO (HL) gaps were analysed to study the correlation between the optical properties of graphene complexes, so TDDFT calculation has been carried out to study the optical properties of nanographene–peptide complexes in aqueous medium. Due to better optical properties of graphene, research interests have been shifted towards achieving improved photoresponse by using graphene as a supporting material. The electron mobility of graphene enables the photo-induced electron transfer in the interacting complex, which results in enhanced behaviour. The absorption wavelength of peptide complexes lies within (137–712 nm), but the absorption wavelength of studied graphene–peptide complexes lies >800 nm range. See Table 4.We find that HL gap of nanographene–peptide complexes are positively correlated to the wavelengths of the studied complexes.| Complexes | λabs (nm) | f | Complexes | λabs (nm) | f |
|---|---|---|---|---|---|
| Graphene | 660.53 | 0.2516 | garg | 989.92 | 0.0215 |
| arg | 230.39 | 0.0122 | gasn | 1076.07 | 0.0312 |
| asn | 137.07 | 0.1247 | ggln | 1192.24 | 0.0036 |
| gln | 149.44 | 0.0280 | ghis-c | 1012.02 | 0.0049 |
| his-c | 261.12 | 0.0727 | glys-c | 872.45 | 0.0021 |
| lys-c | 712.00 | 0.0963 | gphe | 1181.56 | 0.0049 |
| phe | 178.66 | 0.4773 | gtry | 1022.04 | 0.0046 |
| try | 194.82 | 0.6480 | gtyr | 1169.14 | 0.0042 |
| tyr | 181.16 | 0.5686 |
Since the absorption wavelength of studied complexes does not lie in the visible region, we concluded that these complexes can find better application in biosensors rather than the fluorescent materials.
4. Conclusion
First principle calculations have been carried out to study the interactions, electronic and optical properties of eight graphene–peptide complexes. Results indicated strong bond interaction of garg, ggln, glys-c and gphe complexes. We have not observed any correlation between polarizability and bond distance of the studied complexes as shown in a previous study in which polarizability of nucleobase molecules had determined their interaction strength with graphene/CNT.33 Peptides have larger HL gap while nanographene–peptides have smaller HL gap, which showed strong interactions. PDOS figures show that the HOMO, LUMO of these complexes are solely from π electrons. AIM analysis and NCIPLOT results showed strong noncovalent interactions in the studied complexes. TDDFT calculations indicated the applicability of these complexes as biosensors. The absorption wavelength is positively correlated to the HL gap of the complexes. We believe that these studies will be useful for better understanding of peptide binding with planar carbon nanostructures, which has great implications toward developing biosensors. This interfacial graphene–biomolecules interaction permits peptides to exhibit excellent activity for nanobio-technological applications.Conflicts of interest
There are no conflicts to declare.Acknowledgements
RS acknowledges the financial assistance by DST WOSA project (SR/WOS-A/CS-69/2018). RS is also thankful to her Mentor Dr Shrish Tiwari, Bioinformatics, CSIR-Centre for Cellular and Molecular Biology, and Dr G. Narahari Sastry, Director, CSIR-NEIST for the technical support.References
- (a) A. E. Rossini, F. Gala, M. Chinappi and G. Zollo, Nanoscale, 2018, 10(13), 5928–5937 RSC; (b) Y. Y. Hu, S.-L. Sun, S. Muhammad, H.-L. Xu and Z.-M. Su, J. Phys. Chem. C, 2010, 114(46), 19792–19798 CrossRef CAS; (c) H. Chia, K. Muralia, T. D. Lia and S. Thomas, Prog. Nat. Sci.: Mater. Int., 2019, 29, 603–611 CrossRef.
- (a) S. R. Russell and S. A. Claridge, Anal. Bioanal. Chem., 2016, 408, 2649–2658 CrossRef CAS; (b) I. Saada and J. K. Pearson, J. Mol. Struct.: THEOCHEM, 2011, 969, 76–82 CAS; (c) S. Banerjee and D. Bhattacharyya, Comput. Mater. Sci., 2008, 44(1), 41–45 CrossRef CAS.
- (a) C. Chung, Y. K. Kim, D. Shin, S. R. Ryoo, B. H. Hong and D. H. Min, Acc. Chem. Res., 2013, 46, 2211–2224 CrossRef CAS; (b) b. J. Min, C.-W. Lee and H. K. Jeong, J. Korean Phys. Soc., 2015, 67, 507–511 CrossRef CAS; (c) W. J. Jeong, J. Bu, L. J. Kubiatowicz, S. S. Chen, Y. Soo Kim and S. Hong, Nano Convergence, 2018, 5, 38–46 Search PubMed.
- Y. Ohno, K. Maehashi and K. Matsumoto, J. Am. Chem. Soc., 2010, 132, 18012–18013 CAS.
- M. Singh, M. Holzinger, M. Tabrizian, S. Winters, N. C. Berner, S. Cosnier and G. S. Duesberg, J. Am. Chem. Soc., 2015, 137, 2800–2803 CrossRef CAS.
- S. S. Chou, M. De, J. Y. Luo, V. M. Rotello, J. X. Huang and V. P. Dravid, J. Am. Chem. Soc., 2012, 134, 16725–16733 CrossRef CAS.
- Y. H. Ng, I. V. Lightcap, K. Goodwin, M. Matsumura and P. V. Kamat, J. Phys. Chem. Lett., 2010, 1, 2222–2227 CrossRef CAS.
- J. L. Vickery, A. J. Patil and S. Mann, Adv. Mater., 2009, 21, 2180–2184 CrossRef CAS.
- C. Berger, Z. Song, X. Li, X. Wu, N. Brown, C. Naud, D. Mayou, T. Li, J. Hass, A. N. Marchenkov, E. H. Conrad, P. N. First and W. A. de Heer, Science, 2006, 312, 1191–1196 CrossRef CAS.
- J. B. Oostinga, H. B. Heersche, X. Liu, A. F. Morpurgo and L. M. K. Vandersypen, Nat. Mater., 2008, 7, 151–157 CrossRef CAS.
- P. Avouris, Nano Lett., 2010, 10, 4285–4294 CrossRef CAS.
- H. W. ang, Q. Hao, X. Yang, L. Lu and X. Wang, Electrochem. Commun., 2009, 11, 1158–1161 CrossRef.
- C. L iu, Z. Yu, D. Neff, A. Zhamu and B. Z. Jang, Nano Lett., 2010, 10, 4863–4868 CrossRef CAS.
- R. Imran Jafri, N. Rajalakshmi and S. Ramaprabhu, J. Mater. Chem., 2010, 20, 7114 RSC.
- L. Qu, Y. Liu, J. B. Baek and L. Dai, ACS Nano, 2010, 4, 1321–1326 CrossRef CAS.
- X. Q. Zou, W. Shuai, J. Joshua, X. Minyu, W. Qiuming, C. L. Brooks III and C. Zhan, J. Am. Chem. Soc., 2017, 139, 1928–1936 CrossRef CAS.
- M. M. Flocco and S. L. J. Mowbray, J. Mol. Biol., 1994, 235, 709–717 CrossRef CAS.
- G. Duan, V. H. Smith and D. F. Weaver, J. Phys. Chem. A, 2000, 104, 4521–4532 CrossRef CAS.
- G. Toth, C. R. Watts, R. F. Murphy and S. Lovas, Proteins: Struct., Funct., Genet., 2001, 43, 373–381 CAS.
- G. B. McGaughey, M. Gagne and A. K. Rappe, J. Biol. Chem., 1998, 273, 15458–15463 CAS.
- S. K. Burley and G. A. Petsko, Science, 1985, 229, 23–28 CrossRef CAS.
- R. Bhattacharyya, R. P. Saha, U. Samanta and P. Chakrabarti, J. Proteome Res., 2003, 2, 255–263 CrossRef CAS.
- Z. E. Hughes and T. R. Walsh, J. Mater. Chem. B, 2015, 3, 3211–3221 RSC.
- R. B. Pandey, Z. F. Kuang, B. L. Farmer, S. S. Kim and R. R. Naik, Soft Matter, 2012, 8, 9101–9109 RSC.
- A. N. Camden, S. A. Barr and R. J. Berry, J. Phys. Chem. B, 2013, 117, 10691–10697 CrossRef CAS.
- N. Dragneva, W. B. Floriano, D. Stauffer, R. C. Mawhinney, G. Fanchini and O. Rubel, J. Chem. Phys., 2013, 139, 174711 CrossRef CAS.
- C. M. Welch, A. N. Camden, S. A. Barr, G. M. Leuty, G. S. Kedziora and R. J. Berry, J. Chem. Phys., 2015, 143, 045104 CrossRef.
- Y. C ui, S. N. Kim, S. E. Jones, L. L. Wissler, R. R. Naik and M. C. McAlpine, Nano Lett., 2010, 10, 4559–4565 CrossRef CAS.
- C.-H. Lu, J. Li, X. L. Zhang, A. X. Zheng, H. H. Yang, X. Chen and G. N. Chen, Anal. Chem., 2011, 83, 7276–7282 CAS.
- S. K. B hunia and N. R. Jana, ACS Appl. Mater. Interfaces, 2011, 3, 3335–3341 CAS.
- S. N. K im, Z. Kuang, J. M. Slocik, S. E. Jones, Y. Cui, B. L. Farmer, M. C. McAlpine and R. R. Naik, J. Am. Chem. Soc., 2011, 133, 14480–14483 CrossRef CAS.
- L. O u, Y. Luo and G. Wei, J. Phys. Chem. B, 2011, 115, 9813–9822 CrossRef CAS.
- C. Rajesh, C. Majumder, H. Mizuseki and Y. A. Kawazoe, J. Chem. Phys., 2009, 130, 124911 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, W. J. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, K. D. Malick, D. A. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Hallacombe, C. P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, J. A. C.02, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- (a) A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS; (b) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS; (c) Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2006, 120(1–3), 215–241 Search PubMed; (d) J. D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 17 CAS.
- R. Dennington, T. A. Keith and J. M. Millam, GaussView, Version 6, Semichem Inc., Shawnee Mission, KS, 2003 Search PubMed.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093 CrossRef CAS.
- M. Brandbyge, J. L. Mozos, P. Ordejón, J. Taylor and K. Stokbro, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65(16), 165401 CrossRef.
- M. Dion, H. Rydberg, E. Schröder, D. C. Langreth and B. L. Lundqvist, Phys. Rev. Lett., 2004, 92, 246401 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6(1), 15–50 CrossRef CAS.
- P. L. A. Popelier, Atoms in Molecules, An Introduction, PrenticeHall, London, 2000, pp. 100–188 Search PubMed.
- U. Koch and P. L. A. Popelier, J. Phys. Chem., 1995, 99, 9747–9754 CrossRef CAS.
- J. R. Lane, J. Contreras-García, J. P. Piquemal, B. J. Miller and H. G. Kjaergaard, J. Chem. Theory Comput., 2013, 9, 3263–3266 CrossRef CAS.
- J. R. Lane, S. D. Schrøder, G. C. Saunders and H. G. Kjaergaard, J. Phys. Chem. A, 2016, 120, 6371–6378 CrossRef CAS.
- S. D. Schrøder, J. H. Wallberg, J. A. Kroll, Z. Maroun, V. Vaida and H. G. Kjaergaard, J. Phys. Chem. A, 2015, 119, 9692–9702 CrossRef.
- C. L. Andersen, C. S. Jensen, K. Mackeprang, L. Du, S. Jørgensen and H. G. Kjaergaard, J. Phys. Chem. A, 2014, 118, 11074–11082 CrossRef CAS.
- D. L. Thomsen, J. L. Axson, S. D. Schrøder, J. R. Lane, V. Vaida and H. G. Kjaergaard, J. Phys. Chem. A, 2013, 117, 10260–10273 CrossRef CAS.
- (a) R. A. Boto, F. Peccati, R. Laplaza, C. Quan, A. Carbone, J.-P. Piquemal, Y. Maday and J. Contreras-Garcia, NCIPLOT4: A new step towards a fast quantification of noncovalent interactions, 2010 Search PubMed; (b) E. R. Johnson, S. Keinan, P. M. Sanchez, J. C. Garcia, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS; (c) J. Contreras-Garcia, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632 CrossRef CAS.
- E. Espinosa, I. Alkorta, J. Elguero and E. Molins, J. Chem. Phys., 2002, 117, 5529–5542 CrossRef CAS.
- J. G. Feng, H. Z. Dong, L. Yu and L. Dong, J. Mater. Chem. C, 2017, 5, 5984–5994 RSC.
- J. G. Feng, H. Z. Dong, B. Pang, F. Shao, C. K. Zhang, L. Yu and L. Dong, Phys. Chem. Chem. Phys., 2018, 20, 15244–15253 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra07961h |
| This journal is © The Royal Society of Chemistry 2020 |