Open Access Article
Open Access ArticleRemoval of As3+, As5+, Sb3+, and Hg2+ ions from aqueous solutions by pure and co-precipitated akaganeite nanoparticles: adsorption kinetics studies†
Verónica Villacorta *a,
César Augusto Barrero
*a,
César Augusto Barrero a,
María-Belén Turrión
a,
María-Belén Turrión b,
Francisco Lafuenteb,
Jean-Marc Greneche
b,
Francisco Lafuenteb,
Jean-Marc Greneche c and
Karen Edilma García
c and
Karen Edilma García a
a
aSolid State Group, Faculty of Exact and Natural Sciences, University of Antioquia – UdeA, Street 67 N°53-108, Medellín, Colombia. E-mail: vvillacortal@unal.edu.co
bInstitute on Sustainable Forest Management, Department of Agroforestry Sciences, Area of Soil Science and Agricultural Chemistry, University of Valladolid, Palencia, Spain
cInstitut des Molécules et Matériaux du Mans – IMMM UMR CNRS 6283, Université du Maine, Le Mans, Cedex 9, 72085, France
First published on 24th November 2020
Abstract
Adsorption kinetics models have been used to evaluate the adsorption behaviour of pollutants on different materials but there are no reports for the adsorption of As5+, As3+, Sb3+ and Hg2+ on co-precipitated akaganeite nanoparticles which were previously formed in the presence of these ions. In this research, the performance of pure and co-precipitated akaganeite nanoparticles as adsorbents of As3+, As5+, Sb3+ and Hg2+ in aqueous solutions was evaluated using the nonlinear kinetics models of Langmuir, Lagergren, Ho–McKay, Bangham, Elovich and simplified Elovich. In addition, transmission 57Fe Mössbauer spectrometry was used for the first time to compare the physico-chemical properties of akaganeite before and after the adsorption processes. The results showed that co-precipitated akaganeites had much better adsorption capacities than pure akaganeites. On the other hand, the Sb3+ and Hg2+ were the fastest and slowest pollutants respectively adsorbed on all akaganeites. The kinetics models that best described the experimental data for As3+, As5+ and Sb3+ were those of Elovich and simplified Elovich. For Hg2+, the kinetic model that best described the experimental data was that of Bangham. The 300 K and 77 K Mössbauer spectrometry showed only slight variations in some of the hyperfine parameters for the akaganeites after adsorption.
1 Introduction
Akaganeite, the β polymorph of FeOOH, is a natural product of iron corrosion in chloride-containing environments.1,2 This oxyhydroxide has been widely used as a precursor to hematite and other magnetic recording materials3,4 and in the electrocatalysis, pigment, ion-exchange and semiconductor applications.3,5 Furthermore, due to its availability, low cost, large specific surface area, the presence of tunnel sites and the numerous possibilities of synthesis with modified surfaces, akaganeite has been employed as an adsorbent for removing toxic ions such as Zn2+, Pb2+, Cd2+, Cr6+, As3+/As5+, Sb5+, U6+, and antimony and arsenic methylated species from polluted water and nuclear waste streams. In this regard, Guo and co-workers,6 compared the affinity of Sb3+ and Sb5+ for akaganeite. To this end, the authors carried up adsorption experiments at different pH values, for 24 h at 25 °C. The authors reported that the adsorption of Sb3+ was constant over a broad pH range, while the Sb5+ adsorption was favored under acidic conditions. Zhang and Jia,7 synthesized ultra-small and well dispersed akaganeite nanorods and then used them to adsorb As5+. In their kinetic study, the initial As5+ concentrations were 5.20 ppm and the adsorbent dose was 1.0 g L−1. In addition, the suspension was placed into an air incubator at an agitation speed of 150 rpm at 25 °C and a pH of 7.20. The results showed that the adsorption data were well fitted to a pseudo second-order kinetic model. Furthermore, the adsorption rate toward As5+ was very fast, such that most of As5+ could be removed after 1 h. In order to reveal the adsorption mechanism, the authors analysed before and after the adsorbents by FTIR and XPS, and observed that after adsorption the band at 847 cm−1 (assigned to the in-plane bending vibrations of hydroxyl groups of O–H⋯OH2 and O–H⋯Cl hydrogen bonds) was turned weak, and at the same time, a new band at 814 cm−1 was observed. The new band was attributed to As–O vibration of As5+ suggesting the ion-exchange between the hydroxyl groups bonded to the water molecules outside of the tunnels and As5+. Kolbe and co-workers,8 concluded that the best results for the removal of antimonate and arsenate onto akaganeite were achieved under acidic conditions, while the sorption of arsenite had an optimum at pH 7. The maximum loadings varied from 450 mg g−1 (antimonate at pH 2.2) to 2 mg g−1 (trimethyl antimonate at pH 7). Yusan and Erenturk,9 applied the isothermal and kinetics models to explain the U6+ adsorption on akaganeite. Three kinetics models were used to fit the adsorption kinetics data: the pseudo first-order or Lagergren, the pseudo second-order or Ho and McKay and the Morris–Weber intraparticle diffusion models. Kinetics evaluation data showed that the adsorption of U6+ on akaganeite followed well the pseudo second-order kinetic model, highlighting chemical sorption as a step limiting the velocity of adsorption mechanism. Moreover, the authors concluded that the intraparticle diffusion was also the rate-limiting step. Deliyanni and co-workers,10 investigated the zinc removal from aqueous solution by sorption on a nanocrystalline akaganeite. The authors used kinetics models in order to study the mechanism of sorption and potential rate control step. They also observed a complete removal of Zn2+ (10 ppm) at 20 h, pH 6.5 and 25 °C with 1 g L−1 akaganeite concentration. Moreover, the best fit with the experimental data was achieved by application of Elovich's nonlinear kinetic model. Lazaridis and co-workers,11 used nanosized akaganeite to the removal of hexavalent chromium from aqueous solutions. The authors defined the akaganeite sorption capacity from sorption equilibria and sorption kinetics. For the reaction kinetics, the researchers used the pseudo first-order, pseudo second-order and Crank nonlinear adsorption models. Inspection of the regression analysis revealed that intraparticle model yielded a better sum of squares of the residuals than the two reaction kinetics models, and that the second-order kinetic model was superior to the first-order model. They observed a sorption capacity of approximately 9 mg L−1 with akaganeite and Cr6+ concentrations of 1 g L−1 and 10 g L−1, respectively, at 25 °C, pH 6.5 and at 250 minutes. Deliyanni and Matis,12 examined the application of akaganeite for removal of cadmium ions from aqueous solutions through Langmuir and Freundlich sorption isotherms. The evidences obtained by the authors lead to a mechanism of weak chemisorption, which was well modelled by both models.On the other hand, surface-modified akaganeites have shown great potential for environmental applications.13 In this respect, Deliyanni et al.14 developed an adsorbent based on a nanocrystalline–akaganeite hybrid surfactant, which was synthesized using a cationic surfactant, hexadecyl-trimethylammonium bromide, as a modifier. The samples showed a significantly higher adsorption capacity for arsenate than for pure nanocrystalline akaganeite, as well as fast kinetics, which follows a pseudo second-order rate equation. Moreover, the authors observed that adsorption data could not be fitted to the Langmuir equation due to the heterogeneity of the sorbent surface following the modification. Tufo and co-workers,15 studied the adsorption properties of As5+ on Al for Fe substituted akaganeites. The results indicated that Al-substitution enhanced the reactivity of the surface akaganeites towards As-adsorption. Sun and co-workers,16 reported that Zr4+ substituted akaganeites had better adsorption capacities for As3+ and As5+ than pure akaganeites. Harijan and Chandra,17 developed akaganeite nanorods and akaganeite nanorods decorated with graphene oxide sheets at 5%, 10% and 15% for adsorption of phosphate ions from water at pH 7. The FTIR spectra of β-FeOOH nanorods/graphene oxide showed peaks corresponding to akaganeite and a low intense peak corresponding to graphene oxide. When the authors compared the samples after and before of the phosphate adsorption by this technique, they found additional bands corresponding to the P–O stretching vibration in the HPO42− groups. On the other hand, the adsorption experiments showed the maximum removal capacity for an adsorbent dose of 0.4 g L−1, an initial phosphate concentration of 20 ppm, a time of adsorption of 2 h and a temperature of 30 °C. Under these conditions the maximum removal capacity followed the next order: β-FeOOH nanorods/graphene oxide at 5% > β-FeOOH nanorods/graphene oxide at 10% > β-FeOOH > β-FeOOH nanorods/graphene oxide at 15% > graphene oxide. Deliyanni and co-workers,18 prepared and characterized an akaganeite modified with a cationic surfactant. The material was then used as an adsorbent to remove arsenite ions from aqueous solutions. The surfactant modified akaganeite had a much higher arsenite adsorption capacity than the pure akaganeite, which could be attributed to the presence of the surfactant. The kinetics adsorption follows a second-order rate equation and the isothermal sorption the Langmuir and Freundlich models. The maximum adsorption capacity obtained was found between 98 and 100% at pH 7, 25 °C, an adsorbent dose of 1 g L−1, an adsorbate concentration of 10 mg L−1 and 24 h. The authors concluded that arsenite ions reacted with surface OH− functional groups suggesting that specific adsorption occurred. The same authors observed that the maximum adsorption capacity for pure akaganeite under the same conditions was 135.2 mg g−1. Finally, Deliyanni et al.19 synthetized hybrid surfactant akaganeite nanoparticles which showed an efficiency of removal of As3+ from aqueous solution of 100–120 mg g−1 at pH 7.5, 25 °C and a contact time of 2 hours.
According to the bibliography reviewed, most authors have studied the phenomenon of pollutant adsorption on pure akaganeite but only a few on surface-modified akaganeites. We noted that modifying the surface properties of the akaganeites is a good strategy to improve their adsorption properties. One way to do this is to add surfactants and another is to prepare the samples in the presence of different types of cations. We mentioned above that, in the second case, there are reports of akaganeites prepared in the presence of Al3+ and Zr4+ ions. To the best of our knowledge, there are no reports on the use of akaganeite to adsorb Hg2+. Moreover, there are no studies on the adsorption of Sb3+, As5+, and As3+ on modified akaganeites previously co-precipitated in the presence of these ions. In addition, most of the reported works use the isothermal models to define the sorption capacity of akaganeite and for a small number of them, the kinetics models.
In the present study, pure and co-precipitated akaganeites (in the presence of mercury, arsenic and antimony) were used as adsorbents of Sb3+, As5+, As3+ and Hg2+ in aqueous solutions. To understand the adsorption phenomena, we adjust the experimental data to different nonlinear kinetics models. Moreover, the solid samples before and after adsorption were characterized by 57Fe Mössbauer spectrometry at 300 and 77 K. The results showed that the co-precipitated akaganeites had much better adsorption capacities than pure akaganeites, as well as a faster initial average adsorption velocity. The kinetics models that best described the experimental data for As3+, As5+ and Sb3+ adsorbates onto the adsorbents were Elovich and simplified Elovich. In the case of Hg2+ adsorbate was the Bangham nonlinear kinetic model. Mössbauer spectrometry showed slight variations in some of the hyperfine parameters for the akaganeites after adsorption compared to the parameters for the akaganeites before adsorption.
2 Materials and methods
2.1 Adsorbents preparation
Pure and co-precipitated akaganeites were synthesized from 0.05 M FeCl3·6H2O solutions (Merck, EMSURE®, ACS, Reag. Ph Eur.) in the absence and presence of dilute solutions of Hg2+, Sb3+ and As5+ ions at 60 ppm, as described in Villacorta and co-workers.20 The dilute solutions were prepared from standard solutions of Hg(NO3)2, 1000 ppm Hg in 2 M HNO3 (Merck Certipur®), Sb2O3, 1000 ppm Sb in 2 M HCl (Merck Certipur®), and H3AsO4, 1000 ppm As in 0.5 M HNO3 (Merck Certipur®). It is important to mention that the samples were code-named as follows: pAk for pure akaganeite; and Ak60Hg, Ak60Sb and Ak60As for akaganeites co-precipitated with 60 ppm Hg2+, 60 ppm Sb3+ and 60 ppm As5+, respectively.2.2 Physico-chemical characterization of the adsorbents
Pure and co-precipitated akaganeites, prior to adsorption experiments, were characterized by using X-ray diffraction (XRD), high-resolution transmission electron microscopy (TEM) and Raman, IR and Mössbauer spectroscopies. The results obtained by XRD showed that the patterns of co-precipitated samples were similar to that of pure akaganeite, implying that this was the only compound precipitated in all experiments. It is important to highlight that Hg2+, Sb3+ and As5+ did not replace Fe3+ at its crystallographic site, but the pollutants were located at both tunnels and surfaces of akaganeite during the nucleation and growth of the particles. All samples exhibited an acicular morphology, with average particle lengths of 503 ± 39, 29 ± 11, 23 ± 6 and 13 ± 3 nm, and with average particle widths of 107 ± 12, 9 ± 3, 6 ± 2 and 4 ± 1 nm, for pAk, Ak60Hg, Ak60Sb and Ak60As, respectively. From these results, it can be noticed that the pollutants induced dramatic reductions in the particle sizes, and also changed the morphology from nanostructured to nanoparticulated. Now, in order to determine the specific surface area (SSA) of the akaganeites was assumed as a good approximation that the particles exhibit a cylindrical shape. In this way, the SSA can be calculated trough the following equation:
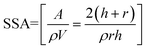 | (1) |
2.3 Kinetics of adsorption
To carry out the adsorption kinetics, solutions of 200 mL at 40 ppm of: (i) As3+ 1000 ppm in NaOH 0.5%, NaCl 0.1% (Merck Certipur); (ii) H3AsO4 in HNO3 0.5 M 1000 ppm As (Merck Certipur®); (iii) Sb2O3 in HCl 2 M 1000 ppm Sb (Merck Certipur®); and (iv) Hg(NO3)2 in HNO3 2 M 1000 ppm Hg (Merck Certipur®), have been brought in contact with 100 mg of pure and co-precipitated akaganeites. Here, visual MINTEQ,21 which is a free software used for solving many kinds of chemical equilibrium problems, was used with the objective to determine the predominant chemical species of Hg2+, As5+, As3+ and Sb3+ formed in the solutions at the actual conditions of adsorption experiments. The values used to perform the simulations were pH: fixed at 2; components names: Hg2+, As5+, As3+ and Sb3+, concentration: 40 mg L−1, temperature: 25 °C and ionic strength: to be calculated.The suspensions were then stirred for 60 minutes at 300 rpm, so that at 1, 3, 6, 9, 12, 20, 40 and 60 minutes, 5 mL aliquots were taken and filtered with a 0.45 μm membrane disc; subsequently, the concentrations of As3+, As5+, Sb3+ and Hg2+ in the aliquots were analyzed by inductively coupled plasma-optical emission spectrometry (ICP-OES) using a Varian 725-ES apparatus.
The temperature of the experiments was controlled at 25 °C, while the pH was about 2. Kolbe and co-workers,8 reported that the best results for the removal of antimonate and arsenate onto akaganeite were achieved under acidic conditions. On the other hand, in the case of acid mine drainage, whose pH can be 2, these pollutants are present, and in nature, mineraloids are the most efficient materials in their decontamination.22
The amount of metal ion adsorbed on the pure and co-precipitated akaganeites at time t, was given by the following equation:
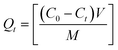 | (2) |
Finally, for the adsorption kinetics, the samples were code-named as follows: pAk-Hg, pAk-Sb and pAk-As3+ for pure akaganeites adsorbing Hg2+, Sb3+ and As3+ pollutants, respectively. Ak60Hg–Hg, Ak60Hg–Sb, Ak60Hg–As3+ and Ak60Hg–As5+ for Ak60Hg samples adsorbing Hg2+, Sb3+, As3+ and As5+ pollutants, respectively. Ak60Sb–Hg, Ak60Sb–Sb, Ak60Sb–As3+ and Ak60Sb–As5+ for Ak60Sb samples adsorbing Hg2+, Sb3+, As3+ and As5+ pollutants, respectively. And, finally, Ak60As–Hg, Ak60As–Sb, Ak60As–As3+ and Ak60As–As5+ for Ak60As samples adsorbing Hg2+, Sb3+, As3+ and As5+ pollutants, respectively.
The experimental data were fitted to the nonlinear kinetics models of Langmuir, Lagergren or pseudo order 1, Bangham, Ho and McKay or pseudo order 2, simplified Elovich and Elovich, with the objective of deciding which model (or models) best describe(s) the data. The equations corresponding to these models are showed in Table S1.†
2.4 Physico-chemical characterization of solids obtained after adsorption
The different akaganeites with adsorbed pollutants were characterized by Mössbauer spectrometry.3 Results and discussion
Regarding the synthesis of akaganeites in the presence of Hg2+, As5+, and Sb3+, it was reported that these pollutants induced changes in the unit cell parameters, the mean crystallite size, the activation energies for akaganeite nucleation and growth and in some vibrational modes.20 All changes were in well agreement with the hypotheses that the pollutants were adsorbed at the surface and in the case of As5+ also at tunnel sites. The average crystallite size determined by Rietveld analysis of the XRD patterns was of 134 ± 19 nm for pure akaganeite (pAk) and of 20 ± 1, 17 ± 1 and 13 ± 1 nm, for Ak60Hg, Ak60Sb and Ak60As, respectively.20In all adsorption kinetics experiments, the pH values were approximately 2 for adsorbing Hg2+, As5+/As3+ and Sb3+. Using the MINTEQ software,21 and considering the pH values of our experiments, we determined that the predominant chemical forms of Hg2+, As5+, As3+ and Sb3+ were: Hg2+ with a total concentration of 96.5%, H3AsO4 and H2AsO4− with a total concentration of 64.8 and 35.2%, respectively, H3AsO3 with a total concentration of 100%, and finally, Sb(OH)2+ and Sb(OH)3 with a total concentration of 20.6 and 79.4%, respectively. These results are consistent with those reported in the literature.23
3.1 Adsorption kinetics
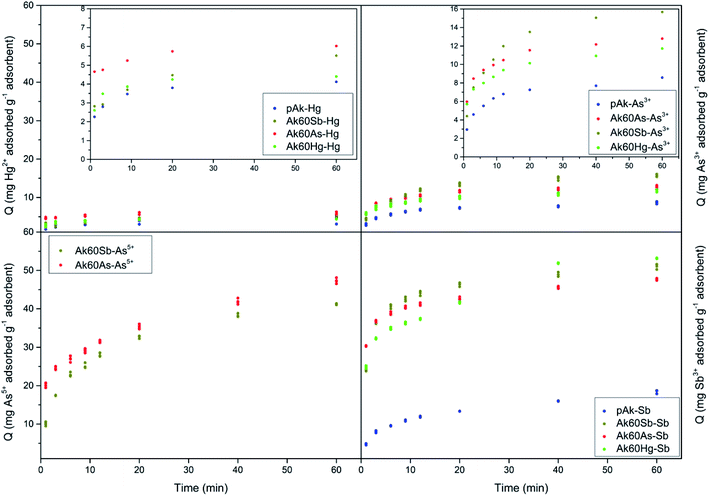
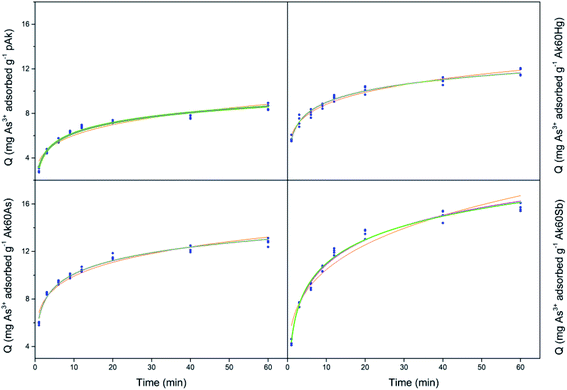
Fig. 1 show the adsorption kinetics of Hg2+, Sb3+, As5+ and As3+ on pure and co-precipitated akaganeites. The adsorption kinetics of As5+ on Ak60Hg were complicated to obtain due to formation of toxic vapours, and therefore are not included.In the construction of the adsorption kinetics for Sb3+ and Hg2+, the three points of the same colour corresponded to Q values collected at the same time and for three different wavelengths of the ICP-OES equipment. In the case of antimony, the readings were at 206.834, 217.582, and 231.146 nm, while mercury at 184.887, 194.164, and 253.652 nm. On the other hand, for As3+ and As5+, the Q data at a given time were collected with four different wavelengths corresponding to four readings at 188.980, 193.696, 197.198 and 234.984 nm.
Now, from Fig. 1, it can be seen that the Q values at 40 and 60 minutes are very similar for co-precipitated samples adsorbing Hg2+. This result could indicate that at 60 minutes the experimental maximum adsorption capacity was probably reached. This situation was different for the co-precipitated samples adsorbing As3+, As5+ and Sb3+ whose kinetics showed a slight continuous increase from 40 to 60 minutes. This result probably suggests the existence of a secondary reaction, surface precipitation or ternary adsorption, which can be seen as the formation of a new surface phase or as a multilayer adsorption due to the continuity of the process beyond adsorption.24–27 In the case of arsenate and arsenite adsorption, it is important to stand out that in agreement with Cornell and Schwertmann,28 the kinetics of adsorption on goethite and ferrihydrite seem to involve two stages: initial rapid adsorption followed by slower adsorption, whose data can be adjusted to the Elovich equation, as in this research was also observed.
For comparative purposes the experimental Q value at 60 minutes was correlated with experimental maximum adsorption capacity, Qmax. Table S2† lists the mean experimental Qmax for the different experiments at t = 60 min. Several interesting observations can be noted from these data. The co-precipitated akaganeites had higher adsorption capacities for the pollutants than pure akageneites. In fact, in the case of Hg2+, As3+ and Sb3+, the co-precipitated akaganeites adsorbed between 1.1 to 1.5, 1.4 to 1.8 and 2.2 to 2.6 times more than the pure akaganeite, respectively. This observation was perhaps due to the fact that the co-precipitated samples had smaller mean particle sizes than pure akaganeite (134 ± 19, 20 ± 1, 17 ± 1 and 13 ± 1 nm for pure akaganeite, Ak60Hg, Ak60Sb and Ak60As, respectively).20 Moreover, the higher adsorption capacity can also be due to the fact that the surface of the co-precipitated akaganeites presented a greater heterogeneity motivated by the presence of different active sites. This idea is in agreement with the structural changes observed in the co-precipitated samples compared with the pure sample due to the incorporation of the pollutants to the surface during the synthesis.20
On the other hand, Sb3+ was the best adsorbed pollutant by pure and co-precipitated akaganeites compared to the other contaminants, while Hg2+ was the least adsorbed one. In fact, the experimental maximum adsorption capacities of pollutants by co-precipitated akaganeites varied, from the highest to the lowest values, in the following order: Sb3+ > As5+ > As3+ > Hg2+. A very interesting result is that the highest experimental Qmax values for a given pollutant were found to be independent of the type of co-precipitated akaganeite, i.e. the type of cation used to synthetized it, suggesting that for the adsorption experiments, the morphological properties of the samples are more important than the type of cations used to prepared it. This result is in good agreement with that reported by Tufo and co-workers,15 who found that the morphological characteristics, in comparison with the Al3+ co-precipitated akaganeites, are the most important factors for the adsorption properties.
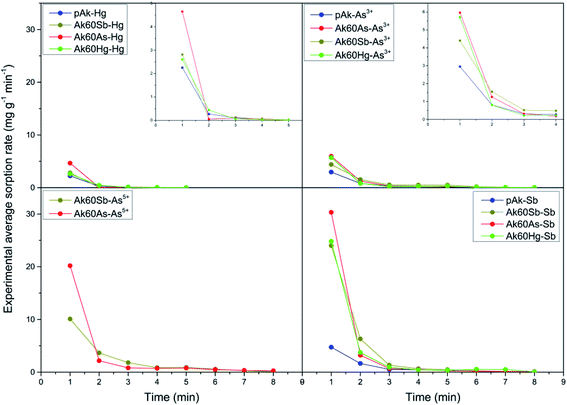
Now, in order to get an idea of the rate at which the pollutants are adsorbed by the adsorbents, we calculated the average sorption velocity, 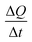 , in mg g−1 min−1, for all samples from the experimental data, using the following equation:
, in mg g−1 min−1, for all samples from the experimental data, using the following equation:
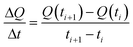 | (3) |
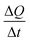 versus ti+1 for the full range of times are shown in Fig. 2. It can be seen that the mean adsorption velocity was very fast at the initial times, and from 3 minutes onwards it went to zero and remained in this value (see also zooms inside graphics of experimental mean sorption rate (mg g−1 min−1) of adsorption of pollutants on akaganeites in the first 6 minutes of adsorption). For all akaganeites, the initial mean sorption velocities of pollutants, from the highest to the lowest, followed the order: Sb3+ > As5+ > As3+ > Hg2+. These results mean that Sb3+ is the most rapidly adsorbed pollutant, while Hg2+ is the slowest adsorbed pollutant by all the akaganeites, in agreement with the order observed above for the maximum adsorption capacity of the pollutants, in which the antimony was the most adsorbed pollutant followed by As5+, As3+ and Hg2+.
versus ti+1 for the full range of times are shown in Fig. 2. It can be seen that the mean adsorption velocity was very fast at the initial times, and from 3 minutes onwards it went to zero and remained in this value (see also zooms inside graphics of experimental mean sorption rate (mg g−1 min−1) of adsorption of pollutants on akaganeites in the first 6 minutes of adsorption). For all akaganeites, the initial mean sorption velocities of pollutants, from the highest to the lowest, followed the order: Sb3+ > As5+ > As3+ > Hg2+. These results mean that Sb3+ is the most rapidly adsorbed pollutant, while Hg2+ is the slowest adsorbed pollutant by all the akaganeites, in agreement with the order observed above for the maximum adsorption capacity of the pollutants, in which the antimony was the most adsorbed pollutant followed by As5+, As3+ and Hg2+.
3.2 Adsorption kinetics models
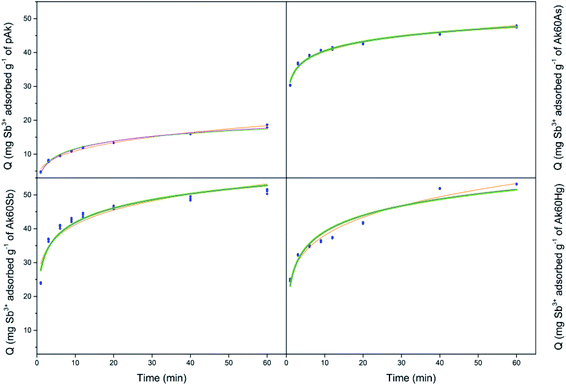
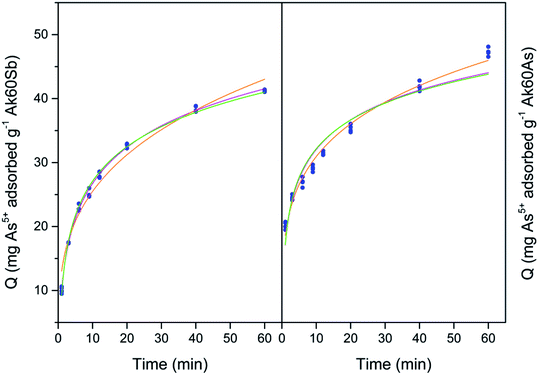
Our next step is to fit the experimental data with different kinetics models, to decide which model(s) correctly describe(s) the data and to better understand the adsorption phenomena. In this study, six nonlinear adsorption kinetics models were used to fit the experimental data. Fig. 3–6 show the adjustment of the experimental data to the nonlinear adsorption kinetics models of Bangham, simplified Elovich and Elovich. The experimental data fit by Langmuir and Ho–McKay kinetics models did not show convergence, and in consequence are not shown here. On the other hand, the fits of the experimental data to the Lagergren model are not shown here because of the high root mean square errors. The values of parameters derived from the adjustments are listed in Table S3.†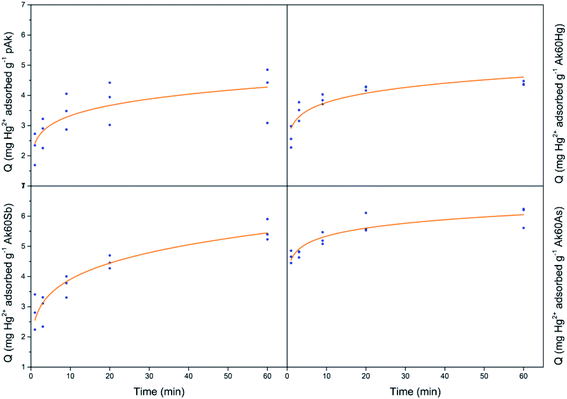 | ||
| Fig. 6 Kinetics of adsorption of Hg2+ onto pAk, Ak60Hg, Ak60Sb, and Ak60As. The experimental data (blue circles) are modelled with Bangham (orange) nonlinear models. | ||
In general, on the basis of a simple visual examination of Fig. 3–6, and on the E values reported in Table S3,† it can be seen that the experimental data are best described for Hg2+ by the Bangham nonlinear kinetic model, and for As3+, As5+ and Sb3+ by Elovich and simplified Elovich nonlinear kinetics models.
According to,29 the Bangham model is an internal diffusion model, meaning that the slowest stage of adsorption refers to diffusion of the adsorbate to active sites located on the adsorbent surface. The values of Qmax obtained from the Bangham equation, 4.2, 4.6, 5.4 and 6.1 mg g−1 to pAk–Hg, Ak60Hg–Hg, Ak60Sb–Hg and Ak60As–Hg, respectively, were very close to those obtained from the experimental Hg adsorption data (see Table S2†).
On the other hand, for Sb3+, As5+ and As3+ the Elovich and simplified Elovich models should be highlighted; indeed, in this case both models are adsorption models in which the slowest step of adsorption is the adsorption itself. In addition, chemisorption prevails over physisorption, and an energetic heterogeneity characterize the surface.29 It is important to recall that α and β parameters refer respectively to the initial sorption rate and an energy activation constant for chemisorption. In Table S3,† it can be observed that the values of α (mg g−1 s−1) increased for co-precipitated akaganeites adsorbing Sb3+, As5+ and As3+ compared with the pure sample. These observations are in agreement with the experimental initial mean sorption rates for Sb3+, As5+ and As3+ adsorption calculated by eqn (2) (see Fig. 2), which changed from the high to the low values in the following order Sb3+ > As5+ > As3+; and with the observation that the Ak60As was the adsorbent on which all adsorbates were adsorbed the fastest during the first minutes (Fig. 2). Similarly, the values of β (g mg−1) decreased in all cases compared with those of the pure sample.
The observations found in the evolution of α and β parameters indicated that As3+, As5+ and Sb3+ probably accessed to the surface of co-precipitated akaganeites easier than to the surface of pure akaganeites, due to the increase of the α parameter and to the decrease of the β parameter compared with those of the pure sample. Some factors that probably influenced the values of α and β parameters are the mean particle size, that was lower for co-precipitated samples compared with pure akaganeite, the heterogeneity of the structure and the different surface active sites.
The agreement between the experimental data and the theoretical predictions based on the Elovich and simplified Elovich models confirms the heterogeneous sorption mechanism that could be responsible for the adsorption of As3+, As5+, and Sb3+ ions. This result is in agreement with the idea of the existence of different adsorption sites, which in the case of akaganeite would refer to tunnel sites and surface sites;16 such as hydroxyl groups28 and in our case the adsorbed As5+ and Sb3+ sites.
On the other hand, the incorporation of the adsorbed species depends fundamentally on the physicochemical characteristics of the adsorbent surface, such as the heterogeneity, specific surface area, the coordination sites, density and arrangement of the functional groups and the surface charge, among others.26,28,30 Moreover, the ionic environment and pH of the solution in contact, the size and nature of adsorbate and the duration of the adsorption, also influence the adsorption process.26,28,30 Here, it is important highlight the relation among the surface charge and the ionic species of the pollutants in solution. According to MINTEQ software, at pH 2 the predominant chemical forms of Hg2+, As5+, As3+ and Sb3+ are: Hg2+ with a total concentration of 96.5%, H3AsO4 and H2AsO4− with total concentrations of 64.8 and 35.2%, respectively, H3AsO3 with a total concentration of 100%, and finally, Sb(OH)2+ and Sb(OH)3 with total concentrations of 20.6 and 79.4%, respectively. In agreement with Deliyanni and co-workers,31 the pzc of akaganeite is approximately 7.3, so below this pH the surface of the akaganeite is positively charged. In this way, the adsorption of As5+ as H2AsO4− could be favoured. However, according with the results obtained in the adsorption kinetics models, the chemisorption prevailed over physisorption and in consequence the formation of internal sphere complexes probably changed the point zero charge since it involved the formation of specific chemical reactions between the surface and the adsorbates.
To complement this information, the free energy of adsorption can be defined as the sum between the chemical energy of adsorption and the electrostatic component: ΔGadsorption = ΔGchemical + ΔGcoulombic.28 In this way, when the affinity between the surface of the material and the ions present in the solution is very high, the chemical component of the adsorption energy predominates, and in consequence the generated bonds have a strong covalent character, causing internal sphere complexes. This situation originates that the adsorption of neutral species or with the same charge of the surface can take place.25,28,30
Finally, the experimental data were less well adjusted to the Lagergren model, which is also an adsorption model where the slowest stage of the process is that of adsorption itself.29 In this model, the saturated monolayer is considered as the maximum adsorption.29 From this result, it could be thought that in adsorption of As3+, As5+, and Sb3+ a multilayer adsorption occurred, due to the loss of the plateau and to the increase of the adsorption (see Fig. 1).
3.3 57Fe Mössbauer spectrometry
In order to better understand the adsorption mechanism, we characterized the pure and co-precipitated akaganeites after the adsorption experiments and compared these results with the properties found for these akaganeites before the adsorption.20 The results of the analysis of the akaganeites obtained after adsorption of pollutants through 300 and 77 K Mössbauer spectrometry are presented in Fig. S1–S6 and in Tables S4 and S5.†Fig. S1–S3† show the 300 K Mössbauer spectra of samples pAk, Ak60Hg, Ak60Sb, and Ak60As after adsorption of Hg2+, As3+ and Sb3+. All spectra were first correctly fitted by introducing two quadrupolar doublets named D1 and D2 and the refined values of hyperfine parameters are listed in Table S4.† It is noted that, within the error bars, the hyperfine parameters (isomer shifts and quadrupole splittings) of the two ferric iron sites for all samples are quite similar. Now, samples pAk and pAk-As3+ showed similar relative spectral areas. On the contrary, the relative spectral areas of the two components for the samples Ak60Hg, Ak60Sb and Ak60As without and with adsorbed pollutants showed some differences. It is important to note that other fitting models can be considered assuming free values of linewidth and/or absorption areas, and/or some constraints: as the hyperfine structure of the quadrupolar spectra is poorly resolved, the main relevant hyperfine parameters are the mean values which are independent of the fitting models. As shown in Table S6,† the mean values of isomer shift and quadrupolar splitting are rather similar.
As shown in Fig. S4–S6,† all spectra obtained at 77 K exhibit rather similar complex hyperfine structures resulting from magnetic sextets composed of asymmetrical lines. The initial fitting procedure consists of four sextets named S1, S2, S3 and S4. These components arise from the existence of four non-equivalent iron sites related to the two monoclinic iron sites (Fe1 and Fe2) in the vicinity of occupied (Cl) or unoccupied (VCl) chloride sites.20 Therefore, S1, S2, S3 and S4 are assigned to Fe1–Cl, Fe2–Cl, Fe1–VCl and Fe2–VCl, respectively. During fitting, the values of the isomer shift, quadrupolar shift, linewidth and absorption area for components S1 and S2 on the one hand, and those for components S3 and S4, on the other hand, can be constrained independently or not, either to be equal, or adjustable. In addition, the values of the hyperfine field were refined without constraint. Finally, many fitting models can be well realized with various sets of hyperfine parameters, leading to similar factors of goodness. At this stage, it remains difficult to establish which of these different models is the best solution. Table S5† shows an example of the values of the hyperfine parameters at 77 K characteristic of the samples pAk, Ak60Hg, Ak60Sb and Ak60As after adsorption of Hg2+, As3+ and Sb3+. Therefore, as in the case of quadrupolar doublets, we need to consider the mean values of each hyperfine parameter, including their respective error bars. They are also given in Table S7;† it is now difficult to establish some significant correlation between such these hyperfine parameters, the nature and content of contaminant, but they show unambiguously the presence of ferric species. The lack of strong evolution can be explained first of all by the low content of contaminant which must preferentially deform the superficial structure, causing thus a small effect.
The results found here suggest that in some cases the adsorption of pollutants by akaganeite slightly modifies certain hyperfine parameters. The isomer shift is the least sensitive parameter. To understand the Mössbauer results, it is worth discussing three aspects: first, how the atomic environment surrounding the Fe3+ ion and its molecular bonding with the ligands affect the hyperfine interactions; second, the relative abundance of iron ions at the surface of akaganeites; and third, the types and distribution of active sites for adsorption. With respect to the first aspect, the p–d electron population of the Fe ion affects the magnitude of the quadrupole shift and the hyperfine magnetic field. The population of this valence shell is affected by the molecular bonding of the iron with its neighbors. In akaganeite, Fe directly bonds to oxygen in the octahedral site. Oxygen share bonding with pollutants located at the surface and with hydrogen, which also bonds to chloride into tunnels and to pollutants at the surface. In summary, the slight variation in some of the hyperfine parameters could be partially explained by the fact that the adsorption of the pollutants at the surface and at tunnel sites, indirectly affects the Fe 3d orbital population. Now, with regard to the second aspect, the small variations in the hyperfine parameters can also be understood if we take into consideration that the adsorption process is mainly a superficial phenomenon, i.e. the pollutants are adsorbed at surface sites, and in the case of akaganeite, also tunnels can be also part of the adsorption sites. Here it is interesting to note that,20 we studied the relative abundance of the surface iron ions with respect to the core irons for the different akaganeites. We found that for a shell thickness of x = 0.2 nm, the shell-volume to particle-volume ratio accounts for 1%, 10%, 14% and 22% for pAk, Ak60Hg, Ak60Sb and As60Ak, respectively. Thus, there are more irons located at the core than at the surface of the akaganeites, therefore explaining the very small variations observed in the hyperfine parameters. Finally, and concerning the third point, it is important to take into account that not all the surface sites available in akaganeite are active for adsorption. In this respect, Song and Boily,32 theoretically and experimentally determined the identity and distribution of the adsorption sites at the surfaces of the akaganeite. They reported that reactions occurring on surfaces sites may involve hydroxyl, oxygen and water groups. In pure akaganeites, terminal (001) and (100) planes expose a mixture of the three types of hydroxyl groups (singly, doubly and triply coordinated to iron). On the other hand, terminal (010) plane exposes a mixture of hydroxyl, oxygen and water groups. Not all of these sites are active for adsorption and their relative abundance is different.
4 Conclusions
In the present work, we have studied the adsorption kinetics of Sb3+, As5+, As3+ and Hg2+ ions in aqueous solutions onto pure and Hg2+, As5+ and Sb3+ co-precipitated akaganeites through adjustment of the experimental data to different nonlinear kinetics models, as well as the characterization of solid samples before and after the adsorption. Carrying out this type of study is important because it generates information about the speciation and fate of this type of pollutants in aqueous environments. At the experimental conditions, and according to MINTEQ software, these ions were adsorbed under the following predominant chemical forms: H3AsO4 and H2AsO4− with total concentrations of 64.8 and 35.2%, respectively, H3AsO3 with a total concentration of 100%, Hg2+ with a total concentration of 96.5% and finally, Sb(OH)2+ and Sb(OH)3 with total concentrations of 20.6 and 79.4%, respectively. We have found that the kinetics models that better described the adsorption experimental data for Sb3+, As5+ and As3+ ions onto pure and co-precipitated akaganeites were Elovich and simplified Elovich nonlinear kinetics models; and for Hg2+ ion the Bangham model. In the case of Hg2+ adsorption, the rate-controlling mechanism of the adsorption process was probably the intraparticle diffusion, whereas in the case of Sb3+, As3+, As5+ adsorption, it was probably of chemical nature. The co-precipitated akaganeites had much better adsorption capacities than pure akaganeites. The maximum adsorption capacities of pollutants onto the co-precipitated akaganeites followed the order: Sb3+ > As5+ > As3+ > Hg2+. The highest Qmax values for a given pollutant were found to be independent of the type of cation used to co-precipitate the akaganeite, suggesting that the morphological properties of akaganeites are important factors in determining their adsorption properties. Sb3+ was the most rapidly adsorbed pollutant, while Hg2+ was the slowest one. Finally, Mössbauer spectrometry showed small variations in some of the hyperfine parameters of akaganeite after adsorption of different pollutants in comparison to akaganeite before adsorption.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The financial support from CODI-Universidad de Antioquia (Estrategia de Sostenibilidad del Grupo de Estado Sólido 2018–2019, ES84180123) is greatly acknowledged.References
- J. E. Post and V. F. Buchwald, Crystal structure refinement of akaganéite, Am. Mineral., 1991, 76, 272–788 CAS.
- S. D. Yusan and S. Akyil, Sorption of uranium (VI) from aqueous solutions by akaganeite, J. Hazard. Mater., 2008, 160, 388–395 CrossRef CAS.
- J. Kim and C. P. Grey, 2H and 7Li Solid-State MAS NMR Study of Local Environments and Lithium Adsorption on the Iron(III) Oxyhydroxide, Akaganeite (β-FeOOH), Chem. Mater., 2010, 22, 5453–5462 CrossRef CAS.
- T. Ishikawa, R. Katoh, A. Yasukawa, K. Kandori, T. Nakayama and F. Yuse, Influences of metal ions on the formation of beta-FeOOH particles, Corros. Sci., 2001, 43, 1727–1738 CrossRef CAS.
- K. Fominykh, D. Böhm, S. Zhang, A. Folger, M. Döblinger, T. Bein, C. Scheu and D. Fattakhova-Rohlfing, Nonagglomerated Iron Oxyhydroxide Akaganeite Nanocrystals Incorporating Extraordinary High Amounts of Different Dopants, Chem. Mater., 2017, 29, 7223–7233 CrossRef CAS.
- X. Guo, Z. Wu, M. He, X. Meng, X. Jin, N. Qiu and J. Zhang, Adsorption of antimony onto iron oxyhydroxides: Adsorption behaviour and surface structure, J. Hazard. Mater., 2014, 276, 339–345 CrossRef CAS.
- Y. X. Zhang and Y. Jia, A facile solution approach for the synthesis of akaganéite (β-FeOOH) nanorods and their ion-exchange mechanism toward As(V) ions, Appl. Surf. Sci., 2014, 290, 102–106 CrossRef CAS.
- F. Kolbe, H. Weiss, P. Morgenstern, R. Wennrich, W. Lorenz, K. Schurk, H. Stanjek and B. Daus, Sorption of aqueous antimony and arsenic species onto akaganeite, J. Colloid Interface Sci., 2011, 357, 460–465 CrossRef CAS.
- S. Yusan and S. A. Erenturk, Adsorption equilibrium and kinetics of U(VI) on beta type of akaganeite, Desalination, 2010, 263, 233–239 CrossRef CAS.
- E. A. Deliyanni, E. N. Peleka and K. A. Matis, Removal of zinc ion from water by sorption onto iron-based nanoadsorbent, J. Hazard. Mater., 2007, 141, 176–184 CrossRef CAS.
- N. K. Lazaridis, D. N. Bakoyannakis and E. A. Deliyanni, Chromium(VI) sorptive removal from aqueous solutions by nanocrystalline akaganeite, Chemosphere, 2005, 58, 65–73 CrossRef CAS.
- E. A. Deliyanni and K. A. Matis, Sorption of Cd ions onto akaganeite-type nanocrystals, Sep. Purif. Technol., 2005, 45, 96–102 CrossRef CAS.
- F. Parvin, S. Y. Rikta and S. M. Tareq, Application of Nanomaterials for the Removal of Heavy Metal from Wastewater, in Nanotechnology in Water and Wastewater Treatment, ed. A. Ahsan and A. F. Ismail, Elsevier, 2019, vol. 137–157, ISBN 9780128139028 Search PubMed.
- E. A. Deliyanni, G. Z. Kyzas and K. A. Matis, Inorganic nanoadsorbent: Akaganeite in wastewater treatment, in Composite Nanoadsorbents, ed. G. Z. Kyzas and A. C. Mitropoulos, Elsevier, 2019, vol. 337–358, ISBN 9780128141328 Search PubMed.
- A. E. Tufo, A. L. Larralde, J. Villarroel-Rocha, K. Sapag and E. E. Sileo, Synthesis and characterization of pure and Al-substituted akaganeites and evaluation of their performance to adsorb As(V), J. Environ. Chem. Eng., 2018, 6, 7044–7053 CrossRef CAS.
- X. Sun, C. Hu, X. Hu, J. Qu and M. Yang, Characterization and adsorption performance of Zr-doped akaganeite for efficient arsenic removal, J. Chem. Technol. Biotechnol., 2013, 88, 629–635 CrossRef CAS.
- D. K. L. Harijan and V. Chandra, Akaganeite nanorods decorated graphene oxide sheets for removal and recovery of aqueous phosphate, J. Water Process Eng., 2017, 19, 120–125 CrossRef.
- E. A. Deliyanni, E. N. Peleka and K. A. Matis, Effect of cationic surfactant on the adsorption of arsenites onto akaganeite nanocrystals, Sep. Sci. Technol., 2007, 42, 993–1012 CrossRef CAS.
- E. A. Deliyanni, L. Nalbandian and K. A. Matis, Adsorptive removal of arsenites by nanocrystalline hybrid surfactant-akaganeite sorbent, J. Colloid Interface Sci., 2006, 302, 458–466 CrossRef CAS.
- V. Villacorta, K. E. García, J.-M. Greneche and C. A. Barrero, Influences of As(V), Sb(III), and Hg(II) ions on the nucleation and growth of akaganeite, CrystEngComm, 2019, 46, 7155–7165 RSC.
- J. P. Gustafsson, Visual MINTEQ 3.1, 2013 Search PubMed.
- K. Ehlert, C. Mikutta, Y. Jin and R. Kretzschmar, Mineralogical Controls on the Bioaccessibility of Arsenic in Fe(III)-As(V) coprecipitates, Environ. Sci. Technol., 2018, 52, 616–627 CrossRef CAS.
- G. K. Schweitzer and L. L. Pesterfield, The aqueous Chemistry of the Elements, Oxford University Press, Inc., New York, 2010 Search PubMed.
- L. Li and R. Stanforth, Distinguishing Adsorption and Surface Precipitation of Phosphate on Goethite (α-FeOOH), J. Colloid Interface Sci., 2000, 230, 12–21 CrossRef CAS.
- S. Goldberg, Surface Complexation Modeling, Reference Module in Earth Systems and Environmental Sciences, 2013, DOI:10.1016/B978-0-12-409548-9.05311-2.
- X. Yang, Y. Wan, Y. Zheng, F. He, Z. Yu, J. Huang, H. Wang, Y. S. Ok, Y. Jiang and B. Gao, Surface functional groups of carbon-based adsorbents and their roles in the removal of heavy metals from aqueous solutions: A critical review, Chem. Eng. J., 2019, 366, 608–621 CrossRef CAS.
- A. Ler and R. Stanforth, Evidence for Surface precipitation of phosphate on goethite, Environ. Sci. Technol., 2003, 37, 2694–2700 CrossRef CAS.
- R. M. Cornell and U. Schwertmann, The Iron Oxides. Structure, Properties, Reactions, Occurrences and Uses, Wiley-VCH Verlag GmbH & Co. KGaA, 2nd edn, 2003 Search PubMed.
- L. Largitte and R. Pasquier, A review of the kinetics adsorption models and their application to the adsorption of lead by an activated carbon, Chem. Eng. Res. Des., 2016, 109, 495–504 CrossRef CAS.
- J. P. Jolivet, Metal Oxide Chemistry and Synthesis. From solution to solid stated, John Wiley & Sons Inc, 1st edn, 1994 Search PubMed.
- E. A. Deliyanni, D. N. Bakoyannakis, A. I. Zouboulis and K. A. Matis, Sorption of As(V) ions by akaganéite-type nanocrystals, Chemosphere, 2003, 50, 155–163 CrossRef CAS.
- X. Song and J. F. Boily, Surface Hydroxyl Identity and Reactivity in Akaganéite, J. Phys. Chem. C, 2011, 115, 17036–17045 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra08075f |
| This journal is © The Royal Society of Chemistry 2020 |