Open Access Article
Open Access ArticleTailored surface composition of Au/Pt nanocatalysts synthesized in microemulsions: a simulation study
Jorge Pérez-Álvarez a,
Concha Tojo
a,
Concha Tojo *a,
David Bucetab and
M. Arturo López-Quintelab
*a,
David Bucetab and
M. Arturo López-Quintelab
aPhysical Chemistry Department, University of Vigo, E-36310, Vigo, Spain. E-mail: jorgperez@alumnos.uvigo.es; ctojo@uvigo.es
bLaboratorio de Magnetismo y Nanotecnología, University of Santiago de Compostela, E-15782, Santiago de Compostela, Spain. E-mail: a.lopez@nanogap.es; buceta.david@gmail.com
First published on 19th November 2020
Abstract
Au/Pt nanoparticles show an optimized catalytic activity when compared with Pt nanoparticles because Pt activity is improved by the presence of Au on the surface. It was checked whether a controllable surface composition can be achieved by the simple strategy of varying the Au![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pt ratio. We present an in-depth kinetic simulation study on the influence of Au
Pt ratio. We present an in-depth kinetic simulation study on the influence of Au![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pt ratio on the formation of Au/Pt nanoparticles synthesized in microemulsions. This study is able to explain the resulting nanoarrangement as a function of kinetic parameters such as Au
Pt ratio on the formation of Au/Pt nanoparticles synthesized in microemulsions. This study is able to explain the resulting nanoarrangement as a function of kinetic parameters such as Au![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pt ratio and intermicellar exchange rate. The role of the micelles as a dosing pump of the Au precursor explains that a higher Au amount results in a Au reduction which takes place over a longer period of time. It implies that Au is deposited until longer stages of the synthesis, so Au is present at the nanoparticle surface. Micelles as reaction media produce a minor impact on Pt due to its slower reduction. These different kinetic behaviours of Au and Pt give rise to a surface composition which can be tailored by tuning the Au
Pt ratio and intermicellar exchange rate. The role of the micelles as a dosing pump of the Au precursor explains that a higher Au amount results in a Au reduction which takes place over a longer period of time. It implies that Au is deposited until longer stages of the synthesis, so Au is present at the nanoparticle surface. Micelles as reaction media produce a minor impact on Pt due to its slower reduction. These different kinetic behaviours of Au and Pt give rise to a surface composition which can be tailored by tuning the Au![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pt ratio. Numerical results on surface composition successfully reproduce experimental data and further support the outcomes of the degree of atomic mixing under different Au
Pt ratio. Numerical results on surface composition successfully reproduce experimental data and further support the outcomes of the degree of atomic mixing under different Au![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pt ratios.
Pt ratios.
1 Introduction
The arrangement of atoms at the surface of catalysts is crucial to understanding the catalytic behaviour, because the material surface determines the reaction sites.1–3 In this vein, special attention has been paid to the development of nanocatalysts composed of two metals, because bimetallic mixtures frequently exhibit enhanced catalytic activities4–7 and may attain new properties.8 The reason is that the interaction between the two metals can give rise to modifications in their electronic states. Thus, the high catalytic activity exhibited by Au/Pt nanoparticles was explained as being due to a readjustment of the d-band in Pt when alloyed materials are formed.9 Specifically, Au/Pt nanocatalysts have been comprehensively investigated as catalysts in oxygen reduction reaction (ORR),10–13 CO electrooxidation14 or methanol oxidation reaction (MOR).10,13,15 In these reactions, Pt catalytic activity is improved by the presence of Au on the surface due to several factors. On one hand, Au exhibits a higher electronegativity than Pt, which could favour an increase of the charge transferred from Pt to Au and, as a consequence, an increase of the d-orbital vacancy in Au/Pt nanoparticles. In fact, the Fermi level of Pt (higher than that of Au) becomes lower due to the transfer of d-electron density from Pt to Au.11,13 This transfer was shown from the binding energy of f-electrons.10 On the second hand, taking into account that the presence of Au produces less d-orbital back donation, the resulting chemical bond between Pt and the reactant would be weaker. For example, the chemisorption of OH is favoured in the presence of Au at the surface, so Pt–OH bonds have further been weakened.11,16 Thus, a significantly enhanced catalytic activity at the nanoparticle surface is observed due to both geometric and electronic effects.17In view of these optimized catalytic properties, Au/Pt nanoparticles of controllable surface composition have received considerable attention, so different methods have been proposed for their preparation. One of the most used methods is the microemulsion route.18–20 The fundamentals of this technique can be summarized as follows: first, micelles are dynamic, and will fuse and redisperse repeatedly such the material located inside micelles becomes mixed. So, metal nanoparticles can be prepared by mixing a microemulsion containing metal precursors and another containing a reducing agent. The basic thought behind this approach is that reverse micelles play as templates and control nanoparticle growth. On the second hand, nanoparticles are built up from a nucleus by adding new atoms, layer by layer. Atoms are deposited on growing particle surface as they are available inside the micelle. In the case of nanoparticles composed by two different metals, the sequence of metal salt reductions will determine the resulting arrangement. That is, if one of the metals is produced much earlier than the other, the resulting nanoparticle shows a metal segregated structure (called core–shell), whose core is composed by the earlier reduced metal, and the shell is build up by the later one. In the case of both metals are produced at the same time, they will be mixed with each other from the beginning, giving rise to an alloyed nanoparticle. The metal ion with a higher reduction potential will be reduced faster, so the general assumption is that the difference in standard reduction potentials determine the final structure.21 Hence, when a one pot method is used and one of the two metals has a clearly higher reduction potential than the other, a core–shell arrangement will be expected. This is the case of simultaneous reduction of AuCl4− (ε0(AuCl4−/Au) = 1.002 V) and PtCl62− (ε0(PtCl62−/Pt) = 0.742 V (ref. 22)), which can produce nanoparticles whose core is mainly composed of Au, and Pt is deposited later building up the surrounding shell. On the contrary, no metal segregation will be expected when both metals have closer reduction potentials (similar reduction rates), as one-pot reductions of Ag+ (ε0(Ag+/Ag) = 0.80 V) and Pd2+ (ε0(Pd2+/Pd) = 0.915 V) in microemulsions, which result in alloyed Ag/Pd nanoparticles.5,23,24
This argumentation, based on kinetics in homogeneous reaction media, was directly employed in nanoparticle formation via microemulsions and was enabled the explanation of experimental results.25 However, this line of reasoning was not entirely correct because microemulsions are compartmentalized reaction media, and the material intermicellar exchange was not taking into account. It was proved that intermicellar exchange rate actively influences the kinetics.26–31 As clear evidence of this, the same pair of metals (such as Au/Ag,32–34 Au/Pt12,25,35,36 or Au/Pd nanoparticles37–39), have been prepared in segregated or non-segregated arrangements just by using different microemulsions, that is, when different intermicellar exchange rates are involved. As a rule, surfactants which provide a high film flexibility around micelles (allowing a faster intermicellar exchange rate) usually facilitate the mix of reactants, giving rise to alloyed bimetallic nanoparticles. In contrast, surfactants that are more rigid lead to better segregated structures.40 Another factor to take into account is the reactants concentration, which plays a basic role in chemical kinetics, and, as a consequence, in the resulting metals segregation. Thus, as concentration rises, a progressive shift from an alloy to a core–shell arrangement has been proved from both experimental and simulation studies on Au/Pt nanoparticles synthesized via microemulsions.41
How reactants concentration and microemulsion composition affects the final Au/Pt nanostructure was previously studied.25,40,42 Both parameters have the disadvantage that they strongly affect final sizes. With the aim of being able to tune the surface composition, an alternative strategy can be modify the molar ratio between Pt and Au precursors. It was proved that the catalytic activity of Au/Pt nanoparticles obtained by electrodeposition and supported on graphene15 was enhanced at a Pt/Au molar ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for both ORR and MOR. In the case of Au/Pt nanoparticles prepared by the polyol method and supported on carbon, the improvement of the catalytic activity for ORR and MOR was found to diminish as the Au amount was higher.13
1 for both ORR and MOR. In the case of Au/Pt nanoparticles prepared by the polyol method and supported on carbon, the improvement of the catalytic activity for ORR and MOR was found to diminish as the Au amount was higher.13
In the paper at hand, our objective is to evaluate whether surface composition can be tuned by varying Au![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pt ratio. Because of the inherent complexity of the microemulsion route, a powerful computer simulation tool was developed for predicting final structures as a function of microemulsion composition, metals nature and the quantity of reagents. Simulation model enables to study chemical kinetics in microemulsions, and provides insight into surface composition. Therefore, with the aim of producing tailor-made Au/Pt nanoparticles, in this contribution we focus on an in-depth kinetic study on the influence of Au
Pt ratio. Because of the inherent complexity of the microemulsion route, a powerful computer simulation tool was developed for predicting final structures as a function of microemulsion composition, metals nature and the quantity of reagents. Simulation model enables to study chemical kinetics in microemulsions, and provides insight into surface composition. Therefore, with the aim of producing tailor-made Au/Pt nanoparticles, in this contribution we focus on an in-depth kinetic study on the influence of Au![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pt ratio on the formation of Au/Pt nanoparticles synthetized in microemulsions and on the surface composition of resulting nanoparticle.
Pt ratio on the formation of Au/Pt nanoparticles synthetized in microemulsions and on the surface composition of resulting nanoparticle.
2 Simulation model
The process of particle formation in reverse micelles is simulated as follows (see details in ref. 42): the reaction media is described as three sets of reverse micelles, each one carrying one type of reagent ([AuCl4]−, [PtCl6]2− and reducing agent, R). Reagents, solved inside the aqueous phase of reverse micelles, are distributed through micelles by a Poisson distribution. The average number of reagents can be changed: 〈c[AuCl4]−〉 = 〈c[PtCl6]2−〉 = 4, 16, 32, and 64 precursors in a micelle, which corresponds to 0.025 M, 0.08 M, 0.16 M and 0.40 M, respectively (calculated in a droplet with a radius of 7.3 nm). The reducing agent is also carried by micelles, and it is always in a great excess ([R] = 10 〈c[AuCl4]−〉). In order to change the proportion of reactants, keeping constant average concentration, the quantity of species are changed as follows: a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Au
1 Au![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pt ratio (50% of Au precursor) at 〈c〉 = 32 reactants/micelle means that an average of 32 [AuCl4]− ions are mixed with 32 [PtCl6]2− ions. So if Au
Pt ratio (50% of Au precursor) at 〈c〉 = 32 reactants/micelle means that an average of 32 [AuCl4]− ions are mixed with 32 [PtCl6]2− ions. So if Au![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pt ratio is 1
Pt ratio is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 (25% of Au precursor) then 〈c[AuCl4]−〉 = 16 must be mixed with 〈c[PtCl6]2−〉 = 48 reactants/micelle, in order to keep the whole averaged concentration 〈c〉 = 32. Once each kind of reactant is distributed in a set of micelles (microemulsion), the three sets are mixed, that is, they would be located at random.
4 (25% of Au precursor) then 〈c[AuCl4]−〉 = 16 must be mixed with 〈c[PtCl6]2−〉 = 48 reactants/micelle, in order to keep the whole averaged concentration 〈c〉 = 32. Once each kind of reactant is distributed in a set of micelles (microemulsion), the three sets are mixed, that is, they would be located at random.
The following step is the redistribution of reactants between micelles. Micelles are in a continuous Brownian motion and can collide. If collision is energetic enough, two micelles can fuse forming a transient dimer connected by an intermicellar water channel, which allows species to pass through. At each Monte Carlo time step, 10% of the micelles in the microemulsion are randomly selected to collide, fuse, exchange material if possible, and then redisperse (breakdown of the dimers). After collision, the material located inside the two colliding micelles is adjusted according to the exchange criteria discussed below. One Monte Carlo step (mcs) is completed when the composition of all colliding micelles is updated.
Once the reactants (metal precursor and reducing agent) are located inside the water phase of the same micelle because of the intermicellar exchange, chemical reduction of metal precursors can start. Due to chemical reduction of metal Au precursor is instantaneous, 100% of [AuCl4]− inside colliding micelles are assumed to be reduced to Au. In the case of [PtCl6]2−, whose standard potential is lower, a successful agreement between experimental and simulation results was found by considering that only 10% of [PtCl6]2− is reduced.41 The remaining [PtCl6]2− and reducing agent will be exchanged and react in a later collision.
2.1 Protocols of material redistribution between colliding micelles
The movement of material must obey the concentration-gradient principle, that is, material goes from the more to the less concentrated micelle. In addition, the material exchange is also subject to other requirements, which allow identifying the microemulsion. On one hand, fused micelles must remain together at least the time the material takes to move through the intermicellar channel. On another hand, the width of the channel must allow the material can cross. Both requirements are directly linked to the flexibility of the surfactant film surrounding microemulsion micelles. Thereby, a highly flexible microemulsion film exhibits both a long-lived dimer stability and a large intermicellar channel. To quantify these characteristics, two parameters are included in the simulation model. In order to simulate the dimer stability, one must keep in mind that a short-lived dimer allow the transfer of a fewer number of atoms than a longer one. From this picture, the dimer stability is included in the model by means of the parameter kex, which quantifies the number of isolated atoms/ions that can be exchanged between micelles during a collision. kex is directly related to the rate of the intermicellar exchange. This parameter mainly concerns to both metal salts and isolated Au or Pt atoms (which are not still aggregated), that will be transferred from the most to the less concentrated micelles, being kex the maximum number of exchanged species. Isolated atoms cross the channel one by one, so channel size is not relevant. On the contrary, the channel size is decisive during the intermicellar exchange of a growing particle (built by aggregation of atoms, that have to cross the channel as a whole). This kind of exchange is controlled by the f parameter, which controls that only growing particles composed by less than f atoms can cross the water channel. Both exchange parameters, kex and f, allow to characterize the microemulsion as follows: a high flexibility of the surfactant film around micelles comprehends not only the fast exchange of isolated atoms/ions (high kex) but also the exchange of big particles (high f).43 As a case in point, a microemulsion composed by 75% isooctane/20% Tergitol/5% water, which provides a flexible film, was adequately characterized by an intermicellar exchange rate kex = 5 (solely a maximum of 5 ions/atoms is allowed to be exchanged by collision),41 together with a channel size f = 30 (solely aggregates smaller than 30 atoms can cross the channel). In the case of a more rigid film, such as provided by a 75% n-heptane/20% AOT/5% water microemulsion, the values kex = 1 and f = 5 were successfully used.24 In the paper at hand, we explore four different microemulsion compositions, defined by f = 5, 15, 30 and 90 associated to kex = 1, 3, 5 and 15, respectively. The last combination (f = 90, kex = 15) corresponds to a very flexible surfactant film, which was included to check whether the behaviour expected in a homogeneous reaction media can be reproduced by considering an extremely high flexibility.2.2 Nanoparticle growth
As the synthesis advances, nanoparticles grow when chemical reductions give rise to Au and Pt atoms inside micelles, that are deposited on the nanoparticle surface. In addition, nanoparticle can also grow by a ripening process, according to which nanoparticle growth is assumed to take place on the bigger particle due to its bigger surface. This possibility is implemented in case of collision between two micelles both carrying an aggregate.2.3 Nanoparticle description
At the end of the synthesis the material carried by all 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 micelles remain invariable after collisions, indicating that particles cannot grow anymore neither by ripening due to nanoparticles sizes, nor by atoms deposition because reagents are exhausted. A simulation run is completed at this stage. It results in a set of micelles carrying a particle or being empty. The sequence of Au and Pt deposition of each particle is stored and divided into ten concentric layers. Then the %Au is determined layer-by-layer to generate spatially resolved data on the Au/Pt distribution inside each nanoparticle. Last of all, data are averaged over 1000 runs. The estimation of final metal distribution is shown by histograms, which represent the number of nanoparticles containing a given percentage of Au in each layer, calculated from the inner layer or nanoparticle core until the nanoparticle surface (outer layer). To simplify the display, a colour pattern is used: 90–100% of Au is depicted in red, 0–10% of Au (mainly Pt) in blue, and 50% Au (50% Pt) in grey. The colours are graded from light to dark as the percentage of pure metal in the layer diminishes. In this way, the nanoparticle metal distribution can be studied from the core to the surface.
000 micelles remain invariable after collisions, indicating that particles cannot grow anymore neither by ripening due to nanoparticles sizes, nor by atoms deposition because reagents are exhausted. A simulation run is completed at this stage. It results in a set of micelles carrying a particle or being empty. The sequence of Au and Pt deposition of each particle is stored and divided into ten concentric layers. Then the %Au is determined layer-by-layer to generate spatially resolved data on the Au/Pt distribution inside each nanoparticle. Last of all, data are averaged over 1000 runs. The estimation of final metal distribution is shown by histograms, which represent the number of nanoparticles containing a given percentage of Au in each layer, calculated from the inner layer or nanoparticle core until the nanoparticle surface (outer layer). To simplify the display, a colour pattern is used: 90–100% of Au is depicted in red, 0–10% of Au (mainly Pt) in blue, and 50% Au (50% Pt) in grey. The colours are graded from light to dark as the percentage of pure metal in the layer diminishes. In this way, the nanoparticle metal distribution can be studied from the core to the surface.
This model was successfully tested by comparing with experimental results of Au/Pt nanoparticles synthesized in 75% isooctane/20% Tergitol/5% water microemulsions (see ref. 41 for details).
3 Results and discussion
For a deeper understanding of how nanoparticle surface composition can be tuned by the simple strategy of changing Au![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pt ratio in feeding solution, first of all we present results on the kinetic behaviour. Then the resulting nanostructures will be analysed, and finally the surface composition will be evaluated and compared with experimental results.
Pt ratio in feeding solution, first of all we present results on the kinetic behaviour. Then the resulting nanostructures will be analysed, and finally the surface composition will be evaluated and compared with experimental results.
3.1 Kinetic study
The consumption of the metal precursor M+ ([AuCl4]− and [PtCl6]2−) was monitored as a function of time, under different Au![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pt ratio, microemulsion compositions and reactants concentrations. The amount of reducing agent (R) was always in a great excess, so its concentration remains basically constant during the course of the reaction. Therefore, the conditions of isolation method are kept and the pseudo first order rate law would be,
Pt ratio, microemulsion compositions and reactants concentrations. The amount of reducing agent (R) was always in a great excess, so its concentration remains basically constant during the course of the reaction. Therefore, the conditions of isolation method are kept and the pseudo first order rate law would be,| v(M+) = k[M+][R] ≈ k[M+][R]0 = kobs[M+] with kobs = k[R] | (1) |
The kinetic study was carried out analyzing how fast the metal precursors are consumed when different initial Au![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
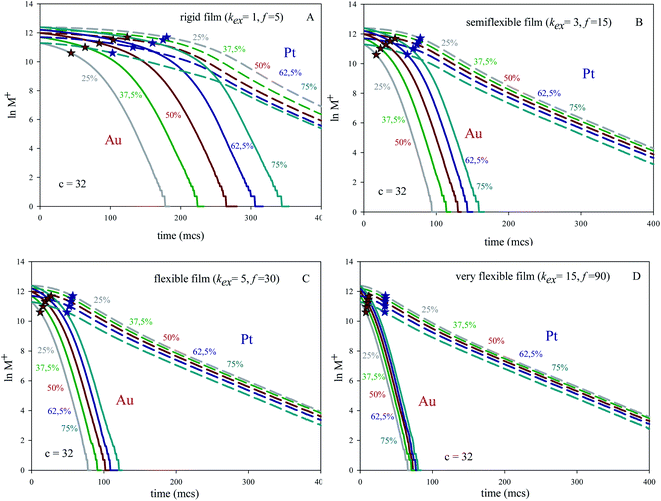
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pt proportion (keeping constant concentration) are mixed using different microemulsions. Fig. 1A shows the logarithmic plot of number of reactants versus time prepared at concentration 〈c〉 = 32 reactants per micelle, and using a rigid film (slow material intermicellar exchange). Fig. 1B and C show results for a growing film flexibility (faster material intermicellar exchange), and Fig. 1D represents the data achieved for an almost homogeneous reaction media (very flexible film). In all cases, the kinetic profiles show a similar trend: after a time lag, the reductions of both Pt and Au obey first order kinetics, as expected. Once the linear regime is reached, the slopes of Au reduction (continuous lines) are higher than the Pt ones (discontinuous lines) because of the faster Au reduction rate. In relation to the influence of Au% in feeding solution, one can observe that the separation between lines at different Au% is always greater for Au than for Pt and this difference diminishes as flexibility increases. That is, all Au curves almost overlap when the intermicellar exchange is very fast, as shown in Fig. 1D. Similar qualitative behaviour has been found for all values of concentration.
Pt proportion (keeping constant concentration) are mixed using different microemulsions. Fig. 1A shows the logarithmic plot of number of reactants versus time prepared at concentration 〈c〉 = 32 reactants per micelle, and using a rigid film (slow material intermicellar exchange). Fig. 1B and C show results for a growing film flexibility (faster material intermicellar exchange), and Fig. 1D represents the data achieved for an almost homogeneous reaction media (very flexible film). In all cases, the kinetic profiles show a similar trend: after a time lag, the reductions of both Pt and Au obey first order kinetics, as expected. Once the linear regime is reached, the slopes of Au reduction (continuous lines) are higher than the Pt ones (discontinuous lines) because of the faster Au reduction rate. In relation to the influence of Au% in feeding solution, one can observe that the separation between lines at different Au% is always greater for Au than for Pt and this difference diminishes as flexibility increases. That is, all Au curves almost overlap when the intermicellar exchange is very fast, as shown in Fig. 1D. Similar qualitative behaviour has been found for all values of concentration.
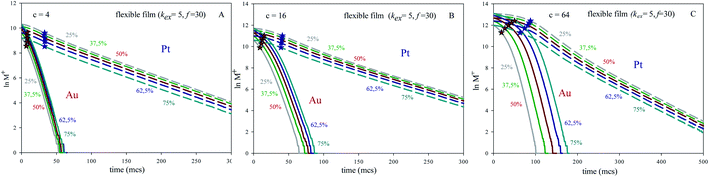
In order to test the influence of concentration, Fig. 2 illustrates the pseudo first order plots obtained for different averaged concentrations and Au![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pt ratio but keeping constant microemulsion composition. It shows results for a flexible film (kex = 5, f = 30). Another values of the flexibility parameters exhibited a similar trend. One can observe that Au lines at different Au% appear closer as averaged concentration is smaller.
Pt ratio but keeping constant microemulsion composition. It shows results for a flexible film (kex = 5, f = 30). Another values of the flexibility parameters exhibited a similar trend. One can observe that Au lines at different Au% appear closer as averaged concentration is smaller.
The approximation of the curves is directly related to the time lag required to attain the linear regime. Taking a closer look on this time lag, and comparing Au and Pt behaviour, the main features are the following: (1) under all studied conditions, the time lag is always longer for Pt reduction than that of Au. (2) Keeping fixed precursors ratio and concentration, the time lag is longer when the film flexibility decreases (see Fig. 1). (3) Keeping fixed concentration, the time lag is longer as the Au% increases for any microemulsion composition (see Fig. 1). (4) Keeping fixed the microemulsion composition and precursors ratio, the time lag is longer as concentration increases (see Fig. 2). To explain this behaviour, compartmentalization of the reaction media has been taken into account. At the beginning of the synthesis, three microemulsions (each one carrying a different reagent) are put together. So that, earlier to chemical reduction can start, the reactants must be redistributed between micelles, in order to allow the reactants encounter within the same micelle. The intermicellar exchange rate, strongly dependent on the microemulsion composition, plays a key role in reactants redistribution, because it determines the ease with which intermicellar channels can be stablished and their stability, which in turn limits transport of material across the channel. That is, the intermicellar exchange rate governs reactants redistribution and the resulting time required to reactants encounter. Thus, a slower exchange rate allows a fewer amount of reactants to be exchanged in each collision. As a result, further collisions are needed in order to the metal precursor and the reducing agent be carried by the same micelle, so they can react. This is why a slower intermicellar rate (rigid film) shows longer lag times than a faster one (see Fig. 1). This outcome was proved for any value of concentration and Au%. Likewise, the time lag almost disappears when a very fast exchange rate is studied (see Fig. 1D), as expected in a non-compartmentalized reaction media.
In relation to why time lag depends also on the reactant amount inside micelles, it must be noted that a highly concentrated micelle will need more collision in order to redistribute reactants, because during each collision only a limited quantity of species can be exchanged. As a result, the time lag is longer as concentration increases (for any Au![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pt ratio) and as the Au content increases (for a constant concentration). Finally, the occupation of micelles will have less influence as the intermicellar exchange rate would be faster, as reflected in the linear regime of the curves, which appears closer as the film is more flexible.
Pt ratio) and as the Au content increases (for a constant concentration). Finally, the occupation of micelles will have less influence as the intermicellar exchange rate would be faster, as reflected in the linear regime of the curves, which appears closer as the film is more flexible.
After the time lag, the pseudo first order rate constants (kobs) can be estimated through the slope of the logarithmic plot. Fig. 3 show kobs as a function of concentration using different surfactant films and different reactants proportion. Because of pseudo first order conditions, kobs should not depend on concentration. This is the behavior shown by Pt reduction, whose value remains constant independently of concentration, intermicellar exchange rate and reactants proportion (see grey discontinuous line at the bottom of Fig. 3). Pt reduction rate is so slow that the reaction is chemically controlled, so the intermicellar exchange rate does not play a decisive role in the kinetics. As a result, kobs behaves as expected in a homogeneous reaction media. Quite to the contrary, Au reduction is deeply dependent on concentration and on intermicellar exchange rate, but there is no significant difference in its behavior when reactants proportion are varied (compare Fig. 3A–C). To explain this unexpected behavior, one must keep in mind that Au reduction is extremely fast, so the limiting step of Au reduction is the intermicellar exchange. In fact, Au reduction is so quick that it requires the use of stopped-flow techniques, because cannot be detected by conventional methods.25 This is the reason why Au reduction is simulated as an instantaneous one (100% of Au precursors inside a micelle are reduced in each collision). But, in order to react, species have to be previously exchanged between micelles. This delay due to reactants redistribution leads to the limiting step of Au reduction was the intermicellar exchange.44 Note that kobs were calculated when the linear regime was reached, that is, its dependence on intermicellar exchange is not only due to the initial redistribution of reactants mentioned above. This means that Au reduction is controlled by the intermicellar exchange during the whole process. This control is more restrictive as concentration increases, because only a limited number of reactants can be exchanged at each collision, so a high amount of reactants results in a longer process. Likewise, the relevance of this exchange control decreases as the flexibility of the surfactant film increases (see Fig. 2), until reach the expected trend in a homogeneous reaction media (extremely fast exchange rate, see grey continuous line in Fig. 3). By comparing Au and Pt curves, one can conclude that using a microemulsion as reaction media has a more or less impact depending on the reduction rate of the metal, since exchange rate strongly controls Au reduction but has virtually no influence on the Pt reduction. The fact that microemulsion strongly affect the Au kinetic behavior is reflected through the resulting arrangement. That is, a bimetallic nanoparticle containing Au can be obtained as a core–shell or as an alloy, just by varying the microemulsion composition (see Table 1 in ref. 40). This is the case for Au/Pt, which was prepared as core–shell nanoparticle using a rigid film12,25 and also as an alloyed one if the film is flexible.35,36,41 Similar behavior has been obtained for Au/Ag32–34 and Au/Pd37,38 nanoparticles, and it was also predicted by simulation.45
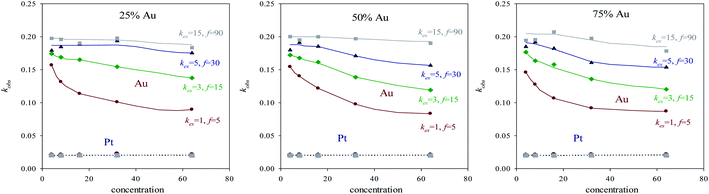 | ||
| Fig. 3 kobs (derived from the slopes of the linear part of plots in Fig. 1) as a function of concentration for different microemulsion compositions. Lines are only a guide to the eye. | ||
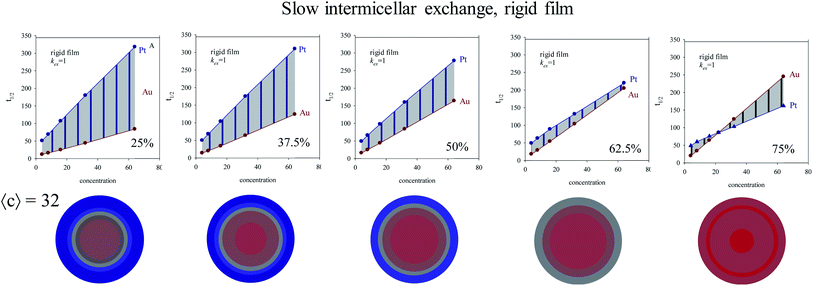
With the aim of examine the relevance of the non-linear regime at initial stages, the half-life was calculated under the different conditions and represented by stars in Fig. 1 and 2 (red and blue stars show the half-live for Au and Pt respectively). Half-live is defined as the time needed for the concentration to decline to half of its initial value, so it is a measurement of whole reaction process, that is, both intermicellar exchange and chemical reduction rate are implicitly taken into consideration. It is interesting to note that the linear regime of Au is generally achieved after half life time, mainly at high reactant content and when rigid films are used (see Fig. 1A). It will be reflected in the resulting nanostructure, because the core and the middle layers were build up before the linear regime is reached. That is, when the inner part of the nanoparticle is being formed, the Au reduction is still not a first-order reaction (except if the film is very flexible) and the Au reduction is controlled by the intermicellar exchange rate.
The half time t1/2 of Au and Pt reductions at different Au![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pt proportion (different % of each metal) versus initial concentration for different microemulsion composition were also studied. Fig. 4 shows results obtained with a 50% each metal (see central column). One can observe that Pt half-time is longer than Au one, due to Pt slower reduction. The separation between half-time of Au and Pt (Δt1/2) is represented by the shadow area. Understanding this separation is key, because it is closely related to final metal segregation, as smaller differences between the Au and Pt halftimes can be associated to mixed structures, and higher differences with core–shell ones42. This is clearly observed in the structures shown in Fig. 4, which represents results for a concentration 〈c[AuCl4]−〉 = 〈c[PtCl6]2−〉 = 4 (left column) and 32 (right column) reactants/micelle. By observing the figures from top to bottom, one can observed that the difference between Au and Pt half-times becomes smaller as the film flexibility is higher (faster exchange rate), giving rise to more mixed nanoarrangements. It agrees with experimental results mentioned above, proving the microemulsion capability to favor a more simultaneous metals reductions when a flexible film is used, which is reflected in the progressive mixture of the two metals.
Pt proportion (different % of each metal) versus initial concentration for different microemulsion composition were also studied. Fig. 4 shows results obtained with a 50% each metal (see central column). One can observe that Pt half-time is longer than Au one, due to Pt slower reduction. The separation between half-time of Au and Pt (Δt1/2) is represented by the shadow area. Understanding this separation is key, because it is closely related to final metal segregation, as smaller differences between the Au and Pt halftimes can be associated to mixed structures, and higher differences with core–shell ones42. This is clearly observed in the structures shown in Fig. 4, which represents results for a concentration 〈c[AuCl4]−〉 = 〈c[PtCl6]2−〉 = 4 (left column) and 32 (right column) reactants/micelle. By observing the figures from top to bottom, one can observed that the difference between Au and Pt half-times becomes smaller as the film flexibility is higher (faster exchange rate), giving rise to more mixed nanoarrangements. It agrees with experimental results mentioned above, proving the microemulsion capability to favor a more simultaneous metals reductions when a flexible film is used, which is reflected in the progressive mixture of the two metals.
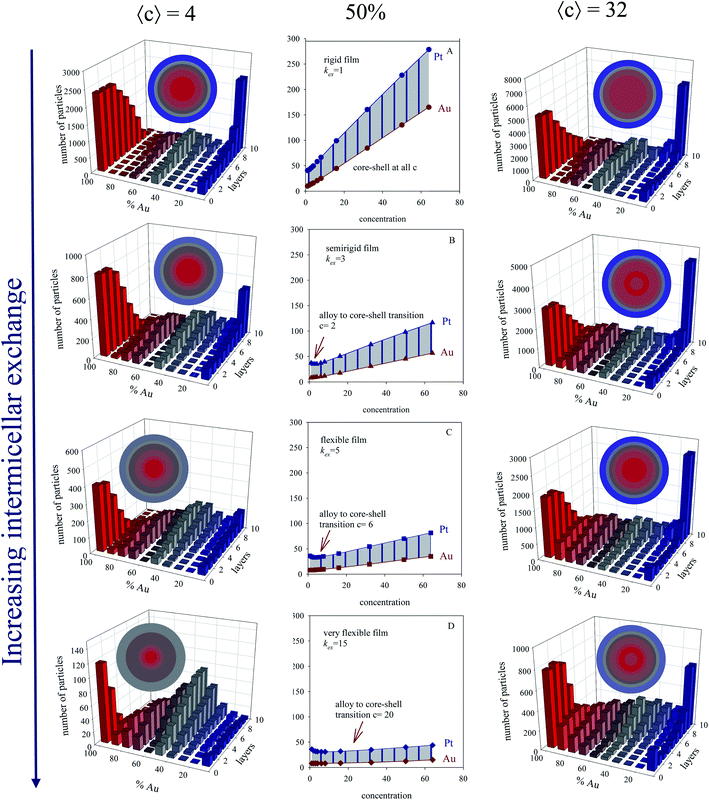 | ||
Fig. 4 First column: histograms obtained at low concentration 〈c〉 = 4, 50% Au, and different microemulsion compositions. Center column: half-time of Au and Pt reductions versus initial concentration for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Au 1 Au![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pt proportion (50% Au), and different microemulsion compositions: (A), (B), (C), and (D) show results for a rigid (kex = 1, f = 5), semiflexible (kex = 3, f = 15), flexible (kex = 5, f = 30) and very flexible (kex = 15, f = 90) surfactant film. Data was adapted with permission from ref. 42. Copyright (2018) Elsevier. Right column: histograms obtained at high concentration 〈c〉 = 32, 50% Au, and different microemulsion compositions. Color pattern: blue (0–45% of Au), grey (45–55% of Au), red (55–100% of Au). Less red means less gold. The nanoparticle structure is also described as concentric layers, keeping the same color pattern. Pt proportion (50% Au), and different microemulsion compositions: (A), (B), (C), and (D) show results for a rigid (kex = 1, f = 5), semiflexible (kex = 3, f = 15), flexible (kex = 5, f = 30) and very flexible (kex = 15, f = 90) surfactant film. Data was adapted with permission from ref. 42. Copyright (2018) Elsevier. Right column: histograms obtained at high concentration 〈c〉 = 32, 50% Au, and different microemulsion compositions. Color pattern: blue (0–45% of Au), grey (45–55% of Au), red (55–100% of Au). Less red means less gold. The nanoparticle structure is also described as concentric layers, keeping the same color pattern. | ||
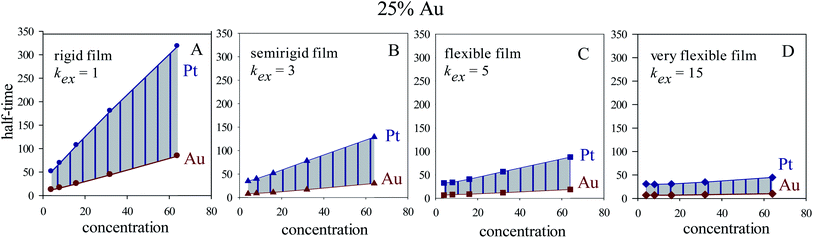
In homogeneous reaction media the half-time of a first order kinetic does not depend on concentration (t1/2 = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2/kobs), as successfully reproduced for very fast intermicellar rate (see Fig. 4D). In microemulsions, half-times also vary with concentration as shown in Fig. 4 (central column). In addition, concentration also influences the separation between Au and Pt half-times. The greater the concentration, the larger the Au and Pt half-times separation, which results in better segregated structures, as experimentally observed.41 This trend is more marked as more rigid the film is (slower exchange rate), and it is even more marked when Au content is decreased, as shown in Fig. 5.
2/kobs), as successfully reproduced for very fast intermicellar rate (see Fig. 4D). In microemulsions, half-times also vary with concentration as shown in Fig. 4 (central column). In addition, concentration also influences the separation between Au and Pt half-times. The greater the concentration, the larger the Au and Pt half-times separation, which results in better segregated structures, as experimentally observed.41 This trend is more marked as more rigid the film is (slower exchange rate), and it is even more marked when Au content is decreased, as shown in Fig. 5.
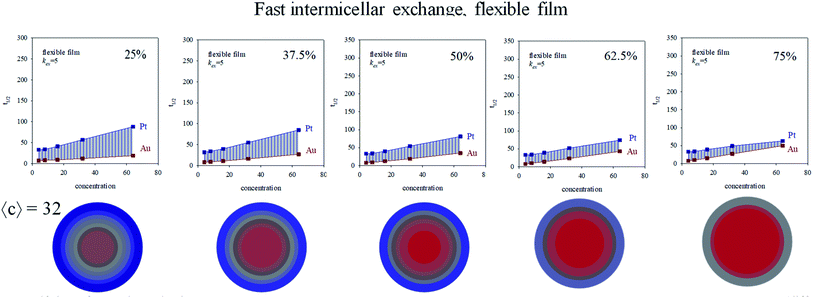
In order to study the influence of reactants proportion Au![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pt on kinetics, intermicellar exchange rate must be kept fixed. Fig. 6 shows half-times versus concentration for different %Au when a flexible film is used. By observing the figures from left to right, the gap between Au and Pt half-times shows the opposite trend, that is, it becomes smaller at high concentration. When this experiment is repeated using a rigid film (slow intermicellar exchange), the tendency is even more pronounced (see Fig. 7). The reason is that the controlling-step of Au reduction is the intermicellar exchange, as mentioned above. Micelles play as dosing pump of Au precursor, so if there is more Au precursor, many collisions are required to make possible the reactants encounter inside the same micelle, and the subsequent chemical reduction. As a result, Au reduction takes place over a longer period of time. This effect will be more pronounced as the exchange rate is slower (compare Fig. 6 and 7). Summarizing, the higher the Au content, the longer the half time.
Pt on kinetics, intermicellar exchange rate must be kept fixed. Fig. 6 shows half-times versus concentration for different %Au when a flexible film is used. By observing the figures from left to right, the gap between Au and Pt half-times shows the opposite trend, that is, it becomes smaller at high concentration. When this experiment is repeated using a rigid film (slow intermicellar exchange), the tendency is even more pronounced (see Fig. 7). The reason is that the controlling-step of Au reduction is the intermicellar exchange, as mentioned above. Micelles play as dosing pump of Au precursor, so if there is more Au precursor, many collisions are required to make possible the reactants encounter inside the same micelle, and the subsequent chemical reduction. As a result, Au reduction takes place over a longer period of time. This effect will be more pronounced as the exchange rate is slower (compare Fig. 6 and 7). Summarizing, the higher the Au content, the longer the half time.
The influence of exchange rate on Pt reduction is expected to be smaller, because Pt reduction rate is mainly chemical controlled. This less impact of exchange rate on Pt reduction rate gives rise to the progressive approach of Au and Pt lines shown in Fig. 5 and 6. The extreme case is represented in Fig. 6 for 75% Au: the line showing Au half time crosses the Pt one, that is, Au half time is longer than Pt one at high Au![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pt ratio. This means that, although Au chemical rate is faster than Pt one, and Au amount is higher than Pt, the microemulsion as reaction media causes Au reduction is taking place during more time.
Pt ratio. This means that, although Au chemical rate is faster than Pt one, and Au amount is higher than Pt, the microemulsion as reaction media causes Au reduction is taking place during more time.
3.2 Structural study
Fig. 6 and 7 also shows the Au/Pt averaged structures for a fixed concentration (〈c〉 = 32 reactants/micelle) and varying Au![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pt ratio and two different microemulsion compositions. Qualitatively similar results were obtained at different concentrations. Correlation between a higher Δt1/2 and a better metal segregation can be clearly observed. In both rigid and flexible films, a low Au% leads to core–shell structures, in which Au builds the inner part of the particle, and Pt locates at the surface, accordingly with the higher differences between Au and Pt half times. Likewise, from 25% to 50% Au, the thickness of the Pt surface is reduced due to the diminution in Pt content. As Au% increases, Au advances towards more external layers, resulting in a progressively higher degree of mix at the surface (more opaque color). At 75% Au, the nanoparticle is mainly composed by gold, covered by a mixed surface if the film is flexible (see last concentric circles in Fig. 6). That is, in accordance with the higher half time of Pt shown in the upper figure, Pt is located mainly at the surface. On the contrary, when the film is rigid, because of the slowness of the intermicellar exchange, Au half times becomes longer than Pt one at high Au% and high 〈c〉 (see Fig. 7, 75%), which means that more Au reaches the surface. This is reflected in nanoparticle structure, whose surface does not present Pt enrichment. There is no metal segregation and the low content of Pt is mixed in all layers. As mentioned above, this behavior can be explained by taking into account the compartmentalization of reaction media: because of micelles play as dosing pump of Au precursor, a higher %Au implies that Au reduction takes place over a longer period of time, so Au will be deposited until longer stages of the process, giving rise to an Au enrichment at the surface.
Pt ratio and two different microemulsion compositions. Qualitatively similar results were obtained at different concentrations. Correlation between a higher Δt1/2 and a better metal segregation can be clearly observed. In both rigid and flexible films, a low Au% leads to core–shell structures, in which Au builds the inner part of the particle, and Pt locates at the surface, accordingly with the higher differences between Au and Pt half times. Likewise, from 25% to 50% Au, the thickness of the Pt surface is reduced due to the diminution in Pt content. As Au% increases, Au advances towards more external layers, resulting in a progressively higher degree of mix at the surface (more opaque color). At 75% Au, the nanoparticle is mainly composed by gold, covered by a mixed surface if the film is flexible (see last concentric circles in Fig. 6). That is, in accordance with the higher half time of Pt shown in the upper figure, Pt is located mainly at the surface. On the contrary, when the film is rigid, because of the slowness of the intermicellar exchange, Au half times becomes longer than Pt one at high Au% and high 〈c〉 (see Fig. 7, 75%), which means that more Au reaches the surface. This is reflected in nanoparticle structure, whose surface does not present Pt enrichment. There is no metal segregation and the low content of Pt is mixed in all layers. As mentioned above, this behavior can be explained by taking into account the compartmentalization of reaction media: because of micelles play as dosing pump of Au precursor, a higher %Au implies that Au reduction takes place over a longer period of time, so Au will be deposited until longer stages of the process, giving rise to an Au enrichment at the surface.
From a conventional kinetic point of view, if media was homogeneous, a larger quantity of Au means a faster Au reduction, so Au would be reduced at the beginning of the synthesis, and then Au would not reach the surface. Quite to the contrary, in microemulsions, Au reduction is controlled by the intermicellar exchange, so a high quantity of Au favors the Au enrichment at the surface. It can be stablished that the final nanoparticle segregation is dictated by the heterogeneity of the reaction media.
Summarizing, a low Au% favor the formation of core–shell structures with mainly Pt at the surface, and a high %Au leads to more mixed ones with an alloyed surface. Specifically, if the goal is a surface containing Au, it is recommended to use a high %Au in the initial mix of reagents.
3.3 Surface composition
Fig. 8 shows the surface composition (expressed as % of Au in the last layer) versus initial composition at two different reagent concentrations. One can observe that when the initial % of Au increases, the quantity of Au at the surface also increases, with the exception of very low %Au values, at which Au is exhausted when the core and middle layers are built and cannot reach the surface. These results are consistent with experimental data on Au/Pt nanocatalysts synthesized at different Au![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pt ratios in a n-heptane/Brij30/water microemulsion.12 In order to determine size distributions, morphologies, crystallographic structures and chemical compositions, the synthesized materials (Pt, Au30Pt70, Au70Pt30, Au80Pt20 and Au) were characterized using transmission electron microscopy (TEM) and X-ray patterns. The direct measurements of particle size on TEM images match well with the results obtained by XRD technique (see Table 1 in ref. 12). These authors found that a high Au content leads to nanoparticles with alloys properties, with a covering surface containing both metals. On the contrary, at low %Au, both metals are clearly separated, and the surface is exclusively composed by Pt, in agreement with simulation results shown in Fig. 6 and 7. In addition, as the Au proportion increases, the superficial composition superficial is closer to the feeding composition. To compare these results with the nanostructures predicted by simulation, experimental data (shown as stars in Fig. 8) are overlapped to simulation data monitored at two different concentration values. Taking into account that the used surfactant was Brij30, which leads to a quite rigid film, the simulation parameters employed to characterize the microemulsion were kex = 1, f = 5. The concentration used in experiments was 0.1 M, but it cannot be calculated in terms of number of reagents in a micelle because the micelle radius is not available. Thus the values calculated for an AOT microemulsion (droplet radius 7.3 nm), which gives a concentration between 〈c〉 = 16 (∼0.08 M) and 〈c〉 = 32 reagents/micelle (∼0.16 M) were shown in Fig. 8. It has to be emphasized that simulation data successfully reproduce the experimental behaviour.
Pt ratios in a n-heptane/Brij30/water microemulsion.12 In order to determine size distributions, morphologies, crystallographic structures and chemical compositions, the synthesized materials (Pt, Au30Pt70, Au70Pt30, Au80Pt20 and Au) were characterized using transmission electron microscopy (TEM) and X-ray patterns. The direct measurements of particle size on TEM images match well with the results obtained by XRD technique (see Table 1 in ref. 12). These authors found that a high Au content leads to nanoparticles with alloys properties, with a covering surface containing both metals. On the contrary, at low %Au, both metals are clearly separated, and the surface is exclusively composed by Pt, in agreement with simulation results shown in Fig. 6 and 7. In addition, as the Au proportion increases, the superficial composition superficial is closer to the feeding composition. To compare these results with the nanostructures predicted by simulation, experimental data (shown as stars in Fig. 8) are overlapped to simulation data monitored at two different concentration values. Taking into account that the used surfactant was Brij30, which leads to a quite rigid film, the simulation parameters employed to characterize the microemulsion were kex = 1, f = 5. The concentration used in experiments was 0.1 M, but it cannot be calculated in terms of number of reagents in a micelle because the micelle radius is not available. Thus the values calculated for an AOT microemulsion (droplet radius 7.3 nm), which gives a concentration between 〈c〉 = 16 (∼0.08 M) and 〈c〉 = 32 reagents/micelle (∼0.16 M) were shown in Fig. 8. It has to be emphasized that simulation data successfully reproduce the experimental behaviour.
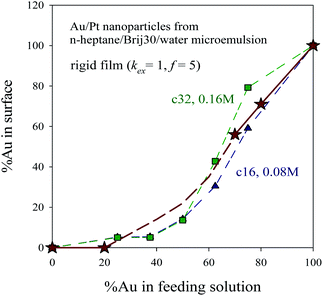 | ||
| Fig. 8 %Au at the surface versus %Au in feeding solution. Synthesis conditions: rigid film (kex = 1, f = 5), 〈c〉 = 32 reactants/micelle ∼0.16 M (green squares) and 〈c〉 = 16 reactants/micelle ∼0.08 M (blue triangles). Stars represent experimental data of Au/Pt nanocatalysts synthesized in a n-heptane/Brij30/water microemulsion, taken from ref. 12. Lines are only guides to the eye. | ||
4 Conclusions
An in-depth kinetic study on the influence of Au![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pt ratio on the formation of Au/Pt nanoparticles synthetized in microemulsions was carried out under different synthesis conditions. The metal distribution in the resulting Au/Pt nanoparticles was explained as a function of kinetic parameters such as Au
Pt ratio on the formation of Au/Pt nanoparticles synthetized in microemulsions was carried out under different synthesis conditions. The metal distribution in the resulting Au/Pt nanoparticles was explained as a function of kinetic parameters such as Au![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pt ratio, intermicellar exchange rate and metal salts concentration. Due to micelles play as dosing pump of Au precursor, a greater Au content implies that Au reduction takes place over a longer period, so Au is deposited until longer stages of the synthesis, resulting in an Au enrichment at the surface. Pt is less affected by compartmentalization of the reaction media due to the slower Pt reduction. These different kinetic behaviors of Au and Pt give rise to a surface composition which can be tailored by tuning the Au
Pt ratio, intermicellar exchange rate and metal salts concentration. Due to micelles play as dosing pump of Au precursor, a greater Au content implies that Au reduction takes place over a longer period, so Au is deposited until longer stages of the synthesis, resulting in an Au enrichment at the surface. Pt is less affected by compartmentalization of the reaction media due to the slower Pt reduction. These different kinetic behaviors of Au and Pt give rise to a surface composition which can be tailored by tuning the Au![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pt ratio. As a guide to experimentalists, core–shell nanoparticles with Pt composed surfaces are obtained when a low Au% is used in feeding solution, and high %Au leads to more mixed structures. Specifically, if the goal is a surface containing Au, it is recommended to use a high %Au in the initial mix of reagents. Simulation results on surface composition under different Au
Pt ratio. As a guide to experimentalists, core–shell nanoparticles with Pt composed surfaces are obtained when a low Au% is used in feeding solution, and high %Au leads to more mixed structures. Specifically, if the goal is a surface containing Au, it is recommended to use a high %Au in the initial mix of reagents. Simulation results on surface composition under different Au![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pt ratio were successfully compared to experimental data.
Pt ratio were successfully compared to experimental data.
In this study, focused on Au/Pt nanoparticles synthesized in microemulsions, the surface composition of the resulting nanoparticles is explained from a kinetic point of view. The thorough-understanding of this synthetic procedure is relevant, because it opens up the improvement for different couple of metals arrangement prediction, that can be implemented for tailor design of other bimetallic nanostructures.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by Consellería de Educación, Universidad y Formación Profesional, Xunta de Galicia (Grupos Ref. Comp. ED431C 2017/22; and AEMAT ED431E2018/08).References
- B. Jiang, Y. Guo, J. Kim, A. E. Whitten, K. Wood, K. Kani, A. E. Rowan, J. Henzie and Y. Yamauchi, J. Am. Chem. Soc., 2018, 140, 12434–12441 CrossRef CAS.
- C. Li, M. Iqbal, B. Jiang, Z. Wang, J. Kim, A. K. Nanjundan, A. E. Whitten, K. Woode and Y. Yamauchi, Chem. Sci., 2019, 10, 4054–4061 RSC.
- C. Li, M. Iqbal, J. Lin, X. Luo, B. Jiang, V. Malgras, K. C.-W. Wu, J. Kim and Y. Yamauchi, Acc. Chem. Res., 2018, 51, 1764–1773 CrossRef CAS.
- J. Xu, T. White, P. Li, C. He, J. Yu, W. Yuan and Y.-F. Han, J. Am. Chem. Soc., 2010, 132, 10398–10406 CrossRef CAS.
- G. Wei, W. Dai, W. Qian, W. Cao and J. Zhang, China Pet. Process. Petrochem. Technol., 2012, 14, 59–67 CAS.
- J. Suntivich, Z. Xu, C. E. Carlton, J. Kim, B. Han, S. W. Lee, N. Bonnet, N. Marzari, L. F. Allard, H. A. Gasteiger, K. Hamad-Schifferli and Y. Shao-Horn, J. Am. Chem. Soc., 2013, 135, 7985–7991 CrossRef CAS.
- C. Li, H. Tan, J. Lin, X. Luo, S. Wang, J. You, Y.-M. Kang, Y. Bando, Y. Yamauchi and J. Kim, Nano Today, 2018, 21, 91–105 CrossRef CAS.
- K. K. Haldar, S. Kundu and A. Patra, ACS Appl. Mater. Interfaces, 2014, 6, 21946–21953 CrossRef CAS.
- F. H. B. Lima, J. Zhang, M. H. Shao, K. Sasaki, M. B. Vukmirovic, E. A. Ticianelli and R. R. Adzic, J. Phys. Chem. C, 2007, 111, 404–410 CrossRef CAS.
- W. Tang, H. Lin, S. Jayaraman, T. F. Jaramillo, G. D. Stucky and E. W. McFarland, J. Phys. Chem. C, 2009, 113, 5014–5024 CrossRef CAS.
- J. Luo, P. N. Njoki, Y. Lin, L. Wang and C. J. Zhong, Electrochem. Commun., 2006, 8, 581–587 CrossRef CAS.
- A. Habrioux, W. Vogel, M. Guinel, L. Guetaz, K. Servat, B. Kokoh and N. Alonso-Vante, Phys. Chem. Chem. Phys., 2009, 11, 3573–3579 RSC.
- S. S. Kumar and K. L. N. Phani, J. Power Sources, 2009, 187, 19–24 CrossRef CAS.
- A. Habrioux, D. Diabate, J. Rousseau, T. W. Napporn, K. Servat, L. Guetaz, A. Trokourey and K. B. Kokoh, Electrocatalysis, 2010, 1, 51–59 CrossRef CAS.
- Y. Hu, H. Zhang, P. Wu, H. Zhang, B. Zhou and C. Cai, Phys. Chem. Chem. Phys., 2011, 13, 4083–4094 RSC.
- J. L. Fernández, D. A. Walsh and A. J. Bard, J. Am. Chem. Soc., 2005, 127, 357–365 CrossRef.
- P. N. Duchesne, Z. Y. Li, C. P. Deming, V. Fung, X. Zhao, J. Yuan, T. Regier, A. Aldalbahi, Z. Almarhoon, S. Chen, D. E. Jiang, N. Zheng and P. Zhang, Nat. Mater., 2018, 17, 1033–1039 CrossRef CAS.
- M. Boutonnet and M. Sanchez-Dominguez, Catal. Today, 2017, 285, 89–103 CrossRef CAS.
- J.-H. Noh and R. Meijboom, J. Colloid Interface Sci., 2014, 415, 57–69 CrossRef CAS.
- K. Holmberg, J. Colloid Interface Sci., 2004, 274, 355–364 CrossRef CAS.
- L. Ström, H. Ström, P. Carlsson, M. Skoglundh and H. Härelind, Langmuir, 2018, 34, 9754–9761 CrossRef.
- J. Feng and C. Zhang, J. Colloid Interface Sci., 2006, 293, 414–420 CrossRef CAS.
- Y. Li, Y. Jiang, M. Chen, H. Liao, R. Huang, Z. Zhou, N. Tian, S. Chen and S. Sun, Chem. Commun., 2012, 48, 9531–9533 RSC.
- F. Heshmatpour, R. Abazari and S. Balalaie, Tetrahedron, 2012, 68, 3001–3011 CrossRef CAS.
- M. Wu, D. Chen and T. Huang, Chem. Mater., 2001, 13, 599–606 CrossRef CAS.
- L. García-Río, J. C. Mejuto and M. Pérez-Lorenzo, J. Phys. Chem. B, 2006, 110, 812–819 CrossRef.
- R. P. Bagwe and K. C. Khilar, Langmuir, 1997, 13, 6432–6438 CrossRef CAS.
- R. P. Bagwe and K. C. Khilar, Langmuir, 2000, 16, 905–910 CrossRef CAS.
- D. G. Angelescu, L. Magno and C. Stubenrauch, J. Phys. Chem. C, 2010, 114, 22069–22078 CrossRef CAS.
- M. Sánchez-Dominguez, M. Boutonnet and C. Solans, J. Nanopart. Res., 2009, 11, 1823–1829 CrossRef.
- M. Sánchez-Dominguez and M. Boutonnet, Catalysts, 2016, 6, 4–8 CrossRef.
- D. Chen and C. Chen, J. Mater. Chem., 2002, 12, 1557–1562 RSC.
- J. Cheng, R. Bordes, E. Olsson and K. Holmberg, Colloids Surf., A, 2013, 436, 823–829 CrossRef CAS.
- A. Pal, S. Shah and S. Devi, Colloids Surf., A, 2007, 302, 483–487 CrossRef CAS.
- P. Hernández-Fernández, S. Rojas, P. Ocón, J. L. Gómez de la Fuente, J. San Fabián, J. Sanza, M. A. Peña, F. J. García-García, P. Terreros and J. L. G. Fierro, J. Phys. Chem. B, 2007, 111, 2913–2923 CrossRef.
- A. Pal, J. Nanostruct. Chem., 2015, 5, 65–69 CrossRef CAS.
- M. Wu, D. Chen and T. Huang, Langmuir, 2001, 17, 3877–3883 CrossRef CAS.
- M. Simoes, S. Baranton and C. Coutanceau, J. Phys. Chem. C, 2009, 113, 13369–13376 CrossRef CAS.
- T. Li, H. Zhou, J. Huang, J. Yin, Z. Chen, D. Liu, N. Zhang and Y. Kuang, Colloids Surf., A, 2014, 463, 55–62 CrossRef CAS.
- C. Tojo, D. Buceta and M. A. López-Quintela, Catalysts, 2017, 7, 1–17 CrossRef.
- D. Buceta, C. Tojo, M. Vukmirovik, F. L. Deepak and M. A. López-Quintela, Langmuir, 2015, 31, 7435–7439 CrossRef CAS.
- C. Tojo, D. Buceta and M. A. López-Quintela, J. Colloid Interface Sci., 2018, 510, 152–161 CrossRef CAS.
- S. Quintillán, C. Tojo, M. C. Blanco and M. A. López-Quintela, Langmuir, 2001, 17, 7251–7254 CrossRef.
- C. Tojo, D. Buceta and M. A. López-Quintela, Nanoscale Res. Lett., 2015, 10, 339–349 CrossRef.
- C. Tojo, M. de Dios and M. A. López-Quintela, J. Phys. Chem. C, 2009, 113, 19145–19154 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2020 |