Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Thermal conductivity of hexagonal BC2P – a first-principles study†
Rajmohan Muthaiah *,
Fatema Tarannum
*,
Fatema Tarannum ,
Roshan Sameer Annam,
Avinash Singh Nayal,
Swapneel Danayat and
Jivtesh Garg
,
Roshan Sameer Annam,
Avinash Singh Nayal,
Swapneel Danayat and
Jivtesh Garg
School of Aerospace and Mechanical Engineering, University of Oklahoma, Norman, OK-73019, USA. E-mail: rajumenr@ou.edu
First published on 23rd November 2020
Abstract
In this work, we report a high thermal conductivity (k) of 162 W m−1 K−1 and 52 W m−1 K−1 at room temperature, along the directions perpendicular and parallel to the c-axis, respectively, of bulk hexagonal BC2P (h-BC2P), using first-principles calculations. We systematically investigate elastic constants, phonon group velocities, phonon linewidths and mode thermal conductivity contributions of transverse acoustic (TA), longitudinal acoustic (LA) and optical phonons. Interestingly, optical phonons are found to make a large contribution of 30.1% to the overall k along a direction perpendicular to the c-axis at 300 K. BC2P is also found to exhibit high thermal conductivity at nanometer length scales. At 300 K, a high k value of ∼47 W m−1 K−1 is computed for h-BC2P at a nanometer length scale of 50 nm, providing avenues for achieving efficient nanoscale heat transfer.
Introduction
High thermal conductivity materials are crucial for achieving efficient thermal management in electronics to improve both performance and reliability.1–8 Carbon based materials such as diamond,9–11 graphene12–14 and stacked-graphene15 (graphene nanoplatelets) exhibit ultrahigh thermal conductivity due to the light mass of carbon (C) atoms and strong C–C bonds. Likewise, boron based III–V compound semiconductors such as boron nitride (BN),16 boron phosphide (BP)17–19 and boron arsenide (BAs)20,21 have very high thermal conductivity due to the light mass of boron atoms and due to a phonon bandgap in vibrational spectra of these materials which suppresses scattering of acoustic phonons by optical phonons thus leading to high acoustic phonon lifetimes. Recently, ultra-high thermal conductivities of 2305 W m−1 K−1 and 4196 W m−1 K−1 were reported22 for bulk ultra-hard hexagonal BC2N (h-BC2N) at 0 GPa and 150 GPa respectively. Similarly, for monolayer BC2N, high thermal conductivities of 1275.79 W m−1 K−1 and 893.9 W m−1 K−1 were reported along the zigzag and armchair directions, respectively.23 These results provide motivation to further explore thermal conductivity of III–IV–V compounds. In this work we explore thermal conductivity of hexagonal BC2P.In this work, thermal conductivity of bulk hexagonal BC2P is computed from first-principles by deriving harmonic (2nd order) and anharmonic (3rd order) interatomic force interactions from first-principles and using them along with an exact solution of the Phonon Boltzmann Transport Equation (PBTE). We find an anisotropic high thermal conductivity (k) of 162 W m−1 K−1 and 52 W m−1 K−1 along directions perpendicular and parallel to c-axis (shown in Fig. 1a) respectively, at 0 GPa. Interestingly, optical phonons are found to contribute 30.1% (∼50 W m−1 K−1) and ∼15% (∼7.54 W m−1 K−1) at 300 K, to overall thermal conductivity along directions perpendicular and parallel to c-axis, respectively, due to their high group velocities. Finally, a high k value of 68 W m−1 K−1 at nanometer length scale of 100 nm (at 300 K) shows that BC2P will be a promising material for thermal management in nanoelectronics.
Computational methods
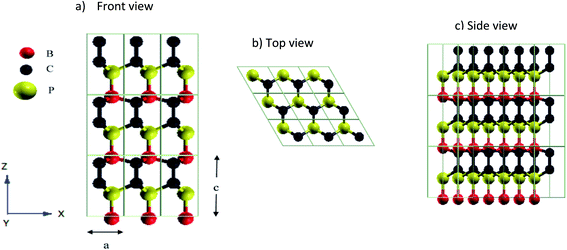
First principles calculations were performed using QUANTUM ESPRESSO24 package. Thermal conductivity was computed by solving Phonon Boltzmann Transport Equation (PBTE) exactly using a variational method. The most important ingredients necessary to predict thermal conductivity, namely the 2nd order and 3rd order interatomic force constants (IFCs), were derived from density-functional perturbation theory (DFPT). These force constants are the second and third-order derivatives of energy with respect to atomic displacements. Computations were performed using norm-conserving pseudopotentials and exchange-correlation was computed in the local density approximation.25 The geometry of the hexagonal BC2P with 4 atoms unit cell, was optimized until forces on all atoms were less than 10−6 Ry per bohr. Plane-wave energy cutoff of 80 Ry and 12 × 12 × 8 Monkhorst–Pack26 k-point mesh were used for electronic structure calculations. Optimized lattice constant (crystal structure of Fig. 1) of BC2P was obtained to be a = 5.2686 bohr with c/a = 1.686.Elastic constants were computed using ‘thermo_pw’ package in QUANTUM-ESPRESSO;24 Voigt–Reuss–Hill approximation27 was used to calculate bulk modulus, shear modulus (G) and Young's Modulus (E). Lattice thermal conductivity is calculated by solving the Phonon Boltzmann Transport Equation (PBTE)28–30 exactly. Expression for thermal conductivity (k) obtained by solving PBTE in the single mode relaxation time (SMRT) approximation31 is given by,
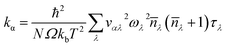 | (1) |
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) λ, and vαλ (=∂ωλ/∂q) are the phonon frequency, equilibrium Bose–Einstein population and group velocity along cartesian direction α, respectively of a phonon mode λ. ωλ,
λ, and vαλ (=∂ωλ/∂q) are the phonon frequency, equilibrium Bose–Einstein population and group velocity along cartesian direction α, respectively of a phonon mode λ. ωλ, ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) λ, and cαλ are derived from the knowledge of phonon dispersion computed using 2nd order IFCs. τλ is the phonon lifetime and is computed using the following equation,
λ, and cαλ are derived from the knowledge of phonon dispersion computed using 2nd order IFCs. τλ is the phonon lifetime and is computed using the following equation,
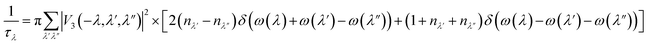 | (2) |
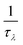 is the anharmonic scattering rate based on the lowest order three phonon interactions and V3(−λ, λ′, λ′′) are the three-phonon coupling matrix elements computed using both harmonic and anharmonic interatomic force constants. Harmonic force constants were calculated using 9 × 9 × 6 q-grid. Anharmonic force constants were computed on a 3 × 3 × 2 q point grid using D3Q28,30,32 package within QUANTUM-ESPRESSO. Acoustic sum rules were imposed on both harmonic and anharmonic interatomic force constants. Phonon linewidth and lattice thermal conductivity were calculated using ‘thermal2’ code within QUANTUM ESPRESSO. For these calculations, a 21 × 21 × 14 q-mesh was used and iterations in the exact solution of the PBTE were performed until Δk between consecutive iterations diminished to below 1.0 × 10−5. Casimir scattering33 is imposed to include the effect of boundary scattering for computing length dependent thermal conductivity.
is the anharmonic scattering rate based on the lowest order three phonon interactions and V3(−λ, λ′, λ′′) are the three-phonon coupling matrix elements computed using both harmonic and anharmonic interatomic force constants. Harmonic force constants were calculated using 9 × 9 × 6 q-grid. Anharmonic force constants were computed on a 3 × 3 × 2 q point grid using D3Q28,30,32 package within QUANTUM-ESPRESSO. Acoustic sum rules were imposed on both harmonic and anharmonic interatomic force constants. Phonon linewidth and lattice thermal conductivity were calculated using ‘thermal2’ code within QUANTUM ESPRESSO. For these calculations, a 21 × 21 × 14 q-mesh was used and iterations in the exact solution of the PBTE were performed until Δk between consecutive iterations diminished to below 1.0 × 10−5. Casimir scattering33 is imposed to include the effect of boundary scattering for computing length dependent thermal conductivity.
Results and discussions
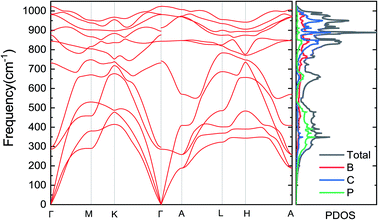
Phonon dispersion and phonon density of states for hexagonal BC2P are shown in Fig. 2. Positive phonon frequencies indicate stability34 of computed h-BC2P crystal structure. Phonon modes at higher frequencies (above 750 cm−1) are mainly dominated by C and B atoms due to light mass and stiff C–C and B–C bonds, whereas P atoms dominate lower frequencies (less than 500 cm−1) due to heavy mass and moderate bond strengths of B–P and C–P. Elastic constants of hexagonal BC2P at 0 GPa are computed to be, C11 = 675 GPa, C33 = 680.6 GPa, C44 = 198 GPa, C66 = 305 GPa, C12 = 65.0 GPa and C13 = 30.8 GPa which satisfies the Born stability criteria35 of C66= (C11 − C12)/2, C11 > C12, C33(C11 + C12) > 2(C13),2 C44 > 0, C66 > 0. Young modulus (E), bulk modulus (B), shear modulus (G) and poisson ratio based on Voigt–Ruess–Hill approximation27 are 582.2 GPa, 253.6 GPa, 260.6 GPa and 0.117 respectively. These values are higher than silicon,36 germanium36 and silicon carbide.37Computed thermal conductivity of the h-BC2P is reported in Fig. 3. Fig. 3a shows the temperature dependent thermal conductivity of h-BC2P along directions perpendicular and parallel to c-axis. At 300 K, computed thermal conductivity of 162 W m−1 K−1, perpendicular to c-axis, is almost 3 times higher than the value, parallel to c-axis, of 52 W m−1 K−1. This is due to the higher phonon frequencies of TA, LA and optical phonons modes, in a direction perpendicular to c-axis, relative to parallel to c-axis, as seen in the computed phonon dispersion. Thermal conductivity of h-BC2N is also higher than that of silicon.38 Perpendicular to c-axis, TA1, TA2 and LA phonon modes contribute 20.1%, 27.5% and 22.3% to overall thermal conductivity while along c-axis, the corresponding contributions are 23%, 30% and 32% to overall k at 300 K. Interestingly, at 300 K, optical phonon modes contribute 30.1% and 15% to overall thermal conductivity, along directions perpendicular and parallel to c-axis, respectively. This contribution is significantly higher than typical semiconductor materials such as silicon, where optical phonons contribute ∼5% to overall k. This is due to the high phonon group velocities of optical phonons (Fig. 4a) and optical phonon linewidths being comparable to that of acoustic phonons, in the frequency range of ∼300–550 cm−1 (Fig. 4b) in BC2P.
 | ||
| Fig. 3 (a) Temperature dependence and (b) length dependence of thermal conductivity along and perpendicular to c-axis of h-BC2P. | ||
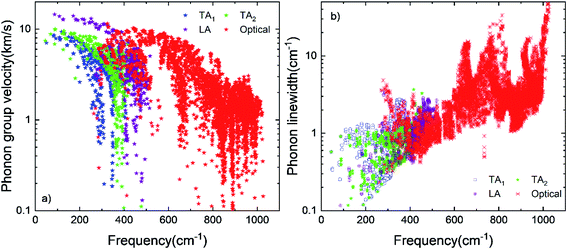 | ||
| Fig. 4 (a) Phonon group velocity and (b) phonon linewidth of TA, LA and optical phonon modes of h-BC2P at 300 K. | ||
An advantage of BC2P is its relatively high thermal conductivity at nanometer length scales. Length dependence of thermal conductivity was calculated by introducing Casimir scattering 1/τboundary = |v|/L, where v is the phonon velocity and L is the system size. Length dependent thermal conductivity is shown in Fig. 3b. We observe that at a length scale of 100 nm, the predicted thermal conductivity of ∼68 W m−1 K−1 is significantly high. This can lead to potential avenues for use of BC2P in nanoscale thermal management applications. This high nanoscale thermal conductivity of BC2P is due to the relatively large k contribution of optical phonons, which typically have meanfreepaths in the nanometer regime.
Conclusion
In this work, thermal conductivity of hexagonal BC2P (h-BC2P) is computed by solving phonon Boltzmann transport equation exactly coupled with force-constants derived from first principles calculations. We report an anisotropic thermal conductivity (k) of 162 W m−1 K−1 and 52 W m−1 K−1 along directions perpendicular and parallel to c-axis of BC2P respectively. This high thermal conductivity is due to the high frequencies and phonon group velocities arising from light mass of the constituent atoms (B, C, P) and stiff C–C, B–C and B–P bonds. Anisotropy in k is due to higher phonon frequencies and group velocities along direction perpendicular to c-axis relative to the parallel direction. Moreover, optical phonon modes are found to contribute significantly to k along directions both perpendicular to c-axis (30.1%) and parallel to c-axis (15%) at 300 K. Finally, a high room temperature thermal conductivity of 68 W m−1 K−1 at 100 nm length scale, makes BC2P attractive for thermal management in nanoelectronics.Conflicts of interest
There are no conflicts to declare.Acknowledgements
R. M, F. T, R. S. A, A. S. N, S. D and J. G would like to acknowledge OU Supercomputing Center for Education Research (OSCER) for providing computational resources. J. G, R. M and F. T acknowledge financial support from NSF CAREER grant, award # 1847129.References
- J. Yeom, M. A. Shannon and T. Singh, Micro-Coolers, in Reference Module in Materials Science and Materials Engineering, Elsevier, 2017 Search PubMed.
- A. L. Moore and L. Shi, Emerging challenges and materials for thermal management of electronics, Mater. Today, 2014, 17(4), 163–174 CrossRef CAS.
- S. S. Kang, in Advanced Cooling for Power Electronics, 2012 7th International Conference on Integrated Power Electronics Systems (CIPS), 6–8 March, 2012, pp. 1–8 Search PubMed.
- A. Bar-Cohen, Thermal management of on-chip hot spots and 3D chip stacks, in 2009 IEEE International Conference on Microwaves, Communications, Antennas and Electronics Systems, 9–11 Nov, 2009, pp. 1–8 Search PubMed.
- S. S. Anandan and V. Ramalingam, in Thermal management of electronics: a review of literature, 2008 Search PubMed.
- A. Bar-Cohen, P. Wang and E. Rahim, Thermal management of high heat flux nanoelectronic chips, Microgravity Sci. Technol., 2007, 19(3), 48–52 CrossRef.
- G. Chen and A. Shakouri, Heat Transfer in Nanostructures for Solid-State Energy Conversion, J. Heat Transfer, 2001, 124(2), 242–252 CrossRef.
- T. J. Lu, Thermal management of high power electronics with phase change cooling, Int. J. Heat Mass Transfer, 2000, 43(13), 2245–2256 CrossRef CAS.
- J. R. Olson, R. O. Pohl, J. W. Vandersande, A. Zoltan, T. R. Anthony and W. F. Banholzer, Thermal conductivity of diamond between 170 and 1200 K and the isotope effect, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47(22), 14850–14856 CrossRef CAS.
- D. G. Onn, A. Witek, Y. Z. Qiu, T. R. Anthony and W. F. Banholzer, Some aspects of the thermal conductivity of isotopically enriched diamond single crystals, Phys. Rev. Lett., 1992, 68(18), 2806–2809 CrossRef CAS.
- A. Ward, D. A. Broido, D. A. Stewart and G. Deinzer, Ab initio theory of the lattice thermal conductivity in diamond, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80(12), 125203 CrossRef.
- J. H. Seol, I. Jo, A. L. Moore, L. Lindsay, Z. H. Aitken, M. T. Pettes, X. Li, Z. Yao, R. Huang, D. Broido, N. Mingo, R. S. Ruoff and L. Shi, Two-Dimensional Phonon Transport in Supported Graphene, Science, 2010, 328(5975), 213–216 CrossRef CAS.
- L. Lindsay, D. A. Broido and N. Mingo, Flexural phonons and thermal transport in graphene, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82(11), 115427 CrossRef.
- D. Nika, E. Pokatilov, A. Askerov and A. Balandin, Phonon Thermal Conduction in Graphene, 2008 Search PubMed.
- A. Balandin, D. Nika, E. Pokatilov and A. Askerov, Comment on 'First principles calculation of lattice thermal conductivity in mono- and bi-layer graphene', 2009, arXiv:0902.0642 Search PubMed.
- K. Chen, B. Song, N. K. Ravichandran, Q. Zheng, X. Chen, H. Lee, H. Sun, S. Li, G. A. G. Udalamatta Gamage, F. Tian, Z. Ding, Q. Song, A. Rai, H. Wu, P. Koirala, A. J. Schmidt, K. Watanabe, B. Lv, Z. Ren, L. Shi, D. G. Cahill, T. Taniguchi, D. Broido and G. Chen, Ultrahigh thermal conductivity in isotope-enriched cubic boron nitride, Science, 2020, 367(6477), 555–559 CrossRef CAS.
- R. Muthaiah and J. Garg, Strain tuned high thermal conductivity in boron phosphide at nanometer length scales – a first-principles study, Phys. Chem. Chem. Phys., 2020, 22(36), 20914–20921 RSC.
- Q. Zheng, S. Li, C. Li, Y. Lv, X. Liu, P. Y. Huang, D. A. Broido, B. Lv and D. G. Cahill, High Thermal Conductivity in Isotopically Enriched Cubic Boron Phosphide, Adv. Funct. Mater., 2018, 28(43), 1805116 CrossRef.
- J. S. Kang, H. Wu and Y. Hu, Thermal Properties and Phonon Spectral Characterization of Synthetic Boron Phosphide for High Thermal Conductivity Applications, Nano Lett., 2017, 17(12), 7507–7514 CrossRef CAS.
- L. Lindsay, D. A. Broido and T. L. Reinecke, First-Principles Determination of Ultrahigh Thermal Conductivity of Boron Arsenide: A Competitor for Diamond?, Phys. Rev. Lett., 2013, 111(2), 025901 CrossRef CAS.
- F. Tian, B. Song, X. Chen, N. K. Ravichandran, Y. Lv, K. Chen, S. Sullivan, J. Kim, Y. Zhou, T.-H. Liu, M. Goni, Z. Ding, J. Sun, G. A. G. Udalamatta Gamage, H. Sun, H. Ziyaee, S. Huyan, L. Deng, J. Zhou, A. J. Schmidt, S. Chen, C.-W. Chu, P. Y. Huang, D. Broido, L. Shi, G. Chen and Z. Ren, Unusual high thermal conductivity in boron arsenide bulk crystals, Science, 2018, 361(6402), 582–585 CrossRef CAS.
- S. Nayeb Sadeghi, S. M. Vaez Allaei, M. Zebarjadi and K. Esfarjani, Ultra-high lattice thermal conductivity and the effect of pressure in superhard hexagonal BC2N, J. Mater. Chem. C, 2020, 21(31), 17306–17313 Search PubMed.
- A. Shafique and Y.-H. Shin, Ultrahigh and anisotropic thermal transport in the hybridized monolayer (BC2N) of boron nitride and graphene: a first-principles study, Phys. Chem. Chem. Phys., 2019, 21(31), 17306–17313 RSC.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials, J. Phys.: Condens. Matter, 2009, 21(39), 395502 CrossRef.
- D. M. Ceperley and B. J. Alder, Ground State of the Electron Gas by a Stochastic Method, Phys. Rev. Lett., 1980, 45(7), 566–569 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13(12), 5188–5192 CrossRef.
- D. H. Chung and W. R. Buessem, The Voigt–Reuss–Hill (VRH) Approximation and the Elastic Moduli of Polycrystalline ZnO, TiO2 (Rutile), and α-Al2O3, J. Appl. Phys., 1968, 39(6), 2777–2782 CrossRef CAS.
- L. Paulatto, I. Errea, M. Calandra and F. Mauri, First-principles calculations of phonon frequencies, lifetimes, and spectral functions from weak to strong anharmonicity: the example of palladium hydrides, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91(5), 054304 CrossRef.
- J. Garg, N. Bonini and N. Marzari, First-Principles Determination of Phonon Lifetimes, Mean Free Paths, and Thermal Conductivities in Crystalline Materials: Pure Silicon and Germanium, in Length-Scale Dependent Phonon Interactions, ed. S. L. Shindé and G. P. Srivastava, Springer New York, New York, NY, 2014, pp. 115–136 Search PubMed.
- G. Fugallo, M. Lazzeri, L. Paulatto and F. Mauri, Ab initio variational approach for evaluating lattice thermal conductivity, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88(4), 045430 CrossRef.
- G. P. Srivastava, The Physics of Phonons, Taylor & Francis, 1990 Search PubMed.
- L. Paulatto, F. Mauri and M. Lazzeri, Anharmonic properties from a generalized third-order ab initio approach: theory and applications to graphite and graphene, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87(21), 214303 CrossRef.
- H. B. G. Casimir, Note on the conduction of heat in crystals, Physica, 1938, 5(6), 495–500 CrossRef.
- I. Etxebarria, J. M. Perez-Mato and G. Madariaga, Lattice dynamics, structural stability, and phase transitions in incommensurate and commensurate A2BX4 materials, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46(5), 2764–2774 CrossRef CAS.
- F. Mouhat and F.-X. Coudert, Necessary and sufficient elastic stability conditions in various crystal systems, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90(22), 224104 CrossRef.
- J. Vanhellemont, A. K. Swarnakar and O. Van der Biest, Temperature Dependent Young's Modulus of Si and Ge, ECS Trans., 2014, 64(11), 283–292 CrossRef CAS.
- E. SCHREIBER and N. SOGA, Elastic Constants of Silicon Carbide, J. Am. Ceram. Soc., 1966, 49(6), 342 CrossRef CAS.
- D. A. Broido, M. Malorny, G. Birner, N. Mingo and D. A. Stewart, Intrinsic lattice thermal conductivity of semiconductors from first principles, Appl. Phys. Lett., 2007, 91(23), 231922 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra08444a |
| This journal is © The Royal Society of Chemistry 2020 |