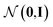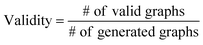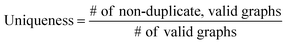Open Access Article
Open Access ArticleScaffold-based molecular design with a graph generative model†
Jaechang
Lim‡
a,
Sang-Yeon
Hwang‡
 a,
Seokhyun
Moon
a,
Seungsu
Kim
b and
Woo Youn
Kim
a,
Seokhyun
Moon
a,
Seungsu
Kim
b and
Woo Youn
Kim
 *ac
*ac
aDepartment of Chemistry, KAIST, 291 Daehak-ro, Yuseong-gu, Daejeon 34141, Republic of Korea. E-mail: wooyoun@kaist.ac.kr
bSchool of Computing, KAIST, 291 Daehak-ro, Yuseong-gu, Daejeon 34141, Republic of Korea
cKI for Artificial Intelligence, KAIST, 291 Daehak-ro, Yuseong-gu, Daejeon 34141, Republic of Korea
First published on 3rd December 2019
Abstract
Searching for new molecules in areas like drug discovery often starts from the core structures of known molecules. Such a method has called for a strategy of designing derivative compounds retaining a particular scaffold as a substructure. On this account, our present work proposes a graph generative model that targets its use in scaffold-based molecular design. Our model accepts a molecular scaffold as input and extends it by sequentially adding atoms and bonds. The generated molecules are then guaranteed to contain the scaffold with certainty, and their properties can be controlled by conditioning the generation process on desired properties. The learned rule of extending molecules can well generalize to arbitrary kinds of scaffolds, including those unseen during learning. In the conditional generation of molecules, our model can simultaneously control multiple chemical properties despite the search space constrained by fixing the substructure. As a demonstration, we applied our model to designing inhibitors of the epidermal growth factor receptor and show that our model can employ a simple semi-supervised extension to broaden its applicability to situations where only a small amount of data is available.
1 Introduction
The goal of molecular design is to find molecules with desirable functionalities. The vast expanse of chemical space offers infinite possibilities of discovering novel molecules in a variety of applications. Yet at the same time, the very infinity is what brings hardships when one intends to find the most promising candidate in an affordable amount of time. In drug discovery, for instance, the number of potential drug-like molecules is estimated to be about 1023 to 1060,1 among which only a few 108s have ever been synthesized.2 Thus, it is practically impossible to discover a new drug through brute-force exploration of chemical space, and the demand for more rational approaches has inevitably surged.A common strategy of rational molecular design is narrowing the search space by starting from a known molecule with potential. Designing new molecules then proceeds by searching for the right combination of functional groups that optimizes the required properties, while the core structure, or scaffold, of the original molecule is purposely retained to preserve the underlying characteristics. This scaffold-based design has been one of the standard approaches in small-molecule drug discovery, where one first identifies a scaffold based on the information of the target protein and probes a library of derivative compounds to find the one showing optimum potency and selectivity.3–5 Molecular design in other areas such as materials chemistry also adopts similar strategies. A conspicuous example is organic electronics, where a typical set of electron-donor and -acceptor moieties is known. The process of properly selecting or combining scaffold moieties, followed by side-chain optimization, leads to designing new constituents in organic light-emitting diodes,6 field-effect transistors,7 photocatalysts8 and solar cells.9 However, although fixing the core structure hugely reduces the search space, it is most likely that, in most real-world applications, the remaining fraction still spans easily beyond the reach of what could be covered by sole human intuition.
Upon the call for more exhaustive and intelligent exploration of chemical space, recent advances in deep generative models have been more and more stimulating the use of the models in in silico molecular design.10,11 All the related studies share a common goal of easing the labor of discovering new molecules in practice.12–31 That said, until today not much attention was given to scaffold-based molecular design, despite its prevalence as described above. One exception is the work by Li et al.,25 where the authors use a fingerprint representation of the scaffolds contained in a molecule. The fingerprint is then used to condition the generation process so that the generated molecules tend to contain desired scaffolds. Another possible way of retaining scaffolds is to learn a continuous representation of molecules.15,17,24,32 Searching the vicinity of a query molecule in the resulting latent space allows generating molecules similar in shape. Generating derivatives of a scaffold can thus be possible if the distance in the learned space well correlates with core-structure similarity.
The described schemes of scaffold-based molecule generation have the following drawbacks. First, categorically representing the scaffold kind of a molecule requires a predefined vocabulary of scaffolds. This imposes a limitation on querying arbitrary kinds of scaffolds when generating molecules. Second, because of their probabilistic nature, both the conditional generation and the latent-space search permit molecules that do not contain desired scaffolds. Lastly, to the best of our knowledge, no work has been shown to control the scaffold and properties of generated molecules at the same time, which is essential in achieving the goal of scaffold-based molecular design.
We here show our development of a generative model that targets its use in scaffold-based molecular design. Our model is a variational autoencoder (VAE)33 that accepts a molecular scaffold as input and extends it to generate derivative molecules. Extending a scaffold is done by sequentially adding new atoms and bonds to due parts of the scaffold. We adopt graphs to represent molecular structures instead of widely used textual formats, such as the simplified molecular-input line-entry system (SMILES).34 This is because a string representation can substantially change throughout our process of sequential extension while graphs can more naturally express how a new atom or bond—i.e., node or edge—is added each time.24 Graph neural networks are used to extract the structural dependencies between nodes and edges, making every decision of adding a new element dependent on the structure of the graph being processed.25,35,36 The properties of generated molecules can be controlled by conditioning the generation process on desired properties. After learning, our model can accept any arbitrary scaffold and generate new molecules, with their properties controlled and core structures retained.
Ideally, generative models without any starting structure, i.e., de novo generative models for molecules, would be more desirable. However, the performance of optimizing a property in de novo generation may significantly drop when the associated structure–property relationship is hard to be learned.18 Such a tendency can get still worse when multiple properties are to be controlled, because acquiring a sufficient amount of data for individual properties is often impractical. By leveraging the properties of a scaffold, our scaffold-based generative model can more easily optimize target properties and preserve desirable characteristics. As an example of the latter, one can retain the synthetic accessibility of the generated molecules by using a scaffold whose synthetic routes are well established—an aspect crucial in in silico design.
Our work contributes to molecular design in two aspects. One, of more practical importance, is our proposal of the model as a tool for scaffold-based molecular design. The other, of more analytical importance, is our exploration of supergraph space. To elaborate the latter, we first note that once a scaffold is to be retained, the set of possible generations only include the molecules whose graphs are supergraphs of the scaffold graph. In other words, fixing a scaffold imposes a strong constraint on the search space, and therefore it shall be meaningful to probe how such a constraint affects the generation performance and property controllability. The first part of our experiments addresses this point. Further divided into three parts, our experiments address (i) the overall generation performance, (ii) the scaffold dependence and (iii) the property controllability of our model. In part (i), we show that our model achieves high rates of validity, uniqueness and novelty in generating molecules. In part (ii), we show that our model consistently shows good performance in extending unobserved as well as observed scaffolds, confirming that our model can build new molecules from smaller ones by learning valid chemical rules, rather than by memorizing the molecule–scaffold matching in the training data. In part (iii), we show that despite the confined search space, our model can control single or multiple properties of generated molecules, with tolerable deviations from targeted values.
Finally, returning to the more practical aspect, we applied our model to designing inhibitors of the human epidermal growth factor receptor (EGFR). We performed semi-supervised learning by incorporating a property predictor to learn from unlabeled molecules as well, which can help treat the frequently encountered problem of data deficiency. As a result, the model was able to generate new inhibitors with improved potency, where 20% of the unique generations showed more than two orders of magnitude decrease in the predicted half-maximal inhibitory concentration. This shows that our model can learn to design molecules in more realistic problems, where the deficiency of available data makes learning hard.
2 Method
2.1 Related work
To define a generative model for molecules, one must choose a molecular representation suitable for feature learning and molecule generation.37 One of the most widely used specifications is SMILES,34 which uses a string of characters to represent a molecule's 2D structure and stereoisomerism. Accordingly, SMILES-based generative models have been developed under various frameworks including language models,12–14 VAEs,15–17,32 adversarial autoencoders18 and generative adversarial networks.19 Some models employed reinforcement learning strategies to augment goal-directed generation.19–23Despite the well-demonstrated successes of SMILES-based models, SMILES has a fundamental limitation in consistently conveying molecular similarity.24 In contrast to SMILES, molecular graphs as a representation can more naturally express the structural characteristics of molecules. Because learning a distribution over graphs imposes more challenging problems like low scalability and non-unique node orderings,25,38 it is only very recently that reports on generative models of graphs—molecular graphs, in particular—began to emerge. The majority of works adopts sequential methods in generating graphs. For instance, the models by Li et al.,25 You et al.26 and Li et al.27 generate a graph by predicting a sequence of graph building actions consisting of node additions and edge additions. Assouel et al.28 and Liu et al.29 similarly adopted the sequential scheme, but their graph generation proceeds through two (fully28 or partially29) separate stages of node initialization and connection. It is also possible to coarse-grain the standard node-by-node generation into a structure-by-structure fashion. The junction tree VAE by Jin et al. generates a tree of molecular fragments and then recovers a full molecular graph through a fine-grained assembly of the fragments.24 Sharply contrasting to the sequential generation scheme is the single-step generation of whole graphs. The models GraphVAE by Simonovsky and Komodakis30 and MolGAN by De Cao and Kipf31 are such, where an adjacency matrix and graph attributes are predicted altogether, generating a graph at one time.
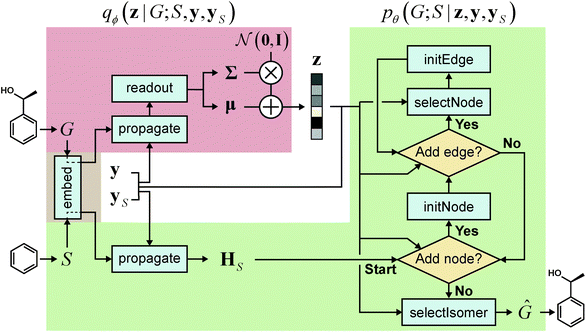
2.2 Overall process and model architecture
Our purpose is to generate molecules with target properties while retaining a given scaffold as a substructure. To this end, we set our generative model to be such that it accepts a graph representation S of a molecular scaffold and generates a graph G that is a supergraph of S. The underlying distribution of G can be expressed as p(G;S). Our notation here intends to manifest the particular relationship, i.e., the supergraph–subgraph relationship, between G and S. We also emphasize that p(G;S) is a distribution of G alone; S acts as a parametric argument, explicitly confining the domain of the distribution. Molecular properties are introduced as a condition, by which the model can define conditional distributions p(G;S|y,yS), where y and yS are the vectors containing the property values of a molecule and its scaffold, respectively. Often in other studies of molecule generation,25,27 a substructure moiety is imposed as a condition, hence defining a conditional distribution p(G|S). Unlike p(G;S), the space of G in the conditional distribution p(G|S) is not explicitly confined by S, and the probabilistic nature also allows G that are not supergraphs of S. On the other hand, the graphs that our model generates according to p(G;S) always contain S as a substructure. As we will see below, our model realizes this by sequentially adding nodes and edges to S. Before we proceed further, we refer the reader to Table 1 for the notations we will use in what follows. Also, when clear distinction is necessary, we will call a molecule a “whole-molecule” to distinguish it from a scaffold.| Notation | Description |
|---|---|
| G | An arbitrary or whole-molecule graph |
| S | A molecular scaffold graph |
| V(G) | The node set of a graph G |
| E(G) | The edge set of a graph G |
| h v | A node feature vector |
| h uv | An edge feature vector |
| H V(G) | {hv:v ∈ V(G)} |
| H E(G) | {huv:(u,v) ∈ E(G)} |
| h G | A readout vector summarizing HV(G) |
| z | A latent vector to be decoded |
| y | The vector of molecular properties of a whole-molecule |
| y S | The vector of molecular properties of a scaffold |
The learning object of our model is a strategy of extending a graph to larger graphs whose distribution follows that of real molecules. We achieve this by training our model to recover the molecules in a dataset from their scaffolds. The scaffold of a molecule can be defined in a deterministic way such as that by Bemis and Murcko,39 which is what we used in our experiments. The construction of a target graph is done by making successive decisions of node and edge additions. The decision at each construction step is drawn from the node features and edge features of the graph at the step. The node features and edge features are recurrently updated to reflect the construction history of the previous steps. The construction process will be further detailed below.
We realized our model as a VAE,33 with the architecture depicted in Fig. 1. The architecture consists of an encoder qϕ and a decoder pθ, parametrized by ϕ and θ, respectively. The encoder encodes a graph G to an encoding vector z and the decoder decodes z to recover G. The decoder requires a scaffold graph S as an additional input, and the actual decoding process runs by sequentially adding nodes and edges to S. The encoding vector z plays its role by consistently affecting its information in updating the node and edge features of a transient graph being processed. Similar to p(G;S), our notation pθ(G;S|z) indicates that candidate generations of our decoder are always a supergraph of S. As for the encoder notation qϕ(z|G;S), we emphasize that the encoder also has a dependence on scaffolds because of the joint optimization of qϕ and pθ.
As a latent variable model, a VAE may have difficulty in generating meaningful samples when the manifold of the learned latent distribution is insufficient to cover all the informative regions.40–42 In generative models for molecules, this difficulty has manifested itself in the form of chemically invalid generated molecules,15,43 and accordingly various SMILES-based43–46 and graph-based24,29,47–49 models have introduced explicit constraints or learning algorithms to enhance the validity of generations. It is possible to incorporate similar constraints or algorithms also in our model; without such, nonetheless, our model shows high chemical validity in the generated graphs (see Section 3.2 below).
2.3 Graph encoding
The goal of graph encoding is to generate a latent vector z of the entire graph G of a whole-molecule. Given the graph G = (V(G), E(G)) of any whole-molecule, we first associate each node v ∈ V(G) with a node feature vector hv and each edge (u,v) ∈ E(G) with an edge feature vector huv. For the initial node and edge features, we choose the atom types and bond types of the molecule. We then embed the initial feature vectors in new vectors with a higher dimension so that the vectors have sufficient capacity to express deep information in and between the nodes and edges. To fully encode the structural information of the molecule, we want every node embedding vector hv to contain not only the sole information of its own node v but also the relationship of v to its neighborhood. This can be done by propagating each node's information to the other nodes in the graph. A large variety of related methods have been devised, each being a particular realization of graph neural networks.35In this work, we implemented the encoder qϕ as a variant of the interaction network.36,50 Our network's algorithm consists of a propagation phase and a readout phase, which we write as
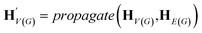 | (1) |
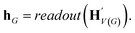 | (2) |
The propagation phase itself consists of two stages. The first stage calculates an aggregated message between each node and its neighbors as
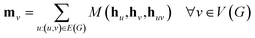 | (3) |
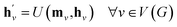 | (4) |
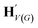 , as written in eqn (1). We iterate the propagation phase a fixed number of times whenever applied, using different sets of parameters at different iteration steps. After the propagation, the readout phase (eqn (2)) computes a weighted sum of the node feature vectors, generating one vector representation hG that summarizes the graph as a whole. Then finally, a latent vector z is sampled from a normal distribution whose mean and variance are inferred from hG.
, as written in eqn (1). We iterate the propagation phase a fixed number of times whenever applied, using different sets of parameters at different iteration steps. After the propagation, the readout phase (eqn (2)) computes a weighted sum of the node feature vectors, generating one vector representation hG that summarizes the graph as a whole. Then finally, a latent vector z is sampled from a normal distribution whose mean and variance are inferred from hG.
The graph propagation can be conditioned by incorporating an additional vector c in calculating aggregated messages. In such a case, the functions M and (accordingly) propagate accept c as an additional argument (i.e., they become M(·,·,·,c) and propagate(·,·,c)). When encoding input graphs, we choose c to be the concatenation of the property vectors y and yS to enable property-controlled generation. During graph decoding, we use the concatenation of y, yS and the latent vector z as the condition vector (see below).
2.4 Graph decoding
The goal of graph decoding is to reconstruct the graph G of a whole-molecule from the latent vector z sampled in the graph encoding phase. Our graph decoding process is motivated by the sequential generation strategy of Li et al.25 In our work, we build the whole-molecule graph G from the scaffold graph G0 (extracted from G by the Bemis–Murcko method39 using the RDKit software51) by successively adding nodes and edges. Here, G0 = S denotes the initial scaffold graph, and we will write Gt to denote any transient (or completed) graph constructed from G0.Our graph decoding starts with preparing and propagating the initial node features of G0. As we do for G, we prepare the initial feature vectors of G0 by embedding the atom types and bond types of the scaffold molecule. This initial embedding is done by the same network (embed in Fig. 1) used for whole-molecules. The initial feature vectors of G0 are then propagated a fixed number of times by another interaction network. As the propagation finishes, the decoder extends G0 by processing it through a loop of node additions and accompanying (inner) loops of edge additions. A concrete description of the process is as follows:
• Stage 1: node addition. Choose an atom type or terminate the building process with estimated probabilities. If an atom type is chosen, add a new node, say w, with the chosen type to the current transient graph Gt and proceed to Stage 2. Otherwise, terminate the building process and return the graph.
• Stage 2: edge addition. Given the new node, choose a bond type or return to Stage 1 with estimated probabilities. If a bond type is chosen, proceed to Stage 3.
• Stage 3: node selection. Select a node, say v, from the existing nodes except w with estimated probabilities. Then, add a new edge (v,w) to Gt with the bond type chosen in Stage 2. Continue the edge addition from Stage 2.
The flow of the whole process is depicted in the right side of Fig. 1. Excluded from Stages 1–3 is the final stage of selecting a suitable isomer, which we describe separately below.
In every stage, the model draws an action by estimating a probability vector on candidate actions. Depending on whether the current stage should add an atom or not (Stage 1), add an edge or not (Stage 2), or select an atom to connect (Stage 3), the probability vector is computed by the corresponding one among the following:
![[p with combining circumflex]](https://www.rsc.org/images/entities/b_char_0070_0302.gif) an = addNode(HV(Gt),HE(Gt),z) an = addNode(HV(Gt),HE(Gt),z) | (5) |
![[p with combining circumflex]](https://www.rsc.org/images/entities/b_char_0070_0302.gif) ae = addEdge(HV(Gt),HE(Gt),z) ae = addEdge(HV(Gt),HE(Gt),z) | (6) |
![[p with combining circumflex]](https://www.rsc.org/images/entities/b_char_0070_0302.gif) sn = selectNode(HV(Gt),HE(Gt),z). sn = selectNode(HV(Gt),HE(Gt),z). | (7) |
The first probability vector ![[p with combining circumflex]](https://www.rsc.org/images/entities/b_char_0070_0302.gif) an is a (na + 1)-length vector, where its elements
an is a (na + 1)-length vector, where its elements ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) an1 to
an1 to 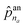 correspond to the probabilities on na atom types, and
correspond to the probabilities on na atom types, and 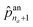 is the termination probability. As for
is the termination probability. As for ![[p with combining circumflex]](https://www.rsc.org/images/entities/b_char_0070_0302.gif) ae, a vector of size nb + 1, its elements
ae, a vector of size nb + 1, its elements ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) ae1 to
ae1 to 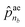 correspond to the probabilities on nb bond types, and
correspond to the probabilities on nb bond types, and 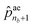 is the probability of stopping the edge addition. Lastly, the i-th element of the third vector
is the probability of stopping the edge addition. Lastly, the i-th element of the third vector ![[p with combining circumflex]](https://www.rsc.org/images/entities/b_char_0070_0302.gif) sn is the probability of connecting the i-th existing node with the lastly added one.
sn is the probability of connecting the i-th existing node with the lastly added one.
When the model decides to add a new node, say w, a corresponding feature vector hw should be added to HV(Gt). To this end, the model prepares an initial feature vector h0w by representing the atom type of w and then incorporates it with the existing node features in HV(Gt) to compute an appropriate hw. Similarly, when a new edge, say (v,w), is added, the model computes hvw from h0vw and HV(Gt) ∪ {hw} to update HE(Gt), where h0vw represents the bond type of (v,w). The corresponding modules for initializing new nodes and edges are as follows:
| hw = initNode(h0w,HV(Gt)) | (8) |
| hvw = initEdge(h0vw,HV(Gt) ∪ hw). | (9) |
The graph building modules addNode, addEdge and selectNode include a preceding step of propagating node features. For instance, the actual operation done by addNode is
| addNode(HV(Gt),HE(Gt),z) = f◦concat(readout◦propagate(k) (HV(Gt),HE(Gt),z),z), | (10) |
![[p with combining circumflex]](https://www.rsc.org/images/entities/b_char_0070_0302.gif) an through a multilayer perceptron f. Likewise, both addEdge and selectNode start with iterated applications of propagate. In this way, node features are recurrently updated every time the transient graph evolves, and the prediction of every building event becomes dependent on the history of the preceding events.
an through a multilayer perceptron f. Likewise, both addEdge and selectNode start with iterated applications of propagate. In this way, node features are recurrently updated every time the transient graph evolves, and the prediction of every building event becomes dependent on the history of the preceding events.
As shown in eqn (10), the graph propagation in addNode (and addEdge and selectNode) incorporates the latent vector z, which encodes a whole-molecule graph G. This makes our model refer to z when making graph building decisions and ultimately reconstruct G by decodingz. If the model is to be conditioned on whole-molecule properties y and scaffold properties yS, one can understand eqn (5)–(7) and (10) as incorporating ![[z with combining tilde]](https://www.rsc.org/images/entities/b_char_007a_0303.gif) = concat(z,y,yS) instead of z.
= concat(z,y,yS) instead of z.
2.5 Molecule generation
When generating new molecules, one needs a scaffold S as an input, and a latent vector z is sampled from the standard normal distribution. Then the decoder generates a new molecular graph Ĝ as a supergraph of S. If one desires to generate molecules with designated molecular properties, the corresponding property vectors y and yS should be provided to condition the building process.2.6 Isomer selection
Molecules can have stereoisomers. Stereoisomers of a molecule have the same connectivity between atoms but different 3D geometries. Consequently, the complete generation of a molecule should also specify the molecule's stereoisomerism. We determine the stereochemical configuration of atoms and bonds after a molecular graph Ĝ is constructed from z.24 The isomer selection module selectIsomer prepares the graphs I of all possible stereoisomers (enumerated by RDKit) whose 2D structures without stereochemical labels are the same as that of Ĝ. All the prepared I include the stereochemical configuration of atoms and bonds in the node and edge features. Then the module estimates the selection probabilities as![[p with combining circumflex]](https://www.rsc.org/images/entities/b_char_0070_0302.gif) si = selectIsomer(Ĝ,z), si = selectIsomer(Ĝ,z), | (11) |
![[p with combining circumflex]](https://www.rsc.org/images/entities/b_char_0070_0302.gif) si are the estimated probabilities of selecting respective I.
si are the estimated probabilities of selecting respective I.
2.7 Objective function
Our objective function has the form of the log-likelihood of an ordinary VAE:33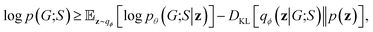 | (12) |
In actual learning, we have a scaffold dataset 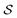 , and for each scaffold
, and for each scaffold  we have a corresponding whole-molecule dataset
we have a corresponding whole-molecule dataset 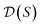 . Note that any set of molecules can produce a scaffold set and a collection of whole-molecule sets: once the scaffolds of all molecules in a pregiven set are defined, producing
. Note that any set of molecules can produce a scaffold set and a collection of whole-molecule sets: once the scaffolds of all molecules in a pregiven set are defined, producing 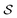 , the molecules of the pregiven set can be grouped into the collection
, the molecules of the pregiven set can be grouped into the collection 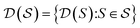 . Using such
. Using such 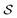 and
and 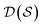 , our objective is to find the optimal values of the parameters ϕ and θ that maximize the right-hand side of eqn (12), hence maximizing
, our objective is to find the optimal values of the parameters ϕ and θ that maximize the right-hand side of eqn (12), hence maximizing 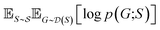 . Here, the double expectation indicates explicitly the dependence of whole-molecule sets D(S) on scaffolds S. That is, according to our definition, defining a scaffold set
. Here, the double expectation indicates explicitly the dependence of whole-molecule sets D(S) on scaffolds S. That is, according to our definition, defining a scaffold set 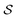 is first, and then each
is first, and then each  defines a whole-molecule set
defines a whole-molecule set 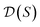 .
.
In the ESI,† we detail our implementation of the modules and their exact operations, along with the algorithm of the full process.
3 Results and discussion
3.1 Datasets and experiments
Our dataset is the synthetic screening compounds (version March 2018) provided by InterBioScreen Ltd.52 The dataset (henceforth the IBS dataset) initially contained the SMILES strings of organic compounds composed of H, C, N, O, F, P, S, Cl and Br atoms. We filtered out the strings containing disconnected ions or fragments and those that cannot be read by RDKit. Our preprocess resulted in 349![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 809 training molecules and 116
809 training molecules and 116![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 603 test molecules. The number of heavy atoms was 27 on average with maximum 132, and the average molecular weight was 389 g mol−1. The number of scaffold kinds was 85
603 test molecules. The number of heavy atoms was 27 on average with maximum 132, and the average molecular weight was 389 g mol−1. The number of scaffold kinds was 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 318 in the training set and 42
318 in the training set and 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 751 in the test set.
751 in the test set.
Our experiments include the training and evaluation of our scaffold-based graph generative model using the stated dataset. For the conditional molecule generation, we used molecular weight (MW), topological polar surface area (TPSA) and octanol–water partition coefficient (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P). We used one, two or all of the three properties to singly or jointly condition the model. We set the learning rate to 0.0001 and trained all instances of the model up to 20 epochs. The other hyperparameters such as the layer dimensions are stated in the ESI.† We used RDKit to calculate the properties of molecules. In what follows, we will omit the units of MW (g mol−1) and TPSA (Å2) for simplicity.
P). We used one, two or all of the three properties to singly or jointly condition the model. We set the learning rate to 0.0001 and trained all instances of the model up to 20 epochs. The other hyperparameters such as the layer dimensions are stated in the ESI.† We used RDKit to calculate the properties of molecules. In what follows, we will omit the units of MW (g mol−1) and TPSA (Å2) for simplicity.
Our source code and dataset are available at https://github.com/jaechanglim/GGM.
3.2 Validity, uniqueness and novelty analysis
The validity, uniqueness and novelty of the generated molecules are basic evaluation metrics of molecular generative models. For the exact meanings of the three metrics, we conform to the following definitions:53We define a graph to be valid if it satisfies basic chemical requirements such as valency. In practice, we use RDKit to determine the validity of generated graphs. It is particularly important for our model to check the metrics above because generating molecules from a scaffold restricts the space of candidate products. We evaluated the models that are singly conditioned on MW, TPSA or log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P by randomly selecting 100 scaffolds from the dataset and generating 100 molecules from each scaffold. The target values (100 values for each property) were randomly sampled from each property's distribution over the dataset. For MW, generating molecules whose MW is smaller than the MW of its scaffold is unnatural, so we excluded those cases from our evaluation.
P by randomly selecting 100 scaffolds from the dataset and generating 100 molecules from each scaffold. The target values (100 values for each property) were randomly sampled from each property's distribution over the dataset. For MW, generating molecules whose MW is smaller than the MW of its scaffold is unnatural, so we excluded those cases from our evaluation.
Table 2 summarizes the validity, uniqueness and novelty of the molecules generated by our models and the results of other molecular generative models for comparison. Note that the comparison here is only approximate because the values by the other models were taken from their respective reports. Despite the strict restriction imposed by scaffolds, our models show high validity, uniqueness and novelty that are comparable to those of the other models. The high uniqueness and novelty are particularly meaningful considering the fact that most of the scaffolds in our training set have only a few whole-molecules. For instance, among the 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 318 scaffolds in the training set, 79
318 scaffolds in the training set, 79![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 scaffolds have less than ten whole-molecules. Therefore, it is unlikely that our model achieved such a high performance by simply memorizing the training set, and we can conclude that our model learns the general chemical rules for extending arbitrary scaffolds.
700 scaffolds have less than ten whole-molecules. Therefore, it is unlikely that our model achieved such a high performance by simply memorizing the training set, and we can conclude that our model learns the general chemical rules for extending arbitrary scaffolds.
3.3 Single-property control
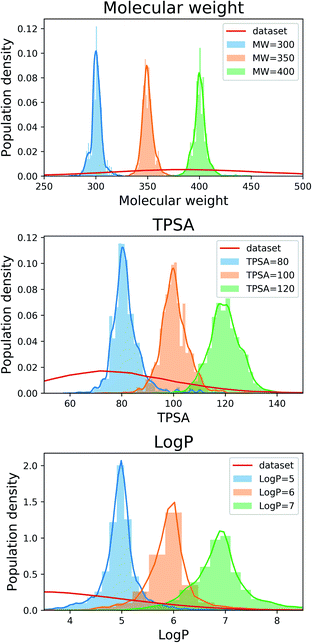
For the next analysis, we tested whether our scaffold-based graph generative model can generate molecules having a specific scaffold and desirable properties simultaneously. Although several molecular generative models have been developed for controlling molecular properties of generated molecules, it would be more challenging to control molecular properties under the constraint imposed by a given scaffold. We set the target values as 80, 100 and 120 for MW, 300, 350 and 400 for TPSA, and 5, 6 and 7 for log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P. For all the nine cases, we used the same 100 scaffolds used for the result in Section 3.2 and generated 100 molecules for each scaffold.
P. For all the nine cases, we used the same 100 scaffolds used for the result in Section 3.2 and generated 100 molecules for each scaffold.
Fig. 2 shows the property distributions of generated molecules. We see that the property distributions are well centered around the target values. This shows that despite the narrowed search space, our model successfully generated new molecules having desired properties. To see how our model extends a given scaffold according to designated property values, we drew some of the generated molecules in Fig. 3. For the target conditions MW = 400, TPSA = 120 and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P = 7, we randomly sampled nine examples using three different scaffolds. The molecules in each row were generated from the same scaffold. We see that the model generates new molecules with designated properties by adding appropriate side chains: for instance, the model added hydrophobic groups to the scaffolds to generate high-log
P = 7, we randomly sampled nine examples using three different scaffolds. The molecules in each row were generated from the same scaffold. We see that the model generates new molecules with designated properties by adding appropriate side chains: for instance, the model added hydrophobic groups to the scaffolds to generate high-log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P molecules, while it added polar functional groups to generate high-TPSA molecules.
P molecules, while it added polar functional groups to generate high-TPSA molecules.
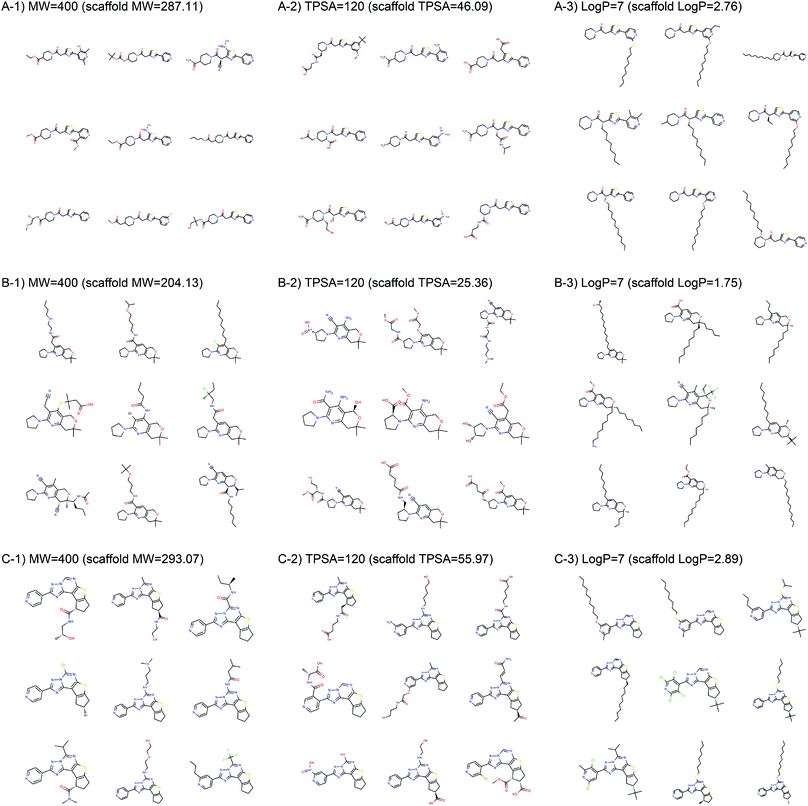 | ||
| Fig. 3 Example molecules generated from three scaffolds. The indicated values are the target conditions of the generation and the property values of the scaffolds. | ||
3.4 Scaffold dependence
Our molecular design process starts from a given scaffold with sequentially adding nodes and edges. So the performance of our model can be affected by the kind of scaffolds. Accordingly, we tested whether our model retains its performance of generating desirable molecules when new scaffolds are given. Specifically, we prepared a set of 100 new scaffolds (henceforth “unseen” scaffolds) that were not included in the training set and an additional set of 100 scaffolds (henceforth “seen” scaffolds) from the training set. We then generated 100 molecules for each scaffold with randomly designated property values. The process is repeated for MW, TPSA and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P.
P.
Table 3 summarizes the validity, uniqueness and MAD of molecules generated from the seen and unseen scaffolds. Here, MAD denotes the mean absolute difference between designated property values and the property values of generated molecules. The result shows no significant difference of the three metrics between the two sets of scaffolds. This shows that our model achieves generalization over arbitrary scaffolds in generating valid molecules with controlled properties.
| Property | Validity (%) | Uniqueness (%) | MAD |
|---|---|---|---|
| MW (seen scaffolds) | 98.4 | 88.6 | 6.72 |
| MW (unseen scaffolds) | 98.4 | 83.5 | 6.09 |
| TPSA (seen scaffolds) | 93.2 | 87.0 | 8.32 |
| TPSA (unseen scaffolds) | 92.5 | 82.9 | 9.82 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P (seen scaffolds) P (seen scaffolds) |
98.2 | 91.1 | 0.28 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P (unseen scaffolds) P (unseen scaffolds) |
97.1 | 87.0 | 0.36 |
3.5 Multi-property control
Designing new molecules seldom requires only one specific molecular property to be controlled. Among others, drug design particularly involves simultaneous control of a multitude of molecular properties. In this regard, we first tested our model's ability of simultaneously controlling two of MW, TPSA and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P. We trained three instances of the model, each being jointly conditioned on MW and TPSA, MW and log
P. We trained three instances of the model, each being jointly conditioned on MW and TPSA, MW and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P, and log
P, and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P and TPSA. We then specified each property with two target values (350 and 450 for MW, 50 and 100 for TPSA, and 2 and 5 for log
P and TPSA. We then specified each property with two target values (350 and 450 for MW, 50 and 100 for TPSA, and 2 and 5 for log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P) and combined them to prepare four generation conditions for each pair. Under every generation condition, we used the randomly sampled 100 scaffolds that we used for the results in Sections 3.2 and 3.3 and generated 100 molecules from each scaffold. We excluded those generations whose target MW is smaller than the MW of the used scaffold.
P) and combined them to prepare four generation conditions for each pair. Under every generation condition, we used the randomly sampled 100 scaffolds that we used for the results in Sections 3.2 and 3.3 and generated 100 molecules from each scaffold. We excluded those generations whose target MW is smaller than the MW of the used scaffold.
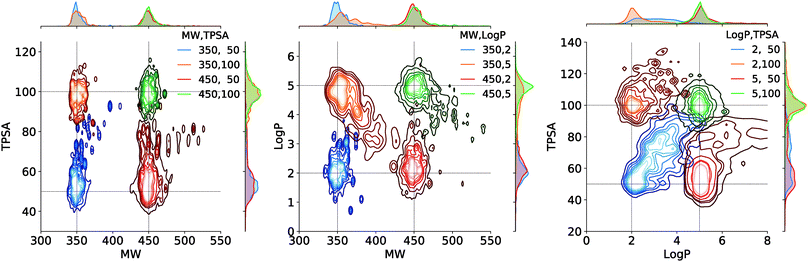
Fig. 4 shows the result of the generations conditioned on MW and TPSA, MW and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P, and log
P, and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P and TPSA. Plotted are the joint distributions of the property values over the generated molecules. Gaussian kernels were used for the kernel density estimation. We see that the modes of the distributions are well located near the point of the target values. As an exception, the distribution by the target (log
P and TPSA. Plotted are the joint distributions of the property values over the generated molecules. Gaussian kernels were used for the kernel density estimation. We see that the modes of the distributions are well located near the point of the target values. As an exception, the distribution by the target (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P, TPSA) = (2, 50) shows a relatively long tail over larger log
P, TPSA) = (2, 50) shows a relatively long tail over larger log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P and TPSA values. This is because log
P and TPSA values. This is because log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P and TPSA have by definition a negative correlation between each other and thus requiring a small value for both can make the generation task unphysical. Intrinsic correlations between molecular properties can even cause seemingly feasible targets to result in dispersed property distributions. An example of such can be the result of another target (log
P and TPSA have by definition a negative correlation between each other and thus requiring a small value for both can make the generation task unphysical. Intrinsic correlations between molecular properties can even cause seemingly feasible targets to result in dispersed property distributions. An example of such can be the result of another target (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P, TPSA) = (5, 50), but we note that in the very case the outliers (in log
P, TPSA) = (5, 50), but we note that in the very case the outliers (in log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P > 5.5 and TPSA > 65 for example) amount to only a minor portion of the total generations, as the contours show.
P > 5.5 and TPSA > 65 for example) amount to only a minor portion of the total generations, as the contours show.
We further tested the conditional generation by incorporating all the three properties. We used the same target values of MW, TPSA and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P as above, resulting in total eight conditions of generation. The rest of the settings, including the scaffold set and the number of generations, were retained. The result is shown in Fig. 5, where we plotted the MW, TPSA and log
P as above, resulting in total eight conditions of generation. The rest of the settings, including the scaffold set and the number of generations, were retained. The result is shown in Fig. 5, where we plotted the MW, TPSA and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P values of the generated molecules. The plot shows that the distributions from different target conditions are well separated from one another. As with the double-property result, all the distributions are well centered around their target values.
P values of the generated molecules. The plot shows that the distributions from different target conditions are well separated from one another. As with the double-property result, all the distributions are well centered around their target values.
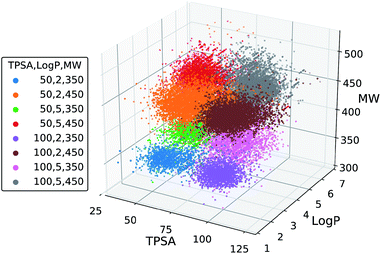 | ||
| Fig. 5 Scatter plot of the property values of generated molecules. The legend lists the eight sets of property values used for the generations. | ||
We also compared the generation performance of our model for single- and multi-property controls in a quantitative way. Table 4 shows the performance statistics of single-, double- and triple-property controls in terms of MAD, validity and novelty. Using the same 100 scaffolds, we generated 100 molecules from each, each time under a randomly designated target condition. As the number of incorporated properties increases from one to two and to three, the overall magnitudes of the descriptors are well preserved. Regarding the slight increases in the MAD values, we attribute them to the additional confinement of chemical space forced by intrinsic correlations between multiple properties. Nevertheless, the magnitudes of the worsening are small compared to the mean values of the properties (389 for MW, 77 for TPSA and 3.6 for log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P).
P).
| Properties | MW | TPSA | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P P |
Validity (%) | Novelty (%) |
|---|---|---|---|---|---|
| MAD | MAD | MAD | |||
| MW | 7.99 | — | — | 98.6 | 98.7 |
| TPSA | — | 8.57 | — | 93.0 | 99.1 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P P |
— | — | 0.29 | 97.8 | 99.3 |
| MW & TPSA | 8.04 | 7.06 | — | 93.5 | 99.4 |
MW & log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P P |
11.59 | — | 0.45 | 97.0 | 99.6 |
TPSA & log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P P |
— | 9.62 | 0.60 | 94.5 | 99.6 |
| All | 16.23 | 10.95 | 0.73 | 93.9 | 99.8 |
3.6 EGFR inhibitor design by semi-supervised learning
Deep learning methods often require millions of labeled data to fully exhibit their power. However, many real-world applications suffer from data deficiency. For instance, in inhibitor design, the available size of binding affinity data for a target protein usually amounts to only a few thousand. One possible approach in such a case is semi-supervised learning, which incorporates a large amount of unlabeled data with a small amount of labeled data for learning. Indeed, Kang and Cho demonstrated the effectiveness of semi-supervised learning in conditional molecular design when only a small portion of molecules in a dataset have property values.16 To see the applicability of our scaffold-based molecular graph generative model in similar situations, we equipped the model with the scheme of semi-supervised learning and tested how well it can design inhibitors of the human EGFR protein, where the data amount is likewise limited.We adopted the semi-supervised VAE16,54 because it can be easily implemented by adding a label predictor to a plain VAE. In semi-supervised VAE, we jointly train the predictor to predict the negative logarithm of half maximal inhibitory concentration (pIC50) values against the human EGFR, together with the VAE part. For labeled molecules, we use the true pIC50 values to train the predictor and also use them in the VAE condition vector. For unlabeled molecules, we only train the VAE part using the pIC50 values predicted by the predictor. To the IBS training molecules we used above, we added 8016 molecules from the ChEMBL database55 to prepare our dataset for semi-supervised learning. The ChEMBL molecules were the ones having pIC50 values, hence labeled, whereas the IBS molecules were unlabeled. Note that each molecule is paired with its extracted scaffold and that all the scaffolds of ChEMBL as well as IBS molecules are treated unlabeled. We divided the ChEMBL molecules into 6025 training molecules and 1991 test molecules, resulting in only 1.7% label ratio in the training set. To efficiently train the predictor, we sampled labeled and unlabeled inputs with the ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 in every batch. After 20 epochs of learning, we chose the 100 scaffolds in the ChEMBL test set whose predicted pIC50 are between 5 and 6, and generated 100 molecules from each scaffold with the target pIC50 value of 8.
5 in every batch. After 20 epochs of learning, we chose the 100 scaffolds in the ChEMBL test set whose predicted pIC50 are between 5 and 6, and generated 100 molecules from each scaffold with the target pIC50 value of 8.
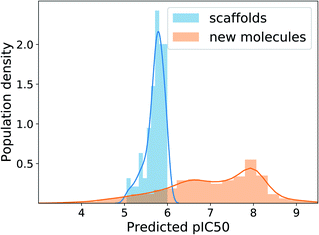
The MAD of pIC50 prediction on the ChEMBL test molecules was 0.58. In the total 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 times of generation, the model showed the validity of 96.6%, uniqueness of 44.9% and novelty of 99.7%. The relatively low uniqueness was expected because using one fixed target value imposes a strict condition on the search space, increasing redundancy in generations. Fig. 6 shows the distributions of predicted pIC50 values of the 100 scaffolds and generated molecules. Although the distribution of generated molecules is centered on values lower than 8 and shows relatively broad dispersion, the mean improvement of pIC50 value compared to the scaffolds is 1.29 (only counting the unique molecules), which amounts to about 19.7 times enhancement of inhibition potency in terms of IC50. Those predicted to have pIC50 larger than 8, which will be of more interest in practice, belong to 20% of the unique generations. These results show the applicability of our model, with minimal extension, to many of the practical situations where the preparation of data becomes problematic.
000 times of generation, the model showed the validity of 96.6%, uniqueness of 44.9% and novelty of 99.7%. The relatively low uniqueness was expected because using one fixed target value imposes a strict condition on the search space, increasing redundancy in generations. Fig. 6 shows the distributions of predicted pIC50 values of the 100 scaffolds and generated molecules. Although the distribution of generated molecules is centered on values lower than 8 and shows relatively broad dispersion, the mean improvement of pIC50 value compared to the scaffolds is 1.29 (only counting the unique molecules), which amounts to about 19.7 times enhancement of inhibition potency in terms of IC50. Those predicted to have pIC50 larger than 8, which will be of more interest in practice, belong to 20% of the unique generations. These results show the applicability of our model, with minimal extension, to many of the practical situations where the preparation of data becomes problematic.
4 Conclusion
In this work, we proposed a scaffold-based molecular graph generative model. Our model generates new molecules from a desired substructure, or scaffold, by sequentially adding new atoms and bonds to the graph of the scaffold. In contrast to other related methods such as probabilistically conditioning a substructure during generation, our strategy naturally guarantees the existence of the scaffold in generated molecules.Because generating molecules from a scaffold can leverage the properties already present in it, optimizing or retaining target properties can be easier than by generating molecules de novo. Suppose a pharmacological activity is targeted to be optimized, then generating the best molecular structure from scratch is likely to be hard because of the property's intricate relationship with molecular structures. In such a case, using a scaffold having moderate activity can make the optimization more feasible. A similar advantage is expected in controlling multiple properties simultaneously. If one's objective is to acquire, for instance, synthetic accessibility of the generated molecule as well as to enhance the activity, using a well-synthesizable scaffold allows the objective to be more focused on the latter, increasing the efficiency of search.
We evaluated our model by examining the validity, uniqueness and novelty of generated molecules. Despite the constraint on the search space imposed by scaffolds, the model showed comparable results with regard to previous SMILES-based and graph-based molecular generative models. Our model consistently worked well in terms of the three metrics when new scaffolds, which were not in the training set, were given. This means that the model achieved good generalization rather than memorizing the pairings between the scaffolds and molecules in the training set. In addition, while retaining the given scaffolds, our model successfully generated new molecules having desired degrees of molecular properties such as the molecular weight, topological polar surface area and octanol–water partition coefficient. The property-controlled generation could incorporate multiple molecular properties simultaneously. We also showed that our model can incorporate semi-supervised learning in applications like designing protein inhibitors, one of the common situations where only a small amount of labeled data is available. From all the results we presented, we believe that our scaffold-based molecular graph generative model provides a practical way of optimizing the functionality of molecules with preserved core structures.
Author contributions
Conceptualization: J. L. and W. Y. K.; Methodology: J. L.; Software, Investigation and Formal Analysis: J. L., S.-Y. H., S. M. and S. K.; Writing – Original Draft: J. L. and S.-Y. H.; Writing – Review & Editing: J. L., S.-Y. H. and W. Y. K.; Supervision: W. Y. K.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (NRF-2017R1E1A1A01078109).References
- P. G. Polishchuk, T. I. Madzhidov and A. Varnek, J. Comput.-Aided Mol. Des., 2013, 27, 675–679 CrossRef CAS PubMed.
- S. Kim, P. A. Thiessen, E. E. Bolton, J. Chen, G. Fu, A. Gindulyte, L. Han, J. He, S. He, B. A. Shoemaker, J. Wang, B. Yu, J. Zhang and S. H. Bryant, Nucleic Acids Res., 2016, 44, D1202–D1213 CrossRef CAS PubMed.
- K. H. Bleicher, Y. Wüthrich, G. Adam, T. Hoffmann and A. J. Sleight, Bioorg. Med. Chem. Lett., 2002, 12, 3073–3076 CrossRef CAS PubMed.
- G. L. Card, L. Blasdel, B. P. England, C. Zhang, Y. Suzuki, S. Gillette, D. Fong, P. N. Ibrahim, D. R. Artis, G. Bollag, M. V. Milburn, S.-H. Kim, J. Schlessinger and K. Y. J. Zhang, Nat. Biotechnol., 2005, 23, 201–207 CrossRef CAS PubMed.
- M. E. Welsch, S. A. Snyder and B. R. Stockwell, Curr. Opin. Chem. Biol., 2010, 14, 347–361 CrossRef CAS PubMed.
- Y. Im, M. Kim, Y. J. Cho, J.-A. Seo, K. S. Yook and J. Y. Lee, Chem. Mater., 2017, 29, 1946–1963 CrossRef CAS.
- J. Dhar, U. Salzner and S. Patil, J. Mater. Chem. C, 2017, 5, 7404–7430 RSC.
- A. Al Mousawi, F. Dumur, P. Garra, J. Toufaily, T. Hamieh, B. Graff, D. Gigmes, J. P. Fouassier and J. Lalevée, Macromolecules, 2017, 50, 2747–2758 CrossRef CAS.
- X. Sun, F. Wu, C. Zhong, L. Zhu and Z. Li, Chem. Sci., 2019, 10, 6899–6907 RSC.
- B. Sanchez-Lengeling and A. Aspuru-Guzik, Science, 2018, 361, 360–365 CrossRef CAS PubMed.
- H. Chen, O. Engkvist, Y. Wang, M. Olivecrona and T. Blaschke, Drug Discovery Today, 2018, 23, 1241–1250 CrossRef PubMed.
- M. H. S. Segler, T. Kogej, C. Tyrchan and M. P. Waller, ACS Cent. Sci., 2018, 4, 120–131 CrossRef CAS PubMed.
- A. Gupta, A. T. Müller, B. J. H. Huisman, J. A. Fuchs, P. Schneider and G. Schneider, Mol. Inf., 2018, 37, 1700111 CrossRef.
- E. J. Bjerrum and B. Sattarov, Biomolecules, 2018, 8(4), 131 CrossRef PubMed.
- R. Gómez-Bombarelli, J. N. Wei, D. Duvenaud, J. M. Hernández-Lobato, B. Sánchez-Lengeling, D. Sheberla, J. Aguilera-Iparraguirre, T. D. Hirzel, R. P. Adams and A. Aspuru-Guzik, ACS Cent. Sci., 2018, 4, 268–276 CrossRef PubMed.
- S. Kang and K. Cho, J. Chem. Inf. Model., 2019, 59, 43–52 CrossRef CAS PubMed.
- J. Lim, S. Ryu, J. W. Kim and W. Y. Kim, J. Cheminf., 2018, 10, 31 Search PubMed.
- D. Polykovskiy, A. Zhebrak, D. Vetrov, Y. Ivanenkov, V. Aladinskiy, P. Mamoshina, M. Bozdaganyan, A. Aliper, A. Zhavoronkov and A. Kadurin, Mol. Pharm., 2018, 15, 4398–4405 CrossRef CAS PubMed.
- G. Lima Guimaraes, B. Sanchez-Lengeling, C. Outeiral, P. L. Cunha Farias and A. Aspuru-Guzik, arXiv e-prints, arXiv:1705.10843, 2017.
- N. Jaques, S. Gu, D. Bahdanau, J. M. Hernández-Lobato, R. E. Turner and D. Eck, Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 2017, pp. 1645–1654 Search PubMed.
- M. Olivecrona, T. Blaschke, O. Engkvist and H. Chen, J. Cheminf., 2017, 9, 48 Search PubMed.
- D. Neil, M. H. S. Segler, L. Guasch, M. Ahmed, D. Plumbley, M. Sellwood and N. Brown, 6th International Conference on Learning Representations, Workshop Track Proceedings, Vancouver, BC, Canada, 2018 Search PubMed.
- M. Popova, O. Isayev and A. Tropsha, Sci. Adv., 2018, 4, eaap7885 CrossRef CAS.
- W. Jin, R. Barzilay and T. Jaakkola, Proceedings of the 35th International Conference on Machine Learning, Stockholmsmässan, Stockholm Sweden, 2018, pp. 2323–2332 Search PubMed.
- Y. Li, O. Vinyals, C. Dyer, R. Pascanu and P. Battaglia, 6th International Conference on Learning Representations, Workshop Track Proceedings, Vancouver, BC, Canada, 2018 Search PubMed.
- J. You, B. Liu, Z. Ying, V. Pande and J. Leskovec, in Advances in Neural Information Processing Systems 31, ed. S. Bengio, H. Wallach, H. Larochelle, K. Grauman, N. Cesa-Bianchi and R. Garnett, Curran Associates, Inc., 2018, pp. 6410–6421 Search PubMed.
- Y. Li, L. Zhang and Z. Liu, J. Cheminf., 2018, 10, 33 Search PubMed.
- R. Assouel, M. Ahmed, M. H. Segler, A. Saffari and Y. Bengio, arXiv e-prints, arXiv:1811.09766, 2018.
- Q. Liu, M. Allamanis, M. Brockschmidt and A. Gaunt, in Advances in Neural Information Processing Systems 31, ed. S. Bengio, H. Wallach, H. Larochelle, K. Grauman, N. Cesa-Bianchi and R. Garnett, Curran Associates, Inc., 2018, pp. 7795–7804 Search PubMed.
- M. Simonovsky and N. Komodakis, Artificial Neural Networks and Machine Learning – ICANN 2018, Cham, Switzerland, 2018, pp. 412–422 Search PubMed.
- N. De Cao and T. Kipf, arXiv e-prints, arXiv:1805.11973, 2018.
- M. Skalic, J. Jiménez, D. Sabbadin and G. De Fabritiis, J. Chem. Inf. Model., 2019, 59, 1205–1214 CrossRef CAS.
- D. P. Kingma and M. Welling, 2nd International Conference on Learning Representations, Banff, AB, Canada, 2014 Search PubMed.
- D. Weininger, J. Chem. Inf. Model., 1988, 28, 31–36 CrossRef CAS.
- Z. Wu, S. Pan, F. Chen, G. Long, C. Zhang and P. S. Yu, arXiv e-prints, arXiv:1901.00596, 2019.
- J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals and G. E. Dahl, Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 2017, pp. 1263–1272 Search PubMed.
- D. Polykovskiy, A. Zhebrak, B. Sanchez-Lengeling, S. Golovanov, O. Tatanov, S. Belyaev, R. Kurbanov, A. Artamonov, V. Aladinskiy, M. Veselov, A. Kadurin, S. Nikolenko, A. Aspuru-Guzik and A. Zhavoronkov, arXiv e-prints, arXiv:1811.12823, 2018.
- J. You, R. Ying, X. Ren, W. Hamilton and J. Leskovec, Proceedings of the 35th International Conference on Machine Learning, Stockholmsmässan, Stockholm Sweden, 2018, pp. 5708–5717 Search PubMed.
- G. W. Bemis and M. A. Murcko, J. Med. Chem., 1996, 39, 2887–2893 CrossRef CAS PubMed.
- A. Makhzani, J. Shlens, N. Jaitly, I. Goodfellow and B. Frey, 4th International Conference on Learning Representations, Workshop Track Proceedings, San Juan, Puerto Rico, 2016 Search PubMed.
- J. He, D. Spokoyny, G. Neubig and T. Berg-Kirkpatrick, 7th International Conference on Learning Representations, Conference Track Proceedings, New Orleans, LA, USA, 2019 Search PubMed.
- I. Goodfellow, arXiv e-prints, arXiv:1701.00160, 2016.
- R.-R. Griffiths and J. M. Hernández Lobato, Chem. Sci., 2020 10.1039/C9SC04026A.
- M. J. Kusner, B. Paige and J. M. Hernández-Lobato, Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 2017, pp. 1945–1954 Search PubMed.
- H. Dai, Y. Tian, B. Dai, S. Skiena and L. Song, 6th International Conference on Learning Representations, Conference Track Proceedings, Vancouver, BC, Canada, 2018 Search PubMed.
- O. Mahmood and J. M. Hernández-Lobato, arXiv e-prints, arXiv:1905.09885, 2019.
- T. Ma, J. Chen and C. Xiao, in Advances in Neural Information Processing Systems 31, ed. S. Bengio, H. Wallach, H. Larochelle, K. Grauman, N. Cesa-Bianchi and R. Garnett, Curran Associates, Inc., 2018, pp. 7113–7124 Search PubMed.
- B. Samanta, A. De, G. Jana, P. K. Chattaraj, N. Ganguly and M. Gomez-Rodriguez, arXiv e-prints, arXiv:1802.05283, 2018.
- Y. Kwon, J. Yoo, Y.-S. Choi, W.-J. Son, D. Lee and S. Kang, J. Cheminf., 2019, 11, 70 Search PubMed.
- P. Battaglia, R. Pascanu, M. Lai, D. Jimenez Rezende and K. Kavukcuoglu, in Advances in Neural Information Processing Systems 29, ed. D. D. Lee, M. Sugiyama, U. V. Luxburg, I. Guyon and R. Garnett, Curran Associates, Inc., 2016, pp. 4502–4510 Search PubMed.
- RDKit: Open-Source Cheminformatics, http://www.rdkit.org Search PubMed.
- InterBioScreen Ltd, http://www.ibscreen.com.
- N. Brown, M. Fiscato, M. H. Segler and A. C. Vaucher, J. Chem. Inf. Model., 2019, 59, 1096–1108 CrossRef CAS PubMed.
- D. P. Kingma, S. Mohamed, D. Jimenez Rezende and M. Welling, in Advances in Neural Information Processing Systems 27, ed. Z. Ghahramani, M. Welling, C. Cortes, N. D. Lawrence and K. Q. Weinberger, Curran Associates, Inc., 2014, pp. 3581–3589 Search PubMed.
- A. Gaulton, L. J. Bellis, A. P. Bento, J. Chambers, M. Davies, A. Hersey, Y. Light, S. McGlinchey, D. Michalovich, B. Al-Lazikani and J. P. Overington, Nucleic Acids Res., 2011, 40, D1100–D1107 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: The full algorithm and implementation of our model, and the hyperparameters used in the experiments. See DOI: 10.1039/c9sc04503a |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2020 |