Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A possible unaccounted source of atmospheric sulfate formation: amine-promoted hydrolysis and non-radical oxidation of sulfur dioxide†
Shixian
Wang
a,
Xiao Cheng
Zeng
 *ba,
Hui
Li
*ba,
Hui
Li
 *a and
Joseph S.
Francisco
*a and
Joseph S.
Francisco
 *c
*c
aBeijing Advanced Innovation Center for Soft Matter Science and Engineering, Beijing University of Chemistry Technology, Beijing 10029, China. E-mail: hli@mail.buct.edu.cn
bDepartment of Chemistry, University of Nebraska-Lincoln, Lincoln, Nebraska, USA 68588. E-mail: xzeng1@unl.edu
cDepartment of Earth and Environmental Sciences, University of Pennsylvania, Philadelphia, Pennsylvania, USA 19104. E-mail: frjoseph@sas.upenn.edu
First published on 10th January 2020
Abstract
Numerous field and laboratory studies have shown that amines, especially dimethylamine (DMA), are crucial to atmospheric particulate nucleation. However, the molecular mechanism by which amines lead to atmospheric particulate formation is still not fully understood. Herein, we show that DMA molecules can also promote the conversion of atmospheric SO2 to sulfate. Based on ab initio simulations, we find that in the presence of DMA, the originally endothermic and kinetically unfavourable hydrolysis reaction between gaseous SO2 and water vapour can become both exothermic and kinetically favourable. The resulting product, bisulfite NH2(CH3)2+·HSO3−, can be readily oxidized by ozone under ambient conditions. Kinetic analysis suggests that the hydrolysis rate of SO2 and DMA with water vapour becomes highly competitive with and comparable to the rate of the reaction between SO2 and OH·, especially under the conditions of heavily polluted air and high humidity. We also find that the oxidants NO2 and N2O5 (whose role in sulfate formation is still under debate) appear to play a much less significant role than ozone in the aqueous oxidation reaction of SO2. The newly identified oxidation mechanism of SO2 promoted by both DMA and O3 provides another important new source of sulfate formation in the atmosphere.
1 Introduction
Sulfuric acid in the atmosphere, mainly produced by the oxidation of gaseous sulfur dioxide, is known as the most important nucleating agent in the earliest stage of atmospheric new particle formation (NPF), as it possesses the lowest vapour pressure (<0.001 mmHg at 298 K) among the gaseous species in the atmosphere.1–9 SO2 in the atmosphere is mainly oxidized by OH· radicals produced from excited oxygen and water vapour.10–12 However, numerous observations indicate that there is insufficient OH· to account for the unexpectedly rapid growth in H2SO4 concentration in the highly polluted atmosphere, in which the high aerosol concentration can actually block solar ultraviolet radiation and lower the concentration of OH· radicals, thereby preventing them from participating in photochemical reactions.5 Moreover, OH· oxidation alone cannot explain the observed level of H2SO4 at nighttime.13On the other hand, although the abundance of the common oxidizing gases O3 and NOx is much higher than that of OH· radicals in the atmosphere, previous ab initio calculations show that the direct oxidation of SO2 by O3/NOx in the gas phase is kinetically unfeasible due to extremely high activation barriers. The hydrolysis of gaseous SO2 is proposed as an alternative reaction pathway to yield H2SO4 because sulfurous acid can be more easily oxidized to sulfuric acid by some moderate oxidants, e.g., ozone and NOx.14–17 However, the hydrolysis of SO2 in the gas phase has also been shown to be both thermodynamically and kinetically unfavourable via high-level quantum mechanical (QM) calculations10,18–20 since the hydrolysis of SO2 with either H2O monomer or dimer is an endothermic process and, again, entails very high energy barriers.10 Hence, new oxidation pathways must be explored to explain the fast conversion of SO2 to atmospheric H2SO4.
Atmospheric bases, such as ammonia (NH3), are another important contributor to initial sulfate aerosols.21 In addition, both cloud chamber studies and field measurements have revealed that atmospheric amines, especially dimethylamine (DMA), also play a surprisingly crucial role in the NPF process, even though their concentrations are two or three orders of magnitude lower than that of NH3.22–30 For example, Almeida et al. detected that a 5 pptv level of DMA can enhance the particle formation rate more than 1000-fold than 250 pptv NH3.8 More recently, Yao et al. reported that H2SO4·DMA·H2O nucleation leads to high NPF rates in urban areas of China.30 Li et al. found that sulfamic acid, produced from SO3 and high concentrations of NH3, can directly participate in H2SO4·DMA clustering.31 Currently, it is widely accepted that DMA, similar to NH3, can further stabilize sulfate clusters through salification with H2SO4. On the other hand, although Liu et al. showed that alkaline gases, such as ammonia, can promote the hydrolysis of SO2 to form H2SO3 (ref. 22) and Chen et al. proposed that alkaline aerosols can trap SO2, then being oxidized by NO2,14 the role played by DMA molecules in atmospheric chemistry is still incompletely understood, despite its fundamental importance for exploring the role of amines in atmospheric chemistry.
Here, we show that atmospheric amines can play a key role in the formation of sulfates at high relative humidity (RH) and low illumination, thereby contributing to enhanced aerosol formation on highly polluted days. Ab initio simulations demonstrate that the presence of methylamine (MA)/DMA molecules leads to exothermic hydrolysis of SO2 with water vapour, without a barrier, to a product that can be oxidized by O3 and NOx. O3 is also found to be a stronger oxidant than NOx in the amine-assisted oxidation of SO2. As a result, the concentration level of atmospheric H2SO4 from aqueous oxidation may be mainly controlled by the concentration of O3 rather than that of NOx. Based on transition state theory (TST) analysis and the observed concentrations of the participating atmospheric species, the rate of the SO2 hydrolysis reaction with the assistance of DMA at 100% RH is even higher than the rate of SO2 oxidization by OH·. This finding may shed new light on the long-standing endeavour to identify the unknown oxidation pathway leading to atmospheric sulfate formation.
2 Results and discussion
2.1 Hydrolysis of SO2 assisted by DMA
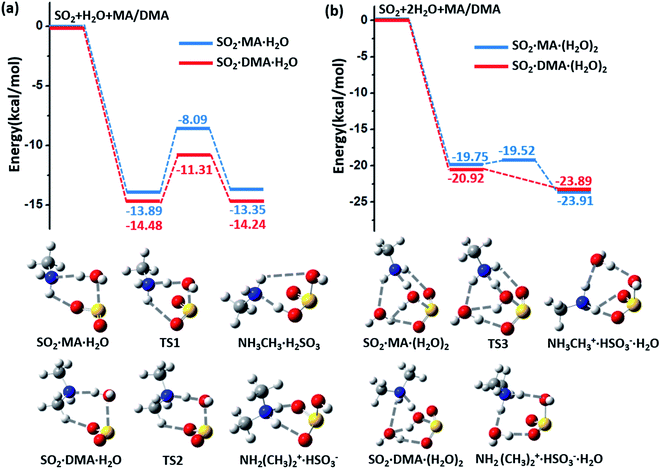
The potential energy surfaces (PESs) for the hydrolysis reaction of SO2, MA/DMA and nH2O (n = 1–3) are shown in Fig. 1(a–b) and S1 in ESI.† In the reaction with the water monomer (Fig. 1(a)), the breaking of the O–H bond of water in the presence of MA and DMA requires activation energies of 5.8 and 3.2 kcal mol−1, respectively, indicating that both reactions can take place quite readily under ambient conditions. In contrast, the process of SO2 + H2O → H2SO3 in the gas phase needs to overcome a high energy barrier of 33.9 kcal mol−1.12 Note that previous quantum-mechanical (QM) calculations showed that atmospheric ammonia can also lower the barrier for the hydrolysis of SO2 to ∼12.0 kcal mol−1.22 However, this energy barrier is still quite high for a reaction to take place at room temperature. According to our calculations, the hydrolysis barriers with MA and DMA are approximately 6.0 and 9.0 kcal mol−1 lower than the barrier with NH3, respectively, suggesting that amines can promote SO2 hydrolysis more strongly than NH3. Furthermore, spontaneous ionization to form HSO3− and NH3CH3+/NH2(CH3)2+ during the hydrolysis reactions is also observed.The energy barrier for hydrolysis can be further lowered by introducing an additional water molecule to the reaction through the formation of a ring structure in the transition state, as shown in Fig. 1(b). The hydrolysis of SO2 with a water dimer and DMA can become barrierless. Likewise, hydrolysis with (H2O)n (n ≥ 3) are also barrierless reactions (ESI Fig. S1†). In addition, increasing the number of water and DMA molecules also promotes further ionization of the already formed H2SO3 and amine molecules. As shown in ESI Fig. S2†(a), H2SO3 is partially ionized to HSO3− in the (DMA)2·H2SO3·(H2O)n, (n = 1–3) clusters, while complete ionization of H2SO3 and DMA to (NH2(CH3)2+)2·SO32− is observed in the presence of (H2O)n (n ≥ 4) with a very low dissociation barrier of 0.24 kcal mol−1 (ESI Fig. S2(b)†). Next, we show that the complete ionization of H2SO3 can benefit its oxidation, a phenomenon that may occur on aerosol surfaces (with high pH) in air with high concentrations of DMA and water.
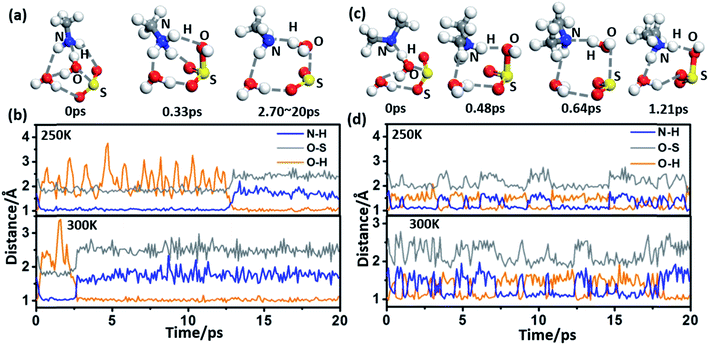
The spontaneous formation and ionization processes of bisulfite/sulfite are confirmed by Born–Oppenheimer molecular dynamics (BOMD) simulation (Fig. 2). As shown by the BOMD trajectories at 300 K in Fig. 2(a), the hydrolysis of SO2 with a water dimer and MA molecule is a very fast process, where the OH bond of a bridging water molecule breaks during the initial 0.33 ps of the BOMD simulation. Meanwhile, the N–H and O–S bond distances decrease to ∼1.07 and ∼1.78 Å, respectively, suggesting the formation of NH3CH3+·HSO3−·H2O. It is observed that the system does not maintain the ionized form and returns back to the molecular state of SO2 after 2.70 ps, indicating the reversible transition between SO2 and HSO3− due to the thermal effect. It is interesting that such a chemical equilibrium can be sensitively regulated by temperature. The simulation system maintains the form of NH3CH3+·HSO3− at 300 K for ∼2.4 ps during the total BOMD simulation time of 20 ps (lower panel in Fig. 2(b)), while the time period that NH3CH3+·HSO3− lasts is approximately six times longer at 250 K (∼12.2 ps) than at 300 K (upper panel in Fig. 2(b)). The BOMD simulation of SO2·DMA·(H2O)2 shows a similar trajectory as that of the SO2·MA·(H2O)2 system (Fig. 2(c) and (d)), where the time periods of the NH2(CH3)2+·HSO3− state are 9.1 and 10.6 ps at 300 and 250 K, respectively. Clearly, lower temperature is beneficial for bisulfite/sulfite formation due to its entropy being lower than that of the loose SO2·H2O cluster.
Previous studies have suggested that heterogeneous reactions on the surface of water droplets play crucial roles in atmospheric chemistry, such as the ionization of N2O4.32,33 Zhong et al. found that SO2 on a water nanodroplet tends to have an S–O bond exposed to the air that can readily react with other gaseous species in the air.34 Here, BOMD simulations also confirm that increasing the size of the water cluster can move the SO2 ↔ HSO3− equilibrium towards the right-hand side. As shown in ESI Fig. S3(a) and (b),† SO2, MA/DMA, and two water molecules quickly convert to NH3CH3+/NH2(CH3)2+·HSO3−·H2O cyclic structures, which remain stable on the water cluster during the BOMD simulation at 300 K. By contrast, no similar structure is formed from SO2 and NH3 during the BOMD simulation (ESI Fig. S3(c)†), implying that the amines have a unique promotion effect on the hydrolysis of SO2. The NH2(CH3)2+·HSO3− complex on the water droplet can also uptake an additional DMA molecule to form (NH2(CH3)2+)2·SO32−, as shown in ESI Fig. S3(d).†
2.2 Oxidation of NH2(CH3)2+·HSO3− and (NH2(CH3)2+)2·SO32− by O3
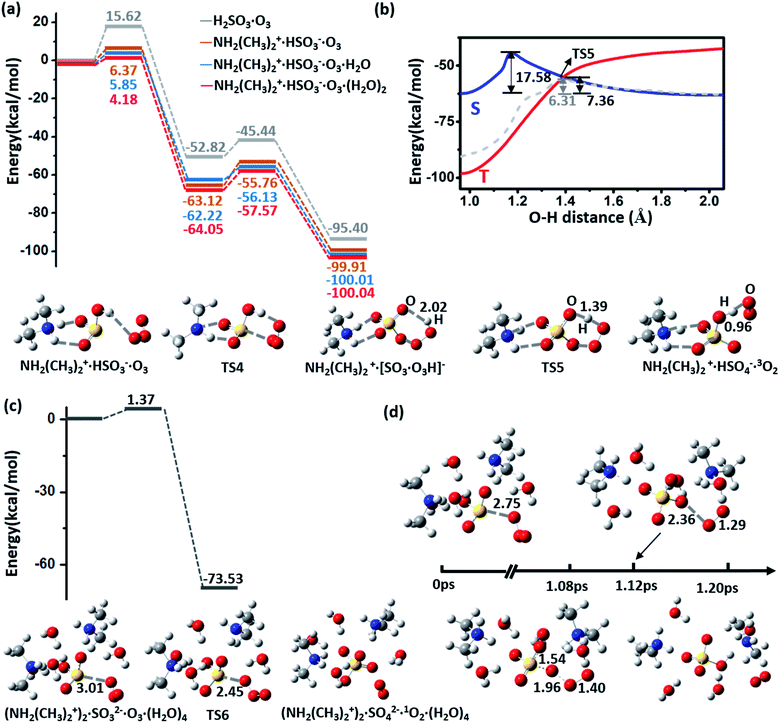
The oxidization process of NH2(CH3)2+·HSO3− by O3 is divided into two steps: (1) Adsorption of O3 and (2) dissociation of [SO3·O3H]−, as shown in the energy profiles in Fig. 3(a) and (b). The oxidation starts from the physical adsorption of O3 with one oxygen atom approaching the HSO3− group (Eads = −3.03 kcal mol−1), and then the O3 molecule is chemically adsorbed to HSO3− by forming a cyclic structure, NH2(CH3)2+· [SO3·O3H]−, as an intermediate state. This process is highly exothermic (ΔE = −63.12 kcal mol−1) and overcomes a low barrier of 6.37 kcal mol−1, which is 9.25 kcal mol−1 lower than the energy barrier without an amine (Fig. 3(a)). This energy barrier can be further lowered by adsorption of additional water molecules, where the energy barrier equals 5.85 and 4.18 kcal mol−1 for one and two H2O molecules, respectively (Fig. 3(a)). Due to the low energy barrier, formation of the NH2(CH3)2+·[SO3·O3H]− complex can spontaneously occur during the BOMD simulation at room temperature (ESI Fig. S4†).As NH2(CH3)2+·[SO3·O3H]− is an extremely stable intermediate state, the dissociation of [SO3·O3H]− needs to overcome a relatively high energy barrier (Ea = 17.58 kcal mol−1) to produce HSO4− and singlet O2 in the spin-restricted calculation (Fig. 3(b)). This barrier seems too high for a room–temperature reaction to occur. However, it is known that unstable singlet O2 in the atmosphere can quickly convert to the triplet ground state35 through collision and that, in particular, the strong spin–orbit interaction of the heavy element sulfur can greatly enhance the spin-flipping rate. Thus, the real dissociation process is accompanied by a spin-flipping process, which can greatly lower the dissociation barrier. Because the O–H stretching vibration corresponds to the main imaginary frequency of the transition state, we scan the energy surface versus the O–H distance (dOH) of [SO3·O3H]−, as shown in Fig. 3(b). The cross-point (dOH = 1.39 Å) between the singlet and triplet Born–Oppenheimer potential surfaces is found to yield a dissociation barrier of 7.36 kcal mol−1, indicating the kinetic feasibility of the oxidation process under ambient conditions. The low dissociation barrier (Ea = 6.31 kcal mol−1) is also confirmed by a calculation at the spin-polarized Perdew–Burke–Ernzerhof (PBE)/plane-wave level,36 as implemented in the Vienna Ab initio Simulation Package (VASP 5.3).37 The dissociation reaction is also highly exothermic (ΔE = −36.79 kcal mol−1). Unlike the barrier to the adsorption of O3, the dissociation barrier is minimally affected by additional vicinal water molecules (Fig. 3(a) and ESI Fig. S5†).
Moreover, the dissociation of HSO3− to SO32−, which generally happens on alkaline aerosol surface, can promote oxidation with O3. A cluster containing one H2SO3, two DMA, and four H2O molecules is chosen to mimic this situation, where the DMA and H2SO3 molecules spontaneously form NH2(CH3)2+ and SO32−. As shown in Fig. 3(c), the oxidation becomes a one-step reaction with an extremely low barrier (Ea = 1.37 kcal mol−1). This oxidation process can be reproduced in the BOMD simulation as well (Fig. 3(d)).
2.3 Oxidation of NH2(CH3)2+·HSO3− with NOx
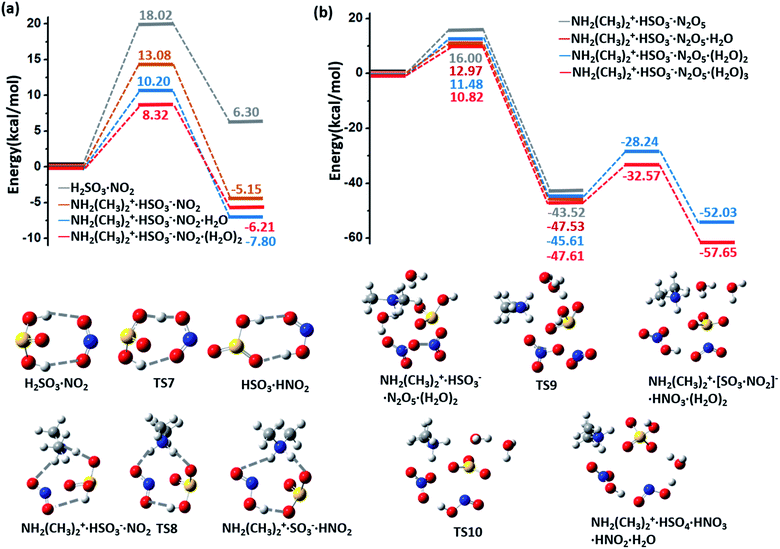
NH2(CH3)2+·HSO3− can be oxidized by NO2 to form the radical NH2(CH3)2+·SO3− and HNO2 (HONO) with an energy barrier of 13.08 kcal mol−1 and a potential energy change of −5.15 kcal mol−1, as shown by the energy profiles and corresponding structures displayed in ESI Fig. 4(a) and S6(a),† respectively. In contrast to this oxidation reaction, the oxidation process without DMA has a relatively higher barrier (18.02 kcal mol−1) and a positive energy change (6.30 kcal mol−1), as shown in Fig. 4(a). Similar to the barrier for O3 oxidation, the barrier for oxidizing NH2(CH3)2+·SO3− with NO2 can be lowered by extra neighbouring water molecules; e.g., the values of the oxidation barrier in the presence of the water monomer and dimer are equal to 10.20 and 8.32 kcal mol−1, respectively. Such a barrier is believed to be even lower on the surface of aqueous aerosols.The NH2(CH3)2+·SO3− radical product is an active radical, so it can easily react with other radicals, such as O2, NO2, and OH˙. For example, our calculations demonstrate that NH2(CH3)2+·SO3−·(H2O)n (n ≥ 1) and another NO2 molecule can spontaneously form a NH2(CH3)2+·HSO4−·(H2O)n−1 cluster (ESI Fig. S6(b)†). In addition, HNO2, the other product of this oxidation reaction, is also an important precursor of OH˙ radicals in the atmosphere.38,39
The potential energy profiles of NH2(CH3)2+·HSO3−·(H2O)n (n = 0–3) oxidized by N2O5, another abundant oxidative NOx species in the atmosphere, are shown in Fig. 4(b) and ESI Fig. S6(c).† Similar to O3 oxidation, the process of (NH2(CH3)2+·HSO3−·(H2O)n + N2O5 → CH2(CH3)2+·HSO4−·(H2O)n−1 + HNO3 + HNO2) is a two-step reaction, where N2O5 first dissociates into a NO2−·NO3+ ion pair and combines with the bisulfite cluster to form a HNO3 molecule and a stable complex [SO3·NO2]− (Fig. 4(b)). The energy barrier of this step also decreases from 16.0 to 10.82 kcal mol−1 as the number of participating water molecule increases (n = 0–3). In the second step, a H2O molecule that attacks the sulfur atom will assist the breaking of [SO3·NO2]−, and the product CH2(CH3)2+·HSO4−·HNO3·HNO2·(H2O)n−1 is finally formed. This step is also an exothermic process (ΔE = −6.42 and −10.04 kcal mol−1 for n = 2 and 3, respectively), and the barrier of this step is weakly affected by the number of water molecules (Ea = 17.37 and 15.04 kcal mol−1 for n = 2 and 3, respectively). Such high energy barriers indicate that N2O5 plays a negligible role in the oxidation of sulfite.
2.4 Kinetics and implications for atmospheric chemistry
The reaction rate constants of hydrolysis reactions are calculated based on TST, as listed in Table 1, and details of this calculation and the reactant concentrations are listed in ESI Tables S1, S2 and S3.† The rate constant for the hydrolysis reaction of SO2·H2O with DMA adopts an inverse relation with temperature, decreasing from 3.35 × 10−10 to 1.39 × 10−11 cm3 molecule−1 s−1 as the temperature changes from 240 to 300 K. According to previous observations, [SO2] and [DMA] are ∼1012 and ∼109 molecules cm−3 in highly polluted air, respectively, while the concentration of H2O decreases from 9.7 × 1017 to 9.0 × 1015 molecules cm−3 at 100% relative humility (RH) as the temperature drops from 300 K to 240 K.7,30,40 On the basis of these parameters, the estimated concentrations of the SO2·H2O and DMA·H2O complexes at 300 K are approximately 3.4 × 108 and 1.9 × 106 molecules cm−3, respectively, and the rate of hydrolysis for SO2 and H2O monomer assisted by DMA is estimated to be 4.8 × 106 molecule cm−3 s−1.| Reaction | k (cm3 molecule−1 s−1) | |||
|---|---|---|---|---|
| 240 K | 260 K | 280 K | 300 K | |
| SO2·H2O + MA | 6.56 × 10−13 | 3.09 × 10−13 | 1.58 × 10−13 | 8.96 × 10−14 |
| SO2·H2O + DMA | 3.35 × 10−10 | 9.42 × 10−11 | 3.21 × 10−11 | 1.39 × 10−11 |
| SO2·(H2O)2 + MA | 3.79 × 10−9 | 3.17 × 10−9 | 1.18 × 10−9 | 4.22 × 10−10 |
| SO2·(H2O)2 + DMA | 9.01 × 10−9 | 7.26 × 10−9 | 5.64 × 10−9 | 4.53 × 10−9 |
It is interesting to compare the rate of SO2 hydrolysis assisted by DMA to the rate of SO2 reacting with OH· radicals under high RH conditions. The latter was previously thought to be the main reaction for SO2 oxidation. Using the average concentration of OH· during the daytime (1 × 106 molecules cm−3), the reaction rate of the oxidation of SO2 by OH˙ based on a previously calculated rate constant (1.3 × 10−12 cm3 molecule−1 s−1 at 300 K and 1 atm)41 is 1.5 × 106 molecule cm−3 s−1, which is lower than the hydrolysis rate. In this case, the consumption of SO2 in the hydrolysis reaction can exceed that in the oxidation reaction with OH· radicals. Similarly, the estimated hydrolysis rate for atmospheric SO2, DMA, and (H2O)2 at 300 K and 100% RH is 2.9 × 106 molecules per cm3 per s, which is also more competitive with the reaction rate of SO2 and OH·. Moreover, the concentration of OH· would be further lowered due to the reduced photochemistry either during heavily polluted periods or at night time, when the hydrolysis reaction would even play an even more crucial role in SO2 oxidation.
The hydration products CH2(CH3)2+·HSO3−·(H2O)n are expected to be oxidized by O3, NO2, and N2O5. The estimated rate constant of the oxidation of CH2(CH3)2+·HSO3−·(H2O)2 by O3 (5.82 × 10−15 cm3 molecule−1 s−1) is 3 orders of magnitude higher than that of the oxidation by NO2 (1.73 × 10−18 cm3 molecule−1 s−1). As the concentrations of O3, NO2 and N2O5 were separately measured to be ∼1012, ∼1012, and ∼1010 molecules cm−3 in haze episodes, respectively,7,42 we can estimate the lifetime of CH2(CH3)2+·HSO3−·(H2O)2 by the expression τ = (k × [oxidant])−1. The lifetime of CH2(CH3)2+·HSO3−·(H2O)2 during oxidation by O3 is ∼1/1000 of that during oxidation by NO2 at 300 K. Considering the much lower oxidation rate constant and concentration of N2O5 than O3 and NO2, the oxidation by N2O5 is negligible. As a result, the proposed hydrolysis of SO2 assisted by DMA in an O3-polluted atmosphere is an important pathway for sulfate formation.
3 Conclusions
In summary, the hydrolysis and oxidation of SO2 promoted by DMA are studied by using QM calculations and BOMD simulations. In both gaseous and heterogeneous environments, SO2 can be easily hydrated with the assistance of DMA and then oxidized by O3, as shown by the overall energy profile in Fig. 5. By contrast, NO2 and N2O5, also viewed as important oxidants in the atmosphere, appear to play a much less important role than O3 in the oxidation of SO2. Kinetic analysis shows that the consumption rate of SO2 during hydrolysis in the presence of DMA can surpass the rate of oxidation with OH· radicals under the conditions of heavily polluted air and high RH.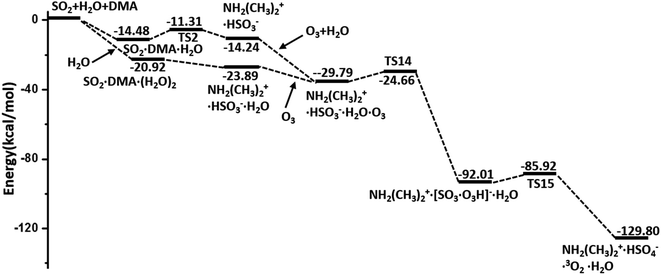 | ||
| Fig. 5 Overall potential energy profiles for the hydrolysis of SO2 promoted by DMA and oxidized by O3 (M06-2X/cc-pVDZ-F12 with ZPE correction). | ||
In the last decade, O3 levels in the global atmosphere, according to field measurements, have greatly increased. For example, it has been reported that the yearly mean concentration of O3 in Chinese megacities increased by 69% from 2006 to 2015.43 The results from this research suggest that the hydrated oxidation of SO2 with amines and O3 has an important role in atmospheric chemistry.
4 Methods
4.1 Details of QM calculations and BOMD simulations
The geometries of the reactant states, transition states, and product states in all the reactions are optimized at the unrestricted M06-2X/cc-pVDZ-F12 level,44–46 which has shown good results on weak interactions and has been widely used in computational studies of atmospheric chemistry.16,46–48 Zero-point energy (ZPE) corrections are included when calculating the potential energies, and intrinsic reaction coordinate (IRC) analysis is carried out to confirm the reaction pathways. WB97XD/cc-pVDZ-F12 and B2PLYPD/def2-TZVP methods are also employed for the total potential energy profiles for comparison, which show great consistency with energy profiles based on M06-2X. All the QM calculations for the reaction pathways are performed by using the Gaussian 09 software package.49 The spin-polarized calculations are performed based on the generalized gradient approximation of the PBE functional, as implemented in the VASP 5.3.37,50–52 A kinetic energy cutoff of 400 eV is chosen for the plane-wave expansion. The cell size for the NH2(CH3)2+·[SO3·O3H] cluster is 15 × 15 × 15 Å3.BOMD simulations are performed in the framework of the Becke–Lee–Yang–Parr (BLYP) functional53,54 with the Quickstep module in CP2K code.55 The Gaussian and plane wave (GPW) basis sets (280 Ry energy cutoff) combined with the Goedecker-Teter-Hutter (GTH) pseudopotential56 are employed to obtain a good balance between computational cost and accuracy. In addition, the dispersion correction is also included to better describe weak intermolecular interactions.57 Periodic boundary conditions are used, and the cell sizes for the SO2·MA/DMA·(H2O)2, NH2(CH3)2+·HSO3−·O3·(H2O)4, and (NH2(CH3)2+)2·SO32−·O3·(H2O)4 systems are 20 × 20 × 20 Å3. A larger cell size (35 × 35 × 35 Å3) is chosen for the hydrolysis reaction of SO2 on the surface of a water nanodroplet containing 100 water molecules. The BOMD simulations are carried out at lower and higher temperatures (250 and 300 K), and the temperatures of the systems are controlled using the Nosé–Hoover thermostat. The time step of BOMD is set to 1.0 fs, which has been proven to achieve sufficient energy conservation for water systems.34,47,58 The reaction process is unchanged with a smaller time step of 0.5 fs (ESI Fig. S7†).
4.2 Calculation of the reaction rate constant
The rate constants of hydrolysis and oxidation reactions are evaluated using TST with Wigner tunnelling corrections.48,59,60 As [SO2][DMA] is negligible relative to [SO2][H2O] and [DMA][H2O], in the hydrolysis reaction of SO2 assisted by DMA, two reaction pathways are considered: H2O first binding to SO2 and first binding to DMA. Because the concentrations of the reactants DMA, SO2, SO2·H2O, and DMA·H2O are critical to the final reaction rates, we estimate the number of SO2·H2O and DMA·H2O complexes by the following expressions: [SO2·H2O] = KSO2·H2O[SO2][H2O] and [DMA·H2O] = KDMA·H2O[DMA][H2O], where KSO2·H2O and KDMA·H2O are the equilibrium constants for the formation of SO2·H2O and DMA·H2O dimers, respectively. The total reaction rate ν can be expressed as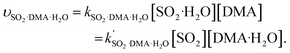 | (1) |
Taking the reaction of SO2·H2O and DMA as an example, the hydrolysis process is represented by
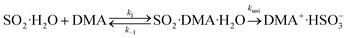 | (2) |
By assuming that the reactant complex SO2·DMA·H2O is in equilibrium with the reactant monomers SO2·H2O and DMA, the total rate constant kSO2·DMA·H2O for the reaction can be written as
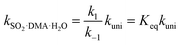 | (3) |
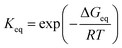 | (4) |
| kuni = Γk2 | (5) |
The tunnelling effect factor Γ is given by Wigner tunnelling corrections,
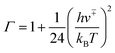 | (6) |
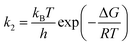 | (7) |
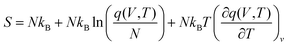 | (8) |
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Dr Jinrong Yang for valuable discussions. HL is thankful for the funding support from the National Natural Science Foundation of China (21773005). JSF and XCZ acknowledge computer support from UNL Holland Computing Center.Notes and references
- F. Bianchi, J. Trostl, H. Junninen, C. Frege, S. Henne, C. R. Hoyle, U. Molteni, E. Herrmann, A. Adamov, N. Bukowiecki, X. Chen, J. Duplissy, M. Gysel, M. Hutterli, J. Kangasluoma, J. Kontkanen, A. Kurten, H. E. Manninen, S. Munch, O. Perakyla, T. Petaja, L. Rondo, C. Williamson, E. Weingartner, J. Curtius, D. R. Worsnop, M. Kulmala, J. Dommen and U. Baltensperger, Science, 2016, 352, 1109–1112 CrossRef CAS.
- M. Kulmala, J. Kontkanen, H. Junninen, K. Lehtipalo, H. E. Manninen, T. Nieminen, T. Petaja, M. Sipila, S. Schobesberger, P. Rantala, A. Franchin, T. Jokinen, E. Jarvinen, M. Aijala, J. Kangasluoma, J. Hakala, P. P. Aalto, P. Paasonen, J. Mikkila, J. Vanhanen, J. Aalto, H. Hakola, U. Makkonen, T. Ruuskanen, R. L. Mauldin 3rd, J. Duplissy, H. Vehkamaki, J. Back, A. Kortelainen, I. Riipinen, T. Kurten, M. V. Johnston, J. N. Smith, M. Ehn, T. F. Mentel, K. E. Lehtinen, A. Laaksonen, V. M. Kerminen and D. R. Worsnop, Science, 2013, 339, 943–946 CrossRef CAS PubMed.
- A. Kürten, F. Bianchi, J. Almeida, O. Kupiainen-Määttä, E. M. Dunne, J. Duplissy, C. Williamson, P. Barmet, M. Breitenlechner, J. Dommen, N. M. Donahue, R. C. Flagan, A. Franchin, H. Gordon, J. Hakala, A. Hansel, M. Heinritzi, L. Ickes, T. Jokinen, J. Kangasluoma, J. Kim, J. Kirkby, A. Kupc, K. Lehtipalo, M. Leiminger, V. Makhmutov, A. Onnela, I. K. Ortega, T. Petäjä, A. P. Praplan, F. Riccobono, M. P. Rissanen, L. Rondo, R. Schnitzhofer, S. Schobesberger, J. N. Smith, G. Steiner, Y. Stozhkov, A. Tomé, J. Tröstl, G. Tsagkogeorgas, P. E. Wagner, D. Wimmer, P. Ye, U. Baltensperger, K. Carslaw, M. Kulmala and J. Curtius, J. Geophys. Res.: Atmos., 2016, 121, 12377–12400 Search PubMed.
- R. Zhang, A. Khalizov, L. Wang, M. Hu and W. Xu, Chem. Rev., 2012, 112, 1957–2011 CrossRef CAS PubMed.
- Y. Cheng, G. Zheng, C. Wei, Q. Mu, B. Zheng, Z. Wang, M. Gao, Q. Zhang, K. He, G. Carmichael, U. Pöschl and H. Su, Sci. Adv., 2016, 2016, e1601530 CrossRef PubMed.
- D. L. Yue, M. Hu, R. Y. Zhang, Z. B. Wang, J. Zheng, Z. J. Wu, A. Wiedensohler, L. Y. He, X. F. Huang and T. Zhu, Atmos. Chem. Phys., 2010, 10, 4953–4960 CrossRef CAS.
- G. J. Zheng, F. K. Duan, H. Su2, Y. L. Ma, Y. Cheng, B. Zheng, Q. Zhang, T. Huang, T. Kimoto, D. Chang, U. Pöschl, Y. F. Cheng and K. B. He, Atmos. Chem. Phys., 2015, 2015, 2969–2983 CrossRef.
- J. Almeida, S. Schobesberger, A. Kurten, I. K. Ortega, O. Kupiainen-Maatta, A. P. Praplan, A. Adamov, A. Amorim, F. Bianchi, M. Breitenlechner, A. David, J. Dommen, N. M. Donahue, A. Downard, E. Dunne, J. Duplissy, S. Ehrhart, R. C. Flagan, A. Franchin, R. Guida, J. Hakala, A. Hansel, M. Heinritzi, H. Henschel, T. Jokinen, H. Junninen, M. Kajos, J. Kangasluoma, H. Keskinen, A. Kupc, T. Kurten, A. N. Kvashin, A. Laaksonen, K. Lehtipalo, M. Leiminger, J. Leppa, V. Loukonen, V. Makhmutov, S. Mathot, M. J. McGrath, T. Nieminen, T. Olenius, A. Onnela, T. Petaja, F. Riccobono, I. Riipinen, M. Rissanen, L. Rondo, T. Ruuskanen, F. D. Santos, N. Sarnela, S. Schallhart, R. Schnitzhofer, J. H. Seinfeld, M. Simon, M. Sipila, Y. Stozhkov, F. Stratmann, A. Tome, J. Trostl, G. Tsagkogeorgas, P. Vaattovaara, Y. Viisanen, A. Virtanen, A. Vrtala, P. E. Wagner, E. Weingartner, H. Wex, C. Williamson, D. Wimmer, P. Ye, T. Yli-Juuti, K. S. Carslaw, M. Kulmala, J. Curtius, U. Baltensperger, D. R. Worsnop, H. Vehkamaki and J. Kirkby, Nature, 2013, 502, 359–363 CrossRef CAS PubMed.
- D. R. Hanson, J. Geophys. Res., 2002, 107, 4158 CrossRef.
- W.-K. Li and M. L. McKee, J. Phys. Chem. A, 1997, 101, 9778–9782 CrossRef CAS.
- J. J. Margitan, J. Phys. Chem. A, 1984, 88, 3314–3318 CrossRef CAS.
- P. H. Wine, R. J. Thompson, A. R. Ravishankara, D. H. Semmes, C. A. Gump, A. Torabi and J. M. Nicovich, J. Phys. Chem., 1983, 88, 2095–2104 CrossRef.
- R. L. Mauldin, T. Berndt, M. Sipila, P. Paasonen, T. Petaja, S. Kim, T. Kurten, F. Stratmann, V. M. Kerminen and M. Kulmala, Nature, 2012, 488, 193–196 CrossRef CAS PubMed.
- Z. Chen, C. Liu, W. Liu, T. Zhang and J. Xu, Sci. Total Environ., 2017, 575, 429–436 CrossRef CAS PubMed.
- F. Sheng, L. Jingjing, C. Yu, T. Fu-Ming, D. Xuemei and L. Jing-yao, RSC Adv., 2018, 8, 7988–7996 RSC.
- H. Zhang, S. Chen, J. Zhong, S. Zhang, Y. Zhang, X. Zhang, Z. Li and X. C. Zeng, Atmos. Environ., 2018, 177, 93–99 CrossRef CAS.
- J. Yang, L. Li, S. Wang, H. Li, J. S. Francisco, X. C. Zeng and Y. Gao, J. Am. Chem. Soc., 2019, 141, 19312–19320 CrossRef CAS PubMed.
- R. Steudel and Y. Steudel, Eur. J. Inorg. Chem., 2009, 2009, 1393–1405 CrossRef.
- T. Loerting and K. R. Liedl, J. Phys. Chem. A, 2001, 105, 5137–5145 CrossRef CAS.
- A. F. Voegele, C. S. Tautermann, C. Rauch, T. Loerting and K. R. Liedl, J. Phys. Chem. A, 2004, 108, 3859–3864 CrossRef CAS.
- J. Kirkby, J. Curtius, J. Almeida, E. Dunne, J. Duplissy, S. Ehrhart, A. Franchin, S. Gagne, L. Ickes, A. Kurten, A. Kupc, A. Metzger, F. Riccobono, L. Rondo, S. Schobesberger, G. Tsagkogeorgas, D. Wimmer, A. Amorim, F. Bianchi, M. Breitenlechner, A. David, J. Dommen, A. Downard, M. Ehn, R. C. Flagan, S. Haider, A. Hansel, D. Hauser, W. Jud, H. Junninen, F. Kreissl, A. Kvashin, A. Laaksonen, K. Lehtipalo, J. Lima, E. R. Lovejoy, V. Makhmutov, S. Mathot, J. Mikkila, P. Minginette, S. Mogo, T. Nieminen, A. Onnela, P. Pereira, T. Petaja, R. Schnitzhofer, J. H. Seinfeld, M. Sipila, Y. Stozhkov, F. Stratmann, A. Tome, J. Vanhanen, Y. Viisanen, A. Vrtala, P. E. Wagner, H. Walther, E. Weingartner, H. Wex, P. M. Winkler, K. S. Carslaw, D. R. Worsnop, U. Baltensperger and M. Kulmala, Nature, 2011, 476, 429–433 CrossRef CAS PubMed.
- J. Liu, S. Fang, W. Liu, M. Wang, F. M. Tao and J. Y. Liu, J. Phys. Chem. A, 2015, 119, 102–111 CrossRef CAS PubMed.
- Y. You, V. P. Kanawade, J. A. de Gouw, A. B. Guenther, S. Madronich, M. R. Sierra-Hernández, M. Lawler, J. N. Smith, S. Takahama, G. Ruggeri, A. Koss, K. Olson, K. Baumann, R. J. Weber, A. Nenes, H. Guo, E. S. Edgerton, L. Porcelli, W. H. Brune, A. H. Goldstein and S. H. Lee, Atmos. Chem. Phys., 2014, 14, 12181–12194 CrossRef.
- J. Zheng, Y. Ma, M. Chen, Q. Zhang, L. Wang, A. F. Khalizov, L. Yao, Z. Wang, X. Wang and L. Chen, Atmos. Environ., 2015, 102, 249–259 CrossRef CAS.
- M. Chen, M. Titcombe, J. Jiang, C. Jen, C. Kuang, M. L. Fischer, F. L. Eisele, J. I. Siepmann, D. R. Hanson, J. Zhao and P. H. McMurry, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 18713–18718 CrossRef CAS PubMed.
- C. Qiu, L. Wang, V. Lal, A. F. Khalizov and R. Zhang, Environ. Sci. Technol., 2011, 45, 4748–4755 CrossRef CAS PubMed.
- S. M. Murphy, A. Sorooshian, J. H. Kroll, N. L. Ng, P. Chhabra, C. Tong, J. D. Surratt, E. Knipping, R. C. Flagan and J. H. Seinfeld, Atmos. Chem. Phys., 2007, 7, 289–349 Search PubMed.
- H. Yu, R. McGraw and S.-H. Lee, Geophys. Res. Lett., 2012, 39, L02807 CrossRef.
- C. Qiu and R. Zhang, Phys. Chem. Chem. Phys., 2013, 15, 5738–5752 RSC.
- L. Yao, O. Garmash, F. Bianchi, J. Zheng, C. Yan., J. Kontkanen, H. Junninen, S. B. Mazon, M. Ehn, P. Paasonen, M. Sipilä, M. Wang, X. Wang, S. Xiao, H. Chen, Y. Lu, B. Zhang, D. Wang, Q. Fu, F. Geng, L. Li, H. Wang, L. Qiao, X. Yang, J. Chen, V.-M. Kerminen, T. Petäjä, D. R. Worsnop, M. Kulmala and L. Wang, Science, 2018, 361, 278–281 CrossRef CAS PubMed.
- H. Li, J. Zhong, H. Vehkamaki, T. Kurten, W. Wang, M. Ge, S. Zhang, Z. Li, X. Zhang, J. S. Francisco and X. C. Zeng, J. Am. Chem. Soc., 2018, 140, 11020–11028 CrossRef CAS PubMed.
- B. J. Finlayson-Pitts, L. M. Wingen, A. L. Sumner, D. Syomin and K. A. Ramazan, Phys. Chem. Chem. Phys., 2003, 5, 223–242 RSC.
- Y. Miller., B. J. Finlayson-Pitts and R. B. Gerber, J. Am. Chem. Soc., 2009, 131, 12180–12185 CrossRef CAS PubMed.
- J. Zhong, C. Zhu, L. Li, G. L. Richmond, J. S. Francisco and X. C. Zeng, J. Am. Chem. Soc., 2017, 139, 17168–17174 CrossRef CAS PubMed.
- C. Schweitzer and R. Schmid, Chem. Rev., 2003, 103, 1685–1757 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. Furthmüller, J. Hafner and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 15606–15622 CrossRef PubMed.
- A. J. M. Anglada, S. Olivella and A. Solé, Phys. Chem. Chem. Phys., 2014, 16, 19437–19445 RSC.
- C. Ye, N. Zhang, H. Gao and X. Zhou, Environ. Sci. Technol., 2017, 51, 6849–6856 CrossRef CAS PubMed.
- M. E. Dunn, E. K. Pokon and G. C. Shields, J. Am. Chem. Soc., 2003, 126, 2647–2653 CrossRef PubMed.
- B. Long, J. L. Bao and D. G. Truhlar, Phys. Chem. Chem. Phys., 2017, 19, 8091–8100 RSC.
- H. Wang, K. Lu, X. Chen, Q. Zhu, Q. Chen, S. Guo, M. Jiang, X. Li, D. Shang, Z. Tan, Y. Wu, Z. Wu, Q. Zou, Y. Zheng, L. Zeng, T. Zhu, M. Hu and Y. Zhang, Environ. Sci. Technol., 2017, 4, 416–420 CAS.
- W. Gao, X. Tie, J. Xu, R. Huang, X. Mao, G. Zhou and L. Chang, Sci. Total Environ., 2017, 603–604, 425–433 CrossRef CAS PubMed.
- C. Hattig, W. Klopper, A. Kohn and D. P. Tew, Chem. Rev., 2012, 112, 4–74 CrossRef PubMed.
- G. Knizia, T. B. Adler and H. J. Werner, J. Chem. Phys., 2009, 130, 054104 CrossRef PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- J. Zhong, H. Li, M. Kumar, J. Liu, L. Liu, X. Zhang, X. C. Zeng and J. S. Francisco, Angew. Chem., Int. Ed. Engl., 2019, 58, 8351–8355 CrossRef CAS PubMed.
- R. Wu, S. Pan, Y. Li and L. Wang, J. Phys. Chem. A, 2014, 118, 4533–4547 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. Staroverov, T. N. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Revision D.01, Gaussian Inc., Wallingford, CT, 2009 Search PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS PubMed.
- G. Kresse and J. FurthmüllerJ, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- J. VandeVondele, F. Mohamed, M. Krack, J. Hutter, M. Sprik and M. Parrinello, J. Chem. Phys., 2005, 122, 14515 CrossRef PubMed.
- G. Lippert, J. Hutter and M. Parrinello, Mol. Phys., 2010, 92, 477–488 CrossRef.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- C. Zhu, M. Kumar, J. Zhong, L. Li, J. S. Francisco and X. C. Zeng, J. Am. Chem. Soc., 2016, 138, 11164–11169 CrossRef CAS PubMed.
- J. Elm, S. Jorgensen, M. Bilde and K. V. Mikkelsen, Phys. Chem. Chem. Phys., 2013, 15, 9636–9645 RSC.
- H. S. Johnston and J. Heicklen, J. Chem. Phys., 1962, 66, 532–533 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sc04756e |
| This journal is © The Royal Society of Chemistry 2020 |