Synthesis of a binary alloy nanoparticle catalyst with an immiscible combination of Rh and Cu assisted by hydrogen spillover on a TiO₂ support

Abstract

This work demonstrated the use of TiO₂ as a promising platform for the synthesis of non-equilibrium RhCu binary alloy nanoparticles (NPs). These metals are regarded as immiscible based on their phase diagram but form NPs with the aid of the significant hydrogen spillover on TiO₂ with concurrent proton–electron transfer. The resulting RhCu/TiO₂ exhibited 2.6 times higher catalytic activity than Rh/TiO₂ during hydrogen production from the hydrolysis of ammonia borane (AB), due to a synergistic effect. Theoretical simulations showed a higher energy value for the adsorption of AB on the RhCu alloy and a lower activation energy for the rate determining N–B bond dissociation by the attack of H₂O during AB hydrolysis compared to monometallic Rh. High-angle annular dark-field scanning transmission electron microscopy and energy-dispersive X-ray spectroscopy confirmed the formation of RhCu alloy NPs with a mean diameter of 2.0 nm on the TiO₂. H₂-temperature programmed reduction and in situ X-ray absorption fine structure analyses at elevated temperature under H₂ demonstrated that Rh³⁺ and Cu²⁺ precursors were simultaneously reduced only on the TiO₂ support. This effect resulted from the improved and limited reducibility of Cu²⁺ and Rh³⁺, respectively. The rate of hydrogen spillover of TiO₂ is faster as compared to γ-Al₂O₃ and MgO as evidenced by sequential H₂/D₂ exchanges during in situ Fourier transform infrared analyses. Density functional theory calculations also showed that the migration of H atoms on TiO₂ proceeds with a lower energy barrier than that on Al₂O₃, and the reduction of Cu²⁺ species is facilitated by H spillover on the support rather than by direct reduction by H₂. These results confirm the vital role of TiO₂ in the formation of the alloy and may represent a new strategy for the synthesis of different non-equilibrium solid solution alloys.

---

Introduction

Over the past decade, metal nanoparticles (NPs) have been studied intensively with regard to a wide range of potential industrial,^1,2 biomedical,^3–5 electronic,^6,7 and catalytic applications.^8–11 This is due to the unique properties of NPs, which are different from those of bulk metals, and the small size effects they exhibit.¹² In addition, binary alloys, whose nanostructure can consist of solid solution, segregated, or core–shell structures, have been widely researched as advanced catalysts because they show superior catalytic activity and selectivity compared to single metal NPs.^12–17 Various geometric and electronic effects can appear as a result of differences in certain characteristics of each metal, such as work functions, ionization potentials, and electronegativity.^14,18,19 These factors can, in turn, have significant effects on the properties of binary alloys. Therefore, the formulations of binary alloys are a vital factor in terms of optimizing their performance.

The replacement of expensive noble metals with low-cost base metals is also an important consideration that affects the economic aspects of these materials. However, there are several combinations of noble and base metals, such as Au–Co, Ru–Ni,²⁰ and Rh–Cu,²¹ that are difficult to process into solid solution alloys based on their phase diagram. Thus, even though such combinations have unexplored potential, the catalytic properties of these solid solution alloys have not yet been elucidated. In this regard, Kitagawa et al. have reported the use of a conventional procedure to synthesize solid solution alloys with immiscible combinations of metals using a polyol method.^17,21,22 In addition, Humphrey et al. also successfully synthesized solid solution alloys by employing a combination of the polyol method and microwave heating.^23,24 These research groups demonstrated that the resulting binary alloys with immiscible combinations show interesting performance and characteristics for specific catalytic reactions. The development of new and facile techniques for the synthesis of such solid solution alloys with immiscible metal combinations remains desirable, even though these NPs are not thermodynamically stable and readily grow to form larger particles.^25,26 One means of mitigating this problem is to fix the NPs on supports having relatively high surface areas, such as metal oxides, so as to maintain their small sizes particularly in the field of catalysis. Interestingly, metal NPs are affected by the supports employed during synthesis and will exhibit different properties depending on the support.^26–28 Therefore, the selection of an appropriate support for use during the growth of metal NPs is very important, and it is crucial to understand the phenomena that occur on various supports.²⁹

Hydrogen spillover is one such phenomenon that is of interest in heterogeneous catalysis. This process involves the surface migration of dissociated H atoms from noble metal particles to nonmetal supports.^30–36 This spillover effect has been widely studied^30,34–36 and applied to catalytic systems and the fabrication of hydrogen storage materials.^37–43 Several types of hydrogenation have been identified in which substrates adsorbed on supports are hydrogenated by activated H atoms generated on metal catalysts and spilled over to supports.^38,42 Hydrogen spillover has also emerged as a promising strategy for high-density hydrogen storage under near-ambient conditions, based on the utilization of carbon-based materials,^39,43 metal–organic frameworks,^40,44 and zeolites.⁴⁵ Hydrogen spillover is initiated by the formation of protons (H⁺) and electrons (e⁻) from H atoms at metal–support interfaces.³⁰ The protons diffuse to O₂⁻ anions to form O–H and H–O–H bonds on the support surface, whereas the electrons simultaneously promote the partial reduction of metals in reducible metal oxides.^46,47 In the case of a TiO₂ support, Ti⁴⁺ ions are partially reduced to Ti³⁺ by the electrons produced by activated H atoms that migrate through the TiO₂ lattice by exchange between Ti³⁺–Ti⁴⁺ pairs.⁴⁸ Consequently, hydrogen spillover rarely occurs on non-reducible supports, since the concurrent transfer of protons and electrons will not proceed on such materials.

Our group has previously reported that a combination of Ru and Ni (which are essentially immiscible at equilibrium due to the positive enthalpy of formation for their solid solution alloy) will form a solid solution alloy on a TiO₂ support when using conventional impregnation and hydrogen reduction procedures.^20,49 This highly specific formation of the binary alloy is believed to involve intraparticle hydrogen spillover from the Ru surface to the Ni surface on the TiO₂ support. This synthesis can be performed without using a polymeric surfactant, and the strong metal–support interaction obtained from the TiO₂ support allows the loading of small size NPs of the alloy.^50,51 However, the mechanism by which solid solution alloys are generated from immiscible metals on a TiO₂ support and the applicable metal combinations remain unclear.

In the work reported herein, we determined that a combination of Rh and Cu, which are also thermodynamically immiscible according to the associated phase diagram (Fig. S1†),⁵² forms binary solid solution alloy NPs on a TiO₂ support. These NPs exhibit superior catalytic performance compared to monometallic Rh during the hydrolysis of ammonia borane (AB) owing to a significant synergistic effect obtained from the two metals. The present study elucidated the specific mechanism responsible for the alloy formation based on in situ characterization by means of H₂ temperature-programmed reduction (TPR), X-ray adsorption fine structure (XAFS) analysis, and Fourier transform infrared (FTIR) spectroscopy. Density functional theory (DFT) calculations were also performed to clarify not only the promotional effect of the RhCu alloy but also the enhanced hydrogen spillover occurring on the TiO₂ support.

Experimental

Materials

Rutile TiO₂ (JRC-TIO-6) and anatase TiO₂ (JRC-TIO-8) were kindly supplied by the Catalysis Society of Japan. MgO was purchased from Wako Pure Chemical Industries, Ltd. Ethanol, RhCl₃, CuCl₂·2H₂O, and ZrO₂ were purchased from Nacalai Tesque. γ-Al₂O₃ was obtained from Strem Chemicals, Inc. Ammonia borane (AB, NH₃BH₃) was obtained from the Aldrich Chemical Co. All commercially available compounds were used as received. Distilled water was employed as the reaction solvent.

Preparation of catalysts

TiO₂ (0.5 g) was added to a mixture of distilled water (50 mL) and ethanol (50 mL), followed by the addition of RhCl₃ (21.0 mg) and CuCl₂·2H₂O (17.1 mg). This mixture was stirred at room temperature for 1 h, after which the solvents were evaporated under vacuum. Finally, the sample was reduced with H₂ at a heating rate of 5 °C min⁻¹ (20 mL min⁻¹, 350 °C) for 2 h to yield RhCu/TiO₂ (Rh 2.0 wt%; Rh : Cu = 1 : 1). RhCu/ZrO₂, RhCu/γ-Al₂O₃, and RhCu/MgO with the same Rh and Cu loadings were also synthesized according to the same procedure.

Characterization

Transmission electron microscopy (TEM) micrographs were obtained with a field emission (FE) TEM instrument (Hf-2000, Hitachi). Scanning transmission electron microscopy (STEM), elemental mapping and line analysis were performed using a JEOL-ARM 200F instrument equipped with a Kevex EDX detector (JED 2300T) operated at 200 kV. Temperature-programmed reduction with H₂ (H₂-TPR) was conducted using a BEL-CAT (BEL Japan, Inc.) instrument by heating 30 mg samples at 5 °C min⁻¹ from 50 to 600 °C under a 5.0% H₂/Ar flow. In these experiments, as-deposited samples before H₂ reduction were employed. Rh K-edge and Cu K-edge in situ X-ray absorption fine structure (XAFS) spectra were recorded in the transmission mode at the 01B1 beamline station in conjunction with a Si (111) monochromator at SPring-8, JASRI, Harima, Japan (proposal numbers 2017A1057 and 2017B1084). In a typical experiment, spectra were acquired while a pellet sample was held in a batch-type in situ XAFS cell. XAFS data were processed using the ATHENA code (Demeter).⁵³ The Fourier transformation (FT) of k³-weighted normalized extended XAFS (EXAFS) data was performed over the range of 3.0 Å < k/Å⁻¹ < 12 Å to obtain the radial structure function.

Hydrolysis of AB

In a typical experiment, a quantity of the RhCu/TiO₂ catalyst (20 mg) combined with 8 mL water was transferred into a Schlenk-type reaction vessel (30 mL) connected to a gas buret. After the system was purged three times with Ar, 2 mL of a 2 mmol aqueous solution of AB was added to the vessel and allowed to react at 30 °C. The reaction was considered to start at the moment that the AB solution was added to the vessel and the reaction progress was monitored periodically. TOF values were defined as (H₂ mol)/((total Rh mol) min).

Evaluation of hydrogen spillover using in situ FTIR

In situ Fourier transform infrared (FTIR) spectra were acquired using a JASCO FT/IR-6600 instrument over the range of 4400–400 cm⁻¹. In each case, an approximately 30 mg quantity of the sample (the as-prepared Rh supported catalyst) was pressed into a self-supported wafer (ϕ10 mm). This wafer was subsequently mounted in a specially designed quartz IR cell (Makuhari Rikagaku Garasu Inc.) equipped with a water-cooling condenser and an electric heater and connected to a gas-exchange system. Spectra were acquired using a previously reported procedure.⁵⁴ The specimen was first reduced at 350 °C under a H₂ flow (20 mL min⁻¹) for 2 h. Following this, the sample was heated under N₂ at 150 °C for 1 h to remove physisorbed water (after which no further changes in the spectrum were observed) and the baseline spectrum was collected.

Spectra were also obtained after the sample was heated under a H₂ atmosphere at 50 °C for 30 min, to ensure equilibration. Following this initial heating step, the gas flow was switched to D₂ for 10 min and then back to H₂ for 10 min. This switching process was repeated again and the resulting three-dimensional changes over time in the peak at 1200 cm⁻¹ (attributed to the δ_D–O–D stretching vibration) were monitored.

DFT calculations

All density functional theory (DFT) calculations were performed with the DMol3 program in the Materials Studio 17.2 software package.^55,56 The generalized gradient approximation (GGA) exchange-correlation functional proposed by Perdew, Burke, and Ernzerhof (PBE) was used to obtain a better understanding of the semiconductor electronic properties of these materials. This function was combined with the double-numerical basis set plus polarization functions (DNP) in conjunction with a cutoff value of 4.0 Å. We adopted the medium level in the DMol³ program for the integration grid. Rh₂₄ and Rh₁₂Cu₁₂ clusters with their (111) facets exposed were selected as models of monometallic and binary clusters, respectively, with the bottom two layers fixed at the corresponding bulk positions and the top layers allowed to relax during geometry optimizations. Adsorption energy values (E_ad) were estimated from the differences between the optimized energies of individual substances and the combined cluster model and AB. E_ad was defined as E_adsorbate + E_cluster − E_{adsorbate/cluster}, where E_adsorbate is the total energy of the free adsorbate, E_cluster is the total energy of the bare cluster and E_{adsorbate/cluster} is the total energy of the adsorbate–cluster system. These activation energy calculations were based on a process previously reported by Peng et al.⁵⁷

Simulations of the reduction of Cu–O groups via H₂ spillover were performed using a TiO₂(101) plane with atomic thickness and a unit cell of 10.929 × 9.188 × 16.394 Å together with a hexagonal Al₂O₃(100) plane with atomic thickness and a unit cell of 9.518 × 12.991 × 14.277 Å. In addition, a γ-Al₂O₃ (100) plane with atomic thickness and a unit cell of 16.826 × 16.136 × 24.318 Å was also used for calculations. Periodic boundary conditions were applied, with some of the top-layer atoms allowed to relax during geometry optimizations and the other layers fixed at the corresponding bulk positions. The slab was separated by a vacuum space with a height of 20 Å and tetrahedral Rh₅ clusters were loaded on the surface of each oxide when modeling H₂ dissociation.

Results and discussion

Synergistic catalytic effect of RhCu/TiO₂

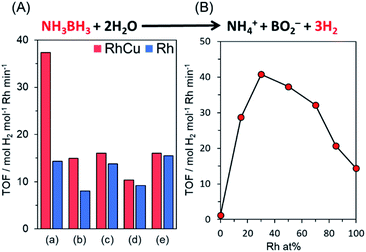
Various Rh, Cu, and RhCu supported catalysts were prepared using a conventional impregnation method. Briefly, aqueous solutions of RhCl₃ and CuCl₂·2H₂O containing ethanol were deposited on various supports, including TiO₂ (rutile: R), TiO₂ (anatase: A), γ-Al₂O₃, ZrO₂, and MgO. The resulting samples were subsequently reduced under a H₂ flow (20 mL min⁻¹) at 350 °C, without applying a prior calcination step.

The catalytic performance of each sample was assessed by monitoring hydrogen production during the hydrolysis of AB. AB was used because this compound has emerged as one of the most practical hydrogen storage compounds due to its high stability as a solid under ambient conditions and superior hydrogen storage capacity (19.6 wt%).^49,58–60Fig. 1A provides the turnover frequency (TOF) values for various Rh and RhCu supported catalysts, while the time courses of reactivities are summarized in Fig. S2.† The RhCu/TiO₂ (R) showed the highest catalytic activity, which was 2.6 times that of a single Rh catalyst, while the other RhCu supported catalysts did not show any significant enhancement as compared to the corresponding Rh catalysts, and the activities of the Cu supported catalysts were negligible (Fig. S2†). The RhCu/TiO₂ (R) exhibited the highest promotional alloying effect (Fig. 1B) when the atomic ratio of Rh and Cu was adjusted to 7 : 3. The volcano-type relationship between activity and composition clearly suggests the formation of a solid solution RhCu alloy structure on the TiO₂ and an unusual synergistic effect originating from the combination of Rh and Cu. Transmission electron microscopy (TEM) images of Rh and RhCu NPs supported on TiO₂ (R) (Fig. S3†) also indicate that the improved activity of the RhCu was not due to the size of the NPs, since the average diameters of the Rh and RhCu NPs were approximately 1.9 and 2.0 nm, respectively.

Fig. 1 (A) TOF values for hydrogen production from AB hydrolysis over Rh and RhCu supported catalysts on (a) TiO₂ (rutile), (b) TiO₂ (anatase), (c) γ-Al₂O₃, (d) ZrO₂ and (e) MgO and (B) TOF values obtained using RhCu supported TiO₂ (R) catalysts with different Rh : Cu ratios (catalytic conditions: catalyst 20 mg, 10 mL 0.2 M aqueous AB solution, 30 °C).

In addition, when Rh/TiO₂ (R) and RhCu/TiO₂ (R) specimens were calcined at 500 °C prior to the H₂ reduction trials, both specimens showed the same level of activity (Fig. S4†). This effect is attributed to the separation of Rh and Cu ions at high temperatures. From these results, it is evident that a unique RhCu binary alloy was formed on the TiO₂ support during simple H₂ reduction at 350 °C. These catalysts supported on TiO₂ (R) were subsequently characterized, as described below (in which TiO₂ (R) is simply referred to as TiO₂).

To investigate the alloying effect of Rh and Cu during AB hydrolysis, DFT calculations were performed based on Rh₂₄ and Rh₁₂Cu₁₂ clusters. During these calculations, the level of the highest occupied molecular orbital (HOMO) could be tuned through the coupling of the electronic structure as the cluster composition was varied. When a portion of the Rh₂₄ cluster was replaced with Cu metal, the HOMO level was found to be raised from −4.069 eV (Rh₂₄) to −3.977 eV (Rh₁₂Cu₁₂). This result suggests that the RhCu alloy is theoretically more electron-rich than monometallic Rh, and this finding is supported by Rh 3d X-ray photoelectron spectroscopy (XPS) analysis of the Rh/TiO₂ and RhCu/TiO₂ (Fig. S5†). In these data, the RhCu/TiO₂ XPS peak is shifted to a lower binding energy compared to that generated by the Rh/TiO₂. This shift is attributed to a change in the electronic state of Rh due to electron donation from the Cu. Charge transfer from Cu atoms to Rh atoms occurs because of the respective electronegativity values of Rh and Cu (2.28 and 1.90). Note that there is no clear difference in the Cu 2p XPS spectra of Cu/TiO₂ and RhCu/TiO₂. Cu⁰ and Cu⁺ are difficult to distinguish because they appeared at almost the same position in XPS spectra. Therefore, even if electrons are transferred from Cu to Rh, we cannot observe a clear change in the Cu 2p XPS spectra because electron-poor Cu⁰ appears at an almost similar position to pure Cu⁰. And, we roughly estimated the ratio of the peak derived from single Rh metal and the RhCu alloy by fitting. The ratio of the peak derived from single Rh metal and the RhCu alloy is estimated to be 42.2% and 57.8%, respectively.

Previous experimental and theoretical studies reported the possible mechanism for AB hydrolysis using metal NPs. Feng et al. observed changes of the Cu state during AB hydrolysis using in situ XAFS, which showed that AB molecules interact with the catalyst firstly and water can approach both the catalyst and AB to attack the N–B bond.⁶¹ Peng et al. demonstrated the plausible AB hydrolysis mechanism using DFT calculations.⁵⁷ Thus, we show the possible mechanism of AB hydrolysis in Fig. 2A, and the details are as follows. In this cycle, the reaction is initiated by the dissociation of the N–B bond in AB, followed by the attack of a H₂O molecule to generate BH₃(OH)⁻ and NH₄⁺. Subsequently, hydrogen is produced by a second attack of H₂O on the BH₃(OH)⁻ ion. Finally, two hydrogen molecules are released from BH₂(OH)₂⁻ accompanied by the formation of BO₂⁻. It should be noted that the final step proceeds readily because the associated energy barrier is lower than those for the other steps. Based on this mechanism, we estimated the activation energy (E_a) values for the first and second steps for Rh₂₄ and Rh₁₂Cu₁₂ clusters (Fig. 2A, Table 1). E_a for the first step was determined to be 24.8 kcal mol⁻¹ on the Rh₁₂Cu₁₂, which is much lower than that on the Rh cluster, for which E_a was 38.5 kcal mol⁻¹. In addition, the E_a values for the second step were lower than those for the first step for both the Rh and RhCu clusters. These results demonstrate that the initial attack by H₂O is the rate determining step during this reaction, and is promoted by the presence of Rh₁₂Cu₁₂ clusters having electron-rich Rh species. Calculated models in the rate-limiting step are shown in Fig. S7.† It is well known that a greater adsorption energy value (E_ad) for the reaction intermediate on the metal catalyst corresponds to a lower reaction barrier, according to the Brønsted–Evans–Polanyi (BEP) relationship.⁶² The E_ad for adsorption on the Rh₁₂Cu₁₂ cluster was calculated to be 22.1 kcal mol⁻¹, which is 1.6 times the value of 14.1 kcal mol⁻¹ for the Rh₂₄ cluster (Fig. 2B, Table 1). Thus, sites comprising neighboring Rh–Cu pairs with an electronic imbalance evidently act to promote interactions with AB molecules, enhancing the catalytic activity.

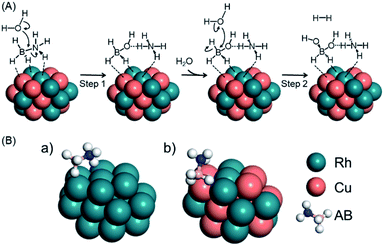Fig. 2 (A) Schematics showing possible processes for AB hydrolysis and (B) the calculated model for the adsorption of AB on (a) Rh24 or (b) Rh12Cu12 clusters with the (111) facet exposed.

Table 1 (A) Activation energy for AB hydrolysis in the reaction pathway in Fig. 2 and (B) adsorption energy of AB on (a) Rh₂₄ or (b) Rh₁₂Cu₁₂ clusters

	Clusters	(A) Activation Energy		(B) Adsorption Energy of AB/kcal mol^−1
		First attack of H2O (step 1)/kcal mol^−1	Second attack of H2O (step 2)/kcal mol^−1
a	Rh24	38.5	10.4	14.1
b	Rh12Cu12	24.8	15.0	22.1

---

Characterization of RhCu/TiO₂

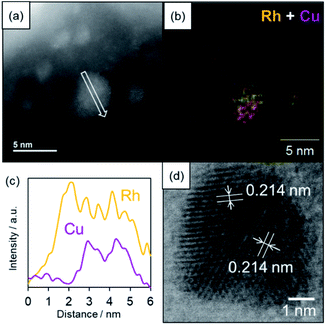
The formation of a solid solution RhCu alloy on the TiO₂ support was confirmed by various characterization experiments. Fig. 3 presents a high-angle annular dark field scanning TEM (HAADF-STEM) image, a bright field STEM (BF-STEM) image, energy dispersive X-ray (EDX) maps, and a line analysis for a RhCu/TiO₂ catalyst after reduction at 350 °C under a H₂ atmosphere. The average size of the RhCu NPs was estimated to be 2.0 nm based on the STEM image, while the EDX maps confirm the formation of a RhCu alloy, since both Rh and Cu signals appeared in the same region. The EDX line analysis shows both Rh and Cu signals in the same area, demonstrating the presence of a solid solution RhCu alloy. Fig S8† presents EDX line analysis of smaller RhCu NPs at around 2–3 nm. The EDX line analysis showed that this nanostructure was found to be a solid solution structure since the Rh and Cu signal appeared at a similar position. However, the atomic ratio of Rh : Cu is 68 : 32 in this particle from the X-ray intensity of Rh and Cu, indicating the formation of the Rh-rich RhCu alloy even in smaller particles. Lattice fringes are evident in the BF-STEM image of the RhCu NPs and the corresponding d spacing was estimated to be 0.214 nm in various regions. This value is almost equal to the average of the spacings of the Rh (111) planes (0.219 nm) and the Cu (111) planes (0.207 nm). These findings again confirm that Rh and Cu form a solid solution structure on the TiO₂.

Fig. 3 HAADF-STEM and BF-STEM images and EDX analysis of the RhCu/TiO₂. (a) A HAADF-STEM image, (b) an EDX map of Rh + Cu in the region indicated in (a), (c) EDX line analysis along the arrow in (a), and (d) a BF-STEM image showing the lattice distances.

The reduction temperatures of the supported metal precursors were determined using H₂-TPR (Fig. S9†). Typically, a Rh precursor will be reduced faster than a Cu precursor because the reduction potential of Rh³⁺ is more positive than that of Cu²⁺ (Cu²⁺ + 2e⁻ → Cu : E₀ = 0.34 vs. RHE, Rh³⁺ + 3e⁻ → Rh : E₀ = 0.76 vs. RHE) although both ions show a positive reduction potential. The reductions of Rh³⁺ species in the Rh/γ-Al₂O₃, Rh/MgO, and Rh/TiO₂ were found to occur at around 70, 120, and 150 °C, respectively. In contrast, the reductions of Cu²⁺ species in the Cu/γ-Al₂O₃ and Cu/MgO were observed to proceed above 300 °C, while reduction in the Cu/TiO₂ occurred at a significantly lower temperature of approximately 240 °C. Interestingly, the RhCu/TiO₂ exhibited two-step reduction peaks approximately at 140 and 210 °C. It is considered that the peak at lower temperature (around 140 °C) represents reduction of some of the Rh³⁺ to Rh⁰ (Rh nuclei) and the peak at higher temperature (around 210 °C) represents simultaneous reduction of other Rh³⁺ and Cu²⁺. This result indicates that the Rh³⁺ and Cu²⁺ precursors were reduced simultaneously on the TiO₂ support to produce a solid solution alloy. A similar trend was also observed on the TiO₂ (A). In contrast, the RhCu/γ-Al₂O₃ and RhCu/MgO specimens produced two reduction peaks, suggesting the individual reductions of Rh³⁺ and Cu²⁺ precursors.

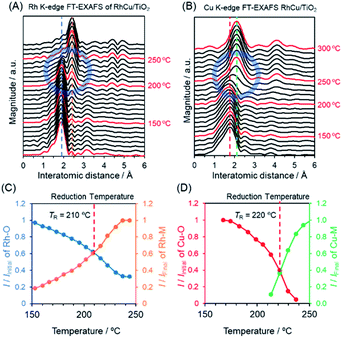
To further elucidate changes in the local structures of the Rh, Cu and RhCu supported catalysts, in situ XAFS analyses were performed during a reduction sequence under H₂ at elevated temperatures (Fig. S10–S15†). The Rh K-edge FT-EXAFS spectrum produced by the RhCu/TiO₂ (Fig. 4A) exhibits a sharp singlet attributed to Rh–O bonds at approximately 1.9 Å below 200 °C, whereas another peak attributed to metallic Rh bonds appeared at approximately 2.4 Å above 200 °C. This transition in the FT-EXAFS spectra demonstrates the reduction of Rh³⁺ on the TiO₂ support. Fig. 4C summarizes changes in the intensities of the peaks ascribed to Rh–O and Rh–Rh(Cu) bonds during heating of the RhCu/TiO₂. The Cu K-edge in situ FT-EXAFS spectra of RhCu/TiO₂ and the changes in the intensities of peaks due to Cu–O and Cu–Cu(Rh) bonds during heating are shown in Fig. 4B and D. Similarly, Fig. S10–S15† present the in situ XAFS spectra acquired from Rh, Cu and RhCu supported on TiO₂, γ-Al₂O₃ and MgO and the transition data for all specimens are shown in Fig. S16–S18.† The intersection between the transitions of two peaks was defined as the reduction temperature (T_R) for each metal precursor on the various supports, and these values are summarized in Table 2.

Fig. 4 In situ FT-EXAFS spectra of the (A) Rh K-edge of RhCu/TiO₂ and (B) Cu K-edge of RhCu/TiO₂ acquired during reduction under H₂ at elevated temperature. Variations in the intensities of peaks attributed to (C) Rh–O and Rh-M (metal) bonds based on the data in (A) and (D) Cu–O and Cu-M bonds based on the data shown in (B). (C and D) Vertical axis shows relative intensity compared to that of initial data (before H₂ reduction) attributed to the Rh–O bond and compared to that of final data (after H₂ reduction) attributed to the Rh–Metal(M) bond.

Table 2 Reduction temperatures of Rh³⁺ and Cu²⁺ supported on TiO₂, γ-Al₂O₃ and MgO as determined based on in situ FT-EXAFS spectra

	Rh K-edge	Cu K-edge
Rh/TiO2	200 °C
Cu/TiO2		280 °C
RhCu/TiO2	210 °C	220 °C
Rh/γ-Al2O3	60 °C
Cu/γ-Al2O3		310 °C
RhCu/γ-Al2O3	130 °C	300 °C
Rh/MgO	130 °C
Cu/MgO		310 °C
RhCu/MgO	130 °C	310 °C

---

The T_R for Rh³⁺ on the Rh/TiO₂ was 200 °C and this value was slightly increased to 210 °C in the case of the RhCu/TiO₂. As expected, the T_R for Cu²⁺ on the Cu/TiO₂ was drastically decreased (from 280 to 220 °C) after mixing with Rh³⁺. The T_R values for Rh³⁺ and Cu²⁺ in the RhCu/TiO₂ were intermediate between those corresponding to the single Rh and Cu samples, which suggests that the two precursors were simultaneously reduced on the TiO₂ surface. However, the T_R values for Cu²⁺ on the γ-Al₂O₃ and MgO supports were above 300 °C, and remained high even after mixing with Rh³⁺. These observations indicate that neither the Rh nor the Cu precursor significantly affects the reduction profile of the other, and that the reductions of these two metals occur individually on the γ-Al₂O₃ and MgO surfaces. In these cases, segregated monometallic NPs and/or Rh_core–Cu_shell-type NPs are presumably obtained as opposed to the binary alloy.

It is unlikely that Cu²⁺ will be reduced as fast as reduction of Rh³⁺ on the TiO₂ support because the reduction potential of Cu is lower than that of Rh. Based on the above results, it is probable that the reductions of Rh³⁺ and Cu²⁺ species on the TiO₂ support proceed via a unique mechanism compared to the mechanisms on the other supports. A mechanism by which Rh³⁺ and Cu²⁺ are reduced on the TiO₂ support can be proposed by considering the contribution of hydrogen spillover from the Rh to the Cu.³⁰ Hydrogen spillover is known to promote the reduction of metals on various supports through hydrogen dissociation on a second precious metal.^31,32 During the initial stage of the reduction, it is thought that pre-reduced Rh nuclei dissociate hydrogen molecules, after which the hydrogen is transferred to the Cu²⁺ precursor by spillover such that the ions are reduced to Cu⁰. Metal oxide supports with reversible reducibility, such as TiO₂, also tend to promote spillover ability.³³

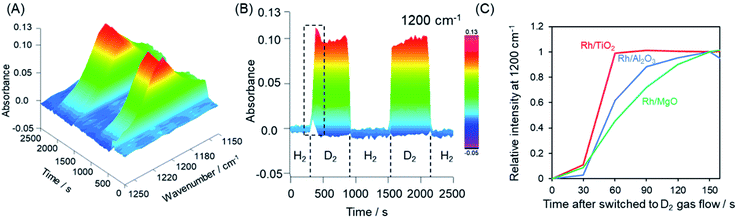
The hydrogen spillover characteristics of the TiO₂, γ-Al₂O₃, and MgO supports were compared by acquiring in situ FTIR spectra during sequential H₂ and D₂ gas flows over Rh supported catalysts. If rapid hydrogen spillover occurred on a support, we would expect to observe rapid exchange between gas phase hydrogen and support protons via the spillover process.⁵⁴ Initially, physisorbed water was removed from the pre-reduced samples over the span of 1 h, after which no further changes in the spectrum were observed. Subsequently, the sample was placed under a H₂ atmosphere and heated at 50 °C, and then allowed to equilibrate. Following this, the gas flow was switched to D₂ instead of H₂ and then back to H₂. This gas exchange procedure was repeated, and the 3D changes over time in the 1200 cm⁻¹ peak (attributed to the δ_D–O–D stretching vibration) are shown in Fig. 5A–C and S19.†Fig. 5C displays the normalized intensity of the 1200 cm⁻¹ peak for Rh supported on TiO₂, γ-Al₂O₃, and MgO supports. After switching from H₂ to D₂, the Rh/MgO required more than 150 s to saturate, while the Rh/γ-Al₂O₃ saturated at approximately 150 s. It should be noted that the increase in the rise in the peak intensity during trials with the Rh/TiO₂ was complete within only 60 s. The process required 30 s for each observation to integrate the data and another several seconds to replace the gases after switching from H₂ to D₂. Thus, the rate of peak saturation for the Rh/TiO₂ was too fast and almost fell below the resolution limitation (30 s) of the in situ FT-IR system after the D₂ gas reached the catalyst. Based on the H-D exchange kinetics, we can conclude that rates of hydrogen spillover on the Rh supported TiO₂ specimen were much higher than thsoe for Rh on non-reducible supports such as γ-Al₂O₃ and MgO.

Fig. 5 (A) 3D and (B) 2D time courses of the changes in the intensity of the peak at 1200 cm⁻¹ attributed to the δ_D–O–D stretching vibration as obtained from in situ FTIR spectra acquired during the H₂ and D₂ gas exchange sequence over Rh/TiO₂. (C) Normalized peak intensities after D₂ gas introduction within the area indicated by dashed lines in (B) for Rh/TiO₂, Rh/Al₂O₃ and Rh/MgO.

Considering these results, we propose a mechanism for the formation of the solid solution RhCu alloy on the TiO₂ support (Fig. 6). During these trials, the sample was heated under a H₂ atmosphere such that Rh³⁺ was partially reduced to generate Rh metal nuclei at around 140 °C. The nuclei seem to be formed at the defect site of TiO₂ and hardly involved in alloy formation since they are stable. Following this, hydrogen was dissociated on the surfaces of these Rh nuclei to form Rh–H species, accompanied by the reduction of Ti⁴⁺ to Ti³⁺ at the metal–support interfaces. Electrons migrated from Ti³⁺ ions to neighboring Ti⁴⁺ ions, which allowed simultaneous proton transfer to O²⁻ anions attached to adjacent Ti⁴⁺. In this manner, the hydrogen rapidly reached both metal ions (Rh³⁺ and Cu²⁺) by moving over the TiO₂ surface, and these ions were reduced at the same time to form RhCu clusters. These clusters then aggregated to produce the non-equilibrium RhCu alloy. This proposed mechanism is supported by the synergistic effect that evidently promotes the catalytic activity of the RhCu/TiO₂ compared to the Rh/TiO₂ following reduction at various temperatures (Fig. S20†). The rate of increase in catalytic activity was found to be significantly dependent on the reduction temperature and increased in the following order: 200 °C (1.38) < 250 °C (2.33) < 300 °C (2.55) < 350 °C (2.60). The decrease of TOF over Rh/TiO₂ and RhCu/TiO₂ catalysts showed an almost similar rate at reduction temperature over 250 °C, indicating that TOF decreases are related to the particle size. Moreover, RhCu/TiO₂ is considered to show a promotional alloying effect at reduction temperature over 220 °C, and in fact, this catalyst suddenly showed more than 2.3 higher activity compared to the Rh/TiO₂ catalyst at reduction temperature over 250 °C, indicating that the activity improvement is due to the formation of the solid solution alloy. This result is consistent with the data obtained by H₂-TPR and in situ XAFS analyses. In addition, the BET surface area of supports was measured to be 100, 338, 185, 11.3 and 2.53 m² g⁻¹ for TiO₂ rutile, TiO₂ anatase, γ-Al₂O₃, ZrO₂ and MgO, respectively. This result showed even if γ-Al₂O₃ which has a higher surface area than TiO₂ rutile is used, the corresponding alloy was not formed. Hence, it can be concluded that the participation of spillover is more important than the distribution of Rh and Cu on the support, for solid solution alloy formation with immiscible Rh and Cu combination.

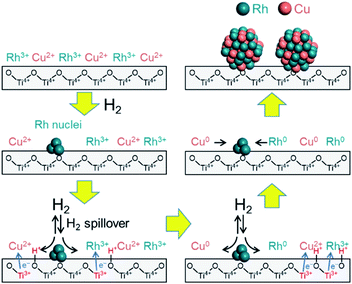Fig. 6 A proposed mechanism for the formation of an immiscible RhCu binary alloy on a TiO₂ support assisted by hydrogen spillover.

DFT calculations were also performed to provide further support for this mechanism by which an immiscible alloy is produced based on the spillover effect. The resulting potential energy profiles are summarized in Fig. 7. Rutile TiO₂ (101) and hexagonal Al₂O₃ (100) planes were chosen as models for this theoretical investigation because of their thermodynamic stability, and Rh₅ clusters were employed as a model of Rh nuclei. Four representative reaction steps were considered for the reduction of Cu²⁺ species on the support through the hydrogen spillover from Rh clusters, according to the above proposed reaction mechanism. These steps included the dissociation of H₂ on a Rh cluster loaded on the support (step 1), the transfer of a dissociated H atom from a Rh cluster to a neighboring O atom on the support (step 2), the migration of a H atom over the support surface (step 3), and the reduction of Cu²⁺ by the spilled H atom on the support (step 4).

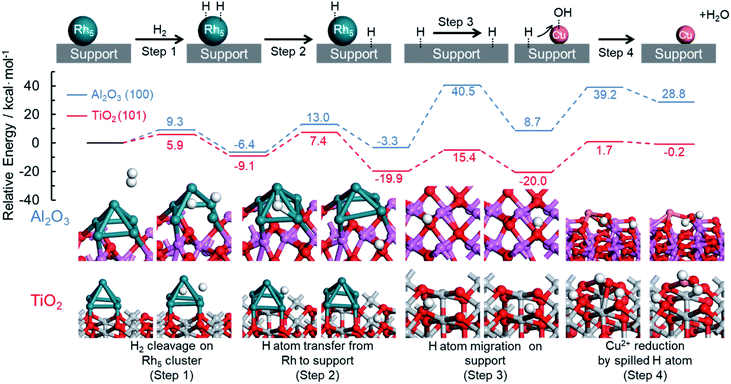Fig. 7 Theoretical pathway for the reduction of Cu species on the TiO₂ and Al₂O₃ supports assisted by hydrogen spillover.

In the case of TiO₂ (101), the dissociation of H₂ on a Rh₅ cluster (step 1) occurs with a barrier of 5.9 kcal mol⁻¹ (Fig. S21†). The E_a associated with H atom transfer from a Rh₅ cluster to a neighboring O atom on the support (step 2) was estimated to be 16.5 kcal mol⁻¹ (Fig. S22†). These values are similar to those obtained using Al₂O₃ (100), for which the E_a values were 9.3 and 19.4 kcal mol⁻¹, respectively. The migration of a H atom over the support surface (step 3) is considered a separate step because of the presence of oxygen sites having different coordination numbers, such as 2-coordinated oxygen (O(2)) or 3-coordinated oxygen (O(3)) sites. The barriers for H atom migration from O(2) to O(2), O(2) to O(3), and O(3) to O(2) were calculated to be 15.0, 37.4, and 12.7 kcal mol⁻¹ on the TiO₂ (101), respectively. These results demonstrate that H atom migration over the TiO₂(101) preferentially occurs at O(2) sites because TiO₂(101) has numerous O(2) sites and because the participation of O(3) is energetically unfavorable. In the case of Al₂O₃(100), the E_a values were determined to be 29.3, 41.7, and 43.8 kcal mol⁻¹ for the transfer pathways from O(2) to O(3), O(3) to O(2), and O(3) to O(3), respectively (Fig. S23†). Since the number of O(2) sites on Al₂O₃ is small, H atom migration on this substrate preferentially occurs at the O(3) sites, and even if an O(2) site is adjacent to O(3) sites, there is a relatively high activation energy for migration from O(2) to O(3) sites. These results clearly suggest that H atom transfer on TiO₂ is energetically more likely to proceed than that on Al₂O₃, and hence the rate of hydrogen spillover is faster on the TiO₂.

With respect to the reduction of Cu²⁺ by the spilled H atom on the support (step 4), we calculated the activation energy for the attack of a neighboring H atom on a Cu–OH group on the support, followed by the loss of H₂O. The E_a values were estimated to be 21.7 and 30.5 kcal mol⁻¹ on the TiO₂(101) and Al₂O₃(100), respectively (Fig. S24†). Taking into account the overall reactions, the reduction of Cu²⁺ species on TiO₂ proceeds with a barrier of 21.7 kcal mol⁻¹ in the presence of Rh, while that on Al₂O₃ requires an activation energy of 43.8 kcal mol⁻¹ even in the presence of Rh. The energy of the final state on the Al₂O₃ appeared to be thermodynamically high since all the steps for reduction of Cu²⁺ with hydrogen spillover from Rh are described together in Fig. 7. In detail, step 2 and step 3 are thermodynamically unfavorable steps which are related to hydrogen migration to the Al₂O₃ surface. Moreover, the same calculations were also performed on the γ-Al₂O₃ model reported by Digne et al., since their structure has been widely accepted for the investigations.^63,64 In the theoretical reduction pathway, H atom migration on the support has the highest activation energy (Fig. S27, Table S1†). The obtained activation energy for the hydrogen migration (38.9 kcal mol⁻¹) is almost similar to a value of our result on hexagonal Al₂O₃ (41.7–43.8 kcal mol⁻¹). In addition, Bokhoven et al. calculated the activation energy of hydrogen spillover on γ-Al₂O₃ using the model reported by Digne.³³ The corresponding value (37.6 kcal mol⁻¹) is the same as our results, indicating the reliability of our calculations. These results produced by the theoretical investigations help to explain the differences in the reduction temperatures for Cu²⁺ species between the RhCu/TiO₂ and RhCu/Al₂O₃. In preliminary work, the energy changes associated with the direct reduction of Cu²⁺ by H₂ molecules on each support were calculated, giving values of 36.8 and 44.7 kcal mol⁻¹ on the TiO₂(101) and Al₂O₃(100), respectively (Fig. S25†). These values correspond to the reduction of Cu/TiO₂ and Cu/Al₂O₃, respectively. The dissociation energies of gaseous H₂ on TiO₂(101) and Al₂O₃(100) without Rh clusters were estimated to be greater than 80 kcal mol⁻¹ (Fig. S26†), and so the reduction of Cu²⁺ must proceed solely due to spilled H atoms in the presence of Rh. These calculated E_a values and the experimental Cu²⁺ reduction temperatures on the TiO₂ and γ-Al₂O₃ determined by in situ XAFS are summarized in Table 3. On the TiO₂ support, the reduction of Cu²⁺ species occurs with an E_a of 21.7 kcal mol⁻¹ in the presence of Rh (210 °C) and with an E_a of 36.8 kcal mol⁻¹ in the absence of Rh (280 °C). On the Al₂O₃ support, these values are 43.8 kcal mol⁻¹ with Rh (300 °C) and 44.7 kcal mol⁻¹ without (310 °C). These correlations between E_a and the experimental reduction temperature are in good agreement with the proposed mechanism for the formation of the solid solution RhCu alloy.

Table 3 (A) Activation energies for various steps during the reduction of Cu²⁺ species assisted by hydrogen spillover on TiO₂ and Al₂O₃ and (B) experimental temperatures for the reduction of Cu²⁺ on the catalyst as determined from in situ XAFS data

	(A) Activation Energy/kcal mol^−1				(B) Reduction Temperature of Cu^2+/°C
	H2 cleavage on the Rh5 cluster	H atom transfer from the Rh5 cluster to the support	H atom migration on the support	Cu^2+ reduction by spilled H atoms
TiO2 (101)	5.9	16.5	15.0	21.7	210 (RhCu/TiO2)
Al2O3 (100)	9.3	19.4	41.7–43.8	30.5	300 (RhCu/γ-Al2O3)
	H2 cleavage on the support			Cu–O reduction by H2 vapor	Reduction temperature/°C
TiO2 (101)	82.3			36.8	280 (Cu/TiO2)
Al2O3 (100)	89.3			44.7	310 (Cu/γ-Al2O3)

---

The phase diagram for Rh and Cu shows that these metals are essentially immiscible at most compositions and do not form solid solution alloys below 600 °C, because of the positive enthalpy of formation of such alloys. Thus, the synthesis of such alloys is difficult using conventional methods. In addition, γ-Al₂O₃, MgO, and ZrO₂ supports do not afford RhCu alloys under the present synthetic conditions, indicating that the use of TiO₂ as a platform for the synthesis of alloy NPs could be a useful means of obtaining solid solution alloy structures with immiscible combinations.

Conclusions

TiO₂ has been demonstrated to be an efficient platform for the formation of a RhCu binary alloy with immiscible combination under H₂ reduction conditions. A RhCu/TiO₂ catalyst synthesized in this manner showed 2.6 times higher activity than Rh/TiO₂ during hydrogen production from the hydrolysis of AB. This activity improvement was not obtained when using other supports. Theoretical studies revealed that the adsorption energy of AB was increased on the RhCu binary alloy, whereas the activation energy for dissociation of the N–B bond (the rate-determining step) was decreased compared to the value obtained using monometallic Rh. This change in the energy barrier is attributed to the formation of negatively charged Rh atoms and positively charged Cu atoms in close proximity to one another. The generation of a RhCu binary alloy on the TiO₂ support was confirmed by HAADF-STEM and EDX observations. Reduction profiles obtained using H₂-TPR and in situ XAFS data suggest the simultaneous reduction of Rh³⁺ and Cu²⁺ species on the TiO₂ support. The rapid H₂/D₂ exchange reaction observed by in situ FT-IR spectroscopy suggests that the rate of hydrogen spillover increased on TiO₂. From these results, we conclude that Rh³⁺ ions are first reduced by H₂ to generate nuclei, after which the dissociation of hydrogen molecules occurs to form hydride species that act as cocatalysts to reduce neighboring Cu²⁺ species. This process is assisted by the hydrogen spillover characteristics of the TiO₂via a coupled proton–electron transfer mechanism. Theoretical simulations provide evidence for the facilitated migration of H atoms on the TiO₂ and show that the spilled H atoms enable the reduction of Cu²⁺ species with a lower activation energy compared to direct H₂ reduction. This study demonstrates a promising approach for the preparation of non-equilibrium solid solution alloys, and we expect that this strategy will be extendable to other combinations of metals that may serve as unique catalysts and/or photocatalysts.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported in part by Grants-in-Aid for Scientific Research (no. A18H020740 and A19H008380) from the Japan Society for the Promotion of Science (JSPS) and MEXT. S.M. thanks JSPS for a Research Fellowship for Young Scientists (no. A19J101530). K.M., Y.K., and H.Y. thank the MEXT program “Elements Strategy Initiative for Catalysts & Batteries (ESICB) (no. JPMXP0112101003)”.

Notes and references

1. H. M. Chen and R.-S. Liu, J. Phys. Chem. C, 2011, 115, 3513–3527.
2. M. A. El-Sayed, Acc. Chem. Res., 2001, 34, 257–264.
3. Y. C. Cao, R. Jin and C. A. Mirkin, Science, 2002, 297, 1536–1540.
4. P. V. Kamat, J. Phys. Chem. B, 2002, 106, 7729–7744.
5. N. L. Rosi, D. A. Giljohann, C. S. Thaxton, A. K. R. Lytton-Jean, M. S. Han and C. A. Mirkin, Science, 2006, 312, 1027–1030.
6. S. Nie and S. R. Emory, Science, 1997, 275, 1102–1106.
7. P. M. Tessier, O. D. Velev, A. T. Kalambur, J. F. Rabolt, A. M. Lenhoff and E. W. Kaler, J. Am. Chem. Soc., 2000, 122, 9554–9555.
8. K. Mori, S. Masuda, H. Tanaka, K. Yoshizawa, M. Che and H. Yamashita, Chem. Commun., 2017, 53, 4677–4680.
9. M. Haruta, N. Yamada, T. Kobayashi and S. Iijima, J. Catal., 1989, 115, 301–309.
10. L. N. Lewis, Chem. Rev., 1993, 93, 2693–2730.
11. A. K. Sinha, S. Seelan, S. Tsubota and M. Haruta, Angew. Chem., Int. Ed., 2004, 116, 1572–1574.
12. A. K. Singh and Q. Xu, ChemCatChem, 2013, 5, 652–676.
13. S. Masuda, K. Mori, Y. Futamura and H. Yamashita, ACS Catal., 2018, 8, 2277–2285.
14. K. Mori, T. Sano, H. Kobayashi and H. Yamashita, J. Am. Chem. Soc., 2018, 140, 8902–8909.
15. K. D. Gilroy, A. Ruditskiy, H. C. Peng, D. Qin and Y. Xia, Chem. Rev., 2016, 116, 10414–10472.
16. T. Mitsudome, T. Urayama, K. Yamazaki, Y. Maehara, J. Yamasaki, K. Gohara, Z. Maeno, T. Mizugaki, K. Jitsukawa and K. Kaneda, ACS Catal., 2015, 6, 666–670.
17. K. Kusada, H. Kobayashi, R. Ikeda, Y. Kubota, M. Takata, S. Toh, T. Yamamoto, S. Matsumura, N. Sumi, K. Sato, K. Nagaoka and H. Kitagawa, J. Am. Chem. Soc., 2014, 136, 1864–1871.
18. T. Yoshii, K. Nakatsuka, Y. Kuwahara, K. Mori and H. Yamashita, RSC Adv., 2017, 7, 22294–22300.
19. M. Miyazaki, S. Furukawa and T. Komatsu, J. Am. Chem. Soc., 2017, 139, 18231–18239.
20. S. Masuda, K. Mori, T. Sano, K. Miyawaki, W.-H. Chiang and H. Yamashita, ChemCatChem, 2018, 10, 3526–3531.
21. T. Komatsu, H. Kobayashi, K. Kusada, Y. Kubota, M. Takata, T. Yamamoto, S. Matsumura, K. Sato, K. Nagaoka and H. Kitagawa, Chem.–Eur. J., 2017, 23, 57–60.
22. B. Huang, H. Kobayashi, T. Yamamoto, S. Matsumura, Y. Nishida, K. Sato, K. Nagaoka, S. Kawaguchi, Y. Kubota and H. Kitagawa, J. Am. Chem. Soc., 2017, 139, 4643–4646.
23. H. Guo, H. Li, K. Jarvis, H. Wan, P. Kunal, S. G. Dunning, Y. Liu, G. Henkelman and S. M. Humphrey, ACS Catal., 2018, 8, 11386–11397.
24. S. García, L. Zhang, G. W. Piburn, G. Henkelman and S. M. Humphrey, ACS Nano, 2014, 8, 11512–11521.
25. X. Yang, Q. Li, E. Lu, Z. Wang, X. Gong, Z. Yu, Y. Guo, L. Wang, Y. Guo, W. Zhan, J. Zhang and S. Dai, Nat. Commun., 2019, 10, 1611.
26. J. Zhang, H. Wang, L. Wang, S. Ali, C. Wang, L. Wang, X. Meng, B. Li, D. S. Su and F. S. Xiao, J. Am. Chem. Soc., 2019, 141, 2975–2983.
27. C. Hernandez Mejia, T. W. van Deelen and K. P. de Jong, Nat. Commun., 2018, 9, 4459.
28. H. Tang, J. Wei, F. Liu, B. Qiao, X. Pan, L. Li, J. Liu, J. Wang and T. Zhang, J. Am. Chem. Soc., 2016, 138, 56–59.
29. L. Liu and A. Corma, Chem. Rev., 2018, 118, 4981–5079.
30. R. Prins, Chem. Rev., 2012, 112, 2714–2738.
31. D. Xu, W. Li, H. Duan, Q. Ge and H. Xu, Catal. Lett., 2005, 102, 229–235.
32. G. Jacobs, J. A. Chaney, P. M. Patterson, T. K. Das and B. H. Davis, Appl. Catal., A, 2004, 264, 203–212.
33. W. Karim, C. Spreafico, A. Kleibert, J. Gobrecht, J. VandeVondele, Y. Ekinci and J. A. van Bokhoven, Nature, 2017, 541, 68–71.
34. C. Spreafico, W. Karim, Y. Ekinci, J. A. van Bokhoven and J. VandeVondele, J. Phys. Chem. C, 2017, 121, 17862–17872.
35. W. C. Conner and J. L. Falconer, Chem. Rev., 1995, 95, 759–788.
36. V. V. Rozanov and O. V. Krylov, Russ. Chem. Rev., 1997, 66, 107–119.
37. S. Ohgoshi, I. Nakamura and Y. wakushima, in Studies in Surface Science and Catalysis, ed. T. lnui, K. Fujimoto, T. Uchijima and M. Masai, Elsevier, 1993, vol. 77, pp. 289–292.
38. J. Im, H. Shin, H. Jang, H. Kim and M. Choi, Nat. Commun., 2014, 5, 3370.
39. H. Nishihara, P.-X. Hou, L.-X. Li, M. Ito, M. Uchiyama, T. Kaburagi, A. Ikura, J. Katamura, T. Kawarada, K. Mizuuchi and T. Kyotani, J. Phys. Chem. C, 2009, 113, 3189–3196.
40. K.-S. Lin, A. K. Adhikari, Y.-H. Su, C.-W. Shu and H.-Y. Chan, Adsorption, 2012, 18, 483–491.
41. Y. Guo, S. Mei, K. Yuan, D.-J. Wang, H.-C. Liu, C.-H. Yan and Y.-W. Zhang, ACS Catal., 2018, 8, 6203–6215.
42. S. Wang, Z.-J. Zhao, X. Chang, J. Zhao, H. Tian, C. Yang, M. Li, Q. Fu, R. Mu and J. Gong, Angew. Chem., Int. Ed., 2019, 131, 7750–7754.
43. H. Nishihara and T. Kyotani, Chem. Commun., 2018, 54, 5648–5673.
44. G. Zhan and H. C. Zeng, Nat. Commun., 2018, 9, 3778.
45. Y. Li and R. T. Yang, J. Phys. Chem. B, 2006, 110, 17175–17181.
46. L. Chen, A. C. Cooper, G. P. Pez and H. Cheng, J. Phys. Chem. C, 2008, 112, 1755–1758.
47. X. Sha, L. Chen, A. C. Cooper, G. P. Pez and H. Cheng, J. Phys. Chem. C, 2009, 113, 11399–11407.
48. T. Huizinga and R. Prins, J. Phys. Chem. C, 1981, 85, 2156–2158.
49. K. Mori, K. Miyawaki and H. Yamashita, ACS Catal., 2016, 6, 3128–3135.
50. S. J. Tauster, S. C. Fung, R. T. K. Baker and J. A. Horsley, Science, 1981, 211, 1121.
51. A. Bruix, J. A. Rodriguez, P. J. Ramírez, S. D. Senanayake, J. Evans, J. B. Park, D. Stacchiola, P. Liu, J. Hrbek and F. Illas, J. Am. Chem. Soc., 2012, 134, 8968–8974.
52. D. J. Chakrabarti and D. E. Laughlin, J. Phase Equilib., 1982, 2, 511–512.
53. B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541.
54. T. Whittaker, K. B. S. Kumar, C. Peterson, M. N. Pollock, L. C. Grabow and B. D. Chandler, J. Am. Chem. Soc., 2018, 140, 16469–16487.
55. B. Delley, J. Chem. Phys., 1990, 92, 508–517.
56. B. Delley, J. Chem. Phys., 2000, 113, 7756–7764.
57. C. Y. Peng, L. Kang, S. Cao, Y. Chen, Z. S. Lin and W. F. Fu, Angew. Chem., Int. Ed., 2015, 54, 15725–15729.
58. K. Fuku, R. Hayashi, S. Takakura, T. Kamegawa, K. Mori and H. Yamashita, Angew. Chem., Int. Ed., 2013, 52, 7446–7450.
59. T. B. Marder, Angew. Chem., Int. Ed., 2007, 46, 8116–8118.
60. A. Staubitz, A. P. M. Robertson and I. Manners, Chem. Rev., 2010, 110, 4079–4124.
61. K. Feng, J. Zhong, B. Zhao, H. Zhang, L. Xu, X. Sun and S.-T. Lee, Angew. Chem., Int. Ed., 2016, 128, 12129–12133.
62. M. Tang, J. Deng, M. Li, X. Li, H. Li, Z. Chen and Y. Wang, Green Chem., 2016, 18, 6082–6090.
63. M. Digne, J. Catal., 2004, 226, 54–68.
64. J. Gu, J. Wang and J. Leszczynski, ACS Omega, 2018, 3, 1881–1888.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sc05612b

---