Collision-induced and complex-mediated roaming dynamics in the H + C₂H₄ → H₂ + C₂H₃ reaction

Abstract

Roaming is a novel mechanism in reaction dynamics. It describes an unusual pathway, which can be quite different from the conventional minimum-energy path, leading to products. While roaming has been reported or suggested in a number of unimolecular reactions, it has been rarely reported for bimolecular reactions. Here, we report a high-level computational study of roaming dynamics in the important bimolecular combustion reaction H + C₂H₄ → H₂ + C₂H₃, using a new, high-level machine learning-based potential energy surface. In addition to the complex-mediated roaming mechanism, a non-complex forming roaming mechanism is found. It can be described as a direct inelastic collision where the departing H atom roams and then abstracts an H atom. We denoted this as “collision-induced” roaming. These two roaming mechanisms have different angular distributions; however, both produce highly internally excited C₂H₃. The roaming pathway leads to remarkably different dynamics as compared with the direct abstraction pathway. A clear signature of the roaming mechanism is highly internally excited C₂H₃, which could be observed experimentally.

---

Introduction

Roaming is a verified unusual pathway leading to unexpected molecular products, which typically bypasses the minimum-energy path associated with a conventional transition state (TS). The first discovery of the roaming mechanism was made more than a decade ago in the photodissociation of H₂CO, where the term “roaming” was coined to describe an alternative pathway for the H₂ + CO molecular channel.^1,2 Such a reaction pathway is initiated by the frustrated dissociation to form radical products, followed by the meandering of the incipient radicals around varied configuration spaces of the moieties in flat regions of the potential energy surface (PES) and ultimately reaching an attractive portion of the PES that leads to intramolecular abstraction and to the molecular products. Since then, the roaming mechanism has attracted much attention, and evidence of roaming has been observed in many other unimolecular dissociation systems^1–16 and also some bimolecular reactions.^17–20

In this work, we report the first full-dimensional reaction dynamics simulations of the important combustion reaction of hydrogen with ethylene, using a new, high-level ab initio PES. These calculations demonstrate the existence of roaming in this bimolecular reaction leading to the molecular hydrogen and vinyl radical. An examination of roaming trajectories uncovers two roaming mechanisms. One is the (usual) complex-mediating one and the second one is non-complex forming. The latter novel mechanism can be described as a direct inelastic collision where the departing H atom roams and then abstracts an H atom. This finding is of general significance because hydrocarbons are ubiquitous and among the most important species in combustion chemistry and atmospheric chemistry.²¹ It is well known that a hydrogen atom might associate with ethylene to form an ethyl radical,^22–27 C₂H₅, which is ∼40 kcal mol⁻¹ below that of H + C₂H₄. A hydrogen atom might also directly abstract another H atom from ethylene via a conventional TS, leading to the vinyl radical and molecular hydrogen.^21,28 The barrier for the direct abstraction of H + C₂H₄ → H₂ + C₂H₃ is roughly 17 kcal mol⁻¹.^26,29

Due to its important role in combustion chemistry,²¹ the kinetics of H + C₂H₄ → C₂H₅/H₂ + C₂H₃ and its reverse have been the subject of interest in both experimental^22–24,28 and theoretical^25–27 investigations for many years. However, the detailed dynamics and reaction mechanism of this fundamentally important reaction remain unclear. Previous theoretical work for the H + C₂H₄ reaction was limited to ab initio calculations of stationary points and reaction paths,^26,27,30 which indicated a direct H atom abstraction pathway leading to H₂ + C₂H₃via a conventional TS, as well as a H atom addition pathway resulting in the ethyl radical, C₂H₅. The reverse decomposition of C₂H₅ can yield H + C₂H₄, but not H₂ + C₂H₃, because no conventional first-order saddle point for the H₂ elimination pathway from the C₂H₅ adduct was found. These quantum chemical calculations explored limited regions of the reaction paths, which were unable to corroborate the reaction mechanism.³¹ Qualitatively, a roaming pathway in alkane dissociation has been suggested.¹⁰ More recently a direct-dynamics study of the unimolecular dissociation of an ethyl radical revealed a roaming pathway leading to H₂ + C₂H₃.¹³ The roaming pathway in this case is perforce the complex-mediated one and thus these calculations could not uncover non-complex forming roaming. In addition, the use of a fairly low level of electronic structure and the propagation of a small number (3600) of trajectories failed to give deep insight and details of the dynamics features, due to the large computational effort this approach entails.

These limited studies of possible roaming in alkyl unimolecular dissociation led us to consider a much more detailed study of the more general bimolecular reaction of an H atom with a hydrocarbon. Specifically, we report a full-dimensional dynamics study of the H + C₂H₄ reaction, employing a new, accurate global PES that describes the C₂H₅ complex as well as a conventional direct abstraction pathway to the H₂ + C₂H₃ products.

The dynamics calculations uncover a collision-induced roaming pathway to these products. This pathway is facilitated by bimolecular collisions, and originates from an extremely short-lived intermediate but by-passes the conventional direct abstraction pathway. Particularly, compared with the unimolecular dissociation of C₂H₅, the bimolecular collision enhanced the roaming pathway by roughly 18% to form H₂ + C₂H₃, due to the fast energy transfer from the collision energy to the internal vibrational excitation of C–H bonds. The details of the roaming pathway are described and in particular an experimentally observable signature of this pathway is reported.

Results and discussion

Full-dimensional potential energy surface

The global PES was fit using the fundamental invariant neural network (FI-NN) approach based on roughly 100 000 ab initio energy points by high level UCCSD(T)-F12a/aug-cc-pVTZ calculations.^32,33 The FI-NN approach uses the fundamental invariants (FIs) as the input vector of the neural network, which is proposed based on the permutationally invariant polynomial (PIP)³⁴ and PIP-NN³⁵ approaches, but minimizes the size of input invariants and efficiently reduces the evaluation time of potential energy, in particular for larger molecular systems with more identical atoms. This fit results in an overall root mean square error (RMSE) of only 13.7 meV (∼0.3 kcal mol⁻¹), representing an unprecedented fitting accuracy for PESs of seven-atom multichannel reactions. Fig. 1 shows relevant stationary-point structures and energies from the PES and direct ab initio calculations, relative to the reagents H + C₂H₄ (with vibrational zero-point energies not included) and corresponding to the relevant product channels. The minimum energy paths were determined by the quadratic steepest descent method.³⁶ As is seen, there is excellent agreement between the PES and UCCSD(T)-F12a/aug-cc-pVTZ results. The maximum fitting error for energy points on the reaction paths is only 0.1 kcal mol⁻¹. The fitting errors of all the data points, optimized geometries and harmonic frequencies of stationary points obtained from the PES and ab initio calculations are shown in the ESI (Fig. S1, S2 and Table S1†). The comparisons made for these critical properties obtained from the current PES and UCCSD(T)-F12a/AVTZ calculations show very good agreement among them.

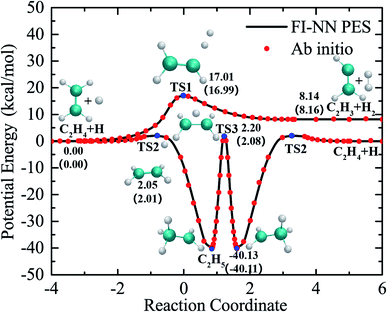Fig. 1 The minimum energy paths of the H + C₂H₄ reaction obtained from the PES (solid lines) and those calculated from the UCCSD(T)-F12a/AVTZ theory (symbols).

As seen in Fig. 1, the collision of H with C₂H₄ can either go over a barrier of 17 kcal mol⁻¹ to directly abstract an H atom from C₂H₄, resulting in H₂ + C₂H₃, or a much lower barrier of roughly 2.0 kcal mol⁻¹ to form the C₂H₅ complex via H atom addition. In the C₂H₅ adduct, which is located at 40 kcal mol⁻¹ below the H + C₂H₄ asymptote, H atom migration can occur between two carbon atoms back and forth via TS3 before decomposition. It is worth noting that there is no direct pathway or conventional first-order saddle point in the reaction leading to H₂ + C₂H₃ from the C₂H₅ complex.

Full-dimensional reaction dynamics simulations

With an accurate, full-dimensional, analytical PES in hand, we can move much further than predicting reaction pathways based on stationary points, and gain deep insight into the reaction mechanisms and also predict observable outcomes of the reaction. To do this, we carried out extensive quasi-classical trajectory (QCT) calculations on the PES, thereby tracking the motion of the atoms. A total of roughly 30 million trajectories were run for C₂H₄ initially in the ground vibrational state, at a collision energy (E_c) of 60 kcal mol⁻¹. Such a high collision energy is also accessible in the experiment.³⁷ Trajectories were also run at collision energies ranging from 30 kcal mol⁻¹ to 70 kcal mol⁻¹. Details of this PES and QCT calculations are given in the ESI.†

The dynamics simulations based on the accurate PES showed that that the major product channel is the hydrogen exchange. As expected, the hydrogen exchange proceeds through a long-lived C₂H₅ complex, in which the incoming H addition to the C–C double bond is followed by another H elimination from the methyl group. During this process, the H atom can also migrate between two carbon atoms before the decomposition of C₂H₅, and finally one H atom of C₂H₄ is substituted by the incoming H atom. The collision between H and C₂H₄ also leads to the direct H atom abstraction in forming the H₂ molecule and C₂H₃, but proceeds through a much higher barrier compared to the H atom addition.

Collision-induced and complex-mediated roaming dynamics

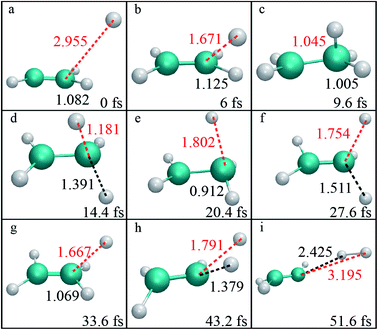
By examination of trajectories, we found a small but significant fraction that leads to H₂via two roaming mechanisms. Snapshots of a typical trajectory illustrating roaming (collision energy of 60 kcal mol⁻¹ with the initial impact parameter b = 0.2 bohr) are shown in Fig. 2. As is shown, the incoming H atom first attacks one carbon atom when approaching ethylene, forming a vibrationally excited C₂H₅ (Fig. 2a–c) in what appears to be simple inelastic scattering. However, subsequently and promptly the H atom detaches from the carbon atom (ethylene), and “roams” almost independently in the region of the C–H bonded complex, which is about to be eliminated (Fig. 2d–f), but finally gets pulled back toward the ethene and picks up a hydrogen atom with an orientation favorable for abstraction to form H₂ (Fig. 2g–i).

Fig. 2 (a–i) Each panel shows the geometry at the reaction time indicated (fs). The internuclear distances (Å) between the incoming H atom and target C atom, and between the detaching H and C atoms are indicated by red and black fonts, respectively.

We found that this typical trajectory finishes within an unexpectedly short reaction time (∼45 fs). The distribution of reaction time for roaming trajectories, which is defined as the duration time for a reactive trajectory proceeding from the reactant side to product side with a distance between two fragments of 6 bohrs, is depicted in Fig. 3, showing a remarkable peak at around 95 fs and a long but small tail up to the time of 4 ps. This feature is quite different from that of a typical complex-forming reaction, which might exhibit much more flat time distributions. Therefore, we also investigated the unimolecular dissociation dynamics of C₂H₅ on this full-dimensional PES. These trajectories were run from the C₂H₅ complex, with the total energy the same as that of the bimolecular collision, and the microcanonical sampling of the initial momenta. As shown in Fig. 3, the reaction time of roaming trajectories from the unimolecular dissociation is distributed over a wide range without any noticeable bias. In addition, we found 18% more probability of roaming trajectories from the bimolecular collision in the reaction leading to H₂ + C₂H₃, than those from the unimolecular dissociation.

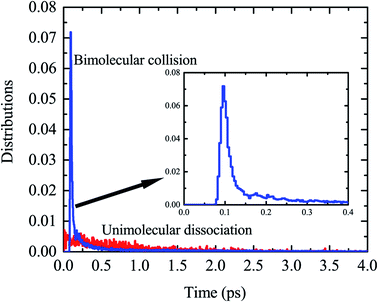Fig. 3 The distributions of reaction time for the H + C₂H₄ bimolecular reaction at E_c = 60 kcal mol⁻¹, together with those for the unimolecular dissociation of C₂H₅ at the same total energy.

Further examination of these trajectories uncovered that the bimolecular collision can facilitate the vibrational excitation of the C–H bonds of the C₂H₅ intermediate in an unexpectedly short time, and thus enhances the roaming process and accelerates the reaction. As shown in the snapshots in Fig. 2, the vibration of one C–H (incoming H) bond is highly excited due to the fast energy transfer from the collision energy, followed by vibrational excitation of another marked C–H bond, and thus the energy from the initial formation of C₂H₅ can be highly localized in the two C–H vibrational modes which facilitates the roaming and intramolecular abstraction. This is quite different from a genuine complex-forming reaction or unimolecular reaction,¹³ in which the intramolecular vibrational energy redistribution among different modes of complex plays an important role. Because of the vibrational excitation of two C–H bonds, the roaming process leading to H₂ + C₂H₃ was finally enhanced and accelerated, resulting in a sharp peak in the reaction time distribution (Fig. 3).

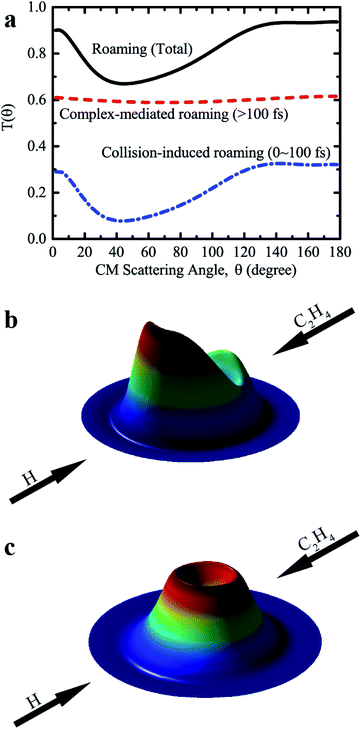
Further analysis revealed that these roaming trajectories were completed in a short reaction time (≤100 fs) yielding mainly the backward-scattered products, as shown in Fig. 4a, with relatively small impact parameters, and also some forward-scattered products for large impact parameter collisions. We name this reaction mechanism as collision-induced roaming (see two complete animations of representative backward and forward scattering trajectories via collision-induced roaming in the ESI†). The unusual roaming pathway was also verified by direct ab initio calculations along selected trajectories. A comparison of potential energies between direct ab initio calculations and fitted results from the FI-NN PES for two representative trajectories (inclusive of the aforementioned trajectory) showing the collision-induced roaming mechanism is displayed in Fig. S3.† The potential energies obtained from the fitted FI-NN PES reproduce considerably well the ab initio data, thereby validating the new findings.

Fig. 4 (a) The angular distribution of H₂ relative to the direction of the incoming H atom, resulting from the collision-induced and complex-mediated roaming mechanisms for the H + C₂H₄ bimolecular reaction at E_c = 60 kcal mol⁻¹. (b) 3D polar plot for the product translational energy and angular distributions via the collision-induced roaming mechanism. (c) The same as (b), except for the complex-mediated roaming mechanism.

When the reaction time increases (>100 fs), these roaming trajectories give rise to a nearly isotropic angular distribution (Fig. 4a), indicating that the long-lived complex-mediated pathway plays a prominent role. Apparently, the scattering with a long-lived complex totally loses the memory of the initial approach direction, and one H atom can also migrate between two carbon atoms and the hydrogen molecule from either two hydrogen atoms of the methyl group of C₂H₅ can be emitted in all the directions without any bias in this complex-mediated roaming mechanism (see one complete animation of the representative complex-mediated roaming trajectory in the ESI†). The total angular distribution of roaming pathways resembles that of collision-induced roaming, due to the isotropic angular distribution of complex-mediated roaming, showing mainly backward scattering as well as substantial contributions from the forward and sideways scattering. 3D polar plots shown in Fig. 4b and c for the product translational energy and angular distributions of H₂ + C₂H₃ from the collision-induced and complex-mediated roaming mechanisms further reflect the remarkably different correlations between the initial (reactant) and final (product) relative velocity vectors.

Roaming versus direct abstraction

It is interesting then to determine the fraction of the roaming pathway at various collision energies, and also the reaction threshold of the roaming pathway. The cross-sections and branching fractions of the direct abstraction and roaming pathways as a function of collision energy are shown in Fig. S4.† We can see that with the increase of the collision energy, the cross-sections of both the direct abstraction and roaming pathways increase, and the branching fraction of the roaming pathway increases as well. The roaming pathway accounts for roughly 16% of the total H₂ + C₂H₃ yield at the collision energy of 60 kcal mol⁻¹. A quite high threshold of roughly 30 kcal mol⁻¹ for the roaming channel is obtained, presumably due to the fact that the product H₂ + C₂H₃ channel lies above the reactants H + C₂H₄ for the title reaction.

As reaction dynamics should be determined by the full-dimensional PES, we have computed and depicted the two-dimensional contour plot of the PES as a function of two CH bonds (RCH₁ and RCH₂) in Fig. S5,† with other coordinates (degrees of freedom) optimized. Note that roaming occurs when the dihedral φ between the plane of C–C–H₁ and C–C–H₂ is larger than 30°, which is quite different from the direct abstraction via TS1 (φ is around 0°), we restricted this dihedral angle to >30° in the optimization to distinguish the roaming channel from the direct abstraction channel. There are 15 degrees of freedom for the H + C₂H₄ reaction, and thus the potential energy optimization performed over these coordinates is highly demanding, which again implies that the current PES is globally smooth and accurate. In addition, the evolution of three typical roaming trajectories is also superimposed on the contour plots of the PES, namely two collision-induced roaming trajectories with an extremely short reaction time and a complex-mediated roaming trajectory with a long-lived complex, as shown in Fig. S5.† As shown in these figures, there is a barrier of around 30 kcal mol⁻¹ from C₂H₅ to H₂ + C₂H₃, which indicates that roaming trajectories can only occur at very high collision energies. To the best of our knowledge, this is also the first time a roaming pathway has been discovered in an endothermic bimolecular reaction. We also investigated the effects of vibrational excitations of various modes of C₂H₄ on the roaming probability. As shown in Fig. S6† for the results at the impact parameter b = 0, we found that the vibrational excitation of C₂H₄ can enhance the roaming reactivity, but is as efficient as the collision energy in enhancing the roaming reactivity.

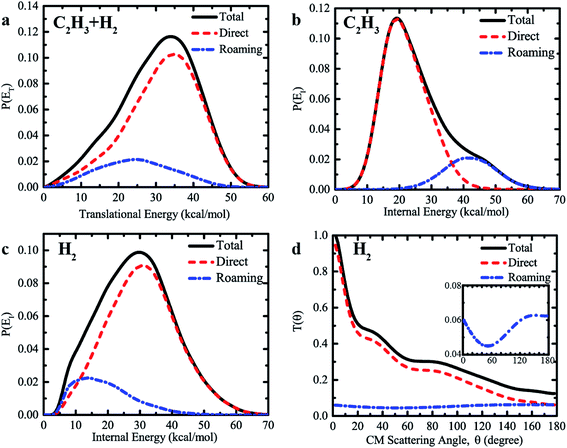
Furthermore, we found substantially different dynamics information produced by the direct abstraction and by the roaming pathway at the collision energy of 60 kcal mol⁻¹. Fig. 5a compares the product translational energy distributions, P(E_T), for the H + C₂H₄ → H₂ + C₂H₃ reaction between the direct abstraction and roaming pathways, together with the total translational energy distributions of the sum of contributions from the two different mechanisms. The P(E_T) from the direct abstraction mechanism has a peak around 35 kcal mol⁻¹, and reaches up to the available energy of roughly 55 kcal mol⁻¹, indicating substantial translational energy release. The behavior of the translational energy distribution of H₂ + C₂H₃ from the direct abstraction pathway supports that the dynamics of this channel is dominated by the exit channel barrier. In contrast, much lower energy is released as the product translational energy via the roaming pathway. As is shown, the translational energy distribution from the roaming pathway peaks at roughly 25 kcal mol⁻¹, and vanishes at the energy of 50 kcal mol⁻¹. The average fraction of the total available energy (50.1 kcal mol⁻¹) released as translational energy from the roaming pathway is 48%, which is lower than the corresponding value of 62% for the direct abstraction. Since the initial formation of the C₂H₅ intermediate, short-lived or long-lived, more energy is channeled into the internal degrees of freedom of C₂H₅, which can also facilitate the high internal (rovibrational) excitation of the products. The total translational energy distribution resembles that from the direct abstraction, due to the relatively small contributions from the roaming pathway.

Fig. 5 (a) Center-of-mass (CM) translational energy distribution of H₂ + C₂H₃ resulting from direct abstraction and roaming pathways at E_c = 60 kcal mol⁻¹. (b) The same as (a), except for the internal energy distribution of C₂H₃. (c) The same as (a), except for the internal energy distribution of H₂. (d) The same as (a), except for the angular distribution of H₂ relative to the direction of the incoming H atom.

We found very different internal energy distributions of the C₂H₃ and H₂ products from the two reaction mechanisms. As shown in Fig. 5b, the internal energy distribution of C₂H₃ from the roaming pathway peaks at a very high energy up to about 42 kcal mol⁻¹, which is remarkably higher than the corresponding result from the direct abstraction. Note that we see much higher internal excitation of C₂H₃ at E_c = 60 kcal mol⁻¹ (corresponding to the photolysis energy of 94.7 kcal mol⁻¹) compared with the limited direct dynamics results of unimolecular dissociation by Matsugi¹³ using even a higher photolysis energy of 114.3 kcal mol⁻¹. The high internal energy region (>40 kcal mol⁻¹) has negligible contributions to the overall internal energy distribution from the direct abstraction. The behavior of distribution curves indicates that much more energy is relaxed into the rovibrational motion of C₂H₃ in the roaming pathway, due to the formation of the highly activated C₂H₅ intermediate. A great fraction (83%) of the available energy is retained in the internal energy of the C₂H₃ radical, given the large number of internal degrees of freedom of C₂H₃. In addition, the large contribution from the roaming pathway at high internal energy gives rise to a shoulder-like structure in the total internal energy distribution above 40 kcal mol⁻¹. Therefore, it is interesting to note that the signature of the roaming mechanism for the H + C₂H₄ → H₂ + C₂H₃ reaction is also manifested as the existence of a distinct shoulder-like feature in the total internal energy distribution of product C₂H₃.

The internal energy distributions of C₂H₃ are in strong contrast to the results of H₂. As shown in Fig. 5c, the distribution of the internal energy of H₂ peaks at roughly 30 kcal mol⁻¹ for the direct abstraction, compared with the corresponding value of 15 kcal mol⁻¹ for the roaming pathway, revealing that the direct abstraction pathway produces H₂ with higher internal energy than that from the roaming pathway. By further comparing the vibrational and rotational state distributions of H₂ (see Fig. S7 and S8†), we found considerably higher vibrational excitation of H₂ and slightly higher rotational excitation of H₂ from the direct abstraction. There are substantial fractions of H₂ in vibrationally excited v = 1 and v = 2 from the direct abstraction, but not the roaming pathway. However, due to the formation of a C₂H₅ intermediate, more available energy is relaxed into the internal degrees of freedom of C₂H₃, leaving very limited rovibrational excitation of H₂ and final translational motion of products from the roaming mechanism.

The angular distributions of H₂ relative to the incoming H resulting from the direct abstraction and roaming mechanisms are displayed in Fig. 5d, together with the total angular distributions of the sum of contributions from the two different mechanisms. The angular distribution for direct H abstraction demonstrates a pronounced forward scattering peak, with relatively small contributions from the sideways and backward scattering. A clear preference for forward scattering implies that stripping plays a dominant role in direct H abstraction of H + C₂H₄ → H₂ + C₂H₃ at the high collision energy of 60 kcal mol⁻¹. The rebound component, which gives reactive scattering in the backward and sideways directions, is quite small. Because of the extremely short reaction time for collision-induced roaming processes, the reaction via roaming results in mainly the backward scattering, with some contributions from both the forward and sideways scattering. This feature is quite different from that of a long-lived complex-forming reaction, for which the angular distribution shows scattering that is symmetric with respect to the forward and backward direction or fully isotropic.

3D polar plots for the product translational energy and angular distributions of H₂ + C₂H₃ arising from the direct abstraction and roaming pathways are shown in Fig. S9.† The very different behaviors of 3D polar plots for the direct abstraction and roaming pathways further reveal a very different partitioning of the total available energy and a correlation between the initial and final relative velocity vectors. The pronounced forward scattering peak for the direct abstraction mainly resides in the high kinetic energy region; however, the mainly backward scattering in the roaming pathway demonstrates relatively lower kinetic energy, suggesting high internal excitation of the products.

Conclusions

The roaming mechanism discovered here for the H + C₂H₄ reaction represents a new pathway in generating molecular hydrogen and vinyl, in addition to direct H abstraction via a conventional transition state. This was accomplished by developing the first fifteen-dimensional PES for the H + C₂H₄ reaction using the FI-NN fitting to a large number of UCCSD(T)-F12a/AVTZ data points, as well as extensive quasi-classical trajectory calculations on this globally accurate PES. We demonstrated that the roaming channel proceeds via a frustrated ethylene + H dissociation from the initially formed C₂H₅ intermediate, followed by the roaming of the H atom to find a favorable orientation to abstract a hydrogen atom from ethene. This is also the first time that a roaming mechanism has been discovered in an endothermic bimolecular reaction.

A collision-induced roaming mechanism is proposed for the H + C₂H₄ reaction, with an unexpectedly short reaction time as well as short-lived C₂H₅ intermediates, because of the efficient and prompt energy transfer from the collision energy to the vibrational excitations of two C–H bonds of the methyl group, exhibiting mainly the backward scattering with some contributions from the forward and sideways scattering. This mechanism is quite different from the complex-mediated roaming mechanism, as found in many unimolecular dissociation systems, where the energy from the initial formation of the long-lived C₂H₅ complex should not be highly localized in specific modes, and the intramolecular vibrational energy redistribution of the complex dominates. A nearly isotropic angular distribution is seen in this complex-mediated roaming mechanism for this reaction. Therefore, the roaming mechanism presented here for the title system is enhanced and accelerated by the bimolecular collision, compared with the unimolecular dissociation. We anticipate that the collision-induced roaming mechanism discovered here also applies to other bimolecular reactions, which is of general significance for our understanding of chemical reactions as well as combustion processes.

Moreover, distinct dynamics information from the roaming and direct abstraction mechanisms was observed in our full-dimensional dynamics simulations. Due to contributions from both the collision-induced and complex-mediated roaming mechanisms, the roaming pathway results in mainly the backward scattering but with substantial contributions from the forward and sideways scattering. In strong contrast, the stripping mechanism dominates in the direct abstraction channel at high collision energy, showing pronounced forward scattering. Compared to the direct abstraction channel, the roaming pathway results in less energy release in product translational motion and internal degrees of freedom of H₂, but predominantly more internal energy of C₂H₃, leading to a clear shoulder-like structure in the total internal energy distribution of C₂H₃ for the title reaction. Note that there is H atom scrambling in roaming trajectories, and thus one can perform an experiment of D + C₂H₄, and detect the H₂ product to investigate dynamical details of roaming, which can be distinguished from the HD product arising from the direct abstraction mechanism. We expect that these predictions can motivate a further dynamical platform of experiment for this important bimolecular reaction in combustion.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China under Grant No. 21722307, 21673233, 21873016, and 21688102, the National Key R&D Program of China (No. 2018YFA0306503), the Strategic Priority Research Program (XDB17010200) of the Chinese Academy of Sciences, the Fundamental Research Funds for the Central Universities (No. DUT18ZD202), and LiaoNing Revitalization Talents Program (XLYC1907190).

References

1. D. Townsend, S. A. Lahankar, S. K. Lee, S. D. Chambreau, A. G. Suits, X. Zhang, J. Rheinecker, L. B. Harding and J. M. Bowman, Science, 2004, 306, 1158.
2. J. M. Bowman, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 16061–16062.
3. M. P. Grubb, M. L. Warter, H. Xiao, S. Maeda, K. Morokuma and S. W. North, Science, 2012, 335, 1075–1078.
4. J. M. Bowman and P. L. Houston, Chem. Soc. Rev., 2017, 46, 7615–7624.
5. P. L. Houston and S. H. Kable, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 16079.
6. B. R. Heazlewood, M. J. T. Jordan, S. H. Kable, T. M. Selby, D. L. Osborn, B. C. Shepler, B. J. Braams and J. M. Bowman, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 12719.
7. B. Fu, B. C. Shepler and J. M. Bowman, J. Am. Chem. Soc., 2011, 133, 7957–7968.
8. N. Ekanayake, T. Severt, M. Nairat, N. P. Weingartz, B. M. Farris, B. Kaderiya, P. Feizollah, B. Jochim, F. Ziaee, K. Borne, K. P. Raju, K. D. Carnes, D. Rolles, A. Rudenko, B. G. Levine, J. E. Jackson, I. Ben-Itzhak and M. Dantus, Nat. Commun., 2018, 9, 5186.
9. E. Kamarchik, L. Koziol, H. Reisler, J. M. Bowman and A. I. Krylov, J. Phys. Chem. Lett., 2010, 1, 3058–3065.
10. L. B. Harding and S. J. Klippenstein, J. Phys. Chem. Lett., 2010, 1, 3016–3020.
11. Y.-C. Han, B. C. Shepler and J. M. Bowman, J. Phys. Chem. Lett., 2011, 2, 1715–1719.
12. S. Maeda, T. Taketsugu and K. Morokuma, J. Phys. Chem. Lett., 2012, 3, 1900–1907.
13. A. Matsugi, J. Phys. Chem. Lett., 2013, 4, 4237–4240.
14. P.-Y. Tsai, K.-C. Hung, H.-K. Li and K.-C. Lin, J. Phys. Chem. Lett., 2014, 5, 190–195.
15. N. Ekanayake, M. Nairat, N. P. Weingartz, M. J. Michie, B. G. Levine and M. Dantus, J. Chem. Phys., 2018, 149, 244310.
16. Y.-C. Han, P.-Y. Tsai, J. M. Bowman and K.-C. Lin, Phys. Chem. Chem. Phys., 2017, 19, 18628–18634.
17. B. Joalland, Y. Shi, A. Kamasah, A. G. Suits and A. M. Mebel, Nat. Commun., 2014, 5, 4064.
18. K. M. Christoffel and J. M. Bowman, J. Phys. Chem. A, 2009, 113, 4138–4144.
19. Á. Bencsura and G. Lendvay, J. Phys. Chem. A, 2012, 116, 4445–4456.
20. A. Li, J. Li and H. Guo, J. Phys. Chem. A, 2013, 117, 5052–5060.
21. J. Warnatz, in Rate Coefficients in the C/H/O System, ed. W. C. Gardiner, Springer New York, New York, NY, 1984, pp. 197–360.
22. J. V. Michael, D. T. Osborne and G. N. Suess, J. Chem. Phys., 1973, 58, 2800–2806.
23. P. D. Lightfoot and M. J. Pilling, J. Phys. Chem., 1987, 91, 3373–3379.
24. M. A. Hanning-Lee, N. J. B. Green, M. J. Pilling and S. H. Robertson, J. Phys. Chem., 1993, 97, 860–870.
25. W. L. Hase, D. M. Ludlow, R. J. Wolf and T. Schlick, J. Phys. Chem., 1981, 85, 958–968.
26. A. M. Mebel, K. Morokuma and M. C. Lin, J. Chem. Phys., 1995, 103, 3440–3449.
27. J. Villà, J. C. Corchado, A. González-Lafont, J. M. Lluch and D. G. Truhlar, J. Phys. Chem. A, 1999, 103, 5061–5074.
28. J. Shao, R. Choudhary, Y. Peng, D. F. Davidson and R. K. Hanson, J. Phys. Chem. A, 2019, 123, 15–20.
29. J. Agarwal, J. M. Turney and H. F. Schaefer, J. Phys. Chem. Lett., 2011, 2, 2587–2592.
30. W. L. Hase, G. Mrowka, R. J. Brudzynski and C. S. Sloane, J. Chem. Phys., 1978, 69, 3548–3562.
31. A. F. Wagner, L. A. Rivera-Rivera, D. Bachellerie, J. W. Perry and D. L. Thompson, J. Phys. Chem. A, 2013, 117, 11624–11639.
32. K. Shao, J. Chen, Z. Zhao and D. H. Zhang, J. Chem. Phys., 2016, 145, 071101.
33. B. Fu and D. H. Zhang, J. Chem. Theory Comput., 2018, 14, 2289–2303.
34. B. J. Braams and J. M. Bowman, Int. Rev. Phys. Chem., 2009, 28, 577–606.
35. B. Jiang, J. Li and H. Guo, Int. Rev. Phys. Chem., 2016, 35, 479–506.
36. J. Q. Sun and K. Ruedenberg, J. Chem. Phys., 1993, 99, 5257–5268.
37. J. M. Smith, M. Nikow, J. Ma, M. J. Wilhelm, Y.-C. Han, A. R. Sharma, J. M. Bowman and H.-L. Dai, J. Am. Chem. Soc., 2014, 136, 1682–1685.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sc05951b

---