Open Access Article
Open Access ArticleChemical control of competing electron transfer pathways in iron tetracyano-polypyridyl photosensitizers†
Kristjan
Kunnus
 *a,
Lin
Li‡
a,
Charles J.
Titus
*a,
Lin
Li‡
a,
Charles J.
Titus
 b,
Sang Jun
Lee
b,
Sang Jun
Lee
 c,
Marco E.
Reinhard
c,
Marco E.
Reinhard
 a,
Sergey
Koroidov§
a,
Kasper S.
Kjær¶
a,
Sergey
Koroidov§
a,
Kasper S.
Kjær¶
 a,
Kiryong
Hong||
a,
Kathryn
Ledbetter
ab,
William B.
Doriese
d,
Galen C.
O'Neil
a,
Kiryong
Hong||
a,
Kathryn
Ledbetter
ab,
William B.
Doriese
d,
Galen C.
O'Neil
 d,
Daniel S.
Swetz
d,
Joel N.
Ullom
d,
Dale
Li
c,
Kent
Irwin
bc,
Dennis
Nordlund
c,
Amy A.
Cordones
*a and
Kelly J.
Gaffney
*a
d,
Daniel S.
Swetz
d,
Joel N.
Ullom
d,
Dale
Li
c,
Kent
Irwin
bc,
Dennis
Nordlund
c,
Amy A.
Cordones
*a and
Kelly J.
Gaffney
*a
aStanford PULSE Institute, SLAC National Accelerator Laboratory, Stanford University, Menlo Park, California 94025, USA. E-mail: kkunnus@stanford.edu; acordon@slac.stanford.edu; kgaffney@slac.stanford.edu
bDepartment of Physics, Stanford University, Stanford, California 94305, USA
cSLAC National Accelerator Laboratory, Menlo Park, California 94025, USA
dNational Institute of Standards and Technology, Boulder, CO 80305, USA
First published on 16th April 2020
Abstract
Photoinduced intramolecular electron transfer dynamics following metal-to-ligand charge-transfer (MLCT) excitation of [Fe(CN)4(2,2′-bipyridine)]2− (1), [Fe(CN)4(2,3-bis(2-pyridyl)pyrazine)]2− (2) and [Fe(CN)4(2,2′-bipyrimidine)]2− (3) were investigated in various solvents with static and time-resolved UV-Visible absorption spectroscopy and Fe 2p3d resonant inelastic X-ray scattering (RIXS). This series of polypyridyl ligands, combined with the strong solvatochromism of the complexes, enables the 1MLCT vertical energy to be varied from 1.64 eV to 2.64 eV and the 3MLCT lifetime to range from 180 fs to 67 ps. The 3MLCT lifetimes in 1 and 2 decrease exponentially as the MLCT energy increases, consistent with electron transfer to the lowest energy triplet metal-centred (3MC) excited state, as established by the Tanabe–Sugano analysis of the Fe 2p3d RIXS data. In contrast, the 3MLCT lifetime in 3 changes non-monotonically with MLCT energy, exhibiting a maximum. This qualitatively distinct behaviour results from a competing 3MLCT → ground state (GS) electron transfer pathway that exhibits energy gap law behaviour. The 3MLCT → GS pathway involves nuclear tunnelling for the high-frequency polypyridyl breathing mode (hν = 1530 cm−1), which is most displaced for complex 3, making this pathway significantly more efficient. Our study demonstrates that the excited state relaxation mechanism of Fe polypyridyl photosensitizers can be readily tuned by ligand and solvent environment. Furthermore, our study reveals that extending charge transfer lifetimes requires control of the relative energies of the 3MLCT and the 3MC states and suppression of the intramolecular distortion of the acceptor ligand in the 3MLCT excited state.
Introduction
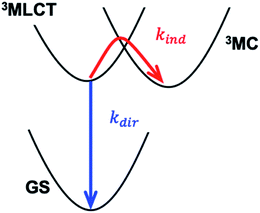
Transition metal complexes with strong charge transfer absorption bands in the visible spectral region can be utilized as photosensitizers for solar energy conversion applications.1 Conventional molecular photosensitizers use noble metals, such as Ru, leading to higher costs and motivating the identification of photosensitizers using abundant metals, such as Fe.2–5 Development of Fe-based photosensitizers has been inhibited by the rapid deactivation of the light absorbing metal-to-ligand charge-transfer (MLCT) states. For instance, the MLCT relaxation occurs in ∼100 fs with unit quantum yield for the Fe analogs of the conventional Ru polypyridyl photosensitizers, and results in the conversion of electronic energy to heat.6–8 Extending the lifetime of MLCT excited states has, therefore, been recognized as one of the key challenges to developing functional Fe-based photosensitizers. This work focuses on understanding the chemical properties dictating MLCT relaxation mechanisms and lifetimes for a class of solvatochromic Fe tetracyano-polypyridyl complexes by tuning ligand composition and solvent environment.The nano- and micro-second lifetimes of Ru(II) and Os(II) polypyridyl complexes usually follow the energy gap law, where the lifetimes increase as the MLCT energy is increased.9–11 This behavior results from a direct 3MLCT → ground state (GS) pathway in the inverted Marcus region, as illustrated by the kdir relaxation pathway in Scheme 1 where the intramolecular electron transfer involves the electron transitioning from the polypyridyl π* orbital to the Fe 3d t2g orbital. In this regime, nuclear tunneling along the high-frequency ligand breathing modes is crucial. Prolonged MLCT lifetimes have been demonstrated by either increasing delocalization of the excited electron over a larger ligand framework, or by increasing the rigidity of the ligand with chemical links between pyridyl rings.12 In contrast, short-lived Fe(II) polypyridyl complexes follow an indirect relaxation pathways facilitated by metal-centered states (MC), as illustrated by kind in Scheme 1 where the intramolecular electron transfer involves the electron transitioning from the polypyridyl π* orbital to the Fe 3d eg orbital.8,13–16 Understanding and controlling the MLCT relaxation rates through low-energy MC states is currently an active field of research.17 A variety of synthetic strategies aiming to modify the Fe–ligand bonding and motions have resulted in longer MLCT lifetimes. These range from destabilization of the MC states by high-symmetry ligand environment with improved π-back-bonding18,19 and introduction of halogen ligand-substituents to sterically hinder the motions facilitating MLCT → MC relaxation.20,21 The most successful approach to date was introduced by the Wärnmark group22–24 and followed by the group of Gros.25,26 This approach utilizes strongly σ-donating N-heterocyclic carbene ligands to destabilize the MC excited states. Chábera et al. reported a luminescent ferric complex with a ligand-to-metal charge-transfer (LMCT) lifetime of 100 ps (ref. 27) and an analogous ferrous complex with 528 ps MLCT lifetime.28 This was further improved by Kjær et al., who demonstrated a 2 ns LMCT lifetime in a Fe(III) complex capable of photoreduction and oxidation.29 Very recently, the longest lifetime of a MLCT-like state in an Fe(II) complex, ∼2.5 ns, was reported by Braun et al.30
The synthetic strategies discussed above focus on manipulating the Fe–ligand bond, reflecting the current consensus that the indirect pathway dominates the MLCT relaxation in Fe photosensitizers. However, cases where the direct pathway is the limiting mechanism for MLCT relaxation, as expected when MLCT states are much lower energy than MC states, have not yet been sufficiently addressed. In a detailed study of Ru cyano-polypyridyl complexes Indelli et al.31 observed a transition between regimes dominated by either the direct or indirect pathway by tuning the MLCT energy. Here we report a similar systematic study on Fe tetracyano-polypyridyl complexes. Consequently, we demonstrate a transition between the direct and indirect pathways controlled by ligand- and solvent-dependent MLCT energy. Distinct from the nano- and microsecond MLCT lifetimes of Ru cyano-polypyridyl complexes, the transition in the studied Fe systems occurs for sub-ns MLCT lifetimes. Therefore, the direct relaxation pathway becomes limiting at significantly shorter MLCT lifetimes than for Ru complexes, indicating that the control of the direct pathway, in addition to the indirect pathway, is crucial for achieving extended MLCT lifetimes.
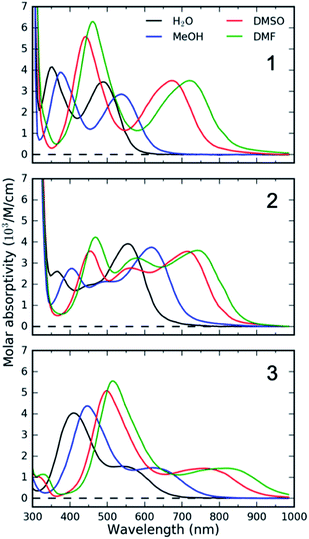
Specifically, we carried out systematic measurements of MLCT lifetime and MLCT and MC state energies for solvatochromic complexes 1, 2, and 3 (Scheme 2) in a large range of solvents. In addition to the study of Indelli et al.,31 this investigation is inspired by early UV-Visible transient absorption experiments on complex 1 by Winkler et al.32 The introduction of strongly coordinating cyanide ligands serves the purpose of increasing the ligand field, thus destabilizing the MC excited states and slowing the MLCT → MC relaxation pathways for this class of complexes. Previously, we have used femtosecond resolution X-ray emission spectroscopy (XES) and UV-Visible transient absorption spectroscopy to investigate the relaxation dynamics and mechanism of the MLCT excited state in Fe cyano-bpy complexes.8,14,33–35 We demonstrated that complex 1 in dimethysulfoxide (DMSO) has a MLCT lifetime of ∼19 ps,36 which has been further confirmed in the work of Jay et al.37 However, the strong solvatochromism of the MLCT state of 138 influences the MLCT relaxation dynamics. We found that in water, the MLCT of 1 decays in ∼100 fs to a 3MC intermediate with a 13 ps lifetime.39 Based on the conjecture that only the MLCT states display significant solvatochromism, that is the 3MC energy and the 3MLCT → 3MC reorganization does not change significantly with changes in polypyridyl ligand and solvent, we focus here on a systematic investigation of the MLCT excitation energy dependence of the MLCT lifetime and relaxation mechanism. We achieve a large range of MLCT energies by changing the electron accepting polypyridyl ligand and the solvent (Fig. 1). Very recently, the effect of polypyridyl ligand π-system conjugation to the MLCT energies was investigated in Fe cyano-polypyridyl complexes computationally.40
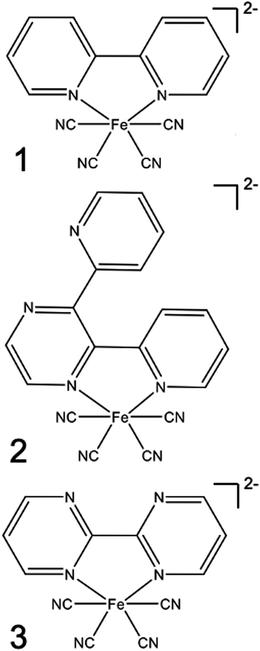 | ||
| Scheme 2 Structural formulas of the complexes [Fe(CN)4(2,2′-bipyridine)]2− (1), [Fe(CN)4(2,3-bis(2-pyridyl)pyrazine)]2− (2), and [Fe(CN)4(2,2′-bipyrimidine)]2−(3). | ||
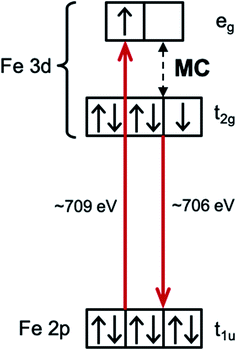
Interpreting the influence of ligand substitution and solvent on the lifetime also requires understanding their influence on the reorganization energy of the MLCT state and the thermodynamic driving force for 3MC formation. The intra- and intermolecular reorganization energies for the MLCT state can be extracted from UV-Visible spectra. This approach has been successfully employed in the Mulliken–Hush analysis of inter-valence electron transfer rates in mixed-valence complexes,41–44 as well as in the vibronic band shape analysis of the absorption and fluorescence spectra.45–48 This approach, however, does not access the driving force and the reorganization energy associated with the MLCT → MC electron transfer reaction. Dipole transitions to the relevant MC states are Laporte and spin-forbidden, and they overlap energetically with the dipole allowed MLCT absorption bands. In order to access the energetics of the relevant MC excited states we utilize resonant inelastic X-ray scattering (RIXS) at the Fe L3-edge (700–715 eV). RIXS provides a powerful spectroscopic technique for measuring low-energy excitations of matter with the element selectivity of X-ray spectroscopy.49 RIXS at 3d transition metal L-edges involves resonant dipole allowed 2p → 3d excitation and de-excitation transitions (Scheme 3). The RIXS final states do not contain a core-hole and the resulting RIXS spectra are dominated by the relevant MC valence excited states.50 Additionally, because MC and MLCT states have electrons excited to different unoccupied molecular orbitals, different final excited states can be accessed by tuning the incident X-ray photon energy to different X-ray absorption resonances. Therefore, a RIXS spectrum measured at the metal L-edge 3d absorption resonance (white line) is dominated by the MC final states, while being completely free of MLCT final states.51 This makes metal L-edge RIXS a highly suitable probe of MC excited state energetics and enables the Tanabe–Sugano analysis of the Fe polypyridyl complexes, a capability we utilize in the present work.
Experimental
Samples
We purchased the potassium salts of complexes 1, 2 and 3 from Allichem Inc. and used them without further purification.52 Complexes 2 and 3 were examined with elemental analysis: 2 (C18H16O3FeK2N8) calc.: C, 37.25; H, 3.82; N, 19.30%. Found: C, 37.04%; H, 2.34%; N, 19.50%. 3 (C12H12O3FeK2N8) calc.: C, 32.01; H, 2.69; N, 24.88%. Found: C, 31.81%; H, 2.18%; N, 24.63%. We exchanged the K+ with tetrabutylammonium (TBA+) to increase the solubility in organic solvents. Firstly, the protonated form of the complexes were prepared following a published procedure.53 The resulting product was reacted with a TBA–OH (Sigma-Aldrich) methanol solution in a stoichiometric amount, which was subsequently dried to retrieve the complexes in the TBA+-form.23UV-Visible absorption
We conducted femtosecond time-resolved UV-Visible transient absorption (TA) and steady-state UV-Visible absorption measurements on various solutions of complexes 1, 2 and 3. We used K+-salts for aqueous solutions and TBA+-salts for all other solutions. Complex 1 was studied in H2O, methanol (MeOH), dimethysulfoxide (DMSO), acetonitrile (MeCN) and dimethylformamide (DMF). Complex 2 was studied in H2O, MeOH, DMSO and DMF. Complex 3 was studied in H2O, MeOH, butanol, hexanol, dichloromethane (DCM), propylene carbonate, pyridine, benzonitrile, DMSO, MeCN, acetone and DMF. All solvents were reagent grade. Concentrations of all the solutions were adjusted to have a maximum absorption in the visible region between 0.3–0.5 OD for a 100 μm path length (concentrations of a few mM). For TA measurements of aqueous solutions we used a recirculating sheet jet with a 100 μm thickness. For all the other samples we used a vibrating 100 μm thick quartz cell without flowing the solution. We measured all of the steady state UV-Visible absorption spectra using a 100 μm quartz cell with a Cary 50 spectrophotometer.TA experiments were carried out using an amplified Ti:sapphire laser system (Coherent Mantis or Vitara oscillator with Coherent Legend Elite Duo) with a 5 kHz repetition rate, 800 nm central wavelength, 2 mJ pulse energy and 40 fs FWHM pulse duration. A portion of the laser pumped an optical parametric amplifier (Spectra-Physics OPA-800C) to generate a near IR signal and idler. We used sum-frequency generation of the signal and 800 nm light to make 500–550 nm pump pulses and frequency doubling of the signal to generate 610–820 nm pump pulses. The pump pulse was directed to the sample through a delay stage, a 2.5 kHz chopper, and a lens, resulting in pump pulses with 200–300 μm focal diameter (FWHM) and fluences of 1–5 mJ cm−2. The pump was overlapped with a white light probe pulse (via supercontinuum generation in 4 mm of CaF2) at the sample position. The probe was transmitted through the sample and imaged on a spectrometer (Horiba Jobin Yvon iHR320, grating 150 grooves per mm). The probe spectrum was recorded at 5 kHz with a NMOS linear image sensor (Hamamatsu, S8380-512Q) simultaneously over the whole 350–750 nm spectral range. The instrument response function was estimated to be ∼100 fs (FWHM). We measured UV-Visible absorption spectra of the solutions before and after the TA experiments to check for photodamage. Most samples showed no optical degradation, with a few exhibiting a few percent reduction in absorption. The differential absorbance (ΔA) was calculated as ΔA = log(Ioff/Ion), where Ion and Ioff are the pumped and unpumped intensity, respectively. We used the cross-phase modulation signal between the pump and the probe to determine t0 for each probe wavelength and to correct for the group velocity dispersion.
Resonant inelastic X-ray scattering
RIXS experiments were carried out at beamline 10−1 at the SSRL storage ring at SLAC National Accelerator Laboratory. Here we utilized a novel energy dispersive X-ray spectrometer based on transition-edge sensor (TES) technology54–57 with >100 times higher detection efficiency compared to conventional grating spectrometers. The endstation and the soft X-ray TES spectrometer57 are described in more detail by Titus et al.58 and Lee et al.59 The employed TES signal processing techniques are described by Fowler et al.60 Powder samples of K+-salt complexes were pressed on carbon tape attached to a sample holder. Samples were kept at room temperature. RIXS maps over the complete Fe L2,3-edge were collected by scanning the incident X-ray energy from 700–735 eV (0.1 eV step, 0.2 eV monochromator bandwidth) and raster scanning over 20 spots on each sample (two monochromator scans on each spot, 1 mm × 1 mm X-ray footprint, average incident flux ∼5 × 1010 photons per s). No beam damage effects were observed in the collected data. The RIXS maps of each sample were acquired for 2 h and 45 min. The incident photon energy was calibrated to match the Fe L3-edge eg-resonance of K4[Fe(CN)6] published by Hocking et al.61X-ray photon energies detected by the TES spectrometer were calibrated with a procedure described by Fowler et al.62 that gives 0.4 eV uncertainty in absolute photon energies. This calibration was refined for Fe 2p3d emission by shifting the elastically scattered photon energy to match the incident photon energy. We estimate that the uncertainty in relative photon energies is below 0.1 eV. The spectral response of the TES spectrometer was measured at 750 eV with elastically scattered light from a gold film (see ESI†). The energy resolution of the TES spectrometer at the Fe L-edge was 2.3 eV (FWHM); over shorter acquisition times but in otherwise similar operating conditions, it is as good as 1.8 eV.59
Results
Below we present the results from three different sets of experiments. Firstly, we performed femtosecond resolution UV-Visible transient absorption (TA) measurements to determine the excited state relaxation dynamics and the 3MLCT lifetimes. Secondly, we carried out band shape analysis of the steady state UV-Visible absorption spectra to quantify the 1/3MLCT excitation energies and the associated intra- and inter-molecular reorganization energies. Thirdly, we performed steady state Fe 2p3d RIXS experiments to establish the MC excited state energies. Results from each of these experiments are described in detail in the following sub-sections.UV-Visible transient absorption
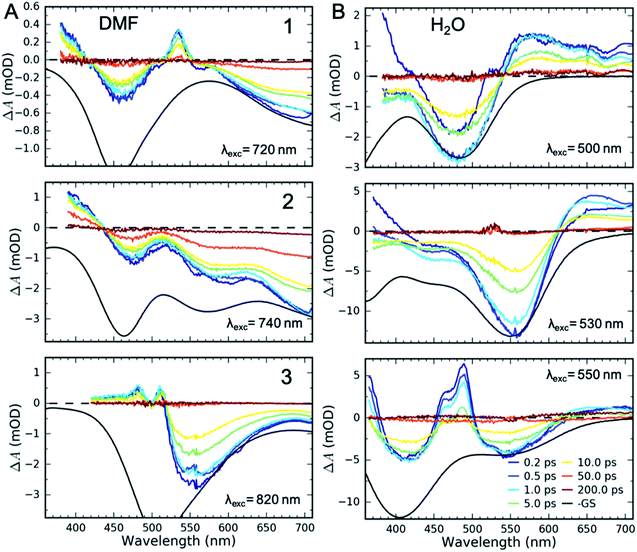
UV-Visible TA experiments were used to probe the photoexcited MLCT state relaxation dynamics of 1, 2 and 3 in various solvents with different solvatochromic effects. In Fig. 2, we display time-resolved difference TA spectra of 1, 2 and 3 in DMF and H2O. Of all the studied solvents, DMF and H2O solutions have the most red- and blue-shifted MLCT absorption spectra, respectively. The complete collection of measured TA data is included in the ESI (Fig. S1–S3†).Characteristic absorption signatures of the MLCT excited states are well established for transition metal polypyridyl complexes and these are very similar to the absorption features of reduced polypyridyl radicals.63,64 This facilitates robust assignment of MLCT relaxation dynamics. We assign the excited state absorption (ESA) feature positioned below 550 nm for all of the measured datasets to intra-ligand transitions of the reduced polypyridyl radicals in the MLCT excited state of the complexes.65 These MLCT ESA features decay concomitantly with the ground state bleach (GSB) recovery in most of the studied solutions of all three complexes (Fig. 2, except 1 and 2 in H2O). In addition, we observe dynamic shifting of the MLCT ESA features on the one ps time scale which we assign to solvation and vibrational energy redistribution (ESI, Fig. S1–S3†). The simultaneous decay of ESA and GSB features confirms no population accumulates in metal-centred (MC) excited states. This is consistent with the previously published results of 1 in acetone and DMSO.32,36 This does not mean MC excited states do not participate in the MLCT relaxation mechanism, only that the lifetime of the 3MLCT state significantly exceeds the lifetime of any MC excited state.
Qualitatively different dynamics are observed in H2O and MeOH solutions of 1 and 2 where the MLCT ESA features associated with the polypyridyl radical decay on the sub-picosecond timescale without GSB recovery. Our recent work combining TA with time-resolved Fe Kα/Kβ X-ray emission spectroscopy (XES) measurements of 1 in H2O determined that the MLCT state decays into a triplet metal-centred (3MC) excited state.39 This 3MC intermediate in 1 lacks the signature ESA of a reduced ligand, while exhibiting a broad ESA to the red of the GSB. Given the similarity of the transient absorption spectra for 1 and 2 in H2O, we also assign the ∼10 ps intermediate of 2 in H2O and MeOH solutions to a 3MC excited state. We observe no population of MC states in any solution of 3.
To accurately determine the time scales of the observed population dynamics, we carried out global fitting of the TA data. The singular value decomposition-based kinetics fitting procedure utilized here has become a standard method for the analysis of 2D TA data.66 A description of the procedure and all of the fit results are presented in the ESI.† A summary of the extracted 3MLCT lifetimes is presented in Table 1. 1 and 2 show more than two orders of magnitude decrease in the 3MLCT lifetime as the MLCT energy increases in hydrogen bonding solvents. 3MLCT lifetimes decrease from 29 ps to 180 fs for complex 1, and from 67 ps to 300 fs for 2. The 67 ps 3MLCT lifetime of 2 in DMF is the longest 3MLCT lifetime observed in polypyridyl-containing Fe complexes.
| Complex | Solvent | E v (eV) | λ cl (eV) | λ q (eV) | E 0 (eV) | Excitation energy | τ (ps) | |
|---|---|---|---|---|---|---|---|---|
| nm | eV | |||||||
| 1 | H2O | 2.64 | 0.33 | 0.19 | 2.12 | 500 | 2.48 | 0.18 |
| MeOH | 2.41 | 0.32 | 0.17 | 1.92 | 520 | 2.38 | 0.22 | |
| DMSO | 1.95 | 0.20 | 0.13 | 1.62 | 670 | 1.85 | 16.5 | |
| MeCN | 1.94 | 0.20 | 0.13 | 1.61 | 720 | 1.73 | 19.3 | |
| DMF | 1.83 | 0.19 | 0.12 | 1.52 | 720 | 1.73 | 28.7 | |
| 2 | H2O | 2.33 | 0.28 | 0.13 | 1.92 | 530 | 2.34 | 0.30 |
| MeOH | 2.10 | 0.24 | 0.12 | 1.73 | 610 | 2.03 | 0.61 | |
| DMSO | 1.83 | 0.19 | 0.11 | 1.53 | 720 | 1.73 | 31.6 | |
| DMF | 1.77 | 0.19 | 0.12 | 1.47 | 740 | 1.68 | 66.9 | |
| 3 | H2O | 2.32 | 0.42 | 0.18 | 1.71 | 550 | 2.25 | 11.9 |
| MeOH | 2.04 | 0.33 | 0.16 | 1.55 | 625 | 1.98 | 16.9 | |
| Butanol | 1.88 | 0.25 | 0.16 | 1.48 | 690 | 1.80 | 20.0 | |
| Hexanol | 1.76 | 0.24 | 0.16 | 1.36 | 670 | 1.85 | 19.9 | |
| DCM | 1.79 | 0.23 | 0.16 | 1.40 | 730 | 1.70 | 20.7 | |
| Propylene carbonate | 1.74 | 0.23 | 0.16 | 1.36 | 750 | 1.65 | 21.4 | |
| Pyridine | 1.76 | 0.24 | 0.16 | 1.36 | 750 | 1.65 | 22.6 | |
| Benzonitrile | 1.75 | 0.24 | 0.16 | 1.35 | 760 | 1.63 | 18.5 | |
| DMSO | 1.73 | 0.22 | 0.15 | 1.36 | 775 | 1.60 | 19.4 | |
| MeCN | 1.73 | 0.24 | 0.15 | 1.34 | 775 | 1.60 | 13.5 | |
| Acetone | 1.70 | 0.25 | 0.16 | 1.29 | 775 | 1.60 | 16.6 | |
| DMF | 1.64 | 0.19 | 0.16 | 1.29 | 820 | 1.51 | 12.7 | |
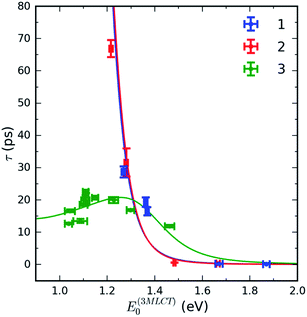
Surprisingly, complex 3 exhibits qualitatively different behaviour. The 3MLCT lifetime dependence of 3 on the 3MLCT energy is non-monotonic and changes only by a factor of two in all solvents (Table 1). The 3MLCT lifetime increases from ∼12 ps at the lowest 3MLCT energy in DMF and reaches a maximum in pyridine solution (∼23 ps), and then it decreases again to ∼12 ps in H2O. The non-monotonic dependence of the 3MLCT lifetime on MLCT excitation energy provides clear evidence that a second relaxation pathway dominates for smaller MLCT excitation energies. The nature of this secondary relaxation pathway and why it depends strongly on polypyridyl ligand will be explained in the Discussion section.
UV-Visible absorption
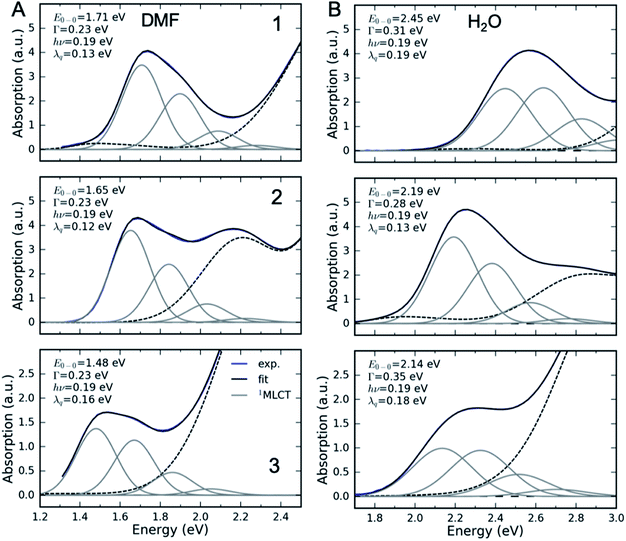
We carried out a vibronic band shape analysis of the lowest-energy 1MLCT UV-Visible absorption features to obtain the 1,3MLCT energies and the reorganization energies associated with the GS → MLCT transitions in all the investigated solutions. Similar vibronic band shape analysis has been successfully applied to the MMCT bands of mixed-valence complexes46 and MLCT bands of Fe and Ru polypyridyl complexes.13,67,68 In particular, the assignment of the band shape of the lowest-energy absorption to a vibronic progression is supported by the polarized low temperature spectra of [Fe(bpy)3]2+,69 and by TDDFT calculations presented in the ESI.† The latter support the conclusion that only one 1MLCT excited state makes a significant contribution to the lowest energy absorption band for all three complexes (ESI, Table S2†). We therefore model the lowest energy absorption with a single high-frequency quantum mode and with an effective classical mode that includes all the low-frequency modes. As clearly shown in Fig. 3, the lowest energy 1MLCT absorption can be accurately fit to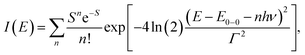 | (1) |
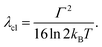 | (2) |
The fully relaxed (minimum) energy of the 1MLCT state with respect to the ground state is E(01MLCT) = E0–0 − λcl = E(v1MLCT) − λq − λcl, where E(01MLCT) and E(v1MLCT) correspond to the structurally relaxed and vertical 1MLCT energies. The energetic parameters directly extracted from the fit are E0–0, Γ, λq and hν (Fig. 3). These fit parameters provide the required input to calculate λcl, E(01MLCT), and E(v1MLCT), all of which are reported in Table 1. Within the experimental uncertainty, the high-frequency vibrational mode has the same frequency of hν = 0.19 ± 0.01 eV (1530 ± 80 cm−1) for 1, 2, and 3 in all solvents. Note that this vibrational frequency agrees well with the polypyridyl intra-ligand breathing mode observed in previous studies of Ru and Fe polypyridyl complexes.13,69,70 For example, a 0.199 eV (1607 cm−1) high frequency mode dominates the vibronic structure of the lowest energy 1MLCT band of [Fe(bpy)3]2+.13
In several measured UV-Visible absorption spectra a low-energy tail is present that cannot be described by the 1MLCT vibronic structure or Gaussian broadening (see 1 in DMF, Fig. 3). Such low-energy features have been observed in Fe polypyridyl complexes and were assigned to the 3MLCT state.13,69 In particular, Kober et al. carried out a detailed analysis of the low-temperature [Fe(bpy)3]2+ UV-Visible absorption spectrum and found that the 3MLCT state is 0.25 eV below the 1MLCT state with a similar vibronic structure.69 Therefore, in the fitting of all our room temperature spectra, we have included a peak that is 0.25 eV below the 1MLCT and has an identical shape to the 1MLCT. This successfully describes the low-energy tail in all the measured spectra. The observed intensity of the 3MLCT peak is typically >50 times smaller than the 1MLCT intensity. Energy of the 3MLCT state is thus E(03MLCT) = E(01MLCT) − 0.25 eV.
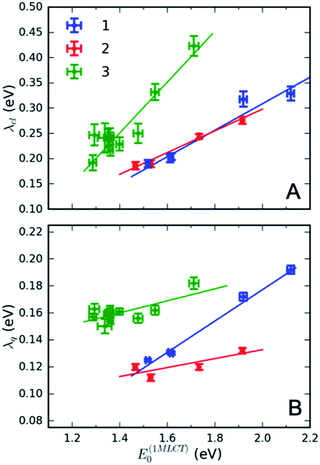
Fig. 4 presents several relevant trends in the classical and high-frequency reorganization energies. Firstly, the solvatochromic effect is strongest in 1, with ΔE0 ≡ E(01MLCT)(H2O) − E(01MLCT)(DMF) = 0.6 eV. In comparison, ΔE0 = 0.45 eV and 0.42 eV in 2 and 3, respectively. These observations are consistent with the study of Toma et al.38 Secondly, the classical reorganization energy λcl increases linearly with the solvatochromic effect (Fig. 4A), but the proportionality between energies is roughly a factor of two larger for 3. Thirdly, the reorganization energy of the high frequency mode λq is significant, accounting for 30–40% of the total reorganization energy. The respective Huang–Rhys factors are between 0.6 and 1. Most importantly, we observe that the reorganization energies of 3 are consistently larger than in 1 and 2. This is particularly evident for λq in weakly interacting solvents (small E(01MLCT)). Although λcl of 3 is similar to 1 and 2 in weakly interacting solvents, in H2O it is significantly larger than in 1 and 2. This likely reflects the two H-bond accepting nitrogen sites on the pyrimidine ligand of 3. As will be addressed in the Discussion section, these larger reorganization energies for the MLCT state of 3 provides an explanation for the qualitatively different MLCT relaxation mechanism for complex 3. Parameters of the linear fits in Fig. 4 are included in the ESI.†
Interestingly, the intramolecular high frequency mode reorganization energy, λq, shows an unexpected difference between protic and aprotic solvents. This can be seen clearly in Fig. 3 when comparing the vibronic progression for complex 1 in DMF and H2O. The MLCT excitation energy also shows strong variation between protic and aprotic solvents. This blue shift in protic solvents has been attributed to direct H-bonding to the cyano ligands that weakens the Fe–CN π-donation and increases the Fe–CN π-back-donation, lowering the energy of the t2g orbitals, and increasing the energy required for the MLCT excitation.39 This change in Fe–CN interaction should also impact the extent of π-back-donation to the polypyridyl ligand, and potentially modify the spatial extent of the MLCT excited state and the magnitude of λq. Additionally, the vibronic progression does not appear distinctly in H2O, as shown in Fig. 3B. This makes differentiating the classical and quantum mechanical reorganization energies more challenging and may provide a systematic uncertainty in the fit not fully captured by the error bars.
Resonant inelastic X-ray scattering
Measuring the relative energy of the 3MLCT and 3MC states is critical to understanding the 3MLCT → 3MC relaxation pathway. While the 1,3MLCT energy can be extracted from the UV-Visible absorption spectrum, this is not possible for the weakly absorbing MC excited states that overlap with the intense 1MLCT bands. Instead, we use Fe 2p3d RIXS to establish the energetics of the MC excited states (Fig. 5). Different from UV-Visible absorption, the Raman selection rules for 2p3d RIXS results predominantly in scattering to MC excited states, providing direct access to the energies of these states. The RIXS spectra in Fig. 5A were recorded at the Fe L3-edge X-ray absorption white-line resonance around 709 eV resulting from transitions from 2p to unoccupied 3d (eg) orbitals (see ESI†). The measured RIXS spectra of all three complexes are very similar. The spectra are dominated by an inelastic scattering feature at ∼3 eV energy transfer, indicated by the light blue line in Fig. 5A. Weak elastic scattering is clearly visible at 0 eV energy transfer. At higher energy transfer, there is a broad feature (centred at 6–7 eV) that can be assigned to decays from occupied ligand orbitals generating ligand-to-metal charge transfer (LMCT) excited states.51,71 For the purposes of this work, we focus on the energies of the MC states observed in the RIXS spectra and in particular to the dominant MC RIXS feature at 3 eV. To accurately obtain these energies we carried out the peak fitting and Tanabe–Sugano analysis described below.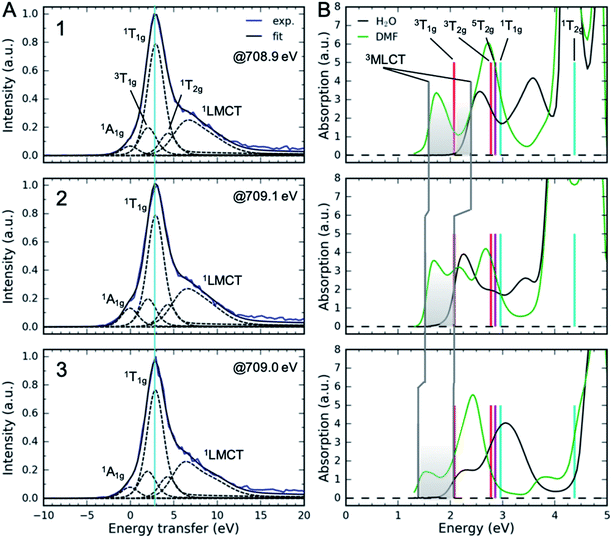 | ||
| Fig. 5 (A) Fe 2p3d resonant inelastic X-ray scattering spectra at the Fe L3-edge eg-resonance. The light blue line corresponds to the vertical energy of the dominant 1T1g RIXS feature. (B) UV-Visible absorption spectra and the vertical energies of MC excited states derived from RIXS (Table 2, average values). Also shown is the 5T2g energy at 2.86 eV. Vertical gray lines correspond to 3MLCT vertical energies. Shaded area shows the range of vertical 3MLCT energies from DMF to H2O covered in different solutions. Labels 1, 2 and 3 correspond to the complexes. | ||
Assignment of the ∼3 eV MC RIXS feature is based on the Tanabe–Sugano energy matrices72 and on previous RIXS studies of similar low spin Fe2+ complexes.51,71 Within the octahedral approximation, the dominant RIXS spectral peak can be unambiguously assigned to the 1T1g (t2g5eg1) excited state. Based on the Tanabe–Sugano energy matrices and the measured TES spectrometer instrument response, we fit the RIXS spectrum using only the octahedral ligand field 10Dq as a free fit parameter to describe the MC state energies (Racah parameters B and C are known, see ESI† for a detailed description of the analysis). The fit provides a robust and accurate measure of 1T1g excited state energy (Fig. 5A). This energy, in conjunction with the known values for the Racah B and C parameters, allows us to calculate the energies of other MC states in the ground state geometry, including the lowest energy 3MC state that is relevant for the indirect MLCT relaxation channel shown in Scheme 1. We label each octahedral MC state manifold according to its octahedral term symbol.
The resulting MC excited state energies extracted from the fitting of the RIXS spectra are summarized in Table 2. The MC state energies of the different complexes are identical within the experimental uncertainties (∼0.1 eV); therefore, all three ligands have very similar ligand fields. We take the averages of these as the best estimate for all three complexes. Thus, any changes in the MLCT lifetime between the complexes should not be related to differences in MC excited state energies. The value of 10Dq, as expected, lies between [Fe(bpy)3]2+ (10Dq = 2.8 eV (ref. 73)) and [Fe(CN)6]4− (10Dq = 4.2 eV (ref. 74)). The lowest energy MC state is 3T1g at 2.07 ± 0.1 eV, which is ∼0.7 eV lower than the second lowest MC state 3T2g. With the vertical MC state energies from Table 2, we can establish the relative energetics of the low energy MC excited states with respect to the MLCT states observed in the UV-Visible absorption (Fig. 5B). The shaded area in Fig. 5B shows the range of vertical 3MLCT energies in various solvents due to the solvatochromic effect. Clearly, the 3MLCT energies are within the same range of the 3T1g energy, providing further support for the importance of the 3MLCT → 3T1g relaxation pathway.
| Complex | 10Dq (eV) | 3T1g (eV) | 3T2g (eV) | 1T1g (eV) | 1T2g (eV) |
|---|---|---|---|---|---|
| 1 | 3.24 | 2.09 | 2.80 | 2.98 | 4.40 |
| 2 | 3.22 | 2.08 | 2.78 | 2.97 | 4.38 |
| 3 | 3.19 | 2.04 | 2.75 | 2.93 | 4.34 |
| Average | 3.22 | 2.07 | 2.78 | 2.96 | 4.38 |
Discussion
Fig. 6 shows the dependence of the 3MLCT lifetime on the 3MLCT minimum energy E(03MLCT). It is evident that complexes 1 and 2 show very similar behaviour, expressed by an exponential increase in lifetime as E(03MLCT) decreases. In contrast, complex 3 behaves differently and shows a non-monotonic lifetime dependence on E(03MLCT). The appearance of a maximum in the lifetime indicates that two independent 3MLCT relaxation pathways occur for 3. The rate of one pathway becomes slower as the reactant 3MLCT energy decreases, whereas the second pathway becomes faster. We demonstrate below that this variation in the 3MLCT lifetimes of complexes 1–3 in a variety of solvents can be understood within the framework of non-adiabatic electron transfer theory. Within this model, we describe two competing pathways for relaxation: an indirect pathway 3MLCT → 3MC → GS involving a 3MC intermediate and a direct relaxation pathway 3MLCT → GS. The indirect 3MLCT → 3MC → GS pathway involves thermally activated barrier crossing in the Marcus normal region, −ΔG > λ. Alternatively, the direct 3MLCT → GS pathway resides in the Marcus inverted region, −ΔG < λ, where nuclear tunneling in high-frequency vibrational modes critically influences the relaxation rate.The total rate of 3MLCT decay is the sum of a direct and an indirect relaxation rate, kdir and kind, shown in Scheme 1:
| ktot = kdir + kind. | (3) |
To address both the classical and quantum mechanical reorganization, we have used the non-adiabatic electron transfer theory developed by Marcus, Jortner and co-workers,75–77
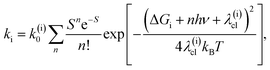 | (4) |
The direct pathway influences strongly the 3MLCT relaxation rate only for complex 3 for the smaller values of the driving force. Nonetheless, evaluation of the 3MLCT → GS rates is more straightforward than the indirect 3MLCT → 3MC rates, because the relevant driving force and reorganization energies can be extracted directly from the UV-Visible absorption spectrum within the Condon approximation. The driving force of the direct pathway in eqn (4) is ΔGdir = − E(03MLCT). Reorganization energies λ(dir)cl = λcl and λq depend linearly on E(01MLCT), described by the fits shown in Fig. 4 for each complex 1, 2 and 3 (ESI, Table S3†). The value of hν extracted from the UV-Visible spectra is constant for all complexes and solutions. This leaves only one free fit parameter, the reaction rate pre-factor, k(dir)0 = (8 ± 1) × 1012 Hz.
The indirect pathway dictates the MLCT relaxation for 1 and 2 in all the solvents we investigated and also determines the MLCT relaxation for complex 3 in solvents where the 3MLCT → 3MC driving force is large. For the indirect pathway, ΔGind = E(03MC) − E(03MLCT)and λ(ind)cl = λ(inner)cl + λcl, where E(03MC) is the 3MC state minimum energy and λ(inner)cl is the inner coordination sphere reorganization energy. E(03MC) and λ(inner)cl are treated as free fit parameters with the identical values for complexes 1–3 and are extracted from the fit of the kind to eqn (4). As noted, the classical reorganization energy λ(ind)cl has two prominent origins, λ(inner)cl and λcl. The constant inner coordination sphere reorganization energy, λ(inner)cl, is associated with the changes in metal–ligand bond lengths and angles upon formation of the 3MC state. The ligand and solvent dependent outer sphere reorganization energy, λcl, is mostly associated with solvation of the 3MLCT state and is extracted from the UV-Visible spectroscopy, identical to the treatment of the direct pathway (Fig. 4). This analysis provides a pre-exponential factor k(ind)0 = (2.1 ± 1.5) × 1013 Hz, a reorganization energy of λ(inner)cl = 0.34 ± 0.16 eV, and E(03MC) = 1.32 ± 0.05 eV.
The reasonableness of the four parameters extracted from the Marcus–Jortner analysis, k(dir)0, k(ind)0, λ(inner)cl and E(03MC) warrant discussion. k(dir)0 is 10–50 times smaller than determined by Indelli et al.31 for Ru dicyano-bipyridine and tricyano-terpyridine complexes. Given that k0 ∝ |V|2 (V is electronic coupling), the smaller pre-factor reflects, at least in part, the smaller spin–orbit coupling in Fe complexes than Ru complexes. The value of λ(inner)cl is consistent with the large changes in inner coordination sphere geometry between the singlet ground state and the 3MC structure predicted by theoretical calculations for polypyridyl 3MC states.73 While we do not have an additional means of experimentally determining the value for E(03MC), we can compare the vertical 3MC state energy for the ground state geometry, E(v3T1g) = 2.07 ± 0.1 eV, extracted from the RIXS measurement, to the 3MC energy at the 3MLCT geometry, E3(MLCT3MC) = E(03MC) + λ(ind)cl + λq = (2.0 − 2.3) ± 0.2 eV, extracted from the rate model analysis and UV-Visible absorption. These values fall in the same range, therefore confirming that the barrierless region of the indirect pathway corresponds to a resonance between the 3MLCT state and the 3T1g manifold.
Given the several assumptions in the modelling, the extracted parameters from the fit in Fig. 6 are likely not unique. However, we can reliably draw some qualitative conclusions. First, inclusion of the 3MLCT → GS pathway explains the difference between complex 3 and complexes 1 and 2. The direct 3MLCT → GS pathway is more prominent in 3 because of the larger λq values in weakly interacting solvents (Fig. 4B). The relatively slow change of the 3MLCT lifetimes at E(03MLCT) < 1.25 eV in 3 is due to compensation of the driving force decrease by the increase in λcl. The model predicts that complex 3 at E(03MLCT) > 1.35 eV has a longer 3MLCT lifetimes than 1 and 2, as observed experimentally, primarily because of the larger classical reorganization energies for complex 3.
The validity of a statistical reaction rate model also warrants comment. Foremost, the large range of lifetimes motivates the Marcus–Jortner analysis. Since the equilibration of the 3MLCT state should occur within a few picoseconds, the assumption of a statistical reaction appears appropriate for most of the relaxation rates. For the fastest MLCT decays, Marcus–Jortner theory will break down, but this most strongly influences the exponential pre-factor and has minimal impact on the free energy values extracted from the analysis.
Closing remarks
We have explored the MLCT excitation energy dependence of the 3MLCT lifetime of heteroleptic Fe tetracyano-polypyridyl complexes by varying the polypyridyl ligand and the solvent to determine how these chemical properties dictate electron transfer rate. These variations generated an eV span of electron transfer driving force and resulted in 3MLCT lifetimes ranging from 0.18 to 67 ps. Over this range, we found that 3MLCT relaxation can proceeds via two competing electron transfer pathways: a direct 3MLCT → GS pathway where the electron in a ligand π* orbital transfers to an Fe t2g orbital and an indirect 3MLCT → 3MC pathway where the electron in a ligand π* orbital transfers to an Fe eg orbital. The latter electron transfer takes place in a normal Marcus regime with a rate that decreases as E(03MLCT) decreases. The reorganization energy for this pathway is large due to considerable intramolecular reorganization associated with the occupation of an anti-bonding eg orbital in the 3MC state. The direct 3MLCT → GS electron transfer takes place in an inverted Marcus regime, with the solvent and the polypyridyl intra-ligand breathing mode reorganizations being coupled to the back-electron transfer. In solvents with smaller MLCT excitation energies, the MLCT relaxation mechanism for [Fe(CN)4(2,2′-bipyrimidine)]2− (complex 3) resembles the energy gap law behaviour of many Ru and Os polypyridyl photosensitizers where the direct pathway dominates the 3MLCT relaxation. The observed 3MLCT lifetimes can be quantitatively described within the framework of a nonadiabatic Marcus–Jortner electron transfer model that includes a classical mode and a single high-frequency quantum mode.We have used Fe 2p3d RIXS measurements to directly probe the low-energy MC excited states that cannot be accessed with conventional UV-Visible spectroscopic methods. Tanabe–Sugano analysis of the experimental Fe 2p3d RIXS data enabled us to determine the approximate octahedral ligand field energy and the energies of all relevant MC states. Comparison of these MC energies to the reorganization energy and equilibrated 3MC energy extracted from the Marcus theory analysis of the MLCT relaxation rate confirms the indirect relaxation pathway proceeds through the lowest energy metal-centered triplet state. The application of RIXS to study chemically relevant systems, often with dilute concentrations and of limited sample quantity, is significantly constrained due to the small cross-sections of RIXS processes and the low efficiencies of soft X-ray spectrometers. The high-efficiency TES spectrometer utilized in this work is expected to considerably expand the applicability of RIXS for studies of chemically relevant systems.
Within the mechanistic model proposed in this work, we consider the factors behind the record-long charge-transfer lifetimes observed in Fe N-heterocyclic carbenes.28,29 The 528 ps 3MLCT lifetime reported by Chábera et al. for a ferrous heterocyclic carbene complexes with low MLCT energy (∼800 nm) agrees well with the model presented here.28 Our model predicts that a similar lifetime can be achieved for Fe tetracyano-polypyridyl complexes if the polypyridyl ligand is modified to have the same MLCT energy, but minimal ligand breathing mode distortion in order to suppress the direct pathway. Curiously, the situation differs for the ferric heterocyclic carbene, where a 2 ns LMCT excited state lifetime has been observed.29 Arrhenius analysis reveals a much smaller free energy barrier (ΔG# = 0.03 eV) for the ferric carbene complex than for the longest MLCT lifetime reported here dominated by the indirect pathway (ΔG# ≈ 0.15 eV for complex 2 in DMF). Instead, the long LMCT lifetime results from the very small pre-exponential factor in the relaxation rate of ∼109 Hz, compared to the ∼1013 Hz we observe for ferrous tetracyano-polypyridyl complexes. This indicates that a key factor behind the record lifetimes in ferric carbene complexes is the spin-forbidden two-electron 2LMCT–4MC electronic coupling, which is apparently 100 times smaller than the spin-allowed one-electron 3MLCT–3MC electronic coupling in similar ferrous complexes.
This work demonstrates that lowering the MLCT energy by decreasing the ligand acceptor orbital energy and the solvent interactions effectively suppresses the indirect 3MLCT → 3MC → GS relaxation pathway and extends the 3MLCT state lifetimes. However, we also observed a change in this behaviour for very low energy MLCT states (E(01MLCT) < 1.5 eV), where decreasing MLCT energy increases the decay rate via the direct 3MLCT → GS pathway, consistent with the well-established energy gap law.9–11 This direct relaxation pathway was not the focus of previous studies of Fe polypyridyl complexes, as the indirect mechanism was reported to dominate in prior systems. Our investigation finds that in addition to suppressing the indirect pathway, factors that decrease the rate of the direct relaxation pathway must also be considered, such as decreasing the solvent and ligand related reorganization energies. Here, synthetic strategies previously devised to slow the rate of MLCT → GS relaxation in 4d and 5d polypyridyl complexes warrant investigation. These include increasing delocalization of the excited electron over a larger ligand framework and increasing the rigidity of the ligand with chemical links between pyridyl rings.12 Both strategies result in longer MLCT lifetimes by decreasing the Huang–Rhys parameter of the intra-ligand vibrational modes, and are therefore expected to be generally effective in supressing the direct relaxation pathway for Fe photosensitizers with low MLCT energy.
Author contributions
KK, AAC and KJG wrote the manuscript with input from all the authors. LL, AAC and KJG conceived the idea and selected the molecules for study. KK, AAC and MER carried out the UV-Visible experiments. KK, SJL, DN, CJT, AAC, SK, KH, KSK and KL carried out the RIXS experiments. KK analyzed the UV-Visible data. KK and CJT analyzed the RIXS data. WBD, GCO, DSS, JNU, DL, KI developed and constructed the TES spectrometer.Conflicts of interest
The authors declare no conflict of interests.Acknowledgements
This work was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Chemical Sciences, Geosciences, and Biosciences Division. Use of the Stanford Synchrotron Radiation Lightsource, SLAC National Accelerator Laboratory, is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Contract No. DE-AC02-76SF00515. LL is supported by the Knut and Alice Wallenberg Foundation Postdoctoral Scholarship Program “The MAX IV synchrotron radiation facility program” (KAW 2012.0359). SK would like to thank the Knut and Alice Wallenberg Foundation (KAW 2014.0370) for financial support. KSK acknowledges the support of the Carlsberg Foundation and the Danish Council for Independent Research. We gratefully acknowledge Joe Fowler, Gene Hilton, Carl Reintsema, and Dan Schmidt in the NIST Quantum Sensors Project for their contribution to the development of the TES spectrometer. KK is thankful for Dr Yizhu Liu for the advice on the counterion exchange procedure.References
- K. Hara and S. Mori, in Handbook of Photovoltaic Science and Engineering, John Wiley & Sons, Ltd, Chichester, UK, 2011, pp. 642–674 Search PubMed.
- Y. Liu, P. Persson, V. Sundström and K. Wärnmark, Acc. Chem. Res., 2016, 49, 1477–1485 CrossRef CAS PubMed.
- W. Zhang and K. J. Gaffney, Acc. Chem. Res., 2015, 48, 1140–1148 CrossRef CAS PubMed.
- C. S. Ponseca, P. Chábera, J. Uhlig, P. Persson and V. Sundström, Chem. Rev., 2017, 117, 10940–11024 CrossRef CAS PubMed.
- J. K. McCusker, Science, 2019, 363, 484–488 CrossRef CAS PubMed.
- T. J. Meyer, Pure Appl. Chem., 1986, 58, 1193–1206 CAS.
- A. Hauser, Top. Curr. Chem., 2004, 234, 155–198 CrossRef CAS.
- J. K. McCusker, K. N. Walda, R. C. Dunn, J. D. Simon, D. Magde and D. N. Hendrickson, J. Am. Chem. Soc., 1993, 115, 298–307 CrossRef CAS.
- R. Englman and J. Jortner, Mol. Phys., 1970, 18, 145–164 CrossRef CAS.
- J. V. Caspar and T. J. Meyer, J. Phys. Chem., 1983, 87, 952–957 CrossRef CAS.
- E. M. Kober, J. V. Caspar, R. S. Lumpkin and T. J. Meyer, J. Phys. Chem., 1986, 90, 3722–3734 CrossRef CAS.
- J. A. Treadway, B. Loeb, R. Lopez, P. A. Anderson, F. R. Keene and T. J. Meyer, Inorg. Chem., 1996, 35, 2242–2246 CrossRef CAS PubMed.
- W. Gawelda, A. Cannizzo, V. T. Pham, F. van Mourik, C. Bressler and M. Chergui, J. Am. Chem. Soc., 2007, 129, 8199–8206 CrossRef CAS PubMed.
- W. Zhang, R. Alonso-Mori, U. Bergmann, C. Bressler, M. Chollet, A. Galler, W. Gawelda, R. G. Hadt, R. W. Hartsock, T. Kroll, K. S. Kjær, K. Kubiček, H. T. Lemke, H. W. Liang, D. a. Meyer, M. M. Nielsen, C. Purser, J. S. Robinson, E. I. Solomon, Z. Sun, D. Sokaras, T. B. van Driel, G. Vankó, T.-C. Weng, D. Zhu and K. J. Gaffney, Nature, 2014, 509, 345–348 CrossRef CAS PubMed.
- K. S. Kjær, T. B. Van Driel, T. C. B. Harlang, K. Kunnus, E. Biasin, K. Ledbetter, R. W. Hartsock, M. E. Reinhard, S. Koroidov, L. Li, M. G. Laursen, F. B. Hansen, P. Vester, M. Christensen, K. Haldrup, M. M. Nielsen, A. O. Dohn, M. I. Pápai, K. B. Møller, P. Chabera, Y. Liu, H. Tatsuno, C. Timm, M. Jarenmark, J. Uhlig, V. Sundstöm, K. Wärnmark, P. Persson, Z. Németh, D. S. Szemes, É. Bajnóczi, G. Vankó, R. Alonso-Mori, J. M. Glownia, S. Nelson, M. Sikorski, D. Sokaras, S. E. Canton, H. T. Lemke and K. J. Gaffney, Chem. Sci., 2019, 10, 5749–5760 RSC.
- K. Zhang, R. Ash, G. S. Girolami and J. Vura-Weis, J. Am. Chem. Soc., 2019, 141, 17180–17188 CrossRef CAS PubMed.
- O. S. Wenger, Chem.–Eur. J., 2019, 25, 6043–6052 CrossRef CAS PubMed.
- L. L. Jamula, A. M. Brown, D. Guo and J. K. McCusker, Inorg. Chem., 2014, 53, 15–17 CrossRef CAS PubMed.
- A. Britz, W. Gawelda, T. A. Assefa, L. L. Jamula, J. T. Yarranton, A. Galler, D. Khakhulin, M. Diez, M. Harder, G. Doumy, A. M. March, É. Bajnóczi, Z. Németh, M. Pápai, E. Rozsályi, D. Sárosiné Szemes, H. Cho, S. Mukherjee, C. Liu, T. K. Kim, R. W. Schoenlein, S. H. Southworth, L. Young, E. Jakubikova, N. Huse, G. Vankó, C. Bressler and J. K. McCusker, Inorg. Chem., 2019, 58, 9341–9350 CrossRef CAS.
- S. G. Shepard, S. M. Fatur, A. K. Rappé and N. H. Damrauer, J. Am. Chem. Soc., 2016, 138, 2949–2952 CrossRef CAS.
- S. M. Fatur, S. G. Shepard, R. F. Higgins, M. P. Shores and N. H. Damrauer, J. Am. Chem. Soc., 2017, 139, 4493–4505 CrossRef CAS PubMed.
- Y. Liu, T. Harlang, S. E. Canton, P. Chábera, K. Suárez-Alcántara, A. Fleckhaus, D. A. Vithanage, E. Göransson, A. Corani, R. Lomoth, V. Sundström and K. Wärnmark, Chem. Commun., 2013, 49, 6412 RSC.
- Y. Liu, K. S. Kjaer, L. A. Fredin, P. Chábera, T. Harlang, S. E. Canton, S. Lidin, J. Zhang, R. Lomoth, K.-E. Bergquist, P. Persson, K. Wärnmark and V. Sundström, Chem.–Eur. J., 2015, 21, 3628–3639 CrossRef CAS PubMed.
- T. C. B. Harlang, Y. Liu, O. Gordivska, L. A. Fredin, C. S. Ponseca, P. Huang, P. Chábera, K. S. Kjaer, H. Mateos, J. Uhlig, R. Lomoth, R. Wallenberg, S. Styring, P. Persson, V. Sundström and K. Wärnmark, Nat. Chem., 2015, 7, 883–889 CrossRef CAS PubMed.
- L. Liu, T. Duchanois, T. Etienne, A. Monari, M. Beley, X. Assfeld, S. Haacke and P. C. Gros, Phys. Chem. Chem. Phys., 2016, 18, 12550–12556 RSC.
- M. Darari, E. Domenichini, A. Francés-Monerris, C. Cebrián, K. Magra, M. Beley, M. Pastore, A. Monari, X. Assfeld, S. Haacke and P. C. Gros, Dalton Trans., 2019, 48, 10915–10926 RSC.
- P. Chábera, Y. Liu, O. Prakash, E. Thyrhaug, A. El Nahhas, A. Honarfar, S. Essén, L. A. Fredin, T. C. B. Harlang, K. S. Kjær, K. Handrup, F. Ericson, H. Tatsuno, K. Morgan, J. Schnadt, L. Häggström, T. Ericsson, A. Sobkowiak, S. Lidin, P. Huang, S. Styring, J. Uhlig, J. Bendix, R. Lomoth, V. Sundström, P. Persson and K. Wärnmark, Nature, 2017, 543, 695–699 CrossRef PubMed.
- P. Chábera, K. S. Kjaer, O. Prakash, A. Honarfar, Y. Liu, L. A. Fredin, T. C. B. Harlang, S. Lidin, J. Uhlig, V. Sundström, R. Lomoth, P. Persson and K. Wärnmark, J. Phys. Chem. Lett., 2018, 9, 459–463 CrossRef PubMed.
- K. S. Kjær, N. Kaul, O. Prakash, P. Chábera, N. W. Rosemann, A. Honarfar, O. Gordivska, L. A. Fredin, K.-E. Bergquist, L. Häggström, T. Ericsson, L. Lindh, A. Yartsev, S. Styring, P. Huang, J. Uhlig, J. Bendix, D. Strand, V. Sundström, P. Persson, R. Lomoth and K. Wärnmark, Science, 2019, 363, 249–253 CrossRef PubMed.
- J. D. Braun, I. B. Lozada, C. Kolodziej, C. Burda, K. M. E. Newman, J. van Lierop, R. L. Davis and D. E. Herbert, Nat. Chem., 2019, 11, 1144–1150 CrossRef CAS PubMed.
- M. T. Indelli, C. A. Bignozzi, F. Scandola and J.-P. Collin, Inorg. Chem., 1998, 37, 6084–6089 CrossRef CAS PubMed.
- J. R. Winkler, C. Creutz and N. Sutin, J. Am. Chem. Soc., 1987, 109, 3470–3471 CrossRef CAS.
- W. Gawelda, A. Cannizzo, V.-T. Pham, F. van Mourik, C. Bressler and M. Chergui, J. Am. Chem. Soc., 2007, 129, 8199–8206 CrossRef CAS PubMed.
- C. Bressler, C. Milne, V.-T. Pham, A. Elnahhas, R. M. van der Veen, W. Gawelda, S. Johnson, P. Beaud, D. Grolimund, M. Kaiser, C. N. Borca, G. Ingold, R. Abela and M. Chergui, Science, 2009, 323, 489–492 CrossRef CAS PubMed.
- G. Auböck and M. Chergui, Nat. Chem., 2015, 7, 629–633 CrossRef PubMed.
- W. Zhang, K. S. Kjær, R. Alonso-Mori, U. Bergmann, M. Chollet, L. A. Fredin, R. G. Hadt, R. W. Hartsock, T. Harlang, T. Kroll, K. Kubiček, H. T. Lemke, H. W. Liang, Y. Liu, M. M. Nielsen, P. Persson, J. S. Robinson, E. I. Solomon, Z. Sun, D. Sokaras, T. B. Van Driel, T. C. Weng, D. Zhu, K. Wärnmark, V. Sundström and K. J. Gaffney, Chem. Sci., 2016, 8, 515–523 RSC.
- R. M. Jay, S. Eckert, V. Vaz da Cruz, M. Fondell, R. Mitzner and A. Föhlisch, Angew. Chem., Int. Ed., 2019, 58, 10742–10746 CrossRef CAS PubMed.
- H. E. Toma and M. S. Takasugi, J. Solution Chem., 1983, 12, 547–561 CrossRef CAS.
- K. S. Kjær, K. Kunnus, T. C. B. Harlang, T. B. Van Driel, K. Ledbetter, R. W. Hartsock, M. E. Reinhard, S. Koroidov, L. Li, M. G. Laursen, E. Biasin, F. B. Hansen, P. Vester, M. Christensen, K. Haldrup, M. M. Nielsen, P. Chabera, Y. Liu, H. Tatsuno, C. Timm, J. Uhlig, V. Sundstöm, Z. Németh, D. S. Szemes, É. Bajnóczi, G. Vankó, R. Alonso-Mori, J. M. Glownia, S. Nelson, M. Sikorski, D. Sokaras, H. T. Lemke, S. E. Canton, K. Wärnmark, P. Persson, A. A. Cordones and K. J. Gaffney, Phys. Chem. Chem. Phys., 2018, 20, 4238–4249 RSC.
- J. Wu, M. Alías and C. de Graaf, Inorganics, 2020, 8, 16 CrossRef.
- R. S. Mulliken, J. Am. Chem. Soc., 1952, 74, 811–824 CrossRef CAS.
- N. S. Hush, Prog. Inorg. Chem., 1967, 8, 391–444 CAS.
- B. S. Brunschwig, C. Creutz and N. Sutin, Chem. Soc. Rev., 2002, 31, 168–184 RSC.
- C. Creutz, M. D. Newton and N. Sutin, J. Photochem. Photobiol., A, 1994, 82, 47–59 CrossRef CAS.
- J. V. Caspar, T. D. Westmoreland, G. H. Allen, P. G. Bradley, T. J. Meyer and W. H. Woodruff, J. Am. Chem. Soc., 1984, 106, 3492–3500 CrossRef CAS.
- K. Tominaga, D. A. V. Kliner, A. E. Johnson, N. E. Levinger and P. F. Barbara, J. Chem. Phys., 1993, 98, 1228–1243 CrossRef CAS.
- Z. Murtaza, D. K. Graff, A. P. Zipp, L. A. Worl, W. E. J. Jones, W. D. Bates and T. J. Meyer, J. Phys. Chem., 1994, 98, 10504–10513 CrossRef CAS.
- A. Ito and T. J. Meyer, Phys. Chem. Chem. Phys., 2012, 14, 13731 RSC.
- L. J. P. Ament, M. van Veenendaal, T. P. Devereaux, J. P. Hill and J. van den Brink, Rev. Mod. Phys., 2011, 83, 705–767 CrossRef CAS.
- S. M. Butorin, J. Electron Spectrosc. Relat. Phenom., 2000, 110–111, 213–233 CrossRef CAS.
- K. Kunnus, W. Zhang, M. G. Delcey, R. V. Pinjari, P. S. Miedema, S. Schreck, W. Quevedo, H. Schröder, A. Föhlisch, K. J. Gaffney, M. Lundberg, M. Odelius and P. Wernet, J. Phys. Chem. B, 2016, 120, 7182–7194 CrossRef CAS PubMed.
- R. R. Ruminski, K. D. Van Tassel and J. D. Petersen, Inorg. Chem., 1984, 23, 4380–4382 CrossRef CAS.
- A. A. Schilt, J. Am. Chem. Soc., 1960, 82, 3000–3005 CrossRef CAS.
- J. N. Ullom and D. A. Bennett, Supercond. Sci. Technol., 2015, 28, 084003 CrossRef.
- J. N. Ullom, W. B. Doriese, D. A. Fischer, J. W. Fowler, G. C. Hilton, C. Jaye, C. Reintsema, D. S. Swetz and D. R. Schmidt, Synchrotron Radiat. News, 2014, 27, 24–27 CrossRef.
- J. Uhlig, W. B. Doriese, J. W. Fowler, D. S. Swetz, C. Jaye, D. A. Fischer, C. D. Reintsema, D. A. Bennett, L. R. Vale, U. Mandal, G. C. O'Neil, L. Miaja-Avila, Y. I. Joe, A. El Nahhas, W. Fullagar, F. Parnefjord Gustafsson, V. Sundström, D. Kurunthu, G. C. Hilton, D. R. Schmidt, J. N. Ullom and IUCr, J. Synchrotron Radiat., 2015, 22, 766–775 CrossRef CAS PubMed.
- W. B. Doriese, P. Abbamonte, B. K. Alpert, D. A. Bennett, E. V. Denison, Y. Fang, D. A. Fischer, C. P. Fitzgerald, J. W. Fowler, J. D. Gard, J. P. Hays-Wehle, G. C. Hilton, C. Jaye, J. L. McChesney, L. Miaja-Avila, K. M. Morgan, Y. I. Joe, G. C. O'Neil, C. D. Reintsema, F. Rodolakis, D. R. Schmidt, H. Tatsuno, J. Uhlig, L. R. Vale, J. N. Ullom and D. S. Swetz, Rev. Sci. Instrum., 2017, 88, 053108 CrossRef CAS PubMed.
- C. J. Titus, M. L. Baker, S. J. Lee, H.-M. Cho, W. B. Doriese, J. W. Fowler, K. Gaffney, J. D. Gard, G. C. Hilton, C. Kenney, J. Knight, D. Li, R. Marks, M. P. Minitti, K. M. Morgan, G. C. O'Neil, C. D. Reintsema, D. R. Schmidt, D. Sokaras, D. S. Swetz, J. N. Ullom, T.-C. Weng, C. Williams, B. A. Young, K. D. Irwin, E. I. Solomon and D. Nordlund, J. Chem. Phys., 2017, 147, 214201 CrossRef PubMed.
- S.-J. Lee, C. J. Titus, R. Alonso Mori, M. L. Baker, D. A. Bennett, H.-M. Cho, W. B. Doriese, J. W. Fowler, K. J. Gaffney, A. Gallo, J. D. Gard, G. C. Hilton, H. Jang, Y. Il Joe, C. J. Kenney, J. Knight, T. Kroll, J.-S. Lee, D. Li, D. Lu, R. Marks, M. P. Minitti, K. M. Morgan, H. Ogasawara, G. C. O'Neil, C. D. Reintsema, D. R. Schmidt, D. Sokaras, J. N. Ullom, T.-C. Weng, C. Williams, B. A. Young, D. S. Swetz, K. D. Irwin and D. Nordlund, Rev. Sci. Instrum., 2019, 90, 113101 CrossRef PubMed.
- J. W. Fowler, B. K. Alpert, W. B. Doriese, Y.-I. Joe, G. C. O'Neil, J. N. Ullom and D. S. Swetz, J. Low Temp. Phys., 2016, 184, 374–381 CrossRef CAS.
- R. K. Hocking, E. C. Wasinger, F. M. F. de Groot, K. O. Hodgson, B. Hedman and E. I. Solomon, J. Am. Chem. Soc., 2006, 128, 10442–10451 CrossRef CAS PubMed.
- J. W. Fowler, B. K. Alpert, D. A. Bennett, W. B. Doriese, J. D. Gard, G. C. Hilton, L. T. Hudson, Y.-I. Joe, K. M. Morgan, G. C. O'Neil, C. D. Reintsema, D. R. Schmidt, D. S. Swetz, C. I. Szabo and J. N. Ullom, Metrologia, 2017, 54, 494–511 CrossRef CAS.
- C. Creutz, Comments Inorg. Chem., 1982, 1, 293–311 CrossRef CAS.
- P. S. Braterman and J. I. Song, J. Org. Chem., 1991, 56, 4678–4682 CrossRef CAS.
- P. S. Braterman, J. I. Song and R. D. Peacock, Inorg. Chem., 1992, 31, 555–559 CrossRef CAS.
- I. H. M. van Stokkum, D. S. Larsen and R. van Grondelle, Biochim. Biophys. Acta, Bioenerg., 2004, 1657, 82–104 CrossRef CAS PubMed.
- N. H. Damrauer, T. R. Boussie, M. Devenney and J. K. McCusker, J. Am. Chem. Soc., 1997, 119, 8253–8268 CrossRef CAS.
- D. W. Thompson, A. Ito and T. J. Meyer, Pure Appl. Chem., 2013, 85, 1257–1305 CAS.
- E. M. Kober and T. J. Meyer, Inorg. Chem., 1982, 21, 3967–3977 CrossRef CAS.
- P. S. Braterman, J. I. Song and R. D. Peacock, Inorg. Chem., 1992, 31, 555–559 CrossRef CAS.
- R. M. Jay, S. Eckert, M. Fondell, P. S. Miedema, J. Norell, A. Pietzsch, W. Quevedo, J. Niskanen, K. Kunnus and A. Föhlisch, Phys. Chem. Chem. Phys., 2018, 20, 27745–27751 RSC.
- Y. Tanabe and S. Sugano, J. Phys. Soc. Jpn., 1954, 9, 766–779 CrossRef CAS.
- C. de Graaf and C. Sousa, Chem.–Eur. J., 2010, 16, 4550–4556 CrossRef CAS PubMed.
- J. J. Alexander and H. B. Gray, J. Am. Chem. Soc., 1968, 90, 4260–4271 CrossRef CAS.
- M. Bixon and J. Jortner, J. Chem. Phys., 1968, 48, 715–726 CrossRef CAS.
- J. Ulstrup and J. Jortner, J. Chem. Phys., 1975, 63, 4358–4368 CrossRef CAS.
- P. Siders and R. A. Marcus, J. Am. Chem. Soc., 1981, 103, 748–752 CrossRef CAS.
- G. C. Walker, E. Aakesson, A. E. Johnson, N. E. Levinger and P. F. Barbara, J. Phys. Chem., 1992, 96, 3728–3736 CrossRef CAS.
- P. J. Reid and P. F. Barbara, J. Phys. Chem., 1995, 99, 3554–3565 CrossRef CAS.
- H. Sumi and R. A. Marcus, J. Chem. Phys., 1986, 84, 4894–4914 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sc06272f |
| ‡ Present Address: Department of Chemistry, Ångström Laboratory, Uppsala University, Box 523, SE-751 20 Uppsala, Sweden. |
| § Present Address: Department of Physics, AlbaNova University Center, Stockholm University, S-10691 Stockholm, Sweden. |
| ¶ Present Address: Department of Chemical Physics, Lund University, P.O. Box 124, 22100 Lund, Sweden. |
| || Present Address: Center for Gas Analysis, Division of Chemical and Medical Metrology, Korea Research Institute of Standards and Science, Daejeon 34113, Republic of Korea. |
| This journal is © The Royal Society of Chemistry 2020 |