Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Understanding the reactivity of polycyclic aromatic hydrocarbons and related compounds
Israel
Fernández
 *
*
Departamento de Química Orgánica I, Centro de Innovación en Química Avanzada (ORFEO-CINQA), Facultad de Ciencias Químicas, Universidad Complutense de Madrid, 28040-Madrid, Spain. E-mail: israel@quim.ucm.es
First published on 1st April 2020
Abstract
This perspective article summarizes recent applications of the combination of the activation strain model of reactivity and the energy decomposition analysis methods to the study of the reactivity of polycyclic aromatic hydrocarbons and related compounds such as cycloparaphenylenes, fullerenes and doped systems. To this end, we have selected representative examples to highlight the usefulness of this relatively novel computational approach to gain quantitative insight into the factors controlling the so far not fully understood reactivity of these species. Issues such as the influence of the size and curvature of the system on the reactivity are covered herein, which is crucial for the rational design of novel compounds with tuneable applications in different fields such as materials science or medicinal chemistry.
1. Introduction
Polycyclic aromatic hydrocarbons (PAHs) are a large family of organic compounds that are typically composed of two or more fused aromatic rings.1,2 These species, which are ubiquitous in modern life, can be divided into two main groups, namely planar PAHs, such as naphthalene, perylene or hexabenzocoronene, and curved PAHs, also known as bowl-shaped PAHs,3–5 such as corannulene or hemifullerene. The relevance and properties of these species are manifold. For instance, PAHs, particularly those having lower molecular weights, are important pollutants that exhibit a significant carcinogenic potency.6,7 On the other hand, many PAHs also possess interesting and tuneable optical and electrochemical properties, which are highly useful in materials science.8 Indeed, a good number of PAHs have been applied as semiconductor materials in organic field-effect transistors,9 light-emitting diodes,10 and even solar cells.11 In addition, PAHs are also ubiquitous components of organic matter in space accounting for a significant percentage of all carbon in the universe.12From the above reasons, it becomes evident that understanding the intrinsic reactivity of PAHs is of crucial importance, especially for the rational design of novel PAHs with potential for application as organic materials. In this sense, different synthetic methods have been developed to produce new PAH derivatives,13 and among them cycloaddition reactions,5,14 transition metal catalysed arylations,15 aryne cyclotrimerizations,16 Scholl reactions,17 and flash vacuum pyrolysis18 should be particularly highlighted. Despite that, in many instances, the factors governing the reactivity of these species are poorly understood which severely hampers the development of new or existing methods for the preparation of novel derivatives with tuneable properties.
Over recent years, we have successfully applied the combined Activation Strain Model (ASM) of reactivity19 and Energy Decomposition Analysis (EDA)20 methods to provide a deeper and quantitative insight into those physical factors controlling the reactivity of PAHs and strongly related species such as cycloparaphenylenes or fullerenes. By means of representative recent applications, this perspective article summarizes the good performance of this relatively novel computational approach in exploring the chemistry of this important family of compounds.
2. The combined activation strain model and energy decomposition analysis approach
The Activation Strain Model (ASM) of reactivity has greatly contributed to our current understanding of fundamental transformations in chemistry, spanning from textbook processes in organic chemistry such as cycloaddition or SN2-reactions to transition metal-mediated reactions and biological processes.19,21 As this approach, also known as distortion/interaction model,19c,22 has been the focus of recent reviews,19 herein we briefly summarize the basics of this methodology.The ASM is a systematic development of the Energy Decomposition Analysis (EDA)20 method (see below) proposed by Morokuma23 and Ziegler and Rauk24 to understand the nature of the chemical bonding in stable molecules. Within the ASM, the height of reaction barriers is described and understood in terms of the original reactants. Thus, the potential energy surface ΔE(ζ) is decomposed, along the reaction coordinate ζ, into the strain (ΔEstrain(ζ)) that derives from the distortion of the individual reactants from their initial equilibrium geometries plus the actual interaction ΔEint(ζ) between the increasingly deformed reactants along the reaction coordinate (eqn (1)):
| ΔE(ζ) = ΔEstrain(ζ) + ΔEint(ζ) | (1) |
It is the interplay between ΔEstrain(ζ) and ΔEint(ζ) that determines if and at which point along ζ a barrier arises, namely, at the point where dΔEstrain(ζ)/dζ = −dΔEint(ζ)/dζ is satisfied.
The ASM method can be combined with the EDA method to quantitatively partition the ΔEint(ζ) term.19 Within this approach, the total interaction between the reactants is further decomposed into the following chemically meaningful terms (eqn (2)):
| ΔEint(ζ) = ΔVelstat(ζ) + ΔEPauli(ζ) + ΔEorb(ζ) + ΔEdisp(ζ) | (2) |
Moreover, the NOCV (Natural Orbital for Chemical Valence)25 extension of the EDA method can also be used for further partitioning the ΔEorb term. The EDA-NOCV approach provides pairwise energy contributions of each pair of interacting orbitals to the total bond energy. Therefore, the EDA-NOCV scheme provides not only qualitative but also quantitative information about the strengths of the most significant orbital interactions between the interacting reactants along the reaction coordinate.
3. Reactivity of planar and curved polycyclic aromatic hydrocarbons
(a) Reactivity of planar PAHs: towards the graphene limit
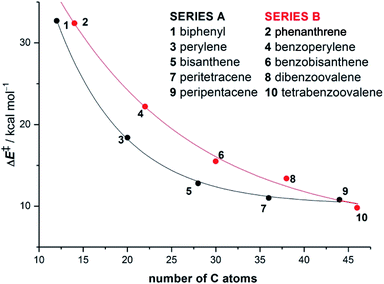
In different studies,26 Scott and co-workers found that the Diels–Alder reactivity in the bay region of PAHs, a metal-free synthetic strategy proposed to grow carbon single-walled armchair nanotubes,26a increases with an increase in the size of the system. Thus, whereas the cycloaddition reaction involving 7,14-dimesitylbisanthene and diethyl acetylenedicarboxylate proceeds with complete conversion at 120 °C for 24 h, a much lower conversion (<50%) was observed for perylene, even when the reaction was conducted at 150 °C for 72 h (Scheme 1).25a Although this size-dependent reactivity has been traditionally ascribed to the nature of the conjugated double bonds in the bay region of the system (i.e. they more and more resemble 1,3-butadiene with an increase in the size of the PAH), very little was known about the factors controlling this clear reactivity trend until our study on the Diels–Alder reactivity of planar PAHs spanning from small systems such as biphenyl or phenanthrene to much larger species such as peripentacene or tetrabenzoovalene.27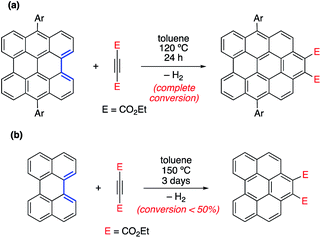 | ||
| Scheme 1 Diels–Alder cycloaddition reactions involving 7,14-dimesitylbisanthene (a) and perylene (b) described by Scott and co-workers (see ref. 26a). | ||
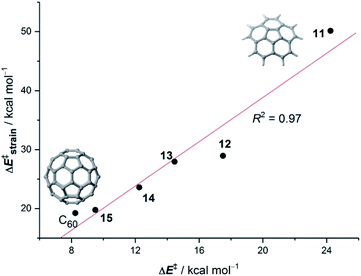
Our calculations indicate that, regardless of the size of the initial PAH, the Diels–Alder reaction with maleic anhydride occurs in a concerted manner through highly synchronous transition states (with the notable exception of the smallest systems whose corresponding transition states are much more asynchronous).27 The corresponding activation barriers steadily decrease when the size of the system is increased. In addition, the transformation becomes more and more exothermic, which is fully consistent with the experimentally observed reactivity enhancement. Interestingly, the change in both energies when going from one PAH to another follows an exponential decay converging toward a final value which seems to be reached for a system having 48–52 atoms (i.e. 18–20 fused six-membered rings) in its structure (Fig. 1). Therefore, we can predict, based on this asymptotic behaviour, a limit for the analogous cycloaddition reaction involving the bay region of a nanographene of ΔE‡ ≈ 10 kcal mol−1 and ΔER ≈ −30 kcal mol−1.
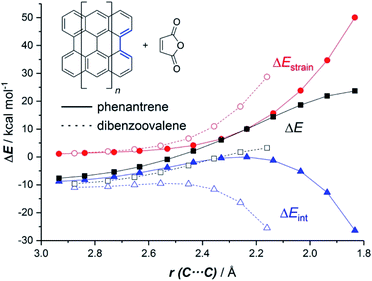
The ASM of reactivity was very helpful in understanding the above reactivity trend. Fig. 2 shows the Activation Strain Diagrams (ASDs) computed for the cycloaddition reactions involving phenanthrene and dibenzoovalene with maleic anhydride from the initial stages of the processes up to the corresponding transition states. As seen in Fig. 2, both systems exhibit rather similar ASDs in the sense that the interaction energy between the reactants (measured using ΔEint) becomes clearly stabilizing at the transition state region, a behaviour which is also found in related Diels–Alder cycloadditions and other pericyclic reactions.28 Despite that, it becomes evident that whereas the strain energy (ΔEstrain) is less destabilizing for the smaller PAH (i.e. it requires less deformation energy to adopt the transition state geometry), the interaction energy is markedly stronger for the process involving dibenzoovalene along the entire reaction coordinate. Therefore, the interaction energy between the deformed reactants is solely the factor controlling the enhanced Diels–Alder reactivity of the larger PAHs.
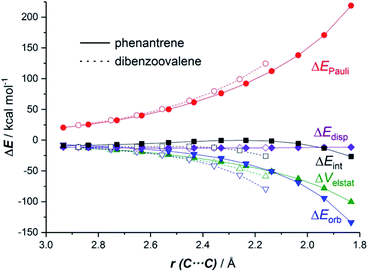
The EDA-NOCV method allowed us to understand the origin of the stronger ΔEint computed for the cycloaddition involving the larger planar PAH dibenzoovalene. As graphically shown in Fig. 3, although the phenanthrene system benefits from a less destabilizing Pauli repulsion (ΔEPauli), the attractive orbital (ΔEorb) and electrostatic (ΔVelstat, although to a much lesser extent) interactions are stronger (i.e. more stabilizing) for the reaction involving dibenzoovalene than for the analogous process involving its smaller counterpart.
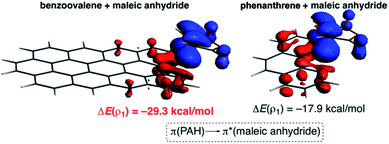
The NOCV extension of the EDA method indicates that two main molecular orbital interactions dominate the ΔEorb term, namely the π(PAH) → π*(dienophile) interaction and the reverse π(dienophile) → π*(PAH) interaction. Not surprisingly, the former interaction is much stronger than the latter, which confirms the normal electron demanding nature of the considered Diels–Alder cycloadditions. Interestingly, both molecular orbital interactions, and especially the direct π(PAH) → π*(dienophile) interaction, are significantly stronger in the process involving dibenzoovalene (Fig. 4). As a result, the total ΔEorb term is stronger for this reaction, which is translated into the computed stronger interaction between the reactants and ultimately, to a lower activation barrier. Therefore, the ASM-EDA(NOCV) method identifies the stronger orbital interactions in the cycloadditions involving larger planar PAHs as the main origin of the enhanced reactivity of these systems compared to their lighter counterparts.
(b) Reactivity of bowl-shaped PAHs: relationship with C60
The Diels–Alder cycloaddition reaction has also been chosen as a representative reaction to understand the effect of the size and curvature on the reactivity of π-curved PAHs.In general, it is found that, similar to planar PAHs, larger systems are systematically more reactive than their smaller counterparts.5,29 The reactivity of these curved systems has been traditionally rationalized by applying Fukui's Frontier Molecular Orbital (FMO) theory30 and the degree of pyramidalization of the trigonal carbon atoms, which can be quantitatively expressed in terms of the angle between the pπ-orbital axis vectors, also known as the POAV index.31 However, these approaches are not always reliable reactivity descriptors for these species, as recently highlighted by Scott.5,29 For this reason, we decided to apply our ASM-EDA approach to gain further insight into the factors controlling the reactivity of these species.32 To this end, we investigated the Diels–Alder reactions between cyclopentadiene and the interior atoms of the bowl-shaped PAHs depicted in Fig. 5, which, similar to C60-fullerene,33,34 regioselectively produce the corresponding [6,6]-cycloadduct (i.e. the reactive C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double-bond of the PAH is that which is shared by two adjacent six-membered rings).5,32
C double-bond of the PAH is that which is shared by two adjacent six-membered rings).5,32
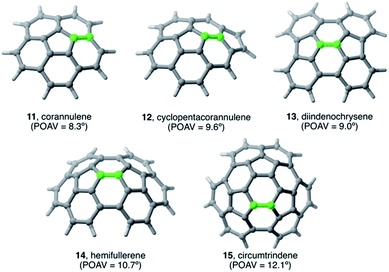 | ||
| Fig. 5 Curved PAHs considered in our study. The reactive [6,6]-bond is highlighted in green (see also ref. 32). | ||
Our calculations indicate that, starting from corannulene, there is a smooth convergence to the C60 energy barrier if the size of the buckybowl is increased. Therefore, both planar and curved PAHs exhibit a similar reactivity trend, i.e. the Diels–Alder reactivity is enhanced with an increase in the size of the system. Despite that, the ASM of reactivity suggests a different origin for this reactivity trend in the case of π-curved PAHs. As shown in Fig. 6, there is a clear linear relationship between the computed activation barriers and the corresponding activation strain energies, 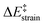 (i.e. the energy required to deform the reactants from their equilibrium geometries to the geometry adopted at the transition state). This finding indicates that larger PAHs already possess a more curved equilibrium geometry which better fits into the geometry of the corresponding transition state. This required lower deformation energy is then translated into the lower activation barriers computed for the cycloaddition reactions involving larger PAHs than those for their smaller counterparts. A similar conclusion, i.e. strain is the key factor controlling the reactivity of curved PAHs, was found by Osuna and Houk35 in a related exhaustive study on the Diels–Alder cycloaddition reactions of s-cis-1,3-butadiene to the different bonds of, among others, corannulene, coronene, and two derivatives that involved four additional five-membered rings added to the periphery of both PAHs to increase their curvature. In that study, the authors also found that the activation strain energy nicely correlates with the barrier heights of the corresponding cycloaddition reactions, therefore confirming the important role of the initial curvature of the PAH in its reactivity.
(i.e. the energy required to deform the reactants from their equilibrium geometries to the geometry adopted at the transition state). This finding indicates that larger PAHs already possess a more curved equilibrium geometry which better fits into the geometry of the corresponding transition state. This required lower deformation energy is then translated into the lower activation barriers computed for the cycloaddition reactions involving larger PAHs than those for their smaller counterparts. A similar conclusion, i.e. strain is the key factor controlling the reactivity of curved PAHs, was found by Osuna and Houk35 in a related exhaustive study on the Diels–Alder cycloaddition reactions of s-cis-1,3-butadiene to the different bonds of, among others, corannulene, coronene, and two derivatives that involved four additional five-membered rings added to the periphery of both PAHs to increase their curvature. In that study, the authors also found that the activation strain energy nicely correlates with the barrier heights of the corresponding cycloaddition reactions, therefore confirming the important role of the initial curvature of the PAH in its reactivity.
4. Reactivity of related species: pyrenophanes, cycloparaphenylenes and larger systems
The results above confirm that the size and curvature have a strong influence on the reactivity of PAHs. To further explore the impact of the initial geometry of the system on the barrier heights, we explored the reactivity of related curved systems such as pyrenophanes and cycloparaphenylenes.(a) Reactivity of pyrenophanes
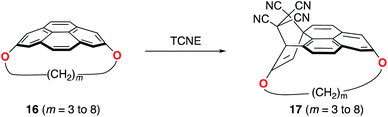
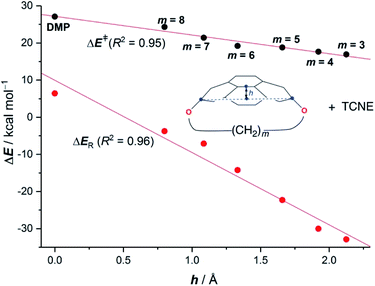
Pyrenophanes are a subgroup of cyclophanes where two nonadjacent positions of pyrene are bridged by an aliphatic chain.36 These species have attracted much attention recently mainly because of the remarkable photophysical and photochemical properties associated with the pyrene nucleus.37,38 In particular, Bodwell and co-workers prepared a series of [n](2,7)pyrenophanes and studied their reactivity in order to prepare new π-curved organic materials.36,39 It was found that the tether connecting the 2 and 7 positions of pyrene has a strong influence on the Diels–Alder reactivity of the system in the sense that systems having long tethers (n = 7, 8) are typically less reactive than those having shorter bridges. Although it is suggested that this reactivity trend is mainly caused by the strain relief during the transformation,39 the ultimate factors controlling the reactivity of these interesting species are not completely understood. For this reason, we explored the influence of the length of the tether on the Diels–Alder reactivity of the (2,7)pyrenophanes depicted in Scheme 2 with tetracyanoethylene (TCNE) as the dienophile (the species used by Bodwell and co-workers in the experiments).40Our calculations clearly indicate that regardless of the length of the bridge, the cycloadditions involving pyrenophanes proceed systematically with a lower barrier and are much more exothermic than the analogous reaction involving the planar 2,7-dimethoxypyrene (DMP) counterpart. This finding strongly suggests that the reactivity of these species is strongly dominated by the curvature of the system. Indeed, very good linear relationships were found when plotting either the activation barriers or reaction energies versus the curvature of the initial pyrenophane, which can be measured using the geometrical parameter h (see Fig. 7 for a definition). This indicates that pyrenophanes with longer tethers possess a low h value, which is then translated into a higher activation barrier. The opposite is found for the systems having shorter tethers (with higher curvatures), which is fully consistent with the experimental observations (see above).36,39
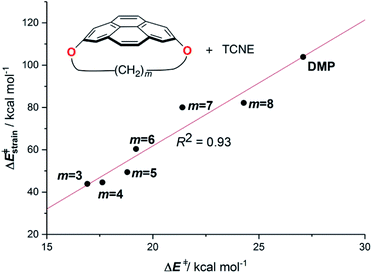
The above plot suggests that the initial bent equilibrium geometry plays a crucial role in determining the reactivity of the (2,7)pyrenophanes. Similar to the bowl-shaped PAHs described above, it is expected that the origin of the lower barriers computed for the processes involving the more bent systems can be found in a much lower strain energy to adopt the corresponding transition state structures. To our delight, a nice linear relationship was found when plotting the computed activation barriers and the corresponding activation strain energies, 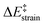 (Fig. 8). This confirms that the systems having higher curvature values already possess a bent initial geometry which better fits into the corresponding transition state geometry, and therefore require a lower deformation energy. In this sense, it is not surprising that the transition states associated with these systems are reached systematically earlier than those associated with pyrenophanes having low h values (i.e. less bent and with longer bridges).
(Fig. 8). This confirms that the systems having higher curvature values already possess a bent initial geometry which better fits into the corresponding transition state geometry, and therefore require a lower deformation energy. In this sense, it is not surprising that the transition states associated with these systems are reached systematically earlier than those associated with pyrenophanes having low h values (i.e. less bent and with longer bridges).
(b) Reactivity of strained-alkyne embedded cycloparaphenylenes
Very recently, Jasti and co-workers prepared a series of strained-alkyne cycloparaphenylenes (CPPs)41 whose size and reactivity can be precisely tuned.42,43 Similar to the pyrenophanes described above, it was experimentally found that the reactivity of the system having seven phenylenes in its structure (18a) is markedly higher than that of its larger counterparts (18c and 18e, Scheme 3). We then decided to apply our ASM-EDA approach to shed more light on the factors controlling the reactivity of these species,44 which is crucial for the design of new strained “clickable” and radially oriented π-rich macrocycles.43 To this end, we considered the Diels–Alder cycloaddition reaction involving cyclopentadiene and the alkyne embedded CPPs 18a–e, having seven to eleven phenylenes in their structures.Similar to the reactivity of pyrenophanes, our calculations confirm that the reactivity of these CPPs steadily decreases with an increase of the size of the system up to the limit of the corresponding planar counterpart diphenylacetylene (DPA). This indicates, once again, that the curvature of the system governs the reactivity of these species in the sense that more bent systems (i.e. smaller systems) are systematically more reactive than their larger congeners. Indeed, very good linear relationships were found again when plotting either the computed activation barriers or reaction energies versus the curvature θ, defined as the difference between the C–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C angle in the linear DPA (180°) and the corresponding angle in the macrocycles 18 (correlation coefficient R2 = 0.99 and 0.92, respectively).44
C angle in the linear DPA (180°) and the corresponding angle in the macrocycles 18 (correlation coefficient R2 = 0.99 and 0.92, respectively).44
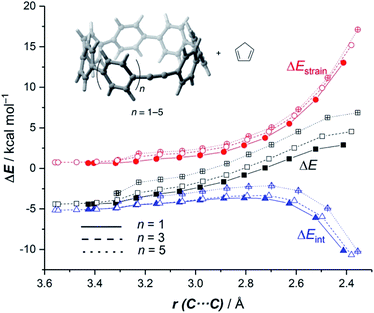
It is again expected that the most curved systems require lower deformation energies, and as a consequence, they exhibit an enhanced reactivity compared to their less curved congeners. According to the ASDs for the processes involving 18a, 18c and 18e, this hypothesis is confirmed as the ΔEstrain curve is clearly less destabilizing for 18a than for 18c and 18e along the entire reaction coordinate (Fig. 9). Despite that, the ASDs suggest that, at variance with other curved PAHs, the difference in reactivity of these CPPs is mainly dominated by the interaction term rather than the deformation energy. For instance, at the same consistent C⋯ C bond forming distance of 2.5 Å, the difference in the ΔEint term (ΔΔEint = 1.2 and 2.6 kcal mol−1 for 18c and 18e, with respect to 18a, respectively) roughly matches the difference in the total energy (ΔΔE = 1.6 and 3.3 kcal mol−1). Therefore, it can be concluded that the initial bent geometry of the system not only leads to a reduced strain energy but also enhances the interaction energy between the deformed reactants.45 This is, according to the EDA method, mainly ascribed to the combination of both stronger electrostatic and orbital interactions.
The ASM-EDA(NOCV) approach has also been particularly useful to understand the reactivity of related larger systems such as fullerenes and carbon nanotubes. In the chemistry of fullerenes, issues such as the influence of the encapsulation of ions or molecules inside the fullerene cage on both the reactivity and regioselectivity have been studied by our group.46,47 Regarding nanotubes, Houk, Lan, and co-workers reported that the interaction energy becomes the major factor controlling the reactivity of single-walled carbon nanotubes of different diameters (4–9,5).48 In a related study, Solà and co-workers explored the influence of the curvature of single-walled carbon nanotubes on their Diels–Alder reactivity with benzyne.49 In this case, it was found that the deformation of the initial reactants in the rate-determining transition states is the key factor governing the chemoselectivity of the process.
5. Influence of the presence of heteroatoms on the reactivity: doped systems
The integration of heteroatoms, especially those belonging to groups 13–16, into the framework of PAHs constitutes a really useful way to modulate their properties.50 Indeed, new systems having potential for application in the fabrication of biomedical and optoelectronic materials have been produced as a result of replacing carbon atoms with heteroatoms. Not surprisingly, such a replacement induces a significant modification of the electronic structure of the system which, of course, greatly affects its reactivity. Despite that, very little is known about the actual influence of the presence of heteroatoms in the structure of PAHs and related systems on their reactivity.In this sense, we recently investigated the reactivity of parent 1,2-borazines and related group 15 and 16 analogues, where a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C group in benzene was replaced by an isoelectronic BN fragment.51 Such C
C group in benzene was replaced by an isoelectronic BN fragment.51 Such C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C/BN replacement in aromatic molecules is particularly attracting considerable interest in materials chemistry and medicinal chemistry.52 For instance, Liu and co-workers reported that, different to benzene, the analogous N-TBS-B-Me-1,2-azaborine (TBS = tert-butyldimethylsilyl) is able to undergo irreversible Diels–Alder reactions with electron-deficient dienophiles such as maleic anhydride or N-methylmaleimide in the presence of AlCl3 as a catalyst at room temperature and with complete endo-diastereoselectivity.53 Our ASM calculations indicate that the enhanced Diels–Alder reactivity of the 1,2-azaborine systems compared to benzene finds its origin not only in a lower strain energy but mainly in the much stronger interaction energy between the reactants along the entire reaction coordinate.51a This can be ascribed to the reduced aromaticity strength in the system induced by the presence of the BN moiety, which makes the 1,2-azaborine a much better diene than the much more aromatic benzene.51b
C/BN replacement in aromatic molecules is particularly attracting considerable interest in materials chemistry and medicinal chemistry.52 For instance, Liu and co-workers reported that, different to benzene, the analogous N-TBS-B-Me-1,2-azaborine (TBS = tert-butyldimethylsilyl) is able to undergo irreversible Diels–Alder reactions with electron-deficient dienophiles such as maleic anhydride or N-methylmaleimide in the presence of AlCl3 as a catalyst at room temperature and with complete endo-diastereoselectivity.53 Our ASM calculations indicate that the enhanced Diels–Alder reactivity of the 1,2-azaborine systems compared to benzene finds its origin not only in a lower strain energy but mainly in the much stronger interaction energy between the reactants along the entire reaction coordinate.51a This can be ascribed to the reduced aromaticity strength in the system induced by the presence of the BN moiety, which makes the 1,2-azaborine a much better diene than the much more aromatic benzene.51b
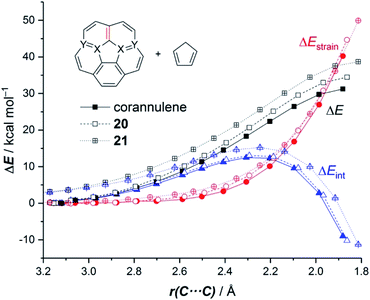
We extended these findings in a recent study aimed to understand the impact of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C/B–N replacement on the reactivity of π-curved PAHs.54 Compared to their BN-embedded planar congeners, these doped curved systems have been comparatively much less explored very likely due to the experimental difficulties associated with their preparation and the lack of knowledge of their intrinsic reactivity. For this reason, we first compared the Diels–Alder reactivity, using cyclopentadiene as the diene, of the parent corannulene with its BN-analogues 20 and 21 (the latter being a model of the experimentally prepared 10b1,18b1-diaza-10b,18b-diboratetrabenzo[a,g,j,m]corannulene)55 (see Fig. 10).
C/B–N replacement on the reactivity of π-curved PAHs.54 Compared to their BN-embedded planar congeners, these doped curved systems have been comparatively much less explored very likely due to the experimental difficulties associated with their preparation and the lack of knowledge of their intrinsic reactivity. For this reason, we first compared the Diels–Alder reactivity, using cyclopentadiene as the diene, of the parent corannulene with its BN-analogues 20 and 21 (the latter being a model of the experimentally prepared 10b1,18b1-diaza-10b,18b-diboratetrabenzo[a,g,j,m]corannulene)55 (see Fig. 10).
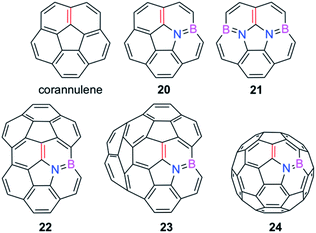 | ||
| Fig. 10 BN-embedded curved PAHs considered in our study. The most reactive [6,6]-bond is highlighted in red (see also ref. 54). | ||
It was found that the presence of the BN fragment induces a significant planarization of the system (bowl-depth decreases from 0.88 Å in corannulene to 0.68 Å in 20, and to 0.26 Å in 21) which is translated into a remarkable reduction of the corresponding bowl-to-bowl inversion barrier. This structural modification results also in a markedly reduced Diels–Alder reactivity with cyclopentadiene (reactivity order: corannulene > 20 > 21). According to the ASM approach, the more curved corannulene benefits from both a less destabilizing strain energy and a stronger interaction between the deformed reactants, which is translated into the computed higher reactivity of this system (Fig. 11). This finding is directly connected to that observed in the reactivity of other curved systems such as strained-alkyne embedded cycloparaphenylenes (see above), where the initial curvature (i.e. pre-distortion) of the system is not only translated into a lower deformation energy but also into a stronger interaction between the reactants. The application of the EDA(NOCV) method indicates that the enhanced interaction computed for the process involving corannulene is caused by both stronger electrostatic and orbital (mainly HOMOdiene–LUMOcorannulene) interactions in a nearly identical manner.54
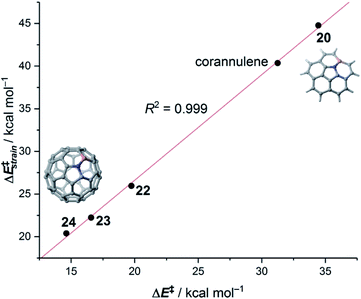
The crucial role of the initial curvature of the system was further confirmed when considering the reactivity of related BN-embedded larger curved PAHs such as BN-hemifullerene 22, BN-circumtrindene 23 and even BN-fullerene 24 (see Fig. 10). Not surprisingly, a steady increase of the Diels–Alder reactivity was found as a consequence of the increasing curvature of the system when going from corannulene or BN-corannulene (less curved systems) to BN-circumtrindene or BN-fullerene. Indeed, a perfect linear correlation, similar to that found for their all-carbon analogues (see Fig. 6), was found when plotting the computed activation barriers versus the corresponding activation strain energies, 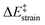 (correlation coefficient R2 = 0.999, Fig. 12). This confirms, once again, that curved PAHs require less deformation energy to adopt the corresponding transition state geometry, which results in lower barrier processes than for the reactions involving less curved systems.
(correlation coefficient R2 = 0.999, Fig. 12). This confirms, once again, that curved PAHs require less deformation energy to adopt the corresponding transition state geometry, which results in lower barrier processes than for the reactions involving less curved systems.
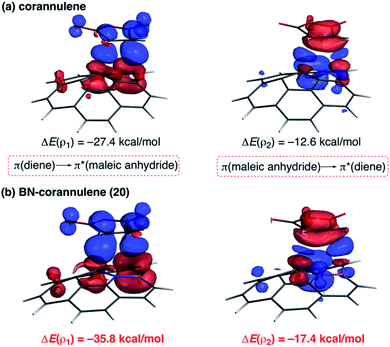
As commented above, the replacement of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C moiety by BN in benzene makes the system a better diene. A similar effect is also found in these π-curved systems. Indeed, at variance with the cycloaddition involving cyclopentadiene, BN-corannulene 20 reacts better (i.e. with a lower activation barrier and more exothermic reaction energy) than corannulene with a dienophile such as maleic anhydride. The ASM method indicates that the reactivity reversal of the BN-system is solely ascribed to the stronger interaction between the reactants along the entire reaction coordinate, which, according to the EDA method, is almost exclusively due to more stabilizing orbital interactions.54 The NOCV extension of the EDA method confirms that the stronger orbital interactions computed for the process involving 20 than for the parent corannulene derive from both the direct π(diene) → π*(dienophile) and the reverse π(dienophile) → π*(diene) molecular orbital interactions, which are comparatively weaker for the process involving corannulene (see Fig. 13). Therefore, it is confirmed that the replacement of a C
C moiety by BN in benzene makes the system a better diene. A similar effect is also found in these π-curved systems. Indeed, at variance with the cycloaddition involving cyclopentadiene, BN-corannulene 20 reacts better (i.e. with a lower activation barrier and more exothermic reaction energy) than corannulene with a dienophile such as maleic anhydride. The ASM method indicates that the reactivity reversal of the BN-system is solely ascribed to the stronger interaction between the reactants along the entire reaction coordinate, which, according to the EDA method, is almost exclusively due to more stabilizing orbital interactions.54 The NOCV extension of the EDA method confirms that the stronger orbital interactions computed for the process involving 20 than for the parent corannulene derive from both the direct π(diene) → π*(dienophile) and the reverse π(dienophile) → π*(diene) molecular orbital interactions, which are comparatively weaker for the process involving corannulene (see Fig. 13). Therefore, it is confirmed that the replacement of a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C fragment by an isoelectronic B–N moiety dramatically modifies the reactivity of the doped PAHs. Thus, whereas the all-carbon system tends to react as a dienophile in Diels–Alder cycloaddition reactions, its BN-counterpart is a better diene in the analogous process with maleic anhydride.56
C fragment by an isoelectronic B–N moiety dramatically modifies the reactivity of the doped PAHs. Thus, whereas the all-carbon system tends to react as a dienophile in Diels–Alder cycloaddition reactions, its BN-counterpart is a better diene in the analogous process with maleic anhydride.56
The effect of the replacement of carbon atoms by heteroatoms was also studied in larger systems such as fullerenes. In particular, we explored the reactivity of azafullerenes, the only class of heterofullerenes that have been synthesized in macroscopic quantities so far57 and that, due to their exceptional energy- and charge-transfer properties, have been employed in organic solar cells.57c,58 Our calculations indicate that, compared to C60, the Diels–Alder reaction with cyclopentadiene involving its doped-counterpart C59NH azafullerene is both kinetically and thermodynamically less favoured.59 This decreased reactivity is ascribed by the ASM-EDA(NOCV) method exclusively to a remarkable reduction of the interaction between the deformed reactants. The presence of the nitrogen atom and the CH fragment significantly modifies the electronic structure of the fullerenic cage and weakens the direct π(cyclopentadiene) → π*(fullerene) molecular orbital interaction. This results in a lower total interaction and therefore, in a higher barrier cycloaddition than for C60.59 This study was also extended to charged systems, C59N+ and C59N−, species prepared or detected experimentally.60,61 Based on the computed barriers, the following Diels–Alder reactivity trend was found: C59N+ > C60 > C59NH > C59N−.62 Once again, the interaction energy between the reactants was found to be the key factor governing the reactivity of these azafullerenes. Despite that, the weaker ΔEint computed for C59NH or C59N− does not derive from weaker orbital interactions but from a more destabilizing Pauli repulsion between closed-shells as a consequence of the presence of two additional π-electrons in these systems compared to C59N+ or C60.62
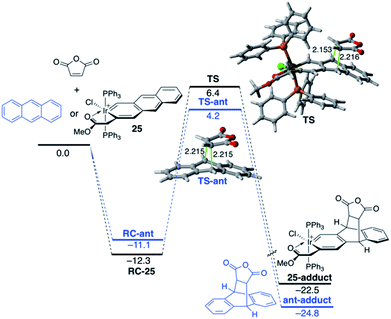
The modification of the electronic structure and reactivity of PAHs is not restricted to the incorporation of group 13–16 heteroatoms. In fact, it can also be achieved by incorporating transition metal fragments in their structures instead. For instance, it was found that the central ring of metallaanthracenes, a particular group of metallabenzenes63 where a CH unit in anthracene is replaced by an isolobal transition-metal fragment, is systematically less reactive than the analogous ring of the parent anthracene in their Diels–Alder cycloaddition reactions with maleic anhydride.64 For instance, Fig. 14 shows the computed reaction profiles for the Diels–Alder reactions involving maleic anhydride and anthracene and iridaanthracene 25, a species recently prepared by Frogley and Wright.65 As clearly seen, the cycloaddition involving 25 is both kinetically (ΔΔE‡ = 3.4 kcal mol−1) and thermodynamically (ΔΔER = 2.3 kcal mol−1) less favoured than the analogous process involving the parent anthracene.
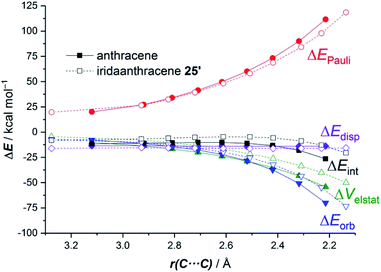
The ASM approach indicates that the cycloaddition involving anthracene, although requires a higher deformation energy, benefits from a much stronger interaction between the reactants along the entire reaction coordinate compared to the process involving its organometallic counterpart 25.64 As graphically shown in Fig. 15, the EDA method indicates that this stronger interaction derives from more stabilizing electrostatic and orbital interactions, the latter resulting mainly from a stronger π(anthracene) → π*(maleic anhydride) molecular orbital interaction.
6. Conclusions and outlook
By means of selected representative applications, in this perspective article we have illustrated the good performance of the combined Activation Strain Model (ASM) of reactivity and Energy Decomposition Analysis (EDA) methods to provide a detailed rationalization of the physical factors controlling the reactivity of PAHs and strongly related species. Issues such as the influence of the size, curvature and the presence of heteroatoms in the system on their reactivity can be easily understood in a quantitative manner using this computational approach, which not only complements but, in many cases, also outperforms other more traditional methods based on the application of FMO arguments or POAV angles. In our opinion, the ASM-EDA(NOCV) methodology can be an extremely useful tool to guide experimentalists towards the development of methods for the preparation of novel PAH derivatives with tuneable properties and potential for application in materials science or medicinal chemistry.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support was provided by the Spanish Ministerio de Economía y Competitividad (MINECO) and FEDER (Grants CTQ2016-78205-P and CTQ2016-81797-REDC).Notes and references
- R. G. Harvey, Polycyclic Aromatic Hydrocarbons, Wiley-VCH, Weinheim, 1997 Search PubMed.
- Polycyclic Arenes and Heteroarenes, ed. Q. Miao, Wiley-VCH, Weinheim, 2016 Search PubMed.
- Fragments of Fullerenes and Carbon Nanotubes: Designed Synthesis, Unusual Reactions, and Coordination Chemistry, ed. M. A. Petrukhina and L. T. Scott, Wiley-VCH, New York, 2011 Search PubMed.
- Y.-T. Wu and J. S. Siegel, Chem. Rev., 2006, 106, 4843 CrossRef.
- L. T. Scott, Chem. Soc. Rev., 2015, 44, 6464 RSC.
- (a) I. J. Keyte, R. M. Harrison and G. Lammel, Chem. Soc. Rev., 2013, 42, 9333 RSC; (b) K.-H. Kim, S. A. Jahan, E. Kabir and R. J. C. Brown, Environ. Int., 2013, 60, 71 CrossRef PubMed.
- R. G. Harvery, Polycyclic Aromatic Hydrocarbons: Chemistry and Carcinogenicity, Cambridge University Press, New York, 1991 Search PubMed.
- (a) J. E. Anthony, Chem. Rev., 2006, 106, 5028 CrossRef; (b) J. E. Anthony, Angew. Chem., Int. Ed., 2008, 47, 452 CrossRef CAS PubMed.
- See, for instance: (a) M. Bendikov, F. Wudl and D. F. Perepichka, Chem. Rev., 2004, 104, 4891 CrossRef CAS; (b) X. Zhan, J. Zhang, S. Tang, Y. Lin, M. Zhao, J. Yang, H.-L. Zhang, Q. Peng, G. Yu and Z. Li, Chem. Commun., 2015, 51, 7156 RSC; (c) C. Li, Y. Wang, T. Zhang, B. Zheng, J. Xu and Q. Miao, Chem.–Asian J., 2019, 14, 1676 CrossRef CAS; (d) G. Liu, C. Xiao, F. Negri, Y. Li and Z. Wang, Angew. Chem., Int. Ed., 2020, 59, 2008 CrossRef CAS.
- Selected examples: (a) C. W. Tang and S. A. VanSlyke, Appl. Phys. Lett., 1987, 51, 913 CrossRef CAS; (b) K. C. Wu, P. J. Ku, C. S. Lin, H. T. Shih, F. I. Wu, M. J. Huang, J. J. Lin, I. C. Chen and C. H. Cheng, Adv. Funct. Mater., 2008, 18, 67 CrossRef CAS; (c) K. M. Omer, S.-Y. Ku, K. T. Wong and A. J. Bard, Angew. Chem., Int. Ed., 2009, 48, 9300 CrossRef CAS; (d) K. H. Lee, J. K. Park, J. H. Seo, S. W. Park, Y. S. Kim, Y. K. Kim and S. S. Yoon, J. Mater. Chem., 2011, 21, 13640 RSC; (e) J. Xiao, S. Liu, Y. Liu, L. Ji, X. Liu, H. Zhang, X. Sun and Q. Zhang, Chem.–Asian J., 2012, 7, 561 CrossRef CAS.
- (a) N. J. Tremblay, A. A. Gorodetsky, M. P. Cox, T. Schiros, B. Kim, R. Steiner, Z. Bullard, A. Sattler, W.-H. So, Y. Itoh, M. F. Toney, H. Ogasawara, A. P. Ramirez, I. Kymissis, M. L. Steigerwald and C. Nuckolls, ChemPhysChem, 2010, 11, 799 CrossRef PubMed; (b) S. Xiao, S. J. Kang, Y. Wu, S. Ahn, J. B. Kim, Y.-L. Loo, T. Siegrist, M. L. Steigerwald, H. Li and C. Nuckolls, Chem. Sci., 2013, 4, 2018 RSC.
- F. Salama, in Organic Matter in Space, Proceedings IAU Symposium, ed. S. Kwok and S. Sandford, 2008, vol. 251, p. 357 Search PubMed.
- R. G. Harvey, Curr. Org. Chem., 2004, 8, 303 CrossRef.
- For a recent review focused mainly on Diels–Alder cycloaddition reactions, see: O. T. Dyan, G. I. Borodkin and P. A. Zaikin, Eur. J. Org. Chem., 2019, 7271 CrossRef.
- (a) W. Hagui, H. Doucet and J.-F. Soulé, Chem, 2019, 5, 2006 CrossRef; (b) R. Dorel and A. M. Echavarren, Acc. Chem. Res., 2019, 52, 1812 CrossRef.
- I. Pozo, E. Guitián, D. Pérez and D. Peña, Acc. Chem. Res., 2019, 52, 2472 CrossRef.
- Representative recent examples: (a) Y. Hu, D. Wang, M. Baumgarten, D. Schollmeyer, K. Müllen and A. Narita, Chem. Commun., 2018, 54, 13575 RSC; (b) C. M. Cruz, I. R. Márquez, I. F. A. Mariz, V. Blanco, C. Sánchez-Sánchez, J. M. Sobrado, J. A. Martín-Gago, J. M. Cuerva, E. Maçôas and A. G. Campaña, Chem. Sci., 2018, 9, 3917 RSC; (c) P. J. Evans, J. Ouyang, L. Favereau, J. Crassous, I. Fernández, J. Perles and N. Martín, Angew. Chem., Int. Ed., 2018, 57, 6774 CrossRef; (d) J. M. Fernández-García, P. J. Evans, S. Medina Rivera, I. Fernández, D. García-Fresnadillo, J. Perles, J. Casado and N. Martín, J. Am. Chem. Soc., 2018, 140, 17168 CrossRef; (e) S. H. Pun, Y. Wang, M. Chu, C. K. Chan, Y. Li, Z. Liu and Q. Miao, J. Am. Chem. Soc., 2019, 141, 9680 CrossRef.
- V. M. Tsefrikas and L. T. Scott, Chem. Rev., 2006, 106, 4868 CrossRef.
- For reviews, see: (a) W.-J. van Zeist and F. M. Bickelhaupt, Org. Biomol. Chem., 2010, 8, 3118 RSC; (b) I. Fernández and F. M. Bickelhaupt, Chem. Soc. Rev., 2014, 43, 4953 RSC; (c) F. M. Bickelhaupt and K. N. Houk, Angew. Chem., Int. Ed., 2017, 56, 10070 CrossRef; see also: (d) I. Fernández, in Discovering the Future of Molecular Sciences, ed. B. Pignataro, Wiley-VCH, Weinheim, 2014, pp. 165–187 Search PubMed.
- For reviews on the EDA method, see: (a) F. M. Bickelhaupt and E. J. Baerends, in Reviews in Computational Chemistry, ed. K. B. Lipkowitz and D. B. Boyd, Wiley-VCH, New York, 2000, vol. 15, pp. 1–86 Search PubMed; (b) M. von Hopffgarten and G. Frenking, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 43 Search PubMed; (c) G. Frenking and F. M. Bickelhaupt, in The Chemical Bond: Fundamental Aspects of Chemical Bonding, ed. G. Frenking and S. Shaik, Wiley-VCH, Weinheim, 2014, pp. 121–158 CrossRef.
- Representative examples: (a) A. P. Bento and F. M. Bickelhaupt, J. Org. Chem., 2007, 72, 2201 CrossRef PubMed; (b) A. P. Bento and F. M. Bickelhaupt, J. Org. Chem., 2008, 73, 7290 CrossRef PubMed; (c) P. H.-Y. Cheong, R. S. Paton, S. M. Bronner, G.-Y. J. Im, N. K. Garg and K. N. Houk, J. Am. Chem. Soc., 2010, 132, 1267 CrossRef PubMed; (d) R. S. Paton, S. Kim, A. G. Ross, S. J. Danishefsky and K. N. Houk, Angew. Chem., Int. Ed., 2011, 50, 10366 CrossRef CAS PubMed; (e) D. Yepes, P. Jaque and I. Fernández, Chem.–Eur. J., 2016, 22, 18801 CrossRef CAS PubMed; (f) A. K. Narsaria, T. A. Hamlin, K. Lammertsma and F. M. Bickelhaupt, Chem.–Eur. J., 2019, 25, 9902 CrossRef CAS PubMed; (g) T. A. Hamlin, I. Fernández and F. M. Bickelhaupt, Angew. Chem., Int. Ed., 2019, 58, 8922 CrossRef CAS.
- (a) D. H. Ess and K. N. Houk, J. Am. Chem. Soc., 2007, 129, 10646 CrossRef CAS; (b) D. H. Ess and K. N. Houk, J. Am. Chem. Soc., 2008, 130, 10187 CrossRef CAS PubMed.
- K. Morokuma, J. Chem. Phys., 1971, 55, 1236 CrossRef CAS.
- T. Ziegler and A. Rauk, Theor. Chim. Acta, 1977, 46, 1 CrossRef CAS.
- (a) M. Mitoraj and A. Michalak, J. Mol. Model., 2007, 13, 347 CrossRef CAS; (b) M. P. Mitoraj, A. Michalak and T. Ziegler, J. Chem. Theory Comput., 2009, 5, 962 CrossRef CAS.
- (a) E. H. Fort, P. M. Donovan and L. T. Scott, J. Am. Chem. Soc., 2009, 131, 16006 CrossRef CAS; (b) E. H. Fort, M. S. Jeffreys and L. T. Scott, Chem. Commun., 2012, 48, 8102 RSC. See also, (c) E. H. Fort and L. T. Scott, Angew. Chem., Int. Ed., 2010, 49, 6626 CrossRef CAS.
- Y. García-Rodeja, M. Solà and I. Fernández, Chem.–Eur. J., 2016, 22, 10572 CrossRef.
- See, for instance: (a) I. Fernández, F. M. Bickelhaupt and F. P. Cossío, Chem.–Eur. J., 2009, 15, 13022 CrossRef PubMed; (b) I. Fernández, F. P. Cossío and F. M. Bickelhaupt, J. Org. Chem., 2011, 76, 2310 CrossRef PubMed; (c) I. Fernández, F. M. Bickelhaupt and F. P. Cossío, Chem.–Eur. J., 2012, 18, 12395 CrossRef PubMed; (d) I. Fernández, Phys. Chem. Chem. Phys., 2014, 16, 7662 RSC; (e) I. Fernández and F. M. Bickelhaupt, Chem.–Asian J., 2016, 11, 3297 CrossRef PubMed.
- H. Y. Cho, R. B. M. Ansems and L. T. Scott, Beilstein J. Org. Chem., 2014, 10, 956 CrossRef.
- (a) K. Fukui, T. Yonezawa and H. Shingu, J. Chem. Phys., 1952, 20, 722 CrossRef CAS; (b) K. Fukui, T. Yonezawa and H. Shingu, J. Chem. Phys., 1954, 22, 1433 CrossRef CAS; (c) K. Fukui, Angew. Chem., Int. Ed., 1982, 21, 801 CrossRef.
- (a) R. C. Haddon and L. T. Scott, Pure Appl. Chem., 1986, 58, 137 CAS; (b) R. C. Haddon, J. Am. Chem. Soc., 1987, 109, 1676 CrossRef CAS; (c) R. C. Haddon, J. Phys. Chem., 1987, 91, 3719 CrossRef CAS.
- Y. García-Rodeja, M. Solà, F. M. Bickelhaupt and I. Fernández, Chem.–Eur. J., 2016, 22, 1368 CrossRef.
- (a) R. Taylor, in The Fullerenes, ed. H. W. Kroto and D. R. M. Walton, Cambridge University Press, Cambridge, 1993, pp. 87–101 Search PubMed; (b) A. Hirsch, The Chemistry of the Fullerenes, Thieme, Stuttgart, 1994 CrossRef.
- For selected computational studies: (a) M. García-Borràs, S. Osuna, M. Swart, J. M. Luis and M. Solà, Chem. Commun., 2013, 49, 1220 RSC; (b) I. Fernández, M. Solà and F. M. Bickelhaupt, Chem.–Eur. J., 2013, 19, 7416 CrossRef PubMed.
- S. Osuna and K. N. Houk, Chem.–Eur. J., 2009, 15, 13219 CrossRef CAS PubMed.
- (a) G. J. Bodwell, G. Venkataramana, and K. S. Unikela, in Fragments of Fullerenes and Carbon Nanotubes: Designed Synthesis, Unusual Reactions and Coordination Chemistry, ed. M. A. Petrukhina and L. T. Scott, Wiley-VCH, New York, 2011, ch. 14 Search PubMed; (b) P. G. Ghasemabadi, T. Yao and G. J. Bodwell, Chem. Soc. Rev., 2015, 44, 6494 RSC.
- (a) F. M. Winnik, Chem. Rev., 1993, 93, 587 CrossRef CAS; (b) S. Karuppannan and J.-C. Chambron, Chem.–Asian J., 2011, 6, 964 CrossRef CAS.
- (a) T. M. Figueira-Duarte and K. Müllen, Chem. Rev., 2011, 111, 7260 CrossRef CAS; (b) J. M. Casas-Solvas, J. D. Howgego and A. P. Davis, Org. Biomol. Chem., 2014, 12, 212 RSC.
- (a) G. J. Bodwell, J. N. Bridson, T. J. Houghton, J. W. J. Kennedy and M. R. Mannion, Chem.–Eur. J., 1999, 5, 1823 CrossRef CAS; (b) G. J. Bodwell, J. J. Fleming, M. R. Mannion and D. O. Miller, J. Org. Chem., 2000, 65, 5360 CrossRef CAS PubMed.
- Y. García-Rodeja and I. Fernández, J. Org. Chem., 2017, 82, 8157 CrossRef.
- For a recent review on CPPs and related species, see: Y. Segawa, D. R. Levine and K. Itami, Acc. Chem. Res., 2019, 52, 2760 CrossRef CAS.
- T. A. Schaub, J. T. Margraf, L. Zakharov, K. Reuter and R. Jasti, Angew. Chem., Int. Ed., 2018, 57, 16348 CrossRef CAS.
- See also the recent review on π-conjugated macrocycles bearing angle-strained alkynes: K. Miji and K. Ohe, Chem.–Eur. J., 2020 DOI:10.1002/chem.201904114.
- Y. García-Rodeja and I. Fernández, J. Org. Chem., 2019, 84, 4330 CrossRef PubMed.
- This finding agrees with a recent report by Houk, Bickelhaupt and co-workers on the reactivity of strained cycloalkynes where pre-distortion not only leads to a reduced strain energy but also enhances the interaction energy between the deformed reactants, see: T. A. Hamlin, B. J. Levandowski, A. K. Narsaria, K. N. Houk and F. M. Bickelhaupt, Chem.–Eur. J., 2019, 25, 6342 CrossRef CAS PubMed.
- (a) I. Fernández, M. Solà and F. M. Bickelhaupt, J. Chem. Theory Comput., 2014, 10, 3863 CrossRef PubMed; (b) F. M. Bickelhaupt, M. Solà and I. Fernández, Chem.–Eur. J., 2015, 21, 5760 CrossRef CAS; (c) Y. García-Rodeja, M. Solà, F. M. Bickelhaupt and I. Fernández, Chem.–Eur. J., 2017, 23, 11030 CrossRef PubMed.
- I. Fernández, Eur. J. Org. Chem., 2018, 1394 CrossRef.
- Y. Li, S. Osuna, M. Garcia-Borrás, X. Qi, S. Liu, K. N. Houk and Y. Lan, Chem.–Eur. J., 2016, 22, 12819 CrossRef CAS PubMed.
- J. P. Martínez, F. Langa, F. M. Bickelhaupt, S. Osuna and M. Solà, J. Phys. Chem. C, 2016, 120, 1716 CrossRef.
- For recent reviews, see: (a) M. Stępień, E. Gońka, M. Żyła and N. Sprutta, Chem. Rev., 2017, 117, 3479 CrossRef PubMed; (b) M. Hirai, N. Tanaka, M. Sakai and S. Yamaguchi, Chem. Rev., 2019, 119, 8291 CrossRef CAS PubMed; (c) U. H. F. Bunz and J. Freudenberg, Acc. Chem. Res., 2019, 52, 1575 CrossRef CAS PubMed.
- (a) Y. García-Rodeja and I. Fernández, J. Org. Chem., 2016, 81, 6554 CrossRef; (b) J. J. Cabrera-Trujillo and I. Fernández, Tetrahedron, 2018, 74, 4289 CrossRef CAS.
- For selected examples, see: (a) S. Furukawa, J. Kobayashi and T. Kawashima, J. Am. Chem. Soc., 2009, 131, 14192 CrossRef CAS PubMed; (b) Q. Tan, S. Higashibayashi, S. Karanjit and H. Sakurai, Nat. Commun., 2012, 3, 891 CrossRef; (c) P. G. Campbell, A. J. V. Marwitz and S. Y. Liu, Angew. Chem., Int. Ed., 2012, 51, 6074 CrossRef CAS; (d) P. O. Dral, M. Kivala and T. Clark, J. Org. Chem., 2013, 78, 1894 CrossRef CAS PubMed; (e) S. Wang, X. Li, X. Hou, Y. Sun and X. Shao, Chem. Commun., 2016, 52, 14486 RSC; (f) H. Helten, Chem.–Eur. J., 2016, 22, 12972 CrossRef CAS PubMed; (g) A. Abengjzar, P. García-García, D. Sucunza, D. Sampedro, A. Pérez-Redondo and J. J. Vaquero, Org. Lett., 2019, 21, 2550 CrossRef PubMed; (h) Z. X. Giustra and S.-Y. Liu, J. Am. Chem. Soc., 2018, 140, 1184 CrossRef CAS.
- R. J. Burford, B. Li, M. Vasiliu, D. A. Dixon and S.-Y. Liu, Angew. Chem., Int. Ed., 2015, 54, 7823 CrossRef CAS PubMed.
- Y. García-Rodeja and I. Fernández, Chem.–Eur. J., 2019, 25, 9771 CrossRef.
- S. Nakatsuka, N. Yasuda and T. Hatekeyama, J. Am. Chem. Soc., 2018, 140, 13562 CrossRef CAS PubMed.
- A similar finding, that is, with corannulene acting as a dienophile, was reported previously, see: P. Jayapal, M. Sundararajan, G. Rajaraman, P. Venuvanalingam, R. Kalagi and S. R. Gadre, J. Phys. Org. Chem., 2008, 21, 146 CrossRef CAS.
- (a) M. Keshavarz-K, R. González, R. G. Hicks, G. Srdanov, V. I. Srdanov, T. G. Collins, J. C. Hummelen, C. Bellavia-Lund, J. Pavlovich, F. Wudl and K. Holczer, Nature, 1996, 383, 147 CrossRef CAS; (b) N. Xin, H. Huang, J. Zhang, Z. Dai and L. Gan, Angew. Chem., Int. Ed., 2012, 51, 6163 CrossRef CAS PubMed. See also the review, (c) G. Rotas and N. Tagmatarchis, Chem.–Eur. J., 2016, 22, 1206 CrossRef CAS PubMed.
- (a) L. Martin-Gomis, G. Rotas, K. Ohkubo, F. Fernández-Lazaro, S. Fukuzumi, N. Tagmatarchis and A. Sastre-Santos, Nanoscale, 2015, 7, 7437 RSC; (b) G. Rotas, G. Charalambidis, L. Glatzl, D. T. Gryko, A. Kahnt, A. G. Coutsolelos and N. Tagmatarchis, Chem. Commun., 2013, 49, 9128 RSC.
- Y. García-Rodeja, M. Solà and I. Fernández, J. Org. Chem., 2017, 82, 754 CrossRef PubMed.
- (a) I. Lamparth, B. Nuber, G. Schick, A. Skiebe, T. Grösser and A. Hirsch, Angew. Chem., Int. Ed., 1995, 34, 2257 CrossRef CAS; (b) K.-C. Kim, F. Hauke, A. Hirsch, P. D. W. Boyd, E. Carter, R. S. Armstrong, P. A. Lay and C. A. Reed, J. Am. Chem. Soc., 2003, 125, 4024 CrossRef CAS PubMed; (c) Y. Hashikawa and Y. Murata, J. Am. Chem. Soc., 2017, 139, 18468 CrossRef CAS PubMed.
- (a) G.-Z. Zhu, Y. Hashikawa, Y. Liu, Q.-F. Zhang, L. Fung Cheung, Y. Murata and L.-S. Wang, J. Phys. Chem. Lett., 2017, 8, 6220 CrossRef CAS PubMed; (b) G.-Z. Zhu, Y. Liu, Y. Hashikawa, Q.-F. Zhang, Y. Murata and L.-S. Wang, Chem. Sci., 2018, 9, 5666 RSC.
- Y. García-Rodeja, M. Solà and I. Fernández, Phys. Chem. Chem. Phys., 2018, 20, 28011 RSC.
- For reviews on metallabenzenes, see: (a) J. R. Bleeke, Chem. Rev., 2001, 101, 1205 CrossRef CAS PubMed; (b) C. W. Landorf and M. M. Haley, Angew. Chem., Int. Ed., 2006, 45, 3914 CrossRef CAS PubMed; (c) A. F. Dalebrook and L. J. Wright, in Advances in Organometallic Chemistry, ed. F. H. Anthony and J. F. Mark, Academic Press, New York, 2012, vol. 60, pp. 93–177 Search PubMed; (d) X.-Y. Cao, Q. Zhao, Z. Lin and H. Xia, Acc. Chem. Res., 2013, 46, 171 CrossRef PubMed; (e) I. Fernández, G. Frenking and G. Merino, Chem. Soc. Rev., 2015, 44, 6452 RSC; (f) Metallabenzenes, an expert view, ed. L. J. Wright, Wiley, Hoboken, 2017 Search PubMed.
- Y. García-Rodeja and I. Fernández, Chem.–Eur. J., 2017, 23, 6634 CrossRef PubMed.
- B. J. Frogley and L. J. Wright, Angew. Chem., Int. Ed., 2017, 56, 143 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2020 |