Strategies for remote enantiocontrol in chiral gold(III) complexes applied to catalytic enantioselective γ,δ-Diels–Alder reactions

Abstract

The use of chiral square planar gold(III) complexes to access enantioenriched products has rarely been applied in asymmetric catalysis. In this context, we report a mechanistic and synthetic investigation into the use of N-heterocyclic (NHC) gold(III) complexes in γ,δ-Diels–Alder reactions of 2,4-dienals with cyclopentadiene. The optimal catalyst bearing a unique 2-chloro-1-naphthyl substituent allowed efficient synthesis of functionally rich carbocycles in good yields, diastereo- and enantioselectivities. Transition state and multivariate linear regression (MLR) analysis of both catalyst and substrate trends using molecular descriptors derived from designer parameter acquisition platforms, reveals attractive non-covalent interactions (NCIs) to be key selectivity determinates. These analyses demonstrate that a putative π–π interaction between the substrate proximal double bond and the catalyst aromatic group is an essential feature for high enantioselectivity.

---

Introduction

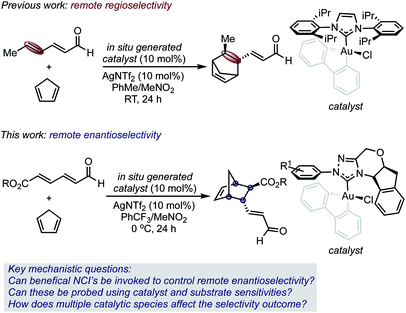
Selective catalysis with transition metal complexes generally requires the transfer of structural information from an ancillary ligand to a transition metal center.¹ As a result of its preferred linear geometry, leveraging the latter to achieve enantioselective homogeneous gold(I) catalysis has proven particularly difficult,² and often requires specialized ligand design.³ It has been hypothesized that this issue could potentially be circumvented by the use of stable gold(III) complexes that, as a result of the square-planar geometry, place an ancillary ligand proximal to the catalyst site.⁴ While some examples of enantioselective gold(III) catalysis have recently been described, support for the concept that these square planar complexes have the ability to leverage selectivity determining non-covalent interactions (NCIs) with substrates in the relevant transition states (TS) remains elusive.^5,6

One of our groups recently demonstrated that such complexes can control site selectivity by promoting additions and cycloadditions to the remote π-bond of 2,4-dienals.^4a For example, gold(III) complexes catalyzed a regioselective Diels–Alder reaction, thereby providing access to structurally complex, cyclic structures from simple substrates (Scheme 1).

Scheme 1 The development of chiral Au(III) complexes for asymmetric Diels–Alder reactions that exhibit γ,δ-selectivity.

The synthetic versatility of the Diels–Alder reaction has inspired a variety of catalytic asymmetric variants; therefore, it is remarkable that 2,4-dienals have yet to be successfully employed as dienophiles in catalytic, enantioselective [4 + 2] cycloadditions with γ,δ-selectivity.^7–9 Despite the exquisite regioselectivity afforded in the gold(III)-catalyzed process, controlling enantioselectivity is more challenging with the site of asymmetric induction distant from the Lewis acid/base interaction.

Given this, we envisioned that this Diels–Alder reaction provided a unique platform to examine the hypothesis that gold(III) complexes can simultaneously control both site and enantioselectivity through remote, attractive NCIs that result from their square planar geometry. In this context, we surmised that the known ability of N-heterocyclic carbene ligands (NHCs) to stabilize gold(III) complexes, combined with their extensive tunability, renders this ligand class an ideal optimization platform.¹⁰ However, the use of chiral NHC gold(III) complexes was projected to involve several additional complications, including the presence of multiple catalytically competent species in solution, which would render the control and interpretation of experimental outcomes difficult. Therefore, the understanding of selectivity discriminants in this process would be important in establishing general design principles for further application of catalyst systems in enantioselective settings.

Herein, we report the development and analysis of a gold(III)-catalyzed asymmetric γ,δ-selective Diels–Alder reaction of 2,4-dienals with cyclopentadiene (Scheme 1). The enantioselectivity outcomes have been rationalized using a combination of DFT and parameterization techniques, which motivated the use of designer transition state (TS) inspired structural descriptor sets.

Results and discussion

Catalyst development and analysis

Our efforts toward applying this strategy in an enantioselective γ,δ-Diels–Alder reaction were initiated with the examination of several common imidazolium ligands on biphenylgold(III) complexes as catalysts¹¹ for the cycloaddition of 2,4-hexadienal (1a) and cyclopentadiene (2) using similar reaction conditions to those previously reported (Fig. 1A).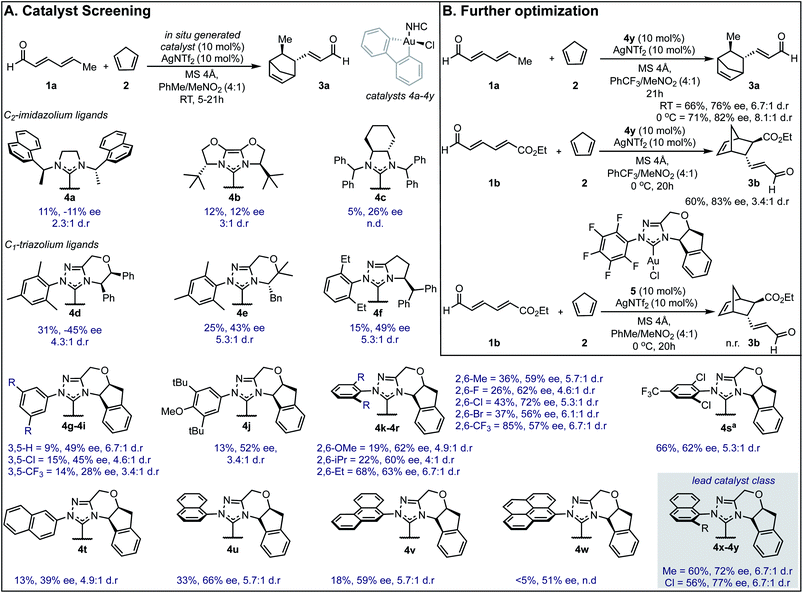

Fig. 1 Reaction optimization data. (A) Catalyst screen identifies 4y as the lead catalyst. Yields were determined as ¹H NMR yields. ^aReaction run at 0 °C. n.d. = not determined, n.r. = no reaction. ee is reported for the major diastereomer. The relative and absolute stereochemistry of 3b was established by comparison of a previously reported sample (see ESI†) and the remainder of the products assigned by analogy. (B) Changing key reaction parameters facilitates further optimization.

When C₂-symmetric imidazolium Au(III) complexes were used, only low ee values were obtained (4a–4c). Next, unsymmetrical chiral triazolium ligands were examined and found to give the product with only modestly improved enantioselectivities (4d–4f). Encouragingly, when more rigid ligands were surveyed, the ee values further increased (4g–4y) and the endo : exo selectivities represented as d.r. remained high. To probe the structural sensitivities, various NHC ligands displaying aromatic substituents with unique substitution patterns were examined. This systematic investigation revealed that bulkier aromatic groups generally afforded higher ee values. Precisely, 2,6-disubstitution was found to be crucial with 2,6-dichlorophenyl affording the highest ee (72% ee) in this catalyst subset, (4k–4r). Further exploration focused on increasing proximal bulk through the introduction of naphthyl substituents wherein 2-chloro-1-naphthyl was revealed to be the lead catalyst affording the product in 77% ee (4y). Interestingly, 2-naphthyl and 9-phenanthryl substituted NHC ligands resulted in lower selectivities (4t and 4v). Several other discrete reaction parameters were explored revealing that using trifluoromethylbenzene (PhCF₃) as solvent gave a similar ee value with a dramatic improvement in conversion (Fig. 1B). Reducing the temperature to 0 °C imparted further improvement in enantioselectivity (from 76% to 82%) without compromising product yield. Additionally, yields could be enhanced by using a more electron deficient substrate, ethyl (2E,4E)-6-oxohexa-2,4-dienoate, 1b, applying this set of reaction conditions. To confirm that in situ reductive elimination¹² of biphenylene from the Au(III) complex to form a potential catalytically competent Au(I) species was not operative, the Au(I) analog, 5, was tested, resulting in no observed product. This experiment also precludes a potential carbophilic Au mechanism, thus, Lewis acid activation of the aldehyde is most plausible.

Intrigued by the sensitivity of the aromatic group on the NHC to enantioselectivity outcomes, we initiated a mechanistic study into interrogating which NCIs impact asymmetric catalysis. We anticipated that a broad scope of techniques would be required to provide a clear picture of how this catalyst system performs. We planned to integrate traditional experimental and density functional theory (DFT) computations with multivariate linear regression (MLR) tools.^13,14 While the TS should reveal key catalyst–substrate interactions that allow efficient transfer of chiral information from catalyst to substrate, a limitation in this approach is that separate calculations for each substrate and catalyst need to be performed. Thus, we viewed MLR analysis as a decisive tool in the interrogation of such interactions in these expanded dimensions.

DFT analysis

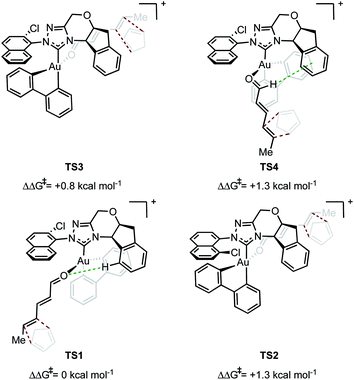
In evaluating the origins of enantioinduction by DFT, all 32 possible C–C forming TSs were located for the reaction shown in Fig. 1A with catalyst 4y. These arise from the following variables; aldehyde orientation (towards or away from the aromatic R substituent), aldehyde coordination site (site 1 as in TS1 or 2 as in TS2 see Fig. 2), cyclopentadiene approach (top or bottom), orientation of cyclopentadiene with respect to the aldehyde (endo or exo) and aromatic group orientation (naphthyl substituent towards the aldehyde or away). Conformers within each family were also explored leading to 109 structures and a corrected free energy spread of 9.6 kcal mol⁻¹. The four lowest TS that led to each of the experimentally observed products are depicted in Fig. 2 (see ESI† for all considered possibilities). The lowest energy TS, TS1, leads to the major product observed experimentally.¹⁵ The TS leading to the opposite enantiomer proceeds via aldehyde coordination at site 2 and is disfavored relative to TS1 by 1.3 kcal mol⁻¹. The computed enantioselectivity arising from TS1 and TS2 is 80% ee, which is in excellent agreement with the experimental value of 77% ee (Fig. 1A). TS2 is destabilized relative to TS1 due to the absence of favorable interactions between the catalyst aromatic group and substrate's proximal double bond (π–π interactions) and a C–H⋯O contact. The lowest energy TS leading to the minor diastereomer is 0.8 kcal mol⁻¹ higher in energy relative to TS1. This corresponds well to the lower experimentally observed endo : exo selectivity than enantioselectivity in the reaction (77% ee vs. 87 : 13 endo : exo). The lowest energy TS leading to the exo diastereomer also proceeds via coordination site 2; therefore, if only one carbene catalyst isomer were present in solution, both higher endo : exo and enantioselectivity would be observed. Our calculations suggest that multiple catalytic species contribute to the overall selectivities. TS4 proceeds via coordination site 1 and similarly to TS1 can engage in several attractive NCIs; however, catalyst distortion deems this a higher energy pathway. In order to test the validity of the results obtained using M06/def2-TZVP//M06/lanl2dz-6-31G(d) as the computational method, key TS were recalculated with M06/def2-TZVP//B3LYP/lanl2dz-6-31G(d). Understanding the form of the potential energy surface (PES) with these conditions would be useful in determining the accuracy of our method, in addition to highlighting any important interactions for stereoinduction. The relative energies of the TS leading to major and minor enantiomeric products between the methods were reasonably altered, reduced to 0.4 kcal mol⁻¹. This disagreement between methods in addition to visual interpretation of the TS (see ESI†) gives us confidence that dispersive interactions are significant stereocontrolling elements and are responsible for the stabilization of TS1. The hybrid DFT, B3LYP method, does not capture this effect.¹⁶ Qualitatively, our calculations support most of the experimental evidence in which catalysts with both large proximal sterics (substituents at the 2 and 6 positions) and extended π systems lead to better performances. In contrast, catalysts with smaller proximal groups that did not introduce the proposed directional and steric effects led to diminished enantioselectivities overall.

Fig. 2 Qualitative models describing the origins of selectivity. Top: exo TS are destabilized relative to endo. Bottom: energetically favorable contacts between catalyst and substrate determine enantioselectivity. Energies calculated in the gas phase at the M06/def2-TZVP//M06/lanl2dz-6-31G(d) level.

Statistical models

While the TS calculations suggest the presence of a number of NCIs dictating the selectivity, a complete mechanistic picture could not be built that was applicable to all catalysts under study. For example, a pyrene-derived catalyst with an extended π system and a large proximal steric profile performed comparably to phenyl. The size and complexity (number of conformations and possibilities to be tried and tested) of the systems under study, makes expanding a traditional computational approach to the study of other catalysts in the series challenging. An alternative strategy is to develop statistical correlations between computationally derived descriptors and experimental performance. This should provide rapid insights into the features important for enantioselectivity for all the catalysts of interest. Owing to its resemblance of the TS, we sought to use the relevant ground states of the carbonyl–NHC–Au(III) complex as an optimal platform for parameter acquisition. We defined the parameter sets as outlined in Fig. 3. Through space interactions between the aromatic substituent and the substrate were isolated from the ground state structures and quantified using the equation, E_int = E_SC − E_cat − E_sub as shown in Fig. 3. E_SC is the energy of the ground state substrate–catalyst complex and this can be dissected into two parts, the catalyst contribution, E_cat and the substrate, E_sub. The difference between these represents, E_int, which is the interaction energy calculated upon complex formation, since the energy to distort the aromatic group and substrate in these isolated forms is both small and consistent (see ESI†).^17,18 This energetic term is a source of more general NCI parameters as not all catalysts in this series exhibit the same features. For example, on inspecting the ground state complexes, the catalyst with large tBu substituents at the 3, 5 positions of the aromatic ring (catalyst 4j, Fig. 1) cannot engage in stacking interactions, instead these are replaced with weaker C–H π interactions. Therefore, these new parameters are a rich source of structural information, which could substantially reduce the number of descriptors required for model development. Sterimol, NBO charges and torsion angles were also acquired from these ground state structures as possible parameters. The dependence of the reaction enantioselectivity on NHC catalysts was investigated by correlation of the selectivities (expressed as ΔΔG^‡). MLR analysis revealed a three-parameter equation to be sufficient to describe the general trends. Techniques such as leave-one-out (LOO) analysis and external validation described the model as relatively robust. As can be seen from Fig. 3B, the selectivity of the reaction is dependent on both large proximal bulk, substituent shape (L and B5) and interaction energies, E_int, which likely describe attractive NCIs, in-line with the analysis from high-level DFT studies of the individual catalyst.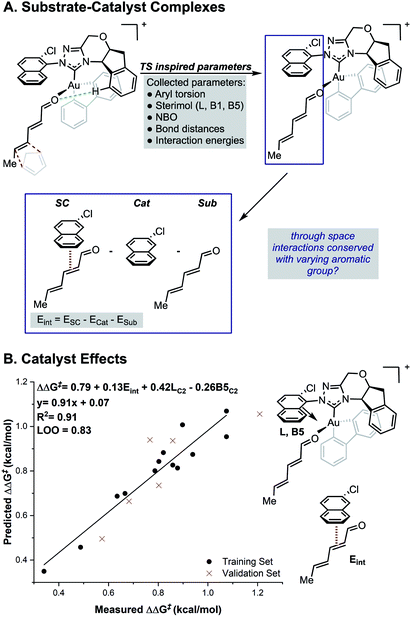

Fig. 3 (A) Deploying substrate–catalyst complexes as parameter acquisition platforms. (B) Steric and interaction energies terms as important selectivity discriminants.

Experimental analysis

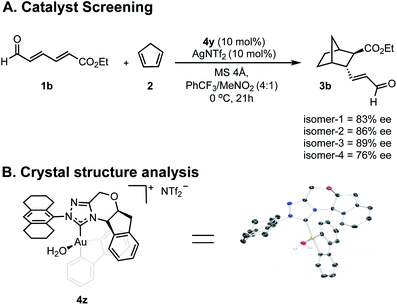
Having greater insight into the origins of enantioinduction, we next focused our efforts on how we could probe the mechanistic details by the experiments summarized in Fig. 4. We performed two types of studies (1) NMR and crystal structure analysis, and (2) enantioselectivity comparisons with different catalyst isomer ratios. Since 4y is composed of four isomers, we first sought to establish the role of the different components in determining the overall enantioselectivity.

Fig. 4 Mechanistic experiments. (A) Reaction under Curtin–Hammett control as suggested by the small changes in ee. (B) X-ray crystal structure analysis establishes the orientation of the biphenyl relative to the carbene.

Envisioning that the individual isomers would exhibit different levels of enantioselectivity, efforts focused on isolating them into pure forms. However, spectroscopic evidence suggested that the isomerization between certain forms can be fast in solution and our isolation efforts were ultimately unsuccessful (see ESI†). Fortunately, samples of isomers in predominant amounts, could be obtained by preparative TLC and as expected each catalyzed the reaction with different levels of enantioselectivity (Fig. 4A). Although the structure of the isomers could not be deduced, the minor enantioselectivity changes, rather than reversal, emphasized these catalyst species are in equilibrium, and their relative thermodynamic stabilities do not determine the stereocontrol (Curtin–Hammett). To further establish the position of the carbene substituents relative to the biphenyl, a new complex was prepared containing an octahydroanthracen-9-yl substituent, 4z. X-ray crystallographic analysis confirms that the lowest energy, carbene catalyst isomer leads to the major product.

Substrate profiling and analysis

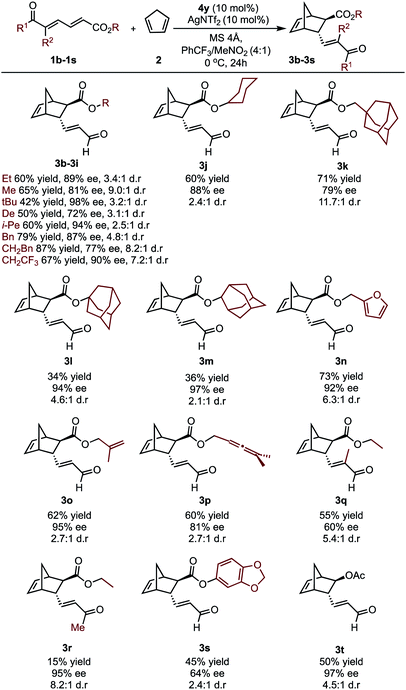
To further investigate whether the key enantioselectivity discriminants translated to a broader range of substrates, using the optimal reaction conditions, the scope of this process was explored as depicted in Table 1 (see ESI† for the determination of absolute configuration of compounds and additional substrates). For these substrates Au(III) activation can presumably occur at either the aldehyde or the ester moiety. However, ester activation requires reaction of the cyclopentadiene at the proximal double bond that is shielded by the catalyst aromatic substituent. As a result, the reaction site is effectively inaccessible, meaning the catalytic mode of activation is likely to be consistent between the two substrate classes. This is further supported by experiment, which determines ester activation to be improbable (see ESI†). Focusing on changes at the ester substituent, in general, incorporating bulky substituents resulted in some of the highest observed enantioselectivities.

Table 1 Substrate scope using catalyst 4y isomer-3. ee and yield is reported for the major diastereomer. The relative and absolute stereochemistry of 3b was established by comparison of a previously reported sample (see ESI) and the remainder of the products assigned by analogy

---

Specifically, alkyl derived ester substituents were well-tolerated, resulting in good to excellent selectivities and moderate to high yields. Interestingly, substrates containing additional unsaturated bonds afforded products 3n–3p cleanly, without intramolecular cyclization. However, increasing the substrate steric profile close to the site of catalyst binding had deleterious effects. This is exemplified by the lower enantioselectivity obtained with the trisubstituted alkene substrate, 1q. Furthermore, when a methyl ketone was used, excellent ee can be obtained; however, lower reactivity resulted in a sharp reduction in yield. The substrate profiling provided us data that could be used to perform MLR with the aim to gain additional information about the features of the substrate that contribute to the enantioselectivity.

In considering the necessary structural requirements for a training set, the ground state structures of (3r). Esters 1b–1s were calculated at the M06-2X/def2-TZVP level of theory and parameters collected (Table 1). Unfortunately, it was not possible to build a readily comprehensible picture of the interactions dictating enantioinduction. This result suggests that the appropriate parameters connecting changes in structure with selectivity were not effectively identified. On the basis of this hypothesis, other platforms for parameter acquisition were examined. We initially investigated the use of uncatalyzed transition states as a consequence of our recent success with this approach.¹⁹ However, we found that for each substrate, the TS failed to accurately resemble that of the catalyzed process, a result of polarization effects introduced by the Au(III). Thus, we sought to amend this strategy to develop a parameter set suited to this complex problem. Transition state analysis with the full catalyst system shows the distinct feature that bond formation is highly asynchronous leading to the question: What simplified “catalyst” structure would exhibit similar effects? In order to devise a protocol which is straightforward to calculate, we selected the simplest model catalyst, a proton. On comparing the series of substrates, it was found that the correct sense of diastereoselectivity was predicted in each case calculated at the M06-2X/6-31G(d,p)//B3LYP/6-31G(d,p) level, suggesting that it reflects the system being probed. To define the parameter library, Sterimol values, bond lengths, dihedral angles were collected on these optimized lowest energy structures to probe the molecular effects. NBO charges were calculated from these structures at the M06-2X/def2TZVP level calculated using NBO6. A simple model consisting of three terms was determined (Fig. 5). The included parameters suggest that strengthening the engagement between the substrate and the catalyst whilst minimizing steric interactions leads to higher enantioselectivities. For example, the negative coefficient with the L term describes likely repulsive interactions between the substituent and the catalyst in TS_major, resulting in a disruption of favorable non-covalent interactions.

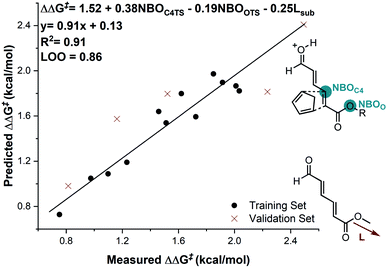Fig. 5 Substrate electron density and steric effects determine enantioselectivity outcomes. Substrate 1c is removed from the correlation.

The inclusion of the substrate 1c, lowers the model correlation coefficient with this substrate performing worse than predicted, a likely consequence of deleterious binding pathways as a function of small ester steric profile. Statistical cross-validation techniques such as LOO and external validation suggest that parameterization of model transition states is an appropriate approach to employ for deeper understanding of important, but subtle NCIs. Consequently, in applying this suite of computational techniques, we were to able uncover both catalyst and substrate sensitivities that affect the enantioselectivity outcome of the reaction, summarized in Fig. 6.

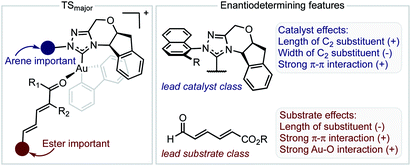Fig. 6 Summary of factors affecting enantioselectivity deduced from mechanistic analysis. The sign determines whether the features contribute negatively or positively.

Conclusions

In summary, we have developed and analyzed, a rare case of enantioselective gold(III) catalysis that can achieve Diels–Alder reactions with exclusive γ,δ-selectivity. The origin of enantioselectivity was investigated by TS and multidimensional correlation analysis, which revealed that a set of subtle, yet, important NCIs are responsible for the observed level of enantioselectivity. In particular, we highlight the ability to demystify MLR correlations based on new TS inspired parameter acquisition platforms. Finally, we demonstrate that these gold(III) complexes are capable of mediating enantioselective transformations through NCIs that have generally eluded their gold(I) counterparts. We anticipate the insight gained from the mechanistic investigations may guide future ligand design for selective gold(III) catalysis.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

M. H. thanks Shanghai Institute of Organic Chemistry (SIOC) and Pharmaron Postdoctoral Fellowship. J. P. R. thanks the EU Horizon 2020 Marie Skłodowska-Curie Fellowship (grant no. 792144), M. S. S. thanks the National Science Foundation (CHE-1763436) and F. D. T. thanks National Institutes of Health (grant R35 GM118190) for support of this work. Computational resources were provided from the Center for High Performance Computing (CHPC) at the University of Utah and the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by the NSF (ACI-1548562) and provided through allocation TG-CHE180003. We thank College of Chemistry's NMR facility, UC Berkeley for resources provided and the staff for their assistance. Instruments in CoC-NMR are supported in part by NIH S10OD024998.

Notes and references

1. For leading references, see: (a) E. N. Jacobsen, A. Pfaltz and H. Yamamoto, Comprehensive Asymmetric Catalysis I-III.: Suppl. I-II, Springer, Berlin, 1999; (b) R. Noyori, Asymmetric Catalysis in Organic Synthesis, Wiley, New York, 1994; (c) I. Ojima, Asymmetric Synthesis, VCH, New York, 1993.
2. A. S. K. Hashmi, Nature, 2007, 449, 292.
3. For recent reviews on enantioselective gold(I) catalysis see: (a) Y. Li, W. Li and J. Zhang, Chem.–Eur. J., 2017, 23, 467; (b) W. Zi and F. D. Toste, Chem. Soc. Rev., 2016, 45, 4567; (c) Y. M. Wang, A. D. Lackner and F. D. Toste, Acc. Chem. Res., 2014, 47, 889; (d) G. Cera and M. Bandini, Isr. J. Chem., 2013, 53, 848.
4. (a) C. Wu, T. Horibe, C. B. Jacobsen and F. D. Toste, Nature, 2015, 517, 449. see also: (b) M. Joost, L. Estévez, K. Miqueu, A. Amgoune and D. Bourissou, Angew. Chem., Int. Ed., 2015, 54, 5236; (c) For an early example of organometallic diarylgold(III) catalysts, see: R. Casado, M. Contel, M. Laguna, P. Romero and S. Sanz, J. Am. Chem. Soc., 2003, 125, 11925.
5. J. Cui, H. Ko, K. Shing, J. Deng, N. C. Lai and M. Wong, Angew. Chem., Int. Ed., 2017, 56, 3074.
6. P. T. Bohan and F. D. Toste, J. Am. Chem. Soc., 2017, 139, 11016.
7. For reviews of enantioselective Diels–Alder reactions involving chiral Lewis acids, see: (a) W. Oppolzer, in Comprehensive Organic Synthesis, ed. B. M. Trost, Pergamon Press, New York, 1991, vol. 5; (b) H. B. Kagan and O. Riant, Chem. Rev., 1992, 92, 1007; (c) L. C. Dias, J. Braz. Chem. Soc., 1997, 8, 289.
8. Recent examples of vinylogous Diels–Alder reactions, see: (a) Z.-J. Jia, H. Jiang, J.-L. Li, B. Gschwend, Q.-Z. Li, X. Yin, J. Grouleff, Y.-C. Chen and K. A. Jørgensen, J. Am. Chem. Soc., 2011, 133, 5053; (b) Z.-J. Jia, Q. Zhou, Q.-Q. Zhou, P.-Q. Chen and Y.-C. Chen, Angew. Chem., Int. Ed., 2011, 50, 8638; (c) K. S. Halskov, T. K. Johansen, R. L. Davis, M. Steurer, F. Jensen and K. A. Jørgensen, J. Am. Chem. Soc., 2012, 134, 12943; (d) Y. Li, F. J. López-Delgado, D. K. B. Jørgensen, R. P. Nielsen, H. Jiang and K. A. Jørgensen, Chem. Commun., 2014, 50, 15689; (e) J. Gu, C. Ma, Q.-Z. Li, W. Du and Y.-C. Chen, Org. Lett., 2014, 16, 3986.
9. X. Tian, N. Hofmann and P. Melchiorre, Angew. Chem., Int. Ed., 2014, 53, 2997.
10. (a) P. Pyykkö and N. Runeberg, Chem.–Asian J., 2006, 1, 623; (b) M. Pažický, A. Loos, M. J. Ferreira, D. Serra, N. Vinokurov, F. Rominger, C. Jäkel, A. S. K. Hashmi and M. Limbach, Organometallics, 2010, 29, 4448.
11. For examples of enantioselective catalysis with chiral NHC gold(I) complexes, see: (a) R. B. Strand, T. Helgerud, T. Solvang, A. Dolva, C. A. Sperger and A. Fiksdahl, Tetrahedron: Asymmetry, 2012, 23, 1350; (b) D. Banerjee, A. K. Buzas, C. Besnard and E. P. Kündig, Organometallics, 2012, 31, 8348; (c) S. Handa and L. M. Slaughter, Angew. Chem., Int. Ed., 2012, 51, 2912; (d) Y. M. Wang, C. N. Kuzniewski, V. Rauniyar, C. Hoong and F. D. Toste, J. Am. Chem. Soc., 2011, 133, 12972; (e) W. Wang, J. Yang, F. Wang and M. Shi, Organometallics, 2011, 30, 3859; (f) Y. Matsumoto, K. B. Selim, H. Nakanishi, K. Yamada, Y. Yamamoto and K. Tomioka, Tetrahedron Lett., 2010, 51, 404.
12. W. J. Wolf, M. S. Winston and F. D. Toste, Nat. Chem., 2014, 6, 159.
13. G.-J. Cheng, X. Zhang, L. W. Chung, L. Xu and Y.-D. Wu, J. Am. Chem. Soc., 2015, 137, 1706.
14. (a) M. S. Sigman, K. C. Harper, E. N. Bess and A. Milo, Acc. Chem. Res., 2016, 49, 1292; (b) C. B. Santiago, J.-Y. Guo and M. S. Sigman, Chem. Sci., 2018, 9, 2398; (c) J. P. Reid and M. S. Sigman, Nat. Rev. Chem., 2018, 2, 290.
15. The absolute stereochemistry of the product was not known throughout the course of the computational investigation. Product stereochemistry was ultimately predicted and confirmed later by experiment.
16. (a) E. R. Johnson, I. D. Mackie and G. A. DiLabio, J. Phys. Org. Chem., 2009, 22, 1127; (b) C. D. Sherrill, Computations of Noncovalent π Interactions, in Reviews in Computational Chemistry, ed. K. B. Lipkowitz and T. R. Cundari, Wiley, New York, 2009, vol. 26, pp. 1– 38; (c) S. Grimme, WIREs Computational Molecular Science, 2011, 1, 211; (d) E. H. Krenske and K. N. Houk, Acc. Chem. Res., 2013, 46, 979.
17. F. M. Bickelhaupt and K. N. Houk, Angew. Chem., Int. Ed., 2017, 56, 10070.
18. Other approaches for calculation of specific attractive non-covalent interaction parameters see: (a) M. Orlandi, J. A. S. Coelho, M. J. Hilton, F. D. Toste and M. S. Sigman, J. Am. Chem. Soc., 2017, 139, 6803; (b) J. A. S. Coelho, A. Matsumoto, M. Orlandi, M. J. Hilton, M. S. Sigman and F. D. Toste, Chem. Sci., 2018, 9, 7153.
19. M. Orlandi, F. D. Toste and M. S. Sigman, Angew. Chem., Int. Ed., 2017, 56, 14080.

---

Footnotes

† Electronic supplementary information (ESI) available. CCDC 1980226. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0sc00497a

‡ Authors contributed equally.

§ Present address: Department of Chemistry, School of Science, Xi'an Key Laboratory of Sustainable Energy Material Chemistry, MOE Key Laboratory for Nonequilibrium Synthesis and Modulation of Condensed Matter, Xi'an Jiaotong University, Xi'an 710049, P. R. China.

---