Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Shape-adaptive single-molecule magnetism and hysteresis up to 14 K in oxide clusterfullerenes Dy2O@C72 and Dy2O@C74 with fused pentagon pairs and flexible Dy–(μ2-O)–Dy angle†
Georgios
Velkos‡
 a,
Wei
Yang‡
b,
Yang-Rong
Yao
c,
Svetlana M.
Sudarkova
ad,
XinYe
Liu
b,
Bernd
Büchner
a,
Stanislav M.
Avdoshenko
a,
Wei
Yang‡
b,
Yang-Rong
Yao
c,
Svetlana M.
Sudarkova
ad,
XinYe
Liu
b,
Bernd
Büchner
a,
Stanislav M.
Avdoshenko
 *a,
Ning
Chen
*a,
Ning
Chen
 *b and
Alexey A.
Popov
*b and
Alexey A.
Popov
 *a
*a
aLeibniz Institute for Solid State and Materials Research Helmholtzstraße 20, 01069 Dresden, Germany. E-mail: s.avdoshenko@ifw-dresden.de; a.popov@ifw-dresden.de
bCollege of Chemistry, Chemical Engineering and Materials Science, Soochow University, Suzhou, Jiangsu 215123, P.R. China. E-mail: chenning@suda.edu.cn
cDepartment of Chemistry, University of Texas at El Paso, 500 W University Avenue, El Paso, Texas 79968, USA
dChemistry Department, Moscow State University, 119991 Moscow, Russia
First published on 20th April 2020
Abstract
Dysprosium oxide clusterfullerenes Dy2O@Cs(10528)–C72 and Dy2O@C2(13333)–C74 are synthesized and characterized by single-crystal X-ray diffraction. Carbon cages of both molecules feature two adjacent pentagon pairs. These pentalene units determine positions of endohedral Dy ions hence the shape of the Dy2O cluster, which is bent in Dy2O@C72 but linear in Dy2O@C74. Both compounds show slow relaxation of magnetization and magnetic hysteresis. Nearly complete cancelation of ferromagnetic dipolar and antiferromagnetic exchange Dy⋯Dy interactions leads to unusual magnetic properties. Dy2O@C74 exhibits zero-field quantum tunneling of magnetization and magnetic hysteresis up to 14 K, the highest temperature among Dy-clusterfullerenes.
Introduction
Endohedral metallofullerenes (EMFs) comprising metal and non-metal atoms in their endohedral species are known as clusterfullerenes.1 Enhanced electrostatic interactions between endohedral lanthanides (Ln) and non-metal ions (Xq−), such as N3−, S2−, or O2−, reinforced by exceptionally short Ln–X bonds result in a strong magnetic anisotropy of Ln ions and lead to the single-molecule magnetism in many Ln-clusterfullerenes.2 Especially Dy-clusterfullerenes are known as robust single molecule magnets (SMMs) with many favourable properties, including thermal and chemical stability, reasonably high blocking temperatures of magnetization, and magnetic hysteresis in bulk samples as well as in monolayers on different substrates.3 Thus, with the improvement of EMF-SMMs, the tremendous progress achieved over the last two decades in the Ln-SMM field4 has a good chance to further advance to the state of device-oriented functional molecular materials.Oxide clusterfullerenes5 with endohedral Ln2O clusters were predicted to have the largest ligand-field splitting in the whole EMF family3g,6 and thus are viable synthetic targets as prospective SMM candidates. Indeed, our recent study of three isomers of Dy2O@C82 revealed their unique magnetic properties.7 The pronounced magnetic anisotropy is combined in these molecules with antiferromagnetic (AFM) exchange interactions, which are the strongest through all dinuclear Dy complexes with non-radical bridging ligands. In this Communication, we report that the encapsulation of the Dy2O cluster in smaller carbon cages has a profound influence on the magnetic properties and leads to the Dy2O@C74 compound with the highest temperature of magnetic hysteresis among clusterfullerene-SMMs.
Results and discussion
Synthesis, molecular and electronic structure
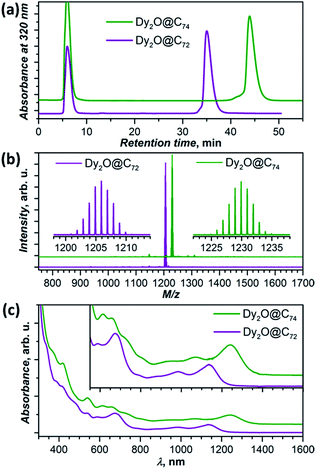
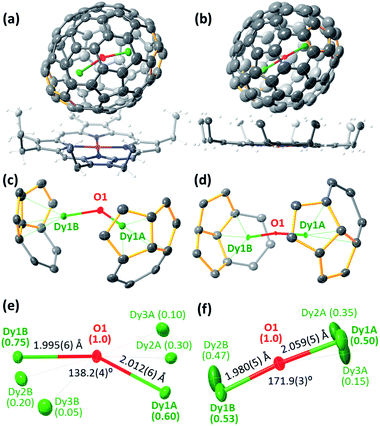
New Dy-oxide clusterfullerenes Dy2O@C72 and Dy2O@C74 were synthesized by arc-discharge evaporation of Dy2O3-filled graphite rods in He/CO2 atmosphere (200/20 Torr) and isolated by multi-step high-performance liquid chromatography (HPLC) as described in ESI.† Basic characterization of the purified Dy2O@C72 and Dy2O@C74, including their HPLC profiles, high-resolution laser desorption ionization mass spectra with characteristic isotopic patterns, and UV-vis-NIR absorption spectra are surveyed in Fig. 1.The molecular structures of Dy2O@C72 and Dy2O@C74 were elucidated by single-crystal X-ray diffraction of co-crystals with NiII(OEP) revealing Cs(10528)–C72 and C2(13333)–C74 carbon cages (Fig. 2a and b).§ Both fullerenes violate the Isolated Pentagon Rule (IPR) and have two pairs of adjacent pentagons, which are stabilized by coordination with Dy ions (Fig. 2c,d). The Cs(10528)–C72 cage was found before in Sc2S@C72,8 Sc2C2@C72,9 and presumably Dy2S@C72.3g The C2(13333)–C74 cage was predicted theoretically as a plausible isomer of Sc2C2@C74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 and was found recently in Ho2O@C74.5c
10 and was found recently in Ho2O@C74.5c
Carbon cages and oxygen atoms are fully ordered in the crystals, but Dy atoms are less ordered with 2–3 sites for each metal atom (Fig. 2e and f). In Dy2O@C72 the Dy–O–Dy angle is 138.2(4)° for the major Dy sites (occupancy 0.60 and 0.75), whereas in Dy2O@C74 the Dy2O cluster is close to the linear shape, similar to the Ho2O cluster in Ho2O@C2(13333)–C74.5c Dy–O bonds are very short, 1.980(5)–2.059(5) Å, but the disorder in Dy positions does not allow detailed analysis. Optimization of the molecular structures performed at the PBE-D level (PAW 4f-in-core potentials, VASP 5.0 code11) resulted in the Dy–O distances and Dy–O–Dy angles of 2.025 Å/138° in Dy2O@C72 and 2.038 Å/180° in Dy2O@C74.
Apparently, the variation of the Dy2O cluster shape from bent to linear is dictated by the Dy⋯Dy distance, which changes from 3.743(1) Å in Dy2O@C72 to 4.030(2) Å in Dy2O@C74 (DFT values are 3.784 and 4.076 Å, respectively). In due turn, the location of Dy atoms inside the fullerene is determined by the arrangement of pentalene units. The distance between centroids of pentalenes in X-ray structures is 8.151 Å in Dy2O@C72 and 8.597 Å in Dy2O@C74. Thus, the shape of the Dy2O cluster is imposed by the fullerene cage form-factor.1c Note that in Dy2O@C82 isomers the cluster is bent despite the larger cage size than in Dy2O@C74: in fact, Dy⋯Dy distances in all Dy2O@C82 structures are shorter than in Dy2O@C74.7 At the same time, the linear shape of the cluster was found in Ho2O@D2d(23)–C84, which also has an elongated shape of the fullerene cage.5d
DFT-based molecular dynamics simulations showed that at 300 K on a timescale of 100 ps metal atoms oscillate near their optimized positions (Fig. S4†). IR spectra calculated from the Fourier transform of the time-dependent dipole moment resemble those computed for the static model and agree well with the experimental spectra (Fig. S5†). Antisymmetric Dy–O stretching vibration is found at 680 cm−1 in Dy2O@C72 and 700 cm−1 in Dy2O@C74.
Electronic absorption spectra of both compounds extend to the near-IR region with the lowest-energy bands at 1137 nm (1.09 eV) in Dy2O@C72 and 1240 nm (1.00 eV) in Dy2O@C74 (Fig. 1c). The spectrum of Dy2O@C72 exhibits a close similarity to the spectra of Sc2S@C72,8 Sc2C2@C72,9 and Dy2S@C723g featuring the same Cs(10528)–C72 cage. However, the cluster composition has a noticeable impact on the lowest energy excitation, found at 1076 nm (Sc2S), 1082 nm (Sc2C2), or 1115 nm (Dy2S). The absorption spectrum of Dy2O@C74 is virtually identical to that of Ho2O@C2(13333)–C74.5c
Further insight into the electronic structure of Dy2O clusterfullerenes is obtained from the electrochemical studies. Cyclic voltammograms are shown in Fig. S6† and redox potentials are listed in Table 1. Both Dy2O@C72 and Dy2O@C74 exhibit one reversible oxidation and three reversible reduction steps as well as poorly reversible fourth reduction and second oxidation steps. DFT calculations show that frontier molecular orbitals of both molecules are localized on their fullerene cages (Fig. S7†), which suggests that the redox processes do not affect the Dy2O cluster. Comparison of the redox potentials of Dy2O@C72 to Sc2S@C72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 and Sc2C2@C72
8 and Sc2C2@C72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 (Table S2†) reveals that the variation of the optical gap discussed above is also reflected in their electrochemical gaps despite the predominant localization of the frontier MOs on the carbon cage in all molecules.
9 (Table S2†) reveals that the variation of the optical gap discussed above is also reflected in their electrochemical gaps despite the predominant localization of the frontier MOs on the carbon cage in all molecules.
| EMF | O–II | O–I | R–I | R–II | R–III | R–IV | GapEC |
|---|---|---|---|---|---|---|---|
| a Measured in TBAPF6/o-dichlorobenzene and referred versus Fe(Cp)2+/0. | |||||||
| Dy2O@C72 | 0.87 | 0.33 | −1.09 | −1.56 | −2.18 | −2.55 | 1.42 |
| Dy2O@C74 | 1.18 | 0.52 | −0.81 | −1.17 | −2.16 | −2.56 | 1.33 |
Magnetic properties
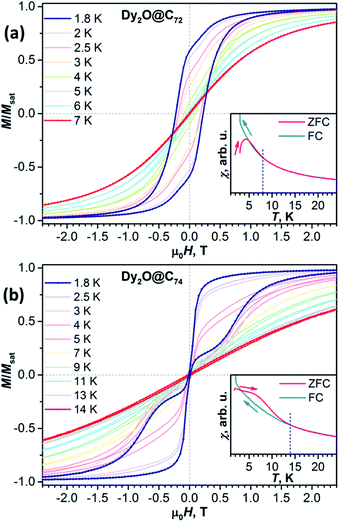
Magnetic hysteresis in Dy2O@C74 closes above 14 K (Fig. S8†). The shape of the hysteresis with the abrupt decay of magnetization near 0 T is different from that of Dy2O@C72 and other dinuclear Dy-clusterfullerenes. Such a “waist-restricted” or “butterfly” hysteresis is characteristic for the quantum tunnelling of magnetization (QTM) in zero field and is common for single-ion magnets, but is not typical for dinuclear SMMs.
Blocking of magnetization is analysed by comparing magnetic susceptibility measured after cooling the sample in zero field (χZFC) and during cooling the sample in field (χFC).13 Blocking temperature TB defined as the peak temperature of χZFC is near 4 K in Dy2O@C72 and 6.7 K in Dy2O@C74 (Fig. 3) when measured in a field of 0.2 T with the temperature sweep rate of 5 K min−1. However, both fullerenes show bifurcation of χZFC and χFC curves (defined as Tirrev13) until noticeably higher temperatures, reaching 8 K for Dy2O@C72 and 14 K for Dy2O@C74. The uncommon shape of χZFC, being higher than χFC, is caused in Dy2O@C74 by the fast QTM at small fields. It should be also noted that TB and Tirrev values are kinetic parameters and depend on the magnetic field, sweep rate, and some technical aspects of the measurements (see Fig. S9–S11† for further measurements and ref. 4d for a more detailed discussion). More universal parameter is the temperature TB100, at which relaxation time of magnetization is 100 s. As determined from the relaxation time measurements described below, TB100 of Dy2O@C72 is 3.4 K in zero field and 2.6 K at 0.2 T. For Dy2O@C74, the TB100 value in zero field is not defined because QTM limits the relaxation time, whereas in the field of 0.2 T the value is 5.0 K.
Relaxation times of magnetization τM below Tirrev (Tables S3–S8 and Fig. S12†) were determined by the stretched exponential fitting of magnetization decay curves recorded after the fast sweep of the magnetic field from 5 T to a required value. Unfortunately, the isolable amounts of the clusterfullerenes are insufficient for the measurement of relaxation times at higher temperatures by AC magnetometry.
Fig. 4a shows the magnetic field dependence of τM measured at a constant temperature. For Dy2O@C72, τM decays fast with the field from 523 s at zero field to 95 s at 0.4 T and then tends to level off. This τM(H) dependence is a clear manifestation of the direct relaxation mechanism. For Dy2O@C74, relaxation rate in 0 T could not be measured because of the fast QTM, and the lowest field studied is 0.05 T. Field dependence at 2.5 K first shows a fast increase of τM from 152 s at 0.05 T to 750–780 s at 0.2–0.35 T. This τM(H) dependence corresponds to the gradual quenching of the QTM by increasing Zeeman splitting. With the further field increase beyond 0.35 T, relaxation accelerates due to the contribution of the direct mechanism as in Dy2O@C72.
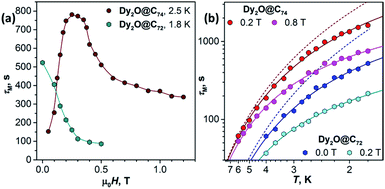 | ||
| Fig. 4 Magnetization relaxation times of Dy2O@C72 and Dy2O@C74: (a) Field dependence of τM at 1.8 K (Dy2O@C72) and 2.5 K (Dy2O@C74). Note that the smallest field for Dy2O@C74 is 0.05 T since the measurements in zero field are not possible because of the fast QTM process; (b) Temperature dependence of τM in two different fields, dots are measured values, solid lines are fits by a combination of Raman and direct mechanisms (eqn (1)), dashed lines are contributions of Raman process for Dy2O@C72 (blue) and Dy2O@74 (red). | ||
The temperature dependence of τM shown in Fig. 4b cannot be described by a direct process alone. Equally good fits are obtained either for a combination of the direct and Raman mechanisms:
| τM−1(T) = Cd,HTnd + CRTnR | (1) |
or by a combination of the direct and Arrhenius process:
| τM−1(T) = Cd,HTnd + τ0−1exp(−Ueff/T) | (2) |
For the direct mechanism nd should be 1, and Cd,H is field-dependent. For each fullerene, temperature dependence was measured in two different fields (Fig. 4b), and then two datasets were fitted jointly either with eqn (1) or with eqn (2) keeping field-independent parameters identical (Fig. S13 and S14†). Eqn (1) gives more physically sound interpretation of the relaxation of magnetization and will be discussed further. For Dy2O@C72, the procedure returned nd = 1.43 ± 0.13, Cd,0 T = (5.2 ± 0.1)·10−4 s−1 K−1.4, Cd,0.2 T = (1.8 ± 0.2)·10−3 s−1 K−1.4, nR = 3.7 ± 0.4, and CR = (8 ± 4)·10−5 s−1 K−3.7. The nd value is higher than 1, which may be due to the phonon bottleneck effect (which increases nd to 2). For Dy2O@C74, we obtained nd = 1.23 ± 0.14, Cd,0.2 T = (1.3 ± 0.3)·10−4 s−1 K−1.25, Cd,0.8 T = (4.9 ± 0.5)·10−4 s−1 K−1.25, nR = 3.28 ± 0.14, and CR = (4 ± 1)·10−5 s−1 K−3.3. For both molecules the direct mechanism dominates at lower temperature and at higher fields, whereas the field-independent Raman process with nR of 3–4 takes over at higher temperatures. These relatively small nR values indicate that optical phonons contribute strongly to the relaxation of magnetization.14 Contribution of the Raman mechanism is shown for each molecule in Fig. 4b. When eqn (2) was used for the fit, Arrhenius processes with effective barriers of 14–16 K were obtained (see ESI†). These values are much smaller than the ligand-field splitting of Dy3+ ions in Dy2O@C2n molecules, but are considerably larger than the energy difference between the states with ferromagnetic and antiferromagnetic coupling of magnetic moments (see below), and thus cannot match the spin energy levels of the system.
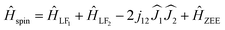 | (3) |
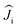 are treated in the |J,mJ〉 basis sets (6H15/2 multiplet). In this notation, the energy difference between FM and AFM-coupled states of the molecule is ΔEAFM–FM = 225j12
are treated in the |J,mJ〉 basis sets (6H15/2 multiplet). In this notation, the energy difference between FM and AFM-coupled states of the molecule is ΔEAFM–FM = 225j12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(α), where α is the angle between quantization axes of two Dy3+ ions.
cos(α), where α is the angle between quantization axes of two Dy3+ ions.
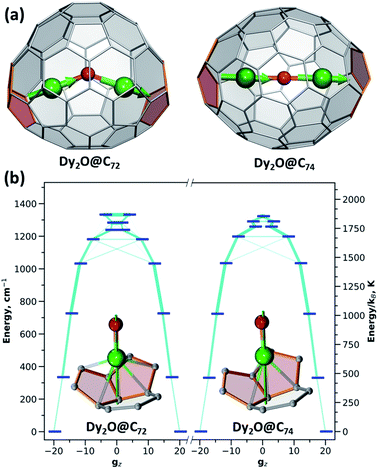
The ligand-field parameters for Dy ions were computed ab initio at the CASSCF(9,7)/SO-RASSI16 level for DyYO@C72 and DyYO@C74 molecules. Given the considerable disorder of experimental structures, DFT-optimized atomic coordinates were used. Ab initio calculations showed that Dy3+ ions in both clusterfullerenes have easy-axis magnetic anisotropy with the quantization axes aligned along the corresponding Dy–O bonds with a deviation of 2°. In |J,mJ〉 representation, the four lowest energy Kramers doublets (KDs) are almost pure states with mJ of 15/2 (ground state), 13/2 (near 340 cm−1), 11/2 (near 720 cm−1), and 9/2 (near 1030 cm−1) (Table S9†). Transition probabilities between these states are thus very low (Fig. 5). Further KDs have a more mixed nature, and at higher temperatures the relaxation of magnetization following the Orbach mechanism is expected to proceed via the fifth KD at 1180–1200 cm−1, which resembles the situation found experimentally in Dy2ScN@C80 with the Orbach barrier of 1206 ± 15 cm−1.3e The overall LF splitting is 1337 cm−1 in Dy2O@C72 and 1329 cm−1 in Dy2O@C74. In brief, both clusterfullerenes have strongly axial magnetic anisotropy with similar energies and state compositions, and their low-temperature magnetic properties are determined exclusively by the ground state KDs.
The coupling constants j12 defining the scale of Dy⋯Dy interactions are determined by fitting of the experimental magnetization curves to eqn (3) (Fig. S15 and S16†). For Dy2O@C72, the best fit is obtained for the ferromagnetic coupling with j12 = 0.009 ± 0.002 cm−1, which gives ΔEAFM–FM = 1.5 ± 0.3 cm−1. For Dy2O@C74, the optimal j12 is less than 0.001 cm−1 with the uncertainty of ±0.002 cm−1. The FM and AFM states in Dy2O@C74 are thus degenerate within |ΔEAFM–FM| < 0.4 cm−1, which means that Dy3+ moments are essentially decoupled.
If a magnetic moment of one of the centers in a dinuclear FM-coupled system is flipped, the system arrives in the AFM-coupled state (and vice versa). As long as the FM and AFM states have a different energy, the ΔEAFM–FMdifference acts as a barrier preventing the QTM, because the latter requires degeneracy of the energy levels. In all dinuclear Dy-clusterfullerenes studied to date the ΔEAFM–FM difference, either positive (FM) or negative (AFM), was large enough to prevent the QTM in zero field. Dy2O@C74 is the first dinuclear Dy-clusterfullerene exhibiting efficient zero-field QTM, which can be explained by the vanishing Dy⋯Dy coupling. In Dy2O@C72, Dy⋯Dy coupling is also weak but still sufficient to quench the QTM in zero field.
The Dy⋯Dy coupling in the Dy2O clusters found in this work – weak FM in Dy2O@C72 and negligible in Dy2O@C74 – is in a sharp contrast with the situation in Dy2O@C82 isomers, featuring strong AFM coupling with ΔEAFM–FM of (5.4–12.9) cm−1.7 Such a large variation of the strength of magnetic interactions in seemingly very similar molecules requires a closer look. The overall Dy⋯Dy coupling in dinuclear spin systems can be divided into exchange and dipolar contributions, ΔEexchAFM–FM and ΔEdipAFM–FM. The latter can be computed exactly when molecular structures and orientations of magnetic moments are known. Using DFT-optimized structures and orientation of quantization axes from ab initio calculations, we obtain ΔEdipAFM–FM of 2.99 cm−1 in Dy2O@C72 and 2.56 cm−1 in Dy2O@C74. Thus, dipolar interactions favour FM arrangement of Dy3+ moments and are of the same size as in Dy2O@C82 isomers with ΔEdipAFM–FM of 2.5–3.0 cm−1. Apparently, small overall coupling in Dy2O@C72,74 results from the cancellation of dipolar coupling by exchange interactions, which are therefore antiferromagnetic. To yield the experimentally determined ΔEAFM–FM energies, ΔEexchAFM–FM values should be −1.5 ± 0.3 cm−1 in Dy2O@C72 and −2.5 ± 0.4 cm−1 in Dy2O@C74. Thus, it is the antiferromagnetic exchange coupling in the Dy2O cluster that is changing strongly from one fullerene to another and is therefore responsible for the considerable variation of the magnetic properties in the series of Dy2O clusterfullerenes. The factors determining exchange interactions in Dy-clusterfullerenes are not very clear yet, and further studies of Dy-oxide clusterfullerenes with different fullerene cages are needed to establish structure–property correlations.
Conclusions
In this work we isolated Dy2O@Cs(10528)–C72 and Dy2O@C2(13333)–C74 clusterfullerenes violating the isolated pentagon rule and characterized their structural, electronic, and magnetic properties. The shape of the Dy2O cluster is determined by the form-factor of the carbon cage and location of pentalene units, leading to the bent cluster in Dy2O@C72 but linear one in Dy2O@C74. Both fullerenes are single molecule magnets showing hysteresis up to 7 K in Dy2O@C72 and 14 K in Dy2O@C74, the latter being the highest temperature among Dy-clusterfullerenes. The magnetic Dy⋯Dy interactions in Dy2O clusters are characterized by the ferromagnetic dipolar coupling counterbalanced by the antiferromagnetic exchange. In Dy2O@C74, these two contributions cancel each other completely leading to decoupled Dy moments and zero-field quantum tunnelling of magnetization. As a result, magnetization of Dy2O@C74 relaxes fast in zero field, but the relaxation becomes slow once the tunnelling is quenched in a finite magnetic field. This study demonstrates that the shape flexibility of the Dy2O cluster and its conformity with the fullerene form-factor is reflected in the substantial variation of the Dy2O-clusterfullerene magnetic properties with the carbon cage. This cage-adaptive SMM behaviour suggests that even stronger variability of magnetic properties may be achieved in future exploration of lanthanide-oxide clusterfullerenes with different carbon cages.Conflicts of interest
There are no conflicts to declare.Acknowledgements
G. Velkos and W. Yang contributed equally to this work. The authors acknowledge funding from the European Union's Horizon 2020 research and innovation programme, European Research Council (grant agreement No. 648295 to A. A. P.), and Marie Skłodowska-Curie action (grant agreement No. 748635 to S. M. A.), and the Deutsche Forschungsgemeinschaft (grants PO 1602/4-1 and 1602/5-1 to A. A. P.). C. N. thanks the National Science Foundation China (NSFC 91961109, 51302178), the NSF of Jiangsu Province (BK20171211), Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD) and the project of scientific and technologic infrastructure of Suzhou (SZS201708). Computational resources were provided by the Center for High Performance Computing at the TU Dresden. We appreciate the help from Dr Anja U. B. Wolter and Sebastian Gaβ in magnetic measurements and technical support with computational resources in IFW Dresden by Ulrike Nitzsche.Notes and references
- (a) S. Yang, T. Wei and F. Jin, Chem. Soc. Rev., 2017, 46, 5005 RSC; (b) A. A. Popov, Endohedral Fullerenes: Electron Transfer and Spin, Springer International Publishing, Cham, 2017 Search PubMed; (c) A. A. Popov, S. Yang and L. Dunsch, Chem. Rev., 2013, 113, 5989 CrossRef CAS PubMed; (d) X. Lu, W. Shen and S. Hu, Chem.–Eur. J., 2020 DOI:10.1002/chem.201905306.
- (a) F. Liu, S. Wang, C.-L. Gao, Q. Deng, X. Zhu, A. Kostanyan, R. Westerström, F. Jin, S.-Y. Xie, A. A. Popov, T. Greber and S. Yang, Angew. Chem., Int. Ed., 2017, 56, 1830 CrossRef CAS PubMed; (b) F. Liu, C.-L. Gao, Q. Deng, X. Zhu, A. Kostanyan, R. Westerström, S. Wang, Y.-Z. Tan, J. Tao, S.-Y. Xie, A. A. Popov and T. Greber, et al. , J. Am. Chem. Soc., 2016, 138, 14764 CrossRef CAS PubMed; (c) R. Westerström, J. Dreiser, C. Piamonteze, M. Muntwiler, S. Weyeneth, K. Krämer, S.-X. Liu, S. Decurtins, A. Popov, S. Yang, L. Dunsch and T. Greber, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 060406 CrossRef; (d) J. Dreiser, R. Westerström, Y. Zhang, A. A. Popov, L. Dunsch, K. Krämer, S.-X. Liu, S. Decurtins and T. Greber, Chem.–Eur. J., 2014, 20, 13536 CrossRef CAS PubMed; (e) R. Westerström, J. Dreiser, C. Piamonteze, M. Muntwiler, S. Weyeneth, H. Brune, S. Rusponi, F. Nolting, A. Popov, S. Yang, L. Dunsch and T. Greber, J. Am. Chem. Soc., 2012, 134, 9840 CrossRef PubMed; (f) T. Wang and C. Wang, Small, 2019, 15, 1901522 CrossRef CAS PubMed; (g) M. Nie, J. Xiong, C. Zhao, H. Meng, K. Zhang, Y. Han, J. Li, B. Wang, L. Feng, C. Wang and T. Wang, Nano Res., 2019, 12, 1727 CrossRef CAS.
- (a) L. Spree and A. A. Popov, Dalton Trans., 2019, 48, 2861 RSC; (b) D. Krylov, F. Liu, A. Brandenburg, L. Spree, V. Bon, S. Kaskel, A. Wolter, B. Buchner, S. Avdoshenko and A. A. Popov, Phys. Chem. Chem. Phys., 2018, 20, 11656 RSC; (c) C. H. Chen, D. S. Krylov, S. M. Avdoshenko, F. Liu, L. Spree, R. Westerström, C. Bulbucan, M. Studniarek, J. Dreiser, A. U. B. Wolter, B. Büchner and A. A. Popov, Nanoscale, 2018, 10, 11287 RSC; (d) C. Schlesier, L. Spree, A. Kostanyan, R. Westerström, A. Brandenburg, A. U. B. Wolter, S. Yang, T. Greber and A. A. Popov, Chem. Commun., 2018, 54, 9730 RSC; (e) D. S. Krylov, F. Liu, S. M. Avdoshenko, L. Spree, B. Weise, A. Waske, A. U. B. Wolter, B. Büchner and A. A. Popov, Chem. Commun., 2017, 53, 7901 RSC; (f) F. Liu, D. S. Krylov, L. Spree, S. M. Avdoshenko, N. A. Samoylova, M. Rosenkranz, A. Kostanyan, T. Greber, A. U. B. Wolter, B. Büchner and A. A. Popov, Nat. Commun., 2017, 8, 16098 CrossRef CAS PubMed; (g) C.-H. Chen, D. S. Krylov, S. M. Avdoshenko, F. Liu, L. Spree, R. Yadav, A. Alvertis, L. Hozoi, K. Nenkov, A. Kostanyan, T. Greber and A. U. B. Wolter, et al. , Chem. Sci., 2017, 8, 6451 RSC; (h) T. Greber, A. P. Seitsonen, A. Hemmi, J. Dreiser, R. Stania, F. Matsui, M. Muntwiler, A. A. Popov and R. Westerström, Phys. Rev. Mater., 2019, 3, 014409 CrossRef CAS; (i) K. Junghans, C. Schlesier, A. Kostanyan, N. A. Samoylova, Q. Deng, M. Rosenkranz, S. Schiemenz, R. Westerström, T. Greber, B. Büchner and A. A. Popov, Angew. Chem., Int. Ed., 2015, 54, 13411 CrossRef CAS PubMed; (j) R. Westerström, A.-C. Uldry, R. Stania, J. Dreiser, C. Piamonteze, M. Muntwiler, F. Matsui, S. Rusponi, H. Brune, S. Yang, A. Popov and B. Büchner, et al. , Phys. Rev. Lett., 2015, 114, 087201 CrossRef PubMed; (k) A. Brandenburg, D. S. Krylov, A. Beger, A. U. B. Wolter, B. Büchner and A. A. Popov, Chem. Commun., 2018, 54, 10683 RSC.
- (a) K. L. M. Harriman, D. Errulat and M. Murugesu, Trends in Chemistry, 2019, 1, 425 CrossRef; (b) A. K. Bar, P. Kalita, M. K. Singh, G. Rajaraman and V. Chandrasekhar, Coord. Chem. Rev., 2018, 367, 163 CrossRef CAS; (c) B. M. Day, F.-S. Guo and R. A. Layfield, Acc. Chem. Res., 2018, 51, 1880 CrossRef CAS PubMed; (d) J.-L. Liu, Y.-C. Chen and M.-L. Tong, Chem. Soc. Rev., 2018, 47, 2431 RSC; (e) Z. Zhu, M. Guo, X.-L. Li and J. Tang, Coord. Chem. Rev., 2019, 378, 350 CrossRef CAS; (f) J. Dreiser, J. Phys.: Condens. Matter, 2015, 27, 183203 CrossRef CAS; (g) S. T. Liddle and J. van Slageren, Chem. Soc. Rev., 2015, 44, 6655 RSC; (h) J. Luzon and R. Sessoli, Dalton Trans., 2012, 41, 13556 RSC; (i) D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110 CrossRef CAS PubMed; (j) C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439 CrossRef CAS PubMed; (k) F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Science, 2018, 362, 1400 CrossRef CAS PubMed; (l) K. R. McClain, C. A. Gould, K. Chakarawet, S. Teat, T. J. Groshens, J. R. Long and B. G. Harvey, Chem. Sci., 2018, 9, 8492 RSC; (m) C. Gould, K. R. McClain, J. Yu, T. J. Groshens, F. Furche, B. G. Harvey and J. R. Long, J. Am. Chem. Soc., 2019, 141, 12967 CrossRef CAS PubMed; (n) F. Liu, G. Velkos, D. S. Krylov, L. Spree, M. Zalibera, R. Ray, N. A. Samoylova, C.-H. Chen, M. Rosenkranz, S. Schiemenz, F. Ziegs and K. Nenkov, et al. , Nat. Commun., 2019, 10, 571 CrossRef CAS PubMed; (o) G. Velkos, D. Krylov, K. Kirkpatrick, L. Spree, V. Dubrovin, B. Büchner, S. Avdoshenko, V. Bezmelnitsyn, S. Davis, P. Faust, J. Duchamp and H. Dorn, et al. , Angew. Chem., Int. Ed., 2019, 58, 5891 CrossRef CAS PubMed; (p) F. Liu, L. Spree, D. S. Krylov, G. Velkos, S. M. Avdoshenko and A. A. Popov, Acc. Chem. Res., 2019, 52, 2981 CrossRef CAS PubMed.
- (a) L. Abella, Y. Wang, A. Rodríguez-Fortea, N. Chen and J. M. Poblet, Inorg. Chim. Acta, 2017, 468, 91 CrossRef CAS; (b) L. Feng, Y. Hao, A. Liu and Z. Slanina, Acc. Chem. Res., 2019, 52, 1802 CrossRef CAS PubMed; (c) A. Liu, M. Nie, Y. Hao, Y. Yang, T. Wang, Z. Slanina, H. Cong, L. Feng, C. Wang and F. Uhlik, Inorg. Chem., 2019, 58, 4774 CrossRef CAS PubMed; (d) H. Cong, A. Liu, Y. Hao, L. Feng, Z. Slanina and F. Uhlik, Inorg. Chem., 2019, 58, 10905 CrossRef CAS PubMed; (e) Q. Tang, L. Abella, Y. Hao, X. Li, Y. Wan, A. Rodríguez-Fortea, J. M. Poblet, L. Feng and N. Chen, Inorg. Chem., 2016, 55, 1926 CrossRef CAS PubMed; (f) Y. Hao, Q. Tang, X. Li, M. Zhang, Y. Wan, L. Feng, N. Chen, Z. Slanina, L. Adamowicz and F. Uhlík, Inorg. Chem., 2016, 55, 11354 CrossRef CAS PubMed; (g) T. Yang, Y. Hao, L. Abella, Q. Tang, X. Li, Y. Wan, A. Rodríguez-Fortea, J. M. Poblet, L. Feng and N. Chen, Chem.–Eur. J., 2015, 21, 11110 CrossRef CAS PubMed; (h) Q. Tang, L. Abella, Y. Hao, X. Li, Y. Wan, A. Rodríguez-Fortea, J. M. Poblet, L. Feng and N. Chen, Inorg. Chem., 2015, 54, 9845 CrossRef CAS PubMed; (i) M. Zhang, Y. Hao, X. Li, L. Feng, T. Yang, Y. Wan, N. Chen, Z. Slanina, F. Uhlik and H. Cong, J. Phys. Chem. C, 2014, 118, 28883 CrossRef CAS; (j) B. Q. Mercado, M. A. Stuart, M. A. Mackey, J. E. Pickens, B. S. Confait, S. Stevenson, M. L. Easterling, R. Valencia, A. Rodriguez-Fortea, J. M. Poblet, M. M. Olmstead and A. L. Balch, J. Am. Chem. Soc., 2010, 132, 12098 CrossRef CAS PubMed.
- M. K. Singh and G. Rajaraman, Chem. Commun., 2016, 52, 14047 RSC.
- W. Yang, G. Velkos, F. Liu, S. M. Sudarkova, Y. Wang, J. Zhuang, H. Zhang, X. Li, X. Zhang, B. Büchner, S. M. Avdoshenko and A. A. Popov, et al. , Adv. Sci., 2019, 6, 1901352 CrossRef CAS PubMed.
- N. Chen, C. M. Beavers, M. Mulet-Gas, A. Rodriguez-Fortea, E. J. Munoz, Y.-Y. Li, M. M. Olmstead, A. L. Balch, J. M. Poblet and L. Echegoyen, J. Am. Chem. Soc., 2012, 134, 7851 CrossRef CAS PubMed.
- Y. Feng, T. Wang, J. Wu, L. Feng, J. Xiang, Y. Ma, Z. Zhang, L. Jiang, C. Shu and C. Wang, Nanoscale, 2013, 5, 6704 RSC.
- P. Zhao, X. Zhao and M. Ehara, Inorg. Chem., 2017, 56, 10195 CrossRef CAS PubMed.
- (a) J. Hafner, J. Comput. Chem., 2008, 29, 2044 CrossRef CAS PubMed; (b) G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS PubMed; (c) G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS; (d) J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed; (e) S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 211 CAS.
- M. Murrie, A. Canaj, S. Dey, O. Cespedes, C. Wilson and G. Rajaraman, Chem. Commun., 2020, 56, 1533 RSC.
- D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, Oxford University Press, New York, 2006 Search PubMed.
- A. Singh and K. N. Shrivastava, Phys. Status Solidi B, 1979, 95, 273 CrossRef CAS.
- N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, J. Comput. Chem., 2013, 34, 1164 CrossRef CAS PubMed.
- (a) F. Aquilante, J. Autschbach, R. K. Carlson, L. F. Chibotaru, M. G. Delcey, L. De Vico, I. F. Galván, N. Ferré, L. M. Frutos, L. Gagliardi, M. Garavelli and A. Giussani, et al. , J. Comput. Chem., 2016, 37, 506 CrossRef CAS PubMed; (b) L. F. Chibotaru and L. Ungur, J. Chem. Phys., 2012, 137, 064112 CrossRef CAS PubMed.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339 CrossRef CAS.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. CCDC 1974305 and 1974314. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0sc00624f |
| ‡ Equal contribution. |
| § Crystals were grown by layering the benzene solution of nickel octaethylporphyrin (Ni(OEP)) onto the CS2 solution of the Dy2O@C2n (2n = 72, 74) isomers. The as-prepared crystals Dy2O@Cs(10528)–C72·Ni(OEP)·2(C6H6) and Dy2O@C2(13333)–C74·Ni(OEP)·C6H6·CS2 were measured with Bruker APEX II at 120 and 173 K, respectively. The structures were solved using direct methods17 and refined on F2 using full-matrix least-squares using the SHELXL2015 crystallographic software package.18 Hydrogen atoms were inserted at calculated positions and constrained with isotropic thermal parameters. The crystal data are presented in Table S1.† The data can be obtained free of charge from the Cambridge Crystallographic Data Centre with CCDC no. 1974305 and 1974314,† respectively. |
| This journal is © The Royal Society of Chemistry 2020 |