Mechanochemical synthesis of glycine oligomers in a virtual rotational diamond anvil cell

Abstract

Mechanochemistry of glycine under compression and shear at room temperature is predicted using quantum-based molecular dynamics (QMD) and a simulation design based on rotational diamond anvil cell (RDAC) experiments. Ensembles of high throughput semiempirical density functional tight binding (DFTB) simulations are used to identify chemical trends and bounds for glycine chemistry during rapid shear under compressive loads of up to 15.6 GPa. Significant chemistry is found to occur during compressive shear above 10 GPa. Recovered products consist of small molecules such as water, structural analogs to glycine, heterocyclic molecules, large oligomers, and polypeptides including the simplest polypeptide glycylglycine at up to 4% mass fraction. The population and size of oligomers generally increases with pressure. A number of oligomeric polypeptide precursors and intermediates are also identified that consist of two or three glycine monomers linked together through C–C, C–N, and/or C–O bridges. Even larger oligomers also form that contain peptide C–N bonds and exhibit branched structures. Many of the product molecules exhibit one or more chiral centers. Our simulations demonstrate that athermal mechanical compressive shearing of glycine is a plausible prebiotic route to forming polypeptides.

---

1 Introduction

Abiotic synthesis of polypeptides is thought to be an important prebiotic stage in the origins of life as such molecules are required to form proteins and more complicated biomolecules.^1–4 Terrestrial and astronomical observations of meteorites and comets have identified the presence of glycine,^5–8 the simplest protein-forming amino acid, which lends support to impacts as a possible source to deliver simple amino acids to ancient Earth and other solar bodies.^2,9–11 In addition to being a viable prebiotic reactant, glycine and its chemistry serve as an important reductionist model for understanding basic polypeptide and protein synthesis in early prebiotic scenarios.^12–24 Theories put forth to explain how glycine forms and reacts under prebiotic conditions to make larger oligomeric structures include thermal cycling at submarine hydrothermal vents,^14,15,18,19 alternating between wet and dry environments,¹³ electron irradiation,²⁵ and impact events.^{16,22,24,26–28} Tidal or tectonic shearing forces within the interiors of planets and moons such as Europa, Enceladus, Triton, and Pluto have also been considered as general drivers of chemistry where subsurface oceans interact with a rocky floor.^29–32 Mechanochemistry can arise during impact events or geological compressive shear scenarios through short-lived deformed or compressive states. This can result in the synthesis of unique materials and metastable molecular compounds due to sudden, highly strained conditions.^33–36

Simulations and experiments on shock-compressed amino acids have demonstrated that polypeptides can form under impact conditions characterized by GPa-range pressure rises and temperature rises of hundreds to thousands of kelvin. Blank et al. performed shock experiments on an aqueous solution of amino acids in the pressure range of 5.1–21 GPa and temperature range of 412–870 K and observed the formation of polypeptides up to dimers.¹⁶ More recently, Sugahara and Mimura performed shock experiments up to 26.3 GPa on cryogenic (77 K) model cometary icy mixtures containing glycine²² and alanine³⁷ and showed oligomerization up to trimers. Sugahara and Mimura also found yields of glycylglycine (diglycine) of up to 1.5% mol ratio of products to reactants and that the yield roughly increases with shock pressure.³⁷ Simulations modeling impacting glycine–water mixtures have shown that even higher pressures and temperatures (48 GPa, 3000 K) can drive the formation larger oligomeric structures that spontaneously rearrange into polyaromatic molecules upon adiabatic expansion.²⁴ Polymerization of dry glycine to form dimers up to 10-mers have also been observed under more modest static pressures ranging from 5–100 MPa at elevated temperatures (423 K) over time frames of 1–32 days.¹⁷ Elevated temperatures appear necessary to drive oligomerization in pure glycine under hydrostatic conditions as Hinton et al. showed that crystalline α-glycine is largely unreactive at room temperature when compressed up to 50 GPa based on Raman spectroscopy and X-ray diffraction measurements.³⁸

A relatively unexplored avenue for prebiotic synthesis is through application of non-hydrostatic (i.e., shear) stresses. Shear stresses can arise in condensed phases due to nonuniform deformations whereby adjacent layers in a fluid or solid are displaced at different rates. This can result in the formation of regions of intense shear deformation, which can lower energetic thresholds for physical and chemical transformations,^39–44 likely in part due to the rapid formation of such highly localized non-equilibrium or mechanochemical conditions. Beyond altering energy landscapes governing stability and kinetics, non-hydrostatic stress loads can also induce plastic deformations in solids when the resulting shear stresses are large. Such stresses can arise during shocks and in macroscopically strained samples, and thus can be expected in both impact-based and tectonic shearing prebiotic synthesis scenarios. One mode for plastic deformation in molecular solids is through shear failure, which can produce shear bands containing disordered or amorphous material.^44–48 Amorphous regions can also form at grain boundaries in polycrystalline samples.⁴⁹ Shear banding through shear failure has been investigated in a number of molecular materials under shock conditions and has been postulated^45–48 and recently demonstrated⁴⁴ to influence the rate at which chemical reactions occur. One cause for increased reactivity is that amorphous materials can exhibit lower reaction activation energies, which leads to faster thermally activated chemistry.⁴⁴ Another possibility that we consider here is that shearing forces have potential to athermally drive reactions in plastically deformed materials through mechanochemistry.

Rotational diamond anvil cells (RDACs) are a specialized experimental tool that can probe sheared material samples under GPa-range compressive loads absent the temperature rise of a shock.^50,51 Similar to a traditional diamond anvil cell, an RDAC compresses a material sample in a small chamber between two gasketed diamonds that is filled with a pressure transmitting medium. Shear is imposed in an RDAC by rotating one of the diamonds with respect to the other, with shear frequently reported in units of “revolutions” of the shearing diamond. When coupled with X-ray diagnostics, RDACs provide a means to study plastic deformations, phase transitions, and even chemistry under controlled conditions.⁵⁰ Compressive shear states accessed in an RDAC were found to drastically lower the room temperature phase transition pressure for the chemically reactive transformation of hexagonal boron-nitride (h)BN to superhard wurtzitic (w)BN by over 40 GPa.⁵² RDAC experiments on molecular organic crystals such as sucrose can induce phase transitions and possibly decomposition reactions at comparatively modest pressures (≤5 GPa).⁵³

Atomistic modeling approaches such as semiempirical quantum-based molecular dynamics (QMD) using density functional tight binding^54–56 (DFTB) can accurately predict chemistry under extreme conditions.^{24,36,44,57–60} Using QMD offers a powerful route to perform computer “experiments” that can help selectively target and interpret more expensive and labor-intensive laboratory experiments. The DFTB method is derived from density functional theory^61,62 (DFT) and offers a competitive balance between computational accuracy and expense that allows for the practical generation of nanoseconds worth of QMD trajectory. This efficiency allows for obtaining ensemble statistics through independent simulations for a given set of conditions, which has proven critical for assessing the wide chemical phase spaces accessible under a variety of non-equilibrium conditions.

We develop a virtual-RDAC (V-RDAC) approach based on QMD that imitates RDAC experiments to model glycine mechanochemistry under compressive shear. The V-RDAC method presented here differs from previous reactive compressive-shear simulations in that we explicitly model diamond-sample interactions rather than imposing shear through deformations of a periodic simulation cell,^42,43,63 which can unrealistically perturb bonds that fall along the cell boundary. This has an advantage in that shearing forces are imposed through a physically realistic interatomic coupling⁵⁰ so that long timescale chemistry under shear can be reliably inferred. Our V-RDAC simulations predict that glycine readily reacts when subject to high strain rate shearing under applied compressive loads greater than ≈7 GPa. Through ensembles of independent simulations we identify the consistent formation of large oligomeric structures including polypeptides and that the mass fraction of oligomers increases as a function of pressure and shear rate. A number of the recovered products exhibit increased chemical complexity beyond simple oligomerization, including the formation of heterocycles and chirality centers.

2 Methods

2.1 General simulation details

Quantum-based molecular dynamics (QMD) simulations were performed using the self-consistent charge DFTB method.^54–56 DFTB is a highly efficient semiempirical approach derived from an expansion of the Kohn–Sham energy⁶² to second order in charge fluctuations. The total DFTB energy is

E_DFTB = E_BS + E_Coul + E_Rep + E_Disp. (1)

Here, E_BS is the electronic band structure energy, which is evaluated within a tight-binding framework,⁶⁴E_Coul captures charge transfer between atoms, E_Rep is an empirical term that accounts for ionic repulsion and Kohn–Sham double counting terms, and E_Disp is an empirical dispersion correction. Parameters for E_BS, E_Coul, and E_Rep were taken from the mio-1-1 parameterization (available at http://www.dftb.org), a typical off-the-shelf parameter set for organic systems. Universal force field dispersion terms⁶⁵ were used for E_Disp.

DFTB-MD simulations were performed using extended Lagrangian Born-Oppenheimer dynamics^66–69 using LAMMPS⁷⁰ with forces and stresses evaluated by the DFTB+ code.⁷¹ The electronic structure was evaluated at the Γ-point only using four self-consistent charge cycles per time step and with Fermi–Dirac thermal smearing⁷² with the electronic temperature set equal to the instantaneous ionic kinetic temperature. All trajectories were integrated using a 0.20 fs time step and a Nosé–Hoover-style thermostat.^73,74 Note that this yields NVT dynamics for portions of the trajectory where the V-RDAC diamond slabs are not translating. We chose to apply a thermostat during the shearing simulations described below to specifically isolate glycine mechanochemistry at a controlled temperature to better match laboratory RDAC experiments. Rapid removal of excess heat from a sheared sample through a thermostat is justified in our V-RDAC simulations as diamond is an exceptionally good thermal conductor.

The DFTB method is rapidly becoming a computational tool of choice for QMD studies of nonequilibrium systems given its efficiency and accuracy relative to DFT and the importance of taking an ensemble-based approach to sample path-dependent chemical processes. Standard DFTB parameter sets such as the one used here provide a reasonable starting point for extrapolating to new conditions and are relatively easy to tune compared to classical force fields given an investment in DFT simulations. Because the DFTB quantum interactions are derived from Kohn–Sham DFT, it generally extrapolates better and is more amenable to refinement than classical reactive force fields. In the case of V-RDAC simulations, one route to develop DFTB parameter sets tuned for shearing conditions would be to force-match the DFTB repulsive potential in eqn (1) to forces from a V-RDAC simulation performed at a DFT level of theory.^23,24,75 Iterative refinement schemes that use DFTB-based QMD as a driver to sample new configurations for which one obtains forces from DFT-level single-point calculations is another promising path towards a semi-automated DFTB model development cycle.

2.2 Virtual rotational diamond anvil cell

Simulations of glycine under compression and shear were performed using the virtual rotational diamond anvil cell (V-RDAC) shown in Fig. 1. The V-RDAC consists of two 2D-periodic diamond crystal slabs with exposed, hydrogen-terminated (111) crystal faces and a material sample contained between them. The hydrogen-terminated (111) face of diamond was calculated to have the lowest surface energy as a function of hydrogen chemical potential.⁷⁷ While the hydrogen-terminated surface likely has a small dipole moment at the diamond/hydrogen interface that could influence chemistry in the sample, this effect is expected to be smaller than with other surface treatments or leaving the diamond unterminated. The generalized crystal-cutting method⁷⁸ (GCCM) was used to obtain an oriented diamond slab in which the target surface normal vector was set to S ‖ [111], which coincides with the crystal face normal vector N₍₁₁₁₎ for cubic crystals such as diamond. An 8-atom cubic primary cell for diamond with DFTB-level optimized lattice length a = 3.555 Å was used as input for the GCCM search. A nearly square slab with 64 carbon atoms was obtained with side lengths x = 8.71 Å and y = 10.05 Å that was oriented such that the surface normal S pointed in the z direction. Terminating hydrogens were placed on both sides of the slab (yielding 96 atoms per slab) and the configuration was optimized in a 3D-periodic cell with the z length was set to 50 Å. This initial slab configuration was replicated and displaced along z to create a large vacuum region and a material sample consisting of twelve randomly oriented and positioned glycine molecules was placed between the two slabs. Upon compression, the initial random placement of glycine molecules leads to a condensed amorphous configuration corresponding to a shear-induced plasticly deformed state within the RDAC. The entire configuration contained 312 atoms. Both diamond slabs were held rigid during all simulations and the sample was treated as flexible. The bottom diamond slab was held fixed and rigid translations of the top diamond were applied to induce compression and shearing on the amorphous glycine sample. Starting from an amorphous state is motivated by the presence of similar disordered regions in sheared molecular crystals^44–48 and polycrystalline samples⁴⁹ and may enhance chemical reactivity relative to the crystal.⁴⁴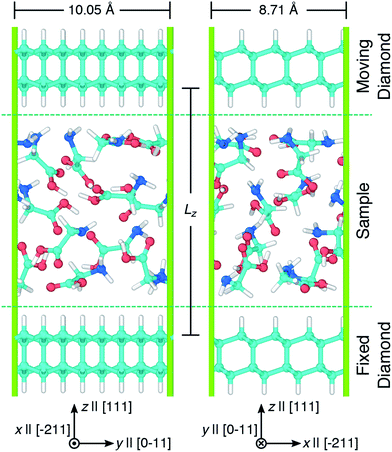

Fig. 1 Snapshots showing two views of the V-RDAC with L_z = 16 Å. Axes highlight the Cartesian lab frame and relevant crystal directions [ijk] in the diamond slabs. Simple shearing was applied to the sample by translating the top diamond along x at specified velocities V_x while holding the bottom diamond fixed. Atom colors are cyan, blue, red, and white for carbon, nitrogen, oxygen, and hydrogen and the periodic simulation cell is drawn with green lines. Snapshots were rendered using OVITO.⁷⁶

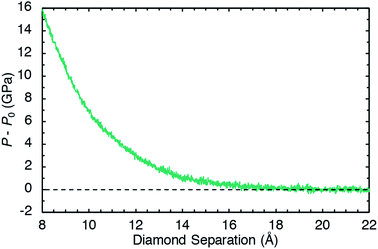
Pressure was applied to the sample through direct manipulation of the diamond separation distance L_z, which was defined to be the displacement between the top-most carbon atoms in the bottom slab and the bottom-most carbon atoms in the top slab. Fig. 2 shows the pressure response during a constant temperature molecular dynamics simulation in which the top diamond was translated at a constant velocity V_z = −1.0 Å ps⁻¹ in the z direction. The (non-zero) system pressure at a large separation distance (L_z = 22 Å) was taken as the reference pressure P₀. Configurations were extracted from the compression simulation at five separation distances (L_z = 8, 9, 10, 11, and 12 Å) to spawn five independent 10 ps NVT unsheared equilibration simulations with fixed diamond slabs. The NVT-average applied pressures for these five separation distances are respectively 15.6, 10.2, 6.7, 4.5, and 2.9 GPa. These five equilibrated configurations were used to spawn ensembles consisting of ten independant shearing simulations at two different shear rates for a total of 100 independent simulations.

Fig. 2 Pressure as a function of diamond separation distance L_z measured with respect to a reference P₀ at L_z = 22 Å obtained from an MD simulation where the top diamond rigidly translates at velocity V_z = −1.0 Å ps⁻¹. The pressure is essentially constant for L_z ≥ 18 Å.

Simple shearing was induced on the amorphous glycine sample at controlled shearing rates by translating the rigid top diamond at a fixed velocity V_x in the x direction. The simple shear rate is defined as

We considered two fixed velocities, V_x = 1.0 Å ps⁻¹ and V_x = 0.5 Å ps⁻¹, which respectively yield shear rates of 1 × 10¹¹ s⁻¹ and 5 × 10¹⁰ s⁻¹ when L_z = 10 Å. While these shear rates are more rapid than those probed in standard RDAC experiments or likely produced in seismic events, they are representative of shear banding in shock impacts^42–45 and also help place an upper bound on the chemistry than can plausibly occur under dynamic conditions. Pressure unloading simulations were performed following shear to gauge product recoverability in which the top diamond slab was translated at velocity V_z = +1.0 Å ps⁻¹ in the z direction for 10 ps. This was followed by a final 10 ps NVT equilibration at ambient pressure. Control simulations were also performed at selected pressures following the same procedure outlined above with the shear rate set to zero (V_x = 0). This provides a baseline for the chemistry under pressure alone to better isolate the influence of shearing.

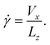2.3 Chemistry analysis

Molecular species were identified in the reactive QMD trajectories using bond distance and lifetime criteria. Atoms were considered bonded if their separation distance fell within a prescribed cutoff for at least 50 fs and molecules were identified as connected components. In our analysis, the bond distance cutoffs were set to 1.8 Å for C–O, C–N, C–C, N–O, N–N, and O–O bonds, 1.3 Å for C–H, N–H, and O–H bonds, and 1.0 Å for H–H bonds. Reducing the cutoffs from 1.8 Å to 1.6 Å and from 1.3 Å to 1.2 Å yielded qualitatively similar trends, described in detail below. Time histories for molecular concentrations and mass fractions were computed for each trajectory. We defined the concentration as the total number of molecules of the same type divided by the total simulation cell volume including vacuum space, which is 10.05 × 8.71 × 50.00 ų = 4376.8 ų. The total volume including vacuum space does not change as the amorphous glycine is compressed. Mass fractions were computed as the total mass of all identical molecules divided by the total mass of the flexible sample (900 a.u.) and is given as a percentage. Both concentrations and mass fractions were averaged over all ten simulations in a given ensemble to obtain better statistics.

3 Results and discussion

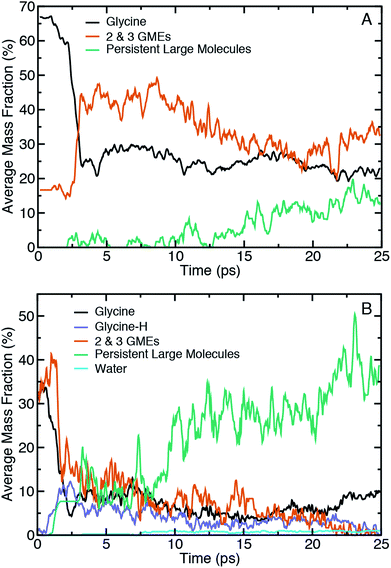
Mechanochemistry of amorphous glycine under compressive shear was predicted through ensembles of QMD simulations using the V-RDAC setup following the procedures described in Section 2.2. The assay of compressive-shear conditions spanned five diamond separation distances L_z (corresponding to 2.9 GPa ≤ P ≤ 15.6 GPa) and two diamond anvil shearing velocities (V_x = 1.0 and 0.5 Å ps⁻¹). Ten independent 25 ps shearing simulations were performed for each condition. Each shearing trajectory was followed by a 10 ps diamond unloading simulation and final 10 ps NVT equilibration at ambient pressure, yielding a total trajectory time of 450 ps for each pressure and shear rate and a grand total of 4.5 ns across all trajectories. Chemical bonding analysis shows that few, if any, reactions occur during the 25 ps shearing portion of the trajectories at the three lowest applied pressures (2.9 GPa, 4.5 GPa, and 6.7 GPa) for both shear rates. In contrast, at the two highest pressures (10.2 GPa and 15.6 GPa) there is significant and dynamically evolving chemistry that predominantly forms oligomers. The qualitative results during shear at the highest shear rate (V_x = 1.0 Å ps⁻¹) are described first, and a more detailed analysis of the chemistry found for each shear rate is described later.

Many distinct molecular species appear in the high-pressure shearing simulations. For the most extreme case at 15.6 GPa, we identified as many as 256 different molecules in a single simulation, although a number of these molecules have lifetimes shorter than 50 fs and are best considered to be transients. To facilitate interpreting these chemically complex trajectories, we initially classify the oligomers into two broad categories. One of these categories corresponds to oligomers with two or more bonded glycine monomers that contain the same number of carbon, nitrogen, and oxygen atoms as an integer number of glycine molecules. We refer to these species as glycine mass equivalents (GMEs) due to their composition. For instance, a 2-GME has the same CNO content as two glycine molecules. Relatively long-lived large molecules and oligomers were also found that we categorize as “persistent large molecules” for the purpose of interpreting chemistry under shearing conditions. The molecules included in this category all had masses greater than glycine, were long-lived enough so that their average mass fraction over the 25 ps shearing simulations was greater than 2%, and are larger than 2- or 3-GMEs. More detailed inspections of chemical trends in the shearing products that we recover at ambient pressure will be made below.

Fig. 3 shows ensemble-averaged time histories of the mass fraction for selected categories of molecules extracted from shearing simulations at V_x = 1.0 Å ps⁻¹ at 10.2 GPa and 15.6 GPa in panels (A) and (B), respectively. The tracked molecular species during shear include glycine, glycine with a missing hydrogen (glycine-H), water, and two classes of oligomeric species defined above. Note that the reported average mass fractions at a given point in time will not necessarily sum to 100% as our analysis neglects species with low average mass fraction and (implicitly) short lifetimes.

Fig. 3 The ensemble-average mass fraction during shear for different types of molecules including glycine, glycine minus a hydrogen atom (glycine-H), the set of 2 and 3 glycine mass equivalents (GMEs), persistent large molecules, and water during the shear simulations at (A) 10.2 GPa and (B) 15.6 GPa. The anvil velocity in both cases is V_x = 1.0 Å ps⁻¹. A block average is taken every 0.02 ps to obtain a smoother trend with time.

Focusing first on the initial state prior to shearing, it is evident that compression alone of amorphous glycine is sufficient to induce some reactivity at these two pressures. The fraction of the system that is distinctly glycine is roughly 67% at 10.2 GPa and 35% at 15.6 GPa. At the same time, there is apparent formation of 2- and 3-GMEs. This might indicate that some backbone altering reactions occur upon compression alone, but could also be partly explained by sensitivity of the bonding analysis to distance cutoff parameters. To better clarify whether the initial mass fractions were an artifact of the chemical analysis, we performed two analogous analyses at the highest pressure in which we either reduced the distance cutoffs or removed the hydrogen atoms to more cleanly identify changes in CNO backbone structures. Plots of the mass fraction time histories obtained through these analyses are provided in Fig. S1 and S2 of the (ESI†) for comparison. Removing hydrogen atoms from the chemical analysis leads to larger initial mass fractions of both glycine (≈42%, an increase of 7%) and the 2- and 3-GMEs. This indicates that the 2- and 3-GMES are not an artifact of the bond distance cutoff criteria for hydrogen. The all-atom analysis using short cutoffs shows that the 2- and 3-GME populations only decrease slightly, demonstrating that the 2- and 3-GMEs are not artifacts of the CNO bond distance cutoff criteria. The mass fraction of glycine decreases by a small amount (to ≈32%, a decrease of 3%) using the short cutoffs, which helps justify our choice of cutoffs. This indicates that some backbone-altering reactions occur upon compression and are not an artifact of chemical analysis. Time history analysis of the pre-shear equilibration trajectories (see Fig. S3 in the ESI†) shows that the system pressure, energy, and chemistry are approximately steady. It should be noted that pressure was applied through a macroscopically fast translation of the diamonds, so one would not necessarily expect similar chemistry in a system compressed very slowly along a quasi-equilibrium path. Extrapolating such a path from QMD is likely to be unreliable given the many orders of magnitude involved, but it could plausibly be approximated as a sequence of structure optimizations.

It is evident that shear initiates a significant amount of chemistry. For instance, within the first 2.5 ps the mass fraction of glycine drops by ≈40% and ≈25% for the lower and higher pressure, respectively. This time delay is at least partially correlated with the time-dependent work done on the sample by the shearing diamonds. As an approximate measure of the work done, the ensemble-averaged change in potential energy during shear for the two shear rates at the two highest pressures is shown in the ESI in Fig. S4,† which reveals that the initial delay for chemical reactions is correlated with an initial increase in potential energy. However, extracting an effective activation energy for shear-induced reactions is difficult to do with precision due to the many physical and chemical processes underlying the potential energy change, including different kinds of chemical reactions, conformational changes, and mechanical work from static and sliding friction. A clear difference with pressure is seen in the time histories for the 2- and 3-GMEs. At 10.2 GPa, there is a rapid increase in the 2- and 3-GME mass fraction after 2.5 ps, after which there is a brief plateau followed by a slow and steady decrease. In contrast, at 15.6 GPa there is initially a sudden increase followed by an effectively monotonic decrease until the mass fraction of 2- and 3-GMEs approaches zero. Decreases in mass fractions of smaller species generally coincide with increases in mass fractions of larger species, with the effect being greatest at the highest pressure. Hydrogen transfer reactions also occur upon shearing at the highest pressure, which leads to the formation of ionic glycine species (e.g., glycine-H) with a reduced number of hydrogens. The fraction of these ionic species reaches a maximum within the first 3 ps of the shearing simulation and steadily declines thereafter. We also note the formation of water at 15.6 GPa beginning at around 7 ps, which indicates that condensation reactions occur.

A dominant trend is the tendency for glycine molecules to oligomerize rather than decompose under shear. This mechanochemical process creates a variety of short-lived and metastable molecular species. Molecular species with short lifetimes could be due to the highly non-equilibrium shearing conditions sampled, but might also indicate that the molecules formed are not particularly stable. To gauge which molecular species formed during shear are (meta)stable and therefore potential recoverable products, we performed additional simulations in which the diamond anvil was unloaded to reduce the pressure to 0 GPa as described in the methods section.

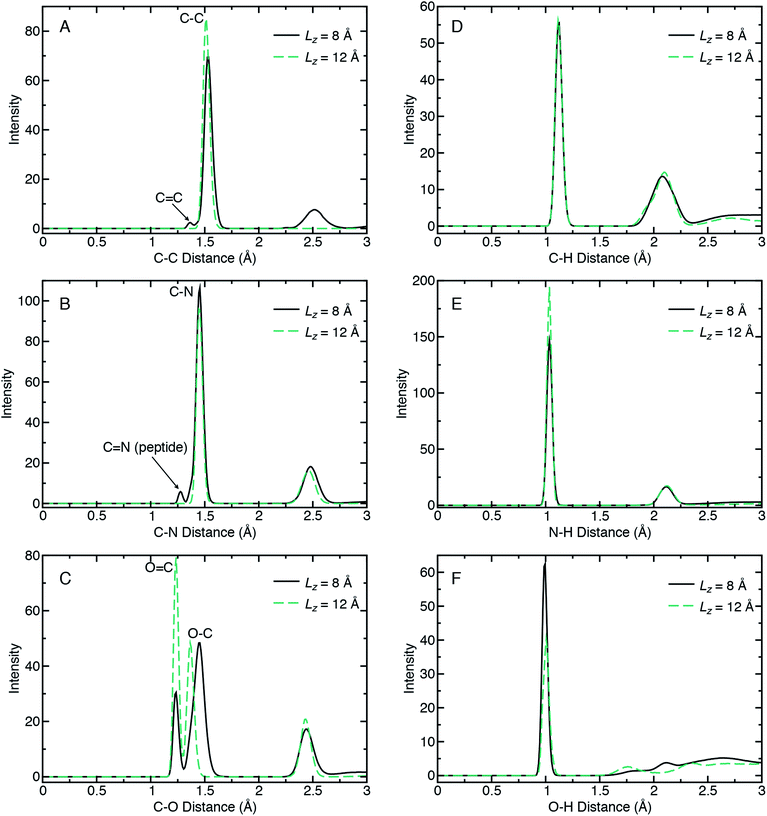
Radial distribution functions (RDFs) can quantify chemical bonding characteristics among the recovered products in terms of a probability density for finding an interaction pair as a function of pair separation distance. When the RDF is calculated for a given pairwise interaction type (e.g., A and B), it yields the probability of finding an atom of type B (or A) at distance R from an atom of type A (or B). Fig. 4 shows RDFs calculated for six interaction types (C–C, C–N, C–O, C–H, N–H, and O–H) for the recovered products obtained from the lowest and highest compression cases (L_z = 12 Å and L_z = 8 Å, respectively) and highest shear rate (V_x = 1.0 Å ps⁻¹). The RDFs were calculated using all ten 10 ps NVT trajectories for a given ensemble. No chemical reactions were observed during these 10 ps, indicating that our set of recovered products are stable on typical QMD timescales. Note that the L_z = 12 Å (2.9 GPa) case corresponds to a system of pure glycine that is predominantly in the neutral charge state.

Fig. 4 Radial distribution functions for recovered products computed from the ensembles of NVT simulations that followed shear at V_x = 1.0 Å ps⁻¹ at diamond separations of L_z = 8 Å and L_z = 12 Å. Interaction pair types are given in the x-axis labels. Panels (A), (B), and (C) in the first column show RDFs for carbon interactions with the heavy atoms C, N, and O. Panels (D), (E), and (F) in the second column show RDFs for hydrogen interactions with the heavy atoms C, N, and O.

Comparison of RDFs for the highly reactive (L_z = 8 Å) and unreactive (L_z = 12 Å) cases reveals a number of changes in chemical bonding structure. Most of these changes are found for the C–C, C–N, and C–O interaction types arranged in the first column of Fig. 4, panels (A)–(C). The C–C RDF in panel (A) clearly reveals the formation of oligomers for L_z = 8 Å, as seen in the new peak at ≈2.5 Å. In contrast, L_z = 12 Å exhibits only a single peak at ≈1.5 Å that corresponds to the C–C bond in glycine. In the reacted case, this C–C peak decreases in intensity, which indicates a loss of C–C bonds, and also splits to form a second small peak at 1.36 Å. This new low-intensity peak indicates a small concentration of C=C double bonds. The most distinctive feature of the C–N RDFs is the appearance of a low-intensity peak at 1.27 Å in the reactive case. This arises from peptidic C=N double bonds from diglycine, larger oligomers, as well as other molecules with C=N double bonds. A more detailed analysis of the exact recovered products is provided later. We note that the predicted C=N bond length of 1.27 Å is a slightly shorter than the peptide bond in α-diglycine crystal (1.32 Å).⁷⁹

The C–O RDF for the unreactive case exhibits three peaks, with the two shortest distance peaks exhibiting narrow distributions. These two correspond to C=O and C–O bonds in the carboxyl group in neutral glycine, due to the O–H bond on one oxygen. The third broader peak arises from 1–3 interactions between oxygen and the non-carboxyl carbon. In the reactive case, the C=O peak decreases in intensity, the C–O peak broadens and shifts to a slightly larger distance, and the third peak remains largely unchanged. The C–O broadening and shift arises due to the formation of O–C–O bridges in the 2 + GMEs and larger oligomers.

From the second column of Fig. 4, we identify only two notable differences in bonds with hydrogen. These are a decrease in the population of N–H bonds and an increase in the population of O–H bonds in the reacted case compared to the unreacted one. Both trends are consistent with the formation of polypeptides and also reflect the propensity for product molecules to exhibit alcohol groups.

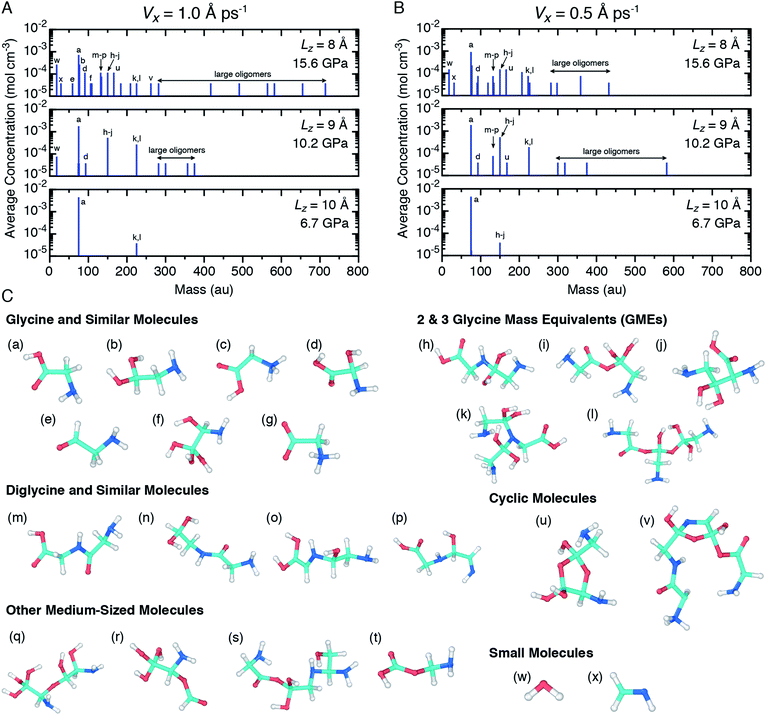
In order to more clearly identify recovered products and also to investigate the pressure and shear rate dependence on the glycine mechanochemistry, ensemble predictions for the mass spectra of recovered products were extracted from the NVT equilibration simulations following shear simulations at both shear rates and are shown in Fig. 5(A) and (B). Configuration snapshots highlighting the chemical diversity of those products are shown in Fig. 5(C). Only glycine was observed as a recovered product for the two lowest pressure cases, so mass spectra plots for those conditions have been omitted from Fig. 5(A) and (B). Readings at the smallest non-zero concentration (3.7 × 10⁻⁵ mol cm⁻³) indicates that only a single molecule of a given mass was identified across all ten independent trajectories. Note that dividing by this amount yields the molecule count in a given ensemble.

Fig. 5 The mass spectrum (on a log scale) of recovered products for shear simulations performed at different pressures and different diamond anvil velocities (A) V_x = 1.0 Å ps⁻¹ and (B) V_x = 0.5 Å ps⁻¹ as well as (C) the representative structures of product molecules. The letters associated with the peaks in (A) and (B) correspond to the structures in (C). The spectra were obtained from the ensembles of the final NVT equilibration simulations at ambient conditions. Molecule categories are described in the text. Dividing the concentrations by 3.7 × 10⁻⁵ mol cm⁻³ yields the molecule count across all ten simulations in a given ensemble.

Several trends are apparent from the mass spectra plots. As the applied pressure increases, the glycine concentration decreases and the concentrations of a variety of other (larger) molecules including diglycine, polypeptides, cyclic molecules, and other large oligomers increases. Concentrations of the 2- and 3-GMEs decreases with pressure from the 10.2 GPa to 15.6 GPa cases, which is consistent with the interpretation of GMEs as reaction intermediates under the reasonable assumption that pressure facilitates rapid chemistry. The dependence of chemistry on the shear rate is less clear. At 10.2 GPa, a larger and more diverse set of products is formed for the slower diamond shearing velocity. In contrast, at 15.6 GPa it is the faster shearing velocity that seemingly leads to larger products. Even with our ensemble approach, there is significant undersampling as many spectral peaks correspond to a single recovered molecule. Thus, we cannot establish a clear trend with shear rate. Analogous ensembles of simulations with a shear rate equal to zero (V_x = 0) were performed at 10.2 GPa and 15.6 GPa and the mass spectra of recovered products are shown in ESI Fig. S5.† Smaller and less diverse products were found when no shear was applied at both pressures, which indicates that shear facilitates the chemistry. Both non-zero shear rates lead to significant chemistry with qualitatively similar features, and thus place bounds on plausible mechanochemistry under very rapid shearing.

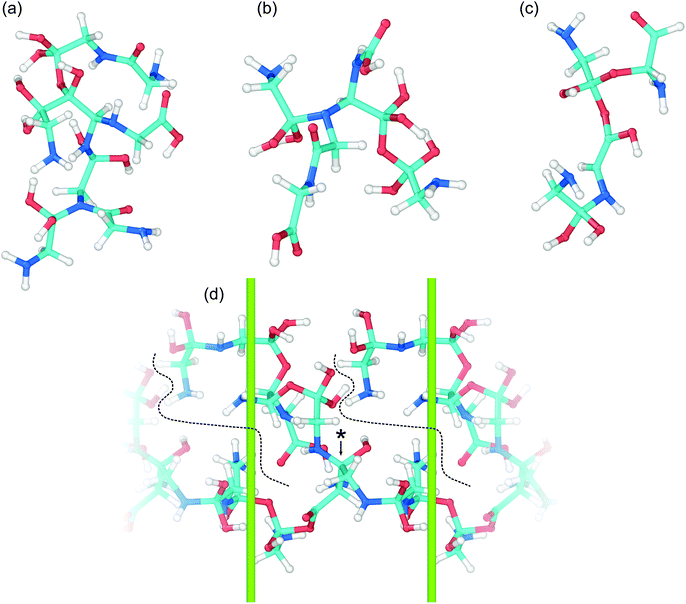
The wide range of different product molecules can be loosely separated into seven categories. The first six categories are shown in Fig. 5(C) and include: (1) glycine and similar molecules, (2) 2- and 3-GMEs, (3) diglycine and similar molecules, (4) cyclic molecules, (5) “other” medium-sized molecules, and (6) small molecules. Fig. 6 shows examples from the seventh category of large oligomers. Molecules were considered similar to glycine if they had the same C–C–N backbone structure, irrespective of oxygen and hydrogen content/placement or CN atom hybridization states. The 2- and 3-GME structures are more diverse and are characterized by containing an equivalent number of C, N, and O atoms to an integer number of glycine molecules. Molecules were considered similar to diglycine if they had the same CNO backbone structure as diglycine, irrespective of hydrogen content/placement or CNO atom hybridization states. If a product molecule contained any small (<10 atom) cyclic structures, it was classified as cyclic. The last three categories sorted remaining molecules that did not fall into categories (1)–(4) based on molecular weight relative to glycine. Small molecules had masses less than glycine, other medium-sized molecules had masses between 1- and 3-GMEs, and the large oligomers had masses greater than 3-GMEs.

Fig. 6 Snapshots of some representative complex large oligomers (a–d) in the recovered products. The large oligomers generally consist of several glycine molecules fused together through C–N, C–C, and/or C–O bridges and in some cases peptide bonds. Example (d) shows a particularly large branched oligomer that spans the dimensions of the simulation cell (green lines). Dashed lines delineate the edges of the oligomer terminated branch and (*) denotes the branching point.

A number of different bonding and functional motifs were found among the various products. Some of the glycine-like molecules contain terminal carboxyl groups (Fig. 5(C)), including the neutral (a) and zwitterionic (g) forms of glycine, whereas others such as (b) and (f) exhibit a terminal sp³ carbon with alcohol groups. Similar trends are seen among the diglycine analogs. Formation of sp³ carbon centers is perhaps not unexpected, as solid carbon allotropes typically exhibit sp³ bonding under high pressure.^80,81 From the product distribution, it is evident that compression and shear can facilitate formation of new peptide (C–N) bonds, yielding diglycine and products with diglycine-like backbones. The highest concentration of diglycine under compressive-shear is found at the highest pressure and shear rate where it is equal to about 1 × 10⁻⁴ mol cm⁻³ (a mass fraction of 4%).

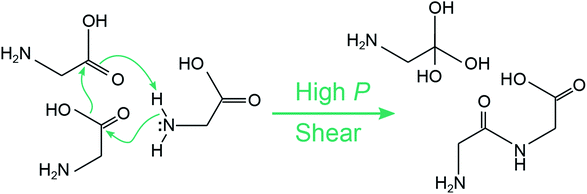
What is perhaps unusual is that diglycine (species (m)) can seemingly form without evolving molecular water, which can be seen upon inspection of the mass spectra for 10.2 GPa and V_x = 0.5 Å ps⁻¹. The formation of diglycine during shear can be seen in ESI Fig. S6,† where it first appears in a single simulation after 1.7 ps of applied shear. We extracted a tentative mechanism for diglycine formation under shear, which is shown in Fig. 7. It is a concerted mechanism that occurs within ≈150 fs and involves three glycine molecules. A hydroxyl group is released from one glycine as an sp³ carbon center forms at the carboxyl group on a neighboring glycine. Simultaneously, a peptide bond forms and a hydrogen is transferred from the amine on a third glycine to form a triol. This results in one diglycine and a triol molecule with sp³ carbon. Under shear, the triol molecule undergoes subsequent reactions and becomes part of a large oligomer. Diglycine was also observed with a higher concentration in the recovered products in the control simulations at 10.2 GPa where no shear was applied, see ESI Fig. S5.† The triol molecule was also found in the recovered products, but no large oligomers or water were present. A time history analysis shown in Fig. S7 of the ESI† reveals that both diglycine and the triol molecule form during the first few ps of the pressure unloading phase, not during the 25 ps while the system is held at static pressure. This could indicate that concerted local motions are required to induce this reaction in amorphous glycine, and that the triol molecule may require compressive shearing to quickly join into a larger oligomer.

Fig. 7 Schematic for the concerted mechanism for 3 glycine molecules to react into diglycine and an intermediate without loss of molecular water that occurs under pressure and shear conditions in amorphous glycine.

Characteristics of the oligomerization process under shear can be inferred from the recovered products. The three 2-GME molecules shown in (h), (i), and (j) are distinguishable in that they respectively involve a C–N, C–O, and C–C bond as the oligomer linkage. The case with C–N linkage (h) is similar to the pre-condensation reaction intermediate for diglycine formation.^19,23 The three different linkage types are likely a consequence of the amorphous starting material and rapid compression and shear rates, with shear forcing bond formation between two glycine molecules respectively oriented in head-to-tail, head-to-head, and tail-to-tail configurations. Despite the idealized amorphous starting configuration, it is not unreasonable to expect similar disordered configurations to arise in crystalline samples as molecular crystals readily form shear bands under complicated stress loads.

Growth of larger GMEs and other large oligomers under shear is not strictly, or even typically, through formation of extended linear structures. The two 3-GMEs shown in (k) and (l) exhibit branched structures, respectively with pseudo-tertiary and -quaternary linkage points at central nitrogen and carbon atoms. Although not a 3-GME, product (s) is a linear oligomer of three glycine molecules linked by C–O and C–N bonds. Inspection of Fig. 6 highlights that growth of larger oligomers involves both branching and linear chain extension. The example in 6(c) is mostly linear, exhibiting only a single quaternary sp³ carbon branch point. The other larger examples all exhibit more branching. Example 6(d) is a notable case in that part of the molecule extends through the periodic boundary, while the rest leads off to a terminated branch at point (*).

Beyond the formation of large oligomeric structures, the set of recovered products highlights that shear is a possible driver for formation of at least two other notable chemical motifs from simple precursors such as glycine. The first of these is synthesis of small heterocycles and the second is formation of chiral centers from achiral precursors. Although cyclic molecules produced in this study have low concentrations, the two identified in our shearing simulations are found in a number of natural products and other biomolecules. Product (u) is a functionalized dioxolane and product (v) is a functionalized amine-terminated oxazole. Dioxalanes are natural products⁸² and oxazoles are parent compounds for a number of heterocyclic aromatic organic molecules.⁸³ Many of the products exhibit one or more chiral centers. Product 6(b) is distinct in that it is a large oligomer without a chiral center. Glycine analog (d) is the smallest chiral molecule among our product distribution, and while it is not an amino acid, it does exhibit the requisite carboxyl-amine form of one. Other larger chiral molecules include 3-GME (l), diglycine analogs (o) and (p), both cyclic molecules, and products (q), (r), and (s).

4 Conclusions

We develop a quantum-based molecular dynamics (QMD) approach to model chemistry inside a rotational diamond anvil cell (RDAC) and apply this approach to predict upper bounds on the compressive-shear induced chemistry of glycine. Our virtual-RDAC (V-RDAC) simulation design explicitly models a material sample placed between hydrogen-terminated (111) crystal faces of diamond that apply compression and simple shear. Ensembles of V-RDAC QMD simulations were performed using semiempirical density functional tight binding (DFTB) to sample reactivity under compressive loads between 2.9 GPa ≤ P ≤ 15.6 GPa at two different shear rates. Although the shear rates are higher than those in typical RDAC experiments, the shear rates could have been experienced in small terrestrial areas in subsurface oceans or in shear bands under dynamic compression on short timescales. The simulations therefore help put bounds on the plausible chemistry that can occur under such dynamic conditions.

Our V-RDAC simulations predict a lower bound on the pressure where glycine undergoes mechanochemical oligomerization of about 10 GPa at room temperature, and oligomerization increases at higher pressures and shear rates. A large variety of molecules appear in the simulations including molecules with new peptide bonds, chains of glycine molecules connected by C–C, C–O, or C–N bridges, large branched oligomers with atomic masses between 300–800 a.u., and cyclic molecules. The polypeptide glycylglycine is found to have a somewhat high average mass fraction of 4% in the recovered products from the simulations at the highest pressure and shear rate. A number of the large oligomers contain peptide bonds along with non-peptidic C–C, C–O, and C–N bridges and branching points at central C or N atoms. These oligomeric species are likely intermediates to peptide-forming condensation reactions and may react further over time scales beyond those accessible with QMD. Many of the molecules formed from sheared compressed glycine exhibit one or more chirality centers. Our study provides a “bottom-up” methodology and prospectus for predicting possible mechanochemical or shear induced prebiotic chemistry that can help bound future RDAC studies as well as determine feasible life-building chemical pathways that might have occurred on early Earth.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank Samantha Clarke and Elissaios Stavrou for many useful discussions. This work was supported by the Laboratory Directed Research and Development Program at LLNL under project 18-LW-036. This work was performed under the auspices of the U.S. Department of Energy by Lawrence Livermore National Laboratory under Contract DE-AC52-07NA27344. Released under IM number LLNL-JRNL-799841.

Notes and references

1. S. L. Miller, Science, 1953, 117, 528–529.
2. C. Chyba and C. Sagan, Nature, 1992, 355, 125–132.
3. W. L. Marshall, Geochim. Cosmochim. Acta, 1994, 58, 2099–2106.
4. G. Danger, R. Plasson and R. Pascal, Chem. Soc. Rev., 2012, 41, 5416–5429.
5. J. Oró, J. Gibert, H. Lichtenstein, S. Wikstrom and D. A. Flory, Nature, 1971, 230, 105–106.
6. M. A. Sephton, Nat. Prod. Rep., 2002, 19, 292–311.
7. J. E. Elsila, D. P. Glavin and J. P. Dworkin, Meteorit. Planet. Sci., 2009, 44, 1323.
8. K. Altwegg, H. Balsiger, A. Bar-Nun, J.-J. Berthelier, A. Bieler, P. Bochsler, C. Briois, U. Calmonte, M. R. Combi, H. Cottin, J. De Keyser, F. Dhooghe, B. Fiethe, S. A. Fuselier, S. Gasc, T. I. Gombosi, K. C. Hansen, M. Haessig, A. Jäckel, E. Kopp, A. Korth, L. Le Roy, U. Mall, B. Marty, O. Mousis, T. Owen, H. Rème, M. Rubin, T. Sémon, C.-Y. Tzou, J. Hunter Waite and P. Wurz, Sci. Adv., 2016, 2, 1–5.
9. A. Brack, Chem. Biodiversity, 2007, 4, 665–679.
10. S. Pizzarello and E. Shock, Cold Spring Harbor Perspect. Biol., 2010, 2, 1–19.
11. P. Schmitt-Kopplin, Z. Gabelica, R. D. Gougeon, A. Fekete, B. Kanawati, M. Harir, I. Gebefuegi, G. Eckel and N. Hertkorn, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 2763–2768.
12. H. Borsook, Adv. Protein Chem., 1953, 8, 127–174.
13. H. Yanagawa, K. Kojima, M. Ito and N. Handa, J. Mol. Evol., 1990, 31, 180–186.
14. E. L. Shock, Geochim. Cosmochim. Acta, 1992, 56, 3481–3491.
15. E.-i. Imai, H. Honda, K. Hatori, A. Brack and K. Matsuno, Science, 1999, 283, 831–833.
16. J. G. Blank, G. H. Miller, M. J. Ahrens and R. E. Winans, Origins Life Evol. Biospheres, 2001, 31, 15–51.
17. S. Ohara, T. Kakegawa and H. Nakazawa, Origins Life Evol. Biospheres, 2007, 37, 215–223.
18. K. H. Lemke, R. J. Rosenbauer and D. K. Bird, Astrobiology, 2009, 9, 141.
19. E. Schreiner, N. N. Nair and D. Marx, J. Am. Chem. Soc., 2009, 131, 13668–13675.
20. K. Sakata, N. Kitadai and T. Yokoyama, Geochim. Cosmochim. Acta, 2010, 74, 6841–6851.
21. E. Van Dornshuld, R. A. Vergenz and G. S. Tschumper, J. Phys. Chem. B, 2014, 118, 8583–8590.
22. H. Sugahara and K. Mimura, Geochem. J., 2014, 48, 51–62.
23. M. P. Kroonblawd, F. Pietrucci, A. M. Saitta and N. Goldman, J. Chem. Theory Comput., 2018, 14, 2207–2218.
24. M. P. Kroonblawd, R. K. Lindsey and N. Goldman, Chem. Sci., 2019, 10, 6091–6098.
25. R. I. Kaiser, A. M. Stockton, Y. S. Kim, E. C. Jensen and R. A. Mathies, Astrophys. J., 2013, 765, 111.
26. N. Goldman, E. J. Reed, L. E. Fried, I.-F. W. Kuo and A. Maiti, Nat. Chem., 2010, 2, 949–954.
27. Z. Martins, M. C. Price, N. Goldman, M. A. Sephton and M. J. Burchell, Nat. Geosci., 2013, 6, 1045–1049.
28. N. Goldman and I. Tamblyn, J. Phys. Chem. A, 2013, 117, 5124–5131.
29. T. Stevens, FEMS Microbiol. Rev., 1997, 20, 327–337.
30. M. Y. Zolotov and E. L. Shock, J. Geophys. Res.: Planets, 2004, 109, E06003.
31. J. R. Spencer, A. C. Barr, L. W. Esposito, P. Helfenstein, A. P. Ingersoll, R. Jaumann, C. P. McKay, F. Nimmo and J. H. Waite, in Enceladus: An Active Cryovolcanic Satellite, ed. M. K. Dougherty, L. W. Esposito and S. M. Krimigis, Springer Netherlands, Dordrecht, 2009, pp. 683–724.
32. Y. Harada, S. Goossens, K. Matsumoto, J. Yan, J. Ping, H. Noda and J. Haruyama, Nat. Geosci., 2014, 7, 569.
33. P. W. Bridgman, Phys. Rev., 1935, 48, 825–847.
34. J. J. Gilman, Science, 1996, 274, 65.
35. S. L. James, C. J. Adams, C. Bolm, D. Braga, P. Collier, T. Friščić, F. Grepioni, K. D. M. Harris, G. Hyett, W. Jones, A. Krebs, J. Mack, L. Maini, A. G. Orpen, I. P. Parkin, W. C. Shearouse, J. W. Steed and D. C. Waddell, Chem. Soc. Rev., 2012, 41, 413–447.
36. M. P. Kroonblawd and N. Goldman, Phys. Rev. B, 2018, 97, 184106.
37. H. Sugahara and K. Mimura, Icarus, 2015, 257, 103–112.
38. J. K. Hinton, S. M. Clarke, B. A. Steele, I.-F. W. Kuo, E. Greenberg, V. B. Prakapenka, M. Kunz, M. P. Kroonblawd and E. Stavrou, CrystEngComm, 2019, 21, 4457–4464.
39. J. J. Gilman and R. W. Armstrong, AIP Conf. Proc., 1994, 309, 199–202.
40. T. Luty, P. Ordon and C. J. Eckhardt, J. Chem. Phys., 2002, 117, 1775.
41. M. M. Kuklja and S. N. Rashkeev, Appl. Phys. Lett., 2007, 90, 151913.
42. S. V. Zybin, W. A. Goddard, P. Xu, A. C. T. van Duin and A. P. Thompson, Appl. Phys. Lett., 2010, 96, 081918.
43. T. Zhou, S. V. Zybin, Y. Liu, F. Huang and W. A. Goddard, J. Appl. Phys., 2012, 111, 124904.
44. M. P. Kroonblawd and L. E. Fried, Phys. Rev. Lett., 2020, 124, 206002.
45. M. J. Cawkwell, T. D. Sewell, L. Zheng and D. L. Thompson, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 014107.
46. J. J. Rimoli, E. Gürses and M. Ortiz, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 014112.
47. R. A. Austin, N. R. Barton, J. E. Reaugh and L. E. Fried, J. Appl. Phys., 2015, 117, 185902.
48. M. J. Cawkwell, N. Mohan, D. J. Luscher and K. J. Ramos, Philos. Mag., 2019, 99, 1079–1089.
49. H. Zhang, D. J. Srolovitz, J. F. Douglas and J. A. Warren, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 7735–7740.
50. Y. Ma, V. I. Levitas and J. Hashemi, J. Phys. Chem. Solids, 2006, 67, 2083–2090.
51. J. A. Ciezak and T. A. Jenkins, Rev. Sci. Instrum., 2011, 82, 073905.
52. C. Ji, V. I. Levitas, H. Zhu, J. Chaudhuri, A. Marathe and Y. Ma, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 19108–19112.
53. J. A. Ciezak-Jenkins and T. A. Jenkins, J. Appl. Phys., 2018, 123, 085901.
54. D. Porezag, T. Frauenheim, T. Köhler, G. Seifert and R. Kaschner, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 12947–12957.
55. M. Elstner, D. Porezag, G. Jungnickel, J. Elsner, M. Haugk, T. Frauenheim, S. Suhai and G. Seifert, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 7260–7268.
56. P. Koskinen and V. Mäkinen, Comput. Mater. Sci., 2009, 47, 237–253.
57. L.-P. Wang, A. Titov, R. McGibbon, F. Liu, V. S. Pande and T. J. Martínez, Nat. Chem., 2014, 6, 1044–1048.
58. M. J. Cawkwell, A. M. N. Niklasson and D. M. Dattelbaum, J. Chem. Phys., 2015, 142, 064512.
59. M. P. Kroonblawd, N. Goldman and J. P. Lewicki, J. Phys. Chem. B, 2018, 122, 12201–12210.
60. E. Martínez, R. Perriot, E. M. Kober, P. Bowlan, M. Powell, S. McGrane and M. J. Cawkwell, J. Chem. Phys., 2019, 150, 244108.
61. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871.
62. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138.
63. B. Steele and J. P. Larentzos, ARL Technical Report, 2016, vol. 0784, p. 24.
64. J. C. Slater and G. F. Koster, Phys. Rev., 1954, 94, 1498–1524.
65. A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. Goddard III and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035.
66. A. M. N. Niklasson, C. J. Tymczak and M. Challacombe, Phys. Rev. Lett., 2006, 97, 123001.
67. A. M. N. Niklasson, Phys. Rev. Lett., 2008, 100, 123004.
68. A. M. N. Niklasson, P. Steneteg, A. Odell, N. Bock, M. Challacombe, C. J. Tymczak, E. Holmström, G. Zheng and V. Weber, J. Chem. Phys., 2009, 130, 214109.
69. G. Zheng, A. M. N. Niklasson and M. Karplus, J. Chem. Phys., 2011, 135, 044122.
70. S. Plimpton, J. Comput. Phys., 1995, 117, 1–19.
71. B. Aradi, B. Hourahine and T. Frauenheim, J. Phys. Chem. A, 2007, 111, 5678–5684.
72. N. D. Mermin, Phys. Rev., 1965, 137, A1441–A1443.
73. S. Nosé, J. Chem. Phys., 1984, 81, 511–519.
74. W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697.
75. N. Goldman, L. E. Fried and L. Koziol, J. Chem. Theory Comput., 2015, 11, 4530–4535.
76. A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2010, 18, 015012.
77. S. Hong and M. Y. Chou, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 6262–6265.
78. M. P. Kroonblawd, N. Mathew, S. Jiang and T. D. Sewell, Comput. Phys. Commun., 2016, 207, 232–242.
79. S. A. Moggach, D. R. Allan, S. Parsons and L. Sawyer, Acta Crystallogr., Sect. B: Struct. Sci., 2006, 62, 310–320.
80. X. Wang, S. Scandolo and R. Car, Phys. Rev. Lett., 2005, 95, 185701.
81. A. A. Correa, S. A. Bonev and G. Galli, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 1204.
82. F. E. Ziegler, C. A. Metcalf, A. Nangia and G. Schulte, J. Am. Chem. Soc., 1993, 115, 2581–2589.
83. I. J. Turchi and M. J. S. Dewar, Chem. Rev., 1975, 75, 389–437.

---

Footnote

† Electronic supplementary information (ESI) available: Validation of chemical analysis. See DOI: 10.1039/d0sc00755b

---