Open Access Article
Open Access ArticleSpin-chemical effects on intramolecular photoinduced charge transfer reactions in bisphenanthroline copper(I)-viologen dyad assemblies†
Megan S.
Lazorski‡§
 *a,
Igor
Schapiro‡¶
*a,
Igor
Schapiro‡¶
 b,
Ross S.
Gaddie
a,
Ammon P.
Lehnig
a,
Mihail
Atanasov
b,
Frank
Neese
b,
Ross S.
Gaddie
a,
Ammon P.
Lehnig
a,
Mihail
Atanasov
b,
Frank
Neese
 *b,
Ulrich E.
Steiner
*b,
Ulrich E.
Steiner
 *c and
C. Michael
Elliott||
a
*c and
C. Michael
Elliott||
a
aDepartment of Chemistry, Colorado State University, Fort Collins, CO 80523, USA. E-mail: mlazorsk@msudenver.edu
bMax Planck Institute for Chemical Energy Conversion, D-45470 Mülheim an der Ruhr, Germany
cDepartment of Chemistry, University of Konstanz, Universitätsstraße 14, Konstanz, 78457, Germany
First published on 12th May 2020
Abstract
Two covalently linked donor–acceptor copper phenanthroline complexes (C–A dyads) of interest for solar energy conversion/storage schemes, [Cu(I)(Rphen(OMV)24+)2]9+ = RC+A48+ with RC+ = [Cu(I)Rphen2]+ involving 2,9-methyl (R = Me) or 2,9-phenyl (R = Ph)-phenanthroline ligands that are 5,6-disubstituted by 4-(n-butoxy) linked methylviologen electron acceptor groups (A2+ = OMV2+), have been synthesized and investigated via quantum chemical calculations and nanosecond laser flash spectroscopy in 1,2-difluorobenzene/methanol (dfb/MeOH) mixtures. Upon photoexcitation, charge transfer (CT) states RC2+A+A36+ are formed in less than one ns and decay by charge recombination on a time scale of 6–45 ns. The CT lifetime of RC2+A+A36+ has a strong dependence on MeOH solvent fraction when R = Me, but is unaffected if R = Ph. This solvent effect is due to coordination of MeOH solvent in MeC+A48+ (i.e. exciplex formation) allowed by conformational flattening of the ligand sphere, which cannot occur in PhC+A48+ having bulkier Phphen ligand framework. Interestingly, the decay time of the CT state increases for both species at low magnetic fields with a maximum increase of ca. 30% at ca. 150 mT, then decreases as the field is increased up to 1500 mT, the highest field investigated. This magnetic field effect (MFE) is due to magnetic modulation of the spin dynamics interconverting 3CT and 1CT states. A quantitative modeling according to the radical pair mechanism involving ab initio multireference calculations of the complexes revealed that the spin process is dominated by the effect of Cu hyperfine coupling. The external magnetic field suppresses the hyperfine coupling induced spin state mixing thereby lengthening the CT decay time. This effect is counteracted by the field dependent processes of T0–S mixing through the Δg-mechanism and by a local mode spin–orbit mechanism. Further, the maximum MFE is limited by a finite rate of direct recombination of 3CT states and the spin-rotational mechanism of spin relaxation. This study provides a first comprehensive characterization of Cu(II)-complex spin chemistry and highlights how spin chemistry can be used to manipulate solar energy harvesting and storage materials.
Introduction
For many decades, trisbipyridineruthenium(II), [Ru(bpy)3]2+ or [RuL3]2+ (L = polypyridyl ligand), has been the prototypical chromophore in many photoinduced charge separation studies due to the combination of its unique photophysical, electrochemical, and coordination properties. Ongoing investigations of [Ru(bpy)3]2+ complexes focus on combining its chromophoric properties with electron donor–acceptor components in covalently linked dyads and triads for potential solar energy conversion and storage applications.1 Unfortunately, ruthenium is not earth-abundant and its inhibitive cost makes commercialization of [RuL3]2+ based technologies unrealistic. A more sustainable sensitizer, bisphenanthrolinecopper(I), [CuP2]+ (P = phen), has thus been thoroughly investigated to replace [RuL3]2+ systems due to similar photophysical and electrochemical properties.2,3As such, [CuP2]+ exhibits a strong metal-to-ligand charge-transfer (MLCT) transition in the visible resulting in a strongly reducing excited state, which can undergo oxidative quenching reactions. However, it is likely that the covalently linked donor–acceptor copper phenanthroline complexes, i.e. C–A dyads of [CuP2]+, have been less investigated than the [RuL3]2+ analogs due to their complex chemistry. As a d10 metal, Cu(I) complexes are often very labile and, when oxidized to d9-Cu(II), undergo pseudo-Jahn–Teller (J–T) distortion.4–9 Consequently, it is often impossible to prepare, isolate, and purify [CuP2]+-type complexes via techniques such as chromatography. Further, in the J–T distorted Cu(II) geometry, Lewis basic solvents or anions can coordinate to form a non-emissive exciplex.5,10–17 Although non-emissive, the exciplex is capable of oxidative quenching by an acceptor, but with a diminished driving force dependent upon the strength of the overall ligand interactions.10–13,16,18–22
Despite lability and J–T distortion issues, examples of photoinduced electron transfer with [CuP2]+-type C–A dyads go back many decades. Unlike [RuL3]2+, persistent, detectable CT product is formed in [CuP2]+-type C–A dyads because the rate of oxidative quenching, kA, is usually faster than non-radiative deactivation of the J–T distorted state.5,23–26 If manipulated correctly, the J–T distortion and ligand lability can be advantageous. Meyer and co-workers reported efficient formation of relatively long-lived (τCT is on the order of a few microseconds in highly coordinating solvents) photoinduced CT products in several Cu(I) bipyridine-viologen-based dyad assemblies.23,25 In these studies, the lifetime of the C+–A− product was demonstrated to be highly solvent dependent, varying by two orders of magnitude between dichloromethane (DCM, shortest) and dimethyl sulfoxide (DMSO, longest). The authors invoke a Marcus theory argument, relating the long CT lifetime to the large reorganization energy requisite for geometric and coordination changes accompanying the recombination reaction.5,23,25,27 The authors left open the question of whether spin restriction has an effect in this regard. On the other hand, the significance of spin effects has been demonstrated and extensively studied in our laboratories for unlinked [Ru(bpy)3]2+/MV2+ dyad systems,28–32 as well as for linked phenazine/[Ru(phen)3]2+/MV2+ triads, where an electron donor is appended to achieve multi-step electron transfer.33–35
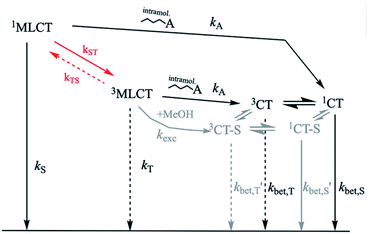
In both, Ru- and Cu-based dyads, the primary events after photoexcitation may be represented by Scheme 1. As a reference for the present study with C–A dyads of copper, we briefly review the specific situation for the ruthenium case. Ultrafast (ps) transient absorption spectroscopy on linked [RuL3]2+-type C–A dyads has demonstrated that forward electron transfer forming the charge transfer (CT) state occurs very fast, but reverse electron transfer regenerating the Ru(II) complex in its ground state is similarly fast, if not faster.36 Thus, no appreciable amount of charge separated product persists. Only an upper limit of ca. 80 ps could be estimated for the time constant of recombination in ref. 37. Data reported by Yonemoto et al. corroborate values on this order of magnitude for covalently linked ruthenium tris(bipyridyl)-viologen dyads.36
In linked [RuL3]2+-type C–A dyads, the dominant MLCT state is a triplet. Forward electron transfer from the 3MLCT to the CT species, C+–A−, results in an overall triplet spin alignment of the unpaired (radical pair (RP)) electrons. The magnetic field dependence of reverse electron transfer kinetics in such systems has greatly expanded the understanding thereof. Since reverse electron transfer, i.e. recombination, from the triplet 3CT state, 3(C+–A−), regenerates the singlet ground state, 1(C–A), spin conversion from triplet 3(C+–A−) to singlet 1(C+–A−) must occur within the CT state before recombination can proceed. The rate of spin-conversion then becomes part of the overall backward electron transfer kinetics, which exhibits a magnetic field dependence according to the field dependence of the triplet/singlet (T/S) conversion process.
This spin-chemical scenario corresponds to the so-called radical pair mechanism,37,38 which describes a magnetic field dependent spin conversion process where interplay between local magnetic interactions, e.g. hyperfine and Zeeman interactions, affect the unpaired electron spins. The major factors determining the magnetic field dependence of T/S conversion kinetics in Ru-based systems are (1) fast electron spin-relaxation and (2) different Zeeman interactions of the Ru(III) complex and MV+ radical resulting from their distinct g-factors. Theoretical analysis of the magnetic field dependence on the CT lifetime in unlinked C–A dyads of [RuL3]2+/MV2+ yielded specific kinetic parameters of the C+…A− state;28–32 particularly, the rate constant of spin-allowed backward electron transfer and spin relaxation. Although these studies dealt with unlinked C–A dyads, the magnetic field dependence of the spin-conversion process should, in principle, also apply to the linked systems where the rate constant of dissociation is zero. Considering the rate of Ru(III) spin relaxation (ca. 19–26 ps) together with the rate of spin-allowed backward electron transfer (ca. 12–30 ps), overall recombination lifetimes of 100–150 ps are predicted for the CT state of the linked [RuL3]3+…MV+ C–A dyads (where L = bpy or phen).30,33
The CT state lifetime, τCT, has a great influence on the utility of the C–A dyads in solar energy conversion/storage applications. To achieve long, functional lifetimes using [RuL3]2+ chromophores, electron transfer from the chromophore to the acceptor must be followed by an additional electron transfer step. Thus, as briefly referenced above, an electron donor can be added to the system to form a donor–chromophore–acceptor (D–C–A) triad. In [RuL3]2+-based D–C–A triads, fast recombination of the CT state (D–C+–A−) is prevented by the second fast electron transfer from the donor to the chromophore: D–C+–A− → D+–C–A−. The greater physical separation between radical species and different spin-chemical interactions in the [RuL3]2+-based D–C–A species enables much longer lifetimes to be achieved.34,39–42 However, as mentioned above, copper C–A dyads can already exhibit longer lifetimes of the C+–A−, CT state. Yet, the question of their spin chemistry is interesting and has not been explored.
Thus, in the present work, we set out to investigate the role of spin-chemical influences on the mechanism of CT formation and relaxation in [CuP2]+ dyads. For our investigations, we prepared the two Cu(I)-based C–A dyad systems shown in Fig. 1. To denote their structure we will use the short hand notation [Cu(I)(Rphen(OMV)24+)2]9+ = RC+A48+ with the complex RC+ = [Cu(I)Rphen2]+ (Rphen = 2,9-dimethyl (R = Me) or 2,9-diphenyl, (R = Ph) phenanthroline), as the photoelectron donor, and four 4-(n-butoxyl) linked methylviologen (A2+ = OMV2+) electron acceptor groups, substituted at the 5,6-positions of the phenanthroline ligands.
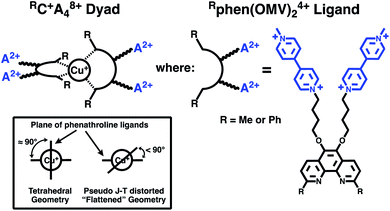 | ||
| Fig. 1 Structures of the synthesized and investigated RC+A48+ dyads and associated Rphen(OMV)24+ acceptor ligands. | ||
These complexes are related to the original complex of Meyer and co-workers,24 but use 2,9-dimethyl-1,10-phenanthroline (dmp) and 2,9-diphenyl-1,10-phenanthroline (dpp) based ligands rather than bipyridine. As reported below, our systems undergo efficient, single-step, photoinduced charge separation to form a CT, in which Cu(I) is oxidized to Cu(II) and the viologen electron acceptor is reduced to the radical mono-cation, MV+˙. We find that the solvent composition influences the lifetime of the CT state in dramatically different ways for the MeC+A48+ and PhC+A48+ dyads. Furthermore, the CT lifetime depends on the applied magnetic field between 0 and 1.5 T. The kinetic MFE is modelled in terms of the radical pair mechanism. The required magnetic parameters of the Cu(II) complexes were obtained from state of the art ab initio multireference calculations performed to elucidate the experimental data.
Experimental and computational methods
All information regarding the reagents, synthesis, and characterization of the ligands and Cu(I) complexes is included in the ESI.†Spectroelectrochemistry
A home-built spectroelectrochemical cell was used to obtain quantitative spectra of the one-electron reduction product, MV+˙, in an Ar-purged 0.1 M tetrabutylammonium hexafluorophosphate (TBA+PF6−)/1,2-difluorobenzene (dfb) solution.43,44 The optically transparent thin layer working electrode (OTTLE) consisted of a rectangular Au mini-grid sandwiched between quartz plates. The prepared cell was mounted in the light path of the Agilent 8453 UV-Vis spectrometer and potential control was afforded via a BAS 100B potentiostat.Laser spectroscopy measurements
The effect of an applied magnetic field on the recombination kinetics of the CT state was also examined by TA spectroscopy. For these experiments, the pump and probe beams were directed through the center of an electromagnet (Model: HV4H, Walker Scientific, Inc.) in a near collinear orientation (Fig. S2 in ESI†). All TA data (in the presence and absence of a magnetic field) were fit using either Origin 7.5 advanced fitting function or a nonlinear regression fitting function in the statistical computing software R46 which fit a differential equation simulating the excitation and subsequent decay of CT state during and after each laser pulse (referred to subsequently as the “ODE fit”). The laser beam profile was measured with a photodiode and approximated to be a normalized (by peak intensity) Gaussian distribution with a FWHM of 4 ns for the ODE fits. Confidence intervals for these fits were produced by investigating the profile log-likelihood function of the fitted model (profile.nls of the {stats} package in R). Details of the signal fits are shown in the ESI.†
Quantum chemical calculations
In addition to the truncated models, calculations of the entire dyad MeC+A48+ were performed. The geometry was optimized at the RI-BP86/def2-SVP level of theory including relativistic effects by ZORA and dispersion correction (DFT-D3BJ).
Results
CT state formation
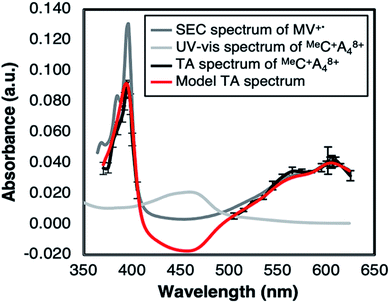
The MLCT emission of the Cu(I) complex is strongly quenched in the RC+A48+ dyads. Compared to Cu(I) complexes without an acceptor moiety, the emission lifetime is ca. 100 ns, but for the RC+A48+ dyads the emission typically decays in < 1 ns (see Fig. S24 in ESI†). The following time constants and relative amplitudes describe the emission profile in dfb solvent fitted with a tri-exponential decay function; MeC+A48+: 0.22 ns (25%), 1.23 ns (51%), 4.13 ns (24%), PhC+A48+: 0.32 ns (84%), 1.25 ns (15%), 10.3 ns (1%). As demonstrated below, the quenching is due to formation of [Cu(II)(Rphen(OMV)2)4+(Rphen(OMV)2)3+˙]9+, the intramolecular CT product. The consistent multi-exponentiality of quenching indicates heterogeneity of the kinetics: two probable causes include, (1) conformational fluctuations of the ROMV4+ acceptor substituents, and (2) multiple stages of ion pair formation, between the strongly charged dyads and the TPFB− counter ions. In the transient absorption (TA) measurement, the first spectrum (Fig. 3) appeared immediately within the time resolution of the experiment. Formation of the proposed CT product was verified for MeC+A48+ by constructing a model spectrum (cf. caption of Fig. 3) of the CT product and comparing it to the spectrum of MV+˙ in the same solvent obtained via spectroelectrochemistry (SEC). As is evident in Fig. 3, the peak positions in the TA spectrum agree well with those of the MV+˙ spectrum from the SEC data. The relative peak intensities deviate from the model, but the difference can be rationalized by considering the effect of the monochromator slit-width on the resolution of the sharp spectral features of MV+˙ at short wavelength (λmax = 396 nm).Solvent effect studies
The recombination kinetics of the photo-induced CT product of the RC+A48+ dyads were studied in dfb/MeOH solvent using TA spectroscopy as described in the Experimental section. The dfb/MeOH solvent system was chosen for three reasons: (A) 1,2-difluorobenzene is particularly stable with respect to radical initiated photochemistry, (B) the complexes having the TPFB counterion are reasonably soluble in weakly Lewis-basic dfb despite the large positive charge (+9), and (C) MeOH should be a reasonably good ligand for Cu(II) but not for Cu(I). Other solvent combinations were less amenable to this study due to solubility issues, photodegradation issues, or complications due to coordination. The TPFB counterion was intentionally chosen not only for solubility purposes, but because the steric bulk of the pentafluorophenyl groups inhibits coordination of the TPFB to the Cu+/2+ metal center in the flattened geometry.The lifetime of the CT state of MeC+A48+ is significantly solvent dependent. As demonstrated in Fig. S5A in the ESI,† the lifetime of the CT state increases with increased MeOH concentration up to a value of ca. 45 ns at a concentration of ca. 5% (v/v) where the effect saturates (%[MeOH] higher than 10% were not considered).
In pure dfb, the lifetime of the CT state formed from PhC+A48+ is essentially the same as for MeC+A48+ (ca. 8.0–9.5 ns). However, in contrast to MeC+A48+, the τCT and absorbance (static or transient) of PhC+A48+ show essentially no solvent dependence with added MeOH. In 5% MeOH/dfb the lifetime is, within experimental error, the same as in 0% MeOH (Fig. 4). This difference is interpreted to indicate the efficacy of the phenyl substituents in the 2,9-positions of the phenanthroline ligand to inhibit MeOH from accessing the metal center relative to the smaller methyl substituents. The difference in steric environment between the two complexes, MeC+A48+ and PhC+A48+, is evident in the quantum chemical calculations provided in Fig. S12 of the ESI.† Moreover, the results with MeC+A48+ are qualitatively in concert with observations reported by Meyer.27,67 The ligands used by Meyer and coworkers had no blocking substituents in the equivalent bipyridine positions (i.e., only H in 6,6′-positions) and an increased τCT with increasing Lewis base strength of the solvent was observed.
Kinetic magnetic field effects
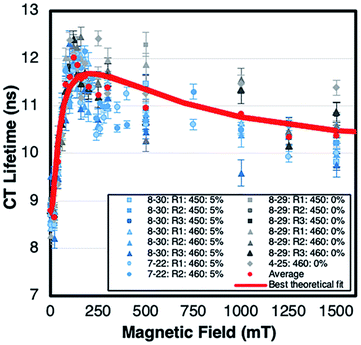
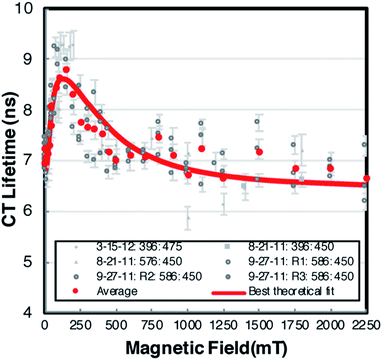
The CT recombination kinetics of both dyads were investigated as a function of applied magnetic field and solvent composition. Fig. 4 shows the CT lifetime of the TA signal at 396 nm (λmax for MV+˙) after excitation at 450 or 460 nm for PhC+A48+ in pure dfb solvent (0% MeOH) and in 5% MeOH. Because of the short lifetime, these data were obtained using the ODE fit to the ΔA vs. time data as described in the Experimental section. Fig. 4 is a compilation of data obtained under various experimental conditions (different samples, days, excitation wavelengths, and trial runs). While there is significant scatter in this large collection of data, clear trends are evident. First, within experimental error, τCT is unaffected by fraction of MeOH, excitation wavelength, and/or laser power over all applied magnetic fields examined. Second, τCT increases from ca. 8.5 ns at 0 mT to 12.0 ns at applied fields of 100–160 mT (p < 0.05 when τCT at 0 and 100 mT were compared via a paired, two-tailed t-test). Yet, as the field is further increased up to ca. 250 mT the lifetime decreases to ca. 11.5 ns, and from 250–1500 mT the lifetime continues to slowly decrease to ca. 10.5 ns (p < 0.05 in both cases when CT lifetimes at 250 and 1500 mT as well as 0 and 1500 mT were compared via paired, two-tailed t-tests).In pure dfb solvent, the MeC+A48+ dyad exhibits qualitatively similar behavior to that of PhC+A48+ as a function of applied magnetic field as shown in Fig. 5. Specifically, τCT increases from ca. 6.5 ns to ca. 8.5 ns between applied fields of 0 and 100–200 mT, then τCT decreases as the field is increased to ca. 500 mT (Fig. 5, p < 0.05 when τCT at 0 and 100 mT are compared via a paired, two-tailed t-test). At that point, the lifetime approximately plateaus at a value of ca. 6.5 ns. One behavioral difference between the two dyads at high magnetic fields is that the τCT of MeC+A48+ returns approximately to its zero-field value whereas τCT for PhC+A48+ is significantly higher at 1500 mT than at zero field. Additionally, like PhC+A48+, the τCT of MeC+A48+ in dfb is insensitive to excitation and monitoring wavelength. The τCT of the PhC+A48+ dyad at zero field is also not dependent on monitoring wavelength, therefore, it is likely that the same is true in an applied field although that was not explicitly investigated. As mentioned previously, the τCT of MeC+A48+ increases when MeOH is incorporated into the solvent mixture, but consistently follows the same qualitative pattern in an applied magnetic field regardless of MeOH concentration (Fig. 6). The combined data presented in Fig. 4–6 ostensibly display a consistent, general pattern in τCT with magnetic field for both RC+A48+ dyads regardless of solvent composition, excitation wavelength, monitoring wavelength, and laser power.
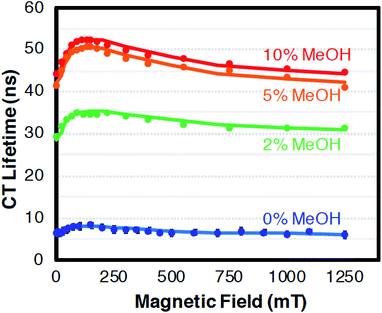 | ||
| Fig. 6 The relative change in CT lifetime (τ) for MeC+A48+ at 396 nm in dfb/X% MeOH with magnetic field after excitation at 475 nm. With exception of the data at 0 and 1250 mT which is shown as calculated from the ODE fits, the values were smoothed using a 3-point moving average. Confidence intervals (95%) for the single field data points are of the same relative magnitude as in Fig. 4 and 5 (<4.2%) and should be approximately reduced by a factor of 13 by the 3-point averaging. Error bars were omitted because they are miniscule on this lifetime scale. The solid lines represent fits with the radical pair model. Solvent dfb with 0% (blue), 2% (green), 5% (orange), 10% (red) MeOH. For parameters cf. Discussion. | ||
Magnetic parameters
To understand the magnetic field effects described above, we need to evaluate the g-tensor and hyperfine tensor components of the Cu(II) complexes. Experimental g- and A-values are available only for the [Cu(dpp)2]2+-complex: g⊥ = 2.07, g‖ = 2.37, and A‖ = 17.7 mT (ref. 68) determined from frozen-solution EPR spectra in CH2Cl2. To complement these values for A⊥ and obtain the corresponding set of parameters for the [Cu(dmp)2]2+-complex, DFT and ab initio multireference calculations were performed (cf. section Experimental and computational methods).g-Tensor
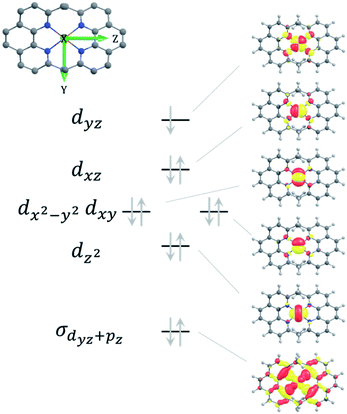
The theoretical g-values along with the directions of the principal axes of the g-tensor for [Cu(dmp)2]2+ and [Cu(dpp)2]2+, are given in Table S3 and Fig. S17, S18 in the ESI,† respectively. For both complexes, the g3 principal axis is the unique molecular axis which bisects the largest of the N–Cu–N bond angles of 139.3° in case of [Cu(dmp)2]2+ and 141.0° in case of [Cu(dpp)2]2+. For all methods, the g-matrix of [Cu(dpp)2]2+ is found to be closer to axial symmetry than for [Cu(dmp)2]2+. As can be seen in Table S3 in the ESI,† the differences between the g-tensor components of the two complexes are below 0.008 at the DFT and at the CASSCF/NEVPT2 level of theory. This small difference in the g tensor can be attributed to the approximate congruence of the CuN4 core in both complexes (see geometrical parameters in Tables S1 and S2 in the ESI†). Hence, we can also expect that the g-values of [Cu(dmp)2]2+ are very close to those of [Cu(dpp)2]2+ and we will use the experimental values of the latter for both complexes in our spin chemical simulation.Hyperfine coupling constants
The dominant hyperfine coupling comes from the Cu-nucleus. The theoretical hyperfine coupling (HFC) constants for the copper in [Cu(dmp)2]2+ and [Cu(dpp)2]2+ are collected in Table S4† and the principal axes are shown in Fig. S19 and S20 in the ESI.† The isotropic A-value values differ by only 0.05 mT between complexes, agreeing with the similarity already observed for the g-tensor, due to the nearly identical local coordination of the copper. The principal value, A1, along the unique molecular axis is negative while the other two values are positive. Overall, the HFC-tensor is nearly axial which is again in line with the g-tensor analyzed above. Based on the quantum chemical results described in detail in the ESI,† the following values for the anisotropic hyperfine couplings of the Cu nuclei in the MeC+A48+ and PhC+A48+ complexes were used in the spin chemical simulations: A‖ = −17.7 mT (the experimental value68 for PhC+A48+, but made negative according to theory) and A⊥ = 2.8 mT (the average value of A2 and A3 for both complexes from the quantum chemical calculations). These values are averaged to an isotropic value of Aiso = −4.0 mT.The HFC tensors of nitrogen in [Cu(dmp)2]2+ and [Cu(dpp)2]2+ are much smaller than those of copper, which is due to the lighter core, smaller polarization at the core level and a negligible A(so) contribution. The pertinent values are listed in the ESI, Table S5.†
Theoretical simulation of MFE
In the ground state, the geometry of [Cu(dmp)2]+ is nearly tetrahedral while the conformation is significantly flattened for [Cu(dpp)2]+, as shown by geometry optimization in this work (see ESI†) and preceding literature.68,70 Vertical excitation to the 1MLCT state causes the [Cu(dmp)2]+-geometry to flatten due to Jahn–Teller distortion. In the case of [Cu(dpp)2]+, excitation exacerbates the pre-existing flattening distortion.71 These structural rearrangements take place within about 0.8 ps and are followed by ISC to the 3MLCT state (rate constant kST) within about 10 ps.14,17,72 As noted earlier,69 the singlet-triplet splitting of the MLCT state is small enough for thermal repopulation of the 1MLCT state to occur and delayed fluorescence to be observed. From the temperature dependence of emission quantum yield and lifetime, McMillin and coworkers estimated some of the rate constants for the [Cu(dmp)2]+ complex in the non-coordinating solvent CH2Cl2. Exploiting the more recent experimental information of kST ≈ 1011 s−1, on the quantum yield of prompt fluorescence,14,17,71 and extending the kinetic approach from ref. 69, it was possible (cf. ESI†) to determine the following absolute values of the rate constants for pure singlet (kS) and pure triplet (kT) recombination as well as the 3MLCT → 1MLCT process (kTS): kS = 4.95 × 109 s−1, kT = 8.8 × 106 s−1, kTS = 4.6 × 107 s−1. The energy gap between 1MLCT and 3MLCT was evaluated to be 1360 cm−1, in fair agreement with a value of 1201 cm−1 obtained by our quantum chemical calculations (cf. ESI†) based on more advanced methods than applied in ref. 14 where a value of 1800 cm−1 was obtained. Experimental evidence for the latter value was provided from the difference of the high and low temperature spectral maxima.14,69 However, as our analysis of the temperature dependent lifetime and quantum yield data in ref. 69 has shown (cf. ESI†), an energy gap of 1800 cm−1 would not comply with a notable contribution of emission from 3MLCT which is inconsistent with spectral evidence. For [Cu(dpp)2]+, in which ISC between 1MLCT/3MLCT is fast,72 our quantum chemical calculations yielded a ΔE value of 1716 cm−1 (cf. ESI†).
For [Cu(dmp)2]+, it is known that a five-coordinate exciplex with a solvent molecule is formed in coordinating solvents such as MeOH. Despite the fact that formation of this structure is complete within a few nanoseconds,26 there is no quantitative information about the rate constant of exciplex formation. At least in solutions having dilute concentrations of a coordinating solvent component, it is unlikely that the process is faster than the initial ISC process in the unsolvated species. Hence, we will assume that solvent coordination occurs on the stage of the unsolvated 3MLCT state, or even after electron transfer and formation of the CT state. In Scheme 2, these processes are indicated in gray.
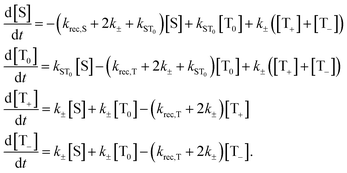 | (1) |
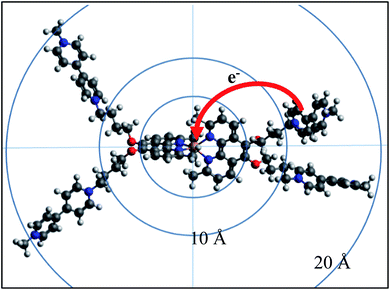 | ||
| Fig. 7 Back electron transfer in, and dimensions of the complex [Cu(II)(Mephen(OMV)2)3+˙(Mephen(OMV)24+)]9+. Structure calculated with geometry optimized at the RI-BP86/def2-SVP level of theory including relativistic effects by ZORA and including dispersion correction (DFT-D3BJ) (cf. ESI†). | ||
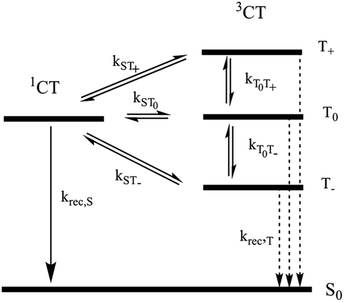
Here, the rate constants kS and kT of singlet and triplet recombination are magnetic field independent, i.e. global parameters for the set of decay curves measured at different fields.
The magnetic field dependence of the rate constants of spin conversion is assumed as follows:
| kST0(B0) = khfc,0 + kΔg(B0) + ksri | (2) |
Here the rate constant khfc,0 is treated as a semiempirical field independent parameter. However, the other two contributions, S/T0-mixing by different Larmor frequencies (kΔg(B0), so-called Δg-mechanism) and by spin-rotational coupling (ksri), are calculated using the magnetic parameters of the system. The former is given by (cf. ESI†):
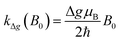 | (3) |
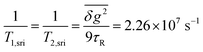 | (4) |
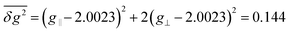 | (5) |
The general relation between the T1 time of a radical and the pertinent rate constants for transitions between S, T0, and T+/T− is given by 1/4T1.73 Hence
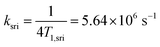 | (6) |
For the field dependent rate constant k±, we consider four possible contributions:
| k±(B0) = khfc(B0) + kgta(B0) + kgta,int(B0) + ksri | (7) |
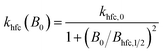 | (8) |
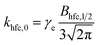 | (9) |
In principle, the Lorentzian form of a function in eqn (8) is suitable for both, coherent and incoherent contributions and we are not introducing a separate Lorentzian term for spin relaxation due to rotational modulation of anisotropic hyperfine coupling. After determining the parameters empirically by fitting the experimental data, their relation to isotropic (coherent) and anisotropic (incoherent) hyperfine interactions will be discussed.
Only the Cu(II)-radical site is considered for the contribution of relaxation by g-tensor anisotropy. From the expression for T1, given for this type of relaxation in the general EPR literature,86 and again taking into account the relation kgta = 1/4T1,gta, we obtain
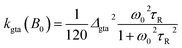 | (10) |
| Δgta = g‖ − g⊥ | (11) |
Actually, the contribution of kgta from rotational modulation of the g-tensor anisotropy is negligible, but we also have to consider modulations of the g-factor by internal vibrational modes, kgta,int(B0). To this end, Δgta in eqn (10) was replaced by an effective value with a modification factor, αint, and the rotational correlation time by an internal correlation time, τint. The contribution of this mechanism is essential to explain the decrease of the CT lifetime at high fields. Both parameters are treated as empirical fitting parameters.
To simulate the kinetic MFE, eqn (1) were numerically solved using Mathematica. The general solution is represented by a tri-exponential decay for the relevant parameter ranges, however, with a dominating contribution of one of the exponentials. An effective decay time, τCT, was obtained by a least-squares fit of a mono-exponential to the calculated tri-exponential (for details cf. ESI†). The effective decay time τCT is a unique function of five parameters:
| τCT = f(Bhfc,1/2, kS, kT, τgta-int, αint) | (12) |
The sets of 5 parameters for each of the best fits shown in Fig. 4–6 are listed in Table 1. From these, we derived the secondary quantities keff = 1/τCT (B = 0), the effective decay rate constant at zero field, kspin-av, the average rate constant of spin conversion, and khfc,0, the effective rate constant of hyperfine induced spin mixing at zero field.
| a Zero field values from the fit agree well with the experimental values. b cf. eqn (13). c Calculated according to eqn (9). | |||||
|---|---|---|---|---|---|
| Complex solvent | PheCA2 dfb | MeCA2 dfb | MeCA2 dfb/2% MeOH | MeCA2 dfb/5% MeOH | MeCA2 dfb/10% MeOH |
| k eff = 1/τCT (B = 0)a | 1.13 × 108 | 1.55 × 108 | 3.4 × 107 | 2.4 × 107 | 2.3 × 107 |
| k rec,S, s−1 | 3.5 × 108 | 5.1 × 108 | 9.6 × 107 | 6.6 × 107 | 6.3 × 107 |
| k rec,T, s−1 | 5.6 × 107 | 8.2 × 107 | 1.5 × 107 | 1.1 × 107 | 1.0 × 107 |
| k spin-av | 1.30 × 108 | 1.9 × 108 | 3.7 × 107 | 2.4 × 107 | 2.3 × 107 |
| B hfc,1/2, mT | 14.9 | 14.3 | 10 | 10 | 10 |
| k hfc,0, s−1c | 3.5 × 108 | 3.3 × 108 | 2.3 × 108 | 2.3 × 108 | 2.3 × 108 |
| τ gta-int, ps | 5.8 | 6.0 | 6.0 | 2.0 | 2.1 |
| α int | 0.47 | 1.2 | 0.5 | 1.1 | 1.0 |
Discussion
Rate constants of singlet and triplet CT recombination
At zero field, the charge recombination rate constants, keff, of both dyads are about 108 s−1 in dfb. For the case of MeC+A48+, small additions of MeOH to the solvent decrease the recombination rate constant by about a factor of 5. This effect seems to saturate between 5% and 10% MeOH, indicating that all dyad molecules have formed an exciplex with MeOH before charge recombination. Our findings are in qualitative accord with previous results from the Meyer group for a [Cu(bpy)2]+ containing dyad with methylviologen,25 who found recombination rate constants on the order of 2–5 × 107 s−1 in the non- or weakly coordinating solvents, CH2Cl2 and MeCN, and values around 106 s−1 in the strongly coordinating solvent DMSO.In ref. 25 the recombination rate constant for the [Cu(bpy)2]+ containing dyads has remained unresolved with respect to the contributions of singlet and triplet recombination and the role of the spin processes. In our case, however, this task could be solved with the help of the kinetic MFE. It is found that direct triplet to singlet ground state recombination is possible, its rate constant being about 1/6 of the spin allowed recombination. Such a behavior seems plausible in view of the spin–orbit coupling effect of the Cu center. The kinetic role of spin conversion between the initial triplet and the singlet charge transfer state can be assessed by comparing keff the effective rate constant of recombination with kspin-av, defined as the average of krec,S and krec,T under spin equilibrium
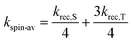 | (13) |
Pertinent values are listed in Table 1. At zero field, the observed value of keff (Table 1, row 1) is less than kspin-av (Table 1, row 4) for the three fastest cases of recombination, i.e.PhC+A48+ or MeC+A48+ in neat dfb and MeC+A48+ in dfb/2% MeOH). This result indicates that spin evolution is a non-negligible kinetic determinant of recombination in these cases. However, when the percentage of MeOH in the solvent is increased to ≥5%, spin equilibrium seems to have been established prior to the recombination process. Nevertheless, with rising magnetic field, the k± process is sufficiently slowed down to make the recombination magnetic field dependent in all cases.
Compared to electron-donor/-acceptor systems with [Ru(bpy)3]2+ or ferrocene as an electron donor,30,87 the spin-allowed backward electron transfer rate constants are several orders of magnitude smaller in the Cu-complex dyads (cf.Table 2). This finding is most likely due to a strongly reduced Franck–Condon factor in the Cu complexes as a result of conformational relaxation of the ligand sphere.
| a Ref. 30 and 32. b Ref. 87 and 94. c This work. d Energy of lowest doublet excitation. e Spin-rotational relaxation time. f Calculated according to eqn (9). g Neglecting the small contribution from magnetic isotopes of Ru and Fe. h Ox˙ = oxonine semiquinone. | |||
|---|---|---|---|
| Complex | [Ru(bpy)3]3+a | [Fe(Cp)2]+b | [Cu(II)(dmp)2]+c |
| d-config. (symmetry) | d5(D3) | d5(D5) | d9(D2) |
| ΔED–D, cm−1d | 600–800 | 270–480 (ref. 90) | 9000 |
| B 0-indep. T1, T2 | 20 ps | 5 ps | 44 nse |
| g ‖, g⊥ | 1.14, 2.64 | 4.35, 1.24 | 2.37, 2.07 (ref. 68) |
| B 1/2(hfc)f (counter radical) | ∼2 mT (MV+˙)g | ∼2 mT (Ox˙)g,h | ∼14 mT (MV+˙) |
| k S, s−1 (counter radical) | 7 × 1010 (MV+˙) | 1012 (Ox˙)h | 3 × 108 (MV+˙) |
Contributions of individual spin conversion mechanisms
A graphical overview of the contributions of the various mechanisms of spin conversion and their magnetic field dependences is shown in Fig. 8. The magnetic field dependence of the lifetime of the CT state, τCT, is determined by the rate constants kST0 and k±. For kST0 we took into account a hyperfine dependent contribution (khfc,0), electron spin relaxation by spin-rotational interaction (ksri) and Δg-dependent coherent S/T0 mixing (Δg-mechanism, kΔg). The latter two were calculated using the magnetic parameters of the complexes, the former was taken from the zero-field value of the empirically fitted rate constant k± since k± and kST0 should be equal at zero field.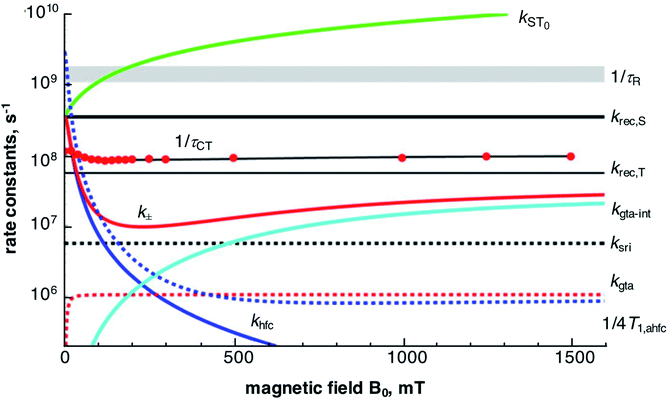 | ||
| Fig. 8 Magnetic field dependence of various contributions to spin dynamics and related parameters for PhC+A48+ in dfb. Red data points: inverse of experimental τCT values with best fit line from Fig. 4 in black. For details cf. text. | ||
The magnetic field dependence of kST0, determined by the Δg-mechanism, corresponds to a monotonic increase with the field. At zero field it is zero, but it increases quickly and supersedes the value of khfc,0 by 45 mT. Noteworthy, the Δg-mechanism causes a field dependence of τCT only up to a field of about 250 mT (cf. Fig. S30 in the ESI†), where it leads to a depression of the τCT maximum by about 6%. At higher fields, this mechanism renders the S/T0 process fast enough to maintain full spin-equilibrium between the two spin states during all stages of decay. Thus, further acceleration of the S/T0 process is not seen as a MFE in the recombination kinetics.
The rate constant k± (cf.eqn (7)) is made up of several contributions: first and foremost, the empirically determined hyperfine coupling contribution, khfc, which effectively comprises both isotropic and anisotropic interactions. Secondly, spin relaxational contributions specific to the Cu(II)-center, viz. rotational modulation of g-tensor anisotropy (kgta) and spin-rotational coupling (ksri); both of which can be calculated directly from the magnetic parameters of the Cu(II)-complex. A further contribution from a spin–orbit coupling related relaxation mechanism modulated by internal motions was also parametrized by an empirical fit and will be discussed below.
The empirical fit according to eqn (8) and (9) of the field dependence of khfc, that mainly determines the increase of τCT with the field up to about 100 mT, yields a Bhfc,1/2 value of 14–15 mT for the two complexes in neat dfb. Now, the role of coherent and incoherent hyperfine induced singlet/triplet mixing on the behavior of khfc(B0) needs to be discussed. As shown in the ESI,† a semiclassical model of spin motion by Schulten and Wolynes,85 and its improved version by Manolopoulos et al.,77,78 can be used to consistently relate coherent hyperfine driven spin motion to the rate constant, khfc,0, of a classical exponential process at both zero field and high field.
According to Schulten and coworkers,85,88 the spin motion is completely determined by the effective hyperfine fields of each radical, I, characterized by the following sum over the nuclei, k
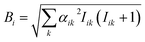 | (14) |
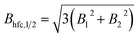 | (15) |
Thus, there is a direct relation between this half field value and spin motion and its approximation by an exponential process (cf. ESI, Section H†).
The coherent spin motion of the Cu(II)…MV+ pair has also been calculated by the improved semiclassical model of Manolopoulos et al.77 (cf. Fig. S28 in the ESI†). The exponential curves derived from the Schulten–Wolynes model fit the curves derived according to Manolopoulos et al. equally well.
For the MV+ radical, the pertinent hyperfine couplings are 0.134 mT (4H), 0.159 mT (4H), 0.401 mT (6H), and 0.425 mT (2N), yielding BMV+ = 1.25 mT. For the Cu nuclei in the MeC+A48+ and PhC+A48+ complexes, we average the anisotropic hyperfine couplings, A‖ = −17.7 mT and A⊥ = 2.8 mT, to an isotropic value of Aiso = −4.0 mT, yielding BCu = 7.8 mT. From these values and eqn (14) and (15) we obtain Bhfc,1/2 = 13.7 mT. This value is in rather good agreement with the Bhfc,1/2 parameter from the best fit for the two complexes in dfb (cf.Table 1). On addition of MeOH, the Bhfc,1/2 value decreases somewhat, which may be indicative of modified spin densities by exciplex formation with the solvent.
Although the coincidence of the empirical Bhfc,1/2 and the theoretical value derived for isotropic hyperfine coupling is gratifying, the role of anisotropic hfc must be considered. If rotational motion is fast, the anisotropic interactions are averaged out and their effect is reduced to spin relaxation, which is slow on the timescale of molecular rotation. As shown in the ESI,† based on Redfield theory, at zero field and low fields the usual theoretical expressions lead to T1 and T2 relaxation times of the Cu(II) center on the order of 0.1 ns. This is significantly shorter than the expected rotational correlation time of about 0.7 ns. Hence, the rotational correlation time comes below the valid range of the Redfield condition, which demands that the resulting relaxation must be slower than the stochastic process inducing it. For the Cu(II) complexes herein, anisotropic hyperfine coupling may lead to spin motion that is faster than or comparable to rotational motion. On the other hand, frozen rotational motion treated by a static averaging of anisotropic hyperfine coupling would not be a good approximation for the present systems either. Actually, it would be most realistic to apply a dynamical theory that treats both quantum dynamical spin motion and (classical) rotational molecular motion on the same time scale. Such a treatment has not been carried out yet for spin chemical problems and is far beyond the scope of the present work. A perturbation treatment based on the Nakajima–Zwanzig equation, recently published by Fay et al.91 might be a promising option, though.
At intermediate fields between ∼50 and ∼200 mT, the Redfield condition for calculating the T1 time of Cu(II) is valid and we can use eqn (S10) (cf. ESI†). In Fig. 8, the field dependence of this contribution to k±, as given by 1/4T1,ahfc, is also shown. This curve runs slightly above the empirical fit line for k±. Thus, spin relaxation due to the rotational modulation of anisotropic hyperfine coupling at the Cu-center can, in fact, account for most of k± up to fields of about 200 mT, above which it drops below the contribution of ksri. We can thus conclude that, different from the purely organic radical pairs investigated in ref. 73, coherent and incoherent contributions of hyperfine coupling to the spin dynamics are largely inseparable for radical pairs with Cu-centered radicals.
In ref. 78, the advanced semiclassical theory of coherent electron spin motion in radical pairs has been developed to a stage that it can be combined with (parametrized) relaxation and different singlet and triplet recombination rates. We have tested it for the present system using the relaxation parameters and reaction rate constants of our model in combination with the hyperfine constants of Cu(II) and MV+ as shown in Fig. S29 (ESI†). For fields up to about 100 mT, coherent hyperfine induced spin motion accounts for about 50–70% of the difference between the observed decay times and the theoretical results obtained if only incoherent contributions would be taken into account. These findings indicate that there must be a contribution to spin mixing neither accounted for by isotropic hyperfine coupling, nor by the Redfield type relaxation processes and hence support the essential role of “slow motional” anisotropic hyperfine coupling in the region up to 100 mT. Above 200 mT spin state mixing by “static” isotropic as well as “slow motional” anisotropic hyperfine coupling seem to be suppressed since the relaxation processes in the Redfield limit are sufficient to account for the magnetic field dependence.
The spin-rotational interaction, represented by a rate constant ksri, is a field-independent contribution to the incoherent part of k±. It can be calculated directly from the magnetic parameters of the Cu-complex and the solvent viscosity (cf. Section H ESI†). The kinetic role of the spin-rotational mechanism is to represent a lower limit to k±. In the region between 100 and 500 mT, its constant value exceeds both the value of khfc and kgta-int and effectively depresses the maximum CT lifetime by about 10%.
The field dependence of τCT indicates an increase of k± at fields higher than about 200 mT. Such a behavior is characteristic of spin relaxation due to modulations of the g-tensor anisotropy. According to eqn (10), the rate constant of such a process increases quadratically with the field and saturates at a level inversely proportional to the correlation time of the modulation source. The correlation time of rotational diffusion is far too long to account for the increase of k± at high fields (cf. red dashed curve in Fig. 8). Therefore, a rotation independent modulation of the g-tensor has been taken into consideration. From the fit, a correlation time of about 6 ps and a modulation depth corresponding to about 0.5 times the full rotational anisotropy of the g-tensor in case of PhC+A48+ and 1.2 times in case of MeC+A48+ seem adequate. The decreasing effect of this mechanism on the CT lifetime at higher fields is illustrated in Fig. S30.† Although the nature of the relaxation process dominating at high field which formally corresponds to an internal modulation of g-tensor anisotropy is not yet clear, we note that similar observations have been made for [RuL3]2+-based D–C–A triads with a phenoselenazine donor and a diquaternary amine acceptor.34,35 In that case, a correlation time of 2 ps and a modulation by the full g-tensor anisotropy have been found.
Cu(II) versus Ru(III), Fe(III), and Co(II) spin chemistry
The present investigation represents the first thorough study of a case of Cu(II) spin chemistry. To make its specifics clear, we compare it with other characteristic cases of paramagnetic transition metal complexes (cf.Table 2), namely Ru(III) in [Ru(bpy)3]3+ and Fe(III) in ferricenium.The different electron configurations of the metal ions and different symmetries of the ligand spheres result in two main consequences: differences in the lowest electronic excitation energies of the paramagnetic complexes (“radicals” that one should better call Kramers doublets, due to their spin–orbit entangled character) and the anisotropy of their g-tensors. In the cases of the d5 metal cores, singly occupied degenerate d-orbitals are involved, leading to a low lying excited Kramers doublet. It is well known that such a situation causes very short, magnetic-field independent, spin relaxation times, due to the so-called Orbach mechanism, operating through thermal excitation of the lowest electronically excited state.29,92,93 Furthermore, the g-tensor components deviate strongly from the free electron value. For the Cu(II) complexes investigated here, a lowest excitation energy of ca. 9000 cm−1 has been calculated, explaining the inefficiency of the Orbach mechanism in this case. Thus, the magnetic field independent spin relaxation is due to spin-rotational interaction and takes much longer than for the Ru(III) and Fe(III) complexes. Additionally, the anisotropy of the g-tensor, though quite large compared to most organic radicals, is much weaker than in the d5 cases. On the other hand, the Cu nucleus exhibits a remarkably strong hyperfine coupling. Together, these differences in the magnetic parameters account for the different spin chemistry of the Cu(II)-complexes: (i) the exclusive Δg-mechanism in the d5 cases, which require very high magnetic fields on the order of 10 T (ref. 30 and 94) to make spin-mixing comparably fast relative to the short spin relaxation time and to the fast reaction rate in the Ru and Fe case, and (ii) hyperfine dominated magnetic field dependence with correspondingly large B1/2 in the case of Cu.
After writing this manuscript, we came across a recent publication by Jones and coworkers95 dealing with the Δg-effect on the RP decay in the photolysis of coenzyme B12. Here the paramagnetic 59Co(II) center plays a very similar role as the Cu(II) center in our Cu-complex systems. Both paramagnetic metal centers exhibit similar, strongly spin–orbit-coupling affected g-values around 2.2 and strong isotropic hyperfine couplings in the 4–7 mT range. In the case of coenzyme B12, the RP is formed in the singlet spin state. The effect of hyperfine induced spin mixing leads to faster 3RP formation and concomitant slower RP recombination, because it is only allowed from the 1RP state. Hence, suppression of spin-mixing by an external magnetic field enhances RP recombination. In the case of our Cu-complexes, the RP originates in the triplet spin state. Here, hyperfine-induced triplet/singlet spin mixing favors RP recombination, a process which is impeded by an external magnetic field to result in a longer RP lifetime.
The Δg-effect, supporting magnetic field driven S/T0 mixing, counteracts and reverts the hyperfine dependent magnetic field effect on the RP lifetime. The 1RP recombination rate in the Cu-complexes is about 10 times longer than in the Co-complex. Hence, the Δg-effect saturates at fairly low fields of about 200 mT (cf. Fig. S30†); the point at which it reaches S/T0 equilibrium during the RP lifetime. In the cobalt case, the Δg-effect continues to develop up to higher fields and also develops a larger amplitude. This different behaviour results from the shorter RP lifetime in the cobalt system which makes S/T0 equilibrium harder to attain than in the Cu systems.
In the Co-case, RP lifetime and rotational correlation time are of similar order of magnitude. Therefore, photoselection and anisotropy effects should matter in the Δg-mechanism, which is not the case for the much longer RP lifetime in the Cu-case. Furthermore, spin-relaxation seems to be unimportant in the Co-case due to the short RP lifetime. On the other hand, it has been shown for the Cu-case that relaxational contributions to spin evolution are essential and that the mechanism of hyperfine anisotropy modulation by rotational diffusion should contribute strongly. In that case, however, normal Redfield theory breaks down, and a consistent theoretical treatment would have to deal with the slow-motional case properly.
Conclusion
In this paper we have presented the first systematic study of radical pair spin chemistry involving a paramagnetic Cu(II) center. In triplet charge transfer (CT) states originating from photoexcitation of donor–acceptor copper(I) phenanthroline complexes the recombination kinetics is found to be magnetic field dependent with a lifetime maximum around 150 mT. The hyperfine and g-tensors of the paramagnetic Cu(II) centers were calculated by ab initio multi reference quantum chemical calculations. Their values, yielding g-values of about 2.2 and isotropic hyperfine couplings of about 4 mT, are on a similar order of magnitude as employed in a recent study of Co(II) spin chemistry with coenzyme B12.95 Characteristic differences between the Cu and the Co systems result, however, from the different order of lifetimes of the radical pairs ranging around 10 ns in the Cu systems and around 0.5 ns in the Co-system. The magnetic field effect (MFE) on the lifetime of the triplet charge transfer state in the Cu-complexes is analyzed in terms of a classical model. Rather than attempting to apply exact quantum models our focus was to provide a first comprehensive survey of the relevant mechanisms effective in this system. It has been found that besides singlet recombination, direct triplet recombination also takes place at a rate about one sixth of the singlet recombination. The MFE on the 3CT lifetime has been shown to comprise contributions of hyperfine coupling and Δg-mechanism, both dominated by the large values of the Cu-center. Furthermore, spin-relaxation by spin-rotational coupling and by an intrinsic spin–orbit coupling mechanism are relevant, the latter causing a decrease of the lifetime of the CT state at higher fields. It turned out that a simple separation of coherent and incoherent spin-mixing by isotropic and anisotropic hyperfine coupling is not possible, because of the slow rotation of the complexes which precludes the application of standard Redfield theory to spin relaxation by the rotational modulation of hyperfine tensor anisotropy. A full quantum mechanical treatment of the coherent and incoherent hyperfine mechanism including relaxation in the slow motional regime is currently being planned.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We would like to thank Dr Niels Damrauer & coworkers for his help acquiring the emission lifetime of Cu(dmp)2 as well as Dr Mykhalo Myahkostupov for his time and expertise regarding the time-resolved emission experiments performed in the labs of Dr Felix Castellano at North Carolina State University. We thank Prof. Peter Hore, Prof. David Manolopoulos and Dr Alan Lewis for putting their computer program to our disposal. The authors also want to acknowledge the incredible work of our collaborator, mentor, and friend: Dr C. Michael Elliott. This article, being one of Dr Elliott's final contributions, is another example of the long-standing, and undeniably prominent influence he has had on advancing our scientific understanding in many fields; particularly, electron transfer in transition metal complexes. Dr Elliott's insight, reason, acumen, and wit are truly missed by all who had the pleasure of knowing and working with him. Finally, we would like to acknowledge our funding sources: Department of Energy – Basic Energy Sciences, Grant Number: DE-FG02-04ER15591.Notes and references
- Photochemical conversion and storage of solar energy, ed. J. S. Connolly, Academic Press, 1981 Search PubMed.
- Y. Zhang, P. Traber, L. Zedler, S. Kupfer, S. Gräfe, M. Schulz, W. Frey, M. Karnahl and B. Dietzek, Phys. Chem. Chem. Phys., 2018, 20, 24843–24857 RSC.
- S. Garakyaraghi, P. D. Crapps, C. E. McCusker and F. N. Castellano, Inorg. Chem., 2016, 55, 10628–10636 CrossRef CAS PubMed.
- K. Kalyanasundaram, Photochemistry of polypyridine and porphyrin complexes, Academic Press, London; San Diego, 1992 Search PubMed.
- D. V. Scaltrito, D. W. Thompson, J. a. O'Callaghan and G. J. Meyer, Coord. Chem. Rev., 2000, 208, 243–266 CrossRef CAS.
- M. Schmittel, C. Michel, S.-X. Liu, D. Schildbach and D. Fenske, Eur. J. Inorg. Chem., 2001, 1155–1166 CrossRef CAS.
- M. Schmittel and A. Ganz, Chem. Commun., 1997, 999–1000 RSC.
- V. Kalsani, M. Schmittel, A. Listorti, A. Gianluca and N. Armaroli, Inorg. Chem., 2006, 45, 2061–2067 CrossRef CAS PubMed.
- Y. Pellegrin, M. Sandroni, E. Blart, A. Planchat, M. Evain, N. C. Bera, M. Kayanuma, M. Sliwa, M. Rebarz, O. Poizat, C. Daniel and F. Odobel, Inorg. Chem., 2011, 50, 11309–11322 CrossRef CAS PubMed.
- C. E. A. Palmer, D. R. McMillin, C. Kirmaier and D. Holten, Inorg. Chem., 1987, 26, 3167–3170 CrossRef CAS.
- R. M. Everly and D. R. McMillin, J. Phys. Chem., 1991, 95, 9071–9075 CrossRef CAS.
- C. E. A. Palmer and D. R. McMillin, Inorg. Chem., 1987, 26, 3837–3840 CrossRef CAS.
- R. M. Everly and D. R. McMillin, Photochem. Photobiol., 1989, 50, 711–716 CrossRef CAS.
- Z. A. Siddique, Y. Yamamoto, T. Ohno and K. Nozaki, Inorg. Chem., 2003, 42, 6366–6378 CrossRef CAS PubMed.
- G. B. Shaw, C. D. Grant, H. Shirota, E. W. Castner Jr, G. J. Meyer and L. X. Chen, J. Am. Chem. Soc., 2007, 129, 2147 CrossRef CAS PubMed.
- D. R. McMillin, J. R. Kirchhoff and K. V. Goodwin, Coord. Chem. Rev., 1985, 64, 83–92 CrossRef CAS.
- M. Iwamura, S. Takeuchi and T. Tahara, J. Am. Chem. Soc., 2007, 129, 5248–5256 CrossRef CAS PubMed.
- D. G. Cuttell, S.-M. Kuang, P. E. Fanwick, D. R. McMillin and R. A. Walton, J. Am. Chem. Soc., 2002, 124, 6–7 CrossRef CAS PubMed.
- C. T. Cunningham, K. L. H. Cunningham, J. F. Michalec and D. R. McMillin, Inorg. Chem., 1999, 38, 4388–4392 CrossRef CAS PubMed.
- N. A. Gothard, M. W. Mara, J. Huang, J. M. Szarko, B. Rolczynski, J. V. Lockard and L. X. Chen, J. Phys. Chem. A, 2012, 116, 1984–1992 CrossRef CAS PubMed.
- B. A. Gandhi, O. Green and J. N. Burstyn, Inorg. Chem., 2007, 46, 3816–3825 CrossRef CAS PubMed.
- M. K. Eggleston, D. R. McMillin, K. S. Koenig and A. J. Pallenberg, Inorg. Chem., 1997, 36, 172–176 CrossRef CAS.
- D. V. Scaltrito, C. A. Kelly, M. Ruthkosky, M. C. Zaros and G. J. Meyer, Inorg. Chem., 2000, 39, 3765–3770 CrossRef CAS PubMed.
- M. Ruthkosky, F. N. Castellano and G. J. Meyer, Inorg. Chem., 1996, 35, 6406–6412 CrossRef CAS PubMed.
- M. Ruthkosky, C. A. Kelly, M. C. Zaros and G. J. Meyer, J. Am. Chem. Soc., 1997, 119, 12004–12005 CrossRef CAS.
- L. X. Chen, G. B. Shaw, I. Novozhilova, T. Liu, G. Jennings, K. Attenkofer, G. J. Meyer and P. Coppens, J. Am. Chem. Soc., 2003, 125, 7022–7034 CrossRef CAS PubMed.
- M. Ruthkosky, C. A. Kelly, F. N. Castellano and G. J. Meyer, Coord. Chem. Rev., 1998, 171, 309–322 CrossRef CAS.
- U. E. Steiner and D. Bürßner, Z. Phys. Chem., 1990, 169, 159–180 CrossRef CAS.
- D. Bürßner, H. J. Wolff and U. E. Steiner, Z. Phys. Chem., 1993, 182, 297–308 CrossRef.
- D. Bürßner, H. J. Wolff and U. E. Steiner, Angew. Chem., Int. Ed., 1994, 33, 1772 CrossRef.
- H. J. Wolff, D. Bürßner and U. E. Steiner, Pure Appl. Chem., 1995, 67, 167 CAS.
- K. A. Hötzer, A. Klingert, T. Klumpp, E. Krissinel, D. Bürßner and U. E. Steiner, J. Phys. Chem. A, 2002, 106, 2207–2217 CrossRef.
- T. Klumpp, M. Linsenmann, S. L. Larson, B. R. Limoges, D. Bürssner, E. B. Krissinel, C. M. Elliott and U. E. Steiner, J. Am. Chem. Soc., 1999, 121, 1076–1087 CrossRef CAS.
- M. T. Rawls, I. Kuprov, C. M. Elliott and U. E. Steiner, in Carbon-centered free radicals and radical cations [electronic resource]: structure, reactivity, and dynamics, ed. M. D. E. Forbes, John Wiley & Sons, Hoboken, NJ, 2010, pp. 205–220 Search PubMed.
- M. T. Rawls, G. Kollmannsberger, C. M. Elliott and U. E. Steiner, J. Phys. Chem. A, 2007, 111, 3485–3496 CrossRef CAS PubMed.
- E. H. Yonemoto, R. L. Riley, Y. Il Kim, S. J. Atherton, R. H. Schmehl and T. E. Mallouk, J. Am. Chem. Soc., 1992, 114, 8081–8087 CrossRef CAS.
- H. Hayashi and S. Nagakura, Bull. Chem. Soc. Jpn., 1984, 57, 322–328 CrossRef CAS.
- U. Steiner and T. Ulrich, Chem. Rev., 1989, 89, 51–147 CrossRef CAS.
- L. F. Cooley, S. L. Larson, C. M. Elliott and D. F. Kelley, J. Phys. Chem., 1991, 95, 10694–10700 CrossRef CAS.
- J. M. Weber, M. T. Rawls, V. J. Mackenzie, B. R. Limoges and C. M. Elliott, J. Am. Chem. Soc., 2007, 129, 313–320 CrossRef CAS PubMed.
- S. L. Larson, C. M. Elliott and D. F. Kelley, J. Phys. Chem., 1995, 99, 6530–6539 CrossRef CAS.
- S. L. Larson, L. F. Cooley, C. M. Elliott and D. F. Kelley, J. Am. Chem. Soc., 1992, 114, 9504–9509 CrossRef CAS.
- R. G. Finke, B. L. Smith, M. W. Droege, C. M. Elliott and E. Hershenhart, J. Organomet. Chem., 1980, 202, C25–C30 CrossRef CAS.
- C. M. Elliott and E. J. Hershenhart, J. Am. Chem. Soc., 1982, 104, 7519–7526 CrossRef CAS.
- K. E. Spettel and N. H. Damrauer, J. Phys. Chem. A, 2014, 118, 10649–10662 CrossRef CAS PubMed.
- M. L. Rizzo, Statistical Computing with R, CRC Press, Boca Raton, 2007 Search PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- E. van Lenthe, A. Ehlers and E.-J. Baerends, J. Chem. Phys., 1999, 110, 8943 CrossRef CAS.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783 CrossRef CAS.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597 CrossRef CAS.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109 CrossRef CAS.
- R. Izsák and F. Neese, J. Chem. Phys., 2011, 135, 144105 CrossRef PubMed.
- K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Theor. Chem. Acc., 1997, 97, 119–124 Search PubMed.
- K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Chem. Phys. Lett., 1995, 240, 283–290 CrossRef CAS.
- S. Vancoillie and K. Pierloot, J. Phys. Chem. A, 2008, 112, 4011–4019 CrossRef CAS PubMed.
- F. Neese, Magn. Reson. Chem., 2004, 42, S187–S198 CrossRef CAS PubMed.
- C. Angeli, R. Cimiraglia and J.-P. Malrieu, J. Chem. Phys., 2002, 117, 9138 CrossRef CAS.
- C. Angeli, S. Borini, M. Cestari and R. Cimiraglia, J. Chem. Phys., 2004, 121, 4043–4049 CrossRef CAS PubMed.
- F. Neese, J. Chem. Phys., 2003, 118, 3939 CrossRef CAS.
- M. Atanasov, D. Ganyushin, K. Sivalingam and F. Neese, in Molecular Electronic Structures of Transition Metal Complexes II, ed. D. M. P. Mingos, P. Day and J. P. Dahl, Springer Berlin Heidelberg, Berlin, Heidelberg, 2012, vol. 143, pp. 149–220 Search PubMed.
- D. Maganas, S. Sottini, P. Kyritsis, E. J. J. Groenen and F. Neese, Inorg. Chem., 2011, 50, 8741–8754 CrossRef CAS PubMed.
- S. K. Singh, M. Atanasov and F. Neese, J. Chem. Theory Comput., 2018, 14, 4662–4677 CrossRef CAS PubMed.
- F. N. Castellano, M. Ruthkosky and G. J. Meyer, Inorg. Chem., 1995, 34, 3–4 CrossRef CAS.
- M. T. Miller, P. K. Gantzel and T. B. Karpishin, Inorg. Chem., 1998, 37, 2285–2290 CrossRef CAS PubMed.
- J. R. Kirchhoff, R. E. J. Gamache, M. W. Blaskie, P. A. A. Del, R. K. Lengel and D. R. McMillin, Inorg. Chem., 1983, 22, 2380–2384 CrossRef CAS.
- F. K. Klemens, C. E. A. Palmer, S. M. Rolland, P. E. Fanwick, D. R. McMillin and J. P. Sauvage, New J. Chem., 1990, 14, 129–133 CAS.
- M. Iwamura, S. Takeuchi and T. Tahara, Phys. Chem. Chem. Phys., 2014, 16, 4143–4155 RSC.
- S. Garakyaraghi, E. O. Danilov, C. E. McCusker and F. N. Castellano, J. Phys. Chem. A, 2015, 119, 3181–3193 CrossRef CAS PubMed.
- J. H. Klein, D. Schmidt, U. E. Steiner and C. Lambert, J. Am. Chem. Soc., 2015, 137, 11011–11021 CrossRef CAS PubMed.
- U. E. Steiner, J. Schäfer, N. N. Lukzen and C. Lambert, J. Phys. Chem. C, 2018, 122, 11701–11708 CrossRef CAS.
- S. Riese, L. Mungenast, A. Schmiedel, M. Holzapfel, N. N. Lukzen, U. E. Steiner and C. Lambert, Mol. Phys., 2019, 117, 2632–2644 CrossRef CAS.
- J. Schäfer, M. Holzapfel, A. Schmiedel, U. E. Steiner and C. Lambert, Phys. Chem. Chem. Phys., 2018, 20, 27093–27104 RSC.
- D. E. Manolopoulos and P. J. Hore, J. Chem. Phys., 2013, 139, 124106 CrossRef CAS PubMed.
- A. M. Lewis, D. E. Manolopoulos and P. J. Hore, J. Chem. Phys., 2014, 141, 44111 CrossRef PubMed.
- A. M. Lewis, T. P. Fay and D. E. Manolopoulos, J. Chem. Phys., 2016, 145, 244101 CrossRef PubMed.
- T. P. Fay, L. P. Lindoy and D. E. Manolopoulos, J. Chem. Phys., 2018, 149, 64107 CrossRef PubMed.
- A. M. Lewis, T. P. Fay, D. E. Manolopoulos, C. Kerpal, S. Richert and C. R. Timmel, J. Chem. Phys., 2018, 149, 034103 CrossRef PubMed.
- A. Horvath, Z. Zsilák and S. Papp, J. Photochem. Photobiol., A, 1989, 50, 129–139 CrossRef CAS.
- P. W. Atkins and D. Kivelson, J. Chem. Phys., 1966, 44, 169 CrossRef CAS.
- S. N. Batchelor, C. W. M. Kay, K. A. McLauchlan and I. A. Shkrob, J. Phys. Chem., 1993, 97, 13250–13258 CrossRef CAS.
- K. Schulten and P. G. Wolynes, J. Chem. Phys., 1978, 68, 3292 CrossRef CAS.
- A. Carrington and A. D. McLachlan, Chapman and Hall, 1967 Search PubMed.
- P. Gilch, W. Haas and U. E. Steiner, Chem. Phys. Lett., 1996, 254, 384–390 CrossRef CAS.
- E.-W. Knapp and K. Schulten, J. Chem. Phys., 1979, 71, 1878 CrossRef CAS.
- U. E. Steiner and H. J. Wolff, in Photochemistry and Photophysics, ed. J. J. Rabek and G. W. Scott, CRC Press, Boca Raton, 1991, vol. IV, pp. 1–130 Search PubMed.
- A. Klingert, PhD Thesis, University of Konstanz, Konstanz, 2004.
- T. P. Fay, L. P. Lindoy and D. E. Manolopoulos, J. Chem. Phys., 2019, 151, 154117 CrossRef PubMed.
- R. Orbach, Proc. Phys. Soc., 1961, 77, 821–826 CrossRef CAS.
- D. Kivelson, J. Chem. Phys., 1993, 45, 1324–1332 CrossRef.
- P. Gilch, F. Pöllinger-Dammer, C. Musewald, M. E. Michel-Beyerle and U. E. Steiner, Science, 1998, 281, 982–984 CrossRef CAS PubMed.
- J. A. Hughes, S. J. O. Hardman, N. S. Scrutton, D. M. Graham, J. R. Woodward and A. R. Jones, J. Chem. Phys., 2019, 151, 201102 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Ligand and copper complex synthesis, optical setup for transient absorption spectroscopy, solvent effects on initial amplitude of MeCA2, quantum chemistry, theoretical calculation of CT decay time, refined analysis of McMillin scheme, emission decay curves, spin motion and spin relaxation. See DOI: 10.1039/d0sc00830c |
| ‡ Equal contribution from both authors |
| § Present address: Department of Chemistry, Metropolitan State University, Denver, CO 80204. |
| ¶ Present address: Fritz Haber Center for Molecular Dynamics Research Institute of Chemistry, The Hebrew University of Jerusalem, Jerusalem 9190401, Israel. |
| || Deceased on July 2nd, 2014. |
| This journal is © The Royal Society of Chemistry 2020 |