Open Access Article
Open Access ArticleMapping the multi-step mechanism of a photoredox catalyzed atom-transfer radical polymerization reaction by direct observation of the reactive intermediates†
Luke
Lewis-Borrell‡
 a,
Mahima
Sneha‡
a,
Mahima
Sneha‡
 a,
Aditi
Bhattacherjee‡§
a,
Aditi
Bhattacherjee‡§
 a,
Ian P.
Clark
b and
Andrew J.
Orr-Ewing
a,
Ian P.
Clark
b and
Andrew J.
Orr-Ewing
 *a
*a
aSchool of Chemistry, University of Bristol, Cantock's Close, Bristol BS8 1TS, UK. E-mail: a.orr-ewing@bristol.ac.uk
bCentral Laser Facility, Research Complex at Harwell, Science and Technology Facilities Council, Rutherford Appleton Laboratory, Harwell Oxford, Didcot, Oxfordshire, OX11 0QX, UK
First published on 16th April 2020
Abstract
The rapid development of new applications of photoredox catalysis has so far outpaced the mechanistic studies important for rational design of new classes of catalysts. Here, we report the use of ultrafast transient absorption spectroscopic methods to reveal both mechanistic and kinetic details of multiple sequential steps involved in an organocatalyzed atom transfer radical polymerization reaction. The polymerization system studied involves a N,N-diaryl dihydrophenazine photocatalyst, a radical initiator (methyl 2-bromopropionate) and a monomer (isoprene). Time-resolved spectroscopic measurements spanning sub-picosecond to microseconds (i.e., almost 8 orders of magnitude of time) track the formation and loss of key reactive intermediates. These measurements identify both the excited state of the photocatalyst responsible for electron transfer and the radical intermediates participating in propagation reactions, as well as quantifying their lifetimes. The outcomes connect the properties of N,N-diaryl dihydrophenazine organic photocatalysts with the rates of sequential steps in the catalytic cycle.
Introduction
The past decade has witnessed renewed interest in the use of photochemistry in chemical synthesis, in particular because of ground breaking developments in photoredox catalysis.1–3 Photoredox cycles commonly use a transition-metal complex (e.g., fac-Ir(ppy)3 or Ru(bpy)3Cl2) as the photo-active catalyst. This complex absorbs visible or near-ultraviolet (UV) light to populate an electronically excited state from which the catalyst drives a single-electron transfer (SET) reaction with an electron donor or acceptor reagent. The one-electron oxidation or reduction initiates a cycle which is closed by a final redox event. Numerous studies have shown how this methodology can access an array of reactions, examples of which include C–H functionalization,4 Ni-based C(sp3)-C(sp2) cross coupling,5 Cu-based stereoselective reactions,6 and an enantioselective Menisci type reaction using a chiral Lewis acid.7 However, catalysts based on Ir and Ru complexes are not sustainable, and a shift towards alternatives is underway.8 One attractive route is the use of organic dyes which can drive the same redox cycles as the metal-centred photocatalysts (PCs).9 Fukuzumi and Nicewicz have pioneered such advances, with example reactions including chlorination,10 bromination,11 oxygenation,12 various forms of anti-Markovnikov additions to alkenes,13–15 C–H amination,16 and strategies for C–H activation of arenes and heteroarenes.17Mechanistic studies have not kept up with the rate of synthetic innovation, but examples are emerging which contribute to the improvement of existing photoredox catalysis schemes or the design of new ones.18–28 One technique well-suited to study photochemical mechanisms is transient absorption spectroscopy, in which a laser pulse of chosen wavelength (the ‘pump’ pulse) selectively excites a PC and the resulting reaction intermediates and photoproducts are monitored in absorption with a probe laser pulse. The probe region most commonly spans either UV/visible or infrared (IR) wavelengths. In this way, reaction pathways may be observed on timescales from hundreds of femtoseconds up to tens of milliseconds.29–31 The resulting advantage is dynamic real-time tracking of short- and longer-lived intermediates, typically spanning picosecond to microsecond lifetimes, allowing identification and kinetic analyses for species impossible to observe with steady state techniques.
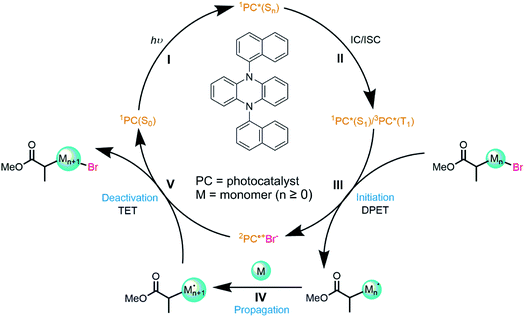
Here, we illustrate the use of transient absorption spectroscopy over extended timescales to follow the multi-step mechanism of a photoredox catalysed reaction. The reactions studied comprise the initiation and propagation steps of an atom transfer radical polymerization (ATRP). Applications of ATRP are benefiting from developments in photoredox catalysis because careful tuning of the photocatalyst, initiator, and polymerization conditions realises unprecedented control over polymer attributes.32–36 The first successful implementation used the popular fac-[Ir(ppy)3] PC,37 but metal-free organic PCs have since been introduced to ATRP to simplify the purification and reduce product toxicity. For example, Hawker and coworkers reported application of the organocatalyst 10-phenylphenothiazine to produce low dispersity poly(methyl methacrylate) (PMMA).38 Miyake and coworkers subsequently employed catalysts with N,N-diaryl dihydrophenazine based architectures differing in their para functionalisation on the phenyl rings (–OMe, –H, –CF3, –CN).39 They hypothesized that excited states with charge transfer (CT) character promoted faster and more efficient SET to the initiator.40 On this basis, two such catalysts were designed with either 1-napthyl or 2-napthyl (PCBN, Fig. 1) groups attached to the dihydrophenazine core and they proved superior to other N,N-diaryl dihydrophenazines in controlling the polymerization of PMMA.39 This design hypothesis has since been used to develop further organic photoredox catalysts for ATRP.41,42
Koyama et al. recently applied ultrafast transient vibrational and electronic absorption spectroscopy (TVAS and TEAS) to study the early stages of selected organocatalyzed ATRP (O-ATRP) reactions developed by Miyake and co-workers.23 The mechanism for this class of reactions is shown in Fig. 1: photoexcitation of the PC is followed by electron transfer (ET) to the initiator, and subsequent radical reaction with the monomer unit grows the polymer which is then deactivated by thermal electron transfer (TET) to an oxidized PC. By focusing on two N,N-diaryl dihydrophenazine catalysts (5,10-bis(4-fluorophenyl)-5,10-dihydrophenazine (abbreviated here to PCF) and 5,10-bisphenyl-5,10-dihydrophenazine (PCH)), Koyama et al. were able to observe steps I–III (Fig. 1) of this cycle on timescales from 100 fs to 1.3 ns. Their study indicated that: (i) electron transfer from the S1 state must compete with short (sub-ns to few ns) S1-state lifetimes because of low quantum yields for ISC to the triplet manifold; (ii) PCs reported to be better catalysts for polymerization control are those that undergo slower electron transfer; (iii) the solvent-dependent relative rates of these dissociative electron transfer reactions follow the expectations of Marcus–Savéant theory, and can be rationalized from the Gibbs energies of the PC excited state and the PC radical cation. Sartor et al. have recently contributed detailed time-dependent studies of the photochemistry of structurally similar phenoxazine PCs.24,43
In the current work, we report a more comprehensive study of an O-ATRP cycle using the organic photocatalyst 5,10-di(naphthalen-1-yl)-5,10-dihydrophenazine (PCBN). This PC was chosen from an array of possible structural modifications of the dihydrophenazine core to explore why it exhibits superior polymerization control to other dihydrophenazine-based PCs.39 We show that short-lived reactive intermediates may be identified and tracked from the initial photoexcitation of the catalyst through to the propagation reaction of the radical, i.e., steps I to IV in Fig. 1. These advances in mechanistic and kinetic studies are achieved using transient absorption spectroscopy in continuous measurements over time domains spanning femtoseconds to microseconds that are greatly extended from the work of Koyama et al. The results provide insights about the influence of the excited state properties of the dihydrophenazine derivatives and the radical reactions they initiate on the performance of organic photoredox catalysed O-ATRP.
Results and discussion
Throughout this study, TVAS and TEAS were used to observe the intermediates in an O-ATRP cycle initiated by exciting the catalyst PCBN with 370 nm light. The intermediates were either tracked in the IR (TVAS) or in the UV/visible (TEAS) spectral region. TEAS measurements on timescales from 100 fs to 1.3 ns used an apparatus at the University of Bristol which has been described elsewhere.44,45 TVAS experiments used a custom-built laser system in the LIFEtime facility at the Rutherford Appleton Laboratory46 to make transient IR spectroscopy measurements over time delays from 300 fs to 10 μs which provided specific information on the chemical participants in sequential reaction steps. In both types of spectroscopic studies, samples were continuously circulated through a Harrick cell using a sealed flow system. Solutions were purged with nitrogen immediately prior to use to minimize the effects of dissolved O2 on the measured kinetics. Further details for each technique are presented in the ESI.†() Light absorption and emission
The photocatalyst PCBN, with the structure shown in Fig. 1, has its lowest energy optically bright transition in the near UV with maximum absorbance at λmax = 370 nm (Fig. S4 of ESI†). This transition was previously assigned to an S0 to S4 excitation with 62% CT character and 30% locally excited (LE) character.23,40 The steady state emission spectra display a strong shift in the wavelengths of maximum emission from 538 nm in toluene to 587 nm in dichloromethane (DCM) and 602 nm in N,N-dimethylformamide (DMF) (Fig. S5†). The emissive S1 state of PCBN is thus argued to be of CT character, an interpretation that is supported by theoretical calculations and prior spectroscopic studies.40(II) Photochemistry of PCBN
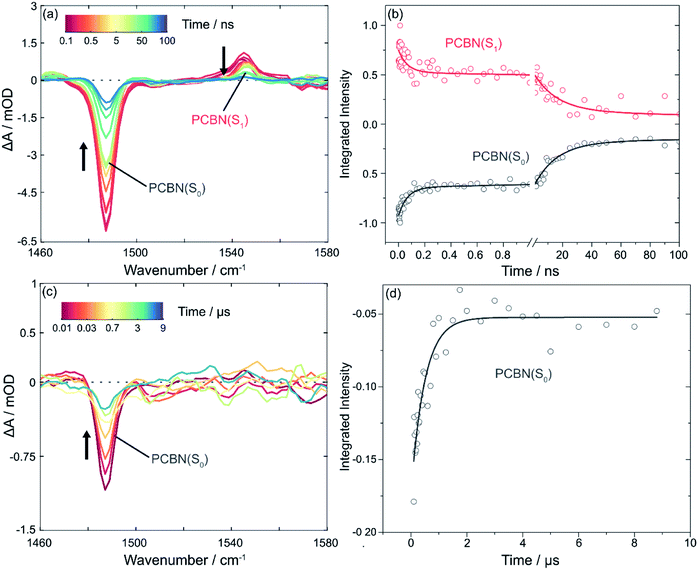
The TVAS spectra measured for PCBN in DCM and displayed in Fig. 2 show two distinct features corresponding to a ground-state bleach (GSB) at 1488 cm−1 and an excited state absorption (ESA) band centred at 1544 cm−1. Based on previous interpretation of the corresponding PCF spectrum,23 the positive feature is assigned to a ring motion of the PCBN (S1) excited state, and the bleach to the photoinduced depletion of a ring motion in the PCBN (S0) ground state. This latter assignment is confirmed by an observed band at 1488 cm−1 in the steady-state IR spectrum of a PCBN solution in DCM (Fig. S1†). The two features have matching kinetics, as shown in Fig. 2(b), with the GSB recovering with time constants of 60 ± 8 ps and 17 ± 1 ns (with one standard error uncertainties derived from the exponential fits) in DCM as the excited state relaxes and the ground state population is recovered. The 17 ns component is attributed to radiative (fluorescent) and perhaps also non-radiative decay from the S1 to the S0 state; this time-constant is solvent dependent, and is 5.2 ± 0.4 ns in DMF and 25 ± 1 ns in toluene-d8. The incomplete ground-state bleach recovery seen in Fig. 2(b) on timescales of ∼100 ns (i.e., ≥4 time constants) suggests that a proportion of the S1-state population transfers to the manifold of triplet states by intersystem crossing, with Φ(T1) = 13 ± 2% (Fig. S10†). TVAS measurements to more-extended time delays (Fig. 2(c and d)) show the residual GSB recovers with a time constant of 0.5 ± 0.1 μs which is indicative of triplet-state relaxation. This time constant is a lower-limit to the T1-state lifetime because triplet quenching may be promoted by small residual amounts of dissolved O2. However, we expect the low concentrations of any dissolved oxygen remaining in our purged solutions to have little effect on the picosecond and nanosecond dynamics.30 A small (∼5%) remaining proportion of unrecovered GSB evident in Fig. 2(c) is thought to stem from excited state reaction with DCM.47 The 60 ps component of S0 recovery must then be associated with a pathway to the ground state accessible only to higher lying singlet states (Sn with n > 1), or to vibrationally hot S1 molecules produced by the internal conversion routes from Sn, in competition with quenching of the excess internal energy above the S1 minimum. A further ultrafast relaxation time constant of 3.4 ± 0.7 ps observed in TEAS data (Fig. S9†) is most likely a consequence of the ultrafast internal conversion, and is not accessible to TVAS measurement because of the lower time resolution. TVAS and TEAS data for PCBN in toluene (Fig. S12†) and DMF (Fig. S13†) show similar behaviour to the DCM solution, except that GSB recovery is complete on nanosecond timescales. This faster GSB recovery suggests that triplet-state pathways are not significant in these two solvents, perhaps because the minor ISC pathway observed in DCM derives from an external heavy atom effect in this chlorinated solvent.(III) Photoinitiated electron transfer from PCBN(S1)
Introduction of the radical initiator Methyl 2-bromopropionate (MBP) gives the transient spectra shown in Fig. 3. While similar to the spectra of Fig. 2, there are three notable differences: (i) the degree of recovery of the GSB feature is less than 25%, signalling that >75% of the PCBN(S1) does not relax to the ground state; (ii) a new band appears at 1552 cm−1 which is assigned to PCBN+˙(D0) (see Fig. S3†); and (iii) a carbonyl band assigned to 2MP˙(D0) grows with centre at 1660 cm−1.23 Both this radical and the PCBN+˙ radical cation are products of an electron transfer reaction (step III of the cycle shown in Fig. 1), accounting for the persistence of the PCBN GSB feature. The matching kinetics of these species are shown in Fig. 3(b) and are consistent with SET from the PCBN(S1) state. The following analysis uses single exponential fitting of the kinetics of bimolecular electron transfer reactions at different concentrations of the acceptor MBP. This exponential fitting of the data is compared to an analysis using a Smoluchowski model of diffusive reactions48,49 in the ESI (Fig. S22†) and the two methods give similar outcomes.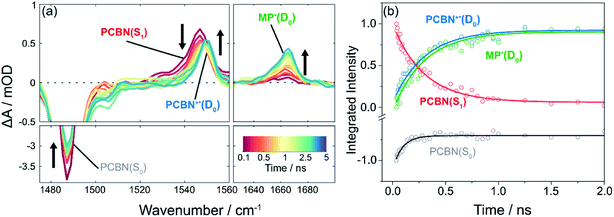 | ||
| Fig. 3 TVAS measurements for the photoexcited-state electron transfer reaction of PCBN with methyl 2-bromopropionate (MBP) following pulsed excitation at 370 nm. (a) TVA spectra for PCBN (2.1 mM) and MBP (0.8 M) in DCM. Black arrows adjacent to features indicate directions of change; (b) Corresponding kinetic traces for PCBN*(S1) (red), PCBN+˙(D0) (blue), PCBN(S0) (grey), 2MP˙(D0) (green) obtained by decomposition of the time-dependent spectra in (a). Integrated intensities have been scaled to maximum magnitudes of 1 at early time. Solid lines are single exponential fits to the data: PCBN*(S1) (red), PCBN+˙(D0) (blue), and 2MP˙(D0) (green) are globally fitted giving a single exponential time constant of τ1 = 0.30 ± 0.01 ns, and PCBN(S0) is fitted separately to the 60 ps time constant revealed by TVAS (Fig. 2) and TEAS (Fig. S9†). | ||
The 2MP˙(D0) radical absorption rises because dissociative electron transfer to MBP causes loss of Br− and it decays on longer timescales by diffusional quenching either with another radical or dissolved O2. Fig. S18† shows how the rise of the radical varies with concentration of MBP in DCM. A linear fit to the MBP-concentration dependence of the derived rate coefficients gives a bimolecular rate coefficient for electron transfer from PCBN(S1) to MBP in DCM of kPET = (2.6 ± 0.3) × 109 dm3 mol−1 s−1. Rate coefficients for electron transfer recorded in DMF (kPET = (1.8 ± 0.1) × 109 dm3 mol−1 s−1) and toluene (kPET = (3.1 ± 0.1) × 109 dm3 mol−1 s−1) do not differ markedly from the value in DCM and their magnitudes indicate a degree of activation control to the kinetics.50 Any variation in these rate coefficients for the three solvents is consistent with greater stabilization of the CT-character S1 state in the more polar solvents, and hence slowing of the ET rate. The diffusion rates are also solvent dependent, and will cause some variation in the kPET values, but the PET reaction rates are not limited by diffusion.
PCBN was proposed as a second-generation catalyst based on design arguments that charge separation in its T1 state would promote fast ET to MBP.39 However, the transient absorption studies reported here point to inefficient ISC (i.e., Φ(T1) = 13 ± 2% in DCM, and no evidence for triplet production in toluene or DMF), ET from the S1 rather than the T1 state of PCBN at the concentrations of the MBP acceptor used, and an ET rate coefficient for PCBN smaller than for catalysts PCF (kPET = (4.4 ± 0.3) × 109 dm3 mol−1 s−1 in DCM) and PCH (kPET = (2.0 ± 0.2) × 1010 dm3 mol−1 s−1 in DCM).23 The excited states of PCF and PCBN involved in ET are of CT character, whereas that for PCH is of LE character.23,40 The trend in the measured PET rate coefficients of kPET(PCH) > kPET(PCF) > kPET(PCBN) is therefore inconsistent with arguments based on CT character and is instead better understood in terms of the Gibbs energy difference between the PC excited state of interest for ET and the PC+˙ radical cation, in accordance with Marcus–Savéant theory (eqn (1)).51–53 For an electron transfer reaction in which the acceptor dissociates into a radical and an anion, the Gibbs energy of activation is estimated using:
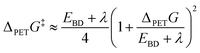 | (1) |
The assumption that the C–Br bond dissociation energy (EBD) in MBP is much greater than the solvent reorganization energy (λ) simplifies the application of this expression. Here, we focus on the effect of changes to the photocatalyst by comparing values of the term accounting for the Gibbs energy for photoinduced dissociative electron transfer:
| ΔPETG = F(E0(PC˙+/PC) − E0(RX/R˙X−)) − E(PC(S1)) − w | (2) |
From eqn (2), we can estimate the changes in this thermodynamic driving force Δ(ΔPETG) for the different PCs. In this expression, F is the Faraday constant, E0(PC˙+/PC) is the PC oxidation potential, E0(RX/R˙X−) is the initiator reduction potential, E(PC(S1)) is the energy of the S1 excited state of the PC (which we argue above to be responsible for the ET reaction) and wis the electrostatic work term.9 The Coulombic attraction between the PC˙+ and Br− accounting for w, and the MBP reduction potential are essentially unchanged for reactions involving PCBN, PCF and PCH, leaving the other factors to determine Δ(ΔPETG). This analysis indicates that ΔPETG values for the PCBN and PCF reactions are 51 and 47 kJ mol−1 smaller in magnitude than for PCH, respectively (see ESI† for details of the calculation), consistent with a degree of activation control for ET from PCF and PCBN whereas the ET reaction of PCH with MBP is diffusion controlled. In comparison to PCF, PCBN is reported to exhibit greater levels of control over polymerization.39 However, our analysis shows that both the rate of electron transfer and the Gibbs energy change for PET do not vary significantly between the two catalysts, suggesting that other factors may influence PCBN's superior polymerization control. One such factor may be efficient deactivation of the polymer chain which is argued to be important in controlling polymerization, although different mechanisms have been proposed.18,40,42
(IV) Propagation reactions
The data presented up to this point have resolved the picosecond timescale excited state photochemistry of PCBN and the nanosecond timescale competition between ground-state recovery and bimolecular electron transfer reactions with the electron acceptor MBP. The subsequent reaction of the resulting 2MP˙(D0) radicals with an added monomer, corresponding to the first propagation step of the catalytic cycle (step IV in Fig. 1), is now addressed. These longer-time measurements are made by following the decay of the absorption of the MP˙ radical over timescales extending beyond 1 μs, as shown in Fig. 4(a). The reaction of MP˙ radicals with dissolved molecular oxygen competes with addition to an unsaturated monomer and therefore necessitates careful purging of the O2 from the sample.30 Measurements made with unpurged and N2-purged samples are compared in Fig. S21† and are consistent with the report by Miyake and co-workers that oxygen inhibited their polymerization reactions.54 In a purged and closed-cycle system, we successfully observed the shortening of the MP˙ lifetime with addition of monomer, chosen to be isoprene because it has no overlapping IR absorption bands in the probe region and has been used previously in ATRP polymerizations.55 Example data are shown in Fig. 4(b). Linear fitting of the pseudo first-order rate constants (see ESI† for a discussion of the kinetic analysis) obtained with different amounts of excess isoprene (at PC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) monomer ratios consistent with conditions used for polymerization reactions) gives a rate coefficient for the first step of the propagation of kprop = (3.1 ± 0.8) × 105 dm3 mol−1 s−1 in DCM. Multiple bimolecular propagation steps extend the subsequent reaction kinetics beyond our observation time window. Theriot et al.39 have suggested that with PCBN as the chosen photocatalyst and methyl methacrylate as a monomer, six propagation steps occur before back-ET to the catalyst and control over polymerization is realised. Completion of the photocatalytic cycle and recovery of the PC(S0) are not evident in our current TVAS measurements because of flow of the sample out of the probe laser volume on these extended time scales and reaction of radical species with residual dissolved O2.
monomer ratios consistent with conditions used for polymerization reactions) gives a rate coefficient for the first step of the propagation of kprop = (3.1 ± 0.8) × 105 dm3 mol−1 s−1 in DCM. Multiple bimolecular propagation steps extend the subsequent reaction kinetics beyond our observation time window. Theriot et al.39 have suggested that with PCBN as the chosen photocatalyst and methyl methacrylate as a monomer, six propagation steps occur before back-ET to the catalyst and control over polymerization is realised. Completion of the photocatalytic cycle and recovery of the PC(S0) are not evident in our current TVAS measurements because of flow of the sample out of the probe laser volume on these extended time scales and reaction of radical species with residual dissolved O2.
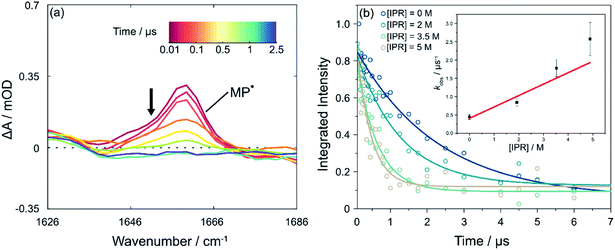 | ||
| Fig. 4 Reaction of the MP radical with isoprene (IPR) in DCM. (a) Transient vibrational absorption spectra showing the extended timescale for decay of the 2MP˙(D0) radical absorption band centred at 1660 cm−1 following pulsed excitation of PCBN at 370 nm. The black arrow adjacent to the MP˙ radical feature indicates the direction of change. (b) Kinetics of decay of 2MP˙(D0) radicals in the presence of IPR on timescales up to 7 μs. Each curve corresponds to a different concentration of isoprene (see legend). The inset is a pseudo-first-order kinetic plot using the model discussed in the ESI,† with a linear fit weighted to account for the uncertainty at each data point. | ||
Conclusion
The current study shows that transient-IR absorption spectroscopy can resolve the sequential photochemical and bimolecular reaction steps involved in a photoredox catalytic cycle spanning time intervals from 300 fs to 10 μs. These measurements reveal the timescales for photocatalyst excited state relaxation by internal conversion and intermolecular electron transfer reaction with a radical initiator, and of radical addition to propagate a growing polymer, from which clear kinetic and mechanistic insights emerge. The excited state responsible for electron transfer is identified, and trends in rate coefficients for dissociative electron transfer reactions are in accord with expectations from Marcus–Savéant theory. Following the PET step to produce reactive radicals for polymerization, competition is observed between radical reactions with dissolved O2 and added alkene monomer highlighting the importance of undertaking O-ATRP polymerizations in O2 free conditions. N,N-diaryl dihydrophenazines with electron donating para substituents tend to have S1 states of LE character and near diffusion-limited PET rates to organobromides such as MBP. In contrast, N-aryl electron withdrawing or delocalizing groups that stabilise electronic states with CT character have the overall effect of decreasing PET rates. These CT-character excited states are also stabilized preferentially by polar solvents. Slower PET rates seem to favour O-ATRP control of polymer dispersity, but the importance of the deactivation step remains under-studied. The transient absorption spectroscopy methodology using multiple IR probe time delays presented here has considerable potential for wider application to unravel the complicated sequential and branching kinetics of many organic chemical reactions promoted by photoredox catalysis.Data availability
Data are available at the University of Bristol data repository, data.bris, at http://10.5523/bris.1bbuxza4dih8f2r16p114vozuo.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research is funded by EPSRC Grant No. EP/R012695/1 and previous ERC Advanced Grant CAPRI 290966. M. S gratefully acknowledges award of a Marie Skłodowska-Curie Fellowship (MARCUS 793799). The authors are grateful to the Science and Technology Facilities Council for access to the LIFEtime Facility at the Rutherford-Appleton Laboratory. We thank the Bristol Chemical Synthesis Centre for Doctoral Training, funded by EPSRC (EP/L015366/1), and the University of Bristol, for a PhD studentship for L. L. B.References
- M. A. Ischay, M. E. Anzovino, J. Du and T. P. Yoon, J. Am. Chem. Soc., 2008, 130, 12886–12887 CrossRef CAS PubMed.
- J. M. R. Narayanam, J. W. Tucker and C. R. J. Stephenson, J. Am. Chem. Soc., 2009, 131, 8756–8757 CrossRef CAS PubMed.
- C. K. Prier, D. A. Rankic and D. W. C. MacMillan, Chem. Rev., 2013, 113, 5322–5363 CrossRef CAS PubMed.
- I. B. Perry, T. F. Brewer, P. J. Sarver, D. M. Schultz, D. A. DiRocco and D. W. C. MacMillan, Nature, 2018, 560, 70–75 CrossRef CAS PubMed.
- Z. Zuo, D. T. Ahneman, L. Chu, J. A. Terrett, A. G. Doyle and D. W. C. MacMillan, Science, 2014, 345, 437–440 CrossRef CAS PubMed.
- D. Wang, N. Zhu, P. Chen, Z. Lin and G. Liu, J. Am. Chem. Soc., 2017, 139, 15632–15635 CrossRef CAS PubMed.
- R. S. J. Proctor, H. J. Davis and R. J. Phipps, Science, 2018, 360, 419–422 CrossRef CAS PubMed.
- A. Hossain, A. Bhattacharyya and O. Reiser, Science, 2019, 364, eaav9713 CrossRef PubMed.
- N. A. Romero and D. A. Nicewicz, Chem. Rev., 2016, 116, 10075–10166 CrossRef CAS PubMed.
- K. Ohkubo, K. Mizushima and S. Fukuzumi, Res. Chem. Intermed., 2013, 39, 205–220 CrossRef CAS.
- K. Ohkubo, K. Mizushima, R. Iwata and S. Fukuzumi, Chem. Sci., 2011, 2, 715–722 RSC.
- K. Ohkubo, T. Kobayashi and S. Fukuzumi, Angew. Chem., Int. Ed., 2011, 50, 8652–8655 CrossRef CAS PubMed.
- D. S. Hamilton and D. A. Nicewicz, J. Am. Chem. Soc., 2012, 134, 18577–18580 CrossRef CAS PubMed.
- T. M. Nguyen and D. A. Nicewicz, J. Am. Chem. Soc., 2013, 135, 9588–9591 CrossRef CAS PubMed.
- A. J. Perkowski and D. A. Nicewicz, J. Am. Chem. Soc., 2013, 135, 10334–10337 CrossRef CAS PubMed.
- N. A. Romero, K. A. Margrey, N. E. Tay and D. A. Nicewicz, Science, 2015, 349, 1326–1330 CrossRef CAS PubMed.
- J. B. McManus and D. A. Nicewicz, J. Am. Chem. Soc., 2017, 139, 2880–2883 CrossRef CAS PubMed.
- X. Pan, C. Fang, M. Fantin, N. Malhotra, W. Y. So, L. A. Peteanu, A. A. Isse, A. Gennaro, P. Liu and K. Matyjaszewski, J. Am. Chem. Soc., 2016, 138, 2411–2425 CrossRef CAS PubMed.
- M. Majek and A. Jacobi von Wangelin, Acc. Chem. Res., 2016, 49, 2316–2327 CrossRef CAS PubMed.
- L. Buzzetti, G. E. M. Crisenza and P. Melchiorre, Angew. Chem., Int. Ed., 2019, 58, 3730–3747 CrossRef CAS PubMed.
- S. Ruccolo, Y. Qin, C. Schnedermann and D. G. Nocera, J. Am. Chem. Soc., 2018, 140, 14926–14937 CrossRef CAS PubMed.
- J. Haimerl, I. Ghosh, B. König, J. Vogelsang and J. M. Lupton, Chem. Sci., 2019, 10, 681–687 RSC.
- D. Koyama, H. J. A. Dale and A. J. Orr-Ewing, J. Am. Chem. Soc., 2018, 140, 1285–1293 CrossRef CAS PubMed.
- S. M. Sartor, B. G. McCarthy, R. M. Pearson, G. M. Miyake and N. H. Damrauer, J. Am. Chem. Soc., 2018, 140, 4778–4781 CrossRef CAS PubMed.
- A. J. Orr-Ewing, Struct. Dyn., 2019, 6, 010901 CrossRef PubMed.
- C. L. Cruz and D. A. Nicewicz, ACS Catal., 2019, 9, 3926–3935 CrossRef CAS.
- N. A. Romero and D. A. Nicewicz, J. Am. Chem. Soc., 2014, 136, 17024–17035 CrossRef CAS PubMed.
- S. P. Pitre, C. D. McTiernan, H. Ismaili and J. C. Scaiano, J. Am. Chem. Soc., 2013, 135, 13286–13289 CrossRef CAS PubMed.
- D. Koyama and A. J. Orr-Ewing, Phys. Chem. Chem. Phys., 2016, 18, 26224–26235 RSC.
- D. Koyama, P. M. Donaldson and A. J. Orr-Ewing, Phys. Chem. Chem. Phys., 2017, 19, 12981–12991 RSC.
- A. Bhattacherjee, M. Sneha, L. Lewis-Borrell, O. Tau, I. P. Clark and A. J. Orr-Ewing, Nat. Commun., 2019, 10, 5152 CrossRef PubMed.
- K. Matyjaszewski and J. Xia, Chem. Rev., 2001, 101, 2921–2990 CrossRef CAS PubMed.
- M. Kato, M. Kamigaito, M. Sawamoto and T. Higashimura, Macromolecules, 1995, 28, 1721–1723 CrossRef CAS.
- J.-S. Wang and K. Matyjaszewski, J. Am. Chem. Soc., 1995, 117, 5614–5615 CrossRef CAS.
- V. Percec and B. Barboiu, Macromolecules, 1995, 28, 7970–7972 CrossRef CAS.
- X. Pan, M. Fantin, F. Yuan and K. Matyjaszewski, Chem. Soc. Rev., 2018, 47, 5457–5490 RSC.
- B. P. Fors and C. J. Hawker, Angew. Chem., Int. Ed., 2012, 51, 8850–8853 CrossRef CAS PubMed.
- N. J. Treat, H. Sprafke, J. W. Kramer, P. G. Clark, B. E. Barton, J. Read de Alaniz, B. P. Fors and C. J. Hawker, J. Am. Chem. Soc., 2014, 136, 16096–16101 CrossRef CAS PubMed.
- J. C. Theriot, C.-H. Lim, H. Yang, M. D. Ryan, C. B. Musgrave and G. M. Miyake, Science, 2016, 352, 1082–1086 CrossRef CAS PubMed.
- C.-H. Lim, M. D. Ryan, B. G. McCarthy, J. C. Theriot, S. M. Sartor, N. H. Damrauer, C. B. Musgrave and G. M. Miyake, J. Am. Chem. Soc., 2017, 139, 348–355 CrossRef CAS PubMed.
- B. G. McCarthy, R. M. Pearson, C.-H. Lim, S. M. Sartor, N. H. Damrauer and G. M. Miyake, J. Am. Chem. Soc., 2018, 140, 5088–5101 CrossRef CAS PubMed.
- V. K. Singh, C. Yu, S. Badgujar, Y. Kim, Y. Kwon, D. Kim, J. Lee, T. Akhter, G. Thangavel, L. S. Park, J. Lee, P. C. Nandajan, R. Wannemacher, B. Milián-Medina, L. Lüer, K. S. Kim, J. Gierschner and M. S. Kwon, Nat. Catal., 2018, 1, 794–804 CrossRef CAS.
- S. M. Sartor, Y. M. Lattke, B. G. McCarthy, G. M. Miyake and N. H. Damrauer, J. Phys. Chem. A, 2019, 123, 4727–4736 CrossRef CAS PubMed.
- M.-H. Kao, R. K. Venkatraman, M. N. R. Ashfold and A. J. Orr-Ewing, Chem. Sci., 2020, 11, 1991 RSC.
- G. M. Roberts, H. J. B. Marroux, M. P. Grubb, M. N. R. Ashfold and A. J. Orr-Ewing, J. Phys. Chem. A, 2014, 118, 11211–11225 CrossRef CAS PubMed.
- G. M. Greetham, P. M. Donaldson, C. Nation, I. V. Sazanovich, I. P. Clark, D. J. Shaw, A. W. Parker and M. Towrie, Appl. Spectrosc., 2016, 70, 645–653 CrossRef CAS PubMed.
- S. Chaudhuri, B. Rudshteyn, M. Prémont-Schwarz, D. Pines, E. Pines, D. Huppert, E. T. J. Nibbering and V. S. Batista, Chem. Phys. Lett., 2017, 683, 49–56 CrossRef CAS.
- T. Kumpulainen, B. Lang, A. Rosspeintner and E. Vauthey, Chem. Rev., 2017, 117, 10826–10939 CrossRef CAS PubMed.
- D. D. Eads, B. G. Dismer and G. R. Fleming, J. Chem. Phys., 1990, 93, 1136–1148 CrossRef CAS.
- A. C. Marco Montalti, L. Prodi and M. Teresa Gandolfi, Handbook of Photochemistry, Taylor & Francis Group, Boca Raton, FL, 3rd edn, 2006 Search PubMed.
- J. M. Saveant, J. Am. Chem. Soc., 1987, 109, 6788–6795 CrossRef CAS.
- R. A. Marcus, J. Chem. Phys., 1956, 24, 966–978 CrossRef CAS.
- R. A. Marcus, J. Chem. Phys., 1965, 43, 679–701 CrossRef CAS.
- B. McCarthy and G. M. Miyake, ACS Macro Lett., 2018, 7, 1016–1021 CrossRef CAS PubMed.
- J. Wootthikanokkhan, M. Peesan and P. Phinyocheep, Eur. Polym. J., 2001, 37, 2063–2071 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc01194k |
| ‡ Authors contributed equally to the work. |
| § Present address: AMOLF, Science Park 104, 1098 XG Amsterdam, The Netherlands. |
| This journal is © The Royal Society of Chemistry 2020 |