Vibrational characterization of a diiron bridging hydride complex – a model for hydrogen catalysis

Abstract

A diiron complex containing a bridging hydride and a protonated terminal thiolate of the form [(μ,κ₂-bdtH)(μ-PPh₂)(μ-H)Fe₂(CO)₅]⁺ has been investigated through ⁵⁷Fe nuclear resonance vibrational spectroscopy (NRVS) and interpreted using density functional theory (DFT) calculations. We report the Fe–μH–Fe wagging mode, and indications for Fe–μD stretching vibrations in the D-isotopologue, observed by ⁵⁷Fe-NRVS. Our combined approach demonstrates an asymmetric sharing of the hydride between the two iron sites that yields two nondegenerate Fe–μH/D stretching vibrations. The studied complex provides an important model relevant to biological hydrogen catalysis intermediates. The complex mimics proposals for the binuclear metal sites in [FeFe] and [NiFe] hydrogenases. It is also an appealing prototype for the ‘Janus intermediate’ of nitrogenase, which has been proposed to contain two bridging Fe–H–Fe hydrides and two protonated sulfurs at the FeMo-cofactor. The significance of observing indirect effects of the bridging hydride, as well as obstacles in its direct observation, is discussed in the context of biological hydrogen intermediates.

---

Introduction

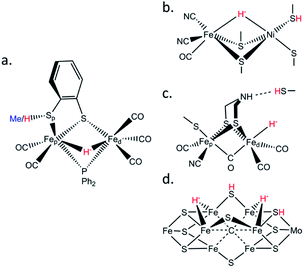
Biological hydrogen catalysis is driven by a ubiquitous and diverse set of enzymes called hydrogenases^1–4 and to a lesser extent by the nitrogenase family.⁵ Hydrogenases reversibly convert molecular hydrogen into reducing power at binuclear [FeFe], binuclear [NiFe],⁶ or mononuclear [Fe] active sites.⁷ Similarly, hydrogen evolution in Mo-nitrogenase occurs at a unique Fe₇MoS₉C cluster called the FeMo-cofactor, and analogous chemistry likely occurs at the Fe(V,Fe)-cofactors.^8,9 The activities of all these enzymes are presumably related by the formation of metastable Fe–H⁻ hydrides and protonation of nearby sulfurs during catalysis (Fig. 1).^6,10,11 Synthesis and characterization of model complexes that can simulate biochemical intermediates and their proton transfer capabilities by the stabilization of transition metal hydrides (M–H⁻) and nearby thiols (–SH) are key to understanding hydrogenase and nitrogenase active site hydrogen catalysis.^10,12–16

Fig. 1 Schematic structures of (a) the μHS(Me/H) synthetic complexes studied in this work; (b) the [NiFe] hydrogenase Ni–R intermediate; (c) the [FeFe] hydrogenase H_hyd intermediate; (d) the nitrogenase Janus intermediate. The iron hydrides and sulfur protonations are labelled in red.

These special –SH/M–H⁻ interactions take various forms. In [FeFe] hydrogenases there is a conserved cysteine situated at the end of a proton transfer chain formed by hydrophilic amino acid residues and water molecules, with the –SH thiol group adjacent to an azadithiolate (ADT) bridge of the [2Fe]_H sub-cluster (Fig. 1c). There is considerable evidence that the ADT bridge plays a critical role in proton acceptance and relay to the catalytic Fe_d site.¹⁷ Moreover, disruption of the proton supply chain in the enzymes from Chlamydomonas reinhardtii (CrHydA1) or Desulfovibrio desulfuricans (DdHydAB) has allowed the transient H_hyd catalytic state to be trapped and unequivocally shown to involve a terminal Fe_d–H⁻ hydride (Fig. 1c).^14,18–21 For [NiFe] hydrogenases, the catalytic Ni–R state has been shown to feature a bridging hydride, with a Ni-bound protonated cysteine sulfur (Fig. 1b).⁶ Finally, in nitrogenases the E₂ state is presumed to have one bridging Fe–H⁻–Fe hydride with a nearby protonated sulfur capable of H₂ release, while two hydrides capable of reductive elimination have been proposed for the E₄ or ‘Janus intermediate’ of the Fe(Mo,V,Fe)-cofactor (Fig. 1d).⁹

To model the aforementioned biological hydrides, previous efforts produced and characterized synthetic protonated thiols coordinated to diiron centers.^22–25 Here we extend this work by exploring ⁵⁷Fe-specific vibrational dynamics for a diiron center with a bridging hydride and a protonated thiol ligand. Specifically, we have characterized the [(μ,κ₂-bdtH)(μ-PPh₂)(μ-H)Fe₂(CO)₅]⁺ (bdt = 1,2-benzenedithiolate) model compound, referred hereafter as ‘μHSH’ (Fig. 1a), and as well its deuterated isotopologue [(μ,κ₂-bdtD)(μ-PPh₂)(μ-D)Fe₂(CO)₅]⁺, μDSD, using nuclear resonance vibrational spectroscopy (NRVS). We also recorded the spectrum of the S-methylated complex: [(μ,κ₂-bdtCH₃)(μ-PPh₂)(μ-H)Fe₂(CO)₅]⁺, here referred to as ‘μHSMe’.

⁵⁷Fe-NRVS is a synchrotron-based technique that observes excitation of an ⁵⁷Fe nucleus together with the excitation/deexcitation of vibrational modes.^26–28 NRVS is essentially the recoil fraction that steals intensity from the recoil-free Mössbauer effect, with the measured intensity for a given normal mode proportional to the ⁵⁷Fe kinetic energy in that mode, ultimately yielding an ⁵⁷Fe partial vibrational density of states (PVDOS). The experimental frequencies and intensities can be directly compared with normal mode calculations from density functional theory (DFT) or even empirical force fields.

The asymmetric diferrous compound μHSH is relevant to the protonated and bridging hydride-bound states proposed for H₂ production in [NiFe] hydrogenases and to the nitrogenase E₂ and E₄ intermediates. It is also a good benchmark for comparison with the NRVS for intermediates in [FeFe] hydrogenase proposed to contain a μ-hydride ligand bridging the Fe_p(II) and Fe_d(II) sites (Fig. S1†).²⁹ In line with a recent interpretation that [FeFe] hydrogenase operates exclusively with bridging CO intermediates,³⁰ the μ-hydride intermediates were attributed to the enzyme's ‘slow cycle’.

Results

NRVS spectra and qualitative assignments

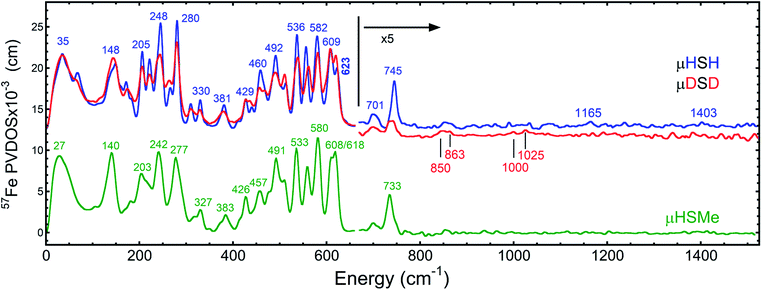
The overall NRVS-derived ⁵⁷Fe-PVDOS for the μHSH, μDSD and μHSMe samples are compared in Fig. 2. Qualitative assignments can be made based on comparison with previous spectra for Fe–S proteins and model compounds. The low energy <200 cm⁻¹ portion of the spectrum is related to acoustic and torsional modes largely involving the bulky Ph and bdt subunits, as well as bending modes at the Fe sites. The next region up to 400 cm⁻¹ comprises predominantly Fe–S and Fe–P stretching modes. The 400–650 cm⁻¹ region has prominent features from modes that are a mix of νFe–CO stretching and δFe–CO bending.

Fig. 2 Top: the NRVS-derived ⁵⁷Fe-PVDOS spectra for μHSH () and its deuterium isotopologue μDSD (), vertically offset by 1 × 10⁻³ cm from each other in the high-energy region. Bottom: the ⁵⁷Fe-PVDOS spectra for μHSMe (). In all cases the high-energy region intensity above 650 cm⁻¹ is multiplied by 5 for visibility. The bands are labelled with their top positions, with those above 800 cm⁻¹ assigned tentatively.

At higher energies, a band at 745 cm⁻¹ is particularly significant – it represents an Fe–H–Fe wagging mode. This assignment is based on comparison with results for similar Fe–μH⁻–Fe synthetic complexes and their computational models,^31,32 as well as Ni–μH⁻–Fe models and the Ni–R state of [NiFe] hydrogenase.¹¹ The significant weakening at this position in the μDSD spectrum supports this assignment; residual intensity likely results from an incomplete H-to-D exchange. Below the 745 cm⁻¹ band is a second candidate wagging mode feature at ∼701 cm⁻¹. Although this energy region coincides with benzene-dithiol modes, their Fe motion is predicted to be low. The energy is also consistent with the predicted hydride wagging motion of a deprotonated species, μHS⁻, based on DFT calculations as described below. For the μHSMe complex, a slight downshift to 733 cm⁻¹ is observed for the main wagging mode feature.

From previous NRVS work on Fe–H/D⁻ complexes,^11,31,32 as well as guidance from the conventional vibrational spectroscopy literature,³³ we expect observation of the Fe–H stretching modes at vibrational energies above 1100 cm⁻¹. There are hints of such features at 1165 cm⁻¹ and 1403 cm⁻¹, but the signal-to-noise is not convincing. Even in the best of cases, these modes are extremely weak in NRVS because they primarily involve the hydride nucleus motion with an almost static Fe partner. Below, we will use DFT calculations to investigate additional factors such as sample heterogeneity and intermolecular coupling that conspire to split the already weak Fe–H stretches into a multitude of even weaker modes that are below the current detection limit.

DFT calculations and quantitative comparisons

The ⁵⁷Fe-PVDOS predictions from the DFT models for μHSH, μDSD, and μHSMe (Fig. S3a and S4†) are compared in Fig. 3, S8 and S9.† The key experimental feature at 745 cm⁻¹, attributed to the Fe–H–Fe wagging mode, is reproduced very well in terms of energy and intensity by the calculated band at 746 cm⁻¹. In this mode, the calculated μH⁻ hydride motion is normal to the ‘Fe–H–Fe’ plane, as shown in Fig. S5 (see additionally ESI for animated vibrational modes, and Fig. S8 for an overlay of the NRVS-observed and DFT-predicted spectra).† A corresponding Fe–D–Fe wagging is not specifically resolved in the NRVS of the deuterated sample.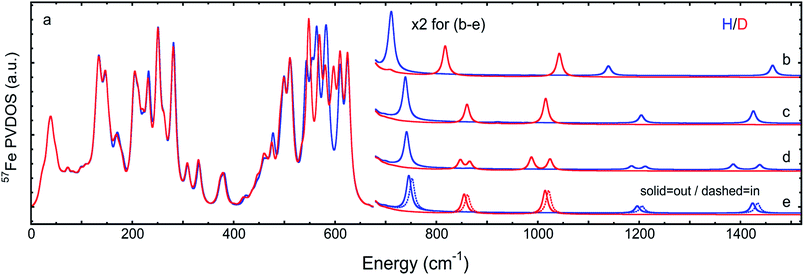

Fig. 3 DFT-based ⁵⁷Fe-PVDOS for different chemical models and their isomers. Left (a): μHSH or μDSD. Right, top to bottom: (b) μHS⁻ or μDS⁻, (c) μHSMe_in or μDSMe_in, (d) [μHSH]₂ or [μDSD]₂, (e) μHSH_invs.μHSH (= μHSH_out) or μDSD_invs.μDSD (= μDSD_out). The high energy region >650 cm⁻¹ (b–e) is multiplied by 2 for visibility. In (a), the intensities <210 cm⁻¹ are based on the [μHSH]₂ or [μDSD]₂ dimer calculations, as explained in the main text and shown in Fig. 5.

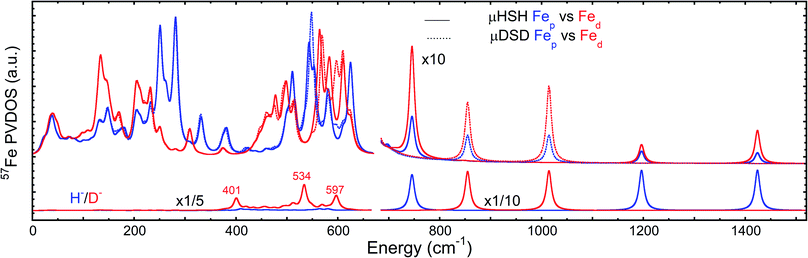
To better understand the differences in these two spectra, we calculated the PVDOS for the bridging H and D nuclei, as shown in Fig. 4 and S7d.† Inspection of these curves reveals three distinct hydride bands, whereas there are only two distinct deuteride bands above 650 cm⁻¹. The intensity for the third deuteride band (corresponding to the wagging motion) is redistributed throughout the 400–600 cm⁻¹ region, indicating significant coupling in the motions of the D nucleus with the five CO ligands. A comparison of the single wagging mode in μHSH with three prominent μDSD modes involving coupled motions is also depicted in Fig. S5.†

Fig. 4 Top: comparison of DFT-predicted ⁵⁷Fe_d and ⁵⁷Fe_p PVDOS for models μHSH and μDSD. Bottom: comparison of DFT-predicted μH/D PVDOS for the same models. The relative intensity multiplication factors (×) are applied for visibility.

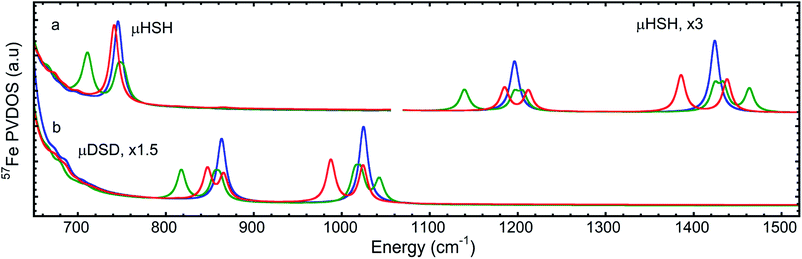
The computed spectrum of μDSD sees shifts of the Fe–H stretching modes at 1424/1196 cm⁻¹ to respectively 1015/855 cm⁻¹. The ⁵⁷Fe-PVDOS intensities of the Fe–D (vs. Fe–H) bands are enhanced due to the amplified ⁵⁷Fe displacements when the heavier deuteride is the bridging ligand, which allows the Fe–D stretching signals to raise above the NRVS noise level (Fig. S11 and S12†). For future NRVS observation of such stretching modes, Fe–D complexes are clearly favored over Fe–H isotopologues.

Asymmetric hydride sharing by Fe_p and Fe_d

We also calculated separate PVDOS for the ⁵⁷Fe_p and ⁵⁷Fe_d nuclei, as shown in Fig. 4 and S7c.† We use this notation for the Fe sites respectively proximal and distal to the thiol, following the notation commonly employed for [FeFe] hydrogenases, see Fig. 1 and S1.† Although both Fe atoms contribute to the vibrational motion, we can discriminate between the two Fe_p/d–μH stretching modes by the Fe–H bond that aligns closest to the μH displacement vector, as shown in Fig. S6 and visualized in the ESI† animations. Breakdown of the DFT ⁵⁷Fe-PVDOS into individual ⁵⁷Fe_p/d contributions demonstrates that the Fe–H modes are asymmetrically comprised of mostly the Fe_d motion. The Fe_d–μH stretching mode is predicted for the high-end of the μHSH spectrum at 1424 cm⁻¹, while the predicted Fe_p–μH stretch is at a lower energy of 1196 cm⁻¹. Experimentally these hydride modes coincide with intensities at 1403 and 1165 cm⁻¹ respectively (Fig. 2 and S7†), however the signal-to-noise is low for these features despite several long acquisition experiments at high incident flux (see ESI Methods†). On the other hand, the two most intense experimental bands at 245/280 cm⁻¹ (Fig. 2) are reproduced by DFT at 251/281 cm⁻¹ (Fig. S7†) and identified as mostly Fe_p–S/P stretching in character – the quantitative agreement with the NRVS experiment indicates a proper modeling of the electronic structure by a low-spin 2Fe(II) core, also consistent with the recorded Mössbauer spectrum, see Fig. S2 and ESI Discussion.†

The deduction that the Fe_d site contributes more NRVS intensity than the Fe_p site in the wagging and stretching hydride modes is supported by the differing Fe–H bond lengths revealed in the DFT-optimized geometry of μHSH, Fe_p–H = 1.73 Å vs. Fe_d–H = 1.65 Å; comparable values and their variations are seen as well in the X-ray structure³⁴ (Table S1†). The ∼0.1 Å difference in the Fe_p/d–H bond lengths as well rationalizes the ∼230 and 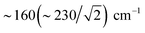splittings in the predicted Fe_p/d–μH and Fe_p/d–μD stretching frequencies.

Conformational heterogeneity of the Fe thiol

We also considered the possibility of alternate structural conformations having an effect on the NRVS profiles. We found from DFT calculations that a local minimum was produced by reorientation of the protonated S_p–H_S thiolate ligand of Fe_p towards the bridging hydride, yielding a ‘μHSH_in’ (or ‘μDSD_in’) structure (Fig. S3a†). The calculated energy difference was a trivial +0.3 kcal mol⁻¹ compared to the above described best-fit model having the S_p–H_S moiety oriented away from the hydride, referred to simply as μHSH (or μDSD). We thus expect μHSH (= μHSH_out) and μHSH_in species to reach an equilibrium and co-exist in the sample crystals. The calculated ⁵⁷Fe-PVDOS for μHSH_in produced an Fe–H–Fe wag at 752 cm⁻¹, upshifted by 6 cm⁻¹ from the spectrum for μHSH (Fig. 3 and S8†). Slightly larger upshifts of 7 cm⁻¹ and 10 cm⁻¹ were predicted for the Fe–D and Fe–H stretching modes, respectively.

Chemical heterogeneity of the Fe thiolate

From previous work with this compound, we know that deprotonation of the S_p–H_S moiety occurs readily (for example, upon solvation of μHSH in THF), and we refer to the resultant thiolate species as ‘μHS⁻’ (Fig. S3a†). DFT calculations on this candidate predict a 35 cm⁻¹ red-shift in the Fe–H–Fe wagging mode to 711 cm⁻¹ (Fig. S8b†). The μHS⁻ model is thus a possible explanation for the weak feature observed at ∼701 cm⁻¹ in the experimental spectrum of μHSH – although a similar, but weaker, feature was observed in μHSMe, implying the source of this intensity need not be limited to the μHS⁻ species in the spectrum of μHSH (Fig. 2, S7a, and S9†).

An even higher degree of hydride sharing asymmetry is calculated for the μHS⁻/μDS⁻ model (Table S1†) and, consequently, larger energy splittings between the predicted bands for the Fe_p/d–μH/D stretches (Fig. 3b and S8b†). Specifically, the Fe_p–μH/D stretches calculated respectively at 818/1138 cm⁻¹ are significantly red-shifted when compared to the best-fit μHSH/μDSD model, due to a stronger Fe_p–S_p bond strength which in turn leads to a weaker adjacent Fe_p–μH⁻ bonding. Notably, the deprotonation of μHSH to μHS⁻ leads to a predicted upshift by 15 cm⁻¹ (332 to 347 cm⁻¹, Fig. S8b†) for the band observed at 330 cm⁻¹ and having the strongest Fe_p–S_p stretching character (see ESI† for these modes animated). Finally, to produce a more realistic simulation of the observed NRVS spectrum, in Fig. 6 and S12† we provide an average of the three DFT models considered above.

Intermolecular coupling – the dimer model

A common weakness of DFT simulations of the NRVS spectra of solids is the lack of predicted intensity in the low-energy regions (<100 cm⁻¹). In solid model complexes, the experimental modes in this region are due to solid matrix motions, and lattice or acoustic modes. In larger biological samples, this energy region corresponds primarily to torsional/dihedral modes and larger scale motions of the protein, and it provides an indicator of coupling between the motion of the ⁵⁷Fe-enriched bioinorganic core and its environment.^18,20,35,36 To partially account for these modes in our calculations, we have used a DFT model based on a dimeric form [μHSH]₂ which is directly available from the crystallographic unit cell in the X-ray structure (Fig. S3b†);³⁴ this approach is justified as the NRVS experiment employed a polycrystalline powder sample.

The vibrational calculation on [μHSH]₂ shows an increased density of normal modes and significant improvement in the low-energy <200 cm⁻¹ region of the predicted NRVS spectrum over that of the μHSH monomer only (Fig. 5 and S10†). Of note is reproduction of the broad experimental feature centered at 35 cm⁻¹ produced by highly-delocalized expansions of the dimer, see Fig. 5 and ESI† for the representative normal mode at 38 cm⁻¹ animated. The intermolecular dispersion interaction plays an important role here, included as a correction to our DFT setup on [μHSH]₂ (see ESI Methods†). The dimer computational model does not capture all of the features in the low-energy region – specifically the prominence at ∼70 cm⁻¹ – which may be reproduced by models accounting for more molecules and/or their structural periodicity, however such a computational effort is beyond the scope of this work.

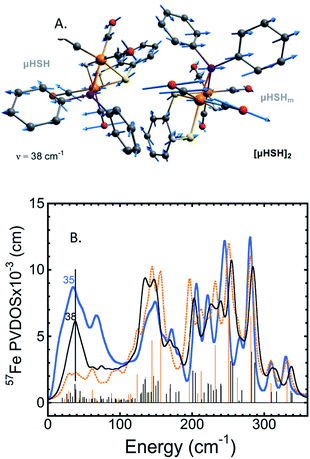Fig. 5 (A) The normal mode calculated at 38 cm⁻¹ showing relative displacements of the two enantiomers comprising the [μHSH]₂ dimer. Actual amplitude of this [μHSH]–[μHSH]_m vibration is ∼0.05 Å. (B) Low-frequency (<350 cm⁻¹) ⁵⁷Fe-PVDOS spectra for the μHSH compound from NRVS experiment (blue) and DFT calculations using [μHSH]₂ dimer (black) and μHSH monomer (orange) models; for the full-range spectra, see Fig. S10.†

Notably, the dimer is composed of μHSH and its mirror-image isomer μHSH_m, or the enantiomer, yet the [μHSH]₂ structure itself does not exhibit a symmetry (higher than C₁). Deviation from the exact mirror-image symmetry between μHSH and μHSH_m effectively splits the Fe–μH/D stretching normal modes >800 cm⁻¹, which are particularly sensitive to even minimal Fe–μH bond length changes of ∼0.01 Å (Table S1†), in line with the hydride mode variations indicated above for the monomer models. This results in a more faithful simulation of their low PVDOS intensities – see the calculated [μHSH]₂/[μDSD]₂vs.μHSH/μDSD spectra compared to the observed H/D sample NRVS data in Fig. 6, S10, and S12.†

Fig. 6 DFT ⁵⁷Fe-PVDOS spectra for the (a) H- (top) and (b) D- (bottom) isotopologues in the iron-hydride bands region >650 cm⁻¹: μHSH monomer (blue), averaged between the three μHSH/μHSH_in/μHS⁻ monomers (green), and the [μHSH]₂ dimer (red) models. The relative intensity multiplication factors (×) are applied for visibility.

Discussion

Our results on the bridging hydride samples show both the strengths and limitations of NRVS for observation of Fe–H normal modes. The experimental and calculated observations demonstrate that the Fe–H–Fe wag mode is sensitive to the chemistry at the Fe–S ligand, reflected by the species-dependent redistribution of intensity in the 690–760 cm⁻¹ region. The DFT calculations suggest the wag mode is even sensitive to the conformation of the SH proton, shifting 6 cm⁻¹ between the ‘in’ and ‘out’ conformers. In the range of the models considered, ∼40 cm⁻¹ upshift of the predicted wag band position is approximately correlated with ∼0.01 Å increase in the adjacent Fe–S bond length (Table S1†). This sensitivity makes NRVS a useful structural probe, but it also means that intensity can be lost by division into multiple channels in cases of sample heterogeneity.

The DFT calculations reveal that Fe–H stretching modes are even more sensitive to variability at the Fe–S ligand than the Fe–H–Fe wag modes. In contrast to the well-defined wag mode, current S/N limitations unfortunately prevented unambiguous experimental assignments of the stretching modes. The predicted position of the lower frequency Fe_p–H stretch mode is especially sensitive to the chemistry at the sulfur ligand adjacent to Fe_p, varying by almost 70 cm⁻¹ in the range of the considered alternatives (S⁻: 1138 cm⁻¹, SH_out: 1195 cm⁻¹, SMe_in: 1204 cm⁻¹, SH_in: 1206 cm⁻¹).

Another result from the DFT calculations is the inequitable sharing of the bridging hydride. This is most directly seen in the optimized ∼0.1 Å Fe–H distance differences. Similar differences have been predicted by DFT previously in the bimetallic cofactors of [FeFe] and [NiFe] hydrogenases and their models.^11,20,32 The difference in Fe_p/d–μH bonding is also reflected in the prediction of two distinct Fe–H stretching modes split by as much as 322 cm⁻¹. Even greater asymmetry was observed in a Ni–μH–Fe model complex, where Ni–H and Fe–H stretches were seen respectively at 954 cm⁻¹ and 1468/1532 cm⁻¹, the latter split by 64 cm⁻¹ due to a conformational heterogeneity in the μ-pdt ligand.¹¹ It is noteworthy that the asymmetry is modulated by the status of the iron-bound sulfur – a larger asymmetry occurs when the sulfur is deprotonated.

The model studies have relevance to proposed [FeFe] hydrogenase intermediates. A terminal hydride state H_hyd has been convincingly assigned using NRVS.^18–20,29 However, bridging hydride species have also been proposed for intermediates named H(s)red using other methods,^29,37 and a recent report has investigated the Hred state using a combination of ⁵⁷Fe-NRVS and other spectroscopies, supported by QM/MM calculations.²⁹ It was proposed that the Hred state contains a bridging Fe_p–μH⁻–Fe_d hydride with its wag distributed among the ∼600–650 cm⁻¹ (Fe–)CO/CN⁻/ADT motions, thus prohibiting its direct observation.

Our experimental results on model compounds found wagging modes at higher frequencies, ranging from 694–702 cm⁻¹ in a sterically congested diiron hydride³² to 733–745 cm⁻¹ for the current samples to 758 cm⁻¹ in a Ni–μH–Fe model complex.¹¹ Of course, structural differences can conspire to move wagging modes to lower frequencies – in a recent study of a complex with an Fe(μ-H)₂Fe core the wagging modes were identified at 455 and 587 cm⁻¹, mostly screened by other NRVS bands.³⁸ For future work with improved S/N, observation of Fe–D and Fe–H stretching modes would be a more rigorous way to test various structural hypotheses.

Summary and outlook

In this work we have characterized the μHSH and μHSMe (and likely μHS⁻) synthetic models with NRVS experiments and DFT calculations. Foremost, we have directly identified the well-separated Fe–H–Fe wagging modes both in the experimental and DFT-simulated spectra. The related Fe–D–Fe wagging modes were found to be heavily mixed with Fe–CO vibrations. The wagging mode displays significant variability that makes it a sensitive test of molecular structure.

Fe–H and Fe–D stretching modes were also scrutinized by DFT modeling for the isomeric μHSH_in/out and deprotonated μHS⁻ forms of μHSH, as well as a [μHSH]₂ dimer relevant to the polycrystalline NRVS sample. These modes exhibit larger frequency and intensity shifts, making them an even more delicate probe of iron-hydride bonding. Their routine application awaits improvements in sample preparation, beamline flux, monochromators, and detectors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was funded by National Institutes of Health Grant GM-65440, National Science Foundation grant CHE 1308384, the Einstein Foundation Berlin grant number EVF-2016-277 (S. P. C.), the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy – EXC 2008 – 390540038 – UniSysCat (V. P.), and the Ministry of Science and Technology of Taiwan and Academia Sinica (AS-SS-108-02-1) (Y.-C.L., M.-H.C). Some computational work was performed under the XSIM project on the CORI computing system at NERSC a U.S. Department of Energy Office of Science User Facility operated under contract no. DE-AC02-05CH11231. Synchrotron experiments were performed at SPring-8 under proposal numbers 2014A2056, 2015A0103-2016B0103, 2016A1154, 2017A1115, 2018A1409 (under JASRI) and 20150048, 20160063 (under RIKEN).

Notes and references

1. P. M. Vignais, B. Billoud and J. Meyer, FEMS Microbiol. Rev., 2001, 25, 455–501.
2. P. M. Vignais and B. Billoud, Chem. Rev., 2007, 107, 4206–4272.
3. W. Lubitz, H. Ogata, O. Rudiger and E. Reijerse, Chem. Rev., 2014, 114, 4081–4148.
4. J. W. Peters, G. J. Schut, E. S. Boyd, D. W. Mulder, E. M. Shepard, J. B. Broderick, P. W. King and M. W. W. Adams, Biochim. Biophys. Acta, Mol. Cell Res., 2015, 1853, 1350–1369.
5. D. Lukoyanov, N. Khadka, Z. Y. Yang, D. R. Dean, L. C. Seefeldt and B. M. Hoffman, J. Am. Chem. Soc., 2016, 138, 1320–1327.
6. H. Ogata, K. Nishikawa and W. Lubitz, Nature, 2015, 520, 571–575.
7. G. F. Huang, T. Wagner, M. D. Wodrich, K. Ataka, E. Bill, U. Ermler, X. L. Hu and S. Shima, Nat. Catal., 2019, 2, 537–543.
8. D. F. Harris, D. A. Lukoyanov, S. Shaw, P. Compton, M. Tokmina-Lukaszewska, B. Bothner, N. Kelleher, D. R. Dean, B. M. Hoffman and L. C. Seefeldt, Biochemistry, 2018, 57, 701–710.
9. D. F. Harris, D. A. Lukoyanov, H. Kallas, C. Trncik, Z. Y. Yang, P. Compton, N. Kelleher, O. Einsle, D. R. Dean, B. M. Hoffman and L. C. Seefeldt, Biochemistry, 2019, 58, 3293–3301.
10. D. Schilter, J. M. Camara, M. T. Huynh, S. Hammes-Schiffer and T. B. Rauchfuss, Chem. Rev., 2016, 116, 8693–8749.
11. H. Ogata, T. Krämer, H. Wang, D. Schilter, V. Pelmenschikov, M. van Gastel, F. Neese, T. B. Rauchfuss, L. B. Gee, A. D. Scott, Y. Yoda, Y. Tanaka, W. Lubitz and S. P. Cramer, Nat. Commun., 2015, 6, 7890.
12. Y. Ohki, Bull. Chem. Soc. Jpn., 2014, 87, 1–19.
13. S. Ogo, Coord. Chem. Rev., 2017, 334, 43–53.
14. S. Rumpel, C. Sommer, E. Reijerse, C. Fares and W. Lubitz, J. Am. Chem. Soc., 2018, 140, 3863–3866.
15. J. A. Denny and M. Y. Darensbourg, Chem. Rev., 2015, 115, 5248–5273.
16. N. A. Arnet, N. Bhuvanesh and M. Y. Darensbourg, J. Biol. Inorg Chem., 2019, 24, 909–917.
17. J. F. Duan, M. Senger, J. Esselborn, V. Engelbrecht, F. Wittkamp, U. P. Apfel, E. Hofmann, S. T. Stripp, T. Happe and M. Winkler, Nat. Commun., 2018, 9, 4726.
18. C. C. Pham, D. W. Mulder, V. Pelmenschikov, P. W. King, M. W. Ratzloff, H. Wang, N. Mishra, E. E. Alp, J. Zhao, M. Y. Hu, K. Tamasaku, Y. Yoda and S. P. Cramer, Angew. Chem. Int. Ed., 2018, 57, 10605–10609.
19. E. J. Reijerse, C. C. Pham, V. Pelmenschikov, R. Gilbert-Wilson, A. Adamska-Venkatesh, J. F. Siebel, L. B. Gee, Y. Yoda, K. Tamasaku, W. Lubitz, T. B. Rauchfuss and S. P. Cramer, J. Am. Chem. Soc., 2017, 139, 4306–4309.
20. V. Pelmenschikov, J. A. Birrell, C. C. Pham, N. Mishra, H. X. Wang, C. Sommer, E. Reijerse, C. P. Richers, K. Tamasaku, Y. Yoda, T. B. Rauchfuss, W. Lubitz and S. P. Cramer, J. Am. Chem. Soc., 2017, 139, 16894–16902.
21. D. W. Mulder, Y. Guo, M. W. Ratzloff and P. W. King, J. Am. Chem. Soc., 2017, 139, 83–86.
22. W. Dong, M. Wang, X. Liu, K. Jin, G. Li, F. Wang and L. Sun, Chem. Commun., 2006, 305–307,  10.1039/B513270C.
23. S. Ezzaher, A. Gogoll, C. Bruhn and S. Ott, Chem. Commun., 2010, 46, 5775–5777.
24. Y.-C. Liu, K.-T. Chu, Y.-L. Huang, C.-H. Hsu, G.-H. Lee, M.-C. Tseng and M.-H. Chiang, ACS Catal., 2016, 6, 2559–2576.
25. U.-P. Apfel, D. Troegel, Y. Halpin, S. Tschierlei, U. Uhlemann, H. Görls, M. Schmitt, J. Popp, P. Dunne, M. Venkatesan, M. Coey, M. Rudolph, J. G. Vos, R. Tacke and W. Weigand, Inorg. Chem., 2010, 49, 10117–10132.
26. T. Petrenko, W. Sturhahn and F. Neese, Hyperfine Interact., 2007, 175, 165–174.
27. W. R. Scheidt, J. F. Li and J. T. Sage, Chem. Rev., 2017, 117, 12532–12563.
28. L. B. Gee, H. X. Wang and S. P. Cramer, in Fe-S Cluster Enzymes, Part B, ed. S. S. David, Academic Press, Cambridge, MA, 1st edn, 2018, vol. 599, ch. 14, pp. 409–425.
29. S. Mebs, J. Duan, F. Wittkamp, S. T. Stripp, T. Happe, U.-P. Apfel, M. Winkler and M. Haumann, Inorg. Chem., 2019, 58, 4000–4013.
30. J. Birrell, V. Pelmenschikov, N. Mishra, H. Wang, Y. Yoda, K. Tamasaku, T. B. Rauchfuss, S. P. Cramer, W. Lubitz and S. DeBeer, J. Am. Chem. Soc., 2020, 142, 222–232.
31. V. Pelmenschikov, L. B. Gee, H. Wang, K. C. MacLeod, S. F. McWilliams, K. L. Skubi, S. P. Cramer and P. L. Holland, Angew. Chem., Int. Ed., 2018, 57, 9367–9371.
32. M. R. Carlson, D. L. Gray, C. P. Richers, W. Wang, P.-H. Zhao, T. B. Rauchfuss, V. Pelmenschikov, C. C. Pham, L. B. Gee, H. Wang and S. P. Cramer, Inorg. Chem., 2018, 57, 1988–2001.
33. K. Nakamoto, Infrared & Raman Spectra of Inorganic & Coordination Compounds, Wiley-Interscience, New York, 5th edn, 1997.
34. Y. C. Liu, K. T. Chu, R. L. Jhang, G. H. Lee and M. H. Chiang, Chem. Commun., 2013, 49, 4743–4745.
35. Y. Xiao, H. Wang, S. J. George, M. C. Smith, M. W. W. Adams, J. F. E. Jenney, W. Sturhahn, E. E. Alp, J. Zhao, Y. Yoda, A. Dey, E. I. Solomon and S. P. Cramer, J. Am. Chem. Soc., 2005, 127, 14596–14606.
36. Y. Xiao, M.-L. Tan, T. Ichiye, H. Wang, Y. Guo, M. C. Smith, J. Meyer, W. Sturhahn, E. E. Alp, J. Zhao, Y. Yoda and S. P. Cramer, Biochemistry, 2008, 47, 6612–6627.
37. P. Chernev, C. Lambertz, A. Brunje, N. Leidel, K. G. V. Sigfridsson, R. Kositzki, C. H. Hsieh, S. L. Yao, R. Schiwon, M. Driess, C. Limberg, T. Happe and M. Haumann, Inorg. Chem., 2014, 53, 12164–12177.
38. V. Pelmenschikov, L. B. Gee, H. Wang, K. C. MacLeod, S. F. McWilliams, K. L. Skubi, S. P. Cramer and P. L. Holland, Angew. Chem., Int. Ed., 2018, 130, 9511–9515.

---

Footnotes

† Electronic supplementary information (ESI) available: Materials and methods, Fig. S1–S12, Table S1, atomic Cartesian coordinates, animated vibrational modes. See DOI: 10.1039/d0sc01290d

‡ These authors contributed equally.

---