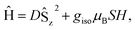Open Access Article
Open Access ArticleAn iron ketimide single-molecule magnet [Fe4(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/h2_char_e001.gif) CPh2)6] with suppressed through-barrier relaxation†
CPh2)6] with suppressed through-barrier relaxation†
Andrew W.
Cook
a,
Joshua D.
Bocarsly
 b,
Richard A.
Lewis
a,
Alexander J.
Touchton
a,
Simona
Morochnik
a and
Trevor W.
Hayton
b,
Richard A.
Lewis
a,
Alexander J.
Touchton
a,
Simona
Morochnik
a and
Trevor W.
Hayton
 *a
*a
aDepartment of Chemistry and Biochemistry, University of California, Santa Barbara, California 93106, USA. E-mail: hayton@chem.ucsb.edu
bMaterials Department and Materials Research Laboratory, University of California, Santa Barbara, Santa Barbara, California 93106, USA
First published on 20th April 2020
Abstract
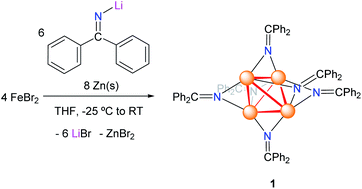
Reaction of FeBr2 with 1.5 equiv. of LiN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CPh2 and 2 equiv. of Zn, in THF, results in the formation of the tetrametallic iron ketimide cluster [Fe4(N
CPh2 and 2 equiv. of Zn, in THF, results in the formation of the tetrametallic iron ketimide cluster [Fe4(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CPh2)6] (1) in moderate yield. Formally, two Fe centers in 1 are Fe(I) and two are Fe(II); however, Mössbauer spectroscopy and SQUID magnetometry suggests that the [Fe4]6+ core of 1 exhibits complete valence electron delocalization, with a thermally-persistent spin ground state of S = 7. AC and DC SQUID magnetometry reveals the presence of slow magnetic relaxation in 1, indicative of single-molecule magnetic (SMM) behaviour with a relaxation barrier of Ueff = 29 cm−1. Remarkably, very little quantum tunnelling or Raman relaxation is observed down to 1.8 K, which leads to an open hysteresis loop and long relaxation times (up to 34 s at 1.8 K and zero field and 440 s at 1.67 kOe). These results suggest that transition metal ketimide clusters represent a promising avenue to create long-lifetime single molecule magnets.
CPh2)6] (1) in moderate yield. Formally, two Fe centers in 1 are Fe(I) and two are Fe(II); however, Mössbauer spectroscopy and SQUID magnetometry suggests that the [Fe4]6+ core of 1 exhibits complete valence electron delocalization, with a thermally-persistent spin ground state of S = 7. AC and DC SQUID magnetometry reveals the presence of slow magnetic relaxation in 1, indicative of single-molecule magnetic (SMM) behaviour with a relaxation barrier of Ueff = 29 cm−1. Remarkably, very little quantum tunnelling or Raman relaxation is observed down to 1.8 K, which leads to an open hysteresis loop and long relaxation times (up to 34 s at 1.8 K and zero field and 440 s at 1.67 kOe). These results suggest that transition metal ketimide clusters represent a promising avenue to create long-lifetime single molecule magnets.
Introduction
The spin-reversal barrier (U) in single-molecule magnets (SMMs) is known to arise from a combination of magnetic anisotropy, D, and spin state, S, according to U = |D|S2 (for integer spin systems). There has therefore been much effort to increase ordering temperatures by maximizing the moments and magnetic anisotropies of SMMs.1,2 However, it is often the case that molecules with large U nevertheless do not show long lifetimes or significant zero-field magnetic hysteresis.1,3–10 In these cases, through-barrier relaxation mechanisms (i.e., quantum tunnelling or Raman relaxation) are typically to blame.While S and D are undoubtedly important in dictating SMM behavior, several groups have also emphasized the importance of achieving a well-separated magnetic ground state to improve SMM performance.4,11–13 In this regard, strong ferromagnetic coupling mediated through direct exchange in transition metal clusters is emerging as a promising strategy for generating large, well-separated magnetic ground states. For example, Betley and co-workers isolated a series of Fe clusters, [(18-crown-6)K(THF)2][(tbsL)Fe3] (tbsLH6 = 1,3,5-(tBuMe2SiNH-o-C6H4NH)3C6H9), [NBu4][(HL)2Fe6(py)2], and [NBu4]2[(HL)2Fe6] (HLH6 = MeC(CH2NHPh-o-NH2)3), with thermally-persistent spin ground states of S = 11/2, 19/2, and 11, respectively,14–17 while Long and co-workers reported a cobalt phosphiniminato complex, [Co4(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PtBu3)4]+, with a S = 9/2 ground state.1 Notably, direct exchange is thought to be responsible for the large spin ground states in these examples. That said, only a narrow range of ligands have been shown to promote direct exchange, including phosphiniminato,1 Betley's hexaamide framework,14–18 diphenylformamidinate (DPhF),19 and guanidinate.20 As a result, the identification of new ligands that could promote these interactions remains an important goal for the field.
PtBu3)4]+, with a S = 9/2 ground state.1 Notably, direct exchange is thought to be responsible for the large spin ground states in these examples. That said, only a narrow range of ligands have been shown to promote direct exchange, including phosphiniminato,1 Betley's hexaamide framework,14–18 diphenylformamidinate (DPhF),19 and guanidinate.20 As a result, the identification of new ligands that could promote these interactions remains an important goal for the field.
In an effort to access a high nuclearity iron cluster, we sought to employ ketimide (−N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CR2) as the supporting ligand. Previously, we had shown that ketimides can be used to promote metal–metal bonding, as seen in the bimetallic complexes [Li(12-crown-4)2][M2(N
CR2) as the supporting ligand. Previously, we had shown that ketimides can be used to promote metal–metal bonding, as seen in the bimetallic complexes [Li(12-crown-4)2][M2(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CtBu2)5] (M = Mn, Fe, Co).21 The Fe example is notable, as magnetic data supported the presence of a double bond between the two Fe centres. Similarly, Hoffman and co-workers isolated a tetrametallic ketimide-supported Cu cluster, [Cu(N
CtBu2)5] (M = Mn, Fe, Co).21 The Fe example is notable, as magnetic data supported the presence of a double bond between the two Fe centres. Similarly, Hoffman and co-workers isolated a tetrametallic ketimide-supported Cu cluster, [Cu(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CtBu2)]4, further highlighting the ability of ketimide ligands to bridge metal centers.22 The ketimide ligand also promotes metal–metal communication via super exchange, as observed for the mixed-valent bimetallic, [Fe2(N
CtBu2)]4, further highlighting the ability of ketimide ligands to bridge metal centers.22 The ketimide ligand also promotes metal–metal communication via super exchange, as observed for the mixed-valent bimetallic, [Fe2(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CtBu2)5],21 which is likely a consequence of the highly covalent metal–ketimide interaction.23 Thus, we hypothesized that ketimides, by virtue of their proclivity to promote M–M bonding and communication, could engender the formation of high nuclearity metal clusters with strong M–M exchange.
CtBu2)5],21 which is likely a consequence of the highly covalent metal–ketimide interaction.23 Thus, we hypothesized that ketimides, by virtue of their proclivity to promote M–M bonding and communication, could engender the formation of high nuclearity metal clusters with strong M–M exchange.
Herein, we report the synthesis and magnetic characterization of the self-assembled, tetrametallic iron ketimide cluster [Fe4(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CPh2)6]. Significantly, we found that this cluster features a room temperature spin ground state of S = 7 – one of the highest thermally-persistent ground states observed for a transition metal cluster – a consequence of strong ferromagnetic direct exchange mediated by its short Fe–Fe bonds. Moreover, this cluster exhibits single-molecule magnet behaviour with a relaxation barrier of Ueff = 29 cm−1. Interestingly, there is no evidence of through-barrier relaxation (quantum tunnelling or Raman relaxation) even down to 1.8 K, and as a result long relaxation times and an open hysteresis loop are observed at this temperature.
CPh2)6]. Significantly, we found that this cluster features a room temperature spin ground state of S = 7 – one of the highest thermally-persistent ground states observed for a transition metal cluster – a consequence of strong ferromagnetic direct exchange mediated by its short Fe–Fe bonds. Moreover, this cluster exhibits single-molecule magnet behaviour with a relaxation barrier of Ueff = 29 cm−1. Interestingly, there is no evidence of through-barrier relaxation (quantum tunnelling or Raman relaxation) even down to 1.8 K, and as a result long relaxation times and an open hysteresis loop are observed at this temperature.
Results and discussion
Addition of lithium diphenylketimide (LiN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CPh2) (1.5 equiv.) to a slurry of FeBr2 (1 equiv.) in THF resulted in the formation of a red-brown solution. Addition of Zn powder (2 equiv.) to the reaction mixture resulted in the gradual colour change to dark-brown, concomitant with the deposition of a dark brown solid. Work-up of the reaction mixture after 18 h resulted in the isolation of the tetrametallic, iron ketimide cluster [Fe4(NC
CPh2) (1.5 equiv.) to a slurry of FeBr2 (1 equiv.) in THF resulted in the formation of a red-brown solution. Addition of Zn powder (2 equiv.) to the reaction mixture resulted in the gradual colour change to dark-brown, concomitant with the deposition of a dark brown solid. Work-up of the reaction mixture after 18 h resulted in the isolation of the tetrametallic, iron ketimide cluster [Fe4(NC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Ph2)6] (1) as a brown microcrystalline solid in 44% yield (Scheme 1). Attempts to perform this reaction in the absence of Zn, or using Fe powder as the reductant, resulted in the formation of complex mixtures, which only contained small amounts of 1.
Ph2)6] (1) as a brown microcrystalline solid in 44% yield (Scheme 1). Attempts to perform this reaction in the absence of Zn, or using Fe powder as the reductant, resulted in the formation of complex mixtures, which only contained small amounts of 1.
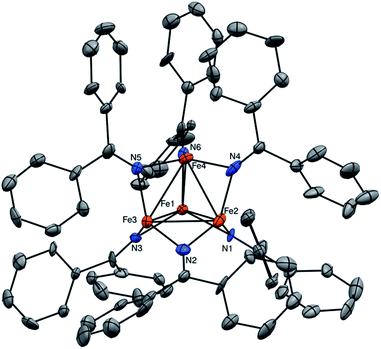
Complex 1 crystallizes as brown plates in the triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) with two independent molecules per unit cell (Fig. 1). 7.5 equiv. of toluene are also incorporated in the unit cell. Each independent molecule of 1 features a tetrahedral [Fe4]6+ core with each edge of the tetrahedron bridged by a ketimide ligand. Ignoring the Fe–Fe bonds, each Fe center has trigonal planar (D3h) geometry with the average ∑N–Fe–N = 357.1°. The Fe–Fe distances range from 2.504(4) to 2.621(4) Å (av. Fe–Fe = 2.56 Å), which are within the range of Fe–Fe bonds.24,25 These values correspond to an average formal shortness ratio (r),26,27 of 1.10, suggestive of the presence of weak single bonds between the Fe centres. For comparison, the closely related cluster, [Fe4(μ-4-MeC6H4)6(THF)4], reported by Neidig and co-workers,28 has an average Fe–Fe distance of 2.47 Å (r = 1.06). Similarly, [MgCl(THF)5][Fe8Me12] has average Fe–Fe distances of 2.433 Å (r = 1.05).29 For further comparison, the only other reported Fe–ketimide complex with an Fe–Fe bond, [Li(12-crown-4)2][Fe2(N
with two independent molecules per unit cell (Fig. 1). 7.5 equiv. of toluene are also incorporated in the unit cell. Each independent molecule of 1 features a tetrahedral [Fe4]6+ core with each edge of the tetrahedron bridged by a ketimide ligand. Ignoring the Fe–Fe bonds, each Fe center has trigonal planar (D3h) geometry with the average ∑N–Fe–N = 357.1°. The Fe–Fe distances range from 2.504(4) to 2.621(4) Å (av. Fe–Fe = 2.56 Å), which are within the range of Fe–Fe bonds.24,25 These values correspond to an average formal shortness ratio (r),26,27 of 1.10, suggestive of the presence of weak single bonds between the Fe centres. For comparison, the closely related cluster, [Fe4(μ-4-MeC6H4)6(THF)4], reported by Neidig and co-workers,28 has an average Fe–Fe distance of 2.47 Å (r = 1.06). Similarly, [MgCl(THF)5][Fe8Me12] has average Fe–Fe distances of 2.433 Å (r = 1.05).29 For further comparison, the only other reported Fe–ketimide complex with an Fe–Fe bond, [Li(12-crown-4)2][Fe2(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CtBu2)]5, was found to have a Fe–Fe distance of 2.433(1) Å with r = 1.05.21 Finally, the Fe–Fe distances for the mixed-valent Fe(II)/Fe(I) clusters reported by Betley and co-workers are also in good agreement with complex 1, with average Fe–Fe distances ranging from 2.46 to 2.65 Å.14,15,17 In contrast to most other multi-metallic Fe clusters, however, which require specially-designed ligands to control nuclearity,14,15,17,18,30 complex 1 spontaneously self-assembles using a simple, commercially available ketimide ligand.
CtBu2)]5, was found to have a Fe–Fe distance of 2.433(1) Å with r = 1.05.21 Finally, the Fe–Fe distances for the mixed-valent Fe(II)/Fe(I) clusters reported by Betley and co-workers are also in good agreement with complex 1, with average Fe–Fe distances ranging from 2.46 to 2.65 Å.14,15,17 In contrast to most other multi-metallic Fe clusters, however, which require specially-designed ligands to control nuclearity,14,15,17,18,30 complex 1 spontaneously self-assembles using a simple, commercially available ketimide ligand.
Complex 1 is sparingly soluble in Et2O, moderately soluble in benzene and toluene, and very soluble in THF. However, the cluster is insoluble in pentane and acetonitrile and rapidly decomposes upon dissolution in CD2Cl2 (Fig. S4†). Its 1H NMR spectrum in C6D6 (Fig. S1†) consists of three, broad paramagnetically-shifted resonances at 57.30, 30.90, and 8.60 ppm, assignable to the o-Ph, m-Ph, and p-Ph environments, respectively. Electrospray ionization mass spectrometry (ESI-MS) of complex 1 in THF, acquired in negative ion mode, is consistent with our proposed formulation (Fig. S7 and S8†). We observe a single major feature at m/z = 1304.2397, which corresponds to [M−] (calcd m/z = 1304.2262). Consistent with its low formal oxidation state, complex 1 is highly air- and moisture-sensitive, but it exhibits reasonable thermal stability. A toluene-d8 solution of 1 heated to 80 °C for 1 h showed no signs of decomposition by 1H NMR spectroscopy (Fig. S5†). This is in contrast to the organometallic Fe4 clusters recently reported by Neidig and co-workers, which rapidly decompose even at 0 °C.28
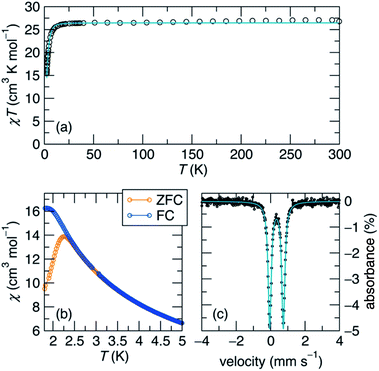
We next endeavoured to explore the magnetism of complex 1 in the solution state via Evans' method31 and in the solid state using superconducting quantum interference device (SQUID) magnetometry. Complex 1 exhibits a solution-state effective magnetic moment of 13.2 μB at 298 K in toluene-d8. In the solid state, the magnetic moment was found to be μeff = 14.64 μB (χMT = 26.56 cm3 K mol−1) at 300 K, which persists until low temperature (Fig. 2a). The magnetic moment of 1 is substantially higher than μeff = 8.83 μB, which is the value expected for two Fe(I) centers and two Fe(II) centers that are magnetically isolated, and is consistent with an S = 7 ground state (14.97 μB, g = 2.0). This value is among the highest reported for an iron cluster to date,15,17 and can be explained by strong electron delocalization via direct exchange.1
A zero-field 57Fe Mössbauer spectrum of complex 1 taken at 90 K (Fig. 2c) reveals a sharp quadrupole doublet with an isomer shift of δ = 0.34 mm s−1 and a quadrupole coupling of ΔEQ = 0.79 mm s−1, in line with other mixed-valent Fe(II)/Fe(I) clusters.14–17,28–30,32,33 Additionally, the presence of a single quadrupole doublet suggests that the Fe valence electrons are fully delocalized across the Fe4 unit on the Mössbauer time scale (107 s−1) at this temperature, in good agreement with our magnetic susceptibility measurements. For comparison, the mixed-valent Fe clusters reported by Neidig and co-workers, [Fe4(μ-C6H5)6(THF)4] and [MgCl(THF)5][Fe8Me12], featured broad doublets with similar isomer shifts of δ = 0.60 and 0.30 mm s−1, and quadrupole couplings of ΔEQ = 0.84 and 0.85 mm s−1, respectively.28,29
At low-temperature, complex 1 displays a splitting between the zero-field-cooled (ZFC) and field-cooled (FC) magnetization vs. temperature curves, indicating magnetic blocking below 2.4 K (Fig. 2b). A magnetic hysteresis loop at 1.8 K (Fig. 3) shows a broad region of hysteresis, with a somewhat narrower hysteresis near zero-field. At a magnetic field measurement sweep rate of 50 Oe s−1, the zero-field coercivity and remnant moment are 3.2 kOe and 3.5 μB, respectively. As is generally the case with SMMs, these values are dependent on the rate at which the magnetic field is swept during the measurement, with more hysteresis seen at higher magnetic sweep rates (Fig. S16†). Nonetheless, hysteresis is still observed even at sweep rates of 20 Oe s−1. The saturated moment at 15 kOe is about 8 μB, which is less than the 14 μB expected for a free S = 7 moment. This difference, as well as the magnetic hysteresis, suggests the presence of magnetic anisotropy, which prevents the free rotation of the magnetic moments. In order to probe this possibility, reduced magnetization data for 1 were fit using the PHI software package34 according to the spin Hamiltonian 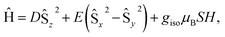 where S = 7, D = −0.75 cm−1, |E/D| = 0.17, and g = 1.92 (Fig. S15†).35
where S = 7, D = −0.75 cm−1, |E/D| = 0.17, and g = 1.92 (Fig. S15†).35
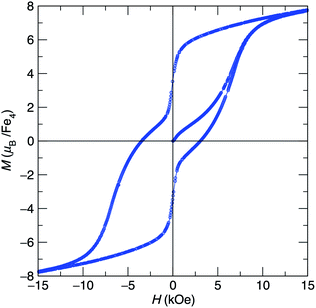 | ||
Fig. 3 Hysteresis loop at 1.8 K for [Fe4(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CPh2)6] (1) showing magnetization vs. applied field cycling from ±70 kOe at a sweep rate of 50 Oe s−1. CPh2)6] (1) showing magnetization vs. applied field cycling from ±70 kOe at a sweep rate of 50 Oe s−1. | ||
To better understand the magnetic relaxation in complex 1, we turned to time-dependent magnetization measurements. AC magnetic susceptibility data at 0 and 1 kOe fields were collected at temperatures between 2 K and 4.4 K and frequencies between 0.1 Hz and 1000 Hz (Fig. 4a). The real and imaginary AC susceptibilities were then fit to a generalized Debye model (eqn S1 and S2†) to extract relaxation times at each temperature. The AC data at each temperature were fit using a single relaxation time with width parameters (α) between 0.07 and 0.34. At temperatures below 2 K, the relaxation times are too long to be probed using this method, so DC saturation–relaxation experiments were used (Fig. 4b), with the sample's magnetic relaxation as a function of time at 0 Oe or 1 kOe being fit to a stretched exponential decay (eqn S3†). At 1.8 K, this procedure reveals substantial lifetimes of 34 seconds at zero field and 275 seconds at 1 kOe.
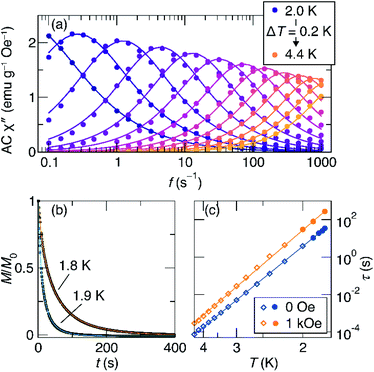 | ||
| Fig. 4 (a) Imaginary part of the AC susceptibility of 1 at zero field as a function of excitation frequency and temperature. The lines shown are fits to the generalized Debye model. (b) DC saturation-decay measurements used to characterize the relaxation at low temperatures, where the relaxation times are long. (c) Arrhenius plot of the relaxation times in zero field (blue) and 1 kOe field (orange). The fits shown are to eqn (1). | ||
The results of the combined AC and DC relaxation measurements are shown in Fig. 4 (additional plots in Fig. S17–S22,† fit parameters in Tables S2–S5†). Fig. 4c shows Arrhenius plots (log(τ) vs. 1/T) of the relaxation times at 0 and 1 kOe applied field. In most single-molecule magnets, such a plot is linear at high temperatures indicating thermally-activated relaxation, and then the relaxation times plateau as the temperature is lowered because through-barrier relaxation mechanisms, including quantum tunnelling and Raman processes, become more efficient than thermal relaxation.1,3,36,37 In the case of 1, surprisingly, both the zero field and 1 kOe data are linear, indicating that the relaxation is dominated by a thermally activated process across the full temperature range studied and across relaxation times spanning six orders of magnitude. This process is described by the equation:
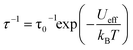 | (1) |
For complex 1, the 0 and 1 kOe field data can be fit well to eqn (1), which gives activation barriers (Ueff) of 27.6(1) and 29.1(1) cm−1, and τ0 values of 9.1(7) × 10−9 and 2.3(1) × 10−8 s, respectively. These values of Ueff compare reasonably well to that calculated from U = |D|S2, where S = 7 and D = −0.75 cm−1 to give U = 37 cm−1. The inclusion of quantum tunnelling, Raman, or direct relaxation terms did not improve the fits, suggesting that these relaxation mechanisms are nearly completely suppressed under the conditions studied. Our data imply a quantum tunnelling relaxation time limit of much greater than 100 s, although measurements at very low temperatures would be needed to accurately determine the tunnelling behaviour.
As mentioned above, we observe increased relaxation times under an applied field of 1 kOe (Fig. 4c). Curiously, this increase does not appear to be related to suppression of quantum tunnelling, as would occur in SMMs where the low-temperature relaxation is dominated by quantum tunnelling. Rather, in this case, the increase in lifetime is apparently due to a decrease in attempt frequency, τ−10, upon application of the magnetic field, given that the slope of the Arrhenius plot remains almost constant. To further probe this behaviour, we measured τ as a function of applied fields between 0 Oe and 10 kOe at 1.8 K (using DC saturation relaxation) and at 3.5 K using (using AC susceptibility). At both temperatures, a very similar field-evolution of τ is observed (Fig. S23†): τ initially increases with increasing field up to around 2 kOe, and then slowly decreases as higher fields are applied. At 1.8 K, a maximum relaxation time of 440 s is observed around H = 1.67 kOe. The consistency of this behaviour at both temperatures further suggests that the changes with field are driven by changes in τ−10, rather than suppression of through-barrier relaxation mechanisms.
In single-molecule magnets, through-barrier relaxation places an upper limit on the relaxation time that can be achieved, even if Ueff is very high. For example, the recently reported tetracobalt cluster, [Co4(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PtBu3)4][B(C6F5)4], shows Ueff = 87 cm−1,1 the largest reported spin-reversal barrier for a transition metal cluster. However, due to quantum tunnelling and Raman relaxation, this complex does not feature long lifetimes at low temperature and shows waist-restricted hysteresis loops with no remnant magnetization at zero field. In contrast, despite its smaller Ueff, complex 1 displays longer relaxation times, which we hypothesize is due to strong ferromagnetic direct exchange coupling that results in a well-separated S = 7 ground state with no accessible low-lying excited states. A similar rationale was used to explain the suppressed quantum tunnelling in a ferromagnetically coupled [Mn6Cr]3+ cluster, whereas quantum tunnelling was present in a different [Mn6Cr]3+ cluster with partially antiferromagnetic interactions.4
PtBu3)4][B(C6F5)4], shows Ueff = 87 cm−1,1 the largest reported spin-reversal barrier for a transition metal cluster. However, due to quantum tunnelling and Raman relaxation, this complex does not feature long lifetimes at low temperature and shows waist-restricted hysteresis loops with no remnant magnetization at zero field. In contrast, despite its smaller Ueff, complex 1 displays longer relaxation times, which we hypothesize is due to strong ferromagnetic direct exchange coupling that results in a well-separated S = 7 ground state with no accessible low-lying excited states. A similar rationale was used to explain the suppressed quantum tunnelling in a ferromagnetically coupled [Mn6Cr]3+ cluster, whereas quantum tunnelling was present in a different [Mn6Cr]3+ cluster with partially antiferromagnetic interactions.4
Conclusions
In conclusion, we have synthesized and characterized the mixed-valent, iron ketimide cluster [Fe4(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CPh2)6] (1). The tetrahedral [Fe4]6+ core of 1 exhibits complete valence electron delocalization, which results in a room temperature spin ground-state of S = 7. Most importantly, our results further confirm that strong ferromagnetic coupling, a consequence of direct metal–metal bonding, results in suppression of through-barrier relaxation, yielding a single molecule magnet with long relaxation times at low temperatures, despite the low anisotropy, D. We suggest that these attractive magnetic properties are a result of the ketimide ligand's ability to promote M–M bonding, coupled with the high covalency of the metal–ketimide interaction. In this regard, the use of ketimide ligands to generate novel metal clusters suggests an exciting new avenue for synthetic chemistry. We also plan to explore the reactivity of 1, especially its use as a template for larger metal clusters.
CPh2)6] (1). The tetrahedral [Fe4]6+ core of 1 exhibits complete valence electron delocalization, which results in a room temperature spin ground-state of S = 7. Most importantly, our results further confirm that strong ferromagnetic coupling, a consequence of direct metal–metal bonding, results in suppression of through-barrier relaxation, yielding a single molecule magnet with long relaxation times at low temperatures, despite the low anisotropy, D. We suggest that these attractive magnetic properties are a result of the ketimide ligand's ability to promote M–M bonding, coupled with the high covalency of the metal–ketimide interaction. In this regard, the use of ketimide ligands to generate novel metal clusters suggests an exciting new avenue for synthetic chemistry. We also plan to explore the reactivity of 1, especially its use as a template for larger metal clusters.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by the National Science Foundation (CHE 1764345). NMR spectra were collected on instruments supported by an NIH Shared Instrumentation Grant (SIG, 1S10OD012077-01A1). ESI mass spectra were acquired at the MRL Shared Experimental Facilities, supported by the MRSEC Program of the NSF under Award No. DMR 1720256 and a member of the NSF-funded Materials Research Facilities Network. Mössbauer spectra were collected with the help of the Ménard lab at UCSB. A. W. C. thanks the Mellichamp Academic Initiative in Sustainability at UCSB for a summer fellowship. J. D. B. is supported by the NSF through DMR 171063. The authors also acknowledge support from the California NanoSystems Institute (CNSI) Challenge Grant program. We thank Dr Guang Wu for help with the X-ray crystallographic analysis.Notes and references
- K. Chakarawet, P. C. Bunting and J. R. Long, J. Am. Chem. Soc., 2018, 140, 2058–2061 CrossRef CAS PubMed.
- P. C. Bunting, M. Atanasov, E. Damgaard-Møller, M. Perfetti, I. Crassee, M. Orlita, J. Overgaard, J. van Slageren, F. Neese and J. R. Long, Science, 2018, 362, eaat7319 CrossRef CAS PubMed.
- J. M. Zadrozny, D. J. Xiao, M. Atanasov, G. J. Long, F. Grandjean, F. Neese and J. R. Long, Nat. Chem., 2013, 5, 577 CrossRef CAS PubMed.
- K.-A. Lippert, C. Mukherjee, J.-P. Broschinski, Y. Lippert, S. Walleck, A. Stammler, H. Bögge, J. Schnack and T. Glaser, Inorg. Chem., 2017, 56, 15119–15129 CrossRef CAS PubMed.
- Y.-S. Ding, N. F. Chilton, R. E. P. Winpenny and Y.-Z. Zheng, Angew. Chem., Int. Ed., 2016, 55, 16071–16074 CrossRef CAS PubMed.
- Y. Rechkemmer, F. D. Breitgoff, M. van der Meer, M. Atanasov, M. Hakl, M. Orlita, P. Neugebauer, F. Neese, B. Sarkar and J. van Slageren, Nat. Commun., 2016, 7, 10467 CrossRef CAS PubMed.
- E. Carl, S. Demeshko, F. Meyer and D. Stalke, Chem.–Eur. J., 2015, 21, 10109–10115 CrossRef CAS PubMed.
- X.-N. Yao, J.-Z. Du, Y.-Q. Zhang, X.-B. Leng, M.-W. Yang, S.-D. Jiang, Z.-X. Wang, Z.-W. Ouyang, L. Deng, B.-W. Wang and S. Gao, J. Am. Chem. Soc., 2017, 139, 373–380 CrossRef CAS PubMed.
- T. Pugh, N. F. Chilton and R. A. Layfield, Angew. Chem., Int. Ed., 2016, 55, 11082–11085 CrossRef CAS PubMed.
- J. Liu, Y.-C. Chen, J.-L. Liu, V. Vieru, L. Ungur, J.-H. Jia, L. F. Chibotaru, Y. Lan, W. Wernsdorfer, S. Gao, X.-M. Chen and M.-L. Tong, J. Am. Chem. Soc., 2016, 138, 5441–5450 CrossRef CAS PubMed.
- T. Glaser, V. Hoeke, K. Gieb, J. Schnack, C. Schröder and P. Müller, Coord. Chem. Rev., 2015, 289–290, 261–278 CrossRef CAS.
- S. Demir, I.-R. Jeon, J. R. Long and T. D. Harris, Coord. Chem. Rev., 2015, 289–290, 149–176 CrossRef CAS.
- D. Gatteschi and R. Sessoli, Angew. Chem., Int. Ed., 2003, 42, 268–297 CrossRef CAS PubMed.
- R. Hernández Sánchez and T. A. Betley, J. Am. Chem. Soc., 2015, 137, 13949–13956 CrossRef PubMed.
- Q. Zhao, T. D. Harris and T. A. Betley, J. Am. Chem. Soc., 2011, 133, 8293–8306 CrossRef CAS PubMed.
- R. Hernández Sánchez, A. K. Bartholomew, T. M. Powers, G. Ménard and T. A. Betley, J. Am. Chem. Soc., 2016, 138, 2235–2243 CrossRef PubMed.
- R. Hernández Sánchez and T. A. Betley, J. Am. Chem. Soc., 2018, 140, 16792–16806 CrossRef PubMed.
- R. Hernández Sánchez, S.-L. Zheng and T. A. Betley, J. Am. Chem. Soc., 2015, 137, 11126–11143 CrossRef PubMed.
- C. M. Zall, D. Zherebetskyy, A. L. Dzubak, E. Bill, L. Gagliardi and C. C. Lu, Inorg. Chem., 2012, 51, 728–736 CrossRef CAS PubMed.
- L. Fohlmeister, S. Liu, C. Schulten, B. Moubaraki, A. Stasch, J. D. Cashion, K. S. Murray, L. Gagliardi and C. Jones, Angew. Chem., Int. Ed., 2012, 51, 8294–8298 CrossRef CAS PubMed.
- R. A. Lewis, S. Morochnik, A. Chapovetsky, G. Wu and T. W. Hayton, Angew. Chem., Int. Ed., 2012, 51, 12772–12775 CrossRef CAS PubMed.
- R. A. D. Soriaga, S. Javed and D. M. Hoffman, J. Cluster Sci., 2010, 21, 567–575 CrossRef CAS.
- P. L. Damon, C. J. Liss, R. A. Lewis, S. Morochnik, D. E. Szpunar, J. Telser and T. W. Hayton, Inorg. Chem., 2015, 54, 10081–10095 CrossRef CAS PubMed.
- S. J. Tereniak and C. Lu, in Molecular Metal-Metal Bonds, ed. S. T.Liddle, 2015 Search PubMed.
- R. H. Duncan Lyngdoh, H. F. Schaefer and R. B. King, Chem. Rev., 2018, 118, 11626–11706 CrossRef CAS PubMed.
- R. J. Eisenhart, P. A. Rudd, N. Planas, D. W. Boyce, R. K. Carlson, W. B. Tolman, E. Bill, L. Gagliardi and C. C. Lu, Inorg. Chem., 2015, 54, 7579–7592 CrossRef CAS PubMed.
- L. Pauling, J. Am. Chem. Soc., 1947, 69, 542–553 CrossRef CAS.
- S. H. Carpenter, T. M. Baker, S. B. Muñoz, W. W. Brennessel and M. L. Neidig, Chem. Sci., 2018, 9, 7931–7939 RSC.
- S. B. Muñoz III, S. L. Daifuku, W. W. Brennessel and M. L. Neidig, J. Am. Chem. Soc., 2016, 138, 7492–7495 CrossRef PubMed.
- R. Hernández Sánchez, A. M. Willis, S.-L. Zheng and T. A. Betley, Angew. Chem., Int. Ed., 2015, 54, 12009–12013 CrossRef PubMed.
- E. M. Schubert, J. Chem. Educ., 1992, 69, 62 CrossRef CAS.
- C. Lichtenberg, I. Garcia Rubio, L. Viciu, M. Adelhardt, K. Meyer, G. Jeschke and H. Grützmacher, Angew. Chem., Int. Ed., 2015, 54, 13012–13017 CrossRef CAS PubMed.
- R. Araake, K. Sakadani, M. Tada, Y. Sakai and Y. Ohki, J. Am. Chem. Soc., 2017, 139, 5596–5606 CrossRef CAS PubMed.
- N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, J. Comput. Chem., 2013, 34, 1164–1175 CrossRef CAS PubMed.
- The value of D calculated using VTVF data differs from that determined from the magnetic susceptibility data (e.g., D = −0.32 cm−1). Similar discrepancies have been observed previously. See, for example, ref. 17. When the two values are not in agreement, those determined using VTVF data are generally regarded as more accurate.
- C. G. Werncke, P. C. Bunting, C. Duhayon, J. R. Long, S. Bontemps and S. Sabo-Etienne, Angew. Chem., Int. Ed., 2015, 54, 245–248 CrossRef CAS PubMed.
- J. M. Zadrozny, D. J. Xiao, J. R. Long, M. Atanasov, F. Neese, F. Grandjean and G. J. Long, Inorg. Chem., 2013, 52, 13123–13131 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Spectroscopic, crystallographic, and magnetic characterization details of 1. CCDC 1957071. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0sc01578d |
| This journal is © The Royal Society of Chemistry 2020 |