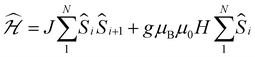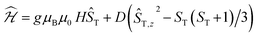Open Access Article
Open Access ArticleLigand field-actuated redox-activity of acetylacetonate†
Morten Gotthold
Vinum‡
 a,
Laura
Voigt‡
a,
Laura
Voigt‡
 a,
Steen H.
Hansen
a,
Colby
Bell
b,
Kensha Marie
Clark
a,
Steen H.
Hansen
a,
Colby
Bell
b,
Kensha Marie
Clark
 b,
René Wugt
Larsen
b,
René Wugt
Larsen
 a and
Kasper S.
Pedersen
a and
Kasper S.
Pedersen
 *a
*a
aDepartment of Chemistry, Technical University of Denmark, Kemitorvet Kgs. Lyngby, DK-2800, Denmark. E-mail: kastp@kemi.dtu.dk
bDepartment of Chemistry, The University of Memphis, Memphis, TN, USA
First published on 16th July 2020
Abstract
The quest for simple ligands that enable multi-electron metal–ligand redox chemistry is driven by a desire to replace noble metals in catalysis and to discover novel chemical reactivity. The vast majority of simple ligand systems display electrochemical potentials impractical for catalytic cycles, illustrating the importance of creating new strategies towards energetically aligned ligand frontier and transition metal d orbitals. We herein demonstrate the ability to chemically control the redox-activity of the ubiquitous acetylacetonate (acac) ligand. By employing the ligand field of high-spin Cr(II) as a switch, we were able to chemically tailor the occurrence of metal–ligand redox events via simple coordination or decoordination of the labile auxiliary ligands. The mechanism of ligand field actuation can be viewed as a destabilization of the dz2 orbital relative to the π* LUMO of acac, which proffers a generalizable strategy to synthetically engineer redox-activity with seemingly redox-inactive ligands.
Introduction
The taming of synergistic metal ion- and ligand-centered redox processes is a crucial first step towards the development of systems having multi-electron redox events using base metals.1 Such systems have the potential to challenge the role of the noble metals in catalysis by providing access to otherwise inaccessible two-electron redox reactivity (e.g. oxidative addition and reductive elimination).1–5 Of particular interest are chelating ligands that both impose steric constraints and enhance the chemical robustness of the transition metal complex, whilst simultaneously having energetically accessible orbitals for reduction or oxidation.6–9 A variety of bidentate ligands have been shown to exhibit beneficial redox-activity and cooperative metal–ligand reactivites. Overwhelmingly, this behavior is monopolized by ligands that form five-membered chelate rings.7,10 Six-membered chelate rings are largely dominated by β-diketonate ligands, the related β-enaminoketonates, and β-diketiminates,11 which are ubiquitous in the chemistry of the s-, p-, d-, and f-block elements. Surprisingly, their redox-activity has remained largely unexplored, despite its potential for exploitation in homogeneous catalysis.12,13 This lacuna arises from the high energy of the ligand LUMO of β-diketiminates, which requires the use of extremely strong reductants.14 Consequently, they partake exclusively in ligand-centered oxidations.14,15 Holland and co-workers demonstrated that the energy of the LUMO can be decreased significantly through the employment of the structurally related formazanate ligands, although strong reductants, as alkali metals, were still needed to induce ligand-centered reduction.16–18 Quite surprisingly, the simple acetylacetonate ligand (acac = monoanion of pentane-2,4-dione) has never been reported to participate in redox events in transition metal chemistry. The existence of an unstable Li+ or Mg2+-bound anion radical, acac˙2−, generated by reduction with n-butyllithium or Grignard reagents, was suggested by EPR spectroscopy; however, it could not be isolated or studied in any further detail.19We recently demonstrated that six-coordinate trans-[Cr(hfac)2L2] (hfac = 1,1,1,5,5,5-hexafluoroacetylacetonate; L = pyrazine, or tetrahydrofuran) is most adequately described as a Cr(III) complex with a single unpaired electron delocalized over two hfac– ligands.20 In contrast, the related square-planar complex [Cr(acac)2], reported in 1958,21 is known to possess an S = 2 spin ground state, which is indicative of a high-spin Cr(II) center.21,22 Herein, we show that introduction of modest σ donors in the vacant, axial positions of [Cr(acac)2] leads to reduction of the acac ligand scaffold (Scheme 1), providing a novel route to chemically control the electronic delocalization and spin-density in a metal-ion complex.
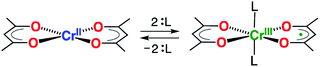 | ||
| Scheme 1 Switching of the redox-state of acetylacetonate by axial coordination/de-coordination at a Cr(II)/Cr(III) center. | ||
Results and discussion
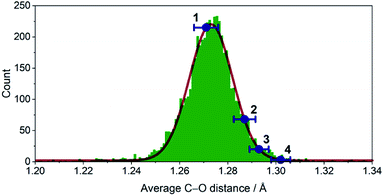
The crystallographic evidence for the existence of a chromium(II) acetylacetonate was reported by Cotton et al. in 1977.22 Sublimation of crude [Cr(acac)2] concomitantly yielded crystalline [Cr(acac)2] and [Cr(acac)3]. We found that reaction of stoichiometric amounts of Li(acac) and CrCl2 in dry, deoxygenated tetrahydrofuran (THF) provides a convenient, direct route to crystalline, brown-orange [Cr(acac)2] (1, see ESI† for details). Our redetermination of the crystal structure of 1 at T = 120 K revealed only a minor thermal contraction as compared to the previously reported room temperature structure.22 Notably, the Cr center resides in a square planar coordination environment that is distantly stacked into a supramolecular chain structure (Fig. 1) with presumably weak [Cr(acac)2]⋯[Cr(acac)2] interactions.1Dissolution of 1 in a selection of weakly coordinating solvents, like THF, toluene, and acetonitrile, leads to only faintly colored solutions (Fig. S1, ESI†). The absorption bands above λ = 500 nm are of low intensity (ε < 200 M−1 cm−1) and are identified as metal-centered d–d transitions. In pyridine, however, an intense, dark coloration of the solution occurs. The UV-vis spectrum (Fig. S1, ESI†) reveals strong optical absorption (ε = 800–13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 M−1 cm−1) through the entire spectral range (200–2300 nm) with an intense charge-transfer band centered at ∼950 nm. The cooling of concentrated pyridine (py) solutions of 1 affords black crystalline specimens, which were identified as trans-[Cr(acac)2(py)2] (3) by single-crystal X-ray diffraction. The average Cr–O bond length in 3 (1.94 Å) is significantly shorter than that of 1 (1.98 Å) despite the lower coordination number in 1. Furthermore, the average C–O bond length is elongated from 1.27 Å in 1 to 1.29 Å in 3 (Fig. 2). This minimalistic structural analysis could suggest an evolution in the electronic structure, bounded by {CrII–(acac)22−} in 1 and {CrIII–(acac)2˙3−} in 3, as the extreme, limiting cases. The formulation of {CrIII–(acac)2˙3−} implies a concurrent occupation of the antibonding LUMO of the acac ligands, which is expected to predominantly elongate the C–O bonds.20 To corroborate this hypothesis, two additional [Cr(acac)2L2] complexes with the axial ligands containing an electron-poor (L = 4-(trifluoromethyl)pyridine = CF3py; 2) and an electron-rich (L = 4-(dimethylamino)pyridine = DMAP; 4) pyridine ring were synthesized and structurally characterized (Fig. 1). The average Cr–N and Cr–O bond lengths in 2–4 vary only slightly (≤0.6%) indicating a common oxidation state of the Cr center. The differences within the series become clearer with the metrics of the acac ligand. Whereas 1 stands apart with the shortest averaged C–O bond of 1.271 Å, the C–O bond elongates by 2.4% from 1, over 2 and 3, to 4 (and by 1.2% from 2 to 4; Fig. 2). Herein, the C–O bond of 4 is within the longest 3% of the averaged C–O bond lengths of all reported acac-based structures (Fig. 2). On the contrary, the C–CH and C–CH3 bond lengths are identical within the experimental accuracy across the entire series 1–4.
000 M−1 cm−1) through the entire spectral range (200–2300 nm) with an intense charge-transfer band centered at ∼950 nm. The cooling of concentrated pyridine (py) solutions of 1 affords black crystalline specimens, which were identified as trans-[Cr(acac)2(py)2] (3) by single-crystal X-ray diffraction. The average Cr–O bond length in 3 (1.94 Å) is significantly shorter than that of 1 (1.98 Å) despite the lower coordination number in 1. Furthermore, the average C–O bond length is elongated from 1.27 Å in 1 to 1.29 Å in 3 (Fig. 2). This minimalistic structural analysis could suggest an evolution in the electronic structure, bounded by {CrII–(acac)22−} in 1 and {CrIII–(acac)2˙3−} in 3, as the extreme, limiting cases. The formulation of {CrIII–(acac)2˙3−} implies a concurrent occupation of the antibonding LUMO of the acac ligands, which is expected to predominantly elongate the C–O bonds.20 To corroborate this hypothesis, two additional [Cr(acac)2L2] complexes with the axial ligands containing an electron-poor (L = 4-(trifluoromethyl)pyridine = CF3py; 2) and an electron-rich (L = 4-(dimethylamino)pyridine = DMAP; 4) pyridine ring were synthesized and structurally characterized (Fig. 1). The average Cr–N and Cr–O bond lengths in 2–4 vary only slightly (≤0.6%) indicating a common oxidation state of the Cr center. The differences within the series become clearer with the metrics of the acac ligand. Whereas 1 stands apart with the shortest averaged C–O bond of 1.271 Å, the C–O bond elongates by 2.4% from 1, over 2 and 3, to 4 (and by 1.2% from 2 to 4; Fig. 2). Herein, the C–O bond of 4 is within the longest 3% of the averaged C–O bond lengths of all reported acac-based structures (Fig. 2). On the contrary, the C–CH and C–CH3 bond lengths are identical within the experimental accuracy across the entire series 1–4.
Cyclic voltammetry of 1–4 was performed in dichloromethane. These experiments revealed only irreversible processes, which for 2–4, likely result from dynamic exchange of the respective pyridine ligands. This interpretation is supported by UV-vis spectroscopy and 1H-NMR spectroscopy. When pyridinic solutions of 3 are titrated with dichloromethane, a drastic decrease in intensity of the charge transfer transitions, which is associated with the loss of pyridine, is observed (Fig. S2, ESI†). Additionally, the 1H-NMR spectra of 2–4 in dichloromethane-d2 (Fig. S3, ESI†) reveal broadened resonances at chemical shifts corresponding to the free pyridines, suggesting dynamic exchange. The observed broadened resonances, which decrease in line width along the 2–4 series, correlate with the donor strength of the pyridine ligand and therefore, implicitly, their lability. It is also noteworthy that 1 is NMR silent and peaks associated with the acac ligand were not observed in any 1H-NMR spectra. In pyridine, cyclic voltammetry of 3, affords a single reversible oxidation at E1/2 = −1.17 V vs.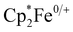 (Fig. S7, ESI†). This large, negative potential is close to that found for the cathodic peak potential in the irreversible reduction of Hacac,23 the reduction potential of the related 1,3-diphenylpropane-1,3-dione,24 and the oxidation potential in [CrIII(hfac)2˙3−(pyrazine)2].20 The oxidation is thus assigned as ligand-centered and corresponding to the formation of trans-[CrIII(acac)2(pyridine)2]+ (3+, Fig. S7, ESI†). 3+ has previously been isolated as the PF6− salt and the RT crystal structure exhibits a slightly longer Cr–O bond length (1.950(2) Å) and a slightly shorter C–O bond length (1.289(2) Å) than those found in 3, supporting the presence of a partially reduced acac-ligand scaffold in 3.25
(Fig. S7, ESI†). This large, negative potential is close to that found for the cathodic peak potential in the irreversible reduction of Hacac,23 the reduction potential of the related 1,3-diphenylpropane-1,3-dione,24 and the oxidation potential in [CrIII(hfac)2˙3−(pyrazine)2].20 The oxidation is thus assigned as ligand-centered and corresponding to the formation of trans-[CrIII(acac)2(pyridine)2]+ (3+, Fig. S7, ESI†). 3+ has previously been isolated as the PF6− salt and the RT crystal structure exhibits a slightly longer Cr–O bond length (1.950(2) Å) and a slightly shorter C–O bond length (1.289(2) Å) than those found in 3, supporting the presence of a partially reduced acac-ligand scaffold in 3.25
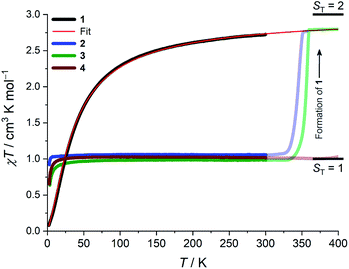
Whilst being known to exhibit an S = 2 ground state at room temperature,21 the magnetic properties of 1 have not previously been studied in any further detail. The room temperature value of the susceptibility-temperature, χT, product for 1 (Fig. 3, black trace) amounts to 2.7 cm3 K mol−1, which is slightly lower than the expected value (3.0 cm3 K mol−1) for a magnetically uncoupled S = 2 ion with a g-factor of 2.0. Upon decreasing temperature, the χT product decreases and almost vanishes at 2 K. The crystal structure of 1 features supramolecular [Cr(acac)2]∞ chains running along the crystallographic b direction with intermolecular distances of Cr⋯Cr = 4.7 Å and Cr⋯Cγ = 3.0 Å (Fig. 1), which provides a pathway for weak intermolecular superexchange interactions. The χT vs. T data can be modelled by the classical Fisher model for S = 2 chains using the isotropic Hamiltonian:26
The data could be modelled with the D/hc parameters of +2.2 cm−1, +4.2 cm−1, and +3.7 cm−1 for 2, 3, and 4, respectively. These values are large for Cr(III) complexes (DCr(III) = 2/3 × D), although not unprecedented.30 Heating 2–4 above room temperature (0.1 K min−1) leads to abrupt increases in the χT products at ∼330 K and ∼340 K for 2 and 3, respectively, which saturate at ∼2.8 cm3 K mol−1 at ∼350 K (2) and ∼360 K (3). The increase in the χT products is followed by a dramatic colour change from almost black to pale orange. Notably, the χT product of 4 experiences only a minuscule increase at the highest attainable temperature (400 K) and no change in color was evident upon returning to RT. Powder X-ray diffraction identifies the heated samples of both 2 and 3 as phase-pure, microcrystalline 1 (Fig. S6, ESI†). This conclusion is supported by the IR spectra that are superimposable to the pristine, as-synthesized 1 (Fig. S4, ESI†). Thermogravimetry coupled to mass spectrometry confirms near-quantitative conversion and the loss of 4-(trifluoromethyl)pyridine and pyridine for 2 and 3, respectively (Fig. S10 and 11, ESI†). The subsequent re-cooling to 2 K demonstrates the irreversibility of the thermal cycling (Fig. S8, ESI†) where the χT product decreases monotonically to 0.08 cm3 K mol−1 at 2 K, identical to the data obtained for as-synthesized 1 (Fig. 3, black trace).
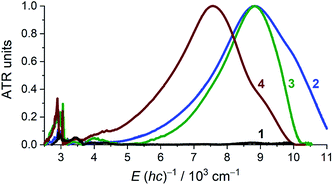
Solid state attenuated total reflection spectra in the mid- and near-infrared (MIR and NIR) spectral range echo the electronic structure conclusions as acquired from crystallography and magnetometry (Fig. 4). For 1, the NIR region is void of absorptions and the only identifiable, narrow bands fall in the mid-IR region where they are assigned as being of vibrational origin. For 2–4, an intense, broad absorption is observed at ∼8800 cm−1 for 2 and 3, and at ∼7600 cm−1 for 4. The spectral maxima of the NIR spectra of 2 and 3 virtually coincide, but the bandwidth is significantly different. Intense NIR excitations are commonly considered as fingerprints of mixed-valency and interpreted as inter-valence charge transfer transitions (IVCTs).31,32 A complete absence of any absorption bands in the NIR energy window in 1 supports the {CrII–(acac)22−} formulation. For 2–4, the crystallographic structure suggests a complete delocalization over the acac ligands, which may, however, be invalidated by crystallographic disorder. According to Hush's theory for symmetrical charge-transfer complexes,33,34 the theoretical bandwidth at half intensity, Δν1/2°, for the IVCT band is related to the energy of the band maximum through Δν1/2° = (2310 × νmax)1/2 (at T = 300 K, and with Δν1/2° and νmax in units of cm−1). The Δν1/2° for 2 (4519), 3 (4512), and 4 (4183) are all larger than the narrow, experimentally obtained Δν1/2 (2: 2776; 3: 1907; 4: 2311), which suggests full delocalization (Robin-Day Class III),35 as observed in other transition metal complexes with organic-based mixed valency.36 Further quantitative analysis of IVCT bands of solid samples is commonly impeded by the often-inaccessible absorption cross-section. For 2–4, the IVCT bands significantly dwarf the dipole-allowed vibrational transitions hinting at a large molar absorptivity of the IVCT bands. The solution spectrum of 3 in pyridine (Fig. S1, ESI†) provides εmax ≈ 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 M−1 cm−1, which is typical for Robin-Day Class III systems, which habitually have εmax values ≥5000 M−1 cm−1.32 Additionally, the determined εmax allows an estimation of the degree of electronic coupling between the two acac-ligand sites through the electron-transfer coupling matrix element HAB = 2.06 × 10−2 × (νmaxεmaxΔν1/2)1/2/rAB. Assuming an electron transfer distance, rAB, of 2.7 Å, corresponding to the closest O⋯O separation across the Cr center in 3, affords HAB ≈ 3600 cm−1 (assuming ε ≈ 13
000 M−1 cm−1, which is typical for Robin-Day Class III systems, which habitually have εmax values ≥5000 M−1 cm−1.32 Additionally, the determined εmax allows an estimation of the degree of electronic coupling between the two acac-ligand sites through the electron-transfer coupling matrix element HAB = 2.06 × 10−2 × (νmaxεmaxΔν1/2)1/2/rAB. Assuming an electron transfer distance, rAB, of 2.7 Å, corresponding to the closest O⋯O separation across the Cr center in 3, affords HAB ≈ 3600 cm−1 (assuming ε ≈ 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 M−1 cm−1 results in the HAB values: 2: ∼4300 cm−1, and 4: ∼3600 cm−1). Such large values of HAB are characteristic for Class III where 2 HAB = νmax is expected, and well obeyed for 2–4.35
000 M−1 cm−1 results in the HAB values: 2: ∼4300 cm−1, and 4: ∼3600 cm−1). Such large values of HAB are characteristic for Class III where 2 HAB = νmax is expected, and well obeyed for 2–4.35
Deeper insight into the electronic structures of 1–4 was acquired through DFT calculations performed on the experimentally determined molecular structures, without any subsequent geometry optimization, and at the TPSSh/def2-TZVP-ZORA level. For 1, the high-spin (HS), S = 2, state is strongly stabilized over the ST = 1 (3,1)-broken-symmetry state (BS; the notation referring to a state with 3 unpaired α-spins on one fragment and 1 unpaired β-spin on a different fragment) (EHS − EBS = −9518 cm−1) in accordance with the preceding experimental results. The Mulliken spin population of the Cr center in 1 (Fig. 5) amounts to 4.1, consistent with the presence of a HS Cr(II) ion. Furthermore, the summed Mulliken spin population for each acac ligand vanishes at −0.05, as expected for a closed-shell ligand. The Kohn–Sham singly occupied molecular spin-orbitals (SOMOs, Fig. S12, ESI†) are all of predominant 3d-character suggesting little admixture with ligand-based π-orbitals. These observations contrast starkly with the situation for 2–4, where the (3,1)-BS states are strongly stabilized relative to the HS states (2: 7248 cm−1; 3: 8078 cm−1; 4: 5656 cm−1), suggesting a ground state formulated as {CrIII–(acac)2˙3−}. Using a superexchange Hamiltonian of the form 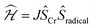 (see ESI† for further details), the calculated energy gaps are translated into superexchange coupling constants, J/hc, of 3943 cm−1, 4366 cm−1, and 3114 cm−1 for 2, 3, and 4, respectively. Whilst the irregular evolution is not straightforward to explain, the magnitudes reflect extremely strong antiferromagnetic interactions, which are approximately one order of magnitude larger than the values estimated experimentally or calculated for other Cr(III)-radical complexes.28,29,37–40 The Mulliken spin-populations of Cr amounts to 2.7 for all three members of the series, 2–4. This value is close to the expected values for an S = 3/2 ion of 3.0 (Fig. 5), and of similar magnitude as several other established Cr(III) complexes with redox-active ligands.28 Despite the close resemblance in the Cr spin density for 2–4, a clear evolution of the Mulliken spin population of the acac ligands and the axial pyridine ligands is observed (Fig. 5). The summed spin density per acac ligand in 2 amounts to 0.2, which is significantly larger than found for 1. For 3, only a slight increase in the acac spin density relative to 2 is found, whereas the integrated acac spin population in 4 of 0.4 approaches the expectation for one electron fully delocalized over two acac moieties (0.5). The evolution of the axial pyridines' spin density counter-balances that of the acac ligand, i.e. showing a gradual decrease in the spin density from a sizable value in 2 of −0.3 to a vanishing value in 4 (−0.06). This trend is as expected based on the electron density of the pyridines. Noticeably, in contrast to 1, for 2–4, the highest energy SOMO is of predominant ligand p-orbital character, whereas the three energetically lower-lying, quasi-degenerate SOMOs all are metal-based and reminiscent of the dxy, dyz, and dzx orbitals (Fig. S13–16, ESI†).
(see ESI† for further details), the calculated energy gaps are translated into superexchange coupling constants, J/hc, of 3943 cm−1, 4366 cm−1, and 3114 cm−1 for 2, 3, and 4, respectively. Whilst the irregular evolution is not straightforward to explain, the magnitudes reflect extremely strong antiferromagnetic interactions, which are approximately one order of magnitude larger than the values estimated experimentally or calculated for other Cr(III)-radical complexes.28,29,37–40 The Mulliken spin-populations of Cr amounts to 2.7 for all three members of the series, 2–4. This value is close to the expected values for an S = 3/2 ion of 3.0 (Fig. 5), and of similar magnitude as several other established Cr(III) complexes with redox-active ligands.28 Despite the close resemblance in the Cr spin density for 2–4, a clear evolution of the Mulliken spin population of the acac ligands and the axial pyridine ligands is observed (Fig. 5). The summed spin density per acac ligand in 2 amounts to 0.2, which is significantly larger than found for 1. For 3, only a slight increase in the acac spin density relative to 2 is found, whereas the integrated acac spin population in 4 of 0.4 approaches the expectation for one electron fully delocalized over two acac moieties (0.5). The evolution of the axial pyridines' spin density counter-balances that of the acac ligand, i.e. showing a gradual decrease in the spin density from a sizable value in 2 of −0.3 to a vanishing value in 4 (−0.06). This trend is as expected based on the electron density of the pyridines. Noticeably, in contrast to 1, for 2–4, the highest energy SOMO is of predominant ligand p-orbital character, whereas the three energetically lower-lying, quasi-degenerate SOMOs all are metal-based and reminiscent of the dxy, dyz, and dzx orbitals (Fig. S13–16, ESI†).
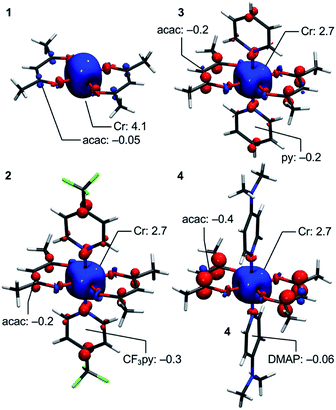 | ||
| Fig. 5 DFT-calculated spin-density plots of the HS-state of 1 and the BS-states of 2–4 shown at an isosurface value of 0.005 a.u. Selected Mulliken spin populations are indicated. | ||
Conclusion
We have demonstrated the redox-activity of the ubiquitous acetylacetonate ligand. The crystallographic, magnetic, spectroscopic, and computational results all point toward the occurrence of concerted metal–ligand redox chemistry in the square-planar [Cr(acac)2] upon axial coordination of moderately donating pyridine ligands. Furthermore, the crystallographically imposed symmetry coupled with Hush analysis indicate electronic delocalization upon coordination, whereby complexes 2–4 can be assigned as Class III mixed-valence systems.31In the ideally square-planar ligand field of 1, the singly occupied dz2 orbital remains energetically low-lying, whereas the pyridines of 2–4 raise the dz2 orbital above the ligand-based LUMO, leading to a partial {CrII–(acac)22−} → {CrIII–(acac)2˙3−} valence tautomerization, whose degree of completion depends on the donor strength of the auxiliary axial ligands. Notably, the valence tautomerization in [Cr(acac)2] is not triggered by more weakly coordinating ligands, which may leave the dz2 orbital energetically well below the acac ligand LUMO. Displacement of the pyridine ligands in 2–4 demonstrates the reversibility of the {CrII–(acac)22−} ⇄ {CrIII–(acac)2˙3−} valence tautomerization process. A handful of transition metal complex families demonstrate temperature-induced valence tautomerism,41,42 but the manifestation of ligand reduction upon alteration of the metal ligand sphere is exceedingly rare.43 It is tempting to consider if mechanical stimuli, mimicking an increased axial ligand field, may actuate redox-activity in 1. Notably, 1 is isomorphous to [Cu(acac)2], which has recently been shown to form easily deformable crystals.44–46 Any similar plasticity in crystals of 1 could be coupled to dramatic changes in both the optical and magnetic properties following the {CrII–(acac)22−} ⇄ {CrIII–(acac)2˙3−} valence tautomerization.
The valence tautomers 2–4 exhibit extremely strong CrIII-radical exchange interactions, as demonstrated by magnetization measurements and DFT calculations. The importance of remarkably strong metal–ligand exchange interactions was recently highlighted as key for acquiring efficient electrocatalysis,47 although the tailoring of superexchange has so far received limited attention in catalysis. Despite the diversity and potency of chromium complexes for organic transformations including, for instance, hydrogenations,48 and carbon–carbon cross-couplings,49 relatively little is known about the exact chemical identity of the active species. For instance, [CrIII(acac)3] was shown to be a potent hydrogenation catalyst only in the presence of a strong reductant.48 Indeed, similar observations were made already in 1971 where the activation of a [CrIII(acac)3] polymerization catalyst with (C2H5)2AlCl provided a putative low-spin CrII complex.50 Considering these reports and the results presented here, it is tantalizing to speculate if valence tautomerism between CrII/III and either the organic co-ligands or the substrate, or both, plays a key role in chromium catalysis.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
K.S.P. thanks the VILLUM Foundation for a VILLUM Young Investigator grant (15374), and the Carlsberg Foundation (CF-17-0637), the Brdr. Hartmann's Foundation and the Torkil Holm foundation for research infrastructure grants. Assoc. Prof. T. J. Sørensen, Assoc. Prof. M. Pittelkow, Prof. J. Bendix (University of Copenhagen), Assoc. Prof. J. Overgaard, Dr B. Richter (Aarhus University), and Mr Ph. Charlie Johansen (Technical University of Denmark) are thanked for experimental assistance and helpful discussions.Notes and references
- D. L. J. Broere, R. Plessius and J. I. Van Der Vlugt, Chem. Soc. Rev., 2015, 44, 6886–6915 RSC.
- V. K. K. Praneeth, M. R. Ringenberg and T. R. Ward, Angew. Chem., Int. Ed., 2012, 51, 10228–10234 CrossRef CAS PubMed.
- P. J. Chirik and K. Wieghardt, Science, 2010, 327, 794–795 CrossRef CAS PubMed.
- O. R. Luca and R. H. Crabtree, Chem. Soc. Rev., 2013, 42, 1440–1459 RSC.
- V. Lyaskovskyy and B. De Bruin, ACS Catal., 2012, 2, 270–279 CrossRef CAS.
- W. Kaim and B. Schwederski, Coord. Chem. Rev., 2010, 254, 1580–1588 CrossRef CAS.
- W. Kaim, Dalton Trans., 2019, 48, 8521–8529 RSC.
- S. Ganguly and A. Ghosh, Acc. Chem. Res., 2019, 52, 2003–2014 CrossRef CAS PubMed.
- R. Eisenberg and H. B. Gray, Inorg. Chem., 2011, 50, 9741–9751 CrossRef CAS PubMed.
- M. M. Khusniyarov, T. Weyhermüller, E. Bill and K. Wieghardt, J. Am. Chem. Soc., 2009, 131, 1208–1221 CrossRef CAS PubMed.
- L. Bourget-Merle, M. F. Lappert and J. R. Severn, Chem. Rev., 2002, 102, 3031–3065 CrossRef CAS PubMed.
- C. Camp and J. Arnold, Dalton Trans., 2016, 45, 14462–14498 RSC.
- R. L. Webster, Dalton Trans., 2017, 46, 4483–4498 RSC.
- M. M. Khusniyarov, E. Bill, T. Weyhermüller, E. Bothe and K. Wieghardt, Angew. Chem., Int. Ed., 2011, 50, 1652–1655 CrossRef CAS PubMed.
- M. P. Marshak, M. B. Chambers and D. G. Nocera, Inorg. Chem., 2012, 51, 11190–11197 CrossRef CAS PubMed.
- D. L. J. Broere, B. Q. Mercado, J. T. Lukens, A. C. Vilbert, G. Banerjee, H. M. C. Lant, S. H. Lee, E. Bill, S. Sproules, K. M. Lancaster and P. L. Holland, Chem. – Eur. J., 2018, 24, 9417–9425 CrossRef CAS PubMed.
- D. L. J. Broere, B. Q. Mercado, E. Bill, K. M. Lancaster, S. Sproules and P. L. Holland, Inorg. Chem., 2018, 57, 9580–9591 CrossRef CAS PubMed.
- M. C. Chang, P. Roewen, R. Travieso-Puente, M. Lutz and E. Otten, Inorg. Chem., 2015, 54, 379–388 CrossRef CAS PubMed.
- A. Staško, A. Tkáč, V. Laurinc and L. Malík, Org. Magn. Reson., 1976, 8, 237–239 CrossRef.
- M. G. Vinum, L. Voigt, C. Bell, D. Mihrin, R. W. Larsen, K. M. Clark and K. S. Pedersen, Chem. – Eur. J., 2020, 26, 2143–2147 CrossRef CAS PubMed.
- G. Costa and A. Puxeddu, J. Inorg. Nucl. Chem., 1958, 8, 104–112 CrossRef CAS.
- F. A. Cotton, C. E. Rice and G. W. Rice, Inorg. Chim. Acta, 1977, 24, 231–234 CrossRef CAS.
- A. Kuhn, K. G. Von Eschwege and J. Conradie, Electrochim. Acta, 2011, 56, 6211–6218 CrossRef CAS.
- R. C. Buchta and D. H. Evans, Anal. Chem., 1968, 40, 2181–2186 CrossRef CAS.
- A. Iino, T. Suzuki and S. Kaizaki, J. Chem. Soc., Dalton Trans., 2003, 3, 4604–4611 RSC.
- M. E. Fisher, Am. J. Phys., 1964, 32, 343–346 CrossRef.
- P. Perlepe, I. Oyarzabal, K. S. Pedersen, P. Negrier, D. Mondieig, M. Rouzières, E. A. Hillard, F. Wilhelm, A. Rogalev, E. A. Suturina, C. Mathonière and R. Clérac, Polyhedron, 2018, 153, 248–253 CrossRef CAS.
- C. C. Scarborough, S. Sproules, C. J. Doonan, K. S. Hagen, T. Weyhermüller and K. Wieghardt, Inorg. Chem., 2012, 51, 6969–6982 CrossRef CAS PubMed.
- C. C. Scarborough, S. Sproules, T. Weyhermüller, S. DeBeer and K. Wieghardt, Inorg. Chem., 2011, 50, 12446–12462 CrossRef CAS PubMed.
- J. Krzystek, G. Kohl, H. B. Hansen, M. Enders and J. Telser, Organometallics, 2019, 38, 2179–2188 CrossRef CAS.
- M. B. Robin and P. Day, Adv. Inorg. Chem. Radiochem., 1968, 10, 247–422 CrossRef.
- D. M. D'Alessandro and F. R. Keene, Chem. Soc. Rev., 2006, 35, 424–440 Search PubMed.
- N. S. Hush, Prog. Inorg. Chem., 1967, 8, 391–444 CAS.
- N. S. Hush, Electrochim. Acta, 1968, 13, 1005–1023 CrossRef CAS.
- B. S. Brunschwig, C. Creutz and N. Sutin, Chem. Soc. Rev., 2002, 31, 168–184 RSC.
- C. C. Lu, E. Bill, T. Weyhermüller, E. Bothe and K. Wieghardt, J. Am. Chem. Soc., 2008, 130, 3181–3197 CrossRef CAS PubMed.
- M. Wang, J. England, T. Weyhermüller, S. L. Kokatam, C. J. Pollock, S. DeBeer, J. Shen, G. P. A. Yap, K. H. Theopold and K. Wieghardt, Inorg. Chem., 2013, 52, 4472–4487 CrossRef CAS PubMed.
- J. A. DeGayner, I. R. Jeon and T. D. Harris, Chem. Sci., 2015, 6, 6639–6648 RSC.
- C. Hua, J. A. DeGayner and T. D. Harris, Inorg. Chem., 2019, 58, 7044–7053 CrossRef CAS PubMed.
- X. Ma, E. Suturina, M. Rouzières, F. Wilhelm, A. Rogalev, R. Clérac and P. Dechambenoit, Chem. Commun., 2020, 56, 4906–4909 RSC.
- D. N. Hendrickson and C. G. Pierpont, in Spin Crossover in Transition Metal Compounds II, Springer Berlin Heidelberg, Berlin, Heidelberg, 2004, pp. 63–95 Search PubMed.
- J. Bendix and K. M. Clark, Angew. Chem., Int. Ed., 2016, 55, 2748–2752 CrossRef CAS PubMed.
- E. J. Schelter, R. Wu, B. L. Scott, J. D. Thompson, T. Cantat, K. D. John, E. R. Batista, D. E. Morris and J. L. Kiplinger, Inorg. Chem., 2010, 49, 924–933 CrossRef CAS PubMed.
- A. Worthy, A. Grosjean, M. C. Pfrunder, Y. Xu, C. Yan, G. Edwards, J. K. Clegg and J. C. McMurtrie, Nat. Chem., 2018, 10, 65–69 CrossRef CAS PubMed.
- A. J. Brock, J. J. Whittaker, J. A. Powell, M. C. Pfrunder, A. Grosjean, S. Parsons, J. C. McMurtrie and J. K. Clegg, Angew. Chem., Int. Ed., 2018, 57, 11325–11328 CrossRef CAS PubMed.
- E. P. Kenny, A. C. Jacko and B. J. Powell, Angew. Chem., Int. Ed., 2019, 58, 15082–15088 CrossRef CAS PubMed.
- J. S. Derrick, M. Loipersberger, D. A. Iovan, P. T. Smith, K. Chakarawet, J. R. Long, M. Head-Gordon and C. J. Chang, ChemRxiv, 2020 DOI:10.26434/chemrxiv.11923176.v1.
- B. Han, P. Ma, X. Cong, H. Chen and X. Zeng, J. Am. Chem. Soc., 2019, 141, 9018–9026 CrossRef CAS PubMed.
- J. Li, Q. Ren, X. Cheng, K. Karaghiosoff and P. Knochel, J. Am. Chem. Soc., 2019, 141, 18127–18135 CrossRef CAS PubMed.
- G. Henrici-Olivé and S. Olivé, Angew. Chem., Int. Ed. Engl., 1971, 10, 776–786 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available: Full experimental details, solution UV-vis spectroscopic data, solid-state IR spectra, NMR spectra, crystallographic details, TGA-MS data, powder X-ray diffraction data, DFT-calculated frontier molecular orbitals. CCDC 1974980–1974983. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0sc01836h |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2020 |

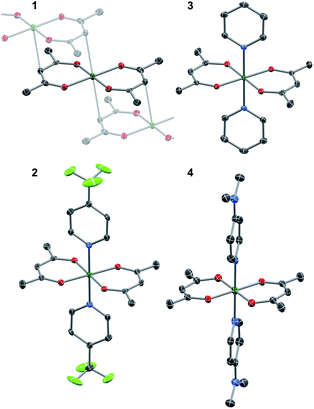
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ): Cr–O 1.947(2), 1.949(2), Cr–N 2.096(3), C–O 1.299(4), 1.305(4).
): Cr–O 1.947(2), 1.949(2), Cr–N 2.096(3), C–O 1.299(4), 1.305(4).