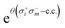Open Access Article
Open Access ArticleHardware efficient quantum algorithms for vibrational structure calculations
Pauline J.
Ollitrault
ab,
Alberto
Baiardi
 b,
Markus
Reiher
b,
Markus
Reiher
 *b and
Ivano
Tavernelli
*b and
Ivano
Tavernelli
 *a
*a
aIBM Quantum, IBM Research – Zurich, Säumerstrasse 4, 8803 Rüschlikon, Switzerland. E-mail: ita@zurich.ibm.com
bLaboratory of Physical Chemistry, ETH Zürich, Vladimir-Prelog-Weg 2, 8093 Zürich, Switzerland. E-mail: markus.reiher@phys.chem.ethz.ch
First published on 11th June 2020
Abstract
We introduce a framework for the calculation of ground and excited state energies of bosonic systems suitable for near-term quantum devices and apply it to molecular vibrational anharmonic Hamiltonians. Our method supports generic reference modal bases and Hamiltonian representations, including the ones that are routinely used in classical vibrational structure calculations. We test different parametrizations of the vibrational wavefunction, which can be encoded in quantum hardware, based either on heuristic circuits or on the bosonic Unitary Coupled Cluster Ansatz. In particular, we define a novel compact heuristic circuit and demonstrate that it provides a good compromise in terms of circuit depth, optimization costs, and accuracy. We evaluate the requirements, number of qubits and circuit depth, for the calculation of vibrational energies on quantum hardware and compare them with state-of-the-art classical vibrational structure algorithms for molecules with up to seven atoms.
1 Introduction
Within the Born–Oppenheimer approximation, a molecular wavefunction is factorized as a product of an electronic part, which is the solution of the electronic Schrödinger equation, and a vibro-rotational one, which is the solution of the nuclear Schrödinger equation in the potential energy surface (PES) generated by sampling the eigenvalues of the electronic Schrödinger equation for different geometries.The nuclear Schrödinger equation is usually solved in two steps, in analogy with its electronic counterpart. A single-particle basis (the basis functions are called, in this case, modals) is obtained either by the harmonic approximation applied to the PES or from a vibrational self-consistent field (VSCF)1–4 calculation. Vibrational anharmonic correlations are added a-posteriori with perturbative5,6 or variational approaches. The latter include Vibrational Configuration Interaction (VCI)7–10 and Vibrational Coupled Cluster (VCC)11,12 and deliver highly-accurate anharmonic energies. Unlike perturbation theories, the accuracy of VCI and VCC can be systematically improved, but their applicability is limited to small molecules with up to about 10 atoms due to their unfavorable scaling with system size. This unfavorable scaling can be tamed either by pruning the VCI basis limiting, for instance, the maximum degree of excitation, or with precontraction algorithms.13–15 Such simplifications make calculations feasible for systems with up to 15–20 atoms. Alternatively, the computational cost of VCI can be reduced with non-linear wavefunction parametrizations. This is the case, for example, of the vibrational Density Matrix Renormalization Group (vDMRG)16,17 which encodes the wavefunction as a matrix product state,18 or of VCC.11
The emerging development of quantum computers has refreshed the prospect of computing energies of large molecules by leveraging the exponentially-large multi-qubit Hilbert space. However, current quantum computers based on superconducting qubits technology have limited coherence times (≈100 μs) and sizable gate error rates (≈2 × 10−2 for a two-qubit gate),19,20 restricting the possible number of operations that can be executed to evolve a quantum state. Under these limitations, hybrid quantum-classical algorithms are the most promising route to calculate molecular energies on quantum hardware. In particular, the ground state energy of a general Hamiltonian can be obtained with quantum circuits of relatively low depth (i.e., a small number of operations) with the Variational Quantum Eigensolver (VQE).21–24 The VQE has already been applied in hardware calculation of the electronic ground state of small molecules25,26 and can also be extended to excited states.27,28
Despite the extensive work on the applications of VQE to the solution of the electronic Schrödinger equation, the extension to vibrational calculations has not yet been fully investigated. Molecular vibrations are described by Bose–Einstein statistics and, therefore, the modal basis must be mapped to the qubits by preserving such symmetry. Moreover, any many-body expansion of a L-mode PES, contains, in principle, up to L-body coupling terms.29,30 The potential energy operator of the nuclear Schrödinger equation is therefore much more complex than the pairwise Coulomb interaction of the electronic Schrödinger equation. McArdle et al.31 adapted the VQE to find the ground state of vibrational Hamiltonians of small molecules on a universal quantum computer based on the unitary extension of the VCC theory (UVCC). In particular, they represent vibrational levels with the so-called compact mapping (the problem of mapping bosonic states to qubits has also been discussed in details in a recent work32). Two key limitations hinder the application of the theory presented in ref. 31 to complex vibrational Hamiltonians. First, the algorithm can be applied only to vibrational ground states and, therefore, does not allow to access vibrational excitation energies that are key for vibrational spectroscopy. Second, it approximates the PES as power series of Cartesian-based normal modes, which relies on harmonic-oscillator eigenfunctions as basis functions. This is an important limitation in the case of strongly anharmonic molecules, whose PES is represented by highly non-compact Taylor expansions. For these systems, the VSCF modals will lead instead to more compact VCC and VCI expansions.
In the present paper, we design a general framework for the calculation of vibrational structures with a quantum algorithm. We introduce the qubit encoding of the vibrational levels based on the generalized second quantization representation11,33 of the nuclear Schrödinger equation that enables the potential to be expressed as a general n-mode expansion.30 We then discuss the parametrization of the vibrational wavefunction introducing a new quantum circuit Ansatz as a compact approximation of UVCC. We emphasize that, although UCC has mostly been applied in electronic-structure calculations34–37 and its extension to vibrational quantum computation has hardly been explored,31 its use for the solution of the vibronic problem is very promising. We discuss how vibrational excited states can be targeted with equation-of-motion (EOM)-based UVCC algorithms.27 Finally, we also discuss the scaling of the UVCC resources in terms of qubits and gate counts as a function of the molecular size and show the resources necessary to compute the vibrational structure of molecules with up to five atoms. The proposed framework offers us the possibility to estimate the hardware requirements that will allow to reach quantum advantage over classical vibrational-structure calculations using near-term quantum computers.
2 Theory
2.1 Second quantization theories for molecular vibrations
The real-space representation of the Watson Hamiltonian for the L modes of a molecular system can be written as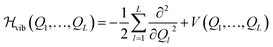 | (1) |
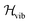 must be mapped to an operator that acts on the states of a given set of Nq qubits in order to calculate its eigenfunctions on quantum hardware. In electronic structure calculations, the mapping is achieved by expressing the non-relativistic electronic Hamiltonian in second quantization, i.e. by projecting it onto the complete set of antisymmetrized occupation number vectors (ONV) generated by a given (finite) set of orbitals. To encode the vibrational Hamiltonian of eqn (1) in a second quantization form defined in eqn (10), we expand the potential V(Q1, …, QL) with the n-body expansion,29,30 as follows:
must be mapped to an operator that acts on the states of a given set of Nq qubits in order to calculate its eigenfunctions on quantum hardware. In electronic structure calculations, the mapping is achieved by expressing the non-relativistic electronic Hamiltonian in second quantization, i.e. by projecting it onto the complete set of antisymmetrized occupation number vectors (ONV) generated by a given (finite) set of orbitals. To encode the vibrational Hamiltonian of eqn (1) in a second quantization form defined in eqn (10), we expand the potential V(Q1, …, QL) with the n-body expansion,29,30 as follows: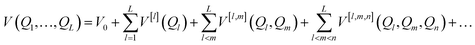 | (2) |
| V[l](Ql) = V(Qeq1, …, Qeql−1, Ql, …, QeqL). | (3) |
Similarly, the two-body potential V[l,m](Ql, Qm) represents the change in the exact PES upon a displacement along the l-th and m-th coordinates, i.e.
| V[l,m](Ql, Qm) = V(Qeq1, …, Ql, …, Qm, …, QeqL) − V[l](Ql) − V[m](Qm). | (4) |
A representation of eqn (1) that is suitable to encode on a quantum computer can be obtained with the so-called canonical quantization38 that maps the l-th normal coordinate Ql and its conjugate momentum Pl to a pair of bosonic creation and annihilation operators (a+l and al) defined as
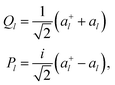 | (5) |
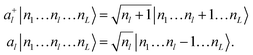 | (6) |
Each index of the ONV |n1…nL〉 is associated to a mode and nl is the degree of excitation of the l-th mode. Different vibrational-structure methods have been derived based on this canonical representation,43,44 including VCC,45–48 although it is not flexible enough to target strongly anharmonic systems. In this formalism the PES V(Q1, …, QL) is expressed as a power series to encode it in a second quantization format based on eqn (5). In addition, the operators of eqn (6) imply that the reference basis set for every mode l is composed by harmonic oscillator eigenfunctions. However, such a basis does not lead to a compact representation of vibrational wavefunctions for strongly anharmonic systems for which modals obtained, for instance, from VSCF1,49 are better suited. The choice of the modal basis may become critical, for instance, when studying high-energy X–H stretching (X being a generic nucleus different from H) modes that are strongly coupled with bending vibrations. Crittenden and co-workers50 highlighted that 10 basis functions are not sufficient to obtain converged VCI energies for C–H stretching modes based on the harmonic reference. Conversely, Bowman and co-workers51 demonstrated for the same system that converged VCI energies can be obtained with only 6 VSCF modals.
A more flexible second quantization form is the so-called n-mode representation introduced by Christiansen.52 Instead of labelling each basis function with a single integer, as in eqn (6), we expand each mode l into a basis of Nl modals (labelled as i1…iNl) which generates an ONV basis for that mode. Let us consider the following, general VCI expansion
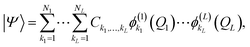 | (7) |
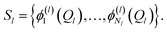 | (8) |
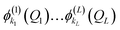 can be encoded as an ONV as
can be encoded as an ONV as| ϕk1(Q1)…ϕkL(QL) ≡ |01…1k1…0N1, 01…1k2…0N2, …, 01…1kL…0NL〉. | (9) |
The full ONV is then given by the expression in eqn (9) where different ONV subspaces are separated by a comma. For each ONV space, we sort the modals in decreasing order of energy. Each mode is described by one and only one basis function, therefore the occupation of each ONV subspace is one.
Based on the representation given in eqn (9), we introduce a pair of creation and annihilation operators per mode l and per basis function kl defined as:
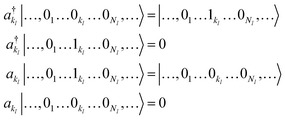 | (10) |
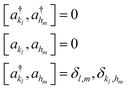 | (11) |
This formalism was introduced for VCC11 and later applied to the multi-configurational time-dependent Hartree method.33 The second quantization form of eqn (1) obtained by expressing the potential as in eqn (2) reads52
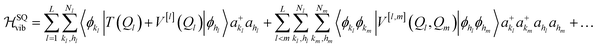 | (12) |
Unlike its electronic-structure counterpart, eqn (12) contains in general coupling terms higher than two-body. Therefore, the number of Pauli terms to be evaluated on the quantum computer scales as 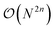 for a n-body truncation, where N is the overall number of modals. We highlight that any PES can be encoded in the n-mode second quantization format provided that the integrals of the PES over the modals are available. Eqn (12) is therefore not restricted to PESs expressed as a power series.
for a n-body truncation, where N is the overall number of modals. We highlight that any PES can be encoded in the n-mode second quantization format provided that the integrals of the PES over the modals are available. Eqn (12) is therefore not restricted to PESs expressed as a power series.
2.2 Wavefunction parametrization
The second quantization formalism introduced in the previous section allows one to express the VCI expansion in terms of ONVs constructed with modals that do not rely on the harmonic approximation. The encoding of such ONVs on a quantum computer is straightforward if based on a one-to-one correspondence between modals and qubits. This mapping extends the “direct mapping” of ref. 31 and 32 beyond harmonic reference basis sets. The Nl modals for a given mode l are represented by a Nl-qubit register. We sort the modals in decreasing order of energy. Therefore, the lowest-energy configuration is represented by the reference ONV state |01…1N1, 01…1N2, …, 01…1NL〉 and is obtained by applying an X gate on the first qubit of each mode register initialized in the vacuum state. The correlated wavefunction is obtained from this reference state by applying a set of excitation operators defined by a given wavefunction Ansatz. We note that a bosonic ONV can be represented with a smaller number of qubits by adopting the compact mapping proposed in the literature.31,32 However, the representation of the elementary raising and lowering operators within such mapping is more complex than in the direct one leading to an increase in the circuit depth and in the number of terms in the Hamiltonian. As we will highlight in the following, current hardware limitations impose short circuit depths because of the accumulation of gate errors, while the possibility of executing gates in parallel favours the use of more qubits. For this reason, in all cases discussed in this work we will adopt the direct mapping of the vibrational modes.In VQE-based electronic-structure quantum-computing two main strategies are available to prepare the wavefunction. The first is based on the CC method and, more precisely, on its unitary formulation (UCC). It provides an intuitive expansion of the wavefunction in terms of excitation operators controlled by an efficiently parametrized circuit.21,53–55 However, this circuit comprises a large number of 2-qubit gates (CNOT gates) and, hence, its practical use is limited by coherence time and the gate error rates. The second approach does not have a classical equivalent and is tailored to quantum hardware. A heuristic wavefunction Ansatz is built concatenating parametrized single-qubit rotations and entangling blocks.25,54 The number of parameters can be increased by repeating the same set of operations (but with independent parameters) d times (where d refers to the circuit depth) to reach the desired accuracy for the ground state energy.
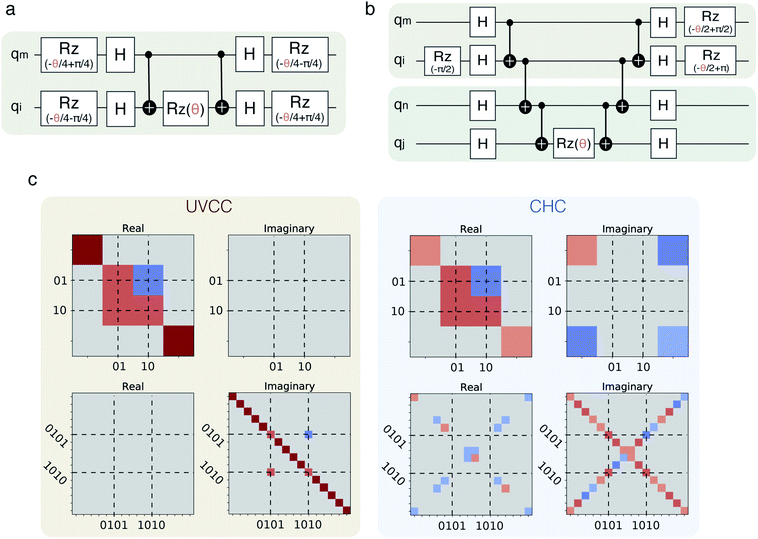
The same strategies can be followed for preparing vibrational wavefunctions. The UVCC circuit can be obtained from the unitary version of the VCC11,31Ansatz:
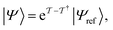 | (13) |
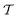 is the cluster operator (and
is the cluster operator (and 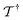 its adjoint) expressed here up to second order as
its adjoint) expressed here up to second order as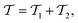 | (14) |
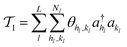 | (15) |
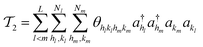 | (16) |
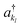 and akl (see eqn (10)) are mapped to the Pauli operators
and akl (see eqn (10)) are mapped to the Pauli operators 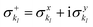 and
and 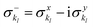 , respectively. In this way, the exponential operator of eqn (13) can be factorized with a Trotter expansion and expressed as a product of quantum gates. Compared to the fermion-to-qubit mappings used in electronic-structure calculations (where the antisymmetry of the wavefunction is encoded in the circuit by applying for instance the Jordan Wigner transformation56) the circuit depth for the implementation of the UVCC Ansatz is greatly reduced. It is interesting to note here that the gate representation of the
, respectively. In this way, the exponential operator of eqn (13) can be factorized with a Trotter expansion and expressed as a product of quantum gates. Compared to the fermion-to-qubit mappings used in electronic-structure calculations (where the antisymmetry of the wavefunction is encoded in the circuit by applying for instance the Jordan Wigner transformation56) the circuit depth for the implementation of the UVCC Ansatz is greatly reduced. It is interesting to note here that the gate representation of the 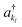 and akl operators is more complex in the previously mentioned compact mapping, in which the qubit representation of the n-th modal is obtained via the binary representation of n. Although Nl modals would be represented by log2(Nl) qubits, instead of Nl qubits as in the direct mapping, the representation of the
and akl operators is more complex in the previously mentioned compact mapping, in which the qubit representation of the n-th modal is obtained via the binary representation of n. Although Nl modals would be represented by log2(Nl) qubits, instead of Nl qubits as in the direct mapping, the representation of the 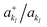 operators would require Nl elementary gates leading in general to deeper circuits for the conventional numbers of modals per mode.
operators would require Nl elementary gates leading in general to deeper circuits for the conventional numbers of modals per mode.
Among the heuristic circuits designed for electronic structure calculation,25,54 we consider here the SwapRZ Ansatz defined as
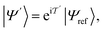 | (17) |
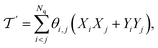 | (18) |
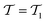 where single excitations are confined to the modal space of the same mode (see eqn (15)). Simultaneous excitations of two different modes (as those included in
where single excitations are confined to the modal space of the same mode (see eqn (15)). Simultaneous excitations of two different modes (as those included in 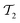 ) are not explicitly captured by the SwapRZ Ansatz with depth 1 and, therefore, we expect that deeper circuits are required to accurately represent the wavefunction.
) are not explicitly captured by the SwapRZ Ansatz with depth 1 and, therefore, we expect that deeper circuits are required to accurately represent the wavefunction.
Another strategy proposed in the context of electronic structure54 is to build the circuit from a layer of Ry and Rz rotations on each qubit followed by a block of CNOT gates entangling all qubits. We refer to the resulting circuit as RYRZ. Note that rotations around the Y axis of each qubit induce a change in both the overall modals occupation and the individual occupation of each mode.
To constrain the optimization to the correct symmetry subspace, both SwapRZ and RYRZ heuristic circuits must be combined to a modified Hamiltonian 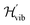 where a penalty function is added to increase the energy of the states with unphysical occupation,54
where a penalty function is added to increase the energy of the states with unphysical occupation,54
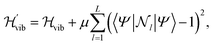 | (19) |
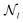 for mode l is defined as
for mode l is defined as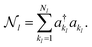 | (20) |
In the next section we will show that the optimization of the wavefunction is much more efficient with the UVCC Ansatz than with the heuristic ones. Therefore, it is desirable to derive a quantum circuit inspired by UVCC that involves a smaller number of CNOT gates, and hence is more suited for near-term quantum calculations.
Given the current coherence time and gate error rates, it is challenging to include double excitations within the UVCC circuit. In fact, each element of 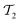 can be decomposed as:
can be decomposed as:
| σ+iσ+jσ−kσ−l − c.c. = 2i(XiYjXkXl + YiXjXkXl + YiYjXkYl + YiYjYkXl − XiXjXkYl − XiXjYkXl − XiYjYkYl − YiXjYkYl). | (21) |
Therefore, the corresponding quantum circuit obtained after exponentiation of the operator given in eqn (21) and its Trotterization contains 8 × 6 CNOT gates per excitation.
Combining the considerations above, we propose to approximate the UVCCSD circuit with a more compact heuristic Ansatz that we name Compact Heuristic for Chemistry (CHC). This circuit exploits the fact that the relations
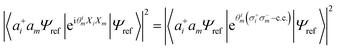 | (22) |
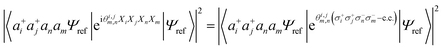 | (23) |
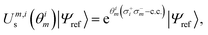 | (24) |
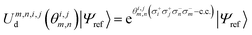 | (25) |
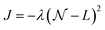 where λ is a variational parameter,
where λ is a variational parameter,  is the number operator, N is the total number of qubits and L the number of modes; this will project out states with occupation number ≠ L. The scaling and performance of the CHC circuit are presented in Section 3.1.
is the number operator, N is the total number of qubits and L the number of modes; this will project out states with occupation number ≠ L. The scaling and performance of the CHC circuit are presented in Section 3.1.
2.3 Extension to excited states
The calculation of the ground state is not sufficient for most vibrational-structure calculations for which vibrational excitation energies must also be considered. This is, for instance, the case of the simulation of vibrational spectra where absorption peaks are located at transition frequencies. Several quantum algorithms have recently been developed for the calculation of electronically excited states.27,57–65 In particular, the quantum EOM (qEOM)27 and the Quantum Subspace Expansion (QSE)61 are straightforward extensions of the VQE algorithm as they do not require any modification of the quantum circuit for the ground state wavefunction, but rather the measurement of additional excitation operators expectation values. Their application in the calculation of the vibrational excited states is relatively simple since the corresponding excitation operators can be written as a product of bosonic raising and lowering operators and directly mapped in the qubit space. Because the qEOM algorithm is free from any approximation (whereas the QSE relies on the Tamm–Dancoff approximation) and directly leads to the transition energies (rather than absolute energies which are not size intensive),27 it becomes the method of choice for the calculation of the vibrational excited states. In this work, we write the excitation operators in terms of the second quantized operators defined in eqn (10) and (11) and straightforwardly map them to tensor products of Pauli operators. Note that the accuracy of qEOM can systematically be improved by increasing the maximum order of the excitation operators up to L in the case of a L-mode system. The inclusion of high order excitations (>2) may become important for PESs that require the inclusion of three- and higher-order terms in the n-body expansion of eqn (2). This increases the size of the pseudo-eigenvalue problem and, therefore, the number of measurements to be performed on the quantum computer.3 Results
As an example system, we choose the carbon dioxide molecule, which is well studied with traditional approaches.66–68 We also estimate the quantum computing resources needed for the simulation of two larger molecules, namely formaldehyde (H2CO) and formic acid (HCOOC).3.1 Ground state calculations with state-of-the-art approaches
We study the UVCC, SwapRZ and RYRZ wavefunction approaches on the PES of CO2 defined by the bending and the symmetric stretching modes. We describe the system Hamiltonian in second quantization as in eqn (12) with two modals per mode where the reference modal basis (see eqn (8)) is obtained as eigenfunctions of the one-body Hamiltonian| (T(Ql) + V[l](Ql))ϕkl(Ql) = εklϕkl(Ql) (l = 1, 2). | (26) |
One could include vibrational correlations in eqn (26) by introducing the averaged two- and higher-order couplings with the other modes in the potential operator, as done in VSCF.49 The resulting set of modals would lead to more compact VCI and VCC expansions than those based on the modals from eqn (26). However, modals obtained from eqn (26) are sufficient to assess the quality of our algorithm and demonstrate that bases different from the harmonic ones can be used. The one-mode basis is then obtained by solving eqn (26), expressing every single-particle basis function as a linear combination of 50 distributed Gaussian functions. We calculate the one- and two-body integrals in the resulting modal basis and express the Hamiltonian as in eqn (12). We optimize the ground-state equilibrium geometry of CO2 using density functional theory with the B3LYP exchange–correlation functional69 and the cc-pVTZ70 basis set. We approximate the PES with a quartic force field calculated by semi-numerical differentiation of the analytical Hessian as implemented in Gaussian.71
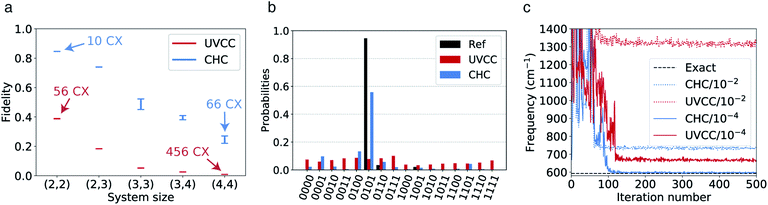
All VQE calculations are run with Qiskit.72 In the calculations using the SwapRZ and RYRZ circuits, we set the penalty term μ in eqn (19) to 105 (we find empirically that values below this threshold do not proscribe the convergence to the vacuum state). In all VQE simulations, we apply the exact unitary matrix representation of the circuit on the reference ONV state (see above) without taking into account sampling, decoherence and gate noise. The VQE parameters are all initialized to zero. We use the constrained optimization by linear approximation (COBYLA)73 optimizer for which no gradient calculation is needed. The results of the simulations are reported in Fig. 2a.
 | ||
| Fig. 2 (a) Convergence of the VQE algorithm for the calculation of the vibrational ground state of CO2 in the 2 modes and 2 modals per node representation of the PES. A penalty term (eqn (19)) is added to the Hamiltonian in order to enforce the conservation of one modal per mode. (b) Same as in (a) but without the addition of the penalty term. | ||
We note that the convergence for both the SwapRZ and the RYRZ circuits is generally slower than with UVCCSD. Convergence is reached after 47 iterations for UVCCSD and only after 8000 iterations for SwapRZ, and after more than 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 for RYRZ. The slow convergence observed with both heuristic approaches is most likely due to the addition of the penalty term in the Hamiltonian (see eqn (19)), which constraints to the optimization. To verify this conjecture and compare the different approaches in an unbiased way, we repeated, when possible, the VQE optimization for the heuristic Ansatz without the penalty term. In the case of the RYRZ circuit, this operation was not successful as the Ansatz, not conserving the overall modal occupation, is converging towards the vacuum state. Conversely, even if the SwapRZ Ansatz also does not ensure the occupation of a single modal per mode, in this case the energy gap between two modals is large enough to prevent the algorithm to converge towards states with the incorrect occupation numbers such as, for instance, the state |11, 00〉. Hence, we performed an optimization with the SwapRZ Ansatz and the original unmodified Hamiltonian to assess the effect of the addition of the penalty term, and compare the results with the UVCC approach (see Fig. 2). To this end we used VQE circuits of depths 1, 2 and 3. The corresponding number of entangling gates is 56, 24, 48, and 72 for the UVCCSD, SwapRZ1, SwapRZ2, and SwapRZ3 Ansatz, which correspond to a number of variational parameters of 3, 14, 24, and 34, respectively. As in the previous case, all parameters are initialized to zero and the optimization is performed with the COBYLA algorithm. The results in Fig. 2b confirm that the penalty term in eqn (19) was the main reason for the slow convergence. Nevertheless, even if the optimization is faster when removing the penalty term, UVCCSD still outperforms SwapRZ for all depths. This result is expected because of the larger number of variational parameters appearing in the heuristic circuits. Moreover, it was pointed out that Barren plateaus may further slow down the convergence of the heuristic Ansatz with the increase of the dimensionality of the system.74,75 However, there is still no clear evidence that Barren plateaus will play an important role when using the UVCC Ansatz, since physically motivated reductions of the number of variational parameters can be applied, at the cost of reducing the accuracy of the calculation.54,55,76–79 Additionally, the convergence rate when working with the UVCC Ansatz for larger, strongly anharmonic molecules may be improved by initializing the VQE parameters with a more accurate guess. As already suggested for the electronic-structure case, such a guess may be constructed from the VMP2 wavefunction.5
000 for RYRZ. The slow convergence observed with both heuristic approaches is most likely due to the addition of the penalty term in the Hamiltonian (see eqn (19)), which constraints to the optimization. To verify this conjecture and compare the different approaches in an unbiased way, we repeated, when possible, the VQE optimization for the heuristic Ansatz without the penalty term. In the case of the RYRZ circuit, this operation was not successful as the Ansatz, not conserving the overall modal occupation, is converging towards the vacuum state. Conversely, even if the SwapRZ Ansatz also does not ensure the occupation of a single modal per mode, in this case the energy gap between two modals is large enough to prevent the algorithm to converge towards states with the incorrect occupation numbers such as, for instance, the state |11, 00〉. Hence, we performed an optimization with the SwapRZ Ansatz and the original unmodified Hamiltonian to assess the effect of the addition of the penalty term, and compare the results with the UVCC approach (see Fig. 2). To this end we used VQE circuits of depths 1, 2 and 3. The corresponding number of entangling gates is 56, 24, 48, and 72 for the UVCCSD, SwapRZ1, SwapRZ2, and SwapRZ3 Ansatz, which correspond to a number of variational parameters of 3, 14, 24, and 34, respectively. As in the previous case, all parameters are initialized to zero and the optimization is performed with the COBYLA algorithm. The results in Fig. 2b confirm that the penalty term in eqn (19) was the main reason for the slow convergence. Nevertheless, even if the optimization is faster when removing the penalty term, UVCCSD still outperforms SwapRZ for all depths. This result is expected because of the larger number of variational parameters appearing in the heuristic circuits. Moreover, it was pointed out that Barren plateaus may further slow down the convergence of the heuristic Ansatz with the increase of the dimensionality of the system.74,75 However, there is still no clear evidence that Barren plateaus will play an important role when using the UVCC Ansatz, since physically motivated reductions of the number of variational parameters can be applied, at the cost of reducing the accuracy of the calculation.54,55,76–79 Additionally, the convergence rate when working with the UVCC Ansatz for larger, strongly anharmonic molecules may be improved by initializing the VQE parameters with a more accurate guess. As already suggested for the electronic-structure case, such a guess may be constructed from the VMP2 wavefunction.5
These observations suggest that an efficient wavefunction Ansatz must be physically motivated and be parametrized by a small number of variational parameters.
3.2 Performance of the CHC Ansatz
To reduce the circuit depth without sacrificing the accuracy, we approximate the UVCC wavefunction with the CHC Ansatz (eqn (24) and (25)). The scaling of UVCC and CHC in terms of number of CNOT gates and number of parameters is shown on Table 1 for three molecules: CO2, H2CO and HCOOC. For all these cases, we constructed the reference modal basis as described for CO2, i.e. from the eigenfunctions of the one-body Hamiltonian of eqn (26), based on geometries optimized with B3LYP/cc-pVTZ and calculating the anharmonic quartic force field by including all third-order and the semi-diagonal fourth-order terms.| Molecule | Modes | Modals | CX UVCC | CX CHC | Parameters |
|---|---|---|---|---|---|
| CO2 | 4 | 2 | 304 | 44 | 10 |
| 4 | 2640 | 348 | 66 | ||
| 6 | 7280 | 940 | 170 | ||
| 8 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 224 224 |
1820 | 322 | ||
| 10 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 472 472 |
2988 | 522 | ||
| H2CO | 6 | 2 | 744 | 102 | 21 |
| 4 | 6552 | 846 | 153 | ||
| 6 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 120 120 |
2310 | 405 | ||
| 8 | 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 448 448 |
4494 | 777 | ||
| 10 | 58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 536 536 |
7398 | 1269 | ||
| HCOOH | 9 | 2 | 1764 | 234 | 45 |
| 4 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 660 660 |
1998 | 351 | ||
| 6 | 43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 380 380 |
5490 | 945 | ||
| 8 | 84![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 924 924 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 710 710 |
1827 | ||
| 10 | 140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 292 292 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 658 658 |
2997 |
We study the CHC circuit for CO2 with different number of modes and modals per mode (see Fig. 3). The results are of reasonable accuracy, with deviations <15 cm−1 compared to the exact diagonalization energies. As expected, CHC works best with two modals per mode since the entangling blocks are always applied to a state of the subspace with the correct symmetry, and therefore it does not create configurations with the wrong number of particles. Errors increase with the number of modals per mode.
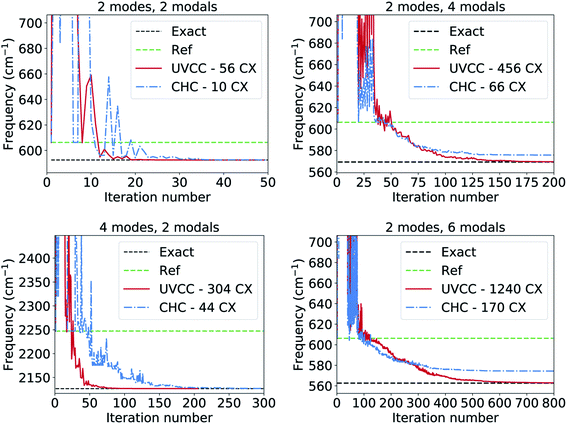 | ||
| Fig. 3 VQE convergence for CO2 with different number of modes and modals based on the UVCC and CHC approaches including single and double excitations. | ||
The CHC approach appears as a promising approximation for the calculation of the vibrational ground state in near-term, noisy quantum computers, offering a favourable balance between accuracy (in the sense of state representability) and sensitivity to noise (e.g., gate errors and qubit decoherence). However, the accuracy decreases with the number of excitations included in the CHC Ansatz. In particular, when the excitations are truncated to second order the error increases as 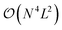 (where N is the number of modals per mode and L the number of modes). Therefore, when scaling to larger systems the error can be controlled by treating parts of the excitations exactly with UVCC and parts with the approximated CHC Ansatz. Moreover, the number of excitations can be reduced using traditional approaches for the selection of the relevant subset.54,55,76–79
(where N is the number of modals per mode and L the number of modes). Therefore, when scaling to larger systems the error can be controlled by treating parts of the excitations exactly with UVCC and parts with the approximated CHC Ansatz. Moreover, the number of excitations can be reduced using traditional approaches for the selection of the relevant subset.54,55,76–79
3.3 Quantum computation of vibrational structures on existing hardware
In the presence of typical hardware noise, the lower accuracy observed for the CHC Ansatz is balanced by the advantage of an implementation that requires a shorter circuit depth. To study this effect, we use both UVCC and CHC circuits in simulations with realistic noise models and in hardware calculations with the 20-qubit processor ibmq_almaden.In the first case, we fix the number of modes to two and progressively increase the number of modals per mode from two to four. The gate angles, {θi}, defining the circuit gates are initiated randomly and restricted within the range −0.2 ≤ θi ≤ 0.2 (for small angles the reference configuration remains largely dominant. Hence, CHC is expected to lead to a reasonable approximation of UVCC for the same set of variational parameters). The noise model includes only depolarization errors for single- and two-qubit gates, for which the corresponding error rates are based on the average gate depolarization error associated to all qubits in the ibmq_almaden 20-qubit device. These are 7 × 10−4, 1.4 × 10−3 and 2.2 × 10−2 for U2, U3 and CNOT gates, respectively. The density matrix, ρ2, obtained from the evolution with noise is used to compute the fidelity, 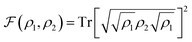 with respect to the density matrix ρ1 of the pure state obtained from the exact simulation with the UVCC Ansatz (note that for both CHC and UVCC, the exact UVCC state is taken as reference as this remains our target in the absence as well as in the presence of the noise). This process is repeated 10 times for different sets of parameters (gate angles). The fidelities obtained with both UVCC and CHC are shown as a function of the system size in Fig. 4a. The corresponding number of CNOT gates is also given in Fig. 4a for two modes and two modals per mode, and for two modes and four modals per mode. These results suggest that in the presence of noise a better accuracy is reached with the CHC Ansatz rather than with the UVCC Ansatz. We repeated the experiment with a quantum processor (ibmq_almaden, 20 qubits) and a system size corresponding to two modes and two modals per mode (for a total of 4 qubits). Fig. 4b shows the histogram of the final states probability distributions corresponding to a single trial (one set of gate parameters) sampled with 8000 measurements. Finally, we performed a VQE optimization to determine the vibrational ground state of CO2 with both Ansatz and using the same error model and error rates described above. In this case, the optimization is performed with the Simultaneous Perturbation Stochastic Approximation (SPSA) algorithm.80 The convergence profiles in presence of noise are shown in Fig. 4c in dotted lines. In both cases, the converged energy values are far from the true ground state energy (dashed line at 592.5 cm−1). However, when repeating the same calculations with smaller error rates (2.2 × 10−4) we achieve a better convergence in both cases (also shown in Fig. 4c in full lines), approaching the exact value with CHC. These results confirm that, with the present level of hardware noise, compact heuristic circuits such as the ones obtained with the CHC Ansatz outperform the original UVCC Ansatz.
with respect to the density matrix ρ1 of the pure state obtained from the exact simulation with the UVCC Ansatz (note that for both CHC and UVCC, the exact UVCC state is taken as reference as this remains our target in the absence as well as in the presence of the noise). This process is repeated 10 times for different sets of parameters (gate angles). The fidelities obtained with both UVCC and CHC are shown as a function of the system size in Fig. 4a. The corresponding number of CNOT gates is also given in Fig. 4a for two modes and two modals per mode, and for two modes and four modals per mode. These results suggest that in the presence of noise a better accuracy is reached with the CHC Ansatz rather than with the UVCC Ansatz. We repeated the experiment with a quantum processor (ibmq_almaden, 20 qubits) and a system size corresponding to two modes and two modals per mode (for a total of 4 qubits). Fig. 4b shows the histogram of the final states probability distributions corresponding to a single trial (one set of gate parameters) sampled with 8000 measurements. Finally, we performed a VQE optimization to determine the vibrational ground state of CO2 with both Ansatz and using the same error model and error rates described above. In this case, the optimization is performed with the Simultaneous Perturbation Stochastic Approximation (SPSA) algorithm.80 The convergence profiles in presence of noise are shown in Fig. 4c in dotted lines. In both cases, the converged energy values are far from the true ground state energy (dashed line at 592.5 cm−1). However, when repeating the same calculations with smaller error rates (2.2 × 10−4) we achieve a better convergence in both cases (also shown in Fig. 4c in full lines), approaching the exact value with CHC. These results confirm that, with the present level of hardware noise, compact heuristic circuits such as the ones obtained with the CHC Ansatz outperform the original UVCC Ansatz.
3.4 Quantum computation of the vibrational excited states of CO2
We calculate the vibrational excitation energies of the CO2 molecule in the following sub-spaces: (A) the 2 bending modes with 2 modals per mode; (B) the 2 bending modes with 4 modals per mode and (C) all 4 modes (i.e., the 2 bending, the symmetric stretching and the antisymmetric stretching modes) with 2 modals per mode. For all three cases, we limit the qEOM operators to 1- and 2-body excitation operators to restrict the number of extra measurements. The ground state is approximated by running a VQE calculation with both UVCC and CHC. The results of these (noise-free) simulations are presented in Table 2. The reference values are obtained from the exact diagonalization of the system Hamiltonian.| Modes | Modals | Reference | UVCC | CHC | |
|---|---|---|---|---|---|
| A | 2 | 2 | 574.441 | 574.450 | 574.441 |
| 1438.778 | 1438.789 | 1438.789 | |||
| 2063.261 | 2063.255 | 2063.269 | |||
| B | 2 | 4 | 496.697 | 496.6680 | 479.2900 |
| 1073.420 | 1073.418 | 1063.520 | |||
| 1460.074 | 1460.084 | 1452.494 | |||
| 1642.996 | 1642.978 | 1634.296 | |||
| 2024.187 | 2024.123 | 2016.191 | |||
| 2498.060 | 2498.037 | 2492.031 | |||
| C | 4 | 2 | 534.908 | 534.682 | 534.774 |
| 559.330 | 559.193 | 559.274 | |||
| 1098.527 | 1121.205 | 1121.298 | |||
| 1267.081 | 1267.910 | 1268.086 | |||
| 1855.895 | 1874.657 | 1874.732 | |||
| 1880.816 | 1901.110 | 1901.130 |
In case (A) all excitation energies are found with an accuracy <1 cm−1. For (B), the accuracy is lower for CHC compared to UVCC. This is expected since for a large number of modals the accuracy of CHC ground state calculations decreases. Finally, case (C) shows that higher order excitations need to be included in 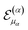 in order to reach an accuracy of about 1 cm−1 for the highest excitation energies with both wavefunction Ansatz.
in order to reach an accuracy of about 1 cm−1 for the highest excitation energies with both wavefunction Ansatz.
4 Discussion
The proposed quantum algorithms for the calculation of the vibrational frequencies support PES representations and modals routinely employed in state-of-the-art traditional calculations. This enables a fair comparison of the scaling of the classical and quantum vibrational structure algorithms that provides an estimate of the resources required to reach a quantum advantage in vibrational-structure calculations. As mentioned in the introduction, large-scale vibrational structure calculations are nowadays possible either with efficient VCI algorithms10,13–15,81 or with non-linear wavefunction parametrizations, as is done in vDMRG16 and VCC.11,12,45,46 The latter algorithm is the direct classical counterpart of our UVCC-based quantum algorithm and will be our reference for comparing the scaling with its quantum counterpart.The scaling of VCC depends on the order of the highest degree of excitation that is included in the 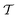 operator (eqn (14)). For instance, VCC[2pt3] comprises all two-mode excitations and treats triple excitations perturbatively and can be applied, in its straightforward formulation, to molecules with up to seven atoms, such as ethylene oxide82 including six modals for each vibrational mode. The simulation of such molecules on quantum hardware would require 90 qubits. The corresponding circuit that includes single and double excitations, and approximates triple excitations with the CHC Ansatz (which we denote as UVCCSD(T)) would contain about 106 CNOT gates. By approximating also the single and double excitations with CHC, the number of 2-qubit gates drops to about 104. Currently, the state-of-the-art quantum hardware comprises about 50 qubits and has a coherence time supporting circuits with no more than 102 CNOT gates. The 2-qubit error rate of about 10−2 is currently the limiting factor for running such circuits in the state-of-the-art hardware. By improving the 2-qubit gate fidelity and according to the estimated evolution of the quantum volume in superconducting quantum computers,83 molecules of the dimensions of ethylene oxide will become accessible using the proposed algorithm within the next generation of quantum hardware.
operator (eqn (14)). For instance, VCC[2pt3] comprises all two-mode excitations and treats triple excitations perturbatively and can be applied, in its straightforward formulation, to molecules with up to seven atoms, such as ethylene oxide82 including six modals for each vibrational mode. The simulation of such molecules on quantum hardware would require 90 qubits. The corresponding circuit that includes single and double excitations, and approximates triple excitations with the CHC Ansatz (which we denote as UVCCSD(T)) would contain about 106 CNOT gates. By approximating also the single and double excitations with CHC, the number of 2-qubit gates drops to about 104. Currently, the state-of-the-art quantum hardware comprises about 50 qubits and has a coherence time supporting circuits with no more than 102 CNOT gates. The 2-qubit error rate of about 10−2 is currently the limiting factor for running such circuits in the state-of-the-art hardware. By improving the 2-qubit gate fidelity and according to the estimated evolution of the quantum volume in superconducting quantum computers,83 molecules of the dimensions of ethylene oxide will become accessible using the proposed algorithm within the next generation of quantum hardware.
Molecules with up to seven atoms and described by a maximum of four-mode excitations can be studied with VCC by adopting a tensor-factorized representation of the amplitudes.84,85 The inclusion of three- and four-body coupling terms in the potential and in the VCC wavefunction leaves the number of qubits required unchanged. However, it also induces a raise in both the circuit depth and the number of measurements i.e., number of terms in the Hamiltonian. For the electronic Hamiltonian, Motta and co-workers showed86 that tensor factorizations can be used to reduce the number of measurements and circuit depth for fermionic systems. We expect that the same holds true also for the vibrational case, and we will consider such extension in future works.
The computational cost of VCC depends also on the choice of the coordinates used to describe the Hamiltonian. It is known that for particular choices, such as local modes87 or VSCF-optimized coordinates, the size of the off-diagonal anharmonic couplings can be significantly reduced. This procedure has been already exploited to speed up traditional VCC calculations88 including only excitations between modes localized on the same portion of the molecules. This simplification has made VCC calculation feasible for systems as large as the water hexamer.88 Our algorithm supports any choice of the reference coordinate system. In the same way, the UVCC circuit can be adapted to a local mode representation by allowing only gates representing excitations for modes localized on nearby portions of the molecule. For instance, in water clusters15 one could apply the UVCC circuit for excitations localized on one water molecule and include an approximated treatment of inter-fragment correlations with CHC.
5 Conclusions
We designed and compared different quantum computing strategies to calculate the vibrational structure of molecular systems amenable to near-term quantum computers. We represented the vibrational wavefunction and PES in the n-mode-based Fock space11,33 that supports an arbitrary one-body reference basis and PES expressed as a generic many-body expansion. This enabled us to overcome the limitations of recent algorithms31,32 that rely on a harmonic-based reference and are, therefore, not flexible enough for strongly anharmonic systems. We compared state-of-the-art circuits to prepare the wavefunction of a two-dimensional Hamiltonian modelling the nuclear dynamics of CO2 and introduced the Compact Heuristic circuit for Chemistry (CHC). On the one hand, the Unitary Vibrational Coupled Cluster (UVCC) delivers the most accurate vibrational energies, but at the price of very deep circuits that are difficult to implement on currently available quantum hardware already for three-atom molecules. On the other hand, heuristic circuits provide less accurate vibrational energies, while being shallower. In this work, we showed how CHC represents a good compromise, combining the advantages of both UVCC and heuristic wavefunction approaches. However, the CHC wavefunction does not fulfill the symmetries of the vibrational Hamiltonian. Therefore one first needs to project it onto the correct symmetry subspace before evaluating the vibrational energy. This effect is only minor for the systems studied here, but we expect it becomes larger for strongly anharmonic molecules. In those cases, a modal basis obtained from a VSCF calculation can significantly improve the accuracy. A second limitation of our algorithm is that each modal is mapped to a different qubit. Therefore, a large portion of the qubit Hilbert space does not correspond to a physically acceptable state. Occupation number vectors based on alternative mappings, such as the ones introduced in ref. 32, produce more compact representations of the vibrational states. However, the reduction in the number of qubits comes at the cost of an increase in the circuit depth for the representation of the wavefunction. Heuristic circuits inspired by the CHC strategy, but adapted to these more compact mappings, could enable the calculation of vibrational energies for molecules with more than three atoms on a state-of-the-art quantum computer. Finally, we extended the quantum Equation Of Motion (qEOM)27 approach to calculate vibrational excitation energies and applied it to the CO2 molecule.This work also sets the fundamentals for the quantum computation of the ground-state energy of interacting fermions and bosons, such as polaronic89 or quantum optics Hamiltonians.90 In the quantum-chemistry context, this is the case of the pre-Born–Oppenheimer molecular Hamiltonian91,92 that has been studied so far with the quantum phase estimation algorithm.93 Moreover, the algorithm can be extended to the time domain (e.g., using the time-dependent Schrödinger formalism of ref. 94) to address quantum dynamics.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by ETH Zürich through the ETH Fellowship No. FEL-49 18-1. The authors acknowledge financial support from the Swiss National Science Foundation (SNF) through the grant No. 200021-179312. IBM, IBM Quantum, Qiskit are trademarks of International Business Machines Corporation, registered in many jurisdictions worldwide. Other product or service names may be trademarks or service marks of IBM or other companies.References
- J. M. Bowman, Self-consistent field energies and wavefunctions for coupled oscillators, J. Chem. Phys., 1978, 68, 608–610 CrossRef CAS.
- G. D. Carney, L. L. Sprandel and C. W. Kern, Variational Approaches to Vibration-Rotation Spectroscopy for Polyatomic Molecules, Adv. Chem. Phys., 1978, 37, 305–379 CAS.
- R. Gerber and M. A. Ratner, A semiclassical self-consistent field (SC SCF) approximation for eigenvalues of coupled-vibration systems, Chem. Phys. Lett., 1979, 68, 195–198 CrossRef CAS.
- T. K. Roy and R. B. Gerber, Vibrational self-consistent field calculations for spectroscopy of biological molecules: new algorithmic developments and applications, Phys. Chem. Chem. Phys., 2013, 15, 9468–9492 RSC.
- O. Christiansen, Møller–Plesset perturbation theory for vibrational wave functions, J. Chem. Phys., 2003, 119, 5773–5781 CrossRef CAS.
- V. Barone, Anharmonic vibrational properties by a fully automated second-order perturbative approach, J. Chem. Phys., 2005, 122, 014108 CrossRef PubMed.
- J. M. Bowman, K. Christoffel and F. Tobin, Application of SCF-CI theory to vibrational motion in polyatomic molecules, J. Phys. Chem., 1979, 83, 905–912 CrossRef CAS.
- T. C. Thompson and D. G. Truhlar, SCF CI calculations for vibrational eigenvalues and wavefunctions of systems exhibiting Fermi resonance, Chem. Phys. Lett., 1980, 75, 87–90 CrossRef CAS.
- K. M. Christoffel and J. M. Bowman, Investigations of self-consistent field, scf ci and virtual stateconfiguration interaction vibrational energies for a model three-mode system, Chem. Phys. Lett., 1982, 85, 220–224 CrossRef CAS.
- M. Neff and G. Rauhut, Toward large scale vibrational configuration interaction calculations, J. Chem. Phys., 2009, 131, 124129 CrossRef PubMed.
- O. Christiansen, Vibrational coupled cluster theory, J. Chem. Phys., 2004, 120, 2149–2159 CrossRef CAS PubMed.
- P. Seidler and O. Christiansen, Automatic derivation and evaluation of vibrational coupled cluster theory equations, J. Chem. Phys., 2009, 131, 234109 CrossRef PubMed.
- D. Oschetzki and G. Rauhut, Pushing the limits in accurate vibrational structure calculations: anharmonic frequencies of lithium fluoride clusters (LiF)n, n = 2–10, Phys. Chem. Chem. Phys., 2014, 16, 16426–16435 RSC.
- P. S. Thomas, T. Carrington, J. Agarwal and H. F. Schaefer, Using an iterative eigensolver and intertwined rank reduction to compute vibrational spectra of molecules with more than a dozen atoms: uracil and naphthalene, J. Chem. Phys., 2018, 149, 064108 CrossRef PubMed.
- Q. Yu and J. M. Bowman, Classical, Thermostated Ring Polymer, and Quantum VSCF/VCI Calculations of IR Spectra of H7O3+ and H9O4+ (Eigen) and Comparison with Experiment, J. Phys. Chem. A, 2019, 123, 1399–1409 CrossRef CAS PubMed.
- A. Baiardi, C. J. Stein, V. Barone and M. Reiher, Vibrational Density Matrix Renormalization Group, J. Chem. Theory Comput., 2017, 13, 3764–3777 CrossRef CAS PubMed.
- A. Baiardi, C. J. Stein, V. Barone and M. Reiher, Optimization of highly excited matrix product states with an application to vibrational spectroscopy, J. Chem. Phys., 2019, 150, 094113 CrossRef PubMed.
- A. Baiardi and M. Reiher, The density matrix renormalization group in chemistry and molecular physics: recent developments and new challenges, J. Chem. Phys., 2020, 152, 040903 CrossRef PubMed.
- IBM Quantum Experience, 2020, https://quantum-computing.ibm.com/.
- Rigetti Computing, 2020, https://rigetti.com/.
- A. Peruzzo, J. McClean, P. Shadbolt, M.-H. Yung, X.-Q. Zhou, P. J. Love, A. Aspuru-Guzik and J. L. O'Brien, A variational eigenvalue solver on a photonic quantum processor, Nat. Commun., 2014, 5, 4213 CrossRef CAS PubMed.
- M.-H. Yung, J. Casanova, A. Mezzacapo, J. Mcclean, L. Lamata, A. Aspuru-Guzik and E. Solano, From transistor to trapped-ion computers for quantum chemistry, Sci. Rep., 2014, 4, 3589 CrossRef PubMed.
- J. R. McClean, J. Romero, R. Babbush and A. Aspuru-Guzik, The theory of variational hybrid quantum-classical algorithms, New J. Phys., 2016, 18, 023023 CrossRef.
- D. Wang, O. Higgott and S. Brierley, Accelerated variational quantum eigensolver, Phys. Rev. Lett., 2019, 122, 140504 CrossRef CAS PubMed.
- A. Kandala, A. Mezzacapo, K. Temme, M. Takita, M. Brink, J. M. Chow and J. M. Gambetta, Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets, Nature, 2017, 549, 242 CrossRef CAS PubMed.
- Y. Nam, J.-S. Chen, N. C. Pisenti, K. Wright, C. Delaney, D. Maslov, K. R. Brown, S. Allen, J. M. Amini, J. Apisdorf, K. M. Beck, A. Blinov, V. Chaplin, M. Chmielewski, C. Collins, S. Debnath, A. M. Ducore, K. M. Hudek, M. Keesan, S. M. Kreikemeier, J. Mizrahi, P. Solomon, M. Williams, J. David Wong-Campos, C. Monroe and J. Kim, Ground-state energy estimation of the water molecule on a trapped ion quantum computer, npj Quantum Inf., 2020, 6, 33 CrossRef.
- P. J. Ollitrault, A. Kandala, C.-F. Chen, P. K. Barkoutsos, A. Mezzacapo, M. Pistoia, S. Sheldon, S. Woerner, J. Gambetta and I. Tavernelli, Quantum equation of motion for computing molecular excitation energies on a noisy quantum processor, arXiv preprint arXiv:1910.12890, 2019.
- J. I. Colless, V. V. Ramasesh, D. Dahlen, M. S. Blok, M. Kimchi-Schwartz, J. McClean, J. Carter, W. De Jong and I. Siddiqi, Computation of molecular spectra on a quantum processor with an error-resilient algorithm, Phys. Rev. X, 2018, 8, 011021 CAS.
- G. M. Chaban, J. O. Jung and R. B. Gerber, Ab initio calculation of anharmonic vibrational states of polyatomic systems: electronic structure combined with vibrational self-consistent field, J. Chem. Phys., 1999, 111, 1823–1829 CrossRef CAS.
- J. Kongsted and O. Christiansen, Automatic generation of force fields and property surfaces for use in variational vibrational calculations of anharmonic vibrational energies and zero-point vibrational averaged properties, J. Chem. Phys., 2006, 125, 124108 CrossRef PubMed.
- S. McArdle, A. Mayorov, X. Shan, S. Benjamin and X. Yuan, Digital quantum simulation of molecular vibrations, Chem. Sci., 2019, 10, 5725–5735 RSC.
- N. P. Sawaya, T. Menke, T. H. Kyaw, S. Johri, A. Aspuru-Guzik and G. G. Guerreschi, Resource-efficient digital quantum simulation of d-level systems for photonic, vibrational, and spin-s Hamiltonians, arXiv preprint arXiv:1909.12847, 2019.
- H. Wang and M. Thoss, Numerically exact quantum dynamics for indistinguishable particles: the multilayer multiconfiguration time-dependent Hartree theory in second quantization representation, J. Chem. Phys., 2009, 131, 24114 CrossRef PubMed.
- A. G. Taube and R. J. Bartlett, New perspectives on unitary coupled-cluster theory, Int. J. Quantum Chem., 2006, 106, 3393–3401 CrossRef CAS.
- R. J. Bartlett and M. Musiał, Coupled-cluster theory in quantum chemistry, Rev. Mod. Phys., 2007, 79, 291 CrossRef CAS.
- J. Lee, W. J. Huggins, M. Head-Gordon and K. B. Whaley, Generalized Unitary Coupled Cluster Wave functions for Quantum Computation, J. Chem. Theory Comput., 2019, 15, 311–324 CrossRef CAS PubMed.
- F. A. Evangelista, G. K.-L. Chan and G. E. Scuseria, Exact parameterization of fermionic wave functions via unitary coupled cluster theory, J. Chem. Phys., 2019, 151, 244112 CrossRef PubMed.
- E. B. Wilson, J. C. Declus and P. C. Cross, in Molecular Vibrations: The Theory of Infrared and Raman Vibrational Spectra, ed. Dover, Dover Publications, new edition, 1980 Search PubMed.
- D. Papousek and M. R. Aliev, in Molecular Vibrational-rotational Spectra: Theory and Applications of High Resolution Infrared, Microwave and Raman Spectroscopy of Polyatomic Molecules, Elsevier Science, 1982 Search PubMed.
- S. Carter, S. J. Culik and J. M. Bowman, Vibrational self-consistent field method for many-mode systems: a new approach and application to the vibrations of CO adsorbed on Cu (100), J. Chem. Phys., 1997, 107, 10458–10469 CrossRef CAS.
- P. Seidler, T. Kaga, K. Yagi, O. Christiansen and K. Hirao, On the coupling strength in potential energy surfaces for vibrational calculations, Chem. Phys. Lett., 2009, 483, 138–142 CrossRef CAS.
- G. Rauhut, Efficient calculation of potential energy surfaces for the generation of vibrational wave functions, J. Chem. Phys., 2004, 121, 9313–9322 CrossRef CAS PubMed.
- M. R. Hermes and S. Hirata, Stochastic algorithm for size-extensive vibrational self-consistent field methods on fully anharmonic potential energy surfaces, J. Chem. Phys., 2014, 141, 244111 CrossRef PubMed.
- S. Hirata and M. R. Hermes, Normal-ordered second-quantized Hamiltonian for molecular vibrations, J. Chem. Phys., 2014, 141, 184111 CrossRef PubMed.
- V. Nagalakshmi, V. Lakshminarayana, G. Sumithra and M. D. Prasad, Coupled cluster description of anharmonic molecular vibrations. application to O3 and SO2, Chem. Phys. Lett., 1994, 217, 279 CrossRef.
- S. Banik, S. Pal and M. D. Prasad, Calculation of vibrational energy of molecule using coupled cluster linear response theory in bosonic representation: convergence studies, J. Chem. Phys., 2008, 129, 134111 CrossRef PubMed.
- J. A. Faucheaux, M. Nooijen and S. Hirata, Similarity-transformed equation-of-motion vibrational coupled-cluster theory, J. Chem. Phys., 2018, 148, 054104 CrossRef PubMed.
- J. A. Faucheaux and S. Hirata, Higher-order diagrammatic vibrational coupled-cluster theory, J. Chem. Phys., 2015, 143, 134105 CrossRef PubMed.
- J. M. Bowman, The self-consistent-field approach to polyatomic vibrations, Acc. Chem. Res., 1986, 19, 202–208 CrossRef CAS.
- M. Sibaev and D. L. Crittenden, PyVCI: a flexible open-source code for calculating accurate molecular infrared spectra, Comput. Phys. Commun., 2016, 203, 290–297 CrossRef CAS.
- S. Carter, A. R. Sharma and J. M. Bowman, First-principles calculations of rovibrational energies, dipole transition intensities and partition function for ethylene using MULTIMODE, J. Chem. Phys., 2012, 137, 154301 CrossRef PubMed.
- O. Christiansen, A second quantization formulation of multimode dynamics, J. Chem. Phys., 2004, 120, 2140–2148 CrossRef CAS PubMed.
- S. McArdle, S. Endo, A. Aspuru-Guzik, S. Benjamin and X. Yuan, Quantum computational chemistry, Rev. Mod. Phys., 2019, 92, 015003 CrossRef.
- P. K. Barkoutsos, J. F. Gonthier, I. Sokolov, N. Moll, G. Salis, A. Fuhrer, M. Ganzhorn, D. J. Egger, M. Troyer, A. Mezzacapo, S. Filipp and I. Tavernelli, Quantum algorithms for electronic structure calculations: particle-hole Hamiltonian and optimized wave-function expansions, Phys. Rev. A, 2018, 98, 022322 CrossRef CAS.
- J. Lee, W. J. Huggins, M. Head-Gordon and K. B. Whaley, Generalized Unitary Coupled Cluster Wave functions for Quantum Computation, J. Chem. Theory Comput., 2018, 15, 311–324 CrossRef PubMed.
- P. Jordan and E. P. Wigner, The Collected Works of Eugene Paul Wigner, Springer, 1993, pp. 109–129 Search PubMed.
- R. M. Parrish, E. G. Hohenstein, P. L. McMahon and T. J. Martínez, Quantum computation of electronic transitions using a variational quantum eigensolver, Phys. Rev. Lett., 2019, 122, 230401 CrossRef CAS PubMed.
- K. M. Nakanishi, K. Mitarai and K. Fujii, Subspace-search variational quantum eigensolver for excited states, Phys. Rev. Res., 2019, 1, 033062 CrossRef.
- I. G. Ryabinkin, S. N. Genin and A. F. Izmaylov, Constrained variational quantum eigensolver: quantum computer search engine in the Fock space, J. Chem. Theory Comput., 2018, 15, 249–255 CrossRef PubMed.
- O. Higgott, D. Wang and S. Brierley, Variational quantum computation of excited states, Quantum, 2019, 3, 156 CrossRef.
- J. R. McClean, M. E. Kimchi-Schwartz, J. Carter and W. A. de Jong, Hybrid quantum-classical hierarchy for mitigation of decoherence and determination of excited states, Phys. Rev. A, 2017, 95, 042308 CrossRef.
- N. H. Stair, R. Huang and F. A. Evangelista, A Multireference Quantum Krylov Algorithm for Strongly Correlated Electrons, arXiv preprint arXiv:1911.05163, 2019.
- R. Santagati, J. Wang, A. A. Gentile, S. Paesani, N. Wiebe, J. R. McClean, S. Morley-Short, P. J. Shadbolt, D. Bonneau, J. W. Silverstone, D. P. Tew, X. Zhou, J. L. O Brien and M. G. Thompson, Witnessing eigenstates for quantum simulation of Hamiltonian spectra, Sci. Adv., 2018, 4, eaap9646 CrossRef PubMed.
- T. Jones, S. Endo, S. McArdle, X. Yuan and S. C. Benjamin, Variational quantum algorithms for discovering Hamiltonian spectra, Phys. Rev. A, 2019, 99, 062304 CrossRef CAS.
- J. Tilly, G. Jones, H. Chen, L. Wossnig and E. Grant, Computation of molecular excited states on IBMQ using a Discriminative Variational Quantum Eigensolver, arXiv preprint arXiv:2001.04941, 2020.
- V. Rodriguez-Garcia, S. Hirata, K. Yagi, K. Hirao, T. Taketsugu, I. Schweigert and M. Tasumi, Fermi resonance in CO2: a combined electronic coupled-cluster and vibrational configuration-interaction prediction, J. Chem. Phys., 2007, 126, 124303 CrossRef PubMed.
- O. Sode, M. Keceli, K. Yagi and S. Hirata, Fermi resonance in solid CO2 under pressure, J. Chem. Phys., 2013, 138, 074501 CrossRef PubMed.
- Q. K. Wang and J. M. Bowman, Two-component, ab initio potential energy surface for CO2—H2O, extension to the hydrate clathrate, CO2@(H2O)20, and VSCF/VCI vibrational analyses of both, J. Chem. Phys., 2017, 147, 161714 CrossRef PubMed.
- A. D. Becke, A new mixing of Hartree–Fock and local density-functional theories, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- T. H. Dunning, Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09 Revision C.01, Gaussian Inc, Wallingford CT, 2009 Search PubMed.
- G. Aleksandrowicz, T. Alexander, P. Barkoutsos, L. Bello, Y. Ben-Haim, D. Bucher, F. J. Cabrera-Hernández, J. Carballo-Franquis, A. Chen, C.-F. Chen, J. M. Chow, A. D. Córcoles-Gonzales, A. J. Cross, A. Cross, J. Cruz-Benito, C. Culver, S. De La Puente González, E. De La Torre, D. Ding, E. Dumitrescu, I. Duran, P. Eendebak, M. Everitt, I. F. Sertage, A. Frisch, A. Fuhrer, J. Gambetta, B. G. Gago, J. Gomez-Mosquera, D. Greenberg, I. Hamamura, V. Havlicek, J. Hellmers, Ł. Herok, H. Horii, S. Hu, T. Imamichi, T. Itoko, A. Javadi-Abhari, N. Kanazawa, A. Karazeev, K. Krsulich, P. Liu, Y. Luh, Y. Maeng, M. Marques, F. J. Martín-Fernández, D. T. McClure, D. McKay, S. Meesala, A. Mezzacapo, N. Moll, D. M. Rodríguez, G. Nannicini, P. Nation, P. Ollitrault, L. J. O'Riordan, H. Paik, J. Pérez, A. Phan, M. Pistoia, V. Prutyanov, M. Reuter, J. Rice, A. R. Davila, R. H. P. Rudy, M. Ryu, N. Sathaye, C. Schnabel, E. Schoute, K. Setia, Y. Shi, A. Silva, Y. Siraichi, S. Sivarajah, J. A. Smolin, M. Soeken, H. Takahashi, I. Tavernelli, C. Taylor, P. Taylour, K. Trabing, M. Treinish, W. Turner, D. Vogt-Lee, C. Vuillot, J. A. Wildstrom, J. Wilson, E. Winston, C. Wood, S. Wood, S. Wörner, I. Y. Akhalwaya and C. Zoufal, Qiskit: An Open-source Framework for Quantum Computing, 2019 Search PubMed.
- M. J. Powell, Advances in optimization and numerical analysis, Springer, 1994, pp. 51–67 Search PubMed.
- J. R. McClean, S. Boixo, V. N. Smelyanskiy, R. Babbush and H. Neven, Barren plateaus in quantum neural network training landscapes, Nat. Commun., 2018, 9, 1–6 CrossRef CAS PubMed.
- M. Cerezo, A. Sone, T. Volkoff, L. Cincio and P. J. Coles, Cost-Function-Dependent Barren Plateaus in Shallow Quantum Neural Networks, arXiv preprint arXiv:2001.00550, 2020.
- H. R. Grimsley, S. E. Economou, E. Barnes and N. J. Mayhall, An adaptive variational algorithm for exact molecular simulations on a quantum computer, Nat. Commun., 2019, 10, 1–9 CrossRef CAS PubMed.
- I. O. Sokolov, P. K. Barkoutsos, P. J. Ollitrault, D. Greenberg, J. Rice, M. Pistoia and I. Tavernelli, Quantum orbital-optimized unitary coupled cluster methods in the strongly correlated regime: Can quantum algorithms outperform their classical equivalents?, J. Chem. Phys., 2020, 152, 124107 CrossRef PubMed.
- T. Takeshita, N. C. Rubin, Z. Jiang, E. Lee, R. Babbush and J. R. McClean, Increasing the representation accuracy of quantum simulations of chemistry without extra quantum resources, Phys. Rev. X, 2020, 10, 011004 CAS.
- A. J. McCaskey, Z. P. Parks, J. Jakowski, S. V. Moore, T. D. Morris, T. S. Humble and R. C. Pooser, Quantum chemistry as a benchmark for near-term quantum computers, npj Quantum Inf., 2019, 5, 1–8 CrossRef.
- J. C. Spall, Adaptive stochastic approximation by the simultaneous perturbation method, IEEE Trans. Autom. Control, 2000, 45, 1839–1853 CrossRef.
- Y. Scribano, D. M. Lauvergnat and D. M. Benoit, Fast vibrational configuration interaction using generalized curvilinear coordinates and self-consistent basis, J. Chem. Phys., 2010, 133, 094103 CrossRef PubMed.
- P. Seidler, E. Matito and O. Christiansen, Vibrational coupled cluster theory with full two-mode and approximate three-mode couplings: the VCC[2pt3] model, J. Chem. Phys., 2009, 131, 034115 CrossRef PubMed.
- A. W. Cross, L. S. Bishop, S. Sheldon, P. D. Nation and J. M. Gambetta, Validating quantum computers using randomized model circuits, Phys. Rev. A, 2019, 100, 032328 CrossRef CAS.
- I. H. Godtliebsen, B. Thomsen and O. Christiansen, Tensor Decomposition and Vibrational Coupled Cluster Theory, J. Phys. Chem. A, 2013, 117, 7267–7279 CrossRef CAS PubMed.
- N. K. Madsen, I. H. Godtliebsen, S. A. Losilla and O. Christiansen, Tensor-decomposed vibrational coupled-cluster theory: enabling large-scale, highly accurate vibrational-structure calculations, J. Chem. Phys., 2018, 148, 024103 CrossRef PubMed.
- M. Motta, E. Ye, J. R. McClean, Z. Li, A. J. Minnich, R. Babbush and G. K.-L. Chan, Low rank representations for quantum simulation of electronic structure, arXiv preprint arXiv:1808.02625, 2018.
- C. R. Jacob and M. Reiher, Localizing normal modes in large molecules, J. Chem. Phys., 2009, 130, 084106 CrossRef PubMed.
- B. Thomsen, K. Yagi and O. Christiansen, Optimized coordinates in vibrational coupled cluster calculations, J. Chem. Phys., 2014, 140, 154102 CrossRef.
- A. Macridin, P. Spentzouris, J. Amundson and R. Harnik, Digital quantum computation of fermion-boson interacting systems, Phys. Rev. A, 2018, 98, 042312 CrossRef CAS.
- A. D. Paolo, P. K. Barkoutsos, I. Tavernelli and A. BlaisVariational Quantum Simulation of Ultrastrong Light-Matter Coupling, arXiv preprint arXiv:1909.08640, 2019.
- S. Bubin, M. Pavanello, W.-C. Tung, K. L. Sharkey and L. Adamowicz, Born–Oppenheimer and Non-Born–Oppenheimer, Atomic and Molecular Calculations with Explicitly Correlated Gaussians, Chem. Rev., 2013, 113, 36–79 CrossRef CAS PubMed.
- E. Mátyus and M. Reiher, Molecular structure calculations: a unified quantum mechanical description of electrons and nuclei using explicitly correlated Gaussian functions and the global vector representation, J. Chem. Phys., 2012, 137, 024104 CrossRef PubMed.
- L. Veis, J. Višňák, H. Nishizawa, H. Nakai and J. Pittner, Quantum chemistry beyond Born–Oppenheimer approximation on a quantum computer: a simulated phase estimation study, Int. J. Quantum Chem., 2016, 116, 1328–1336 CrossRef CAS.
- Y. Li and S. C. Benjamin, Efficient Variational Quantum Simulator Incorporating Active Error Minimization, Phys. Rev. X, 2017, 7, 021050 Search PubMed.
| This journal is © The Royal Society of Chemistry 2020 |