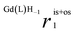Acid-catalyzed proton exchange as a novel approach for relaxivity enhancement in Gd-HPDO3A-like complexes

Abstract

A current challenge in medical diagnostics is how to obtain high MRI relaxation enhancement using Gd^III-based contrast agents (CAs) containing the minimum concentration of Gd^III ions. We report that in GdHPDO3A-like complexes a primary amide group located in close proximity to the coordinated hydroxyl group can provide a strong relaxivity enhancement at slightly acidic pH. A maximum relaxivity of r₁ = 9.8 mM⁻¹ s⁻¹ (20 MHz, 298 K) at acidic pH was achieved, which is more than double that of clinically approved MRI contrast agents under identical conditions. This effect was found to strongly depend on the number of amide protons, i.e. it decreases with a secondary amide group and almost completely vanishes with a tertiary amide. This relaxivity enhancement is attributed to an acid-catalyzed proton exchange process between the metal-coordinated OH group, the amide protons and second sphere water molecules. The mechanism and kinetics of the corresponding H⁺ assisted exchange process are discussed in detail and a novel simultaneous double-site proton exchange mechanism is proposed. Furthermore, ¹H and ¹⁷O NMR relaxometry, Chemical Exchange Saturation Transfer (CEST) on the corresponding Eu^III complexes, and thermodynamic and kinetic studies are reported. These highlight the optimal physico-chemical properties required to achieve high relaxivity with this series of Gd^III-complexes. Thus, proton exchange provides an important opportunity to enhance the relaxivity of contrast agents, providing that labile protons close to the paramagnetic center can contribute.

---

Introduction

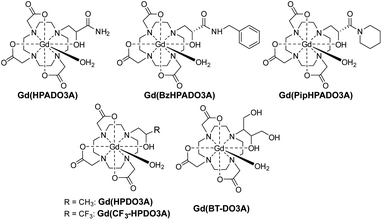
Gd³⁺ based MRI contrast agents (CAs) are used in about 40–50% of clinical scans to increase the tissue contrast in relaxation weighted images, by shortening the relaxation times of the water molecules in their proximity. Although some of these CAs have successfully been on the market for more than 30 years, strategies to obtain high MRI relaxation enhancement with the minimum concentration of Gd^III are still a challenge in the field of medical diagnostics.^1,2 The exchange of the mobile protons from a Gd^III complex with the bulk water is one of the processes able to enhance the nuclear relaxation rate of solvent water protons.³ Among the clinically approved Gd^III CAs, Gd(HPDO3A) [HPDO3A = 10-(2-hydroxypropyl)-1,4,7,10-tetra-azacyclododecane-1,4,7-triacetic acid; Scheme 1] is a neutral complex featuring a coordinated hydroxyl group and a water molecule, both of which contain protons responsible for transferring the paramagnetism of the Gd^III ion to bulk water.⁴ Typically, the hydroxyl proton of Gd(HPDO3A) is involved in slow exchange with the bulk water at physiological pH. Thus, Ln(HPDO3A) complexes have been used for Chemical Exchange Saturation Transfer (CEST) MRI applications, exploiting the –OH group as a saturable pool of protons.⁵ The relatively short Gd–OH bond distance (Gd–OH: 2.32 Å, Gd–OH₂: 2.51 Å)⁶ results in a stronger contribution to the relaxivity (r₁) than that of the coordinated water molecule.⁷ At pH > 10, the interplay of the short exchange lifetime of the hydroxyl proton (τ_M = 1/k_ex = 1/k_OH[OH⁻], where k_OH = 5.2 × 10⁹ M⁻¹ s⁻¹) with the short Gd–OH distance leads to a substantial base-catalyzed proton exchange contribution to r₁ (Δr₁ = 1.2 mM⁻¹ s⁻¹).⁷ Moreover, it has recently been shown that the proton exchange of the hydroxyl group in Gd(CF₃-HPDO3A) (Scheme 1) can be accelerated by the basic component of buffers (e.g. phosphate, carbonate and HEPES) allowing a slight increase in r₁ even at neutral pH.⁷ Also, the introduction of an appropriate group in close proximity to the metal ion has been shown to modulate r₁ by restricting rotation about the Gd–O_w bond or by accelerating proton exchange.^8,9 Acid-catalysed proton exchange has also been observed in the case of Gd(DOTA-tetrakis-N-methylacetamide), a tripositive Gd^III complex with a very slow water exchange rate (k_ex = 4.5 × 10⁴ s⁻¹). The value of r₁ is doubled at pH ≈ 1 compared to neutral pH,¹⁰ while the rate constant of the acid-catalyzed exchange of the inner-sphere water protons, k_H, is 2.4 × 10⁶ M⁻¹ s⁻¹. Also, in the case of Gd(DOTA), lowering the temperature to 273 K, and thus reducing k_ex, resulted in a slight increase of r₁ due to acid-catalysed proton exchange.³

Scheme 1 The Gd^III complexes synthesized and discussed in the present work.

In this work, we expanded the group of HPDO3A-like ligands by replacing the methyl group in the ordinary hydroxypropyl arm of HPDO3A with electron-withdrawing amide groups. Our ultimate goal was to investigate the effect of labile amide protons in the proximity of the coordinated hydroxyl group on the proton exchange relaxation enhancement. Thus, three new GdHPDO3A-like complexes containing primary, secondary and tertiary amides (Gd(HPADO3A), Gd(BzHPADO3A) and Gd(PipHPADO3A), Scheme 1) were synthesized and investigated by ¹H and ¹⁷O NMR relaxometry as well as CEST, and solution thermodynamic and kinetic studies.

Results and discussion

Synthesis

The ligand HPADO3A was obtained from the ring opening of glycidamide with the secondary amine of DO3A(tBuO)₃, followed by deprotection of the t-butyl esters with trifluoroacetic acid (TFA) and dichloromethane (DCM). The ligands containing secondary and tertiary amides were prepared by the reaction of DO3A(tBuO)₃ and methyl (2R)-glycidate, followed by aminolysis with benzylamine (BzHPADO3A) or piperidine (PipHPADO3A). Then, the final ligands were obtained by deprotection of the t-butyl esters using TFA/DCM (1 : 1) and the Gd^III complexes by the reaction of the ligand with GdCl₃ at pH = 7.0 in aqueous solution.

pH dependence of relaxivity

The relaxivity vs. pH profiles of the three Gd-HPADO3A complexes, measured at 20 MHz and 298 K (Fig. 1), show a significant change in the r₁ values at pH 6–7. At pH > 7, the r₁ values for all three Gd^III-complexes are similar and comparable to those measured for Gd(HPDO3A) and related systems. However, significant differences were found in the r₁ values at acidic pH; the relaxivity is very high for Gd(HPADO3A) (r₁ = 9.8 mM⁻¹ s⁻¹) and it gradually decreases by reducing the number of amide protons on the ligands. Thus, a remarkable enhancement is detectable for Gd(HPADO3A) in the physiologically relevant 7.4–5.5 pH range (Δr₁ = 5.5 mM⁻¹ s⁻¹ from pH 5 to 7.4). This Δr₁ is similar to those found for the well-known pH-responsive systems such as Gd^III-complexes of DO3A-sulfonamides (Δr₁ ≈ 5.5),¹¹ or DO3A-aminoethyl-derivatives (Δr₁ ≈ 3.4).¹² In these examples, the variation of r₁ was attributed to a change of hydration state of the Gd^III complex from q = 2 to q ≈ 0, under acidic and basic conditions, respectively. In contrast, the large Δr₁ of Gd(HPADO3A) cannot be explained by the change of the hydration state, because the inner-sphere water molecule remains coordinated in the entire pH range as confirmed by ¹⁷O NMR studies (see below and the ESI†).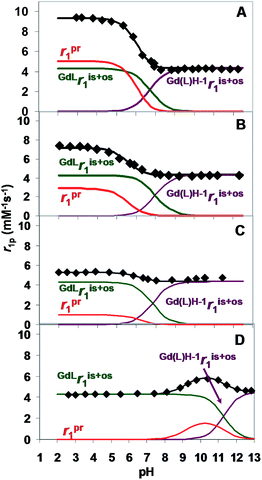

Fig. 1 Relaxivity of Gd(HPADO3A) (A), Gd(BzHPADO3A) (B), Gd(PipHPADO3A) (C) and Gd(HPDO3A) (D) as a function of pH ([GdL] = 1.0 mM, 20 MHz, 0.15 M NaCl, 298 K).

Analysis of the proton exchange mechanism

Under acidic conditions, the higher relaxivity is presumably due to the proton exchange between the –OH group of Gd(HPADO3A) and the bulk. The overall relaxivity, r₁, is given by eqn (1):

r₁ = r^is₁ + r^os₁ + r^pr₁ (1)

where r^is₁, r^os₁ and r^pr₁ are the relaxivity components due to the inner and outer sphere water molecules and the –OH group, respectively. r^pr₁ can be expressed as follows:⁷where c is the concentration of the complex, and T^H_1P and τ_p are the longitudinal relaxation time and the lifetime of the –OH proton, respectively. The characteristic pH dependence of r₁ can be interpreted by considering the deprotonation of the complex at around pH 6–7 and the acid-catalyzed proton exchange of the –OH proton. The protonation constants of GdHPADO3A-derivatives (K_Gd(L)H−1) were determined by pH-potentiometry: log K_Gd(L)H−1 = 6.73(4), 7.08(5) and 6.82(2) for Gd(HPADO3A), Gd(BzHPADO3A) and Gd(PipHPADO3A), respectively (log K_Gd(L)H−1 = 11.34(4) in the case of Gd(HPDO3A)). The basicity of GdHPADO3A-derivatives is significantly lower than that of Gd(HPDO3A) due to the electron withdrawing effect of the amide group in the pendant arm. Upon decreasing the pH, the molar ratio of the protonated form increases and the proton exchange between the coordinated OH group and the bulk becomes increasingly significant and, as a consequence, the relaxivity increases. However, eventually this effect becomes relaxation controlled (T^H_1P ≫ τ_p) and the relaxivity becomes constant. Interestingly, the N-substitution strongly influences the r₁ of this series of Gd^III-complexes under acidic conditions (pH < 5.0), as the r₁ decreases from the primary amide, Gd(HPADO3A), to the tertiary amide, Gd(PipHPADO3A). An inspection of Fig. 1 reveals that the enhancement of the relaxivity is proportional to the number of protons of the –OH and amide groups (N). This implies that a fast exchange is operative between the OH and NH protons, because the protons originally located in the NH group need to be transferred and exposed to the magnetic field of the paramagnetic centre.

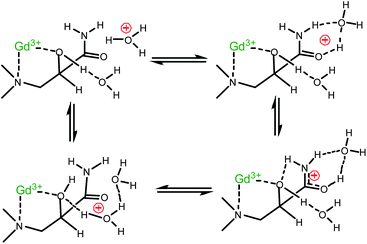
The typical protonation constant (log K^H) of the amide group is in the range of −1.92 to +0.37,¹³ and it is reasonable to assume that the protonated Gd(L)H⁺ species forms at a negligible concentration at pH 5.0–6.0. Accordingly, the standard proton transfer process via the acid–base equilibrium of the Gd(L)H⁺ complex cannot be operative in the enhancement of the relaxivity. Thus, in order to rationalize the observations, we propose the mechanism shown in Scheme 2. It takes into account that the labile protons are involved in secondary interactions with the bulk. We assume that the encounter of the carbonyl oxygen with H₃O⁺ induces an internal proton transfer between the amide and –OH groups and, consequently, between –OH and the bulk. Instead of the formation of the protonated Gd(L)H⁺ species, a concerted rearrangement of the hydrogen bonds takes place, which effectively exchanges protons between GdL and the bulk.

Scheme 2 Mechanism of the H⁺ assisted exchange of –OH and –CONH_n– protons of Gd(HPADO3A). The free rotation around the C2–C3 σ bond of the pendant arm guarantees the same mechanism for both enantiomers at C2.

The noted relaxation effect is absent in the case of Gd(CF₃-HPDO3A) (Scheme 1), although the basicity of the –OH group in this complex (log K_Gd(L)H−1 = 6.90(4))⁷ is very similar to that of the GdHPADO3A-derivatives. This corroborates the conclusion that the acid-catalyzed proton exchange and the enhanced relaxivity are due to the presence of the labile amide protons in the vicinity of the –OH group. This interpretation is also supported by the CEST spectra of the Eu^III complexes with HPADO3A-derivatives (Fig. 2, S15 and S16†). In this case, fast proton exchange between the OH and amide protons results in a broad coalesced signal at ∼26 ppm under acidic conditions. The interaction between hydroxyl and amide groups vanishes upon deprotonation of the OH group and the corresponding CEST signal disappears.

Fig. 2 (A) Z-spectra and (B) ST%-spectra of Eu(HPADO3A) (20 mM) in water at different pH values; (C) ST% effect for Eu(HPADO3A), in water as a function of pH; (D) ST-weighted, CEST map capillaries filled with Eu(HPADO3A) (20 mM) in water at various pH values (1: pH 4.6; 2: pH 5.5; 3: pH 5.9; 4: pH 6.5; 5: pH 6.7; 6: pH 7.0; 7: pH 7.5; 8: water).

The mechanism proposed is also consistent with earlier studies on proton exchange processes of several amides with water.¹⁴ The acid and base catalysis in such processes was interpreted by considering the (de)protonation of the amide group via the formation of H-bonded complexes between the proton donors and acceptors.¹⁵ This mechanism requires the diffusion-controlled formation of a H-bonded complex and subsequently the rapid separation of the corresponding conjugate acid and base.¹⁶

In accordance with Scheme 2, the rate of proton exchange is ν_H = k_H[H₃O⁺][GdL]. Because of the fast internal rearrangement, the alcoholic –OH and amide –CONH_n– protons cannot be distinguished and their lifetime is τ_p = (k_H[H⁺])⁻¹. Thus, eqn (2) can be rewritten as follows:

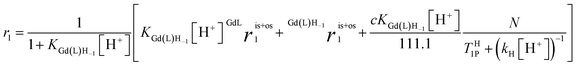where N is the number of labile protons (N = 1–3)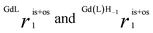, and are the sum of r^is₁ and r^os₁, for GdL and Gd(L)H₋₁. The experimental data (Fig. 1) were fitted to eqn (3) and the results are listed in Table 1.

Table 1 Kinetic and relaxation parameters for the proton exchange reactions of the Gd^III complexes of HPADO3A, BzHPADO3A and PipHPADO3A compared to Gd(HPDO3A) (20 MHz, 0.15 M NaCl, 298 K)

			T 1P ^H × 10^6	k H × 10^−11	k OH × 10^−10	k +B × 10^−9
	mM^−1 s^−1	mM^−1 s^−1	s	M^−1 s^−1	M^−1 s^−1	M^−1 s^−1
HPA-DO3A	4.57 ± 0.07	4.32 ± 0.03	5.6 ± 0.2	2.1 ± 0.2	—	1.8 ± 0.3
BzHPA-DO3A			5.7 ± 0.4	0.8 ± 0.2	—	2.5 ± 0.5
PipHPA-DO3A			5 ± 1	1.0 ± 0.3	—	2.3 ± 0.8
HP-DO3A	4.28 ± 0.01	4.54 ± 0.03	5.0 ± 0.1	—	1.0 ± 0.1	—

---

The H⁺ assisted exchange of the labile protons of GdHPADO3A-derivatives is characterized by very similar k_H and T^H_1P values (Table 1), confirming analogous behaviour of these complexes. In each system, k_H is about an order of magnitude larger than the typical rate constants for diffusion-controlled proton exchange processes between conjugate acid–base pairs. This lends strong support to the simultaneous double-site exchange mechanism proposed in Scheme 2. The results also verify that the proton relaxation enhancement of GdHPADO3A-derivatives, under acidic conditions, is exchange controlled (T^H_1P ≪ 1/(k_H[H⁺])) at pH > 5.0 and relaxation controlled (T^H_1P ≫ 1/(k_OH[H⁺])) at pH < 5.0.

In order to obtain further information on the mechanism of the acid–base catalysed proton-exchange processes of GdHPADO3A-derivatives, the relaxivity of Gd^III-complexes was measured in the absence and in the presence of NH₄Cl at pH = 6.0, 298 K and 20 MHz (Fig. S6†). The [NH₄Cl] dependent relaxation enhancement can readily be interpreted by considering that NH₃, as a Brønsted base, catalyzes the exchange of the –OH proton. The corresponding rate constant is k_+B. These are practically the same for the three GdHPADO3A-derivatives and very similar to k_OH, which characterizes the OH⁻ ion assisted, diffusion-controlled proton-exchange process of the hydroxyl proton in Gd(HPDO3A) (Table 1). This result clearly confirms that the exchange between NH₃ and the labile protons of Gd(HPADO3A) derivatives proceeds via the general base catalysed proton transfer mechanism.¹⁶

CEST experiments

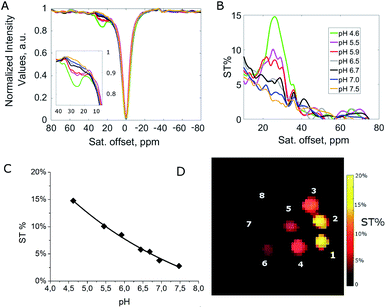
Further insight into the mechanism of the acid–base catalyzed proton-exchange process was obtained by Chemical Exchange Saturation Transfer Magnetic Resonance Imaging (CEST-MRI) experiments, on Eu^III complexes of HPADO3A-derivatives at variable pH (Fig. 2 and S13–S16†). A clear decrease of ST% effect was observed by moving from acidic to basic pH. This seems to be consistent with deprotonation of the coordinated hydroxyl group. In particular, for a 20 mM water solution of Eu(HPADO3A), one CEST peak is present at 26 ppm, with an ST% that decreases from 14.9% at pH = 4.6 to ca. 2% at pH = 7.5 (B₁ = 12 μT). In order to evaluate the presence of two distinguishable peaks, the Z-spectrum of EuHPADO3A was acquired at low temperature (278 ± 2 K) and pH 4.5 by using a pre-saturation pulse of 6 μT. As reported in Fig. S15,† two peaks are clearly detectable, belonging to the two exchangeable pools of protons. Upon increasing the temperature, there is an increase of exchange rate and coalescence of the two peaks. Analogously, upon using higher B₁ fields (e.g. 12 μT) there is a broadening of the signals that are no more distinguishable. This behaviour was also confirmed by Z- and ST-spectral simulation of the Eu(HPADO3A) complex by using Bloch equations modified for chemical exchange¹⁷ considering a three-pool exchange system with bulk water at zero, –OH at 30 and –NH₂ at 25 ppm.

The same pH dependence as for Eu(HPADO3A) was observed for Eu(BzHPADO3A), but the ST% measured under the same conditions as those for Eu(HPADO3A) (pH 4.6 and 20 mM) was lower (8.2%) due to the presence of two exchangeable protons instead of three (Fig. S15†). On the other hand, for Eu(PipHPADO3A) the CEST signal was too weak to be observed (Fig. S16†). This pH dependent behaviour is also shown clearly in Fig. 2C through the CEST-MR image of phantoms containing Eu(HPADO3A) at different pH values, as previously highlighted in the case of a dimeric Eu₂(HPADO3A)₂ complex.¹⁸

Relaxometric analysis

A detailed ¹H and ¹⁷O NMR relaxometric study (including NMRD profiles at 298 and 310 K, temperature dependence of the ¹⁷O NMR transverse relaxation rate, R₂, and paramagnetic shift, Δω, of the solvent water, Fig. 3 and S7–S12†) was carried out under both acidic and neutral conditions. A least-square fit of the data was carried out using the established theory of paramagnetic relaxation. This is expressed by the Solomon–Bloembergen–Morgan and Freed equations,¹⁹ for the inner sphere (IS) and outer sphere (OS) proton relaxation mechanisms, respectively, and the Swift–Connick²⁰ theory for ¹⁷O relaxation. The NMRD profiles at acidic pH were fitted adding a fixed proton exchange contribution of r₁ (r^pr₁) to the equations (Table 2). Moreover, the contribution of second sphere (SS) water molecules, H-bonded to the amide group, was also considered (r^GdH(SS) = 3.5 Å, q^SS = 3–5). Such a mechanism was also previously reported for the dimeric Gd₂(HPADO3A)₂ complex where the increase of r₁ could be explained only by taking into account the contribution of 4 SS water molecules.¹⁸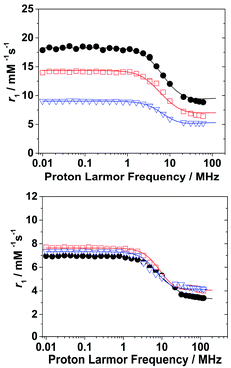

Fig. 3 ¹H NMRD profiles of Gd(HPADO3A) (black circles), Gd(Bz-HPADO3A) (red squares) and Gd(pip-HPADO3A) (blue triangles) at pH 4.2 (top) and 7.4 (below).

Table 2 Selected best-fit parameters obtained from the analysis of the 1/T₁¹H NMRD profiles (298 and 310 K) and ¹⁷O NMR data for Gd(HPADO3A), Gd(BzHPADO3A), and Gd(PipHPADO3A)

Parameter^a	Gd(HPADO3A)		Gd(BzHPADO3A)		Gd(PipHPADO3A)
	pH 4.2	pH 7.4	pH 4.2	pH 7.4	pH 4.2	pH 7.4
a The parameters fixed in the fitting procedure are q = 1, rGdO = 2.5 Å, rGdH = 3.0 Å, aGdH = 4.0 Å, ^298DGdH = 2.25 × 10^−5 cm^2 s^−1, ER = 18 kJ mol^−1, Ev = 1 kJ mol^−1, and rGdH(SS) = 3.5 Å.^18 b These values were fixed considering the value obtained for Gd(HPADO3A) at pH 4.2.
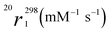
	9.8 (2)	4.3 (1)	7.2 (1)	4.5 (1)	5.3 (2)	4.6 (1)
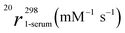
	—	6.7 (1)	—	7.7 (1)	—	8.5 (1)
r 1 ^pr 298 (mM^−1 s^−1)	4.99 (2)	—	2.87 (2)	—	1.12 (3)	—
Δ ^2 (10^19 s^−2)	12.0 (7)	8.5 (1.1)	6.8 (1.6)	10.2 (1.4)	10.1 (1.0)	3.5 (9)
τ ^298V (ps)	4.5 (6)	13.8 (8)	5.0 (9)	13.1 (9)	10.4 (7)	25.2 (9)
τ ^298M (ns)	24.5 (5)	20.2 (2.4)	21.6^b	24.2 (2.1)	21.6^b	45.0 (1.4)
τ ^298R (ps)	62.0 (1.2)	62.0 (1.3)	70.8 (2.1)	70.8 (1.5)	82.2 (1.5)	82.2 (2.0)
ΔHM (kJ mol^−1)	15.5 (7)	14.9 (9)	—	13.0 (5)	—	7.5 (3)
A/h (10^6 rad s^−1)	−3.4 (1)	−3.4 (1)	−3.4^b	−3.4 (1)	−3.4^b	−3.4 (1)
q ^SS	5	5	4	4	3	3
τ ^SSR (ps)	30.0 (2.5)	12.7 (9)	24.5 (2.1)	23.2 (1.0)	24.0 (1.3)	10.1 (9)

---

In all complexes, the coordinated water molecule is in fast exchange with the bulk (τ_M in the range 21.6–45.0 ns, Table 2), with values comparable to the dimeric complex Gd₂(HPADO3A)₂ (ref. 18) and the recently reported Gd(HPDO3MA) (Scheme 1),²¹ but almost one order of magnitude faster than in the case of Gd(HPDO3A).⁴ Furthermore, the presence of an important second sphere contribution supports the proton exchange mechanism shown in Scheme 2. In this mechanism, SS water molecules have a strong interaction with the amide groups and are involved in the proton exchange between the hydroxyl and amide groups. The rotational correlation time of these SS water molecules – τ^SS_R ∼ 10–30 ps – is in line with the values reported in the literature.²²

The relaxivity was also measured (pH 7.4, 298 K and 20 MHz) by dissolving the three complexes in reconstituted human serum (Seronorm). The r₁ values reported in Table 2 are higher than those measured in pure water; in particular, a 56% increase is observed for Gd(HPADO3A), 71% for Gd(BzHPADO3A) and 85% for Gd(PipHPADO3A). The significant r₁ increase observed in serum can be attributed to two factors: (i) the presence of endogenous anions that can contribute to the relaxivity by catalysing the proton exchange⁷ and (ii) the interaction of the Gd-complex with serum proteins such as Human Serum Albumin (HSA). In particular, for Gd(BzHPADO3A) and Gd(PipHPADO3A), the interaction with HSA of the benzyl and piperidine moieties, respectively, and the formation of slowly tumbling supramolecular adducts, contributes to the strong relaxivity increase.

Thermodynamic and kinetic study on GdHPADO3A

The in vivo application requires very robust Gd^III-complexes, which must be characterised by high thermodynamic stability and kinetic inertness, to avoid the transmetallation or transchelation reactions with competing endogenous species.^1,2 The stability and protonation constants of the Ca^II-, Zn^II-, Cu^II- and Gd^III-complexes of HPADO3A, and the protonation constants of Gd(BzHPADO3A) and Gd(PipHPADO3A), were calculated using pH-potentiometric and spectrophotometric data (Table 3). Experimental details, as well as the definitions and equations used for the evaluation of the equilibrium and kinetic data, are provided in the ESI.†

Table 3 Stability and protonation constants of Ca^II-, Zn^II-, Cu^II- and Gd^III complexes formed with HPADO3A compared with literature data on HPDO3A, BT-DO3A and DOTA ligands (298 K)

	HPADO3A	DOTA^a	HPDO3A^c	BT-DO3A^d
a Ref. 24. b Ref. 25, 0.1 M NaCl, 298 K. c Ref. 26. d Ref. 27. e pGd = −log[Gd]free, [Gd^3+] = 1 μM, [L] = 10 μM, pH = 7.4 (ref. 28). *Spectrophotometry, I = [Na^+] + [H^+] = 0.15, [H^+] ≤ 0.15 M; Gd(BzHPADO3A): log KGd(L)H−1 = 7.08 (5); Gd(PipHPADO3A): log KGd(L)H−1 = 6.82 (2), 0.15 M NaCl, 298 K;^a 0.1 M NaCl.
I	0.15 M NaCl	0.1 M KCl	0.1 M Me4NCl	0.1 M NaCl
CaL	12.13 (4)	16.37	14.83	12.1
Ca(L)H−1	11.50 (6)	—	—	—
ZnL	17.18 (3)	18.7	19.37	17.0
Zn(L)H−1	10.79 (5)	10.62	—	—
*CuL	21.53 (2)	22.72	22.84	19.1
Cu(L)H−1	10.55 (2)	—	—	—
GdL	18.41 (2)	24.7^b	23.8	18.7
Gd(L)H−1	6.73 (4)	—	11.36^d	9.48
pGd^e	16.88	22.09	18.16	15.63

---

The stability constants of Gd^III-, Ca^II-, Zn^II- and Cu^II-HPADO3A complexes (Table 3) are about 1–5 orders of magnitude smaller than those of the corresponding DOTA and HPDO3A complexes, but similar to those of BT-DO3A complexes (Scheme 1). In our study, the experiments were performed in 0.15 M NaCl solution to obtain the equilibrium data near physiological conditions and therefore, the equilibrium constants are presumably smaller than they would be in 0.1 M KCl or Me₄NCl, due to the formation of Na^I-complexes (e.g. log K_Na(DOTA) = 4.38).²³ The similarity of log K_GdL values for Gd(HPADO3A) and Gd(BT-DO3A) is reasonable, because the coordinated alcoholic –OH group of the ligands has a similar, albeit minor role in the Gd^III–ligand interaction. On the other hand, the interaction of the alkoxide donor with Gd^III ions is stronger than with Ca^II, Zn^II and Cu^II ions, resulting in significantly lower log K_Gd(L)H−1 values. Moreover, the lower log K_Gd(L)H−1 value results in a conditional stability (pGd) of Gd(HPADO3A) about one unit higher than that of Gd(BT-DO3A).

The kinetic inertness of lanthanide(III)-complexes is also a very important requirement for in vivo application in order to avoid the possible release of free Ln³⁺ ions and ligands in living systems. The dissociation of Ln(DOTA)-like complexes is exceptionally slow and generally occurs through a proton-assisted path without the direct involvement of endogenous metal ions (e.g. Ca^II, Zn^II, Cu^II and Fe^III).^27,29,30 The dissociation reactions of Gd(HPADO3A) were monitored by ¹H-NMR relaxometry (400 MHz and 298 K) in 0.01–1.0 M HCl solution to establish pseudo-first-order kinetics conditions. The increase in the value of the pseudo-first order rate constant (k_d) with increasing concentration of H⁺ (Fig. S5†) can be interpreted by the proton assisted dissociation of Gd(HPADO3A) (k₁) via the formation of the protonated Gd(HHPADO3A) intermediate (the protonation presumably occurs on the carboxylate group).^27,29,30 As shown in Table 4, the k₁ of Gd(HPADO3A) is about 5 and 90 times higher than that of Gd(BT-DO3A) and Gd(DOTA), respectively. The dissociation rate constant (k_d) of Gd(HPADO3A) calculated near physiological conditions (pH = 7.4, 298 K) is approximately two times lower than that of Gd(HPDO3A), i.e. the former complex is somewhat more inert. The dissociation most likely occurs via proton transfer, from the –COOH group to the N-atom of the ring in the protonated Gd(HHPADO3A) intermediate, resulting in the displacement of the Gd^III ion from the coordination cage. This is the result of the stronger coordination of the –OH group to the metal centre in Gd(HPADO3A), than in Gd(HPDO3A), making the proton transfer to the macrocyclic N-atom less favourable. Finally, a comparison of the half-lives (t_1/2 = ln 2/k_d) proves the superior kinetic inertness of Gd(HPADO3A) compared to Gd(HPDO3A).

Table 4 Rate constants (k_i) and half-lives (t_1/2 = ln 2/k_d) characterising the dissociation reactions of Gd(HPADO3A), Gd(DOTA), Gd(HPDO3A) and Gd(BT-DO3A) complexes at 298 K

	Gd(HPA-DO3A)	Gd(DOTA)^a	Gd(HP-DO3A)^a	Gd(BT-DO3A)^b
a Ref. 30b, 0.15 M NaCl, 298 K. b Ref. 27, 0.1 M NaCl, 298 K.
k 1 (M^−1 s^−1)	(1.6 ± 0.1) ×10^−4	1.8 ×10^−6	2.9 × 10^−4	2.8 × 10^−5
k d (s^−1) at pH = 7.4	6.41 × 10^−12	7.28 × 10^−14	1.15 × 10^−11	1.35 × 10^−12
t 1/2 (hour) at pH = 7.4	3.00 × 10^7	2.64 × 10^9	1.67 × 10^7	1.42 × 10^8

---

Conclusions

In conclusion, we have shown that acid-catalyzed proton exchange processes can strongly enhance the relaxivity and saturation transfer of Ln^III complexes, when amide protons are present in the proximity of the metal ion coordinated hydroxyl group. A mechanism to explain such behaviour was proposed, which involves protonation, hydrogen-bonding with second sphere water molecules, and a concerted rearrangement of the hydrogen bonds. Moreover, fitting the r₁vs. pH curves allowed the kinetic parameters for the simultaneous double-site proton exchange process to be obtained. This resulted in a k_H value ca. 10 times larger than the typical rate constants for diffusion-controlled proton-exchange, between conjugate acid–base pairs.

Both relaxation and saturation transfer enhancements are pH dependent and they disappear when the hydroxyl group deprotonates at pH 6–7. However, a ¹H and ¹⁷O NMR relaxometric study, at both acidic and neutral pH, demonstrated that no evident differences exist in the relaxation parameters such as τ_M, ΔH_M and τ_R. The water exchange rate is fast (τ_M ≈ 20 ns) in all complexes and a second sphere contribution was considered, to fit the NMRD data.

Furthermore, Gd(HPADO3A) was shown to maintain, and even improve, the thermodynamic stability and kinetic inertness compared to the clinically approved Gd(HPDO3A). This indicates that the presence of the amide substituents attached to the hydroxy-propyl side chain does not alter the thermodynamic and kinetic properties of the resulting Gd^III-complexes.

Finally, it must be emphasised that the acid-catalysed proton exchange is an important approach for relaxivity enhancement. It opens the way for the design of several innovative chemical structures, not only in Ln^III-based agents, but also for other paramagnetic metal complexes that can improve their MRI efficiency via this mechanism. Moreover, the modulation of these proton exchange processes may allow the determination of important physico-chemical parameters (e.g. pH, temperature, concentration of important anions and cations, etc.) in vivo, by classical T₁, CEST-MRI or a combination of these techniques.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

IF acknowledges the Hungarian National Research, Development and Innovation Office (K-124983). LT acknowledges Università del Piemonte Orientale (Ricerca locale 2019). The authors especially thank Laszlo Zekany (University of Debrecen) for help with the simulation of the Z-spectra.

References

1. J. Wahsner, E. M. Gale, A. Rodríguez-Rodríguez and P. Caravan, Chem. Rev., 2019, 119, 957.
2. T. J. Clough, L. Jiang, K.-L. Wong and N. J. Long, Nat. Commun., 2019, 10, 1420.
3. S. Aime, M. Botta, M. Fasano and E. Terreno, Acc. Chem. Res., 1999, 32, 941.
4. D. Delli Castelli, M. C. Caligara, M. Botta, E. Terreno and S. Aime, Inorg. Chem., 2013, 52, 7130.
5. D. Delli Castelli, E. Terreno and S. Aime, Angew. Chem., Int. Ed., 2011, 50, 1798.
6. K. Kumar, C. A. Chang, L. C. Francesconi, D. D. Dischino, M. F. Malley, J. Z. Gougoutas and M. F. Tweedle, Inorg. Chem., 1994, 33, 3567.
7. S. Aime, S. Baroni, D. Delli Castelli, E. Brücher, I. Fábián, S. Colombo Serra, A. Fringuello Mingo, R. Napolitano, L. Lattuada, F. Tedoldi and Z. Baranyai, Inorg. Chem., 2018, 57, 5567.
8. E. Boros, R. Srinivas, H.-K. Kim, A. M. Raitsimring, A. V. Astashkin, O. G. Poluektov, J. Niklas, A. D. Horning, B. Tidos and P. Caravan, Angew. Chem., Int. Ed., 2017, 56, 5603.
9. (a) I. M. Carnovale, M. L. Lolli, S. C. Serra, A. F. Mingo, R. Napolitano, V. Boi, N. Guidolin, L. Lattuada, F. Tedoldi, Z. Baranyai and S. Aime, Chem. Commun., 2018, 54, 10056; (b) L. Leone, D. Esteban-Gomez, C. Platas-Iglesias, M. Milanesio and L. Tei, Chem. Commun., 2019, 55, 513.
10. S. Aime, A. Barge, M. Botta, D. Parker and A. S. De Sousa, J. Am. Chem. Soc., 1997, 119, 4767.
11. (a) M. P. Lowe, D. Parker, O. Reany, S. Aime, M. Botta, G. Castellano, E. Gianolio and R. Pagliarin, J. Am. Chem. Soc., 2001, 123, 7601; (b) N. Vologdin, G. A. Rolla, M. Botta and L. Tei, Org. Biomol. Chem., 2013, 11, 1683.
12. (a) G. B. Giovenzana, R. Negri, G. A. Rolla and L. Tei, Eur. J. Inorg. Chem., 2012, 2035; (b) Z. Baranyai, G. A. Rolla, R. Negri, A. Forgacs, G. B. Giovenzana and L. Tei, Chem.–Eur. J., 2014, 20, 2933.
13. A. R. Goldfarb, A. Mele and N. Gutstbin, J. Am. Chem. Soc., 1955, 77, 6194.
14. R. S. Molday and R. G. Kallen, J. Am. Chem. Soc., 1972, 94, 6739.
15. A. Berger, A. Loewenstein and S. Meiboom, J. Am. Chem. Soc., 1959, 81, 62.
16. M. Eigen, Angew. Chem., Int. Ed., 1964, 3, 1.
17. D. E. Woessner, S. Zhang, M. E. Merritt and A. Dean Sherry, Magn. Reson. Med., 2005, 53, 790.
18. L. Leone, G. Ferrauto, M. Cossi, M. Botta and L. Tei, Front. Chem., 2018, 6, 158.
19. (a) N. B. Solomon, J. Chem. Phys., 1956, 25, 261; (b) N. Bloembergen and L. O. Morgan, J. Chem. Phys., 1961, 34, 842; (c) J. H. Freed, J. Chem. Phys., 1978, 68, 4034.
20. (a) T. J. Swift and R. E. Connick, J. Chem. Phys., 1962, 37, 307; (b) T. J. Swift and R. E. Connick, J. Chem. Phys., 1964, 41, 2553.
21. G. Ferrauto, D. Delli Castelli, L. Leone, M. Botta, S. Aime, Z. Baranyai and L. Tei, Chem.–Eur. J., 2019, 25, 4184.
22. M. Botta, Eur. J. Inorg. Chem., 2000, 399.
23. R. Delgado and J. J. R. F. Da Silva, Talanta, 1982, 29, 815.
24. E. T. Clarke and A. E. Martell, Inorg. Chim. Acta, 1991, 190, 27.
25. W. P. Cacheris, S. K. Nickle and A. D. Sherry, Inorg. Chem., 1987, 26, 958.
26. K. Kumar, M. F. Tweedle, M. F. Malley and J. Z. Gougoutas, Inorg. Chem., 1995, 34, 6472.
27. E. Toth, R. Kiraly, J. Platzek, B. Raduchel and E. Brucher, Inorg. Chim. Acta, 1996, 249, 191.
28. S. Hajela, M. Botta, S. Giraudo, J. Xu, K. N. Raymond and S. Aime, J. Am. Chem. Soc., 2000, 122, 11228.
29. É. Tóth, E. Brücher, I. Lázár and I. Tóth, Inorg. Chem., 1994, 33, 4070.
30. (a) K. Kumar, T. Jin, X. Wang, F. Desreux and M. F. Tweedle, Inorg. Chem., 1994, 33, 3823; (b) Z. Baranyai, Z. Pálinkás, F. Uggeri, A. Maiocchi, S. Aime and E. Brücher, Chem.–Eur. J., 2012, 18, 16426.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental details: synthetic procedures, thermodynamic, kinetic and relaxivity parameters of Gd complexes, CEST spectra and images, ¹H and ¹³C NMR spectra, LC-MS traces and HRMS of ligands and complexes. See DOI: 10.1039/d0sc02174a

---