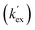Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Unusually high α-proton acidity of prolyl residues in cyclic peptides†
Oliver R.
Maguire‡
 a,
Bethany
Taylor
a,
Eleanor M.
Higgins
a,
Matthew
Rees
b,
Steven L.
Cobb
a,
Bethany
Taylor
a,
Eleanor M.
Higgins
a,
Matthew
Rees
b,
Steven L.
Cobb
 a,
Nigel S.
Simpkins
a,
Nigel S.
Simpkins
 b,
Christopher J.
Hayes
b,
Christopher J.
Hayes
 c and
AnnMarie C.
O'Donoghue
c and
AnnMarie C.
O'Donoghue
 *a
*a
aDepartment of Chemistry, Durham University, South Road, Durham DH1 3LE, UK. E-mail: annmarie.odonoghue@durham.ac.uk
bSchool of Chemistry, University of Birmingham, Edgbaston, Birmingham, B15 2TT, UK
cSchool of Chemistry, University of Nottingham, University Park, Nottingham, NG7 2RD, UK
First published on 2nd July 2020
Abstract
The acidity of the α-proton in peptides has an essential role in numerous biochemical reactions and underpins their stereochemical integrity, which is critical to their biological function. We report a detailed kinetic and computational study of the acidity of the α-proton in two cyclic peptide systems: diketopiperazine (DKP) and triketopiperazine (TKP). The kinetic acidity (protofugality) of the α-protons were determined though hydrogen deuterium exchange studies in aqueous solutions. The acidities of the α-proton in prolyl residues were increased by 3–89 fold relative to other amino acid residues (prolyl > glycyl ≫ alanyl > tyrosyl). Experimental and computational evidence for the stereoelectronic origins of this enhanced prolyl reactivity is presented. TKPs were 106-fold more reactive than their DKP analogues towards deprotonation, which we attribute to the advanced development of aromaticity in the earlier transition state for proton transfer in these cases. A Brønsted linear free energy analysis of the reaction data was conducted to provide estimates of α-proton pKas.
Introduction
Proline is unique amongst the proteinogenic amino acids in its ability to induce structural and conformational modifications in proteins.1 These unique characteristics are often linked to proline being the only proteinogenic amino acid with a secondary N-terminal amino functionality. The resulting effect this has upon conformations of (a) the cis–trans isomers of the prolyl amide bond, and, (b) the endo/exo ring pucker of the pyrrolidine ring of proline, which links nitrogen to the α-carbon position, combine together to play a crucial role in the establishment of the correct secondary structure during protein folding.2,3 The rate of Xaa-Pro cis/trans isomerism has been shown to be a rate-limiting step in the folding of proteins.4,5 Additionally, the proliferation of prolyl residues in the enzymes of thermophilic organisms has been linked to enhanced protein stabilities in more extreme host environments.6,7Many of the contributions that prolyl residues make to protein structure and stability are underpinned by stereoelectronic effects. The gauche effect from substitution of the 4-position plays an important role in the endo/exo ring pucker of the pyrrolidine ring which affects protein structure.2,3,8,9 The cumulative effects of n-to-π* interactions from proline and 4-hydroxyproline residues have been shown to contribute significantly to protein stability, as exemplified in the case of collagen.2,10,11
The unique chemistry of proline is not confined to influences on protein structures and stabilities. Proline and small-molecule derivatives have been widely shown to be efficient, stereoselective catalysts for a range of (bio)organic transformations.12–17 The superior abilities of proline derivatives as organocatalysts compared with other amino acids is often ascribed to the increased nucleophilicity of the prolyl secondary amine and influence on cis/trans isomerism in enamine intermediates.18–24 Mayr and co-workers have demonstrated a 100-fold increased nucleophilicity of the secondary amino group of proline towards reaction with diarylcarbenium ions relative to the primary amino groups of other amino acids.25 Myers and Raines recently reported a detailed kinetic study of the hydrogen–deuterium exchange reactions of cyclohexanone catalysed by proline derivatives in aqueous solution. Their kinetic structure–activity analysis demonstrated that inter- and intramolecular electrostatic interactions involving charged and electron-rich atoms derived from the proline catalyst, cyclohexanone substrate and buffer can have dramatic influences on catalytic activity.26 Moreover, Xaa-Pro bonds are a highly conserved structural motif for catalytically active peptides27–32 for which cis/trans isomerization has been directly linked to the stereoselectivity of the peptide catalyst.33 Finally, the enhanced catalytic ability of proline has broader implications in the origin of chirality in prebiotic chemistry.34–41 For example, Blackmond and co-workers reported that L-proline alkyl ammonium salts can induce the formation of an enantiomeric excess of D-sugars in the formose reaction.42
Herein we report an additional unique property of proline in the substantial enhancement of the acidity of its α-proton relative to other amino acids in cyclic peptide systems. As the simplest examples of cyclic peptides, we have chosen 2,5-diketopiperazine (DKP) and triketopiperazine (TKP) systems (Fig. 1). We undertook a series of hydrogen–deuterium exchange studies to determine the kinetic lability, or protofugality,43 of the α-protons in these DKPs and TKPs. Second order rate constants for base-catalysed exchange were observed to be substantially higher for prolyl containing DKPs and TKPs. Furthermore, the TKPs were orders of magnitude more kinetically labile towards deprotonation than DKPs. Rate constants for deprotonation could be correlated using the Brønsted linear free energy relationship to shed light on the enhanced acidities (protofugalities) in these cyclic peptide systems and to provide estimates of α-carbon acid pKas. Electronic structure calculations replicated experimental trends and led to further insight into the stereochemical origins of the enhanced lability of the prolyl α-protons in these DKPs and the role of aromaticity in the deprotonation of TKP α-protons. These data provide new insight into the fundamental properties of prolyl-containing cyclic peptide systems to inform synthetic and biological applications for which the stereochemical integrity of peptide derivatives, both in solution and in vivo, is crucial.44–46
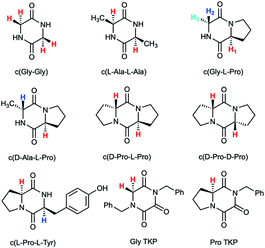 | ||
| Fig. 1 Diketopiperazines (DKPs) and triketopiperazines (TKPs) used in our hydrogen–deuterium exchange study of α-protons. The exchangeable protons of interest are highlighted. | ||
Results and discussion
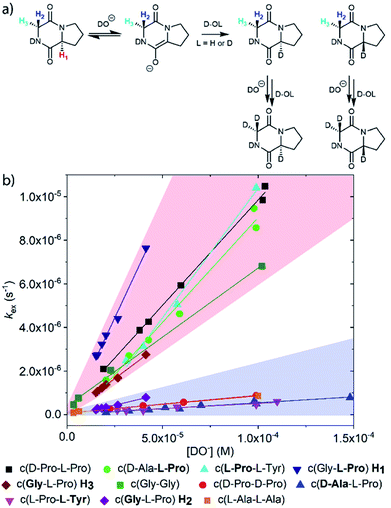
Deuterium exchange of diketopiperazines (DKPs)
DKPs are small cyclic dipeptides found in many natural products and are also common by-products in solid phase peptide synthesis.44 Owing to their prevalence in pharmaceutically important compounds and their non-planar structure, DKPs have acquired the status of privileged structures in medicinal chemistry.44,47 We determined the reactivity towards deprotonation of the α-protons for a range of 2,5-DKPs in Fig. 1, which were prepared readily by cyclisation of appropriate protected linear peptides or were commercially available (ESI†). The reactions were analysed by 1H NMR spectroscopy in carbonate or 3-chloroquinuclidine buffered D2O solutions in the pD range 9.35–10.94 at 25 °C and ionic strength I = 1.0 (KCl). Outside this pD range, the exchange reactions were either too fast or slow for NMR kinetic analysis. The unambiguous observation of hydrogen–deuterium exchange supports a mechanism involving enolate formation (Fig. 2a), where exchange is accompanied by epimerization (see ESI† for details of kinetic evaluation). Fig. 2b shows the dependence of the observed first order rate constants of exchange, kex (s−1), upon deuteroxide concentration for the DKPs. A clear first order dependence on deuteroxide concentration is observed, however, no significant additional general base catalysis of exchange was detectable. The slopes of linear fits of the H/D-exchange kinetic data are the second order rate constants for deuteroxide catalysed exchange, kDO (M−1 s−1) (Table 1).| k DO (M−1 s−1) | k HO (M−1 s−1) | k rel | pKad | |
|---|---|---|---|---|
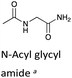
| a H/D-exchange kinetic data for N-acyl glycyl amide, a linear analogue of a DKP, is included for comparison.48 b Calculated from experimental kDO values using a secondary solvent isotope effect kDO/kHO = 2.00 (see text). c k rel = relative rate constants for deprotonation compared to value for linear N-acyl glycyl amide as reference. The krel values have been statistically corrected for the number of exchangeable protons. d Interpolated values from a Brønsted analysis (see text). | ||||
| c(Gly–Gly) | 6.33 × 10−2 | 3.17 × 10−2 | 12.2 | 20.9 |
| c(L-Ala–L-Ala) | 7.80 × 10−3 | 3.90 × 10−3 | 3.00 | 22.7 |
| c(Gly–L-Pro) | 1.87 × 10−1 | 9.35 × 10−2 | 144 | 18.8 |
| c(H2-Gly–L-Pro) | 2.09 × 10−2 | 1.05 × 10−2 | 16.2 | 21.2 |
| c(H3-Gly–L-Pro) | 6.59 × 10−2 | 3.30 × 10−2 | 50.8 | 19.9 |
| c(D-Ala–L-Pro) | 9.45 × 10−2 | 4.73 × 10−2 | 72.8 | 19.6 |
| c(D-Ala–L-Pro) | 5.51 × 10−3 | 2.76 × 10−3 | 4.25 | 22.6 |
| c(D-Pro–L-Pro) | 9.69 × 10−2 | 4.85 × 10−2 | 37.3 | 20.0 |
| c(D-Pro–D-Pro) | 8.62 × 10−3 | 4.31 × 10−3 | 3.30 | 22.6 |
| c(L-Pro–L-Tyr) | 1.19 × 10−1 | 5.95 × 10−2 | 91.5 | 19.3 |
| c(L-Pro–L-Tyr) | 2.09 × 10−3 | 1.05 × 10−3 | 1.60 | 23.7 |
|
2.6 × 10−3 | 1.3 × 10−3 | 1.00 | 23.9 |
The comparison of reactivities towards deprotonation by a common base, DO−, allows for the determination of a DKP Brønsted kinetic acidity scale (or protofugality scale).43 The observed kinetic acidity (protofugalities) (kDO) of the DKP amino acid residues fall into two broad regions with Pro and Gly (red region) being substantially more kinetically acidic than Ala and Tyr (blue region) according to the following acidity trend:
| Pro > Gly ≫ Ala > Tyr |
The Gly and Ala residues follow expected trends with Ala being less acidic than Gly due to inductive destabilisation by the electron donating methyl group of the carbanion/enolate formed upon deprotonation by DO−. The lower reactivity of Tyr could be due to the significant geometric rearrangement required upon enolate formation, which raises the barrier to deprotonation. The phenol(ate) ring of Tyr prefers a folded conformation over the DKP ring in the keto form.49 The change from sp3 to sp2 hybridisation upon enolate formation would enforce a more open conformation of the phenol(ate) ring with greater solvent exposure and an associated entropic penalty.50
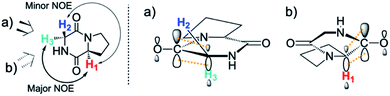
By contrast, the prolyl residues were more acidic than all other DKP residues with kDO from 3–89-fold larger (apart from c(D-Pro–D-Pro)). A stereoelectronic effect is proposed as the major origin of the enhanced rates of deprotonation (higher protofugalities) of the Pro Cα-protons in DKPs. Evidence for the contribution of a stereoelectronic effect initially came from the two glycyl α-protons H2 and H3 in c(Gly–L-Pro), which were found to have a 3.1-fold difference in reactivity towards DO− (H2: kDO = 2.09 × 10−2 M−1 s−1; H3: kDO = 6.59 × 10−2 M−1 s−1). The higher 1H NMR chemical shift of the glycyl H3 proton (4.03 ppm) relative to the H2 proton (3.74 ppm) suggests a greater elongation of the C–H3 bond possibly as a result of an enhanced σC–H to 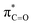 interaction (Fig. 3a).
interaction (Fig. 3a).
This stereoelectronic effect can also be present for the Pro α-proton in c(Gly–L-Pro) (H1, Fig. 3b) to explain the substantially increased reactivity towards deprotonation. The additional conformational restrictions imposed by the pyrrolidine ring predisposes Pro residues towards an optimal stereoelectronic alignment of the σC–H and 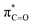 orbitals for deprotonation of the Pro α-proton. The NOESY spectrum of c(Gly–L-Pro) in Fig. S1.†36 Shows the glycyl H3 α-proton at 4.03 ppm has a larger coefficient of interaction with the prolyl H1 α-proton at 4.17 ppm than the glycyl H2 α-proton at 3.74 ppm. This suggests that H1 in c(Gly–L-Pro) lies on the same face of the DKP as H3, which similarly enhances the orbital overlap between the σC–H and
orbitals for deprotonation of the Pro α-proton. The NOESY spectrum of c(Gly–L-Pro) in Fig. S1.†36 Shows the glycyl H3 α-proton at 4.03 ppm has a larger coefficient of interaction with the prolyl H1 α-proton at 4.17 ppm than the glycyl H2 α-proton at 3.74 ppm. This suggests that H1 in c(Gly–L-Pro) lies on the same face of the DKP as H3, which similarly enhances the orbital overlap between the σC–H and 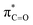 , lowering the barrier to enolate formation.
, lowering the barrier to enolate formation.
To gain further insight into the stereoelectronic effect we performed electronic calculations with c(Gly–L-Pro) at the BMK/6-31+g(d) level. An NBO analysis shows that the computed C–H bond lengths increased in the order C–H2 < C–H3 < C–H1 which is in agreement with the observed lability order of C–H1 > C–H3 > C–H2 (Table 2). The calculated structures confirmed that the prolyl H1 and glycyl H3 are located on the same face of the DKP ring. The computed structures and energies of enolates resulting from DKP deprotonation also corroborate the deuterium exchange kinetic data. The Pro-derived enolate is 2.6 kcal mol−1 more stable than the Gly-enolate formed from c(Gly–L-Pro).
Larger kDO values are also observed for c(D-Ala–L-Pro), c(D-Pro–L-Pro) and c(L-Pro–L-Tyr). The absence of such an effect in c(D-Pro–D-Pro) can be attributed to the inter-dependent conformational preferences between the two pyrrolidine and DKP rings in the Pro–Pro case.51 Fig. S3.1† compares the starting DKPs and transition state structures for deprotonation of both c(D-Pro–L-Pro) and c(D-Pro–D-Pro) by LiOH using a solvation model for water at the BMK/6-31+g(d) level. The energies of the two transition states are similar. The main difference in activation barriers comes from the difference in energies of the two DKP starting materials with the central DKP ring of c(D-Pro–D-Pro) adopting a boat conformation and the pyrrolidine ring a more stable envelope conformation. By contrast, the planar DKP ring of c(D-Pro–L-Pro) enforces a less-stable half-chair pyrrolidine conformation increasing the energy of the reactant.
To our knowledge, there has been no reported kinetic study of the H/D exchange reactions of the α-protons of DKPs in biologically-relevant aqueous solution, although the acidity of the amide protons have been studied.52 Coote and Easton have examined the H/D exchange reactions of Gly, Ala and Leu-derived DKPs in non-aqueous d6-acetone with DBU as base at 50 °C.53 Their results indicated that N-substitution had a greater effect upon the acidity of the remote, as opposed to the adjacent, α-protons in the DKP ring.54 In our study the additional N-substitution derived from the pyrrolidine ring of Pro does not reduce the acidity of the remote α-protons of glycine and alanine residues relative to c(Gly–Gly) and c(L-Ala–L-Ala), respectively. However, as prolyl residues were not studied by Coote and Easton, a direct comparison is not possible.
Cyclisation effects on proton transfer
To further assess the effect of cyclisation, we can compare our data for the DKPs with analogous data for linear peptide derivatives. Richard and co-workers have reported extensive, detailed studies of the H/D-exchange reactions of non-cyclic amino acids and peptides in aqueous solution.48,55–60 We have chosen to compare our data with their reported kDO value48 for the Gly α-protons of N-acyl glycyl amide as a reference (krel, Table 1), owing to its overall neutrality and equivalent chain atoms to the central DKP ring. With the exception of the Tyr residue of c(L-Pro–L-Tyr), all other amino acid residues show a significant increase in kinetic acidity (protofugality) upon cyclisation to a DKP.In particular, it can be calculated that the prolyl α-proton in a DKP experiences the largest increase in kDO compared to the linear system by over two orders of magnitude (krel = 144). Richard and co-workers reported near identical kDO values (∼4.5 × 10−5 M−1 s−1) for the amino acids glycine and proline showing the lack of any significant stereoelectronic effects prior to cyclisation.60 Our new data highlights that cyclisation of a peptide substantially increases the labilities of the α-protons, which can be further enhanced by stereoelectronic factors especially in the case of Pro residues.
Deuterium exchange of triketopiperazines (TKPs)
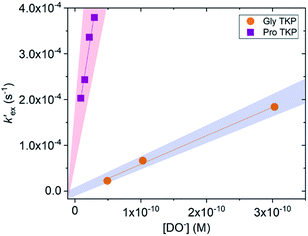
To further explore the enhanced acidity of the prolyl α-protons we also undertook deuterium exchange studies of the α-protons in two TKP systems (Fig. 1). TKPs are masked amino acids of similar structure to DKPs but with a carbonyl at the C2-position instead of a second sp3 α-carbon (Fig. 1).61 TKPs have recently been demonstrated to be excellent substrates in organocatalytic asymmetric Michael addition reactions. This has enabled highly enantioselective access to chiral TKPs and DKPs,62 α-CF3 amides,63 bicyclo[2.2.2]diazaoctanes related to the prenylated alkaloid family,64 prolinamides and 2,7-diazabicyclo[2.2.1]heptanes.65 To the best of our knowledge there has been no reported H/D-exchange reaction of TKPs in any solvent.The H/D-exchange reactions of the TKPs were six orders of magnitude faster than observed for all the DKPs. At pD values above 6, the H/D-exchange reactions were too fast to follow by 1H NMR spectroscopy and significant hydrolytic ring-opening was observed. The H/D-exchange could be monitored in acetate buffers in the pD range 4.76–6.29 at 25 °C and ionic strength, I = 0.06 (KCl) for the prolyl TKP and I = 0.2 (KCl) for the glycyl TKP. Rates of deuterium exchange continued to decrease at lower pDs. Owing to the poor solubility of both TKPs in fully aqueous solution, kinetic studies were performed with a 40% d3-MeCN co-solvent (ESI†).
Unlike the DKPs, significant general base catalysis was observed for the TKPs. The kDO values are obtained as the slope of a plot of buffer-independent 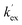 values against DO− concentration (Fig. 4). Individual
values against DO− concentration (Fig. 4). Individual 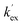 were obtained as y-axis intercepts of plots of kobsex values versus buffer concentration ([AcO−]) at a constant pD (†). The kDO values were ∼106-fold higher for both TKPs compared with all the DKPs (Table 3). Furthermore, the prolyl effect was also observed in the TKPs, with the prolyl TKP being 17-fold more acidic than the glycyl TKP, indicating the generality of the prolyl effect in cyclic systems.
were obtained as y-axis intercepts of plots of kobsex values versus buffer concentration ([AcO−]) at a constant pD (†). The kDO values were ∼106-fold higher for both TKPs compared with all the DKPs (Table 3). Furthermore, the prolyl effect was also observed in the TKPs, with the prolyl TKP being 17-fold more acidic than the glycyl TKP, indicating the generality of the prolyl effect in cyclic systems.
| k AcO− (M−1 s−1) | k DO (M−1 s−1) | k HO (M−1 s−1) | |
|---|---|---|---|
| a k AcO− is the second order rate constant for deprotonation by acetate anion and was obtained as the slope of kobsexversus buffer concentration plots at pD 6.28 for Gly TKP and pD 4.76–5.28 for Pro TKP. b A secondary solvent isotope effect of kDO/kHO = 1.46 was used to convert kDO to kHO. | |||
| Gly TKP | 7.21 × 10−2 | 5.09 × 105 | 6.40 × 104 |
| Pro TKP | 1.61 × 10−2 | 8.99 × 106 | 1.14 × 106 |
The six orders of magnitude increase in kDO is markedly larger than would be expected from an increased inductive effect caused by the inclusion of an additional carbonyl in the TKP versus DKP rings. Similarly, the 40% d3-MeCN co-solvent is expected to alter the observed rate constant by no more than ∼10-fold based on previous H/D-exchange studies of a range of carbon acids.66 The rate constants for enolate formation in TKPs (kDO = 5.09 × 105 to 8.99 × 106 M−1 s−1) are closer to that for the formation of the aromatic phenolate anion from cyclohexa-2,5-dienone (kHO = 2.0 × 106 M−1 s−1).67
In order to account for this significant rate enhancement, the contribution of aromaticity to transition state stabilisation is invoked. Our BMK/6-31+G calculations revealed the highly delocalised nature of the HOMO of the TKP enolate (Fig. 5, S3.2.4 and S3.2.5†), which clearly shares the same features as 2,3,6-trihydroxypyrazine, a structurally comparable aromatic model compound. The role of aromaticity in transition state stabilisation is well known e.g. for Diels–Alder reactions.68 A computational analysis of the contribution that aromaticity makes to the stability of the transition state for carbon acid deprotonation has been performed by Bernasconi and co-workers.69 Based upon these calculations, Bernasconi concluded that only minor progress in the formation of the product aromatic molecular orbitals is required in order for the transition state to take advantage of aromaticity for stabilisation. This is also supported by experimental observations.70–74 Thus, aromatic character could potentially stabilise the transition state for formation of the TKP enolate, prior to significant solvent reorganisation, explaining the substantially enhanced acidity of the α-protons.
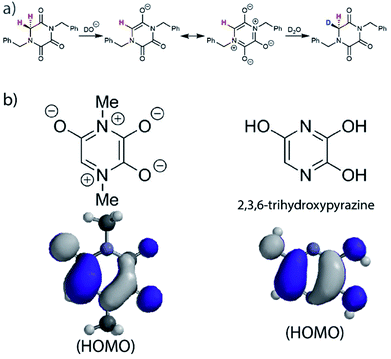 | ||
| Fig. 5 (a) Proposed mechanism of hydrogen–deuterium exchange via enolate formation for Gly TKP; (b) resonance structures and HOMOs for the fully delocalised TKP enolate and 2,3,6-trihydroxypyrazine. | ||
Brønsted linear free energy analysis: estimates for the α-carbon acid pKas
The kinetic acidities (protofugalities) (kDO) measured above can be correlated to the thermodynamic pKas of the carbon acids through a Brønsted linear free energy relationship (LFER). For the series of neutral α-carbonyl compounds in Fig. 6a, Richard and co-workers have reported an extended linear Brønsted correlation between experimental rate constants for hydroxide-catalysed α-deprotonation (kHO) and the corresponding carbon acid pKas of a series of α-carbonyl acids (eqn (1); Fig. 6b, □) with β = −0.401.77,78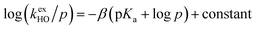 | (1) |
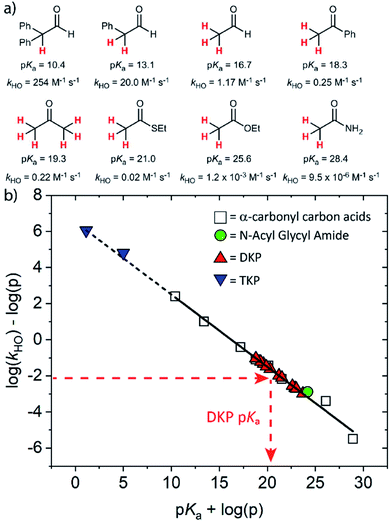 | ||
Fig. 6 (a) α-Carbonyl compounds (□) used to construct the Brønsted LFER below with data from Richard and co-workers;48,57–60,75–77 (b) Brønsted linear free energy relationship between log(kHO/p) and pKa for the series of α-carbonyl carbon acids above (□). The data is fitted with log(kHO/p) = −0.401pKa + log(p) + 6.51 (—) where p = number of acidic α-CH protons. Kinetic data for the DKPs ( ) and N-acyl glycyl amide ( ) and N-acyl glycyl amide ( ) can be used to interpolate corresponding pKa values using eqn (1), whereas kinetic data for TKPs ( ) can be used to interpolate corresponding pKa values using eqn (1), whereas kinetic data for TKPs ( ) would require significant extrapolation. ) would require significant extrapolation. | ||
As DKPs are also neutral α-carbonyl acids, estimates of pKa values can therefore be obtained from combining the experimental kDO values for DKPs measured herein with the Brønsted LFER (Fig. 6b,  ). This assumes that a constant intrinsic barrier to proton transfer with changes in pKa, which underpins the linear Brønsted correlation observed for the series in Fig. 6a, also applies to the DKPs. Prior to use of the kDO values on the Brønsted LFER, it is necessary to correct for a secondary solvent isotope effect (which typically range from kDO/kHO = 1.36–2.40).57,75 We used an intermediate secondary solvent isotope effect of kDO/kHO = 2.0 to estimate the kHO values in Table 1, which is consistent with a specific base-catalysed proton transfer process.48,57 The interpolated pKa values in Table 1 fall in the following ranges: pKa (Pro) = 18.8–22.6; pKa (Gly) = 19.9–21.2; pKa (Ala) = 22.6–22.7; pKa (Tyr) = 23.7.
). This assumes that a constant intrinsic barrier to proton transfer with changes in pKa, which underpins the linear Brønsted correlation observed for the series in Fig. 6a, also applies to the DKPs. Prior to use of the kDO values on the Brønsted LFER, it is necessary to correct for a secondary solvent isotope effect (which typically range from kDO/kHO = 1.36–2.40).57,75 We used an intermediate secondary solvent isotope effect of kDO/kHO = 2.0 to estimate the kHO values in Table 1, which is consistent with a specific base-catalysed proton transfer process.48,57 The interpolated pKa values in Table 1 fall in the following ranges: pKa (Pro) = 18.8–22.6; pKa (Gly) = 19.9–21.2; pKa (Ala) = 22.6–22.7; pKa (Tyr) = 23.7.
Consistent with the observed higher rate constants for exchange for the Pro residues, the interpolated pKas were 2–4 units lower than for other residues. Coote and Easton have previously calculated the α-carbon pKas of c(Gly–Gly) and c(L-Ala–L-Ala) DKPs computationally as 24.0 and 26.1, respectively.54 The 3–4 unit difference from the interpolated values could potentially result from the solvation model used in computational calculations, or alternatively from the need to account for enhanced stereoelectronic effects upon cyclisation.
Using the same Brønsted analysis for TKPs requires an extensive 3–4 unit extrapolation ( ) beyond the data in the existing correlation to predicted pKas of 5.00 and 1.13 for the glycyl and prolyl TKPs, respectively (Fig. 6b,
) beyond the data in the existing correlation to predicted pKas of 5.00 and 1.13 for the glycyl and prolyl TKPs, respectively (Fig. 6b,  ). These extremely low predicted values would require the observation of the TKP enolate for pD values ≥ pKa, and rate-constants for re-protonation/deuteration should be slow relative to deprotonation. In our NMR experiments, deuterium exchange was clearly evident by the observation of an upfield triplet owing to α-CHD of the mono-deuterated glycyl TKP (Fig. S2.1†) showing that facile reprotonation occurs. Furthermore, no additional new NMR peaks were present that could be attributed to TKP enolate in both the glycyl and prolyl cases. This clearly demonstrates that the above Brønsted analysis is not appropriate for TKPs and highlights the significant difference of these systems from both DKPs and simple, non-cyclic α-carbonyl acids.
). These extremely low predicted values would require the observation of the TKP enolate for pD values ≥ pKa, and rate-constants for re-protonation/deuteration should be slow relative to deprotonation. In our NMR experiments, deuterium exchange was clearly evident by the observation of an upfield triplet owing to α-CHD of the mono-deuterated glycyl TKP (Fig. S2.1†) showing that facile reprotonation occurs. Furthermore, no additional new NMR peaks were present that could be attributed to TKP enolate in both the glycyl and prolyl cases. This clearly demonstrates that the above Brønsted analysis is not appropriate for TKPs and highlights the significant difference of these systems from both DKPs and simple, non-cyclic α-carbonyl acids.
Biological relevance
In addition to highlighting the uniquely high kinetic lability and acidity of α-protons in prolyl-containing cyclic peptides, these new data also present an alternative rationale for the origin of catalysis in amino acid-utilising enzymes. The carbon acidity of α-carbonyl compounds is crucial to many key biological reactions and an understanding of how enzymes enhance the rate of deprotonation is vital to probing metabolic processes.55,79 The restrictions on the conformation of an amino acid residue within a DKP has been shown herein to enhance the lability of the α-proton by up to 144-fold relative to a linear, non-cyclic reference, thereby reducing the barrier to deprotonation by up to ∼12.1 kJ mol−1. In the more restricted environment of an enzyme active site, a reduction in conformational mobility could similarly allow for enhanced σC–H and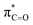 interactions in non-cyclic, linear peptides and particularly for prolyl-containing systems. This provides an alternative potential origin for enzymatic rate enhancement in non-co-factor dependent amino acid racemases.60,80 Recently, a new type of prolyl hydroxylation at the Cα-position was identified in the active site of polysaccharide deacetylases.81 The enhanced acidity of the prolyl group identified here could in principle aid the oxidation of the Cα-position by molecular oxygen in order to form the 2-hydroxyproline.82
interactions in non-cyclic, linear peptides and particularly for prolyl-containing systems. This provides an alternative potential origin for enzymatic rate enhancement in non-co-factor dependent amino acid racemases.60,80 Recently, a new type of prolyl hydroxylation at the Cα-position was identified in the active site of polysaccharide deacetylases.81 The enhanced acidity of the prolyl group identified here could in principle aid the oxidation of the Cα-position by molecular oxygen in order to form the 2-hydroxyproline.82
Conclusions
We have demonstrated herein that the α-protons in Pro residues in DKP cyclic peptides have unexpectedly high rate constants of deprotonation, between 3 – 89-fold greater than other DKP amino acid residues studied. Evidence for the stereoelectronic origins of this prolyl effect was presented. Furthermore, our data highlights that cyclisation of a linear peptide substantially increases the labilities of the α-protons, which can be further enhanced by stereoelectronic factors especially in the case of Pro residues. Brønsted analysis was performed to provide estimates of DKP pKas.Our study also reveals the exceptionally enhanced α-kinetic acidity by up to six orders of magnitude of TKP cyclic peptides relative to DKPs, which can be rationalised by invoking an aromatic-like transition state for deprotonation in the former case. Rate constants for proton transfer in the TKPs are similar to that for the formation of the aromatic phenolate anion from cyclohexa-2,5-dienone. In TKP systems the enhanced acidity of the prolyl residue was also observed.
Our results thus demonstrate a new unique property for the chemistry of proline derivatives: the enhanced acidity of prolyl residue α-protons. The observation of this effect in both DKPs and TKPs indicates the generality of this effect in cyclic peptides. Future work by us will additionally probe the interplay between the effect of 4-Pro substitution, usually attributed to the gauche effect, and α-proton kinetic acidity.
Experimental
Synthetic procedures, preparation of solutions, NMR and kinetic methods to monitor deuterium exchange reactions, kinetic evaluation and electronic structure calculations are found in the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful for the help of Drs Alan Kenwright, Catharine Heffernan and Juan Aguilar (Durham NMR service). The authors thank EPSRC for a studentship for ORM (EPSRC DTA, 1213247).Notes and references
- M. W. MacArthur and J. M. Thornton, J. Mol. Biol., 1991, 218, 397–412 CrossRef CAS PubMed
.
- L. E. Bretscher, C. L. Jenkins, K. M. Taylor, M. L. DeRider and R. T. Raines, J. Am. Chem. Soc., 2001, 123, 777–778 CrossRef CAS PubMed
.
- S. J. M. Verhoork, P. M. Killoran and C. R. Coxon, Biochemistry, 2018, 57, 6132–6143 CrossRef CAS PubMed
.
- G. Fischer, Chem. Soc. Rev., 2000, 29, 119–127 RSC
.
- W. J. Wedemeyer, E. Welker and H. A. Scheraga, Biochemistry, 2002, 41, 14637–14644 CrossRef CAS PubMed
.
- L. Sawle and K. Ghosh, Biophys. J., 2011, 101, 217–227 CrossRef CAS
.
- C. Vieille and G. J. Zeikus, Microbiol. Mol. Biol. Rev., 2001, 65, 1 CrossRef CAS PubMed
.
- B. Holzberger, S. Obeid, W. Welte, K. Diederichs and A. Marx, Chem. Sci., 2012, 3, 2924–2931 RSC
.
- P. K. Mykhailiuk, V. Kubyshkin, T. Bach and N. Budisa, J. Org. Chem., 2017, 82, 8831–8841 CrossRef CAS PubMed
.
- R. W. Newberry and R. T. Raines, Acc. Chem. Res., 2017, 50, 1838–1846 CrossRef CAS PubMed
.
- R. W. Newberry, B. VanVeller, I. A. Guzei and R. T. Raines, J. Am. Chem. Soc., 2013, 135, 7843–7846 CrossRef CAS PubMed
.
- B. List, R. A. Lerner and C. F. Barbas, J. Am. Chem. Soc., 2000, 122, 2395–2396 CrossRef CAS
.
- A. Bøgevig, K. Juhl, N. Kumaragurubaran, W. Zhuang and K. A. Jørgensen, Angew. Chem., Int. Ed., 2002, 41, 1790–1793 CrossRef
.
- G. Zhong, Angew. Chem., Int. Ed., 2003, 42, 4247–4250 CrossRef CAS PubMed
.
- S. P. Brown, M. P. Brochu, C. J. Sinz and D. W. C. MacMillan, J. Am. Chem. Soc., 2003, 125, 10808–10809 CrossRef CAS PubMed
.
- S. Mukherjee, J. W. Yang, S. Hoffmann and B. List, Chem. Rev., 2007, 107, 5471–5569 CrossRef CAS PubMed
.
- R. J. Spears, R. L. Brabham, D. Budhadev, T. Keenan, S. McKenna, J. Walton, J. A. Brannigan, A. M. Brzozowski, A. J. Wilkinson, M. Plevin and M. A. Fascione, Chem. Sci., 2018, 9, 5585–5593 RSC
.
- H. Iwamura, D. H. Wells, S. P. Mathew, M. Klussmann, A. Armstrong and D. G. Blackmond, J. Am. Chem. Soc., 2004, 126, 16312–16313 CrossRef CAS PubMed
.
- S. P. Mathew, H. Iwamura and D. G. Blackmond, Angew. Chem., Int. Ed., 2004, 43, 3317–3321 CrossRef CAS PubMed
.
- M. B. Schmid, K. Zeitler and R. M. Gschwind, Angew. Chem., Int. Ed., 2010, 49, 4997–5003 CrossRef CAS PubMed
.
- J. E. Hein, J. Burés, Y.-h. Lam, M. Hughes, K. N. Houk, A. Armstrong and D. G. Blackmond, Org. Lett., 2011, 13, 5644–5647 CrossRef CAS PubMed
.
- M. B. Schmid, K. Zeitler and R. M. Gschwind, Chem. Sci., 2011, 2, 1793–1803 RSC
.
- J. Burés, A. Armstrong and D. G. Blackmond, Acc. Chem. Res., 2016, 49, 214–222 CrossRef PubMed
.
- P. Renzi, J. Hioe and R. M. Gschwind, Acc. Chem. Res., 2017, 50, 2936–2948 CrossRef CAS PubMed
.
- F. Brotzel and H. Mayr, Org. Bio. Chem., 2007, 5, 3814–3820 RSC
.
- E. L. Myers, M. J. Palte and R. T. Raines, J. Org. Chem., 2019, 84, 1247–1256 CrossRef CAS PubMed
.
- P. Krattiger, R. Kovasy, J. D. Revell, S. Ivan and H. Wennemers, Org. Lett., 2005, 7, 1101–1103 CrossRef CAS PubMed
.
- V. D'Elia, H. Zwicknagl and O. Reiser, J. Org. Chem., 2008, 73, 3262–3265 CrossRef PubMed
.
- M. Wiesner, J. D. Revell and H. Wennemers, Angew. Chem., Int. Ed., 2008, 47, 1871–1874 CrossRef CAS PubMed
.
- M. Wiesner, J. D. Revell, S. Tonazzi and H. Wennemers, J. Am. Chem. Soc., 2008, 130, 5610–5611 CrossRef CAS PubMed
.
- C. E. Grünenfelder, J. K. Kisunzu and H. Wennemers, Angew. Chem., Int. Ed., 2016, 55, 8571–8574 CrossRef PubMed
.
- A. J. Metrano, N. C. Abascal, B. Q. Mercado, E. K. Paulson, A. E. Hurtley and S. J. Miller, J. Am. Chem. Soc., 2017, 139, 492–516 CrossRef CAS PubMed
.
- T. Schnitzer and H. Wennemers, J. Am. Chem. Soc., 2017, 139, 15356–15362 CrossRef CAS PubMed
.
- J. Kofoed, J.-L. Reymond and T. Darbre, Org. Bio. Chem., 2005, 3, 1850–1855 RSC
.
- M. Klussmann, A. J. P. White, A. Armstrong and D. G. Blackmond, Angew. Chem., Int. Ed., 2006, 45, 7985–7989 CrossRef PubMed
.
- Y. Hayashi, M. Matsuzawa, J. Yamaguchi, S. Yonehara, Y. Matsumoto, M. Shoji, D. Hashizume and H. Koshino, Angew. Chem., Int. Ed., 2006, 45, 4593–4597 CrossRef CAS PubMed
.
- M. Klussmann, T. Izumi, A. J. P. White, A. Armstrong and D. G. Blackmond, J. Am. Chem. Soc., 2007, 129, 7657–7660 CrossRef CAS PubMed
.
- R. Breslow and Z.-L. Cheng, Proc. Nat. Acad. Sci. USA., 2010, 107, 5723 CrossRef CAS PubMed
.
- J. E. Hein, E. Tse and D. G. Blackmond, Nat. Chem., 2011, 3, 704 CrossRef CAS PubMed
.
- R. Breslow, V. Ramalingam and C. Appayee, Orig. Life Evol. Biospheres, 2013, 43, 323–329 CrossRef PubMed
.
- J. Ying, R. Lin, P. Xu, Y. Wu, Y. Liu and Y. Zhao, Sci. Rep., 2018, 8, 936 CrossRef PubMed
.
- J. E. Hein and D. G. Blackmond, Acc. Chem. Res., 2012, 45, 2045–2054 CrossRef CAS PubMed
.
- H. Mayr and A. R. Ofial, Acc. Chem. Res., 2016, 49, 952–965 CrossRef CAS PubMed
.
- A. D. Borthwick, Chem. Rev., 2012, 112, 3641–3716 CrossRef CAS PubMed
.
- D. S. Nielsen, N. E. Shepherd, W. Xu, A. J. Lucke, M. J. Stoermer and D. P. Fairlie, Chem. Rev., 2017, 117, 8094–8128 CrossRef CAS PubMed
.
- P. G. Dougherty, A. Sahni and D. Pei, Chem. Rev., 2019, 119, 10241–10287 CrossRef CAS PubMed
.
- M. Saleki, N. Colgin, J. A. Kirby, S. L. Cobb and S. Ali, Med. Chem. Commun., 2013, 4, 860–864 RSC
.
- A. Rios, J. P. Richard and T. L. Amyes, J. Am. Chem. Soc., 2002, 124, 8251–8259 CrossRef CAS PubMed
.
- P. E. Young, V. Madison and E. R. Blout, J. Am. Chem. Soc., 1976, 98, 5365–5371 CrossRef CAS PubMed
.
- V. Madison, P. E. Young and E. R. Blout, J. Am. Chem. Soc., 1976, 98, 5358–5364 CrossRef CAS PubMed
.
- C. Eguchi and A. Kakuta, J. Am. Chem. Soc., 1974, 96, 3985–3989 CrossRef CAS PubMed
.
- W. R. Forsyth and A. D. Robertson, J. Am. Chem. Soc., 1996, 118, 2694–2698 CrossRef CAS
.
- J. Ho, M. L. Coote and C. J. Easton, J. Org. Chem., 2011, 76, 5907–5914 CrossRef CAS PubMed
.
- J. Ho, C. J. Easton and M. L. Coote, J. Am. Chem. Soc., 2010, 132, 5515–5521 CrossRef CAS PubMed
.
- J. P. Richard and T. L. Amyes, Curr. Opin. Chem. Biol., 2001, 5, 626–633 CrossRef CAS PubMed
.
- J. P. Richard, T. L. Amyes and M. M. Toteva, Acc. Chem. Res., 2001, 34, 981–988 CrossRef CAS PubMed
.
- A. Rios, T. L. Amyes and J. P. Richard, J. Am. Chem. Soc., 2000, 122, 9373–9385 CrossRef CAS
.
- A. Rios, J. Crugeiras, T. L. Amyes and J. P. Richard, J. Am. Chem. Soc., 2001, 123, 7949–7950 CrossRef CAS PubMed
.
- A. Rios and J. P. Richard, J. Am. Chem. Soc., 1997, 119, 8375–8376 CrossRef CAS
.
- G. Williams, E. P. Maziarz, T. L. Amyes, T. D. Wood and J. P. Richard, Biochemistry, 2003, 42, 8354–8361 CrossRef CAS PubMed
.
- P. D. Bailey, N. Bannister, M. Bernad, S. Blanchard and A. N. Boa, J. Chem. Soc. Perk. Trans., 2001, 1, 3245–3251 Search PubMed
.
- A. Cabanillas, C. D. Davies, L. Male and N. S. Simpkins, Chem. Sci., 2015, 6, 1350–1354 RSC
.
- R. W. Foster, E. N. Lenz, N. S. Simpkins and D. Stead, Chem. Eur. J., 2017, 23, 8810–8813 CrossRef CAS PubMed
.
- M. Rees, N. S. Simpkins and L. Male, Org. Lett., 2017, 19, 1338–1341 CrossRef CAS PubMed
.
- G. R. Peczkowski, P. G. E. Craven, D. Stead and N. S. Simpkins, Chem. Commun., 2019, 55, 4214–4217 RSC
.
- R. S. Massey, C. J. Collett, A. G. Lindsay, A. D. Smith and A. C. O'Donoghue, J. Am. Chem. Soc., 2012, 134, 20421–20432 CrossRef CAS PubMed
.
- M. Capponi, I. G. Gut, B. Hellrung, G. Persy and J. Wirz, Can. J. Chem., 1999, 77, 605–613 CrossRef CAS
.
- M. Manoharan, F. De Proft and P. Geerlings, J. Chem. Soc., Perkin Trans., 2000, 2, 1767–1773 RSC
, see references therein.
- C. F. Bernasconi, P. J. Wenzel and M. L. Ragains, J. Am. Chem. Soc., 2008, 130, 4934–4944 CrossRef CAS PubMed
.
- T. Tsuji, M. Okuyama, M. Ohkita, H. Kawai and T. Suzuki, J. Am. Chem. Soc., 2003, 125, 951–961 CrossRef CAS PubMed
.
- A. J. Kresge and Q. Meng, J. Am. Chem. Soc., 2002, 124, 9189–9198 CrossRef CAS PubMed
.
- C. F. Bernasconi, M. Ali and J. C. Gunter, J. Am. Chem. Soc., 2003, 125, 151–157 CrossRef CAS PubMed
.
- C. F. Bernasconi and H. Zheng, J. Org. Chem., 2006, 71, 8203–8211 CrossRef CAS PubMed
.
- C. F. Bernasconi and M. Pérez-Lorenzo, J. Am. Chem. Soc., 2007, 129, 2704–2712 CrossRef CAS PubMed
.
- T. L. Amyes and J. P. Richard, J. Am. Chem. Soc., 1996, 118, 3129–3141 CrossRef CAS
.
- J. P. Richard, G. Williams and J. Gao, J. Am. Chem. Soc., 1999, 121, 715–726 CrossRef CAS
.
- J. P. Richard, G. Williams, A. C. O'Donoghue and T. L. Amyes, J. Am. Chem. Soc., 2002, 124, 2957–2968 CrossRef CAS PubMed
.
-
J. R. Keeffe and A. J. Kresge, Kinetics and mechanism of enolization and ketonization, 1990 Search PubMed
.
- A. C. Eliot and J. F. Kirsch, Annu. Rev. Biochem., 2004, 73, 383–415 CrossRef CAS PubMed
.
- C. Fischer, Y.-C. Ahn and J. C. Vederas, Nat. Prod. Rep., 2019, 36, 1687–1705 RSC
.
- V. E. Fadouloglou, S. Balomenou, M. Aivaliotis, D. Kotsifaki, S. Arnaouteli, A. Tomatsidou, G. Efstathiou, N. Kountourakis, S. Miliara, M. Griniezaki, A. Tsalafouta, S. A. Pergantis, I. G. Boneca, N. M. Glykos, V. Bouriotis and M. Kokkinidis, J. Am. Chem. Soc., 2017, 139, 5330–5337 CrossRef CAS PubMed
.
- P. F. Widboom, E. N. Fielding, Y. Liu and S. D. Bruner, Nature, 2007, 447, 342–345 CrossRef CAS PubMed
.
Footnotes |
| † Electronic supplementary information (ESI) available: Synthetic and kinetic methods, kinetic data fitting and computational analysis. See DOI: 10.1039/d0sc02508a |
| ‡ Current address: Radboud University Nijmegen, Institute for Molecules and Materials, Heyendaalseweg 135, 6525 AJ Nijmegen, The Netherlands. |
| This journal is © The Royal Society of Chemistry 2020 |