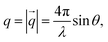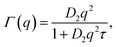Open Access Article
Open Access ArticleA neutron scattering perspective on the structure, softness and dynamics of the ligand shell of PbS nanocrystals in solution†‡
Tilo
Seydel
 a,
Michael Marek
Koza
a,
Michael Marek
Koza
 a,
Olga
Matsarskaia
a,
Olga
Matsarskaia
 a,
Alexander
André
b,
Santanu
Maiti§
a,
Alexander
André
b,
Santanu
Maiti§
 c,
Michelle
Weber
b,
Ralf
Schweins
c,
Michelle
Weber
b,
Ralf
Schweins
 a,
Sylvain
Prévost¶
a,
Sylvain
Prévost¶
 d,
Frank
Schreiber
d,
Frank
Schreiber
 ce and
Marcus
Scheele
ce and
Marcus
Scheele
 *be
*be
aInstitut Max von Laue - Paul Langevin (ILL), 71 Avenue des Martyrs, CS 20156, 38042 Grenoble Cedex 9, France
bInstitute of Physical and Theoretical Chemistry, University of Tübingen, Auf der Morgenstelle 18, 72076 Tübingen, Germany. E-mail: marcus.scheele@uni-tuebingen.de
cInstitute of Applied Physics, University of Tübingen, Auf der Morgenstelle 10, 72076 Tübingen, Germany
dESRF - The European Synchrotron, 71 Avenue des Martyrs, CS 40220, 38043 Grenoble Cedex 9, France
eCenter for Light-Matter Interaction, Sensors & Analytics LISA+, University of Tübingen, Auf der Morgenstelle 15, 72076 Tübingen, Germany
First published on 3rd August 2020
Abstract
Small-angle neutron and X-ray scattering, neutron backscattering and neutron time-of-flight spectroscopy are applied to reveal the structure of the ligand shell, the temperature-dependent diffusion properties and the phonon spectrum of PbS nanocrystals functionalized with oleic acid in deuterated hexane. The nanocrystals decorated with oleic acid as well as the desorbed ligand molecules exhibit simple Brownian diffusion with a Stokes–Einstein temperature-dependence and inhibited freezing. Ligand molecules desorbed from the surface show strong spatial confinement. The phonon spectrum of oleic acid adsorbed to the nanocrystal surface exhibits hybrid modes with a predominant Pb-character. Low-energy surface modes of the NCs are prominent and indicate a large mechanical softness in solution. This work provides comprehensive insights into the ligand–particle interaction of colloidal nanocrystals in solution and highlights its effect on the diffusion and vibrational properties as well as their mechanical softness.
A. Introduction
Electron–phonon interactions greatly influence the optoelectronic properties of semiconductor nanocrystals (NCs).1 The occurrence of a phonon bottle-neck and the associated feasibility of multi-exciton generation in NCs is an important consequence of their vibrational properties, which requires a detailed understanding for an exploitation in optoelectronic devices.2 Recent investigations of the phonon spectrum of PbS NCs indicate that mechanical softness due to dangling bonds and other defects on the surface of the NCs invokes a large density of low-energy phonons with strong coupling rates to electrons.3,4 It has been argued that these low-energy phonons may be responsible for the surprisingly fast electron relaxation rates in many semiconductor NCs and that their distribution is linked to the chemical nature and structure of the ligand shell.5,6 While these studies were performed in the solid state and after ligand exchange with short cross-linkers such as 1,2-ethanedithiol, methanethiol or halide ions, no comparable knowledge exists about the phonon spectrum of PbS NCs in solution, terminated with its native ligand oleic acid (OA). In related work, the structure of the ligand shell of OA-terminated NCs has been explored to some degree in the solid state, but remains scarcely studied in solution.7–10Any understanding of the structure of the ligand shell in solution requires an account for dynamic phenomena, possibly different forms of diffusion, ligand desorption and structural changes of the ligand shell, for instance due to a change in temperature.11,12 Previous studies of the diffusion of NCs in solution by electron microscopy have revealed orders of magnitude smaller diffusion coefficients (D) than predicted by the Stokes–Einstein equation.13–18 In contrast, diffusion ordered nuclear magnetic resonance spectroscopy (DOSY-NMR) of NC solutions yielded D values in good agreement with Stokes–Einstein.11,19–21 NMR studies also revealed a strong solvent-dependence of the solvation of the ligand sphere, which would in turn affect the particle diameter and D value.8 Molecular dynamics simulations have introduced several different models for the structure of a typical NC ligand shell in the solid state, ranging from fully erected ligand molecules (“spiky ball” model) over bundles of unfolded ligands (“coiled spiky ball”) to a layer of collapsed ligands (“wet hair” model).9 For relatively bulky molecules like OA, the wet hair configuration has been identified as the most stable structure. In contrast, small angle neutron scattering (SANS) on metal NCs implied that a fully unfolded ligand structure prevails in solution.10,22
In this context, a number of fundamental questions arise. Is the structure of the ligand shell in solution identical to that in the solid state? How confined are ligands bound to the surface? Is the mechanical softness of the NCs, that is, a large density of low-energy phonons, also present in solution? How do these properties vary with temperature, especially close to phase transitions of the ligand or the solvent? Is there evidence for a correlation between changes of the dynamics or the structure with variations of the phonon spectrum?
We address these questions for PbS NCs with a radius of 3.3 nm, terminated with OA in d14-hexane by applying a combination of several neutron scattering and spectroscopic techniques. With SANS and small angle X-ray scattering (SAXS), we determine the width of the ligand sphere. By quasi-elastic neutron scattering (QENS), we derive the temperature-dependent diffusion coefficients of the NCs, distinguish between the dynamics of adsorbed and desorbed ligands, derive the mean-free-path of the bound ligands and determine structural changes of the ligand shell between 183–295 K. We use inelastic neutron spectroscopy (INS) to record the generalized density of states (GDOS) between 100 K and 239 K and show for the first time that surface phonons of the NCs as well as vibrations of the ligands can be recorded in solution.
B. Methodology
While details of the experimental procedures are provided in the ESI,† here we briefly summarize the most important aspects of the scattering experiments performed in this work.Small-angle neutron and X-ray scattering (SANS and SAXS)
Scattering contrast in SAXS is provided by the difference in electron density, which makes SAXS the ideal tool for determining the structure of the NC cores due to their large density of heavy Pb atoms against a background of light elements (d14-hexane or oleic acid).23 In contrast, the scattering cross-section for neutrons varies non-monotonically with the isotope number.24 As detailed in the ESI (Fig. S4†), the SANS signal and the resulting scattering contrast is dominated by scattering of the H-rich ligands, considering that the solvent is deuterated with 99% isotope purity.Quasi-elastic neutron scattering (QENS)
QENS is a powerful method for studying the diffusion of organic matter in solution, which is based on energy-resolved scattering of neutrons by the H nuclei.25 Crucially, QENS accesses the Fourier transform of the intermediate scattering function. Thus, for instance, simple diffusion processes resulting in single exponential decays of the intermediate scattering function translate into Lorentzian line broadenings visible in the QENS signal. More generally, diffusion of the molecules during the scattering event invokes a broadening of the elastic scattering line, which allows to extract the diffusion coefficient D. This method can be employed for a wide range of momentum transfers q, at which the energy transfer ω of the neutrons to the sample is recorded. The q dependence of the scattering signal contains information on the confinement geometry of the diffusive motion of the scatterers, specifically its elastic incoherent structure factor (EISF) A0(q). The EISF is the long-time limit of the intermediate scattering function and a rough estimate for the mean-free-path. The number of Lorentzian functions giving rise to this broadening as well as the dependence of this broadening on the momentum transfer q inform on the number of underlying superimposed diffusion processes as well as on their geometrical characteristics. Therefore, q-dependent QENS experiments can determine the degree of confinement of a diffusing scatterer.26Selecting a fixed energy transfer window at the very high energy resolution of 0.8 μeV FWHM of the backscattering experiment allows to follow changes in the scattering intensity with temperature, which contains information on slowed diffusion due to freezing and possible phase changes. These scans only require a recording time on the order of one minute per temperature step and can, thus, be acquired much more quickly than full QENS spectra with a recording time of several hours per spectrum. Elastic fixed window scans (EFWS, energy transfer = 0 μeV) monitor intensity changes of scatterers which are stationary over the observed time scale of a few nanoseconds. Inelastic fixed window scans (IFWS, energy transfer ≠ 0 μeV) exclusively record intensity changes due to the dynamics of the scatterers. Thus, IFWS vs. EFWS experiments allow distinguishing temperature-dependent changes in the bulk diffusion properties between fast and slow scatterers, such as free OA vs. OA bound to the surface of NCs.
Inelastic neutron scattering (INS) by time-of-flight spectroscopy
A time-of-flight (TOF) experiment employs the velocity change of neutrons during scattering from a sample to calculate the energy exchange. The high-energy limit for TOF spectroscopy is much larger (on the order of one to hundreds of meV) than for the backscattering experiment employed during QENS, which includes not only the energy range of solvent diffusion (e.g. d14-hexane) but also that of vibrational excitations. Basically, vibrations are related to the chemical bonding and their frequencies are a measure of the bond strength. The distribution of vibrational excitations contains information on the chemical interaction between the NCs and the adsorbed OA molecules. In case of a strong interaction, we expect the formation of hybrid vibrational modes, procuring a renormalization of the bulk vibrational spectra of the individual systems. As the contribution of Pb and S to the recorded signal is negligible according to its weak relative neutron scattering power in the specimen (see Table S3 and Fig. S4 in ESI† for details), INS monitors the vibration of OA with high sensitivity. The inelastic response and its changes are provided in the form of the spectral distribution to which we refer to as the generalized density of states (GDOS).C. Results
Oleic acid (OA)-capped PbS NCs are dissolved in d14-hexane to yield a stable colloidal solution with a concentration of 140 μmol L−1, corresponding to a volume fraction of 1.6% (for details, see ESI†). SANS and SAXS of PbS/OA/d14-hexane are shown in Fig. 1 as functions of the momentum transferwhere 2θ is the scattering angle and λ is the incoming wavelength. The different onsets of the oscillations in the SANS and SAXS data starting at q ≈ 1 nm−1 reflect the different sensitivities of the two techniques to the PbS core and the OA shell as explained in the Methodology section. From the SAXS data, we calculate the radius of the PbS core as 33 Å and the thickness of the OA shell as 18 Å from SANS. The latter value roughly corresponds to one molecular length of OA (19.5 Å; from universal force field calculations). It is also consistent with a SANS/SAXS study on oleylamine-capped Au NCs in toluene, which reported 17 Å for the width of this similar ligand sphere.10
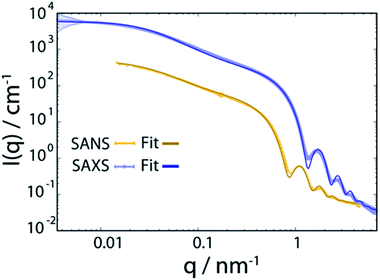 | ||
| Fig. 1 Small angle neutron and X-ray scattering (SANS and SAXS) spectra of PbS NCs decorated with oleic acid in d14-hexane at 298 K. The bold lines are fits to the data and are described in detail in the ESI.† | ||
We model the SANS and SAXS data in Fig. 1 with core–shell spheres, a fraction of which is included in mass fractal aggregates (for details, see ESI†). Both datasets display a large excess of scattering intensity at low q compared to the scattering expected from well-dispersed core–shell spheres. The SAXS data indicate the exclusive presence of elongated aggregates as evidenced by the power-law decay of the intensity at mid q that follows ISAXS(q) ≈ q−1, as it is typical for rod-like scatterers with a fractal dimension close to 1. The SANS data, however, are different and allow to discard the hypothesis that all particles are part of rod-like clusters. By simultaneously fitting the SANS and SAXS data, we establish that there are two populations in the PbS/OA/d14-hexane sample: (1) a large majority of spherical monomers corresponding to well-dispersed NCs and (2) a smaller fraction (21%) of NC aggregates. We calculate the OA/PbS ratio in the aggregates to be ∼30% smaller than that in the well-dispersed NCs, indicating that partial ligand deficiency may be responsible for this finding. Such ligand deficiency is often invoked by slow and irreversible changes of the inorganic surface of the NCs, e.g. by aging due to exposure to air or radicals.8,27
Fig. 2 displays the QENS signal recorded on IN16B at q = 0.29, 0.44 and 0.82 Å−1, and T = 239 K, of OA-decorated PbS NCs in d14-hexane (left column, orange circles). For comparison, we also measure solutions of 35 mmol L−1 OA in d14-hexane without PbS NCs (right column, blue circles). The concentration of free OA in the OA/d14-hexane reference sample is chosen to match the nominal concentration of bound OA on the NC surface in the PbS/OA/d14-hexane sample measurement (for details, see ESI†). The significant broadening of the QENS peak visible in the PbS/OA/d14-hexane spectrum (Fig. 2, left column) indicates diffusion on a nanosecond time scale. A narrower QENS peak is also visible for the OA/d14-hexane sample (Fig. 2, right column).
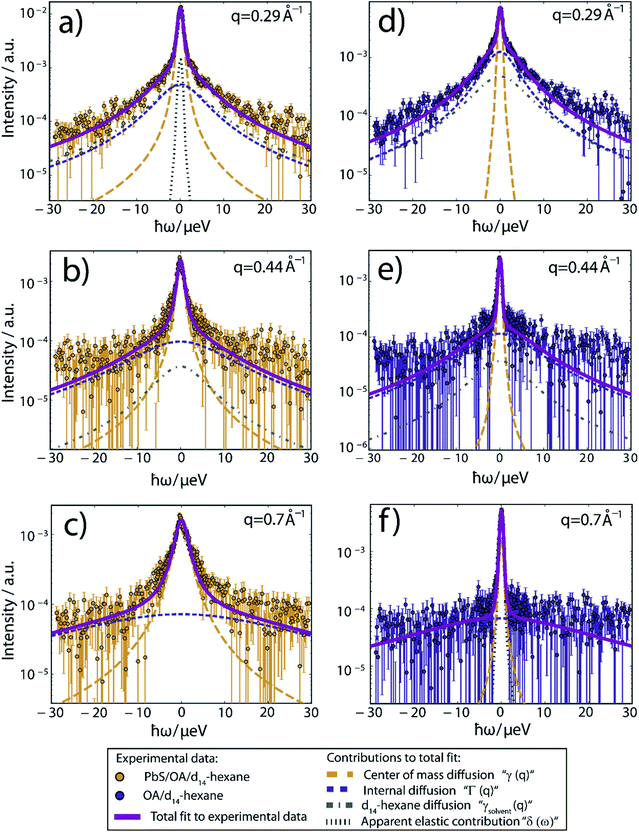 | ||
| Fig. 2 QENS spectra at T = 239 K and three different scattering vectors. (a–c) Experimental data of PbS/OA/d14-hexane and (d–f) of OA/d14-hexane. A sloped background arising from instrument and sample contributions has been subtracted in all cases. Solid lines represent fits to the experimental data, composed of the Lorentzian contributions from the center-of-mass diffusion, internal diffusion, d14-hexane solvent and an apparent elastic contribution represented by dashed lines according to the model described by eqn (1) in the ESI.† The apparent elastic contribution and the d14-hexane diffusion are not visible on all plots due to the low signal and rapid broadening of the d14-hexane signal with rising q. The d14-hexane contribution has been rescaled by the effective excluded volume of OA. All data has been binned by pairs of two channels for small (|ħω| < 5.85 μeV) and by groups of four channels for large absolute values of the energy transfer, respectively, subsequent to fitting for better visibility. | ||
While details are provided in the ESI,† we fit the QENS spectra according to a heuristic model, which assumes three Lorentzian contributions due to (1) a center-of-mass diffusion of the NCs (or alternatively of OA vesicles, cf. further below), (2) internal diffusion of OA molecules moving along the NC surface and (3) a solvent diffusion background.28 The three Lorentzian contributions give rise to a line broadening, characterized by the widths γ(q), Γ(q) and γsolvent(q), respectively. The center-of-mass diffusion and internal diffusion are assumed to be convoluted, being represented by the sum γ + Γ. The contribution by the center-of-mass diffusion scales with the scalar fit parameter 0 ≤ A0(q) ≤ 1, which is the Elastic Incoherent Structure Factor (EISF) associated with the spatially confined diffusion of OA. In addition, we include a delta-function δ(ω) due to an apparent elastic contribution, e.g. by the sample container and/or very large objects that appear essentially immobile on the time scale accessible to IN16B (e.g. the agglomerates observed in SAXS, Fig. 1). These four contributions are displayed in Fig. 2 as dashed lines. Their convolution according to the heuristic model is depicted as solid lines for PbS/OA/d14-hexane and OA/d14-hexane (purple) as well as for pure d14-hexane (black). The excellent fit to the experimental QENS data supports the applicability of the model.
We now use the Lorentzian widths, γ(q) and Γ(q), to extract the corresponding scalar diffusion coefficients for the center-of-mass diffusion (D1) and internal diffusion (D2). Since the incoherent scattering from the OA dominates the signal in our experiment, the observed diffusion coefficients represent the self-diffusion or, synonymously, tracer diffusion of the diffusing objects. Moreover, since the observation or coherence time of our experiment amounts to a few nanoseconds, as given by the Fourier transform of its energy resolution, collisions between diffusing nanoparticles are negligible. In colloid physics, this regime of negligible collisions is denoted short-time diffusion.29 We assume Fickian diffusion and impose γ(q) = D1q2. Similarly, we test different assumptions for Γ(q), namely the so-called jump-diffusion
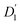 (orange circles). We speculate that these small values arise from nearly immobile OA vesicles suspended in d14-hexane. In this picture, which will be corroborated by the discussion of the fixed-window data in the following section, large OA vesicles form only in the absence of the PbS nanoparticles, whilst the OA decorates the PbS in their presence.
(orange circles). We speculate that these small values arise from nearly immobile OA vesicles suspended in d14-hexane. In this picture, which will be corroborated by the discussion of the fixed-window data in the following section, large OA vesicles form only in the absence of the PbS nanoparticles, whilst the OA decorates the PbS in their presence.
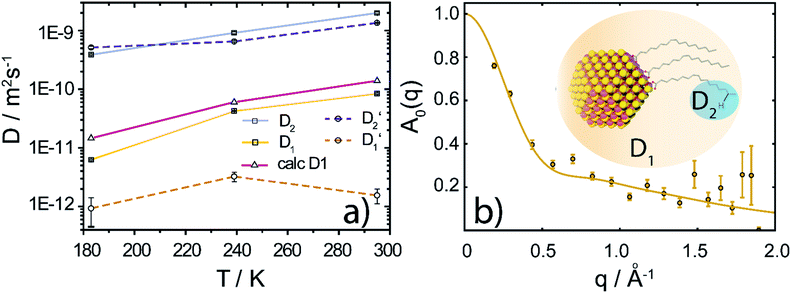 | ||
Fig. 3 (a) Diffusion coefficients in d14-hexane extracted from the QENS fit in Fig. 2. Center-of-mass diffusion of PbS/OA NCs (D1) or OA vesicles 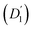 in orange; internal diffusion of OA on the NC surface (D2) or within OA vesicles in orange; internal diffusion of OA on the NC surface (D2) or within OA vesicles 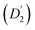 in blue. Calculated diffusion coefficient for the PbS/OA NCs according to the Stokes–Einstein equation in purple. (b) A0(q) at 295 K for PbS/OA in d14-hexane obtained from the fit of the QENS spectra (symbols). The solid line represents a qualitative fit according to the heuristic model given in ref. 32 and 33 under the assumption of diffusion in a sphere with a smeared-out radius R of 6.5 ± 0.4 Å, including a background of immobile scatterers. The inset is an idealized schematic of the two diffusion processes present in the PbS/OA/d14-hexane sample. in blue. Calculated diffusion coefficient for the PbS/OA NCs according to the Stokes–Einstein equation in purple. (b) A0(q) at 295 K for PbS/OA in d14-hexane obtained from the fit of the QENS spectra (symbols). The solid line represents a qualitative fit according to the heuristic model given in ref. 32 and 33 under the assumption of diffusion in a sphere with a smeared-out radius R of 6.5 ± 0.4 Å, including a background of immobile scatterers. The inset is an idealized schematic of the two diffusion processes present in the PbS/OA/d14-hexane sample. | ||
The evaluation of the internal diffusion contribution to the QENS fits yields similar D2 values for both, the PbS/OA/d14-hexane (D2, blue squares) and OA/d14-hexane (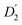 , blue circles) samples in Fig. 3a. We speculate that D2 and
, blue circles) samples in Fig. 3a. We speculate that D2 and 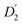 are associated with the diffusion of OA along the surfaces of the PbS NCs (PbS/OA/d14-hexane sample) and within the OA vesicle membranes (OA/d14-hexane sample), respectively. This speculative picture would describe two-dimensional Fickian diffusion within a surface. The picture is supported by the corresponding hydrodynamic radii calculated by the Stokes–Einstein equation summarized in Table 1 in the presence of PbS (r2) and for OA/d14-hexane only
are associated with the diffusion of OA along the surfaces of the PbS NCs (PbS/OA/d14-hexane sample) and within the OA vesicle membranes (OA/d14-hexane sample), respectively. This speculative picture would describe two-dimensional Fickian diffusion within a surface. The picture is supported by the corresponding hydrodynamic radii calculated by the Stokes–Einstein equation summarized in Table 1 in the presence of PbS (r2) and for OA/d14-hexane only 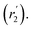 The nominal radii of 3.2 Å and 3.6 Å are in good agreement with the previously reported value of 3.1 Å for similar fatty acids in hexane at 298 K.31
The nominal radii of 3.2 Å and 3.6 Å are in good agreement with the previously reported value of 3.1 Å for similar fatty acids in hexane at 298 K.31
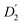 in Fig. 3a and the Stokes–Einstein equation. r2 represents the radii in the presence of the NCs, while
in Fig. 3a and the Stokes–Einstein equation. r2 represents the radii in the presence of the NCs, while 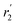 stands for the calculated radii without the NCs. For comparison, we note the literature value for the radius of similar fatty acids reported in ref. 31
stands for the calculated radii without the NCs. For comparison, we note the literature value for the radius of similar fatty acids reported in ref. 31
| 183 K | 239 K | 295 K | |
|---|---|---|---|
| r 2 (PbS/OA/d14-hexane) | 1.4 Å | 3.3 Å | 3.2 Å |
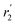 (OA/d14-hexane) (OA/d14-hexane) |
0.8 Å | 3.4 Å | 3.6 Å |
| r (OA/hexane), ref. 31 | 3.1 Å |
To further investigate the spatial confinement of the internal OA diffusion, we utilize the EISF A0(q) obtained by fitting the QENS data, which is depicted in Fig. 3b for the PbS/OA/d14-hexane sample. We emphasize that the EISF is contained as additional information in the fit result of the QENS data, which automatically results from the same model along with the information on the diffusion coefficients. The EISF data is fit with a heuristic model described in ref. 32 and 33, which assumes a superposition of confined diffusion with a characteristic mean-free-path d and molecular reorientation jumps. From the onset of the rise in the EISF data towards q = 0, we gauge the mean-free-path as r = 2π/onset = 9 Å at 295 K. The corresponding fit of the data is obtained with a mean value for r of 6.6 ± 1.9 Å. The reasonable agreement between these two independent estimates supports the applicability of the model. We note that the significant standard deviation in the A0(q) prevents a more involved modeling and correction for the Debye–Waller factor.
At 239 K, the fit of A0(q) is less stable (see Fig. S1†), presumably due to the growing contribution of large NC agglomerates (cf. the SAXS data in Fig. 1). The generally higher A0(q) values at 239 K compared to 295 K indicate that a smaller fraction of OA is mobile at lower temperature. We note that at 183 K, A0(q) is mostly flat and no stable fit may be obtained, which is why we omit it here. We argue that at this low temperature, the OA molecules are fully immobilized, which prevents a meaningful analysis of A0(q). Furthermore, a similar analysis applied to the OA/d14-hexane data does not result in a discernable onset for any of the three temperatures. Overall, the presence of reasonable onsets for mean free paths in the PbS/OA/d14-hexane sample and their absence for OA/d14-hexane suggests that the diffusion of OA is confined to the surface of the NCs.
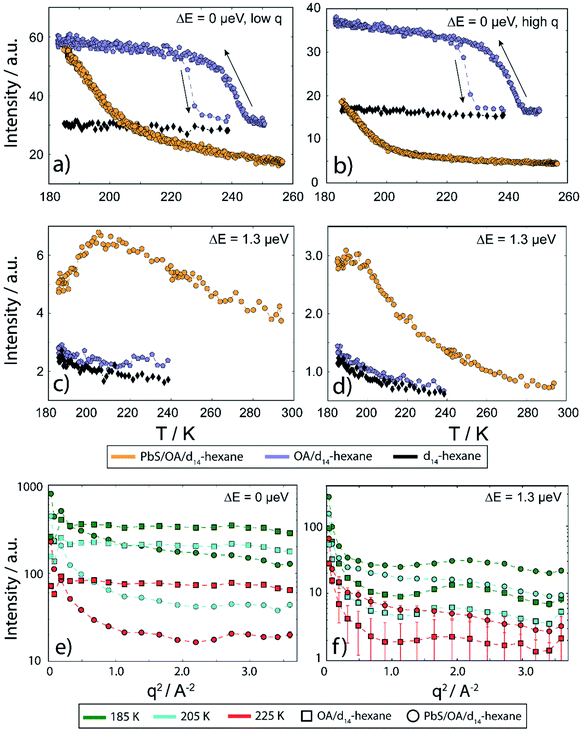
In Fig. 4, we display EFWS (Fig. 4a and b) and IFWS (Fig. 4c and d) for the fixed q-ranges 0.44–0.82 Å−1 and 1.39–1.65 Å−1 of PbS/OA/d14-hexane, OA/d14-hexane and d14-hexane versus the sample temperature. The OA/d14-hexane mixture evidences a freezing step between 230–220 K which may be associated with immobilized OA, e.g. due to the formation of OA clusters (Fig. 4a and b; blue circles). As is typical for freezing transitions, the melting during heating occurs at a higher temperature than the freezing during cooling, as evidenced by the hysteresis (about 10–15 K in this case). Note that the freezing point of pure OA is significantly above this temperature window (278 K). For a discussion of phase transitions in these systems and the comparison bulk vs. surface (flat) vs. surface (curved), see ref. 34 and 35 and therein. There is no significant QENS broadening on the ns scale even at 239 K for this mixture, consistent with the absence of a strong signal or changes in the IFWS (Fig. 4c and d; blue circles). The absence of Bragg scattering below the freezing step at 230–220 K suggests that the elastic scattering arises solely from incoherent scattering of OA and not from d14-hexane that remains liquid (cf. also Fig. 4e and f). In line with this observation, pure d14-hexane shows no significant change in the inspected temperature range in EFWS scans (Fig. 4a and b; black circles) and only very minute changes in the IFWS (Fig. 4c and d; black circles). We note that the diffusion of hexane slows down significantly towards the lower end of our temperature window, entering the detectable range of the QENS experiment performed here as illustrated by the rise of the signal represented by black diamonds in Fig. 4c and d towards low temperatures.
In the presence of PbS NCs, we observe no freezing step in the elastic signal (Fig. 4a and b; orange circles). Instead, the elastic intensity gradually increases with decreasing temperature. Moreover, the IFWS exhibits a maximum in its temperature-dependence, at least for some values of q (Fig. 4c and d; orange circles). These observations are consistent with the strong nanosecond QENS signal seen at lower temperature, which can be understood in terms of a gradual change of the center-of-mass diffusion (Fig. 3a and S2†).
As depicted in Fig. 4e and f, the fixed window scans can be further illustrated by slices along q for the three temperatures 225 K (blue lines), 205 K (green lines) and 185 K (purple lines), comparing PbS/OA/d14-hexane (orange circles) and OA/d14-hexane (blue squares), respectively. The elastic signal (Fig. 4e) resembles the behavior of a harmonic solid for the OA/d14-hexane sample, as evidenced by the straight lines in the logarithmic plot versus q2. In contrast, the q2-dependence of the signal from PbS/OA/d14-hexane strongly deviates from a straight line in this plot, supporting the presence of diffusive behavior. The inelastic signal in Fig. 4f illustrates the overall much weaker intensity of OA/d14-hexane compared to PbS/OA/d14-hexane, which is in line with the interpretation of the elastic signal.
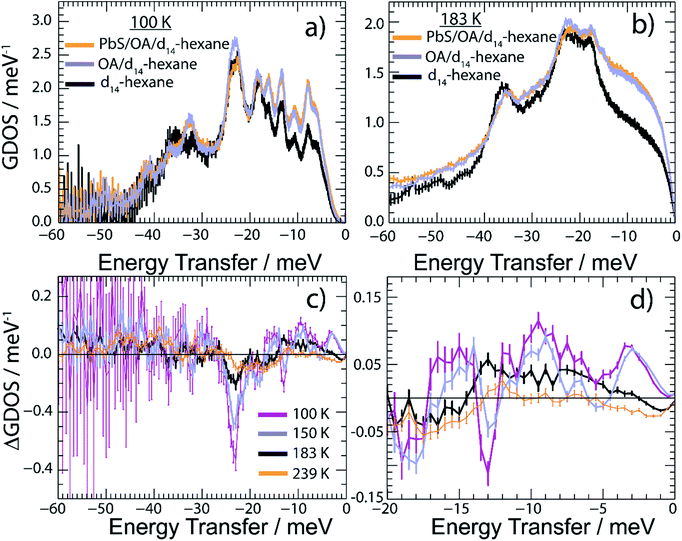
We report in Fig. 5 the vibrational properties of the PbS/OA/d14-hexane, OA/d14-hexane and d14-hexane specimens. For convenience, the GDOS of PbS/OA/d14-hexane and OA/d14-hexane displayed in Fig. 5a at 100 K and Fig. 5b at 183 K are normalized to 60 vibrational modes corresponding to the vibrational degrees of freedom of a hexane molecule. We recall that the scattering contribution from PbS is insignificant in the present experiment (see Table S3 in ESI†). The GDOS of d14-hexane is however corrected for the absent OA contribution. In the solid state at 100 K, the frozen solvent d14-hexane dominates the spectral density in any of the specimens evidenced by the number and position of distinguishable peaks. They are well defined indicating their long lifetimes. This property changes visibly above the melting point of d14-hexane (Fig. 5b). Note that all GDOS preserve their relative intensities, however, they are strongly altered towards rather featureless profiles. As expected, the liquid state of d14-hexane opens up effective relaxation channels for the vibrational modes. As a consequence, the inter-molecular bonds are short-lived leading to the enhanced broadening of their characteristic vibrational peaks and a complete loss of definition in the experimental spectra. This is less the case for the localized intra-molecular vibrations. Thus, we may associate the remaining characteristic maxima in the GDOS at 183 K with some intra-molecular properties determined by the C–H and C–D bonds. We may further conclude that the additional sharp peaks obvious in the frozen state are determined by the inter-molecular interactions.
Comparing the GDOS of PbS/OA/d14-hexane and OA/d14-hexane, we observe that the presence of the PbS NCs results in an additional, however weak, intensity gain below 12 meV and a visible intensity loss up to the peak of highest intensity at 20–28 meV. Thus, there is a renormalization of vibrational modes of the OA/d14-hexane system in the presence of the PbS NCs such that less high-frequency but more low-frequency vibrations are present. Note that the energy range of up to 28 meV matches very well with the range of excitations in PbS.6 It is worth highlighting that the DOS of PbS is dominated by Pb vibrations below ∼12 meV and by S vibrations above ∼12 meV.6 We conjecture that this spectral separation is the reason for the renormalization of the OA/d14-hexane modes towards lower energies, as the OA molecules are attached to the predominantly Pb terminated NCs.36 These properties are highlighted in Fig. 5c and d, which report the difference GDOS (ΔGDOS) of PbS/OA/d14-hexane and OA/d14-hexane at different temperatures. Note that due to the normalization of both GDOS to the same number of modes the total ΔGDOS is null. Deviations from the zero line towards positive and negative values signify the respective spectral gains and losses induced by the renormalization. In the temperature-regime of solid d14-hexane, the GDOS of PbS/OA/d14-hexane outnumbers the modes in OA/d14-hexane below 18 meV and vice versa above 18 meV. Upon heating, the mode differences become progressively less pronounced. Above the melting point of d14-hexane (178 K), the clearly textured profile of the ΔGDOS changes into a monotone smooth distribution of weak intensity variation at the highest T. We corroborate this finding further in Fig. S5 of the ESI† by integrating ΔGDOS over three specific energy ranges and find that at highest T the integrated signals approach zero. The loss of ΔGDOS contrast in the liquid state signifies the progressive decoupling of the OA/d14-hexane dynamics from the NCs. The loss of texture highlights the reduction in the lifetime of vibrational excitations and promotes thus a closer matchable spectral distributions of the solvent with and without PbS NCs.
D. Discussion
This work provides a comprehensive analysis of the structure, dynamics and vibrational properties of the OA ligand shell of PbS NCs in solution. The SANS and SAXS data (Fig. 1) illustrate that the structure of the OA-ligand sphere resembles the previously described “spiky ball” or “coiled spiky ball” model. This picture is different from the solid state where the collapsed “hair ball”-morphology is believed to be the more stable configuration and a ligand shell thickness of approx. 1.0 nm was measured.9 The QENS data (Fig. 2) reveal that the OA molecules exhibit a dynamic adsorption/desorption equilibrium at the surface of the NCs, which manifests itself in a slow, collective center-of-mass diffusion with the NCs and a fast internal diffusion of desorbed, individual OA molecules (Fig. 3a). Both processes can be described with simple Brownian motion. The center-of-mass diffusion and its temperature-dependence are only 50% smaller than predicted by the Stokes–Einstein model and in good agreement with previous 1H-DOSY experiments.21 These results suggest that the orders of magnitude smaller diffusion constants obtained for NCs in electron microscopy studies originated from the confined sample volume (∼100 nm thickness) and was thus not intrinsic to the material.13–18 The remaining deviation from the expected dilute-limit Stokes–Einstein diffusion may be due to crowding effects.20 We find evidence for such crowding in the fit of the SAXS/SANS data in Fig. 1, which indicates the co-existence of individual NCs and clusters of NCs formed by diffusion-limited cluster aggregation.The internal diffusion of OA in the presence of the NCs is of similar magnitude to that of free, pure OA, however, it is spatially confined to a radius of <10 Å (Fig. 3b), indicating a strong interaction with the NC surface. The fixed window scans (Fig. 4a and b) further confirm such interaction, which manifests itself in a complete suppression of the phase transformation at ∼230 K otherwise observed for pure OA in d14-hexane. This indicates that the formation of OA clusters to nucleate crystallization is indeed inhibited by the NCs. The very small center-of-mass diffusion constant found only for pure OA in d14-hexane (Fig. 3a) is a sign of vesicle formation.
The vibrational properties in Fig. 5 show clear signs of hybrid modes formed by the surface of the PbS NCs and OA. From their mean energy, it follows that these hybrid modes have mainly Pb-character, which is consistent with previous simulations of preferred OA-binding to Pb surface sites.37 The nanocrystalline character of PbS becomes apparent in the ΔGDOS maximum at energies as low as ∼3 meV (Fig. 5d), which are the transverse acoustic modes of Pb at the surface of the NCs.6 These modes appear at slightly lower energies than those reported for 1,2-ethanedithiol functionalization of PbS NCs, indicating an even softer NC surface. Due to the smaller spring constant, this should lead to strong electron–phonon coupling, including the mostly unwanted by-pass of a phonon bottleneck.4 To prevent this coupling, ligands which mechanically stabilize the surface of the NCs would be beneficial, which is an important conclusion of this study.
E. Conclusions
We have studied the temperature-dependent diffusion and phonon spectrum of PbS nanocrystals surface-functionalized with oleic acid in d14-hexane solution by neutron backscattering, time-of-flight spectroscopy and small-angle scattering. Our results indicate Brownian diffusion of the nanocrystals and a structure of the ligand shell which differs from that in the solid state. Desorbed ligand molecules also follow simple Brownian diffusion, but their motion is confined to a mean radius <10 Å, and freezing is inhibited due to the presence of the nanocrystals. The phonon spectrum of the ligand shell exhibits hybrid modes, indicating a preferential binding to Pb-surface sites. Strong low energy phonon modes are consistent with large mechanical softness of the NC surface, which in comparison to recent studies in the solid state appears to be even more pronounced in solution.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful for financial support by the DFG under grants SCHE1905/4 and SCHR700/25. This work has received funding by the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (grant agreement No 802822). We wish to thank the ILL for making their excellent facilities available to us. FS wishes to thank the ILL for their hospitality during his sabbatical stay. The ID02 team at ESRF, especially Theyencheri Narayanan, is gratefully acknowledged for providing in-house beam time.Notes and references
- (a) D. Li, Z. L. Wang and Z. Wang, J. Phys. Chem. Lett., 2018, 6795 CrossRef CAS PubMed; (b) C. Delerue, G. Allan and M. Lannoo, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 1138 CrossRef; (c) J. Ramade, L. M. Andriambariarijaona, V. Steinmetz, N. Goubet, L. Legrand, T. Barisien, F. Bernardot, C. Testelin, E. Lhuillier, A. Bramati and M. Chamarro, Appl. Phys. Lett., 2018, 112, 72104 CrossRef; (d) A. L. Efros, V. A. Kharchenko and M. Rosen, Solid State Commun., 1995, 93, 281 CrossRef CAS; (e) J. M. Pietryga, Y.-S. Park, J. Lim, A. F. Fidler, W. K. Bae, S. Brovelli and V. I. Klimov, Chem. Rev., 2016, 116, 10513 CrossRef CAS PubMed; (f) T. D. Krauss and F. W. Wise, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 9860 CrossRef CAS; (g) E. M. Janke, N. E. Williams, C. She, D. Zherebetskyy, M. H. Hudson, L. Wang, D. J. Gosztola, R. D. Schaller, B. Lee, C. Sun, G. S. Engel and D. V. Talapin, J. Am. Chem. Soc., 2018, 140, 15791 CrossRef CAS PubMed.
- (a) M. Li, R. Begum, J. Fu, Q. Xu, T. M. Koh, S. A. Veldhuis, M. Grätzel, N. Mathews, S. Mhaisalkar and T. C. Sum, Nat. Commun., 2018, 9, 4197 CrossRef PubMed; (b) M. T. Trinh, A. J. Houtepen, J. M. Schins, T. Hanrath, J. Piris, W. Knulst, A. P. L. M. Goossens and L. D. A. Siebbeles, Nano Lett., 2008, 8, 1713 CrossRef PubMed; (c) P. Han and G. Bester, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 085305 CrossRef; (d) V. I. Klimov and D. W. McBranch, Phys. Rev. Lett., 1998, 80, 4028 CrossRef CAS; (e) A. Pandey and P. Guyot-Sionnest, Science, 2008, 322, 929 CrossRef CAS PubMed.
- R. D. Schaller, J. M. Pietryga, S. V. Goupalov, M. A. Petruska, S. A. Ivanov and V. I. Klimov, Phys. Rev. Lett., 2005, 95, 196401 CrossRef PubMed.
- D. Bozyigit, N. Yazdani, M. Yarema, O. Yarema, W. M. M. Lin, S. Volk, K. Vuttivorakulchai, M. Luisier, F. Juranyi and V. Wood, Nature, 2016, 531, 618 CrossRef CAS PubMed.
- N. Yazdani, D. Bozyigit, K. Vuttivorakulchai, M. Luisier, I. Infante and V. Wood, Nano Lett., 2018, 18, 2233 CrossRef CAS PubMed.
- N. Yazdani, T. Nguyen-Thanh, M. Yarema, W. M. M. Lin, R. Gao, O. Yarema, A. Bosak and V. Wood, J. Phys. Chem. Lett., 2018, 9, 1561 CrossRef CAS PubMed.
- (a) P. Simon, L. Bahrig, I. A. Baburin, P. Formanek, F. Röder, J. Sickmann, S. G. Hickey, A. Eychmüller, H. Lichte, R. Kniep and E. Rosseeva, Adv. Mater., 2014, 26, 3042 CrossRef CAS PubMed; (b) A. Konrad, M. Metzger, A. M. Kern, M. Brecht and A. J. Meixner, Nanoscale, 2015, 7, 10204 RSC.
- J. de Roo, N. Yazdani, E. Drijvers, A. Lauria, J. Maes, J. S. Owen, I. van Driessche, M. Niederberger, V. Wood, J. C. Martins, I. Infante and Z. Hens, Chem. Mater., 2018, 30, 5485 CrossRef CAS.
- N. Geva, J. J. Shepherd, L. Nienhaus, M. G. Bawendi and T. van Voorhis, J. Phys. Chem. C, 2018, 122, 26267 CrossRef CAS.
- B. T. Diroll, K. M. Weigandt, D. Jishkariani, M. Cargnello, R. J. Murphy, L. A. Hough, C. B. Murray and B. Donnio, Nano Lett., 2015, 15, 8008 CrossRef CAS PubMed.
- B. Fritzinger, R. K. Capek, K. Lambert, J. C. Martins and Z. Hens, J. Am. Chem. Soc., 2010, 132, 10195 CrossRef CAS PubMed.
- (a) X. Ji, D. Copenhaver, C. Sichmeller and X. Peng, J. Am. Chem. Soc., 2008, 130, 5726 CrossRef CAS PubMed; (b) C. Bullen and P. Mulvaney, Langmuir, 2006, 22, 3007 CrossRef CAS PubMed; (c) M. B. Teunis, T. Liyanage, S. Dolai, B. B. Muhoberac, R. Sardar and M. Agarwal, Chem. Mater., 2017, 29, 8838 CrossRef CAS.
- T. J. Woehl and T. Prozorov, J. Phys. Chem. C, 2015, 119, 21261 CrossRef CAS.
- L. R. Parent, E. Bakalis, M. Proetto, Y. Li, C. Park, F. Zerbetto and N. C. Gianneschi, Acc. Chem. Res., 2018, 51, 3 CrossRef CAS PubMed.
- J. Lu, Z. Aabdin, N. D. Loh, D. Bhattacharya and U. Mirsaidov, Nano Lett., 2014, 14, 2111 CrossRef CAS PubMed.
- H. Zheng, S. A. Claridge, A. M. Minor, A. P. Alivisatos and U. Dahmen, Nano Lett., 2009, 9, 2460 CrossRef CAS PubMed.
- A. Verch, M. Pfaff and N. de Jonge, Langmuir, 2015, 31, 6956 CrossRef CAS PubMed.
- P. Y. Kim, A. E. Ribbe, T. P. Russell and D. A. Hoagland, ACS Nano, 2016, 10, 6257 CrossRef CAS PubMed.
- (a) Z. Hens and J. C. Martins, Chem. Mater., 2013, 25, 1211 CrossRef CAS; (b) R. Dierick, F. van den Broeck, K. de Nolf, Q. Zhao, A. Vantomme, J. C. Martins and Z. Hens, Chem. Mater., 2014, 26, 5950 CrossRef CAS.
- I. Moreels, Y. Justo, B. de Geyter, K. Haustraete, J. C. Martins and Z. Hens, ACS Nano, 2011, 5, 2004 CrossRef CAS PubMed.
- I. Moreels, B. Fritzinger, J. C. Martins and Z. Hens, J. Am. Chem. Soc., 2008, 130, 15081 CrossRef CAS PubMed.
- Z. Luo, D. Marson, Q. K. Ong, A. Loiudice, J. Kohlbrecher, A. Radulescu, A. Krause-Heuer, T. Darwish, S. Balog, R. Buonsanti, D. I. Svergun, P. Posocco and F. Stellacci, Nat. Commun., 2018, 9, 1343 CrossRef PubMed.
- Neutrons, X-rays and light. Scattering methods applied to soft condensed matter, ed. P. Lindner and T. Zemb, North-Holland Elsevier, Amsterdam, 1st edn, 2002 Search PubMed.
- V. F. Sears, Neutron News, 1992, 3, 26 CrossRef.
- M. Grimaldo, F. Roosen-Runge, F. Zhang, F. Schreiber and T. Seydel, Q. Rev. Biophys., 2019, 52, e7 CrossRef.
- M. Bée, Phys. B, 1992, 182, 323 CrossRef.
- M. L. Kessler and J. L. Dempsey, Chem. Mater., 2020, 32, 2561 CrossRef CAS.
- (a) M. Grimaldo, F. Roosen-Runge, N. Jalarvo, M. Zamponi, F. Zanini, M. Hennig, F. Zhang, F. Schreiber and T. Seydel, EPJ Web Conf., 2015, 83, 2005 CrossRef; (b) K. S. Singwi and A. Sjölander, Phys. Rev., 1960, 119, 863 CrossRef CAS.
- A. J. Banchio and G. Nägele, J. Chem. Phys., 2008, 128, 104903 CrossRef PubMed.
- S. Mitra, V. K. Sharma, V. Garcia-Sakai, A. Orecchini, T. Seydel, M. Johnson and R. Mukhopadhyay, J. Phys. Chem. B, 2016, 120, 3777 CrossRef CAS PubMed.
- M. Iwahashi, Y. Yamaguchi, Y. Ogura and M. Suzuki, Bull. Chem. Soc. Jpn., 1990, 63, 2154 CrossRef CAS.
- M. Grimaldo, F. Roosen-Runge, M. Hennig, F. Zanini, F. Zhang, N. Jalarvo, M. Zamponi, F. Schreiber and T. Seydel, Phys. Chem. Chem. Phys., 2015, 17, 4645 RSC.
- F. Volino, J.-C. Perrin and S. Lyonnard, J. Phys. Chem. B, 2006, 110, 11217 CrossRef CAS PubMed.
- V. M. Kaganer, H. Möhwald and P. Dutta, Rev. Mod. Phys., 1999, 71, 779 CrossRef CAS.
- F. Schreiber, Prog. Surf. Sci., 2000, 65, 151 CrossRef CAS.
- I. Moreels, K. Lambert, D. Smeets, D. de Muynck, T. Nollet, J. C. Martins, F. Vanhaecke, A. Vantomme, C. Delerue, G. Allan and Z. Hens, ACS Nano, 2009, 3, 3023 CrossRef CAS PubMed.
- D. Zherebetskyy, M. Scheele, Y. Zhang, N. Bronstein, C. Thompson, D. Britt, M. Salmeron, P. Alivisatos and L.-W. Wang, Science, 2014, 344, 1380 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: (1) Methods, (2) details on data fitting, (3) calculation of the scattering power, (4) calculation of the concentration of free oleic acid in solution, (5) estimation of the number of desorbed ligands, (6) calculation of the volume fraction, (7) temperature-dependent redistribution of phonon modes, (8) characteristic vibrational energies in the solid and liquid state, Fig. S1: EISF at 239 K and 295 K, Fig. S2: Additional fixed-window data, Fig. S3: Qualitative scheme describing the results of the SAXS/SANS fitting, Fig. S4: Scattering power values, Fig. S5: Temperature-dependent relative difference in the number of phonon modes, Fig. S6: GDOS of d14-hexane at 100 K, Fig. S7 and S8: QENS data from IN5, Fig. S9: Diffusion of d14-hexane. See DOI: 10.1039/d0sc02636k |
| ‡ The neutron data can be accessed at: http://doi.ill.fr/10.5291/ILL-DATA.9-10-1514 (IN5) and http://doi.ill.fr/10.5291/ILL-DATA.9-12-498 (IN16B and D11). |
| § Present address: Jülich Centre for Neutron Science (JCNS-1), Forschungszentrum Jülich GmbH52425 Jülich, Germany. |
| ¶ Present address: Institut Max von Laue - Paul Langevin (ILL), CS20156, 38042 Grenoble Cedex 9, France. |
| This journal is © The Royal Society of Chemistry 2020 |