 Open Access Article
Open Access ArticleEnthalpic and entropic contributions to the basicity of cycloalkylamines†
Charles L.
Perrin
 * and
Annadka
Shrinidhi
* and
Annadka
Shrinidhi
Department of Chemistry & Biochemistry, University of California—San Diego, La Jolla, California 92093-0358, USA. E-mail: cperrin@ucsd.edu
First published on 29th July 2020
Abstract
Large-ring cycloalkylamines are slightly less basic than other cycloalkylamines such as cyclohexylamine, even though all have tetrahedral carbons and are strain-free. To understand why, enthalpy and entropy for protonation of a series of cycloalkylamines were accurately determined by isothermal titration calorimetry in 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 methanol–water. The study required resolving a discrepancy between these measurements and those in pure water. The data show that the lower basicity of large-ring cycloalkylamines is not due to enthalpy but to a more negative entropy of protonation. Computations show that this can be attributed in part to an entropy of conformational mixing, but the dominant contribution is steric hindrance to solvation, also corroborated by computation.
1 methanol–water. The study required resolving a discrepancy between these measurements and those in pure water. The data show that the lower basicity of large-ring cycloalkylamines is not due to enthalpy but to a more negative entropy of protonation. Computations show that this can be attributed in part to an entropy of conformational mixing, but the dominant contribution is steric hindrance to solvation, also corroborated by computation.
Introduction
Cycloalkanes CnH2n and their derivatives are abundant in natural products1 and fuels,2 they are precursors to cyclic products,3 and they and their derivatives are frequent targets of synthesis, where macrocycles are a particular challenge,4–6 often to serve as receptors for small molecules and ions.7–9 They have been a holy grail for many physical-organic chemists to study their structure and reactivity.10–12Their rings have been classified as small (n = 3–4), common (n = 5–7), medium (n = 8–12), and large (n ≥ 13).13,14 Small rings suffer from angle strain, as proposed by Baeyer.15 Cyclohexane (n = 6) has minimum strain owing to its chair conformation, with tetrahedral bond angles and with staggered bonds that eliminate torsional strain.16 Beyond cyclohexane the situation becomes complicated. Medium rings suffer from a combination of expanded bond angles, torsional strain, and transannular repulsion. In large rings those strains diminish, and the rings become strain-free for n ≥ 14.
Acid–base behavior can be a sensitive probe for angle strain, separate from torsional strain and transannular repulsion, because the effective electronegativity of a carbon depends on its hybridization. Indeed, titrations of cyclo-propyl-, -butyl-, and -pentyl-amines showed a reduced basicity attributable to their smaller CCC angles.17,18 Basicities of larger cycloalkylamines had also been measured, with medium-ring amines ca. 0.2 pK units more basic than cyclohexylamine and large-ring amines ca. 0.3 pK units less basic.19 However, these variations are hardly greater than the errors, so no conclusions were drawn.
Amine basicity is a topic of enduring interest. It probes medium effects,20 it is correlated with nucleophilicity,21,22 and it determines suitability for CO2 capture.23 Besides, basicity is sensitive to push–pull effects of electron donors,24 and also responsible for the formation of NXN halogen bonds from halonium ions25 and of NHN hydrogen bonds as in protonated 1,8-bis(dimethylamino)naphthalene (“Proton Sponge”), whose symmetry is a matter of controversy.26,27 Cycloalkylamines provide a more homogeneous series of homologs than do the more extensively studied azacycloalkanes, (CH2)nNH,28,29 where not only ring strain and torsional strain but also nitrogen's hybridization is affected by the ring size. Besides, those studies have not been extended to large rings.
Subsequently relative basicities of cycloalkylamines were measured,30 using a highly accurate NMR titration method.31Fig. 1 displays pKa's relative to (CH3)2CHNH3+.32 The data confirm the reduced basicity of small-ring amines, the slightly increased basicity of medium-ring amines, and the slightly lower basicity for large-ring amines. However, this last comparison was puzzling, because large-ring amines are free of angle strain, torsional strain, and transannular repulsion and ought to have the same basicity as cyclohexylamine.
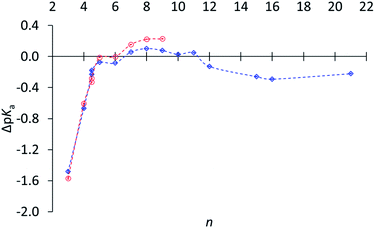 | ||
Fig. 1 ΔpKa of (CH2)n−1CHNH3+vs. n (and including exo- and endo-2-norbornyl at n = 4.5) in water ( ) and in 3 ) and in 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 methanol–water ( 1 methanol–water ( ), relative to (CH3)2CHNH3+ (1·H+), adapted from ref. 30. ), relative to (CH3)2CHNH3+ (1·H+), adapted from ref. 30. | ||
It would be an oversight to dismiss this comparison as too small to be worth addressing, especially inasmuch as secondary isotope effects are even smaller but are widely valued as informative. Although the difference corresponds to less than a twofold lower basicity for the large-ring amines relative to medium-ring amines, it is accurately measured (0.22 ± 0.05), and the error bars in Fig. 1 are too small to be seen. This difference is a puzzle, because the hybridization and torsional-strain environments of the –NH2 are identical in all these large-ring and medium-ring amines, and so are those of the –NH3+. This experimentally measured difference is a serious challenge to our claim to understand the relation between molecular structure and chemical reactivity.
It was therefore suggested that the lower basicity of a large-ring amine might be due to conformational restrictions on its ammonium ion.30 This is reasonable, since the necessity of solvent access to a positive charge should constrain the ring, whereas in cyclohexylammonium ion the ring is rigidly tethered away from the nitrogen. Such a conformational origin would be manifested in the entropy, and separation into entropic and enthalpic contributions has been used to explain some anomalies of amine basicity.33
In principle enthalpy and entropy contributions to basicity could be separated by measuring the temperature dependence of ΔpKa. Unfortunately, the error in ΔS° was found to be too large to draw any conclusion.30 Therefore we have now undertaken to measure enthalpies of protonation of cycloalkylamines by isothermal titration calorimetry (ITC). Then entropies could be determined from free energies evaluated from ΔpKa. We now report that the reason large-ring amines are measurably less basic than the other amines is that their ΔS° of protonation is slightly but significantly more negative.
Results
The reliability of our ITC measurements is supported by their excellent agreement with previously measured enthalpies of protonation,34 as shown in Table S4.† However, those measurements were limited to small-ring amines in aqueous solution, where the large-ring amines of interest are not soluble. Consequently it was necessary to measure enthalpies in aqueous methanol. The choice of 75% methanol was a practical one, to ensure solubility of both the amine and its protonated form.Table S7† lists the pKa and observed enthalpies for amine protonation in untreated 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 methanol–water. The baffling result is that the exothermicity of protonation of cycloalkylamines decreases with increasing ring size. In particular, protonation of cyclopropylamine (1) is the most exothermic of all, even though this is the least basic. Moreover, this is exactly the opposite of what is observed in water (Table S4†).
1 methanol–water. The baffling result is that the exothermicity of protonation of cycloalkylamines decreases with increasing ring size. In particular, protonation of cyclopropylamine (1) is the most exothermic of all, even though this is the least basic. Moreover, this is exactly the opposite of what is observed in water (Table S4†).
Table 1 lists the pKa, enthalpy, free-energy, and entropy values for protonation of amines in 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 methanol–water that had been purged with N2. (For clarity the boldface label for a cycloalkylamine designates n, the number of carbons in the ring.) The enthalpies of protonation of iPrNH2 (1) and cycloalkylamines 3, 5, and 6 are 0.4 ± 0.1 kcal mol−1 less negative than those measured in pure water (Table S4†), but they follow the same relative order. In particular protonation of cyclopropylamine (3) is the least exothermic, opposite to the result in untreated methanol–water (Table S7†) but consistent with expectations based on its lower basicity.
1 methanol–water that had been purged with N2. (For clarity the boldface label for a cycloalkylamine designates n, the number of carbons in the ring.) The enthalpies of protonation of iPrNH2 (1) and cycloalkylamines 3, 5, and 6 are 0.4 ± 0.1 kcal mol−1 less negative than those measured in pure water (Table S4†), but they follow the same relative order. In particular protonation of cyclopropylamine (3) is the least exothermic, opposite to the result in untreated methanol–water (Table S7†) but consistent with expectations based on its lower basicity.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 methanol–water at T = 25.0 °C
1 methanol–water at T = 25.0 °C
| Amine | pKa | −ΔH° | −ΔG° | ΔS° |
|---|---|---|---|---|
| 1 | 10.268 ± 0.005 | 13.57 ± 0.04 | 14.008 ± 0.007 | 1.47 ± 0.13 |
| 3 | 8.788 ± 0.007 | 11.47 ± 0.05 | 11.989 ± 0.010 | 1.73 ± 0.18 |
| 4 | 9.602 ± 0.005 | 12.88 ± 0.05 | 13.099 ± 0.007 | 0.75 ± 0.18 |
| 5 | 10.195 ± 0.003 | 13.84 ± 0.04 | 13.908 ± 0.004 | 0.23 ± 0.15 |
| 6 | 10.185 ± 0.003 | 13.88 ± 0.05 | 13.895 ± 0.004 | 0.05 ± 0.18 |
| 7 | 10.327 ± 0.002 | 14.09 ± 0.06 | 14.089 ± 0.003 | 0.01 ± 0.20 |
| 8 | 10.371 ± 0.002 | 14.13 ± 0.04 | 14.149 ± 0.003 | 0.05 ± 0.13 |
| 9 | 10.347 ± 0.004 | 14.11 ± 0.07 | 14.116 ± 0.005 | 0.03 ± 0.22 |
| 10 | 10.296 ± 0.003 | 14.04 ± 0.04 | 14.046 ± 0.004 | 0.02 ± 0.15 |
| 11 | 10.317 ± 0.003 | 14.08 ± 0.04 | 14.075 ± 0.004 | 0.00 ± 0.15 |
| 12 | 10.141 ± 0.004 | 14.00 ± 0.05 | 13.835 ± 0.005 | −0.55 ± 0.17 |
| 15 | 10.009 ± 0.004 | 13.88 ± 0.05 | 13.655 ± 0.005 | −0.76 ± 0.16 |
| 16 | 9.977 ± 0.004 | 13.87 ± 0.06 | 13.611 ± 0.006 | −0.86 ± 0.19 |
| 21 | 10.047 ± 0.004 | 13.97 ± 0.04 | 13.707 ± 0.005 | −0.88 ± 0.15 |
As the ring size increases, the enthalpies of protonation in Table 1 become even more negative, reach a minimum at n = 8 and increase slightly for the large rings, as can be seen in Fig. 2. A key result is that ΔH° for the large rings is essentially the same as for the common rings. Therefore the lower basicity of the large rings cannot be due to a lower exothermicity of protonation.
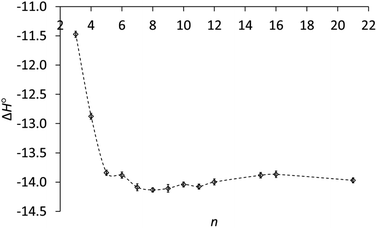 | ||
Fig. 2 Enthalpy of protonation (ΔH°, kcal mol−1) of cycloalkylamines (CH2)n−1CHNH2 in 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 methanol–water vs. ring size (n). 1 methanol–water vs. ring size (n). | ||
Fig. 3 shows how the entropy of protonation depends on ring size. The key result is that the entropy of protonation is high for cyclopropylamine (3) but decreases abruptly to become almost zero for common and medium rings (5–11) and then decreases further to become negative for large rings (12, 15, 16, 21). The average ΔS° for n ≥ 12 is −0.76 ± 0.15 cal mol−1 K−1, significantly more negative than the +0.03 ± 0.02 cal mol−1 K−1 for n = 6–11. Although the individual variations in entropy are not much larger than the experimental errors, the averages are consistent with this classification according to ring size. The data conclusively show that although ΔS° is very near zero for 6–11, ΔS° is slightly but significantly negative for large-ring amines 12, 15, 16, and 21.
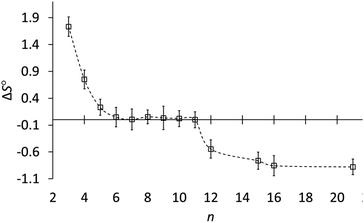 | ||
Fig. 3 Entropy of protonation (ΔS°, cal mol−1 K−1) of cycloalkylamines (CH2)n−1CHNH2 in 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 methanol–water vs. ring size (n). 1 methanol–water vs. ring size (n). | ||
Discussion
The contradiction between the order of enthalpies of protonation in water (Table S4†) versus their reverse order in aqueous methanol (Table S7†) was baffling. How can protonation of the least basic amine, cyclopropylamine, be, as expected, the least exothermic in water, but the most exothermic in 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 methanol–water? For weeks we considered many fanciful rationalizations involving solvent sorting in this mixed solvent.35,36 However, the same anomaly appears with 100% methanol, as shown in Table S8,† so this is not a consequence of solvent sorting. Eventually we recognized that experiments at submillimolar concentrations carry perils due to trace impurities, even though all amines were carefully purified.
1 methanol–water? For weeks we considered many fanciful rationalizations involving solvent sorting in this mixed solvent.35,36 However, the same anomaly appears with 100% methanol, as shown in Table S8,† so this is not a consequence of solvent sorting. Eventually we recognized that experiments at submillimolar concentrations carry perils due to trace impurities, even though all amines were carefully purified.
The impurity must be weakly acidic, to react with the more basic amines and reduce their apparent heat of protonation, while interfering with cyclopropylamine to a lesser extent. Moreover, the effect of that impurity should be greater in aqueous methanol than in water.
Carbon dioxide is just such an impurity, currently present in the atmosphere at a global-warming level of 414 ppm.37 Indeed, amines are effective for selective CO2 chemisorption through carbamate formation.38 The solubility of CO2 in 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 methanol–water can be estimated as 4 × 10−5 M, but only 1 × 10−5 M in water, based on extrapolations from data obtained at much higher pressures.39 The higher concentration in aqueous methanol is in a range to interfere with measurements of heats of protonation, whereas this is less of a problem in water. Therefore all amines were stored and used under N2, and solvents for ITC were bubbled with N2 to remove CO2. Fortunately this precaution confirmed the expected parallelism of the enthalpies of protonation between water and aqueous methanol, and it saved us from publishing an embarrassing blunder. And when this result was told to colleagues, their usual response was “How did you ever think of that?”
1 methanol–water can be estimated as 4 × 10−5 M, but only 1 × 10−5 M in water, based on extrapolations from data obtained at much higher pressures.39 The higher concentration in aqueous methanol is in a range to interfere with measurements of heats of protonation, whereas this is less of a problem in water. Therefore all amines were stored and used under N2, and solvents for ITC were bubbled with N2 to remove CO2. Fortunately this precaution confirmed the expected parallelism of the enthalpies of protonation between water and aqueous methanol, and it saved us from publishing an embarrassing blunder. And when this result was told to colleagues, their usual response was “How did you ever think of that?”
The enthalpies in Table 1 generally parallel basicities. The small-ring amines 3 and 4 are the least basic, owing to smaller C–C–C angles and increased s character in their C–N bonds.17 Correspondingly, protonation of these amines is the least exothermic. The parallelism for the other amines is not perfect. The slightly more basic medium-ring amines 7–11 show an average enthalpy of protonation of 14.1 ± 0.05 kcal mol−1, slightly greater than the 13.9 ± 0.05 kcal mol−1 average for common-ring (5, 6) and large-ring (15, 16, 21) amines. However, the enthalpies of protonation are the same for these latter two groups, even though the large-ring amines are less basic. Why?
Rather than focus on enthalpies, it is more informative to compare entropies of protonation (Table 1). Whereas ΔS° is very near zero for common- and medium-ring amines, it is negative for large-ring amines 12–21. This, finally, is the reason why large-ring amines are slightly less basic than the other amines, even though all carbons for n > 4 are tetrahedral.
How does entropy contribute? It may depend on two interrelated effects, solvation and conformational restrictions. Solvation is definitely involved, because in the gas phase cyclohexadecylamine (16) is calculated (HF6-31G(d), data not shown) to be 3 kcal mol−1 more basic than cyclohexylamine (6), opposite to the order in solution. Similarly, the experimental gas-phase basicity of acyclic amines increases with addition of distant methyl groups.40
However, the role of solvation in decreasing the basicity of large-ring amines is difficult to specify, so we first focus on conformational restrictions. We choose the specific case of a sixteen-membered ring, which benefits from the simplification that it has few distinct positions for substitution.41 The three stable conformers of 16·H+ are shown in Fig. 4 as corner, edge, and center. Inversion of configuration in the latter two is unfavorable because it forces the bulky substituent into the interior of the ring, but inversion of configuration in corner produces an equivalent structure. Also edge is paired with an enantiomer. Therefore there are a total of 2, 2, and 1 conformers of corner, edge, and center, respectively, along each of the four sides, and many more conformations of the corresponding amine 16.
Structures and energies were calculated with B3LYP/6-31+G(d,p), a level that provides improved energies of isomerization across a wide range of organic molecules,42 and with B3LYP/aug-cc-pVDZ, recommended for cyclohexylamine.43 Solvation was accounted for with the polarized-continuum model, which is recognized as imperfect for cations and amines in a hydrogen-bonding solvent like aqueous methanol. The calculated energies of all the low-lying conformers of 6, 6·H+, 16, and 16·H+ are listed in Tables S1–S3.† They can be correlated with the number of steric repulsions between NH and a CH five bonds away. In particular, center is destabilized, reducing the number of populated conformers of 16·H+.
Energies in Tables S1–S3† were converted to molar entropies of mixing, according to eqn (1), where Xi = mole fraction of conformer i at 25.0 °C. This ought to be calculated as exp(−Grel/RT)/Σexp(−Grel/RT), but free-energy calculations with the B3LYP/aug-cc-pVDZ basis set require an inordinate amount of computer time to calculate 144 or 147 normal modes. Therefore energies were used to calculate mole fractions for this basis set. To test whether this simplification creates error, mole fractions were calculated with the B3LYP/6-31+G(d,p) basis set using both sets of energies. Table 2 lists the calculated entropies of conformational mixing for 6, 6·H+, 16, and 16·H+. Comparison of the B3LYP/6-31+G(d,p) entropies shows that the error in using energies rather than free energies is negligible. This is reasonable inasmuch as the zero-point energies and thermal corrections are nearly the same for each conformation of an amine as for its protonated form, as can also be seen from the similarities between the Grel values in Table S1† and the Erel values in Table S2.†
Smix = −RΣXi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(Xi) ln(Xi) | (1) |
The calculated entropy of conformational mixing for 6, 2.18 cal mol−1 K−1, is almost identical to R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(3), because 6 has three nearly isoenergetic conformers, related by C–N rotation. Likewise, the calculated Smix for 16, 5.31–5.33 cal mol−1 K−1, is very close to 5.38 cal mol−1 K−1, which is R
ln(3), because 6 has three nearly isoenergetic conformers, related by C–N rotation. Likewise, the calculated Smix for 16, 5.31–5.33 cal mol−1 K−1, is very close to 5.38 cal mol−1 K−1, which is R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(15), because 16 has fifteen nearly isoenergetic conformers. It is only 16·H+ that deviates from a statistical mixture of five conformers, but its calculated Smix of 2.98–3.02 cal mol−1 K−1 is not so different from 3.20 cal mol−1 K−1, which is R
ln(15), because 16 has fifteen nearly isoenergetic conformers. It is only 16·H+ that deviates from a statistical mixture of five conformers, but its calculated Smix of 2.98–3.02 cal mol−1 K−1 is not so different from 3.20 cal mol−1 K−1, which is R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(5).
ln(5).
Those values lead to a calculated contribution of −2.32 ± 0.01 cal mol−1 K−1 to the entropy of mixing for protonation of 16. These values are slightly more negative than the contribution of −2.18 cal mol−1 K−1 calculated for protonation of 6. Therefore entropy of mixing does contribute to reducing the basicity of large-ring amines.
However, that difference is significantly less than the difference between −0.76 ± 0.15 cal mol−1 K−1, the average ΔS° for n ≥ 12, and the 0.03 ± 0.02 cal mol−1 K−1 for n = 6–11. This discrepancy is not due to any inadequacy of these basis sets, because so negative a ΔS° would require 16 edge·H+ to be destabilized by ∼1.0 kcal mol−1 and 16 center·H+ by ∼2.0 kcal mol−1, unrealistically higher than the calculated energies in Tables S1–S3.† Nor is the discrepancy due to our choice of 16 for calculations, because other large rings are just as unlikely to deviate from a nearly statistical population of conformers. Therefore although conformational restrictions do contribute to the negative ΔS° for n ≥ 12, we conclude that they are not dominant. We must admit that our original explanation, in terms of the number of conformations available,19 is wrong.
If conformational restriction and entropy of mixing are not sufficient to account for the negative ΔS° of protonation for n ≥ 12, what does? We conclude that steric hindrance to solvation must also contribute, as is seen in protein–ligand binding.44 The computations support this explanation: Table S9† lists the calculated short NH-to-CH distances in cyclohexylammonium ion (6·H+) and in the three conformers of cyclohexadecylammonium ion (16·H+) of Fig. 4. In 6·H+ there are only 2.5 Å four-bond distances, because the –NH3+ is held rigidly away from the ring. In contrast, in 16·H+ there are also some five-bond distances that are shorter, around 2.2 Å, comparable to the 2.3 Å five-bond NH-to-CH distances calculated for the axial conformer of 6·H+. Those nearby CH hydrogens hinder the solvation of the NH+, so that the solvent organization to accommodate that hindrance leads to a negative ΔS° and correspondingly a measurably lower basicity for the large-ring amines. Moreover, a further contrast is that ΔS° of protonation is positive for 3 and 4 because the small rings hold the CH farther from the NH+ and enable solvent access.
Finally, we can return to the question of why the enthalpies of protonation are the same for common-ring (5, 6) and large-ring (15, 16, 21) amines, even though the latter are less basic. This question was deferred in favor of a consideration of the entropies of protonation. Yet if steric hindrance to solvation is responsible for the difference in basicities, why does this not manifest itself in the enthalpy? The paradigm for this behavior is the greater aqueous acidity of formic acid over acetic acid, owing to steric hindrance to ionic solvation and appearing in the entropy, not the enthalpy.14 Thus we can understand why the lower basicity of large-ring amines resides in the entropy and not at all in the enthalpy.
Experimental section
Enthalpies of protonation of cycloalkylamines were determined by isothermal titration calorimetry (ITC) with a VP-ITC instrument (MicroCal, Inc.).45 The reference cell of the calorimeter was filled with 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 methanol–water, and a solution of the amine in 3
1 methanol–water, and a solution of the amine in 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 methanol–water was placed in the sample cell under UHP nitrogen gas atmosphere. A 3
1 methanol–water was placed in the sample cell under UHP nitrogen gas atmosphere. A 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 methanol–water solution of p-toluenesulfonic acid was then added in a series of 30 injections. The heats of dilution of each amine and of p-toluenesulfonic acid were measured independently. The ITC data were analyzed and fitted by the Origin 7.0 software adapted for ITC data analysis (MicroCal, Inc.). All titrations were performed in duplicate or triplicate. Further details are presented in ESI.†
1 methanol–water solution of p-toluenesulfonic acid was then added in a series of 30 injections. The heats of dilution of each amine and of p-toluenesulfonic acid were measured independently. The ITC data were analyzed and fitted by the Origin 7.0 software adapted for ITC data analysis (MicroCal, Inc.). All titrations were performed in duplicate or triplicate. Further details are presented in ESI.†
Conclusions
In summary, ΔH° values for protonation of cycloalkylamines were accurately measured by isothermal calorimetry and combined with highly accurate ΔpKa values to evaluate ΔS° of protonation. The data show that the lower basicity of large-ring amines is not due to enthalpy but to a more negative entropy of protonation. Computations show that this can be attributed in part to conformational restrictions, but the dominant contribution is steric hindrance to ionic solvation, also corroborated by computation.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by grants CHE124B, CHEFFPE, and CHE63CP to CLP from the UCSD Academic Senate and Department of Chemistry & Biochemistry. We are indebted to Dr Yongxuan Su for access to a Departmental VP-ITC instrument.Notes and references
- B. M. Fraga, Nat. Prod. Rep., 2003, 20, 392–413 RSC.
- H. Schobert, Chemistry of Fossil Fuels and Biofuels, Cambridge University Press, New York, 2013 Search PubMed.
- A. Banerjee, S. Sarkar and B. K. Patel, Org. Biomol. Chem., 2017, 15, 505–530 RSC.
- A. K. Yudin, Chem. Sci, 2015, 6, 30–49 RSC.
- J. R. Donald and W. P. Unsworth, Chem.–Eur. J., 2017, 23, 8780–8799 Search PubMed.
- K. T. Mortensen, T. J. Osberger, T. A. King, H. F. Sore and D. R. Spring, Chem. Rev., 2019, 119, 10288–10317 CrossRef CAS PubMed.
- M.-K. Chung, K. Severin, S. J. Lee, M. L. Waters and M. R. Gagné, Chem. Sci., 2011, 2, 744–747 RSC.
- A. Akdeniz, T. Minami, S. Watanabe, M. Yokoyama, T. Ema and P. Anzenbacher, Chem. Sci., 2016, 7, 2016–2022 RSC.
- L. Qin, A. Hartley, P. Turner, R. B. P. Elmes and K. A. Jolliffe, Chem. Sci., 2016, 7, 4563–4572 RSC.
- S. Patai and Z. Rappoport, The Chemistry of Alkanes and Cycloalkanes, John Wiley & Sons, New York, 1992 Search PubMed.
- A. Paul, C. S. Wannere, V. Kasalova, P. V. R. Schleyer and H. F. Schaefer, J. Am. Chem. Soc., 2005, 127, 15457–15469 CrossRef CAS PubMed.
- M. B. Smith and J. March, March's Advanced Organic Chemistry: Reactions, Mechanisms, and Structure, John Wiley & Sons, New York, 2007 Search PubMed.
- J. F. Liebman and A. Greenberg, Chem. Rev., 1976, 76, 311–365 CrossRef CAS.
- E. V. Anslyn and D. A. Dougherty, Modern Physical Organic Chemistry, University Science Books, California, 2006 Search PubMed.
- A. Baeyer, Chem. Ber., 1885, 18, 2269–2281 CrossRef.
- E. L. Eliel and S. H. Wilen, Stereochemistry of Organic Compounds, John Wiley & Sons, New York, 2008 Search PubMed.
- J. D. Roberts and V. C. Chambers, J. Am. Chem. Soc., 1951, 73, 5030–5034 CrossRef CAS.
- K. B. Wiberg, B. S. Ross, J. J. Isbell and N. McMurdie, J. Org. Chem., 1993, 58, 1372–1376 CrossRef CAS.
- V. Prelog, M. Fausy El-Neweihy and O. Häfliger, Helv. Chim. Acta, 1950, 33, 365–369 CrossRef CAS.
- S. Tshepelevitsh, A. Kütt, M. Lõkov, I. Kaljurand, J. Saame, A. Heering, P. G. Plieger, R. Vianello and I. Leito, Eur. J. Org. Chem., 2019, 2019, 6735–6748 CrossRef CAS.
- H. K. Hall and R. B. Bates, Tetrahedron Lett., 2012, 53, 1830–1832 CrossRef CAS.
- F. An, B. Maji, E. Min, A. R. Ofial and H. Mayr, J. Am. Chem. Soc., 2020, 142, 1526–1547 CrossRef CAS PubMed.
- X. Yang, R. J. Rees, W. Conway, G. Puxty, Q. Yang and D. A. Winkler, Chem. Rev., 2017, 117, 9524–9593 CrossRef CAS PubMed.
- E. D. Raczyńska, J.-F. Gal and P.-C. Maria, Chem. Rev., 2016, 116, 13454–13511 CrossRef PubMed.
- A. Karim, M. Reitti, A.-C. C. Carlsson, J. Gräfenstein and M. Erdélyi, Chem. Sci., 2014, 5, 3226–3233 RSC.
- C. L. Perrin and B. K. Ohta, J. Am. Chem. Soc., 2001, 123, 6520–6526 CrossRef CAS PubMed.
- M. Nadal-Ferret, R. Gelabert, M. Moreno and J. M. Lluch, J. Am. Chem. Soc., 2014, 136, 3542–3552 CrossRef CAS PubMed.
- T. Ohwada, H. Hirao and A. Ogawa, J. Org. Chem., 2004, 69, 7486–7494 CrossRef CAS PubMed.
- N. Radić, I. Despotović and R. J. C. C. A. Vianello, Croat. Chem. Acta, 2012, 85, 495–504 CrossRef.
- C. L. Perrin, M. A. Fabian and I. A. Rivero, Tetrahedron, 1999, 55, 5773–5780 CrossRef CAS.
- C. L. Perrin and M. A. Fabian, Anal. Chem., 1996, 68, 2127–2134 CrossRef CAS PubMed.
- In these figures the dashed lines have no significance but are to guide the eye..
- E. M. Arnett, F. M. Jones, M. Taagepera, W. G. Henderson, J. L. Beauchamp, D. Holtz and R. W. Taft, J. Am. Chem. Soc., 1972, 94, 4724–4726 CrossRef CAS.
- J. J. Christensen, R. M. Izatt, D. P. Wrathall and L. D. Hansen, J. Chem. Soc. A, 1969, 1212–1223 RSC.
- R. Ta-Shma and Z. Rappoport, in Adv. Phys. Org. Chem., ed. D. Bethell, Academic Press, 1992, vol. 27, pp. 239–291 Search PubMed.
- D. González-Salgado, K. Zemánková, E. G. Noya and E. Lomba, J. Chem. Phys., 2016, 144, 184505 CrossRef PubMed.
- https://scripps.ucsd.edu/programs/keelingcurve .
- R. W. Flaig, T. M. Osborn Popp, A. M. Fracaroli, E. A. Kapustin, M. J. Kalmutzki, R. M. Altamimi, F. Fathieh, J. A. Reimer and O. M. Yaghi, J. Am. Chem. Soc., 2017, 139, 12125–12128 CrossRef CAS PubMed.
- J. Xia, M. Jödecke, Á. Pérez-Salado Kamps and G. Maurer, J. Chem. Eng. Data, 2004, 49, 1756–1759 CrossRef CAS.
- D. H. Aue, H. M. Webb and M. T. Bowers, J. Am. Chem. Soc., 1975, 97, 4137–4139 CrossRef CAS.
- J. Dale, J. Chem. Soc., 1963, 93–111 RSC.
- J. Tirado-Rives and W. L. Jorgensen, J. Chem. Theory Comput., 2008, 4, 297–306 CrossRef CAS PubMed.
- L. I. N. Tomé, M. T. S. Rosado, M. Ermelinda, S. Eusébio and J. S. Redinha, J. Mol. Struct.: THEOCHEM, 2007, 804, 65–74 CrossRef.
- M. L. Verteramo, O. Stenström, M. M. Ignjatović, O. Caldararu, M. A. Olsson, F. Manzoni, H. Leffler, E. Oksanen, D. T. Logan, U. J. Nilsson, U. Ryde and M. Akke, J. Am. Chem. Soc., 2019, 141, 2012–2026 CrossRef CAS PubMed.
- VP-ITC MicroCalorimeter, User's Manual, Microcal Inc., Northampton, 2003 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental procedures, calculations, Tables S1–S9, Fig. S1–S9, and references (PDF). See DOI: 10.1039/d0sc02931a |
| This journal is © The Royal Society of Chemistry 2020 |

