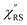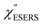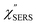Open Access Article
Open Access ArticleElectronic and vibrational surface-enhanced Raman scattering: from atomically defined Au(111) and (100) to roughened Au†
Motoharu
Inagaki‡
a,
Taichi
Isogai
a,
Kenta
Motobayashi
 a,
Kai-Qiang
Lin
a,
Kai-Qiang
Lin
 b,
Bin
Ren
b,
Bin
Ren
 c and
Katsuyoshi
Ikeda
c and
Katsuyoshi
Ikeda
 *ad
*ad
aDepartment of Physical Science and Engineering, Nagoya Institute of Technology, Gokiso, Showa, Nagoya 466-8555, Japan. E-mail: kikeda@nitech.ac.jp
bInstitut für Experimentelle und Angewandte Physik, Universität Regensburg, Regensburg, Germany
cState Key Laboratory of Physical Chemistry of Solid Surfaces, Collaborative Innovation Center of Chemistry for Energy Materials (iChEM), College of Chemistry and Chemical Engineering, Xiamen University, Xiamen 361005, China
dFrontier Research Institute for Materials Science (FRIMS), Nagoya Institute of Technology, Gokiso, Showa, Nagoya 466-8555, Japan
First published on 3rd August 2020
Abstract
In surface-enhanced Raman spectra, vibrational peaks are superimposed on a background continuum, which is known as one major experimental anomaly. This is problematic in assessing vibrational information especially in the low Raman-shift region below 200 cm−1, where the background signals dominate. Herein, we present a rigorous comparison of normal Raman and surface-enhanced Raman spectra for atomically defined surfaces of Au(111) or Au(100) with and without molecular adsorbates. It is clearly shown that the origin of the background continuum is well explained by a local field enhancement of electronic Raman scattering in the conduction band of Au. In the low Raman-shift region, electronic Raman scattering gains additional intensity, probably due to a relaxation in the conservation of momentum rule through momentum transfer from surface roughness. Based on the mechanism for generation of the spectral background, we also present a practical method to extract electronic and vibrational information at the metal/dielectric interface from the measured raw spectra by reducing the thermal factor, the scattering efficiency factor and the Purcell factor over wide ranges in both the Stokes and the anti-Stokes branches. This method enables us not only to analyse concealed vibrational features in the low Raman-shift region but also to estimate more reliable local temperatures from surface-enhanced Raman spectra.
1. Introduction
Plasmonic metal nanostructures can confine optical photons (optical far-fields) in their nanoscale cavities through photon-plasmon coupling.1–3 When a molecule is exposed to such nano-confined photons (optical near-fields), inelastic scattering of photons by molecular vibrations, i.e., Vibrational Raman Scattering (VRS), is largely enhanced in intensity by a factor of 106–1010.4–9 This plasmonic enhancement effect, typically referred to as Surface-Enhanced Raman Scattering (SERS), enables us to obtain chemical information not only with high detection sensitivity at the single-molecule level but also with high spatial resolution beyond the diffraction limit.10–14 It is, however, known that vibrational SERS (VSERS) signals are always superimposed on a background continuum;15–17 this often limits the signal-to-noise ratio in SERS spectroscopy. The origin of the background continuum is still under discussion, although this phenomenon has been recognized as one of the major experimental anomalies since the discovery of SERS.18 There are two predominant mechanisms for generation of the spectral background: inelastic scattering of photons by conduction electrons in a metal substrate, i.e., Electronic Raman Scattering (ERS),18–21 and photoluminescence (PL).22–25 In most SERS studies, however, the background continuum has been just ignored or subtracted from the raw spectra without any theoretical basis for doing this.26 In particular, there is a dearth of information on electronic SERS (ESERS).Recently, normal Raman Scattering (RS) spectroscopy (plasmonic enhancement absent) using a conventional single-monochromator has been shown to be applicable even in the low Raman-shift region below 100 cm−1 (3 THz in vibration frequency), owing to technical advances made in manufacturing ultra-narrow band optical notch filters.27–29 In contrast, SERS spectroscopy remains unexploited in this low Raman-shift spectral region because the background continuum dominates in this region,30–35 leading to a difficulty in analysing the VSERS signals. In the research fields of surface science such as catalysis and electrochemistry, surface-selective spectroscopy for such low-energy vibrations is of particular importance, because useful information on weak forces such as intermolecular interactions36,37 and substrate/molecule interactions can be provided.30,31,38 Low-energy ERS is also a crucial tool in condensed matter physics, giving access to strongly correlated systems and collective modes such as Cooper pairs and charge density waves.39 Nevertheless, studies on the SERS background have been mostly carried out in the high Raman-shift region.19–25,40 Due to a lack of information on the low Raman-shift region, theoretical treatment of the background continuum is considered to be insufficient. Hence, a rigorous investigation of VSERS and ESERS over a wide spectral range including the low Raman-shift region may provide deeper insights into the SERS mechanism.
SERS spectroscopy is normally conducted using SERS-active metal nanostructures to benefit from the highly confined optical near-fields.41–43 Actually, this has prevented us from improving our fundamental knowledge about SERS mechanisms. In conventional SERS spectroscopy, for example, roughened metal surfaces or colloidal aggregates have been commonly used as SERS-active substrates, resulting in low reproducibility of SERS spectra with respect to intensity and appearance. Even when well-tailored metal nanostructures are employed, their atomistic surface structures, which affect substrate/molecule interactions, are not very controllable. In this regard, the use of a well-defined single crystalline metal surface should advance our understanding of SERS mechanisms. The so-called nanoparticle-on-mirror structure is quite useful for observing such a defined flat metal surface; when Au nanoparticles are nearly in touch with a flat single crystalline metal substrate, each nanoparticle creates a SERS-hotspot on the surface.44–50 For example, Ikeda et al. demonstrated that VSERS spectra for various metal surfaces were indeed dependent on the atomistic surface features.17,29,51,52 Li et al. reported on in situ VSERS observation of electrochemical reactions at single crystalline Pt electrodes.49,53 For ESERS, however, there are only limited spectroscopic studies on such atomically defined surfaces.54
Herein, we present a thorough comparison of RS and SERS on Au(111) and Au(100) with and without molecular adsorbates, along with a theoretical framework to analyse both VSERS and ESERS. Strong evidence is provided to support the contention that the background continuum under moderate continuous wave (CW) excitation can be ascribed to ESERS rather than PL. Weak VSERS signals, concealed by large ESERS signals in the low Raman-shift region, can be extracted from the measured SERS spectra by reducing the Bose–Einstein thermal factor, the scattering efficiency factor and the Purcell factor, according to the mechanism of the background generation. Moreover, this method can be generalized to conventional SERS spectroscopy conducted on a roughened Au surface. Accordingly, more reliable local temperatures can be estimated from SERS spectra, which have often been overestimated in previous studies. The present work provides a practical method for performing in situ spectroscopic studies of various interface phenomena, and sheds more light on the SERS mechanism.
2. Methods
2.1 Theoretical treatment of RS and SERS
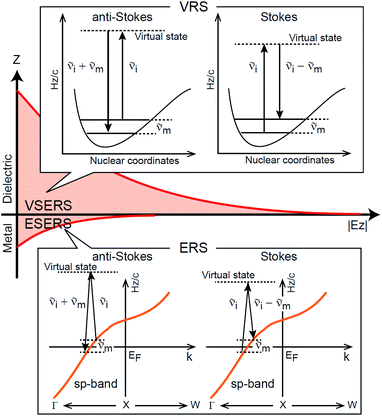
First, we focus on elucidating the theoretical treatment of VRS and ERS (plasmonic enhancement absent), and VSERS and ESERS (plasmonic enhancement present). A schematic of the relationships between these four scattering processes for the SERS model is shown in Fig. 1. It is emphasized that plotting of the Raman spectrum on the frequency-axis is preferable to the wavenumber-axis, given the physical meanings of frequency (energy) and wavenumber (momentum). In this paper, however, physical quantities are described using “wavenumber”; photon energy and Raman shifts are described using the absolute wavenumber (![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) > 0 in cm−1) and the relative wavenumber (
> 0 in cm−1) and the relative wavenumber (![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) Δ in cm−1), respectively, by considering the connection to traditional wavenumber plotting. Given the time reversal symmetry of light scattering, the ratio of the VRS intensities of the Stokes and anti-Stokes branches can be expressed in the well-known form:55
Δ in cm−1), respectively, by considering the connection to traditional wavenumber plotting. Given the time reversal symmetry of light scattering, the ratio of the VRS intensities of the Stokes and anti-Stokes branches can be expressed in the well-known form:55Anti-Stokes/Stokes = [n(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) m)]/[n( m)]/[n(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) m) + 1] = exp(−hc m) + 1] = exp(−hc![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) m/kBT). m/kBT). | (1) |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) m is the molecular vibration energy in cm−1, and n(
m is the molecular vibration energy in cm−1, and n(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) m) is the Bose–Einstein distribution described as n(
m) is the Bose–Einstein distribution described as n(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) m) = [exp(hc
m) = [exp(hc![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) m/kBT) − 1]−1, where h, c and kB are Planck's constant, the velocity of light and the Boltzmann constant, respectively. In VRS spectroscopy, eqn (1) is widely used to estimate the local temperature of a measured sample. Importantly, this relation holds for ERS;
m/kBT) − 1]−1, where h, c and kB are Planck's constant, the velocity of light and the Boltzmann constant, respectively. In VRS spectroscopy, eqn (1) is widely used to estimate the local temperature of a measured sample. Importantly, this relation holds for ERS; ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) m for ERS corresponds to the energy difference between the initial and final states of scattered electrons in the conduction band of a metal. The microscopic origin of the general Bose–Einstein weighting for both VRS and ERS is related to the thermal occupation of photon states.55,56 Therefore, the power spectrum for VRS or ERS in traditional wavenumber plotting, is connected with the imaginary part of the dynamic susceptibility,
m for ERS corresponds to the energy difference between the initial and final states of scattered electrons in the conduction band of a metal. The microscopic origin of the general Bose–Einstein weighting for both VRS and ERS is related to the thermal occupation of photon states.55,56 Therefore, the power spectrum for VRS or ERS in traditional wavenumber plotting, is connected with the imaginary part of the dynamic susceptibility, 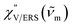 , by the following expressions:21,24,38,57
, by the following expressions:21,24,38,57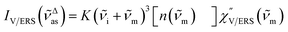 | (2) |
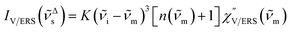 | (3) |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) i is the photon energy for the incident laser (
i is the photon energy for the incident laser (![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) i = 1/632.8 nm = 15
i = 1/632.8 nm = 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 802.8 cm−1), and
802.8 cm−1), and ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) Δas and
Δas and ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) Δs are the Raman shifts in the anti-Stokes and Stokes branches, i.e.,
Δs are the Raman shifts in the anti-Stokes and Stokes branches, i.e., ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) Δas = −
Δas = −![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) m and
m and ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) Δs =
Δs = ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) m. The cubic terms of the scattered photon energies, (
m. The cubic terms of the scattered photon energies, (![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) i +
i + ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) m)3 and (
m)3 and (![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) i −
i − ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) m)3, express the scattering efficiency factors for the anti-Stokes and Stokes processes, respectively; the cubic weighting is valid when the signals are measured using a photon counter.
m)3, express the scattering efficiency factors for the anti-Stokes and Stokes processes, respectively; the cubic weighting is valid when the signals are measured using a photon counter. 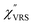 is given by the vibrational states of polyatomic molecules, leading to discrete vibrational features in the VRS spectra.
is given by the vibrational states of polyatomic molecules, leading to discrete vibrational features in the VRS spectra. 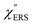 is determined by integrating the thermally occupied electronic states, which are described by the Fermi–Dirac function, over the distribution of excited wave vectors, resulting in a source for the broad continuum in the ERS spectra (
is determined by integrating the thermally occupied electronic states, which are described by the Fermi–Dirac function, over the distribution of excited wave vectors, resulting in a source for the broad continuum in the ERS spectra (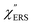 depends on the excitation energy or temperature, unlike
depends on the excitation energy or temperature, unlike 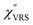 ).57–59 [n(
).57–59 [n(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) m)] and [n(
m)] and [n(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) m) + 1] correspond to the thermal factors for the anti-Stokes and Stokes processes, respectively. K is an instrument constant. Note that eqn (1) can be obtained from eqn (2) and (3) by neglecting the small difference in the scattering efficiency factors.
m) + 1] correspond to the thermal factors for the anti-Stokes and Stokes processes, respectively. K is an instrument constant. Note that eqn (1) can be obtained from eqn (2) and (3) by neglecting the small difference in the scattering efficiency factors.
Here, it is assumed that the SERS signals consist of VSERS and ESERS signals; that is, the SERS background originates solely from plasmon-enhanced ERS signals. For SERS, eqn (2) and (3) are modified using the local field enhancement, f ≡ |Enear-field/Efar-field|. This has been extensively discussed for VSERS. Here, we assume that this treatment is also applicable for ESERS. Note that the magnitude of f should be different for VSERS and ESERS because the near-field distribution is asymmetric across the metal/dielectric interface, as illustrated in Fig. 1. Therefore, the power spectrum for VSERS or ESERS, i.e., V/ESERS, is expressed as follows:20,60
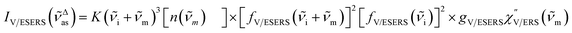 | (4) |
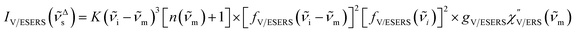 | (5) |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) m because free electrons are the source of ERS. [fV/ESERS(
m because free electrons are the source of ERS. [fV/ESERS(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) i)]2 and [fV/ESERS(
i)]2 and [fV/ESERS(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) i ±
i ± ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) m)]2 describe the field confinement effect for incident photons and the Purcell factor for scattering photons, respectively.5 Here, we define
m)]2 describe the field confinement effect for incident photons and the Purcell factor for scattering photons, respectively.5 Here, we define 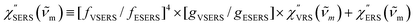 . The overall SERS signal, ISERS = IVSERS + IESERS, can then be simplified as follows:
. The overall SERS signal, ISERS = IVSERS + IESERS, can then be simplified as follows: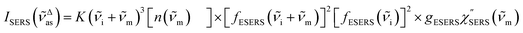 | (6) |
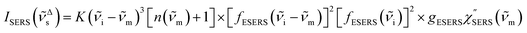 | (7) |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) i ±
i ± ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) m)]2 × [fESERS(
m)]2 × [fESERS(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) i)]2 × gESERS experimentally by measuring both the ESERS and the ERS spectra for the same metal surface with and without nanostructures. Then, the Purcell factor can be deduced from the measured SERS spectra using [IESERS/IERS]:
i)]2 × gESERS experimentally by measuring both the ESERS and the ERS spectra for the same metal surface with and without nanostructures. Then, the Purcell factor can be deduced from the measured SERS spectra using [IESERS/IERS]: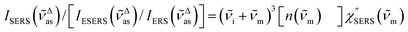 | (8) |
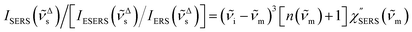 | (9) |
2.2 Experimental procedure
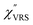 ,
, 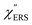 and
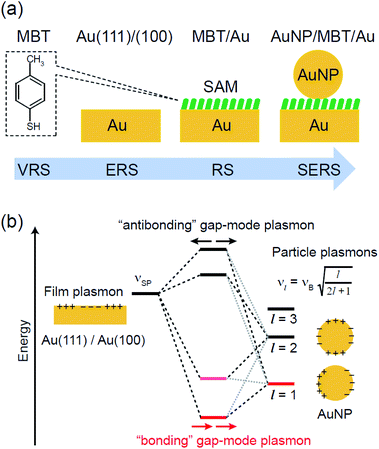
and 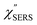 were obtained according to the procedure illustrated in Fig. 2(a). First, the VRS spectrum for molecules of 4-methylbenzenethiol (MBT) and the ERS spectra for bare Au(111) and Au(100) were measured separately, and then the
were obtained according to the procedure illustrated in Fig. 2(a). First, the VRS spectrum for molecules of 4-methylbenzenethiol (MBT) and the ERS spectra for bare Au(111) and Au(100) were measured separately, and then the 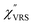 and
and 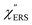 spectra were calculated using eqn (2) and (3). Next, self-assembled monolayers (SAMs) of MBT were formed on these Au surfaces. Normal RS spectra for these modified surfaces, i.e., MBT/Au(111) and MBT/Au(100), were measured, and the respective
spectra were calculated using eqn (2) and (3). Next, self-assembled monolayers (SAMs) of MBT were formed on these Au surfaces. Normal RS spectra for these modified surfaces, i.e., MBT/Au(111) and MBT/Au(100), were measured, and the respective 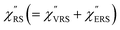 spectra were also calculated. It is noted that
spectra were also calculated. It is noted that 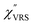 and
and 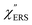 for the MBT/Au system should deviate from those of the individual systems because of the chemical interaction between MBT and Au. Therefore, SERS spectra for bare Au and MBT/Au must be analysed in eqn (8) and (9) using the ERS spectra for bare Au and MBT/Au, respectively. Finally, nanoparticle-on-mirror structures were formed by deposition of Au nanoparticles (AuNP) on these surfaces, i.e., AuNP/MBT/Au(111) and AuNP/MBT/Au(100).17 The plasmonic resonance property of these structures can be understood by plasmon coupling between film plasmons (a propagating surface plasmon mode) on a flat Au surface and particle plasmons (localized surface plasmon modes) on an AuNP, as shown in Fig. 2(b).44,45 This SERS technique is sometimes called gap-mode SERS because the coupled plasmon mode is referred to as gap-mode plasmons. Given that the gap distance in this structure is well-defined by the thickness of MBT-SAM, the plasmon resonance energy can be tuned by varying the diameter of the AuNPs.63,64 The
for the MBT/Au system should deviate from those of the individual systems because of the chemical interaction between MBT and Au. Therefore, SERS spectra for bare Au and MBT/Au must be analysed in eqn (8) and (9) using the ERS spectra for bare Au and MBT/Au, respectively. Finally, nanoparticle-on-mirror structures were formed by deposition of Au nanoparticles (AuNP) on these surfaces, i.e., AuNP/MBT/Au(111) and AuNP/MBT/Au(100).17 The plasmonic resonance property of these structures can be understood by plasmon coupling between film plasmons (a propagating surface plasmon mode) on a flat Au surface and particle plasmons (localized surface plasmon modes) on an AuNP, as shown in Fig. 2(b).44,45 This SERS technique is sometimes called gap-mode SERS because the coupled plasmon mode is referred to as gap-mode plasmons. Given that the gap distance in this structure is well-defined by the thickness of MBT-SAM, the plasmon resonance energy can be tuned by varying the diameter of the AuNPs.63,64 The 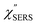 can be obtained using eqn (8) and (9) if the background continuum originated solely from the ERS.
can be obtained using eqn (8) and (9) if the background continuum originated solely from the ERS.
2.3 Sample preparation and Raman measurements
A single crystalline Au bead was fabricated by melting the end of an Au wire (diameter 0.8 mm; purity 99.999%); four (111) and one (100) facets appeared on top of the bead crystal after slow cooling of the Au bead.17 SERS measurements on the (111) and (100) faces were conducted at these small facets under microscope observation. An electrochemically roughened polycrystalline Au surface was also used as a conventional SERS substrate. The roughening process65 was conducted in 0.1 M KCl solution by applying potential cycles (−0.3 to 1.2 V vs. Ag/AgCl) using a function generator (WF1948, NF Corporation). These surfaces were self-assembly covered with molecular monolayers by immersing the substrates in 1 mM MBT (Aldrich) ethanoic solution for 2 hours. To induce SERS activity at the Au(111) and (100) surfaces, citrate-capped AuNPs with different diameters were physisorbed on top of the monolayers by immersion of the sample into Au colloidal solution (Tanaka precious metals) for 2 hours. SERS spectra were measured using a home-built inverted microscope Raman system with an objective (40×, 0.6 N.A.).26 He–Ne laser radiation (632.8 nm) was filtered using an ultra-narrow band laser-line filter with a bandwidth of less than 0.4 nm FWHM (reflecting volume Bragg grating (VBG) line filter, OptiGrate Corp). The excitation laser power at the focal point was typically less than 0.14 mW for SERS and 1.2 mW for RS. The backscattered Raman signals from the sample were monitored by a CCD-polychromator system (PIXIS 100BR eX-I & IsoPlane, Princeton Instruments) after Rayleigh scattered light was removed by two ultra-narrow band VBG notch filters (OptiGrate Corp).3. Results and discussion
3.1 Normal Raman spectra
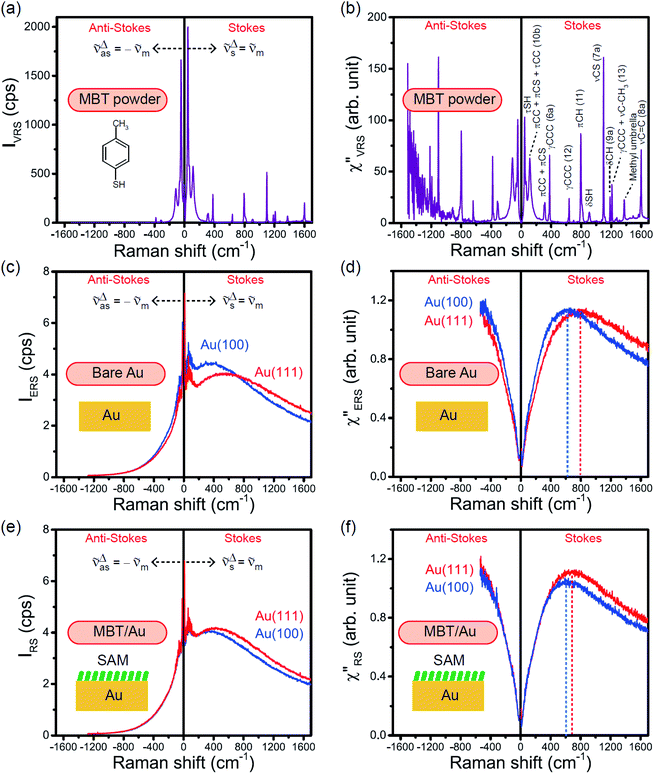
The measured VRS spectrum for solid crystalline MBT is presented in Fig. 3(a). In this raw spectrum, the peak intensities in the anti-Stokes branch rapidly decrease with increasing![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) m, compared with those in the Stokes branch. This typical behavior is as expected from eqn (1). Indeed, the appearance of the
m, compared with those in the Stokes branch. This typical behavior is as expected from eqn (1). Indeed, the appearance of the 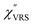 spectrum for MBT shown in Fig. 3(b), which was calculated using eqn (2) and (3) at T = 300 K, is nearly symmetric for the Stokes and the anti-Stokes branches. As is known, this high symmetry in the
spectrum for MBT shown in Fig. 3(b), which was calculated using eqn (2) and (3) at T = 300 K, is nearly symmetric for the Stokes and the anti-Stokes branches. As is known, this high symmetry in the 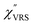 spectrum means that the thermal factor was effectively reduced from the measured spectrum. A similar tendency is found in the broad ERS spectra for the Au surfaces, as shown in Fig. 3(c) and (d), although accurate calculation of
spectrum means that the thermal factor was effectively reduced from the measured spectrum. A similar tendency is found in the broad ERS spectra for the Au surfaces, as shown in Fig. 3(c) and (d), although accurate calculation of 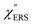 was difficult in the anti-Stokes branch of
was difficult in the anti-Stokes branch of ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) m > 500 cm−1 due to the extremely weak signal intensities. It is emphasized that the symmetry between the anti-Stokes and the Stokes branches after taking out the thermal factor is not expected from the PL expression, indicating that the observed signals at the Au surfaces indeed originated from ERS.24 This can be further confirmed by the dependence of
m > 500 cm−1 due to the extremely weak signal intensities. It is emphasized that the symmetry between the anti-Stokes and the Stokes branches after taking out the thermal factor is not expected from the PL expression, indicating that the observed signals at the Au surfaces indeed originated from ERS.24 This can be further confirmed by the dependence of 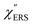 on the excitation energy, as shown in Fig. S1.†58,59 Interestingly, the spectral maximum for
on the excitation energy, as shown in Fig. S1.†58,59 Interestingly, the spectral maximum for 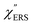 was apparently dependent on the crystal orientation, that is, 810 cm−1 for Au(111) and 638 cm−1 for Au(100). The source of inelastic ERS in normal metals is conduction electrons.38 Therefore, the orientation dependence of
was apparently dependent on the crystal orientation, that is, 810 cm−1 for Au(111) and 638 cm−1 for Au(100). The source of inelastic ERS in normal metals is conduction electrons.38 Therefore, the orientation dependence of 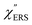 is related to the difference in the sp-projected surface density of states between Au(111) and Au(100). Incidentally, the rapid drop in intensity in the low Raman-shift region is a common feature of ERS in normal metals; light-induced charge fluctuations, which are needed for conservation of momentum in ERS transitions, are largely screened by Coulomb interactions in this region.57 The measured and calculated spectra for MBT/Au(111) and MBT/Au(100) are also presented in Fig. 3(e) and (f). The VRS signals from the MBT monolayers should be below the detection limit in normal RS spectra, hence, the measured broad spectra can be ascribed to ERS signals from the Au/MBT interfaces. For MBT/Au(111), the spectral maximum was red-shifted to 696 cm−1. However, for MBT/Au(100), the spectral intensity decreased for the entire region. Since formation of thiol monolayers is known to induce lifting of the surface reconstruction,66–68 one can expect that these changes of
is related to the difference in the sp-projected surface density of states between Au(111) and Au(100). Incidentally, the rapid drop in intensity in the low Raman-shift region is a common feature of ERS in normal metals; light-induced charge fluctuations, which are needed for conservation of momentum in ERS transitions, are largely screened by Coulomb interactions in this region.57 The measured and calculated spectra for MBT/Au(111) and MBT/Au(100) are also presented in Fig. 3(e) and (f). The VRS signals from the MBT monolayers should be below the detection limit in normal RS spectra, hence, the measured broad spectra can be ascribed to ERS signals from the Au/MBT interfaces. For MBT/Au(111), the spectral maximum was red-shifted to 696 cm−1. However, for MBT/Au(100), the spectral intensity decreased for the entire region. Since formation of thiol monolayers is known to induce lifting of the surface reconstruction,66–68 one can expect that these changes of 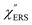 with and without MBT are related to adsorbate-induced changes in surface electronic structures (note the change of the dielectric environment due to MBT adsorption was not significant in the ellipsometry measurements). To the best of our knowledge, there is no report on such adsorbate-induced changes in ERS spectra. This will be discussed elsewhere, although this phenomenon is interesting from the viewpoint of surface spectroscopy.
with and without MBT are related to adsorbate-induced changes in surface electronic structures (note the change of the dielectric environment due to MBT adsorption was not significant in the ellipsometry measurements). To the best of our knowledge, there is no report on such adsorbate-induced changes in ERS spectra. This will be discussed elsewhere, although this phenomenon is interesting from the viewpoint of surface spectroscopy.
3.2 Surface-enhanced Raman spectra
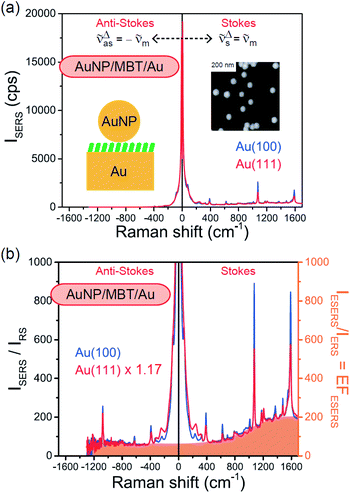
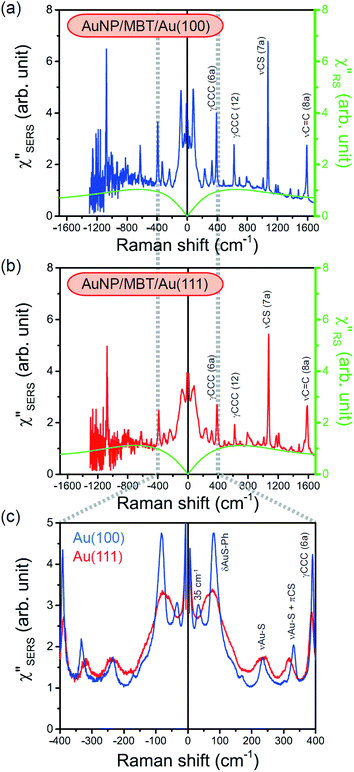
Both the VRS and the ERS signals from MBT/Au(111) and MBT/Au(100) are enhanced by the local fields created using deposited AuNPs. Fig. 4(a) shows the SERS spectra for AuNP/MBT/Au(111) and AuNP/MBT/Au(100), measured using AuNPs with a diameter of 60 nm. The distinct VSERS bands of MBT are now observed in the high Raman-shift region, along with the broad background continuum. It may be also noted that the background intensity is extremely large in the low Raman-shift region. This is indeed a serious problem in a practical vibrational study when the raw spectra are used for analysis; this will be discussed later. When the spectra for AuNP/MBT/Au(111) and AuNP/MBT/(100) are divided by the RS spectra for MBT/Au(111) and MBT/(100), respectively, the respective background profiles become very similar, as shown in Fig. 4(b). This result strongly supports the contention that the background continuum is associated with ESERS from the metal substrate. (Although ESERS signals from individual AuNPs may also contribute to the overall ESERS features, this would be same for Au(111) and Au(100).) It is noted here that the background profile of ISERS/IRS corresponds to IESERS/IERS = [fESERS(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) i ±
i ± ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) m)]2 × [fESERS(
m)]2 × [fESERS(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) i)]2 × gESERS, because the RS signals from MBT/Au mainly consist of ERS from MBT/Au. This “surface-averaged” enhancement factor for ESERS (EFESERS) is dependent on the surface density of the deposited AuNP.17,51,69 If it is assumed that the effective size of each SERS hotspot is the same as the diameter of the AuNP, the EFESERS per hotspot can be estimated to be in the order of 102–103 for this nanoparticle-on-mirror system. In previous reports, the enhancement factor for VSERS (EFVSERS) per hotspot was estimated to be 105–106 for the same system.17,51 The ratio between EFESERS and EFVSERS seems to be reasonable based on the asymmetric profile of the near-fields at the metal/dielectric interface.
i)]2 × gESERS, because the RS signals from MBT/Au mainly consist of ERS from MBT/Au. This “surface-averaged” enhancement factor for ESERS (EFESERS) is dependent on the surface density of the deposited AuNP.17,51,69 If it is assumed that the effective size of each SERS hotspot is the same as the diameter of the AuNP, the EFESERS per hotspot can be estimated to be in the order of 102–103 for this nanoparticle-on-mirror system. In previous reports, the enhancement factor for VSERS (EFVSERS) per hotspot was estimated to be 105–106 for the same system.17,51 The ratio between EFESERS and EFVSERS seems to be reasonable based on the asymmetric profile of the near-fields at the metal/dielectric interface.
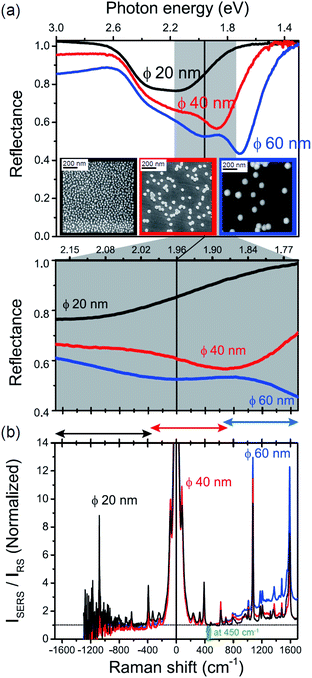
The origin of the SERS background can be further confirmed by changing the plasmon resonances of the AuNPs/MBT/Au. Fig. 5(a) shows the reflectance spectra of AuNP(ϕ 20 nm)/MBT/Au, AuNP(ϕ 40 nm)/MBT/Au, and AuNP(ϕ 60 nm)/MBT/Au. With increasing size of the AuNPs, the plasmon resonance energy is considerably red-shifted as a result of stronger plasmon coupling;63,64 the plasmon resonance band is found at 2.2 eV for ϕ 20 nm, which is located in the anti-Stokes branch, at 1.9 eV for ϕ 40 nm, which corresponds to the low Raman-shift region, and at 1.7 eV for ϕ 60 nm, which is located in the Stokes branch. (Note that the difference in the surface density of the AuNPs does not affect the plasmon resonance band because most of the AuNPs are well isolated from the other AuNPs. Thus, the higher surface density only contributes to the higher SERS intensities. A crystal orientation dependence of the plasmon resonance band was not clearly observed in this system.17,51) Here, the SERS spectra of AuNP/MBT/Au(100) for the different size AuNPs were divided by the same RS spectra of MBT/Au(100) in order to reduce the contribution of the 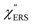 for MBT/Au (the raw SERS spectra are shown in Fig. S2†). In the high Raman-shift region of the Stokes branch, both the VSERS peaks and the ESERS background are larger for ϕ 60 nm than for the other diameters, as shown in Fig. 5(b). However, those signals in the anti-Stokes branch are apparently more intense for ϕ 20 nm than for other diameters. (For details, see Fig. S2.†) these trends, which are in accord with the plasmon resonance features, indicate that both VRS and ERS signals certainly gain intensity from plasmon resonances. Recently, Ren et al. has also pointed out the correlation of spectral profiles between the SERS background on Au nanoparticles and the broad emission from Au(111), although the origin of the emission from Au(111) was not assigned.40 It is also the case for the current model that the SERS spectra consist of VSERS and ESERS signals.
for MBT/Au (the raw SERS spectra are shown in Fig. S2†). In the high Raman-shift region of the Stokes branch, both the VSERS peaks and the ESERS background are larger for ϕ 60 nm than for the other diameters, as shown in Fig. 5(b). However, those signals in the anti-Stokes branch are apparently more intense for ϕ 20 nm than for other diameters. (For details, see Fig. S2.†) these trends, which are in accord with the plasmon resonance features, indicate that both VRS and ERS signals certainly gain intensity from plasmon resonances. Recently, Ren et al. has also pointed out the correlation of spectral profiles between the SERS background on Au nanoparticles and the broad emission from Au(111), although the origin of the emission from Au(111) was not assigned.40 It is also the case for the current model that the SERS spectra consist of VSERS and ESERS signals.
Now, one can obtain 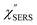 spectra from the measured SERS spectra using eqn (8) and (9) after division by EFESERS (= ISERS/IRS). In a practical analysis, care is needed regarding treatment of the very weak intensities of IERS (or IRS) in the high Raman-shift region of the anti-Stokes branch, in order to achieve a reliable analysis. The
spectra from the measured SERS spectra using eqn (8) and (9) after division by EFESERS (= ISERS/IRS). In a practical analysis, care is needed regarding treatment of the very weak intensities of IERS (or IRS) in the high Raman-shift region of the anti-Stokes branch, in order to achieve a reliable analysis. The 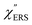 spectrum obtained from the Stokes branch can be used to regenerate the anti-Stokes IERS (or IRS) spectrum using eqn (2) (see Fig. S3†). This reprocessing significantly improves the quality of the spectrum conversion in the anti-Stokes branch. Fig. 6 shows the
spectrum obtained from the Stokes branch can be used to regenerate the anti-Stokes IERS (or IRS) spectrum using eqn (2) (see Fig. S3†). This reprocessing significantly improves the quality of the spectrum conversion in the anti-Stokes branch. Fig. 6 shows the 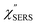 spectra for AuNP(ϕ 40 nm)/MBT/Au(111) and AuNP(ϕ 40 nm)/MBT/(100), which were calculated viaeqn (8) and (9) using T = 300 K. The spectral features are nearly symmetric for the Stokes and anti-Stokes branches, suggesting that the obtained
spectra for AuNP(ϕ 40 nm)/MBT/Au(111) and AuNP(ϕ 40 nm)/MBT/(100), which were calculated viaeqn (8) and (9) using T = 300 K. The spectral features are nearly symmetric for the Stokes and anti-Stokes branches, suggesting that the obtained 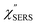 are indeed reliable. The important point to note is that both the vibrational peaks and the background continuum become symmetric after applying the same procedure. This gives strong evidence to support the contention that the background continuum can be ascribed to ESERS rather than PL, because such a symmetry for the background is not expected in the PL expression.24 Among the spectral features of
are indeed reliable. The important point to note is that both the vibrational peaks and the background continuum become symmetric after applying the same procedure. This gives strong evidence to support the contention that the background continuum can be ascribed to ESERS rather than PL, because such a symmetry for the background is not expected in the PL expression.24 Among the spectral features of 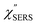 , we focus first on the ESERS continuum. The background continuum profile is well traced by the
, we focus first on the ESERS continuum. The background continuum profile is well traced by the 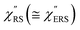 for MBT/Au. Actually, this profile has a large impact in terms of being able to estimate the local temperature in SERS spectroscopy. As already explained, eqn (1) is not valid for the measured SERS spectra due to the Purcell factor. Nevertheless, the local temperature has often been estimated by fitting the anti-Stokes ESERS signals with the Boltzmann distribution.19,20 However, such a fitting apparently overestimates the local temperature because of the
for MBT/Au. Actually, this profile has a large impact in terms of being able to estimate the local temperature in SERS spectroscopy. As already explained, eqn (1) is not valid for the measured SERS spectra due to the Purcell factor. Nevertheless, the local temperature has often been estimated by fitting the anti-Stokes ESERS signals with the Boltzmann distribution.19,20 However, such a fitting apparently overestimates the local temperature because of the 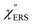 feature. As shown in Fig. S1,† for example, if the Boltzmann function is assumed for the anti-Stokes ESERS profiles, the apparent local temperatures are estimated to be T = 346 K for ϕ 20 nm, 315 K for ϕ 40 nm, and 304 K for ϕ 60 nm. It is emphasized again that the
feature. As shown in Fig. S1,† for example, if the Boltzmann function is assumed for the anti-Stokes ESERS profiles, the apparent local temperatures are estimated to be T = 346 K for ϕ 20 nm, 315 K for ϕ 40 nm, and 304 K for ϕ 60 nm. It is emphasized again that the 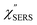 spectra in this figure were obtained using T = 300 K. Next, we focus on the VSERS features in Fig. 6. The differences of
spectra in this figure were obtained using T = 300 K. Next, we focus on the VSERS features in Fig. 6. The differences of 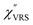 with and without a Au substrate can be seen mainly in the appearance of Au–S related vibrations and in the disappearance of S–H related vibrations from the comparison with Fig. 3(b). In the high Raman-shift region, i.e., in the so-called fingerprint region, VSERS peaks are quite similar between Au(111) and Au(100). In the low Raman-shift region, in contrast, the VSERS peaks are apparently dependent on the crystal orientation; most of the differences are found in the Au–S related vibrations such as νAu–S. Such low-energy “extramolecular” vibrations should be more sensitive to the atomistic differences of the substrate, compared with high-energy “intramolecular” vibrations. As reported previously, the dominant Au–S bonding structure may be assigned to bridge adsorption on Au(100) and hollow adsorption on Au(111).29,67–70 Importantly, the ability to analyse VSERS signals in the low Raman-shift region is considerably improved in the
with and without a Au substrate can be seen mainly in the appearance of Au–S related vibrations and in the disappearance of S–H related vibrations from the comparison with Fig. 3(b). In the high Raman-shift region, i.e., in the so-called fingerprint region, VSERS peaks are quite similar between Au(111) and Au(100). In the low Raman-shift region, in contrast, the VSERS peaks are apparently dependent on the crystal orientation; most of the differences are found in the Au–S related vibrations such as νAu–S. Such low-energy “extramolecular” vibrations should be more sensitive to the atomistic differences of the substrate, compared with high-energy “intramolecular” vibrations. As reported previously, the dominant Au–S bonding structure may be assigned to bridge adsorption on Au(100) and hollow adsorption on Au(111).29,67–70 Importantly, the ability to analyse VSERS signals in the low Raman-shift region is considerably improved in the 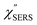 spectra, compared with the raw SERS spectra. As shown in Fig. 6(c), a small vibrational peak at 35 cm−1 is, for example, clearly observed in the
spectra, compared with the raw SERS spectra. As shown in Fig. 6(c), a small vibrational peak at 35 cm−1 is, for example, clearly observed in the 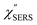 spectrum for (100), while this peak is completely concealed in the raw SERS spectrum. A detailed assignment of the low Raman-shift VSERS features is still ongoing.
spectrum for (100), while this peak is completely concealed in the raw SERS spectrum. A detailed assignment of the low Raman-shift VSERS features is still ongoing.
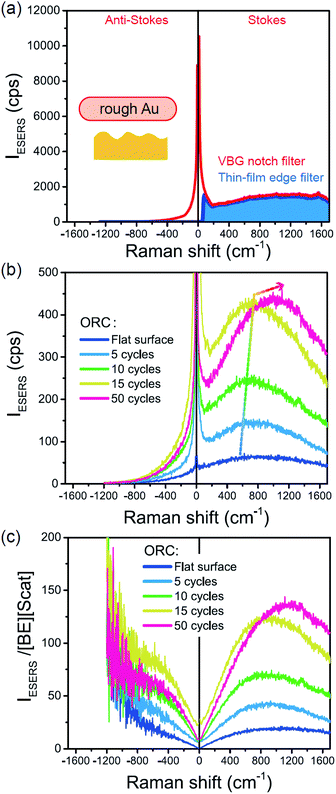
Next, we consider the SERS spectra measured on conventional rough Au surfaces. The ESERS spectra for an electrochemically roughened Au surface obtained using different optical filters are presented in Fig. 7(a). The spectrum obtained using the ultra-narrow band notch filter exhibits very intense signals in the low Raman-shift region, as already shown in Fig. 4 and 5. When the conventional edge filter is used for ESERS observation, the low Raman-shift signals are, of course, eliminated from the spectrum. Importantly, the tail of the low Raman-shift background signals can be still seen in the spectrum, indicating that this feature is not due to the leakage of Rayleigh scattered photons but due to inelastically scattered photons. Actually, the background in this low Raman-shift region is unexpectedly large, and it is not eliminated after reduction of the Bose–Einstein thermal factor unlike the normal ERS for Au (see Fig. S4†). To investigate this, electrochemical roughening of a flat Au surface was observed by in situ SERS spectroscopy. Fig. 7(b) shows a series of ESERS spectra of polycrystalline Au monitored for application of oxidation and reduction cycles (ORCs) in 0.1 M KCl solution.65 Before application of the ORCs, there was no characteristic features in the low Raman-shift region. When the ORC was applied, very distinct features rapidly evolved in this region along with an increase in the broad continuum. For the broad continuum, this spectral variation can be simply explained by plasmonic local field enhancement, as already discussed; this is more clearly seen in Fig. 7(c) where the thermal factor and the scattering efficiency factor are reduced. At the initial stage of the ORCs, the spectral features are rather symmetric between the Stokes and the anti-Stokes branches of the reduced spectra, meaning that the contribution of the wavenumber-dependent Purcell factor is rather small. With an increase in the number of ORCs applied, however, the spectral profile becomes asymmetric along a red-shift of the spectral maximum in the Stokes branch. This is due to the evolution of the plasmon-active surface roughness. In contrast, the appearance of the sharp features, especially in the initial stage of the ORCs, cannot be explained only by conventional local field enhancement. In the case of normal ERS (plasmonic enhancement absent), the momentum difference is conserved by light-induced charge fluctuations.38,58,59 Hence, the ERS cross sections significantly decrease in the low Raman-shift region, due to Coulomb screening. In other words, the ERS intensity can be enhanced if the momentum conservation rule is relaxed. There are two possible mechanisms for relaxation of momentum conservation in a plasmonic system: momentum transfer from nano-confined photons or from microscopic surface roughness. Actually, nano-confined photons, i.e., plasmon polaritons, have a very large momentum compared with free-propagating photons, according to the uncertainly principle. There are indeed several reports on plasmon-mediated optical transitions.21,71,72 As shown in Fig. 7, however, the evolution of the sharp features is more rapid than that of the plasmon resonance. For example, the ESERS spectrum after 5 ORCs exhibits the distinctive sharp feature in the low Raman-shift region, but the local field enhancement is still small. Therefore, the predominant mechanism for the extra enhancement of ERS in the low Raman-shift region is the relaxation of the usual momentum conservation rule by momentum transfer from the microscopic surface roughness18 (The decrease in the intensity of the sharp feature after 50 cycles is just a transitional change due to the red-shift of the plasmon resonance. After successive ORCs, this feature eventually becomes very intense as shown in Fig. 7(a)). Further investigation will be necessary to confirm this.
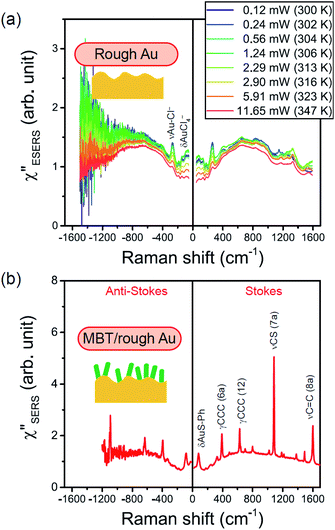
From the above, it is clear that the SERS mechanism proposed for the nanoparticle-on-mirror system is applicable to roughened surfaces of polycrystalline Au, despite the ill-defined plasmon resonances. Fig. 8 shows calculated results for 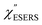 for rough Au and
for rough Au and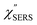 for MBT/rough Au, obtained using the same procedure applied for Fig. 6. For the
for MBT/rough Au, obtained using the same procedure applied for Fig. 6. For the 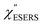 spectra in Fig. 8(a), each spectrum was measured using different excitation powers; laser-induced local heating was assumed in this measurement given the high excitation power. The local temperature for each spectrum was estimated by fitting via optimization of the symmetry between the Stokes and the anti-Stokes branches, after removing the same Purcell factor. As shown in Fig. 8(a), the dependence of the ESERS signals on laser excitation power is well explained by assuming laser-induced local heating. Under CW excitation, therefore, ERS is the dominant source for the SERS background while the intraband PL seems to be dominant for strong pulsed laser excitation.24 Incidentally, the vibrational features in the low Raman-shift region are ascribed to chloride complexs created by the ORCs.35,38 These peaks decreased in intensity with increasing laser pump power, probably due to surface migration induced by local heating. (The small features in the high Raman-shift region were caused by surface contaminants, which are unavoidable in SERS measurements under ambient conditions.) In previous SERS studies, the local temperature has often been estimated by Boltzmann fitting of the anti-Stokes branch of the SERS spectra.19,20 As already mentioned, this leads to overestimation of the local temperature. In Fig. 8(a), for example, the local temperature, under illumination with laser radiation of 11.65 mW, was estimated to be 347 K (for details, see ESI†). In the Boltzmann fitting, however, the apparent local temperature was 363 K because the
spectra in Fig. 8(a), each spectrum was measured using different excitation powers; laser-induced local heating was assumed in this measurement given the high excitation power. The local temperature for each spectrum was estimated by fitting via optimization of the symmetry between the Stokes and the anti-Stokes branches, after removing the same Purcell factor. As shown in Fig. 8(a), the dependence of the ESERS signals on laser excitation power is well explained by assuming laser-induced local heating. Under CW excitation, therefore, ERS is the dominant source for the SERS background while the intraband PL seems to be dominant for strong pulsed laser excitation.24 Incidentally, the vibrational features in the low Raman-shift region are ascribed to chloride complexs created by the ORCs.35,38 These peaks decreased in intensity with increasing laser pump power, probably due to surface migration induced by local heating. (The small features in the high Raman-shift region were caused by surface contaminants, which are unavoidable in SERS measurements under ambient conditions.) In previous SERS studies, the local temperature has often been estimated by Boltzmann fitting of the anti-Stokes branch of the SERS spectra.19,20 As already mentioned, this leads to overestimation of the local temperature. In Fig. 8(a), for example, the local temperature, under illumination with laser radiation of 11.65 mW, was estimated to be 347 K (for details, see ESI†). In the Boltzmann fitting, however, the apparent local temperature was 363 K because the 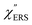 feature was not taken into account. Clearly, the present method is more reliable for estimation of the local temperature. This tendency is the same even when molecular adsorbates exist on the surface. In Fig. 8(b), the appearance of the
feature was not taken into account. Clearly, the present method is more reliable for estimation of the local temperature. This tendency is the same even when molecular adsorbates exist on the surface. In Fig. 8(b), the appearance of the 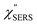 spectrum for MBT/rough Au is similar to that for MBT/Au(111) or Au(100) in Fig. 6, suggesting that the calculation result is indeed reliable. However, the symmetry of the vibrational peaks between the Stokes and the anti-Stokes branches is relatively low, compared with that for the background continuum. This is probably due to the inhomogeneous distribution of MBT molecules on the rough surface; while every SERS-active hotspot emits ESERS signals regardless of MBT adsorption, some of hotspots may not emit VSERS signals given the absence of MBT. Accordingly, the frequency dependence of the “averaged” Purcell factor might be slightly different for ESERS and VSERS. However, it is noted that low-energy vibrations such as δAuS–Ph can be well revealed by this procedure. The analytical method proposed in this paper is useful for analysing vibrational features in practical SERS spectroscopy.
spectrum for MBT/rough Au is similar to that for MBT/Au(111) or Au(100) in Fig. 6, suggesting that the calculation result is indeed reliable. However, the symmetry of the vibrational peaks between the Stokes and the anti-Stokes branches is relatively low, compared with that for the background continuum. This is probably due to the inhomogeneous distribution of MBT molecules on the rough surface; while every SERS-active hotspot emits ESERS signals regardless of MBT adsorption, some of hotspots may not emit VSERS signals given the absence of MBT. Accordingly, the frequency dependence of the “averaged” Purcell factor might be slightly different for ESERS and VSERS. However, it is noted that low-energy vibrations such as δAuS–Ph can be well revealed by this procedure. The analytical method proposed in this paper is useful for analysing vibrational features in practical SERS spectroscopy.
Conclusions
In conclusion, SERS spectra are well explained by plasmonic enhancement of both vibrational and electronic Raman scattering at metal/dielectric interfaces. The discrete vibrational peaks in SERS spectra are ascribed to inelastic scattering of nano-confined photons by molecular vibrations. The broad background continuum with sharp features in the low Raman-shift region is not ascribed to PL but to inelastic scattering of nano-confined photons by conduction electrons in the metal substrate, because of the correlation between the anti-Stokes and the Stokes branches. The spectral profile of the SERS background is influenced not only by the enhanced local fields but also by momentum transfer from the surface roughness. To extract both vibrational and electronic information from measured SERS spectra, it is essential to reduce the Bose-Einstein thermal factor, the scattering efficiency factor and the Purcell factor. The Purcell factor can be determined by comparison of the electronic Raman spectra with and without plasmonic nanostructures. Low-energy vibrations in the raw SERS spectra are concealed by the intense background, but are uncovered by calculating their susceptibilities. In this work, we were able to analyse vibrational features down to 10 cm−1 in the SERS spectra. Our strategy offers a novel route to obtain rich information and new knowledge on buried interfaces at the molecular level.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported in part by Grant-in-Aid for Scientific Research (c) (No. JP15K05372) and Challenging Research (Exploratory) (No. 18K18999) from JSPS, and also by The Hibi Science Foundation, Japan.Notes and references
- J. A. Schuller, E. S. Barnard, W. Y. Chul Jun, J. S. White and M. L. Brongersma, Nat. Mater., 2010, 9, 193–204 CrossRef CAS PubMed.
- N. J. Halas, S. Lal, W.-S. Chang, S. Link and P. Nordlander, Chem. Rev., 2011, 111, 3913–3961 CrossRef CAS PubMed.
- W. L. Barnes, A. Dereux and T. W. Ebbesen, Nature, 2003, 424, 824–830 CrossRef CAS PubMed.
- M. Fleischmann, P. J. Hendra and A. J. McQuillan, Chem. Phys. Lett., 1974, 26, 163–166 CrossRef CAS.
- B. Pettinger, J. Chem. Phys., 1986, 85, 7442–7451 CrossRef CAS.
- M. Moskovits, J. Raman Spectrosc., 2005, 36, 485–496 CrossRef CAS.
- J. Yang, J. C. Dong, V. Vinod Kumar, J. F. Li and Z. Q. Tian, Curr. Opin. Electrochem., 2017, 1, 16–21 CrossRef.
- S. M. Morton, D. W. Silverstein and L. Jensen, Chem. Rev., 2011, 111, 3962–3994 CrossRef CAS PubMed.
- S. A. Maier, Plasmonics: Fundamentals and Applications, Springer, New York, 2007, p. 159 Search PubMed.
- S. Nie and R. Emory, Science, 1997, 275, 1102–1106 CrossRef CAS PubMed.
- K. Kneipp, Y. Wang, H. Kneipp, L. T. Perelman, I. Itzkan, R. R. Dasari and M. S. Feld, Phys. Rev. Lett., 1997, 78, 1667–1670 CrossRef CAS.
- A. B. Zrimsek, N. Chiang, M. Mattei, S. Zaleski, M. O. McAnally, C. T. Chapman, A. –I. Henry, G. C. Schatz and R. P. Van Duyne, Chem. Rev., 2017, 117, 7583–7613 CrossRef CAS PubMed.
- H.-S. Su, X. –G. Zhang, J. –J. Sun, X. Jin, D. –Y. Wu, X. –B. Lian, J. –H. Zhong and B. Ren, Angew. Chem., Int. Ed., 2018, 57, 13177–13181 CrossRef CAS PubMed.
- J. Lee, N. Tallarida, X. Chen, P. Liu, L. Jensen and V. A. Apkarian, ACS Nano, 2017, 11, 11466–11474 CrossRef CAS PubMed.
- S. Mahajan, R. M. Cole, J. D. Speed, S. H. Pelfrey, A. E. Russell, P. N. Bartlett, S. M. Barnett and J. J. Baumberg, J. Phys. Chem. C, 2010, 114, 7242–7250 CrossRef CAS.
- C. Farcau and S. Astilean, Chem. Commun., 2011, 47, 3861–3863 RSC.
- K. Ikeda, S. Suzuki and K. Uosaki, J. Am. Chem. Soc., 2013, 135, 17387–17392 CrossRef CAS PubMed.
- A. Otto, J. Timper, J. Billmann, G. Kovacs and I. Pockrand, Surf. Sci., 1980, 92, L55–L57 CrossRef CAS.
- J. T. Hugall and J. J. Baumberg, Nano Lett., 2015, 15, 2600–2604 CrossRef CAS PubMed.
- K. T. Crampton, A. Fast, E. O. Potma and V. A. Apkarian, Nano Lett., 2018, 18, 5791–5796 CrossRef CAS PubMed.
- S. Dey, M. Banik, E. Hulkko, K. Rodriguez, V. A. Apkarian, M. Galperin and A. Nitzan, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 035411 CrossRef.
- M. R. Beversluis, A. Bouhelier and L. Novotny, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 115433 CrossRef.
- Y. –Y. Cai, E. Sung, R. Zhang, L. J. Tauzin, J. G. Liu, B. Ostovar, Y. Zhang, W. –S. Chang, P. Nordlander and S. Link, Nano Lett., 2019, 19, 1067–1073 CrossRef PubMed.
- L. Roloff, P. Klemm, I. Gronwald, R. Huber, J. M. Lupton and S. Bange, Nano Lett., 2017, 17, 7914–7919 CrossRef CAS PubMed.
- K.-Q. Lin, J. Yi, S. Hu, J. –J. Sun, J. –T. Zheng, X. Wang and B. Ren, ACS Photonics, 2016, 3, 1248–1255 CrossRef CAS.
- Z. M. Zhang, S. Chen, Y. Z. Liang, Z. X. Liu, Q. M. Zhang, L. X. Ding, F. Ye and H. Zhou, J. Raman Spectrosc., 2010, 41, 659–669 CrossRef CAS.
- A. L. Glebov, O. Mokhun, A. Rapaport, S. Vergnole, V. Smirnov and L. B. Glebov, Proc. SPIE, 2012, 8428, 84280C CrossRef.
- P. H. Tan, W. P. Han, W. J. Zhao, Z. H. Wu, K. Chang, H. Wang, Y. F. Wang, N. Bonini, N. Marzari, N. Pugno, G. Savini, A. Lombardo and A. C. Ferrari, Nat. Mater., 2012, 11, 294–300 CrossRef CAS PubMed.
- J. Ibáñez, A. Rapaport, C. Boney, R. Oliva, R. Cuscó, A. Bensaoula and L. Artús, J. Raman Spectrosc., 2012, 43, 237–240 CrossRef.
- M. Inagaki, K. Motobayashi and K. Ikeda, J. Phys. Chem. Lett., 2017, 8, 4236–4240 CrossRef CAS PubMed.
- M. Inagaki, K. Motobayashi and K. Ikeda, Curr. Opin. Electrochem., 2019, 17, 143–148 CrossRef CAS.
- D. A. Weitz, T. J. Gramila and A. Z. Genack, Phys. Rev. Lett., 1980, 45, 355–358 CrossRef CAS.
- G. Bachelier, J. Margueritat, A. Mlayah, J. Gonzalo and C. N. Afonso, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 235419 CrossRef.
- H. Portales, L. Saviot, E. Duval, M. Fujii, S. Hayashi, N. Del Fatti and F. Vallee, J. Chem. Phys., 2001, 115, 3444–3447 CrossRef CAS.
- B. H. Loo, J. Phys. Chem., 1982, 86, 433–437 CrossRef CAS.
- K. Fumino, S. Reimann and R. Ludwig, Phys. Chem. Chem. Phys., 2014, 16, 21903–21929 RSC.
- K. Iwata, H. Okajima, S. Saha and H. Hamaguchi, Acc. Chem. Res., 2007, 40, 1174–1181 CrossRef CAS PubMed.
- H. Seki, J. Electron Spectrosc. Relat. Phenom., 1986, 39, 289–310 CrossRef CAS.
- T. P. Devereaux and R. Hackl, Rev. Mod. Phys., 2007, 79, 175–233 CrossRef CAS.
- K. –Q. Lin, J. Yi, J. –H. Zhong, S. Hu, B. –J. Liu, J. –Y. Liu, C. Zong, Z. –C. Lei, X. Wang, J. Aizpurua, R. Esteban and B. Ren, Nat. Commun., 2017, 8, 14891 CrossRef CAS PubMed.
- L. Zhang, W. Dong, Z. Tang, J. Song, H. Xia and H. Sun, Opt. Lett., 2010, 35, 3297 CrossRef CAS PubMed.
- Z. Zhu, H. Meng, W. Liu, X. Liu, J. Gong, X. Qiu, L. Jiang, D. Wang and Z. Tang, Angew. Chem., Int. Ed., 2011, 50, 1593 CrossRef CAS PubMed.
- L. He, Y. Liu, Y. Xiong, J. Zheng, Y. Liu and Z. Tang, Angew. Chem., Int. Ed., 2013, 52, 3741 CrossRef CAS PubMed.
- P. K. Aravind and H. Metiu, J. Phys. Chem., 1982, 86, 5076–5084 CrossRef CAS.
- P. Nordlander and E. Prodan, Nano Lett., 2004, 4, 2209–2213 CrossRef CAS.
- J. K. Daniels and G. Chumanov, J. Phys. Chem. B, 2005, 109, 17936–17942 CrossRef CAS PubMed.
- K. Kim and J. K. Yoon, J. Phys. Chem. B, 2005, 109, 20731–20736 CrossRef CAS PubMed.
- K. Ikeda, N. Fujimoto, H. Uehara and K. Uosaki, Chem. Phys. Lett., 2008, 460, 205–208 CrossRef CAS.
- J. F. Li, Y. F. Huang, Y. Ding, Z. L. Yang, S. B. Li, Z. S. Zhou, F. R. Fan, W. Zhang, Z. Y. Zhou, D. Y. Wu, B. Ren, Z. L. Wang and Z. Q. Tian, Nature, 2010, 464, 392–395 CrossRef CAS PubMed.
- D. P. Butcher, S. P. Boulos, C. J. Murphy, R. C. Ambrosio and A. A. Gewirth, J. Phys. Chem. C, 2012, 116, 5128–5140 CrossRef CAS.
- K. Ikeda, S. Suzuki and K. Uosaki, Nano Lett., 2011, 11, 1716–1722 CrossRef CAS PubMed.
- J. Hu, M. Tanabe, J. Sato, K. Uosaki and K. Ikeda, J. Am. Chem. Soc., 2014, 136, 10299–10307 CrossRef CAS PubMed.
- J. C. Dong, X. G. Zhang, V. Briega-Martos, X. Jin, J. Yang, S. Chen, Z. L. Yang, D. Y. Wu, J. M. Feliu, C. T. Williams, Z. Q. Tian and J. F. Li, Nat. Energy, 2019, 4, 60–67 CrossRef CAS.
- A. Bruckbauer and A. Otto, J. Raman Spectrosc., 1998, 29, 665 CrossRef CAS.
- R. Loudon, J. Raman Spectrosc., 1978, 7, 10 CrossRef CAS.
- V. Branchina, M. D. Liberto and I. Lodato, Phys. Rev. E, 2010, 81, 011120 CrossRef PubMed.
- Y. S. Ponosov and S. V. Streltsov, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 045138 CrossRef.
- Y. S. Ponosov and S. V. Streltsov, JEPT Lett, 2011, 94, 437–441 CAS.
- V. N. Kostur, Z. Phys. B, 1992, 89, 149–159 CrossRef CAS.
- M. K. Schmidt, R. Esteban, A. González-Tudela, G. Giedke and J. Aizpurua, ACS Nano, 2016, 10, 6291–6298 CrossRef CAS PubMed.
- T. Hümmer, F. J. García-Vidal, L. Martín-Moreno and D. Zueco, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 115419 CrossRef.
- A. F. Koenderink, Opt. Lett., 2010, 35, 4208–4210 CrossRef CAS PubMed.
- K. Ikeda, K. Takahashi, T. Masuda, H. Kobori, M. Kanehara, T. Teranishi and K. Uosaki, J. Phys. Chem. C, 2012, 116, 20806–20811 CrossRef CAS.
- F. Benz, R. Chikkaraddy, A. Salmon, H. Ohadi, B. de Nijs, J. Mertens, C. Carnegie, R. W. Bowman and J. J. Baumberg, J. Phys. Chem. Lett., 2016, 7, 2264–2269 CrossRef CAS PubMed.
- Z. –Q. Tian, B. Ren and D. –Y. Wu, J. Phys. Chem. B, 2002, 106, 9463–9483 CrossRef CAS.
- G. Nenchev, B. Diaconescu, F. Hagelberg and K. Pohl, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 081401 CrossRef.
- S. M. Driver, T. Zhang and D. A. King, Angew. Chem., Int. Ed., 2007, 46, 700–703 CrossRef CAS PubMed.
- C. Vericat, M. E. Vela, G. Benitez, P. Carro and R. C. Salvarezza, Chem. Soc. Rev., 2010, 39, 1805–1834 RSC.
- S. Mubeen, S. Zhang, N. Kim, S. Lee, S. Krämer, H. Xu and M. Moskovits, Nano Lett., 2012, 12, 2088–2094 CrossRef CAS PubMed.
- J. Nara, S. Higai, Y. Morikawa and T. Ohno, J. Chem. Phys., 2004, 120, 6705–6711 CrossRef CAS PubMed.
- K. Ikeda, M. Takase, N. Hayazawa, S. Kawata, K. Murakoshi and K. Uosaki, J. Am. Chem. Soc., 2013, 135, 11489–11492 CrossRef CAS PubMed.
- M. V. Balois, N. Hayazawa, S. Yasuda, K. Ikeda, B. Yang, E. Kazuma, Y. Yokota, Y. Kim and T. Tanaka, npj 2D Mater. Appl., 2019, 38 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc02976a |
| ‡ Present address: Asahi Intecc Co. Ltd. Akatsuki-cho, Seto, Aichi 489-0071, Japan. |
| This journal is © The Royal Society of Chemistry 2020 |