Open Access Article
Open Access ArticlePolymorph exploration of bismuth stannate using first-principles phonon mode mapping†
Warda
Rahim
 ab,
Jonathan M.
Skelton
c,
Christopher N.
Savory
ab,
Jonathan M.
Skelton
c,
Christopher N.
Savory
 ab,
Ivana R.
Evans
ab,
Ivana R.
Evans
 d,
John S. O.
Evans
d,
Aron
Walsh
d,
John S. O.
Evans
d,
Aron
Walsh
 ef and
David O.
Scanlon
ef and
David O.
Scanlon
 *abg
*abg
aDepartment of Chemistry, University College London, 20 Gordon Street, London WC1H 0AJ, UK. E-mail: d.scanlon@ucl.ac.uk
bThomas Young Centre, University College London, Gower Street, London WC1E 6BT, UK
cDepartment of Chemistry, University of Manchester, Oxford Road, Manchester M13 9PL, UK
dDepartment of Chemistry, University Science Site, Durham University, South Road, Durham DH1 3LE, UK
eDepartment of Materials, Imperial College London, Exhibition Road, London SW7 2AZ, UK
fDepartment of Materials Science and Engineering, Yonsei University, Seoul 03722, Korea
gDiamond Light Source Ltd., Diamond House, Harwell Science and Innovation Campus, Didcot, Oxfordshire OX11 0DE, UK
First published on 6th July 2020
Abstract
Accurately modelling polymorphism in crystalline solids remains a key challenge in computational chemistry. In this work, we apply a theoretically-rigorous phonon mode-mapping approach to understand the polymorphism in the ternary metal oxide Bi2Sn2O7. Starting from the high-temperature cubic pyrochlore aristotype, we systematically explore the structural potential-energy surface and recover the two known low-temperature phases alongside three new metastable phases, together with the transition pathways connecting them. This first-principles lattice-dynamics method is completely general and provides a practical means to identify and characterise the stable polymorphs and phase transitions in materials with complex crystal structures.
1 Introduction
Predicting polymorphism using first-principles methods is a fundamental challenge in materials discovery.1–3 The ability to search for and identify polymorphs computationally both helps avoid experimental complications from poor-quality samples and low-resolution characterisation, and also accelerates the development of functional materials.Group-theoretical methods have successfully been used to characterise the lower-symmetry phases derived by distorting the archetypal cubic ABX3/A2BB′X6 perovskite phase by tilting and distorting the BX6/B′X6 octahedra.4–8 Predicting polymorphs in complex multi-component systems presents a major challenge, as the number of degrees of freedom often makes ab initio exploration prohibitively expensive.
In this study, we remap the problem of identifying polymorphs of the ternary metal oxide Bi2Sn2O7 from a search over atom positions in real space to collective atomic displacements in phonon space.9 This results in an efficient and unbiased computational approach to predicting the polymorphs of the ternary oxide Bi2Sn2O7, which is generally applicable to other complex systems where conventional approaches such as random searching or genetic algorithms are not practical.10–14
1.1 Crystal chemistry of bismuth stannate
The ideal A2B2O6O′ pyrochlore structure in the Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group has eight formula units in the unit cell. The four unique atomic sites, viz. the A-site cation (+2 or +3), B-site cation (+4 or +5), and two inequivalent oxygen sites (O and O′), are present at the 16c, 16d, 48f and 8a Wyckoff positions, respectively.15 The inequivalent O sites can be understood as two interpenetrating oxide sublattices.16 The B-site cation forms corner-sharing BO6 octahedra, while the A-site cation adopts an anti-cristobalite geometry based on corner-sharing A4O′ tetrahedra with linear O′–A–O′ bonds. The interpenetration of the oxide sublattices results in distorted hexagonal bipyramidal coordination at the A-site, with six longer equatorial A–O bonds and two shorter axial A–O′ bonds (Fig. 1).
m space group has eight formula units in the unit cell. The four unique atomic sites, viz. the A-site cation (+2 or +3), B-site cation (+4 or +5), and two inequivalent oxygen sites (O and O′), are present at the 16c, 16d, 48f and 8a Wyckoff positions, respectively.15 The inequivalent O sites can be understood as two interpenetrating oxide sublattices.16 The B-site cation forms corner-sharing BO6 octahedra, while the A-site cation adopts an anti-cristobalite geometry based on corner-sharing A4O′ tetrahedra with linear O′–A–O′ bonds. The interpenetration of the oxide sublattices results in distorted hexagonal bipyramidal coordination at the A-site, with six longer equatorial A–O bonds and two shorter axial A–O′ bonds (Fig. 1).
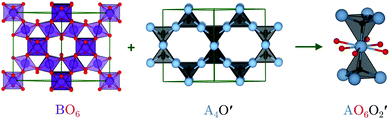 | ||
| Fig. 1 Pyrochlore structure showing the two oxide sublattices forming a corner-sharing network of BO6 octahedra and an anti-cristobalite network of corner-sharing A4O′ tetrahedra. Interpenetration of the two networks results in a bipyramidal hexagonal A-site coordination environment with 6 equatorial O and two axial O′. The atoms are coloured as follows: A-site – blue, B-site – purple, O – red, and O′ – black. The images were generated using VESTA.17 | ||
Bi2Sn2O7 is unique in undergoing symmetry-lowering phase transitions on cooling and has three well-characterised polymorphs: the high-temperature cubic γ phase undergoes a second-order phase transition to β-Bi2Sn2O7 above 900 K, followed by a first-order phase transition to α-Bi2Sn2O7 around 390 K.18 γ-Bi2Sn2O7 possesses the standard cubic pyrochlore structure with the Bi3+ cations displaced from the ideal crystallographic sites.19 While the structure of γ-Bi2Sn2O7 is undisputed, characterising the structures of β- and α-Bi2Sn2O7 has been a significant challenge.
The first structural model for α-Bi2Sn2O7 was a non-centrosymmetric monoclinic P1c1 structure with 352 atoms per cell20 (αold). Three assumptions were used to solve the structure: (1) that β-Bi2Sn2O7 has a face-centred cubic structure, (2) that β- and α-Bi2Sn2O7 are second-harmonic generation active; and (3) that the three phases have group–subgroup relations.18
New insight was obtained very recently from high-resolution X-ray and neutron powder diffraction.16 Though the neutron data showed β to be metrically cubic, small peak splittings in the X-ray data indicated a lower-symmetry structure. An exhaustive symmetry-adapted distortion mode approach was used to enumerate all the candidate structures between the high-symmetry γ parent and a base P1 child structure using ISODISTORT.21,22 All the candidate structures were then tested against room-temperature and ∼470 K X-ray and neutron data, based on which an orthorhombic Aba2 structure with 176 atoms in the conventional cell was suggested for β-Bi2Sn2O7 together with a simplified Cc structure with 88 atoms per cell for α-Bi2Sn2O7 (αnew). The four structures, viz. γ, β, αold and αnew, are shown in Fig. 2.
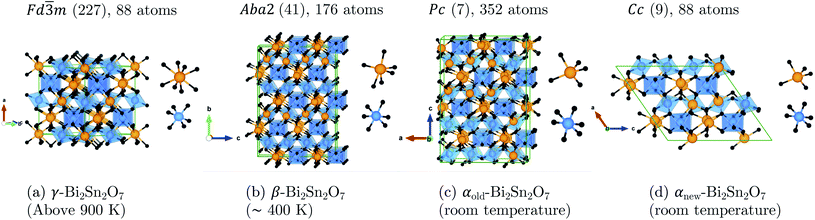 | ||
| Fig. 2 Unit cells of (a) the cubic pyrochlore γ-Bi2Sn2O7 structure with statistically averaged Bi3+ displacements and the distorted (b) β, (c) αold, and (d) αnew structures. All four structures are aligned along the SnO6 octahedra to show the increasingly-irregular Bi chains as the temperature decreases. The insets show the cation coordination in each structure. The atoms are coloured as follows: Bi – orange, Sn – blue, O and O′ – black. These images were generated using VESTA.17 | ||
2 Results and discussion
2.1 Phonon mode mapping procedure
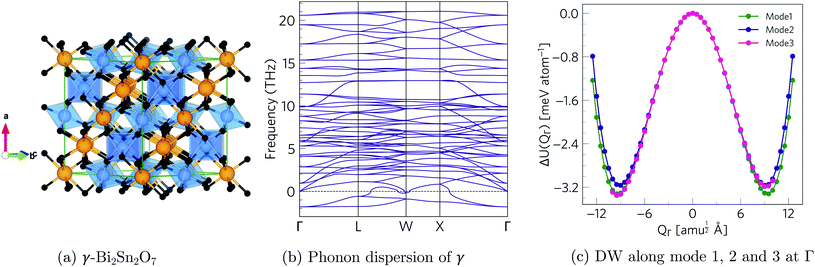
Starting from the high-temperature γ structure, we employ an ab initio approach to systematically identify the energy minima on the structural potential-energy surface (PES) of Bi2Sn2O7.The harmonic phonon dispersion of γ-Bi2Sn2O7 is evaluated using the supercell finite-displacement method23,24 with the Phonopy package.25 Imaginary harmonic modes in the dispersion indicate dynamical instabilities in the form of collective atomic displacements that lower the energy. We use the ModeMap code26 to map the energy as a function of the normal-mode coordinate Q (distortion amplitude) along the imaginary-mode eigenvectors and to locate the energy minimum along the mode. This structure is then relaxed and a subsequent phonon calculation performed to check for additional imaginary modes. Repeating this procedure iteratively across all the imaginary modes in the parent γ and child structure(s) until each branch terminates in a dynamically-stable structure with no imaginary modes allows the sequence of intermediate structures connecting the γ and low-temperature α-phases to be systematically enumerated while also identifying other (meta-)stable polymorphs.
We use plane-wave density-functional theory with the PBEsol functional for the force calculations, as PBEsol has been shown to give accurate structures and phonon frequencies.26–30 Full details of the computational modelling and mode-mapping procedure are given in the ESI.†
2.2 Distorting the cubic aristotype
The phonon dispersion of γ-Bi2Sn2O7 shows imaginary modes at four phonon wavevectors, viz. a triply-degenerate mode at Γ, doubly-degenerate modes at W and X, and single- and a doubly-degenerate modes at L (Fig. 3). The wavevector defines the periodicity of the distortion, and the qΓ = (0, 0, 0) wavevector is commensurate with the unit cell and the distortions therefore do not change the cell volume. We therefore began our exploration by mapping the three Γ-point modes to obtain the typical double-well potential-energy curves shown in Fig. 3. The three imaginary modes lead to minima 3.17–3.35 meV per atom lower in energy than γ-Bi2Sn2O7.After relaxation we obtain an orthorhombic Ima2 structure with 44 atoms per cell. The dispersion of this structure has imaginary modes at four wavevectors, viz. Γ, R, X and T. Mapping the Γ-point instability leads to a 44-atom monoclinic Cc structure with a single imaginary mode at 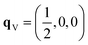 (Fig. S3 and S4†). For this mode, a complete distortion period requires a 2 × 1 × 1 supercell, and mapping yields the 88-atom Cc αnew structure.16 (Calculated: a = 13.108 Å, b = 7.559 Å, c = 13.115 Å and β = 109.6°; measured:16a = 13.155 Å, b = 7.541 Å, c = 13.146 Å and β = 110.04°.) Our method therefore yields the room-temperature αnew polymorph from the high-temperature γ phase in three mode-mapping steps. The phonon dispersion of αnew has no imaginary modes, indicating it to be a dynamically-stable energy minimum.
(Fig. S3 and S4†). For this mode, a complete distortion period requires a 2 × 1 × 1 supercell, and mapping yields the 88-atom Cc αnew structure.16 (Calculated: a = 13.108 Å, b = 7.559 Å, c = 13.115 Å and β = 109.6°; measured:16a = 13.155 Å, b = 7.541 Å, c = 13.146 Å and β = 110.04°.) Our method therefore yields the room-temperature αnew polymorph from the high-temperature γ phase in three mode-mapping steps. The phonon dispersion of αnew has no imaginary modes, indicating it to be a dynamically-stable energy minimum.
Since each of the instabilities in γ-Bi2Sn2O7 represents different possible transition pathways, we mapped all the independent imaginary modes to try and locate the β phase or other stable polymorphs. The instabilities at X and W were mapped in 2 × 1 × 2 and 2 × 4 × 4 supercells, respectively, commensurate with the 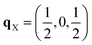 and
and 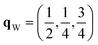 wavevectors (Fig. 4). The instability at X leads in a single step to a dynamically-stable P212121 structure with 44 atoms per cell via a double-well with a depth of ∼0.714 meV per atom. The W-point instability leads to a dynamically-stable Pna21 structure via a double-well potential with a depth of ∼0.388 meV per atom, again with 44 atoms per cell. Neither polymorph has yet been identified experimentally, and we refer to the P212121 and Pna21 structures as δ-Bi2Sn2O7 and ε-Bi2Sn2O7 respectively. The δ and ε phases are 0.87 and 1.45 meV per atom higher in energy than αnew and are thus metastable.
wavevectors (Fig. 4). The instability at X leads in a single step to a dynamically-stable P212121 structure with 44 atoms per cell via a double-well with a depth of ∼0.714 meV per atom. The W-point instability leads to a dynamically-stable Pna21 structure via a double-well potential with a depth of ∼0.388 meV per atom, again with 44 atoms per cell. Neither polymorph has yet been identified experimentally, and we refer to the P212121 and Pna21 structures as δ-Bi2Sn2O7 and ε-Bi2Sn2O7 respectively. The δ and ε phases are 0.87 and 1.45 meV per atom higher in energy than αnew and are thus metastable.
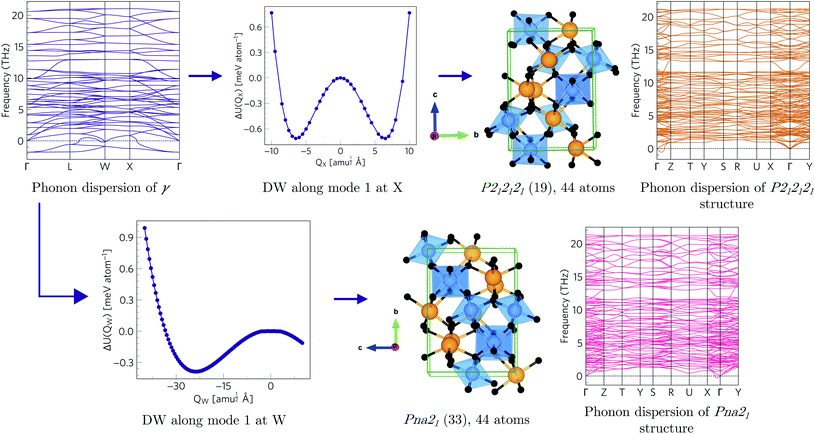 | ||
| Fig. 4 Transition pathways starting from the X- and W-point instabilities in the γ-Bi2Sn2O7 dispersion (top left). The X-point instability leads to a P212121 structure (top row) while the W-point mode leads to a Pna21 structure (bottom row). Both structures are dynamically stable with no imaginary modes in the dispersions. (The imaginary acoustic mode along the Γ → Z path in the P212121 is an interpolation artefact – see ESI.†) | ||
Finally, mapping the L-point instability in γ-Bi2Sn2O7 in a 2 × 2 × 2 supercell also leads to the αnew structure in two steps via an intermediate R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c (167) phase with 132 atoms per unit cell (Fig. S6†).
c (167) phase with 132 atoms per unit cell (Fig. S6†).
We next proceeded to analyse the other instabilities present in the intermediate structures (Fig. S7–S10†). Several pathways end in αnew, while several others lead to the intermediate-temperature β phase.16 More pathways lead to αnew, suggesting it may be more accessible on the PES.
The dispersion of β-Bi2Sn2O7 has imaginary modes at the Γ and Y wavevectors. Both double-well potentials have a very shallow depth of ∼7 × 10−3 meV per atom and lead to a stable Cc structure with 176 atoms per cell (ζ-Bi2Sn2O7; Fig. S11†). This indicates that the β phase is likely a thermal average of equivalent lower-symmetry ζ structures.
To investigate this, we performed Rietveld analysis of a series of powder diffraction patterns collected from 300–1100 K in which the isotropic atomic displacement parameters (ADPs) of the inequivalent Bi sites were independently refined (4 in α, 5 in β, 1 in γ). The ADPs can provide valuable structural information,31–33 and while this analysis pushes the information content of powder diffraction to its limits, we find that the Bi4 and Bi5 atoms, which disorder during the phase transition, have ADPs in the β phase comparable to those in γ-Bi2Sn2O7 and much larger than the other Bi atoms (Fig. S12†). Similarly, the calculated ADPs for β-Bi2Sn2O7 predict large-amplitude displacements of these atoms.
We further tested the model against the data in ref. 16 with a Rietveld methodology such that the R-factors are directly comparable. Splitting the Bi4 site produces an excellent fit to the neutron and X-ray powder diffraction data and reduces Rwp from 4.355% without splitting to 4.176%. This is also lower than the 4.201% obtained by reducing the symmetry to monoclinic. This provides further evidence that the site is dynamically disordered, as predicted by our calculations, and indicates that ζ-Bi2Sn2O7 represents the true local structure of the intermediate-temperature phase.
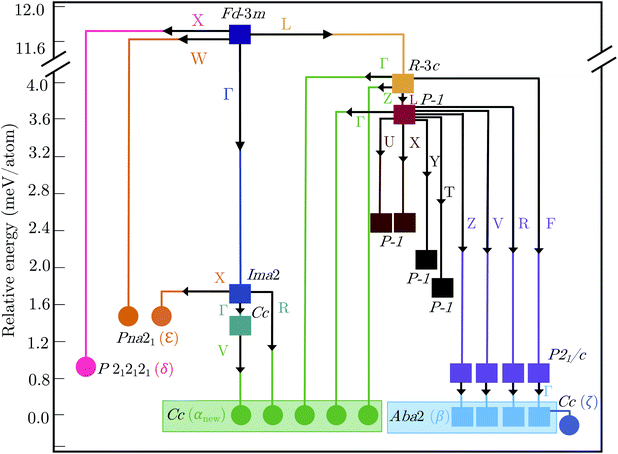
2.3 Polymorph map
Fig. 5 shows the complete polymorph map for Bi2Sn2O7 as a tree diagram. Each branch connects intermediate structures linked by continuous atomic displacements and terminates at structures with no dynamical instabilities. The energies decrease along all pathways with no energetic barriers. Apart from the two new metastable δ and ε phases, all other branches lead to α- and β-/ζ-Bi2Sn2O7. A series of intermediate P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) structures with dynamical instabilities were also identified, but the instabilities were not mapped. From their position on the diagram, however, we can infer that they would likely lead to α- or β-Bi2Sn2O7.
structures with dynamical instabilities were also identified, but the instabilities were not mapped. From their position on the diagram, however, we can infer that they would likely lead to α- or β-Bi2Sn2O7.
The small energy separations between minima highlight the complexity of the PES and indicate that different synthesis conditions may yield different polymorphs by changing the free-energy landscape during crystal formation.34 With the exception of β- and ζ-Bi2Sn2O7, all the structures are higher in energy than αnew. However, these energies are the lattice energies from athermal electronic-structure calculations, and free-energy contributions from lattice vibrations and temperature effects are likely to change the energetic ordering. β- and ζ-Bi2Sn2O7 are predicted to be only 0.1 and 0.19 meV per atom lower in energy than the α phase, respectively, and taken together with the experimental data this suggests that αnew is the global energy minimum on the PES.
Future work may employ the quasi-harmonic approximation (QHA) to compute the temperature-dependent Gibbs free energy G and obtain a more accurate free-energy landscape, improved relative stabilities, and predicted phase-transition temperatures.35
2.4 Chemical explanation of distortions
The structural distortions underlying the polymorphism in Bi2Sn2O7 are driven by the stereochemically-active Bi 6s lone pair. Interaction of the Bi 6s and O 2p states produces filled antibonding orbitals at the top of the valence band, which facilitate coupling to the metal 6p states.36 This hybridisation is symmetry forbidden in the cubic γ phase, but instantaneous symmetry breaking from vibrations allows the Bi 6p and Bi 6s/O 2p states to couple. This stabilises the filled antibonding orbital and offsets the increase in energy from the structural distortion, thereby favouring lower-symmetry structures.37–40This model is supported from the symmetry-mode analysis of the diffraction data by the larger amplitudes of distortion modes associated with Bi4O′ tetrahedra compared to those of SnO6 octahedra.16 This is also consistent with the eigenvectors of the imaginary modes involved in the γ → αnew transition path (Fig. S13†), which show coupled rotations of the Bi and O′ atoms with very little movement of Sn.
3 Conclusions
We have employed a first-principles lattice-dynamics approach to systematically explore the structural PES of Bi2Sn2O7 starting from the high-temperature cubic pyrochlore aristotype. We recover the known phases from diffraction measurements and identify three new dynamically-stable polymorphs that may be targets for future experimental syntheses. We further demonstrate that the intermediate-temperature β polymorph is a crystallographic average over a lower-symmetry ζ minimum, the structure of which is supported by the diffraction data.Bi2Sn2O7 is the most complex system yet to be solved using a computational approach, highlighting the strength of our mode-mapping technique for complex multiternary structures, and this approach could be readily extended to other materials with high-symmetry parent structures such as leucite/pollucite,41 moganite42 and andorite.43
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Calculations were performed on the Archer HPC system, via the UK Materials Chemistry Consortium (EPSRC EP/L000202), and the UCL Legion and Grace facilities. We are also grateful for resources from UK Materials and Molecular Modelling Hub (EPSRC EP/P020194/1). WR is grateful to University College London for awarding the PhD scholarship. JMS is supported by a University of Manchester Presidential Fellowship.Notes and references
- J. Maddox, Nature, 1988, 201, 335 Search PubMed.
- A. van de Walle, Nat. Mater., 2005, 4, 362 CrossRef CAS PubMed.
- N. L. Abraham and M. I. J. Probert, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 224104 CrossRef.
- C. J. Howard and H. T. Stokes, Acta Crystallogr., Sect. B: Struct. Sci., 1998, 54, 782 CrossRef.
- H. T. Stokes, E. H. Kisi, D. M. Hatch and C. J. Howard, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 934 CrossRef PubMed.
- C. J. Howard and M. A. Carpenter, Acta Crystallogr., Sect. B: Struct. Sci., 2010, 66, 40 CrossRef CAS PubMed.
- B. Orayech, I. Urcelay-Olabarria, G. A. López, O. Fabelo, A. Faik and J. M. Igartua, Dalton Trans., 2015, 44, 13867 RSC.
- J. Young, A. Stroppa, S. Picozzi and J. M. Rondinelli, Dalton Trans., 2015, 44, 10644 RSC.
- A. Togo and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 184104 CrossRef.
- C. J. Pickard and R. J. Needs, J. Phys.: Condens. Matter, 2011, 23, 053201 CrossRef PubMed.
- A. E. Eiben and J. E. Smith, in Introd. to Evol. Comput., Springer, Berlin, Heidelberg, 2015, p. 25 Search PubMed.
- N. L. Abraham and M. I. J. Probert, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 224104 CrossRef.
- S. Q. Wu, M. Ji, C.-Z. Wang, M. C. Nguyen, X. Zhao, K. Umemoto, R. M. Wentzcovitch and K.-M. Ho, J. Phys.: Condens. Matter, 2013, 26, 035402 CrossRef PubMed.
- S. Y. Chen, F. Zheng, S. Q. Wu and Z. Z. Zhu, Curr. Appl. Phys., 2017, 17, 454 CrossRef.
- B. J. Kennedy, B. A. Hunter and C. J. Howard, J. Solid State Chem., 1997, 130, 58 CrossRef CAS.
- J. W. Lewis, J. L. Payne, I. R. Evans, H. T. Stokes, B. J. Campbell and J. S. O. Evans, J. Am. Chem. Soc., 2016, 138, 8031 CrossRef CAS PubMed.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272 CrossRef CAS.
- R. D. Shannon, J. D. Berlein, J. L. Gillson, G. A. Jon and A. W. Sleight, J. Phys. Chem. Solids, 1980, 41, 117 CrossRef CAS.
- V. Kahlenberg, Z. Kristallogr., 1997, 212, 297 CAS.
- I. R. Evans, J. A. K. Howard and J. S. O. Evans, J. Mater. Chem., 2003, 13, 2098 RSC.
- B. J. Campbell, H. T. Stokes, D. E. Tanner and D. M. Hatch, J. Appl. Crystallogr., 2006, 39, 607 CrossRef CAS.
- H. T. Stokes, D. M. Hatch and B. J. Campbell, ISOTROPY Software Suite, 2017, http://stokes.byu.edu/isotropy.html Search PubMed.
- K. Parlinski, Z. Q. Li and Y. Kawazoe, Phys. Rev. Lett., 1997, 78, 4063 CrossRef CAS.
- G. Kresse, J. Furthmüller and J. Hafner, Europhys. Lett., 1995, 32, 729 CrossRef CAS.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1 CrossRef CAS.
- J. M. Skelton, L. A. Burton, S. C. Parker, A. Walsh, C.-E. Kim, A. Soon, J. Buckeridge, A. A. Sokol, C. R. A. Catlow, A. Togo and I. Tanaka, Phys. Rev. Lett., 2016, 117, 075502 CrossRef PubMed.
- J. M. Skelton, D. Tiana, S. C. Parker, A. Togo, I. Tanaka and A. Walsh, J. Chem. Phys., 2015, 143, 64710 CrossRef PubMed.
- A. M. Ganose, K. T. Butler, A. Walsh and D. O. Scanlon, J. Mater. Chem. A, 2016, 4, 2060 RSC.
- M. A. Tumelero, L. C. Benetti, E. Isoppo, R. Faccio, G. Zangari and A. A. Pasa, J. Phys. Chem. C, 2016, 120, 11797 CrossRef CAS.
- C. N. Savory, A. M. Ganose and D. O. Scanlon, Chem. Mater., 2017, 29, 5156 CrossRef CAS.
- A. E. Phillips, G. J. Halder, K. W. Chapman, A. L. Goodwin and C. J. Kepert, J. Am. Chem. Soc., 2010, 132, 10 CrossRef CAS PubMed.
- E. E. McCabe, D. G. Free, B. G. Mendis, J. S. Higgins and J. S. O. Evans, Chem. Mater., 2010, 22, 6171 CrossRef CAS.
- S. Lee and H. Xu, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2019, 75, 160 CrossRef CAS.
- W. Sun, S. T. Dacek, S. P. Ong, G. Hautier, A. Jain, W. D. Richards, A. C. Gamst, K. A. Persson and G. Ceder, Sci. Adv., 2016, 2, e1600225 CrossRef PubMed.
- E. Lora Da Silva, J. M. Skelton, S. C. Parker and A. Walsh, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 144107 CrossRef.
- A. Walsh, D. J. Payne, R. G. Egdell and G. W. Watson, Chem. Soc. Rev., 2011, 40, 4455 RSC.
- A. Walsh and G. W. Watson, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 235114 CrossRef.
- A. Walsh and G. W. Watson, J. Solid State Chem., 2005, 178, 1422 CrossRef CAS.
- A. Walsh, G. W. Watson, D. J. Payne, G. Atkinson and R. G. Egdell, J. Mater. Chem., 2006, 16, 3452 RSC.
- A. Walsh and G. W. Watson, Chem. Mater., 2007, 19, 5158 CrossRef CAS.
- K. S. Knight and C. M. B. Henderson, Phys. Chem. Miner., 2019, 46, 595 CrossRef CAS.
- J. Haines, C. Chateau, J. M. Léger, A. Le Sauze, N. Diot, R. Marchand and S. Hull, Acta Crystallogr., Sect. B: Struct. Sci., 1999, 55, 677 CrossRef PubMed.
- M. Nespolo, T. Ozawa, Y. Kawasaki and K. Sugiyama, J. Mineral. Petrol. Sci., 2012, 107, 226 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc02995e |
| This journal is © The Royal Society of Chemistry 2020 |