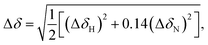Structural impact of GTP binding on downstream KRAS signaling

Abstract

Oncogenic RAS proteins, involved in ∼30% of human tumors, are molecular switches of various signal transduction pathways. Here we apply a new protocol for the NMR study of KRAS in its (inactive) GDP- and (activated) GTP-bound form, allowing a comprehensive analysis of the backbone dynamics of its WT-, G12C- and G12D variants. We found that Tyr32 shows opposite mobility with respect to the backbone of its surroundings: it is more flexible in the GDP-bound form while more rigid in GTP-complexes (especially in WT- and G12D-GTP). Using the G12C/Y32F double mutant, we showed that the presence of the hydroxyl group of Tyr32 has a marked effect on the G12C-KRAS-GTP system as well. Molecular dynamics simulations indicate that Tyr32 is linked to the γ-phosphate of GTP in the activated states – an arrangement shown, using QM/MM calculations, to support catalysis. Anchoring Tyr32 to the γ-phosphate contributes to the capture of the catalytic waters participating in the intrinsic hydrolysis of GTP and supports a simultaneous triple proton transfer step (catalytic water → assisting water → Tyr32 → O1G of the γ-phosphate) leading to straightforward product formation. The coupled flip of negatively charged residues of switch I toward the inside of the effector binding pocket potentiates ligand recognition, while positioning of Thr35 to enter the coordination sphere of the Mg²⁺ widens the pocket. Position 12 mutations do not disturb the capture of Tyr32 by the γ-phosphate, but (partially) displace Gln61, which opens up the catalytic pocket and destabilizes catalytic water molecules thus impairing intrinsic hydrolysis.

---

Introduction

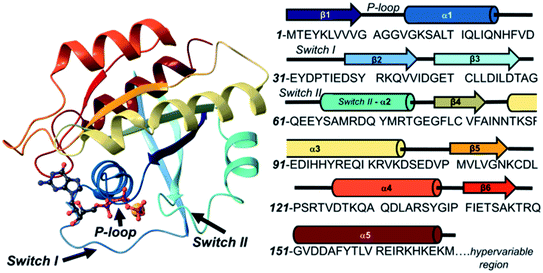
RAS oncogenes found in oncogenic retroviruses were the first human oncogenes identified encoding the oncoproteins of HRAS and KRAS.^1,2 Together with the NRAS of neuroblastomas³ these RAS proteins harbor oncogenic mutations involved in almost 30% of human tumors.⁴ RAS proteins are membrane-bound GTPases that form interactions with a high number of effector proteins including TIAM1, PI3K, RAF, RALGDS and PLCs.⁵ These signaling pathways control cell growth, motility, migration, differentiation, proliferation and survival which makes RAS a molecular integrator of oncogenic signaling. Mutations in codons 12, 13 and 61 increase the relative amount of the GTP-bound active form that activates pro-oncogenic signaling pathways.⁴ Since RAS is regulated by a cycle balancing between activation by guanine nucleotide exchange factors (GEFs such as the protein SOS) and inactivation by GTPase activating proteins (GAPs such as p120GAP), oncogenic mutations might impair either the intrinsic GTPase activity and/or might inhibit the processes of regulatory protein mediated nucleotide exchange and hydrolysis.⁶ Besides KRAS other small G-proteins such as RAP, RAN, RHO, RAB, etc. play key roles in signal transduction cascades which structurally are very homologous to RAS proteins.⁷

The structure of RAS proteins shows three major domains of decreasing sequence similarity, namely the effector-binding lobe (residues 1–85, similarity 100%), the allosteric lobe (residues 86–168, similarity 86%) – jointly constituting the G-domain – and the hypervariable region (HVR, residues 166–188/189, similarity 15%) (Fig. 1). The effector lobe is responsible for the recruitment and activation of effector proteins; however, the molecular mechanism of this process remains largely unknown.^8,9 The structure of the sequentially conserved G-domain is similar for all the RAS proteins and contains four main regions that include the phosphate binding loop (P-loop, residues 10–17), switch I (residues 25–40), switch II (residues 57–76) and nucleobase binding loops (residues 116–120 and 145–147).^10–12

Fig. 1 Schematic structure and sequence of KRAS-4B. Secondary structural elements from β1 through β4 form the effector lobe (residues 1–85), while the allosteric lobe is created by α3 to α5 (residues 86–168).

Structural investigations on RAS activation are notoriously difficult. Despite the large number of available X-ray structures and thorough NMR studies, the molecular details of the highly organized conformational rearrangements at the switch regions still remain to be clarified. Although these changes are responsible for the exposure of the effector binding site, and consequently for oncogenic activation, their elucidation at the atomic level is challenged by multiple factors. On one hand, crystal structures do not provide a clear picture since the conformationally flexible switch I and switch II regions are often shaped and restricted in mobility by crystal contacts, show high B-factors if no such contacts are established (ESI Fig. 1†), or are simply unresolved and missing from electron density maps (ESI Fig. 2 and 3†). Furthermore, data collection for the GTP-bound active form is complicated by the hydrolysis of the nucleotide. To avoid this, small G-protein investigators use GTP analogues in most cases, though it has been shown that they behave somewhat differently from GTP itself.^13–15 In a recent study, to avoid this problem, GEF protein (SOS) was added to the native HRAS-GTP NMR sample.¹⁶ However, since GEF displaces the switch I region in its entirety (by over 10 Å) and remodels switch II¹⁷ – even if it is added to the samples in minimal amounts – the results thus derived might be altered from the RAS-GTP native state. These limitations prevent clarifying what steps constitute the transition to the active form, which features of the activated state are recognized by the downstream partners and the conformational criteria of inactivation – thus, the exact mechanism of the rise and shutdown of the growth signal.

The motivation of our work came from two major sources. First, investigating the molecular mechanism of RAS activation might clarify the structural details of oncogenic signaling that would help to understand the activation of downstream signaling pathways involving the recruitment of effector proteins. More importantly, however, identifying the conformational signal could serve as the basis of inhibitor design – targeting the effector binding conformation directly. Indeed, most of the drug discovery efforts are based on enhancing GTP hydrolysis, influencing nucleotide exchange or inhibiting RAS–effector interactions.^6,10,18

We developed a set of conditions that enabled us to work with the native KRAS-GDP/GTP systems, and guaranteed full GDP–GTP exchange by passing through the nucleotide free form. We applied an integrated structural biology approach, combining multidimensional NMR measurements with molecular modeling (MD and QM/MM relying on the pool of the relevant X-ray structures). We chose to study the wild type KRAS protein and two oncogenic mutations (G12C and G12D variants) that affect the intrinsic GTP hydrolysis rates differently while inhibiting GAP-mediated hydrolysis to a similar extent.

Our data revealed that the most significant change evoked by nucleotide exchange is the pivotal flip of Tyr32 (and the adjoining residues e.g. Thr35) of the switch I region. The results explain the effect of oncogenic P-loop mutations on intrinsic hydrolysis rates and effector protein binding capability and highlight the role of binding site waters during the activation process.

Materials and methods

Expression and purification of ¹⁵N-labeled KRAS (1–169) WT, G12C and G12D mutants as well as the G12C–Y32F double mutant protein and ¹³C, ¹⁵N-labeled G12C mutant were performed by using a method published¹⁹ in the nucleotide free form. GDP and GTP were added during sample preparation for NMR measurements. NMR samples contained the protein of interest in 0.3–1.0 mM concentration, 2–5 mM GDP (a minimum of five-fold excess with respect to the protein) or 80–100 mM GTP (a minimum of 100-fold excess with respect to the protein), 10 mM EDTA, 15 mM MgCl₂ (in 5 mM excess with respect to EDTA), 3 mM NaN₃ in PBS buffer, 10% D₂O, and 1% DSS standard, and the pH was set to 7.4. The spectra of the stable GTP bound forms were acquired using an unusually high excess of GTP. Due to the ratio of the GTP intrinsic hydrolysis and GDP–GTP autoexchange, under these extreme conditions, we could detect changeless ¹H, ¹⁵N-HSQC spectra for as long as 3–4 days. This protocol did not require the use of any other added protein as the method was published recently.¹⁶

NMR measurements were performed at 298 K on a Bruker Avance III 700 MHz spectrometer equipped with a 5 mm Prodigy TCI H&F-C/N-D, z-gradient probe head operating at 700.05 MHz for ¹H-, 70.94 MHz for ¹⁵N- and 176.03 MHz for ¹³C-nuclei. Temperature was calibrated using a standard methanol solution.²⁰ All chemical shifts were referenced with respect to the internal ¹H-resonance of DSS, and ¹³C, ¹⁵N-chemical shifts were referenced indirectly using the corresponding gyromagnetic ratios according to IUPAC convention.²¹ Sequence specific assignments of backbone ¹H- and ¹⁵N-nuclei of GDP-bound forms were used from our previous work.¹⁹ In the case of GTP-bound forms, assignments were performed based on the 3D BEST-HNCO, BEST-HNCA, BEST-HN(CO)CA, BEST-HNCACB and CC(CO)NH spectra of the G12C mutant (its backbone and sidechain ¹³C nucleus assignment was determined as well). These results were transferred to WT and G12D using 3D NOESY-HSQC spectra, using mixing times of 120–150 ms. All the assigned resonances were deposited in the BMRB database with the following entries: 28021 (WT-GTP), 28015 (G12C-GTP), and 28022 (G12D-GTP) ¹H, ¹⁵N-HSQC spectra of KRAS-G12C and G12C–Y32F mutants were compared in both GDP and GTP-bound forms. All spectra were processed with the Bruker TOPSPIN program and analyzed by using CARA (ETH Zürich).²²

Standard backbone ¹⁵N-relaxation experiments (T₁, T₂ and steady state ¹H–¹⁵N HetNOE) were performed using ¹⁵N-labeled WT, G12C and G12D mutants for both GDP- and GTP-bound forms. A typical set of spectra in the 0.1–4.5 s and 0.017–0.678 s range were recorded in 10 points for both T₁ and T₂ measurements. The spectra were processed using TOPSPIN. The longitudinal (R₁) and transverse (R₂) relaxation rates were determined by fitting the cross-peak intensities as a function of the delay to a single-exponential decay using NMRFAM-SPARKY software.²³ The heteronuclear NOE values were obtained from the ratio of the peak intensities of saturated and unsaturated cross-peaks.

The obtained relaxation results were further analyzed by reduced spectral density mapping analysis²⁴ and extended Lipari–Szabo model-free formalism.^25–27 Reduced spectral density mapping analysis results in three different spectral density values characterizing the distribution of slow, medium and fast time scale motions of each residue's backbone N–H vector: J(0) for slow, J(ω_N) for medium, and J(0.87ω_H) = J(ω_h) for fast time scales. Model-free analysis can be performed using an isotropic approach, assuming the molecule is approximately spherical, or using an anisotropic approach (axially anisotropic or fully anisotropic) based on the exact 3D structure of the protein. The analysis provides the global rotational correlation time (τ_c) that characterizes the tumbling motion of the molecule as a whole and for each residue a generalized order parameter (S²) describing how restricted the motion of its backbone N–H vector is. Further optional per-residue parameters can be obtained depending on which model of 1–5 are best fitted to the data: correlation time for internal motion (τ_e) characterizing a motion faster than the time scale of global tumbling and the exchange parameter (R_ex) describing chemical or conformational exchange processes on a slower time scale than the global tumbling motion, here carried out using FAST-Modelfree software,²⁸ the automated version of Modelfree 4.2 (ref. 29 and 30) using the isotropic approach, were used for Lipari–Szabo model-free analysis with a constant 1.02 Å for N–H bond length and −172 ppm for ¹⁵N-chemical shift anisotropy.³¹ The data for KRAS monomers were derived using the isotropic approach, while for dimeric forms of KRAS-WT, the axially anisotropic approach was used. The results of dynamics measurements and analysis were also deposited in the BMRB database with the previously given entries.

Molecular dynamics (MD) simulations were started from two different crystal structures: 4obe (WT KRAS/GDP) for the GDP- and 3k8y (WT/HRAS-GNP) for the GTP-bound forms.^32,33 In the latter case the HRAS variant was selected because no WT KRAS/GTP-analogue structure is currently available that does not contain unresolved segments. Furthermore, in this structure the conformation of both Tyr32 and Gln61 indicates that it is in a truly activated conformation. Also, the authors identified 2 water molecules that they felt were catalytically important,³² and carrying out the simulation from a starting conformation nearly identical to theirs (aside from the HRAS → KRAS mutations and the GppNHp → GTP switch) also allowed us to compare the MD derived water-cluster around the active site to that determined experimentally. KRAS and HRAS share 94% sequence identity in the 1–169 region studied here; the HRAS → KRAS transformation involved a total of 10 changes, none of them in, or near, the switch I–II regions.

All mutations and modifications were introduced into the wild type (WT) structures without any further changes, using Maestro (Schrödinger Suite (Schrödinger Release 2019-3: Maestro, Schrödinger, LLC, New York, NY, 2019)). Maestro was also used for generating the figures shown in the text. Simulations were carried out as implemented in GROMACS,³⁴ using the AMBER-ff99SBildnp* force field. The system was solvated with OPC water molecules³⁵ in dodecahedral boxes with a size allowing 10 Å between any protein atom and the box. The total charge was neutralized and physiological salt concentration (0.15 M) set using Na⁺ and Cl⁻ ions. Energy minimization of the starting structures was followed by sequential relaxation of constraints on protein atoms in three steps and an additional NVT step (100 ps) to stabilize pressure. Trajectories of 600–1200 ns NPT simulations at 310 K and 1 bar were recorded for further analysis (collecting snapshots at every 4 ps). Simulations satisfactorily reproduced the crystal structures and the experimental B-factors (see ESI Fig. 1†). For illustrating the effect of nucleotide exchange on the switch I region, snapshots were clustered³⁶ based on the conformation of the main-chain atoms of residues 10–48 for the last 300 ns of the trajectories using a 1 Å cutoff. MD and NMR results were compared using the CoNSEnsX+ server.³⁷

QM/MM calculations were carried out for KRAS-GTP complexes using Jaguar.^38,39 The B3LYP/LACV3P* method was used in combination with OPLS3-based molecular mechanics.⁴⁰ The starting system was derived from the mid-structure of the first cluster from the KRAS-GTP MD simulation (based on the full main-chain using a 1 Å cutoff). All waters that reach within 12 Å of any protein atom were kept. The quantum region was composed of the entire GTP, the Mg²⁺ ion, 4 water molecules (catalytic and assisting water, and 2 waters coordinated with the Mg²⁺ ion) and the sidechains of Lys16, Set17, Tyr32, Thr35, Gln61 and Lys117, forming a neutral system. The MM region was divided into two parts: residues 11–40, 55–76 and 117; GTP and the Mg²⁺ ion and all waters within 6 Å of these moved freely during optimization, while all the rest were kept frozen. The hydrolysis reaction was modeled by moving the catalytic water from PG_GTP–OW_{catalytic-water} distance of 3.4 Å to 1.4 Å in 0.1 Å steps. Forward and backward scans were repeated several times to smooth inconsistencies, and since proton transfer lags behind both during the forward and the backward scans, a minimum energy path was chosen from the scan-points of both. The scan-grid was downscaled to 0.02 Å within ± 1 Å of the TS-like structure. The Y32F* model was created by in silico mutation of Tyr32 without any further modification.

Results and discussion

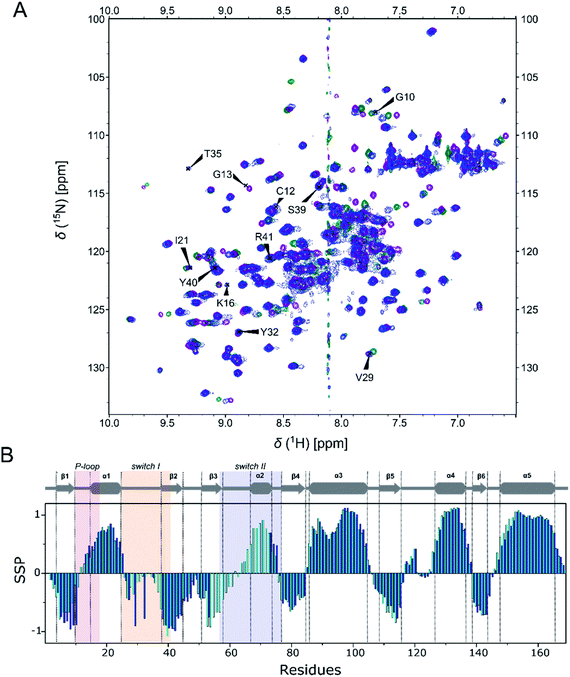
In this study we considered three systems, WT KRAS and two of its oncogenic mutants, G12C and G12D, for which structural information is available and which are known to differently affect intrinsic hydrolysis rates: while G12C only moderately affects it, G12D severely limits the unassisted GTP-hydrolysis of KRAS.⁴¹

The NMR structural characterization of RAS-GTP proteins is hindered by NMR-signal broadening due to intermediate exchange, which, in the most interesting regions, leads to undetectable or unassignable signals.^42,43 We also encountered this problem, but have succeeded in detecting and assigning several new resonances within the P-loop and switch I regions of KRAS. Most probably this is because we used – for the first time – the physiological GTP ligand for which the binding site was optimized (without adding extra protein partners) and had a homogeneous sample due to complete nucleotide exchange. We took great care to ascertain that the signals in ¹H, ¹⁵N-HSQC spectra indeed belong to the GTP-bound KRAS protein (see ESI Fig. 4†). In short: the already assigned^19,44 and stable ¹H, ¹⁵N-HSQC spectra of the GDP-bound form of all three variants were recorded (affording signal set 1). EDTA was added to the samples, and they were in turn diluted using the buffer solution to remove excess GDP. To these systems GTP and Mg²⁺ were subsequently added. This brought about the appearance of a new set of signals (KRAS-GTP: signal set 2) besides the signals of the KRAS-GDP (signal set 1). The samples were incubated for 3 days and then re-measured, showing a homogeneous state analogous to the original (signal set 1), confirming the hydrolysis of KRAS-bound GTP to GDP via the intrinsic GTPase activity of KRAS. Samples used for NMR dynamics measurements were prepared by first adding EDTA to remove the Mg²⁺ and the remnant nucleotide and then resupplying the Mg²⁺ and a great excess of GTP. The ¹H, ¹⁵N-HSQC spectra then recoded only contained signal set 2 and remained stable for 3–4 days due to the shifted equilibrium of GTP intrinsic hydrolysis and nucleotide autoexchange. Based on the appearance of only two signal sets, the contribution of the nucleotide-free form to the spectra could also be ruled out. This form is expected to undergo significant rearrangement in the switch I region,^45,46 which would have differentiated it from both signal set 1 and signal set 2. Using this methodology we could assign, in the case of KRAS-G12C-GTP – for example – hitherto undetected signals of Gly10, Cys12, Gly13, Lys16, Ile21, Val29, Tyr32, Thr35, Ser39, Tyr40, and Arg41 (Fig. 2A), although in some cases the resonance was still too broad to gain information about chemical shifts of the side chains. Signals remaining unassigned were of Val8, Ala11, Gly13, Gln22, Asp30, Glu31, Asp33, Ile36, Glu37, Asp38, Thr87, and Val103 as well as signals of the switch II region (Asp54–Arg73). In total 80.6% of the non-proline residues (133 of 165) were detected and assigned in the ¹H, ¹⁵N-HSQC spectrum (exceeding that (76.4%) of a recently published study concerning the non-native GppNHp-bound KRAS-G12C).⁴⁷ Similarly, 80.0% and 78.2% of all non-proline residues were detected and assigned in the ¹H, ¹⁵N-HSQC spectrum of WT-GTP and G12D-GTP structures, respectively, also the highest fraction hitherto obtained. Resonance assignment is complex as there are two conformational states of the GTP-bound form of KRAS, namely that of state 1 and state 2. The main difference between these two forms is in the conformation of switch I, which is released from the active site in state 1, leading to a GTP-loaded but still inactive conformation.⁴⁸ Interestingly, the relative population of state 1 and state 2 has recently been shown to be mutation-sensitive, the oncogenic G12D mutation – for example – seems to shift the equilibrium toward the fully activated state 2 form.^49,50 The exchange between the two states results in some minor peaks with very low intensity in the ¹H, ¹⁵N-HSQC spectra which remained unassigned, but their presence confirms the slow exchange between them. In contrast to the GTP-bound forms, there was no severe line broadening in the ¹H, ¹⁵N-HSQC spectra of GDP-bound states, allowing the assignment of 98–99% of non-proline residues for all of the three variants.¹⁹

Fig. 2 (A) Assigned ¹H, ¹⁵N-HSQC spectra of the GTP-bound KRAS-WT (dark green), G12C mutant (blue) and G12D mutant (purple). The assignment of the newly detected and assigned crosspeaks of the KRAS-G12C mutant is shown (the full assignment is deposited in BMRB, access number: 28015). (B) Secondary structure propensities (SSP) of the GTP-bound KRAS-G12C (blue) compared with the GDP-bound form (cyan) along with the residue numbers. Secondary structure elements are drawn above the graph, and the P-loop (light red, residues 10–17), switch I (yellow, residues 25–40) and switch II (light blue, residues 57–76) units are depicted.

The triple resonance experiments performed for KRAS-G12C-GTP allowed us to compare the NMR chemical shift-based secondary structure propensities (SSP)⁵¹ to those of the GDP-bound form¹⁹ (Fig. 2B). This analysis confirmed that the secondary structures of the well-defined regions of GDP- and GTP-bound forms do not differ notably. We carried out detailed studies on the backbone dynamics of the three variants (WT, G12C and G12D) in both GDP- and GTP-bound forms. We investigated the fast backbone dynamics of KRAS by determining the standard R₁, R₂ and HetNOE relaxation parameters. Surprisingly, position 12 mutations only cause local variations in the dynamics in the presence of either nucleotide. However, when comparing the GDP to the GTP-bound form, we found significant differences (Table 1 and Fig. 3).

Table 1 Averaged relaxation parameters (R₁, R₂ and HetNOE) determined for KRAS-WT, G12C and G12D in both GDP- and GTP-bound forms. Additional dynamic properties were calculated with the Lipari–Szabo model-free and reduced spectral density analysis: τ_c (global correlation time), S² (generalized order parameters) and J(ω_h): the spectral density functions of fast motions

	KRAS-WT		KRAS-G12C		KRAS-G12D
	+GDP	+GTP	+GDP	+GTP	+GDP	+GTP
R 1 (s^−1)	0.97 ± 0.05	0.85 ± 0.08	0.99 ± 0.06	0.85 ± 0.07	0.95 ± 0.06	0.82 ± 0.07
R 2 (s^−1)	13.85 ± 2.00	16.94 ± 3.12	14.16 ± 2.01	16.57 ± 2.63	14.83 ± 3.37	17.54 ± 2.76
HetNOE	0.79 ± 0.10	0.75 ± 0.14	0.79 ± 0.10	0.77 ± 0.13	0.78 ± 0.10	0.76 ± 0.13
τ c (ns)	9.95	12.33	9.97	11.97	10.44	12.59
S ^2	0.82 ± 0.07	0.85 ± 0.09	0.84 ± 0.08	0.84 ± 0.08	0.84 ± 0.07	0.85 ± 0.08
J(ωh) (ps rad^−1)	3.26 ± 1.92	3.33 ± 2.29	3.30 ± 1.86	3.22 ± 2.34	3.35 ± 1.85	3.11 ± 1.94

---

Fig. 3 Relaxation parameters of the KRAS WT (light green/green), G12C mutant (cyan/blue), and G12D mutant (lilac/purple) in GDP-bound (left) and GTP-bound forms (right). (A) R₁, longitudinal relaxation rates, (B) R₂, transverse relaxation rates and (C) steady-state heteronuclear ¹H–¹⁵N NOE data are plotted against the residue sequence numbers. No dynamics data are reported for several residues due to their signal-broadening (in the GTP-bound forms) or signal overlapping. P-loop (light red, residues 10–17), switch I (yellow, residues 25–40) and switch II (light blue, residues 57–76) are shown in colored rectangles (R₂/R₁ and R₂ × R₁ values are shown in ESI Fig. 5,† for individual values of the most interesting switch I residues see ESI Table 1†).

R ₁ and R₂ values suggest a general trend in the global motions of the molecules: the former significantly decreased, while the latter increased when going from the GDP- to GTP-bound form arising from the increased global correlation time (τ_c) of GTP-bound forms. Since it is clear from previous crystallographic and NMR results that the overall shape and size of RAS proteins do not change substantially on nucleotide exchange, the significantly different global tumbling of the GDP- and GTP-bound forms could either arise from a drastic difference in viscosity of the samples or via dimerization or oligomerization processes that only involve one of them, or – in case of the GTP-bound state – via contamination by aggregates of the nucleotide-free form that transiently appears during nucleotide exchange. This latter possibility could be excluded by showing that the samples containing the nucleotide-free form are monomeric (see ESI Fig. 6†). A change in viscosity could be suspected, because – to counteract the intrinsic hydrolysis of GTP – the samples of the GTP-bound forms contained approximately 40-fold greater amount of the nucleotide than those of the GDP-bound forms. However, neither increasing the GDP concentration, nor decreasing that of GTP caused significant changes in the detected line-width of the ¹H, ¹⁵N-HSQC spectra (see ESI Fig. 7†). On the other hand, dimerization/oligomerization of RAS proteins in complex with GTP-analogues has already been described.^52,53 Determining whether the GTP-bound samples were truly free from significant levels of dimeric forms was critical for the interpretation of our results, since while oligomers of extended size are not detected by the NMR methodology applied by us, dimerization could lead to spectral changes comparable in magnitude to those caused by nucleotide exchange or mutation. To determine the oligomeric state of our samples, we first carried out size exclusion chromatography. The results indicated that while the GDP-bound state is a homogeneous solution of the monomeric form, the sample of the GTP-bound WT KRAS contained high-molecular-weight oligomers besides the monomer form – although the presence of dimers was not detected (see ESI Fig. 8D†). Accordingly, room temperature incubation of the samples led to the appearance of visible aggregates in the case of the GTP-containing sample, while the GDP-bound form remained stable in solution. Next we compared the spectra of 300 μM and 30 μM solutions of ¹⁵N-KRAS-G12C-GTP according to the method of Muratcioglu et al.⁵² In the case of the diluted sample ¹H, ¹⁵N-SOFAST-HMQC measurements had to be carried out to reduce the measurement time, which does not allow detailed analysis of the results, but is sufficient for comparison with the standard ¹H, ¹⁵N-HSQC spectrum. The combined chemical shift difference⁵⁴ value was calculated for each residue using the following expression,

where Δδ_H and Δδ_N are the detected differences of ¹H and ¹⁵N chemical shifts (see ESI Fig. 8A and B†). Δδ > 0.15 was found in the case of Glu3, Tyr4, Gly10, Thr20, His27, Arg41, Asp108 and His166, indicating that at higher concentration some intermolecular interactions are indeed formed. However, since the most affected residues are not clustered spatially but are scattered over distant regions of the surface, a mixture of different dimeric forms must be present in the solution (see ESI Fig. 8C†). Considering all the findings, we propose that in concentrated solutions of the G-domain of KRAS-GTP, transiently appearing dimeric forms are present which self-assemble into more stable oligomers and insoluble aggregates. The concentration of the dimeric forms seems to be closer to the ∼10% determined recently using ultraviolet photodissociation mass spectrometry measurements,⁵³ instead of being the dominant component of the solution (as was seen by Muratcioglu et al.,⁵²) but their presence, nevertheless, supplies a rational explanation for the observed difference in the global correlation times of our GDP- and GTP-loaded samples. HetNOE values were found to be slightly higher in the GDP complex indicating a slight increase in global rigidity upon GTP-hydrolysis. Standard deviations of all relaxation parameters are lower in KRAS-GDP in the case of all three variants which is in line with the decreased dynamic variability. Furthermore, transverse relaxation rates of the switch I region are higher in all GDP-bound forms, most significantly in the case of the G12D mutant (Glu37 has an extremely high R₂ value: 45.7 s⁻¹), confirming the slow conformational exchange in the region. We note that while such an extreme R₂ value in the GTP-bound forms has not been found, the resonance signal of several residues in this region could not be assigned or broadened beyond the detection limit. Based on HetNOE parameters, three distinct flexible regions can be distinguished in the GDP-bound forms: Gly60–Ser65 (switch II), Lys104–Met111 and Ser122–Thr124. Interestingly, within the switch I region only Tyr32 has a very small HetNOE value (0.39, 0.42 and 0.50 for WT, G12C and G12D mutants, respectively) indicating its high flexibility in contrast to the surrounding residues with average values of 0.79, 0.79 and 0.78 for the WT and G12C and G12D mutants, respectively (Table 1 and Fig. 3). In GTP-bound forms, switch II shows motions in the intermediate time regime and consequently its signals are completely broadened. The other two flexible regions are similar in position to those assigned in the GDP-bound forms: Lys104–Met111 (identical region) and Ser122–Gln129 (slightly extended region). These regions are located on the opposite side of the protein, near where it binds to the membrane, and have been shown to exert an allosteric effect on the binding site.^32,55–57 Within the switch I region, Tyr32 has a higher HetNOE value (0.93, 0.75 and 0.92 in the WT and G12C and G12D mutants, respectively compared to those of the GDP-complexes) indicating the increased rigidity of this residue in all three variants in the ps–ns time scale. In the GTP-bound forms the majority of residues in the switch I region are in intermediate exchange too, causing signal broadening similar to that seen in switch II.

The obtained relaxation parameters were further analyzed by the Lipari–Szabo model-free analysis and by reduced spectral density mapping (Table 1 and Fig. 3). Elevated τ_c values of GTP-bound states originate from the dimerization/oligomerization process as discussed previously. The G12D mutant has the highest τ_c in both GDP- and GTP-bound forms, whilst the lowest value belongs to WT in GDP-bound and G12C in GTP-bound states suggesting differences in the global shape of the WT and the G12C and G12D mutants. No significant difference was found in the average generalized order parameters (S²) between GDP- and GTP-bound forms in any of the three variants. The same regions appear to be flexible which was determined based on HetNOE values. These flexible regions are evidenced by fast internal motions characterized by τ_e parameters, most characteristic of the WT-GTP complex. For the latter protein, to describe internal motion properly, the involvement of τ_e is needed for 35 residues, while for G12C and G12D only 20 and 22 residues, respectively. Therefore Gly12 site mutations seem to reduce the fast time scale motions in the ps–ns time range (Fig. 4B). The slow motions in the mutants are focused in the allosteric regions.

Fig. 4 Selected dynamic properties of KRAS WT (light green/green), G12C mutant (cyan/blue), G12D mutant (lilac/purple) in GDP-bound (left) and GTP-bound forms (right): (A) generalized order parameter, S², (B) correlation times for internal motions, τ_e, and (C) slow exchange rates, R_ex, all of them derived from the Lipari–Szabo model-free formalism. (D) Spectral density values of fast timescale motions according to the reduced spectral density mapping method, J(ω_h). P-loop (light red, residues 10–17), switch I (yellow, residues 25–40) and switch II (light blue, residues 57–76) are shown in colored rectangles (for individual values of the most interesting switch I residues see ESI Table 1†).

While there is no significant difference in the fast motions between the three proteins in GDP-bound states, slow motions in the μs–ms time range (characterized by R_ex (Fig. 4C)) differ notably. It is WT-KRAS-GDP that possesses the most residues engaged in slow-time scale motions, namely for 34 residues the motions are characterized by R_ex, while in the case of G12C and G12D it is 10 and 21 residues, respectively.

Switch I residues of all the three variants show slow-time scale motions; however in the G12D mutant the values tend to be higher than those in the WT and G12C variants: the largest R_ex value measured is also in this region, describing the motion of Glu37 of G12D-KRAS-GDP. In the switch I region, Tyr32 (G12D)/Asp33 (in WT and G12C) show slow time-scale motions. Thr35 participates in slow motions in WT and G12D-KRAS-GDP and is not detected in the G12C variant. The most outstanding slow movement or exchange in the P-loop belongs to Gly13 of the G12C mutant, next to the site of the mutation. The motion of the Gly15 residue can be described by using a slow time scale parameter R_ex only in the case of KRAS-G12D-GDP forms (model 3), but not in KRAS-WT-GDP and KRAS-G12C-GDP mutants (model 1 was used in both cases), while the motion of the Ser17 residue can be characterized by an R_ex parameter in both KRAS-WT-GDP and KRAS-G12D-GDP forms (model 3 in both), but not in the KRAS-G12C-GDP mutant (model 1). This suggests that slow motions in the P-loop are the most relevant in KRAS-G12D-GDP and the least in KRAS-G12C-GDP; thus in the G12C form Gly13 might be involved in chemical/conformational exchange processes instead of slow motions.

To test the robustness of the results we repeated the Lipari–Szabo model-free analysis using the axial anisotropy approach using dimer-models instead of the monomeric form of KRAS-WT-GDP. We built dimer models using the two arrangements proposed in the work of Muratcioglu et al.:⁵² the α- and the β-dimer. We obtained very similar results when using either model to those derived by the isotropic approach (ESI Fig. 9†).

Flexible regions were also confirmed by the reduced spectral density mapping. The spectral density parameters referring to the propensity of fast motions (J(ω_h)) reinforce the three flexible regions (Gly60–Ser65 in switch II, Ser106–Met111 and Ser122–Arg123) (Fig. 4D). In the GDP-bound forms Tyr32 is highly flexible (J(ω_h) values are 9.77, 9.17 and 8.68 ps rad⁻¹, while the averages are 3.26, 3.30 and 3.35 ps rad⁻¹ for the WT and G12C and G12D mutants, respectively). In the GTP-bound state, the flexibility of Tyr32 is similar to or even less than the average flexibility (J(ω_h) values are 1.10, 3.33 and 1.12 ps rad⁻¹ while the averages are 3.33, 3.22 and 3.11 ps rad⁻¹ for the WT and G12C and G12D mutants, respectively). Thus, it appears that the dynamics of Tyr32 – detected at its backbone amide NH – notably deviates from those of every other residue of switch I in the GDP-bound forms where its flexibility exceeds that of the surroundings. However, it becomes even more anchored than the neighboring residues (in the case of the WT and G12D variant) in the GTP-bound forms.

To further elaborate the effect of the Tyr32 side chain, and to specifically clarify whether its presence has a marked effect on the structural ensemble of the KRAS-G12C system too, we have designed a double mutant, namely that of G12C/Y32F and compared the relevant chemical shifts (¹H, ¹⁵N-HSQC spectra) to those of the G12C mutant, both in the GDP- and GTP-bound states (Fig. 5A). In the case of the GDP-bound form significant changes were found mostly in switch I, in the proximity of the mutated Tyr32. In total, 29 of the assigned 164 resonances shifted slightly or even significantly primarily in the vicinity of Tyr32. In contrast, in the GTP-bound form more than half of the signals were shifted (89 of the assigned 133 signals) involving even far-lying sites (Fig. 5B). This is a clear indication of the key role of the –OH group of Tyr32 in the stabilization of the GTP-bound form. A similar conclusion was reached by Buhrman et al. in the case of the WT HRAS, where the Y32F mutation resulted in over a 2-fold decrease in the GTP hydrolysis rate – thus leading to the destabilization of the catalytically competent form. They found that, in the presence of a non-hydrolysable GTP analogue (GppNHp), the switch I region is distant from the active site and F32 points inward the switch I loop, in a conformation reminiscent of the GDP-loaded state.³²

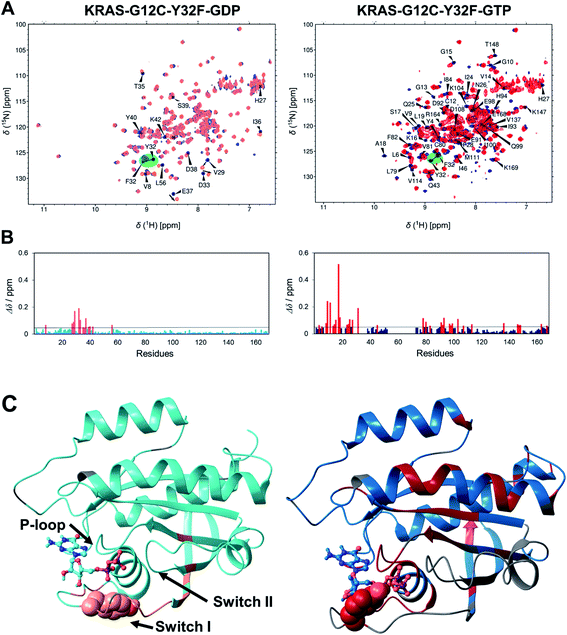Fig. 5 (A) Overlaid ¹H, ¹⁵N-HSQC spectra of KRAS-G12C-GDP (blue; left) and KRAS-G12C-Y32F-GDP (light red; left) and those of KRAS-G12C-GTP (dark blue; right) and KRAS-G12C-Y32F-GTP (red; right). Assignment is shown for the G12C mutant and only for those resonances which shifted significantly (Δδ > 0.05 ppm). The mutated Y32 → F32 is highlighted. (B) Combined chemical shift differences upon G12C/Y32F mutation along the sequence for GDP and GTP-bound forms. Δδ values are calculated according to Williamson.⁵⁴ Residues for which Δδ > 0.05 ppm are colored red (GDP-bound form: left; GTP-bound form: right). (C) 3D distribution of the residues affected by the Y32F mutation (shown on the MD derived structures of the KRAS-G12C-GDP (left) and KRAS-G12C-GTP (right)): residues with significant Δδ shifts of the GDP-bound forms are colored light red (left) and those of the GTP-bound forms are colored red (right), those residues for which a signal could not be identified are shown in gray, and residues with negligible chemical shift upon mutation are colored cyan (left) and darker blue (right). The mutated Tyr32 is shown in CPK and the nucleotide is shown in ball-and-stick representation.

In the GDP-bound RAS enzymes, Tyr32 points away from the nucleotide binding site, interacting with Tyr40 within the loop created by the switch I residues. Experimental information concerning the role of Tyr32 in the formation of the active, GTP-bound state of RAS proteins, however, is scarce due to the intrinsic hydrolysis of the physiological nucleotide, which hinders the detailed analysis of this state. The crystal structure of the HRAS-GTP complex was determined in an elegant study some twenty years ago.⁵⁸ Using a caged-GTP variant (R-1-(2-nitrophenyl)-ethyl-GTP ester) the authors generated the active form within the crystal lattice by irradiation. However, due to a peculiar artifact this structure does not clarify the active, solution state conformation of Tyr32. In the crystal, each Tyr32 flips from the inner switch I region toward the nucleotide binding site but is captured in a tight H-bond (at 2.7 Å) by the neighboring monomer placed in the vicinity by crystal-packing, specifically by the O1G atom of the γ-phosphate of the neighboring GTP (ESI Fig. 10†). Curiously, this conformation of HRAS is very similar to that assumed in the HRAS-GAP complex,⁵⁹ thus it was proposed that it might represent a GAP-compatible, less stable, and thus sparsely sampled sub-state of the activated, GTP-loaded form of HRAS.⁶⁰ Recently, the GTP-bound form of KRAS was also explored in a comprehensive study of WT and mutant variants using both GTP and its various non-hydrolysable analogues.⁶¹ However, in these experiments GTP (or its analogue) was simply diffused into the preformed crystals of GDP-loaded KRAS – a methodology that does not guarantee complete nucleotide exchange. Accordingly, the structures reflect more the transition from the GDP- to the GTP-bound form and less the final stabilized activated state. In fact, both switch I and II are destabilized and have poorly localized electron density. The conformation of Tyr32 is seen as unchanged by nucleotide exchange; however a nearly 2-fold increase in its (relative) B-factors indicates that its position, distant from the nucleotide binding site, is far from certain. Reviewing all structures concerning the GTP-bound state (WT and mutant forms in complex with GTP or its analogues, excluding those crystal structures where switch I directly interacts with neighboring monomers) three distinct positions of Tyr32 (and the adjoining switch I region) can be found: (i) it remains secured within the switch I loop interacting primarily with Tyr40 (a GDP-complex-like state), (ii) it is flipped from this spot to the vicinity of the γ-phosphate of GTP, but points into the solvent and (iii) its hydroxyl group forms a direct H-bond to one of the oxygens of the γ-phosphate (ESI Fig. 11†).

Since our NMR results indicated a distinct change in the environment and flexibility of Tyr32 on nucleotide exchange, we considered the latter two possibilities to be plausible. Because nucleotide exchange and the corresponding conformational changes proceed ineffectively without the aid of the exchange factors, we expected this Tyr32-related conformational change to be substantial.

To generate unbiased and directly comparable models for the GDP and GTP-bound forms of WT, G12C and G12D KRAS, we carried out MD simulations starting from two crystal structures, one for each nucleotide-bound form.^32,33 For representing the GTP-bound state we chose a structure where Tyr32 is near, but not directly coordinated with the γ-phosphate of GTP (O1G_GTP–OH_Tyr32 distance of 4.3 Å).

The MD results were compared to NMR backbone dynamics data using S² values and C′, C^α and C^β chemical shifts (calculated from MD ensembles) for the G12C mutant in both the GDP- and GTP bound states since ¹³C chemical shifts were determined only for this system. The calculated and the measured data were in good agreement (as can be seen in ESI Fig. 12†).

Similarly to the NMR results, we found little structural consequence of the mutations in the core structure of KRAS in either the GDP- or the GTP-bound states (ESI Fig. 1†). The high flexibility of the switch regions is apparent, especially in the GDP-complexes. The overall effect of nucleotide exchange is a more defined structure – both the overall and especially the local conformational heterogeneity of the switch I region is considerably reduced in the GTP complexes (Table 2 and ESI Fig. 1†).

Table 2 Clustering of the snapshots of the last 300 ns of the equilibrium trajectory of the MD simulations, based on the conformation of the backbone atoms along the full sequence (1st column) and just between residues 10–48, an extended region containing switch I (2nd column). The values of the 1^st column are provided as a reference, to illustrate the greater conformational variability of the switch I region in both the GDP- and the GTP-bound states. It can also be seen that the GDP → GTP switch lowered the conformational heterogeneity in the case of all three variants, according to both measures. Per residue average B-factors were also calculated for each system – these can be seen in ESI Fig. 1

	Full-sequence	Residue 10–48
WT-GDP	23	170
WT-GTP	7	49
G12C-GDP	21	91
G12C-GTP	12	52
G12D-GDP	21	144
G12D-GTP	10	85

---

In all three GDP complexes Tyr32 points into the loop created by switch I residues, bound directly or through a water to Asp38 or Tyr40, wedged between Ile21, Val29 and Ile36, blocking the entrance of the effector binding pocket below the plane of the nucleotide (Fig. 6A and B). Its secured binding within the switch I loop might be surprising in light of the HetNOE value indicating that its backbone amide NH assumes a number of different conformations, much more so than its immediate surroundings. The conformational heterogeneity of the switch I region does not reach that of switch II, but there is a variability which is created by the flapping movement of the segment following Tyr32. In fact, the backbone twists slightly, precisely at Tyr32. Since the motion of residues 32–36 involves the nearly rigid-body flapping of the entire, well-defined segment that is immersed into the solvent, the backbone amide NH vectors in this region will not experience a significant change in their chemical environment even if they fluctuate around their average positions. However, the amide H of Tyr32 is close to the α-phosphate of GDP and as it tilts, performing its hinge function, it passes through a broad distribution of NH–O1A/O2A distances between 3 and 7 Å. This produces not only conformationally but electrostatically quite different environments, which might be the reason why the flexibility (fast timescale motions) of the switch I region is detected only at Tyr32 (ESI Fig. 13†).

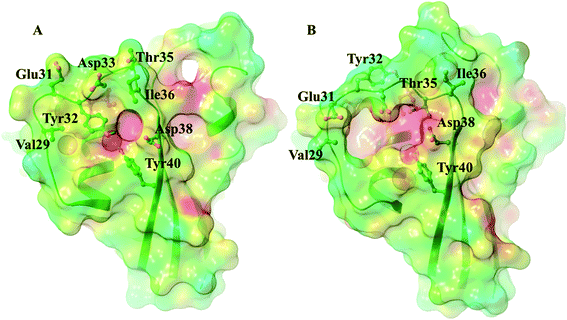Fig. 6 The effect of nucleotide exchange on the structure of WT and mutant KRAS proteins in the MD simulations: rearrangement of the effector binding pocket on nucleotide exchange (WT-KRAS shown as an example, mid-structure of the most populated cluster). In the presence of GDP Tyr32 blocks the pocket (A), while in the GTP-bound state (B) the binding site becomes approachable (surfaces colored according to electrostatic potential (red: negative, blue positive)). For an overview of the structures of all three variants in the GDP- and GTP-bound states see ESI Fig. 1.†

In the GTP-bound states, Tyr32 is flipped from its position within the effector binding site to the opposite side of switch I and binds directly to the O1G atom of the γ-phosphate (with OH_Tyr32–O1G_GTP distances of 2.6 ± 0.1 Å, 2.6 ± 0.1 Å and 2.7 ± 0.4 Å in the case of the WT-, G12C- and G12D-KRAS-GTP complexes) – in accordance with the significant change in its HetNOE and J(ω_h) values in the GTP-bound forms in our NMR measurements and the previous findings based on both crystallographic^62–65 and theoretical approaches.^60,66 This new connection results in the rearrangement of the surrounding residues as well, most significantly those of Glu31, Asp33, Thr35 and Asp38, which flip toward the inner side of the effector binding pocket, creating a significant change – the entrance becomes more spacious and lined by negatively charged groups in the GTP complexes (Fig. 6), potentiating the binding site for the docking of the effector proteins which anchor to RAS through positively charged amino acids.⁶⁷

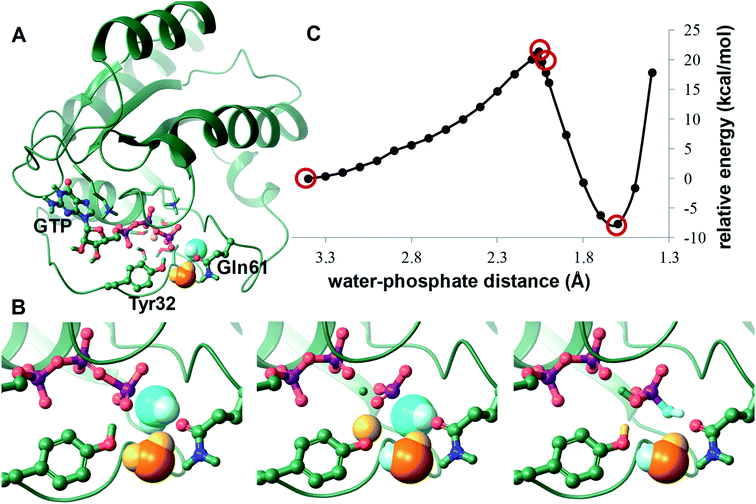
Anchoring of Tyr32 to O1G of GTP causes a further significant change in the case of WT-KRAS. This completes the trapping of the catalytic water pair near the γ-phosphate.⁶⁸ According to the generally accepted mechanism, the catalytic reaction is aided by two waters: a catalytic water serving as the nucleophile and an assisting water that functions as the general base. Following the attack of the catalytic water on the phosphorus of the γ-phosphate, a proton shuffle takes place. The proton released by the catalytic water on binding to the phosphorus is accepted by the assisting water (activated by Gln61), which in turn protonates one of the oxygens of the γ-phosphate, resulting in a doubly protonated H₂PO₄⁻ and GDP as the products.^69–71

In our simulations, in the WT-KRAS-GTP complex with the Tyr32–GTP H-bond intact, the protein matrix creates a binding pocket for the nucleotide and the catalytic waters, sheltering them from the bulk solvent (Fig. 7).

Fig. 7 Trapping of the catalytic and assisting waters in the GTP-bound complex of (A) WT-, (B) G12C- and (C) G12D-KRAS (the mid-structures of the most populated clusters of the simulations are shown). The active site pocket containing the catalytic water pair (shown in CPK with the oxygens colored cyan) is closed in the case of the WT (A), while open toward the solvent in the case of the mutant systems (B) and (C). The solvent accessible surface – shown in mesh – was calculated for the non-hydrogen atoms of the protein, excluding GTP, Mg²⁺ and the water molecules.

The first water spot (always occupied) places the catalytic water at a distance of 3.3 ± 0.1 Å from the γ-phosphorus atom of GTP. This water primarily interacts with the backbone amides of switch II residues of Gly60 and Gln61. The second water molecule, at 2.8 ± 0.1 Å from the first one, is secured between the O1G oxygen of the γ-phosphate, the OE1 atom of Gln61 and the hydroxyl of Tyr32 forming an H-bond with these centers in 100%, 68.6% and 97.4% of the snapshots, respectively. Thus, this second water is positioned ideally for accepting a proton from the catalytic water and passing it on to the detaching γ-phosphate.

Interestingly, two water molecules in very similar positions can also be seen in the crystal structure of the HRAS-GppNHp complex (PDB: 3k8y)³² that was used for building the starting model for our simulation. This structure presents a conformation stabilized by the capture of an acetate-Ca²⁺ ion pair at the allosteric ligand binding site (formed between α3, β5 and α4 (see Fig. 1 and 8.)). There is a crystal water at 3.3 and 3.1 Å from the amides of Gly60 and Gln61 and another that is within 2.8 Å of Tyr32–OH, Gln61–OE1 and the O1G atom of the γ-phosphate. As Tyr32 is not bound directly to the nucleotide, the two captured waters are too far (4.2 Å) for interaction. This prompted the authors to propose that the catalytic reaction is initiated by a proton transfer from the catalytic water to the γ-phosphate directly, which disagrees with the QM/MM derived mechanisms of others.^67,69,70 Instead, we suggest that both of these water molecules are required for the catalysis. If Tyr32 shifts to the position seen in our simulations and pulls the coordinated water molecule along, then both waters participate in the proton shuffle mechanism of hydrolysis (Fig. 8).

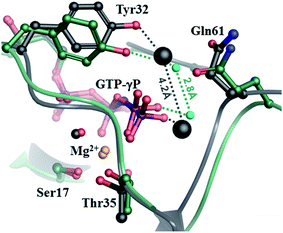Fig. 8 Comparison of the crystal structure of the HRAS–GppNHp complex³² with the MD derived WT-KRAS-GTP structure (the mid-structure of the most populated cluster of the simulation). The crystal structure is shown in dark gray with the crystal waters shown in CPK, while the calculated conformer is colored in green, with cyan spheres indicating the position of the oxygen atoms of the catalytic and assisting waters.

In the case of the mutants, the situation is slightly different. Either sidechain present at position 12 clashes with Gln61, which is thus displaced by ∼1 Å (with the Pγ_GTP–CD1_Q61 distance increasing from 6.5 ± 0.6 Å to 7.3 ± 0.7 Å in both cases) causing further rearrangement of the 61–67 segment of switch II. This rearrangement opens up the active site pocket toward the solvent (Fig. 7). Both catalytic water positions remain occupied in the GTP-bound forms of both G12C and G12D mutants, albeit in a continual exchange. While in the case of the WT-GTP complex, there are two waters that spend more than 80% of the last 300 ns of the simulation time within the active site pocket, in the case of the G12C–GTP complex the longest fraction of time spent within the pocket by a water molecule is 65.6%, and in the case of G12D–GTP, 43.9%. Retaining the water molecules in the case of the WT–GTP complex results in protein-like B-factors for both the catalytic and the assisting water (ESI Fig. 14†). The difference seen between the two mutants is likely the result of the Cys12 sidechain of G12C-KRAS-GTP H-bonding to the catalytic water in nearly a third of the snapshots (32.6%) providing additional stabilization for it within the pocket. The Asp12 sidechain of the G12D–GTP complex reaches into the solvent (in 59.6% of the snapshots the carboxylate moiety has no protein contacts) without providing such support. Comparing these findings to the intrinsic hydrolysis rates of the three forms (6.8 × 10⁻⁴ s⁻¹, 5.0 × 10⁻⁴ s⁻¹ and 1.9 × 10⁻⁴ s⁻¹ for WT-, G12C- and G12D-KRAS, respectively),³³ we can conclude that the distancing of Gln61 from the active center and the destabilization of the water molecules participating in catalysis might be the reason for the loss of catalytic efficiency.

To support the catalytic relevance of the derived activated conformation we carried out QM/MM calculations for the GTP hydrolysis step – considering the presence of Tyr32 in the active site for the first time. Experimentally determined intrinsic hydrolysis rates for WT-HRAS and KRAS enzymes vary between 2.1 × 10⁻⁴ s⁻¹ and 6.8 × 10⁻⁴ s⁻¹,^41,72,73 corresponding to an activation energy of approximately 22 kcal mol⁻¹. Using the MD derived arrangement of the WT-KRAS active site, the activation energy of the catalytic water approaching the phosphorus of the γ-phosphate of GTP – in a simple scan of their distance – afforded a 21.4 kcal mol⁻¹ single barrier at 2.06 Å separation, which also results in the lengthening of the PG–O3B bond (GDP–P_i bond) to 1.98 Å. Further advance of the water prompts a triple proton shuffle, leading to a H₂PO₄⁻ product state. Tyr32 participates in this step: the proton of the catalytic water is passed on to the assisting water, which in turn protonates Tyr32, prompting donation of its proton to the γ-phosphate in a single step (Fig. 9).

Fig. 9 Mechanism of the WT-KRAS catalyzed intrinsic GTP-hydrolysis in the presence of Tyr32. (A) The QM region (Lys16, Ser17, Tyr32, Thr35, Gln61, Lys117, Mg²⁺-ion, GTP and 4 water molecules) shown is explicitly in the reactant state (r(O_{wat-catlaytic}–P_γ-phosphate) = 3.4 Å). The catalytic water is shown in cyan and the assisting water in orange. (B) Further characteristic points of the scan are: r = 2.06 Å (left), r = 2.04 Å (middle) and r = 1.6 Å (right). (C) Calculated energies along the reaction profile (points corresponding to stages shown in (A) and (B) are circled in red).

The product thus achieved is quite reminiscent of the PROD2 state of the reaction derived by Grigorenko et al.⁶⁹ In their study – in the absence of Tyr32 – this state was reached from a transient product (PROD1) by rearrangement of the H-bond motif around the phosphate (requiring negligible activation energy). This suggests that the reaction proceeds quite effectively in the absence of Tyr32 also, but it requires a further rearrangement step to stabilize the product state.

To investigate the role of Tyr32 in supporting catalysis, we created a computational mutant (Y32F*) simply by exchanging the –OH group of the tyrosine to an –H, keeping the rest of the system unchanged. Our very local computational mutation (Y32F*) did not cause a significant change in the reaction profile (with a 22.1 kcal mol⁻¹ barrier) as expected, but it did lead to a less stable product state (ESI Fig. 15†) – supporting the notion that hydrolysis is possible in the absence of Tyr32 as well. Thus, our QM/MM calculations indicate that direct bonding of Tyr32 to the γ-phosphate of GTP is not an “anti-catalytic” arrangement as was previously suggested.^55,61,74 Indeed, it does not hinder the attack of the catalytic water and contributes to straightforward product formation. However, it does seem that even though the –OH group of Tyr32 is positioned very similarly to the Arg finger of GAP that provides electrostatic enhancement to the hydrolysis reaction, this is not the case for Tyr32; the significance of the Tyr32–GTP connection lies in creating a local environment that binds and activates the catalytic waters and in facilitating product formation.

Finally, we analyzed the arrangement of binding hot spots of the GTP complex of wild type and mutant KRAS proteins. Although similar analysis has been published by the Mattos group⁷⁵ their work used FTMAP⁷⁶ on HRAS structures co-crystallized with the GTP analogue GppNHp. Having structural information on the native, GTP-bound state of KRAS prompted us to investigate the architecture of the available hot spots. Our calculations confirmed the results of the Mattos group identifying multiple hot spots on the protein surface. In addition to the nucleotide binding site FTMAP predicted allosteric sites at the α2–β2 groove close to the effector binding loop and also at the α2–α3 groove (ESI Fig. 16†). In fact, both of these sites were validated by KRAS-inhibitor complexes; the former is used by small fragments that inhibit GEF binding⁷⁷ and pyrazolopyrimidine-based KRAS inhibitors drastically lower its affinity toward effector protein RAF⁷⁸ (ESI Fig. 17†), and the latter serves as the binding site of ARS compounds.⁷⁹ Our study revealed that Tyr32 flips over the nucleotide binding site in GTP-bound activated complexes and gets closer to the ARS site. Since FTMAP predicted here a strong binding hot spot for the oncogenic mutants, covalent inhibitors targeting Tyr32 would represent an alternative strategy for mutant specific KRAS inhibitors. These covalent inhibitors would bind to the validated hot spot located in the α2–α3 groove and label Tyr32 irreversibly, preventing its ligation to the γ-phosphate and, through this, the emergence of the conformational signal prompting the binding of the effector proteins.

Conclusion

Oncogenic mutations protrude from the surface of RAS as a knob and obstruct the docking of the Arg-finger of GAP.⁸⁰ This Arg sidechain of GAP passes close to the P-loop of RAS and thus it clashes into any sidechain at position 12; therefore any residue different from the WT glycine at this position is a hindrance to GAP reaching the phosphates of RAS-bound GTP. However, the presence of the Arg-finger is required for effective GTP hydrolysis: it grants an electrostatic boost to the reaction. Thus blocking its entrance into the nucleotide binding pocket provides a straightforward explanation as to the detrimental effect of Gly12 mutations. But it is less clear how the intrinsic hydrolysis rates (in the absence of GAP) are affected by these variants that leave the backbone of the P-loop unchanged and carry sidechains at position 12 that point into the solvent and away from the catalytic site.

NMR measurements allowed a detailed analysis of the changes in structure and dynamics taking place in WT KRAS and its G12C and G12D mutants on nucleotide exchange. The results of HetNOE measurements and data analysis by reduced spectral density mapping singled out Tyr32 as a central contributor to the changes. We found that it is by far the most flexible switch I residue of the GDP-bound forms and the most rigid of the GTP-complexed states of WT and G12D mutant KRASs, while also proving to be crucial for the stability of the G12C–GTP complex – as demonstrated using the G12C–Y32F variant.

Combining our NMR and molecular modeling results, we propose that the capture of Tyr32 by the terminal phosphate of GTP is one of the key steps of RAS activation. It enlarges and switches the polarization of the effector binding loop preparing it for the docking of downstream partners and it contributes to the capture, positioning and activation of the catalytic waters. We found that closing of the active site pocket and securing water molecules is upset to varying degrees by position 12 mutations – in agreement with the experimental findings concerning their reduced intrinsic hydrolysis capacities.

For assuring controllability, RAS proteins were engineered to be “poor” enzymes thus providing the possibility of a wide range of different regulatory functions to oversee emergence of the growth signal. The most basic enzymatic functions of these small GTPases – nucleotide binding and hydrolysis – are carried out very ineffectively on their own and are assisted by exchange factors and GTPase activator proteins, themselves under tight regulation. It was recently shown that the RAS function can also be disrupted in an independent regulatory cycle by phosphorylation of Tyr32 and Tyr64 by impairing RAF binding but also lowering the rate of intrinsic GTP hydrolysis. Catalytic activity is reinstated by dephosphorylation.⁸¹ Inhibition of dephosphorylation was shown to suppress cancerous growth evoked by RAS mutations.^82–85 In the work of Kano et al.⁸¹ the authors point out that phosphorylation also lowers the rate of intrinsic GTP hydrolysis. This finding was an ideal test for our proposed active form; thus we also carried out MD simulations for WT-, G12D- and G12V-pKRAS, phosphorylated at Tyr32, and the WT phosphorylated at both Tyr32 and Tyr64 in the GTP-bound states. The results indicate that in pKRAS-GTP complexes, the connection between pTyr32 and GTP is lost, and the opening of the active site further destabilizes the water network of the active site, which we've shown to be essential for catalysis: there is only a single water captured in the catalytic pocket of the WT protein phosphorylated at Tyr32, and none in the case of the mutants or the doubly phosphorylated WT (which is the physiological state before dephosphorylation by SHP2) (see ESI Fig. 18†). This lends support to our results: WT-KRAS is more effective in the intrinsic hydrolysis of GTP than mutants or phosphorylated forms because its active site captures both catalytically essential water molecules. In our WT-KRAS-GTP model Tyr64 is also quite close to the active site; in fact it plays a role in forming the pocket that captures the active waters – therefore its phosphorylation would also contribute to the destabilizing of the “switched-on” conformation.

Our hot spot analysis on the mutant KRAS proteins revealed that a similar effect might be achieved by the covalent modification of Tyr32. The vicinity of the strong binding hot spot in the GTP-bound structure of the oncogenic mutants might open new opportunities for designing Tyr32 targeting covalent inhibitors. Similarly to its phosphorylation, irreversible binding to Tyr 32 might also stall the GTPase cycle and probably impairs binding to effectors. Our efforts now focus on the discovery of this novel type of KRAS inhibitor with significant therapeutic potential.

Abbreviations

BMRB	Biological magnetic resonance data bank
DSS	Sodium trimethylsilylpropanesulfonate
GDP	Guanosine diphosphate
GTP	Guanosine triphosphate
GppNHp	5′-Guanylyl-imidodiphosphate
HetNOE	Heteronuclear Overhauser effect
HSQC	Heteronuclear single quantum coherence
BEST	Band-selective excitation short-transient
MD	Molecular dynamics
NOESY	Nuclear Overhauser effect spectroscopy
PDB	Protein data bank
QM/MM	Quantum mechanics/molecular mechanics simulation
SSP	Secondary structure propensities
TOCSY	Total correlation spectroscopy
WT	Wild type

Author contributions

D. K. M., G. P., G. M. K. and A. P. designed the research; I. V. produced the proteins, G. P. performed NMR measurements, D. K. M. and Z. O. performed MD simulations, D. K. M. performed QM/MM simulations; D. K. M. and G. P. analyzed the data; and D. K. M., G. P., Z. O., G. M. K. and A. P. wrote the paper.

Funding sources

The National Research, Development and Innovation Office of Hungary (grant numbers: NVKP_16-1-2016-0020, OTKA K116904, and OTKA K116305) and the Hungarian Ministry of Human Capacities and co-financed by the European Regional Development Fund (VEKOP-2.3.2-16-2017-00014) and HunProtEx.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We are grateful to Orsolya Tőke and László Buday (RCNS, Hungary) for carefully reading the manuscript and for the useful discussions.

References

1. J. J. Harvey, An Unidentified Virus Which Causes the Rapid Production of Tumours in Mice, Nature, 1964, 204(4963), 1104–1105,  DOI:10.1038/2041104b0.
2. W. H. Kirsten and L. A. Mayer, Morphologic Responses to a Murine Erythroblastosis Virus, J. Natl. Cancer Inst., 1967, 39(2), 311–335.
3. A. Hall, C. J. Marshall, N. K. Spurr and R. A. Weiss, Identification of Transforming Gene in Two Human Sarcoma Cell Lines as a New Member of the Ras Gene Family Located on Chromosome 1, Nature, 1983, 303(5916), 396–400,  DOI:10.1038/303396a0.
4. A. D. Cox, S. W. Fesik, A. C. Kimmelman, J. Luo and C. J. Der, Drugging the Undruggable RAS: Mission Possible?, Nat. Rev. Drug Discovery, 2014, 13(11), 828–851,  DOI:10.1038/nrd4389.
5. G. A. Hobbs, C. J. Der and K. L. Rossman, RAS Isoforms and Mutations in Cancer at a Glance, J. Cell Sci., 2016, 129(7), 1287–1292,  DOI:10.1242/jcs.182873.
6. R. Spencer-Smith and J. P. O'Bryan, Direct Inhibition of RAS: Quest for the Holy Grail?, Semin. Cancer Biol., 2019, 54, 138–148,  DOI:10.1016/j.semcancer.2017.12.005.
7. A. M. Rojas, G. Fuentes, A. Rausell and A. Valencia, The Ras Protein Superfamily: Evolutionary Tree and Role of Conserved Amino Acids, J. Cell Biol., 2012, 196(2), 189–201,  DOI:10.1083/jcb.201103008.
8. B. E. Hall, D. Bar-Sagi and N. Nassar, The Structural Basis for the Transition from Ras-GTP to Ras-GDP, Proc. Natl. Acad. Sci. U. S. A., 2002, 99(19), 12138–12142,  DOI:10.1073/pnas.192453199.
9. M. V. Milburn, L. Tong, A. M. deVos, A. Brünger, Z. Yamaizumi, S. Nishimura and S. H. Kim, Molecular Switch for Signal Transduction: Structural Differences between Active and Inactive Forms of Protooncogenic Ras Proteins, Science, 1990, 247(4945), 939–945,  DOI:10.1126/science.2406906.
10. J. M. L. Ostrem and K. M. Shokat, Direct Small-Molecule Inhibitors of KRAS: From Structural Insights to Mechanism-Based Design, Nat. Rev. Drug Discovery, 2016, 15(11), 771–785,  DOI:10.1038/nrd.2016.139.
11. S. Lu, H. Jang, S. Muratcioglu, A. Gursoy, O. Keskin, R. Nussinov and J. Zhang, Ras Conformational Ensembles, Allostery, and Signaling, Chem. Rev., 2016, 116(11), 6607–6665,  DOI:10.1021/acs.chemrev.5b00542.
12. P. A. Boriack-Sjodin, S. M. Margarit, D. Bar-Sagi and J. Kuriyan, The Structural Basis of the Activation of Ras by Sos, Nature, 1998, 394(6691), 337–343,  DOI:10.1038/28548.
13. M. Spoerner, C. Hozsa, J. A. Poetzl, K. Reiss, P. Ganser, M. Geyer and H. R. Kalbitzer, Conformational States of Human Rat Sarcoma (Ras) Protein Complexed with Its Natural Ligand GTP and Their Role for Effector Interaction and GTP Hydrolysis, J. Biol. Chem., 2010, 285(51), 39768–39778,  DOI:10.1074/jbc.M110.145235.
14. D. Long, C. B. Marshall, G. Bouvignies, M. T. Mazhab-Jafari, M. J. Smith, M. Ikura and L. E. Kay, A Comparative CEST NMR Study of Slow Conformational Dynamics of Small GTPases Complexed with GTP and GTP Analogues, Angew. Chem., Int. Ed., 2013, 52(41), 10771–10774,  DOI:10.1002/anie.201305434.
15. D. Liu, X. Chen and D. Long, NMR-Derived Conformational Ensemble of State 1 of Activated Ras Reveals Insights into a Druggable Pocket, J. Phys. Chem. Lett., 2020, 11(9), 3642–3646,  DOI:10.1021/acs.jpclett.0c00858.
16. X. Chen, H. Yao, H. Wang, Y. Mao, D. Liu and D. Long, Extending the Lifetime of Native GTP-Bound Ras for Site-Resolved NMR Measurements: Quantifying the Allosteric Dynamics, Angew. Chem., Int. Ed., 2019, 58(9), 2730–2733,  DOI:10.1002/anie.201812902.
17. R. C. Hillig, B. Sautier, J. Schroeder, D. Moosmayer, A. Hilpmann, C. M. Stegmann, N. D. Werbeck, H. Briem, U. Boemer, J. Weiske, V. Badock, J. Mastouri, K. Petersen, G. Siemeister, J. D. Kahmann, D. Wegener, N. Böhnke, K. Eis, K. Graham, L. Wortmann, F. Nussbaum and B. Bader, Discovery of Potent SOS1 Inhibitors That Block RAS Activation via Disruption of the RAS-SOS1 Interaction, Proc. Natl. Acad. Sci. U. S. A., 2019, 116(7), 2551–2560,  DOI:10.1073/pnas.1812963116.
18. F. McCormick, Progress in Targeting RAS with Small Molecule Drugs, Biochem. J., 2019, 476(2), 365–374,  DOI:10.1042/BCJ20170441.
19. G. Pálfy, I. Vida and A. Perczel, 1H, 15N Backbone Assignment and Comparative Analysis of the Wild Type and G12C, G12D, G12V Mutants of K-Ras Bound to GDP at Physiological pH, Biomol. NMR Assignments, 2020, 14(1), 1–7,  DOI:10.1007/s12104-019-09909-7.
20. C. Ammann, P. Meier and A. Merbach, A Simple Multinuclear NMR Thermometer, J. Magn. Reson., 1982, 46(2), 319–321,  DOI:10.1016/0022-2364(82)90147-0.
21. D. S. Wishart, C. G. Bigam, J. Yao, F. Abildgaard, H. J. Dyson, E. Oldfield, J. L. Markley and B. D. Sykes, ¹H, ¹³C and ¹⁵N Chemical Shift Referencing in Biomolecular NMR, J. Biomol. NMR, 1995, 6(2), 135–140,  DOI:10.1007/bf00211777.
22. R. L. J. Keller, The computer aided resonance assignment tutorial, Cantina Verlag, Goldau, 2004.
23. W. Lee, M. Tonelli and J. L. Markley, NMRFAM-SPARKY: Enhanced Software for Biomolecular NMR Spectroscopy, Bioinformatics, 2015, 31(8), 1325–1327,  DOI:10.1093/bioinformatics/btu830.
24. N. A. Farrow, O. Zhang, A. Szabo, D. A. Torchia and L. E. Kay, Spectral Density Function Mapping Using 15N Relaxation Data Exclusively, J. Biomol. NMR, 1995, 6(2), 153–162,  DOI:10.1007/BF00211779.
25. G. Lipari and A. Szabo, Model-Free Approach to the Interpretation of Nuclear Magnetic Resonance Relaxation in Macromolecules. 1. Theory and Range of Validity, J. Am. Chem. Soc., 1982, 104(17), 4546–4559,  DOI:10.1021/ja00381a009.
26. G. Lipari and A. Szabo, Model-Free Approach to the Interpretation of Nuclear Magnetic Resonance Relaxation in Macromolecules. 2. Analysis of Experimental Results, J. Am. Chem. Soc., 1982, 104(17), 4559–4570,  DOI:10.1021/ja00381a010.
27. G. M. Clore, P. C. Driscoll, P. T. Wingfield and A. M. Gronenborn, Analysis of the Backbone Dynamics of Interleukin-1.Beta. Using Two-Dimensional Inverse Detected Heteronuclear Nitrogen-15-Proton NMR Spectroscopy, Biochemistry, 1990, 29(32), 7387–7401,  DOI:10.1021/bi00484a006.
28. R. Cole and J. P. Loria, FAST-Modelfree: A Program for Rapid Automated Analysis of Solution NMR Spin-Relaxation Data, J. Biomol. NMR, 2003, 26(3), 203–213,  DOI:10.1023/A:1023808801134.
29. A. M. Mandel, M. Akke and A. G. Palmer III, Backbone Dynamics Of Escherichia Coli Ribonuclease HI: Correlations with Structure and Function in an Active Enzyme, J. Mol. Biol., 1995, 246(1), 144–163,  DOI:10.1006/jmbi.1994.0073.
30. A. G. Palmer, M. Rance and P. E. Wright, Intramolecular Motions of a Zinc Finger DNA-Binding Domain from Xfin Characterized by Proton-Detected Natural Abundance Carbon-13 Heteronuclear NMR Spectroscopy, J. Am. Chem. Soc., 1991, 113(12), 4371–4380,  DOI:10.1021/ja00012a001.
31. D. M. Korzhnev, M. Billeter, A. S. Arseniev and V. Y. Orekhov, NMR Studies of Brownian Tumbling and Internal Motions in Proteins, Prog. Nucl. Magn. Reson. Spectrosc., 2001, 38(3), 197–266,  DOI:10.1016/S0079-6565(00)00028-5.
32. G. Buhrman, G. Holzapfel, G. Fetics and C. Mattos, Allosteric modulation of Ras positions Q61 for a direct role in catalysis, Proc. Natl. Acad. Sci. U. S. A., 2010, 107(11), 4931–4936,  DOI:10.1073/pnas.0912226107.
33. J. C. Hunter, D. Gurbani, S. B. Ficarro, M. A. Carrasco, S. M. Lim, H. G. Choi, T. Xie, J. A. Marto, Z. Chen, N. S. Gray and K. D. Westover, In situ selectivity profiling and crystal structure of SML-8-73-1, an active site inhibitor of oncogenic K-Ras G12C, Proc. Natl. Acad. Sci. U. S. A., 2014, 111(24), 8895–8900,  DOI:10.1073/pnas.1404639111.
34. S. Pronk, S. Páll, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M. R. Shirts, J. C. Smith, P. M. Kasson, D. van der Spoel, B. Hess and E. Lindahl, GROMACS 4.5: A High-Throughput and Highly Parallel Open Source Molecular Simulation Toolkit, Bioinformatics, 2013, 29(7), 845–854,  DOI:10.1093/bioinformatics/btt055.
35. S. Izadi, R. Anandakrishnan and A. V. Onufriev, Building Water Models: A Different Approach, J. Phys. Chem. Lett., 2014, 5(21), 3863–3871,  DOI:10.1021/jz501780a.
36. X. Daura, K. Gademann, B. Jaun, D. Seebach, W. F. V. Gunsteren and A. E. Mark, Peptide folding: When simulation meets experiment, Angew. Chem., Int. Ed., 1999, 38(1–2), 236–240,  DOI:10.1002/(SICI)1521-3773(19990115)38:1/2<236::AID-ANIE236>3.0.CO;2-M.
37. D. Dudola, B. Kovács and Z. Gáspári, CoNSEnsX⁺ Webserver for the Analysis of Protein Structural Ensembles Reflecting Experimentally Determined Internal Dynamics, J. Chem. Inf. Model., 2017, 57(8), 1728–1734,  DOI:10.1021/acs.jcim.7b00066.
38. A. D. Bochevarov, E. Harder, T. F. Hughes, J. R. Greenwood, D. A. Braden, D. M. Philipp, D. Rinaldo, M. D. Halls, J. Zhang and R. A. Friesner, Jaguar: A High-Performance Quantum Chemistry Software Program with Strengths in Life and Materials Sciences, Int. J. Quantum Chem., 2013, 113(18), 2110–2142,  DOI:10.1002/qua.24481.
39. Schrödinger Release 2019-2: Jaguar, Schrödinger LLC, New York, NY, 2019.
40. E. Harder, W. Damm, J. Maple, C. Wu, M. Reboul, J. Y. Xiang, L. Wang, D. Lupyan, M. K. Dahlgren, J. L. Knight, J. W. Kaus, D. S. Cerutti, G. Krilov, W. L. Jorgensen, R. Abel and R. A. Friesner, OPLS3: A Force Field Providing Broad Coverage of Drug-like Small Molecules and Proteins, J. Chem. Theory Comput., 2016, 12(1), 281–296,  DOI:10.1021/acs.jctc.5b00864.
41. J. C. Hunter, A. Manandhar, M. A. Carrasco, D. Gurbani, S. Gondi and K. D. Westover, Biochemical and Structural Analysis of Common Cancer-Associated KRAS Mutations, Mol. Cancer Res., 2015, 13(9), 1325–1335,  DOI:10.1158/1541-7786.MCR-15-0203.
42. Y. Ito, K. Yamasaki, J. Iwahara, T. Terada, A. Kamiya, M. Shirouzu, Y. Muto, G. Kawai, S. Yokoyama, E. D. Laue, M. Wälchli, T. Shibata, S. Nishimura and T. Miyazawa, Regional Polysterism in the GTP-Bound Form of the Human c-Ha-Ras Protein, Biochemistry, 1997, 36(30), 9109–9119,  DOI:10.1021/bi970296u.
43. M. J. Smith, B. G. Neel and M. Ikura, NMR-Based Functional Profiling of RASopathies and Oncogenic RAS Mutations, Proc. Natl. Acad. Sci. U. S. A., 2013, 110(12), 4574–4579,  DOI:10.1073/pnas.1218173110.
44. A. K. Sharma, S. J. Lee, A. C. Rigby and S. A. Townson, NMR ¹H,¹³C, ¹⁵N backbone and ¹³C side chain resonance assignment of the G12C mutant of human K-Ras bound to GDP, Biomol. NMR Assignments, 2018, 12(2), 269–272,  DOI:10.1007/s12104-018-9821-8.
45. H. Sondermann, S. M. Soisson, S. Boykevisch, S.-S. Yang, D. Bar-Sagi and J. Kuriyan, Structural analysis of autoinhibition in the Ras activator Son of sevenless, Cell, 2004, 119(3), 393–405,  DOI:10.1016/j.cell.2004.10.005.
46. S. Dharmaiah, T. H. Tran, S. Messing, C. Agamasu, W. K. Gillette, W. Yan, T. Waybright, P. Alexander, D. Esposito, D. V. Nissley, F. McCormick, A. G. Stephen and D. K. Simanshu, Structures of N-terminally processed KRAS provide insight into the role of N-acetylation, Sci. Rep., 2019, 9(1), 10512,  DOI:10.1038/s41598-019-46846-w.
47. A. K. Sharma, S.-J. Lee, M. Zhou, A. C. Rigby and S. A. Townson, NMR ¹H, ¹³C, ¹⁵N Resonance Assignment of the G12C Mutant of Human K-Ras Bound to GppNHp, Biomol. NMR Assignments, 2019, 13(1), 227–231,  DOI:10.1007/s12104-019-09882-1.
48. H. R. Kalbitzer, M. Spoerner, P. Ganser, C. Hozsa and W. Kremer, Fundamental Link between Folding States and Functional States of Proteins, J. Am. Chem. Soc., 2009, 131(46), 16714–16719,  DOI:10.1021/ja904314q.
49. A. Sayyed-Ahmad, P. Prakash and A. A. Gorfe, Distinct dynamics and interaction patterns in H- and K-Ras oncogenic P-loop mutants, Proteins, 2017, 85(9), 1618–1632,  DOI:10.1002/prot.25317.
50. J. A. Parker, A. Y. Volmar, S. Pavlopoulos and C. Mattos, K-Ras Populates Conformational States Differently from Its Isoform H-Ras and Oncogenic Mutant K-RasG12D, Structure, 2018, 26(6), 810–820.e4,  DOI:10.1016/j.str.2018.03.018.
51. J. A. Marsh, V. K. Singh, Z. Jia and J. D. Forman-Kay, Sensitivity of Secondary Structure Propensities to Sequence Differences between α- and γ-Synuclein: Implications for Fibrillation, Protein Sci., 2006, 15(12), 2795–2804,  DOI:10.1110/ps.062465306.
52. S. Muratcioglu, T. S. Chavan, B. C. Freed, H. Jang, L. Khavrutskii, R. N. Freed, M. A. Dyba, K. Stefanisko, S. G. Tarasov, A. Gursoy, O. Keskin, N. I. Tarasova, V. Gaponenko and R. Nussinov, GTP-Dependent K-Ras Dimerization, Structure, 2015, 23(7), 1325–1335,  DOI:10.1016/j.str.2015.04.019.
53. M. R. Mehaffey, C. L. Schardon, E. T. Novelli, M. B. Cammarata, L. J. Webb, W. Fast and J. S. Brodbelt, Investigation of GTP-dependent dimerization of G12X K-Ras variants using ultraviolet photodissociation mass spectrometry, Chem. Sci., 2019, 10(34), 8025–8034,  10.1039/c9sc01032g.
54. M. P. Williamson, Using chemical shift perturbation to characterise ligand binding, Prog. Nucl. Magn. Reson. Spectrosc., 2013, 73, 1–16,  DOI:10.1016/j.pnmrs.2013.02.001.
55. B. J. Grant, A. A. Gorfe and J. A. McCammon, Ras Conformational Switching: Simulating Nucleotide-Dependent Conformational Transitions with Accelerated Molecular Dynamics, PLoS Comput. Biol., 2009, 5(3), e1000325,  DOI:10.1371/journal.pcbi.1000325.
56. C. O'Connor and E. L. Kovrigin, Global Conformational Dynamics in Ras, Biochemistry, 2008, 47(39), 10244–10246,  DOI:10.1021/bi801076c.
57. J. S. Fraser, H. Van Den Bedem, A. J. Samelson, P. T. Lang, J. M. Holton, N. Echols and T. Alber, Accessing Protein Conformational Ensembles Using Room-Temperature X-Ray Crystallography, Proc. Natl. Acad. Sci. U. S. A., 2011, 108(39), 16247–16252,  DOI:10.1073/pnas.1111325108.
58. A. J. Scheidig, C. Burmester and R. S. Goody, The Pre-Hydrolysis State of P21(Ras) in Complex with GTP: New Insights into the Role of Water Molecules in the GTP Hydrolysis Reaction of Ras-like Proteins, Structure, 1999, 7(11), 1311–1324,  DOI:10.1016/S0969-2126(00)80021-0.
59. K. Scheffzek, M. R. Ahmadian, W. Kabsch, L. Wiesmüller, A. Lautwein, F. Schmitz and A. Wittinghofer, The Ras-RasGAP Complex: Structural Basis for GTPase Activation and Its Loss in Oncogenic Ras Mutants, Science, 1997, 277(5324), 333–338,  DOI:10.1126/science.277.5324.333.
60. Y. Li, Y. Zhang, F. Großerüschkamp, S. Stephan, Q. Cui, C. Kötting, F. Xia and K. Gerwert, Specific Substates of Ras To Interact with GAPs and Effectors: Revealed by Theoretical Simulations and FTIR Experiments, J. Phys. Chem. Lett., 2018, 9(6), 1312–1317,  DOI:10.1021/acs.jpclett.8b00342.
61. S. Xu, B. N. Long, G. H. Boris, A. Chen, S. Ni and M. A. Kennedy, Structural Insight into the Rearrangement of the Switch i Region in GTP-Bound G12A K-Ras, Acta Crystallogr., Sect. D: Struct. Biol., 2017, 73(12), 970–984,  DOI:10.1107/S2059798317015418.
62. M. E. Welsch, M. E. Welsch, A. Kaplan, J. M. Chambers, M. E. Stokes, P. H. Bos, A. Zask, Y. Zhang, M. Sanchez-Martin, M. A. Badgley, C. S. Huang, T. H. Tran, H. Akkiraju, L. M. Brown, R. Nandakumar, S. Cremers, W. S. Yang, L. Tong, K. P. Olive, A. Ferrando and B. R. Stockwell, Multivalent Small-Molecule Pan-RAS Inhibitors, Cell, 2017, 168(5), 878–889.e29,  DOI:10.1016/j.cell.2017.02.006.
63. S. Xu, B. N. Long, G. H. Boris, A. Chen, S. Ni and M. A. Kennedy, Structural insight into the rearrangement of the switch I region in GTP-bound G12A K-Ras, Acta Crystallogr., Sect. D: Struct. Biol., 2017, 73(Pt 12), 970–984,  DOI:10.1107/S2059798317015418.
64. G. Buhrman, G. Wink and C. Mattos, Transformation Efficiency of RasQ61 Mutants Linked to Structural Features of the Switch Regions in the Presence of Raf, Structure, 2007, 15(12), 1618–1629,  DOI:10.1016/j.str.2007.10.011.
65. S. Matsumoto, N. Miyano, S. Baba, J. Liao, T. Kawamura, C. Tsuda, A. Takeda, M. Yamamoto, T. Kumasaka, T. Kataoka and F. Shima, Molecular Mechanism for Conformational Dynamics of Ras-GTP Elucidated from In-Situ Structural Transition in Crystal, Sci. Rep., 2016, 6(1), 1–12,  DOI:10.1038/srep25931.
66. S. Lu, H. Jang, R. Nussinov and J. Zhang, The Structural Basis of Oncogenic Mutations G12, G13 and Q61 in Small GTPase K-Ras4B, Sci. Rep., 2016, 6, 1–15,  DOI:10.1038/srep21949.
67. D. Filchtinski, O. Sharabi, A. Rüppel, I. R. Vetter, C. Herrmann and J. M. Shifman, What Makes Ras an Efficient Molecular Switch: A Computational, Biophysical, and Structural Study of Ras-GDP Interactions with Mutants of Raf, J. Mol. Biol., 2010, 399(3), 422–435,  DOI:10.1016/j.jmb.2010.03.046.
68. M. Chakrabarti, H. Jang and R. Nussinov, Comparison of the Conformations of KRAS Isoforms, K-Ras4A and K-Ras4B, Points to Similarities and Significant Differences, J. Phys. Chem. B, 2016, 120(4), 667–679,  DOI:10.1021/acs.jpcb.5b11110.
69. B. L. Grigorenko, A. V. Nenumkhin, M. S. Shadrina, I. A. Topol and S. K. Burt, Mechanisms of Guanosine Triphosphate Hydrolysis by Ras and Ras-GAP Proteins as Rationalized by Ab Initio QM/MM Simulations, Proteins: Struct., Funct., Genet., 2007, 66(2), 456–466,  DOI:10.1002/prot.21228.
70. A. Shurki and A. Warshel, Why Does the Ras Switch “Break” by Oncogenic Mutations?, Proteins: Struct., Funct., Genet., 2004, 55(1), 1–10,  DOI:10.1002/prot.20004.
71. S. C. L. Kamerlin, P. K. Sharma, R. B. Prasad and A. Warshel, Why Nature Really Chose Phosphate, Q. Rev. Biophys., 2013, 46(1), 1–132,  DOI:10.1017/S0033583512000157.
72. T. Schweins, M. Geyer, K. Scheffzek, A. Warshel, H. R. Kalbitzer and A. Wittinghofer, Substrate-Assisted Catalysis as a Mechanism for Gtp Hydrolysis of P21ras and Other GTP-Binding Proteins, Nat. Struct. Biol., 1995, 2(1), 36–44,  DOI:10.1038/nsb0195-36.
73. M. Wey, J. Lee, S. S. Jeong, J. Kim and J. Heo, Kinetic Mechanisms of Mutation-Dependent Harvey Ras Activation and Their Relevance for the Development of Costello Syndrome, Biochemistry, 2013, 52(47), 8465–8479,  DOI:10.1021/bi400679q.
74. S. K. Fetics, H. Guterres, B. M. Kearney, G. Buhrman, B. Ma, R. Nussinov and C. Mattos, Allosteric Effects of the Oncogenic Rasq61l Mutant on Raf-RBD, Structure, 2015, 23(3), 505–516,  DOI:10.1016/j.str.2014.12.017.
75. G. Buhrman, C. O'Connor, B. Zerbe, B. M. Kearney, R. Napoleon, E. A. Kovrigina, S. Vajda, D. Kozakov, E. L. Kovrigin and C. Mattos, Analysis of Binding Site Hot Spots on the Surface of Ras GTPase, J. Mol. Biol., 2011, 413(4), 773–789,  DOI:10.1016/j.jmb.2011.09.011.
76. D. Kozakov, L. E. Grove, D. R. Hall, T. Bohnuud, S. E. Mottarella, L. Luo, B. Xia, D. Beglov and S. Vajda, The FTMap Family of Web Servers for Determining and Characterizing Ligand-Binding Hot Spots of Proteins, Nat. Protoc., 2015, 10(5), 733–755,  DOI:10.1038/nprot.2015.043.
77. T. Maurer, L. S. Garrenton, A. Oh, K. Pitts, D. J. Anderson, N. J. Skelton, B. P. Fauber, B. Pan, S. Malek, D. Stokoe, M. J. C. Ludlam, K. K. Bowman, J. Wu, A. M. Giannetti, M. A. Starovasnik, I. Mellman, P. K. Jackson, J. Rudolph, W. Wang and G. Fang, Small-Molecule Ligands Bind to a Distinct Pocket in Ras and Inhibit SOS-Mediated Nucleotide Exchange Activity, Proc. Natl. Acad. Sci. U. S. A., 2012, 109(14), 5299–5304,  DOI:10.1073/pnas.1116510109.
78. M. J. McCarthy, C. V. Pagba, P. Prakash, A. K. Naji, D. van der Hoeven, H. Liang, A. K. Gupta, Y. Zhou, K.-J. Cho, J. F. Hancock and A. A. Gofre, Discovery of High-Affinity Noncovalent Allosteric KRAS Inhibitors That Disrupt Effector Binding, ACS Omega, 2019, 4(2), 2921–2930,  DOI:10.1021/acsomega.8b03308.
79. M. P. Patricelli, M. R. Janes, L.-S. Li, R. Hansen, U. Peters, L. V. Kessler, Y. Chen, J. M. Kucharski, J. Feng, T. Ely, J. H. Chen, S. J. Firdaus, A. Babbar, P. Ren and Y. Liu, Selective Inhibition of Oncogenic KRAS Output with Small Molecules Targeting the Inactive State, Cancer Discovery, 2016, 6(3), 316–329,  DOI:10.1158/2159-8290.CD-15-1105.
80. M. Klähn, E. Rosta and A. Warshel, On the Mechanism of Hydrolysis of Phosphate Monoesters Dianions in Solutions and Proteins, J. Am. Chem. Soc., 2006, 128(47), 15310–15323,  DOI:10.1021/ja065470t.
81. Y. Kano, T. Gebregiworgis, C. B. Marshall, N. Radulovich, B. P. K. Poon, J. St-Germain, J. D. Cook, I. Valencia-Sama, B. M. M. Grant, S. G. Herrera, J. Miao, B. Raught, M. S. Irwin, J. E. Lee, J. J. Yeh, Z. Y. Zhang, M. S. Tsao, M. Ikura and M. Ohh, Tyrosyl Phosphorylation of KRAS Stalls GTPase Cycle via Alteration of Switch I and II Conformation, Nat. Commun., 2019, 10(1), 224,  DOI:10.1038/s41467-018-08115-8.
82. S. Mainardi, A. Mulero-Sánchez, A. Prahallad, G. Germano, A. Bosma, P. Krimpenfort, C. Lieftink, J. D. Steinberg, N. De Wit, S. Gonçalves-Ribeiro, E. Nadal, A. Bardelli, A. Villanueva and R. Bernards, SHP2 Is Required for Growth of KRAS-Mutant Non-Small-Cell Lung Cancer in Vivo Letter, Nat. Med., 2018, 24(7), 961–967,  DOI:10.1038/s41591-018-0023-9.
83. D. A. Ruess, G. J. Heynen, K. J. Ciecielski, J. Ai, A. Berninger, D. Kabacaoglu, K. Görgülü, Z. Dantes, S. M. Wörmann, K. N. Diakopoulos, A. F. Karpathaki, M. Kowalska, E. Kaya-Aksoy, L. Song, E. A. Z. Van Der Laan, M. P. López-Alberca, M. Nazaré, M. Reichert, D. Saur, M. M. Erkan, U. T. Hopt, B. Sainz, W. Birchmeier, R. M. Schmid, M. Lesina and H. Algül, Mutant KRAS-Driven Cancers Depend on PTPN11/SHP2 Phosphatase, Nat. Med., 2018, 24(7), 954–960,  DOI:10.1038/s41591-018-0024-8.
84. G. S. Wong, J. Zhou, J. B. Liu, Z. Wu, X. Xu, T. Li, D. Xu, S. E. Schumacher, J. Puschhof, J. McFarland, C. Zou, A. Dulak, L. Henderson, P. Xu, E. O'Day, R. Rendak, W. L. Liao, F. Cecchi, T. Hembrough, S. Schwartz, C. Szeto, A. K. Rustgi, K. K. Wong, J. A. Diehl, K. Jensen, F. Graziano, A. Ruzzo, S. Fereshetian, P. Mertins, S. A. Carr, R. Beroukhim, K. Nakamura, E. Oki, M. Watanabe, H. Baba, Y. Imamura, D. Catenacci and A. J. Bass, Targeting Wild-Type KRAS-Amplified Gastroesophageal Cancer through Combined MEK and SHP2 Inhibition, Nat. Med., 2018, 24(7), 968–977,  DOI:10.1038/s41591-018-0022-x.
85. C. Fedele, H. Ran, B. Diskin, W. Wei, J. Jen, M. J. Geer, K. Araki, U. Ozerdem, D. M. Simeone, G. Miller, B. G. Neel and K. H. Tang, Shp2 Inhibition Prevents Adaptive Resistance to Mek Inhibitors in Multiple Cancer Models, Cancer Discovery, 2018, 8(10), 1237–1249,  DOI:10.1158/2159-8290.CD-18-0444.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc03441j

---