Open Access Article
Open Access ArticleEngineering micromechanics of soft porous crystals for negative gas adsorption†
Simon
Krause
 *ab,
Jack D.
Evans
*ab,
Jack D.
Evans
 *a,
Volodymyr
Bon
*a,
Volodymyr
Bon
 a,
Irena
Senkovska
a,
Sebastian
Ehrling
a,
Irena
Senkovska
a,
Sebastian
Ehrling
 a,
Paul
Iacomi
a,
Paul
Iacomi
 ce,
Daniel M.
Többens
d,
Dirk
Wallacher
ce,
Daniel M.
Többens
d,
Dirk
Wallacher
 d,
Manfred S.
Weiss
d,
Manfred S.
Weiss
 d,
Bin
Zheng
d,
Bin
Zheng
 ef,
Pascal G.
Yot
ef,
Pascal G.
Yot
 e,
Guillaume
Maurin
e,
Guillaume
Maurin
 e,
Philip L.
Llewellyn
e,
Philip L.
Llewellyn
 c,
François-Xavier
Coudert
c,
François-Xavier
Coudert
 g and
Stefan
Kaskel
g and
Stefan
Kaskel
 *a
*a
aFaculty of Chemistry and Food Chemistry, TU Dresden, Bergstrasse 66, 01069, Dresden, Germany. E-mail: jack.evans@tu-dresden.de; Stefan.kaskel@tu-dresden.de
bCentre for Systems Chemistry, Stratingh Institute for Chemistry, University of Groningen, Nijenborgh 4, 9747 AG Groningen, The Netherlands. E-mail: simon.krause@rug.nl
cAix-Marseille Univ., CNRS, MADIREL (UMR 7246), 13013, Marseille, France
dHelmholtz-Zentrum Berlin für Materialien und Energie, Hahn-Meitner-Platz 1, 14109, Berlin, Germany
eICGM, Univ. Montpellier, CNRS, ENSCM, Montpellier, France
fSchool of Materials Science and Engineering, Xi'an University of Science and Technology, Xi'an 710054, PR China
gChimie ParisTech, PSL University, CNRS, Institut de Recherche de Chimie Paris, 75005, Paris, France
First published on 24th August 2020
Abstract
Framework materials at the molecular level, such as metal–organic frameworks (MOF), were recently found to exhibit exotic and counterintuitive micromechanical properties. Stimulated by host–guest interactions, these so-called soft porous crystals can display counterintuitive adsorption phenomena such as negative gas adsorption (NGA). NGA materials are bistable frameworks where the occurrence of a metastable overloaded state leads to pressure amplification upon a sudden framework contraction. How can we control activation barriers and energetics via functionalization of the molecular building blocks that dictate the frameworks' mechanical response? In this work we tune the elastic and inelastic properties of building blocks at the molecular level and analyze the mechanical response of the resulting frameworks. From a set of 11 frameworks, we demonstrate that widening of the backbone increases stiffness, while elongation of the building blocks results in a decrease in critical yield stress of buckling. We further functionalize the backbone by incorporation of sp3 hybridized carbon atoms to soften the molecular building blocks, or stiffen them with sp2 and sp carbons. Computational modeling shows how these modifications of the building blocks tune the activation barriers within the energy landscape of the guest-free bistable frameworks. Only frameworks with free energy barriers in the range of 800 to 1100 kJ mol−1 per unit cell, and moderate yield stress of 0.6 to 1.2 nN for single ligand buckling, exhibit adsorption-induced contraction and negative gas adsorption. Advanced experimental in situ methodologies give detailed insights into the structural transitions and the adsorption behavior. The new framework DUT-160 shows the highest magnitude of NGA ever observed for nitrogen adsorption at 77 K. Our computational and experimental analysis of the energetics and mechanical response functions of porous frameworks is an important step towards tuning activation barriers in dynamic framework materials and provides critical design principles for molecular building blocks leading to pressure amplifying materials.
Introduction
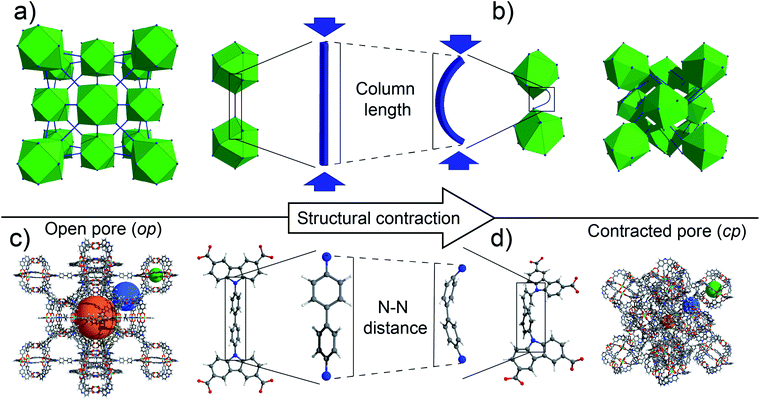
Designer materials on the macro and nanoscale have taken the spotlight in recent years with fantastical properties approaching those described in science fiction. Macro- and microscopic mechanical metamaterials have captured the imagination of many researchers with many demonstrating unnatural properties, such as negative effective bulk modulus1 and negative effective mass density.2 This has poised their utilization in seemingly absurd applications, including unfeelability cloaks.3 Mechanical metamaterials derive their interesting properties primarily from specific framework architectures and topologies combined with the mechanical properties of the construction materials such as polymers, ceramics or metals fabricated into struts and nodes on the length scale of millimetres to sub-micrometres.4 In comparison, the construction of ordered 3D frameworks by self-assembly of molecular building blocks represents a straightforward bottom-up methodology for building framework architectures at the nanoscale (in the range of 0.5 to 5 nm).5 As such, metal–organic frameworks (MOFs) or covalent organic frameworks (COFs) can be understood as molecular analogues to macroscopic framework materials. Interestingly, many of these crystalline frameworks demonstrate unusual mechanical properties6 including negative Poisson's ratio7 or negative linear compressibility8 and are thus considered nanoscopic mechanical metamaterials.6 Notably, the molecular-scale architecture of these “meta-MOFs” routinely produces responses difficult to engineer on the macroscale, such as negative thermal expansion (NTE)9–11 and other optical phenomena.12,13 While most of these properties are based on elastic deformations of the crystal lattice, several MOFs are known to undergo large scale inelastic transitions under preservation of the framework connectivity. These so-called soft porous crystals (SPCs)14 or flexible MOFs15 exhibit strong deformation of the lattice in particular upon adsorption or desorption of guest species.16 Such guest-induced transitions are specific to nanoscopic metamaterials, as they rely on enhanced host–guest interactions due to confinement at the molecular scale. As a consequence, SPCs can exhibit exotic adsorption properties with application in the area of gas storage, separation and sensing.17–26 Despite extensive knowledge about the mechanical properties of polymers and metals typically used in the construction of macroscopic metamaterials and the advancing understanding of the mechanical properties of nanoscopic materials such as poly(ethylene glycol),27 DNA,28 or carbon nanotubes,29 little is known regarding the mechanical behaviour of individual small molecules and their influence on the elastic and inelastic response of molecular crystalline frameworks.30,31In 2016, we discovered the counterintuitive adsorption phenomenon termed negative gas adsorption (NGA) in the flexible MOF named DUT-49 (Dresden University of Technology No. 49).32 NGA occurs during the course of guest adsorption with increasing gas pressure when a metastable overloaded state suddenly collapses by cooperative adsorption-induced buckling of molecular struts throughout the framework, resulting in framework contraction.33 In the process of this pore contraction, gas adsorbed in the overloaded metastable state is expelled from the solid, resulting in the counterintuitive release of gas with increasing pressure upon adsorption. Computational analysis showed that this behaviour can in principle be observed for other porous materials if their mechanical properties allow for bistability.34 We subsequently investigated molecular changes to the DUT-49 structure in an effort to tune or change the inelastic mechanical response involved in this phenomenon. Motivated by the macroscopic understanding of columnar buckling, in recent studies we considered shortening35 and elongation of the molecular struts.36 We demonstrated by density functional theory (DFT) calculations and experimental investigations that the characteristic yield stress could be tuned, leading to three frameworks with rigid characteristics in the gas physisorption experiments and a new framework, DUT-50, that also exhibits NGA.36 However, all these materials are based on 1,4-phenylene backbones which are buckled in the process of structural compression (Fig. 1).
In NGA materials such as DUT-49 and DUT-50, the linker plays the key role of a molecular hinge enabling the dynamic framework transformation. It is therefore essential, for a rational design of novel NGA materials, to balance the linkers micromechanics as being stiff enough to stabilize the op structure of the guest-free and metastable overloaded state, but also soft enough to allow for the guest-induced contraction.
In order to identify linker backbones providing the ideal mechanical properties for NGA, we apply in the present study a combined computational and experimental approach to probe the elastic and inelastic properties of a series of molecular building units with different chemical bond-motifs typical for molecular frameworks. We link the single molecule buckling behaviour to the mechanical properties of a series of 10 isoreticular metal–organic frameworks. Both their mechanical and adsorption-induced inelastic structural transitions are unravelled by advanced in situ characterization, and their structural behaviour is rationalized using computational methods. Based on these results we quantify the essential micromechanical features of the molecular building blocks leading to new NGA frameworks, of which three are presented in this work.
Results
Computational analysis of mechanical properties of different ligand motives
To investigate the effect of various chemical bonding-motifs on the elastic properties, independent of the framework topology, we selected the framework type of DUT-49.37 The DUT-49 network is constructed by the linkage of tetra-connective carbazole-based ligands (L49) to a copper paddle wheel to result in a framework with composition Cu2(L49) and fcu topology.37 When exposed to hydrostatic pressure via a pressure transmitting medium such as mercury, which is unable to penetrate the pores in the operating range of pressure, the open pore form of DUT-49 (op) exhibits volumetric compression by over 50% in a contracted pore (cp) state and beyond.35 A guest-induced response is observed when DUT-49 is exposed to various gases, close to their respective standard boiling points.38 In this case, the adsorption stress of the confined adsorbate imposes an internal contractive pressure which also leads to an inelastic contraction of the framework.32,39,40 In contrast to hydrostatic compression, this transition was found to be fully repeatable and can be followed via in situ diffraction and spectroscopic methods.32,36 Experimental observations were combined with computational modelling to establish the molecular mechanism of this unusual structural contraction. The linear ligand-backbone (Fig. 1b) is observed to undergo buckling upon contraction of the framework. Recently, we have demonstrated that the length of this phenylene-based building unit in L49 dictates the inelastic response of the framework.36 This behaviour can be rationalized by Euler's formula of critical load (1), Pcrit, commonly applied in the characterisation of macroscopic columns,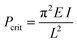 | (1) |
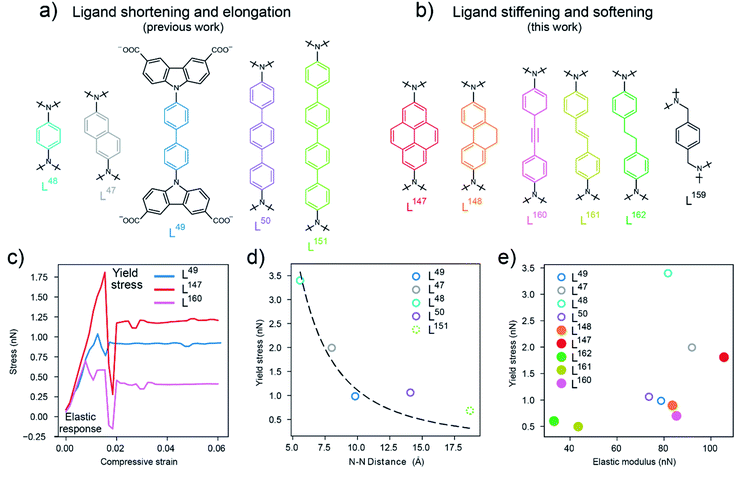 | ||
| Fig. 2 (a) Biscarbazol ligand subunits used in previously reported DUT-49-type frameworks,36 (b) biscarbazol ligand subunits that are novel in this work. (c) Stress–strain profiles for the ligands in DUT-49 (L49), DUT-147 (L147) and DUT-160 (L160) with the elastic response region and yield stress labelled, (d) correlation of the yield stress (calculated by DFT) and ligand length illustrated by the N–N distance in the ligand backbone. Dashed line represents a fit of eqn (1) with varying length, (e) comparison of the yield stress and elastic modulus of the ligands investigated in this study (filled symbols) and previously reported ligands36 (open symbols), L159 not included. | ||
Based on these observations we were interested in how the mechanical response of DUT-49-type frameworks can be rationally tuned by changing the elastic properties of the ligand backbone via chemical functionalization. Intuitively, to increase stiffness and Pcrit in a macroscopic column one would increase its thickness or use a stiffer material, but how can these properties be manipulated on the molecular level? We deliberately chose to follow two approaches. First, by enhancing the ligand “thickness” by increasing the area of sp2 conjugated backbone and introduction of alkane side groups which is expected to enhance stiffness. Second, by breaking the sp2 conjugation and introducing sp3 hybridised carbon atoms to increase softness. To investigate these effects of chemical functionalisation we introduced a para-substituted 9,10-dihydrophenanthrene-derived (L148) and pyrene-derived (L147) backbone which is expected to rigidify the central C–C bond in the backbone of the biphenylene-based ligand L49 in DUT-49. Additionally, to analyse the impact of hybridization of the carbon atoms in the ligand backbone, we introduced alkyne (L160), alkene (L161) and alkane (L162, L159) functionalities (Fig. 2b). While L147 and L148 exhibit the same length as L49, the other ligands are comparable in length to L50. DFT calculations were employed to study the application of axial strain on these ligands, generating characteristic stress–strain profiles. These simulations indicate the elastic modulus (or stiffness), within the elastic regime, and the yield stress related to the non-elastic buckling behaviour of the ligands (Fig. 2c). As expected, and shown in Fig. 2e, in the series of biphenylene-derived ligands, L147 exhibits the highest elastic modulus of 110 nN originating from the rigidified backbone. L148 only shows a slight increase in elasticity over L49 with an elastic modulus around 80 nN demonstrating the structural similarity and flexibility of the sidechain. In the series of different hybridisation L160 (with 84 nN) exhibits a twofold increase in elasticity compared to L161; and L162 without full conjugation in the backbone shows the lowest elastic modulus, in the range of 30 nN. Interestingly, the yield stress of functionalized ligands is found to be in a rather small range of 0.5 to 2 nN compared to the series of elongated ligands, with phenylene-based backbone, which spans from 0.8 to 3.5 nN. Consequently, the functionalisation of the ligand backbone allows to rationally tune the elastic properties with comparable yield stress (horizontal trend in Fig. 2e) while elongation of a phenylene-based ligand allows to manipulate the yield stress independent of the elastic properties (vertical trend in Fig. 2e). This analysis demonstrates how the elastic and inelastic properties of molecular building blocks can be manipulated by both elongation and chemical exchange of the backbone constituents leading to stiffening and softening. Notably, the loss of linearity and sp2 hybridization in the backbone has the biggest influence on both elasticity and yield stress producing an extremely soft molecular unit to an extent where the ligand no longer exhibits a linear conformation, as in L159 (ESI Fig. 20†).
Synthesis and characterisation of metal–organic frameworks
To link the elastic and inelastic behaviour of the molecular ligands to the mechanical properties of the corresponding frameworks, the proposed ligands and their corresponding Cu(II)-based MOFs (DUT-147, DUT-148, DUT-159, DUT-160, DUT-161, DUT-162) were synthesized based on procedures previously described for DUT-49 and elongated derivatives.36 With the exception of DUT-159 all frameworks are found to crystallize in cubic symmetry with the fcu topology expected for DUT-49-type structures.37 The ligand backbones are found to be disordered over two (in case of DUT-147 and DUT-160) and four (DUT-148, DUT-161 and DUT-162) positions consistent with the symmetry of Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group. Interestingly, while introduction of two CH2 groups in the backbone of L162 results in the formation of a framework with fcu topology and linear backbone, the introduction of two CH2 groups adjacent to the carbazole nitrogen in L159 distorts the linear conformation and results in the formation of a drastically different structure. The substituted carbazole-3,6-dicarboxylate units in DUT-159 no longer form cuboctahedral cages as in DUT-49 but 2D kagome-type sheets that are pillared by the 1,4-bismethylenebenzene backbones in L159. DUT-159 thus represents a 3D framework based on kagome lattices previously reported in DUT-158 (composition Cu(cdc), cdc = 9H-carbazole 3,6-dicarboxylate)41 (ESI Fig. 20†). This demonstrates that the incorporation of sp3-hybridized carbon atoms in the spacing unit not only softens the ligand backbone but also affects the formation of highly symmetrical supermolecular building blocks.
m space group. Interestingly, while introduction of two CH2 groups in the backbone of L162 results in the formation of a framework with fcu topology and linear backbone, the introduction of two CH2 groups adjacent to the carbazole nitrogen in L159 distorts the linear conformation and results in the formation of a drastically different structure. The substituted carbazole-3,6-dicarboxylate units in DUT-159 no longer form cuboctahedral cages as in DUT-49 but 2D kagome-type sheets that are pillared by the 1,4-bismethylenebenzene backbones in L159. DUT-159 thus represents a 3D framework based on kagome lattices previously reported in DUT-158 (composition Cu(cdc), cdc = 9H-carbazole 3,6-dicarboxylate)41 (ESI Fig. 20†). This demonstrates that the incorporation of sp3-hybridized carbon atoms in the spacing unit not only softens the ligand backbone but also affects the formation of highly symmetrical supermolecular building blocks.
Crystal size and shape are important parameters to control as they significantly impact adsorption-induced structural transitions in flexible MOFs in general,42–45 and DUT-49 in particular.39 A representative size distribution obtained via scanning electron microscopy is shown in ESI Fig. 9–14.† Crystal morphologies range from cubic to cuboctahedral with mean sizes in the range of 4–7 μm, similar to those previously chosen to analyse NGA in DUT-49 and DUT-50 samples.36 Bulk powders of the MOFs were further characterized by powder X-ray diffraction (ESI Fig. 3–8†), elemental analysis (ESI Table 3†), and thermogravimetric analysis (ESI Fig. 2†).
To characterize the mechanical properties independently of the guest species, MOF samples were desolvated by applying a supercritical activation protocol previously used on DUT-49 and related materials.36 With the exception of DUT-159, all other materials show preservation of the op structure upon solvent removal investigated by PXRD (ESI Fig. 3–8†). DUT-159 was found to lose long-range structural ordering upon removal of the solvent from the pores indicating that the previously discussed soft nature of the ligand is transferred to the framework, which in this case seems to be stabilized by the presence of solvent in the pore space. The lack of crystallinity does not allow further characterization in the context of this work and DUT-159 is thus not further considered in the following discussion. In the remaining series of five new DUT-49-type structures, the experimentally observed ligand lengths of the respective op phases obtained by MD simulations correspond well to the values derived from DFT simulations of the free single ligand molecules (Table 1).
| Material | Ligand N⋯N spacing op (Å) (exp) | Ligand N⋯N spacing op (Å) (sim) | Ligand N⋯N spacing cp (Å) (exp) | Ligand N⋯N spacing cp (Å) (sim) | Unit cell volume (Å3) op (exp) | Unit cell volume (Å3) op (sim) | Unit cell volume (Å3) cp (exp) | Unit cell Volume (Å3) cp (sim) | Contraction (%) (exp) | Contraction (%) (sim) |
|---|---|---|---|---|---|---|---|---|---|---|
| DUT-49 | 9.945(4) | 9.92 | 9.630(2) | 9.31 | 101![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 117(19) 117(19) |
97![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 153 153 |
47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 281(5) 281(5) |
46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 287 287 |
53 | 52 |
| DUT-147 | 9.868(5) | 9.85 | 9.535(3) | 9.34 | 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 221(35) 221(35) |
99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 781 781 |
48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 998(7) 998(7) |
48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
51 | 52 |
| DUT-148 | 9.907(4) | 9.91 | 9.720(2) | 9.14 | 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 804(35) 804(35) |
99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 806 806 |
47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 979(8) 979(8) |
48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 971 971 |
52 | 51 |
| DUT-160 | 12.438(4) | 12.4 | 11.455(4) | 11.6 | 125![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 827(44) 827(44) |
125![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 669 669 |
51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 186(10) 186(10) |
59![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 127 127 |
59 | 53 |
| DUT-161 | 12.215(4) | 12.3 | 11.105(4) | 11.1 | 123![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 209(43) 209(43) |
119![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 947 947 |
45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 898(8) 898(8) |
53![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 082 082 |
63 | 56 |
| DUT-162 | 12.128(6) | 12.2 | n.a. | 9.82 | 121![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 950(42) 950(42) |
122![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 682 682 |
n.a. | 48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 339 339 |
n.a. | 61 |
| DUT-50 | 14.273(7) | 14.4 | 13.593(3) | 13.2 | 145![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 781(51) 781(51) |
141![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 092 092 |
58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 062(4) 062(4) |
58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 557 557 |
60 | 58 |
Computational and experimental analysis of mechanical properties of metal–organic frameworks
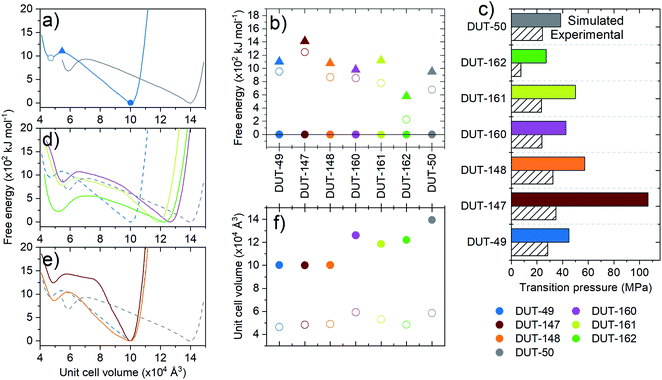
To explore the dynamics of the framework materials, we performed classical molecular dynamics (MD) simulations similar to our previous studies on DUT-49.35,36 The simulations employed established forcefields,46 not specially produced or optimized for the systems at hand, which qualitatively reproduce the lattice parameters observed experimentally (Table 1). We computed a series of pressure–volume curves at 300 K, which represent the response of the framework under increasing hydrostatic compression, using previously reported protocols.35 The pressure–volume curves thus give access to the underlying free energy surface of the frameworks with respect to volume. All materials presented in this work demonstrate a bistable nature with a local minimum, ΔFcp, at reduced unit cell volume and estimated activation barriers, ΔF‡ (op → cp), in the range of DUT-49 (ΔF‡ = 1000 kJ moluc−1 (uc = unit cell), ΔFcp = 950 kJ moluc−1) with the exception of DUT-162 (ΔF‡ = 580 kJ mol−1, ΔFcp = 220 kJ moluc−1) and DUT-147 (ΔF‡ = 1420 kJ moluc−1, ΔFcp = 1240 kJ moluc−1, Fig. 3).This analysis demonstrates structural bistability, as in each case a second minimum is identified with significantly reduced unit cell and pore volume. This is a key prerequisite for NGA materials, but it also requires the presence of sufficiently large activation barriers promoting the metastable overloaded state. In order to experimentally probe the mechanical response and bistability of these MOFs, compression via mercury intrusion was performed on desolvated crystalline MOF powders of the series of functionalized MOFs (ESI Fig. 18 and 19†). From the intrusion curves the inelastic transition pressure for hydrostatic compression of the op-phases can be estimated as a first approach to quantify and rationalize the framework micromechanics as predicted by computer simulations. The computational analysis of the inelastic yield stress of the ligands is well reflected in the trend of experimental transition pressure for structural contraction of the corresponding MOF materials, and also agrees well with the computationally predicted values (Fig. 3c) confirming the general relationship of the microscopic mechanism at play. DUT-160 and -161 exhibit transition pressures comparable to DUT-50 in the range of 24 MPa while DUT-148 and 147 exhibit a slight increase with 32 MPa and 35 MPa, respectively over DUT-49 (30 MPa). DUT-162, however, exhibits by far the lowest transition pressure of all materials tested (less than 10 MPa). From a molecular perspective the application of sp3 hybridized carbon atoms in the backbone not only severely softens the framework but can also prevent the formation of the desired framework topology due to enhanced degrees of freedom in the ligand structure. Extended aromatic systems on the other hand were found to yield the most stable configurations with a slight decrease in stability upon introduction of stilbene-type motives.
Analysis of adsorption properties by experiment and simulation
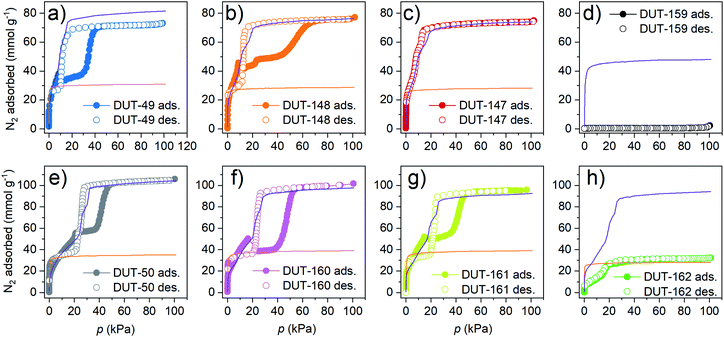
In the published literature, DUT-49 and DUT-50 are so far unique in their ability to sustain a guest-overloaded metastable state before they undergo adsorption-induced structural contraction leading to NGA and pressure amplification. According to previous experimental36 and computational studies,34 tuning and balancing the activation barrier and energetic separation of the two states is essential to maintain the overloaded metastable state without disabling the adsorption-induced contraction. Mechanically and energetically this means DUT-148, 160, 161, 162 are promising materials for NGA, having activation barriers in the same range as DUT-49 and 50 (around 1000 kJ moluc−1).To test the porosity of the bulk materials and potential occurrence of adsorption-induced transitions, the desolvated MOF powders were analysed using nitrogen physisorption at 77 K. Grand Canonical Monte Carlo (GCMC) simulations for op and cp phase greatly facilitate the interpretation of the experimental adsorption isotherms (description of the simulation procedures and CIF files in ESI†) (Fig. 4).
DUT-160 and DUT-161 stand out as highly porous materials with specific pore volumes up to 3.38 and 3.2 cm3 g−1 and geometrically accessible surface areas of 5342 and 5229 m2 g−1, respectively determined by Zeo++ calculations47 from the simulated crystal structures (ESI Table 11†).
With regard to adsorption-induced transitions, the recorded N2 adsorption isotherms at 77 K reflect three different scenarios. The rigid DUT-147 exhibits a reversible type IVb isotherm without any indication of structural contraction (and, in particular, no hysteresis loop typically associated with such structural transition). DUT-148, 160 and 161 are dynamic and exhibit characteristic NGA steps around 10–20 kPa, followed by a plateau at intermediate pressures and a steep increase in uptake at approximately 50 kPa. Upon desorption a wide hysteresis in the pressure range of 50–20 kPa is observed. This is a remarkable finding as so far, NGA steps induced by N2 at 77 K were only observed for DUT-49.39 Hence, DUT-148, 160, and 161 represent three new NGA materials demonstrating counterintuitive N2 pressure amplification at 77 K. Of the three DUT-148 and DUT-161 exhibit incomplete contraction of the bulk sample upon NGA evident by the deviation in uptake of experimental and simulated isotherm at intermediate pressure and previously described for DUT-50.36 For DUT-148 this can be assigned to the formation of phase mixtures which will be discussed below. Further softening of the backbone as in DUT-162, leads to a different scenario and significantly decreased uptake. Crumbled crystals are detected in SEM indicating deformation upon solvent removal (ESI Fig. 14†). However, PXRDs do not confirm complete collapse of the crystals. The remaining porosity in the bulk sample and comparison to the simulated isotherm indicate that ca. 60% of the DUT-162 bulk undergoes collapse likely upon solvent removal. Whether this collapse occurs partially in individual crystals or the bulk powder consists of a mixture of completely collapsed and non-collapsed crystals could not be determined. The reduced porosity explains the gradient slope and low volumetric compression of DUT-162 in the mercury intrusion experiments (ESI Fig. 19†). Hence, in this system backbone softening exceeds a critical value to maintain the open porosity. Similarly, DUT-159 exhibits a strong decrease in uptake compared to the simulated isotherm which further supports the framework collapse upon solvent removal. Replication of the synthesis and activation procedure on a second sample of DUT-159 and DUT-162 supported these findings rendering DUT-162 the lower limit of stability required to obtain a non-collapsed guest free DUT-49-type framework. Upon desorption DUT-49, 148, 50, 160 and 161 exhibit an inverse (Z-type) hysteresis in which the desorption branch intersects the adsorption branch indicating desorption-induced contraction. The good agreement of low-pressure desorption branches with the simulated isotherms of the cp phases indicates complete structural contraction upon desorption in contrast to the adsorption behaviour.
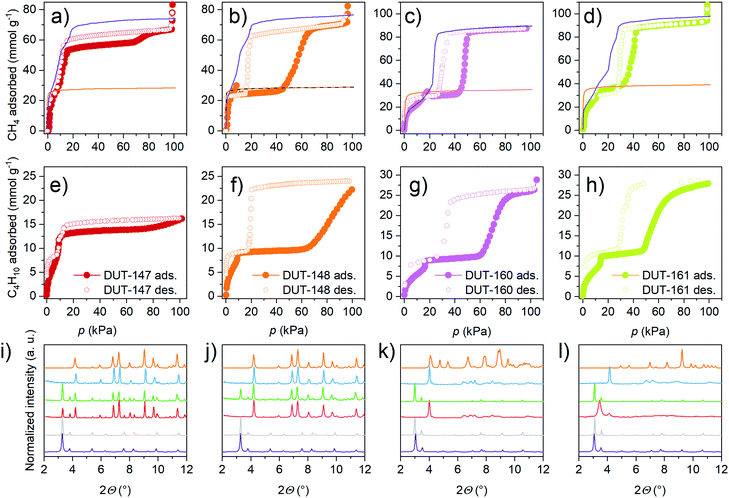
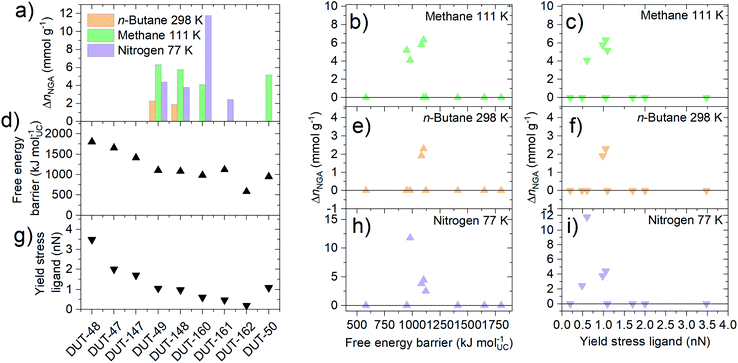
NGA in DUT-49 was initially observed upon adsorption of methane at 111 K and n-butane at 298 K (ref. 32) and strongly depends on the adsorption temperature and nature of the adsorbate.38 The magnitude of NGA, which is proposed to be correlated to the barrier of structural transformation,48 is defined by the released amount of gas upon structural contraction, ΔnNGA, which is the difference in uptake of gas in the op phase before contraction, nop, minus the uptake in the cp phase after contraction, ncp. Methane adsorption at 111 K in DUT-49 yields a relatively large NGA step of ΔnNGA = 6.3 mmol g−1, adsorption of n-butane at 273 K was found to result in structural contraction without NGA due to enhanced adsorption-induced stress. Conversely, nitrogen adsorption at 77 K yielded an intermediate NGA step of 4.4 mmol g−1 due to incomplete contraction caused by lower adsorption-induced stress partly reflected by the adsorption enthalpy.39,49 To further investigate the response of the series of materials in this study against increased adsorption-induced stress, adsorption experiments with methane adsorption at 111 K and n-butane adsorption at 273 K were conducted (Fig. 5).
Interestingly, under these conditions even DUT-147 as the most rigid framework shows a narrow hysteresis in the pressure range of 10–60 kPa for both adsorption of methane at 111 K and n-butane at 273 K, indicating a partial contraction. Isotherms of DUT-148, 160 and 161 exhibit wide hysteresis at intermediate pressures for both methane and n-butane adsorption. Interestingly, only methane isotherms at 111 K of DUT-148 and DUT-160 show NGA steps similar to DUT-49.32 The absence of NGA steps in DUT-161 upon adsorption of methane at 111 K and n-butane at 273 K is consistent with the observations made for DUT-50.36 These findings reflect the close energetic relationship of DUT-50 and DUT-161 which exhibit the lowest activation barriers of the series and the relationship of DUT-49 with DUT-148 and DUT-160 with slightly enhanced barriers (Fig. 3).
The fundamental driving force of the adsorption-induced contraction in DUT-49-type frameworks is the enhanced interactions of the fluid inside the contracted pore diameter in the cp phase.32 In a previous study we could correlate the non-monotonic enthalpy profile to the pore filling mechanism in the op phase by in situ calorimetry experiments and computational analysis.35,36,49 While elongation of the ligand backbone was found to strongly influence the adsorption energetics due to the change in pore size,36 the effect of chemical functionalization on the adsorption enthalpy profile is less clear. In situ calorimetry experiments in parallel to the adsorption of n-butane at 303 K for DUT-148, 147 and 160 (ESI Fig. 34†) show that the enthalpy curves of DUT-148 and DUT-147 match the previously reported data of DUT-49 demonstrating that the functionalization of the ligand backbone does not impact the solid–fluid interactions in the op phase. This is further confirmed by comparing enthalpy curves of DUT-160 to DUT-49 and DUT-50: the average adsorption enthalpy in the op phase is found to decrease with increasing pore size. This finding is also supported by adsorption enthalpy curves simulated for methane adsorption at 111 K for the op and cp phases (ESI Fig. 35†). Thus, the applied ligand functionalization has neglectable influence on the adsorption energetics of the op and cp phase and the observed adsorption behavior and adsorption-induced contraction can be attributed primarily to the mechanical characteristics of the solid. Structures that exhibit enhanced mechanical stability (DUT-48, 47, 147) are found to be non-contractable under these conditions while the structure of softened MOFs (DUT-159, 162) cannot be retained upon solvent removal. In the intermediate range of mechanical stability (DUT-49, 148, 160, 161, 50) adsorption-induced structural contraction and in some cases NGA occurs. This finding underpins the importance of balancing mechanical stiffness for pressure amplifying materials towards adsorption–responsive transitions.
Elucidation of adsorption-induced structural transitions by in situ powder X-ray diffraction
The interpretation of adsorption-induced transformations is also supported by in situ PXRD studies in parallel to the adsorption of n-butane at 273 K for DUT-147 and DUT-148 (full datasets ESI Fig. 21,† selected patterns in Fig. 5) and methane at 111 K for DUT-160 and DUT-161. Remarkably, DUT-147 undergoes partial contraction around 10 kPa and incomplete reopening at increased pressure up to 95 kPa. Upon desorption, the DUT-147 sample undergoes partial contraction in the pressure range of 12–9 kPa and complete contraction is observed at pressures below 1 kPa. Interestingly, the desorption-induced stress can trigger phase transitions which are otherwise not observed during adsorption, revealing a different mechanism for the adsorption and desorption processes in these bistable systems. As phase mixtures occur during adsorption but not upon desorption this indicates that gas loading, in addition to previously mentioned crystal size effects,39 can have a strong influence on the bulk adsorption properties in DUT-49-type systems. DUT-148 shows complete contraction of the bulk sample at intermediate pressures upon adsorption of n-butane at 273 K.Experimental crystal structures of DUT-147cp and DUT-148cp could be refined by Rietveld methods based on PXRD pattern collected at 15 kPa loading with n-butane at 273 K (ESI Fig. 28 and 30†). The unit cell parameters and conformational changes in the ligand are very similar to DUT-49cp (Table 1) and the modelled values. However, in both, DUT-148 and 147 incomplete reopening of the cp phase is observed even at pressures close to saturation. This indicates a high barrier for the cp–op transformation in these systems possibly caused by the strong host–guest interactions.
In situ PXRD patterns recorded for DUT-160 in parallel to adsorption of n-butane at 273 K show complete transformation of the op phase (ESI Fig. 25†). However, the quality of the PXRD pattern is drastically reduced with severe loss in intensity and broadening of the remaining peaks. Similar observations for DUT-50 were attributed to the relatively high adsorption temperature in which the increased mobility of the elongated ligands causes increased disorder in the framework of the strained cp phase.36In situ PXRD patterns recorded for DUT-160 and DUT-161 (ESI Fig. 24 and 26,† selected patterns in Fig. 5) in parallel to methane adsorption at 111 K show improved quality but still severe broadening compared to patterns collected for DUT-148cp. Both materials show complete op–cp transition at 17 kPa and presence of cp phase in the pressure range of 17–35 kPa. At elevated pressures the samples undergo reopening with phase pure op phases at saturation pressure. PXRD patterns obtained for DUT-161cp during adsorption are different from the pattern obtained for DUT-160cp during desorption for which the patterns of DUT-161cp are comparable to DUT-160cp at pressures below 10 kPa. In both cases the quality of the PXRD patterns did not allow for Rietveld refinement. Instead, structural models for DUT-160cp and DUT-161cp were simulated based on the unit cell parameters, obtained from the Le Bail fit of the PXRD patterns and show good agreement with the simulated models. The fact that the cp phase in DUT-160 and 161 shows only few reflections with low intensity in PXRD but still can transform back to a crystalline op phase at elevated pressures (Fig. 5k and l) demonstrates the preservation of framework connectivity and the cooperativity of the transition.
In situ PXRD patterns recorded during adsorption of nitrogen at 75 K in DUT-148 shows that at 10 kPa the op phase transforms to a mixture of op, cp and intermediate pore (ip) structures. These observations were previously also made for nitrogen adsorption in DUT-49.39 With increasing pressure in the range of 12 to 20 kPa the ip phases expand gradually to the op phase thus producing multiple steps in the isotherm. The cp phase of the remaining phase mixture, is only completely reopened at around 50 kPa forming phase pure DUT-148op at pressures beyond 70 kPa (ESI Fig. 33†).
The magnitude of negative gas adsorption
Adsorption-induced contraction and the resulting adsorption behavior, including NGA, can be thought of as a response of the framework to different levels of adsorption-induced stress. From the adsorption experiments reported above, we can derive that softer frameworks contract at lower adsorption-induced stress levels present upon adsorption of N2 at 77 K. On the other hand, stiffer frameworks only undergo contraction at increased stress levels that can be present during n-butane adsorption at 273 K. However, in order for NGA transitions to occur, the framework not only needs to undergo adsorption-induced contraction, but that contraction needs to occur at a pressure/loading beyond the intersection of the op and cp. So far, three scenarios have been observed for the investigated materials upon gas adsorption of nitrogen (77 K), methane (111 K) and n-butane (273 K): (i) absence of structural transitions indicated by the lack of hysteresis; (ii) structural contraction without NGA transition indicated by a wide hysteresis; and (iii) structural contraction with NGA transition indicated by the presence of a drop in uptake at intermediate pressure. Interestingly, NGA is only found to occur in materials with free energy barriers and yield stress of single ligand buckling in the range of 800 to 1100 kJ mol−1 and 0.6 to 1.2 nN, respectively (Fig. 6).The similar three scenarios were also found to occur for DUT-49 upon changing the adsorption temperature. There, NGA was only found to occur in a narrow range of temperature for a given adsorbate.38 In fact, while structural contraction in the absence of NGA was observed for DUT-49, 148, 160, 161, 50 upon adsorption of n-butane at 273 K, NGA is observed in DUT-49 and 148 at 298 K (ESI Fig. 15†), DUT-161 only exhibits NGA upon adsorption of nitrogen at 77 K and methane at 111 K. DUT-50 is found to show NGA only upon adsorption of methane at 111 K. DUT-160 exhibits NGA upon adsorption of methane at 111 K, as well as a very large NGA step of almost 12 mmol g−1 upon adsorption of nitrogen at 77 K: this is the highest value reported, almost twice compared to the largest value found so far in DUT-49.39 However, we cannot from this dataset establish a clear and direct correlation between the magnitude of ΔnNGA, the adsorption conditions, and the mechanical properties of the frameworks.
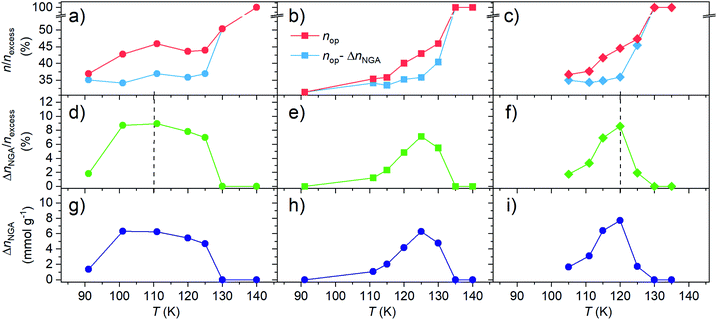
For DUT-49 we previously found that, in the 91–150 K temperature range, the maximum adsorption-induced stress increases with decreasing adsorption temperature promoting adsorption-induced contraction at lower adsorption temperature. We also showed that the critical stress for contraction is shifted towards lower adsorption pressure closer to the intersection of the op–cp isotherm and as a consequence ΔnNGA is found to decrease with decreasing adsorption temperature. To test whether this behavior is universal and present in other DUT-49-type systems, and whether a correlation between ΔnNGA and the mechanical properties of the framework can be made, we conducted variable methane adsorption in the range of 90–140 K for DUT-50 (ESI Fig. 17†) and DUT-160 (ESI Fig. 16†). For each material, the experiments were conducted on a single sample. To avoid irreversible contraction upon desorption at isothermal conditions, which was found to be the case in DUT-49, -50 and 160 by in situ PXRD (ESI Fig. 33†), the pores of the samples were saturated with methane (>3 MPa) and heated beyond the supercritical temperature of methane (>150 K). Methane was subsequently removed from the pores in dynamic vacuum (<10–2 kPa) at elevated temperature >190 K and samples could subsequently be reused for adsorption experiments at lower temperatures. This procedure resembles the initial supercritical activation using CO2 and allows to repeat NGA transitions for samples undergoing irreversible contraction under sub-critical guest removal conditions at lower temperature. For each isotherm recorded at different temperatures parameters important to NGA are derived and shown in Fig. 7.
Both DUT-50 and DUT-160 exhibit a similar temperature dependence of ΔnNGA upon adsorption of methane. In all cases ΔnNGA reaches a maximum with a more defined maximum in DUT-150 and 160 compared to DUT-49. Interestingly, the temperature at which ΔnNGA reaches its maximum is governed by the mechanical characteristics of the corresponding framework. For DUT-49 which is the most robust of the three, a maximum is observed in the range of 110–115 K while DUT-50 and 160 a maximum is observed at 120–125 K. This is in line with the previously discussed correlation between the adsorption temperature, the critical adsorption stress and the framework rigidity. To investigate the influence of the variation in pore volume present upon elongation of the ligand, ΔnNGA was normalized to the excess uptake of the op phase, nexcess, at 0.95 relative pressure. Interestingly, each material exhibits a maximum of ΔnNGA around 10%. Considering the total uptake of the cp phase is around 30% of nexcess of the op phase there would still be a lot of theoretical potential for an increase in ΔnNGA under these conditions. Thus, we investigated the evolution of ΔnNGA as a function of nop and ncp. The analysis clearly shows that the increase in ΔnNGA with increasing temperature is a result of the increase in nop before contraction while ncp is almost constant in the analyzed temperature range. Although the variable temperature analysis in DUT-50 and 160 supports the earlier findings of DUT-49, a wider dataset potentially involving different adsorbates is still needed to derive a quantitative relationship of the framework micromechanics and their NGA response.
Conclusion
In summary, by controlled tuning of the elastic and inelastic characteristics of a series of ligands under uniaxial strain and implementation into a DUT-49-type fcu network, it is possible to manipulate the counterintuitive negative gas adsorption response and pressure amplification behaviour in adsorption induced structural transformations. Shortening and widening of the ligand backbone is observed to increase stiffness while incorporation of acetylene, ethylene, and sp3 hybridized groups in the ligand backbone increases softness. The inelastic transition of the frameworks and metastable states controlled by free energy barriers for framework compression and yield stress for single ligand buckling lead to NGA. According to computational estimations, these free energy barriers are in the range of 800 to 1100 kJ mol−1 per unit cell or 33 to 46 kJ mol−1 per linker with moderate yield stress (0.6 to 1.2 nN) which is essential to preserve an overloaded metastable state without suppressing the framework transformation. By balancing the elasticity of the ligand, the magnitude of gas expulsion (ΔnNGA) from the metastable state is boosted, as demonstrated for the new framework DUT-160. However, the degree of metastability and pressure amplification is also critically affected by the gas composition, the adsorption temperature and porosity of the porous solid.These new findings provide fundamental insights for understanding the impact of chemical constitution on the mechanical properties of molecular building blocks. While the mechanical properties of more rigid50 but also structurally flexible15 porous solids have recently gained interest, this study provides fundamental design principles towards softening and rigidifying molecular building blocks. The deliberate design of transformation barriers has important implications for applications of flexible porous frameworks as mechanical actuators, valves, selective adsorbents, sensors and switchable catalysts.48 In addition, this work might provide the foundation to rationally tune the flexible properties of macroscopic single crystals. McMurtrie and co-workers recently demonstrated the potential to transform macroscopic deformation into molecular structural change of an individual single crystal,51 a property which seems strongly related to the present work. Yet, the current study only probes molecular mechanical effects and transformations in a single framework topology on the molecular- and microscopic level and the striking analogy to macro and microscopic mechanical metamaterials may serve as an inspiration for the future design of novel counterintuitive framework response functions and crystal deformations. In this sense topological engineering and the art of building block design enable unforeseen opportunities at different length scales.
Notes
MOF materials are abbreviated DUT (Dresden University of Technology) followed by a serial number, corresponding ligands are abbreviated L with the corresponding DUT serial number as superscript, open, contracted, and intermediate pore states are abbreviated op, ip, and cp, respectively. Energy values for framework contraction are given in kJ mol−1 per unit cell which is abbreviated to kJ moluc−1 (uc = unit cell).Conflicts of interest
The authors have no conflict of interest to declare.Acknowledgements
This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 Research and Innovation Programme (Grant agreement No. 742743). The authors thank the BMBF (No. 05K16OD1) and ANR/DFG Programme FUN for financial support and Helmholtz-Zentrum Berlin für Materialien und Energie for allocated beam time at KMC-2 and MX Beamlines and travel funding. S. Krause and J. D. E. acknowledge the support of the Alexander von Humboldt foundation. F.-X. C. is supported by ANR under project “MATAREB” (ANR-18-CE29-0009-01). Access to HPC platforms was provided by a GENCI grant (A0070807069) and the Center for Information Services and High Performance Computing (ZIH) at TU Dresden. P. I. and P. L. L. received funding from the European Union's Horizon 2020 Research and Innovation Program under the Marie Sklodowska-Curie grant agreement No. 641887 (project acronym: DEFNET).References
- S. H. Lee, C. M. Park, Y. M. Seo, Z. G. Wang and C. K. Kim, J. Phys.: Condens. Matter, 2009, 21, 175704 CrossRef.
- Z. Yang, J. Mei, M. Yang, N. H. Chan and P. Sheng, Phys. Rev. Lett., 2008, 101, 204301 CrossRef CAS.
- T. Bückmann, M. Thiel, M. Kadic, R. Schittny and M. Wegener, Nat. Commun., 2014, 5, 4130 CrossRef.
- M. Kadic, G. W. Milton, M. van Hecke and M. Wegener, Nat. Rev. Phys., 2019, 1, 198–210 CrossRef.
- O. M. Yaghi, ACS Cent. Sci., 2019, 5, 1295–1300 CrossRef CAS.
- F.-X. Coudert and J. D. Evans, Coord. Chem. Rev., 2019, 388, 48–62 CrossRef CAS.
- E. Jin, I. S. Lee, D. Kim, H. Lee, W.-D. Jang, M. S. Lah, S. K. Min and W. Choe, Sci. Adv., 2019, 5, 4119 CrossRef.
- W. Li, M. R. Probert, M. Kosa, T. D. Bennett, A. Thirumurugan, R. P. Burwood, M. Parinello, J. A. K. Howard and A. K. Cheetham, J. Am. Chem. Soc., 2012, 134, 11940–11943 CrossRef CAS.
- J. D. Evans, J. P. Dürholt, S. Kaskel and R. Schmid, J. Mater. Chem. A, 2019, 7, 24019–24026 RSC.
- N. C. Burtch, S. J. Baxter, J. Heinen, A. Bird, A. Schneemann, D. Dubbeldam and A. P. Wilkinson, Adv. Funct. Mater., 2019, 29, 1904669 CrossRef CAS.
- C. S. Coates and A. L. Goodwin, Mater. Horiz., 2018, 6, 211–218 RSC.
- L. R. Mingabudinova, V. V. Vinogradov, V. A. Milichko, E. Hey-Hawkins and A. V. Vinogradov, Chem. Soc. Rev., 2016, 45, 5408–5431 RSC.
- Q. R. S. Miller, S. K. Nune, H. T. Schaef, K. W. Jung, K. M. Denslow, M. S. Prowant, P. F. Martin and B. P. McGrail, ACS Appl. Mater. Interfaces, 2018, 10, 44226–44230 CrossRef CAS.
- S. Horike, S. Shimomura and S. Kitagawa, Nat. Chem., 2009, 1, 695 CrossRef CAS.
- A. Schneemann, V. Bon, I. Schwedler, I. Senkovska, S. Kaskel and R. A. Fischer, Chem. Soc. Rev., 2014, 43, 6062–6096 RSC.
- S. Krause, N. Hosono and S. Kitagawa, Angew. Chem., Int. Ed., 2020, 59, 15325–15341 CrossRef CAS.
- H. Furukawa, K. E. Cordova, M. O'Keeffe and O. M. Yaghi, Science, 2013, 341, 1230444 CrossRef.
- H. Robatjazi, D. Weinberg, D. F. Swearer, C. Jacobson, M. Zhang, S. Tian, L. Zhou, P. Nordlander and N. J. Halas, Sci. Adv., 2019, 5, 5340 CrossRef.
- M. Ding, R. W. Flaig, H.-L. Jiang and O. M. Yaghi, Chem. Soc. Rev., 2019, 48, 2783–2828 RSC.
- J. Liu, L. Chen, H. Cui, J. Zhang, L. Zhang and C.-Y. Su, Chem. Soc. Rev., 2014, 43, 6011–6061 RSC.
- Y. Cui, J. Zhang, H. He and G. Qian, Chem. Soc. Rev., 2018, 47, 5740–5785 RSC.
- A. H. Chughtai, N. Ahmad, H. A. Younus, A. Laypkov and F. Verpoort, Chem. Soc. Rev., 2015, 44, 6804–6849 RSC.
- A. Dhakshinamoorthy, Z. Li and H. Garcia, Chem. Soc. Rev., 2018, 47, 8134–8172 RSC.
- W. Zhao, L. Xia and X. Liu, CrystEngComm, 2018, 20, 1613–1634 RSC.
- N. A. Khan, Z. Hasan and S. H. Jhung, Coord. Chem. Rev., 2018, 376, 20–45 CrossRef CAS.
- I. Stassen, N. Burtch, A. Talin, P. Falcaro, M. Allendorf and R. Ameloot, Chem. Soc. Rev., 2017, 46, 3185–3241 RSC.
- A. Dittmore, D. B. McIntosh, S. Halliday and O. A. Saleh, Phys. Rev. Lett., 2011, 107, 148301 CrossRef.
- C. Bustamante, Z. Bryant and S. B. Smith, Nature, 2003, 421, 423–427 CrossRef.
- A. Takakura, K. Beppu, T. Nishihara, A. Fukui, T. Kozeki, T. Namazu, Y. Miyauchi and K. Itami, Nat. Commun., 2019, 10, 3040 CrossRef.
- A. U. Ortiz, A. Boutin, A. H. Fuchs and F.-X. Coudert, J. Chem. Phys., 2013, 138, 174703 CrossRef.
- E. V. Alexandrov, A. V. Goltsev, R. A. Eremin and V. A. Blatov, J. Phys. Chem. C, 2019, 123, 24651–24658 CrossRef CAS.
- S. Krause, V. Bon, I. Senkovska, U. Stoeck, D. Wallacher, D. M. Többens, S. Zander, R. S. Pillai, G. Maurin, F.-X. Coudert and S. Kaskel, Nature, 2016, 532, 348–352 CrossRef CAS.
- J. D. Evans, L. Bocquet and F.-X. Coudert, Chem, 2016, 1, 873–886 CAS.
- J. D. Evans, S. Krause, S. Kaskel, M. B. Sweatman and L. Sarkisov, Chem. Sci., 2019, 10, 5011–5017 RSC.
- S. Krause, J. D. Evans, V. Bon, I. Senkovska, S. Ehrling, U. Stoeck, P. G. Yot, P. Iacomi, P. Llewellyn, G. Maurin, F.-X. Coudert and S. Kaskel, J. Phys. Chem. C, 2018, 33, 19171–19179 CrossRef.
- S. Krause, J. D. Evans, V. Bon, I. Senkovska, P. Iacomi, F. Kolbe, S. Ehrling, E. Troschke, J. Getzschmann, D. M. Többens, A. Franz, D. Wallacher, P. G. Yot, G. Maurin, E. Brunner, P. L. Llewellyn, F.-X. Coudert and S. Kaskel, Nat. Commun., 2019, 10, 3632 CrossRef.
- U. Stoeck, S. Krause, V. Bon, I. Senkovska and S. Kaskel, Chem. Commun., 2012, 48, 10841–10843 RSC.
- S. Krause, J. D. Evans, V. Bon, I. Senkovska, F.-X. Coudert, D. M. Többens, D. Wallacher, N. Grimm and S. Kaskel, Faraday Discuss., 2020 10.1039/D0FD00013B.
- S. Krause, V. Bon, I. Senkovska, D. M. Többens, D. Wallacher, R. S. Pillai, G. Maurin and S. Kaskel, Nat. Commun., 2018, 9, 1573 CrossRef.
- J. Schaber, S. Krause, S. Paasch, I. Senkovska, V. Bon, D. M. Többens, D. Wallacher, S. Kaskel and E. Brunner, J. Phys. Chem. C, 2017, 121, 5195–5200 CrossRef CAS.
- S. Krause, F. S. Reuter, S. Ehrling, V. Bon, I. Senkovska, S. Kaskel and E. Brunner, Chem. Mater., 2020, 32, 4641–4650 CrossRef CAS.
- C. Zhang, J. A. Gee, D. S. Sholl and R. P. Lively, J. Phys. Chem. C, 2014, 118, 20727–20733 CrossRef CAS.
- S. Tanaka, K. Fujita, Y. Miyake, M. Miyamoto, Y. Hasegawa, T. Makino, S. Van der Perre, J. Cousin Saint Remi, T. Van Assche, G. V. Baron and J. F. M. Denayer, J. Phys. Chem. C, 2015, 119, 28430–28439 CrossRef CAS.
- S. Krause, V. Bon, H. Du, R. E. Dunin-Borkowski, U. Stoeck, I. Senkovska and S. Kaskel, Beilstein J. Nanotechnol., 2019, 10, 1737–1744 CrossRef CAS.
- N. Kavoosi, V. Bon, I. Senkovska, S. Krause, C. Atzori, F. Bonino, J. Pallmann, S. Paasch, E. Brunner and S. Kaskel, Dalton Trans., 2017, 4685–4695 RSC.
- S. Bureekaew, S. Amirjalayer, M. Tafipolsky, C. Spickermann, T. K. Roy and R. Schmid, Phys. Status Solidi B, 2013, 250, 1128–1141 CrossRef CAS.
- T. F. Willems, C. H. Rycroft, M. Kazi, J. C. Meza and M. Haranczyk, Microporous Mesoporous Mater., 2012, 149, 134–141 CrossRef CAS.
- J. D. Evans, V. Bon, I. Senkovska, H.-C. Lee and S. Kaskel, Nat. Commun., 2020, 11, 2690 CrossRef CAS.
- P. Iacomi, B. Zheng, S. Krause, S. Kaskel, G. Maurin and P. L. Llewellyn, Chem. Mater., 2020, 32, 3489–3498 CrossRef CAS.
- L. R. Redfern and O. K. Farha, Chem. Sci., 2019, 10, 10666–10679 RSC.
- A. Worthy, A. Grosjean, M. C. Pfrunder, Y. Xu, C. Yan, G. Edwards, J. K. Clegg and J. C. McMurtrie, Nat. Chem., 2018, 10, 65–69 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2003150, 2003151, 2003152, 2003153, 2003154, and 2003155 contain the supplementary crystallographic data for DUT-147, DUT-148, DUT-159, DUT-160 and DUT-161 correspondingly. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0sc03727c |
| This journal is © The Royal Society of Chemistry 2020 |