Topological prediction of palladium coordination cages

Abstract

The preparation of functionalized, heteroleptic Pd_xL_2x coordination cages is desirable for catalytic and optoelectronic applications. Current rational design of these cages uses the angle between metal-binding (∠B) sites of the di(pyridyl)arene linker to predict the topology of homoleptic cages obtained via non-covalent chemistry. However, this model neglects the contributions of steric bulk between the pyridyl residues—a prerequisite for endohedrally functionalized cages, and fails to rationalize heteroleptic cages. We describe a classical mechanics (CM) approach to predict the topological outcomes of Pd_xL_2x coordination cage formation with arbitrary linker combinations, accounting for the electronic effects of coordination and steric effects of linker structure. Initial validation of our CM method with reported homoleptic Pd₁₂^LFu₂₄ (^LFu = 2,5-bis(pyridyl)furan) assembly suggested the formation of a minor topology Pd₁₅^LFu₃₀, identified experimentally by mass spectrometry. Application to heteroleptic cage systems employing mixtures of ^LFu (∠B = 127°) and its thiophene congener ^LTh (∠B = 149° ∠B_exp = 152.4°) enabled prediction of Pd₁₂L₂₄ and Pd₂₄L₄₈ coordination cages formation, reliably emulating experimental data. Finally, the topological outcome for exohedrally (^LEx) and endohedrally (^LEn) functionalized heteroleptic Pd_xL_2x coordination cages were predicted to assess the effect of steric bulk on both topological outcomes and coordination cage yields, with comparisons drawn to experimental data.

---

Introduction

Spherical coordination cages of type Pd_xL_2x are formed by the self-assembly of palladium ions and organic bipyridine linkers in regular geometric patterns.¹ The dynamic nature of Pd–pyridyl coordination has enabled the isolation of Pd_xL_2x assemblies featuring 2–60 metal centers, isolated as the thermodynamic minima of possible structures.¹ The internal and external surfaces can be independently functionalized to modulate the sphere environment at the nanoscale for applications.² Previous reports detail a range of novel properties for guest binding,³ facilitating chemical reactions,⁴ modifying catalytic processes,^5–7 electrochemistry,⁸ and optoelectronic applications.⁹ These useful properties are derived from the topology of the assembly,¹ creating a significant interest in predicting topological results of self-assembly processes that ultimately lead to production of uniform assemblies of singular topology. Previously, Hay and Young described a model to predict the topology of coordination assemblies based on geometric properties of the metal center and organic linker.¹⁰ This model was adapted by Fujita and coworkers, using the bend angle (∠B) of the bipyridine linker to predict the topology of the thermodynamic product, applying it to describe spherical cages containing 3–60 metal centers as a principle for rational design.¹¹ While this approach is sufficient for most homoleptic cages, the model fails to describe assemblies derived from asymmetric, flexible or sterically demanding linkers. This shortcoming is apparent in modern efforts to design heteroleptic cages that feature multiple functional groups to control the assembly outcome in a trial-and-error manner, especially when asymmetric linkers steric bulk or shape-complementarity are employed.^12–14 The latter strategy, employed by Clever and colleagues, is especially promising for the design of small M₂L₄ cages with divergent functionalities.¹² A more robust model would provide a better basis of rational design for these new structures, and the application of shape-complementarity to larger designs, motivating the aim of our research.

The process of self-assembly leads to formation of supramolecular structures with the most thermodynamically stable topology,¹¹ and a means to identify this product computationally would allow prediction of topologies prior to the experimental identification. While previous efforts have used computational methods to simulate the formation process,¹⁵ and determine the guest binding properties of cages,¹⁵ there is no available method for in silico screening to identify the preferred topology produced from an arbitrary linker, or set of linkers. Such a method would have practical applications as a tool for the rational design of highly functionalized cage assemblies, and furthermore provide further insight into known assemblies. Distinguishing the true thermodynamic products from trapped states and the identification of minor products are important issues in this regard. A viable method of in silico screening requires accuracy in estimating the free energy coupled with expediency to effectively guide experimental work. Given the size of the assemblies, numerous topologies and permutations of linker combinations, classical mechanics methods are well suited to practically address this task, with modern methodologies showing marked success in describing these assemblies.^15–17

Here, we report a strategy that utilizes force field parameters for individual linkers from DFT structure optimization to estimate the relative free energies across 40 topologies containing 3–30 metal centers. The validity of our approach was demonstrated by a detailed study of the topological preferences of homoleptic and heteroleptic assemblies derived from reported linkers. The feasibility of our method is demonstrated by the study of novel heteroleptic assemblies featuring a sterically demanding linker bearing endohedral functionalization. These topological predictions of our CM method are supported by experimental observations.

Methods

Experimental details

Linkers ^LFu, ^LTh, ^LEx, and ^LEn were synthesized following standard procedures detailed in the ESI (Section D†).^2,18 Homoleptic assemblies were formed with a total linker concentration of 10 mM and 0.55 equivalents of Pd(CH₃CN)₄(BF₄)₂, at room temperature (^LFu and ^LTh) or 50 °C (^LEx and ^LEn) after 16 hours in CD₃CN. The resulting clear solutions were filtered (0.45 μm, PTFE syringe filter), following analysis by NMR and ESI-HRMS. Details of the experimental procedures and subsequent analyses are given in the ESI (Sections E–H†). ¹H NMR spectra were measured using either a Bruker DRX 500 (500 MHz) or a Bruker DRX 300 (300 MHz) at 25 °C unless otherwise noted for variable temperature experiments. DOSY NMR spectra were obtained using LED bipolar pulse gradients with a diffusion delay time of 0.1 seconds at 25 °C. Mass spectra were collected on a high-resolution time-of-flight Bruker Impact II ESI-HRMS. Detection was in positive-ion mode with a source voltage between 4 and 6 kV. Samples were prepared in CD₃CN with a total linker concentration of 10 mM and a Pd(CH₃CN)₄(BF₄)₂ concentration of 5.5 mM, and then analyzed by NMR and ESI–HRMS directly.

Computational details

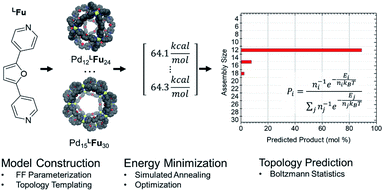
CM calculations were carried out using an Amber-type forcefield¹⁹ and structural annealing and optimization were completed with the GPU-enabled Amber16 software suite,²⁰ with run parameters provided in the ESI (Section B†). CM forcefield parameters were developed directly with a model system (Fig. 1).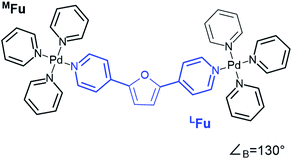

Fig. 1 An example of a model system used for DFT dynamics studies (see also Fig. S1†). This model, ^MFu, features the linker ^LFu (blue) coordinated to tris-pyridyl Pd²⁺ centers. The bend angle of the complex is measured from the B3LYP/def2-TZV minimized structure, deviating slightly from the free linker due to electronic effects of metal coordination. Structures, charge assignments (Fig. S2†), dynamics trajectories (Fig. S3†) and other data for model complexes of linkers are provided in the ESI (Section A†).

The optimized structure of the model system was used for charge fitting based on the RESP method employed by antechamber.²⁰ Lennard Jones potentials for organic atom centers were assigned by GAFF atom type,²¹ palladium centers were parameterized according to previous reports.²² Bond, angle and torsion terms were fit using a genetic algorithm.²³ Models of the complete cages were assembled by least-squares fitting placement of the individual linkers in accordance to a template using ProFit.²⁴

The fitting and validation data sets were obtained from trajectories generated using GFN2-xTB,²⁵ supplemented by single point energies of each trajectory frame computed by DFT at a B3LYP/def2-TZV level of theory using Gaussian 16 rev. C.²⁶ A complete discussion of the parameterization (Scheme S1†) and validation (Table S1†) is provided in the ESI (Section A†). While only topologies containing 3–30 metal centers are considered, this approach is readily extended to Pd₂L₄ based assemblies, as also discussed in the ESI (Section K†).

Results and discussion

Topological survey procedure

In this study we considered the four linkers shown in Fig. 2. ^LFu (∠B = 127°) and ^LTh (∠B = 149°) have been previously reported and shown to form both homoleptic and heteroleptic assemblies.²⁴ Furthermore, as the favored topology of the heteroleptic assemblies depends on the composition of linkers in the assembly, this system offers an ideal test for method development. Linkers ^LEx and ^LEn are novel linkers featuring exohedral and endohedral functionalization respectively. While these two linkers possess similar bend angles, the latter is sterically strained, which may impact the topological outcome of self-assembly.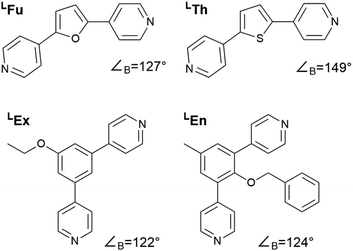

Fig. 2 Structures of the bipyridyl linker molecules used in this study. Bend angles, ∠B, are estimated from B3LYP/def2-TZV minimized structures.

Amber type forcefield parameters were developed for the four linkers employed in this study (Fig. 2), which reproduced the relative free energies for the model complex reliable compared to semi-empirical methods (Table S1†). These linker models were then used to construct assembly models in accordance to templated defined for polyhedra containing 3–30 vertices representing many of the known cage topologies. These structures could then be annealed (2 ns) and optimized (10 000 steps) expediently to produce a minimum energy structure for each topology, provided in detail in the ESI (Table S4†). The relative energy of these structures was analyzed using a Boltzmann statistical model, with each topology considered a microstate for a given linker weighted by the number of linkers involved as depicted in Scheme 1.

Scheme 1 Flow chart for topological prediction of homoleptic assemblies featuring the formation of homoleptic Pd_x^LFu_2x assemblies. The linker structure is used to construct a library of possible assembly outcomes, which are subjected to a simulated annealing and structural optimization procedure using implicit solvation. The resulting minimum energies, E, are treated as microstates, and the topological distribution is determined using Boltzmann statistics with a weighting factor ‘n’ corresponding to the number of linker components in the assembly.

A majority of Pd_xL_2x assemblies reported are homoleptic in nature due to the ease of assembly and subsequent analysis. This simple case was used in order to validate our topological survey approach. Specially the method was validated for linkers ^LFu (∠B = 127°) and ^LTh (∠B = 149°). The former has been reported to afford a single topology, Pd₁₂^LFu₂₄, while the latter is recently known to form a mixture, Pd₂₄^LTh₄₈ and Pd₃₀^LTh₆₀. These assemblies have been sufficiently characterized by NMR, HRMS, and crystallographic means providing clear and definite knowledge of the assembly outcomes.^18,27

Our model predicted a majority (89.1%) presence of M₁₂L₂₄ homoleptic assemblies using linker ^LFu, which is observed experimentally (Fig. 3). Additionally, our model predicted the presence of a minor (7.8%) Pd₁₅L₃₀ product. We experimentally investigated the minor Pd₁₅L₃₀ species by reproducing assemblies based on reported protocols¹⁸ and subsequent characterization of the Pd_xL_2x assembly distribution by DOSY NMR (Fig. S13†) and CSI-HRMS (Fig. S14†). DOSY NMR revealed a single species (log₁₀ D = −9.23), consistent with the presence of Pd₁₂^LFu₂₄ as previously reported. ESI-HRMS revealed the presence of a Pd₁₅^LFu₃₀ assembly (Fig. 3).

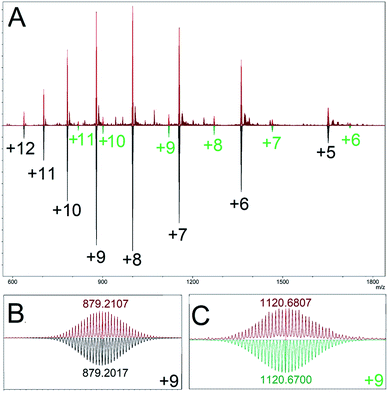Fig. 3 (A) ESI-HRMS characterization of the homoleptic assembly products of linker ^LFu (red), top. Mass simulations indicate multiple charged species matching simulations for Pd₁₂^LFu₂₄, (black), and Pd₁₅^LFu₃₀, (green) species. Bottom, an expanded view of the isotope distributions observed for (B) Pd₁₂^LFu₂₄(BF₄)₁₃⁹⁺, and (C) Pd₁₅^LFu₃₀(BF₄)₂₁⁹⁺, species, annotated with the center peak m/z either observed (red) or calculated (black or green). Data is further detailed in the ESI (Fig. S15†).

Fortuitously, the relative intensity of this minor species (9.4% of Pd₁₅^LFu₃₀) correlates well to the prediction of Pd₁₅^LFu₃₀ abundance (8.7%) from our computational model, as detailed in the ESI (Table S3†). This highlights the inability of DOSY NMR to distinguish between coexisting Pd₁₂ and Pd₁₅ species originating from significant overlap of the NMR resonances, similar size (and therefore, diffusion coefficient) and the disparity between their relative populations. We applied our method to the Pd_xL_2x assemblies formed with linker ^LTh (∠B = 149°), reported to generate larger M₂₄L₄₈ and M₃₀L₆₀ assemblies.²⁷ The modelling results of the homoleptic assembly formed with linker ^LTh predict the formation of assemblies with either M₂₄L₄₈ (67.0%) or M₃₀L₆₀ (32.8%) topologies, further detailed in the ESI (Table S4†).

Initial experimental reports of these assemblies afforded only the M₂₄L₄₈ structure which was characterized by NMR, HRMS, and crystallographic means.²⁴ However, later work afforded a mixture which included both M₂₄L₄₈ and M₃₀L₆₀ topologies, the latter of which was additionally characterized by NMR, HRMS, and crystallographic means.²⁷ Our CM approach was unaffected by the kinetic differences for forming either topologies and the resulting topological distribution contain these two species at relative populations in good agreement with the experimentally reported data.

Topological prediction of heteroleptic Pd_xL_2x assembly distribution

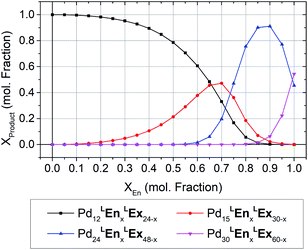
The formation of heteroleptic assemblies is a significant motivation for topological prediction as there is no apparent rule to predict the assembly outcome for the combination of two dissimilar linkers. Therefore, we expanded our survey to consider assemblies composed of two linkers, randomly distributed over the edges of the polyhedral templates. To validate this extension, we considered the previously reported heteroleptic assemblies of ^LTh and ^LFu.¹⁸

A new approach was needed in order to identify the topological preference of mixtures of linkers at arbitrary compositions using a linear of the relative free energy for each topology at various compositions (Fig. 4). This approach is further detailed in the ESI (Section C†).

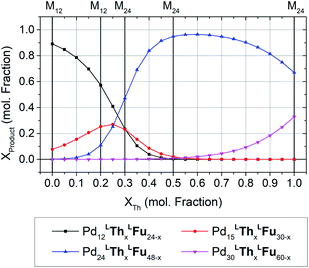Fig. 4 The topological preferences of heteroleptic cages composed of ^LFu and ^LTh with the four most major products shown. Referenced experimentally determined topological outcomes shown on upper axis at the reported experimental composition. Preferences at arbitrary compositions were predicted by linear interpolation of the model forcefield energy, and subsequent application of Boltzmann statistical analysis. This procedure is detailed further in the ESI (Section C†), with included analysis and discussion of the fitting results for heteroleptic assemblies of ^LFu and ^LTh.

Our model predicts that heteroleptic assemblies with a M₁₂L₂₄ topology are produced from mixtures of ^LFu and ^LTh containing less than 27% of ^LTh. At this critical concentration a transition in topological preference is observed, shifting towards the M₂₄L₄₈ topology. This critical composition is in agreement with the previous report observing the transition occurring at 0.2–0.3 mole fraction ^LTh.¹⁸ The model predicts greater preference for the M₁₅L₃₀ topology at this critical point, suggesting it may be an important intermediate between the two topologies.

The effect of endohedral functionalization on topological distribution

Moving beyond the bend angle, we used our model to study the topological effect of endohedral and exohedral substituents. Linker ^LEx features external ornamentation that should impart minimal effect on Pd_xL_2x assembly topology, as homoleptic assemblies of similar linkers have been reported to form M₁₂L₂₄ topologies.² Linker ^LEn, with internal functionalization demonstrate the same apparent bend angle as ^LEx suggesting the same topology should form. However, reports of a similar linker featuring a methoxy substituent by Fujita et al., concluded that Pd_xL_2x assembly formation is inhibited assemblies due to the steric encumbrance imparted by substituents in this position.² To maximize this steric effect, a benzyl group was selected in the design of linker ^LEn.

Shown in Fig. 5, our topological prediction shows the M₁₂L₂₄ topologies are favored over a large range of compositions, as would be suggested by the bend angle. Interestingly, at mixtures containing a larger proportion of ^LEn, the formation of larger topologies (i.e. M₂₄L₄₈ or M₃₀L₆₀) are favored. As the ^LEn bend angle (∠B = 124°) favors M₁₂L₂₄ topologies, the preference towards larger assemblies can only be ascribed to the effect of the steric bulk.

Fig. 5 The modeled topologic preference of heteroleptic assemblies of linkers ^LEx and ^LEn. The M₁₂L₂₄ is the most preferred topology at lower compositions, with successively larger topologies, M₁₅L₃₀ to M₃₀L₆₀, preferred with increasing ^LEn.

As expected, homoleptic assemblies were successfully formed with ^LEx, evidenced by the characteristic shift of α-pyridyl proton resonances in ¹H NMR. Subsequent characterization of the assembly by DOSY NMR revealed a hydrodynamic radius of 16.4 Å, identical to the radius found for the Pd₁₂^LEx₂₄ model (Table S4†). Finally, isotope pattern analysis within the ESI-HRMS data enabled for unambiguous assignment of Pd₁₂^LEx₂₄ cage topologies (Fig. S19†).

Similarly, homoleptic assemblies of ^LEn were successfully formed on the basis of the characteristic downfield shift of α-pyridyl proton resonances, and the absence of free building block in ¹H NMR. However, DOSY NMR indicated that resulting assemblies possess a radius of 27.8 Å (Fig. S22†). While this value is significantly larger than the 17.6 Å predicted by our model of Pd₁₂^LEn₂₄ cages, it is a reasonable radius for Pd₃₀^LEn₆₀ assemblies. Unfortunately, the difficulty in reliably ionizing this species meant that it's presence could not be confirmed by ESI-HRMS, thus the composition of the assembly (or assemblies) formed experimentally remains ambiguous. These limitations of ESI-HRMS are known for the analysis of larger assemblies, experimentally limiting the pursuit of these structures.²⁷

Heteroleptic assemblies were formed using five different ratios of ^LEx : ^LEn linkers, incorporating 4–20 of ^LEn (mole fractions 0.14–0.86) and 20–4 ^LEx (Fig. 6). The formation of these assemblies was confirmed by the characteristic downfield shift of the α-pyridyl proton (ca. 9.05 to 9.25 ppm). DOSY NMR indicated that the resulting assemblies were larger than expected for M₁₂L₂₄ topologies (r_H 18–21 Å), but within expectations for M₂₄L₄₈ or M₃₀L₆₀ topologies (r_H 23–26 Å). These data are provided in the ESI (Section H†). It is well documented that intermediate polymeric species present during assembly formation are NMR silent,^28,29 and therefore can be excluded as a major product.

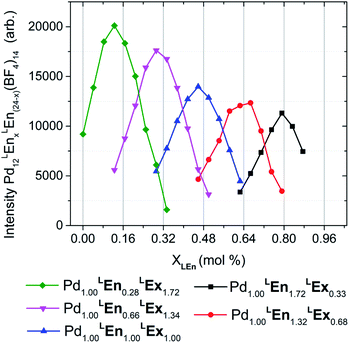Fig. 6 Distributions of heteroleptic assemblies observed by ESI-HRMS. Assembly product mixtures were formed in deuterated acetonitrile from 10.0 mM total concentration of ^LEn and ^LEx with 5.0 mM of Pd(BF₄)₂ and were directly analyzed without dilution by ESI-HRMS. The observed mass spectra of Pd₁₂^LEn_(x)^LEx_(24−x)·(BF₄)₁₄¹⁰⁺ species suggests a single product topology. These results are further detailed in the ESI (Section H†).

Mass analysis of the heteroleptic assemblies were found to include 0–21 ^LEn randomly incorporated into the assembly structure with an average ratio corresponding to the composition of the reaction mixture, summarized by Fig. 6. Mass analysis yielded only compositions with a stoichiometry of Pd₁₂^LEn_x^LEx_(24−x), corresponding only to the Pd₁₂L₂₄ topologies. This contradicts the DOSY NMR results indicating the formation of larger species containing 24–30 metal centers. Interestingly the overall intensity of the mass signal decreases with the increase in ^LEn content. If this decrease were due to simple differences in assembly formation, ionizability, or instrument response, a bias should be observed in the distributions of Pd₁₂^LEn_x^LEx_(24−x) species formed. Alternatively, this diminished intensity can be attributed to the presence of a secondary species—plausibly Pd₂₄^LEn_x^LEx_(48−x) or Pd₃₀^LEn_x^LEx_(60−x) cages—which are beyond the current limits of this particular ESI-HRMS analytical technique and therefore cannot be conclusively characterized.

Impaired dihedral rotation and long-range topological effects

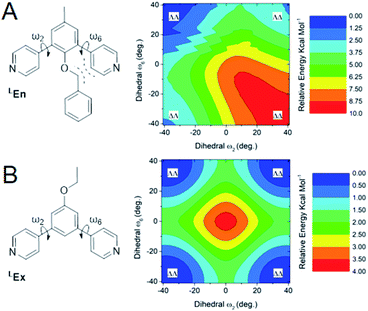
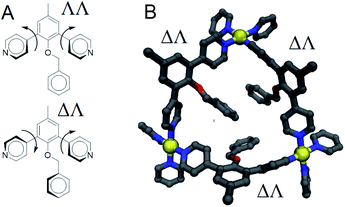
From the above data we surmise that heteroleptic assemblies of ^LEn and ^LEx form under conditions similar to other palladium–pyridyl coordination cages. Furthermore, these cages possess a larger topology due to the steric effects of the endohedral functionalization of ^LEn. To understand the mechanism of this steric effect and its impact on topological preferences for heteroleptic assemblies, relaxed potential energy surfaces were computed for the pyridyl–arene dihedral rotation using DFT at a B3LYP/def2-TZV theory level as illustrated in Fig. 7.

Fig. 7 Computed free energy surfaces of dihedral rotations of model systems for ^LEn (A) and ^LEx (B). Left, simple drawing of the model system showing the dihedral rotation (arrows), and expected source steric hinderance (dashed lines). Right, potential energy surfaces produced from a relaxed scan of the dihedral angles (ω₂, ω₆) between ±40° from coplanarity in 28 steps of 3° for each dihedral angle. These DFT calculations were conducted at a B3LYP/def2-TZV level of theory, with the color contour corresponding to the relative free energy of each dihedral pair in kcal mol⁻¹.

While relaxed scans were used, the method converges to local minima resulting in the distinct ΛΛ and ΔΔ atropisomers shown in Fig. 8A. These potential energy surfaces reveal that the pyridyl–arene dihedral rotations for the sterically demanding ^LEn are asymmetric compared to ^LEx. The structures generated from this scan were analyzed using our CM parameters, producing similar results as shown in the ESI (Section J†).

Fig. 8 (A) Drawing showing ΛΛ and ΔΛ atropisomers of ^LEn with out-of-plane rotation shown. (B) Ball and stick model renders of a triangular face from our molecular mechanics model of a cuboctahedral Pd₁₂^LEn₂₄ cage including neighboring linker pyridyl groups shown showing requirement for ΔΛ isomers to accommodate the propeller angle about the palladium coordination site. Model features atoms colored by element: carbon as grey; nitrogen, blue; oxygen, red; and palladium as yellow. Hydrogen atoms were omitted from the rendering for clarity.

The DFT potential energy surface shows that ΔΛ or ΛΔ isomers of ^LEn are less favorable by 2.2 kcal mol⁻¹. The preference for the ΛΛ atropoisomer is easily rationalized by the minimization of steric interactions between the pyridyl groups and the endohedral benzyl functionality. Similarly, the high energy ΔΔ isomer forces the pyridyl groups to rotate into the endohedral benzyl functionality, and therefore such conformation is not physically accessible.

Reproduction of these dihedral scans using our CM method produces similar minima with ΔΛ or ΛΔ isomers being only 1.2 kcal mol⁻¹ higher in energy, as discussed in detail in the ESI (Section J†). Contrary to the computed preference of the ΛΛ isomer, our CM models of assemblies feature predominantly ΔΛ or ΛΔ isomers shown in Fig. 8.

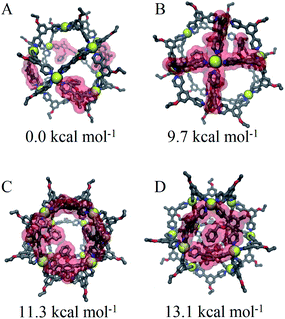
We speculate that this arrangement is a requirement for coordination to satisfy coordination and results in a destabilization of cages proportional to the number of triangular faces involved. This aggregate effect was modelled directly using our CM approach to consider specific arrangements of linkers for Pd₁₂^LEn₄^LEx₂₀ assemblies following the same annealing and optimization methodology used for previously. The relative free energies were computed for four different distributions representative of the intuitive outcomes for different degrees of interaction between ^LEn linkers.

Based on our model, the non-interacting arrangement (Fig. 9A) is significantly more favorable than co-coordinated or co-facial arrangements (Fig. 9B–D). However, the possibility of forming these favorable arrangements becomes insignificant with increasing ^LEn content, necessitating the more accessible co-facial arrangements. The relative free energy of co-facial ^LEn on a triangular face (Fig. 9D) were less favored compared to the co-facial square (Fig. 9C) arrangements by 1.8 kcal mol⁻¹ per linker. In turn this accounts for the observation that assemblies of ^LEn form larger topologies (i.e. M₂₄L₄₈ and M₃₀L₆₀) as they feature a smaller proportion of triangular faces (8/26 and 8/38 faces, respectively) compared to M₁₂L₂₄ (8/14 faces) topologies. Similarly, the incorporation of the more adaptable ^LEx alleviates permits the formation of spherical cages with a smaller M₁₂L₂₄ topology that would otherwise be favored by the natural bend angle of both linkers.

Fig. 9 Renders of CM optimized structures of Pd₁₂^LEn₄^LEx₂₀ with forcefield energy per linker relative to the minimum structure. (A) Distributed at distant, non-interacting positions, (B) interaction at a palladium center, (C) interaction as a square face, and (D) interaction as a triangular face, with one distant non-facial linker. Ball-and-stick models of linkers are colored by atom type (carbon (grey), nitrogen (blue) and oxygen (red)) with hydrogen atoms omitted for clarity. Yellow vdW volume spheres (yellow) are shown for palladium centers. A red vdW surface highlights the interacting ^LEn within the structure.

These computational results account for the experimental observations of heteroleptic assemblies for ^LEx and ^LEn, where DOSY NMR shows the formation of a larger complex, and the mass spectra results which present an unexpected loss of intensity. While it is unfortunate that available experimental methods cannot fully characterize and quantitatively assess these larger species, our CM model provides deeper insight into these assemblies and is well supported by both higher-level calculations and available experimental evidence.

Conclusions

In this work we produced a forcefield for pyridyl–palladium complexes as found in a number of coordination assemblies. This forcefield offers significant improvements to accurately estimates of relative free energies of palladium–pyridyl complexes. Using these estimates, we could predict the topological preferences of two previously reported bis-pyridyl linkers, ^LTh and ^LFu, reproducing experimentally observed topological preferences for their homoleptic and heteroleptic assemblies. From our results we found a novel minority M₁₅L₃₀ topology which we characterized experimentally. These outcomes demonstrate the viability of a classical mechanics based in silico screening for these topological outcomes.

This approach was then used to determine the topological outcome of heteroleptic assemblies formed from two novel linkers, ^LEx and ^LEn, respectively featuring exohedral and endohedral functionalization. This study demonstrated the pronounced effect of steric bulk proximal to metal binding sites in topological outcomes and assembly yields, as confirmed by experimental study with high resolution mass spectrometry. These heteroleptic assemblies demonstrate a novel strategy for the inclusion of sterically demanding functionalization within coordination cages, and highlight the effectiveness of our classical mechanics methodology to aid in assembly design.

Future work aims to apply these computational approaches to provide more detailed insight in the formation of these self-assembled nanospheres, and to extend these approaches to include to better suit the analysis of applied supramolecular structures.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We extend a special thanks to our colleague, Ms. Eline Meijer, for her insightful comments, and providing initial motivation for forming the novel heteroleptic assemblies presented here. This paper is dedicated to Prof. P. H. Dixneuf for his scientific and organisational contributions to field of organometallic chemistry and catalysis. We thank the European Research Council (ERC Adv. Grant 339786-5354 NAT_CAT) and the sustainable chemistry research program from the University of Amsterdam for financial support.

References

1. For reviews, see: (a) K. Harris, D. Fujita and M. Fujita, Chem. Commun., 2013, 49, 6703–6712; (b) S. R. Seidel and P. J. Stang, Acc. Chem. Res., 2002, 35, 972–983; (c) R. A. S. Vasdev, D. Preston and J. D. Crowley, Chem.–Asian J., 2017, 12, 2513–2523; (d) T. K. Ronson, S. Zarra, S. P. Black and J. R. Nitschke, Chem. Commun., 2013, 49, 2476–2490; (e) S. J. Dalgarno, N. P. Power and J. L. Atwood, Coord. Chem. Rev., 2008, 258, 825–841.
2. S. Löffler, J. Lübben, A. Wuttke, R. A. Mata, M. John, B. Dittrich and G. H. Clever, Chem. Sci., 2016, 7, 4676–4684.
3. (a) M. Han, D. M. Engelhard and G. H. Clever, Chem. Soc. Rev., 2014, 43, 1848–1860; (b) F. J. Rizzuto, L. K. S. von Krbek and J. R. Nitschke, Nat. Rev. Chem., 2019, 3, 204–222; (c) Y. Ueda, H. Ito, D. Fujita and M. Fujita, J. Am. Chem. Soc., 2017, 139, 6090–6093.
4. For examples of catalytic cages, see: (a) M. D. Pluth, R. G. Bergman and K. N. Raymond, Science, 2007, 316, 85–88; (b) M. Yoshizawa, M. Tamura and M. Fujita, Science, 2006, 312, 251–254; (c) M. D. Ward and P. R. Raithby, Chem. Soc. Rev., 2013, 42, 1619–1636; (d) Y. Ueda, H. Ito, D. Fujita and M. Fujita, J. Am. Chem. Soc., 2017, 139, 6090–6093; (e) Y. Fang, J. Powell, E. Li, Q. Wang, Z. Perry, A. Kirchon, X. Yang, Z. Xiao, C. Zhu, L. Zhang, F. Huang and H. Zhou, Chem. Soc. Rev., 2019, 48, 4707–4730; (f) L. Holloway, P. Bogie, Y. Lyon, C. Ngai, T. Miller, R. Julian and R. Hooley, J. Am. Chem. Soc., 2018, 140, 8078–8081; (g) W. Cullen, M. Misuraca, C. Hunter, M. Williams and M. Ward, Nat. Chem., 2016, 8, 231–236; (h) C. Tan, J. Jiao, Y. Liu and Y. Cui, Angew. Chem., Int. Ed., 2017, 8, 2085–2090; (i) H. Takezawa, K. Shitozawa and M. Fujita, Nat. Chem., 2020, 12, 574–578; (j) See also ref. 16d.
5. For reviews, see: (a) V. Mouarrawis, R. Plessi11us, J. I. van der Vlugt and J. N. H. Reek, Front. Chem., 2018, 6, 623; (b) A. C. H. Jans, X. Caumes and J. N. H. Reek, ChemCatChem, 2019, 11, 287–297; (c) S. H. A. M. Leenders, R. Gramage–Doria, B. de Bruin and J. N. H. Reek, Chem. Soc. Rev., 2015, 44, 433–448; (d) M. Yoshizawa, J. K. Klosterman and M. Fujita, Angew. Chem., Int. Ed., 2009, 48, 3418–3438; (e) M. J. Wiester, P. A. Ulmann and C. A. Mirkin, Angew. Chem., Int. Ed., 2011, 50, 114–137; (f) M. Raynal, P. Ballester, A. Vidal–Ferran and P. W. N. M. van Leeuwen, Chem. Soc. Rev., 2014, 43, 1734–1787; (g) C. J. Brown, F. D. Toste, R. G. Bergman and K. N. Raymond, Chem. Rev., 2015, 115, 3012–3035; (h) D. M. Vriezema, M. Comellas Aragonès, J. A. A. W. Elemans, J. J. L. M. Cornelissen, A. E. Rowan and R. J. M. Nolte, Chem. Rev., 2005, 105, 1445–1489; (i) S. Zarra, D. M. Wood, D. A. Roberts and J. R. Nitschke, Chem. Soc. Rev., 2015, 44, 419–432; (j) R. J. Hooley and J. Rebek Jr, Chem. Biol., 2009, 16, 255–264; (k) D. Fiedler, D. H. Leung, R. G. Bergman and K. N. Raymond, Acc. Chem. Res., 2005, 38, 349–358; (l) L. J. Jongkind, X. Caumes, A. P. T. Hartendorp and J. N. H. Reek, Acc. Chem. Res., 2018, 51, 2115–2128.
6. For examples on metal catalyzed processes in cages, see: (a) M. Otte, P. F. Kuijpers, O. Troeppner, I. Ivanović-Burmazović, J. N. H. Reek and B. de Bruin, Chem.–Eur. J., 2013, 19, 10170–10178; (b) L. J. Jongkind, J. A. A. W. Elemans and J. N. H. Reek, Angew. Chem., Int. Ed., 2019, 58, 2696–2699; (c) C. Arroniz, G. Chaubet and E. Anderson, ACS Catal., 2018, 8, 8290–8295; (d) Q. He, X. Li, L. Chen, L. Zhang, W. Wang and C. Y. Su, ACS Catal., 2013, 3, 1–9; (e) V. Welborn, W. Li and T. Head-Gordon, Nat. Commun., 2020, 11, 415; (f) T. A. Bender, R. G. Bergman, K. N. Raymond and F. D. Toste, J. Am. Chem. Soc., 2019, 141, 11806–11810.
7. For catalysis in M₁₂L₂₄ spheres, see: (a) Q. Q. Wang, S. Gonell, S. H. A. M. Leenders, M. Dürr, I. Ivanović-Burmazović and J. N. H. Reek, Nat. Chem., 2016, 8, 225–230; (b) R. Gramage-Doria, J. Hessels, S. H. A. M. Leenders, O. Tröppner, M. Dürr, I. Ivanović-Burmazović and J. N. H. Reek, Angew. Chem., Int. Ed., 2014, 53, 13380–13384; (c) F. Yu, D. Poole III, S. Mathew, N. Yan, J. Hessels, N. Orth, I. Ivanović-Burmazović and J. N. H. Reek, Angew. Chem., Int. Ed., 2018, 57, 11247–11251; (d) S. Gonell, X. Caumes, N. Orth, I. Ivanović-Burmazović and J. N. H. Reek, Chem. Sci., 2019, 10, 1316–1321; (e) R. Zaffaroni, N. Orth, I. Ivanović-Burmazović and J. N. H. Reek, Angew. Chem., Int. Ed., 2020, 59, 18485–18489.
8. For examples of electrocatalysis within coordination assemblies, see: (a) R. Zaffaroni, E. O. Bobylev, R. Plessius, J. I. van der Vlugt and J. N. H. Reek, J. Am. Chem. Soc., 2020, 142, 8837–8847; (b) C. J. Bruns, D. Fujita, M. Hoshino, S. Sato, J. F. Stoddart and M. Fujita, J. Am. Chem. Soc., 2014, 136, 12027–12034.
9. For examples of electro-optical applications of coordination assemblies, see: (a) X. Yan, P. Wei, Y. Liu, M. Wang, C. Chen, J. Zhao, G. Li, M. L. Saha, Z. Zhou, Z. An, X. Li and P. J. Stang, J. Am. Chem. Soc., 2019, 141, 9673–9679; (b) J. Y. Ryu, J. M. Lee, N. Van Nghia, K. M. Lee, S. Lee, M. H. Lee, P. J. Stang and J. Lee, Inorg. Chem., 2018, 57, 11696–11703; (c) D. Fujita, Y. Ueda, S. Sato, N. Mizuno, T. Kumasaka and M. Fujita, Nature, 2016, 540, 563–566.
10. N. J. Young and B. P. Hay, Chem. Commun., 2013, 49, 1354–1379.
11. J. Bunzen, J. Iwasa, P. Bonakdarzadeh, E. Numata, K. Rissanen, S. Sato and M. Fujita, Angew. Chem., Int. Ed., 2012, 51, 3161–3163.
12. For examples of shape-complimentary M₂L₄ cages, see: (a) W. Bloch, Y. Abe, J. Holstein, C. M. Wandtke, B. Dittrich and G. H. Clever, J. Am. Chem. Soc., 2016, 138, 13750–13755; (b) S. Saha, B. Holzapfel, Y. T. Chen, K. Terlinden, P. Lill, C. Gatsogiannis, H. Rehag and G. H. Clever, J. Am. Chem. Soc., 2018, 140(50), 17384–17388; (c) R. Zhu, W. Bloch, J. Holstein, S. Mandal, L. V. Schafer and G. H. Clever, Chem.–Eur. J., 2018, 24(49), 12976–12982; (d) R. J. Li, J. Holstein, W. Hiller, J. Andreasson and G. H. Clever, J. Am. Chem. Soc., 2019, 141(5), 2097–2103; (e) B. Chen, J. J. Holstein, S. Horiuchi, W. G. Hiller and G. H. Clever, J. Am. Chem. Soc., 2019, 141, 8907–8913.
13. L. R. MacGillivray and J. L. Atwood, Angew. Chem., Int. Ed., 1999, 38, 1018–1033.
14. J. E. M. Lewis and J. D. Crowley, ChemPlusChem, 2020, 85, 815–820.
15. For relevant studies classical mechanics dynamics of Pd_xL_2x coordination assemblies using non-bonded metal centers, see: (a) M. Yoneya, T. Yamaguchi, S. Sato and M. Fujita, J. Am. Chem. Soc., 2012, 134, 14401–14407; (b) M. Yoneya, S. Tsuzuki, T. Yamaguchi, S. Sato and M. Fujita, ACS Nano, 2014, 8, 1290–1296; (c) Y. Tachi, S. Sato, M. Yoneya, M. Fujita and Y. Okamoto, Chem. Phys. Lett., 2019, 714, 185–189.
16. For examples of classical mechanics, semi-empirical and DFT studies to study coordination assembly host-guest chemistry, see: (a) T. A. Young, R. Gheorghe and F. Duarte, J. Chem. Inf. Model., 2020, 60(7), 3546–3557; (b) V. Marti-Centelles, F. Duarte and P. J. Lusby, Isr. J. Chem., 2019, 59, 257–266; (c) R. L. Spicer, A. D. Stergiou, T. A. Young, F. Duarte, M. D. Symes and P. J. Lusby, J. Am. Chem. Soc., 2020, 142, 2134–2139; (d) T. A. Young, V. Marti-Centelles, J. Wang, P. J. Lusby and F. Duarte, J. Am. Chem. Soc., 2020, 142(3), 1300–1310.
17. In regards to modern methodological development in structural discovery and improved mechanics forcefields, refer to: (a) P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192; (b) S. Spicher and S. Grimme, Angew. Chem., Int. Ed., 2020, 59(36), 15665–15673; (c) See also ref. 25.
18. Q. F. Sun, J. Iwasa, D. Ogawa, Y. Ishido, S. Sato, T. Ozeki, Y. Sei, K. Yamaguchi and M. Fujita, Science, 2010, 328, 1144–1147.
19. D. A. Case, T. E. Cheatham, T. Darden, H. Gohlke, R. Luo, K. M. Merz, A. Onufriev, C. Simmerling, B. Wang and R. J. Woods, J. Comput. Chem., 2005, 26, 1668–1688.
20. A. W. Götz, M. J. Williamson, D. Xu, D. Poole, S. Le Grand and R. C. Walker, J. Chem. Theory Comput., 2012, 8, 1542–1555.
21. J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174.
22. P. Li, B. P. Roberts, D. K. Chakravorty and K. M. Merz, J. Chem. Theory Comput., 2013, 9, 2733–2748.
23. R. M. Betz and R. C. Walker, J. Comput. Chem., 2015, 36, 79–87.
24. A. D. McLachlan, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1982, 38, 871–873.
25. C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671.
26. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
27. D. Fujita, Y. Ueda, S. Sato, H. Yokoyama, N. Mizuno, T. Kumasaka and M. Fujita, Chem, 2016, 1, 91–101.
28. S. Kai, T. Shigeta, T. Kojima and S. Hiraoka, Chem.–Asian J., 2017, 12, 3203–3207.
29. M. Tominaga, K. Suzuki, M. Kawano, T. Kusukawa, T. Ozeki, S. Sakamoto, K. Yamaguchi and M. Fujita, Angew. Chem., Int. Ed., 2004, 43, 5621–5625.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc03992f

---