Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A family of diastereomeric dodecanuclear coordination cages based on inversion of chirality of individual triangular cyclic helicate faces†
Stephen P.
Argent
*ab,
Fiona C.
Jackson
a,
Ho Man
Chan
a,
Sam
Meyrick
a,
Christopher G. P.
Taylor
 a,
Tanya K.
Ronson
a,
Tanya K.
Ronson
 c,
Jonathan P.
Rourke
c,
Jonathan P.
Rourke
 d and
Michael D.
Ward
d and
Michael D.
Ward
 *a
*a
aDepartment of Chemistry, University of Warwick, Coventry CV4 7AL, UK. E-mail: m.d.ward@warwick.ac.uk
bSchool of Chemistry, University of Nottingham, University Park, Nottingham NG7 2RD, UK. E-mail: stephen.argent@nottingham.ac.uk
cUniversity Chemistry Laboratory, University of Cambridge, Lensfield Road, Cambridge CB2 1EW, UK
dSchool of Chemistry, Cardiff University, Main Building, Park Place, Cardiff CF10 3AT, UK
First published on 8th September 2020
Abstract
The dodecanuclear coordination cage [Cd12(Lnaph)12(Lmes)4](BF4)24 consists of a set of four triangular, trinuclear helical panels {Cd3(μ-Lnaph)3}6+ (based on ditopic bridging ligands Lnaph), which are connected by four tritopic ligands Lmes. The result is that the four triangular helical panels and the four Lmes-capped triangular faces of the cuboctahedral core form two alternating subsets of the eight triangular faces of the cuboctahedron. Crystallographic investigations revealed that the triangular helicate faces can have ‘clockwise’ (C) or ‘anticlockwise’ (A) helicity, and that the helicity of each face can vary independently of the others as they are mechanically separated. This generates a set of three diastereoisomers in which all four cyclic helicate faces in the cuboctahedron have the same chirality (AAAA/CCCC enantiomers with T symmetry; AAAC/CCCA enantiomers with C3 symmetry; and achiral AACC with S4 symmetry). This mirrors the known behaviour of many simpler M4L6 tetrahedral cages which can likewise exist as T, C3 or S4 isomers according to the sense of tris-chelate chirality around each individual metal centre: but here it is translated onto a much larger scale by the four chiral units being entire trinuclear helicate faces rather than single metal centres. 1H NMR spectroscopy confirms the presence of the three diastereoisomers with their different molecular symmetries in a ratio slightly different from what is expected on purely statistical grounds; and 1H NMR measurements on a non-equilibrium sample (enriched by manual crystal-picking before preparing the solution) showed that the distribution does not change over several weeks in solution, indicating the kinetic inertness of the cage assemblies.
Introduction
The assembly of combinations of metal ions and multi-topic bridging ligands into coordination cages is now a mature field which has afforded a huge range of beautiful species of interest for their structural diversity1–5 and the functions arising from their host–guest chemistry.2 A large subset of these, based on square planar Pd(II)/Pt(II) and rigid linear or panel-like planar ligands,3 illustrate how elaborate structures can be assembled with a high degree of predictability once the underlying structural and geometric principles are appreciated. In contrast, the use of octahedral tris-chelate vertices provides two additional sources of structural diversity which are less predictable. These are (i) the possibility of fac/mer isomerism at individual metal centres in a multinuclear assembly,4 and (ii) the chirality at each centre associated with the configuration in which the three chelate units assemble around the metal. Chirality in large self-assembled systems is a highly important and topical field.5An interesting consequence of incorporation of multiple octahedral tris-chelate metal centres into cages is the possibility of diastereoisomerism arising from inversion of configuration at one centre but not others, affording a family of related but structurally distinct complexes. This is best illustrated by some examples of M4L6 tetrahedral complexes in which bis-bidentate bridging ligands span the cage edges. Usually such tetrahedral cages form homochiral assemblies (as racemates), i.e. they have ΛΛΛΛ/ΔΔΔΔ configurations with T molecular symmetry.6 However they can also sometimes form with one vertex inverted with respect to the other three, i.e. they have ΛΛΛΔ/ΔΔΔΛ configurations with C3 molecular symmetry; or two vertices can be inverted giving achiral ΛΛΔΔ assemblies with S4 molecular symmetry. A few such systems where all three diastereoisomers are present in equilibrium have been reported.7
Here, we report a novel extension of this principle in the form of a diastereomeric family of dodecanuclear cuboctahedral coordination cages in which the structural variation is provided not by inversion of individual metal vertices, but by inversion of chirality of entire triangular cyclic helicate faces. Inverting the chirality of entire triangular panels, independently of one another, in a polyhedral assembly provides an intriguing addition to the structural diversity of these cages. Using purely organic assemblies and covalent bond formation, Cao and co-workers have demonstrated how different enantiomers of a three-fold symmetric truxene unit could be incorporated into the triangular faces of an octahedral assembly, with different diastereoisomers of the cage being formed according to the disposition of truxene units of different chirality around the faces.8 The examples we report here, based on self-assembly using achiral ligands and labile metal ions, constitute the first such example in the field of metal-directed assembly of coordination cages. All three diastereomeric forms of the cuboctahedral cage have been identified and structurally characterised, with 1H and 113Cd NMR spectroscopy confirming the existence of the mixture of diastereomers in solution.
Results and discussion
Several years ago we reported the assembly and crystal structures of some unusual cuboctahedral cage complexes that formed by selection of two different ligands from a mixture during the assembly process (Scheme 1 and Fig. 1).9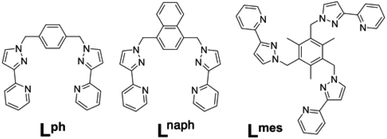 | ||
| Scheme 1 Structural formulae of the face-capping ligand Lmes and the edge-bridging ligands Lph and Lnaph referred to in this paper. | ||
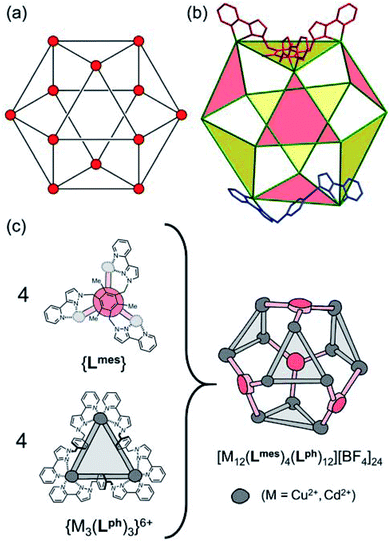 | ||
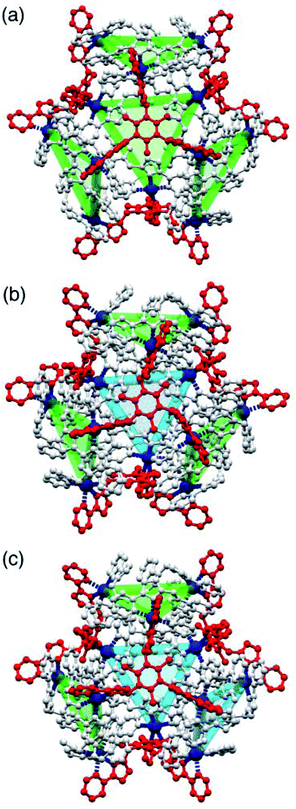
| Fig. 1 (a) An idealised cuboctahedron; (b) partial crystal structure of [Cu12(Lph)12(Lmes)4](BF4)24 (taken from ref. 9b) emphasising the cuboctahedral Cu12 core with the four triangular faces capped by tritopic ligands Lmes coloured yellow, and the alternate four triangular faces – which are Cu3(μ-Lph)3 cyclic helicates – coloured pink; (c) additional sketch emphasising the disposition of the four M3(μ-Lph)3 cyclic helicate faces in these structures (grey triangles) and the four Lmes ligands which connect them (red). | ||
The complexes [M12(Lph)12(Lmes)4]X24 (M = Cu, Cd; X = ClO4 or BF4) contain a cuboctahedral core of twelve M(II) ions which contains eight triangular faces and six square faces. The cuboctahedral structure may be considered as derived from a cube, with the eight corners truncated to reveal triangular faces whose vertices meet exactly in the centre of what used to be an edge of the cube. With all vertices equivalent but with two different types of face, the cuboctahedron is one of the class of Archimedean solids. The two types of ligand (ditopic Lph is edge-bridging and tritopic Lmes is face-capping) are associated with different subsets of the eight triangular faces; these eight faces can thus be split into two subsets of four (Fig. 1b), which alternate around the cage and each describe a tetrahedron. In one subset of four triangular faces, each face is capped by a tripodal Lmes ligand. In the other subset, each of the four triangular faces contains a set of three Lph ligands around the edges, with all ligands having a helical twist such that each triangular face is a M3(μ-Lph)3 cyclic helicate.9 The assembly can be regarded as a tetrahedral array of four M3(μ-Lph)3 cyclic helicates, each with a vacant site for an additional chelating ligand at each metal ion, connected by four Lmes ligands: this way of considering the structure is emphasised in Fig. 1c.
For the Cd12 cage of this type that we reported earlier,9 we observed three 113Cd environments by NMR, implying a loss of regular cuboctahedral symmetry in which all metal ions would be equivalent. This was unexpected and a consequence of the fact that two of the four triangular cyclic helical faces have ‘clockwise’ helicity (which we denote ‘C’) and the other two have ‘anticlockwise’ helicity (which we denote ‘A’) giving a CCAA combination of face chiralities. This results in (non-crystallographic) S4 molecular symmetry such that one quarter of each cage – i.e. a subset of three metal ions and the associated ligands – is unique.9,10 As this structural type was the only product isolated for each of the original [M12(Lph)12(Lmes)4]X24 cages9 no particular significance was attached to this at the time, but it becomes relevant to this new work.
Motivated by the ability of some members of our cage family to act as excellent hosts for small molecule guests,11 we have revisited this cuboctahedral cage structure with the intention of investigating its host/guest chemistry. We also wished to incorporate fluorophores into the ligand array which might act as luminescent reporters of guest binding, or which might perform photoinduced electron transfer or energy transfer to bound guests in the manner that we have recently demonstrated with different photo-active cages.12 Accordingly we used the same methodology as was used for preparation of the original cuboctahedral complexes [M12(Lph)12(Lmes)4]X24,9 but have replaced the edge-bridging ligand Lph with Lnaph (Scheme 1)13 to incorporate the fluorescent groups that we wanted. Examination of the structures of the original cages [M12(Lph)12(Lmes)4]X24 indicated that incorporation of the additional aromatic rings by replacing Lph with Lnaph should not present a significant steric barrier to cage assembly, and so it proved.
Reaction of Lnaph, Lmes and Cd(BF4)2 in a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
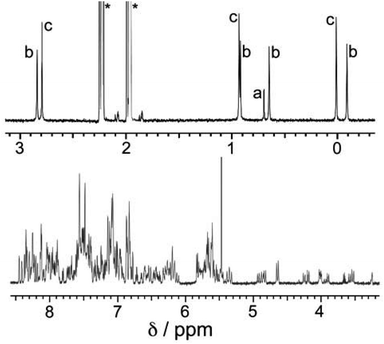
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 ratio, as required for assembly of the desired cuboctahedral cage, in acetonitrile followed by rapid precipitation upon addition of diisopropyl ether afforded a colourless crystalline solid which proved to the desired product [Cd12(Lnaph)12(Lmes)4](BF4)24. ES mass spectrometry confirmed the formulation, showing a characteristic sequence of peaks corresponding to {[Cd12(Lnaph)12(Lmes)4](BF4)24−n}n+ (n = 4–9), i.e. the intact cage cation associated with varying numbers of anions (Fig. S1†). 1H NMR spectroscopy (Fig. 2) revealed a very complex spectrum with numerous sub-spectra of different intensities, clearly indicating the presence of a mixture of species. This is particularly clearly apparent in the 0–3 ppm region where the signals for the methyl groups of Lmes appear; these provide a much more convenient diagnostic handle than the aromatic region where numerous signals overlap.
3 ratio, as required for assembly of the desired cuboctahedral cage, in acetonitrile followed by rapid precipitation upon addition of diisopropyl ether afforded a colourless crystalline solid which proved to the desired product [Cd12(Lnaph)12(Lmes)4](BF4)24. ES mass spectrometry confirmed the formulation, showing a characteristic sequence of peaks corresponding to {[Cd12(Lnaph)12(Lmes)4](BF4)24−n}n+ (n = 4–9), i.e. the intact cage cation associated with varying numbers of anions (Fig. S1†). 1H NMR spectroscopy (Fig. 2) revealed a very complex spectrum with numerous sub-spectra of different intensities, clearly indicating the presence of a mixture of species. This is particularly clearly apparent in the 0–3 ppm region where the signals for the methyl groups of Lmes appear; these provide a much more convenient diagnostic handle than the aromatic region where numerous signals overlap.
Recrystallisation of the material by slow diffusion of di(isopropyl)ether vapour into a solution of the material in MeCN afforded single crystals with different habits: unit cell determination on many of these revealed that three different unit cells could be identified consistently, all occurring as a mixture in each batch of crystals. Accordingly we collected all three data sets and found on solving and refining the structures that we have isolated three different diastereoisomers of the expected cuboctahedral cage [Cd12(Lnaph)12(Lmes)4](BF4)24, with the differences arising from the helicity of the individual Cd3(μ2-Lnaph)3 helicate faces. We will give a general overview of this first to illustrate the principle before discussing the individual structures in detail.
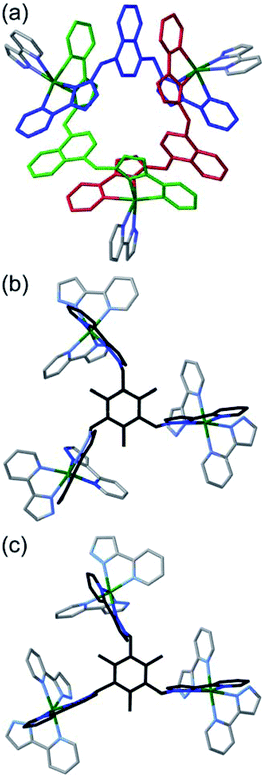
The array of metal ions in a regular cuboctahedron has the same symmetry as a cube, i.e. point group Oh, with all twelve vertices equivalent (Fig. 1). This is not affected by the presence of the Lmes ligands on four of the eight triangular faces, as these triangular ligands are capable – when coordinated in a face-capping mode – of preserving the threefold rotational symmetry through those faces. The isomerism arises from the fact that each of the four Cd3(μ-Lnaph)3 helicate faces can have ‘clockwise’ (C) or ‘anticlockwise’ (A) helicity, and, crucially, that these can vary independently of one another. Each Cd3(μ2-Lnaph)3 face (pink in Fig. 1b) is connected via a shared vertex to three Cd3(μ3-Lmes) faces (yellow in Fig. 1b) in which coordination of the achiral, tripodal Lmes ligand is not affected by the sense of rotation of these Cd3(μ2-Lnaph)3 faces; each chelating arm in Lmes will occupy the same two coordination sites of each of its Cd(II) ions, even if the other two chelating pyrazolyl-pyridine units (from Lnaph) have their positions changed to invert the chirality at that metal centre. Changing the helicity around one Cd3(μ2-Lnaph)3 face does not, therefore, trigger any ongoing requirements for major changes in ligand coordination elsewhere: the four cyclic helicate Cd3(μ2-Lnaph)3 faces are mechanically decoupled from one another and can act independently in this respect.
The consequences of this are illustrated in cartoon form in Fig. 3. The two enantiomers of the cyclic helicate faces are shaded blue or green, and these are connected by the Lmes tripodal ligands (red). With four cyclic helicate faces arranged in a tetrahedron around the cuboctahedral core, the different combinations of helicity mirror exactly what happens in smaller M4L6 cages described above which can occur as a mixture of T, C3 and S4 isomers depending on whether individual metal tris-chelate centres have Λ or Δ configurations. Thus the cuboctahedron containing four chiral cyclic helicate Cd3(μ2-Lnaph)3 faces can in principle exist as a homochiral T-symmetric isomer CCCC/AAAA (which are of course enantiomers); a C3-symmetric ACCC/CAAA isomer in which one of the Cd3(μ2-Lnaph)3 faces has the opposite helicity to the other three; and the S4-symmetric AACC/CCAA isomer. This is shown in Fig. 3b which also emphasises the degeneracies of these structures, i.e. the numbers of ways in which they can form by random aggregation of the cyclic helicate faces (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 for the T, C3 and S4 isomers respectively).
3 for the T, C3 and S4 isomers respectively).
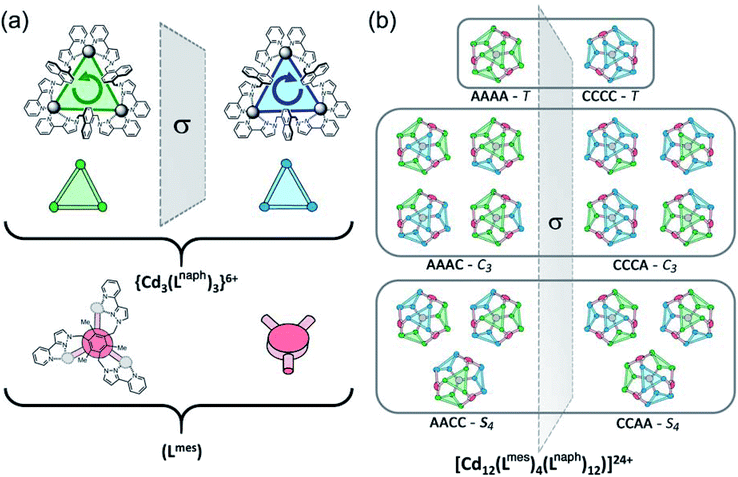 | ||
Fig. 3 Graphical illustration of the different stereoisomers of the cage and their degeneracies: (a) illustration of the two different chiralities of the cyclic helicate triangular panels, shown as green (anticlockwise, A) and blue (clockwise, B) panels, with the connecting tripodal ligands Lmes shown in red; (b) illustration of the different ways in which these chiral panels can assemble into a cuboctahedral Cd12 array, highlighting both the different enantiomers within each diastereoisomeric structure (left and right of the central mirror plane) and the number of ways in which each diastereoisomer can be achieved (degeneracy) based on random assembly of chiral panels. Bearing in mind that the AACC and CCAA isomers in Fig. 3(b) are identical as this isomer is achiral, we can see that the five stereoisomers AAAA, AAAC, AACC, ACCC and CCCC would have a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binomial distribution if assembly of the A and C chiral faces were completely random. For spectroscopic purposes, given that the two enantiomers AAAA/CCCC and the two enantiomers AAAC/CCCA are equivalent by NMR spectroscopy, this would give a 2 1 binomial distribution if assembly of the A and C chiral faces were completely random. For spectroscopic purposes, given that the two enantiomers AAAA/CCCC and the two enantiomers AAAC/CCCA are equivalent by NMR spectroscopy, this would give a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 (= 1 6 (= 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3) expected ratio of diastereoisomers, see main text. 3) expected ratio of diastereoisomers, see main text. | ||
More subtly, in these diastereomers the environments of the Lmes ligands will be different. In the T isomer these four ligands are all equivalent and all retain their threefold symmetry, such that one third of an Lmes ligand and one Cd atom – one twelfth of the assembly – are unique and all 12 Cd atoms are equivalent. In the C3 isomer (AAAC and its enantiomer) one Lmes ligand on the C3 axis is adjacent to three equivalent ‘A’ helical faces and retains its threefold symmetry; the other three Lmes ligands are all adjacent to two ‘A’ and one ‘C’ helical faces: they are equivalent to one another but different from the first one, and have lost their internal symmetry. This means that there are 1.333 independent Lmes ligands (four independent pyrazolyl-pyridine chelating arms) and hence four independent Cd atom environments (one third of the assembly). Finally in the AACC isomer all four Lmes ligands are equivalent, as each one is adjacent to an A/A/C (or the enantiomeric A/C/C) set of helical faces, but have no internal symmetry. Thus there is 1 unique Lmes ligand and hence three independent Cd atom environments (one quarter of the assembly) in this diastereomer. These considerations are important for understanding the NMR spectra which will be discussed later.
One of the crystal morphologies had the cubic space group F23, and this turned out to be the T symmetry isomer with a homochiral arrangement of the four identical Cd3(μ2-Lnaph)3 faces (Fig. 4 and 5). F23 is a chiral space group: the absolute configuration could not be determined reliably due to a combination of twinning and low resolution of the diffraction data, but the homochiral arrangement of all metal centres is clear, with the asymmetric unit containing one twelfth of the cage structure (one metal ion, one Lnaph ligand and one third of an Lmes ligand). A view of the entire assembly is in Fig. 4a, and views looking onto the Lmes-capped face and the Cd3(μ2-Lnaph)3 cyclic helicate face are in Fig. 5. It is clear that the cyclic helicate arrays are stabilised by π-stacking with the naphthyl group of one ligand sandwiched between the coordinated pyrazolyl-pyridine units of the other two. The Cd⋯Cd separations within the helicate faces and the Lmes-capped faces are 9.97 Å and 11.41 Å respectively.
The crystals that grow in space group P21/n turned out to be the C3 symmetric AAAC/CCCA isomer (Fig. 4b). In this case the idealised molecular symmetry is not reflected in the crystal structure, with all 12 Cd(II) ions being crystallographically inequivalent and hence the asymmetric unit containing an entire molecule. Nonetheless it is clear that one cyclic helicate face has the opposite helical chirality to the other three: this results in one Lmes ligand having (non-crystallographic) threefold symmetry and the other three Lmes ligands being significantly distorted away from this (Fig. 4b). As in the previous example, the Cd⋯Cd separations around the cyclic helicate faces (9.94–10.41 Å; average 10.16 Å) are considerably shorter than those on the Lmes-capped faces (average 11.38 Å, with a much wider spread from 10.35 to 12.56 Å). Finally, the crystals that grow in space group C2/c were the S4-symmetric AACC isomer (Fig. 4c). The crystallographic symmetry (six independent metal ions, i.e. half of the molecule astride a twofold rotation axis) is again lower than the ideal molecular symmetry (with three metal ions, one quarter of the molecule, constituting the asymmetric unit) but the presence of two ‘C’ helicate and two ‘A’ helicate faces is clear. This molecular symmetry requires that all four cyclic helicate faces are structurally equivalent but with all three metal ions within each cyclic helicate being inequivalent; consequently the four Lmes ligands are likewise equivalent to one another but have no internal symmetry and those triangular faces have significantly different Cd⋯Cd separations in them. The Cd⋯Cd separations around the helicate faces average 10.06 Å and fall in a very narrow range (10.04–10.09 Å) whereas those on the Lmes-capped faces are on average longer (11.44 Å) and spread over a wider range (11.04–12.18 Å).
The crystal structures of the three isomers show that the cage molecules enclose large voids whose total volumes can be determined by applying the PLATON-SOLV routine to sets of coordinates from which all solvent and anion entities have been removed and cage apertures artificially blocked. The total volumes of isomers AAAA, AAAC and AACC calculated in this way are 1036, 1121 and 1047 Å3 respectively. These minor variations in cavity volumes follow the trend of variations in the volumes of the convex alpha shape defined by the coordinates of the twelve cadmium cations for the isomers: 2872, 2975 and 2951 Å3 respectively. Whilst the cage contents and surrounding residues of isomer AAAA cannot be determined from the weak low resolution diffraction data, the contents of the other two cage isomers AAAC and AACC are observed to be a mixture of tetrafluoroborate counterions and solvent molecules (Table S2†). The crystal structures of isomers AAAC and AACC both reveal numerous associations between the cage exterior and interior surfaces with water and acetonitrile solvent residues, mediated by multiple weak C–H⋯O and C–H⋯N hydrogen bonds (Fig. S6–S11†).
We can now understand the 1H NMR spectrum (Fig. 2). Although the aromatic region is too complex to provide useful information, the signals from the methyl groups on the Lmes ligands (0–3 ppm region) are completely diagnostic as they correlate exactly with the number of Cd environments. Thus for the T symmetry isomer we expect one signal arising from all 12 equivalent methyl groups; for the C3 isomer we expect four different signals, each from three equivalent methyl groups; and for the S4 isomer we expect three different signals, each from four equivalent methyl groups. A mixture of the three isomers would therefore contain eight signals (sets of 1 + 3 + 4) and this is clear in Fig. 2. The relative intensities of these will depend on the abundance of each isomer in the mixture, which in turn depends not just on simple thermodynamic stability issues but also on the degeneracy of each structure.
A simple calculation‡ suggests that if the distribution of cyclic helicate units amongst the ensemble of the cages were purely statistical, all eight signals from methyl groups would end up with the same intensity. From the 1H NMR spectrum this is clearly not the case with the signal for the T isomer being relatively weak and the three signals for the S4 isomer being relatively abundant, with an overall isomer distribution of 5% (T), 47.5% (C3) and 47.5% (S4) (Fig. 2). This could reflect small differences in thermodynamic stability between the diastereoisomers or could be a kinetic effect associated with different solubilities and crystallisation rates of the three components: we return to this point below. This ratio is repeatable between multiple crystalline samples. The 113Cd NMR spectrum (Fig. 6) should follow exactly the same pattern to that found for the methyl groups in the 1H NMR spectrum. Although the very similar environments of the Cd(II) ions will lead to only small differences in chemical shift, we do observe a number of different resonances. Though the signals are not fully resolved, we can identify signals for the different Cd environments with different intensities, partially overlapping but approximately consistent with the 1H NMR spectrum.
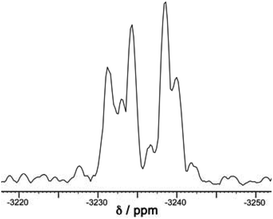 | ||
| Fig. 6 The 113Cd NMR spectrum of freshly prepared [Cd12(Lnaph)12(Lmes)4](BF4)24 (mixture of isomers) in CD3CN. This spectrum is a 1D projection of the F2 dimension taken from the 8.51–6.36 ppm region of the 1H dimension of the 600 MHz 1H–113Cd HMBC spectrum (full spectra available in the ESI†). The broad peaks of overlapping 113Cd environments preclude a full deconvolution so we cannot see clear sets of 1, 3 and 4 signals that match the methyl groups in the 1H NMR spectrum (Fig. 2), but the spectrum is approximately consistent with the expected number and relative intensities of Cd(II) environments. | ||
Examination of batches of crystals under an optical microscope revealed visibly distinct block-like and teeth-like crystals. Manual selection of the block-like crystals afforded samples which NMR spectroscopy showed to be dominantly the S4-symmetric stereoisomer; after multiple attempts we were able to obtain a sample of a small number of crystals whose NMR spectrum contained only the three signals (denoted ‘c’ in Fig. 7a) associated with the methyl groups of that isomer (Fig. 7b). Whilst the signal at 0.9 ppm is partly obscured by a solvent impurity, the other two signals at 0.0 and 2.8 ppm are clear; and equally clearly the signals ‘a’ and ‘b’ arising from the T and C3 isomers are absent. Spectra recorded again of this sample after 1 week and then 7 weeks showed no change, implying that the S4 isomer is kinetically trapped at RT. Manual selection of the teeth-like crystals was less successful at separating the isomers: the NMR spectrum of these samples showed the presence of all three stereoisomers, albeit in a ratio different from that of the bulk sample. The spectrum shown in Fig. 7c shows an excess of the T isomer (signal ‘a’), and a deficiency of the S4 isomer (signals ‘c’), compared to the as-synthesised mixture (Fig. 7a). Again this is kinetically trapped at room temperature, with the non-equilibrium spectrum shown in Fig. 7c not changing significantly after weeks in CD3CN solution.
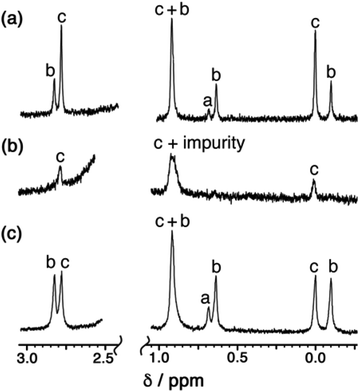 | ||
| Fig. 7 400 MHz 1H NMR spectra in CD3CN of (a) a recrystallised sample of [Cd12(Lnaph)12(Lmes)4](BF4)24 before manual separation of crystal morphologies (this is the same as the spectrum in Fig. 2 except at 400 MHz and is replicated here to aid comparison with the spectra below); (b) manually separated crystals with teeth-like morphology; and (c) manually separated crystals with block morphology. Spectra (b) and (c) of manually selected crystals did not change appreciably over a period of six weeks at room temperature. | ||
The Cd12 cage assembly system is clearly kinetically inert at RT despite the fact that it is based on individually labile Cd(II) ions. Inverting the chirality of a whole triangular helical panel would require a substantial degree of ligand dissociation as the first step which would present a high activation energy barrier: we have shown before that cages of this general type are very slow (weeks/months) to undergo structural rearrangements14 or ligand exchange reactions,15 and the same is true of other families self-assembled cages.16
Finally, the question arises as to whether the isomer proportions observed in the bulk crystalline sample when it is redissolved (Fig. 2) constitute a thermodynamic minimum, or whether this distribution is a kinetic artefact of the crystallisation process arising from different solubilities of the three isomers. Two experiments suggest that the proportions in the spectrum in Fig. 2 are at, or close to, the thermodynamic minimum. Firstly, we followed the assembly by 1H NMR spectroscopy without crystallisation of the components, by combining Cd(BF4)2 and the two ligands in the correct proportions in CD3CN in an NMR tube; the slow appearance of the various methyl signals associated with the Cd12 cage between 0 and 3 ppm provided a simple way to follow the assembly process. After 1 h we could see the first signs of the appearance of these signals; and after 2 days the spectrum had stopped evolving (see ESI, Fig. S13†). The spectrum generated by in situ assembly was noisy due to solubility limitations of the components so the isomer ratio cannot be determined with high precision, but all three isomers have clearly formed in this experiment in a ratio similar to what was observed in Fig. 2 from the redissolved crystalline sample.
Secondly, we heated a sample of redissolved crystalline material in CD3CN to 65 °C for 90 minutes. At this temperature we could see small changes in the proportions of the isomers, with a slight increase in the proportion of the S4 isomer which then stopped when a new equilibrium was reached after 90 minutes (see ESI, Fig. S14†). Returning the sample to RT resulted in this new slightly changed distribution being kinetically trapped as no further change occurred: the fact that ‘unlocking’ the cage by heating to 65 °C resulted in only a small change in the equilibrium position – which might reasonably be ascribed to the temperature change – implies that the starting solution (prepared from redissolved crystals) was close to equilibrium in the first place.
Conclusion
In conclusion, we have structurally characterised a unique set of three diastereomeric Cd12 coordination cages (T, C3 or S4 symmetry) based on an overall cuboctahedral array of metal ions with a combination of edge-bridging (ditopic) and face-capping (tritopic) ligands, but displaying different combinations of chirality around the four triangular cyclic helicate faces. In contrast to previous examples of tetrahedral M4L6 cages where the presence of T, C3 or S4 symmetry is dictated by the tris-chelate configuration of chelating ligands around the individual metal centres, in this M12 cage it arises from the different cyclic helicate arrangements associated with the four triangular Cd3(μ2-Lnaph)3 faces. This source of diastereoisomerism is new to the field of coordination cages and has provided here a set of molecular containers of essentially the same shape and size, but with different cavity chirality. Partial separation of diastereoisomers by manual selection of crystals of different habits was possible. Given the interest in use of chiral molecular containers for various applications based on chiral molecular recognition,5 this represents an intriguing and potentially valuable new source of structural diversity. The cages are highly kinetically inert despite being based on labile Cd(II) ions, with non-equilibrium samples generated by manual selection of crystals with different habits showing no change in their isomer ratio by NMR spectroscopy during weeks at RT.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the University of Warwick, and EPSRC (grant EP/N031555/1), for financial support for this work.Notes and references
- (a) T. R. Cook and P. J. Stang, Chem. Rev., 2015, 115, 7001 CrossRef CAS; (b) T. R. Cook, Y.-R. Zheng and P. J. Stang, Chem. Rev., 2013, 113, 734 CrossRef CAS; (c) R. Chakrabarty, P. S. Mukherjee and P. J. Stang, Chem. Rev., 2011, 111, 6810 CrossRef CAS; (d) M. M. J. Smulders, I. A. Riddell, C. Browne and J. R. Nitschke, Chem. Soc. Rev., 2013, 42, 1728 RSC.
- (a) M. D. Ward and P. R. Raithby, Chem. Soc. Rev., 2013, 42, 1619 RSC; (b) Y. Fang, J. A. Powell, E. Li, Q. Wang, Z. Perry, A. Kirchon, X. Yang, Z. Xiao, C. Zhu, L. Zhang, F. Huang and H.-C. Zhou, Chem. Soc. Rev., 2019, 48, 4707 RSC; (c) C. J. Brown, F. D. Toste, R. G. Bergman and K. N. Raymond, Chem. Rev., 2015, 115, 3012 CrossRef CAS; (d) C. Deraedt and D. Astruc, Coord. Chem. Rev., 2016, 324, 106 CrossRef CAS; (e) D. Zhang, T. K. Ronson and J. R. Nitschke, Acc. Chem. Res., 2018, 51, 2423 CrossRef CAS; (f) M. Yoshizawa, J. K. Klosterman and M. Fujita, Angew. Chem., Int. Ed., 2009, 48, 3418 CrossRef CAS.
- (a) M. Fujita, Struct. Bonding, 2000, 96, 177 CrossRef CAS; (b) M. Fujita, M. Tominaga, A. Hori and B. Therrien, Acc. Chem. Res., 2005, 38, 369 CrossRef CAS; (c) B. H. Northrop, Y.-R. Zheng, K.-W. Chi and P. J. Stang, Acc. Chem. Res., 2009, 42, 1554 CrossRef CAS.
- (a) A. J. Metherell and M. D. Ward, Dalton Trans., 2016, 45, 16096 RSC; (b) A. J. Metherell, W. Cullen, A. Stephenson, C. A. Hunter and M. D. Ward, Dalton Trans., 2014, 43, 71 RSC.
- (a) L.-J. Chen, H.-B. Yang and M. Shionoya, Chem. Soc. Rev., 2017, 46, 2555 RSC; (b) H. Jedrzejewska and A. Szumna, Chem. Rev., 2017, 117, 4863 CrossRef CAS; (c) D. Bradshaw, J. B. Claridge, E. J. Cussen, T. J. Prior and M. J. Rosseinsky, Acc. Chem. Res., 2005, 38, 273 CrossRef CAS; (d) B. Sun, S. S. Nurttila and J. N. H. Reek, Chem.–Eur. J., 2018, 24, 14693 CrossRef CAS; (e) L.-Y. Bao, S.-J. Hao, S.-F. Xi, X. Yan, H.-X. Zhang, R. Shen and Z.-G. Guo, Chem. Commun., 2018, 54, 8725 RSC; (f) Y. Yang, Y. Wu, J.-H. Jia, X.-Y. Zheng, Q. Zhang, K.-C. Xiong, Z.-M. Zhang and Q.-M. Wang, Cryst. Growth Des., 2018, 18, 4555 CrossRef CAS; (g) T. Tateishi, T. Kojima and S. Hiraoka, Commun. Chem., 2018, 1, 20 CrossRef; (h) J. Jiao, C. Tan, Z. Li, Y. Liu, X. Han and Y. Cui, J. Am. Chem. Soc., 2018, 140, 2251 CrossRef CAS; (i) C. Tian, J. Jiao, Y. Liu, X. Han and Y. Cui, Angew. Chem., Int. Ed., 2018, 57, 2085 CrossRef; (j) A. M. Castilla, W. J. Ramsay and J. R. Nitschke, Acc. Chem. Res., 2014, 47, 2063 CrossRef CAS; (k) T. D. Hamilton and L. R. MacGillivray, Cryst. Growth Des., 2004, 4, 419 CrossRef CAS.
- (a) D. L. Caulder, R. E. Powers, T. N. Parac and K. N. Raymond, Angew. Chem., Int. Ed., 1998, 37, 1840 CrossRef CAS; (b) P. Mal, D. Schultz, K. Beyeh, K. Rissanen and J. R. Nitschke, Angew. Chem., Int. Ed., 2008, 47, 8297 CrossRef CAS; (c) I. S. Tidmarsh, B. F. Taylor, M. J. Hardie, L. Russo, W. Clegg and M. D. Ward, New J. Chem., 2009, 33, 366 RSC; (d) R. W. Saalfrank, B. Demleitner, H. Glaser, H. Maid, D. Bathelt, F. Hampel, W. Bauer and M. Teichert, Chem.–Eur. J., 2002, 8, 2679 CrossRef CAS; (e) L. Li, A. R. Craze, O. Mustonen, H. Zenno, J. J. Whittaker, S. Hayami, L. F. Lindoy, C. E. Marjo, J. K. Clegg, J. R. Aldrich-Wright and F. Li, Dalton Trans., 2019, 48, 9935 RSC; (f) C. R. K. Glasson, G. V. Meehan, J. K. Clegg, L. F. Lindoy, P. Turner, M. B. Duriska and R. Willis, Chem. Commun., 2008, 1190 RSC.
- (a) W. Meng, J. K. Clegg, J. D. Thoburn and J. R. Nitschke, J. Am. Chem. Soc., 2011, 133, 13652 CrossRef CAS; (b) T. Beissel, R. E. Powers, T. N. Parac and K. N. Raymond, J. Am. Chem. Soc., 1999, 121, 4200 CrossRef CAS.
- (a) P. Zhang, X. Wang, W. Xuan, P. Peng, Z. Li, R. Lu, S. Wu, Z. Tian and X. Cu, Chem. Commun., 2018, 54, 4685 RSC; (b) X. Wang, Y. Wang, H. Yang, H. Fang, R. Chen, Y. Sun, N. Zhang, K. Tan, X. Lu, Z. Tian and X. Cao, Nat. Commun., 2016, 7, 12469 CrossRef.
- (a) S. P. Argent, H. Adams, T. Riis-Johannessen, J. C. Jeffery, L. P. Harding and M. D. Ward, J. Am. Chem. Soc., 2006, 128, 72 CrossRef CAS; (b) I. S. Tidmarsh, T. B. Faust, H. Adams, L. P. Harding, L. Russo, W. Clegg and M. D. Ward, J. Am. Chem. Soc., 2008, 130, 15167 CrossRef CAS.
- This aspect of the chirality of the cuboctahedra was not noticed in the first reported examples (ref. 8) as only a single isomer was isolated.
- (a) M. D. Ward, C. A. Hunter and N. H. Williams, Acc. Chem. Res., 2018, 51, 2073 CrossRef CAS; (b) M. D. Ward, C. A. Hunter and N. H. Williams, Chem. Lett., 2017, 46, 2 CrossRef CAS.
- (a) J. S. Train, A. B. Wragg, A. J. Auty, A. J. Metherell, D. Chekulaev, C. G. P. Taylor, S. P. Argent, J. A. Weinstein and M. D. Ward, Inorg. Chem., 2019, 58, 2386 CrossRef CAS; (b) J. R. Piper, L. Cletheroe, C. G. P. Taylor, A. J. Metherell, J. A. Weinstein, I. V. Sazanovich and M. D. Ward, Chem. Commun., 2017, 53, 408 RSC.
- A. Stephenson, D. Sykes and M. D. Ward, Dalton Trans., 2013, 42, 6756 RSC.
- (a) M. D. Ward, Chem. Commun., 2009, 4487 RSC; (b) A. Stephenson, S. P. Argent, T. Riis-Johannessen, I. S. Tidmarsh and M. D. Ward, J. Am. Chem. Soc., 2011, 133, 858 CrossRef CAS.
- B. R. Hall, L. E. Manck, I. S. Tidmarsh, A. Stephenson, B. F. Taylor, E. J. Blaikie, D. A. Vander Griend and M. D. Ward, Dalton Trans., 2011, 40, 12132 RSC.
- (a) A. J. Terpin, M. Ziegler, D. W. Johnson and K. N. Raymond, Angew. Chem., Int. Ed., 2001, 40, 157 CrossRef CAS; (b) S. Sato, Y. Ishido and M. Fujita, J. Am. Chem. Soc., 2009, 131, 6064 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Synthesis, mass spectrometry, X-ray crystallography details, geometric analysis of cage polyhedra, and more details of NMR spectra. CCDC 2009535–2009537. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0sc04347h |
‡ The T isomer requires four cyclic helicates of the same chirality to come together which can only occur in two ways (to give the AAAA/CCCC enantiomers); the arrangement of AAAC or CCCA faces in the C3 isomer has fourfold degeneracy for each enantiomer, giving 8 possibilities; and the arrangement of AACC faces in the achiral S4 isomer has sixfold degeneracy with no enantiomer. Thus if there are no steric preferences, and the assembly is dictated simply by chance combination of helical triangular faces with either chirality, the expected 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of five stereoisomers (Fig. 3b) would result in T, C3 and S4 diastereoisomers forming in the ratio 2 1 ratio of five stereoisomers (Fig. 3b) would result in T, C3 and S4 diastereoisomers forming in the ratio 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 (= 1 6 (= 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3), i.e. 12.5% (T) 3), i.e. 12.5% (T)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50% (C3) 50% (C3)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 37.5% (S4) of the total population. We also need to factor into this the previous observation that the relative intensities of each methyl signal for the T, C3 and S4 isomers are, respectively, one signal with intensity 12; four signals of intensity 3; and three signals of intensity 4. We then end up with an expected set of relative intensities as follows: one signal (relative intensity 12) for the T isomer; four signals (relative intensity 12 each) for the C3 isomer; and three signals (relative intensity 12 each) for the S4 isomer – i.e. all eight methyl signals should have the same intensity if assembly of the mixture of cage stereoisomers were purely statistical. 37.5% (S4) of the total population. We also need to factor into this the previous observation that the relative intensities of each methyl signal for the T, C3 and S4 isomers are, respectively, one signal with intensity 12; four signals of intensity 3; and three signals of intensity 4. We then end up with an expected set of relative intensities as follows: one signal (relative intensity 12) for the T isomer; four signals (relative intensity 12 each) for the C3 isomer; and three signals (relative intensity 12 each) for the S4 isomer – i.e. all eight methyl signals should have the same intensity if assembly of the mixture of cage stereoisomers were purely statistical. |
| This journal is © The Royal Society of Chemistry 2020 |