Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Transferrable property relationships between magnetic exchange coupling and molecular conductance†
Martin L.
Kirk
 *ab,
Ranjana
Dangi
a,
Diana
Habel-Rodriguez
a,
Jing
Yang
a,
David A.
Shultz
*c and
Jinyuan
Zhang‡
c
*ab,
Ranjana
Dangi
a,
Diana
Habel-Rodriguez
a,
Jing
Yang
a,
David A.
Shultz
*c and
Jinyuan
Zhang‡
c
aDepartment of Chemistry and Chemical Biology, The University of New Mexico, MSC03 2060, 1 University of New Mexico, Albuquerque, New Mexico 87131-0001, USA. E-mail: mkirk@unm.edu
bCenter for High Technology Materials, The University of New Mexico, Albuquerque, New Mexico 87106, USA
cDepartment of Chemistry, North Carolina State University, Raleigh, North Carolina 27695-8204, USA. E-mail: shultz@ncsu.edu
First published on 8th October 2020
Abstract
Calculated conductance through Aun–S–Bridge–S–Aun (Bridge = organic σ/π-system) constructs are compared to experimentally-determined magnetic exchange coupling parameters in a series of TpCum,MeZnSQ–Bridge–NN complexes, where TpCum,Me = hydro-tris(3-cumenyl-1-methylpyrazolyl)borate ancillary ligand, Zn = diamagnetic zinc(II), SQ = semiquinone (S = 1/2), and NN = nitronylnitroxide radical (S = 1/2). We find that there is a nonlinear functional relationship between the biradical magnetic exchange coupling, JD→A, and the computed conductance, gmb. Although different bridge types (monomer vs. dimer) do not lie on the same JD→Avs. gmb, curve, there is a scale invariance between the monomeric and dimeric bridges which shows that the two data sets are related by a proportionate scaling of JD→A. For exchange and conductance mediated by a given bridge fragment, we find that the ratio of distance dependent decay constants for conductance (βg) and magnetic exchange coupling (βJ) does not equal unity, indicating that inherent differences in the tunneling energy gaps, Δε, and the bridge–bridge electronic coupling, HBB, are not directly transferrable properties as they relate to exchange and conductance. The results of these observations are described in valence bond terms, with resonance structure contributions to the ground state bridge wavefunction being different for SQ–Bridge–NN and Aun–S–Bridge–S–Aun systems.
Introduction
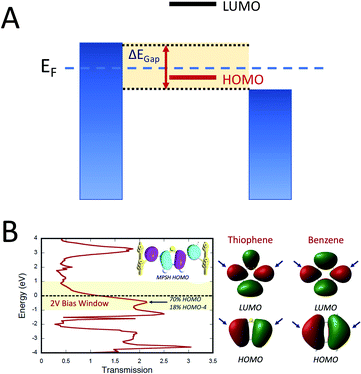
Electron transport in single-molecule devices is typically interrogated via a combination of experimental and computational probes of conductance using Metal–Bridge–Metal (M–B–M) junctions (Fig. 1A).1–14 To account for inherent variations in molecule–electrode binding geometries, the experimental determination of conductance (gmb) typically requires hundreds to thousands of individual conductance measurements in order to construct conductance histograms, which allow researchers to determine both conductance distributions and the most probable conductance value.15 Since conductance calculations often utilize a single M–B–M geometry and the molecular geometry in the actual junction is unknown, this can make direct comparisons between theory and experiment difficult to interpret. As a result, studies that correlate single-molecule conductance with physical observables such as electron transfer rate constants (kD→A)2,4,5,14,16 and magnetic exchange couplings (JD→A)1,17–20 continue to be a topic of current research. A primary impact of these efforts will be to provide key insight into orbital pathways for charge transport through molecules, which is difficult to achieve using traditional approaches. These correlations, coupled with the determination of transferable property relationships, are expected to facilitate improved molecular design concepts for molecular electronics and spintronics.The crux of these transferable property relationships was first described by Nitzan,21 who derived a relationship between gmb and kD→A at parity of the molecular bridge. With some approximations, Nitzan was able to show that conductance could be related to the square of the D–A electronic coupling matrix element, HD→A2 (HD→A2 = |HDBHBA|2|GB(E)|2), for electron transfer (eqn (1)–(4)).21
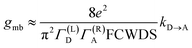 | (1) |
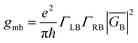 | (2) |
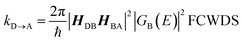 | (3) |
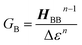 | (4) |
| JD→A ∝ HD→A2 ∝ kD→A ∝ gmb | (5) |
This leads to a corresponding relationship between these parameters and the distance decay constants (βi) for electron transfer, conductance, and magnetic exchange as indicated in eqn (6),
| kD→A ∝ gmb ∝ JD→A ∝ exp(−βi × nL) | (6) |
There is both experimental and computational support for a correlation between kD→A, gmb and JD→A.14,17,22–31 Beratan and Waldeck4,5 have built on Nitzan's work to show that the relationship between kD→A and gmb is nonlinear for alkane and peptide nucleic acid oligomer bridges, but they are related by a power law dependence. Their work supports an argument that the bridge Green's function, GB, is not the same for electron transfer and conductance. As a result, Beratan and Waldeck4,5 were able to show that the distance decay constants for kD→A and gmb are, in general, inequivalent and a linear relationship between kD→A and gmb will only occur if the individual βi are identical.
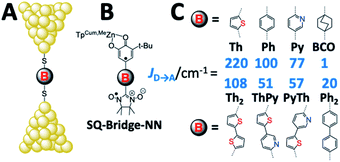
Since the magnetic exchange interaction (JD→A) is proportional to HD→A2viaeqn (5),32–36 we have initiated experiments designed to explore the correlation of JD→A between donor–acceptor biradical centers that are spanned by molecular bridge units (D–B–A biradicals = SQ–Bridge–NN; SQ = S = 1/2 semiquinone, and NN = S = 1/2 nitronylnitroxide radical, Fig. 1B and C)1,17–20,26,35–40 with computed molecular conductance values, gmb.1 An advantage to understanding the magnitude of gmb by correlating with experimental JD→A parameters is highlighted by the fact that the variable-temperature magnetic susceptibility measurements used to determine JD→A are performed on solid-state samples with known geometries that have been determined by X-ray crystallography. Thus, there is a single conformation present that contributes to JD→A. Unlike experimental conductance measurements in a contact geometry and solution electron transfer rate measurements, the magnitude of JD→A determined by solid state magnetic susceptibility measurements is not affected by structural and solvent bath induced inhomogeneities or by decoherence effects.
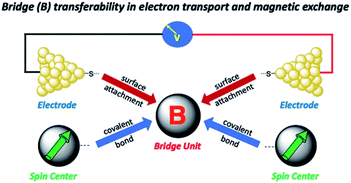
Relating molecular orbital pathways for JD→A to orbital transport channels for gmb has its own set of challenges, and these include (1) differences in the molecular fragments covalently attached to the bridge unit, (2) the molecular identity of surfactant groups, (3) variations in surface contacts, (4) the choice of electrode material and surface morphology, and (5) inhomogeneities in molecular structure (e.g., conformation) and in contact geometries. As alluded to above, an important related question was recently posited by Herrmann,14 which concerns the transferability of geometric and electronic structure contributions of the bridge moiety to kD→A, gmb, and JD→A (Fig. 2). Herein, we address these difficulties and the concept of bridge electronic structure transferability between conductance and exchange. We then use our results to explicitly determine distance decay constants (βg) for gmb from prior studies that have determined the distance dependence of JD→A. Our results are described in valence bond terms, with resonance structure contributions to the ground state bridge wavefunction being different for SQ–Bridge–NN and Aun–S–Bridge–S–Aun systems. This provides a path forward for understanding the power law relationship between gmb and JD→A in the absence of structural inhomogeneities and decoherence effects.
Experimental
General
The synthesis and characterization of SQ–BCO–NN, SQ–Ph–NN, SQ–Th–NN, SQ–Ph2–NN, SQ–Py–Th–NN, and SQ–Th2–NN have been published previously.1,17,20,26,35,39,41,42 See the ESI† for the preparation and characterization (spectroscopic data, X-ray crystal structure, and magnetic characterization) of the pyridyl-bridged biradical complex, SQ–Py–NN.Resonance Raman spectroscopy
Solution (methylene chloride) resonance Raman spectra were collected in either a 180° backscattering (780 nm) or 90° scattering geometry using 407 nm excitation from a Coherent Innova 70 Kr+ (1 W) ion laser. The scattered radiation was passed through a longpass filter (Semrock RazorEdge) to remove Rayleigh scattered laser light and then dispersed onto a liquid nitrogen-cooled Infrared Associates CCD detector using a Princeton Acton spectrograph. The laser power at the sample was typically kept between 40 and 100 mW in order to prevent possible photo- and thermal degradation of the sample. The sample was sealed in a glass capillary tube and spun with a custom-made sample holder. All data were scan-averaged, and any individual data set with vibrational bands compromised by cosmic events were discarded.Molecular electronic structure calculations
Thiophene and benzene calculations were performed at the density functional level of theory using the Gaussian 09W software package.43 Input files were prepared using the molecular builder function in GaussView. Calculations employed the B3LYP hybrid exchange–correlation functional and a 6-31g(d′,p′) split valence basis set with polarizability functions was used for all atoms. Frontier molecular orbitals (MOs) were generated from fully optimized ground states.Transport calculations
Transport calculations were performed using ATK 2016.0 v16.0,44–46 as detailed in our earlier work.1 The device configuration consists of the left Au electrode, the molecular bridge (scattering region), and the right Au electrode. Both the left and right gold electrodes consist of nine layers with each layer comprised of a 3 × 3 array of Au(111) atoms, for a total of 81 gold atoms per electrode. For the electrodes, the C or z direction is periodic in the system. This is also the direction of electron transport. Initial geometry optimizations of the bridge molecules BCO, Py, Ph, Th, Ph2, Py-Th, Th2 were performed using Gaussian 09 (ref. 43) with a 6-31g(d′,p′) basis set and the B3LYP functional. Electrode surfaces were constructed by cleaving the bulk crystal and using a copy of this to form the second electrode. The molecule was then placed on the surface of the left electrode and subsequently connected to the right electrode through terminal sulfur atoms to create the final device geometry. Prior to creating the final device geometry, the bulk configuration was optimized using a single-zeta basis set for the gold atoms (to save computational time) and a double zeta basis set for all other atoms. The optimization was performed using ATK-DFT with a Perdew–Zunger local density approximation (LDA-PZ) exchange–correlation. After this bulk optimization, the configuration was converted into a final device geometry for all subsequent calculations. A 5 × 5 × 51 K-point sampling has been used in x, y, z-directions, respectively. The boundary conditions were Dirichlet (fixed boundary condition) in the z direction, which is the direction of transport. The boundary conditions in the x and y directions were disabled so they could not be changed but the default parameterization is periodic for the x and y directions. The NEGF formalism was used to calculate the non-equilibrium electron density of the central region of the device.The Landauer–Büttiker formula47 relates transmission probabilities to conductance, gmb (gmb = I/V). This formula is used to calculate the voltage dependent current, I(V), across a molecular junction, which is determined by integrating the transmission function, T(E,V), according to eqn (7).47
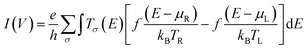 | (7) |
Results and discussion
Exchange coupling in SQ–Bridge–NN complexes
Magnetic exchange coupling constants (JD→A) for the monomeric SQ–Bridge–NN biradical complexes (Fig. 1B and C) SQ–BCO–NN, SQ–Ph–NN, SQ–Th–NN,17,20,26,41 and for the dimeric bridge molecules SQ–Py–Th–NN,1SQ–Ph2–NN,17 and SQ–Th2–NN17 have previously been determined by magnetic susceptibility measurements. The dimer exchange spin Hamiltonian (eqn (8)):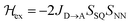 | (8) |
Exchange coupling within the context of a valence bond configuration interaction model
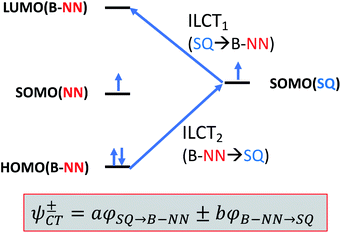
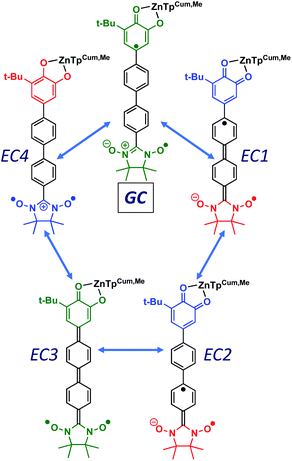
Given the geometric structures of these SQ–Bridge–NN biradicals, we can conveniently divide them into two distinct bridge categories: the first possesses single-ring molecular bridges, while the second contains two-ring molecular bridges where each bridge ring is connected to the other via a σ-bond. The electronic origins of π-mediated exchange coupling in SQ–Ph–NN and σ-mediated exchange in SQ–BCO–NN have been rigorously evaluated using a combination of spectroscopy, magnetic susceptibility, and theory.19,20,26,39,41,50 For π-mediated exchange, a valence-bond configuration interaction (VBCI) model has been used.19,20,35,36 Within the context of more traditional orbital pathways for understanding exchange coupling, the VBCI method conveniently illustrates how specific excited state configurations admix with the ground configuration to affect the magnitude of JD→A. The NN(SOMO), SQ(SOMO), NN–Bridge(HOMO), and the NN–Bridge(LUMO) (Fig. 3) orbitals form a convenient minimal active space to generate the ground and excited state configurations that contribute to JD→A for conjugated SQ–Bridge–NN systems. Previous work has demonstrated the crucial role of the LUMO(B–NN) in determining the magnitude of JD→A.17,19,20,35,36,39 Resonance structures that illustrate both the spin and the charge distributions of ground state SQ–Ph2–NN configurations and excited state configurations that arise from one-electron promotions within this active space are shown in Fig. 4. Here, the ground SQ–Bridge–NN configuration is represented by GC, EC1 and EC2 represent the configuration that results from an intraligand SQ(SOMO) → NN–Bridge(LUMO) electron promotion, and the NN–Bridge(HOMO) → SQ(SOMO) one-electron promotion is represented by the EC3 and EC4 resonance structures. Similar resonance structures can be drawn for other SQ–Bridge–NN biradical complexes. For the conjugated SQ–Bridge–NN systems discussed here, the charge transfer configuration generated by the intraligand SQ(SOMO) → NN–Bridge(LUMO) one-electron promotion (EC1 and EC2) has been shown to be the dominant contributor to the ground state ferromagnetic exchange coupling in SQ–Ph–NN, with the NN–Bridge(HOMO) → SQ(SOMO) (EC3 and EC4) playing a less important role.17,19,20,35,36,39 The relative contributions of these two intraligand charge transfer (ILCT) configurations will be dependent on the nature of the bridge. The use of more electron donating bridge molecules (e.g., thiophene) is expected to increase the relative NN–Bridge(HOMO) → SQ(SOMO) charge transfer contribution to the magnetic exchange by raising the energy of the bridge HOMO and LUMO orbitals. In addition, we have shown that bond torsions which disrupt Ph–NN π-coupling result in the ILCT transition being shifted to higher energy, with a concomitant reduction in the ILCT intensity relative to configurations that possess more planar Ph–NN conformations.41 As a result, an ILCT transition is not observed in SQ–BCO–NN and the lack of a CT feature in the visible region of the electronic absorption spectrum correlates with the weak σ-mediated exchange coupling.26,41 Our understanding of how the bridge HOMO and LUMO orbitals affect the magnitude of both JD→A and HD→A allow us to begin an assessment of how these orbitals contribute to the transferability of JD→A, kD→A, and HD→A to conductance in a biased electron transport configuration (Fig. 2).Correlation of exchange and conductance
Electron transport calculations have been performed on M–B–M constructs (Aun–S–Bridge–S–Aun) in order to compare the magnitude of bridge-mediated JD→A with gmb (i.e., current). In the transport computations, the bridge molecules in Fig. 1C are connected to voltage-biased Au electrodes via thiol anchoring groups. Thus, the bridges are the molecular fragments depicted in Fig. 1C with sulfur atoms attached to the bridge carbons. These calculations treat the M–B–M ensemble at the SCF level with the computational results being interpreted in terms of the Landauer–Büttiker formula, which relates transmission probabilities to conductance, gmb, according to eqn (7).47 In marked contrast to the dominant role of the bridge LUMO in SQ–Bridge–NN biradical magnetic superexchange coupling, the dominant orbital contributions to our computed conductance values are the bridge HOMOs. This is clearly illustrated in Fig. 5, where the bias-dependent transmission coefficient for M–Th–M (note that Th is a dithiol in the M–B–M construct) is largest for occupied energy levels that are comprised of thiophene bridge HOMOs. This derives from the bridge HOMOs being effectively pinned to the electrode Fermi level.48,51,52 The molecular HOMO character is clearly present in the molecular projected self-consistent Hamiltonian (MPSH) state contributions to the transmission at energies just below the Fermi level for M–Th–M and M–Ph–M (Fig. 5 and S3†). Closer inspection of the MPSH HOMO reveals the presence of anchor sulfur p-orbital contributions, which represent a key difference in the nature of the orbitals that promote M–B–M conductance vs. SQ–Bridge–NN magnetic exchange.Following the work of Beratan,53 Yoshizawa and coworkers54,55 have conveniently related the zeroth order Green's function for the bridge 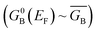 to the MO coefficients of the bridge orbitals, the Fermi energy, and the individual MO energy levels according to:
to the MO coefficients of the bridge orbitals, the Fermi energy, and the individual MO energy levels according to:
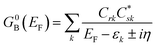 | (9) |
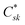 correspond to the MO coefficients for the sulfur atoms located on the left- and right-hand side of the bridge molecule that directly connects to the electrodes. We note that these sulfur atoms are connected to the same carbon atoms of the organic bridge as the SQ-donor and NN-acceptor moieties in our SQ–Bridge–NN biradical systems (Fig. 5B, right). The sulfur orbital contributions to the MPSH states are important in modulating the conductance, since they directly connect the electrodes to the molecule and allow for delocalization of the bridge wavefunction in the scattering region.55 When considering only the HOMO contributions to the conductance, eqn (9) reduces to:55
correspond to the MO coefficients for the sulfur atoms located on the left- and right-hand side of the bridge molecule that directly connects to the electrodes. We note that these sulfur atoms are connected to the same carbon atoms of the organic bridge as the SQ-donor and NN-acceptor moieties in our SQ–Bridge–NN biradical systems (Fig. 5B, right). The sulfur orbital contributions to the MPSH states are important in modulating the conductance, since they directly connect the electrodes to the molecule and allow for delocalization of the bridge wavefunction in the scattering region.55 When considering only the HOMO contributions to the conductance, eqn (9) reduces to:55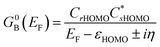 | (10) |
Thus, our a priori expectation is a difference in bridge-mediated coupling for conductance and magnetic exchange that results from the importance of sulfur atom character in the M–B–M MPSH HOMOs and the importance of the bridge LUMO that facilitates magnetic exchange in SQ–Bridge–NN biradicals.
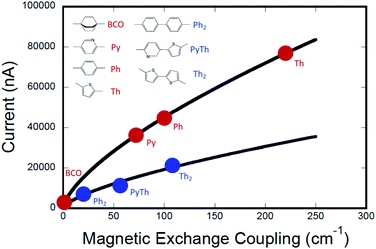
The computed conductance as a function of the experimentally determined SQ–Bridge–NN magnetic exchange coupling constants using monomeric and dimeric bridge molecules is presented in Fig. 6. We have fit these data to the power law expression:
| gmb = a(cJ0D→A)γ | (11) |
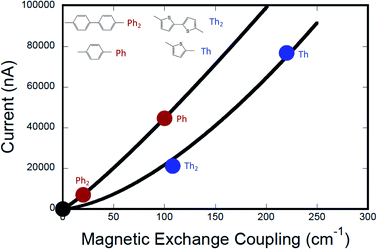
Fig. 7 shows the computed current as a function of magnetic exchange coupling for thiophene and phenylene bridges (0–2 bridge units). Following the formalism of Beratan and Waldeck,5 these data have been fit to eqn (12),
| gmb = [gL=0(J0D→A)−βg/βJ](JD→A)βg/βJ | (12) |
The relationship between gmb and JD→A for thiophenes is markedly more nonlinear than what we observe in the phenylene data. Eqn (13) describes how differences in these exponential
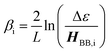 | (13) |
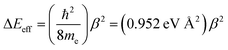 | (14) |
Beratan and Waldeck elegantly attributed their observed deviations in βg/βET from unity to a combination of charge transfer energy barrier differences between electron transfer in D–B–A ensembles and electron transport in M–B–M configurations, bath-induced decoherences on the bridge molecule, and bridge–bridge electronic coupling (HBB).4,5 Their work comparing conductance values and electron transfer rate constants indicated that differences in effective barrier heights derive from differences between the electrode work function in a transport geometry and donor/acceptor redox potentials in D–B–A systems.4,5 With respect to βi values, differences in the work function and redox potentials derive from different values for Δε. In general, due to the interdependence of Δε and HBB on βi values it is difficult to separate these individual contributions to ΔEeff.58
Since decoherence effects are not important for the JD→Avs. gmb correlation presented here, the dominant contributors to the nonlinearity between JD→A and gmb must relate to differences in bridge–bridge electronic coupling (HBB) and the tunneling energy gaps (Δε). For our SQ–Bridge–NN biradical complexes, we have used the ILCT energy as an approximation to the tunneling energy gap. This ILCT transition energy increases going from SQ–Ph–NN to SQ–Ph2–NN and decreases when going from SQ–Th–NN to SQ–Th2–NN.17 This contributes to the observed differences in βJ between SQ–(Ph)n–NN and SQ–(Th)n–NN, but also contributes to the magnitude of βg/βJ and differences in ΔEeff for magnetic exchange coupling and conductance.
Previously, we used magnetic susceptibility measurements to determine ΔEeff for superexchange-mediated magnetic coupling in SQ–Bridge–NN biradical systems, and this yielded ΔEeff = 1173 cm−1 and 373 cm−1 for phenylene and thiophene bridges, respectively.17 Given the conductance to magnetic exchange distance decay ratios (βg/βJ) for phenylenes and thiophenes determined here, we compute conductance barrier heights (ΔEeff) of 1555 cm−1 and 941 cm−1 for phenylene and thiophene bridges that span electrodes in a transport geometry. This translates to a decrease in ΔEeff for magnetic exchange coupling of ∼25% (phenylenes) and ∼60% (thiophenes) when compared to conductance values using these same organic bridge fragments. Our βJ values determined from magnetic susceptibility experiments (βJ = 0.39 Å−1 (Phn); βJ = 0.22 Å−1 (Thn))17 and the magnitude of βg/βJ determined in this work reveal the corresponding βg values for conductance using these molecular bridges (Table 1). The βg = 0.45 Å−1 value we determine for para-phenylene bridges is very close to the βg = 0.42 Å−1 value determined by conducting probe atomic force microscopy on oligo(para-phenylene)-monothiols suspended between metal contacts.59 Additionally, the βg = 0.35 Å−1 value that we have determined for oligothiophene bridges is also in good agreement with conductance studies performed on thiophene bridges with repeat units (n) equal to 1, 2, 3 and 5 (βg = 0.29 Å−1).60
| Compound/device | Parameter | Value |
|---|---|---|
| a Data calculated using distances R0 from X-ray crystal structures of SQ–Bridgen–NN with one single bond included = 4.30 Å (Ph) and 3.87 Å (Th). b n = 1 and 2. c Consistent with HBB,J > HBB,g and/or Δεg > ΔεJ. | ||
| M–Phn–Mb | β g | 0.45 Å−1 |
| ΔEeff | 1555 cm−1 | |
| Δεg/HBB,g | 2.63 (>ΔεJ/HBB,J)c | |
| SQ–Phn–NN , 17 | β J | 0.39 Å−1 |
| ΔEeff | 1168 cm−1 | |
| ΔεJ/HBB,J | 2.31 | |
| M–Thn–Mb | β g | 0.35 Å−1 |
| ΔEeff | 941 cm−1 | |
| Δεg/HBB,g | 1.79 (>ΔεJ/HBB,J)c | |
| SQ–Thn–NN , 17 | β J | 0.22 Å−1 |
| ΔEeff | 372 cm−1 | |
| ΔεJ/HBB,J | 1.53 | |
Resonance contribution to bridge mediated conductance and exchange
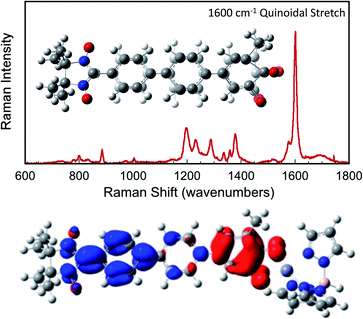
Since βi and ΔEeff are also a function of HBB, the bridge–bridge electronic coupling, differences in the nature of the frontier bridge MOs that promote both gmb and JD→A will also affect the magnitude of the distance decay constants. It is generally assumed that the bridge–bridge electronic couplings encountered in electron transfer, conductance, and magnetic exchange are equivalent, and the donor, acceptor, and electrode contacts do not affect the magnitude of HBB. However, this assumption may not be true. A convenient vehicle for understanding electronic structure contributions to βi values is the use of contributing resonance structures to highlight excited state configurations that mix with the ground state configuration within a valence bond framework.41,61–64As introduced above, the resonance structures shown in Fig. 4 describe the charge and spin distributions of the ground state configuration (GC) and four excited state configurations (ECs) for the SQ–Ph2–NN biradical complex. Quinoidal EC1 and EC3 possess enhanced Ph–Ph π-coupling, which provides a mechanism for increasing the magnitude of HBB. Contributions of resonance structures EC1–EC4 to the ground state all lead to enhanced magnetic exchange coupling in SQ–Bridge–NN biradicals. This occurs via a combination of B–B, D–B, and B–A electronic couplings (HBB, HDB, HBA), which are different than those provided by the coupling of these same bridge molecules with the electrodes (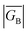 , ΓLB, ΓRB). This is partly due to the fact that only high energy zwitterionic and biradical resonance structures can be drawn for the S–Ph–Ph–S electrode linkage. In contrast, these CT configurations lead to a low-energy ILCT state at ∼24
, ΓLB, ΓRB). This is partly due to the fact that only high energy zwitterionic and biradical resonance structures can be drawn for the S–Ph–Ph–S electrode linkage. In contrast, these CT configurations lead to a low-energy ILCT state at ∼24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 in SQ–Bridge–NN biradicals, which has been shown to admix with the electronic ground state by resonance Raman spectroscopy.20,41 Specifically, the effect of this enhanced electronic coupling has been observed in SQ–Bridge–NN biradical compounds by optical pumping into the excited state ILCT and observing a large resonance enhancement of the phenylene quinoidal stretching vibration, which decreases in intensity with increased SQ–Bridge and Bridge–NN bond torsions.41 For di-bridged SQ–Ph2–NN, a large resonance enhancement of the 1600 cm−1 quinoidal stretch is also observed when pumping into the SQ → Ph–NN ILCT band17 (Fig. 8). The nature of the charge transfer is indicated by the computed electron density difference map (EDDM) in Fig. 8, which shows net charge transfer from the SQ donor (red) to the Ph–NN acceptor fragment (blue). Thus, the nature of the charge transfer in di-bridged SQ–Ph2–NN is analogous to what has been observed previously in the mono-bridged SQ–Ph–NN biradical,20,39 highlighting quinoidal resonance structure contributions to the ground state wavefunction.
000 cm−1 in SQ–Bridge–NN biradicals, which has been shown to admix with the electronic ground state by resonance Raman spectroscopy.20,41 Specifically, the effect of this enhanced electronic coupling has been observed in SQ–Bridge–NN biradical compounds by optical pumping into the excited state ILCT and observing a large resonance enhancement of the phenylene quinoidal stretching vibration, which decreases in intensity with increased SQ–Bridge and Bridge–NN bond torsions.41 For di-bridged SQ–Ph2–NN, a large resonance enhancement of the 1600 cm−1 quinoidal stretch is also observed when pumping into the SQ → Ph–NN ILCT band17 (Fig. 8). The nature of the charge transfer is indicated by the computed electron density difference map (EDDM) in Fig. 8, which shows net charge transfer from the SQ donor (red) to the Ph–NN acceptor fragment (blue). Thus, the nature of the charge transfer in di-bridged SQ–Ph2–NN is analogous to what has been observed previously in the mono-bridged SQ–Ph–NN biradical,20,39 highlighting quinoidal resonance structure contributions to the ground state wavefunction.
Conclusions
This work provides a detailed account of the transferability of electronic coupling with regard to exchange coupling and conductance. We have developed an electronic structure description of the functional relationship between JD→A and gmb, which we observed to be nonlinear (βg/βJ ≠ 1). Plots of JD→Avs. gmb for monomeric and dimeric bridges lie on different curves due to a scale invariance between these bridge types, which indicates a proportionate scaling of the exchange interaction, JD→A. Our gmbvs. JD→A data yield βg/βJ = 1.15 for the phenylene series and βg/βJ = 1.58 for the thiophene series, and these ratios accurately replicate recently reported β-values for electron transport through oligothiophene and oligophenylene bridges.59,60 In addition, these βg/βJ ratios have been used to determine conductance tunneling barrier heights for oligo-phenylenes (ΔEeff = 1555 cm−1) and oligo-thiophenes (ΔEeff = 941 cm−1) that span electrodes in a transport geometry. This translates to a decrease in effective barrier heights ΔEeff for magnetic exchange coupling of ∼25% for phenylenes and ∼60% for thiophenes when compared to conductance values using these same organic bridge fragments.Tunneling gaps and bridge–bridge electronic coupling, HBB, calculated from experimental data for the phenylene- and thiophene series provide a convincing explanation for the more pronounced gmbvs. JD→A nonlinearity observed in the thiophene series compared to the phenylene series. Additionally, resonance Raman spectroscopy indicates that HBB may be enhanced by quinoidal resonance structure contributions in SQ–Bridge–NN biradicals relative to M–B–M devices for conductance. Namely, contributions from ECN resonance structures (Fig. 4) are expected to be more pronounced for SQ–Thn–NN than for SQ–Phn–NN or Aun–S–Bridge–S–Aun constructs.
Resonance enhancement of the bridge quinoidal stretching mode illustrates the key bridge distortion that is the hallmark of a large HBB, and the magnitude of this excited state distortion is proportional to the degree of SQ → B–NN charge transfer, which contributes to the magnitude of the magnetic exchange interaction in SQ–Bridge–NN biradicals. From a valence bond/resonance perspective, contributing ECN resonance structures accurately reflect both the spin- and charge distribution of low-lying SQ–Bridge–NN CT states, for which the corresponding quinoidal bridge-containing excited states in M–Bridge–M constructs lie far higher in energy. With respect to the importance of quinoidal resonance contributions, aromaticity has been shown to reduce conductance values in single molecule junctions.65 Critically, the quinoidal resonance structure contributions in Fig. 4 result in diminished aromaticity and contribute more to exchange than to conductance, leading to γ ≠ 1 and βg/βJ > 1 for these molecular bridges.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
M. L. K. acknowledges NSF (CHE-1900237) for financial support. D. A. S. acknowledges financial support from NSF (CHE-1931291 and CHE-1764181). The authors thank the UNM Center for Advanced Research Computing, supported in part by the NSF, for providing high performance computing resources used in this work.Notes and references
- M. L. Kirk, D. A. Shultz, J. Y. Zhang, R. Dangi, L. Ingersol, J. Yang, N. S. Finney, R. D. Sommer and L. Wojtas, Chem. Sci., 2017, 8, 5408–5415 RSC.
- Y. Tsuji, R. Movassagh, S. Datta and R. Hoffmann, ACS Nano, 2015, 9, 11109–11120 CrossRef CAS.
- J. L. Xia, B. Capozzi, S. J. Wei, M. Strange, A. Batra, J. R. Moreno, R. J. Amir, E. Amir, G. C. Solomon, L. Venkataraman and L. M. Campos, Nano Lett., 2014, 14, 2941–2945 CrossRef CAS.
- R. Venkatramani, E. Wierzbinski, D. H. Waldeck and D. N. Beratan, Faraday Discuss., 2014, 174, 57–78 RSC.
- E. Wierzbinski, R. Venkatramani, K. L. Davis, S. Bezer, J. Kong, Y. J. Xing, E. Borguet, C. Achim, D. N. Beratan and D. H. Waldeck, ACS Nano, 2013, 7, 5391–5401 CrossRef CAS.
- W. B. Chen, J. R. Widawsky, H. Vazquez, S. T. Schneebeli, M. S. Hybertsen, R. Breslow and L. Venkataraman, J. Am. Chem. Soc., 2011, 133, 17160–17163 CrossRef CAS.
- E. D. Fung, D. Gelbwaser, J. Taylor, J. Low, J. L. Xia, I. Davydenko, L. M. Campos, S. Marder, U. Peskin and L. Venkataraman, Nano Lett., 2019, 19, 2555–2561 CrossRef.
- W. D. Ding, M. Koepf, C. Koenigsmann, A. Batra, L. Venkataraman, C. F. A. Negre, G. W. Brudvig, R. H. Crabtree, C. A. Schmuttenmaer and V. S. Batista, J. Chem. Theory Comput., 2015, 11, 5888–5896 CrossRef CAS.
- P. Darancet, J. R. Widawsky, H. J. Choi, L. Venkataraman and J. B. Neaton, Nano Lett., 2012, 12, 6250–6254 CrossRef CAS.
- S. V. Aradhya, J. S. Meisner, M. Krikorian, S. Ahn, R. Parameswaran, M. L. Steigerwald, C. Nuckolls and L. Venkataraman, Nano Lett., 2012, 12, 1643–1647 CrossRef CAS.
- S. Schneebeli, M. Kamenetska, F. Foss, H. Vazquez, R. Skouta, M. Hybertsen, L. Venkataraman and R. Breslow, Org. Lett., 2010, 12, 4114–4117 CrossRef CAS.
- M. Kamenetska, S. Y. Quek, A. C. Whalley, M. L. Steigerwald, H. J. Choi, S. G. Louie, C. Nuckolls, M. S. Hybertsen, J. B. Neaton and L. Venkataraman, J. Am. Chem. Soc., 2010, 132, 6817–6821 CrossRef CAS.
- L. Venkataraman, Nat. Nanotechnol., 2008, 3, 187–188 CrossRef CAS.
- C. Herrmann, J. Phys. Chem. A, 2019, 123, 10205–10223 CrossRef CAS.
- L. Venkataraman, J. E. Klare, I. W. Tam, C. Nuckolls, M. S. Hybertsen and M. L. Steigerwald, Nano Lett., 2006, 6, 458–462 CrossRef CAS.
- C. Joachim and M. A. Ratner, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 8801 CrossRef CAS.
- M. L. Kirk, D. A. Shultz, D. E. Stasiw, G. F. Lewis, G. B. Wang, C. L. Brannen, R. D. Sommer and P. D. Boyle, J. Am. Chem. Soc., 2013, 135, 17144–17154 CrossRef CAS.
- M. L. Kirk, D. A. Shultz, D. E. Stasiw, D. Habel-Rodriguez, B. Stein and P. D. Boyle, J. Am. Chem. Soc., 2013, 135, 14713–14725 CrossRef CAS.
- M. L. Kirk and D. A. Shultz, Coord. Chem. Rev., 2013, 257, 218–233 CrossRef CAS.
- M. L. Kirk, D. A. Shultz, E. C. Depperman, D. Habel-Rodriguez and R. D. Schmidt, J. Am. Chem. Soc., 2012, 134, 7812–7819 CrossRef CAS.
- A. Nitzan, J. Phys. Chem. A, 2001, 105, 2677–2679 CrossRef CAS.
- A. B. Ricks, G. C. Solomon, M. T. Colvin, A. M. Scott, K. Chen, M. A. Ratner and M. R. Wasielewski, J. Am. Chem. Soc., 2010, 132, 15427–15434 CrossRef CAS.
- E. A. Weiss, M. J. Ahrens, L. E. Sinks, A. V. Gusev, M. A. Ratner and M. R. Wasielewski, J. Am. Chem. Soc., 2004, 126, 5577 CrossRef CAS.
- J. Proppe and C. Herrmann, J. Comput. Chem., 2015, 36, 201–209 CrossRef CAS.
- C. Herrmann and J. Elmisz, Chem. Commun., 2013, 49, 10456–10458 RSC.
- D. E. Stasiw, J. Y. Zhang, G. B. Wang, R. Dangi, B. W. Stein, D. A. Shultz, M. L. Kirk, L. Wojtas and R. D. Sommer, J. Am. Chem. Soc., 2015, 137, 9222–9225 CrossRef CAS.
- S. Nishizawa, J. Hasegawa and K. Matsuda, Chem. Lett., 2014, 43, 530–532 CrossRef CAS.
- S. Nishizawa, J. Hasegawa and K. Matsuda, Chem. Phys. Lett., 2013, 555, 187–190 CrossRef CAS.
- S. Nishizawa, J. Hasegawa and K. Matsuda, J. Phys. Chem. C, 2013, 117, 26280–26286 CrossRef CAS.
- M. Shinomiya, K. Higashiguchi and K. Matsuda, J. Org. Chem., 2013, 78, 9282–9290 CrossRef CAS.
- Y. Tsuji, R. Hoffmann, M. Strange and G. C. Solomon, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, E413–E419 CrossRef CAS.
- P. W. Anderson, Phys. Rev., 1950, 79, 350–356 CrossRef.
- H. A. Kramers, Physica, 1934, 1, 182–192 CrossRef CAS.
- P. J. Hay, J. C. Thibeault and R. Hoffmann, J. Am. Chem. Soc., 1975, 97, 4884–4899 CrossRef CAS.
- M. L. Kirk, D. A. Shultz, E. C. Depperman and C. L. Brannen, J. Am. Chem. Soc., 2007, 129, 1937–1943 CrossRef CAS.
- M. L. Kirk, D. A. Shultz and E. C. Depperman, Polyhedron, 2005, 24, 2880–2884 CrossRef CAS.
- T. Steenbock, D. A. Shultz, M. L. Kirk and C. Herrmann, J. Phys. Chem. A, 2017, 121, 216–225 CrossRef CAS.
- M. L. Kirk and D. A. Shultz, Coord. Chem. Rev., 2013, 257, 218–233 CrossRef CAS.
- M. L. Kirk, D. A. Shultz, D. Habel-Rodriguez, R. D. Schmidt and U. Sullivan, J. Phys. Chem. B, 2010, 114, 14712–14716 CrossRef CAS.
- D. A. Shultz, K. E. Vostrikova, S. H. Bodnar, H. J. Koo, M. H. Whangbo, M. L. Kirk, E. C. Depperman and J. W. Kampf, J. Am. Chem. Soc., 2003, 125, 1607–1617 CrossRef CAS.
- D. A. Shultz, M. L. Kirk, J. Y. Zhang, D. E. Stasiw, G. B. Wang, J. Yang, D. Habel-Rodriguez, B. W. Stein and R. D. Sommer, J. Am. Chem. Soc., 2020, 142, 4916–4924 CrossRef CAS.
- M. L. Kirk and D. A. Shultz, Coord. Chem. Rev., 2013, 257, 218–233 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- S. Smidstrup, T. Markussen, P. Vancraeyveld, J. Wellendorff, J. Schneider, T. Gunst, B. Verstichel, D. Stradi, P. A. Khomyakov, U. G. Vej-Hansen, M.-E. Lee, S. T. Chill, F. Rasmussen, G. Penazzi, F. Corsetti, A. Ojanpera, K. Jensen, M. L. N. Palsgaard, U. Martinez, A. Blom, M. Brandbyge and K. Stokbro, J. Phys.: Condens. Matter, 2019, 32, 015901 CrossRef.
- M. Brandbyge, J.-L. Mozos, P. Ordejon, J. Taylor and K. Stokbro, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 165401 CrossRef.
- J. M. Soler, E. Artacho, J. D. Gale, A. Garcia, J. Junquera, P. Ordejon and D. Sanchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745–2779 CrossRef CAS.
- M. Büttiker, Y. Imry, R. Landauer and S. Pinhas, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 6207–6215 CrossRef.
- C. Van Dyck and M. A. Ratner, Nano Lett., 2015, 15, 1577–1584 CrossRef CAS.
- J. Taylor, H. Guo and J. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245407 CrossRef.
- E. C. Depperman, S. H. Bodnar, K. E. Vostrikova, D. A. Shultz and M. L. Kirk, J. Am. Chem. Soc., 2001, 123, 3133 CrossRef CAS.
- C. Van Dyck and M. A. Ratner, J. Phys. Chem. C, 2017, 121, 3013–3024 CrossRef CAS.
- C. Van Dyck, V. Geskin and J. Cornil, Adv. Funct. Mater., 2014, 24, 6154–6165 CrossRef CAS.
- S. Priyadarshy, S. S. Skourtis, S. M. Risser and D. N. Beratan, J. Chem. Phys., 1996, 104, 9473–9481 CrossRef CAS.
- K. Yoshizawa, T. Tada and A. Staykov, J. Am. Chem. Soc., 2008, 130, 9406–9413 CrossRef CAS.
- Y. Tsuji, A. Staykov and K. Yoshizawa, J. Am. Chem. Soc., 2011, 133, 5955–5965 CrossRef CAS.
- H. B. Gray and J. R. Winkler, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 3534 CrossRef CAS.
- O. S. Wenger, Acc. Chem. Res., 2011, 44, 25–35 CrossRef CAS.
- O. S. Wenger, Chem. Soc. Rev., 2011, 40, 3538–3550 RSC.
- D. J. Wold, R. Haag, M. A. Rampi and C. D. Frisbie, J. Phys. Chem. B, 2002, 106, 2813–2816 CrossRef CAS.
- B. Capozzi, E. J. Dell, T. C. Berkelbach, D. R. Reichman, L. Venkataraman and L. M. Campos, J. Am. Chem. Soc., 2014, 136, 10486–10492 CrossRef CAS.
- L. Pauling and G. W. Wheland, J. Chem. Phys., 1933, 1, 362–374 CrossRef CAS.
- G. W. Wheland and L. Pauling, J. Am. Chem. Soc., 1935, 57, 2086–2095 CrossRef CAS.
- L. Pauling, The Nature of the Chemical Bond, Cornell University Press, Ithaca, NY, 3rd edn, 1960 Search PubMed.
- F. Weinhold and C. R. Landis, Valency and bonding: a natural bond orbital donor–acceptor perspective, Cambridge University Press, Cambridge, UK; New York, 2005 Search PubMed.
- W. B. Chen, H. X. Li, J. R. Widawsky, C. Appayee, L. Venkataraman and R. Breslow, J. Am. Chem. Soc., 2014, 136, 918–920 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Computed phenylene I–V plot and MPSH HOMO, synthesis, characterization, crystal structure, and magnetic data for SQ–Py–NN. CCDC 2022006 and 2022007. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0sc04350h |
| ‡ Current address: Beijing National Laboratory for Molecular Sciences, CAS Key Laboratory of Organic Solids, Institute of Chemistry, Chinese Academy of Sciences, Beijing 100190, China. |
| This journal is © The Royal Society of Chemistry 2020 |