DOI:
10.1039/D0SC04495D
(Minireview)
Chem. Sci., 2020,
11, 12994-13007
Correlated motion and mechanical gearing in amphidynamic crystalline molecular machines
Received
15th August 2020
, Accepted 15th October 2020
First published on 21st October 2020
Abstract
In this review we highlight the recent efforts towards the development of molecular gears with an emphasis on building molecular gears in the solid state and the role that molecular gearing and correlated motions may play in the function of crystalline molecular machines. We discuss current molecular and crystal engineering strategies, challenges associated with engineering correlated motion in crystals, and outline experimental and theoretical tools to explore gearing dynamics while highlighting key advances made to date.
1. Introduction
During the past couple of decades in the development of artificial molecular machines, efforts have been made to synthesize analogues of macroscopic machines or to emulate the function of biomolecular machines.1,2 It has been shown that the synergistic and synchronized behaviour of molecular components performing sophisticated functions may lead to the development of molecular pumps,3 unidirectional motors,4,5a and emergent dipolar rotary arrays5a,b (Fig. 1). Some of the earliest and most iconic structures in the realm of artificial molecular machines are molecular gears that transmit motion, forces and energy from one component to another in a correlated manner. For example, two-component bevel gears consisting of meshed three-bladed triptycene rotators linked by a single atom or cis-alkene derivative were reported and thoroughly analysed in the mid-1980s (Fig. 2a, left).6 Despite the continued efforts to take advantage of various intermolecular forces, degrees of freedom and chemical processes to study correlated motion or gearing, there are relatively simple aspects of molecular gears that are still poorly understood. Namely, a relatively simple structural modification of the two triptycene gears along parallel axes in molecular analogues of macroscopic spur gear (Fig. 2a, right) is yet to be demonstrated with high gearing fidelity (Fgear). Gearing fidelity is defined as the number of disrotatory, gearing rotations that occur per conrotatory, slipping rotations (kgear/kslippage), and is the primary figure of merit for determining the efficiency of a molecular gear.7Fgear is invariably determined by the relative energies of the slippage and gearing transition states compared to the ground state for two gearing rotators (Fig. 2b).
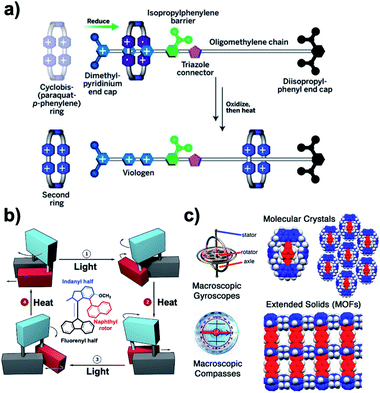 |
| | Fig. 1 (a) A molecular pump threads a ring on a dumbbell-shaped molecule and then repeats the process. Pluses and dots represent the oxidized and reduced forms of charged groups, respectively. (b) A rotary motor powered by photochemical and thermal stimuli. The motor is coupled with a single bond to a passive rotor consisting of a naphthalene paddle. (c) Structure of a macroscopic gyroscope illustrating its stator, rotator, and axle, compared with the topologies and space-filling model of potential crystal-forming molecular rotors with closed and open topologies. The blue color is used to represent the stator, and the red color is used to highlight the axle and the rotator (adapted from ref. 3–5). | |
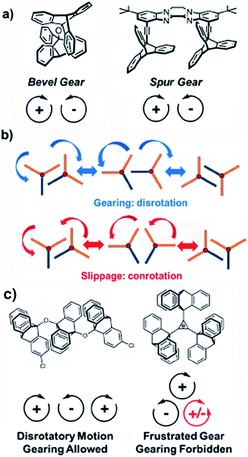 |
| | Fig. 2 (a) Bevel and spur gears. (b) Transition states and trajectories for geared or slipping rotations, and (c) multi-gear systems that illustrate parity laws for molecular gears. | |
Considering the symmetry requirements of gearing rotors, it can be shown that linear gear chains may have any number of intermeshed rotators, but cyclic arrangements of gears require an even parity of rotators to function. In cyclic systems containing an odd number of gears, one gear will ultimately interact with two others that have out of phase rotations and the triad will be unable to fulfill the requirement for disrotatory motion. This will lead to a frustrated gear that is unable to rotate (Fig. 2c).8 Utilizing these principles, recent work has led to the development of more complex multi-gear systems with cyclic arrays of four or six triptycenes, sometimes with tunable functionalities, suggesting that various structural solutions can be found.9 Here we examine the potential of building molecular gears in the crystalline solid state, and the role that molecular gearing and correlated motions may play in the function of crystalline molecular machines.
2. Amphidynamic crystals
Our group and others have shown the promise of the crystalline solid state as a platform for the development of functional smart materials and molecular machines.10 Due to their long-range order and relatively strong mechanical and electronic molecular coupling, crystals are able to transduce different forms of energy across length scales that cover several orders of magnitude. Crystalline solids also offer opportunities to take advantage of emergent properties that can lead to complex functions, such as the modulation of mechanical,10a electric,10b magnetic,10c acoustic,10d and optical10e properties. A promising strategy to enable dynamics in the solid state involves the use of amphidynamic crystals, a condensed phase that combines crystalline order and liquid-like dynamics, built with lattice-forming elements linked to components that can undergo fast motion. The position of amphidynamic crystals in a general phase order–molecular motion phase diagram is illustrated in Fig. 3. They possess the periodicity and long-range order of crystals with elements that are as dynamic as liquids, but maintain well-defined trajectories. Amphidynamic crystals are the opposite of glasses, which lack order and motion, but display higher order and faster motion than those commonly seen in plastic crystals and liquid crystals.
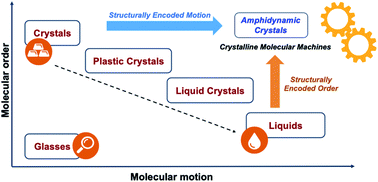 |
| | Fig. 3 Phase order–molecular motion phase diagram illustrating possible forms of condensed-phase matter. Crystalline molecular machines would require architectures that warrant a combination of structurally encoded order and structurally encoded motion leading to desirable dynamic processes. | |
3. Strategies for engineering motion in crystalline solids
One of the most intuitive types of amphidynamic crystals is formed by arrays of molecular rotors based on rigid stators linked by an axle to rapidly moving or reorienting components that play the role of a rotator, as shown in Fig. 1c.2 In our previous work, we proposed that the design of amphidynamic crystals relies on three general principles shown in Fig. 4.
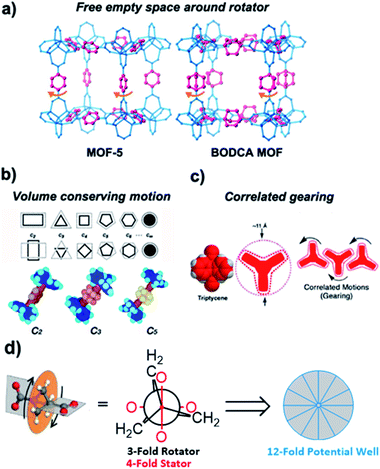 |
| | Fig. 4 The three main structural strategies for the design of amphidynamic crystals: (a) free empty space around rotator, (b) volume conserving motion, and (c) correlated gearing (adapted from ref. 2b). (d) Newman projection depicting how a 3-fold symmetrical rotator mismatching with a 4-fold symmetrical stator creates a 12-fold potential well with vanishingly low barriers to rotation (adapted from ref. 12a). | |
The first is based on the availability of empty volume to accommodate rotary elements undergoing large angular displacements, as can be found in porous crystals.11 We have shown that cavities with large free volumes in metal–organic frameworks (MOFs, Fig. 4a) pose no steric barriers, and that rotational dynamics under those conditions are limited by the intrinsic barriers of the bonds that link the stator and the rotator.2b The second principle applies in close-packed crystals and relies on the use of high symmetry, volume-conserving rotary elements that are able to move with minimal changes in shape. This principle is based on the fact that the energy difference between the rotational ground and transition states will become smaller in a close-packed environment as the two structures become more similar. As shown in Fig. 4b, this occurs with molecular rotators with polygonal cross sections that approach the cross section of their own volume of revolution. An increase in the rotational symmetry also results in a larger number of degenerate ground states with shorter angular displacements between them. The effect of increasing volume conservation in the cross section of the rotator can be appreciated by comparing molecular rotors with the same triphenylsilyl stator and either a C2-symmetric para-phenylene, a C3-symmetric bicyclo[2.2.2]octane, or a C5-symmetric para-carborane, which have activation energies of 8.5 kcal mol−1, 3.57 kcal mol−1 and 2.92 kcal mol−1, respectively. It was also shown by our group as well as Sozzani et al. that if the symmetry of the rotator mismatches with the symmetry of the struts in metal–organic frameworks, frustrated rotational dynamics can be achieved resulting in hyperfast dynamics even at very low temperatures (Fig. 4d).12 For example, the three-fold trigonal symmetry a bicyclopentane rotor and the fourth-fold symmetry generated by the orthogonal carboxylate arrangement in a Zn-MOF resulted in a shallow potential energy surface with an activation barrier to rotation of only 6.2 cal mol−1 and no stable conformations allowing for continuous rotation exceeding rates of 1010 Hz, even at temperatures below 2 K.12a
Furthermore, computational models suggests that small low-symmetry components, such as 1,4-disubstituted benzenes, undergo hindered rotation in closed-packed molecular crystals by taking advantage of “crystal fluidity”, which depends on the volume fluctuations that occur as the result of correlated displacement of neighboring molecules creating transient cavities.8 Finally, and related to the concept of crystal fluidity, the third and more challenging principle relies on the implementation of correlated motions where the displacement of any one element depends on the displacement of its neighbors, such as it occurs in the case of molecular gears (Fig. 4c). From a strict structural perspective, the design of crystalline molecular gears will require the placement of adjacent rotators in a manner that they give up their individual degrees of freedom to enter a regime where the velocity and direction of one rotator determines the velocity and direction of its neighbor(s).
4. Correlated motion in crystalline solids
The correlated motion of two or more molecular rotors is entropically disfavored due to the reduction of microstates that occurs when they transition from being independent to acting as a geared ensemble. The entropy cost for molecular gears in solution is further amplified in the solid state where extended domains of molecular rotators must interact with one another within a crystal. Most notably, structural solutions that allow for adjacent rotators to remain in sterically meshed configurations while having the space needed for rotation will be challenging to achieve. As such, in addition to controlling the rotator position in the crystal lattice, full control of crystal density and mobility will be necessary to engineer correlated motion in amphidynamic systems. Plausible strategies in the case of molecular crystal can be based on the use of supramolecular templates that align adjacent rotors, as shown by Setaka et al.,13 and by the design of discrete molecular multirotor gears with shapes that are conducive to low packing densities, as suggested by Gould et al.14 In essence, one would start with the design of a two, three, or larger gear train attached to bulky stators that can enable geared rotation of the discrete multirotor system, as shown with a triptycene dirotor gear in Fig. 5a. One may expect that with a suitable lattice-forming stator this structural concept will lead to the formation of amphidynamic crystals with arrays of dual rotor molecular gears, as illustrated in Fig. 5b. Alternatively, a promising solution for the construction of amphidynamic crystals with gearing moieties could be based on porous architectures such as MOFs, with functional rotators acting as struts linked by coordination bonds to secondary binding units (SBUs) composed of static metal clusters.15 A schematic example in Fig. 5b and c involves chains of triptycene rotators linked to metal centers in a manner that their blades can act as interdigitated cogs. Variations can be envisioned by maintaining the same SBUs with ligands of different lengths to create isoreticular MOF cavities with different pore dimensions.15
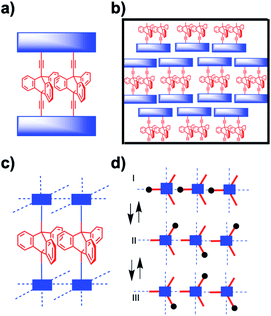 |
| | Fig. 5 Schematic representation of (a) a di-triptycene dirotor gear in the form of a macrocycle with a shared stator and (b) the corresponding molecular crystal. (c) Side view of a MOF crystal with triptycene linkers aligned as extended gear chains and, (d) a top indicating three stages of gearing with rotors from left to right moving clockwise, counterclockwise, and clockwise. | |
For the design of molecular rotors with cogged rotators our group has utilized pillared paddlewheel metal–organic frameworks with Zn2(CO2)4 clusters, as shown in Fig. 6a. Our strategy to create the free volume necessary for triptycene gears to rotate relied on relatively long 9,10-bis(2-(4-pyridyl))-ethynyltriptycene pillars and 9,10-triptycene dicarboxylate ligands, which form very dense layers that are known to prevent the formation of interpenetrating lattices.15 We discovered that the distance between the center of adjacent triptycene rotators was ca. 11 Å, which is just about the same length as its diameter of revolution, so that rotation of each unit is independent (Fig. 6b). This was indeed shown to be the case even though the rotation was strongly affected by solvent, which increased its effective viscosity by about four orders of magnitude as compared to that in the bulk. Other similar studies explored how switchable rotational dynamics can be achieved by gas molecule absorption in porous coordination polymers,16a organosilica architectures,16b,c porous aromatic frameworks,16d and molecular crystals.16e,f In other MOF systems such as MIL-101(Cr), solvent absorption and subsequent coordination to the unsaturated Cr3O metal sites (CUS) changed the electronic state and the geometry of the phenylene linker that resulted in its enhanced rate of rotation. Notably, this study performed by Stepanov and coworkers, showcased a strategy to control linker rotational dynamics via solvent molecules acting as molecular gear-levers.17
 |
| | Fig. 6 (a) Amphidynamic crystals composed of spacer, metal cluster and rotor units; (b and c) spacer site can be modified by installing different dicarboxylates such as terephthalate, biphenyl-4,4′-dicarboxylate, and triptycene-9,10-dicaboxylate. | |
Shown in Fig. 6c is a promising structural solution for the development of a molecular gear crystal. An increase in the length of the cogs from one benzene ring to two in going from triptycene to tri-benzotriptycene enlarges the volume of revolution beyond the inter-rotor distance in the lattice, such that rotation can only occur in a correlated gearing motion. While it is easy to show that the proper gearing parity exists as one connects multiple four-fold circular gear trains, one may expect that the energetics of rotation will be highly demanding from both enthalpic and entropic perspectives.
5. Experimental methods to study rotational dynamics in crystalline solids
The experimental determination of molecular rotation relies on the observation of differences between the various rotational states.18 When analyzed in an internal molecular frame of reference, rotational states must be structurally isomeric, such that they can be identified and their rates of exchange analyzed as a function of temperature. An example with a hypothetical 9-(ortho-tert-butyl-phenyl)-triptycene molecular rotor in Fig. 7 illustrates a set of rotational states, 1a, 1b and 1c, which are degenerate and non-distinguishable in Set I where the three substituents are identical (X = Y = Z).
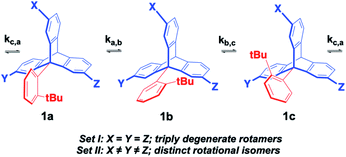 |
| | Fig. 7 Desymmetrization of 2,7,14-trisubstituted-9-triptycene achieved by introducing different substituents to the X, Y and Z positions, making them non-equivalent. Synthesis and dynamic studies have been done on similar triptycene derivatives.19 | |
By contrast, rotational isomers 1a, 1b and 1c become distinguishable in Set II when the structure is de-symmetrized by making the three triptycene blades different, with X ≠ Y ≠ Z. Notably, such relatively small structural changes require the use of high-resolution dynamic NMR with each isomer being identified by a characteristic signal (or set of signals) with chemical shifts δa, δb, δc, such that changes in chemical shift (Δδ) as a function of temperature can be analyzed in terms of the various rotational site exchange rates (ka,b, kb,c, kc,a). The rate and temperature data can be used for the determination of rotational activation barriers (Ea) and pre-exponential factors (k0) by taking advantage of the Arrhenius equation (eqn (1)):
| | 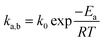 | (1) |
Unfortunately, the dynamic range of the method relies on the difference in chemical shift between rotational states, which depends on the signal dispersion of the magnetic nucleus observed, which typically varies from ca. 0–100 Hz for 1H NMR to ca. 0–1000 Hz for 13C NMR. For that reason, rotational dynamics by variable temperature NMR in solution are only possible for very slow molecular rotors (rotational time constants slower than microseconds) with relatively high-energy barriers (ca. 10–20 kcal mol−1).20 Similarly, slow rotational dynamics in the solid state can be measured by performing variable temperature high-resolution cross polarization and magic angle spinning (CPMAS) NMR measurements, typically taking advantage of the 13C nuclei in the structure of the rotator (VT CPMAS 13C NMR). A key difference with solution measurements is that chemical shifts in the crystalline state are defined by the site symmetry of the lattice rather than by the time-averaged site symmetry of the molecular rotator. For example, the 13C CPMAS spectrum of bis(tritylethynyl)cubyl molecular rotor 2 measured at 263 K was shown to have three signals assigned to the cubyl carbons a, b and c, which are equivalent in solution but not in the crystal.21 Coincident molecular and crystal inversion centers demand that the top of the rotor is equivalent to the bottom, such that inversion-center-related carbons a and a′ are crystallographically and magnetically equivalent, but different from carbon atoms b and c and their symmetry related signals. As shown in Fig. 8, increasing the temperature in small increments up to 288 K causes the three signals to coalesce in a manner that depends on the rotational site exchange, which can be readily simulated with commercially available computer programs. An Arrhenius plot of the natural logarithm of the rotational exchange rate vs. the inverse temperature indicates a relatively high activation barrier Ea = 12.6 kcal mol−1 and a normal pre-exponential factor k0 = 9.63 × 1011 s−1.
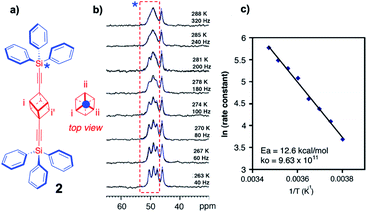 |
| | Fig. 8 (a) Structure of bis(tritylethynyl)cubyl molecular rotor 2 and a projection of the 1,4-cubanediyl group along its rotational axis, along with (b) the experimentally observed and simulated VT 13C CP-MAS spectra (superimposed), and (c) the Arrhenius plot of the rotational exchange rate (adapted from ref. 21). | |
Considering that NMR measurements in single crystals and polycrystalline samples can be carried out without spinning, and at very low temperatures (e.g., 4 K), fast rotational motion with very low barriers can be measured with confidence by doing measurements at cryogenic temperatures. Intermediate exchange rates on the order of 104–107 s−1 (10 kHz to 10 MHz) can be readily determined by taking advantage of 2H-labeled samples and variable temperature quadrupolar echo 2H NMR followed by the simulation of the spectrum that considers the rates and trajectories of the rotational exchange process. While a detailed description of the method is beyond the scope of this review, there are excellent descriptions in the literature.22 In very general terms, the method relies on changes in the direction of the C–2H bond vector in the laboratory frame of reference as determined by the external magnetic field. The example in Fig. 9 illustrates the results obtained with a polycrystalline sample of 1,4-bis(2-triphenylsilylethynyl)-d4-benzene 3 with measurements carried out between 207 K and 321 K (Fig. 9b). In this case, the spectra were simulated with a model that considers Brownian rotation of the phenylene group with 180° jumps between two degenerate minima at frequencies that range between ca. 103 s−1 (or “static”) and ca. 2 × 107 s−1. The method is particularly powerful because chemical equivalence or non-equivalence within a local frame of reference are not important and spectral changes are only observed when the orientation of C–2H bond vector changes as a result of internal molecular rotation, even when macroscopic crystals are static. An Arrhenius plot in Fig. 9c revealed a solid state activation barrier Ea = 8.5 kcal mol−1 and pre-exponential factor A = 1.1 × 1013 s−1.
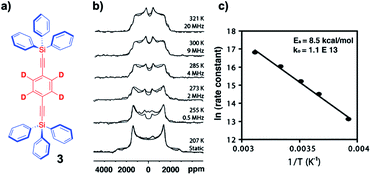 |
| | Fig. 9 (a) Structure of a 1,4-bis(2-triphenylsilylethynyl)-d4-benzene molecular rotor, (b) the corresponding experimental and simulated VT-quadrupolar echo 2H NMR spectra (superimposed), and (c) the Arrhenius plot of the exchange data (adapted from ref. 21). | |
Extremely small rotational barriers leading to ultrafast rotational motion can be conveniently documented by taking advantage of variable temperature spin lattice relaxation due to the modulation of dipolar interactions by rotational motion, which reaches an optimal value when molecular Brownian rotational jumping rates (τc−1) approach the Larmor frequency (ω0) of the nucleus being observed. In the case of molecular rotors bearing 1H nuclei, observations are commonly made with spectrometers operating at frequencies (νL = ω0/2π) that vary from ca. 10 MHz to 600 MHz, which help determine rotations with time constants in the range of ca. 107 s−1 to 6 × 108 s−1. An example is shown in Fig. 10 with two closely related halogen-bonded supramolecular rotors with 1,4-diazabicyclo[2.2.2]octane (dabco) acting as the rotator and either 2-bromoethynyl-triphenylmethane (4Br) or 2-iodoethynyl-triphenylmethane (4I) acting as the stator.23 Measurements with 4Br were carried out between 40 K and 155 K (indicated with rhombs) and measurements with 4I were in the range from 80 K to 165 K (marked with circles).
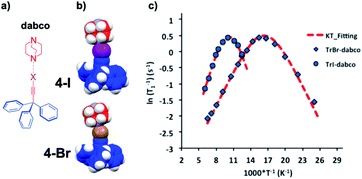 |
| | Fig. 10 (a) Line formula and (b) space-filling models of halogen-bonded supramolecular rotors of 1,4-diazabicyclo[2.2.2]octane (dabco) with 2-bromoethynyl-triphenylmethane (4Br) and 2-iodoethynyl-triphenylmethane (4I). (c) Variable temperature 1H T1 NMR spin–lattice relaxation data of 4Br between 40 K and 155 K and 4I between 80 K and 165 K with their corresponding Kubo–Tomita fits revealing activation energies Ea = 0.71 kcal mol−1 and 1.15 kcal mol−1, respectively (adapted from ref. 23). | |
The experimental data can be fitted to the Kubo–Tomita relaxation expression (eqn (2)),
| | 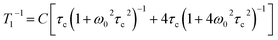 | (2) |
| | 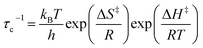 | (3) |
which relates the macroscopic relaxation times (
T1−1) to the molecular rotational dynamics (
τc) with respect to spectrometer frequency (
ω0), such that one is able to obtain activation energy and pre-exponential values by assuming that
τc follows an Arrhenius behavior (
eqn (1)). Alternatively, one can use the Eyring equation (
eqn (3)) to determine activation enthalpies and activation entropies. In the case of
4Br an
4I our group was able to establish that the activation entropy for rotation is small and negative (Δ
S‡ = −3.0 cal mol
−1 K
−1) for both dynamic systems, while there is almost a 2-fold difference in activation enthalpies, with
4I having a higher activation enthalpy (Δ
H‡ = 0.95 kcal mol
−1) than
4Br (Δ
H‡ = 0.54 kcal mol
−1), which can be understood in terms of subtle differences in steric interactions.
The activation energies (Ea) or enthalpies (ΔH‡) obtained by the methods described above reflect the intrinsic electronic barriers and steric hindrance that a molecular rotor must overcome in order to go from one orientation to another. By contrast, the pre-exponential factor of a Brownian rotor (k0), sometimes referred to as its “attempt frequency”, reflects the upper limit for rotation between adjacent minima that a given molecule can undergo in a particular environment. Its value can be determined from the moment of inertia of a hypothetical free rotor, or from the frequency of the torsional mode that turns into rotations when sufficient thermal energy is provided. For small molecular rotors such as those analyzed in this review the theoretical pre-exponential factor takes values on the order of 1011–1013 s−1, which corresponds to the rate that would occur in the hypothetical scenario where there are no intrinsic steric or electronic barriers.
6. Computational methods to study rotational dynamics in amphidynamic systems
Computational studies of artificial molecular machines can give an overview of the energy barriers associated with different dynamic processes, facilitate the interpretation of experimental results, or explore correlated dynamics for processes that are outside the experimentally accessible time scales. Calculations rely on theoretical models that account for key intra- and inter-molecular interactions which determine the trajectories of motion as molecules overcome barriers between energy minima, or explore full multidimensional hypersurfaces. The cost of computational analyses scales with the size of the system, accuracy and sophistication of the theoretical models. They may range from relatively simple and inexpensive force field methods to more complex density functional theory and ab initio quantum mechanical calculations.
6.1. Intrinsic rotational barriers in free-volume MOFs
In the case of crystalline molecular rotors, theoretical insight may be gained from very simple models that address the intrinsic gas phase barriers along the rotational potential in free volume environments. For example, high level DFT gas phase calculations of a minimalistic model based on two Zn clusters, the bridging 1,4-phenylenedicarboxylate rotator, and ten formate groups [Zn4O(O2CH)5O2C–C6H4–CO2(O2CH)5Zn4O] help explain the slow rotation determined by 2H NMR in the spacious phenylene rotator of MOF-5 (Fig. 4). The potential energy surface has two coplanar minima related by 180° rotation and connected through barriers located at an angular displacements of 90°.24 While an experimental barrier of ca. 11 kcal mol−1 is overestimated by computational values that range between ca. 14–16 kcal mol−1 depending on the basis set and level of theory, calculations account well for the dynamic behavior of the rotator and help infer experimental trajectories that avoid a double transition state (or second order saddle point).24c,d Similarly, a nearly barrierless 6-fold degenerate potential with activation energies of ca. 0.1–0.3 kcal mol−1 was calculated for 1,4-bicyclo[2.2.2]octane dicarboxylate acting as a rotator in the Zn-paddle wheel BODCA-MOF (Fig. 4).12b A minimalistic model using the hybrid functionals M062X/6-311+G(d) and ωB97XD/6-311+G(d) in this case matched very well experimental values in the range of 0.12 and 0.29 kcal mol−1.
6.2. Rotational barriers in close-packed molecular crystals using discrete cluster models
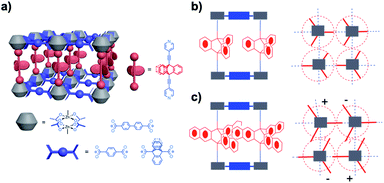
Calculations of rotational barriers in molecular crystals have utilized models that consider crystal packing density, rigidity and periodicity based on structural parameters available from single crystal X-ray diffraction. Computational models may involve discrete molecular clusters where a central molecular rotor is surrounded by neighboring molecules (or fragments of molecules) that preserve all the van der Waals interactions between the rotator and its environment. Energies are calculated as the rotator is driven in steps of a few degrees to explore its entire rotational potential. Several studies by Batail and co-workers and our group have employed this computational approach.25 One example from our group involves potential energy calculations as a function of the central phenylene rotation in crystals of 1,4-bis(3,3,3-triphenylpropynyl)benzene (5).26 Our model was built with 3 × 3 × 3 clusters of molecules constructed directly from X-ray crystallographic data of a crystal with benzene (5B) and a solvent-free pseudopolymorph (5SF) (Fig. 11a). The two structures were studied assuming rigid and increasingly relaxed crystal lattices to evaluate the effect of rigidity on the changes in rotational energy. In the rigid lattice model, all atoms in the cluster were fixed, except for the six carbon and four hydrogen atoms of the central rotator. This simple approximation led to unrealistic sawtooth potentials with large changes in energy (Fig. 11b). Relaxed models allowed for an increased number of conformational degrees of freedom. It was shown that conformational oscillations of all the molecules in the two clusters reduced the height of the barriers to the experimental values of ca. 12 kcal mol−1. The resulting computational data disclosed the role of correlated motion in molecular crystals, a phenomenon that we now refer to as “crystal fluidity”. Changes in atomic positions with respect to the equilibrium structure were observed for all molecules in the cluster as a function of rotator's dihedral angle, with the largest displacement observed when the rotator was at its transition state (90° off the plane). Specifically, atomic displacements were dependent on the distance from the central rotator, with structural perturbations radiating outward from the rotary event. Additionally, in the solvated system (5B), the 180° flipping motion of the rotator is coupled to a 60° geared rotation of the solvent benzene molecules, suggesting a crystalline molecular gear.27
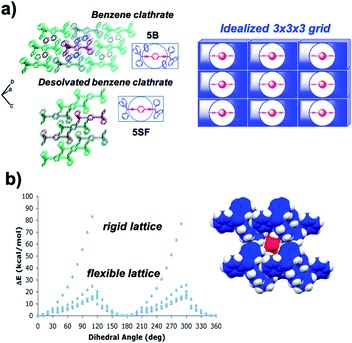 |
| | Fig. 11 (a) Crystal packing structures of the benzene clathrate 5B (top) and desolvated form 5SF (bottom). The structures as shown are analogous to the schematic depiction of an idealized 3 × 3 × 3 lattice (right) constituting a 27-rotor molecule assembly. (b) Correlated motion in crystalline benzene clathrate that accounted for varying degrees of freedom within a crystal lattice and approximated rotational barriers in a rigid or flexible lattice, respectively. Calculations were performed using molecular dynamics simulations (adapted from ref. 26). | |
6.3. Molecular dynamics and periodic boundary conditions in close-packed molecular crystals
While dynamics in crystalline solids may be approximated by means of a large molecular cluster, as discussed above, the size of the computational model can be significantly reduced to a primitive cell when combined with periodic boundary conditions (PBC). Periodic boundary conditions impose artificial periodicity repeated in all directions on the simulated cell to account for the continuum properties of the system. When PBC are employed, any atom or molecule that leaves the box through a particular face, reenters the system at the same point of the face directly opposite. One can anticipate that molecular dynamics simulations of amphidynamic systems based on PBC would describe a model of an infinite lattice of molecular rotors undergoing their motion in a coherent manner, in effect assuming a multicomponent geared system, rather than one susceptible to structural and dynamic fluctuations through the crystal lattice. An example of this computational model was reported by Kolomeisky et al. to study how intramolecular interactions between a triphenylsilyl stator and four different rotators, including phenylene (Phe 3), cubyl (Cub 2), bicyclo[2.2.2]octane (BCO 6), and para-carborane (Carbor 7) (Fig. 12a) affect rotational dynamics.28 Each simulation cell contained 4 molecular rotors, with 124 periodic images of the original cell. The impact of flexibility on the dynamic properties of the system was studied by considering four types of coarse-graining representations of molecular rotors that differed by the size of what was defined to be rigid, and included the central rotator (Flex) and extended portions of the axle (Flex1, Flex2 and Rod, Fig. 12b). Results indicated that more flexible rotors were able to find the most energetically favorable packing configuration which resulted in the overall smaller free volume around the rotator unit. As a result, steric hindrance emerging from the rotator interactions with its neighbors contributed to high activation barriers and high attempt frequency (Fig. 12c). Indeed, the BCO 6 and Carbor 7 amphidynamic crystals with relatively large free volumes displayed high rotational speed because of lower activation barriers. While molecular dynamics simulations with PBC are able to give a reasonable picture of local environment of molecular rotors, such simulations might have to be coupled with additional approximations that may account for the stochastic nature of molecular machines.
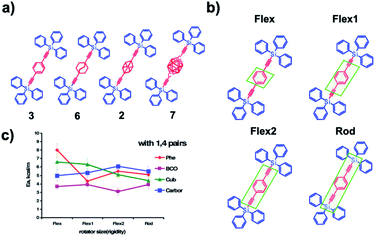 |
| | Fig. 12 (a) Molecular gyroscopes studied Phe, BCO, Cub, and Carbor. (b) Various coarse-grain representations of the rotator part in Phe molecular gyroscope. These representations are labelled as: Flex, Flex1, Flex2, Rod, and they differ by the size of the central rotator rigid segment. The rigid segment is the smallest in Flex and the largest in Rod. (c) Rotational activation energies for different molecular rotors as a function of flexibility with nonbonded interactions in 1,4 pairs of terminal atoms involved in each dihedral angle (adapted from ref. 28). | |
6.4. Bias sampling via metadynamics simulations
In instances were correlated motion can be defined with specific collective variables, an enhanced sampling technique called metadynamics could be utilized to construct potential energy hypersurfaces. The method allows for an efficient energy landscape sampling via an introduction of a time-dependent bias potential acting on the chosen variables and propagating the system on the potential energy surface in an accelerated fashion. This advanced molecular dynamics technique was utilized in studying crowded molecular media such as octafluoronaphthalene plastic crystals,29a,b interdigitated metal–organic rotor {Li4+(1−)4(H2O)8}·2DMF crystals29c or systems that are characterized by dynamics of interconversion between gearing and slippage such as norbornane based molecular spur gear.29d Metadynamics simulations were shown to support the interpretation of the experimental results, or provide evidence of correlated dynamics in instances where gearing time scales are outside the experimentally accessible range. For example, in the study by Batail et al. DFT metadynamics studies29c revealed strongly interrelated series of rotational motions in a densely-packed crystalline environment of the metal–organic rotor, {Li4+(1−)4(H2O)8}·2DMF and were in a great agreement with VT NMR results. On the other hand, in the study of norbornane 8 spur gears,29d VT NMR studies at temperatures as low as 213 K showed no phase isomer formation and thus 2D metadynamics calculations were performed to understand the gearing/slippage energetic profile. Defining a dihedral angle for each triptycene in an intermeshed gear system and repeatedly introducing the bias potential allowed for a good estimation of the free energy of the process. A simultaneous increase in dihedral angle in both rotors (same direction) or independent rotation of one gear were attributed to slippage trajectories, while a decrease in dihedral angle for one rotator and an increase for the other (opposite directions) was associated with geared rotation (Fig. 13). The results indicated that norbornane spur gear has a lower barrier for slippage (2 kcal mol−1) than the barrier for gearing (5.4 kcal mol−1), and therefore was undergoing predominantly slippage-type dynamics.
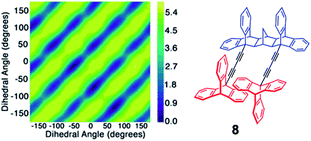 |
| | Fig. 13 2D metadynamics simulations for molecular spur gears with triptycene rotators and a norbornane-based stator. Top-left to bottom-right diagonals represent the lowest energy trajectory for gearing, with dihedral angles changing in positive and negative direction (adapted from ref. 29d). | |
7. Experimental determination of molecular gearing in crystalline solids
While the experimental determination of molecular gearing in the solid state can be based on analogous measurements, correlated motions with matched rotational frequencies and parity are expected to have characteristic dynamics. As mentioned earlier, gearing implies a reduction in entropy as the result of a reduction in the number of microstates as n rotors, each with m rotational states, independently give rise to mn degenerate states, which reduce to the same number of states as a single rotator, m1, when they become part of a linear gear train. A very simple illustration of this is shown in Fig. 14 with a single symmetric toothed rotor with n = 3 (Fig. 14a), a set of two independent rotors that would have mn = 32 = 9 independent rotational states (Fig. 14b), and two geared rotators with m1 = 31 = 3 states (Fig. 14c). The contribution to the change of activation entropy that occurs as a result of a reduction in the number of degrees of freedom connecting the various rotational states can be appreciated by considering the change in symmetry number (σ) from isolated (σi) to geared systems (σg). In the hypothetical case in Fig. 14, the negative change in entropy ΔS‡ ≈ R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(3/9) = −2.15 cal mol−1 K−1, will be manifested in an Eyring plot by a reduction in the value of the intercept. Indeed, several literature examples for correlated motion and molecular gearing in solution have shown that gearing is characterized by a negative activation entropy, which is also manifested in the form of small values in the pre-exponential factor of an Arrhenius plot.30 Notably, one example reporting activation parameters for a gear slipping process shows the activation entropy to be close to zero.31
ln(3/9) = −2.15 cal mol−1 K−1, will be manifested in an Eyring plot by a reduction in the value of the intercept. Indeed, several literature examples for correlated motion and molecular gearing in solution have shown that gearing is characterized by a negative activation entropy, which is also manifested in the form of small values in the pre-exponential factor of an Arrhenius plot.30 Notably, one example reporting activation parameters for a gear slipping process shows the activation entropy to be close to zero.31
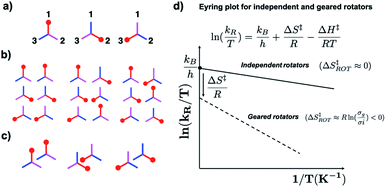 |
| | Fig. 14 (a) Illustration of an independent molecular rotor with three degenerate rotational states where each blade can occupy sites 1, 2 and 3, (b) the nine degenerate states that can be occupied by two independent rotators, and (c) the three states of two geared rotors. (d) Qualitative expectations of changes in intercept and slope of the Eyring plots of independent (i) and geared (g) molecular rotors. A smaller intercept is the result of a negative activation entropy due the reduction in the number of microstates in going from independent to gear rotors, and a steeper slop is the result of differences in activation enthalpies resulting from changes in the volume of independent and geared rotors. | |
Furthermore, one may expect rotational barriers in molecular crystals to depend on the surface area of the rotator and the contacts it makes with its close neighbors. For that reason, the activation enthalpy needed for the correlated motion of two rotators will be greater than an equivalent system with free rotation, as illustrated in Fig. 14d by the different slopes of the hypothetical independent and geared rotors. One can also appreciate that the activation enthalpy and entropy will grow increasingly unfavorable as the number of gears in a gear train increases. Similarly, one can expect that activation enthalpy will be greater and the activation entropy increasingly negative as the number of cogs increases in a particular gear.
8. Studies of correlated dynamics in crystalline molecular gears
8.1. A crystalline slipping gear train
The observation of molecular gears in the solid state has been proposed in a small number of cases based on the spatial arrangement of rotating units. Supporting evidence generally comes from computational data and experimental measurements. An early example comes from the benzene-containing crystals of 1,4-bis(triphenylethynyl)benzene molecular rotor 5 discussed in Section 6.2. The dumbbell-shaped molecular rotor 5 was shown to crystallize in parallel chains of tilted rotors with two benzene molecules occupying the space between adjacent neighbors (Fig. 15).27 Benzene molecules in the crystal were shown to exist as parallel-displaced dimers, with their edges making van der Waals contacts with the phenylene rotators on each side. A simple mechanical model based on the crystal structure where phenylenes and benzene molecules can be seen as gears in a gear train (Fig. 15, left), suggests that the clockwise rotation of the phenylene on the left, labeled with a C, should lead to the anticlockwise rotation of the closest benzene molecule to the right, indicated with the label A. In principle, this motion could be transmitted to the off-axis benzene molecule below, causing it to turn in the clockwise direction. This hypothetical gear chain would continue with anticlockwise rotation of the phenylene group leading to clockwise rotation of the next benzene molecule, and so on.
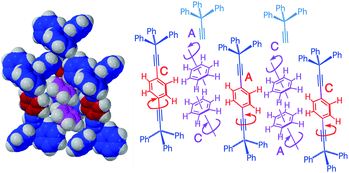 |
| | Fig. 15 (Left) Space-filling model and (right) line formulas illustrating the packing arrangement of rotor 5 and the enclathrated benzene dimer. The angle formed by the phenylene 1,4-axis and the benzene molecules 6-fold axes is 59.7°. Arrows and letter C and A indicate hypothetical clockwise and anticlockwise rotation, respectively (adapted from ref. 27). | |
Interestingly, the computational model based on a flexible cluster using classical force field methods as described above, confirmed that the 180° rotation of a phenylene group results in the concerted 60° rotation of the neighboring benzene molecules (Fig. 15). Experimental measurements showed that in-plane rotation of the benzene molecule occurs at frequencies that are greater than the upper limit of the quadrupolar echo 2H NMR experiment, krot > 107 s−1. In contrast, rotation of the phenylene group in the benzene clathrate using VT 13C CPMAS NMR was shown to occur in the krot ≈ 103 s−1 regime, with an activation energy Ea = 12.8 kcal mol−1.31 Given the difference of over four orders of magnitude between fast benzene and slow phenylene rotators, and considering the normal value of the pre-exponential factor for rotation of the phenylene group, we concluded that this particular array of molecular rotors behaves like a slipping gear train.
8.2. Spiral gear in a supramolecular 12-crown[4]ether rotor assembly
A recent study on the structure and dynamics of supramolecular salts of 12-crown-4-ether hosting a di-protonated salt of diazabicylo[2.2.2]octane (DABCO) with either tetrafluoroborate (2BF4−) or perchlorate (2ClO4−) anions, led the authors to suggest a network of geared 12-crown-4-ethers.33 A schematic representing the crystal structure in Fig. 16a highlights the intermeshed zig-zag alignment of the (12-crown-4)2DABCOH22+, with the counterions surrounding DABCOH22+ omitted for clarity. VT solid state 2H NMR experiments confirmed the ultrafast independent rotational motion of the globular DABCOH22+ groups at the center of the complex, while VT 13C CPMAS showed a much slower rotational motion of the 12-crown-4. It was suggested that the slower process corresponds to rotational site exchange of the 12-crown-4 methylene groups rather than a less likely crown inversion process. The authors also note that the adjacent 12-crown-4 molecules are locked and, therefore, must rotate in a concerted manner by transferring their instantaneous angular momentum to adjacent 12-crown-4 that are aligned in either parallel (Fig. 16b) or perpendicular fashion (Fig. 16c).
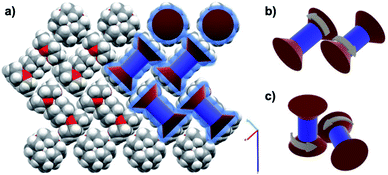 |
| | Fig. 16 (a) Crystal packing of the [(12-crown-4)2·DABCOH2]2+ units. Schematics of the suggested geared motion between (b) antiparallel and (c) perpendicular ethers (adapted from ref. 32). | |
8.3. Correlated motion between pairs of bicyclo[2.2.2]octane rotors
In an elegant study addressing an unusual polarizability leading to interesting non-linear optical effects, Batail and coworkers proposed remarkable gearing dynamics in molecular dirotor 9, which entails a molecular rod with two outer pyridines and two three-cogged 1,4-bis(ethynyl)-bicyclo[2.2.2]octane (BCO) paddle wheel-shaped gears spaced by a diyne linker (Fig. 17a).34 Monoclinic crystals in the space group C2/c were characterized by molecular rods forming infinite molecular chains, as shown in Fig. 17. By performing variable-temperature 1H spin–lattice relaxation NMR experiments, Batail and coworkers observed two dynamic processes involving the same number of molecular rotors. Fitting the temperature dependence of the relaxation rate to the Kubo–Tomita relaxation expression (eqn (2)) revealed activation barriers of 1.85 kcal mol−1 (pre-exponential factor A = 1.82 × 1012 s−1) and 6.1 kcal mol−1 (pre-exponential factor A = 8.3 × 1012 s−1). Based on the crystal structure, it was suggested that the two barriers were associated with rotational motion emerging from two different equilibrium positions that differ by a 60° rotation of the BCO groups with an occupancy ratio of 88![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12 at room temperature. It was proposed that the lower energy barrier was associated with synchronized gearing motion between two adjacent BCOs, while the higher barrier was due to neighboring BCOs “rubbing” against each other in an asynchronous fashion. Support for this hypothesis was found in a computational model based on a cluster containing the molecular rod with two BCO units surrounded by neighboring molecules with H⋯H contacts shorter than 2.8 Å. DFT-based calculations indicated that having two rotors occupy minority sites (m·m) is energetically unfavorable by 5.0 kcal mol−1 as compared to having the two rotors in majority sites (M·M). The mixed structure with one rotor in each site (m·M or M·m) was shown to have an energy penalty of only 1.5 kcal mol−1. Noting that these values are close to the experimental barriers, the authors suggested that the low barrier rotation is likely to arise when rotors in the (M·M) ground state follow a trajectory that goes through a barrier that is analogous to the structure of the (m·M) pair, while the slower rotation with a higher energy barrier would occur in trajectories that pass through structures that resemble the (m·m) rotor pair. Support for this hypothesis was obtained from DFT calculations simulating synchronous and asynchronous motion, which led to calculated barriers of 1.08 and 4.88 kcal mol−1, respectively (not indicated in the figure).
12 at room temperature. It was proposed that the lower energy barrier was associated with synchronized gearing motion between two adjacent BCOs, while the higher barrier was due to neighboring BCOs “rubbing” against each other in an asynchronous fashion. Support for this hypothesis was found in a computational model based on a cluster containing the molecular rod with two BCO units surrounded by neighboring molecules with H⋯H contacts shorter than 2.8 Å. DFT-based calculations indicated that having two rotors occupy minority sites (m·m) is energetically unfavorable by 5.0 kcal mol−1 as compared to having the two rotors in majority sites (M·M). The mixed structure with one rotor in each site (m·M or M·m) was shown to have an energy penalty of only 1.5 kcal mol−1. Noting that these values are close to the experimental barriers, the authors suggested that the low barrier rotation is likely to arise when rotors in the (M·M) ground state follow a trajectory that goes through a barrier that is analogous to the structure of the (m·M) pair, while the slower rotation with a higher energy barrier would occur in trajectories that pass through structures that resemble the (m·m) rotor pair. Support for this hypothesis was obtained from DFT calculations simulating synchronous and asynchronous motion, which led to calculated barriers of 1.08 and 4.88 kcal mol−1, respectively (not indicated in the figure).
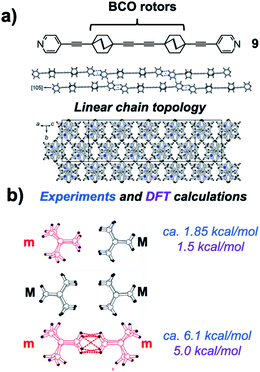 |
| | Fig. 17 Crystalline arrays of pairs of the rod-like molecules (a) 1,4-bis(ethylnyl)bicyclo[1.1.1]octane (BCO) and (b) intermolecular interactions propose to affect correlated rotational dynamics (adapted from ref. 33). | |
It is expected that intermolecular interactions between pairs of BCO rotors along different trajectories should give rise to different barriers. However, given that the two trajectories start from a common ground state, the lower barrier trajectory for the synchronous gearing pathway would have to be functional at low temperatures, but become “disrupted” when the asynchronous rubbing process takes place at higher temperatures. The system would have to transition from a very efficient synchronous gear into one that slows down significantly at higher temperature as the asynchronous rotation begins. It is interesting to also point out that the experimental pre-exponential factors of 1.8 × 1012 s−1 and 8.3 × 1012 s−1 are not consistent with a correlated process where independent degrees of rotational freedom are surrendered, but with internal dynamics determined by a simple site-exchange process. It appears that more data will be needed in order to pin this process down.
8.4. Gear dynamics in a crystalline 1D helical rotor arrays
Substantial evidence of molecular gearing in a 1D crystalline rotor arrays was obtained by a combination of single crystal X-ray diffraction, solid state NMR, and the formation of mixed crystals as a simple strategy to probe for correlated dynamics. While investigating a set of molecular systems built with p-phenylene rotators and ethynyl-substituted steroids as the stator, we came across the molecular rotor 9 with a central p-phenylene rotator flanked by two mestranol moieties acting as the stator (Fig. 18).35 Single crystal X-ray diffraction analysis revealed that structure 9 adopts a U-shape conformation (Fig. 18a) and packs as a nested 1D-helical array of molecular rotors with each phenylene group having a center-to-center distance of 4.9 Å to its neighboring rotators (Fig. 18b and c). Such distance is much longer than van der Waals contact, but not long enough to allow for free rotation. The orientation of the phenylenes was shown to be disordered over two positions related by an 85°/95° rotation (Fig. 18d).
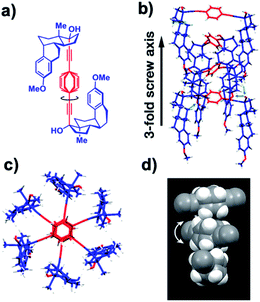 |
| | Fig. 18 (a) Structure and solid state conformation of mestranol molecular rotor 9. (b) Packing motif in the form of 1D chains of nested molecular rotors. (c) View long the axis of the 1D-chain highlighting a 120° rotation between adjacent rotors corresponding to the space group P6. (d) Space filling model of the phenylene groups showing rotational disorder over two position related by 85°/96° (adapted from ref. 34). | |
Quadrupolar echo 2H NMR measurements carried out at 296 K to explore rotational motion in crystals of 9 resulted in a narrow spectrum consistent with fast dynamics and exchange between multiple sites (Fig. 19a). Spectral simulations were obtained only when using a counterintuitive model that included 180° rotations in the fast exchange regime (>107 s−1) and a slower 85° tilting motion in ca. 106 s−1 regime. While the two-fold flipping (180° rotation) is consistent with the rotational C2 symmetry of the phenylene group, the slower 85° tilting process can be attributed to the exchange between the two equilibrium sites. The kinematics of this process can be understood in terms of the model shown in Fig. 19b, where a rotator undergoes fast 180° rotations at a given site (coordinate A), and after six or seven such rotations switches by an angle of 85°/95°, before continuing the fast 180° rotations in the other site (coordinate B). Further VT NMR analysis at temperatures as low as 155 K revealed that the 180° rotations remain in the fast exchange regime, but the 85°/95° rotations can be slowed down because of a relatively low enthalpic barrier (2.2 kcal mol−1) and a relatively unfavorable activation entropy of −23 cal mol−1 K−1 (Fig. 19c). These results are strong indication of a highly organized switching mechanism between the two sites in the 1D channel.
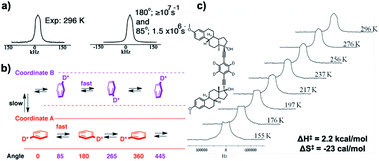 |
| | Fig. 19 (a) Quadrupolar echo 2H NMR spectrum of molecular rotor 9 at 296 K and a simulated spectrum corresponding to a kinematic process that involves 180° rotations in the fast exchange regime (>107 s−1) combined with 85°/95° jumps in the intermediate exchange regime (1.5 × 106 s−1). (b) Representation of the this process in terms of two coordinates that correspond to rotation in each of the two disordered sites, labelled as coordinate A and coordinate B. (c) Variable temperature 2H NMR spectra corresponding to a process that retains fast 180° rotations and slow 85°/95° jumps varying from 2 × 104 s−1 at 155 K to 1.2 × 106 s−1 at 296 K, which reveal a low activation enthalpy and large and negative activation entropy (adapted from ref. 34). | |
Considering that highly organized switching motion should involve several correlated molecular rotors, potentially in the form of highly organized domains, our group explored substitutional solid solutions of mestranol rotor 9 acting as host with a slightly larger 2,3-difluorophenylene rotator analog (F2Ph) added as a guest.35b Both the dynamics of the phenylene-d4 host and the difluorophenylene-d2 guest were explored with crystals having the guest in quantities varying from 1% to 20%, which were obtained by slow solvent evaporation. Solid solutions with as little as 1% to 5%, F2Ph seemed to facilitate the 85°/95° switching process, as shown by narrower spectra, a reduction of the activation enthalpies (1.4 or 1.6 kcal mol−1), and an activation entropy that was slightly less negative (−19.0 cal mol−1 K−1). This simple observation confirms a process where molecular rotation is influenced by long-range interactions in the channel, indicating that rotation at any given site is not an independent process. Notably, higher guest loadings with one of every five molecular rotors replaced by a larger difluorophenylene guest (20%) resulted in broader spectra and suggested that high loadings lead to jamming in the channel.
Kinematics of this system changed and the NMR spectra for both phenylene and difluorophenylene broadened out at lower temperatures (Fig. 20a). Line shape analysis for the labeled host showed that even though the rotations for the phenylene were slowed down at lower temperatures, the trajectories mapping out the fast 180° and the slow 85° processes were not affected by the 2,3-difluorophenylene guest. By contrast, spectral simulations for the deuterated difluorophenylene failed when the same mechanism was assumed. The key distinction was that the difluorophenylene rotator was unable to occupy one of the sites that had been otherwise available to the phenylene rotator. The dynamics of the difluorophenylene rotator could be qualitatively accounted for by an exchange process consisting of only three sites. Furthermore, the activation parameters for the difluorophenylene were dramatically altered with a small and positive activation entropy of ca. 1.0 cal mol−1 K−1. This result suggests that the difluorophenylene rotation is not correlated, but occurs independently. The experimental evidence available to date has been interpreted in terms of the model shown in Fig. 20b, with a central phenylene rotator flanked by its two closest neighbors in the chain. A black dot in the space-filling model and on the red bars that represent the phenylene rotors indicates their orientation with respect to 180° rotation. The two structures at the top and bottom rows in Fig. 20b represent a 180° flip of the central phenylene in the sites that have a different tilt. We hypothesize that the transition state associated with such rotation requires an oscillation of phenylenes above and below their plane. By contrast, changing the tilt of the central rotator requires a transition state where the two nearby neighbors must align along the direction of the channel. Overall, the level of organization required for these two processes is quite different. Fast 180° rotation requires minimal motion of the neighboring molecules in the chain while the slow tilting requires a high level of order extended along the channel. To date, this work represents the strongest evidence for a solid-state gearing event.
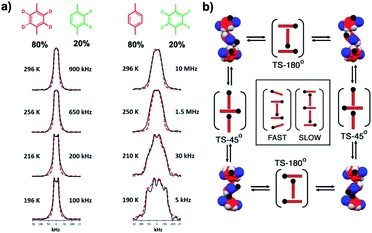 |
| | Fig. 20 (a) Quadrupolar echo 46 MHz 2H NMR spectra of the deuterated phenylene rotor recorded in a solid solution with 20% of the difluorophenylene guest between 196 K and 296 K. The black solid lines correspond to the experimental spectra and the red dotted lines to the simulation. The frequencies shown in the simulated spectra correspond to the 85°/95° switch, as the 180° jumps remain in the fast exchange limit, above 10 MHz. (b) Mechanism for the rotation of the difluorophenylene rotator in the 1D column of molecular rotor (adapted from ref. 35b). | |
9. Conclusions and future perspective
While elegant solutions have been found for the design of discrete, isolated molecular gears in solution, engineering isolated and extended gears in the crystalline state is in its infancy. We believe that the most viable approach towards realizing molecular gears in the solid state is by utilizing amphidynamic crystals. A new set of design strategies for bringing molecular gears to the solid state are outlined here with the special emphasis on the importance of intermolecular interactions that facilitate gearing dynamics and control framework flexibility. With these strategies and by the careful selection of the rotator and lattice elements, different dynamic regimes can be obtained. Energetic parameters for systems that display dynamic gearing can be obtained experimentally using variable temperature NMR. Computational approaches such as quantum mechanics and molecular dynamics simulations can be utilized to construct potential energy hypersurfaces that provide useful information on gearing mechanism. Future research approaches should address the main challenges associated with installing gears in the solid state such as achieving a fine balance between the lattice geometry and rotator position as well as creating favourable electrostatic interactions between each rotator. Building on the strategies of the previous attempts to design molecular gears in solution and utilizing amphidynamic crystals as a flexible framework to accommodate gearing dynamics will allow researchers to synthesize systems with higher levels of dynamic complexity that rival macroscopic gear trains.
Conflicts of interest
The authors declare no competing interests.
Acknowledgements
This work was supported by National Science Foundation Grants NSF DMR 1700471 and CHE-1855342.
Notes and references
- V. Balzani, A. Credi, F. Raymo and J. F. Stoddart, Angew. Chem., Int. Ed., 2000, 39, 3348–3391 CrossRef CAS.
-
(a) C. S. Vogelsberg and M. A. Garcia-Garibay, Chem. Soc. Rev., 2012, 41, 1892–1910 RSC;
(b) M. E. Howe and M. A. Garcia-Garibay, J. Org. Chem., 2019, 84, 9835–9849 CrossRef CAS;
(c) M. A. Garcia-Garibay, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 10771–10776 CrossRef CAS.
-
(a) C. Cheng, P. R. McGonigal, S. T. Schneebeli, H. Li, N. A. Vermeulen, C. Ke and F. J. Stoddart, Nat. Nanotechnol., 2015, 10, 547–553 CrossRef CAS;
(b) K. Zhu, C. A. O'Keefe, V. N. Vukotic, R. W. Schurko and S. J. Loeb, Nat. Chem., 2015, 7, 514–519 CrossRef CAS.
- W. Danowski, T. van Leeuwen, S. Abdolahzadeh, D. Roke, W. R. Browne, S. J. Wezenberg and B. L. Feringa, Nat. Nanotechnol., 2019, 14, 488–494 CrossRef CAS.
-
(a) J. Michl and E. C. H. Sykes, ACS Nano, 2009, 3, 1042–1048 CrossRef CAS;
(b) R. D. Horansky, L. I. Clarke, E. B. Winston, J. C. Price, S. D. Karlen, P. D. Jarowski, R. Santillan and M. A. Garcia-Garibay, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 054306 CrossRef.
-
(a) H. Iwamura and K. Mislow, Acc. Chem. Res., 1988, 21, 175–182 CrossRef CAS;
(b) Y. Kawada and H. Iwamura, Tetrahedron Lett., 1981, 22, 1533–1536 CrossRef CAS;
(c) Y. Kawada and H. Iwamura, J. Am. Chem. Soc., 1983, 105, 1449–1459 CrossRef CAS;
(d) Y. Kawada, H. Sakai, M. Oguri and G. Koga, Tetrahedron Lett., 1994, 35, 139–142 CrossRef CAS;
(e) W. Setaka, T. Nirengi, C. Kabuto and M. Kira, J. Am. Chem. Soc., 2008, 2, 15762–15763 CrossRef.
-
(a) D. K. Frantz, A. Linden, K. K. Baldridge and J. S. Siegel, J. Am. Chem. Soc., 2012, 134, 1528–1535 CrossRef CAS;
(b) F. Huang, G. Wang, L. Ma, Y. Wang, X. Chen, Y. Che and H. Jiang, J. Org. Chem., 2017, 82, 12106–12111 CrossRef CAS;
(c) S. Toyota, T. Shimizu, T. Iwanaga and K. Wakamatsu, Chem. Lett., 2011, 40, 312–314 CrossRef CAS.
-
(a) J. M. Chance, J. H. Geiger, Y. Okamoto, R. Aburatani and K. Mislow, J. Am. Chem. Soc., 1990, 112, 3540–3547 CrossRef CAS;
(b) N. Koga, Y. Kawada and H. Iwamura, J. Am. Chem. Soc., 1983, 105, 5498–5499 CrossRef CAS.
-
(a) H. Ube, R. Yamada, J. I. Ishida, H. Sato, M. Shiro and M. Shionoya, J. Am. Chem. Soc., 2017, 139, 16470–16473 CrossRef CAS;
(b) H. Ube, Y. Yasuda, H. Sato and M. Shionoya, Nat. Commun., 2017, 8, 1 CrossRef;
(c) K. Sanada, H. Ube and M. Shionoya, J. Am. Chem. Soc., 2016, 138, 2945–2948 CrossRef CAS.
-
(a) A. Colin-Molina, D. P. Karothu, M. J. Jellen, R. A. Toscano, M. A. Garcia-Garibay, P. Naumov and B. Rodríguez-Molina, Matter, 2019, 1, 1033 CrossRef;
(b) A. S. Tayi, A. Kaeser, M. Matsumoto, T. Aida and S. I. Stupp, Nat. Chem., 2015, 7, 281 CrossRef CAS;
(c) J. S. Miller, Mater. Today, 2014, 17, 224–235 CrossRef CAS;
(d) P. Naumov, S. Chizhik, M. K. Panda, N. K. Nath and E. Boldyreva, Chem. Rev., 2015, 115, 12440–12490 CrossRef CAS;
(e) M. Jin, S. Yamamoto, T. Seki, H. Ito and M. A. Garcia-Garibay, Angew. Chem., Int. Ed., 2019, 131, 18003–18010 CrossRef.
-
(a) A. Comotti, S. Bracco and P. Sozzani, Acc. Chem. Res., 2016, 49, 1701–1710 CrossRef CAS;
(b) D. I. Kolokolov, H. Jobic, A. G. Stepanov, V. Guillerm, T. Devic, C. Serre and G. Férey, Angew. Chem., Int. Ed., 2010, 49, 4791–4794 CrossRef CAS;
(c) J. A. Rodríguez-Velamazán, M. A. González, J. A. Real, M. Castro, M. C. Muñoz, A. B. Gaspar, R. Ohtani, M. Ohba, K. Yoneda, Y. Hijikata, N. Yanai, M. Mizuno, H. Ando and S. Kitagawa, J. Am. Chem. Soc., 2012, 134, 5083–5089 CrossRef;
(d) S. Bracco, F. Castiglioni, A. Comotti, S. Galli, M. Negroni, A. Maspero and P. Sozzani, Chem.–Eur. J., 2017, 23, 11211–11215 Search PubMed.
-
(a) J. Perego, S. Bracco, M. Negroni, C. X. Bezuidenhout, G. Prando, P. Carretta, A. Comotti and P. Sozzani, Nat. Chem., 2020, 12, 845–851 CrossRef CAS;
(b) C. S. Vogelsberg, F. J. Uribe-Romo, A. S. Lipton, S. Yang, K. N. Houk, S. Brown and M. A. Garcia-Garibay, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 13613–13618 CrossRef CAS.
- N. Tanaka, Y. Inagaki, K. Yamaguchi and W. Setaka, Cryst. Growth Des., 2019, 20, 1097–1102 CrossRef.
- S. L. Gould, R. B. Rodriguez and M. A. Garcia-Garibay, Tetrahedron, 2008, 64, 8336–8345 CrossRef CAS.
- X. Jiang, H.-B. Duan, S. I. Khan and M. A. Garcia-Garibay, ACS Cent. Sci., 2016, 2, 608–613 CrossRef CAS.
-
(a) S. Horike, R. Matsuda, D. Tanaka, S. Matsubara, M. Mizuno, K. Endo and S. Kitagawa, Angew. Chem., Int. Ed. Engl., 2006, 45, 7226–7230 CrossRef CAS;
(b) A. Comotti, S. Bracco, P. Valsesia, M. Beretta and P. Sozzani, Angew. Chem., Int. Ed., 2010, 49, 1804–1808 CrossRef;
(c) S. Bracco, M. Beretta, A. Cattaneo, A. Comotti, A. Falqui, K. Zhao, C. Rogers and P. Sozzani, Angew. Chem., Int. Ed., 2015, 54, 4855–4859 CrossRef;
(d) A. Comotti, S. Bracco, T. Ben, S. Qiu and P. Sozzani, Angew. Chem., Int. Ed., 2014, 53, 1061–1065 CrossRef;
(e) S. Bracco, T. Miyano, M. Negroni, I. Bassanetti, L. Marchio, P. Sozzani, N. Tohnai and A. Comotti, Chem. Commun., 2017, 53, 7776–7779 RSC;
(f) A. Comotti, S. Bracco, A. Yamamoto, M. Beretta, T. Hirukawa, N. Tohnai, M. Miyata and P. Sozzani, J. Am. Chem. Soc., 2014, 136, 618–621 CrossRef CAS.
- A. E. Khudozhitkov, S. S. Arzumanov, D. I. Kolokolov, O. A. Kholdeeva, D. Freude and A. G. Stepanov, Chem.–Eur. J., 2019, 25, 10808–108012 CrossRef CAS.
-
(a)
C. A. Fyfe, Solid State NMR for Chemists, CFC Press, Guelph, Ontario, 1983 Search PubMed;
(b) P. Schanda and M. Ernst, Prog. Nucl. Magn. Reson. Spectrosc., 2016, 96, 1–46 CrossRef CAS;
(c) S. P. Brown and H. W. Spiess, Chem. Rev., 2001, 101, 4125–4156 CrossRef CAS;
(d) P. A. Beckmann, A. I. Hill, E. B. Kohler and H. Yu, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 11098 CrossRef CAS.
-
(a) M. Nakamura and N. Oki, Bull. Chem. Soc. Jpn., 1975, 48, 2106–2111 CrossRef CAS;
(b) K. Nikitin, J. Muldoon, H. M. Bunz and M. J. McGlinchey, Chem.–Eur. J., 2015, 21, 4664–4670 CrossRef CAS;
(c) K. Nikitin, H. Müller-Bunz, Y. Ortin, J. Muldoon and M. J. McGlinchey, J. Am. Chem. Soc., 2010, 132, 17617–17622 CrossRef CAS.
- I. Liepuoniute, J. N. Sanders, M. A. Garcia-Garibay and K. N. Houk, J. Org. Chem., 2020, 85, 8695–8701 CrossRef CAS.
- S. D. Karlen, H. Reyes, R. E. Taylor, S. I. Khan, M. F. Hawthorne and M. A. Garcia-Garibay, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 14973–14977 CrossRef CAS.
-
(a)
G. L. Hoatson and R. L. Vold, 2H-NMR spectroscopy of solids and liquid crystals. Solid State NMR III, ed. B. Blümich, Springer, New York, 1994, pp. 1–67 Search PubMed;
(b) V. Macho, L. Brombacher and H. W. Spiess, The NMR-WEBLAB: An Internet approach to NMR lineshape analysis, Appl. Magn. Reson., 2001, 20, 405–432 CrossRef CAS;
(c) R. Kubo and K. Tomita, A general theory of magnetic resonance absorption, J. Phys. Soc. Jpn., 1954, 9, 888–919 CrossRef CAS;
(d)
J. Sandstruöm, Dynamic NMR Spectroscopy, Academic, New York, 1983 Search PubMed.
- L. Catalano, S. Pérez-Estrada, H.-H. Wang, A. J. L. Ayitou, S. I. Khan, G. Terraneo, P. Metrangolo, S. Brown and M. A. Garcia-Garibay, J. Am. Chem. Soc., 2017, 139, 843–848 CrossRef CAS.
-
(a) M. Tafipolsky, S. Amrjalayer and R. Schmid, J. Comput. Chem., 2007, 28, 1169–1176 CrossRef CAS;
(b) T. Kawaguchi, A. Mamada, Y. Hosokawa and F. Horii, Polymer, 1998, 39, 2725–2732 CrossRef CAS;
(c) L. D. Speakman, B. N. Papas, H. L. Woodcock and H. F. Schaefer III, J. Chem. Phys., 2004, 120, 4247–4250 CrossRef CAS;
(d) I. Liepuoniute, C. M. Huynh, S. Pérez-Estrada, Y. Wang, S. I. Khan, K. N. Houk and M. A. Garcia-Garibay, J. Phys. Chem. C, 2020, 28, 15391–15398 CrossRef.
-
(a) C. Lemouchi, H. M. Yamamoto, R. Kato, S. Simonov, L. Zorina, A. Rodríguez-Fortea, E. Canadell, P. Wzietek, K. Iliopoulos, D. Gindre, M. Chrysos and P. Batail, Cryst. Growth Des., 2014, 14, 3375–3383 CrossRef CAS;
(b) S. Simonov, L. Zorina, P. Wzietek, A. Rodríguez-Fortea, E. Canadell, C. Mézière, G. Bastien, C. Lemouchi, M. A. Garcia-Garibay and P. Batail, Nano Lett., 2018, 18, 3780–3784 CrossRef CAS;
(c) J. Kaleta, J. Michl, C. Mézière, S. Simonov, L. Zorina, P. Wzietek, A. Rodríguez-Fortea, E. Canadell and P. Batail, CrystEngComm, 2015, 17, 7829 RSC.
- P. D. Jarowski, K. N. Houk and M. A. Garcia-Garibay, J. Am. Chem. Soc., 2007, 129, 3110–3117 CrossRef CAS.
- Z. Dominguez, H. Dang, M. J. Strouse and M. A. Garcia-Garibay, J. Am. Chem. Soc., 2002, 124, 7719–7727 CrossRef CAS.
- A. V. Akimov and A. B. Kolomeisky, J. Phys. Chem. C, 2011, 115, 13584–13591 CrossRef CAS.
-
(a) A. J. Ilott, S. Palucha, P. Hodgkinson and M. R. J. Wilson, J. Phys. Chem. B, 2013, 117, 12286–12295 CrossRef CAS;
(b) A. J. Ilott, S. Palucha, A. S. Batsanov, M. R. Wilson and P. Hodgkinson, J. Am. Chem. Soc., 2010, 132, 5179–5185 CrossRef CAS;
(c) A. Rodríguez-Fortea, E. Canadell, P. Wzietek, C. Lemouchi, M. Allain, L. Zorina and P. Batail, Nanoscale, 2020, 12, 8294–8302 RSC;
(d) X. Jiang, S. Yang, M. J. Jellen, K. N. Houk and M. Garcia-Garibay, Org. Lett., 2020, 22, 4049–4052 CrossRef CAS.
-
(a) T. Tseng, H. F. G. Lu, C. Y. Kao, C. W. Chiu, I. Chao, C. Prabhakar and J.-S. Yang, J. Org. Chem., 2017, 82, 5354–5366 CrossRef CAS;
(b) M. Nakamura, K. Kishimoto, Y. Kobori, T. Abe, K. Yoza and K. Kobayashi, J. Am. Chem. Soc., 2016, 138, 12564–12577 CrossRef CAS;
(c) S. Ogi, T. Ikeda, R. Wakabayashi, S. Shinkai and M. A. Takeuchi, Chem.–Eur. J., 2010, 16, 8285–8290 CrossRef CAS;
(d) S. Hayashi, T. Nakamoto, M. Minoura and W. Nakanishi, J. Org. Chem., 2009, 74, 4763–4771 CrossRef CAS.
- K. Okamura, Y. Inagaki, H. Momma, E. Kwon and W. Setaka, J. Org. Chem., 2019, 84, 14636–14643 CrossRef CAS.
- S. D. Karlen and M. A. Garcia-Garibay, Chem. Commun., 2005,(2), 189–191 RSC.
- L. Fornasari, A. Olejniczak, F. Rossi, S. d'Agostino, M. R. Chierotti, R. Gobetto, A. Katrusiak and D. Braga, Chem.–Eur. J., 2020, 26, 5061–5069 CrossRef CAS.
- C. Lemouchi, K. Iliopoulos, L. Zorina, S. Simonov, P. Wzietek, T. Cauchy, A. Rodríguez-Fortea, E. Canadell, J. Kaleta, J. Michl, D. Gindre, M. Chrysos and P. Batail, J. Am. Chem. Soc., 2013, 135, 9366–9376 CrossRef CAS.
-
(a) B. Rodríguez-Molina, N. Farfán, M. Romero, J. M. Méndez-Stivalet, R. Santillan and M. A. Garcia-Garibay, J. Am. Chem. Soc., 2011, 133, 7280–7283 CrossRef;
(b) S. Pérez-Estrada, B. Rodríguez-Molina, E. F. Maverick, S. I. Khan and M. A. Garcia-Garibay, J. Am. Chem. Soc., 2019, 141, 2413–2420 CrossRef;
(c) S. Pérez-Estrada, B. Rodríguez-Molina, L. Xiao, R. Santillan, G. Jiménez-Osés, K. N. Houk and M. A. Garcia-Garibay, J. Am. Chem. Soc., 2015, 137, 2175–2178 CrossRef.
Footnote |
| † These authors contributed equally. |
|
| This journal is © The Royal Society of Chemistry 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ,
Marcus J.
Jellen†
,
Marcus J.
Jellen†
 and
Miguel A.
Garcia-Garibay
and
Miguel A.
Garcia-Garibay
 *
*




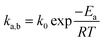



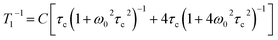
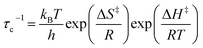



![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(3/9) = −2.15 cal mol−1 K−1, will be manifested in an Eyring plot by a reduction in the value of the intercept. Indeed, several literature examples for correlated motion and molecular gearing in solution have shown that gearing is characterized by a negative activation entropy, which is also manifested in the form of small values in the pre-exponential factor of an Arrhenius plot.30 Notably, one example reporting activation parameters for a gear slipping process shows the activation entropy to be close to zero.31
ln(3/9) = −2.15 cal mol−1 K−1, will be manifested in an Eyring plot by a reduction in the value of the intercept. Indeed, several literature examples for correlated motion and molecular gearing in solution have shown that gearing is characterized by a negative activation entropy, which is also manifested in the form of small values in the pre-exponential factor of an Arrhenius plot.30 Notably, one example reporting activation parameters for a gear slipping process shows the activation entropy to be close to zero.31


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12 at room temperature. It was proposed that the lower energy barrier was associated with synchronized gearing motion between two adjacent BCOs, while the higher barrier was due to neighboring BCOs “rubbing” against each other in an asynchronous fashion. Support for this hypothesis was found in a computational model based on a cluster containing the molecular rod with two BCO units surrounded by neighboring molecules with H⋯H contacts shorter than 2.8 Å. DFT-based calculations indicated that having two rotors occupy minority sites (m·m) is energetically unfavorable by 5.0 kcal mol−1 as compared to having the two rotors in majority sites (M·M). The mixed structure with one rotor in each site (m·M or M·m) was shown to have an energy penalty of only 1.5 kcal mol−1. Noting that these values are close to the experimental barriers, the authors suggested that the low barrier rotation is likely to arise when rotors in the (M·M) ground state follow a trajectory that goes through a barrier that is analogous to the structure of the (m·M) pair, while the slower rotation with a higher energy barrier would occur in trajectories that pass through structures that resemble the (m·m) rotor pair. Support for this hypothesis was obtained from DFT calculations simulating synchronous and asynchronous motion, which led to calculated barriers of 1.08 and 4.88 kcal mol−1, respectively (not indicated in the figure).
12 at room temperature. It was proposed that the lower energy barrier was associated with synchronized gearing motion between two adjacent BCOs, while the higher barrier was due to neighboring BCOs “rubbing” against each other in an asynchronous fashion. Support for this hypothesis was found in a computational model based on a cluster containing the molecular rod with two BCO units surrounded by neighboring molecules with H⋯H contacts shorter than 2.8 Å. DFT-based calculations indicated that having two rotors occupy minority sites (m·m) is energetically unfavorable by 5.0 kcal mol−1 as compared to having the two rotors in majority sites (M·M). The mixed structure with one rotor in each site (m·M or M·m) was shown to have an energy penalty of only 1.5 kcal mol−1. Noting that these values are close to the experimental barriers, the authors suggested that the low barrier rotation is likely to arise when rotors in the (M·M) ground state follow a trajectory that goes through a barrier that is analogous to the structure of the (m·M) pair, while the slower rotation with a higher energy barrier would occur in trajectories that pass through structures that resemble the (m·m) rotor pair. Support for this hypothesis was obtained from DFT calculations simulating synchronous and asynchronous motion, which led to calculated barriers of 1.08 and 4.88 kcal mol−1, respectively (not indicated in the figure).








