Open Access Article
Open Access ArticleA critical analysis of electrospray techniques for the determination of accelerated rates and mechanisms of chemical reactions in droplets†
Grazia
Rovelli
 a,
Michael I.
Jacobs‡
ab,
Megan D.
Willis
a,
Michael I.
Jacobs‡
ab,
Megan D.
Willis
 a,
Rebecca J.
Rapf§
a,
Alexander M.
Prophet
ab and
Kevin R.
Wilson
a,
Rebecca J.
Rapf§
a,
Alexander M.
Prophet
ab and
Kevin R.
Wilson
 *a
*a
aChemical Sciences Division, Lawrence Berkeley National Laboratory, Berkeley, 94720, CA, USA. E-mail: krwilson@lbl.gov
bDepartment of Chemistry, University of California, Berkeley, 94720, CA, USA
First published on 26th October 2020
Abstract
Electrospray and Electrosonic Spray Ionization Mass Spectrometry (ESI-MS and ESSI-MS) have been widely used to report evidence that many chemical reactions in micro- and nano-droplets are dramatically accelerated by factors of ∼102 to 106 relative to macroscale bulk solutions. Despite electrospray's relative simplicity to both generate and detect reaction products in charged droplets using mass spectrometry, substantial complexity exists in how the electrospray process itself impacts the interpretation of the mechanism of these observed accelerated rates. ESI and ESSI are both coupled multi-phase processes, in which analytes in small charged droplets are transferred and detected as gas-phase ions with a mass spectrometer. As such, quantitative examination is needed to evaluate the impact of multiple experimental factors on the magnitude and mechanisms of reaction acceleration. These include: (1) evaporative concentration of reactants as a function of droplet size and initial concentration, (2) competition from gas-phase chemistry and reactions on experimental surfaces, (3) differences in ionization efficiency and ion transmission and (4) droplet charge. We examine (1–4) using numerical models, new ESI/ESSI-MS experimental data, and prior literature to assess the limitations of these approaches and the experimental best practices required to robustly interpret acceleration factors in micro- and nano-droplets produced by ESI and ESSI.
1. Introduction
A significant number of studies have observed that chemical reactions confined in micro- and nano-droplets proceed at significantly faster rates than those in macroscopic bulk solutions. Several approaches are used to study in-droplet chemistry, which include electrospray (ESI),1–7 nano-ESI (nESI)8–14 and electrosonic spray (ESSI)15–29 ionization mass spectrometry (MS). These techniques produce droplets from a solution containing the reaction mixture, which is then directed towards a MS inlet for chemical characterization. In droplet fusion mass spectrometry,15,30–32 two droplet plumes, each containing a reactant, are mixed in free space prior to entering the MS inlet.Accelerated reaction rates are also observed in millimeter-sized droplets levitated either acoustically33 or by the Leidenfrost effect,19,34,35 as well as for evaporating droplets deposited on a surface.36 Reaction rate acceleration has also been reported in other less commonly used approaches, including atomized sub-micron droplets suspended in an environmental chamber,37 guided collisions of electrodynamically levitated micron-sized charged droplets,38 thin-films,36,39,40 desorption ESI (DESI) MS,41 laser ablation ESI-MS,42 paper spray MS,11,43 droplet imbibition,44 and micro-emulsions.45
In this work, we focus on the growing body of literature using ESI/ESSI-MS to investigate reaction rates and mechanisms in nano- and micro-droplets. ESI, nESI and ESSI-MS have been applied to study a diverse set of unimolecular,8,13,14,20,30 bimolecular4,5,7,9,12,14–17,19,25,26,28,29,31 and termolecular1,23 organic reactions. These include complexation,15 cycloaddition,9 and ring-opening reactions,4 phosphorylation,21 hydrogen–deuterium exchange,10 protein folding and unfolding,8,13,14,30 reduction24 and oxidation6,22,25 reactions, as well as the formation of inorganic aggregates.32 When compared to the same reactions conducted in macroscale containers, reactions in ESI/ESSI micro- and nano-droplets are observed to proceed significantly faster, with reported acceleration factors in the ∼102 to 106 range.47
Although many of these prior studies report evidence that reactivity is altered in ESI/ESSI droplets, the underlying reasons for the accelerated rates and, in some cases, altered reaction mechanisms remain unclear.48 The aim of this work is to provide further insight into potential acceleration mechanisms using numerical modelling, new experimental observations, and analysis of the existing literature. We break down the processes occurring in ESI/ESSI droplet plumes and discuss how the often competing multi-phase kinetics of each step affect the accelerated reaction rates observed in the literature. To do so, the paper is organized as follows. In Section 2 we illustrate the coupling of gas- and condensed-phase processes (i.e. multi-phase) inherent to the ESI process itself, providing a framework for the discussion of possible acceleration mechanisms in Section 3. Section 4 presents a detailed analysis of each of the ESI processes described in Section 2: (1) droplet evaporation, (2) the competition between in-droplet chemistry and reactions in the gas-phase or on experimental surfaces, (3) challenges related to ionization efficiency of different analytes and ion transmission and (4) effects of droplet charge. We demonstrate that all these factors need to be carefully considered to robustly interpret the mechanism underlying accelerated reaction rates in ESI/ESSI experiments.
2. Multi-phase processes in electrospray and sonic spray droplets plumes
ESI-, nESI- and ESSI-MS are similar techniques for the generation of charged micro- and nano-droplets, in which ions are transferred to the gas-phase for analysis by mass spectrometry. Shown in Fig. 1 is an illustration of a typical ESI setup used for measuring the kinetics of a generic bimolecular reaction: A + B → C. Reactants A and B are dissolved in a pure or mixed solvent (most commonly water, ethanol, and/or methanol) and the reaction mixture is delivered to a capillary emitter tip to form charged droplets. The reaction time is controlled by varying the distance between the emitter and the MS inlet, usually over a few centimeters, but sometimes up to 1 m by introducing a transfer tube.17,28,42 Reaction kinetics are typically obtained by measuring the ion intensity corresponding to product C as a function of the distance between the MS inlet and the droplet source. Distance is converted to reaction time using droplet velocity. This approach differs from the use of ESI, nESI and ESSI-MS for offline reaction monitoring,18,49 where the emitter tip is kept close to the MS inlet (typically at a distance of a few millimeters) to minimize droplet travel time.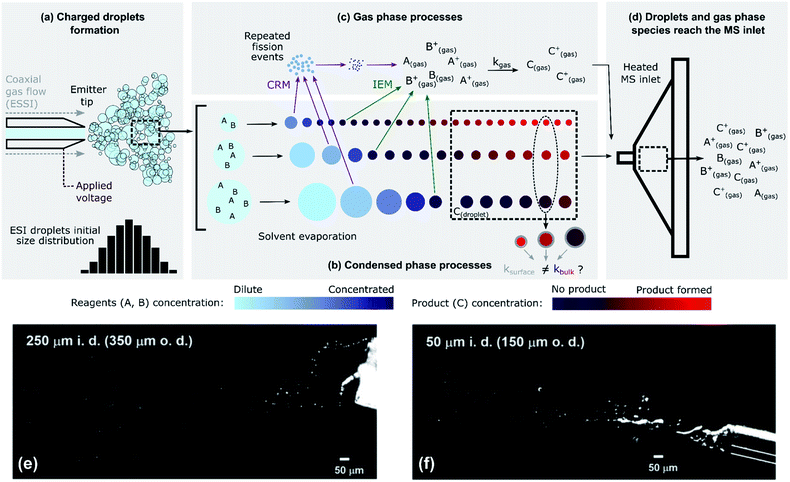 | ||
Fig. 1 The complex, multi-phase processes present during ESI-MS. (a) Droplets are formed from a capillary emitter tip by applying a voltage (ESI/nESI) and/or a high-pressure coaxial gas flow (ESSI); droplets are formed with a certain size distribution. (b) Rapid solvent evaporation causes a decrease in the sizes of the droplets. In this schematic, reactants are considered non-volatile. In the condensed phase, the concentration of reagents can increase because of solvent evaporation and the amount of product formed can be a function of droplet size (Section 4.2); condensed-phase reactions can occur in the bulk (kbulk) or at the surface (ksurface) regions of the droplets. (c) Charged ESI droplets undergo repeated fission events (charge residual model, CRM) that produce smaller progeny droplets, and reagent ions can be directly emitted into the gas-phase (ion emission model, IEM). Gas-phase reactivity can occur with a certain kgas. (d) Gas-phase species and droplets reach the MS inlet. The colour scales qualitatively represent the concentration of reagents A and B (cyan/blue) and of product C (purple/red) in the ESI droplets. (e) and (f) Imaging of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 MeOH/H2O ESSI microdroplets plumes (120 psi N2 gas flow, 5 μL min−1 solvent flow rate, +5 kV applied to the emitter tip) formed with two capillaries with 250 μm and a 50 μm inner diameters (i.d.) and 350 μm and a 150 μm outer diameters (o.d.), respectively.4 Adapted with permission from ref. 4. Copyright (2020) American Chemical Society. 1 MeOH/H2O ESSI microdroplets plumes (120 psi N2 gas flow, 5 μL min−1 solvent flow rate, +5 kV applied to the emitter tip) formed with two capillaries with 250 μm and a 50 μm inner diameters (i.d.) and 350 μm and a 150 μm outer diameters (o.d.), respectively.4 Adapted with permission from ref. 4. Copyright (2020) American Chemical Society. | ||
Fig. 1 illustrates the coupling of gas- and liquid-phase (i.e. multi-phase) processes that occur as droplets are formed and travel to the MS inlet. The liquid jet formed at the tip of the capillary emitter is broken up into droplets by an applied voltage (ESI and nESI) and/or by a high-pressure coaxial sheath gas flow (ESSI), which facilitates droplet formation as well as charging. The resulting droplet properties (size, charge and velocity distributions) depend on the emitter tip diameter, flow rate, sheath gas pressure and applied voltage.50–54 The process of droplet formation is complex and the spray conditions are not always stable, sometimes resulting in pulsating or burst spray modes.52Fig. 1e and f illustrates this complexity with two snapshots of ESSI plumes4 where bursts of liquid and droplets are observed.
Fig. 1b shows droplets shrinking before reaching the MS inlet. This is due to solvent evaporation, possible reactant evaporation, fission events and direct emission of ions into the gas-phase. The extent of solvent evaporation depends on volatility, with size-dependent kinetics. For example, small droplets (∼100s of nm in diameter) of a highly volatile solvent (e.g. methanol or ethanol) can completely evaporate and enter the MS inlet as gas-phase species. Larger droplets (typically up to ∼10 or 20 μm in diameter) composed of a less volatile solvent (e.g. water) remain nearly unchanged during transit and will be vaporized within the MS inlet. This means that the degree of evaporative enrichment of reactants A and B is both a function of size (as indicated by the cyan/blue reagent concentration scale in Fig. 1b) and solvent composition, which is discussed quantitatively in Section 4.5. Additionally, Fig. 1b shows that droplets eventually reach a constant size, if the reactants are non-volatile. However, this is not always the case and solvent evaporation can be accompanied by the substantial loss of reactants to the gas-phase, as considered in Section 4.3.
As the droplets shrink, their surface charge density approaches the Rayleigh limit, leading to direct ion emission and/or to the spontaneous ejection of smaller offspring droplets that continue to evaporate and undergo subsequent fission events.55 These processes are described by the ion emission model (IEM)56 and charge residue model (CRM,57Fig. 1c), respectively. However, the physical mechanisms (IEM vs. CRM) explaining the conversion of solvated species within droplets to gas-phase ions still remain somewhat unclear and may not be universal, since the exact mechanism will likely depend upon the solvent, chemical species and droplet charge evolution.50,58 The net result of evaporation, repeated fission events and direct ion emission is to increase the concentration of reagents (A and B) in the droplets as well as the gas-phase.
Once both reactants and products in the condensed- and gas-phase reach the heated MS inlet (Fig. 1d), all residual solvent is evaporated. There have been reports indicating that reactivity is halted by this sudden desolvation process,4,5,7,30 but given the high temperatures within the inlet, ion–molecule reactions in this region cannot be completely excluded. For example, the observation of product distributions changing with MS inlet temperature may be indicative of additional gas-phase chemistry occurring in the inlet.5,17
The competing multi-phase processes illustrated in Fig. 1 suggest that understanding the accelerated formation of product in ESI/ESSI-MS requires a detailed evaluation of the spatial–temporal evolution of reactants, products and solvent in both the gas and condensed phases. There are several possibilities, with potentially competitive timescales, of where the A + B reaction might occur: inside a droplet, at its surface, and/or in the gas phase during transit to or inside the MS-inlet. Additional complexity arises due to the inherent polydispersity of droplets produced in ESI/ESSI sources, since many of the potential acceleration mechanisms (e.g. evaporation and surface reaction) and multi-phase processes (e.g. droplet fission or ion emission) scale with droplet size. When ESI/ESSI-MS methods are used to investigate reaction acceleration mechanisms in droplets, it is crucial to account for these dynamic and competing multi-phase processes for an accurate interpretation of the observations.
3. Possible competing reaction acceleration mechanisms in ESI/ESSI droplets
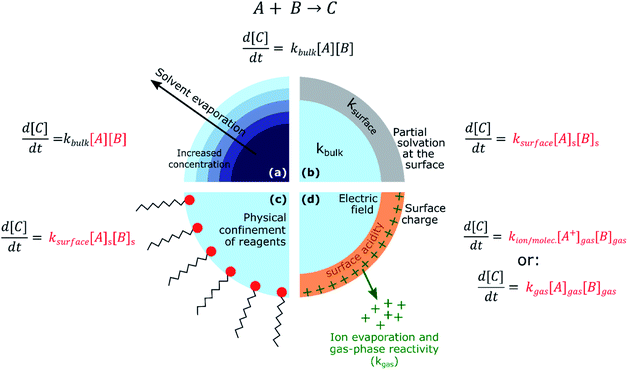
From consideration of the multi-phase steps in Fig. 1, it follows that there are several mechanisms for the observed accelerated reaction rates in ESI/ESSI droplets. These mechanisms are summarized in Fig. 2, again using a generic bimolecular reaction (A + B → C). The rapid evaporation of solvent increases the concentration of reactants (Fig. 2a), potentially reaching supersaturated states in a droplet that are inaccessible in bulk solutions.59 Increased concentration of A and B naturally results in faster formation rates of product C (d[C]/dt = kbulk[A][B]).The fraction of molecules at the droplet surface compared to its bulk is much larger than in a macroscopic vessel (see for example Fig. 1 in ref. 60). Thus, surface reactions or equilibria could play a more substantial role in governing the overall chemical transformations occurring in micro- and nano-droplets, compared to bulk solutions. It has been shown that partial solvation of A and B molecules at the air–liquid interface (Fig. 2b) can modify the Gibbs free energy of the reactants relative to the products,45 resulting in larger surface rate constants for A + B compared with the bulk (ksurface > kbulk). Narendra et al.61 used quantum mechanical methods to explore how partially solvated reagent molecules and transition states at the air–vacuum interface can accelerate reaction rates. For example, they found that reactant molecules at the interface of a nanometer-sized methanol clusters had broader energy distributions than when located in the bulk. The increase in energy for certain surface orientations was calculated to be as high as 1.6 eV. This increase in energy was attributed to configurations that had lower degree of solvation of the charged site on the reactant molecule. From these calculations, Narendra et al.61 estimated an upper bound of ksurfacevs. kbulk enhancement of 104.
If reactants are surface active (e.g. surfactants, hydrophobic molecules, etc.Fig. 2c), their surface enrichment further increases the reaction rate (i.e. [A]s > [A], [B]s > [B]). Moreover, specific orientation of reactants and solvent molecules at the interface resulting in decrease in entropy has also been implicated in faster reaction kinetics.49 In addition, stable pH gradients were observed in neutral droplets,62 which could lead to differential (acid or base) catalysis at the droplet surface compared to its bulk. The exact nature of the air–water interface of charged droplets remains debated,2,63–66 with some studies reporting that the air–water interface is basic,67,68 while others found a larger surface affinity for protons.69,70 A detailed description of these unknowns can be found in the review by Agmon et al.66 and references therein. The acceleration of a few acid-catalysed15,71,72 and base-catalysed72 reactions have been observed in ESI/ESSI droplets, where pH gradients and different surface affinity of protons and hydroxide ions could play an important role.
Finally, Fig. 2d shows that ESI, nESI and ESSI droplets are charged50 and strong electric fields could be present in these micron- and nanometer-sized compartments.73 The excess charge resides at the surface of a charged droplet, simply due to electrostatic repulsion between charges of the same sign.58 Charged species can reside up to a few monolayers depth, depending on the exact nature of the charges species.58 Additionally, the excess surface charge is predicted to rearrange ionic species in the droplet interior, resulting in an electric field with a specific radial profile.73 It has been observed that strong electric fields stabilize charge separation in a transition state during single molecule experiments74,75 and a similar mechanism could occur at the charged droplet interface, thus resulting in faster rates. Charge could also be responsible for local changes in pH at the surface of charged droplets.
As illustrated in Fig. 1, evaporating ESI, nESI and ESSI droplets eject charged species into the gas-phase (IEM),56 potentially introducing gas-phase and ion–molecule reactions (Fig. 2d). Since there is no way to determine where the reaction has occurred (i.e. gas-phase vs. droplet) from the mass spectra alone, the presence of gas-phase chemistry complicates the identification and quantification of in-droplet chemistry. This is particularly true of ion–molecule reactions that are often collision-limited and orders of magnitude faster than diffusion-controlled condensed phase reactions (i.e. kion/molec. ≫ kbulk).
The relative importance of each mechanism summarized in Fig. 2 remains relatively unexplored.47 Additionally, the dominant mechanism(s) likely depend on the specific chemical reaction,47 droplet size distribution and solvent properties (e.g. vapor pressure). Although separating and exploring each of these factors to isolate the governing reaction acceleration mechanism(s) is experimentally challenging, the growing body of literature motivates an in-depth analysis of the relative importance of these coupled steps that are intrinsic to these ESI-type techniques. The goal of this critical review and analysis is to: (1) provide a context for future work aimed at elucidating the underlying mechanisms for accelerated reactions in ESI/ESSI droplets and (2) provide a better understanding of the possible ramifications of chemistry observed in ESI droplets for transformations occurring in environmental and biological micro- and nano-compartments.
4. Analysis of the multi-phase processes responsible for reaction acceleration in ESI-, nESI- and ESSI-MS
In the following sections we present a critical analysis of the application of ESI-, nESI- and ESSI-MS to study reaction kinetics in droplets, with particular focus on (1) the impact of increased reagent concentrations due to solvent evaporation and droplet lifetimes, (2) competing gas-phase reactions and reactivity on experimental surfaces, (3) ionization efficiencies and ion transmission, and (4) charged droplet surface and strong electric fields in micro- and nano-droplets.4.1 Numerical modelling of simultaneous in-droplet reaction and evaporation
Solvent evaporation and the resulting increased concentration of reagents can be one of the key factors determining the accelerated reaction rates observed in ESI/ESSI droplets.49,72 Here, we discuss to what extent this evaporation is significant for methanol droplets of varying initial size (ESI vs. nESI) and concentration. We also compare solvents of different vapor pressure (methanol vs. water) and we consider the case of volatile reactants. We demonstrate that high reagent concentrations caused by solvent evaporation can account for a few orders of magnitude in the overall observed acceleration rates in ESI, nESI and ESSI-MS experiments, specifically up to 5 × 105 for 500 nm diameter methanol droplets with a starting reagent concentration of 10 μM.To quantitatively assess these aspects, we couple droplet evaporation and reaction in a numerical model. Evaporation of solvent from a single pure-component droplet is described by integrating Maxwell's equation:76
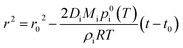 | (1) |
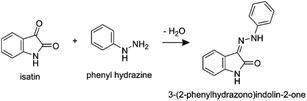
We couple solvent evaporation described by eqn (1) to a simultaneous bimolecular chemical reaction. For the discussion that follows, the hydrazone formation reaction from isatin and phenyl hydrazine12,18 is selected as a model system:
 | (2) |
This reaction was chosen for two reasons. First, bulk solution kinetics are reported in Bain et al.,18 which allows for a direct comparison between the reaction in a macroscopic solution to that in a droplet. Second, for this reaction Marsh et al.12 report significant trends of increasing conversion rates with decreasing droplet size and concentration.
The hydrazone formation reaction is bimolecular with the following rate law:
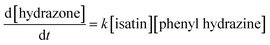 | (3) |
At each simulation time step (0.1 μs) we compute changes in droplet size and composition due to evaporation (eqn (1)) and reaction (eqn (3)). To make sure the chosen time step was small enough to avoid numerical artifacts, we confirmed that a smaller time step of 0.01 μs produced the same simulations results. The concentrations of the reactants and product are updated at every time step, which accounts for changes in concentration due to both reaction and the decrease in droplet volume due to solvent evaporation. For the comparisons to reactions in bulk solutions presented in Sections 4.2 and 4.4, eqn (3) is solved considering the initial bulk solution concentrations and evaporation is omitted.
We note that our modelling approach is purely focused on determining the contribution of solvent evaporation to the observed accelerated reaction rates in Fig. 2a, and any possible alteration of reaction kinetics due to the processes described in Fig. 2b–d are not considered.
4.2 Model results: solvent evaporation leads to larger acceleration factors in smaller droplets
Fig. 3 shows results for the evaporation of methanol droplets with initial diameters from 200 to 4000 nm. The droplets contain equimolar quantities of isatin and phenyl hydrazine (10 mM), with both reagents assumed non-volatile. The temporal evolution of the diameter for each initial droplet size (d0) is shown in Fig. 3a. The r2-slope in the evaporation model (eqn (1)) is constant, but Fig. 3a shows that the overall methanol evaporation timescale is size-dependent and faster for smaller droplets. As an example, Fig. 3a shows that for two droplets with initial diameter of 200 (violet line) and 3000 nm (orange line) methanol evaporation is complete after ∼0.05 and 1.5 ms, respectively. The corresponding increased reagent concentration is shown in Fig. 3b: in all the cases, the final concentration reached within the droplets is ∼5 M, which corresponds to the ‘neat’ reagents. This is an increase by a factor of 500 from the initial concentration. | ||
| Fig. 3 Evaporation of methanol droplets containing isatin and phenyl hydrazine (both 10 mM), calculated with eqn (1), and simultaneous reaction (eqn (3)). Time evolution of droplet diameter (a), reagent concentration in droplets and in bulk solution (grey dashed line) (b), product conversion ratio in droplets and in bulk solution (grey dashed line, right y-axis) (c) and calculated acceleration factor (d) for droplets with initial diameters of 200–4000 nm (purple to red color scale) are shown. The acceleration factors in (d) are calculated by dividing the conversion ratio in droplets and that in the bulk solution from panel (c) at each point in time. Reagents are considered non-volatile. | ||
Fig. 3c shows the product conversion ratio as a function of time, calculated using the molar ratio of the product (nhydrazone(t)) and one of the reactants, (n0,isatin(t0)):
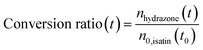 | (4) |
A conversion ratio of 1 indicates reaction has come to completion. Fig. 3c shows that smaller droplets achieve higher conversion ratios at faster timescales than larger droplets, due to the fact that complete methanol evaporation is faster in smaller droplets (Fig. 3a). As a comparison, the conversion ratio estimated for the same reaction conducted in the bulk (dashed line) is shown in Fig. 3c. A conversion ratio of 1.1 × 10−5 is reached over timescales relevant for ESI-MS experiments (25 ms) in a bulk solution. This is because there is no solvent evaporation in the bulk simulation.
Finally, the droplet acceleration factors as a function of initial d0 relative to the bulk solution are shown in Fig. 3d. The acceleration factor is calculated as the ratio between the conversion ratio in droplets and that in the bulk solution from Fig. 3c. For each droplet size, acceleration factors tend towards 500, which simply originates from the factor of 500 increase in reactant concentration due to the solvent evaporation shown in Fig. 3b. Fig. 3d illustrates that smaller droplets obtain their maximum acceleration factors more rapidly. For example, at t = 10 ms the acceleration factor for a droplet with initial diameter of 200 nm is ∼500, whereas for a droplet with initial diameter of 4000 nm it is ∼350. This result simply reflects the shorter times required for complete evaporation of methanol from the droplet. In Section S4 of the ESI† we provide a detailed explanation of the temporal trends of the acceleration factors in Fig. 3d.
Bain et al.18 reported an acceleration factor of 104 for the hydrazone formation reaction measured by nESI-MS with a droplet flight time of 10 ms. Marsh et al.12 found that the magnitude of the rate enhancement for this reaction depended upon droplet size, with smaller droplets exhibiting larger acceleration factors. Fig. 3 shows that increased reagent concentrations from rapid solvent evaporation can explain both the observed trend in acceleration factors with droplet size and a significant portion of the magnitude of the acceleration. Lee et al.24 and Yan et al.22 also observed larger enhancements in reaction rates with decreasing droplet size. These size dependent trends are often presented as evidence that surface reactions (see Fig. 2b) are responsible for accelerated reaction rates in droplets, due to higher surface-to-volume ratios the smaller the droplet size. However, Fig. 3 shows that solvent evaporation can produce the same size-dependent trends, which would be difficult to distinguish from surface reactions in polydisperse evaporating ESI/ESSI droplets. To show that the conclusion drawn from Fig. 3 are general and applicable to the polydisperse droplet distributions studied in ESI experiments, we have simulated the evolution of three droplet size distributions centered at 500, 2000 and 5000 nm (see Fig. S3a†). The trend in the acceleration factors found in Fig. S3b† for the polydisperse case is consistent with the size-dependent acceleration factors observed for single droplet sizes in Fig. 3d, with smaller sizes resulting in larger acceleration factors obtained over shorter timescales.
4.3 Model results: complete evaporation of solvent and reactants
A further factor to be accounted for is the potential for complete evaporation of both the solvent and reactants from ESI, nESI and ESSI droplets prior to reaching the MS inlet. This is especially relevant when transfer capillaries or tubes (up to ∼100 cm)17,28,42 are used to increase reaction timescales by lengthening the distance to the MS-inlet. In Fig. S4,† we consider the same reaction as in Fig. 3 but consider the more realistic case where phenyl hydrazine is volatile, since its vapor pressure (3.43 Pa at 293 K)78 is non-negligible. Isatin and the hydrazone product are still assumed non-volatile. In this case, we estimate that droplets with diameters smaller than 1 μm have a lifetime of less than 1 ms. This is in contrast with the estimated travel time of 17 ms reported by Marsh et al.,12 for emitter to MS inlet distance up to 10 cm and a reported droplet velocity of 6 m s−1 for typical nESI droplets.18 Although our simple evaporation model does not account for the Kelvin effect, the occurrence of repeated fission events and the enhancement of mass transfer due droplet motion through the surrounding gas-phase, these factors would result in even shorter droplet lifetimes than those estimated in Fig. S4.† Thus, our simulated lifetimes are upper limits (see Section S1 in the ESI† for full discussion).Furthermore, as discussed in Section 2, according to the CRM model57 evaporating charged ESI/ESSI droplets undergo repeated fission events when approaching the Rayleigh limit. The resulting progeny droplets are estimated to have a size that is ∼10% of the parent droplet55 (e.g. from a 1 μm radius parent droplet, 20 droplets of 100 nm or smaller are formed with every fission event, see example in Fig. S5†). These smaller droplets have much shorter lifetimes than the parent droplet. Fig. S4† shows that a 100 nm diameter progeny droplet has a lifetime of ∼40 μs, compared to a lifetime of ∼900 μs for the 1000 nm diameter parent droplet.
In Fig. S6† we estimate the amounts of isatin and phenyl hydrazine transferred to the gas-phase from three initial droplets size distributions centered at diameters of 500, 1500 and 2500 nm with initial reactant concentrations of 10 mM, assuming a vapor pressure for phenyl hydrazine of 3.43 Pa.78 Isatin and the hydrazone product are considered non-volatile and only transferred to the gas-phase by coulombic explosion when the phenyl hydrazine has completely evaporated. For the smaller size distribution, 80% of phenyl hydrazine is transferred to the gas-phase by t = 0.25 ms and both reagents have fully evaporated by t = 0.5 ms. Overall, the evaporation of reactants can result in an increased potential for gas-phase reactions. Gas-phase chemistry may be faster than the corresponding reaction in solution and could interfere with any assessment or quantification of in-droplet chemistry, as discussed below in Section 4.8.
4.4 Model results: lower initial concentrations lead to larger acceleration factors
We extend our analysis to consider how variable initial reagent concentration impacts the measured acceleration factors. In Fig. 4, we consider five droplets with the same initial diameter (d0 = 1000 nm) but with different isatin/phenyl hydrazine equimolar starting concentrations, ranging from 10 μM to 100 mM. Phenyl hydrazine, isatin and the hydrazone product are all assumed to be non-volatile in this case. Droplets with lower initial concentrations start at a condition that is further away from the ‘neat’ reagent concentration (∼5 M). Fig. 4a shows that although the methanol evaporation timescale is the same in all cases (indicated by a vertical dashed line), the least concentrated droplets undergo a much larger relative increase in reagent concentration (light blue) than the more concentrated cases (dark blue). For example, a 0.01 mM droplet increases its concentration by a factor of 5 × 105, whereas for a 10 mM droplet the increase is by a factor of 500. This is reflected in Fig. 4b where correspondingly larger computed acceleration factors for droplets with lower initial concentrations are observed. These results are consistent with literature observations that have previously attributed these concentration trends solely to an increased role of surface reactions.12,24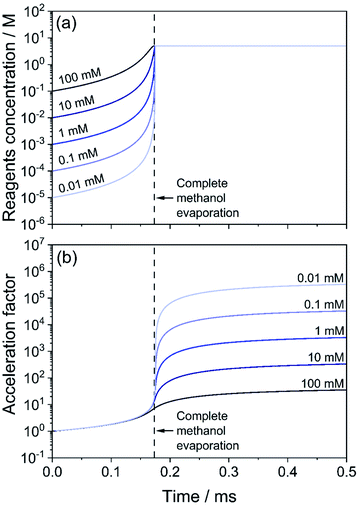 | ||
| Fig. 4 Effect of initial solution concentration of reagents on the acceleration factor for the hydrazone formation reaction in eqn (2). Droplets of initial size d0 = 1000 nm with methanol as the solvent are considered. Initial concentration in the droplets is between 100 mM (dark blue) and 0.01 mM (light blue). (a) Temporal evolution of the concentration of reagents (isatin and phenyl hydrazine). (b) Acceleration factor calculated as the ratio of the product formed in droplets and for the same reaction (with the same reagent concentrations) in a bulk solution. The vertical dashed line indicates when the evaporation of methanol is complete. | ||
Reaction rate enhancements on the order of ∼102 to 106 are reported from ESI/ESSI-MS experiments in the literature,49 and are often attributed to increased reactivity at the droplet surface. Taking the effects of evaporation, size, and concentration trends from our modelling results together, we conclude that at a significant portion of the reported acceleration factors can be explained by evaporative enrichment of reactants (Fig. 2a). This is especially true for small initial droplet sizes (1–2 μm and less) and commonly used volatile solvents (i.e., methanol and ethanol).
We summarize these findings in Fig. 5. Fig. 5a shows the acceleration factors for the model hydrazone formation reaction in methanol droplets as a function of droplet diameter (t = 2 ms, 10 mM reactants concentration). Fig. 5b illustrates how the acceleration factor depends on the initial reagent concentration (t = 0.5 ms, 1000 nm initial diameter). Overall, Fig. 5 shows that acceleration factors increase with both decreasing size and decreasing initial concentration. Both trends are driven by reactant enrichment due to rapid solvent evaporation.
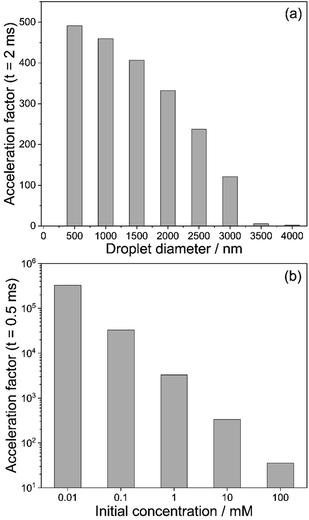 | ||
| Fig. 5 (a) Calculated acceleration factors for the hydrazone formation reaction in eqn (2) extracted from Fig. 3d at t = 2 ms as a function of initial droplet diameter. The reagent concentration is 10 mM and solvent is methanol. (b) Calculated acceleration factors for the hydrazone formation reaction in eqn (2) extracted from Fig. 4b at t = 0.5 ms as a function of initial reagent concentration. The initial droplet diameter is 1000 nm. | ||
These trends in reaction acceleration with size and concentration are qualitatively similar to those expected when surface reactions dominate the acceleration mechanism, as reported for micro-compartments in the absence of evaporation.45 This implies that in ESI experiments, where evaporation is occurring, it would be very difficult to distinguish accelerated chemistry due to surface reactions from bulk reaction rates that are enhanced due to evaporative enrichment of reactants.
4.5 Droplet size and velocity distributions of ESI, nESI and ESSI droplets
Having demonstrated that acceleration factors are dependent on droplet size, we now consider more realistic polydisperse size distributions of droplets produced in ESI, nESI and ESSI sources. Experimentally, the droplet size distribution can be shifted by either varying the emitter capillary internal diameter or, in the case of sonic spray, by varying the pressure of the coaxial sheath gas. There is very little systematic information on how changing these parameters affects the average diameter of droplets, their size and charge distributions, and their velocity. Droplet velocity is intimately connected to the droplet size distribution and it is typically used to infer reaction timescales. Often, the ratio between the time required to produce the same amount of product in the bulk vs. in droplets is used to estimate the magnitude of acceleration in droplets, making it crucial that the droplet velocity is well-characterized. ESI, nESI and ESSI droplet sizes and velocities are measured either by high-speed cameras46,54 or with phase Doppler anemometry.52,53,79In the ESI (Section S3),† we present a review of several literature studies focused on the determination of ESI, nESI and ESSI-MS droplets size and velocity distributions. Comparison of results from different studies is necessarily qualitative since velocity depends on droplet size, ESI flow rate,8 emitter tip size, coaxial gas pressure, and travel distance (i.e. the velocity might not be constant throughout the droplet travel time42,53). This literature review can be summarized as follows: (1) typical droplet velocities are in the range ∼1–20 m s−1;12,42,51–54,80 (2) larger droplets travel faster than smaller droplets;52 (3) ESI, nESI and ESSI size distributions can be broad (up to tens of μm)51,54 and smaller sizes may not be observable in all experimental setups.54 We recommend that these factors should be carefully taken into account when computing acceleration factors obtained with ESI, nESI and ESSI droplets. For example, overestimating the droplet velocity by one order of magnitude would result in a one order of magnitude uncertainty in the reaction timescale and therefore in an overestimate in the acceleration factor by a factor of 10.
In addition, overestimation of the droplet velocity can lead to an underestimate of their lifetime and therefore to an underestimate of the extent of solvent evaporation and the resulting increase in concentration of reagents. This is clearly shown in Fig. S7,† where the evaporation of water and methanol is simulated for droplets with initial diameters of 2 and 14 μm and travelling over a distance of 5 mm to the MS inlet. For the 14 μm water and methanol droplets in Fig. S7b,† at t = 1 ms the percentage of volume lost is ∼1% and ∼4%, respectively. This indicates both that the evaporation of solvent is negligible for large droplets and that the uncertainty in the assumed velocity is not relevant to determine the magnitude of solvent evaporation. Conversely, Fig. S7a† shows that the evaporation is considerable for the 2 μm droplets, with volume loss of ∼38% for a water droplet and >90% for a methanol droplet. In the case of a 2 μm methanol droplet, velocities of 84, 20, 10 and 5 m s−1 result in estimated loss of volume of 9%, 36%, 72% and >90%, respectively. This clearly indicates that the uncertainty in velocity for small droplets is significant on the estimated extent of solvent evaporation.
Below we further evaluate how droplet velocity can influence collision dynamics in droplet fusion MS experiments.
4.6 Droplet fission in droplet fusion mass spectrometry
Droplet fusion mass spectrometry has been used to observe accelerated rates of the acid-induced unfolding of cytochrome c,46 its complexation with maltose,15 the acid demetallation of chlorophyll31 and the formation of gold nanostructures.32 In the experimental setup shown in Fig. 6a and b, two ESSI sources were used to generate two separate streams of droplets, each containing one reagent. The two droplet streams are mixed, and the resulting stream is directed to the inlet of a mass spectrometer for chemical analysis.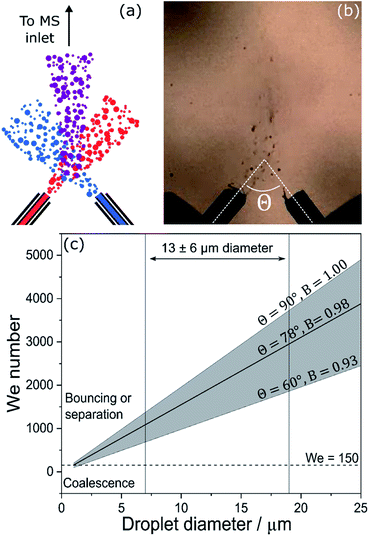 | ||
| Fig. 6 Schematics (a) and still frame (b) from Lee et al.46 showing the microdroplet fusion mass spectrometry setup. (c) Weber number (We) calculated for the collision of two equally-sized aerosol droplets with variable colliding angle, θ; the diameter range of 13 ± 6 μm indicated by Lee et al.46 is shown for reference. The horizontal dashed line at We = 150 separates regions where coalescence or bouncing/separation are expected to occur. | ||
These experiments assume that a large percentage of the droplets (reported as 70%)46 in the two streams will undergo fusion events. The high-speed camera images and videos (Fig. 6b and videos from Lee et al.46) show that the mixing of the two streams is quite turbulent and the generation of the two droplets streams is rather unstable. The interpretation of these results depends upon the nature and outcome of the droplet collision. To do so, two factors are considered: droplet velocity and charge.
A collision of two single droplets can have four different outcomes:81 full coalescence (i.e. fusion), bouncing, stretching separation and reflexive separation, with the last two forming smaller satellite droplets,82 as shown in Fig. S8.† These outcomes depend on the relative velocity, collision angle, absolute size, and the ratios of the diameters of the two colliding droplets. The Weber number (We) is used to evaluate the relative effect of inertia and surface tension at the interface between two fluids, such as in the case of two droplets colliding. The Weber number is defined as:
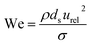 | (5) |
Fig. 6c shows We as a function of droplet diameter.46 A recent review on the outcomes of the collisions within sprays81 indicates that complete coalescence for non-viscous droplets is only observed when We < 150 and essentially never occurs for B > 0.7. Collisions of droplets in the size and velocity range reported by Lee et al.46 (13 ± 6 μm in diameter, as indicated in Fig. 6c) are characterized by We values in excess of 1000, for all angles and B values considered. This is an order of magnitude larger than is required for successful full coalescence. The dashed line in Fig. 6c indicates that at a velocity of 84 m s−1, successful complete coalescence would only be possible for droplets smaller than ∼1 μm, which may go undetected if a camera is used for droplet sizing.46
Therefore, under the experimental conditions in Lee et al.,46 there will be very few instances of successful complete droplet coalescence (i.e. fusion). Rather it is highly likely that the dominant processes under their experimental conditions are bouncing, stretching separation, and reflexive separation, all of which result in the disintegration of the original droplets after collision and the subsequent formation of smaller satellite droplets. This scenario is also supported by data on colliding micro-droplet streams,83 which observed coalescence only for velocities < 7 m s−1 and We < 30.
Experiments and modelling on impinging sprays82 have shown that the average size of droplets exiting the mixing region are significantly smaller than the initial average diameter (from ∼100 μm to ∼30 μm). These considerations strongly suggest that the majority of droplets that reach the MS inlet in these microdroplet fusion experiments are smaller than has been previously reported, which will result in faster evaporation (Section 4.2) and possibly larger contributions from gas-phase chemistry (Section 4.8).
Finally, there is some ambiguity about the role of charge in droplet fusion MS experiments. Both ESSI capillaries are generally subjected to an equal and positive voltage up to +5 kV,15,31,32,46 resulting in two streams of positively charged droplets. It is unclear what effect repulsion between similarly charged droplets has on microdroplets in fusion MS experiments.
4.7 Discussion: solvent evaporation, reagent concentration, droplet size and velocity
We have shown that rapid solvent evaporation and the subsequent increased concentration of reagents can be a substantial factor in reaction rate acceleration in droplets, particularly for small sizes, low initial concentrations and highly volatile solvents (e.g. methanol/ethanol vs. water).To observe potential enhancement of reaction kinetics in droplets due to unique processes taking place at a droplet's surface, droplet size and velocity distributions are essential variables to control in ESI, nESI and ESSI-MS experiments. We have discussed how the complexity of the multiphase processes inherent in ESI/ESSI plumes and in microdroplet fusion MS makes this challenging and we suggest that at least a portion of acceleration factors reported as high as 106 to 107 can be explained by the effects described above. As a comparison, it is interesting that in experiments where solvent evaporation is controlled (e.g. merging micro-droplets38 and micro-emulsions45) the observed increase in rate constant is smaller (25% and 45-fold enhancement, respectively).
Quantum mechanical modelling indicates that partial solvation of molecules at the air–vacuum interface can contribute to the accelerated formation of hydrazone product in nESI droplets, with an estimated upper bound of surface rate constant enhancement of 104.61 Additionally, modelling compartmentalized reactions in microemulsions45 we estimated that the forward rate constant for the equilibrium formation of imine is enhanced by a factor of 102 at the oil–water interface.60 Importantly, we note that the overall observed reaction rate in droplets is a result of both reactions at the surface and in the bulk of a droplet, which occur concurrently. Therefore, the observed reaction rate is governed by both the surface and bulk rate constants and a rate constant enhancement of 104 at the surface would effectively result in a smaller overall rate acceleration factor. This suggests that surface reactions likely play a relevant role in reaction acceleration in droplets, but it is challenging to establish the magnitude of their contribution while rapid solvent evaporation is occurring.
Furthermore, given the estimated droplet lifetimes are in the micro- and millisecond regimes from the ESI/ESSI literature, some considerations on the kinetics and timescales of reagent adsorption to the droplet surface relative to droplet lifetimes are important. For the surface to have a predominant role in the observed reaction rates within ESI, nESI and ESSI droplets, reagent molecules need sufficient time to diffuse to the droplet surface after its formation from a bulk liquid jet. This process is governed by the intrinsic surface adsorption kinetics of the reagent molecules.
As an example, Fig. S9† shows the simulated60 surface partitioning timescale for pimelic acid within two aqueous droplets (15 and 50 mM, 10 μm diameter). Equilibrium surface coverage is reached only after ∼40 ms, which is longer than typical timescales accessed with ESI/ESSI-MS experiments (from ∼10 μs to ∼20 ms). This result qualitatively demonstrates possible incomplete adsorption of reagent molecules within ESI/ESSI droplets, which raises questions about the actual contribution of surface reactivity to observed accelerated rates in ESI/ESSI-MS experiments. We note here that ESI, nESI and ESSI droplets are rapidly evaporating, whereas the example in Fig. S9† considers a droplet with constant volume. A further factor to consider is the possible formation of concentration gradients caused by rapid evaporation. It was observed that quickly evaporating aqueous NaCl micro-droplets develop a concentration gradient due to competing surface recession and solute diffusion rates.84 These observations suggest that, in order to be able to evaluate the contribution of all these competing and dynamic processes to observed accelerated rates, a complete modelling framework is required that fully describes the kinetics of reagents partitioning to the droplet surface, rapid evaporation of solvent, possible increase in viscosity resulting in slower diffusion of both reagent and solvent molecules, and simultaneous chemical reactivity. Existing multi-phase aerosol models85,86 could be expanded to describe these processes in ESI/ESSI droplets.
4.8 Competing gas-phase and in-droplets reactions in ESI/ESSI-MS
Jacobs et al.87 and Gallo et al.2 have shown that gas-phase chemistry can potentially dominate the formation of products in the ESI/ESSI-MS ionization region, which complicates the quantification and determination of the reaction rate enhancement in droplets. To further evaluate the potential for the formation of reaction products in the gas-phase, we examined the epoxide ring opening4 and ribonucleoside synthesis reactions21 previously reported in the literature. To do this we use the experimental approach designed by Jacobs et al.87 to independently measure in-droplet vs. gas-phase chemistry.Two different setups87 are used and shown in Fig. 7. Fig. 7a shows the ‘reagents in the same compartment’ configuration, where droplets from a solution containing both reactants are formed with one atomizer (Model 3076, TSI, Inc., operated at 700 sccm) and vaporized in an annular heater prior ionization. Fig. 7b shows the ‘reagents in separate compartments’ setup, which separates the two reactants into two different atomizers, so that they never reside in the same droplet. After passing the two droplet streams through separate heaters, reactants are introduced into the ionization region as gas-phase species. Any products that are detected in this configuration must arise solely from gas-phase reactions in the ionization region or within the MS inlet. In both configurations, an ESI source (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 by volume methanol
1 by volume methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water, 3.5 kV, 3 μL min−1) is used to ionize the gas-phase molecules in the mixing region and products are detected using a Q-Exactive Orbitrap mass spectrometer (Thermo Fisher, Inc.).
water, 3.5 kV, 3 μL min−1) is used to ionize the gas-phase molecules in the mixing region and products are detected using a Q-Exactive Orbitrap mass spectrometer (Thermo Fisher, Inc.).
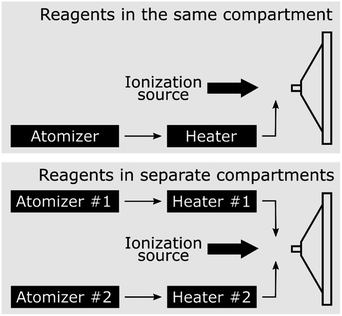 | ||
| Fig. 7 (a) ‘Reagents in the same compartment’ and (b) ‘reagents in separate compartments’ setups, as designed by Jacobs et al.87 | ||
In our previous work,87 using the setups described above, we examined the droplet-induced phosphorylation of glucose, ribose and fructose, showing that a substantial fraction of product ions previously21 attributed to in-droplet chemistry actually originated from gas-phase reactions. Here, these measurements are extended to the synthesis of a ribonucleoside (uridine) from the reaction of phosphorylated ribose and uracil:
 | (6) |
In-droplet production of uridine21 and other ribonucleosides88 has been observed in charged ESSI droplets at room temperature and atmospheric pressure, with a reported yield of ∼2.5% for uridine.21
First, a solution containing uracil (10 mM), H3PO4 (15 mM) and ribose (15 mM) is atomized using the setup in Fig. 7a. Then, with the setup in Fig. 7b, a solution with uracil and H3PO4 is atomized separately from a second solution containing ribose. Fig. 8 shows the mass spectra recorded with the two configurations, where peaks at m/z = 245.07 were previously assigned to uridine21 (full peak attribution is given in Table S1†). The two mass spectra in Fig. 8 are identical, in agreement with our previous experiments on the phosphorylation of several sugars.87 These results indicate that products observed from reagents residing in the same micro-droplet (Fig. 7a) can also arise when the reactive constituents never reside in the same droplet (Fig. 7b) and must therefore, at least partially, originate from gas-phase reactions.
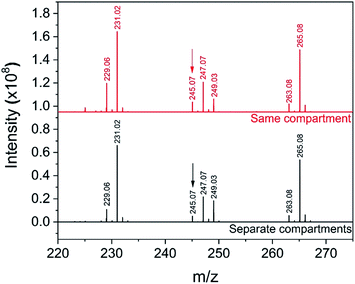 | ||
| Fig. 8 Mass spectra from the reaction of ribosylation of uracil with the ‘reagents in the same compartment’ setup (a) and the ‘reagents in separate compartments’ configuration (b). The peak at m/z = 245.07 was previously assigned to uridine21 and is indicated with an arrow; the full peak attribution can be found in Table S1.† | ||
Additionally, we consider an epoxide ring opening reaction between limonene oxide and morpholine:
 | (7) |
Lai et al.4 reported an acceleration factor of ∼105 for this reaction with ESSI-MS (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 by volume methanol/water, applied voltage +5 kV, 5 μL min−1 flow rate, 120 psi coaxial sheath N2 pressure, 50 and 250 μm i.d. capillaries).
1 by volume methanol/water, applied voltage +5 kV, 5 μL min−1 flow rate, 120 psi coaxial sheath N2 pressure, 50 and 250 μm i.d. capillaries).
Fig. 9 shows the mass spectra for individual reactant solutions (50 mM in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v MeOH/H2O), where peaks corresponding to morpholine (m/z = 88.07, [M + H+]+) and limonene oxide (m/z = 153.12, [M + H+]+ and m/z = 135.11, [M − H2O + H+]+) are observed. The mass spectra obtained for the reaction mixture with and without compartmentalization as described above are also shown. With the ‘reagents in the same compartment’ setup, a new peak attributable to products A and B (eqn (7), m/z = 240.19, [M + H+]+) appears, consistent with previous observations.4 Attribution of the two peaks at m/z = 258.19 and 272.21 is not clear, and it is not possible to compare the spectra obtained in this work to those by Lai et al.,4 who reported m/z only up to 250.
1 v/v MeOH/H2O), where peaks corresponding to morpholine (m/z = 88.07, [M + H+]+) and limonene oxide (m/z = 153.12, [M + H+]+ and m/z = 135.11, [M − H2O + H+]+) are observed. The mass spectra obtained for the reaction mixture with and without compartmentalization as described above are also shown. With the ‘reagents in the same compartment’ setup, a new peak attributable to products A and B (eqn (7), m/z = 240.19, [M + H+]+) appears, consistent with previous observations.4 Attribution of the two peaks at m/z = 258.19 and 272.21 is not clear, and it is not possible to compare the spectra obtained in this work to those by Lai et al.,4 who reported m/z only up to 250.
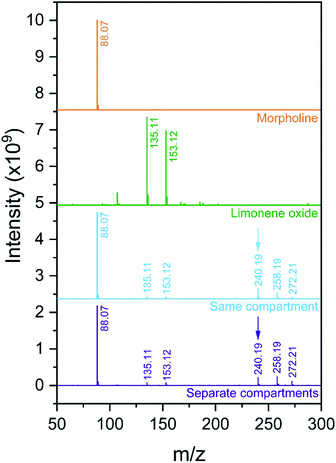 | ||
| Fig. 9 Mass spectra obtained for morpholine and limonene oxide individually, and from experiments with the configurations in Fig. 7a (‘same compartment’) and Fig. 7b (‘separate compartments’). The product peak at m/z = 240.19 is indicated with an arrow. | ||
The product peak at m/z = 240.19 (together with the two unattributed peaks at m/z = 258.19 and 272.21) also appears in the ‘reagents in separate compartments’ configuration, which indicates that the reactants do not need to reside in the same micro-droplet for peaks at expected product masses to be detected. Similar to the observations described for the ribosylation of uracil, this result implies that gas-phase reactions are substantial and cannot be ruled out. Therefore, it is not possible to definitively attribute the formation of product peaks solely to in-droplet reactivity.
Fig. S10† shows the Collision-Induced Dissociation (CID) spectrum of the product ion (m/z = 240.19) from the atomization experiments compared with that from ESSI-MS experiments (where limonene oxide and morpholine are sprayed together from an ESSI source). CID is used in tandem mass spectrometry to induce the fragmentation of selected ions by colliding them with a buffer gas, with the aim of gaining structural information on the selected ions.89 The CID spectra from the atomization experiments, from both configurations in Fig. 7, show only one ion (m/z 88.07), which is attributed to morpholine. The lack of any signal from the parent ion or a fragment that includes components from both reagents suggests the new ion observed at m/z 240.19 is not a new molecular species, but rather a cluster between limonene oxide and morpholine. If the parent ion corresponded to a covalently bound species, some parent ion signal should persist in the CID spectrum, especially at low collision energies, which is not the case for these atomizer experiments. Conversely, the CID spectrum from the ESSI-MS experiment shows the parent ion (m/z 240.19), a dehydration product (m/z 222.18), and the morpholine ion (m/z 88.07), suggesting at least some portion of the parent ion is a new molecular species. The difference between the two CID spectra in Fig. S10† demonstrates (1) the ease with which potential clusters can be identified as new reaction products and (2) that formation of a covalently bound product is somehow unique to ESI conditions.
It was reported that with no voltage applied to the ESSI source the concentration of the morpholine-substituted product was enhanced.4 To further investigate this finding, we considered the same set of experiments from the literature as function of applied voltage to the ESSI source (see Fig. S11 and S12†), additionally collecting the CID spectra of m/z 240.19 at different ESSI voltages (Fig. S13†). The difference in fragment intensities (m/z = 222.18 vs. m/z = 88.07, Fig. S13†) as a function of the applied voltage suggests that the identities of the ions contributing to the peak at m/z 240.19 in the initial mass spectra vary with charge applied and could include some product from gas-phase reactions. Taking the results from atomization experiments and CID spectra together, it is clear that contributions from gas-phase chemistry and ion clustering must be unambiguously ruled out when mass spectrometry is used to identify and quantify new reaction products attributed to in-droplet chemistry.
Our results on both the ribosylation of uracil and on the epoxide ring opening reaction highlight the complexity of possible multi-phase chemistry in ESI/ESSI that needs to be accounted for to correctly interpret the results from such experiments. Therefore, it is crucial that ESI/ESSI-MS experimental protocols include basic control experiments required to distinguish between products formed from in-droplet chemistry from those originating in the gas-phase. We note here that the title of the original publication reporting ESSI describes it as “A gentle technique for […] studying ion–molecule reactions at atmospheric pressure”.90 Takáts and co-authors also state that “under these conditions, even the evaporation of species having low vapor pressures becomes feasible”.90 Application of a technique (and by extension, of ESI and nESI) specifically developed to study ion–molecule reactions in the gas-phase for the study of reaction acceleration in droplets should be done cautiously and with suitable controls.
4.9 Reactions on experimental surfaces
Transfer tubes of various lengths, up to 1 m, are often introduced to extend reaction timescales and improve transmission of droplets to the MS inlet.17,28,42 Transfer tubes, however, introduce another potential location where reactions can occur.Accelerated reaction rates were observed in ESSI droplets for the Hantzsch synthesis of a dihydropyridine derivative from benzaldehyde, ethyl acetoacetate and ammonium acetate:17,28
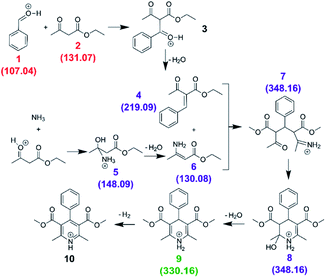 | (8) |
We first carried out the reaction in the bulk (10 mM ethyl acetoacetate and ammonium acetate and 5 mM benzaldehyde in ethanol, under reflux for 24 hours). As shown in Fig. 10a, for the bulk reaction we detected a small signal from the reactants (m/z = 107.04 and 131.07, [M + H]+ ions), a few reaction intermediates (m/z = 130.08, 148.09, 219.09 and 348.16, all [M + H]+) and the hydrogenated form of product 9 (m/z = 330.16, [M + H]+). We attribute the remaining grey peaks in Fig. 10a to clustering and/or contaminants.
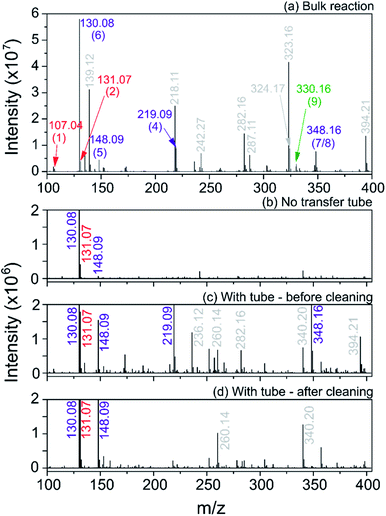 | ||
| Fig. 10 Mass spectra for the Hantzsch synthesis conducted in the bulk (a) and in ESSI droplets with no transfer tube (b), with a 55 cm tube before cleaning (c) and after cleaning with acetone wash (d). Label color (same as in eqn (8)): red = reagents, purple = reaction intermediates, green = product, grey = peaks from impurities. In parentheses the labels for each reagent, intermediate and product molecule from eqn (8); all ions are [M + H]+. | ||
We then conducted the reaction in ESSI droplets using 3.3 mM ethyl acetoacetate and ammonium acetate, 1.7 mM benzaldehyde, 2.5% (v/v) formic acid in ethanol. The emitter was positioned 55 cm away from the inlet of the mass spectrometer. Fig. 10b shows the mass spectrum recorded without a transfer tube. Only intermediates 5 and 6 were observed in the ‘no tube’ configuration and no condensation product (9/10) is visible, which is likely a result of poor transfer of ions to the mass spectrometer.
A 55 cm long, ¼′′ diameter stainless steel transfer tube was placed between the ESSI source and the inlet of the mass spectrometer to guide the droplets to the mass spectrometer and increase signal. The same transfer tube was used over the course of multiple days. Comparing the mass spectra in Fig. 10b and c, the reaction appears to proceed further when the 55 cm tubing is present, with two additional peaks appearing at m/z = 219.09 and 348.16, attributed to intermediates 4 and 7/8. This observation could be due to better transfer efficiency of the droplets to the MS inlet. However, the data shown in Fig. 10d suggests an alternative explanation: after a thorough cleaning of the transfer tube with acetone, the peaks from intermediates and other impurities disappear. This suggests unwanted chemistry possibly originating from deposition of reactants on the walls of the transfer tube. As droplets from the ESSI source move through the transfer tube, they can impact its walls and create a thin film of starting material. Solvent evaporation, surface and gas-phase reactions could lead to faster observed reaction rates within the film on the walls of the transfer tube.36,39,40 After reaction within the film for a period of time, products could be picked up from the walls of the transfer tube by ESSI droplets (i.e. via desorption electrospray ionization (DESI)) and detected. Thorough washing of the transfer tube immediately before experimentation minimizes (but does not eliminate) the possibility for multiple sources of reaction products.
These results highlight the possible interference of unwanted chemistry occurring on the walls of transfer tubes, which might obscure in-droplet chemistry, and suggest that care needs to be taken to ensure that unwanted reactions on experimental surfaces are minimized.
4.10 Ionization efficiency of reagents and products
Quantitative interpretation of ESI, nESI and ESSI-MS data for the investigation of accelerated reaction rates in droplets is further complicated by the use of MS signal intensity as a proxy for reagent and product concentrations. Ionization efficiencies in ESI/ESSI-MS are governed by both the properties of the solvent, such as pH, and the molecular characteristics of the analyte, including surface affinity and polarity, the presence of acidic or basic functional groups, and pKa.91–93 Ionization efficiencies in mixtures can also be limited by charge competition, or ion suppression, leading to a non-linear responses to analyte concentration.94–96 Overall, ionization efficiencies can span orders of magnitude for very different molecules and because of matrix effects.Quantitative conclusions are not possible without considering differential ionization efficiencies, and some recent studies4,6,21,24 have included such corrections in order to draw more quantitative conclusions from the ESI/ESSI-MS signals. Below we discuss the implications of not accounting for ionization efficiencies with an example from the literature.
We consider the reaction between isatin and phenyl hydrazine (eqn (2)) as reported by Marsh et al.12 (nESI with 1, 5 and 20 μm capillary i.d., +2 kV applied voltage, solutions in methanol). To study the reaction acceleration vs. droplet size (Fig. 3b in ref. 12), solutions containing 100 mM of phenyl hydrazine and 3 mM of isatin were sprayed using capillaries of variable internal diameter. Formation of the phenylhydrazone product was observed and conversion ratios up to ∼70% for smaller droplets were reported. These conversion ratios were calculated by dividing the hydrazone product peak intensity by the sum of the product and phenyl hydrazine peak intensities. For non-equimolar amounts of reactants in solution, the conversion ratio should be calculated against the limiting reagent (in this case isatin, 3 mM), but this was not the case.12 It is unphysical that up to 70% of phenyl hydrazine is converted to product, since there is simply not enough isatin present to do this. The maximum possible conversion ratio calculated against the phenyl hydrazine peak intensity for these reaction conditions is 3%.
This result is attributable to two factors: (1) no peak is observed in the mass spectrum for the limiting reagent (isatin), presumably due to poor ionization efficiency; (2) no correction accounting for ionization efficiency was applied to either the hydrazine product or the phenyl hydrazine peak intensities, resulting in unphysical conversion ratios. This example shows that quantitative conclusions derived from qualitative ESI, nESI and ESSI-MS experiments must be interpreted with some caution when the different ionization efficiencies of products and reactants are not accounted for.
4.11 Ion transmission and data normalization
Ion transmission and measured signal intensities are known to decay steeply with increasing distance between the ESI emitter tip and MS inlet97–99 because of the expansion and subsequent dilution of the droplet plume.97 This becomes problematic when the distance between the MS inlet and the emitter tip is increased to access longer droplet lifetimes, and correspondingly longer reaction timescales. As discussed in Section 4.9, in some cases a transfer tube is used for distances up to ∼1 m.17,28,42 However, when the distance is only increased a few cm, no transfer tube is placed in the setup and ion transmission decreases with increasing distance. If the emitter and MS-inlet are considered as point sources, then the dilution of the droplet plume is expected to scale inversely with the square of the distance. It is common practice at each position or time point in the reaction to report peak intensities normalized against the highest peak in each spectrum6,10,11,15,17,18,20,21,24,27–30,40,63 and/or the ratio of a product peak and a reactant peak.5,12,17,21,30,41 This makes it difficult to evaluate the overall loss of signal due to transmission effects from the consumption of reactants due to a chemical reaction. Thus, reporting the formation of a product as ‘normalized abundance’ might be confounding the actual concentration trends of reagents and product as a function of distance from the MS inlet.A similar effect is found when the voltage applied to the emitter tip is varied. Fig. S14† shows the intensity of the product peak formed in the epoxide ring opening reaction between limonene oxide and morpholine (m/z = 240.19, intensities taken from the data in Fig. S11†) as a function of applied voltage to the ESSI source. The absolute ion intensities span 3 orders of magnitude (ranging from 104 to 107 at 0 and 5 kV applied, respectively), and generally increase with increasing applied voltage. This result implies that the quantification of reagents and products from measurements that vary the applied voltage should be done carefully. Calibration with an internal standard conducted at a single voltage might not be applicable over a wide range of signal intensities and ionization conditions.
We recommend that raw ion counts be presented in ESI, nESI ESSI-MS experiments, to allow readers to appreciate this signal decay with distance and variable applied voltage and the possible effects of data normalization.
4.12 Charge, strong electric fields and ‘electrochemical ESI’
The presence of charge and/or strong electric fields in ESI, nESI and ESSI droplets are often invoked as possible contributors to accelerated reaction rates in droplets (Fig. 2d). An analysis of the ESI literature shows that electrochemical reactions in ESI droplets are in fact well-known. In most cases, the ESI conditions (i.e. the applied voltage) are selected to prevent redox reactions within the capillary emitter, but ESI can also be used for explicit electrochemical studies.100 The application of ESI to the study of redox reactions is commonly referred to as ‘Electrochemical ESI’.101,102 A demonstration of the redox processes occurring within an ESI source was shown by Xu et al.,103 who found that the minimum voltage needed to observe the oxidized form of a series of metallocenes depends linearly on their redox potentials.Redox reactions have shown accelerated rates in ESI/ESSI droplets. Zare and co-workers have considered a few examples of oxidation and reduction reactions in aqueous droplets.6,24,25 They have observed that these reactions proceed spontaneously without the addition of a catalyst or voltage to the capillary emitter tip. This unexpected reactivity in aqueous droplets is hypothesized to arise from the large electric field naturally present at the air–water interface. The electric field is proposed to promote auto-ionization of water and of OH− ions to form an OH˙ radical plus an electron, which then proceed to react with molecules in solution6,24 or to spontaneously form H2O2.25 This explanation could be plausible considering the well-known occurrence of redox reactivity in charged ESI droplets discussed above. However, Lee and co-authors24 also observed the spontaneous reduction of pyruvate and other organic molecules in “pure water” micro-droplets formed “without applying external charges” using ESSI.
Importantly, Zilch et al.50 observed that ESSI droplets are effectively charged, even without an external voltage being applied to the capillary tip. The net charge on sonic sprayed droplets is thought to arise from their aerodynamic breakup.50 The measured charge on ESSI droplets was ∼1 fC (∼104 electrons per droplet), with positively charged droplets more abundant than negatively charged ones.50 For comparison, the average charge on ESI droplets is 10–100 fC (∼105 to 106 electrons per droplet).50,51 It is also worth noting that even though the absolute charge on ESSI droplets is smaller than on ESI droplets, as solvent evaporates the surface charge density still increases, eventually reaching the Rayleigh limit and emitting ions directly into the gas-phase. The presence of charge on ESSI droplets should perhaps be unsurprising since sonic spray (without external voltage) is routinely used as an ion source for mass spectrometry.
From the above considerations on the charge state of ESSI droplets, we consider the spontaneous reduction of pyruvate and other molecules reported by Lee and coauthors.24 One interesting result in their work is the dependence of the reduction efficiency of pyruvate on the external voltage applied to the sonic spray emitter (see Fig. S16 in their work24). They observed that negative applied voltages resulted in reduction efficiencies similar to the “0 V” case, whereas a positive voltage suppressed the reduction efficiency almost completely. The observations by Zilch et al.50 showed that the natural charge distribution of ESSI droplets is shifted towards positive charges, but a significant fraction of negatively charged droplets remains present, and thus might be responsible for the redox chemistry observed by Lee et al.24
When considering ESSI droplets generated with no externally applied voltage, we suggest it is inaccurate to compare reactivity in “pure water” with that in micro-droplets formed “without applying external charges”.24 Similarly to Gallo et al.,2 we recommend that the presence of charge in sonic sprayed droplets should be acknowledged and accounted for when interpreting the observations of redox reactivity in droplets.
In addition to the absolute charge distribution of ESI/ESSI droplets, the radial distribution of charge within a single droplet needs to be considered. Excess charges within a spherical droplet distribute at near-surface molecular layers (more or less close to the actual surface, depending on the chemical nature of the charged species).58 The profile of the electric field within a droplet resulting from this surficial charge distribution is a function of droplet size and concentration of charges.73 Measured electric field strengths were in the range of 0.2–1 V nm−1 for charged nanodroplets104 and in the order of 107 V nm−1 at the oil–water interface of rhodamine microemulsions.105
It was reported that strong electric fields accelerate single molecule reactions by stabilizing charge separation in the transition state.74,75 By analogy, strong fields may have similar effects within nano- and micro-droplets. Furthermore, stable pH gradients have been reported in neutral droplets by Wei et al.,62 indicating that even within neutral droplets the distribution of the charged species might not be homogeneous. However, some question exists63,106,107 about whether the surface-enhanced Raman spectroscopy technique used by Wei et al.62 is actually measuring pH (i.e., the activity of protons) or concentration of H+. Measuring the pH of microdroplets is a surely challenging task,108,109 and further investigation is needed to clarify the role of pH in the acceleration of reaction rates in droplets.
The particular radial distribution of charges within both droplets with a net charge and neutral droplets could play a relevant role in the acceleration of reaction rates at the surface. However, it needs to be acknowledged here that significant debate exists around the exact chemical–physical nature of the air–water interface of neutral aqueous systems.64 Contrasting results from both experiments and theoretical calculations66 currently result in conflicting conclusions on the estimated electrostatic potential at a water surface.26 Further clarity on these aspects is necessary to allow a definitive determination of the role of charge and electric fields in the acceleration of reaction rates within nano- and micro-droplets.
5. Conclusions
This work aims to elucidate the competing multi-phase processes occurring in ESI/ESSI-MS experiments. We evaluated how the substantial complexity present in these experiments impact the interpretation of the underlying mechanisms for reaction rate acceleration in nano- and micro-droplets.We demonstrated the impact of several factors that complicate the interpretation of ESI/ESSI reaction rate acceleration:
1. Increased reagent concentrations due to solvent evaporation can account for a substantial fraction of the ∼102 to 106 acceleration factors reported in the literature.47
2. Concurrent solvent and reagent evaporation, uncertainties in droplet size and velocity distributions all affect the estimated ESI, nESI and ESSI droplet lifetimes and inferred rate enhancement.
3. The competing kinetics of droplet evaporation, reagent diffusion and adsorption to the surface require further modelling to evaluate the spatial–temporal distribution of reagent molecules at the droplet surface in the bulk- and gas-phases.
4. Results from new measurements demonstrate that gas-phase reactions and reactions on the walls of transfer tubes do occur and cannot be neglected in ESI/ESSI-MS experiments.
5. Variable reagent and product ionization efficiencies, clustering of reagents and decay of ion transmission over long distances between the capillary emitter and the MS inlet all impact interpretation of reaction rate acceleration.
6. Charge and potentially high electric fields within both ESI and ESSI droplets can drive chemistry in micro-droplets; the occurrence of redox activity in ESI is a well-established phenomenon that is exploited in electrochemical ESI.
ESI and ESSI-MS have likely been so widely applied to study the chemical–physical behavior of droplets because they require small amounts of reagents, the necessary equipment is readily available in many laboratories and they are relatively simple to perform. However, it is important to distinguish between experimental practicality and the underlying highly complex multi-phase system that these techniques create. Our analysis and review shows that a number of experimental and data analysis controls are needed in order to draw more robust and quantitative conclusions about the mechanism of reaction rate acceleration observed in ESI/ESSI droplets. We have aimed to provide recommendations for best experimental practices throughout this work.
Ideally, any experimental technique for the study of chemical reactions in droplets should have the following features:
1. Control of solvent evaporation.
2. Well-defined droplet size and concentration of reagents.
3. Access to a wide range of sizes and concentrations.
4. Controlled reaction initiation and timescale.
5. Online detection of products.
6. Quantification of competing gas-phase reactions.
Some of the less commonly used approaches (environmental chambers,37 guided collisions of charged micro-droplets,38 droplet micro-emulsions45) possess some or all of the desirable requirements listed above. For this reason, they have the potential of contributing to the understanding of the acceleration of reaction rates in droplets and of the role of surface processes. In addition to experiments, modelling the kinetics of reactions within droplets and at interfaces can help clarify our understanding of the mechanisms leading to reaction acceleration in micro- and nano-compartments. A few recent examples of such contributions include the kinetic modelling of reactions in microemulsions,60 molecular dynamics simulations of a cycloaddition reaction at the water–graphene interface,110 quantum mechanical calculations of the energies of desolvated molecules at the water–vacuum interface61 and estimation of the magnitude of electric fields in microdroplets.73
Finally, there is an important distinction between two different objectives that one might have when studying the acceleration of reaction rates in aerosolized nano- and micro-droplets. One goal could be to establish effective methods to synthesize large quantities of product that would otherwise require long reaction times in the bulk, expensive catalysts, and high temperature and/or pressure. Such a goal warrants optimizing the ESI/ESSI-MS experimental conditions for the fastest and highest reaction yield, and knowledge of the underlying physical–chemical processes that lead to the enhanced formation of desired products would not necessarily be required. There have been some exciting recent developments in this field with the formation of large product quantities from preparative synthesis with electrosprayed or sonic sprayed reaction mixtures, up to 3 g per hour.22,111,112
The distinct goal of understanding the mechanism of reaction rate enhancement in droplets, and how the various possible factors shown in Fig. 2 contribute to such enhancement, requires mastery of the multi-phase kinetics present in the ESI/ESSI-MS experiments. Observations of reaction rate enhancement by the droplet surface are likely confounded in many ESI/ESSI-MS experiments by one or several of the effects discussed in this work. Moreover, there is an open debate on whether the interfaces of ESI/ESSI charged droplets accurately represent the air–water interface of atmospheric droplets.2,65,113 For these reasons, we suggest caution when drawing general mechanistic conclusions from ESI/ESSI-MS experiments. Similarly, drawing broad conclusions about the role droplet surfaces in atmospheric aerosols and cloud droplets, environmental chemistry at interfaces or prebiotic chemistry, from results obtained by charged ESI, nESI and ESSI droplets should be done cautiously.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Condensed Phase and Interfacial Molecular Science Program, in the Chemical Sciences Geosciences and Biosciences Division of the Office of Basic Energy Sciences of the U.S. Department of Energy (Contract No. DE-AC02-05CH11231). M. I. J. was supported by an NSF Graduate Research Fellowship under DGE-1106400. M. D. W. acknowledges support from a Natural Sciences and Engineering Research Council of Canada (NSERC) postdoctoral fellowship (PDF-516746-2018).References
- N. Sahota, D. I. Abusalim, M. L. Wang, C. J. Brown, Z. Zhang, T. J. El-Baba, S. P. Cook and D. E. Clemmer, Chem. Sci., 2019, 10, 4822–4827 RSC.
- A. Gallo, A. S. F. Farinha, M. Dinis, A. Emwas, A. Santana, R. J. Nielsen, W. A. Goddard and H. Mishra, Chem. Sci., 2019, 10, 2566–2577 RSC.
- A. Colussi and S. Enami, Atmosphere, 2019, 10, 47 CrossRef CAS.
- Y. H. Lai, S. Sathyamoorthi, R. M. Bain and R. N. Zare, J. Am. Soc. Mass Spectrom., 2018, 29, 1036–1043 CrossRef CAS.
- S. Banerjee and R. N. Zare, J. Phys. Chem. A, 2019, 123, 7704–7709 CrossRef CAS.
- D. Gao, F. Jin, J. K. Lee and R. N. Zare, Chem. Sci., 2019, 10, 10965–11148 RSC.
- R. M. Bain, S. T. Ayrton and R. G. Cooks, J. Am. Soc. Mass Spectrom., 2017, 28, 1359–1364 CrossRef CAS.
- D. N. Mortensen and E. R. Williams, J. Am. Chem. Soc., 2016, 138, 3453–3460 CrossRef CAS.
- R. M. Bain, S. Sathyamoorthi and R. N. Zare, Angew. Chem., Int. Ed., 2017, 56, 15083–15087 CrossRef CAS.
- E. T. Jansson, Y.-H. Lai, J. G. Santiago and R. N. Zare, JACS, 2017, 139, 6851–6854 CrossRef CAS.
- K. Iyer, J. Yi, A. Bogdan, N. Talaty, S. W. Djuric and R. G. Cooks, React. Chem. Eng., 2018, 3, 206–209 RSC.
- B. M. Marsh, K. Iyer and R. G. Cooks, J. Am. Soc. Mass Spectrom., 2019, 30, 2022–2030 CrossRef CAS.
- D. N. Mortensen and E. R. Williams, Anal. Chem., 2016, 88, 9662–9668 CrossRef CAS.
- D. N. Mortensen and E. R. Williams, Anal. Chem., 2015, 87, 1281–1287 CrossRef CAS.
- J. K. Lee, S. Banerjee, H. G. Nam and R. N. Zare, Q. Rev. Biophys., 2015, 48, 437–444 CrossRef CAS.
- S. Banerjee and R. N. Zare, Angew. Chem., Int. Ed., 2015, 54, 14795–14799 CrossRef CAS.
- R. M. Bain, C. J. Pulliam and R. G. Cooks, Chem. Sci., 2015, 6, 397–401 RSC.
- R. M. Bain, C. J. Pulliam, S. T. Ayrton, K. Bain and R. G. Cooks, Rapid Commun. Mass Spectrom., 2016, 30, 1875–1878 CrossRef CAS.
- M. Wleklinski, C. E. Falcone, B. P. Loren, Z. Jaman, K. Iyer, H. S. Ewan, S. H. Hyun, D. H. Thompson and R. G. Cooks, Eur. J. Org. Chem., 2016, 5480–5484 CrossRef CAS.
- P. W. Fedick, R. M. Bain, K. Bain, T. F. Mehari and R. G. Cooks, Int. J. Mass Spectrom., 2018, 430, 98–103 CrossRef CAS.
- I. Nam, J. K. Lee, H. G. Nam and R. N. Zare, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 201714896 Search PubMed.
- X. Yan, Y. H. Lai and R. N. Zare, Chem. Sci., 2018, 9, 5207–5211 RSC.
- E. Gnanamani, X. Yan and R. N. Zare, Angew. Chem., Int. Ed., 2020, 59, 3069–3072 CrossRef CAS.
- J. K. Lee, D. Samanta, H. G. Nam and R. N. Zare, J. Am. Chem. Soc., 2019, 141, 10585–10589 CrossRef CAS.
- J. K. Lee, K. L. Walker, H. S. Han, J. Kang, F. B. Prinz, R. M. Waymouth, H. G. Nam and R. N. Zare, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 19294–19298 CrossRef CAS.
- X. Zhong, H. Chen and R. N. Zare, Nat. Commun., 2020, 11, 1049 CrossRef CAS.
- T. Müller, A. Badu-Tawiah and R. G. Cooks, Angew. Chem., Int. Ed., 2012, 51, 11832–11835 CrossRef.
- R. M. Bain, C. J. Pulliam, S. A. Raab and R. G. Cooks, J. Chem. Educ., 2015, 92, 2146–2151 CrossRef CAS.
- S. Enami, Y. Sakamoto and A. J. Colussi, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 623–628 CrossRef CAS.
- J. K. Lee, S. Kim, H. G. Nam and R. N. Zare, PNAS, 2015, 112, 3898–3903 CrossRef CAS.
- J. K. Lee, H. G. Nam and R. N. Zare, Q. Rev. Biophys., 2017, 50, 1–7 CrossRef CAS.
- J. K. Lee, D. Samanta, H. G. Nam and R. N. Zare, Nat. Commun., 2018, 9, 1–9 CrossRef.
- E. A. Crawford, C. Esen and D. A. Volmer, Anal. Chem., 2016, 88, 8396–8403 CrossRef CAS.
- R. M. Bain, C. J. Pulliam, F. Thery and R. G. Cooks, Angew. Chem., Int. Ed., 2016, 55, 10478–10482 CrossRef CAS.
- Y. Li, Y. Liu, H. Gao, R. Helmy, W. P. Wuelfing, C. J. Welch and R. G. Cooks, Chem.–Eur. J., 2018, 24, 7349–7353 CrossRef CAS.
- A. K. Badu-Tawiah, D. I. Campbell and R. G. Cooks, J. Am. Soc. Mass Spectrom., 2012, 23, 1461–1468 CrossRef CAS.
- A. D. Castañeda, Z. Li, T. Joo, K. Benham, B. T. Burcar, R. Krishnamurthy, C. L. Liotta, N. L. Ng and T. M. Orlando, Sci. Rep., 2019, 9, 13527 CrossRef.
- M. I. Jacobs, J. F. Davies, L. Lee, R. D. Davis, F. Houle and K. R. Wilson, Anal. Chem., 2017, 89, 12511–12519 CrossRef CAS.
- Y. Li, X. Yan and R. G. Cooks, Angew. Chem., Int. Ed., 2016, 55, 3433–3437 CrossRef CAS.
- Z. Wei, X. Zhang, J. Wang, S. Zhang, X. Zhang and R. G. Cooks, Chem. Sci., 2018, 9, 7779–7786 RSC.
- M. Girod, E. Moyano, D. I. Campbell and R. G. Cooks, Chem. Sci., 2011, 2, 501–510 RSC.
- F. A. M. G. Van Geenen, M. C. R. Franssen, H. Zuilhof and M. W. F. Nielen, Anal. Chem., 2018, 90, 10409–10416 CrossRef CAS.
- R. M. Bain, C. J. Pulliam, S. A. Raab and R. G. Cooks, J. Chem. Educ., 2016, 93, 340–344 CrossRef CAS.
- T. Sahraeian, D. S. Kulyk and A. K. Badu-Tawiah, Langmuir, 2019, 35, 14451–14457 CrossRef CAS.
- A. Fallah-Araghi, K. Meguellati, J.-C. Baret, A. El Harrak, T. Mangeat, M. Karplus, S. Ladame, C. M. Marques and A. D. Griffiths, Phys. Rev. Lett., 2014, 112, 28301 CrossRef.
- J. K. Lee, S. Kim, H. G. Nam and R. N. Zare, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 3898–3903 CrossRef CAS.
- S. Banerjee, E. Gnanamani, X. Yan and R. N. Zare, Analyst, 2017, 142, 1399–1402 RSC.
- B. R. Bzdek, J. P. Reid and M. I. Cotterell, Commun. Chem., 2020, 3, 105 CrossRef CAS.
- Z. Wei, Y. Li, R. G. Cooks and X. Yan, Annu. Rev. Phys. Chem., 2020, 71, 31–51 CrossRef CAS.
- L. W. Zilch, J. T. Maze, J. W. Smith, G. E. Ewing and M. F. Jarrold, J. Phys. Chem. A, 2008, 112, 13352–13363 CrossRef CAS.
- J. N. Smith, R. C. Flagan and J. L. Beauchamp, J. Phys. Chem. A, 2002, 106, 9957–9967 CrossRef CAS.
- P. Nemes, I. Marginean and A. Vertes, Anal. Chem., 2007, 79, 3105–3116 CrossRef CAS.
- Z. Olumee, J. H. Callahan and A. Vertes, J. Phys. Chem. A, 1998, 102, 9154–9160 CrossRef CAS.
- A. Stindt, C. Warschat, A. Bierstedt, U. Panne and J. Riedel, Eur. J. Mass Spectrom., 2014, 20, 21–29 CrossRef CAS.
- L. Tang and P. Kebarle, Anal. Chem., 1993, 65, 3654–3668 CrossRef CAS.
- J. V. Iribarne and B. A. Thomson, J. Chem. Phys., 1976, 64, 2287–2294 CrossRef CAS.
- L. L. Mack, P. Kralik, A. Rheude and M. Dole, J. Chem. Phys., 1970, 52, 4977–4986 CrossRef CAS.
- L. Konermann, E. Ahadi, A. D. Rodriguez and S. Vahidi, Anal. Chem., 2013, 85, 2–9 CrossRef CAS.
- J. H. Seinfeld and S. N. Pandis, Atmospheric Chemistry and Physics: From Air Pollution to Climate Change, Wiley, 2006 Search PubMed.
- K. R. Wilson, A. M. Prophet, G. Rovelli, M. D. Willis, R. J. Rapf and M. I. Jacobs, Chem. Sci., 2020, 11, 8533–8545 RSC.
- N. Narendra, X. Chen, J. Wang, J. Charles, R. G. Cooks and T. Kubis, J. Phys. Chem. A, 2020, 124, 4984–4989 CrossRef CAS.
- H. Wei, E. P. Vejerano, W. Leng, Q. Huang, M. R. Willner, L. C. Marr and P. J. Vikesland, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 7272–7277 CrossRef CAS.
- A. J. Colussi, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E7887 CrossRef CAS.
- R. J. Saykally, Nat. Chem., 2013, 5, 82–84 CrossRef CAS.
- A. Gallo, A. S. F. Farinha, M. Dinis, A. Emwas, A. Santana, R. J. Nielsen, W. A. Goddard and H. Mishra, Chem. Sci., 2019, 10, 8253–8255 RSC.
- N. Agmon, H. J. Bakker, R. K. Campen, R. H. Henchman, P. Pohl, S. Roke, M. Thämer and A. Hassanali, Chem. Rev., 2016, 116, 7642–7672 CrossRef CAS.
- S. Enami, M. R. Hoffmann and A. J. Colussi, J. Phys. Chem. Lett., 2010, 1, 1599–1604 CrossRef CAS.
- H. Mishra, S. Enami, R. J. Nielsen, L. A. Stewart, M. R. Hoffmann, W. A. Goddard and A. J. Colussi, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 18679–18683 CrossRef CAS.
- Y. L. S. Tse, C. Chen, G. E. Lindberg, R. Kumar and G. A. Voth, J. Am. Chem. Soc., 2015, 137, 12610–12616 CrossRef CAS.
- V. Buch, A. Milet, R. Vácha, P. Jungwirth and J. P. Devlin, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 7342–7347 CrossRef CAS.
- S. Banerjee and R. N. Zare, Angew. Chem., Int. Ed., 2015, 54, 14795–14799 CrossRef CAS.
- R. D. Espy, M. Wleklinski, X. Yan and R. G. Cooks, TrAC, Trends Anal. Chem., 2014, 57, 135–146 CrossRef CAS.
- C. F. Chamberlayne and R. N. Zare, J. Chem. Phys., 2020, 152, 184702 CrossRef CAS.
- S. Ciampi, N. Darwish, H. M. Aitken, I. Díez-Perez and M. L. Coote, Chem. Soc. Rev., 2018, 47, 5146–5164 RSC.
- A. C. Aragonès, N. L. Haworth, N. Darwish, S. Ciampi, N. J. Bloomfield, G. G. Wallace, I. Diez-Perez and M. L. Coote, Nature, 2016, 531, 88–91 CrossRef.
- E. J. Davis, Adv. Chem. Eng., 1992, 18, 1–94 CAS.
- F. K. A. Gregson, M. Ordoubadi, R. E. H. Miles, A. Haddrell, D. Barona, D. Lewis, T. Church, R. Vehring and J. P. Reid, Phys. Chem. Chem. Phys., 2019, 21, 9709–9719 RSC.
- C. L. Yaws, Handbook of Vapor Pressure, Gulf Publishing Co., Houston, TX, 1994, vol. 2 – C5 to C7 Compounds Search PubMed.
- R. L. Grimm and J. L. Beauchamp, J. Phys. Chem. A, 2010, 114, 1411–1419 CrossRef CAS.
- R. M. Bain, C. J. Pulliam, S. T. Ayrton, K. Bain and R. G. Cooks, Rapid Commun. Mass Spectrom., 2016, 30, 1875–1878 CrossRef CAS.
- M. Sommerfeld and L. Pasternak, Int. J. Multiphase Flow, 2019, 117, 182–205 CrossRef CAS.
- S. Kim, D. J. Lee and C. S. Lee, Int. J. Multiphase Flow, 2009, 35, 533–549 CrossRef CAS.
- R. D. Davis, M. I. Jacobs, F. A. Houle and K. R. Wilson, Anal. Chem., 2017, 89, 12494–12501 CrossRef CAS.
- F. K. A. Gregson, J. F. Robinson, R. E. H. Miles, C. P. Royall and J. P. Reid, J. Phys. Chem. B, 2018, 123, 266–276 CrossRef.
- M. Shiraiwa, C. Pfrang, T. Koop and U. Pöschl, Atmos. Chem. Phys., 2012, 12, 2777–2794 CrossRef CAS.
- A. A. Wiegel, M. J. Liu, W. D. Hinsberg, K. R. Wilson and F. A. Houle, Phys. Chem. Chem. Phys., 2017, 19, 6814–6830 RSC.
- M. I. Jacobs, R. D. Davis, R. J. Rapf and K. R. Wilson, J. Am. Soc. Mass Spectrom., 2019, 30, 339–343 CrossRef CAS.
- I. Nam, H. G. Nam and R. N. Zare, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 36–40 CrossRef CAS.
- M. M. Safarov, A. V Kartavchenko and M. A. Zaripova, J. Eng. Phys. Thermophys., 1995, 68, 252–254 CrossRef.
- Z. Takáts, J. M. Wiseman, B. Gologan and R. G. Cooks, Anal. Chem., 2004, 76, 4050–4058 CrossRef.
- N. B. Cech and C. G. Enke, Anal. Chem., 2000, 72, 2717–2723 CrossRef CAS.
- N. B. Cech and C. G. Enke, Mass Spectrom. Rev., 2001, 20, 362–387 CrossRef CAS.
- N. B. Cech and C. G. Enke, Anal. Chem., 2001, 73, 4632–4639 CrossRef CAS.
- K. Tang, J. S. Page and R. D. Smith, J. Am. Soc. Mass Spectrom., 2004, 15, 1416–1423 CrossRef CAS.
- R. King, R. Bonfiglio, C. Fernandez-Metzler, C. Miller-Stein and T. Olah, J. Am. Soc. Mass Spectrom., 2000, 11, 942–950 CrossRef CAS.
- C. G. Enke, Anal. Chem., 1997, 69, 4885–4893 CrossRef CAS.
- J. S. Page, R. T. Kelly, K. Tang and R. D. Smith, J. Am. Soc. Mass Spectrom., 2007, 18, 1582–1590 CrossRef CAS.
- I. Marginean, R. T. Kelly, D. C. Prior, B. L. LaMarche, K. Tang and R. D. Smith, Anal. Chem., 2008, 80, 6573–6579 CrossRef CAS.
- L. C. Chen, S. Tsutsui, T. Naito, S. Ninomiya and K. Hiraoka, J. Mass Spectrom., 2018, 53, 400–407 CrossRef CAS.
- H. Oberacher, F. Pitterl, R. Erb and S. Plattner, Mass Spectrom. Rev., 2015, 34, 64–92 CrossRef CAS.
- G. J. Van Berkel, J. Am. Soc. Mass Spectrom., 2000, 11, 951–960 CrossRef CAS.
- G. J. Van Berkel and V. Kertesz, Anal. Chem., 2007, 79, 5510–5520 CrossRef CAS.
- X. Xu, S. P. Nolan and R. B. Cole, Anal. Chem., 1994, 66, 119–125 CrossRef CAS.
- C. J. Hogan, P. Biswas and D. R. Chen, J. Phys. Chem. B, 2009, 113, 970–976 CrossRef CAS.
- H. Xiong, J. K. Lee, R. N. Zare and W. Min, J. Phys. Chem. Lett., 2020, 11, 7423–7428 CrossRef CAS.
- E. M. Coddens, K. J. Angle and V. H. Grassian, J. Phys. Chem. Lett., 2019, 10, 4476–4483 CrossRef CAS.
- P. J. Vikesland, H. Wei, Q. Huang, H. Guo and L. C. Marr, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E7888–E7889 CrossRef CAS.
- H. O. T. Pye, A. Nenes, B. Alexander, A. P. Ault, M. C. Barth, S. L. Clegg, J. L. Collett, K. M. Fahey, C. J. Hennigan, H. Herrmann, M. Kanakidou, J. T. Kelly, I. T. Ku, V. Faye McNeill, N. Riemer, T. Schaefer, G. Shi, A. Tilgner, J. T. Walker, T. Wang, R. Weber, J. Xing, R. A. Zaveri and A. Zuend, The acidity of atmospheric particles and clouds, Atmos. Chem. Phys., 2020, 20, 4809–4888 CrossRef CAS.
- A. P. Ault, Acc. Chem. Res., 2020, 53, 1703–1714 CrossRef CAS.
- L. Ruiz Pestana, H. Hao and T. Head-Gordon, Nano Lett., 2019, 20, 606–611 CrossRef.
- H. Nie, Z. Wei, L. Qiu, X. Chen, D. T. Holden and R. G. Cooks, Chem. Sci., 2020, 11, 2356–2361 RSC.
- C. Liu, J. Li, H. Chen and R. N. Zare, Chem. Sci., 2019, 10, 9367–9373 RSC.
- A. J. Colussi and S. Enami, Chem. Sci., 2019, 10, 8253–8255 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc04611f |
| ‡ Now at: Beckman Institute, University of Illinois, 61801, Urbana-Champaign, IL, USA. |
| § Now at: Department of Chemistry, Trinity University, San Antonio, 78212, TX, USA. |
| This journal is © The Royal Society of Chemistry 2020 |