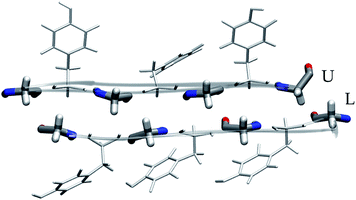
Open Access Article
Open Access ArticleAtomistic fibrillar architectures of polar prion-inspired heptapeptides†
Francesca
Peccati
 *a,
Marta
Díaz-Caballero
*a,
Marta
Díaz-Caballero
 bc,
Susanna
Navarro
bc,
Susanna
Navarro
 bc,
Luis
Rodríguez-Santiago
bc,
Luis
Rodríguez-Santiago
 d,
Salvador
Ventura
d,
Salvador
Ventura
 bce and
Mariona
Sodupe
bce and
Mariona
Sodupe
 d
d
aCenter for Cooperative Research in Biosciences (CIC bioGUNE), Basque Research and Technology Alliance (BRTA), Bizkaia Technology Park, Building 801A, 48160 Derio, Spain. E-mail: fpeccati@cicbiogune.es; Tel: +34 4469/946 572 538
bInstitut de Biotecnologia i Biomedicina, Universitat Autònoma de Barcelona, 08193 Bellaterra, Spain
cDepartament de Bioquímica i Biologia Molecular, Universitat Autònoma de Barcelona, 08193 Bellaterra, Spain
dDepartament de Química, Universitat Autònoma de Barcelona, 08193 Bellaterra, Spain
eICREA, Passeig Lluís Companys 23, E-08010 Barcelona, Spain
First published on 2nd November 2020
Abstract
This article provides the computational prediction of the atomistic architectures resulting from self-assembly of the polar heptapeptide sequences NYNYNYN, SYSYSYS and GYGYGYG. Using a combination of molecular dynamics and a newly developed tool for non-covalent interaction analysis, we uncover the properties of a new class of bionanomaterials, including hydrogen-bonded polar zippers, and the relationship between peptide composition, fibril geometry and weak interaction networks. Our results, corroborated by experimental observations, provide the basis for the rational design of prion-inspired nanomaterials.
1 Introduction
The cross-β spine is a common motif of amyloid fibrils; it is composed of two sandwiched β-sheets, each resulting from the lateral stacking of peptide segments. At the contact region between the β-sheets, side chains form a tight, solvent-excluded interface called a steric zipper.1–3 This regular repeat of stacked strands arranged perpendicular to the fibril growth axis represents the structural basis of amyloid fibrils. Furthermore, this apparently simple organization contains the key to the polymorphism of amyloid fibrils, i.e. the ability of the same polypeptide sequence to yield a variety of different three-dimensional architectures.2,4 Indeed, this heterogeneity arises from a multiplicity of possible polypeptide arrangements and conformations, all lying in a narrow energy range. Also short peptides have the ability to self-assemble in various dispositions with distinct probabilities, giving rise to fibrils with different morphologies; these morphologies, in turn, can translate into different mechanical properties, highlighting the importance of having accurate knowledge of the atomistic structure for revealing the experimental results and designing new systems.5,6Formation of fibrils with hydrophobic steric zippers as a consequence of protein misfolding and aggregation is a fundamental aspect of pathogenic amyloids involved in neurodegenerative diseases (e.g. amyloid-β in Alzheimer's disease and α-synuclein in Parkinson's disease).7,8
One of the key aspects of amyloids is the fact that they represent a thermodynamic well in the conformational landscape: when a protein attains an amyloid state, the aggregation process cannot be easily reversed due to a high enthalpic cost, and the aggregated state, corresponding to a specific polymorph, can recruit new monomers, providing the means for fibril propagation. The preference for a specific polymorph among all the possible supra-structures is fine-tuned by the local environment in such a way that two different Alzheimer's disease patients may show different amyloid-β polymorphs.9–11 Once a certain fibrillar length is attained, structural interconversion is no longer observed.12
A different behavior is observed in functional prions: yeast prions are capable of switching between a soluble and an amyloid state, where globular domains remain unmodified and self-assembly takes place at the level of the so-called prion domains (PrDs), intrinsically disordered sequences rich in polar residues such as asparagine and glutamine and deficient in hydrophobic amino acids. This reversibility, which sets these systems apart from classic amyloid fibrils, makes them excellent candidates for the design of nanomaterials that can be activated by aggregation while maintaining a specific function encoded in the untouched globular domain. To understand and develop the full potential of PrDs in nanotechnology, it is necessary to analyze, at the molecular level, the aggregation patterns of prion domains.13,14
On this point, the intrinsic disorder of amyloid and prion aggregates represents a big challenge for computational techniques,15–17 as they need to describe accurately both covalent bonding and the more elusive non-covalent interactions.18,19 In this work, we employ our recently developed non-covalent interaction integral technique, which allows fast estimation of non-covalent interaction strengths in biomolecular systems to address the relative stability of prion-inspired aggregates.20,21 In a recent study, we designed a series of minimalist prion-inspired polar heptapeptides that, despite their small size, recapitulate the properties of full-length PrDs, spontaneously self-assembling into highly ordered non-toxic amyloid fibrils under physiological conditions.22 Here, we address the atomistic structure of their cross-β spines.
2 Methodology
2.1 Computational methods
MD simulations were performed with the Amber suite, using the ff14SB force field.23,24 A slow equilibration protocol was set up to relax the initial fibrillar architecture to a temperature of 300 K. Since the initial inter-sheet distance is set to a large value to avoid steric clashes, equilibration involves short low temperature unrestrained dynamics bursts to allow the fibril model to pack side chains at the steric zipper (see the ESI†). Production was run as 100 ns NPT dynamics, at a constant temperature of 300 K and removing all restraints, with the Langevin thermostat and Monte Carlo barostat.25,26 A rectangular solvent box was built around each fibril model with TIP3P waters27 with a minimum 12 Å buffer between the solvent and the simulation box. As all fibril models are neutral, no ion was added. Calculation of the relative energy of fibril architectures was performed by extracting 100 snapshots from the 100 ns production trajectory, stripping water molecules and running a 500 step geometry relaxation on each frame using the generalized Born implicit solvent model to attenuate steric clashes.28,29 NCIPLOT analysis to obtain semiquantitative information on the relative stability of lateral and inter-sheet contacts was performed on the snapshots extracted from the molecular dynamics simulations as discussed in ref. 20, 21 and 30. This information is given in the form of non-covalent interaction (NCI) integrals, which have been shown to provide a semiquantitative measure of the interaction strength.30 NCI integrals are presented for the so-called van der Waals region, which covers most of the NCIs, and is comparatively weak and the so-called attractive region, which accounts for the contribution of the strongest NCIs, involving high electron densities (e.g. strong hydrogen bonds). These integrals provide for each frame a descriptor of the collective strength of intra-sheet and inter-sheet NCIs and can be used to compare the relative stabilization of different fibril models of the same system.NCIs can be identified by analyzing the electron density, ρ(r), and its reduced density gradient (eqn (1))
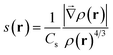 | (1) |
2.2 Experimental techniques
3 Results and discussion
3.1 Model generation
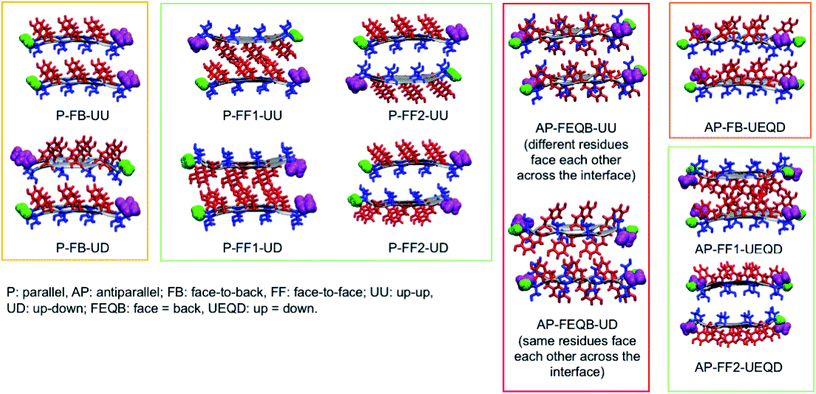
To generate all possible fibrillar architectures we used an in-house code that computes the Cartesian coordinates of steric zippers of any length applying rigid rotations and translations to the coordinates of an individual strand. The length of each β-sheet was set to 20 strands, so that each fibril model is composed of 40 strands. For each heptapeptide, we ran molecular dynamics simulations on the eleven non-equivalent possible fibrillar architectures and computed their relative energies on 100 frames sampled with a constant stride.
Of these models, we analyzed the relative stability, non-covalent interaction networks and geometrical features. As far as the latter are concerned, we analyzed the twist angle, which measures the rotation of subsequent strands around the fibril's main axis, and the tilt angle, which measures the linearity of the main axis. The formal definition of these angles is given in the ESI.†
3.2 Relative stabilities
| Model | NY7 (sd) | SY7 (sd) | GY7 (sd) |
|---|---|---|---|
| AP-FEQB-UD | 10.50 (0.57) | 13.59 (0.60) | 9.23 (0.34) |
| AP-FEQB-UU | 9.46 (0.56) | 12.40 (0.65) | 8.05 (0.47) |
| AP-FB-UEQD | 8.31 (0.70) | 12.59 (0.74) | 13.40 (0.65) |
| AP-FF1-UEQD | 11.96 (0.54) | 16.04 (0.39) | 17.97 (1.16) |
| AP-FF2-UEQD | 9.67 (0.61) | 2.28 (0.43) | 0.00 (0.57) |
| P-FB-UU | 3.14 (0.69) | 12.41 (0.50) | 12.37 (0.29) |
| P-FB-UD | 2.00 (0.77) | 9.72 (0.49) | 15.02 (0.44) |
| P-FF1-UD | 11.16 (1.48) | 19.52 (0.78) | 21.24 (1.24) |
| P-FF1-UU | 8.23 (0.91) | 18.23 (0.71) | 22.28 (0.55) |
| P-FF2-UD | 0.79 (0.33) | 0.87 (0.30) | 6.64 (0.74) |
| P-FF2-UU | 0.00 (0.26) | 0.00 (0.57) | 9.73 (0.49) |
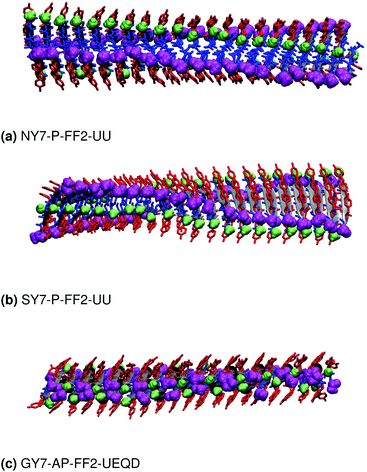
These results indicate that despite the common features of the three heptapeptides (length, residue alternation and presence of three tyrosines), the composition affects the preferred steric zipper architecture. Also, they show that if an amino acid capable of forming strong hydrogen bonds such as serine, asparagine, or glycine is present alongside tyrosine residues, tyrosines will remain exposed to the solvent and the other residue will be packed at the interface. The evolution of the twist angles of NY7, SY7, and GY7 and along the MD trajectories is shown in Fig. S7–S9.† The results indicate a large variability both among different heptapeptides and among fibril models. In general, our models become flatter in the order GY7 < SY7 < NY7, with NY7 yielding the flattest fibrils of the set.
3.3 NY7 fibrils
| Name | i-BB-SC | Avgd | i-SC HB | Avgd | i-NCIvdw | i-NCIa | Twist | Tilt |
|---|---|---|---|---|---|---|---|---|
| NY7-AP-FEQB-UD | 0 | — | 17 | 2.74 | 56.08 | 7.67 | 161.82 | 4.75 |
| NY7-AP-FEQB-UU | 0 | — | 4 | 2.79 | 59.03 | 6.99 | 161.91 | 3.08 |
| NY7-AP-FB-UEQD | 0 | — | 25 | 2.74 | 63.12 | 11.41 | 164.25 | 4.31 |
| NY7-AP-FF1-UEQD | 0 | — | 13 | 2.83 | 57.70 | 7.33 | 166.12 | 1.70 |
| NY7-AP-FF2-UEQD | 5 | 2.84 | 36 | 2.84 | 69.32 | 14.91 | 159.06 | 2.18 |
| NY7-P-FB-UU | 4 | 2.79 | 20 | 2.73 | 59.89 | 9.95 | 16.63 | 1.39 |
| NY7-P-FB-UD | 0 | — | 23 | 2.85 | 64.33 | 7.90 | 10.11 | 5.79 |
| NY7-P-FF1-UD | — | — | — | — | — | — | — | — |
| NY7-P-FF1-UU | 0 | — | 72 | 2.81 | 84.18 | 12.29 | 32.46 | 1.63 |
| NY7-P-FF2-UD | 0 | — | 59 | 2.86 | 64.45 | 16.35 | 20.56 | 1.27 |
| NY7-P-FF2-UU | 0 | — | 31 | 2.87 | 83.25 | 17.54 | 15.94 | 1.16 |
| SY7-AP-FEQB-UD | 3 | 2.77 | 20 | 2.80 | 72.31 | 9.11 | 162.87 | 4.75 |
| SY7-AP-FEQB-UU | 0 | — | 3 | 2.81 | 56.03 | 4.68 | 109.84 | 6.62 |
| SY7-AP-FB-UEQD | 8 | 2.77 | 25 | 2.80 | 76.47 | 11.79 | 166.20 | 6.99 |
| SY7-AP-FF1-UEQD | 0 | — | 12 | 2.83 | 57.84 | 7.72 | 171.13 | 1.78 |
| SY7-AP-FF2-UEQD | 19 | 2.72 | 13 | 2.79 | 109.10 | 16.15 | 172.43 | 2.51 |
| SY7-P-FB-UU | 36 | 2.77 | 30 | 2.77 | 93.69 | 17.16 | 12.71 | 8.15 |
| SY7-P-FB-UD | 0 | — | 74 | 2.75 | 81.36 | 16.70 | 11.63 | 2.54 |
| SY7-P-FF1-UD | — | — | — | — | — | — | — | — |
| SY7-P-FF1-UU | 0 | — | 71 | 2.81 | 83.13 | 12.79 | 24.19 | 1.51 |
| SY7-P-FF2-UD | 121 | 2.70 | 17 | 2.77 | 134.89 | 21.57 | 63.66 | 4.27 |
| SY7-P-FF2-UU | 38 | 2.76 | 69 | 2.72 | 114.81 | 21.09 | 37.80 | 1.94 |
| GY7-AP-FEQB-UD | 26 | 2.77 | 0 | — | 90.04 | 10.50 | 131.59 | 4.65 |
| GY7-AP-FEQB-UU | 16 | 2.78 | 0 | — | 99.80 | 10.81 | 169.98 | 6.02 |
| GY7-AP-FB-UEQD | 22 | 2.76 | 0 | — | 78.82 | 8.58 | 128.48 | 7.49 |
| GY7-AP-FF1-UEQD | — | — | — | — | — | — | — | — |
| GY7-AP-FF2-UEQD | 0 | — | 0 | — | 104.69 | 7.65 | 169.40 | 1.97 |
| GY7-P-FB-UU | 57 | 2.72 | 0 | — | 82.45 | 10.59 | 19.41 | 4.57 |
| GY7-P-FB-UD | 7 | 2.75 | 0 | — | 76.92 | 8.61 | 54.12 | 4.86 |
| GY7-P-FF1-UD | — | — | — | — | — | — | — | — |
| GY7-P-FF1-UU | — | — | — | — | — | — | — | — |
| GY7-P-FF2-UD | 0 | — | 0 | — | 102.37 | 5.80 | 31.33 | 5.99 |
| GY7-P-FF2-UU | 0 | — | 0 | — | 90.84 | 5.51 | 60.35 | 3.87 |
3.4 SY7 fibrils
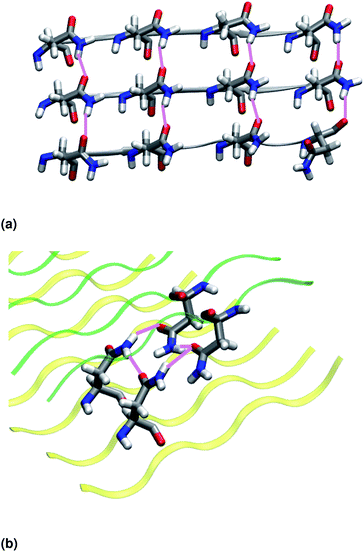
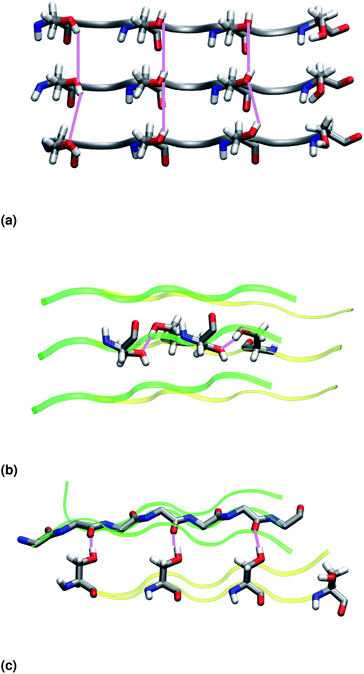
Similar to NY7, the P-FF1-UD model that packs tyrosines at the interface is unstable and disaggregates along the MD trajectory. In the preferred models, P-FF2-UU and P-FF2-UD, tyrosine residues remain exposed to the solvent, and serine residues are packed at the polar zipper, forming a strong network of intra-sheet (Fig. 4a) and inter-sheet (Fig. 4b and c) hydrogen bonds, as already observed for NY7. However, there is a significant difference between NY7 and SY7, which originates from the distinct steric hindrance of asparagine and serine: while inter-sheet hydrogen bonds in NY7-P-FF2-UU and NY7-P-FF2-UD exclusively involve asparagine side chains, in SY7 models they can involve not only serine side chains (Fig. 4b), but also backbone carbonyl groups (Fig. 4c). These contacts (named i-BB-SC in Table 2) are established across the steric zipper involving on one side the hydroxyl group of a serine side chain and on the other a backbone carbonyl group.
Furthermore, we find it interesting that the energetically equivalent SY7-P-FF2-UU and SY7-P-FF2-UD steric zippers present such different twist angles. While the mechanical properties of the nano-fibrils cannot be extrapolated from our simulations on the bilayer – they depend on the overall morphology of the assembly of several bilayer units – we expect SY7-P-FF2-UU and SY7-P-FF2-UD to coexist in the nanofibril yielding a flexible morphology35 modulated by the extent of inter-sheet side chain-backbone hydrogen bonds. Similar considerations can be drawn for NY7, where the P-FF2-UU and P-FF2-UD arrangements are essentially energetically equivalent but less marked differences are observed between the two organizations.
3.5 GY7 fibrils
3.6 Comparison with experiment
The design, synthesis and characterization of NY7, SY7 and GY7 fibrils were published in ref. 22. In this section we provide new TEM images of the three types of fibrils and reassess their interpretation in light of the computational results. TEM analysis reveals the presence of fibrils for NY7, SY7 and GY7 peptides (Fig. 6a–c). NY7 and SY7 fibrils differ significantly in length, with SY7 fibrils being longer. This fact might correspond to the higher structural flexibility of SY7 fibrils, as calculated, which would decrease their brittleness, relative to the likely more rigid NY7 fibrils. GY7 (Fig. 6c) fibrils appear thinner and less electrodense than those of NY7 and SY7 peptides, which will be consistent with a shorter inter β-sheet distance in GY7 fibrils, once they are assembled.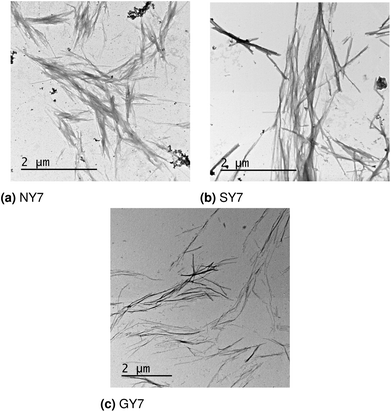 | ||
| Fig. 6 Electron microscopy images of (a) NY7, (b) SY7 and (c) GY7 fibrils.22 | ||
3.7 Validation
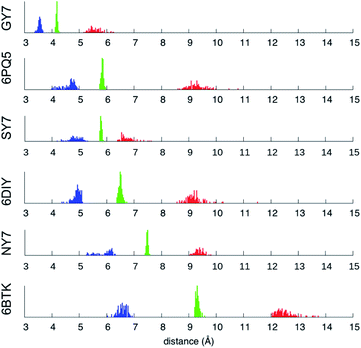 | ||
| Fig. 7 Minimum (blue), mean (green) and maximum (red) inter-sheet distance distribution along the MD trajectories of NY7-P-FF2-UU, SY7-P-FF2-UU, GY7-AP-FF2-UEQD and the validation set. | ||
Averaging over the 100 frames yields a single value for each MD trajectory, presented in Table 3 and compared with the crystallographic distance for the validation set. To ensure comparability between calculated and crystallographic data, crystallographic inter-sheet distances were computed with the same protocol operating on the biological assembly as downloaded from the Protein Data Bank. The results shown in Table 3 show an excellent agreement between the calculated and crystallographic data for the validation set, confirming the quality of our MD protocol. Noticeably, GY7's inter-sheet distance is comparable with that of a prion structure. Indeed, the recently solved partial prion sequence of PDB 6PQ5 (ref. 37) shows an average inter-sheet distance of 5.8 Å, corresponding to a steric zipper of alanine residues. The predicted average inter-sheet distance of GY7-AP-FF2-UEQD is 4.2 Å, less than 2 Å shorter than that of 6PQ5, which is consistent with the smaller size of glycine over alanine side chains. Thus, steric zippers with a short inter-sheet distance exist, but resolution of their structure has started to become possible only in the last few years due to methodological advances (cryo-EM).38
4 Conclusions
Using the newly developed non-covalent interaction integral method in combination with classical molecular dynamics, we have identified the most favorable polar zipper architectures resulting from the self-assembly of three heptapeptides containing tyrosine and (i) asparagine, (ii) serine and (iii) glycine. We have shown that polar residues (asparagine and serine) are packed at the interface between β-sheets, yielding a strong network of hydrogen bonds and stabilizing the resulting architectures over those that pack tyrosine at the interface. Furthermore, while asparagine polar zippers are stabilized by hydrogen bonds involving side chains only, serine polar zippers can form hydrogen bonds between backbone and side chain groups on opposite β-sheets. In general, fibril stability correlates with large intra- and inter-sheet van der Waals integrals, and for SY7 with the number of stable inter-sheet side chain–side chain and side chain–backbone hydrogen bonds. In SY7, larger twist angles correlate with a higher side chain–backbone/side chain–side chain ratio of stable inter-sheet hydrogen bonds. We have also shown that glycines, known as secondary structure breakers, can form a tight steric zipper (∼4 Å), yielding stable nanofibrils. Overall, we have demonstrated that computational techniques can predict the atomistic structure of novel prion-like assemblies with the peptide sequence as the only initial input. These predicted structures match experimental information even in highly atypical cases: we predict the first glycine steric zipper, which, like the recently resolved alanine zipper,37 is unthinkable within the framework of classic amyloid hydrophobic zippers. In this way, we show that our approach, which does not rely on structural databases, is able to tackle such new classes of non-classical steric zippers. We believe that these results will encourage the application of computational techniques, and in particular non-covalent interaction analysis, to interpret experimental results and provide the necessary physico-chemical insight to aid the rational design of related nanomaterials.Conflicts of interest
There are no conflicts to declare.Acknowledgements
FP acknowledges the financial support from CALSIMLAB under the public grant ANR-11-LABX-0037-01 overseen by the French National Research Agency (ANR) as part of the Investissements d'Avenir program (reference: ANR-11-IDEX-0004-02). MS and LRS gratefully acknowledge the financial support from the MINECO (CTQ2017-89132-P) and the Generalitat de Catalunya (2017SGR1323). SV gratefully acknowledges the financial support from the MINECO (BIO2016-78310-R) and ICREA (ICREA-Academia 2015 to S. V.). MDC gratefully acknowledges the financial support from the Spanish Ministry of Science and Innovation via a doctoral grant (FPU14/05786). SV, MDC and SN gratefully acknowledge the Servei de Microscopia from the Universitat Autònoma de Barcelona for their technical support.Notes and references
- R. Nelson, M. R. Sawaya, M. Balbirnie, A. O. Madsen, C. Riekel, R. Grothe and D. Eisenberg, Nature, 2005, 435, 773–778 CrossRef CAS.
- J.-P. Colletier, A. Laganowsky, M. Landau, M. Zhao, A. B. Soriaga, L. Goldschmidt, D. Flot, D. Cascio, M. R. Sawaya and D. Eisenberg, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 16938–16943 CrossRef CAS.
- D. S. Eisenberg and M. R. Sawaya, Annu. Rev. Biochem., 2017, 86, 69–95 CrossRef CAS.
- M. Fändrich, J. Meinhardt and N. Grigorieff, Prion, 2009, 3, 89–93 CrossRef.
- Y. Raz, B. Rubinov, M. Matmor, H. Rapaport, G. Ashkenasy and Y. Miller, Chem. Commun., 2013, 49, 6561–6563 RSC.
- Y. Miller, B. Ma and R. Nussinov, J. Phys. Chem. B, 2015, 119, 482–490 CrossRef CAS.
- E. M. Rocha, B. D. Miranda and L. H. Sanders, Neurobiol. Dis., 2018, 109, 249–257 CrossRef CAS.
- M. Castello and S. Soriano, Ageing Res. Rev., 2014, 13, 10–12 CrossRef CAS.
- A. T. Petkova, W.-M. Yau and R. Tycko, Biochemistry, 2006, 45, 498–512 CrossRef CAS.
- A. K. Paravastu, R. D. Leapman, W.-M. Yau and R. Tycko, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 18349–18354 CrossRef CAS.
- J.-X. Lu, W. Qiang, W.-M. Yau, C. D. Schwieters, S. C. Meredith and R. Tycko, Cell, 2013, 154, 1257–1268 CrossRef CAS.
- R. Tycko, Protein Sci., 2014, 23, 1528–1539 CrossRef CAS.
- W. Wang, S. Navarro, R. A. Azizyan, M. Baño Polo, S. A. Esperante, A. V. Kajava and S. Ventura, Nanoscale, 2019, 11, 12680–12694 RSC.
- X.-M. Zhou, A. Entwistle, H. Zhang, A. P. Jackson, T. O. Mason, U. Shimanovich, T. P. J. Knowles, A. T. Smith, E. B. Sawyer and S. Perrett, ChemCatChem, 2014, 6, 1961–1968 CrossRef CAS.
- I. M. Ilie and A. Caflisch, Chem. Rev., 2019, 119, 6956–6993 CrossRef CAS.
- F. Musiani and A. Giorgetti, Early Stage Protein Misfolding and Amyloid Aggregation, Academic Press, 2017, vol. 329, pp. 49–77 Search PubMed.
- N. V. Dovidchenko and O. V. Galzitskaya, in Computational Approaches to Identification of Aggregation Sites and the Mechanism of Amyloid Growth, ed. O. Gursky, Springer International Publishing, Cham, 2015, pp. 213–239 Search PubMed.
- J. Černý and P. Hobza, Phys. Chem. Chem. Phys., 2007, 9, 5291–5303 RSC.
- K. E. Riley and P. Hobza, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 3–17 CAS.
- R. A. Boto, F. Peccati, R. Laplaza, C. Quan, A. Carbone, J.-P. Piquemal, Y. Maday and J. Contreras-García, J. Chem. Theory Comput., 2020, 16, 4150–4158 CrossRef CAS.
- F. Peccati, J. Chem. Inf. Model., 2020, 60, 6–10 CrossRef CAS.
- M. Díaz-Caballero, S. Navarro, I. Fuentes, F. Teixidor and S. Ventura, ACS Nano, 2018, 12, 5394–5407 CrossRef.
- D. A. Case, R. M. Betz, W. Botello-Smith, D. S. Cerutti, T. E. Cheatham, T. Darden, R. E. Duke, T. J. Giese, H. Gohlke and A. W. Goetz, et al., AMBER16, 2016 Search PubMed.
- J. A. Maier, C. Martinez, K. Kasavajhala, L. Wickstrom, K. E. Hauser and C. Simmerling, J. Chem. Theory Comput., 2015, 11, 3696–3713 CrossRef CAS.
- R. J. Loncharich, B. R. Brooks and R. W. Pastor, Biopolymers, 1992, 32, 523–535 CrossRef CAS.
- J. Åqvist, P. Wennerström, M. Nervall, S. Bjelic and B. O. Brandsdal, Chem. Phys. Lett., 2004, 384, 288–294 CrossRef.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- A. Onufriev, D. Bashford and D. A. Case, Proteins: Struct., Funct., Bioinf., 2004, 55, 383–394 CrossRef CAS.
- A. Onufriev, D. Bashford and D. A. Case, J. Phys. Chem. B, 2000, 104, 3712–3720 CrossRef CAS.
- F. Peccati, E. Desmedt and J. Contreras-García, Comput. Theor. Chem., 2019, 1159, 23–26 CrossRef CAS.
- X. Periole, T. Huber, A. Bonito-Oliva, K. C. Aberg, P. C. A. van der Wel, T. P. Sakmar and S. J. Marrink, J. Phys. Chem. B, 2018, 122, 1081–1091 CrossRef CAS.
- M. R. Sawaya, S. Sambashivan, R. Nelson, M. I. Ivanova, S. A. Sievers, M. I. Apostol, M. J. Thompson, M. Balbirnie, J. J. W. Wiltzius, H. T. McFarlane, A. O. Madsen, C. Riekel and D. Eisenberg, Nature, 2007, 447, 453–457 CrossRef CAS.
- M. Gallagher-Jones, C. Glynn, D. R. Boyer, M. W. Martynowycz, E. Hernandez, J. Miao, C.-T. Zee, I. V. Novikova, L. Goldschmidt, H. T. McFarlane, G. F. Helguera, J. E. Evans, M. R. Sawaya, D. Cascio, D. S. Eisenberg, T. Gonen and J. A. Rodriguez, Nat. Struct. Mol. Biol., 2018, 25, 131–134 CrossRef CAS.
- Y. Maréchal, The Hydrogen Bond and the Water Molecule, Elsevier, 2007, pp. 25–47 Search PubMed.
- R. Song, X. Wu, B. Xue, Y. Yang, W. Huang, G. Zeng, J. Wang, W. Li, Y. Cao, W. Wang, J. Lu and H. Dong, J. Am. Chem. Soc., 2019, 141, 223–231 CrossRef CAS.
- B. Brumshtein, S. R. Esswein, M. R. Sawaya, G. Rosenberg, A. T. Ly, M. Landau and D. S. Eisenberg, J. Biol. Chem., 2018, 293, 19659–19671 CrossRef CAS.
- C. Glynn, M. R. Sawaya, P. Ge, M. Gallagher-Jones, C. W. Short, R. Bowman, M. Apostol, Z. H. Zhou, D. S. Eisenberg and J. A. Rodriguez, Nat. Struct. Mol. Biol., 2020, 27, 417–423 CrossRef CAS.
- E. Nwanochie and V. Uversky, Int. J. Mol. Sci., 2019, 20, 4186 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Structural analysis of NY7, SY7 and GY7 fibrils. See DOI: 10.1039/d0sc05638c |
| This journal is © The Royal Society of Chemistry 2020 |