Arrested dynamics of the dipolar hard sphere model
Luis F.
Elizondo-Aguilera†
 *a,
Ernesto C.
Cortés-Morales†
b,
Pablo F.
Zubieta Rico†
*a,
Ernesto C.
Cortés-Morales†
b,
Pablo F.
Zubieta Rico†
 b,
Magdaleno
Medina-Noyola†
b,
Ramón
Castañeda-Priego†
c,
Thomas
Voigtmann†
b,
Magdaleno
Medina-Noyola†
b,
Ramón
Castañeda-Priego†
c,
Thomas
Voigtmann†
 ad and
Gabriel
Pérez-Ángel†
e
ad and
Gabriel
Pérez-Ángel†
e
aInstitut für Materialphysik im Weltraum, Deutsches Zentrum für Luft-und Raumfahrt (DLR), 51170 Köln, Germany. E-mail: luisfer.elizondo@gmail.com
bInstituto de Física, Universidad Autónoma de San Luis Potosí, Av. Manuel Nava 6, Zona Universitaria, 78290 San Luis Potosí, Mexico
cDepartamento de Ingeniería Física, División de Ciencias e Ingenierías, Universidad de Guanajuato, Loma del Bosque 103, 37150 León, Mexico
dDepartment of Physics, Heinrich-Heine-Universität Düsseldorf, Universitätsstraße 1, 40225 Düsseldorf, Germany
eDepartamento de Física Aplicada, CINVESTAV del IPN, A. P. 73 “Cordemex”, 97310 Mérida, Yucatán, Mexico
First published on 14th November 2019
Abstract
We report the combined results of molecular dynamics simulations and theoretical calculations concerning various dynamical arrest transitions in a model system representing a dipolar fluid, namely, N (soft core) rigid spheres interacting through a truncated dipole–dipole potential. By exploring different regimes of concentration and temperature, we find three distinct scenarios for the slowing down of the dynamics of the translational and orientational degrees of freedom: at low (η = 0.2) and intermediate (η = 0.4) volume fractions, both dynamics are strongly coupled and become simultaneously arrested upon cooling. At high concentrations (η ≥ 0.6), the translational dynamics shows the features of an ordinary glass transition, either by compressing or cooling down the system, but with the orientations remaining ergodic, thus indicating the existence of partially arrested states. In this density regime, but at lower temperatures, the relaxation of the orientational dynamics also freezes. The physical scenario provided by the simulations is discussed and compared against results obtained with the self-consistent generalized Langevin equation theory, and both provide a consistent description of the dynamical arrest transitions in the system. Our results are summarized in an arrested states diagram which qualitatively organizes the simulation data and provides a generic picture of the glass transitions of a dipolar fluid.
The substantial progress in the synthesis and fabrication of anisotropic colloids,1–4 along with their unique ability for self-assembly and structural reconfiguration,2,3,5–7 provides a route for the design of new specialized materials with novel physical properties and with specific functionalities of high technological interest. Colloids of non-spherical shapes have long been known, but recognition that anisotropy in interactions constitutes another potential tool for engineering particular targeted structures has brought a widespread research enthusiasm in dipolar systems.5–16 Even at thermodynamic equilibrium conditions and in the absence of external fields, dipolar suspensions tend to assemble into energetically favorable head-to-tail configurations and typically display a rich structural, dynamical and phase behavior arising from the complex and highly anisotropic nature of the dipolar interaction.11–22
The current interest in structures of increasing complexity, however, has also triggered investigations of self-assembly under non-equilibrium conditions.23–26 Colloidal suspensions, in particular, have been observed to undergo distinct transitions to non-crystalline amorphous states. At high densities, for instance, they can form glassy states, where the main underlying physical mechanism for dynamical arrest is nearest-neighbor caging inhibiting individual motion.27,28 At low densities, they may also undergo gelation by increasing the mutual interactions among particles, prompting long-lived physical (reversible) bonding between particles, which thus facilitates the formation of percolated networks capable of sustaining weak mechanical stresses.29–32 Striking similarities, but also fundamental differences, have been highlighted between the microscopic dynamics and the mechanical response of both gels and glasses.30,31
Dipolar colloids have been the subject of numerous investigations based on computer simulations.10,18–22,33,34 Goyal et al., for example, carried out molecular dynamics (MD) studies aimed at outlining the equilibrium phase diagram in the packing fraction (η) vs. temperature (T) plane of monocomponent fluids of hard spheres (HS) with embedded dipoles20 and of binary mixtures with difference in size and dipolar moment.21,22 One of the most interesting aspects of such diagrams is the observation that, besides different crystalline (e.g., fcc-hcp-bct), fluid and string-fluid equilibrium phases, a region of percolated networks of crossed-links chains exists, occurring at intermediate temperatures and at nearly all the volume fractions considered, thus describing a region of gel-like states. In addition, Blaak et al.,18,19 demonstrated that, at low densities (η < 0.1), a slight elongation of the particles into dumbbells favors branching of dipolar chains, and hence, space-spanning networking towards the gel state. It was also highlighted that this behavior is accompanied by a noteworthy slowing down of the translational dynamics, closely resembling well known features of physical (reversible) gelation in systems with short-ranged but spherically-symmetric depletion attractions,32 just as it occurs in the case of colloid-polymer mixtures35,36 and systems with adhesive (sticky) interactions.37,38
The theoretical modeling of the dynamical arrest of dipolar fluids is not abundant. Schilling and Scheidsteger39 applied the mode coupling theory (MCT) of the glass transition (GT) to predict the existence of several dynamical arrest transitions in a dipolar HS fluid and outlined the corresponding non-equilibrium states diagram. More recently, the same essential features were also observed within the self-consistent generalized Langevin equation (SCGLE) theory.40 To date, however, characterizations of the glassy and gel behavior of dipolar liquids, based on the simultaneous use of simulations and theoretical approaches, are rather scarce. In addition, and to the best of our knowledge, presently there are no experimental results reporting on glassy dynamics of dipolar colloidal suspensions in the absence of external fields and covering the supercooled and high density regime. Thus, it remains to be understood whether the competition between caging and bonding, along with the highly anisotropic character of the interactions (which couples translational and orientational motion) mediates the various dynamical arrest transitions. In particular, the role of the orientational dynamics in the glass transitions has not been fully determined.
A collection of N rigid spheres of diameter σ bearing a dipolar moment μ is clearly one of the simplest representations of a dipolar fluid, a model that possesses a remarkable theoretical significance,41,42 since it combines both spherical entropic and anisotropic energetic interactions. Notwithstanding its apparent conceptual simplicity, the distinct glassy behavior of such system is far from being completely understood. Hence, a main aim of this work is to report the results of extensive MD simulations carried out on a slightly simplified version of this model, introduced for practical convenience. We refer to a system of spherical particles whose repulsive-core interaction is given by the so-called Weeks–Chandler–Andersen (WCA) potential.43 For simplicity, and in order to focus on the effect of anisotropy in the interactions, rather than on their long-range nature, the particles further interact by a truncated dipole–dipole potential. For this model, we have investigated different regimes of concentration and temperature where – on the basis of previous theoretical39,40 and simulation18–22 results – various dynamical arrest transitions are expected to occur.
Therefore, instead of considering equilibrium phases, in this contribution we are specifically interested in investigating those morphological transformations driven by conditions of dynamical arrest. In particular, we find three types of transitions: (i) the simultaneous arrest of the dynamics of both the translational (TDF) and orientational degrees of freedom (ODF), occurring at low and intermediate concentrations upon lowering the temperature; (ii) an ordinary GT for the translational dynamics, occurring at high densities and high-to-intermediate temperatures, but where the relaxation of the orientational dynamics remains ergodic; and (iii) the subsequent arrest of the ODF in a positionally frozen structure of particles, occurring also at high densities but lower temperatures. Our findings thus suggest the existence of at least three different GTs in the parameters space (η,T*), which describe distinct microscopical underlying mechanisms for arrest.
Besides the analysis of the dynamics of the TDF, given in terms of observables such as the self-part of the Fourier transform of the van Hove correlation function and the mean square displacement, we also consider explicitly the dynamics of the ODF of the model towards the GT. The latter is described in terms of a proper set of orientationally sensitive correlation functions39–42 and the corresponding angular mean square deviations. As we show below, this allows us to unravel important features of the dynamical arrest transitions of a dipolar fluid not fully described in previous investigations.
Finally, to provide a stronger physical insight, we complement the MD simulation results with a theoretical analysis based on the SCGLE theory40 of dynamical arrest. We particularly focus on the study of the so-called non ergodicity parameters, describing the long-time dynamics of the fluid in the vicinity of each glass transition, and summarized in an arrested state diagram, which organizes qualitatively our results from simulations. The physical scenario emerging from the theory is in remarkable agreement with the features observed in the simulations, thus providing a consistent physical description of dynamical arrest.
1 Simulations: methodological aspects
The standard tools of MD cannot be directly applied to simulate a dipolar hard-sphere (DHS) fluid due to the mismatch between the discontinuous HS potential and the soft dipolar contribution. The former can be properly approached only via an event-driven algorithm,44,45 whereas the latter requires a continuous-time approach. One may use a Monte Carlo (MC) sampling considering both hard and soft potentials, but this only would be useful if our main purpose were the determination of the static properties. The absence of a well defined time variable in MC simulations, however, renders the evaluation of dynamical quantities complicated (MC time is nevertheless used some times, see, for instance, ref. 46). To circumvent these limitations, we have introduced a set of simplifying modifications to the pair interactions between dipolar spheres. Similarly, rather than simulating an exhaustive catalog of physical properties, here we shall focus on the dynamical properties associated with the (translational and rotational) Brownian motion and tracer diffusion properties, as explained in what follows.1.1 Model system
We have simulated a system of N spherical particles in a volume V, with a pairwise interaction potential between particles (labeled as a and b) given by| Uab(ra,μa;rb,μb) =UabWCA(|rb − ra|) + UabTD(rb − ra,μa,μb). | (1) |
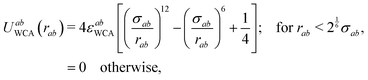 | (2) |
The second term on the right side of eqn (1) represents the anistropic dipolar contribution to the interaction. In order to avoid all the complexities inherent to the specialized treatment of long-ranged (∼1/r3) interactions,48 we have considered a truncated dipolar potential which is written as
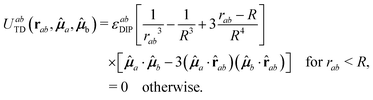 | (3) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ab = rab/rab,
ab = rab/rab, ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) a ≡ μa/μa, R is a cut-off distance for the dipolar interaction and εabDIP = μaμb. In this work we are setting R = 3σave. The magnitude of a given dipole moment is proportional to its diameter to the power 3/2, that is, μi = μ0(σi/σave)3/2 (i = 1, 2), where μ0 is a common dipole scale taken here as μ0 = 1. The reason to introduce this dependence is to keep the interaction at contact (i.e., for rab ≈ σab) approximately the same for all contacts, be they between large dipoles, small dipoles, or a small dipole with a large one; otherwise the attraction at contact between small dipoles is substantially larger than the one between large dipoles, and segregation phenomena may appear. For simplicity, all dipoles are assumed to have mass m = 1 (this sets the mass scale) and moment of inertia I = 1/10, and the scale of the WCA potential is set by εabWCA = 1 for all a, b = 1, 2, fixing in this way both energy and time scales.
a ≡ μa/μa, R is a cut-off distance for the dipolar interaction and εabDIP = μaμb. In this work we are setting R = 3σave. The magnitude of a given dipole moment is proportional to its diameter to the power 3/2, that is, μi = μ0(σi/σave)3/2 (i = 1, 2), where μ0 is a common dipole scale taken here as μ0 = 1. The reason to introduce this dependence is to keep the interaction at contact (i.e., for rab ≈ σab) approximately the same for all contacts, be they between large dipoles, small dipoles, or a small dipole with a large one; otherwise the attraction at contact between small dipoles is substantially larger than the one between large dipoles, and segregation phenomena may appear. For simplicity, all dipoles are assumed to have mass m = 1 (this sets the mass scale) and moment of inertia I = 1/10, and the scale of the WCA potential is set by εabWCA = 1 for all a, b = 1, 2, fixing in this way both energy and time scales.
1.2 Physical observables
In this contribution we focus on the single particle dynamics, which is sampled with better statistics than collective dynamics. Specifically, we consider the self-part of the generalized intermediate scattering functions (ISFs) and mean square deviations defined below as a measure of translational and rotational diffusion. To monitor the stability of the simulations, we have also checked translational and rotational kinetic energies, potential energies, and pressure. To verify the stationarity of the simulation runs and check for possible aging effects, instead, we have followed the protocol described below (see Section 1.3)Also reviewed, and of special interest, are those quantities that may signal a breakdown of the homogeneity or the isotropy of the fluid. To test for possible crystallization, we have used the q4, q6, Q4 and Q6 orientational order parameters defined by Steinhardt and Nelson.49,50 To look for possible segregation, instead, we introduce a simple “sameness” parameter, which measures how many dipoles of the same size are within a cut-off distance of any given dipole, compared to how many dipoles of the other size can be found. More concretely, this is defined for the a-th dipole as 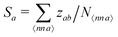 , where we take zab = 1 if dipoles a and b are of the same size, and zab = −1 otherwise. Here the sum is taken over all nearest neighbors (nn) to a, as defined by the cut-off distance, and N〈nn
, where we take zab = 1 if dipoles a and b are of the same size, and zab = −1 otherwise. Here the sum is taken over all nearest neighbors (nn) to a, as defined by the cut-off distance, and N〈nn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a〉 is the number of those nearest neighbors. It is also quite important to check the variance in S, since a small value for this variance indicates some degree of ordering. The cutoff distance used here is the same one employed for the aforementioned Steinhard–Nelson order parameters, and has been taken for our purposes as the distance for the first minimum in the pair distribution function, g(r), which is larger than σ1. Finally, we also monitor the total magnetization,
a〉 is the number of those nearest neighbors. It is also quite important to check the variance in S, since a small value for this variance indicates some degree of ordering. The cutoff distance used here is the same one employed for the aforementioned Steinhard–Nelson order parameters, and has been taken for our purposes as the distance for the first minimum in the pair distribution function, g(r), which is larger than σ1. Finally, we also monitor the total magnetization, 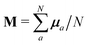 , so we can rule out any long range orientation of the dipoles. In all the states considered below 〈M〉 ≈ 0, and no crystallization or particle segregation occurs.
, so we can rule out any long range orientation of the dipoles. In all the states considered below 〈M〉 ≈ 0, and no crystallization or particle segregation occurs.
Let us now discuss the mean squared deviations. For the TDF, the common definition of the mean squared displacement (MSD) is used,
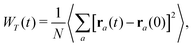 | (4) |
The description of rotational diffusion is slightly more complex. Recall that in this case, the ODF are described by the set {![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) 1(t),
1(t),![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) 2(t),…,
2(t),…,![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) N(t)} ∈ S2, where each of the vectors
N(t)} ∈ S2, where each of the vectors ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) a(t) describe a point over the unit sphere S2. As it is immediately apparent, the long-time limit of the diffusion of such points over a spherical surface is a static homogeneous covering, which gives a WR(t) that saturates to a constant after a sufficiently long time.51 There have been various efforts to define different ways of measuring diffusion over a spherical surface. In particular, there is a method that generates a vector Δ
a(t) describe a point over the unit sphere S2. As it is immediately apparent, the long-time limit of the diffusion of such points over a spherical surface is a static homogeneous covering, which gives a WR(t) that saturates to a constant after a sufficiently long time.51 There have been various efforts to define different ways of measuring diffusion over a spherical surface. In particular, there is a method that generates a vector Δ![[small phi, Greek, vector]](https://www.rsc.org/images/entities/i_char_e13a.gif) (t) tangential to the surface and normal to the direction of displacement, and with the magnitude of the traversed angle. One then concatenates these vectorial increments to obtain a total displacement vector
(t) tangential to the surface and normal to the direction of displacement, and with the magnitude of the traversed angle. One then concatenates these vectorial increments to obtain a total displacement vector ![[small phi, Greek, vector]](https://www.rsc.org/images/entities/i_char_e13a.gif) (t).52 This measure of diffusion does not saturate and, for small angular increments Δϕ, gives a linear behavior in the long time limit, i.e., Wϕ(t) = 4Dϕt. However, since the Δ
(t).52 This measure of diffusion does not saturate and, for small angular increments Δϕ, gives a linear behavior in the long time limit, i.e., Wϕ(t) = 4Dϕt. However, since the Δ![[small phi, Greek, vector]](https://www.rsc.org/images/entities/i_char_e13a.gif) contributions are all tangential to the surface of the sphere, their sum
contributions are all tangential to the surface of the sphere, their sum ![[small phi, Greek, vector]](https://www.rsc.org/images/entities/i_char_e13a.gif) drifts away from the surface for any finite displacements, and thus, ends up predicting normal diffusion even in cases where there is clear arrest and where the dipoles cannot deviate more than a small fraction of π from its original orientation. We therefore stick with a measure of rotational diffusion that saturates and identify arrest as those cases where a rotational MSD does not reach (or takes an exceedingly long time to reach) its saturation value. Specifically, we have considered the mean square deviations (see Appendix A)
drifts away from the surface for any finite displacements, and thus, ends up predicting normal diffusion even in cases where there is clear arrest and where the dipoles cannot deviate more than a small fraction of π from its original orientation. We therefore stick with a measure of rotational diffusion that saturates and identify arrest as those cases where a rotational MSD does not reach (or takes an exceedingly long time to reach) its saturation value. Specifically, we have considered the mean square deviations (see Appendix A)
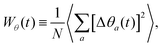 | (5) |
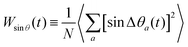 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ(t), however, is important because it allows to develop a closed formula to obtain the rotational diffusion coefficient from simulations (see eqn (16) and (18) in Appendix A).
θ(t), however, is important because it allows to develop a closed formula to obtain the rotational diffusion coefficient from simulations (see eqn (16) and (18) in Appendix A).
With respect to the correlation functions, there is a common approach which, for completeness, is briefly reviewed here. Details are carefully discussed in ref. 39, 40 and 42. One starts by considering a microscopical density of particles at position r and orientation ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) , at time t, defined by
, at time t, defined by
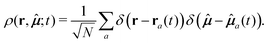 | (7) |
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) at time t = 0, and r′,
at time t = 0, and r′, ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) ′ at time t, it is customary to consider the coefficients of the Fourier transform and spherical harmonics expansion of ρ(r,
′ at time t, it is customary to consider the coefficients of the Fourier transform and spherical harmonics expansion of ρ(r,![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) ;t),42 commonly referred to as tensorial density modes, and given by
;t),42 commonly referred to as tensorial density modes, and given by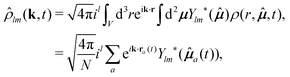 | (8) |
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) ) are spherical harmonics and k is the scattering vector. From here, the fundamental correlators are defined by a family of intermediate scattering functions (ISFs) of the form39,40
) are spherical harmonics and k is the scattering vector. From here, the fundamental correlators are defined by a family of intermediate scattering functions (ISFs) of the form39,40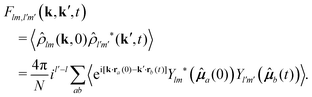 | (9) |
Up to now no assumptions have been made about the fluid. However, one knows that in an homogeneous system, a van Hove correlation function does not depend on two vectors r and r′ separately, but only on the displacement |r − r′|. As a result, the corresponding ISFs will only depend on one wavevector k, instead of the two appearing, for instance, in eqn (9). Furthermore, in an isotropic system the van Hove function does not depend on the two full sets of angles defining the orientations ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) and
and ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) ′, but only on three angular variables.42 Following the form of the anisotropic dipolar interaction, an appealing choice is to use the projections of
′, but only on three angular variables.42 Following the form of the anisotropic dipolar interaction, an appealing choice is to use the projections of ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) and
and ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) ′ over the line connecting the two dipoles (assuming some orientation for this line which, at the end, results irrelevant), and the dihedral angle between them. This is equivalent to choosing the line between the two particles as the ẑ axis, a prescription referred to as the interaction frame.42 Going again into Fourier space, an equivalent procedure is to rotate the coordinate system so that the wavevector k points in the direction of the ẑ axis, also called the k-frame choice41 As discussed in ref. 39, for an isotropic space and using well-known properties of spherical harmonics, this choice imposes several restrictions on Flm,l′m′. The most important of them being that, for a nonzero correlator, one only needs to consider m = m′. In this way, one gets a right counting of variables, since the ISF now uses just three orientational indices. We are then left with correlators of the form
′ over the line connecting the two dipoles (assuming some orientation for this line which, at the end, results irrelevant), and the dihedral angle between them. This is equivalent to choosing the line between the two particles as the ẑ axis, a prescription referred to as the interaction frame.42 Going again into Fourier space, an equivalent procedure is to rotate the coordinate system so that the wavevector k points in the direction of the ẑ axis, also called the k-frame choice41 As discussed in ref. 39, for an isotropic space and using well-known properties of spherical harmonics, this choice imposes several restrictions on Flm,l′m′. The most important of them being that, for a nonzero correlator, one only needs to consider m = m′. In this way, one gets a right counting of variables, since the ISF now uses just three orientational indices. We are then left with correlators of the form
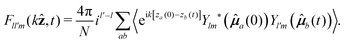 | (10) |
Finally, and as indicated before, in this contribution we are interested only in the self part of these correlation functions, that is, the correlators of the positions and orientations of a single particle,
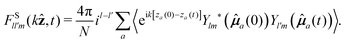 | (11) |
There are additional restrictions for Fll′m(kẑ,t).39 Two of them are worth mentioning here: (i) these correlation functions are zero unless l − l′ is even, and (ii), Fll′m is zero at time t = 0 unless l′ = l.
1.3 Molecular dynamics simulations
We have considered a Newtonian MD that uses the velocity-Verlet integrator, for both translations and rotations. Both sets of degrees of freedom are coupled to stochastic thermostats that performs velocity re-scaling in the same spirit as the Bussi–Donadio–Parrinello thermostat.53 Two thermostats are used because, in general, the evolution timescales for translations and rotations are different, and the system tends to show a difference in temperatures analogous to the Hot-Solvent/Cold-Solute problem that is pervasive in other applications of MD, when some type of velocity rescaling is used with only one thermostat.54We have simulated a total of N dipolar particles (N1 = N2 = N/2) in a cubic box of volume V, with periodic boundary conditions. The effective packing fraction, η = Nπ(σ13 + σ23)/12V, and the scaled temperature, T* ≡ kBT/εabWCA, were used to explore different points in the (η,T*) plane. Specifically, we have investigated state points along four different Paths. Three of them consist in fixing the volume fraction to the values η = 0.2 (Path 1), 0.4 (Path 2) and 0.6 (Path 3), and varying the temperature in the range 0.2 ≤ T* ≤ 2. In addition, we also considered the isotherm T* = 1 and varied the concentration as 0.2 ≤ η ≤ 0.7 (Path 4). With exception of the state point (η = 0.6, T = 0.63), we have considered N1 = N2 = 4096 for a total of 8192 particles, a number large enough so we have not detected any changes in the behavior of the fluid when halving N (for the aforementioned state point along Path 3, we have considered N1 = N2 = 2048). For each state point investigated, 8 different seeds (realizations) of the system have been used to explore the available phase space and to improve statistics. The time increment for T* = 1 was set to dt1 = 5 × 10−4, and for other temperatures we use 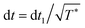 . The computing of the self ISFs has been carried out performing, for each configuration considered, the sum indicated in eqn (11) taking as the vertical direction each of the three coordinate axes, that is, using the original coordinates and then performing the two cyclic rotations xyz → zxy → yzx. These correlators are real when we consider both possible orientations for the z axis.
. The computing of the self ISFs has been carried out performing, for each configuration considered, the sum indicated in eqn (11) taking as the vertical direction each of the three coordinate axes, that is, using the original coordinates and then performing the two cyclic rotations xyz → zxy → yzx. These correlators are real when we consider both possible orientations for the z axis.
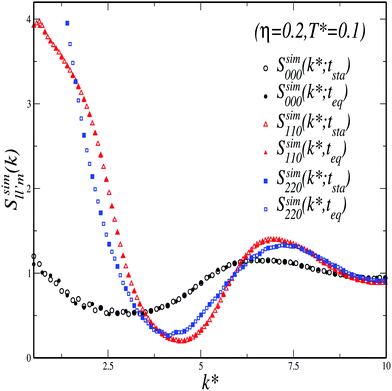
We start from a random, non-overlapping configuration and then run the simulations for a transient time, tsta, long enough to acquire stable values for the pressure and potential energy of the system. To assess the stationarity of the samples, we proceed as follows: after verifying that pressure, potential and kinetic energies are stable, we use the configuration obtained at tsta to calculate the static structure factor. We then let the samples evolve for an equilibration time, teq, of roughly 106 time units. During this time, we have monitored the evolution of the ISFs and MSDs. At the end of this equilibration run, we use the final configuration and calculate again the static structure correlations, in order to compare against those obtained at tsta (see Fig. 11 in Appendix B). We do not observe any crucial difference between the structure obtained at tsta and teq. This was taken as the criteria to consider a sample stationary. At the end of any production run, the system was cooled to a lower temperature (or compressed to a higher density, according to the case) and the procedure was reiterated.
2 Simulation results
We now present the results of the described simulations, regarding the dynamical properties associated with the translational and rotational degrees of freedom.2.1 Translational dynamics
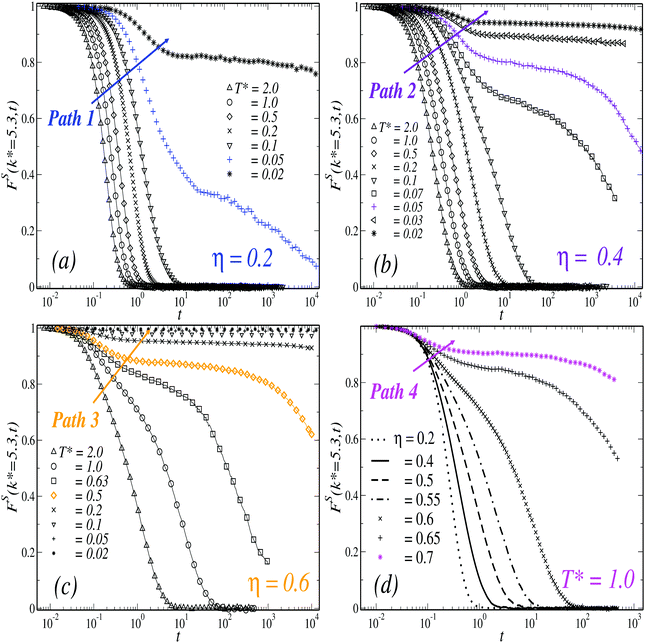
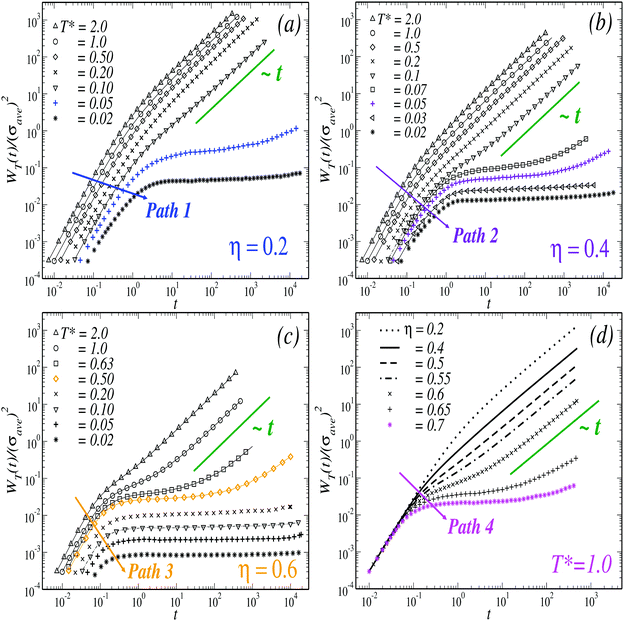
To study the dynamics of the TDF of the model we considered the purely translational self-ISF, FS000(k,t) ≡ FS(k,t), and the MSD, WT(t). As indicated above, both observables were investigated at different state points of the (η,T*) parameters space, organized for clarity in four paths that approach dynamical arrest in different ways. In Fig. 1, we summarize the results obtained for FS(k* = 5.3,t), with k* ≡ kσave, at the three isochores corresponding to (a) η = 0.2, (b) η = 0.4 and (c) η = 0.6, and along the isotherm (d) T* = 1.At the lowest density considered and high temperatures, the system's behavior resembles that of a dilute HS gas (see also Fig. 3(a)). Lowering T* at fixed η (i.e., following the solid arrow of Fig. 1(a) from left to right, Path 1), a gradual slowing down in the relaxation dynamics is observed. Specifically at T* = 0.05, FS shows an inflection point and a stretched relaxation which remains finite over the time-scale of the simulations, thus indicating dynamical arrest. Slightly below, at T* = 0.02, the arrest of the dynamics of the TDF becomes more noticeable with the emergence of a high plateau, which remains practically constant up to three decades in time.
Upon increasing the concentration to η = 0.4 (Fig. 1(b), Path 2) one finds similar features. Within the range 0.1 ≤ T* ≤ 2, FS becomes only moderately slower with respect to the previous case at comparable temperatures. At lower values, T* = 0.07, the self-ISF develops a second slower decay mode, and the relaxation-time increases dramatically with small variations in T*. A transient plateau appears at T* = 0.05, where this correlation function barely changes over three decades and remains finite at the longest time of the simulation. The height of this plateau, however, is noticeably larger in comparison to that found along the isochore η = 0.2 at the same temperature. This suggests that the state point (η = 0.4, T* = 0.05) is closer to conditions of dynamical arrest than (η = 0.2, T* = 0.05). In addition, the appearance of a higher plateau is typically associated to the formation of a mechanically stronger glassy state. It is worth stressing that, despite the small differences in the dynamics of the TDF along Paths 1 and 2, a concomitant change in the structure of the system is also observed upon increasing η from 0.2 to 0.4. These effects can be appreciated, for instance, from the evolution of the radial distribution function, g(r), along both isochores. This will be discussed below in Section 2.2.
Along the isochore η = 0.6 (Fig. 1(c), Path 3), in contrast, the relaxation of FS becomes substantially slower upon decreasing temperature in the whole T* range explored. Lowering down to T* = 0.63, for instance, accounts for an increment of about three decades in the relaxation time of FS with respect to T* = 2. This correlation function becomes arrested and develops a high plateau at T* = 0.5 (and below). Noticeably, this temperature is larger than those found along the two previous cases (roughly, one order of magnitude) and accounts for the strong influence of crowding in the dynamical arrest of the translational dynamics. These effects can be also emphasized by considering the results along the isotherm T* = 1 (Fig. 1(d), Path 4), where the features of a HS GT (i.e., density-driven) are displayed. In this case, the slowing down of the relaxation dynamics is observed for concentrations η ≥ 0.6, where FS develops a two-steps relaxation pattern and eventually a non-decaying plateau at η = 0.7. Therefore, the results along Paths 3 and 4 support the interpretation that the critical temperature for the arrest of the translational dynamics represents a rapidly increasing function of η at high densities.
Besides the information provided by the self-ISF, one can also consider the evolution of the MSD, WT(t), along Paths 1–4. Both quantities are connected in the low-wave-vector limit, but the MSD represents an easily interpreted observable quantifying particle mobility and long-ranged transport. The corresponding data are displayed in Fig. 2 and consistently describe the physical scenario outlined by FS. Along the isochores η = 0.2 and η = 0.4 (Fig. 2(a) and (b), respectively), WT(t) undergoes the typical evolution from ballistic (∼t2) to diffusive (∼t) behavior for 0.1 ≤ T* ≤ 2. At lower temperatures, the particles virtually cease to diffuse and the MSD develops transient plateaus followed by the emergence of a small subdiffusive regime for longer times. In both paths, this occurs at T* ≈ 0.05, and flat plateaus extending the observation time of the simulation appear for lower temperature.
 | ||
| Fig. 2 Mean square displacements, W*(t) (in units of σave2), corresponding to the isochores: (a) η = 0.2, (b) η = 0.4, and (c) η = 0.6 and the same temperatures as in Fig. 1; and for the isotherm (d) T* = 1.0. From left to right, the solid black arrows intersect the curves in order of decreasing temperature or increasing density. The (green) solid lines are a guide to the eye. | ||
As it might be expected from the results for FS along Path 3, the MSD shows arrest at T* = 0.5 for the isochore η = 0.6 (Fig. 2(c)). Similarly, in the case of the isotherm T* = 1, WT(t) shows a slowing down with increasing density and develops plateaus for η ≥ 0.65. This confirms that FS and W(t) provide the same physical scenario regarding the dynamical arrest of the TDF.
Close to conditions of arrest, the long-time value of the MSD allows to estimate the maximum possible displacement of the particles. In the case of dense systems described by steep repulsive potentials, the square-root of this value (up to a factor) is commonly referred to as the localization length, l, and represents a measurement of the local confinement, since it provides the displacement inside nearest-neighbor cages. In a colloidal HS glass, for instance, one typically finds values lHS ∼ 0.1σHS. Furthermore, in the case of systems with short-ranged attractions, a reduction of the localization length at fixed density, normally indicates the passage from localization due to caging to one due to bonding. As we discuss in Section 3, the results of Fig. 2(c) along Path 3 describe consistently these features, and are also in remarkable agreement with the predictions of the SCGLE for the behavior of this quantity (see Fig. 9).
Let us anticipate at this point, however, that the localization length extracted from simulations at time scales corresponding to the plateau (which indicates transient caging), i.e., 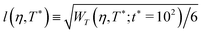 , shows that the particles become slightly more localized upon increasing η from 0.2 to 0.4 and approaching dynamical arrest, whereas for both l(η = 0.6, T* = 0.5) and l(η = 0.7, T* = 1) one finds essentially the same value, l ≈ 0.1σave. Furthermore, along Path 3 one observes a substantial reduction of l(η = 0.6,T*) for T* < 0.5.
, shows that the particles become slightly more localized upon increasing η from 0.2 to 0.4 and approaching dynamical arrest, whereas for both l(η = 0.6, T* = 0.5) and l(η = 0.7, T* = 1) one finds essentially the same value, l ≈ 0.1σave. Furthermore, along Path 3 one observes a substantial reduction of l(η = 0.6,T*) for T* < 0.5.
In summary, the results for FS(k*,t) and WT(t) outline the main features of the dynamical arrest transitions of the TDF of the simulated model. At low and intermediate concentrations, the dynamics freezes at nearly the same temperature, but showing small deviations in the localization length, the corresponding relaxation times, decay patterns and, as we show in what follows, also at the structural level. The results for the high density regime, instead, show that the critical temperature for dynamical arrest behaves as a monotonically and rapidly increasing function of the concentration, and that the dynamics of the TDF undergo a GT in the fashion of a HS system.
2.2 Radial distribution function
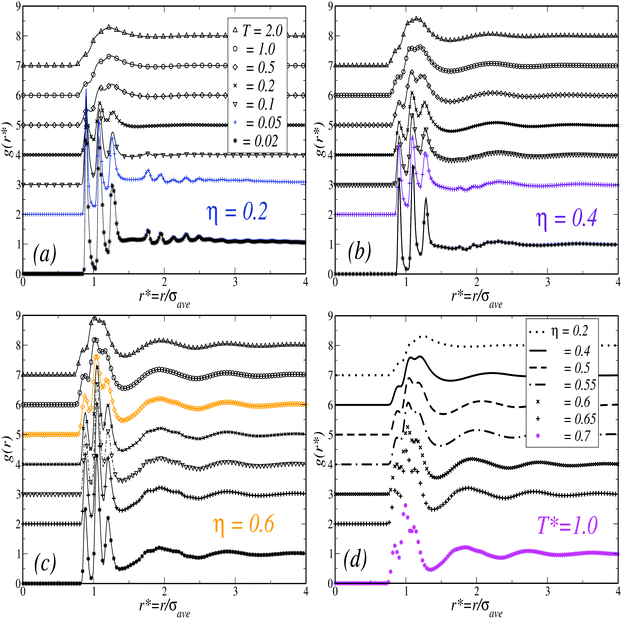
Besides the analysis of the translational dynamics, we have monitored the structural behavior of the simulated fluid, represented by the radial distribution function g(r), and along the four paths considered. The results are shown in Fig. 3 (data are shifted in the vertical axis for clarity).At the isochore η = 0.2 (Path 1, Fig. 3(a)) and high temperatures, g(r) exhibits a single broad peak centered at r ≈ 1.2σave, beyond which it attains its asymptotic unit value. Upon cooling, this first diffuse peak evolves into the superposition of the nearest-neighbor peaks of g11(r), g12(r), and g22(r), separated from each other by approximately ±σave/6. At T* = 0.05 and below, the amplitudes of the three peaks become noticeable higher. At the same time, one observes the emergence of an additional train of smaller peaks, now centered at r ≈ 2σave representing the second-nearest neighbor shell. The various individual peaks in this train correspond to the combinations of small and large particles in an approximately linear configuration. This may be indicative of the tendency of the particles to associate in linear trimers and small chains, leading to the emergence of heterogeneous structures as the temperature decreases, i.e., upon an increase of the dipolar interactions. As already suggested by previous works, this also could be related to the formation of percolation networks of crossed-links dipolar chains towards the gelation transition,20–22 however, a detailed discussion of such effects is beyond the scope of this work. Therefore, we will restrict the discussion to the concomitant effects arising from this structural behavior but only at the level of the dynamics of both the TDF and ODF.
By increasing the volume fraction to η = 0.4, the structure evolves to that of a liquid (Path 2, Fig. 3(b)), characterized by the emergence of a main peak and followed by other well-separated, but smaller, secondary peaks. Importantly, the small oscillations around r ≈ 2σave observed in g(r) along Path 1 and at low temperatures disappear. Finally, at both the isochore η = 0.6 (Path 3, Fig. 3(c)) and the isotherm T* = 1 (Path 4, Fig. 3(d)), g(r) presents the typical evolution in a dense liquid with short ranged repulsion.
2.3 Orientational dynamics
We now turn our discussion to the dynamics of the ODF. For this, we have considered a set of orientationally sensitive correlation functions, , with l = l′ > 0 and defined by eqn (11); and the angular mean squared deviations, Wθ(t) and Wsin
, with l = l′ > 0 and defined by eqn (11); and the angular mean squared deviations, Wθ(t) and Wsin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ(t), given by eqn (5) and (6). Let us mention in advance that both FS221 and FS222 provide essentially the same information as FS220. Hence, for simplicity, we will restrict ourselves to the analysis of ISFs of rank 1 ≤ l = l′ ≤ 2, and we specifically focus on the analysis of the correlation functions FS110(k,t), FS111(k,t), and FS220(k,t). As mentioned before, a similar behavior is encountered for Wθ(t) and Wsin
θ(t), given by eqn (5) and (6). Let us mention in advance that both FS221 and FS222 provide essentially the same information as FS220. Hence, for simplicity, we will restrict ourselves to the analysis of ISFs of rank 1 ≤ l = l′ ≤ 2, and we specifically focus on the analysis of the correlation functions FS110(k,t), FS111(k,t), and FS220(k,t). As mentioned before, a similar behavior is encountered for Wθ(t) and Wsin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ(t), so we only report the former.
θ(t), so we only report the former.
The results for the orientational ISFs along the three isochores previously considered (Paths 1, 2, 3), also evaluated at k* = 5.3, are summarized in Fig. 4. At either low (first column, Fig. 4(a), (d) and (g)) or intermediate concentration (middle column, Fig. 4(b), (e) and (h)) FS110, FS111, and FS220 display essentially the same relaxation patterns and become gradually slower with decreasing temperature. Remarkably, all the correlation functions also follow the same trends of FS along Paths 1 and 2, including their eventual arrest at T* = 0.05 (for clarity, the arrested behavior of FS is displayed again in Fig. 4(a)–(c) as the dashed lines). These features indicate a strong coupling in the dynamics of the TDF and ODF, thus evidencing their simultaneous arrest upon cooling.
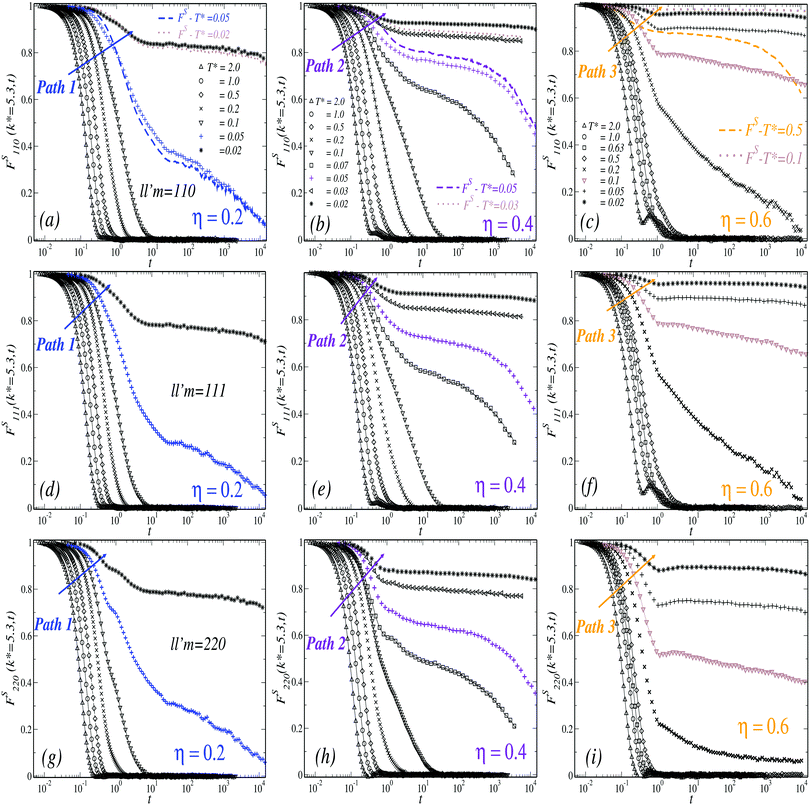 | ||
| Fig. 4 Time evolution of the correlation functions F110(k*,t), F111(k*,t) and F220(k*,t), evaluated at k* = 5.3, at three different concentrations η = 0.2 (a), (d) and (g), η = 0.4 (b), (e) and (h), η = 0.6 (c), (f) and (i), and at different temperatures (as indicated). For reference, the dashed lines in (a)–(c) illustrate the arrested behavior of FS(k,t) previously shown in Fig. 1. | ||
This is to be contrasted with the scenario observed for η = 0.6 (right column in Fig. 4). First, let us notice that the orientational ISFs remain ergodic (i.e., decay to zero) at T* = 0.5 (open diamonds in Fig. 4(c), (f) and (i)), whilst FS undergoes dynamical arrest (dashed line of Fig. 4(c)). Lowering the temperature to T* = 0.2, FS110 and FS111 develop transient plateaus, which hardly decay to zero in the time scale of the simulations, whereas FS220 develops a slightly different relaxation pattern characterized by a fast initial decay and followed by a stretched relaxation. These features indicate the existence of a transition to partially arrested states for the fluid, where the dynamics of the TDF undergoes a GT whereas the ODF remain ergodic. Furthermore, at T* = 0.1 the three correlation functions also become arrested (open down triangles), indicating another type of transition where the ODF may undergo a GT starting from a partially arrested state. Notice that this transition for the ODF occurs at a slightly higher temperature with respect to Paths 1 and 2.
The existence of partially arrested states is also illustrated by the results shown in Fig. 5 for the orientational ISFs along the isotherm T* = 1, where the three correlation functions remain ergodic and practically unaffected by increasing the concentration up to η = 0.7. This is in clear contrast with the behavior of FS, which hardly relaxes to zero for η = 0.65 and becomes arrested at η ≥ 0.7, as already shown in Fig. 1(d).
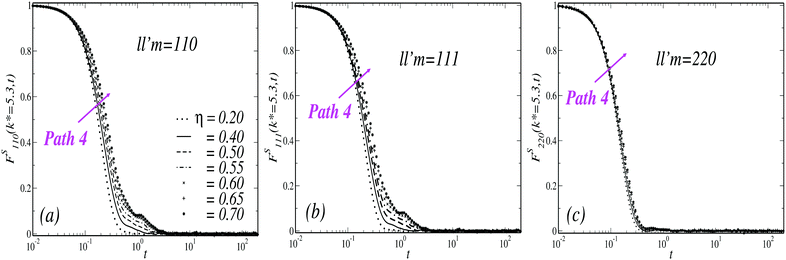 | ||
| Fig. 5 Time evolution of the correlation functions (a) F110(k*,t), (b) F111(k*,t) and (c) F220(k*,t) evaluated at k* = 5.3, along the isotherm T* = 1, for different concentrations (as indicated). | ||
The angular MSD, Wθ(t), describes consistently the same scenario for the arrest of the orientational dynamics. Along Paths 1 and 2 (Fig. 6(a) and (b), respectively) Wθ(t) reaches its ergodic saturation value within the range 0.1 ≤ T* ≤ 2. As it may be expected, the time elapsed to reach this limit becomes progressively larger with decreasing temperature. Below this range, Wθ(t) saturates to a smaller value, thus indicating arrest in the diffusion of the ODF. For the isochore η = 0.6, the angular MSD rapidly reaches the ergodic value for temperatures down to T* = 0.5. At T* = 0.2, however, this requires the whole time-window of the simulations. For even lower temperatures, within the same time window, Wθ(t) appears fully arrested. Finally, this observable remains unaffected at the isochore T* = 1.0 (Fig. 6(d)).
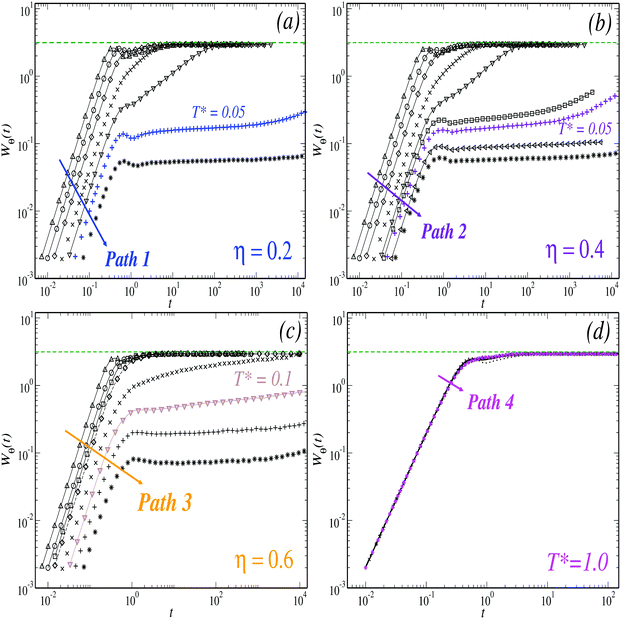 | ||
| Fig. 6 Behavior of the angular mean square displacement, Wθ(t), at the three isochores (a) η = 0.2, (b) η = 0.4 and (c) η = 0.6, for different temperatures; and for the isotherm (d) T* = 1.0 (symbols are used exactly as in Fig. 4 and 5 above to represent the state points). The (green) dashed horizontal lines indicate the ergodic long time value of Wθ and are used as guide to the eye. | ||
To summarize, the MD simulations exhibit three different scenarios for dynamical arrest in the model. The first was observed to occur at low and intermediate concentrations upon lowering the temperature, and is mainly characterized by the simultaneous arrest of the TDF and ODF, with both dynamics being strongly coupled. The critical temperature of this transition does not vary significantly with η, but a qualitative evolution of the structural behavior (signaled by the radial distribution function, g(r)) and a small reduction of the localization length with increasing η are observed. A second scenario is observed at high densities and high-to-intermediate temperatures, where only the dynamics of the TDF undergoes arrest whilst the ODF remain ergodic. This indicates the possibility of partially arrested states to occur, either through an isochorical drop in temperature, or an isothermal compression. This transition presents the features of the GT in dense HS fluids such as a remarkable increase of the relaxation time upon small increments in density (with only moderate changes in the structural behavior) and a typical localization length of l ∼ 0.1σave. Finally, a third possibility involves the arrest of the orientational dynamics by cooling down the system from a partially arrested state. This was observed to occur at temperatures only slightly higher with respect to those describing simultaneous arrest and is accompanied by a significant reduction of the localization length of the particles.
3 Theoretical development
To provide a more comprehensive picture of the dynamical arrest transitions of a dipolar fluid, we now consider the SCGLE theory.40 Specifically, we use this theoretical framework to obtain the GT lines in the parameters space of the simulated system, leading to the development of an arrested states diagram which identifies the regions of the (η,T*)-plane where the system remains ergodic, the regions where it becomes dynamically arrested and the boundaries between such regions. This kinetic arrest diagram complements the usual equilibrium phase diagram.20–22 As we show in what follows, the physical scenario outlined by the SCGLE describes consistently the main features of dynamical arrest observed in the simulations, despite the various approximations considered in the theoretical development, and organizes qualitatively the different state points and paths studied with MD, thus providing mutual support between the results of the two independent approaches.The use of the SCGLE for this purpose is particularly helpful because a precise determination of GT points from simulations is notoriously difficult. As one approaches a transition, one typically encounters severe instabilities and very slow dynamics that may present a strong history dependence, and both render the required computational time excessively large. Furthermore, the common protocols to estimate GT points in simulations are normally based on extrapolations of either the divergence of the relaxation time of the ISFs or the diffusion coefficients, and are therefore prone to errors, since this intrinsically involves a large uncertainty in the choice of the specific extrapolation function and the fit range.
3.1 Non-ergodicity parameters (NEPS) and arrested states diagram
We briefly recall some technical aspects regarding the determination of GT lines within the SCGLE (for more details the reader is referred to Appendix C and ref. 40). The theory provides equations describing the wave-vector dependence and time evolution of the diagonal (l = l′) ISFs, Fll′m(k,t)δll′ ≡ Flm(k,t), and their corresponding self counterparts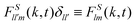 . Within well defined approximations,40 these equations involve the two memory friction functions ΔζT*(t) and ΔζR*(t), which characterize, respectively, the translational and rotational diffusion of a tracer particle.55 In turn, the functions Δζα*(t) (α = T, R) can be written as functionals of Flm(k,t) and FSlm(k,t), thus defining a self-consistent system of equations for both the ISFs and the memory functions. These are eqn (31)–(34) of Appendix C.
. Within well defined approximations,40 these equations involve the two memory friction functions ΔζT*(t) and ΔζR*(t), which characterize, respectively, the translational and rotational diffusion of a tracer particle.55 In turn, the functions Δζα*(t) (α = T, R) can be written as functionals of Flm(k,t) and FSlm(k,t), thus defining a self-consistent system of equations for both the ISFs and the memory functions. These are eqn (31)–(34) of Appendix C.
Close to conditions of dynamical arrest, a generic asymptotic solution can be derived, leading to a closed set of equations for the non-decaying k-components of both Flm(k,t) and FSlm(k,t), commonly referred to as non-ergodicity parameters (NEPs), and defined as limt→∞Flm(k,t)/Flm(k,t = 0) ≡ flm(k) and limt→∞FSlm(k,t) ≡ fSlm(k). This solution also provides the asymptotic long-time behavior of the aforementioned memory friction functions, allowing to define the two dynamic order parameters γα ≡ D0α/limt→∞Δζα*(t), α = T, R. The quantity γT, in particular, is related to the long-time limit of the translational MSD, limt→∞WT(t). The SCGLE equations for the NEPs are summarized by eqn (38)–(42) (see Appendix C).
In terms of these quantities, fully ergodic (fluid) states are described by the condition that all the NEPs are equal to zero. Any other solution indicates loss of ergodicity (i.e., dynamical arrest) in one or both degrees of freedom. For instance, the conditions f00(k) ≠ 0, fS00(k) ≠ 0, γT−1 ≠ 0, along with flm(k) = fSlm(k) = 0 (for l ≥ 1, m = −l,…,0,…,l) and γR−1 = 0 describe partially arrested states, where only the TDF undergo a GT, whereas the dynamics of the ODF remains ergodic. Similarly, the condition that all the NEPs are simultaneously different from zero describes arrest in both degrees of freedom, i.e., fully arrested states.
To solve eqn (38)–(42) one requires the previous determination of the diagonal elements, Slm(k), of the spherical harmonics expansion of the static structure factor (SSF) S(k,μ,μ′), at each state point of the parameters space (notice that Sll′m(k) = Fll′m(k, t = 0) and Sll′m(k)δll′ ≡ (Slm(k))). In general, this might pose a non-trivial problem on its own. To simplify the theoretical calculations as much as possible, we have approximated the Slm(k) components of the simulated model system by a softened-core version of Wertheim's solution for the mean spherical approximation (MSA) of a dipolar hard-sphere fluid (DHS).41 The specific details of this procedure are provided in Appendix B along with a comparison against MD results for these quantities (see Fig. 10), however, it is worth to stress that, within this approximation, the only non-zero components of the SSF are the elements S00(k), S10(k) and S11(k). This, in turn, imposes a cutoff for the indexes l and m of the NEPs, where the remaining terms are f00(k), f10(k), f11(k), fS00(k) and fS10(k) = fS11(k).
For the numerical calculation of the NEPs, we discretize wavenumber integrals (eqn (41) and (42)) by an equidistant grid of M = 213 points. An implied large-k cutoff K = 50k* was selected to be reasonably large to not affect our results qualitatively, thus giving a grid spacing 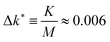 . To obtain the NEPs we proceed as follows: first, we solve eqn (41) and (42) for the two order parameters, γT and γR, using a standard iterative scheme at each state point of the states space. We typically demand a numerical precision of 10−7 in the determination of the finite values for γT and γR. Notice that, according to eqn (38) and (39), this implicitly determines the remaining NEPs.
. To obtain the NEPs we proceed as follows: first, we solve eqn (41) and (42) for the two order parameters, γT and γR, using a standard iterative scheme at each state point of the states space. We typically demand a numerical precision of 10−7 in the determination of the finite values for γT and γR. Notice that, according to eqn (38) and (39), this implicitly determines the remaining NEPs.
This procedure leads to the identification of three kinetically different regions separated by three distinct transition lines. Our results are summarized in Fig. 7, where we also show the location of the state points and paths investigated via MD. Based on the theory, the (η,T*)-space can be partitioned as follows: a fluid region (I), where the dynamics of both TDF and ODF remain ergodic (i.e., f00(k) = f10(k) = f11(k) = 0,fS00(k) = fS10(k) = 0, and γT−1 = γR−1 = 0). This region is delimited by two different boundaries. One of these boundaries (black solid line) describes the transitions to fully arrested states (II), where all the NEPs become finite simultaneously, so both degrees of freedom are dynamically arrested. The second boundary (blue dashed-pointed line), instead, describes the transitions to partially arrested states (III), where only the TDF dynamics undergo arrest (f00(k) ≠ 0, fS00(k) ≠ 0 and γT-finite, as indicated above) whereas the ODF remain ergodic (i.e., f10(k) = f11(k) = fS10 = 0 and γR−1 = 0). Furthermore, a third line (red dashed) separates regions II and III, where the flm(k), fSlm(k) (l = 1, m = 0, 1) and γR−1 become finite, thus describing the arrest of the ODF under the condition that the TDF were previously arrested.
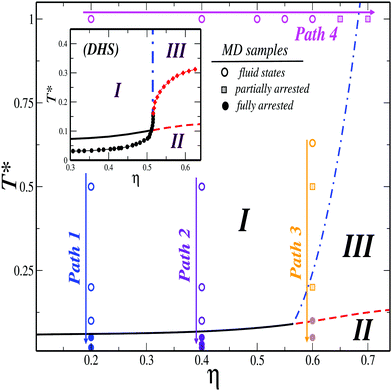 | ||
| Fig. 7 State diagram of the dipolar fluid. The different symbols and arrows denote, respectively, the state points and paths studied via MD simulations. Open circles are used to represent the ergodic samples, half-filled circles describe samples where partially arrested states are observed, solid circles account for full arrest. The lines delimiting regions I, II and III are predictions of the SCGLE for three distinct GT lines using the approximation described in Appendix B for the static structure factor projections, Slm(k). Inset: Results of the SCGLE (lines) and MCT (solid symbols) for the GTs of a DHS fluid reported, respectively, in ref. 40 and 39. | ||
The I → II transition line represents the behavior of the critical temperature, 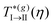 , as a function of the volume fraction, and as predicted by the SCGLE. It describes a monotonically (and very slowly) increasing function of η and, noticeably,
, as a function of the volume fraction, and as predicted by the SCGLE. It describes a monotonically (and very slowly) increasing function of η and, noticeably, 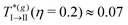 and
and 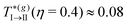 , which is in remarkable agreement with our previous findings with MD along Paths 1 and 2. The theory also predicts that this line bifurcates into two distinct lines upon increasing the concentration (η ≈ 0.57). The branch describing the I → III transition shows that the critical temperature
, which is in remarkable agreement with our previous findings with MD along Paths 1 and 2. The theory also predicts that this line bifurcates into two distinct lines upon increasing the concentration (η ≈ 0.57). The branch describing the I → III transition shows that the critical temperature 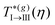 increases significantly with small increments in η. This implies strong effects of crowding in the slowing down of the translational motion, leading to the decoupling of the orientational dynamics, and indicates that the localization of particles is due to caging. These features are consistent with the scenario outlined by the simulations along Paths 3 and 4, although some small differences are observed. For example, the theory seems to slightly overestimate the critical volume fraction of the bifurcation point and the locus of the I → III transition line. This may be attributed to deviations of the simplified model assumed in the theory from the simulated system, and also to the approximations made to determine the structure factor projections, Slm(k). Nevertheless, the overall physical scenario is qualitatively the same.
increases significantly with small increments in η. This implies strong effects of crowding in the slowing down of the translational motion, leading to the decoupling of the orientational dynamics, and indicates that the localization of particles is due to caging. These features are consistent with the scenario outlined by the simulations along Paths 3 and 4, although some small differences are observed. For example, the theory seems to slightly overestimate the critical volume fraction of the bifurcation point and the locus of the I → III transition line. This may be attributed to deviations of the simplified model assumed in the theory from the simulated system, and also to the approximations made to determine the structure factor projections, Slm(k). Nevertheless, the overall physical scenario is qualitatively the same.
Starting from a state point inside the partially arrested region III and decreasing the temperature, one eventually crosses the III → II transition line, below which the orientational dynamics of the positionally-frozen dipoles also becomes arrested. Hence, this line describes a scenario similar to a spin glass-like transition. Notice that the critical temperature 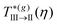 appears almost independent on η and satisfies
appears almost independent on η and satisfies 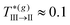 , a value in good quantitative agreement with the simulation results for Path 3. Furthermore, the results of MD for the MSD along this path (Fig. 2(c)) showed how the localization length, l(η = 0.6,T*), first becomes of order l ≈ 0.1σave, crossing the I → III transition (which is indicative of a HS-like glass transition for the TDF), and that a further decrease in temperature leads to a noticeable reduction of this quantity approaching the III → II transition. As mentioned above, this is the typical signature of the passage from caging to bonding in the localization of the particles, and both SCGLE and MD describe consistently this scenario, as we show further below (see Fig. 9).
, a value in good quantitative agreement with the simulation results for Path 3. Furthermore, the results of MD for the MSD along this path (Fig. 2(c)) showed how the localization length, l(η = 0.6,T*), first becomes of order l ≈ 0.1σave, crossing the I → III transition (which is indicative of a HS-like glass transition for the TDF), and that a further decrease in temperature leads to a noticeable reduction of this quantity approaching the III → II transition. As mentioned above, this is the typical signature of the passage from caging to bonding in the localization of the particles, and both SCGLE and MD describe consistently this scenario, as we show further below (see Fig. 9).
Before discussing the k-dependence of the NEPs, let us compare the arrested states diagram just presented against similar predictions of both SCGLE and MCT corresponding to a DHS model,39,40i.e., a system where the short-ranged and purely repulsive contribution to the potential is represented by a discontinuous (athermal) HS potential, and not by the soft (thermal) WCA interaction considered in both theory and simulations in this work. This is shown in the inset of Fig. 7. Qualitatively, both theories provide the same prediction, namely, that the parameter space can be partitioned in the same three distinct regions. Only minor (and rather irrelevant) differences are observed between the diagrams provided by both theories for the DHS system, and they concern to the specific location of the I → II transition line (black solid for SCGLE, black circles for MCT) and of the III → II one (red dotted line for SCGLE, red diamonds for MCT), as well as the locus of the point at which all the transition lines meet. The topology of these two diagrams, however, is identical. More crucially, such topology also coincides with that predicted by the SCGLE for the Stockmayer fluid considered in the simulations. The vertical (blue dashed-dotted) line in the inset of Fig. 7 describing the I → III transition coincides in both theories upon a tuning of the only free parameter of the SCGLE. We refer to the a-parameter used in the cutoff wavevector of the SCGLE approximation for the translational irreducible memory kernel (see Appendix C). In general, the theory allows flexibility in the choice of this parameter, and this can be chosen in order to fine-tune a comparison between the SCGLE and both simulations or MCT. We found that the value a = 1.3 represents a good compromise for the comparison with simulations, whereas a = 1.941 was used for the comparison against MCT.40
Thus, the main difference between the diagrams for soft and hard-core only refers to the slope of the I–III transition line. In the case of the DHS model, this is described by a vertical line at η(g)DHS ≈ 0.52, which results from the athermal nature of the discontinuous HS potential and, consequently, of the I–III transition. The fact that the topology of the three diagrams presented in Fig. 7 is identical, along with the consistency between the results provided by both SCGLE and MD for the dynamical arrest transitions of the Stockmayer fluid, allow us to reach an important observation. In the model considered for the theory, forces and torques are described by a genuine dipole–dipole potential (see Appendix B), that is, one considers a r−3 contribution in all the space. In the simulated system, in contrast, we have truncated this interaction for simplicity. This suggests that the topology of the dynamical arrest diagram of a dipolar fluid is essentially determined by the anisotropy of the dipolar tensor D(rab,![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) a,
a,![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) b) ≡
b) ≡ ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) a·
a·![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) b − 3(
b − 3(![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) a·
a·![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ab)(
ab)(![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) b·
b·![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ab) (see eqn (3) above), but not by the long-range behavior of the pair potential. This provides support to the systematic use of truncated anisotropic potentials for the study of glassy behavior in dipolar systems which, as mentioned before, simplifies considerably the simulations, since one avoids the specialized treatment of long-ranged forces and torques.
ab) (see eqn (3) above), but not by the long-range behavior of the pair potential. This provides support to the systematic use of truncated anisotropic potentials for the study of glassy behavior in dipolar systems which, as mentioned before, simplifies considerably the simulations, since one avoids the specialized treatment of long-ranged forces and torques.
We now turn the discussion to the NEPs. Fig. 8(a)–(c) show the k-dependence of the functions f00(k), f10(k) and f11(k), respectively, as predicted by the SCGLE at the intersections of each of the paths considered in MD with the distinct transition lines. At the crossing point of Path 1 (η = 0.2) with the I → II transition, f00(k) describes a monotonic decaying function of k, related to very small variations in the corresponding structure factor, S00(k) (Fig. 8(d)). Upon increasing the concentration to Path 2 (η = 0.4), f00(k) develops oscillations that are roughly in phase with the corresponding S00(k). Thus, and despite one crosses the same transition line, the behavior of both f00(k) and S00(k) along Path 2 is indicative of medium-range order induced by the short ranged repulsion which becomes more predominant with increasing density. Notice that this is also in agreement with the scenario provided by MD in terms of g(r), as shown in Fig. 3(a) and (b). Crossing the I → III transition line, either along Path 3 or 4, one finds essentially the same behavior for f00(k), where the modulations of the static structure factor become more noticeable. Finally, following Path 3 towards the III → II transition, one observes the emergence of larger values for f00(k) in comparison to the previous cases, along with a larger spectrum of non-decaying components which exceed the limit of the k-window considered. This feature is indicative of arrest in the collective dynamics at smaller length scales.
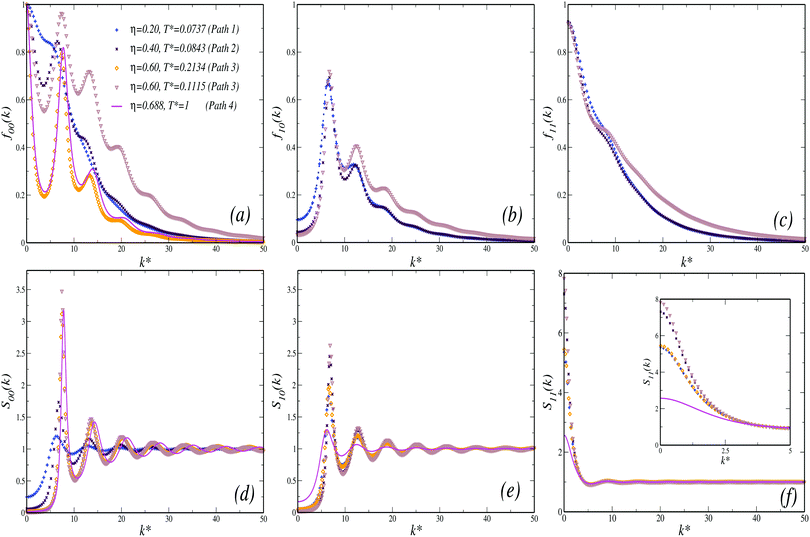 | ||
| Fig. 8 Upper panels: Wave vector dependence (in units of k* = kσave) of the collective non-ergodicity parameters (a) f00(k), (b) f10(k) and (c) f11(k), evaluated at the intersections of the four Paths considered in MD with the transition lines shown in Fig. 7 (as indicated) and as predicted by the SCGLE. Lower panels: corresponding spherical harmonics projections (d) S00(k), (e) S10(k) and (f) S11(k) as provided by the approximation discussed in Appendix B. Inset in (f) shows a zoom of the low-k* region. | ||
Unlike f00(k), the NEPs f10(k) and f11(k) display essentially the same k-dependence at all the relevant crossing points, as shown in Fig. 8(b) and (c), respectively (notice that both NEPs remain zero at the I → III transition). For f10(k), oscillations inherited from the corresponding static structure factor projection, S10(k), appear but, differently from f00(k), one finds small values of this NEP for k → 0. This is to be contrasted against the behavior of f11(k), which describes a monotonically decreasing function of k, similar to the static structure component S11(k), and both showing a large signal at low k. Both parameters emphasize thus the strong coupling between the dynamics of the TDF and ODF along the I → II and III → II transitions and the decoupling of the dynamics at the I → III transition line.
We finally consider the NEPs associated to the self dynamics. In principle, this can be done in terms of the k dependence of the functions fS00(k) and fS10(k) = fS11(k) at the crossing points. In general, the typical behavior found for fS00(k) is that of a monotonically decaying function of k that interpolates through the oscillations of f00(k), and the width of the fS00(k)-vs.-k curve provides an estimation of the localization length. However, the SCGLE already provides an equation for l(η,T*) (eqn (41)), allowing for a more efficient and direct comparison against the results from simulations (recall that the quantities FS000(k,t) and WT(t) are intimately related in the k → 0 limit). In Fig. 9 we display the behavior of l(η(g),T*(g)), calculated along the three distinct transition lines, and as predicted by the SCGLE. According to the theory, along the I → II (solid) line the localization length of a tracer particle becomes progressively smaller with increasing density. At the bifurcation point (η ≈ 0.57), this quantity shows distinct behavior depending on the branch considered. For instance, following the III → II transition line (dashed), l(η(g),T*(g)) continues decreasing with η, whereas along the I → III (pointed-dashed) line the localization length discontinuously jumps to values ∼10−1 and remains constant, thus indicating a characteristic cage size of approximately 10% the size of the particles, a well known feature of a HS glass (sometimes referred to as the Lindemann criterion for melting). In the same figure we also show estimates for the same quantity, extracted from MD simulations as 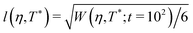 at the points previously identified as dynamically arrested in Fig. 2. Despite the quantitative differences found between simulations and theory (the latter tends to underestimate the value of the localization length provided by MD), these results are in good overall agreement.
at the points previously identified as dynamically arrested in Fig. 2. Despite the quantitative differences found between simulations and theory (the latter tends to underestimate the value of the localization length provided by MD), these results are in good overall agreement.
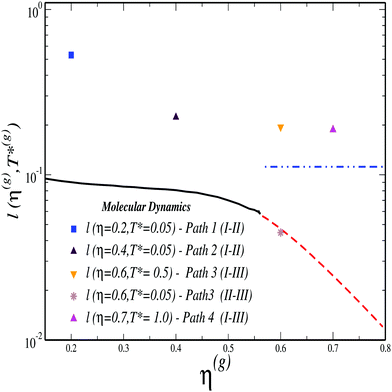 | ||
Fig. 9 Localization length, l(η(g),T*(g)), calculated at the transition lines of Fig. 7 as predicted by the SCGLE (solid, dashed and pointed-dashed lines). Symbols represent estimates for the same quantity obtained from the results of Fig. 2 as 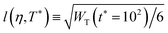 at state points close to each transition studied (as indicated). at state points close to each transition studied (as indicated). | ||
4 Conclusions
Molecular dynamics simulations and theoretical calculations were combined to investigate the glassy behavior and different non-equilibrium phases and transitions in a dipolar fluid. The system was modeled as a collection of N spherical particles interacting via a soft-repulsive potential coated with an anisotropic contribution that retains the directional features of the dipole–dipole forces, but which neglects its long-ranged character. This is a reasonable approximation for dipolar colloids suspended in highly dielectric solvents. An advantage of this modeling procedure is that the simulations are not too computationally exhaustive.We have studied the dynamics associated to the translational and orientational degrees of freedom, at different regions of the parameter space of the system, and considering distinct pathways to dynamical arrest. The detailed analysis of several correlation functions and of two types of mean square deviations along the distinct paths, provided evidence of the occurrence of three types of dynamical arrest transitions in a dipolar fluid.
At small and intermediate volume fractions, one observes the simultaneous arrest of the dynamics of both degrees of freedom on cooling, occurring at a critical temperature T(g)I→II ≈ 0.05. Despite some qualitative changes observed in the structure of the simulated system, this transition seems to not depend crucially on the concentration. Both simulations and theory support this interpretation. At high concentration, instead, a bifurcation scenario for the glass transition is found. In this regime, a decoupling in the dynamics of each degree of freedom leads to another type of transition describing partially arrested states, where only the translational motion becomes arrested, but with the orientations remaining ergodic. In this regard, it is also important to notice that neither in the simulations nor in the theory we observed any hint of the other possible mixed state, in which the translational motion remains ergodic, but with the orientations become arrested. Finally, a third kind of transition can be reached starting from a partially arrested state and decreasing the temperature, with the orientational correlations displaying arrest under the condition that the translational dynamics was already arrested.
The physical scenario outlined by the simulations is qualitatively (and semi quantitatively) consistent with the results of the SCGLE theory. The latter, however, allows us to develop a more generic description of dynamical arrest in the dipolar fluid. This was conveniently summarized in an arrested states diagram, which results topologically identical to that of a dipolar hard sphere fluid, where different short and long-range interactions are considered. This indicates that our results may be generic to systems with competing dynamics arising from dipolar anisotropic forces and torques. These observations could also be relevant for the understanding of glassy dynamics in a wider range of colloidal systems dealing with higher order multipolar contributions (for instance, quadrupolar moments) or more complicated interactions (Janus particles).
Let us also mention that the present work is also an essential and unavoidable first step in a more ambitious program towards a deeper study of the non-equilibrium and nonstationary phenomena, such as the kinetics of the aging associated with these transitions. As it happens, the SCGLE formalism has recently been extended to describe non-stationary non-equilibrium structural relaxation processes, such as aging or the dependence of the dynamical and structural properties on the protocol of fabrication, in liquids constituted by particles interacting through non spherical potentials.56 The resulting non-equilibrium self-consistent generalized Langevin equation theory (NE-SCGLE), aimed at describing non-equilibrium phenomena in general, leads in particular to a simple and intuitive (but still generic) description of the essential behavior of glass-forming dipolar liquids near and beyond its dynamical arrest transitions. This renders the description of the nonequilibrium processes occurring in a colloidal dispersion after an instantaneous temperature quench possible, with the most interesting prediction being the aging processes occurring when full equilibration is prevented by conditions of dynamical arrest. In this regard, the development of the arrest diagram presented in this contribution, and its validation by independent results obtained with the assistance molecular dynamics simulations constitutes a crucial step in developing a full description of dynamical arrest in dipolar liquids.
In addition, previous applications of the NE-SCGLE for spherically symmetric potentials, and more concretely, for the case of attractive potentials, have shown the ability of this non equilibrium theory to describe the main fingerprints of the formation of gel states by the process of arrested spinodal decomposition.57 Thus we expect that the extension carried out in ref. 56, along with the results presented in this contribution, would provide the main elements to attempt a thorough characterization of the complex interplay between phase separation and dynamical arrest towards the gel transition in dipolar colloidal suspensions.
Finally, we also expect that the results of this work might serve to locate and reinterpret previous results dealing with both equilibrium and arrested dynamics in dipolar fluids, and as a benchmark for future tests in similar models with competitive dynamics arising from distinct degrees of freedom. The information provided in this work might be also relevant for the rational design of technologically important materials based in ferrofluids, considering dipolar systems as prototypical models.
Conflicts of interest
There are no conflicts to declare.Appendix A: mean square deviations and rotational diffusion coefficients
To extract rotational diffusion coefficients from saturating MSDs one can start with the solution of Fick's equation for the orientational microscopic density, ρ(θ,ϕ,t), on a spherical surface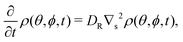 | (12) |
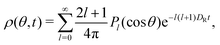 | (13) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) being Legendre polynomials. Using this solution, one can calculate the mean square deviation in the polar angle, Wθ(t) ≡ 〈θ2(t)〉, via integration
θ) being Legendre polynomials. Using this solution, one can calculate the mean square deviation in the polar angle, Wθ(t) ≡ 〈θ2(t)〉, via integration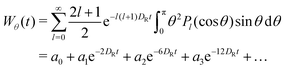 | (14) |
| log(a0 − Wθ(t)) = log|a1| − 2DRt + log(1 + b2e−4DRt +…), | (15) |
| log(a0 − Wθ(t)) ≈ const. − 2DRt. | (16) |
Using the orthogonality of the Legendre polynomials, Perrin also found a closed form for Wsin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ(t) ≡ 〈sin2
θ(t) ≡ 〈sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ(t)〉, which reads
θ(t)〉, which reads
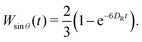 | (17) |
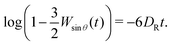 | (18) |
B Determination of the static structure factor projections for a dipolar soft sphere fluid
B.1 Mean spherical approximation for a soft-core dipolar fluid
The solution of the equations for the non-ergodicity parameters (eqn (31)–(34) and (41), (42) below) requires the previous determination of the spherical harmonics projections, Slm(k), of the static structure factor, or equivalently, the projections, clm(k), of the direct correlation function. Both quantities are related through the Ornstein–Zernike (OZ) equation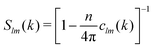 .
.
For this, one starts by identifying the system of interest, which thus require the specific form of the two-particle potential of interaction, Uab(rab,![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) a,
a,![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) b). To represent the simulated system, such pairwise potential should possess the generic form (see eqn (1))
b). To represent the simulated system, such pairwise potential should possess the generic form (see eqn (1))
Uab(rab,![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) a, a,![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) b) = UabREP(rab) + UabDIP(rab, b) = UabREP(rab) + UabDIP(rab,![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) a, a,![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) b), b), | (19) |
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) a,
a,![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) b) an anisotropic dipolar contribution. This generic representation includes as a particular case the dipolar hard-sphere model (DHS), where UabREP is given by the discontinuous hard-sphere potential and UabDIP by the dipole–dipole potential, but it also includes other possible systems. For instance, under some circumstances it may be necessary to consider some degree of softness in the purely repulsive part, just as it happens in the case of the Stockmayer potential,59 which replaces UabREP by a Lennard-Jones potential. In general, any such departure from the DHS reference potential will destroy the analytical convenience provided by the solution of Wertheim for the Mean Spherical Approximation (MSA),41 which renders the calculation of the functions clm(k) straightforward.
b) an anisotropic dipolar contribution. This generic representation includes as a particular case the dipolar hard-sphere model (DHS), where UabREP is given by the discontinuous hard-sphere potential and UabDIP by the dipole–dipole potential, but it also includes other possible systems. For instance, under some circumstances it may be necessary to consider some degree of softness in the purely repulsive part, just as it happens in the case of the Stockmayer potential,59 which replaces UabREP by a Lennard-Jones potential. In general, any such departure from the DHS reference potential will destroy the analytical convenience provided by the solution of Wertheim for the Mean Spherical Approximation (MSA),41 which renders the calculation of the functions clm(k) straightforward.
A simplified version of the Stockmayer potential that allows to exploit the analytical simplicity of Wertheim's solution consists in replacing UabREP by the WCA potential of eqn (2). In this manner, the generic potential given by eqn (19) can be written as the following soft-sphere dipolar potential
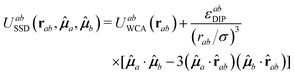 | (20) |
In the spirit of the WCA treatment of soft-core interactions,60 we may assume that the properties of the soft-core dipolar potential of eqn (20) can be approximated by those of an effective DHS potential UeffDHS(rab,![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) a,
a,![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) b) with a state-dependent effective diameter σeff(n,T), i.e., by a system with a potential of interaction
b) with a state-dependent effective diameter σeff(n,T), i.e., by a system with a potential of interaction
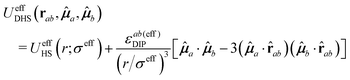 | (21) |
Therefore, within these assumptions, the direct correlation function cSSD(rab,![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) a,
a,![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) b;n,T) of a soft dipolar system with a potential defined by eqn (20) can be approximated by the direct correlation function of an effective DHS system, ceffDHS(rab,
b;n,T) of a soft dipolar system with a potential defined by eqn (20) can be approximated by the direct correlation function of an effective DHS system, ceffDHS(rab,![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) a,
a,![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) b;n,T). In dimensionless units, this approximation reads
b;n,T). In dimensionless units, this approximation reads
cSSD(r/σ,![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) 1, 1,![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) 2;n*,T*) ≈ cDHS(r/λσ, 2;n*,T*) ≈ cDHS(r/λσ,![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) 1, 1,![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) 2;λ3n*,λ−3T*). 2;λ3n*,λ−3T*). | (22) |
Within the MSA, the explicit form of the dipolar potential indicates that the only non-zero spherical harmonics projections, cll′m(k), of the Fourier transform of the direct correlation function are the digonal components c000(k) ≡ c00(k), c110(k) ≡ c10(k), c111(k) ≡ c11(k). This, in turn, imposes a cut off in the indexes l and m of the non-ergodicity parameters provided by the SCGLE.
B.2 Static structure factor components Slm(k): comparison between MSA and simulations
To assess the accuracy of the soft-cored MSA approach discussed above, we have also determined spherical harmonics projections of the static structure factor (SSF), S(k,![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) ,
,![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) ′), from simulations. For the sake of clarity, let us denote such projections as
′), from simulations. For the sake of clarity, let us denote such projections as 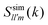 in order to distinguish them from those provided by MSA, hereafter denoted as
in order to distinguish them from those provided by MSA, hereafter denoted as 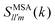 .
.
In general, one has to be careful in the choice of a reference system for the spherical harmonics expansion of the SSF. In Wertheim's theory, the functions 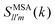 are obtained in the so called k-frame, whereas, for technical convenience, the functions
are obtained in the so called k-frame, whereas, for technical convenience, the functions 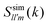 defined below were calculated from simulation configurations described in an intermolecular frame. In essence, in the k-frame description, one chooses the direction
defined below were calculated from simulation configurations described in an intermolecular frame. In essence, in the k-frame description, one chooses the direction ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) k of the wave vector k = k
k of the wave vector k = k![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) k as the polar axis to refer both rotations and orientations (see for instance ref. 39 and 41). This reference system is useful to simplify many theoretical calculations and allows to easily determine self dynamical properties in simulations. However, it is difficult to implement in simulations to calculate collective properties (structural and dynamical). Thus, for the functions
k as the polar axis to refer both rotations and orientations (see for instance ref. 39 and 41). This reference system is useful to simplify many theoretical calculations and allows to easily determine self dynamical properties in simulations. However, it is difficult to implement in simulations to calculate collective properties (structural and dynamical). Thus, for the functions 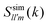 we have considered the intermolecular frame, where the vector rab ≡ ra − rb is chosen as the polar axis.
we have considered the intermolecular frame, where the vector rab ≡ ra − rb is chosen as the polar axis.
Let us now summarize the procedure to compare results from Wertheim's theory and simulations. MSA only provides the isotropic projections of the SSF, such that
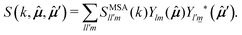 | (23) |
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) ,
,![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) ′), however, can also be generically written as a spherical harmonics expansion in the intermolecular frame. Such expansion reads (see eqn (3.B9) of ref. 42)
′), however, can also be generically written as a spherical harmonics expansion in the intermolecular frame. Such expansion reads (see eqn (3.B9) of ref. 42)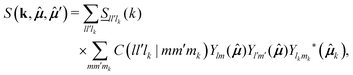 | (24) |
![[S with combining low line]](https://www.rsc.org/images/entities/i_char_0053_0332.gif) ll′lk(k) are determined from S(k,
ll′lk(k) are determined from S(k,![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) ,
,![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) ′) ≡ 〈ρ(k,
′) ≡ 〈ρ(k,![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) ;t = 0)ρ*(
;t = 0)ρ*(![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) ;t = 0)〉, with ρ(k,
;t = 0)〉, with ρ(k,![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) ;t = 0) being the t = 0 value of the Fourier transform of the microscopic density defined in eqn (7). A straightforward calculation leads to
;t = 0) being the t = 0 value of the Fourier transform of the microscopic density defined in eqn (7). A straightforward calculation leads to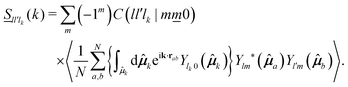 | (25) |
In general, the coefficients ![[S with combining low line]](https://www.rsc.org/images/entities/i_char_0053_0332.gif) ll′lk(k) of the spherical harmonics expansion in the intermolecular frame are related to those of the k-frame via the relation42
ll′lk(k) of the spherical harmonics expansion in the intermolecular frame are related to those of the k-frame via the relation42
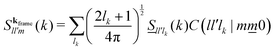 | (26) |
Conversely, if the 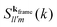 functions are known, the functions
functions are known, the functions ![[S with combining low line]](https://www.rsc.org/images/entities/i_char_0053_0332.gif) ll′lk(k) can be determined via
ll′lk(k) can be determined via
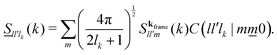 | (27) |
In order to compare against MSA results, in the simulations we have only considered isotropic contributions of the form
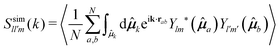 | (28) |
![[m with combining low line]](https://www.rsc.org/images/entities/i_char_006d_0332.gif) 0) (that needs to be considered in the summation on the index m in eqn (25)), corresponds to terms of order lk = 0 in (25). More specifically, one gets
0) (that needs to be considered in the summation on the index m in eqn (25)), corresponds to terms of order lk = 0 in (25). More specifically, one gets | (29) |
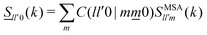 | (30) |
Therefore, a comparison between MSA and MD results can be performed in terms of the expansion coefficients ![[S with combining low line]](https://www.rsc.org/images/entities/i_char_0053_0332.gif) 000(k) and
000(k) and ![[S with combining low line]](https://www.rsc.org/images/entities/i_char_0053_0332.gif) 110(k). Fig. 10 displays the results obtained for these functions calculated at distinct state points. From eqn (25) one sees that the function
110(k). Fig. 10 displays the results obtained for these functions calculated at distinct state points. From eqn (25) one sees that the function ![[S with combining low line]](https://www.rsc.org/images/entities/i_char_0053_0332.gif) 000(k) corresponds to the standard definition of the SSF, S(k), in systems with spherically symmetric interactions. Of course, for l = l′ = 0, the choice of a reference frame is irrelevant. At low density, only a diffuse peak appears in
000(k) corresponds to the standard definition of the SSF, S(k), in systems with spherically symmetric interactions. Of course, for l = l′ = 0, the choice of a reference frame is irrelevant. At low density, only a diffuse peak appears in ![[S with combining low line]](https://www.rsc.org/images/entities/i_char_0053_0332.gif) 000(k) at k* ≈ 7, beyond which this function attains its asymptotic unit value. As expected, such peak becomes noticeable higher with increasing density, and oscillations appear signaling medium range order. The overall behavior of this function, as provided by MD (empty circles), is well captured by the soft-cored MSA (solid lines), only with some small differences. The most relevant are the exact position of the main peak, k000max (which MSA seems to slightly overestimate), and the k → 0 value (only slightly underestimated by our approximation).
000(k) at k* ≈ 7, beyond which this function attains its asymptotic unit value. As expected, such peak becomes noticeable higher with increasing density, and oscillations appear signaling medium range order. The overall behavior of this function, as provided by MD (empty circles), is well captured by the soft-cored MSA (solid lines), only with some small differences. The most relevant are the exact position of the main peak, k000max (which MSA seems to slightly overestimate), and the k → 0 value (only slightly underestimated by our approximation).
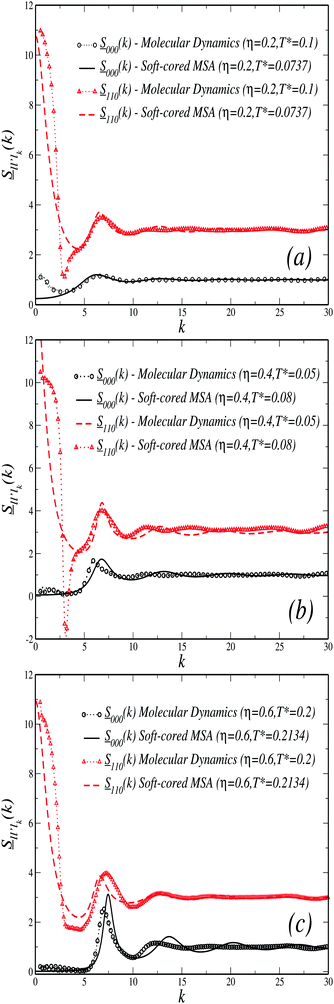 | ||
Fig. 10 Static structure factor coefficients ![[S with combining low line]](https://www.rsc.org/images/entities/i_char_0053_0332.gif) 00lk=0(k) and 00lk=0(k) and ![[S with combining low line]](https://www.rsc.org/images/entities/i_char_0053_0332.gif) 11lk=0(k) as a function of the scaled wave vector number, k*, provided by MD simulations (symbols, eqn (29) and the soft-cored MSA (lines, eqn (30)) at different state points (as indicated) close to the GT). 11lk=0(k) as a function of the scaled wave vector number, k*, provided by MD simulations (symbols, eqn (29) and the soft-cored MSA (lines, eqn (30)) at different state points (as indicated) close to the GT). | ||
For the function ![[S with combining low line]](https://www.rsc.org/images/entities/i_char_0053_0332.gif) 111(k) the overall behavior is also very similar in MD and MSA, with only small deviations for one of the state points considered. Since this projection is in reality a superposition of the functions S110(k), S111(k) and S11−1(k), calculated in each reference frame, they account for the influence of the orientational degrees of freedom in the structure of the system. The physical interpretation of this function, however, is subtle and, consequently, beyond the scope of the present work.
111(k) the overall behavior is also very similar in MD and MSA, with only small deviations for one of the state points considered. Since this projection is in reality a superposition of the functions S110(k), S111(k) and S11−1(k), calculated in each reference frame, they account for the influence of the orientational degrees of freedom in the structure of the system. The physical interpretation of this function, however, is subtle and, consequently, beyond the scope of the present work.
B.3 Equilibration of the samples
To guarantee the stationarity of the simulation runs, we have used the protocol described at the end of Section 1.3. This involves the calculation of the static structure projections, , using the configurations at both the end of the stabilization transient time, tsta, and also at the end of the equilibration run, teq. Fig. 11 displays exemplary results obtained for the state point (η = 0.2, T* = 0.1).
, using the configurations at both the end of the stabilization transient time, tsta, and also at the end of the equilibration run, teq. Fig. 11 displays exemplary results obtained for the state point (η = 0.2, T* = 0.1).
C SCGLE theory for Brownian fluids of non-spherical particles
The SCGLE theory of colloid dynamics and dynamical arrest has been previously extended for the description of Brownian fluids constituted by particles interacting through non-spherical potentials. For more details the reader is referred to ref. 40. In its simplest version, the SCGLE formalism provides a closed set of time evolution equations for the diagonal components (l = l′, m = m′) Flm(k,t) and FSlm, of the ISFs defined in eqn (10) and (11). Written in the Laplace space, such equations read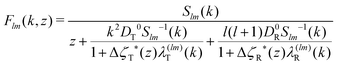 | (31) |
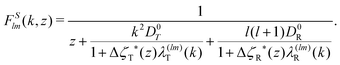 | (32) |
On the other hand, within a well defined set of approximations (discussed in Appendix A of ref. 40) the memory functions Δζα*(t) (α = T, R) may be written as
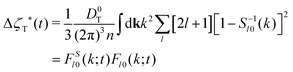 | (33) |
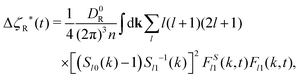 | (34) |
The closed set of coupled eqn (31)–(34) constitute the equilibrium non spherical version of the SCGLE theory, whose solution provides the full wave vector and time dependence of the dynamic correlation functions Flm(k;t) and FSlm(k;t) and of the memory functions Δζα*(t) (α = T, R). These equations may be numerically solved using standard methods once the projections Slm(k) of the static structure factor are provided. Under some circumstances, however, one may only be interested in identifying and locating the regions in state space of a given system that correspond to the various possible ergodic or non ergodic phases, involving the dynamical arrest of the dynamics of the translational and orientational degrees of freedom. For this purpose it is possible to derive equations for the so-called non-ergodicity parameters, i.e., the equations for the long-time stationary solutions of eqn (31)–(34). These are written in terms of the non-decaying components of the ISFS, defined as
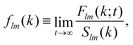 | (35) |
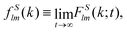 | (36) |
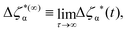 | (37) |
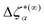 .
.
It is not difficult to show that the resulting equations can be written as
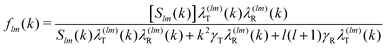 | (38) |
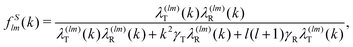 | (39) |
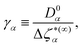 | (40) |
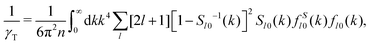 | (41) |
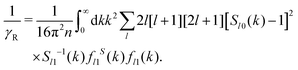 | (42) |
Fully ergodic states are thus described by the condition that all the non-ergodicity parameters are zero, so the dynamic order parameters γT and γR are both infinite. Any other possible solution of these bifurcation equations indicate total or partial loss of ergodicity. For instance, the conditions f00(k) ≠ 0, = fS00(k) ≠ 0, γT−1 ≠ 0, along with flm(k) = fSlm(k) = 0 (l ≥ 1, m = −l,…,0,…l) and γR−1 = 0 correspond to a partially arrested state in which the dynamics of the translational degrees of freedom undergo arrest, whereas the orientational degrees of freedom remain ergodic. The condition that all the non-ergodicity are simultaneously different from zero, in contrast, describes fully arrested states, where both dynamics become arrested.
Acknowledgements
L. F. E. A. acknowledges financial support from the German Academic Exchange Service (DAAD) through the DLR-DAAD programme under grant no. 212. M. M. N., R. C. P. and G. P. A. acknowledge the financial support provided by the Consejo Nacional de Ciencia y Tecnología (CONACYT, México) through grants no. 237425 and 287067, 242364, CB-A1-S-22362 (“Fondo Sectorial de Investigación para la Educación”), and LANIMFE 299043. The authors thank to Centro de Investigaciones y Estuidos Avanzados (CINVESTAV, México) to allow for the use of the computing clusters KUKULKAN and ABACUS for the simulations.References
- S. Glotzer and M. Solomon, Nat. Mater., 2007, 6, 557–562 CrossRef
.
- A. Walther and A. Müller, Chem. Rev., 2013, 113, 5194–5261 CrossRef CAS PubMed
.
- J. Zhang, B. Grzybowski and S. Granick, Langmuir, 2017, 33, 6964–6977 CrossRef CAS
.
- O. Cayre, V. Paunov and O. Velev, Chem. Commun., 2003, 2296–2297 RSC
.
- S. Safran, Nat. Mater., 2013, 2, 71–72 CrossRef
.
- A. Nych, U. Ognysta, M. Škarabot, S. Žumer and I. Muševič, Nat. Commun., 2013, 4, 71–72 Search PubMed
.
- K. Butter, P. Bomans, P. Frederik, G. Vroege and A. Philipse, Nat. Mater., 2003, 2, 88–91 CrossRef CAS
.
- T. Tlusty and S. Safran, Science, 2000, 290, 1328 CrossRef CAS
.
- K. Klokkenburg, B. Erné, A. Wiedenmann, A. Petukhov and A. Philipse, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 051408 CrossRef
.
- L. Rovigatti, J. Russo and F. Sciortino, Soft Matter, 2012, 8, 6310 RSC
.
- S. M. Cattes, S. Klapp and M. Schoen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 052127 CrossRef
.
- J. Sindt and P. Camp, J. Chem. Phys., 2015, 143, 024501 CrossRef
.
- K. K. K. Koperwas, K. Adrjanowicz, Z. Wojnarowska, A. Jedrzejowska, J. Knapik and M. Paluch, Sci. Rep., 2016, 6, 36934 CrossRef CAS
.
- J. Weis and D. Levesque, Adv. Polym. Sci., 2005, 185, 163–225 CrossRef CAS
.
- L. Belloni and J. Puibasset, J. Chem. Phys., 2017, 147, 224110 CrossRef
.
- A. Yethiraj and A. van Blaaderen, Nature, 2003, 421, 513–517 CrossRef CAS
.
- P. de Gennes and P. Picus, Phys. Kondens. Mater., 1970, 11, 189–198 CrossRef CAS
.
- R. Blaak, M. Miller and J.-P. Hansen, Europhys. Lett., 2007, 78, 26002 CrossRef
.
- M. Miller, R. Blaak, C. Lumb and J.-P. Hansen, J. Chem. Phys., 2009, 130, 114507 CrossRef
.
- A. Goyal, C. Hall and O. Velev, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 031401 CrossRef
.
- A. Goyal, C. Hall and O. Velev, J. Chem. Phys., 2009, 133, 064511 CrossRef
.
- A. Goyal, C. Hall and O. Velev, Soft Matter, 2010, 6, 480–484 RSC
.
- V. Testard, L. Berthier and W. Kob, J. Chem. Phys., 2014, 140, 164502 CrossRef
.
- F. Varrato, L. D. Michele, M. Belushkin, N. Dorsaz, S. Nathan, E. Eiser and G. Foffi, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 19155–19160 CrossRef CAS
.
- E. Kim, K. Stratford, R. Adhikari and A. Cates, Langmuir, 2008, 24, 6549–6556 CrossRef CAS
.
- K. Stratford, R. Adhikari, J.-C. D. I. Pagonabarraga and M. Cates, Science, 2005, 309, 2198–2201 CrossRef CAS
.
- P. Pusey and W. van Megen, Phys. Rev. Lett., 1987, 59, 2083 CrossRef CAS
.
- W. van Megen and P. Pusey, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 43, 5429 CrossRef CAS
.
- G. Foffi, E. Zaccarelli, P. Tartaglia, F. Sciortino and K. Dawson, Progr. Colloidal Sci., 2001, 118, 221–225 CAS
.
- E. Zacarelli and W. K. Poon, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15203–15208 CrossRef
.
- R. Pastore, A. de Candia, A. Fierro, M. P. Ciamarra and A. Coniglio, J. Stat. Mech.: Theory Exp., 2016, 074011 CrossRef
.
- F. Sciortino and E. Zacarelli, Curr. Opin. Colloid Interface Sci., 2017, 30, 90–96 CrossRef CAS
.
- A. Hynnien and M. Dijkstra, Phys. Rev. Lett., 2005, 94, 138303 CrossRef
.
- L. Rovigatti, J. Russo and F. Sciortino, Phys. Rev. Lett., 2011, 107, 237801 CrossRef
.
- K. Pham, A. Puertas, S. E. J. Bergenholtz, A. Moussaïd, P. Pusey, A. Schofield, M. Cates, M. Fuchs and W. Poon, Science, 2002, 296, 104 CrossRef CAS
.
- J. Bergenholtz, W. C. K. Poon and M. Fuchs, Langmuir, 2003, 19, 4493–4503 CrossRef CAS
.
- A. Eberle, R. Castañeda-Priego, J. M. Kim and N. Wagner, Langmuir, 2011, 28, 1866–1878 CrossRef
.
- A. Eberle, R. Castañeda-Priego and N. Wagner, Phys. Rev. Lett., 2011, 106, 105704 CrossRef
.
- R. Schilling and T. Scheidsteger, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 56, 2932 CrossRef CAS
.
- L. Elizondo-Aguilera, P. F. Z. Rico, H. R. Estrada and O. Alarcón-Waess, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 052301 CrossRef CAS
.
- M. S. Wertheim, J. Chem. Phys., 1971, 55, 4291–4298 CrossRef CAS
.
-
C. G. Gray and K. E. Gubbins, Theory of Molecular Fluids Vol. I: Fundamentals, Oxford University Press, New York, 1984 Search PubMed
.
- J. D. Weeks, D. Chandler and H. C. Andersen, J. Chem. Phys., 1971, 54, 5231 CrossRef
.
- B. J. Alder and T. E. Wainwright, J. Chem. Phys., 1959, 31, 459 CrossRef CAS
.
- B. D. Lubachevsky, J. Comput. Phys., 1991, 94, 255 CrossRef
.
- L. Berthier and W. Kob, J. Phys.: Condens. Matter, 2007, 19, 205130 CrossRef
.
- L. Berthier and W. A. Witten, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 021502 CrossRef
.
-
M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Clarendon Press, 1989 Search PubMed
.
- P. J. Steinhardt, D. R. Nelson and M. Ronchetti, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 28, 784 CrossRef CAS
.
- P. R. ten Wolde, M. J. Ruiz-Montero and D. Frenkel, J. Chem. Phys., 1996, 104, 9932 CrossRef CAS
.
- P. Castro-Villareal, A. Villada-Balbuena, J. Méndez, R. Castaneda-Priego and S. Estrada-Jiménez, J. Chem. Phys., 2014, 140, 214115 CrossRef
.
- M. G. Mazza, N. Giovambattista, H. E. Stanley and F. W. Starr, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 031203 CrossRef
.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef
.
- A. Cheng and K. M. Merz, J. Phys. Chem., 1996, 100(5), 1927–1937 CrossRef CAS
.
- M. Hernández-Contreras and M. Medina-Noyola, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 54, 6573 CrossRef
.
- E. Cortés-Morales, L. Elizondo-Aguilera and M. Medina-Noyola, J. Phys. Chem. B, 2016, 120, 7975–7987 CrossRef
.
- J. Olais-Govea, L. López-Flores and M. Medina-Noyola, J. Chem. Phys., 2015, 143, 174505 CrossRef
.
-
F. Perrin, Etude mathematique du mouvement, Thesis, Universite de Paris, Physique Mathematique, 1928 Search PubMed
.
- W. Stockmayer, J. Chem. Phys., 1941, 9, 348 Search PubMed
.
-
J. Hansen and I. McDonald, Theory of Simple Liquids, Academic Press, London, 2nd edn, 1986 Search PubMed
.
Footnote |
| † All authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2020 |