Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Arrested dynamics in a model peptide hydrogel system†
Axel
Rüter
 *a,
Stefan
Kuczera
*a,
Stefan
Kuczera
 a,
Luigi
Gentile
a,
Luigi
Gentile
 b and
Ulf
Olsson
a
b and
Ulf
Olsson
a
aDivision of Physical Chemistry, Lund University, SE-22100 Lund, Sweden. E-mail: axel.rueter@fkem1.lu.se; Tel: +46 46 2228188
bDepartment of Chemistry, University of Bari Aldo Moro, I-70121 Bari, Italy
First published on 26th February 2020
Abstract
We report here on a peptide hydrogel system, which in contrast to most other such systems, is made up of relatively short fibrillar aggregates, discussing resemblance with colloidal rods. The synthetic model peptides A8K and A10K, where A denotes alanine and K lysine, self-assemble in aqueous solutions into ribbon-like aggregates having an average length 〈L〉 on the order of 100 nm and with a diameter d ≈ 6 nm. The aggregates can be seen as weakly charged rigid rods and they undergo an isotropic to nematic phase transition at higher concentrations. Translational motion perpendicular to the rod axis gets strongly hindered when the concentration is increased above the overlap concentration. Similarly, the rotational motion is hindered, leading to very long stress relaxation times. The peptide self-assembly is driven by hydrophobic interactions and due to a net peptide charge the system is colloidally stable. However, at the same time short range, presumably hydrophobic, attractive interactions appear to affect the rheology of the system. Upon screening the long range electrostatic repulsion, with the addition of salt, the hydrophobic attraction becomes more dominant and we observe a transition from a repulsive glassy state to an attractive gel-state of the rod-like peptide aggregates.
1 Introduction
Fiber dispersions are interesting due to the strong rheological effects that can be observed already at very low concentrations.1 In fact, gelation or glass formation can be obtained at a solid content of only a fraction of percent.2–6 Materials of such low molecular weight content, where the continuous solvent is water, are often referred to as hydrogels. A specific class of anisotropic colloidal particles forming hydrogels are self-assembled peptide fibers, where peptides are the individual building blocks which spontaneously assemble into long one-dimensional fiber-like structures. These fibers may further interact with one another to form higher level assemblies or networks with varying mechanical properties. The biocompatibility and often high tunability make these fibrous networks of great interest for biomedical applications, such as drug delivery, implantable materials or as scaffolds for tissue regeneration.7–10Fiber forming peptides can be found in nature. They are typical hallmarks of neurodegenerative diseases such as Alzheimer's and Parkison's11,12 but are also found in many other protein systems.5,13–16 All these fibers appear to contain some sort of laminated β-sheet structure. Inspiration has been taken from these naturally occurring systems and the same or similar structural motifs have been used when designing peptides for controlled self-assembly.3,6,17,18 It has been found that the mechanical properties of the fibers as well as the macroscopical mechanical properties of their assemblies is strongly correlated to the structural motifs that are present within the fibers.19
Most peptide hydrogel systems consist of a network of many micrometer long fibers having contour lengths, L, that are much longer than their persistence length lp, which in turn can vary from tens of nanometers to tens of micrometers.5,20 The elasticity of these hydrogel systems can often successfully be described using theory developed for flexible and semi-flexible polymers,21 with fiber rigidity and network mesh size being the important parameters. However, fiber–fiber interactions also affect the stiffness of the network.1,22,23 Peptides typically contain both charged and hydrophobic amino acid, giving rise to simultaneous long range electrostatic repulsion and short range attractive interactions. Recent work indicate that increasing the relative strength of attractive interactions leads to a stiffer network due to an increase in fiber–fiber contacts, that decreases the entanglement length in the network.22
In the present paper we have characterized peptide hydrogels that unlike most other systems are composed of relatively short, 〈L〉 ≈ 100 nm, and rigid fibrillar aggregates. The synthetic A8K and A10K peptides, where A is alanine and K is lysine self-assemble into weakly charged twisted ribbon aggregates, consisting of approximately N = 15 laminated β-sheets.24,25 These aggregates are crystalline,26 making them highly rigid, and they therefore offer an interesting model system for studying the behavior of weakly charged colloidal rods that also exhibit a short range attractive interaction due to their hydrophobicity. Tuning the electrostatic repulsion by the addition of electrolyte allows for exploring this peptide hydrogel system from a repulsive glassy state at low salt content, to a heterogeneous gel state at a higher salt content where interactions are predominantly attractive. We here adopt the terminology that a gel is a material with arrested dynamics due to attractive “sticky” interactions, while in a glass the dynamics has been arrested because of repulsive excluded volume interactions.1,27,28
2 Materials and methods
2.1 Materials
The model peptides A8K and A10K were purchased from CPC Scientific as a lyophilized powder. The peptides were delivered as trifluoroacetate (TFA) salts at a purity of roughly 98% and were used without further purification. The peptides have one TFA counterion and can therefore be described for example as (NH2–AnK–COOH)+TFA−. Samples were prepared by mixing the amorphous powder in either water or D2O, the latter chosen for the possibility to perform nuclear magnetic resonance (NMR) measurements. Sample volume fractions were calculated from mass fractions and previously reported peptide densities.242.2 Dynamic lights scattering
Dynamic light scattering was measured on an CGF-8F compact goniometer system from ALV Gmbh, Langen, Germany. The system includes a CW He–Ne gas laser with a wavelength λ = 632.8 nm and an output power of 22 mW. The laser intensity is automatically attenuated and detected by a fiber optical near-monomodal detection system splitting up the signal on two avalanche photodiodes in pseudo-cross correlation arrangement. An ALV-7004 multiple tau digital correlator is used for the time correlation function of the scattered intensity. 8 samples in water in the concentration range 0.00034 < ϕ < 0.028 were measured at four different angles. The 4 lowest concentration were measured for 300 s while the higher concentrations, showing slower dynamics, were measured for 600 s.The experiment measures the intensity auto correlation function g(2)(t) from which we construct C(t) = (g(2)(t) − 1)/β = |g(1)(t)|2. Here, β is an instrumental constant, close to unity, g(1)(t) is the correlation function of the electric field, and the second equality corresponds to the so called Siegert relation.29C(t) is then defined in the interval 0 ≤ C(t) ≤ 1. All experiments were performed at 25 °C.
2.3 Rheology
Rheology was performed on a stress-controlled Anton Paar Physica MCR 301 rheometer with a Peltier system for temperature control. A cone-plate geometry Anton Paar CP25-1 tool with a diameter of 25 mm and an angle of 1° was used together with a water vapor solvent trap. All measurements were performed at 25 °C. Gel-like samples were loaded using a spatula whereas more viscous samples were loaded using a syringe. Before the start of each measurement a 20 min time sweep was performed at ω = 1 rad s−1 and γ = 1% to ensure that apparent steady state was reached after loading.Oscillatory measurements were performed at 1% strain in the linear viscoelastic regime, determined from amplitude sweeps at a frequency of 1 rad s−1. Steady shear flow curves were acquired by step-wise increasing the shear rate and awaiting steady state before the measurement point was collected. To determine the recovery time of the gel-like material after high shear a shear step measurement was performed where a half hour time sweep at γ = 1% and ω = 1 rad s−1 was followed by a 1 minute shear step at ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 1000 s−1 and a 1 h time sweep with the same parameters as previously mentioned.
= 1000 s−1 and a 1 h time sweep with the same parameters as previously mentioned.
All samples used for rheological measurements including various salt concentrations were diluted from a concentration ϕ ≥ 0.035 and further aged approximately 20 h.
2.4 Small angle X-ray scattering
Small and wide angle X-ray scattering (SAXS/WAXS) experiments were performed on a Saxslab Ganesha instrument, equipped with JJ X-ray system Aps pinhole, an X-ray microsource with a wavelength λ = 1.54 nm, and a movable two-dimensional 300k Pilatus detector (Dectris Ltd, Switzerland). Three detector sample-to-detector distances were used for data collection and the azimuthally averaged scattering intensities, I(q), as a function of the scattering vector q = (4π/λ)sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/2 where θ is the angle between the scattered beam and the incoming beam. Measured scattering intensities were put to absolute scale using a built-in calibration procedure of the instrument. All experiments were performed at 25 °C.
θ/2 where θ is the angle between the scattered beam and the incoming beam. Measured scattering intensities were put to absolute scale using a built-in calibration procedure of the instrument. All experiments were performed at 25 °C.
3 Results and discussion
3.1 Ribbon phase behavior
A8K and A10K form twisted ribbon aggregates of laminated β-sheets when dissolved in water. These ribbons have a cross-section of circa 4 × 8 nm2, and are typically about 100 nm long for A10K, and roughly 180 nm, for A8K.24,25 The cross-section is strikingly monodisperse, a fact that can be explained as a compromise between hydrophobic interactions and a torsional deformation that stretches the β-sheet hydrogen bonds.25,30 The ribbons form at a critical aggregation concentration, ϕcac, which is 0.001 for A8K and 5 × 10−6 for A10K, measured in volume fraction.24 Due to the fact that the ribbons are crystalline,24–26 they are also highly rigid, and can be viewed as charged rigid rods. At lower concentrations, the solution phase is isotropic. However, when increasing the concentration a transition to an anisotropic phase, presumably nematic, occurs. Fig. 1 shows a number of samples of A10K in water, viewed in transmitted light between crossed polarizers. A transition from an isotropic solution to an anisotropic birefringent phase is observed as the volume fraction, ϕ, is increased above approximately 0.02. | ||
| Fig. 1 Photographs of A10K between cross-polarizers. For samples above roughly ϕ ≈ 0.02 the samples are clearly birefringent, indicating a transition from an isotropic to a nematic phase. | ||
Surprisingly the same isotropic-to-nematic phase transition is estimated to ϕIN ≈ 0.1 in the case of A8K, in spite of the fact that the A10K ribbons are shorter. These values can be compared with Onsager's prediction for the hard rods, where the isotropic-to-nematic transition occurs at ϕIN ≈ 4d/L,31d being the rod diameter and L its length. For A8K the average L/d ≈ 180/6 ≈ 30 from which we expect the transition at circa ϕ ≈ 0.13 only slightly higher than the observed value. For A10K, which has a smaller aspect ratio L/d ≈ 100/6 ≈ 15, the Onsager model predicts the transition to occur at a higher concentration ϕIN ≈ 0.25, while we experimentally observe the transition already at ϕIN ≈ 0.02.
This can be understood from the fact that the ribbons carry a net charge. Due to the electrostatic interparticle repulsion, the rods will act as if they have an effectively larger diameter, implying a decrease in the effective aspect ratio.31–33 In addition, the electrostatic interaction destabilizes the nematic phase.32 For two rods arranged side by side, the electrostatic potential is highest when they are parallel and lowest when the angle between them is 90°. The increased effective diameter however also corresponds to a larger effective volume fraction and the overall effect of the electrostatic interaction is that the isotropic-to-nematic transition moves to a lower concentration.32
The situation regarding electrostatic interactions is here however somewhat complicated. The peptides have one TFA counterion and can therefore be described for example as (NH2–AnK–COOH)+TFA−. When the peptides self-assemble, a certain fraction (≈50%) of the peptide ions dissociate a proton and become electroneutral.34 When doing so, the solution becomes acidic, as trifluoroacetic acid is a relatively strong acid, pKa ≈ 1.35 This implies that the ionic strength of the solution varies with the peptide concentration, as [H+] ≈ 0.5(c − cs), where c is the peptide molar concentration and cs is the monomer solubility. The pH reaches ≈2 at ϕ ≈ 0.028. In addition, there is the screening from the peptide monomers. In the case of A10K, cs = 7 μM,24 corresponding to ϕcac ≈ 5 × 10−6, which is very low. cs has however been found to be an order of magnitude higher because of unaggregated monomers.36 For A8K on the other hand, the solubility is then almost one order of magnitude higher, cs = 2 mM.24 Thus, there is a higher ionic strength in the A8K system compared to A10K, resulting in a shift of the isotropic-to-nematic transition to higher concentrations.
It is further important to keep in mind that the background screening electrolyte concentration, due to [H+] increases with c. Thus, electrostatic interactions become increasingly screened the higher the peptide concentration. Because of this, and because the aggregate lengths are polydisperse, the isotropic–nematic two phase region is expected to be wide. We refrain from a more detailed analysis of the electrostatics, but conclude that with A8K the interactions are more screened compared to A10K. We also note that the dynamics at higher concentrations are very slow (vide infra), and it is very difficult to establish an equilibrium state. The system can be trapped in a more or less isotropic glass.
3.2 Arrested diffusion
Rod-like particles in solution have translational and rotational degrees of freedom. In dilute conditions, diffusion is unhindered. However, as the concentration is increased, in particular above the overlap concentration, ϕ* ≈ 6(d/L)2, certain degrees of freedom become significantly hindered. For translational diffusion we may consider diffusion parallel and perpendicular to the rod axis, as statistically independent diffusion modes, with diffusion coefficients D‖ and D⊥, respectively. At infinite dilution the friction coefficients of these two diffusion modes only differ by a factor of 2 (D‖/D⊥ = 2). Calculations of the diffusion coefficients were first made by Broersma.37–40 Slightly different values of some coefficients were later proposed by Tirado et al.41 Following Broersma, we consider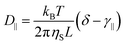 | (1a) |
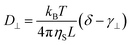 | (1b) |
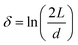 | (2a) |
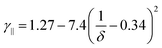 | (2b) |
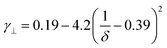 | (2c) |
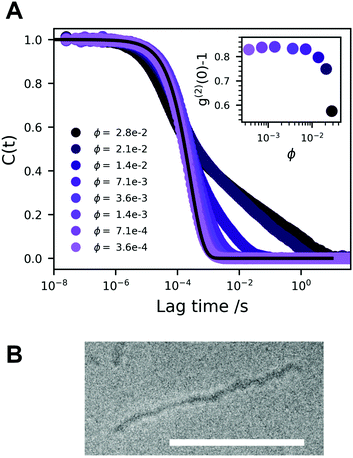
In Fig. 2A we present a normalized correlation function C(t), obtained from DLS experiments, for different concentrations of A10K. For the lowest concentration, the separation of modes is not clearly seen and the measured correlation function is consistent with only a single diffusion mode being only an average of the parallel and perpendicular modes. In this case, the diffusion coefficient is given by42
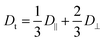 | (3) |
With increasing concentration, we see the appearance of a slow mode, clearly visible for ϕ > 0.01. At the highest concentration, ϕ = 0.028, the correlation function still decays to zero, but very slowly requiring several seconds. At these highest concentrations, the sampling time was 600 s. This indicates that the system approaches an arrested or jammed state. At the highest concentrations, ϕ > 0.02, the intercept, g(2)(0) − 1, shown in the inset in Fig. 2A, decreases. This further indicates that the system is becoming non-ergodic.43 All modes are diffusive as relaxation rates are proportional to q2, Fig. S1 (ESI†), q being the magnitude of the scattering vector. Some deviation is seen at high concentration and low q, but this is likely due to too short measurement times when the decay time becomes very long. We see no sign of rotational diffusion in the present data. But this is not expected as qL < 1. Attempts to detect the rotational diffusion using depolarized (vertical–horizontal, VH) light scattering were made, but the signal was too weak.
Jamming and dynamic arrest have been studied extensively with spherical colloids.44,45 Similar bimodal decays are observed in the vicinity of a glass transition, that are interpreted in terms of α and β structural relaxation, respectively. The fast α relaxation corresponds to the rattling motion of particles trapped within the cage of nearest neighboring particles. The slow β-relaxation corresponds to the occasional opening of the cage due to the collective motion of the neighboring particles.
There are, however, some particular differences. Spheres jam at much higher volume fractions.44,45 The hard sphere glass transition occurs at ϕ = 0.58. While this can be considered merely as a quantitative difference, there is also a significant qualitative difference. For the spherical geometry, both the local short time diffusion as well as the long time diffusion is isotropic, and when the system jams, all three translational degrees of freedom become arrested simultaneously. For anisotropic rod-like particles, on the other hand, the perpendicular diffusion is strongly hindered in crowded conditions, while the parallel diffusion may be essentially unhindered. For rod-like particles, rotation, with diffusion coefficient Dr, is also important, and like the perpendicular diffusion, the rotation also become strongly hindered above the overlap concentration.46
In a previous study,24 the fast and slow decays were interpreted as being associated with D‖ and D⊥, respectively. A similar interpretation was also made recently in a study of cellulose nanocrystals.47 Another possible source of slow mode could be the self-diffusion, as the particles are highly polydisperse.48 Self-diffusion modes have been observed clearly for example for polydisperse microemulsion droplets.49 Kang and Dhont studied the dynamics of charged fd virus particles (L/d ≈ 100) approaching the glass transition.50,51 A significant slowing down was observed with increasing concentration in the liquid state, followed by an abrupt vitrification when crossing the glass transition. In their experiments, however, no clear time-scale separation of two modes were observed.
To summarize, we conclude that the A10K dispersions approach a state of non-ergodicity and dynamic arrest at ϕ ≈ 0.03. SAXS experiments have shown that interactions are significantly repulsive,25 and the arrested state should be a repulsive glass. There is still significant motion in the glassy state as seen by the apparent β-relaxation. Interestingly, the systems shows a non-ergodic behavior even though the particles are essentially free to diffuse parallel to their axis. Perpendicular diffusion and rotation, however, are expected to be strongly hindered.
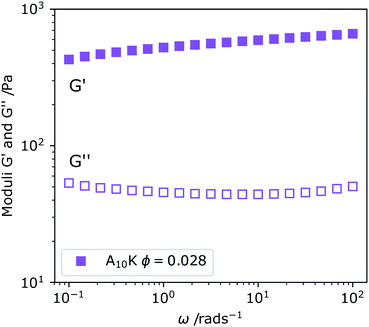
In Fig. 3 we show the linear viscoelastic spectrum obtained for ϕ = 0.028 of A10K ribbons. We observe that G′ ≫ G′′, where G′ is the storage modulus and G′′ the loss modulus. This is indicative of a system that behaves as an elastic solid rather than a viscous liquid. Furthermore, but both the moduli are independent of the deformation frequency, ω, within the frequency window of the experiment, covering three orders of magnitude. The frequency independence implies that τ ≫ ωmin−1 = 100 s. This should be compared to the time it takes to diffuse its contour length, L2/D‖ ≈ 10−5 s, where we have used L ≈ 100 nm and D‖ ≈ 10−11 m2 s−1 where D‖ is taken from the data of Fig. 2A. A striking difference.
When an isotropic system of homogeneously distributed rigid rods is subjected to an applied shear stress, an anisotropic distribution of rod orientations is induced. Relaxation of this anisotropy, back to the isotropic state is done by particle rotation alone, as the translational degrees of freedom, parallel and perpendicular to the rod axis, do not change orientation.52 The characteristic stress relaxation time is therefore τ ∼ 1/Dr. This clearly differentiates rigid rod systems from systems of flexible chains with internal degrees of freedom. In melts or solutions of entangled flexible chains the stress is typically relaxed by reptation,53 where chains diffuse along their contour (parallel diffusion) within a tube defined by entanglements with neighboring chains. Typically, flexible chains need only to escape the original tube in order to completely relax the stress and the induced anisotropy and the τ is essentially the time it takes for a tube renewal, referred to as the reptation time, τrep ≈ L2/Drep, where Drep is the reptation diffusion coefficient, similar to D‖ discussed above. Rigid rods, on the other hand, must diffuse many times their own contour length in order to relax the stress, as for each tube renewal there is only a minor rotation, depending on the concentration (crowding). For this reason, very long τ, due to very low Dr, are obtained even for relatively short rods. A striking difference compared to flexible chains where corresponding glassy states are not obtained in semi-dilute solutions.
3.3 Linear viscoelastic regime
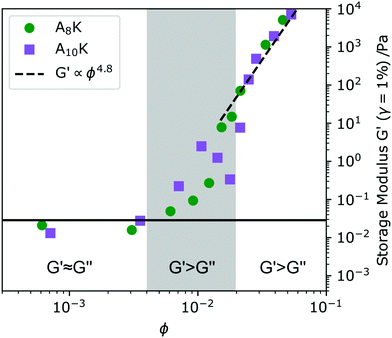
The onset of the dynamical arrest can also be studied by probing the viscoelastic properties of the system. Measurements of A8K and A10K were performed with small amplitude oscillatory shear (SAOS) rheology in the linear viscoelastic regime, where no plastic deformation occurs. By studying the dynamic moduli G′ and G′′ as a function of concentration we obtain information about when the system transforms from a viscous liquid to an elastic solid.54,55 In viscous liquids the input energy is dissipated as heat and G′ < G′′. Elastic solids on the other hand, where the energy is stored shows G′ > G′′. At the transition between the two regimes, G′ ≈ G′′, the characteristic viscoelastic relaxation time is typically found. In Fig. 4 values of G′ are obtained at 1% strain and 1 rad s−1 are shown versus ϕ. At low enough concentration, roughly ϕ < 0.005, the A8K and A10K aggregate dispersions show G′ ≈ G′′, however the absolute values of G′ are noisy and close to the instrumental limit. Therefore, we classify the system in this concentration regime as a viscous liquid.At ϕ ≈ 0.005 the response starts to become predominantly elastic (G′ > G′′), and we identify this as the overlap concentration ϕ* ≈ (d/L)2. Here, the system is till ergodic and we do not yet see any significant slow mode in DLS, Fig. 2A. Increasing the concentration further, the ratio G′/G′′ increases. For ϕ > 0.02, we have G′ ≫ G′′ and the system is also becoming non-ergodic and show the presence of very slow dynamics in DLS, Fig. 2A.
ϕ ≈ 0.02 also corresponds with the visually observed liquid to gel transition. At the transition concentration (ϕ = 0.02) we further observe the proportionality G′ ∝ G′′ ∝ ω(∼0.5), reminiscent of the criteria of the Winter–Chambon principle for when a system transitions into a fully percolated network.56 The viscoelastic relaxation time in this high concentrated regime, ϕ > 0.02, becomes practically infinite and G′ is above 103 Pa, not uncommon for peptide hydrogels.15,57 Representative amplitude and frequency sweeps from this regime can be found in Fig. 5C and D.
An interesting observation is the particularly strong concentration dependence G′ ∝ ϕn. A power of n = 4.8 was fitted to the high concentration data and is shown as a dashed line in Fig. 4. Models describing the scaling behavior of the plateau modulus as a function of concentration for semi-flexible and rigid polymers and rod dispersions show a power-law behavior where n ≈ 2–2.5 depending on fiber properties.21,58 These models have also been shown to hold for other fibril forming peptide model systems, such as the MAX1 system3 and the RADA16-II,4 for amyloid fibrils formed from proteins such as β-lactoglobulin16 and lysozyme14 and for other biologically relevant fibrillar systems such as actin.59
One of few reports of a peptide system deviating from the previously mentioned theoretical scaling behavior is the octapeptide FEFEFKFK,60 where a scaling behavior of G′ ∝ C3.7 was found for systems at pH = 4 whereas higher and lower pH showed a lower power. When the peptides fibrils became less charged at a specific pH, they could laterally aggregate and become more rigid. This would lead to a higher concentration dependence of G′.
A strong concentration dependence of the storage modulus has also been found in carboxylated nano-crystalline cellulose (NCC) systems61,62 where scaling behaviors with n ≥ 3 are found. The NCC systems studied are very similar to the peptide aggregates found in the A8K and the A10K system. They are not only charged stabilized and show a similar aspect ratio, but are also highly crystalline and thus very rigid. Inspired by the cellulose work,61 Hill proposed a model for the storage modulus of rigid rod networks, allowing for the effects of repulsive or attractive interparticle interactions.23 In this model G′ is given by
| G′ ∼ βEϕ11/3(1 + αϕ)10/3 | (4) |
The mechanical properties of β-sheet containing fibers have a strong correlation to the density of hydrogen bonds in the cross-section of the fiber. The more regular and tightly packed the hydrogen bonds are, the higher E the fiber will have.63 A rough method of determining the E has been given by Knowles et al.,19 where the E is estimated by a product of the hydrogen bond lengths of within the β-sheet, δβ, the hydrogen bond density, ζ, and a hydrogen bond spring constant, kH. The parameters regarding the geometry of the hydrogen bond have been investigated previously and have been determined to δβ = 0.45 nm and ζ = 1/(0.51 × 0.35) nm−2. Using kH = 13 N m−1, as suggested by Knowles et al.,19 results in E ≈ 32 GPa for both the AnK peptides in this work. This value is similar to the Young's modulus estimated for spider silk,64 but larger when compared to amyloid fibrils where different values of Young's modulus have been reported (0.3–4 GPa).65,66 We also note that an estimate of E for the A8K and A10K fibres is higher than that for NCC used as the example system by Hill (5.5 GPa).23,61
Finally we note that from a simple fit of G′ = Aϕ4.8 the high concentration data in Fig. 4 we obtain A ≈ 30 GPa, which is similar to the estimated value of the Young's modulus presented above. This is consistent with the ideas of Hill23 and eqn (4) that the dominating local fibril deformation is elongation.
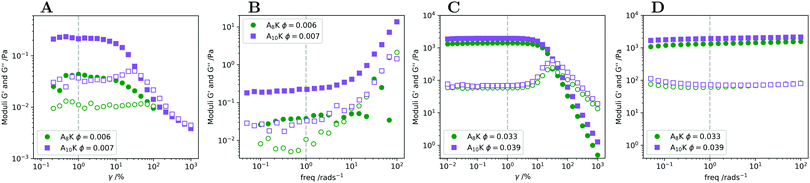
As seen in Fig. 4 and 5, the rheological response is essentially the same for A8K and A10K for a given ϕ. This in spite that A10K samples are birefringent for ϕ > 0.02. A8K samples showed no birefringence within the concentration range studied using rheology. This shows that the effect of ordering in A10K is small. Possibly, because we are dealing with a two phase region where the amount of ordered domains is small.
3.4 Repulsive and attractive fibril interactions
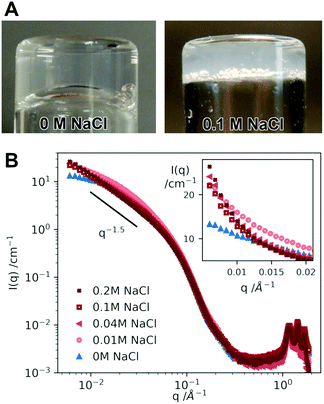
As suggested above, the A8K and A10K aggregates are hydrophobic, which influences the rheological behavior. In pure water they are sufficiently charged to provide colloidal stability,24,25 but when screening the long range electrostatic interaction by the addition of salt, the short range attractive interactions become predominant and the rods aggregate into clusters. The samples then strongly scatter light and become turbid. With pure water, the samples are highly transparent. This change is visualized in Fig. 6A comparing two samples of A10K ϕ ≈ 0.025 in pure water and 0.1 M NaCl. It is also possible to observe this change in interactions upon the addition of salt from small angle X-ray scattering (SAXS) measurements. In Fig. 6B we present SAXS patterns of A10K ϕ = 0.025 recorded in different aqueous concentrations of NaCl, varying from 0 to 0.2 M.The scattered intensity in a small angle scattering experiment, I(q), is proportional to a product of the average single particle scattering function, often referred to as the form factor 〈P(q)〉, and the effective structure factor, Seff(q), that contains information on solution structure and hence interparticle interactions. We use the word effective here, because a system with size polydispersity should strictly be considered as a multicomponent system where all different cross correlations should be taken into account as a sum of partial structure factors. Using this approximation we get67
| I(q) = ϕΔρ2Vp〈P(q)〉Seff(q) | (5) |
In the so called thermodynamic limit of q = 0, the effective structure factor can be interpreted in terms of an effective osmotic compressibility, Seff(0) = kBT〈Vp〉(∂π/∂ϕ)−1, where π denotes the osmotic pressure. For repulsive interparticle interactions Seff(0) < 1, and the effect of the repulsive interaction is to decrease the scattering intensity at smaller q-values. If interactions, on the other hand are predominantly attractive, Seff(0) > 1, resulting in an increased scattering at smaller q-values. Seff(0) = 1 corresponds to an ideal solution.
The A8K and A10K systems have been quantitatively characterized in water by SAXS previously, both with respect to 〈P(q)〉 and Seff(q).24,25 From those experiments it was concluded that interactions are repulsive (Seff(0) < 1). From 〈P(q)〉 it was concluded that the fibril cross section was biaxial and that it can be described as elliptical with semi-axes of 1.8 nm and 4 nm.24,25 With this information at hand we compare the scattering curves obtained at different NaCl concentrations, that are shown in Fig. 6B. The data cover a q-range of roughly 3 orders of magnitude including both the small angle regime with information of the aggregate morphology and interactions as well as the wide angle regime (high q) where the diffraction peaks show that the aggregates are crystalline. The diffraction peaks can be indexed to a two dimensional oblique unit cell.26
First of all we note that the different scattering curves completely superimpose for q > 0.07 Å−1. From this we can conclude that the individual fibrils are not affected by the addition of salt. Changes in I(q) are only observed at lower q, which we interpret as resulting from changes in Seff(q). The low q scattering is highlighted in the inset of Fig. 6B. The addition of salt leads to an increase in the small q scattering, indicating a crossover to attractive interactions. We do not have access to sufficiently low q-values to determine Seff(0). For the highest salt concentrations, 0.1 and 0.2 M, the small angle scattering shows a power law with I(q) ∼ q−1.5. These samples are also very turbid in visible light suggesting that the attractive interactions have become predominant and the fibrils have aggregated further into clusters, resulting in a heterogeneous fibrillar network. The power −1.5 can possibly be interpreted as a fractal dimension of the fiber clusters.1,68
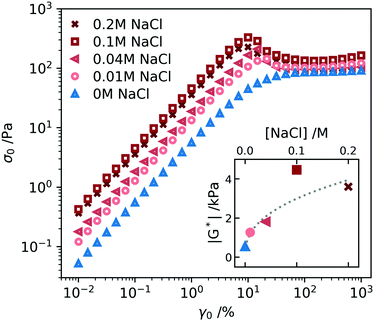
Also the non-linear rheology of a ϕ = 0.025 A10K sample depends on the electrolyte concentration. In Fig. 7 we present the variation of the stress amplitude, σ0, as a function of the strain amplitude, γ0, in oscillatory shear experiments at the different NaCl concentrations. The oscillation frequency used was ω = 1 rad s−1. In the linear regime, at lower γ, we can extract the dynamic shear modulus |G*| = σ0/γ0. The variation of the modulus with the NaCl concentration is plotted as an inset in Fig. 7. |G*| first increases with increasing salt concentration and then essentially levels off. A similar value is obtained at 0.1 and 0.2 M salt. This value is approximately an order of magnitude larger compared to the value at zero salt. The increase in |G*| with increasing salt concentration is understood as an increase in the entanglement density due to the increase of hydrophobic contacts when the electrostatic repulsion gets screened.22,69 A similar increase in network stiffness is also observed in α-synuclein hydrogels when decreasing the fibril charge density by pH.70 Moreover, similar salt effects are observed for nanocrystalline cellulose.69
Frequency sweeps were also performed with the samples containing salt, and the results are presented in Fig. S2 (ESI†). The samples with salt showed the same features as the sample without salt, Fig. 3, with essentially no frequency dependence within the frequency window. However, G′ increases with increasing salt concentration similar to the behavior of G*, shown as an inset in Fig. 7.
We also see in Fig. 7 that the addition of salt leads to the build up of a stress overshoot at γ0 ≈ 10%. This is consistent with the transition from predominantly repulsive to predominantly attractive interactions. In the attractive gel, an additional stress is needed to overcome the attractive hydrophobic force and pull particles apart inducing a flow.55
As has been shown above, we observe a transition from a homogeneous network in water to a more heterogeneous state with voids in the overlapping network giving rise to an increased turbidity. We can understand this as follows. When screening the electrostatic interactions, the short range attraction becomes the dominating interaction and the system starts to undergo a liquid–liquid (i.e. “liquid–gas”) phase separation where the rods get concentrated in one phase coexisting with a dilute or excess solvent phase. However, a full macroscopic phase separation is not obtained. The process gets at some point arrested resulting in the kinetically trapped gel state.28
3.5 Flow properties
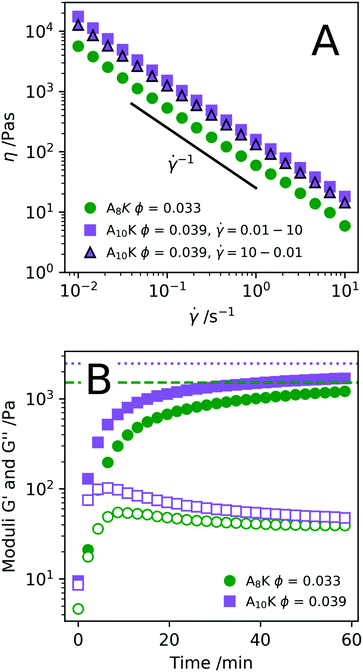
Knowing how peptide hydrogels respond to shear is important to correctly assess future applicability. Materials that are injected by syringe are typically subjected to extremely high shear rates, which can have a high impact on the material. By rheological flow curves and shear rate step measurements it is possible to a certain degree to simulate the process of injection through a needle.71,72 In Fig. 8A we present the viscosity η as a function of shear rate![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) for two samples, A8K ϕ = 0.033 and A10K ϕ = 0.039 respectively. As can be seen, both samples show a strong shear-thinning behavior, with essentially η ∝
for two samples, A8K ϕ = 0.033 and A10K ϕ = 0.039 respectively. As can be seen, both samples show a strong shear-thinning behavior, with essentially η ∝ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) −1 over the whole range of shear rates investigated. This corresponds to the maximum possible shear thinning and implies a constant shear stress, σ, within the range of
−1 over the whole range of shear rates investigated. This corresponds to the maximum possible shear thinning and implies a constant shear stress, σ, within the range of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) .
.
These types of systems are shear thinning because the rod-like aggregates align in the shear flow.26,73 A question that remains is whether this alignment is continuous, with an order parameter describing the degree of alignment, that is homogeneous throughout the gap, or whether the alignment is discontinuous. The latter case implies shear banding in the gradient direction,74 where a fully aligned nematic state, N, of relatively low viscosity, coexisting with a highly viscous isotropic network state, I. The present experiments where performed on a stress controlled rheometer but in a simulated rate controlled mode. In this case the set ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) is a weighted average (lever rule),
is a weighted average (lever rule), ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = (1 − fN)
= (1 − fN)![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) I + fN
I + fN![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) N, where fN is the fraction of aligned nematic state in the gap, and
N, where fN is the fraction of aligned nematic state in the gap, and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) I and
I and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) N, with
N, with ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ≪
≪ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) N, are the shear rates of the isotropic and aligned nematic states, respectively. With
N, are the shear rates of the isotropic and aligned nematic states, respectively. With ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) I and
I and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) N being fixed, fN increases from 0 to 1 in the range
N being fixed, fN increases from 0 to 1 in the range ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) I <
I < ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) <
< ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) N. Such a scenario with a shear induced nematic state has been found and studied extensively in wormlike micelle systems.75–77 In the present system, it is known that the aggregates align in shear flow,26 but the detailed nature of the alignment remains to be investigated.
N. Such a scenario with a shear induced nematic state has been found and studied extensively in wormlike micelle systems.75–77 In the present system, it is known that the aggregates align in shear flow,26 but the detailed nature of the alignment remains to be investigated.
Shearing the samples at a high shear rate result in a low viscosity, presumably an aligned (nematic) state. After cessation of flow, the sample is expected to relax back to its initial state of a stiff network. The kinetics of this recovery is of interest for some hydrogel applications, for example for injected subcutaneous drug deposition. In Fig. 8B we have plotted the elastic and storage modulus obtained from an oscillatory experiment as a function of time after pre-shearing the samples at ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 1000 s−1 for 60 s. The elastic modulus measured directly before the pre-shear is shown as the horizontal lines. Roughly 75–80% of the elastic modulus is recovered within 1 h. This reversibility is also shown by the fact that the flow curve in Fig. 8A for A10K ϕ = 0.039 is near to identical both as
= 1000 s−1 for 60 s. The elastic modulus measured directly before the pre-shear is shown as the horizontal lines. Roughly 75–80% of the elastic modulus is recovered within 1 h. This reversibility is also shown by the fact that the flow curve in Fig. 8A for A10K ϕ = 0.039 is near to identical both as ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) is increased and when
is increased and when ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) is decreased. Interestingly, the moduli are G′ ≈ G′′ ≈ 0 just after the pre-shear (t = 0) indicating that the network is completely disentangled and a fully aligned nematic state has been achieved.
is decreased. Interestingly, the moduli are G′ ≈ G′′ ≈ 0 just after the pre-shear (t = 0) indicating that the network is completely disentangled and a fully aligned nematic state has been achieved.
Shear-thinning as a response to increased shear rate is, as previously stated, typical behavior for rod dispersions as the rods align along the direction of the flow. This behavior has recently been explained thoroughly for various viruses.73 Many studied peptide fibril systems however have long fibres where alignment is not possible due to the large number of entanglement points. For the MAX1 peptide system the shear thinning instead occurs by the fracturing of the network and not of alignment of fibres.71 Due to the shorter aggregate lengths in these systems, alignment has been shown to take place,26 this does however not exclude network fracturing.
4 Conclusions
Self-assembled peptide hydrogels are interesting biomaterials with a range of potential applications.7–10 Typically, such systems consist of micrometer long fibrils forming a transient network.3,6,15 Here, we have shown that peptide hydrogels can also be obtained with relatively short, 100–200 nm fibrils, corresponding to an aspect ratio L/d of roughly 20. These peptide aggregates can be viewed as rigid rods with a sticky hydrophobic surface that are still colloidally stable due to a net charge. Thus in water, these hydrophobic but charged aggregates interact through a combination of a long range repulsion and a short range attraction like in other similar systems,22,69,78 and where both interactions are significant. There are strong similarities to the classical DLVO potential although here the attraction is mainly due to sticky hydrophobic interactions rather than van der Waals interactions.With increasing concentration, above the overlap concentration ϕ*, the rotational diffusion becomes increasingly hindered and Dr gradually approaches zero. In water, the repulsive electrostatic interaction still provides colloidal stability, and we identify the system as a repulsive glass, where the rotational degree of freedom has been arrested. In the present system, the short range attraction still seems to be significant, increasing the density of effective aggregate contacts leading to an increased network stiffness and a strong concentration dependence of the elastic modulus (G′ ∼ ϕ4.8).23 When screening the electrostatic repulsion by the addition of salt, the attractive hydrophobic interactions becomes predominant and the system crosses over from a repulsive glass to a gel state. A similar behavior has previously been reported for nanocrystalline cellulose having a similar aspect ratio as the peptide aggregates here.69
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research is funded by the Knut and Alice Wallenberg Foundation, grant number KAW 2014.0052.References
- M. J. Solomon and P. T. Spicer, Soft Matter, 2010, 6, 1391–1400 RSC.
- K. Kang and J. K. G. Dhont, Soft Matter, 2013, 9, 4401–4411 RSC.
- J. P. Schneider, D. J. Pochan, B. Ozbas, K. Rajagopal, L. Pakstis and J. Kretsinger, J. Am. Chem. Soc., 2002, 124, 15030–15037 CrossRef CAS PubMed.
- M. Owczarz, S. Bolisetty, R. Mezzenga and P. Arosio, J. Colloid Interface Sci., 2015, 437, 244–251 CrossRef CAS PubMed.
- J.-M. Jung and R. Mezzenga, Langmuir, 2010, 26, 504–514 CrossRef CAS PubMed.
- A. Aggeli, M. Bell, N. Boden, J. N. Keen, T. C. B. McLeish, I. Nyrkova, S. E. Radford and A. Semenov, J. Mater. Chem., 1997, 7, 1135–1145 RSC.
- B. V. Slaughter, S. S. Khurshid, O. Z. Fisher, A. Khademhosseini and N. A. Peppas, Adv. Mater., 2009, 21, 3307–3329 CrossRef CAS PubMed.
- R. G. Ellis-Behnke, Y.-X. Liang, S.-W. You, D. K. C. Tay, S. Zhang, K.-F. So and G. E. Schneider, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 5054–5059 CrossRef CAS PubMed.
- C. A. E. Hauser and S. Zhang, Chem. Soc. Rev., 2010, 39, 2780–2790 RSC.
- A. Dasgupta, J. H. Mondal and D. Das, RSC Adv., 2013, 3, 9117–9149 RSC.
- V. Castelletto, I. W. Hamley and P. J. F. Harris, Biophys. Chem., 2008, 138, 29–35 CrossRef CAS PubMed.
- L. C. Serpell, Biochim. Biophys. Acta, Mol. Basis Dis., 2000, 1502, 16–30 CrossRef CAS.
- S. Zhang, T. Holmes, C. Lockshin and A. Rich, Proc. Natl. Acad. Sci. U. S. A., 1993, 90, 3334–3338 CrossRef CAS PubMed.
- H. Yan, H. Frielinghaus, A. Nykanen, J. Ruokolainen, A. Saiani and A. F. Miller, Soft Matter, 2008, 4, 1313–1325 RSC.
- B. Frohm, J. E. DeNizio, D. S. M. Lee, L. Gentile, U. Olsson, J. Malm, K. S. Åkerfeldt and S. Linse, Soft Matter, 2015, 11, 414–421 RSC.
- Y. Cao, S. Bolisetty, J. Adamcik and R. Mezzenga, Phys. Rev. Lett., 2018, 120, 158103 CrossRef CAS PubMed.
- H. Yokoi, T. Kinoshita and S. Zhang, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 8414–8419 CrossRef CAS PubMed.
- G. von Maltzahn, S. Vauthey, S. Santoso and S. Zhang, Langmuir, 2003, 19, 4332–4337 CrossRef CAS.
- T. P. Knowles, A. W. Fitzpatrick, S. Meehan, H. R. Mott, M. Vendruscolo, C. M. Dobson and M. E. Welland, Science, 2007, 318, 1900–1903 CrossRef CAS PubMed.
- B. Ozbas, K. Rajagopal, J. P. Schneider and D. J. Pochan, Phys. Rev. Lett., 2004, 93, 268106 CrossRef PubMed.
- F. C. MacKintosh, J. Käs and P. A. Janmey, Phys. Rev. Lett., 1995, 75, 4425–4428 CrossRef CAS PubMed.
- S. A. Semerdzhiev, S. Lindhoud, A. Stefanovic, V. Subramaniam, P. van der Schoot and M. M. A. E. Claessens, Phys. Rev. Lett., 2018, 120, 208102 CrossRef CAS PubMed.
- R. J. Hill, Biomacromolecules, 2008, 9, 2963–2966 CrossRef CAS PubMed.
- Ç. Ç. Cenker, S. Bucak and U. Olsson, Langmuir, 2014, 30, 10072–10079 CrossRef PubMed.
- A. Rüter, S. Kuczera, D. J. Pochan and U. Olsson, Langmuir, 2019, 5802–5808 CrossRef PubMed.
- S. Kuczera, A. Rüter, K. Roger and U. Olsson, ChemPhysChem, 2020 DOI:10.1002/cphc.201901126.
- V. Trappe and P. Sandkhler, Curr. Opin. Colloid Interface Sci., 2004, 8, 494–500 CrossRef CAS.
- E. Zaccarelli, J. Phys.: Condens. Matter, 2007, 19, 323101 CrossRef.
- K. Schätzel, Appl. Phys. B: Photophys. Laser Chem., 1987, 42, 193–213 CrossRef.
- I. A. Nyrkova, A. N. Semenov, A. Aggeli and N. Boden, Eur. Phys. J. B, 2000, 17, 481–497 CrossRef CAS.
- L. Onsager, Ann. N. Y. Acad. Sci., 1949, 51, 627–659 CrossRef CAS.
- A. Stroobants, H. N. W. Lekkerkerker and T. Odijk, Macromolecules, 1986, 19, 2232–2238 CrossRef CAS.
- R. Mezzenga, J.-M. Jung and J. Adamcik, Langmuir, 2010, 26, 10401–10405 CrossRef CAS PubMed.
- M. Koder Hamid, A. Rüter, S. Kuczera and U. Olsson, to be submitted.
- J. B. Milne and T. J. Parker, J. Solution Chem., 1981, 10, 479–487 CrossRef CAS.
- A. Rüter and U. Olsson, to be submitted.
- S. Broersma, J. Chem. Phys., 1960, 32, 1626–1631 CrossRef CAS.
- S. Broersma, J. Chem. Phys., 1960, 32, 1632–1635 CrossRef CAS.
- J. Newman, H. L. Swinney and L. A. Day, J. Mol. Biol., 1977, 116, 593–603 CrossRef CAS PubMed.
- S. Broersma, J. Chem. Phys., 1981, 74, 6989–6990 CrossRef.
- M. M. Tirado, C. L. Martínez and J. G. de la Torre, J. Chem. Phys., 1984, 81, 2047–2052 CrossRef.
- B. J. Berne and R. Pecora, Dynamic Light Scattering: With Applications to Chemistry, Biology, and Physics, Wiley, 1976 Search PubMed.
- P. N. Pusey and W. Van Megen, Phys. A, 1989, 157, 705–741 CrossRef CAS.
- W. C. K. Poon, MRS Bull., 2004, 29, 96–99 CrossRef CAS.
- P. N. Pusey and W. van Megen, Nature, 1986, 320, 340–342 CrossRef CAS.
- M. Doi and S. F. Edwards, J. Chem. Soc., Faraday Trans. 2, 1978, 74, 560–570 RSC.
- J. Van Rie, C. Schütz, A. Gençer, S. Lombardo, U. Gasser, S. Kumar, G. Salazar-Alvarez, K. Kang and W. Thielemans, Langmuir, 2019, 35, 2289–2302 CrossRef CAS PubMed.
- P. N. Pusey, H. M. Fijnaut and A. Vrij, J. Chem. Phys., 1982, 77, 4270–4281 CrossRef CAS.
- Y. Hattori, H. Ushiki, L. Courbin and P. Panizza, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 021504 CrossRef CAS PubMed.
- K. Kang and J. K. G. Dhont, Phys. Rev. Lett., 2013, 110, 015901 CrossRef CAS PubMed.
- K. Kang and J. K. G. Dhont, Soft Matter, 2013, 9, 4401–4411 RSC.
- M. Doi, Soft Matter Physics, OUP, Oxford, 2013 Search PubMed.
- P.-G. d. Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, Ithaca, NY, 1979 Search PubMed.
- R. G. Larson, The structure and rheology of complex fluids, Oxford University Press, New York, 1999 Search PubMed.
- J. Mewis and N. J. Wagner, Colloidal Suspension Rheology, Cambridge University Press, Cambridge, 2011 Search PubMed.
- H. H. Winter and F. Chambon, J. Rheol., 1986, 30, 367–382 CrossRef CAS.
- C. Yan and D. J. Pochan, Chem. Soc. Rev., 2010, 39, 3528–3540 RSC.
- J. L. Jones and C. M. Marques, J. Phys., 1990, 51, 1113–1127 CrossRef CAS.
- M. L. Gardel, J. H. Shin, F. C. MacKintosh, L. Mahadevan, P. Matsudaira and D. A. Weitz, Science, 2004, 304, 1301–1305 CrossRef CAS PubMed.
- S. Boothroyd, A. F. Miller and A. Saiani, Faraday Discuss., 2013, 166, 195–207 RSC.
- M. Pääkkö, M. Ankerfors, H. Kosonen, A. Nykänen, S. Ahola, M. Österberg, J. Ruokolainen, J. Laine, P. T. Larsson, O. Ikkala and T. Lindström, Biomacromolecules, 2007, 8, 1934–1941 CrossRef PubMed.
- L. Jowkarderis and T. G. M. van de Ven, Carbohydr. Polym., 2015, 123, 416–423 CrossRef CAS PubMed.
- G. Lamour, R. Nassar, P. H. Chan, G. Bozkurt, J. Li, J. M. Bui, C. K. Yip, T. Mayor, H. Li, H. Wu and J. A. Gsponer, Biophys. J., 2017, 112, 584–594 CrossRef CAS PubMed.
- D. Porter, J. Guan and F. Vollrath, Adv. Mater., 2013, 25, 1275–1279 CrossRef CAS PubMed.
- J. Adamcik, C. Lara, I. Usov, J. S. Jeong, F. S. Ruggeri, G. Dietler, H. A. Lashuel, I. W. Hamley and R. Mezzenga, Nanoscale, 2012, 4, 4426–4429 RSC.
- N. Sasaki, Y. Saitoh, R. K. Sharma and K. Furusawa, Int. J. Biol. Macromol., 2016, 92, 240–245 CrossRef CAS PubMed.
- Neutrons, X-Rays and Light: Scattering methods applied to soft condensed matter, ed. P. Lindner and T. Zhemb, Elsevier Science B.V., Amsterdam, 2002 Search PubMed.
- B. Hammouda, J. Appl. Crystallogr., 2010, 43, 1474–1478 CrossRef CAS.
- Y. Xu, A. D. Atrens and J. R. Stokes, Soft Matter, 2018, 14, 1953–1963 RSC.
- B. H. Pogostin, S. Linse and O. Ulf, Langmuir, 2019, 35, 16536–16544 CrossRef CAS PubMed.
- C. Yan, A. Altunbas, T. Yucel, R. P. Nagarkar, J. P. Schneider and D. J. Pochan, Soft Matter, 2010, 6, 5143–5156 RSC.
- S. Wan, S. Borland, S. M. Richardson, C. L. R. Merry, A. Saiani and J. E. Gough, Acta Biomater., 2016, 46, 29–40 CrossRef CAS PubMed.
- C. Lang, J. Kohlbrecher, L. Porcar, A. Radulescu, K. Sellinghoff, J. K. G. Dhont and M. P. Lettinga, Macromolecules, 2019, 52, 9604–9612 CrossRef CAS.
- P. D. Olmsted, Rheol. Acta, 2008, 47, 283–300 CrossRef CAS.
- J. Berret and D. C. Roux, J. Rheol., 1995, 39, 725–741 CrossRef CAS.
- U. Olsson, J. Börjesson, R. Angelico, A. Ceglie and G. Palazzo, Soft Matter, 2010, 6, 1769–1777 RSC.
- R. Angelico, U. Olsson, K. Mortensen, L. Ambrosone, G. Palazzo and A. Ceglie, J. Phys. Chem. B, 2002, 106, 2426–2428 CrossRef CAS.
- A. Stradner, H. Sedgwick, F. Cardinaux, W. C. K. Poon, S. U. Egelhaaf and P. Schurtenberger, Nature, 2004, 432, 492–495 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sm02244a |
| This journal is © The Royal Society of Chemistry 2020 |