Open Access Article
Open Access ArticleSwitchable self-assembled capillary structures
Nicolas
Vandewalle
 *a,
Martin
Poty
a,
Nathan
Vanesse
a,
Jérémie
Caprasse
b,
Thomas
Defize
b and
Christine
Jérôme
b
*a,
Martin
Poty
a,
Nathan
Vanesse
a,
Jérémie
Caprasse
b,
Thomas
Defize
b and
Christine
Jérôme
b
aGRASP, CESAM Research Unit, Institute of Physics B5a, University of Liège, B4000 Liège, Belgium. E-mail: nvandewalle@uliege.be
bCERM, CESAM Research Unit, Institute of Chemistry B6a, University of Liège, B4000 Liège, Belgium
First published on 14th October 2020
Abstract
Capillarity driven self-assembly is a way to create spontaneous structures along liquid interfaces in between bottom-up and top-down fabrication methods. Based on multipolar capillary interactions between elementary floating object, simple to complex structures can been achieved by designing objects with specific 3D shapes. We show herein that a switchable self-assembled structure can be obtained with a shape memory polymer. At a defined temperature of the liquid, the 3D shape of each elementary floating object changes, modifying the capillary interactions thus forcing the stable structure to disassemble and to form a new arrangement. Based on simulations and experiments, we study how this cooperative behavior induces metastable complex configurations.
1 Introduction
The spontaneous generation of order in systems made of numerous components, called self-assembly, is ubiquitous in biology and chemistry at the molecular level. Examples range from the formation of crystals to the formation of complex molecules. Self-assembly is now being intensely studied in chemistry, biology and materials engineering.1 Moreover, self-assembly is also encountered from the micrometer up to the centimeter scales, offering opportunities to generate 2D and 3D elaborated structures with low cost and simple manipulations.2 Extensive research demonstrated that the self-assembly of small-scale structures can be achieved along liquid interfaces, opening ways to inexpensive manufacture processes in between bottom-up and top-down forms of fabrication.3–9Capillary driven self-assembly consists in suspending small objects at the water–air interface. Depending on the object weight, hydrophobicity and surface tension, the interface is slightly deformed, inducing a net force between the particles.10–14 Vella and Mahadevan14 rationalized this interaction for spheres, while Kralchevsky11,12 considered non-spherical particles. In both approaches, any liquid deformation around an object (or a particle) defines a so-called capillary charge, and the interaction between two objects is given by the product of the capillary charges as well as a decreasing (Bessel) function of the object interdistance. While a spherical particle is characterized by a single capillary charge, a non-spherical particle could be characterized by a sum of capillary charges leading to multipolar effects.13 Those multipolar interactions involve torque and orientational effects in addition to attractive/repulsive interactions.13,15 Such multipolar effects were considered for example to explain the particular natural patterns forming along water–air interfaces with mosquito eggs and whirligig beetles.16
Based on multipolar capillary interactions, sophisticated self-assembled structures can therefore be envisioned, as already tested by our group.7,8 In these earlier works, we 3D printed branched objects for producing either positive or negative charges located at the tips of the branches. We proved that large and ordered self-assemblies can be programmed by designing the shape of the objects: square and triangular lattices have been achieved.7
A step forward is to achieve a remotely configurable self-assembly. Changing the shape of the composing particles modifies the interactions between them and enables us to provoke or prevent the assembly. A programmable, reconfigurable and switchable self-assembly can thus be reached.17 Earlier studies proposed to change the density of the liquid by adding salts.18 The resulting modification of particle buoyancy triggers the reconfiguration of the assembly. More recently, we proposed to use an external magnetic field to actuate capillary charges placed on floating elastic objects,19 allowing for reversing the self-assembling process.
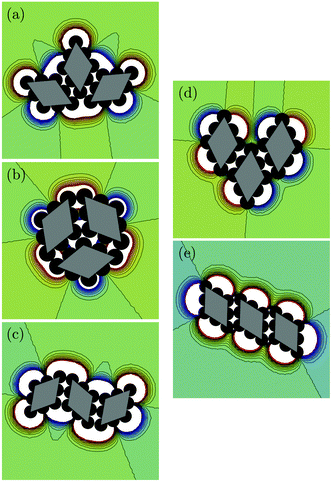
The aim of this paper is to study the self-assembly of objects whose multipolar capillary interactions can be modified/activated by shape shifting using shape-memory polymer as material for manufacturing the objects. We study the different stable and metastable patterns that can be achieved, as the one illustrated in Fig. 1. Our work aims to provide original patterns by remotely switching the shape of objects.
2 Multipoles
According to ref. 14, the cylindrical liquid profile, being the liquid elevation zi, at a position![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) from a spherical particle i centered on
from a spherical particle i centered on ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i, is given by
i, is given by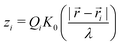 | (1) |
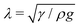 , over which the liquid surface is deformed, is called the capillary length, which depends on surface tension γ, liquid density ρ and Earth gravitational acceleration g. This characteristic length is close to λ = 2.7 mm for water/air interfaces. When two distant particles, labelled i and j, are floating at the liquid surface, the interaction potential is given by
, over which the liquid surface is deformed, is called the capillary length, which depends on surface tension γ, liquid density ρ and Earth gravitational acceleration g. This characteristic length is close to λ = 2.7 mm for water/air interfaces. When two distant particles, labelled i and j, are floating at the liquid surface, the interaction potential is given by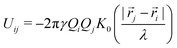 | (2) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i −
i − ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) j| ≫ λ), the decay of K0 looks like an exponential decay.
j| ≫ λ), the decay of K0 looks like an exponential decay.
When the object shape differs from a sphere,15 or when the object is larger than the capillary length,19 a superposition of capillary charges, has been proposed for describing the deformation of the liquid. The liquid elevation at position ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) around the object i is given by
around the object i is given by
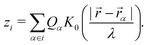 | (3) |
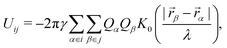 | (4) |
In order to create a pattern, we 3D printed many multipolar objects having a rhombus shape. The internal angles of the rhombus are 60° and 120°. The side length is 1 cm, being much larger than the capillary length λ. The rhombus thickness is 0.5 mm. Those elementary units are floating thanks to partial wetting. In addition, we imposed positive and negative curvatures. In fact, we created two different types of rhombus, as illustrated in Fig. 2. The first type, as illustrated in Fig. 2(a), considers a positive and a negative curvature along the diagonals of the rhombus for creating respectively positive or negative capillary charges at the vertices. The second type of rhombus, as seen on Fig. 2(b), has curvatures along the medians of the rhombus for creating large liquid deformations along the sides of the rhombus.
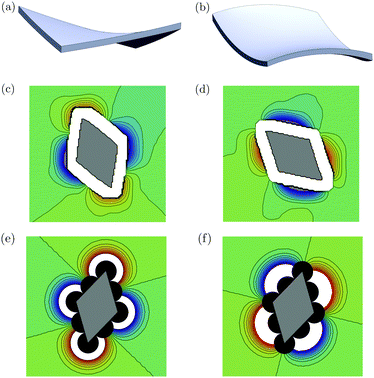 | ||
| Fig. 2 (a) 3D view of a rhombus tile curved along the diagonals, with opposite curvatures. (b) 3D view of the same rhombus tile curved along the medians, with opposite curvatures. (c and d) Experimental profilometry of the liquid interface deformation around objects (a and b), respectively. The blue-green-red color scale indicates the elevation of the liquid interface in arbitrary units. Blue (red) corresponds to a negative (positive) capillary charge, while the green color corresponds to a flat unperturbed interface. The white region around each rhombus corresponds to high slopes characterized by large uncertainties within this profilometry method. (e and f) Using the same color code, simulation of the liquid elevation with eqn (3) in our simulations with objects corresponding to (a and b) respectively. Each rhombus is simulated using non-overlapping disks shown in black and associated to a capillary charge. | ||
Before building elaborated structures, we characterized the liquid interface deformation around each basic elements using a profilometry technique.21 The experimental method is based on refraction of light through the deformed interface. A pattern is placed below the system and is recorded with zero deformation of the interface. When one or more objects are placed on the liquid interface, light refraction will modify the image of the pattern. By image correlation analysis, it is possible to obtain the gradients of the interface. By integration, the liquid profile is obtained. Liquid elevations of at least 10 μm are detected. Experimental liquid profiles around the particles are shown in a color scale in Fig. 2(c and d): red for positive deformation and blue for negative deformation.
The liquid elevation z around single floating tiles is shown in Fig. 2. The white region around each rhombus corresponds to strong gradients involving some indetermination of the liquid elevation after integration. Close to the objects, strong deviation from a flat interface are seen either at the vertices (c) or along the sides of the rhombus (d), as expected. Positive and negative capillary charges forming a quadrupolar system could be considered. Moreover, a slight negative capillary charge should be considered coming from the weight of the tile itself. Indeed, a non-curved tile deforms slightly the interface and a weak capillary interaction is observed between uncurved objects.
We have also considered a numerical model which considers rhombus shape made of 9 non-overlapping disks. One disk is placed at the center of the rhombus. Four disks corresponds to vertices. Four disks corresponds to the middle of the edges. Each disk could be the center of a capillary charge, as described by eqn (3). Two typical objects are shown in Fig. 2(e and f). A small grey rhombus is superimposed in order to give the orientation of the object. However, the object should be considered as the union of all disks. By placing capillary charges either at the vertices of the rhombus or along the sides of the rhombus, we obtain a good approximation of the liquid profile obtained in our experiments, as shown in Fig. 2. Please remark that the ninth capillary charge in the particle center is considered in order to provide a slight negative charge and attraction between objects. In the following work, we will consider this model in order to simulate capillary driven self-assemblies.
More capillary charges can be considered for describing the rhombus objects but this will inevitably increase the computation times when calculating the interaction potential eqn (4). We present herein the results with the minimum possible of charges in order to reproduce experimental observations. Moreover, adding more disks for modeling rhombi implies shorter interdistances that could result in another choice for the potential (4).
3 Self-assembled patterns
Considering both types of 3D printed objects, two different self-assembled patterns are obtained in experiments. Objects are placed at random on the water–air interface. Interactions drive the system into ordered clusters within seconds and without mechanical agitation. The more compact obtained experimental structures are illustrated in Fig. 3(a and b) when 12 floating objects comes together. A similar kind of self-assembled lattice has already been obtained in our earlier work on branched floating objects.7 In fact, lacunes, i.e. missing tiles, may be present in the lattice and they are mainly due to initial conditions, i.e. initial positions and orientations of the particles. A small agitation of the water–air interface provides some annealing for the structure leading to a more compact and more symmetrical raft.19 The key ingredient for reaching lattices is the use of both positive and negative charges on the objects allowing for both attractive and repulsive motions during self-assembly. It should be remarked that neighboring rhombi are still separated by a very thin layer of liquid at equilibrium, i.e. they are not completely in contact. This is probably due to the wavy contact line along the edge, leading to a repulsive interaction at short range.22 | ||
| Fig. 3 Self-assemblies formed by 12 identical rhombi. Each rhombus has an edge length of 1 cm, giving a scale to the pictures. (a) Rhombille tiling obtained with tiles of Fig. 2(a), involving vertex–vertex interactions. (b) Isohedral tiling obtained with rhombi of Fig. 2(b), involving edge–edge interactions. | ||
Rhombille tiling, as shown in Fig. 3(a), is obtained for vertex–vertex interactions. The rhombille tiling can be viewed as a regular hexagonal structure, each hexagon being made of three rhombi.23 The hexagonal lattice has a symmetry p6m, while the hexagon centers have a symmetry p3m1, meaning that 3-fold and 6-fold local symmetries coexist in the structure.
When edge–edge interactions are dominating the system, the particles self-assemble into a 4-fold isohedral structure,23 as shown in Fig. 3(b). The lattice is formed by the simple translation of the rhombus along the air–water interface. It is remarkable that completely different symmetries can be reached using similar rhombi objects but having different curvatures.
Based on the objects of Fig. 2(e and f) possessing 9 capillary charges, numerical simulations of self-assembly were performed. The objects are initially placed with random positions and orientations in the horizontal plane. The so-called steepest descent algorithm searches for small translations and rotations of the particles among numerous random moves, allowing only minimization of capillary energy, as given by eqn (4). Whatever the values of the charges Qα in eqn (4), the minimum is obtained when objects comes into contact. The resulting pattern is therefore independent on the scale of charge, i.e. the scale of interface deformation along the vertical z-axis.
Typical results for three interacting objects are shown in Fig. 4 for both types of rhombus. As expected, rhombille and isohedral patterns are obtained, therefore validating such a model. Although a low number of objects is considered, many different patterns result from self-assembly, emphasizing the importance of the initial conditions. All resulting patterns are illustrated in Fig. 4. Increasing the number of particles in simulations involve more defects in the lattices such that annealing is needed. Nevertheless, low number of objects are enough to show the symmetry of expected patterns. One should nevertheless remark that the isohedral pattern is not perfect, since there is a slight shift between neighboring rhombi. This effect, also observed in the picture of Fig. 3(b), can be reduced by considering smaller disks for the capillary charges describing the shape of the objects.
4 Switching behavior
Instead of 3D printing rigid tiles with specific curvatures, we 3D printed the negative of these tiles in order to create molds. A polymer can therefore be pressed in the molds. A shape-memory polymer has been developed for our purpose. Four-arm star-shaped poly-ε-caprolactone end-capped by reactive functions, i.e. furan or maleimide moieties, have been used for the preparation of the shape-memory particles (see Fig. 5). The functionalization of commercially available PCL-4OH chain-ends by maleimide or furan moieties to get the PCL-4MAL and PCL-4FUR, respectively, is a well optimized and already published process.24,25 It was applied to PCL-4OH of a molar mass of 8000 g mol−1.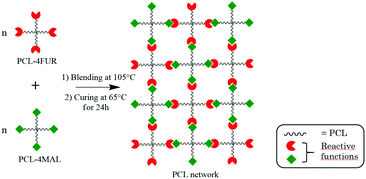 | ||
| Fig. 5 Network formation using the Diels–Alder cycloaddition between furan and maleimide as reactive functions at the chain-ends of 4-arm star-shape PCL. | ||
In order to get the temperature triggered shape-memory objects, they were made of cross-linked semi-crystalline PCL. The chemically cross-linked PCL network is formed by mechanical mixing of an equimolar blend of PCL-4MAL and PCL-4FUR at 105 °C, followed by a thermal post-curing at 65 °C in a mold to allow Diels–Alder adduct formation leading to the network (Fig. 5). More precisely, 1 g of PCL-4FUR and 1 g of PCL-4MAL (Mn 8000 g mol−1) stars were introduced in a 10 mL vial and molten at 105 °C in an oven. Few milligrams of carbon black were added in order to have a better contrast for future pictures and videos. Then the mixture was mechanically blended and collected in a home-made 3D-printed mold (see Fig. 6b), then cured at 65 °C during 24 h to obtain a crosslinked material. After this step, the formed PCL network has memorized the edge–edge shape (permanent shape) of the particles.
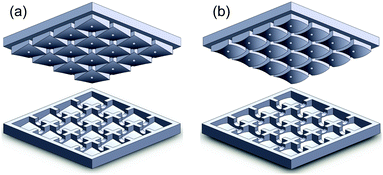 | ||
| Fig. 6 Design of the molds used to give to the shape-memory particles: (a) the vertex–vertex temporary shape and (b) the edge–edge permanent shape. | ||
Then, these objects are heated again at 60 °C, i.e. above the melting temperature of the PCL network and placed in a second mold (Fig. 6a) to give them their vertex–vertex temporary shape after cooling in the mold at ambient temperature.
We decided to switch from vertex–vertex to edge–edge rhombus types. The melting temperature is around Tm = 60 °C. The water is therefore progressively heated from the bottom using electrical resistors. The increase of temperature may have two effects: (i) a modification of surface tension and (ii) the appearance of convective cells. We assume that they are weak effects. Indeed, the capillary length changes only by 4% in the temperature range such that the objects are still much larger than λ. By heating from below, convective rolls may appear below the interface, providing some agitation. If present, this source of fluid motion is however unable to separate the tiles from each other just before the transition. Once the transition temperature is reached, the change of symmetry is observed within a few seconds. A typical sequence of self-disassembly and reassembly into a new structure is given in Fig. 7. Starting from 6 rhombi in a flower configuration, i.e. with a 6-fold vertex in the center, the rhombi start to slide along each other and then rotate to switch to an isohedral lattice.
Changing the symmetry involves both fundamental moves for each rhombus: translation and rotation. When capillary charges migrate from vertices to edges, the translation of a rhombus along the edge of another one is cost effective with respect to the capillary energy. Indeed, the slight negative charge of each object favors translation for objects nearly in contact before rotations, as seen in the first stages shown in Fig. 7. Rotational events appears at the end of the shape switching process when capillary charges involve larger torques. At this step of the process, the centres of rotation correspond roughly to the tips of each rhombus.
We performed many experiments, varying the number of tiles as well as the initial configurations. We start from compact configurations only (without lacunes) but with a variable number of tiles. Two major behaviors should be distinguished. The first one, often encountered for a large number of tiles, is illustrated by the remarkable structure of Fig. 1 being the last step of a rearrangement starting from Fig. 3(a). In fact, the system is stuck in a metastable situation far from the expected isohedral structure. The transition is therefore incomplete. In fact, the migration of the capillary charges from vertices to edge centers allows for translation of tiles along the edges. However, the rotation of tiles is forbidden since particles are always in close interaction with two other neighbors, even in the last step of capillary charge migration. This behavior has been simulated starting from 3 tiles forming a compact rhombille structure, as shown in the top row of Fig. 8. During the capillary charge migration along the edges, they move cooperatively forming a triangular shape in the center. The liquid deformation there is important since the superposition of three charges is observed there. Each rhombus has still 2 neighbors, but the rotation of each rhombus is unlikely since they are attracted towards the center of the triangle. The self-assembly of Fig. 1 is therefore a metastable configuration. In order to obtain the isohedral structure, this configuration should be annealed by interface fluctuations/agitation for separating objects from each other, allowing for rotations.
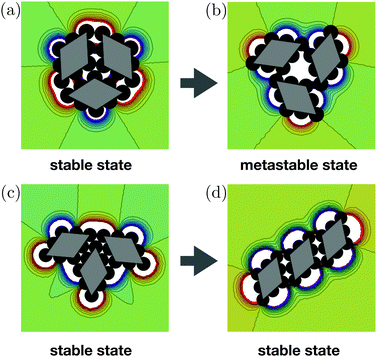 | ||
| Fig. 8 Two initial different stable rhombic states are driven to a single stable isohedral state when capillary charges are transferred from vertices to sides. For the first compact configuration (a), a metastable state (b) is obtained for which three rhombi form a triangular configurations, as observed in Fig. 1. Another configuration (c) leads to a perfect isohedral stable state (d). The blue-green-red color scale indicates the elevation of the liquid interface in arbitrary units. Blue (red) corresponds to a negative (positive) capillary charge, while the green color corresponds to a flat unperturbed interface. | ||
The second behavior is the one of Fig. 7: isohedral lattice is obtained at the end of the process. For that case, each rhombus has the opportunity to rotate. This has been simulated starting with three tiles, as shown in the bottom row of Fig. 8. From that experimental and numerical results, we can conclude that the initial configuration determines the occurrence or not of the metastable configuration.
5 Conclusions
In summary, we performed experiments and simulations for the capillary driven self-assembly of rhombic tiles, forming lattices. The curvature of the particles induce specific positions for the capillary charges involving different interactions and self-assembled lattices.By using a shape memory polymer for creating particles, the self-assembly becomes responsive to the temperature of the liquid. The capillary charges can be transferred from vertices to edges. The resulting patterns disassemble and self-assemble again into new configurations, including metastable states.
The numerical simulations based on multipolar capillary charges are able to capture all observed phenomena, and could be applied to any other self-assembling objects forming complex structures.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by the CESAM Research Unit of the University of Liège.Notes and references
- G. M. Whitesides and B. Grzybowski, Science, 2002, 295, 2418–2421 CrossRef CAS.
- M. Boncheva, D. A. Bruzewicz and G. M. Whitesides, Pure Appl. Chem., 2003, 75, 621–630 CAS.
- N. Bowden, S. R. Oliver and G. M. Whitesides, J. Phys. Chem., 2000, 104, 2714–2724 CrossRef CAS.
- N. Bowden, F. Arias, T. Deng and G. M. Whitesides, Langmuir, 2001, 17, 1757–1765 CrossRef CAS.
- P. W. Rothemund, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 984–989 CrossRef CAS.
- M. Mastrangeli, W. Ruythooren, J. P. Celis and C. V. Hoof, IEEE Trans. Compon., Packag., Manuf. Technol., 2010, 1, 133–149 Search PubMed.
- M. Poty, G. Lumay and N. Vandewalle, New J. Phys., 2014, 16, 023013 CrossRef.
- N. Vandewalle, N. Obara and G. Lumay, Eur. Phys. J. E: Soft Matter Biol. Phys., 2013, 36, 127 CrossRef CAS.
- G. Lumay, N. Obara, F. Weyer and N. Vandewalle, Soft Matter, 2013, 9, 2420–2425 RSC.
- M. M. Nicolson, Proc. Cambridge Philos. Soc., 1949, 45, 288–295 CrossRef.
- P. A. Kralchevsky and K. Nagayama, Adv. Colloid Interface Sci., 2000, 85, 145–192 CrossRef CAS.
- P. A. Kralchevsky and N. D. Denkov, Curr. Opin. Colloid Interface Sci., 2001, 6, 383–401 CrossRef CAS.
- K. D. Danov and P. A. Kralchevsky, Adv. Colloid Interface Sci., 2010, 154, 91–103 CrossRef CAS.
- D. Vella and L. Mahadevan, Am. J. Phys., 2005, 73, 817–825 CrossRef.
- L. Botto, E. P. Lewandowski, M. Cavallaro and K. J. Stebe, Soft Matter, 2012, 8, 9957–9971 RSC.
- J. Voise, M. Schindler, J. Casas and E. Raphael, J. R. Soc., Interface, 2011, 8, 1357–1366 CrossRef.
- J. Bae, N. P. Bende, A. A. Evans, J. H. Na, C. D. Santangelo and R. C. Hayward, Mater. Horiz., 2017, 4, 228–235 RSC.
- C. Mao, V. R. Thalladi, D. B. Wolfe, S. Whitesides and G. M. Whitesides, J. Am. Chem. Soc., 2002, 124, 14508–14509 CrossRef CAS.
- J. Metzmacher, M. Poty, G. Lumay and N. Vandewalle, Eur. Phys. J. E: Soft Matter Biol. Phys., 2017, 40, 108 CrossRef CAS.
- H. Cooray, P. Cicuta and D. Vella, J. Phys.: Condens. Matter, 2012, 24, 284104 CrossRef.
- F. Moisy, M. Rabaud and K. Salsac, Exp. Fluids, 2009, 46, 1021 CrossRef.
- L. Yao, L. Botto, M. Cavallaro, B. J. Bleier, V. Garbin and K. J. Stebe, Soft Matter, 2013, 9, 779 RSC.
- Tilings and patterns, ed. B. Grunbaum and G. C. Shepard, Freeman, 1987 Search PubMed.
- T. Defize, R. Riva, J. M. Raquez, P. Dubois, C. Jérôme and M. Alexandre, Macromol. Rapid Commun., 2011, 32, 1264–1269 CrossRef CAS.
- T. Defize, R. Riva, J. M. Thomassin, C. Jérôme and M. Alexandre, Macromol. Symp., 2011, 309, 154–161 CrossRef.
| This journal is © The Royal Society of Chemistry 2020 |