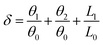Hydrogen peroxide synthesis on porous graphitic carbon nitride using water as a hydrogen source†
Yongyong
Cao
a,
Guobing
Zhou
b,
Xianlang
Chen
a,
Qi
Qiao
b,
Chenxia
Zhao
a,
Xiang
Sun
a,
Xing
Zhong
 a,
Guilin
Zhuang
a,
Guilin
Zhuang
 a,
Shengwei
Deng
a,
Zhongzhe
Wei
a,
Zihao
Yao
a,
Liangliang
Huang
a,
Shengwei
Deng
a,
Zhongzhe
Wei
a,
Zihao
Yao
a,
Liangliang
Huang
 *b and
Jianguo
Wang
*b and
Jianguo
Wang
 *a
*a
aInstitute of Industrial Catalysis, College of Chemical Engineering, State Key Laboratory Breeding Base of Green-Chemical Synthesis Technology, Zhejiang University of Technology, Hangzhou 310032, China. E-mail: jgw@zjut.edu.cn
bSchool of Chemical, Biological and Materials Engineering, University of Oklahoma, Norman, Oklahoma 73019, USA. E-mail: HLL@ou.edu
First published on 28th October 2019
Abstract
Using water as a hydrogen source is a promising strategy for alternative hydrogen peroxide (H2O2) synthesis. By a series of ab initio molecular dynamics (AIMD) simulations and reactive molecular dynamics (RxMD) calculations, fundamental details have been revealed regarding how liquid water interacts with oxygen on a metal-free carbon nitride catalyst, and the two-step reaction mechanism of H2O2 synthesis. Metal-free porous graphitic carbon nitride (g-C5N2) catalysts are also systematically screened by using a thermodynamics approach through the ab initio density functional theory (DFT) method. Key results include: (a) pristine g-C5N2 is most active to catalyze the H2O/O2 reaction and produce H2O2; (b) the adsorption and activation of water at unsaturated carbon sites of g-C5N2 are critical to initiate the H2O/O2 reaction, producing HOO* intermediates; (c) interfacial free water and adsorbed water at g-C5N2 form a synergetic proton transfer cluster to promote HOO* intermediates to form H2O2. To the best of our knowledge, this work presents long-needed theoretical details of direct H2O2 synthesis via the water/oxygen system, which can guide further optimization of carbon-based catalysts for oxygen reduction reactions.
1. Introduction
Hydrogen peroxide (H2O2) has been extensively used for pulp bleaching, wastewater treatment and green oxidization for chemical synthesis.1–3 With the increasing global demand, how to synthesize H2O2via economic and environment friendly processes is a pressing topic. Currently, over 95% of H2O2 is produced using an indirect process, involving energy-intensive multistep anthraquinone oxidation and reduction reactions.1,4 The industrialized process requires a complex and large-scale infrastructure and causes severe pollution to the environment due to the utilization of aromatic chemicals.5 Since the last decade, direct synthesis of H2O2via a two-proton hydrogen/oxygen reaction has attracted much attention.6,7 Various metal and metal oxide catalysts have been proposed and optimized, among which Pd based alloys and nanoparticles seem to be most promising.8–11 Unfortunately, this method is limited by the heavy use of strong acids and halides, which would promote metal catalyst leaching and as-produced H2O2 requires further purification.8 In addition, the hydrogen explosion risk at the operational high pressure continues to be a safety hazard and prevents its commercial scale implementation.12Direct H2O2 synthesis under ambient conditions, utilizing water as a hydrogen source and combining electrocatalysis or photocatalysis techniques, has witnessed tremendous research efforts recently.13–17 Kato et al.18 prepared an Fe–Ru bifunctional catalyst to produce H2O2 from H2O and O2via visible-light photocatalytic reactions. They observed that H2O adsorption on Fe sites is critical to the following O2/H2O reaction. Electrochemically, H2O2 synthesis from H2O and O2 is a typical two-proton/two-electron (2H+/2e−) oxygen reduction reaction (ORR).19 A number of catalysts have been developed with promising efficiency for electrochemical ORR processes, including noble metal-based electrocatalysts (Au,20 Pt21 and Pd17), single-atom catalysts (Pt@TiN22), metal oxide catalysts (Fe3O4 (ref. 23) and Mn–Ru oxide24) and carbon-based electrocatalysts (N-doped, or B, N co-doped mesoporous carbon25–28).
Carbon-based catalysts have been considered as an efficient low-cost, metal-free alternative for green and renewable processes.29–33 For H2O2 synthesis from H2O and O2, Cui et al.34 reported that oxidized carbon nanotubes (CNTs) exhibited a higher selectivity and a better activity for the two-electron oxygen reduction reaction. Yang and co-workers35 found that epoxy and ring ether groups of graphene oxide exhibit an outstanding electrochemical HO2− production, achieving a good activity (overpotential <10 mV), an excellent selectivity(≈100%) and a satisfactory stability (over 15 h at 0.45 V in alkaline media). Despite this encouraging progress of carbon-based catalysts for direct H2O2 synthesis, detailed fundamental understandings are still incomplete. To just name a few, what is the exact catalytic role of carbon-based materials? what is the critical initial step of H2O2 synthesis, water adsorption or oxygen interaction with the catalyst? Is it a one-step reaction or a subsequent two-step proton/electron reaction mechanism? what is the role of the liquid/solid interface?
In this work we report a computational study to reveal the reaction mechanism of direct synthesis of H2O2 by a H2O/O2 reaction on porous graphitic carbon nitride (g-C5N2). Also known as an Aza-fused π-conjugated microporous polymer (Aza-CMP), g-C5N2 has a large number of pyridinic nitrogen dopants at zigzag edges, a large surface area, a high pore/volume ratio, and a high electrical conductivity.36–38 Through a series of AIMD, RxMD and ab initio DFT calculations, the following key results have been elucidated: (a) pristine and hydrogenated g-C5N2 catalysts have been screened and the most effective catalyst is partially hydrogenated metastable g-C5N2; (b) positively charged carbon sites preferentially chemisorb water molecules, which is critical to promote the H2O/O2 interaction and generate HOO* intermediates towards H2O2 production; (c) a collection of near-surface water molecules could form a proton transfer chain, thus conveniently promoting the reaction of HOO* intermediates to form H2O2.
2. Models and simulation methods
2.1 ReaxFF based reactive molecular dynamics simulation
Developed by van Duin and co-workers, the ReaxFF force field provides affordable and accurate atomic details of reactive complex systems.39,40 With a bond order concept, ReaxFF force field parameters have been fitted to reproduce ab initio quantum mechanics calculations. Therefore, ReaxFF based reactive molecular dynamics (RxMD) simulations can describe reaction systems with a similar accuracy to ab initio quantum mechanics methods, and effectively handle systems of hundreds of thousands of molecules. The C/N/O/H ReaxFF force field parameters in this work are extracted from the literature.41 The structural information of g-C5N2 has been obtained by both RxMD and ab initio DFT calculations. As presented in Fig S1,† the results of characteristic bonds and angles agree quantitatively well with each other. It is also worth noting that RxMD simulations were performed where only 500 water and 25 oxygen molecules were placed in the simulation box at 300.0 K. The simulation results indicated that this process was only a simple physical mix, and no OOH* and H2O2 can be observed after 5 ns (Fig. S2†). RxMD simulations were performed with the LAMMPS software package.42 A canonical ensemble was applied where the number of molecules (N), the volume (V), and the temperature (T) remained constant throughout the calculations. The temperature (300.0 K) was maintained by the Nosé–Hoover method with a damping coefficient of 100.0 fs.43,44 The initial velocities of water and oxygen molecules were assigned according to the Boltzmann distribution. g-C5N2 was treated as a flexible solid substrate during the calculation. Newton's equation was integrated by the velocity Verlet algorithm with a time step of 0.25 fs.45 A bond-order change of 20% of the original bond length was used to identify the connectivity and molecular species and monitor the system evolution as a function of simulation time.As illustrated in Fig. 1a, a 2 × 2 supercell was constructed based on the optimized primitive unit cell of g-C5N2 containing 30C and 12 N atoms. The simulation box was composed of a single sheet of g-C5N2, 68.98 Å (y) × 57.71 Å (x), placed in the middle, and a mixture of 500 water molecules and 25 oxygen molecules, as shown in Fig. 1b. The z dimension of the simulation box was 30.0 Å, so that the interaction between neighboring g-C5N2 sheets is negligible. Periodic boundary conditions were applied along the x, y, and z directions. For each RxMD simulation, the system (water, oxygen and g-C5N2) was firstly relaxed to optimize the structures, followed by a 2.0 ns calculation to further equilibrate the system. After that, the data were collected for 200 ps for analysis. It is worth noting that there was no restriction on the system: all g-C5N2, water and oxygen molecules were allowed to relax and move during the simulation.
 | ||
| Fig. 1 The illustrations of (a) the initial configurations of a 2 × 2 g-C5N2 supercell. (b) The simulation box of g-C5N2, H2O and O2 molecules. | ||
2.2 Ab initio DFT and ab initio MD calculations
Three sets of ab initio quantum mechanics calculations have been performed to: (I) screen and evaluate the structural stability of pristine and hydrogenated g-C5N2 models; (II) search and reveal H2O/O2 reaction mechanism details, such as the transition state, the reaction pathway and the activation energy barrier; (III) generate the reaction trajectory and dynamics properties, to compare with RxMD calculation results, and to identify the two-proton/two-electron (2H+/2e−) reaction process.Geometry optimization and transition state calculation were performed by the ab initio DFT method via the Vienna ab initio simulation package (VASP).46–48 The exchange-correlation functional was treated via the generalized gradient approximation (GGA) method with Perdew–Burke–Ernzerhof (PBE).49 Empirical D3 Grimme's method (DFT-D3) was adopted to improve the description of van der Waals interactions in all calculations.50 The planewave kinetic energy cutoff was 450.0 eV. Geometries were optimized until the residual forces were smaller than 0.05 eV Å−1. A 5 × 5 × 1 grid was used for k-point sampling, according to the Monkhorst–Pack method.51 A vacuum of 20.0 Å was added to the z direction to avoid mirror image interactions. The climbing image-modified nudged elastic band (CI-NEB) method was used to evaluate the activation energies of different reaction paths.52 A total of 55 g-C5N2 models were generated to represent pristine and all possible hydrogenations in terms of coverage and distribution of hydrogen atoms. Optimized structures and the corresponding equilibrium energies are summarized in Fig. S3 and Table S1 of the ESI.†
Ab initio molecular dynamics (AIMD) calculations were performed by using the CP2K package.49,53 The system (g-C5N2, water and oxygen) was maintained at 300.0 K using the canonical (NVT) ensemble, where the temperature was controlled via the Nosé–Hoover thermostat.43,54 Each calculation was performed for 2.0 ps with a time step of 0.25 fs. The wave functions were expanded in an optimized double-ζ Gaussian basis set.55 The electrostatic energy cutoff for an auxiliary plane wave basis set was 360.0 Ry.56 Van der Waals interactions were corrected by the Grimme algorithm (DFT-D3).50
2.3 Choice of three simulation methods
While the overall goal of this work is to reveal how water and oxygen react on a carbon nitride catalyst (g-C5N2) to produce hydrogen peroxide, the thermal stability of the catalyst and the diffusion/reaction coupled complex process are worth exploring. Thus, we take advantage of three adopted simulation methods to understand the system. First of all, to mimic experimental g-C5N2 and provide insight into catalyst screening and optimization, a series of ab initio DFT calculations were performed to calculate the Gibbs free energy and evaluate the thermal stability of all g-C5N2 models. Secondly, it is critical to understand the first step of the reaction, the energy barrier and the reaction pathway. Thus, ab initio quantum mechanics methods are appropriate choices. Along this direction, we have performed ab initio DFT and AIMD calculations. Thirdly, H2O2 synthesis is a complex process and it occurs at the gas/liquid/solid interface. Obviously, the adsorption and diffusion of reactants (H2O and O2) to the solid interface (g-C5N2) could be significant parameters. Additionally, after the synthesis reaction, the competitive desorption of H2O2 from the solid interface is also vital to a successful separation and purification of the H2O2 product. The ReaxFF potential has become a powerful computational tool to explore the chemisorption and reactions of complex systems. More importantly, RxMD simulations not only can describe systems composed of hundreds of thousands of atoms but also can archive a trajectory to the time sale of microseconds. Therefore, RxMD was adopted to study such a complex and multiscale system. The three methods complement each other and provide insights from different perspectives.3. Results and discussion
3.1 Gibbs free energy calculation and thermal stability of g-C5N2 models
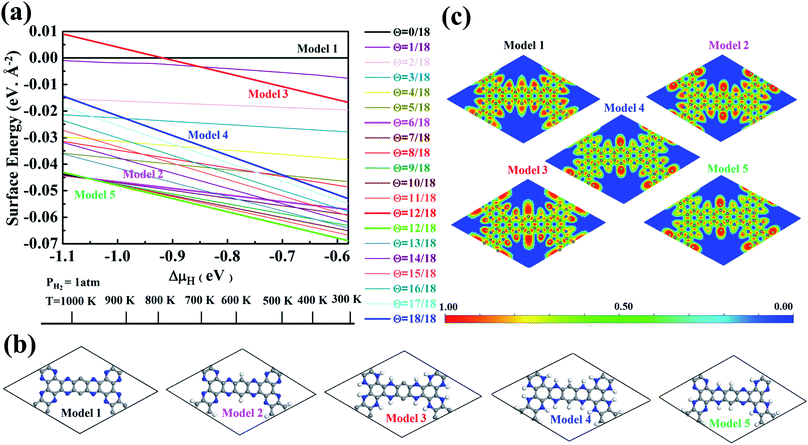
The stability of 55 g-C5N2 models was firstly investigated by the ab initio DFT based thermodynamics approach.57–59 The most stable model generally has the lowest Gibbs free energy. In this work, the surface energy (Ω) is calculated according to eqn (1):60,61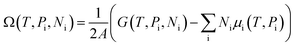 | (1) |
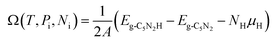 | (2) |
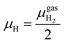 | (3) |
At the studied temperature of 300.0 K, the gas-phase hydrogen could be treated as an ideal gas. Therefore, the chemical potential could be calculated by using eqn (4):
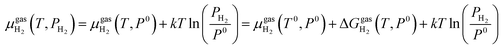 | (4) |
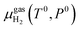 is the chemical potential of the hydrogen molecule in the standard state (T0 = 298.15 K, P0 = 1 atm),
is the chemical potential of the hydrogen molecule in the standard state (T0 = 298.15 K, P0 = 1 atm), 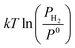 is the pressure-dependent term.
is the pressure-dependent term. 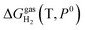 is the temperature-dependent term, referring to the Gibbs free energy change when the temperature changes from T0 = 298.15 K to T = 300.0 K (see Table S2†), while keeping the pressure at P0:
is the temperature-dependent term, referring to the Gibbs free energy change when the temperature changes from T0 = 298.15 K to T = 300.0 K (see Table S2†), while keeping the pressure at P0: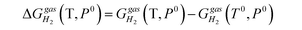 | (5) |
The chemical potential of the hydrogen molecule under standard state conditions is:
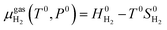 | (6) |
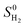 is obtained from the NIST thermodynamic tables,62 and
is obtained from the NIST thermodynamic tables,62 and 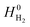 is calculated using experimental data of heat of formation of water:
is calculated using experimental data of heat of formation of water: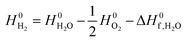 | (7) |
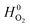 and
and 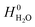 are adopted from the literature. The oxygen gas entropy
are adopted from the literature. The oxygen gas entropy 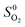 in the standard state is from experimental data. Hence, eqn (2) and (3) yield:
in the standard state is from experimental data. Hence, eqn (2) and (3) yield: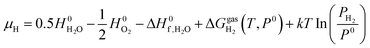 | (8) |
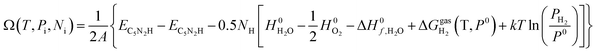 | (9) |
As shown in Fig. S3 and Table S1,† the proposed models are constructed based on the degree of hydrogenation, that is, the number of hydrogen atoms added to pristine g-C5N2. When multiple candidates exist for a same degree of hydrogenation, the most stable model (with the lowest Gibbs free energy) is then selected as the representative one. With this information, 19 out of the total 55 possible g-C5N2 models were selected for the Gibbs free energy calculation to evaluate their thermal stability. The calculations were performed under atmospheric conditions, as a function of variation of hydrogen chemical potential from −0.58 eV to −1.10 eV, which corresponds to the temperature range of 300.0 to 1100.0 K. As shown in Fig. 2a, the Gibbs free energy was expressed as a function of temperature at a fixed partial pressure of hydrogen, PH2 = 1 atm. A more negative Gibbs free energy indicates a better thermal stability of the g-C5N2 model. In addition, the negative slope suggests that the thermal stability generally declines when the temperature increases. According to the Gibbs free energy calculation, the hydrogen coverage (i.e., the degree of hydrogenation) affects the thermal stability. But the dependence is not linear according to the results in Fig. 2a. This is probably due to different activities of C and N sites of g-C5N2. The same degree of hydrogenation could have different hydrogen distributions from C and N sites.
In this work, we selected five models to study their catalytic roles in H2O2 synthesis. As illustrated in Fig. 2b, the models represent respectively pristine (Model 1, no hydrogenation), C-site full hydrogenation (Model 2), N-site full hydrogenation (Model 3), full hydrogenation (Model 4, both C and N sites hydrogenated), and partial hydrogenation (Model 5, C sites fully and N sites partially hydrogenated), which is the most stable model from the Gibbs free energy calculation. The electron localization function (ELF) analysis in Fig. 2c shows the distribution of electrons of the models, where sites with higher electron densities (red color) are preferential to interact with H2O and O2 molecules.
3.2 Preferential water adsorption on g-C5N2
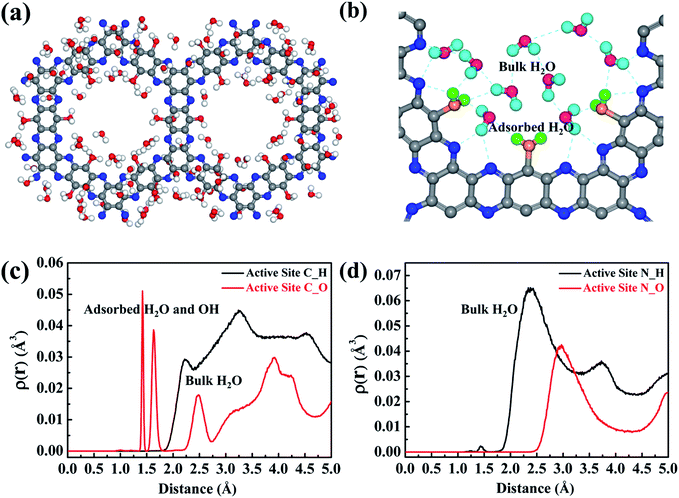
In order to elucidate which reactant (H2O or O2) initiates the reaction, the H2O/g-C5N2 and O2/g-C5N2 systems have been studied separately with the pristine Model 1. Ab initio DFT calculations reveal that O2 and H2O adsorption at the pores of g-C5N2 has stronger binding energies than that of the basal plane of g-C5N2 (Fig. S4†). The adsorption energy is respectively −1.68 eV and −1.14 eV for H2O/g-C5N2 and O2/g-C5N2 at the unsaturated C site, suggesting a preferential interaction between H2O and g-C5N2. The comparison was performed using RxMD simulations where 500H2O molecules or 50O2 molecules were placed to interact with pristine g-C5N2 (Model 1) at 300.0 K. For the O2/g-C5N2 system, only 4 O2 molecules were adsorbed at unsaturated C sites. No preferential interaction between O2/N sites was observed, see Fig. S5 of the ESI.† Meanwhile, for the H2O/g-C5N2 system, as shown in Fig. 3a, water was preferentially distributed to form an ordered ring configuration along the pores of pristine g-C5N2. This phenomenon was also observed via ab initio DFT calculation. A zoom-in snapshot of Fig. 3b clearly reveals three types of water molecules in the system, namely, adsorbed water at unsaturated C sites, water molecules near g-C5N2 which form a hydrogen bonding network with adsorbed water, and bulk water not shown in Fig. 3b for clarity. The Bader charge analysis in Fig. S6† demonstrates that uncoordinated carbon of pristine g-C5N2 carriers a positive charge of 0.18 e by average. This confirms that positively charged carbon of g-C5N2 interacts strongly with water through its negatively charged oxygen atom.The distributions of water near C and N sites are shown in Fig. 3c and d, respectively. In Fig. 3c, the first two peaks around 1.50 Å are from absorbed water. As illustrated in Fig. 3b, adsorbed water generally adopts the ‘v’ configuration, atop of C sites. The adsorbed water still demonstrates a certain degree of freedom, which results in two close peaks at 1.50 Å. The peaks around 2.5 Å and 3.7 Å come from hydrogen-bonded water molecules. Limited by the pore size of g-C5N2, diameter ∼13.82 Å, only two layers of hydrogen bonds (HB) are allowed, as illustrated by the dotted circles in Fig. 3b. The distribution analysis around N sites revealed one significant peak at around 2.97 Å, which represents hydrogen bonds between two adsorbed water molecules. Due to the negative charge, hydrogen of water stays closer to the N sites, at 2.38 Å.
3.3 Reaction mechanism for direct H2O2 synthesis
A series of RxMD and AIMD simulations have been performed to reveal the reaction mechanism of H2O and O2 on g-C5N2 catalysts and the complete process of direct H2O2 synthesis. Fig. 4 presents key snapshots of a representative RxMD simulation, demonstrating how one H2O2 molecule was synthesized by a two-step reaction of H2O/O2 on pristine g-C5N2 (Model 1). It is worth noting that during the RxMD simulation, oxygen and hydrogen were assigned different colors to facilitate tracking of the reaction progress: adsorbed water, oxygen-yellow and hydrogen-green; near surface HB bonded water, oxygen-pink and hydrogen-turquoise; gas-phase oxygen-red. As shown in Fig. 4, step 1 illustrates a critical configuration where water molecules were adsorbed at unsaturated C sites of the pore, and gas-phase oxygen molecules were closer to adsorbed water. From step 1 to step 3, the interaction between O2 and adsorbed water was witnessed by the OH bond length, changing from 2.037 Å to 1.591 Å, and eventually leading to the dissociation of the adsorbed water and the formation of the OOH* intermediate.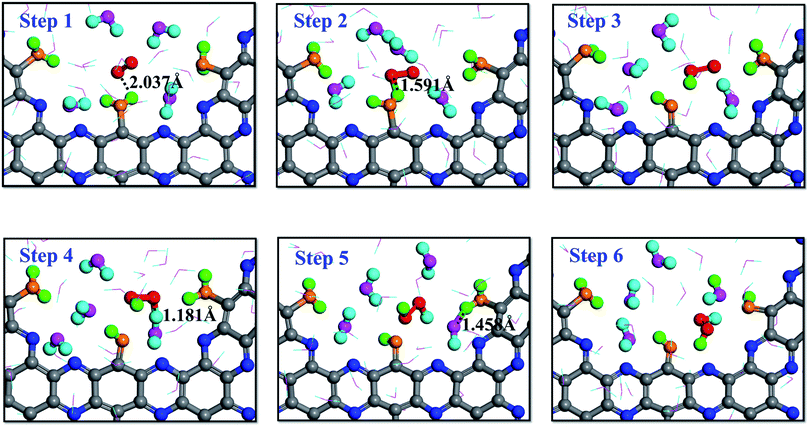 | ||
| Fig. 4 Proton transfer mechanism (PTM) on the dehydrogenated g-C5N2 system: the hydrogen atoms of H2O2 come from adsorbed water and bulk water, respectively. | ||
Snapshots from step 4 to step 6 revealed an interesting proton exchange mechanism involving the newly generated OOH* intermediate, a nearby water molecule and another adsorbed water molecule from the neighboring C site. While the overall result is that one oxygen molecule interacts with two adsorbed water molecules to directly synthesize one H2O2 molecule, the snapshot of step 6 clearly shows that the two hydrogen atoms of the H2O2 molecule came from two different proton donors, which is convincing evidence of the proton exchange event involving near surface water molecules.
It is interesting to note that a different reaction mechanism was also observed from the simulation trajectory, where the O2 molecule interacted successively with two adsorbed H2O molecules. As shown by the trajectory snapshots in Fig. 5, the configuration of step 2 is critical: the O2 molecule diffused to the location where it could simultaneously interact with two adsorbed water molecules. The HOO* intermediate was then produced as a result of the interactions. In addition, since the intermediate was still very close to the other adsorbed water molecule, it could receive the second proton and lead the reaction to completion to produce one H2O2 molecule. The color of hydrogen atoms of H2O2, step 6 in Fig. 5, clearly demonstrates that no free or hydrogen bonded water participated in the two-step reaction process.
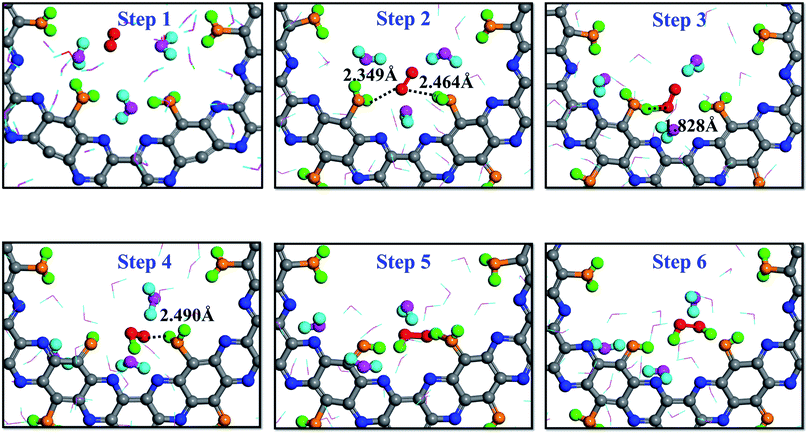 | ||
| Fig. 5 Direct formation mechanism (DFM) on the dehydrogenated g-C5N2 system: the H atoms of H2O2 both come from adsorbed H2O. | ||
The snapshots shown in Fig. 6 are from the AIMD calculation of 5 O2 molecules, 20H2O molecules and a pristine g-C5N2 model. It is worth noting that, due to the high computational cost, there were fewer oxygen and water molecules in the AIMD calculations. But both RxMD and AIMD were performed at 300.0 K with the same g-C5N2 model. The analyses of AIMD and RxMD trajectories give the same conclusion, that is, the first critical step is H2O adsorption at edge unsaturated C sites, followed by O2 interaction with adsorbed water to form a HOO* intermediate. Then, different hydrogen suppliers can interact with HOO* to produce H2O2. Simultaneously, the interaction between adsorbed water and nearby water molecules was also observed, sequentially producing a hydronium ion (H3O+, step 5) and then a Zundel cation (H5O2+, step 6). H2O2 was eventually synthesized as a reaction product between HOO* and H5O2+, as illustrated by steps 8 and 9 in Fig. 6. As the reaction proceeded, OH* or O* would be accumulated on the unsaturated edge-C sites. It is probably challenging to regenerate g-C5N2 by the H2O/O2 system as used in this work. However, convenient techniques are available to recycle the catalyst. Removing OH*/O* and regenerating active sites of carbon-based catalysts can be achieved by electrocatalytic reactions. For example, for 4-electron ORR processes,63–65 adsorbed OH* is hydrogenated and removed in the form of H2O. Liang and co-workers studied the 4-electron ORR of nitrogen doped graphene (N-graphene). Their results demonstrated that the removal of adsorbed OH* from the N-graphene surface that is covered by O with a 1/6 monolayer surface oxygen coverage has a small energy barrier of 0.32 eV in the water solution phase.66 The regeneration depends closely on the form of deactivated g-C5N2 catalysts, the concentration of H3O+ and the applied voltage. To validate the general regeneration process, a proof-of-concept calculation is designed in this work, to mimic a separate electrocatalytic treatment after the successful H2O2 production, to remove surface OH and O groups and regenerate the active carbon sites of g-C5N2. As shown in Fig. S7(a),† six H2O and two H3O+ molecules are placed at the pore of the deactivated g-C5N2 where its edge nitrogen sites are fully hydrogenated and carbon sites are alternatively bonded with OH and O. The AIMD simulation results in Fig. S7(b) and (c)† show that within 0.2 ps H3O+ interacts with oxygen-containing functional groups at edge carbon sites, transforming OH* and O* back to adsorbed water at edge carbon sites, thus regenerating the g-C5N2 catalyst for the next cycle of H2O2 production.
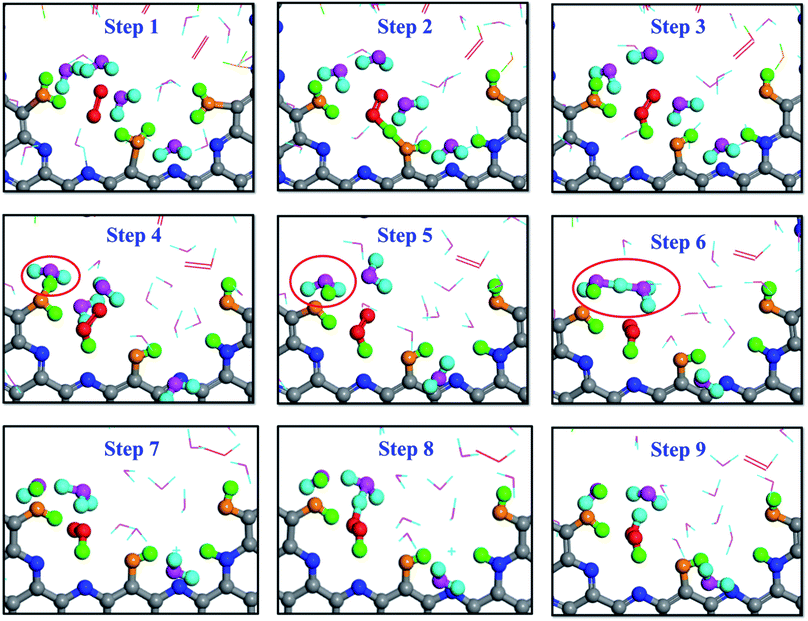 | ||
| Fig. 6 Snapshots of H2O2 production on dehydrogenated g-C5N2 described by the AIMD simulations. Structures corresponding to the reaction path followed by PTM. | ||
Both RxMD and AIMD reveal the same overall reaction mechanism which can be generally described by two sequential steps: (a) the formation of HOO* intermediates, from the interactions between oxygen and adsorbed water; (b) the completion of H2O2 synthesis, by the proton transfer between HOO* and chain-cluster water (or second adsorbed water); (c) H2O* regeneration, by interactions between residual OH* and H3O+ molecules. The key steps are summarized below:
H2O adsorption:
| H2O(bulk) + g-C5N2 → g-C5N2 *H2O(ad) | (R1) |
HOO* formation:
| O2(gas) + H2O(ad) → HOO*(bulk) + –OH(dec) | (R2) |
H2O2 formation:
| HOO*(bulk) + H2O(chain) → H2O2(bulk) + –OH(dec) | (R3.1) |
| HOO*(bulk) + *H2O(ad) → H2O2(bulk) + –OH(dec) | (R3.2) |
H2O chain:
| Hydronium ion: *H2O(ad) + H2O(bulk) → H3O+(bulk) + –OH(dec) | (R3.1a) |
| Zundel cation: H3O+(bulk)+ H2O(bulk) → H5O2+(bulk) | (R3.1b) |
| H2O* regeneration: OH* + H3O+(bulk) → H2O(ad) + H2O(bulk) | (R4) |
For other studied g-C5N2 models where N- or C-sites are hydrogenated, H2O2 was produced by a similar reaction mechanism. The complete process was recorded for a few H2O2 molecules, as shown in Fig. S8–11.† Hydrogenated N-sites (Model 3 and Model 4) are potential proton providers. Different H2O2 molecules have been identified from the calculations: (a) H2O2 synthesized by interacting with an absorbed water and a hydrogenated N-site (Model 3), Fig. S8;† (b) H2O2 synthesized by receiving two hydrogens from the same adsorbed water molecule (Model 3), Fig. S9† (c) H2O2 synthesized by interacting with an absorbed water and a hydrogenated N-site, via a H2O proton transfer chain (Model 4), Fig. S10;† (d) H2O2 synthesized by directly interacting with two hydrogenated N-sites (Model 4), Fig. S11.† Goclon and Winkler67 reported that the oxygen reduction proceeds through a one-step two-electron direct process with a 2.15 eV energy barrier on the amino functionalized g-C3N4 structure. In contrast, for the hydrogenated g-C3N4 catalyst, the two-step single-electron indirect H2O2 synthesis has an energy barrier of 1.78 eV. This indicates that the O2 molecule can directly interact with hydrogenated sites to produce H2O2.
Both RxMD and AIMD calculations confirm the direct H2O2 synthesis from chemisorbed water and gaseous colliding oxygen molecules, which is known as the Eley–Rideal (ER) reaction. A direct ER reaction is generally expected to occur only when there is a rather small activation barrier to the reaction, such as a gas-phase radical reactant which undergoes an exothermic reaction. In this work, we adopted the CI-NEB method to study the reaction pathway and activation energy for producing HOO* intermediates and H2O2.
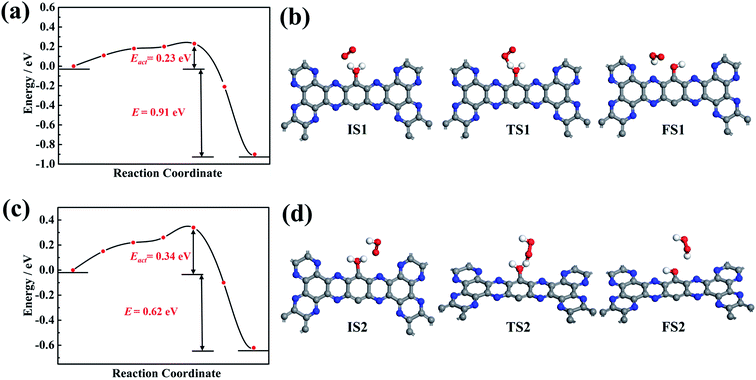
As shown in Fig. 7a, for the HOO* intermediate, the initial configuration in the system has a gaseous O2 and one adsorbed H2O molecule at g-C5N2. While the final configuration has a HOO* intermediate and OH-functionalized g-C5N2. For the initial configuration, upon water adsorption at the unsaturated C sites, the O–H bond was elongated, changing from 0.972 Å of the bulk to 1.110 Å. The transition state was identified in which the gaseous O2 was interacting with the adsorbed water, to the extent that the adsorbed water has two equally elongated O–H bonds, one with the gaseous O2 and the other from the adsorbed water. The calculation revealed that the activation energy (Eact) for HOO* formation was 0.23 eV, and the overall reaction was exothermic, releasing 0.91 eV from the system. The exothermic nature indicates that the proton transfer from adsorbed water to a nearby O2 molecule is energetically favored.
Fig. 7b shows the reaction pathway by which the HOO* intermediate received the second proton to generate a H2O2 molecule. As revealed by RxMD and AIMD calculations, this reaction generally involves ‘free’ water molecules to transfer protons from adsorbed water. It was also observed, see Fig. 5, that the gaseous O2 could interact successively with two adsorbed H2O molecules to produce a H2O2 molecule, which does not require much diffusion of the HOO* intermediate. It is also worth pointing out that there is no ‘free’ water considered in the CI-NEB calculations, and only the direct reaction between HOO* and adsorbed water to form H2O2 was calculated. The result suggested that a larger activation energy (0.34 eV) was necessary to overcome the reaction barrier. But the overall reaction was also exothermic, discharging 0.63 eV from the system.
3.4 Proton transfer along hydrogen bonds
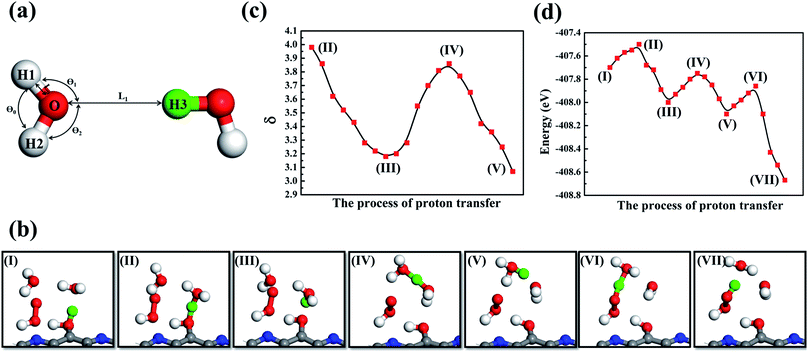
Proton transfer is essential to many aqueous processes, from ion channel function to enzymatic reactions.68–70 Especially for photocatalytic71,72 and electrocatalytic reactions,73,74 simultaneous gain or loss of electrons and protons frequently occur in aqueous solutions. Nevertheless, not enough emphasis has been placed on the effect of proton transfer in aqueous reactions. Experimentally, direct observation of proton transfer is challenging due to the short lifetime of intermediates and the difficulty of distinguishing protons, electrons and their coupling with solvent molecules. For example, Yu and co-workers75 investigated the Langmuir–Hinshelwood (LH) and ER mechanisms for the ORR on graphene sheets. They performed ab initio DFT calculations to mimic ER reactions under an alkaline environment, with H shuttling through one or two water molecules. Other theoretical efforts of understanding proton transfer mechanisms have been summarized in recent reviews.76–85 It has been demonstrated that the proton transfer can largely determine the energy profile and reaction pathway. However, as far as we are aware, there is no quantitative description of proton transfer in ORR processes.Here, we propose a proton transfer descriptor based on the structural information of involved water molecules. As illustrated in Fig. 8a, the descriptor δ describes the geometric requirement, assuming that proton transfer occurs when the oxygen atoms of water molecules have three identical hydrogen atoms nearby. Therefore, breaking O–H bonds and exchanging hydrogen atoms (protons) require a negligible energy penalty. The δ value is estimated by using the equation:
Previous studies observed Eigen (H9O4+)86,87 and H5O2+ (ref. 88) evolution from bulk water. This suggests that proton transfer events involving two or three water molecules are energetically favorable. In this work, dehydrogenated carbon sites provide localized positive charge centers, which promote H2O adsorption and subsequent H5O2+ ion formation (Fig. 8b). Representative snapshots in Fig. 8b demonstrate how near-surface water molecules participate in proton transfer events and promote the HOO* intermediate to receive a proton and thus produce H2O2. The AIMD trajectory reveals that two bulk water molecules are involved in this proton transfer process (Fig. 8b(I)): firstly, as shown in Fig. 8b(II), the adsorbed H2O interacted with a nearby bulk H2O molecule to form a hydronium H3O+ and an OH functional group of g-C5N2, and after that the adsorbed water gave up the proton (green color), see Fig. 8b(III). The hydronium H3O+ then interacted with another bulk water molecule to form a H5O2+ cation, as shown in Fig. 8b(IV). It is worth noting that the oxygen–oxygen distance, between the second bulk water molecule and the previously formed H3O+, is about 2.70 Å which is within a typical hydrogen bond cutoff.89 This suggests that the second water molecule could easily accept a hydrogen atom from H3O+, forming a new hydronium H3O+, see Fig. 8b(V). Since the new H3O+ was much closer to the HOO* intermediate, it easily gives up a proton to HOO* to promote the formation of H2O2 (Fig. 8b(VI and VII)). Additionally, direct proton exchange was also observed between adsorbed H2O molecules and g-C5N2, see Fig. S12.†
It has been reported89 that a Zundel proton is formed when two water molecules, the oxygen–oxygen distance, are within 1.35 Å. To quantify proton transfer events, we adopted the same cut-off of 1.35 Å to determine whether a proton transfer event could occur between two water molecules. In addition, since the four atoms of the hydronium ion H3O+ adopt a trigonal pyramidal geometry, an angular term is necessary to describe proton transfer events. Using the definition of φ, the dynamics trajectory was monitored. As shown in Fig. 8b, in the process of forming the first H3O+, the value of the bulk and adsorbed H2O molecules gradually decreases (II to III), eventually reaching the minimum where the bulk water molecule accepted a proton from the adsorbed water, forming H3O+. From (III to IV) of Fig. 8b, the H3O+ interacted with a second water molecule, firstly forming the Zundel proton H5O2+, where increased to reach the maximum at (IV). The value then decreased and reached the minimum again, where the H5O2+ decomposed to a new H3O+. The function is similar to the double-minimum potentials that are often used to describe hydrogen bonds and can provide a handy description of proton transfer dynamics. In addition, to better interpret the proton transfer and the H2O2 formation, energetics information of each snapshot has been obtained via ab initio DFT. As shown in Fig. 8d, three energy barriers were identified for one successful proton transfer and one HOO hydrogenation event. The energy barrier of forming the first and second H3O+ is 0.20 eV and 0.25 eV (Fig. 8d(I–V)), respectively. More importantly, *HOO only needed to overcome a barrier of 0.24 eV to form H2O2 by proton transfer.
3.5 H2O2 evolution on different g-C5N2 surfaces
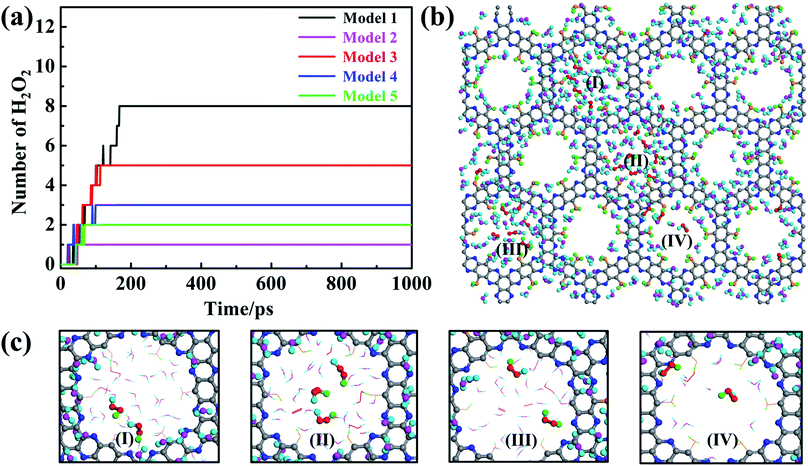
The aforementioned results have clearly demonstrated that pristine dehydrogenated g-C5N2 is effective to catalyze the H2O/O2 reaction and produce H2O2. The two-step reaction mechanism depends critically on both adsorbed water (at unsaturated C sites) and free water (near the pores of g-C5N2). It is important to evaluate the catalytic performance of other models where C and N sites are partially or fully hydrogenated. Similar to Sec. 2.1, 500H2O and 25 O2 molecules were randomly placed on both sides of the g-C5N2 model, of the size 68.98 Å (y) × 57.71 Å (x). RxMD calculations were performed at 300.0 K for all five models and the results are shown in Fig. 9a. Firstly, g-C5N2 showed a general catalytic activity to H2O/O2 reactions and H2O2 was produced from all five systems. The best yield (eight H2O2) was from the pristine g-C5N2 (Model 1, no hydrogenation). And two different types of H2O2 molecules were synthesized from different hydrogen resources, see Fig. 9c. This phenomenon was also observed in AIMD simulations of Model 3 (Fig. S8 and S9†) and Model 4 (Fig. S10 and S11†). However, only five H2O2 molecules were produced in Model 3 where the C-sites are not hydrogenated and the N sites are fully hydrogenated. The following two observations could explain this result: (a) the transition state calculation indicated that the activation energy of O2 reaction with H of the edge-N-H species is 0.58 eV (Fig S14(a)†), which is higher than that of O2 reaction with adsorbed water at the edge C sites. The activation energy for HOO* and H2O2 formation was respectively only 0.23 eV and 0.32 eV for Model 1. Thus, O2 shall preferentially interact with the adsorbed H2O. (b) As shown in Fig S8,† AIMD calculations reveal that when adsorbed H2O of edge C sites and hydrogenated H of edge N sites coexist, O2 preferentially reacted with adsorbed H2O to form HOO* intermediates. Those HOO* intermediates could then capture H from those edge N sites to form H2O2. Based on these observations, we conclude that O2 reaction with two adsorbed water molecules, as shown for Model 1, is energetically favored and that Model 1 is more active than Mode 3 for the studied H2O2 synthesis.For Model 2 (C-site fully hydrogenated), Model 4 (C-site and N-site fully hydrogenated) and Model 5 (the most stable model, with C sites fully and N sites partially hydrogenated), the yield is relatively lower, only 1, 3 and 2H2O2 molecules were produced respectively during the simulation of 1000 ps. According to AIMD results, O2 can only capture protons from the hydrogenated N sites due to the very stable C–H bonds. In addition, the adsorption configurations of H2O and O2 on Model 5 have been optimized via ab initio DFT calculations based on Bader charge analysis (Fig. S13a†). The adsorption energy of O2 is −0.95 eV (Fig. S13b†), and that of H2O is only −0.05 eV (Fig. S13c†). Stronger O2 adsorption can significantly weaken the bond energy of O2, which will reduce the selectivity of H2O2 and produce water as a side reaction product. Thus, the number of formed H2O2 molecules of Model 4 are more than that of Model 2 and Model 5 with all the edge-C sites hydrogenated.
Although the Gibbs free energy was calculated to evaluate possible g-C5N2 hydrogenation, other factors, such as defects and solutions, could also affect the stability and reactivity of g-C5N2 catalysts. If one only considers the best reactivity, as shown in Fig. 9a, the pristine g-C5N2, in which neither edge nitrogen nor carbon sites are hydrogenated, demonstrates the best catalytic performance, while the most stable g-C5N2 model (Model 5) has a relatively poor catalytic performance towards H2O2 synthesis. The activity is the major contributor to H2O2 synthesis, but the successful application of g-C5N2 materials shall also depend strongly on the stability. Regardless of the mechanism or yield of H2O2 formation analysis, both suggest that unsaturated edge carbon sites do not promote immediate water dissociation and could be reactivated afterwards. We expect that those unsaturated edge sites are available both from the synthesized g-C5N2 and during the process of catalyzing H2O/O2 reactions.
4. Conclusion
In summary, this work represents a computational study of direct H2O2 synthesis from H2O and O2 on a metal-free porous graphitic carbon nitride catalyst. Through a combination of ab initio molecular dynamics simulation, reactive molecular dynamics (RxMD) calculation, and the ab inito density functional theory based thermodynamics approach, g-C5N2 models with different hydrogenation have been examined to catalyze H2O/O2 reactions for H2O2 production. The Gibbs free energy calculation and the thermal stability discussion of various g-C5N2 models could be a general protocol to screen and evaluate carbon-based materials which are doped with a wide range of other elements. The two-step reaction mechanism has been elucidated, which involves sequentially the adsorption and activation of water at unsaturated C sites of g-C5N2, producing HOO* intermediates, and synergetic proton transfer to promote HOO*-to-H2O2 reactions, via clusters of free and adsorbed water. Other fundamental facts include that pristine g-C5N2 is the most active catalyst and that a preferential water adsorption (instead of oxygen adsorption) on g-C5N2 is critical to direct H2O2 synthesis. Future development of new catalysts could take this as a general criterion to design reactive sites and optimize catalyst geometry, to simultaneously favor water activation at reactive sites and water-chain assisted fast proton transfer processes. This work paves the way for using carbon-based sustainable catalysts for direct H2O2 synthesis via this promising water/oxygen strategy. In addition, the fundamental insight could also shed light on selecting and designing other green catalysts for heterogeneous oxygen hydrogenation reactions.Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
Y. Y. Cao and J. G. Wang acknowledge the support by the National Natural Science Foundation of China (Grant No 21625604, 21671172, 21776251 and 21706229). L.L. Huang acknowledges the U.S. National Science Foundation (NSF) for support through Grant CHE-1710102. We are very pleased to thank the OU Supercomputing Center for Education & Research (OSCER) at the University of Oklahoma for their dedicated support.References
- J. M. Campos-Martin, G. Blanco-Brieva and J. L. G. Fierro, Angew. Chem., Int. Ed., 2006, 45, 6962–6984 CrossRef CAS PubMed.
- E. Brillas, I. Sires and M. A. Oturan, Chem. Rev., 2009, 109, 6570–6631 CrossRef CAS PubMed.
- N. Agarwal, S. J. Freakley, R. U. McVicker, S. M. Althahban and N. Dimitratos, Science, 2017, 358, 223–227 CrossRef CAS PubMed.
- Y. Yi, L. Wang, G. Li and H. Guo, Catal. Sci. Technol., 2016, 6, 1593–1610 RSC.
- J. Garcia-Serna, T. Moreno, P. Biasi, M. J. Cocero, J. P. Mikkola and T. O. Salmi, Green Chem., 2014, 16, 2320–2343 RSC.
- J. K. Edwards, B. Solsona, E. N. Ntainjua, A. F. Carley, A. A. Herzing, C. J. Kiely and G. J. Hutchings, Science, 2009, 323, 1037–1041 CrossRef CAS PubMed.
- Q. Liu, J. C. Bauer, R. E. Schaak and J. H. Lunsford, Angew. Chem., Int. Ed., 2008, 47, 6221–6224 CrossRef CAS.
- G. M. Lari, B. Puertolas, M. Shahrokhi, N. Lopez and J. Perez-Ramirez, Angew. Chem., Int. Ed., 2017, 56, 1775–1779 CrossRef CAS PubMed.
- J. S. Jirkovský, I. Panas, E. Ahlberg, M. Halasa, S. Romani and D. J. Schiffrin, J. Am. Chem. Soc., 2011, 133, 19432–19441 CrossRef PubMed.
- I. Kim, M.-g. Seo, C. Choi, J. S. Kim, E. Jung, G.-H. Han, J.-C. Lee, S. S. Han, J.-P. Ahn, Y. Jung, K.-Y. Lee and T. Yu, ACS Appl. Mater. Interfaces, 2018, 10, 38109–38116 CrossRef CAS.
- E. Pizzutilo, S. J. Freakley, S. Cherevko, S. Venkatesan, G. J. Hutchings, C. H. Liebscher, G. Dehm and K. J. J. Mayrhofer, ACS Catal., 2017, 7, 5699–5705 CrossRef CAS.
- Y. Shiraishi, Y. Kofuji, H. Sakamoto, S. Tanaka, S. Ichikawa and T. Hirai, ACS Catal., 2015, 5, 3058–3066 CrossRef CAS.
- Y. Isaka, Y. Kawase, Y. Kuwahara, K. Mori and H. Yamashita, Angew. Chem., Int. Ed., 2019, 58, 5402–5406 CrossRef CAS.
- S. Zhao, T. Guo, X. Li, T. Xu, B. Yang and X. Zhao, Appl. Catal., B, 2018, 224, 725–732 CrossRef CAS.
- M. Gryszel, A. Markov, M. Vagin and E. D. Głowacki, J. Mater. Chem. A, 2018, 6, 24709–24716 RSC.
- X. Shi, S. Siahrostami, G.-L. Li, Y. Zhang, P. Chakthranont, F. Studt, T. F. Jaramillo, X. Zheng and J. K. Nørskov, Nat. Commun., 2017, 8, 701 CrossRef.
- S. Siahrostami, A. Verdaguer-Casadevall, M. Karamad, D. Deiana, P. Malacrida, B. Wickman, M. Escudero-Escribano, E. A. Paoli, R. Frydendal, T. W. Hansen, I. Chorkendorff, I. E. L. Stephens and J. Rossmeisl, Nat. Mater., 2013, 12, 1137–1143 CrossRef CAS PubMed.
- S. Kato, J. Jung, T. Suenobu and S. Fukuzumi, Energy Environ. Sci., 2013, 6, 3756 RSC.
- I. Yamanaka and T. Murayama, Angew. Chem., Int. Ed., 2008, 47, 1900–1902 CrossRef CAS PubMed.
- H. Jing, Q. F. Zhang, N. Large, C. M. Yu, D. A. Blom, P. Nordlander and H. Wang, Nano Lett., 2014, 14, 3674–3682 CrossRef CAS.
- C. H. Choi, H. C. Kwon, S. Yook, H. Shin, H. Kim and M. Choi, J. Phys. Chem. C, 2014, 118, 30063–30070 CrossRef CAS.
- S. Yang, J. Kim, Y. J. Tak, A. Soon and H. Lee, Angew. Chem., Int. Ed., 2016, 55, 2058–2062 CrossRef CAS.
- W. R. P. Barros, Q. L. Wei, G. X. Zhang, S. H. Sun, M. R. V. Lanza and A. C. Tavares, Electrochim. Acta, 2015, 162, 263–270 CrossRef CAS.
- M. B. Zakaria, C. Li, M. Pramanik, Y. Tsujimoto, M. Hu, V. Malgras, S. Tominaka and Y. Yamauchi, J. Mater. Chem. A, 2016, 4, 9266–9274 RSC.
- S. Chen, Z. Chen, S. Siahrostami, D. Higgins, D. Nordlund, D. Sokaras, T. R. Kim, Y. Liu, X. Yan, E. Nilsson, R. Sinclair, J. K. Nørskov, T. F. Jaramillo and Z. Bao, J. Am. Chem. Soc., 2018, 140, 7851–7859 CrossRef CAS.
- T.-P. Fellinger, F. Hasché, P. Strasser and M. Antonietti, J. Am. Chem. Soc., 2012, 134, 4072–4075 CrossRef CAS.
- L. Han, Y. Sun, S. Li, C. Cheng, C. E. Halbig, P. Feicht, J. L. Hübner, P. Strasser and S. Eigler, ACS Catal., 2019, 9, 1283–1288 CrossRef CAS.
- J. Park, Y. Nabae, T. Hayakawa and M. a. Kakimoto, ACS Catal., 2014, 4, 3749–3754 CrossRef CAS.
- Y. Cao, S. Deng, Q. Fang, X. Sun, C. Zhao, J. Zheng, Y. Gao, H. Zhuo, Y. Li, Z. Yao, Z. Wei, X. Zhong, G. Zhuang and J. Wang, Nanotechnology, 2019, 30, 335403 CrossRef CAS.
- K. Gong, F. Du, Z. Xia, M. Durstock and L. Dai, Science, 2009, 323, 760–764 CrossRef CAS.
- Z. Pan, K. Wang, Y. Wang, P. Tsiakaras and S. Song, Appl. Catal., B, 2018, 237, 392–400 CrossRef CAS.
- L. Tao, Q. Wang, S. Dou, Z. Ma, J. Huo, S. Wang and L. Dai, Chem. Commun., 2016, 52, 2764–2767 RSC.
- P. Zhang, D. Sun, A. Cho, S. Weon, S. Lee, J. Lee, J. W. Han, D.-P. Kim and W. Choi, Nat. Commun., 2019, 10, 940 CrossRef.
- Z. Lu, G. Chen, S. Siahrostami, Z. Chen, K. Liu, J. Xie, L. Liao, T. Wu, D. Lin, Y. Liu, T. F. Jaramillo, J. K. Norskov and Y. Cui, Nat. Catal., 2018, 1, 156–162 CrossRef CAS.
- H. W. Kim, M. B. Ross, N. Kornienko, L. Zhang, J. Guo, P. Yang and B. D. McCloskey, Nat. Catal., 2018, 1, 282–290 CrossRef.
- V. Briega-Martos, A. Ferre-Vilaplana, A. de la Peña, J. L. Segura, F. Zamora, J. M. Feliu and E. Herrero, ACS Catal., 2016, 7, 1015–1024 CrossRef.
- Y. Kou, Y. Xu, Z. Guo and D. Jiang, Angew. Chem., Int. Ed., 2011, 50, 8753–8757 CrossRef CAS PubMed.
- Z.-D. Yang, W. Wu and X. C. Zeng, J. Mater. Chem. C, 2014, 2, 2902–2907 RSC.
- A. C. T. van Duin, S. Dasgupta, F. Lorant and W. A. Goddard, J. Phys. Chem. A, 2001, 105, 9396–9409 CrossRef CAS.
- K. Chenoweth, A. C. T. van Duin and W. A. Goddard III, J. Phys. Chem. A, 2008, 112, 1040–1053 CrossRef CAS.
- L. L. Huang, M. Seredych, T. J. Bandosz, A. C. T. van Duin, X. H. Lu and K. E. Gubbins, J. Chem. Phys., 2013, 139, 194707 CrossRef.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- S. Nose, J. Chem. Phys., 1984, 81, 511–519 CrossRef CAS.
- W. G. Hoover, Phys. Rev. A, 1985, 31, 1695–1697 CrossRef PubMed.
- L. Verlet, Phys. Rev., 1967, 159, 98–103 CrossRef CAS.
- P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- R. A. Evarestov and V. P. Smirnov, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 233101 CrossRef.
- G. Henkelman, B. P. Uberuaga and H. Jonsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128 CrossRef CAS.
- W. G. Hoover, Phys. Rev. A, 1985, 31, 1695–1697 CrossRef PubMed.
- J. VandeVondele and J. Hutter, J. Chem. Phys., 2007, 127, 114105 CrossRef.
- G. Lippert, J. Hutter and M. Parrinello, Mol. Phys., 1997, 92, 477–487 CrossRef CAS.
- F. Bottin, F. Finocchi and C. Noguera, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 13 CrossRef.
- E. Heifets, S. Piskunov, E. A. Kotomin, Y. F. Zhukovskii and D. E. Ellis, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 13 Search PubMed.
- Q. Cai, J.-g. Wang, Y. Wang and D. Mei, J. Phys. Chem. C, 2016, 120, 19087–19096 CrossRef CAS.
- D. Gao, H. Zhou, F. Cai, D. Wang, Y. Hu, B. Jiang, W.-B. Cai, X. Chen, R. Si, F. Yang, S. Miao, J. Wang, G. Wang and X. Bao, Nano Res., 2017, 10, 2181–2191 CrossRef CAS.
- K. Reuter and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 045407 CrossRef.
- http://https://webbook.nist.gov/ .
- R. Cao, J.-S. Lee, M. Liu and J. Cho, Adv. Energy Mater., 2012, 2, 816–829 CrossRef CAS.
- Z. L. Wang, D. Xu, J. J. Xu and X. B. Zhang, Chem. Soc. Rev., 2014, 43, 7746–7786 RSC.
- R. Ma, G. Lin, Y. Zhou, Q. Liu, T. Zhang, G. Shan, M. Yang and J. Wang, npj Comput. Mater., 2019, 5, 78 CrossRef.
- L. Yu, X. Pan, X. Cao, P. Hu and X. Bao, J. Catal., 2011, 282, 183–190 CrossRef CAS.
- J. Goclon and K. Winkler, Appl. Surf. Sci., 2018, 462, 134–141 CrossRef CAS.
- O. Gerlits, T. Wymore, A. Das, C. H. Shen, J. M. Parks, J. C. Smith, K. L. Weiss, D. A. Keen, M. P. Blakeley, J. M. Louis, P. Langan, I. T. Weber and A. Kovalevsky, Angew. Chem., Int. Ed., 2016, 55, 4924–4927 CrossRef CAS.
- C. T. Supuran, Biochem. J., 2016, 473, 2023–2032 CrossRef CAS.
- E. Nango, A. Royant, M. Kubo, T. Nakane, C. Wickstrand, T. Kimura, T. Tanaka, K. Tono, C. Y. Song, R. Tanaka, T. Arima, A. Yamashita, J. Kobayashi, T. Hosaka, E. Mizohata, P. Nogly, M. Sugahara, D. Nam, T. Nomura, T. Shimamura, D. Im, T. Fujiwara, Y. Yamanaka, B. Jeon, T. Nishizawa, K. Oda, M. Fukuda, R. Andersson, P. Bath, R. Dods, J. Davidsson, S. Matsuoka, S. Kawatake, M. Murata, O. Nureki, S. Owada, T. Kameshima, T. Hatsui, Y. Joti, G. Schertler, M. Yabashi, A. N. Bondar, J. Standfuss, R. Neutze and S. Iwata, Science, 2016, 354, 1552–1557 CrossRef CAS.
- C. Chen, T. Shi, W. Chang and J. Zhao, ChemCatChem, 2015, 7, 724–731 CrossRef CAS.
- K. Yamamoto and K. Takatsuka, Phys. Chem. Chem. Phys., 2018, 20, 6708–6725 RSC.
- A. Badalyan and S. S. Stahl, Nature, 2016, 535, 406–410 CrossRef CAS.
- C. W. Lee, J. S. Hong, K. D. Yang, K. Jin, J. H. Lee, H.-Y. Ahn, H. Seo, N.-E. Sung and K. T. Nam, ACS Catal., 2018, 8, 931–937 CrossRef CAS.
- Q. Ly, B. V. Merinov, H. Xiao, W. A. Goddard and T. H. Yu, J. Phys. Chem. C, 2017, 121, 24408–24417 CrossRef CAS.
- M. T. M. Koper, Chem. Sci., 2013, 4, 2710–2723 RSC.
- U. W. Schmitt and G. A. Voth, J. Chem. Phys., 1999, 111, 9361–9381 CrossRef CAS.
- S. Hammes-Schiffer, Acc. Chem. Res., 2001, 34, 273–281 CrossRef CAS.
- J. M. Saveant, Acc. Chem. Res., 1993, 26, 455–461 CrossRef CAS.
- S. Scheiner, Acc. Chem. Res., 1985, 18, 174–180 CrossRef CAS.
- M. H. V. Huynh and T. J. Meyer, Chem. Rev., 2007, 107, 5004–5064 CrossRef CAS.
- D. R. Weinberg, C. J. Gagliardi, J. F. Hull, C. F. Murphy, C. A. Kent, B. C. Westlake, A. Paul, D. H. Ess, D. G. McCafferty and T. J. Meyer, Chem. Rev., 2012, 112, 4016–4093 CrossRef CAS.
- R. I. Cukier and D. G. Nocera, Annu. Rev. Phys. Chem., 1998, 49, 337–369 CrossRef CAS.
- J. M. Mayer, Annu. Rev. Phys. Chem., 2004, 55, 363–390 CrossRef CAS PubMed.
- S. Hammes-Schiffer and A. A. Stuchebrukhov, Chem. Rev., 2010, 110, 6939–6960 CrossRef CAS PubMed.
- M. Eigen, Angew. Chem., 1963, 75, 489–508 CrossRef CAS.
- M. Eigen, Angew. Chem., Int. Ed., 1964, 3, 1–72 CrossRef.
- G. Zundel, Adv. Chem. Phys., 2000, 111, 1–217 CAS.
- D. Marx, ChemPhysChem, 2006, 7, 1848–1870 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ta08103h |
| This journal is © The Royal Society of Chemistry 2020 |