Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Solvothermal synthesis of Sn3N4 as a high capacity sodium-ion anode: theoretical and experimental study of its storage mechanism†
Samuel D. S.
Fitch
a,
Giannantonio
Cibin
b,
Steven P.
Hepplestone
cd,
Nuria
Garcia-Araez
 a and
Andrew L.
Hector
a and
Andrew L.
Hector
 *a
*a
aSchool of Chemistry, University of Southampton, Southampton SO17 1BJ, UK. E-mail: A.L.Hector@soton.ac.uk
bDiamond Light Source Ltd, Diamond House, Harwell Science and Innovation Campus, Didcot, Oxfordshire OX11 0DE, UK
cSchool of Physics and Astronomy, University of Exeter, Stocker Road, Exeter EX4 4QL, UK
dDeregallera Ltd, Unit 2 De Clare Court, Pontygwindy Industrial Estate, Caerphilly CF83 3HU, UK
First published on 21st July 2020
Abstract
A new simple and scalable method to synthesise spinel-structured Sn3N4 has been developed using SnCl4 and LiNH2 precursors under solvothermal conditions. Nanocrystalline Sn3N4 with a crystallite size < 10 nm was produced and tested as anode material in sodium half cells, demonstrating a very high reversible (de-sodiation) capacity of ∼850 mA h g−1 measured over 50 cycles, the highest reported reversible capacity for a sodium anode apart from sodium itself. Ex situ X-ray absorption spectroscopy and X-ray diffraction show that the electrochemical reactions are reversible and that Sn3N4 is recovered upon re-oxidation. X-ray diffraction shows that the peaks associated with Sn3N4 reflections become narrower during discharge (reduction), evidencing that the smaller Sn3N4 particles are primarily involved in the electrochemical reactions, and broadening of the peaks is reversibly recovered upon oxidation. The analysis of the near edge X-ray absorption data (XANES) shows that the Sn oxidation state decreases during reduction and nearly recovers the initial value during oxidation. DFT calculations suggest that the insertion of Na into the Sn3N4 surface followed by substitution of tetrahedral Sn by Na is energetically favourable, and evidence of the removal of tetrahedral Sn from the spinel Sn3N4 structure is obtained from the analysis of the extended X-ray absorption fine-structure (EXAFS) measurements of reduced electrodes, which also show the recovery of the pristine structure at the end of oxidation. DFT also shows that Sn substitution by Na is only favourable at the Sn3N4 surface (not for bulk Sn3N4), in agreement with the electrochemical characterisation that shows that controlling the nanoparticle size is crucial to achieve full utilisation of Sn3N4 (and thus high capacity).
Introduction
Use of lithium-ion batteries (LIBs) in electrical energy storage is undergoing rapid growth due to their high energy density and long cycling stability. However, demand for battery grade lithium carbonate has up driven costs for manufacturing LIBs.1,2 The renewed interest in sodium-ion batteries (SIBs) is in part due to the high abundance, low cost and wide geographical distribution of the alkali metal. Sodium is the sixth most abundant element and is found both in sea water and in various mineral forms.3,4 The metal shares physico-chemical properties with lithium, and sodium analogues of LIB positive electrode (cathode) materials, including layered transition metal oxides (NaxMO2 where M = Ni, Co, Mn etc.) and polyanionic compounds such as NaFePO4, often perform well.5–9For SIBs, the anode is still a considerable challenge. For LIBs, the standard anode material is graphite, however the larger ionic radius of sodium ions (1.02 Å for Na+, 0.76 Å for Li+) leads to sluggish reaction kinetics, lower capacities and poor cycling stability in sodium-ion cells. Other carbon materials in the form of amorphous and hard carbon are able to accommodate sodium ions, delivering reversible capacities of up to ∼350 mA h g−1.10–12
Tin-based alloying materials have been studied as alternative anodes for SIBs. The full sodiation of Sn to Na15Sn4 has a theoretical capacity of 847 mA h g−1.13,14 However, Sn undergoes a volume variation of 420% during alloying/dealloying with Na. The large volume change imposed on the metallic Sn particles leads to pulverization, delamination and loss of conduction pathways, although nanostructuring does improve stability. Tin-based binary materials (e.g. SnO2, SnS, Sn4P3) can mitigate the stresses imposed on the electrode by the formation of a matrix structure during initial reduction (Sn + NaxMy),15–20 as well as offering possible extra capacity by the combination of conversion and alloying processes. The most studied of these is SnO2, owing to its high theoretical capacity (1378 mA h g−1), low redox potential and ease of synthesis.21,22 However, the material suffers from a large initial irreversible capacity loss, low electronic conductivity and poor cyclability.23–25 Nano-structuring of conversion materials and formation of composites with carbon structures have yielded significant improvements in their electrochemical performance. Some of the best of these are summarised in Table 1.
| Material | Current (mA g−1) | First sodiation capacity (mA h g−1) | First de-sodiation capacity (mA h g−1) | Final de-sodiation capacity (mA h g−1)/no. of cycles |
|---|---|---|---|---|
| Sn/graphite composite26 | 50 | 580 | 410 | 360/20 |
| C–SnO2–C hollow core/shell/shell27 | 100 | 1200 | 620 | 420/30 |
| Amorphous SnO2 on C nanotubes28 | 100 | 1110 | 630 | 590/50 |
| SnS–acetylene black composite29 | 100 | 760 | 500 | 530/80 |
| Sn4P3 nanoparticles on reduced graphene oxide30 | 100 | 1600 | 780 | 640/100 |
| Sn4P3 nanoparticles in a cube-shaped carbon shell31 | 100 | 1430 | 750 | 700/50 |
Even higher capacities are, in principle, obtainable with tin nitride (Sn3N4). Sn3N4 has a tuneable band gap and applications in photocatalysis, chemical sensing and solid state LIBs have been suggested.32–35 As an anode material in SIBs, the conversion of Sn3N4 to Sn and Na3N followed by full alloying of Sn to Na15Sn4 would result in a capacity of 1512 mA h g−1. Previously we produced bulk nanocrystalline Sn3N4 by ammonolysis of a tin dialkylamide and demonstrated a reversible (de-sodiation) capacity of 270 mA h g−1 after 50 cycles at 50 mA g−1 with a coulombic efficiency close to 95%.36Ex situ diffraction measurements on cycled electrodes suggested that a significant fraction of the material was not involved in the electrochemical processes. Consequently, it was envisioned that smaller crystallite sizes could produce larger capacities. This is now demonstrated in this work, together with a theoretical and experimental study of the reaction mechanism.
Recent years have expanded the list of tools capable of predicting new phases of materials using first principles calculations.37,38 Their application to the interaction of Na with Sn compounds has attracted considerable theoretical interest. An initial study in 2011 by Chevrier et al. used first-principle calculations to predict the voltage profile of the process of sodiation of Sn by formation of NaxSny compounds.39 Later experimental studies using X-ray diffraction and operando TEM corroborated the formation of Na15Sn4 as the crystalline phase of maximum sodiation.40–42 Further theoretical work combined with Mössbauer and X-ray absorption spectroscopies shed light into the reaction mechanism of Sn sodiation.43,44 A decisive in-depth examination of the reaction pathway by Stratford et al. using ab initio random structure searching and operando XRD, PDF and NMR characterization identified the structure of the intermediate NaxSny compounds and showed that the final product Na15Sn4 can store additional sodium atoms as an off-stoichiometry product Na15+xSn4.45
Theoretical studies have also been very useful for understanding the compounds formed with Na and N. The formation of metastable Na3N was predicted from theoretical considerations and later demonstrated in practice by synthetic routes using atomic co-deposition or reactions of sodium with active nitrogen, it was also shown that Na3N decomposes at ∼100 °C.46–50 On the other hand, sodium azide (NaN3) is a well-known stable compound of Na and N and it is manufactured at around 250 tonnes per year, with the main application in car airbags.51,52 A theoretical study using global structure optimization identified a new compound, sodium azenide (Na2N2), which was predicted to be stable (that is, it had a negative enthalpy of formation from the respective elements Na and N2),53 but the experimental synthesis of Na2N2 has not been reported. Finally, theoretical and experimental studies on the tertiary compounds of NaxSnyNz are currently limited, but ab initio calculations by Sun et al. showed that a phase of NaSnN is thermodynamically stable54 and this was subsequently demonstrated experimentally.55
Herein we report a joint theoretical and experimental study of the application of Sn3N4 as a high capacity anode material in SIB, using a new synthesis method to make Sn3N4 microcrystalline and nanocrystalline powders. The capacity achieved with nanocrystalline Sn3N4 over 50 cycles exceeds those for anodes reported to date. The underlying mechanism is interrogated using first principle methods and experimental characterization (XRD, EXAFS and XANES).
Experimental
Synthesis of Sn3N4 was carried out under anaerobic conditions using either a nitrogen-filled glovebox or Schlenk line techniques. Benzene (Aldrich) was refluxed over sodium for 8 h, distilled and stored under nitrogen. SnCl4 (Aldrich) was short-path distilled. LiNH2 was obtained by reacting nBuLi (1.6 mol dm−3 in hexane, 500 cm3, Aldrich) with ammonia (distilled from a ∼100 cm3 sodium/liquid ammonia solution) at 0 °C, filtering the white solid product and drying in vacuo. Solvothermal synthesis was performed in a 75 cm3 autoclave (Parr 4740CH), with a silica liner reducing the internal volume to ∼60 cm3. SnCl4 (0.60 g, 2.3 mmol) was placed in the silica liner and covered by 30 cm3 of benzene. LiNH2 (0.21 g, 9.2 mmol) was added and stirred. The autoclave was sealed and heated for 12 hours at temperatures as discussed later (300 to 430 °C). Typically, ∼50 atm pressure was developed during heating. After cooling to room temperature, the autoclave was opened and the solid was washed with deionised water (50 ml) and MeOH (20 ml) to remove the LiCl by-product. The powder was then washed further with HCl (3 mol dm−3, 30 ml) to remove any tin metal formed by thermal decomposition of the metal nitride.Electrode preparation involved homogenizing the Sn3N4 active material (75%) with acetylene black (20%, Shawingan black, 100%-compressed, Chevron) and sodium alginate (5%, Aldrich) dissolved in deionised water. The slurry was cast onto Cu foil (17.5 μm thick, 99.9% purity, Goodfellow Ltd) using a K bar (wet thickness of 200 μm) and dried at room temperature. The coated foil was punched into circular discs (11 mm diameter) and pressed at 10 tonnes to obtain the Sn3N4 electrode. Typical mass loadings of electrodes prepared in this way were 0.5–1.0 mg cm−2. Swagelok cells were assembled in an argon-filled glove box. Sodium half-cells were prepared by cutting a fresh face of sodium metal (Aldrich, 99% purity) and rolling to produce sodium foil counter-electrodes, with two microfiber filter (Whatman, GF/F grade) separators soaked in 120 μl of 1 mol dm−3 NaPF6 (Aldrich, anhydrous) in a 47.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 47.5
47.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 by wt mixture of ethylene carbonate (EC), diethyl carbonate (DEC) and fluoroethylene carbonate (FEC) (all Aldrich, 99%, anhydrous or vacuum distilled before use). Electrochemical testing was performed with a BioLogic MPG multi-channel potentiostat. Galvanostatic cycling was carried out at 25 °C at various rates of charge/discharge within the potential range of 10 mV to 2.5 V vs. the sodium metal counter-electrode.
5 by wt mixture of ethylene carbonate (EC), diethyl carbonate (DEC) and fluoroethylene carbonate (FEC) (all Aldrich, 99%, anhydrous or vacuum distilled before use). Electrochemical testing was performed with a BioLogic MPG multi-channel potentiostat. Galvanostatic cycling was carried out at 25 °C at various rates of charge/discharge within the potential range of 10 mV to 2.5 V vs. the sodium metal counter-electrode.
Powder X-ray diffraction (XRD) measurements were recorded on a Bruker D2 Phaser using Cu-Kα radiation (λ = 1.5418 Å) in Bragg–Brentano geometry. The reflections present were identified by comparison with the ICSD database and patterns refined using the GSAS package.56 Scale factor, background, lattice parameter, zero point correction, thermal displacement parameters, nitrogen atom positions, crystallite size broadening and isotropic strain. An Al2O3 standard collected in the same geometry was used to define the Gaussian instrumental peak shape, with the crystallite size obtained from the Lorentzian crystallite size broadening terms.57 In two-phase fits containing two crystallite sizes, the tin thermal displacement parameters were constrained to a single value and the nitrogen thermal displacements were fixed. Transmission electron microscopy (TEM) was carried out with a FEI Technai12 (120 kV) on samples that were dispersed into propanol with ultrasound and dropped onto carbon grids. Bulk elemental CHN combustion analysis was obtained from Medac Ltd, and the values are reported in weight percentages. The XRD patterns of the pristine electrodes show some small, unidentified impurity peaks, which are formed during the homogenizing process in electrode preparation, but additional diffraction studies with electrodes prepared without the homogenizing step show the same reactions (see ESI, Fig. S1†).
For ex situ measurements before and after galvanostatic cycling, microcrystalline tin nitride electrodes were cycled in Na half-cells to specific potentials of interest at 200 mA g−1. The Swagelok cells were disassembled in an argon-filled glovebox as soon as the target potential had been reached. The electrodes were rinsed with anhydrous DEC solvent and allowed to dry. Ex situ X-ray diffraction patterns collected in a sealed XRD sample holder (Bruker, loaded in the glove box) were collected in grazing incidence geometry (1° incidence angle) with Cu-Kα radiation (λ = 1.5418 Å) using a Rigaku Smartlab with Hypix 2D detector. Near-edge (XANES) and extended fine-structure (EXAFS) X-ray absorption measurements in sealed polyfoil pouches were made at the B18 beamline of Diamond Light Source across the Sn K-edge region from 28.8 to 30.0 keV. Tin standards were produced by preparing inks with Sn, SnO2, SnO (Aldrich) and Na4Sn powders diluted with acetylene black to match the respective mass loadings of the tin nitride electrodes. The Na4Sn standard was prepared in a nitrogen-filled glovebox where a slight excess of Na (4.4 equiv., Aldrich, 99% purity) and Sn (Aldrich) was loaded into a furnace tube and sealed, following a previously reported synthesis method for Na4Sn.58 The tube was placed into a furnace at 300 °C and heated for 1 hour under flowing N2. After heating, the sample was transferred to the glovebox before diluting with acetylene black to produce the Na4Sn standard. The Sn edge positions were obtained as the first inflexion point of the respective XANES absorption spectra, and the EXAFS data has been fitted using two independent Sn–N coordination shells, similarly to previous studies of Sn3N4.59
Targeted compounds of known composition and structure were simulated from first principles as implemented in the Vienna Ab initio Simulation Program (VASP).60 This approach is based upon density functional theory (DFT), and the PBE and HSE06 functionals were considered with the projected augmented waves method used for the pseudopotentials.61,62 An energy cut-off of 600 eV and a minimum of a 4 × 4 × 4 (2 × 2 × 2) Monkhorst–Pack k-grid were used. The total energy of each system was minimised with respect to the internal coordinates and the lattice parameters, with a force tolerance of 0.01 eV Å−1. All charge analysis was performed using the Bader scheme.63 Two functionals were considered here. PBE is a highly suitable functional for geometric considerations, whereas for chemical accuracy one would consider HSE06. In general, whilst broad trends can be extrapolated from a PBE result, the chemically accurate results require HSE06. To investigate the reaction pathways, we calculated the energies of the different compounds following the standard approach.64 The reactions of Na with the Sn or N2 can be written as:
| xNa + (1 − x)Sn → NaxSn1−x | (1) |
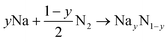 | (2) |
| Ef = E(NaxSn1−x) − xE(Na) − (1−x)E(Sn) | (3) |
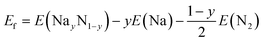 | (4) |
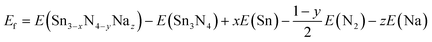 | (5) |
Results and discussion
Solvothermal synthesis of Sn3N4
Solvothermal synthesis has become an effective, well-controlled route for the preparation of crystalline metal nitrides.65–67 By heating reactants in a solvent medium inside a sealed autoclave, metathesis reactions can proceed at mild temperatures due to the solvent absorbing heat produced in the exothermic reactions.68–70 Thermal decomposition of the formed metal nitrides is also significantly reduced under solvothermal conditions, and the products are usually crystalline.20,71,72 Sn3N4 was synthesised via a simple and easily-scalable solvothermal method with defined particle size via a solvothermal metathesis reaction, with benzene employed as the solvent owing to its stability under solvothermal conditions:73,74| 3SnCl4 + 12LiNH2 → Sn3N4 + 12LiCl + 8NH3 | (6) |
XRD and TEM were employed to characterise the product of the solvothermal reaction. Sn3N4 crystallises with the cubic spinel structure (Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) with a reported lattice parameter of 9.037(3) Å.75 Powder X-ray diffraction (XRD) patterns of the brown products produced in solvothermal reactions at 300, 350 and 430 °C are displayed in Fig. 1, all showing the peak positions of the Sn3N4 reference. The good match of the XRD peak positions of the Sn3N4 reference and the samples here produced, demonstrates the success in the synthesis of phase pure Sn3N4 for all the reaction conditions here explored (the absence of other peaks demonstrate that no other crystalline impurities are present). In addition, for the sample produced at 430 °C, all the XRD peaks are symmetrical and narrow, demonstrating that the sample is made of crystalline particles in the micron size range; this material will be referred to as microcrystalline Sn3N4 in the following text. A Rietveld fit to this XRD pattern (Rwp = 5.0%, Rp = 3.4%) yielded a lattice parameter of 9.0549(2) Å and an average crystallite size of 310(40) nm (ESI, Fig. S2 and Table S1†). TEM micrographs corroborate this crystallite size (Fig. 2a).
m) with a reported lattice parameter of 9.037(3) Å.75 Powder X-ray diffraction (XRD) patterns of the brown products produced in solvothermal reactions at 300, 350 and 430 °C are displayed in Fig. 1, all showing the peak positions of the Sn3N4 reference. The good match of the XRD peak positions of the Sn3N4 reference and the samples here produced, demonstrates the success in the synthesis of phase pure Sn3N4 for all the reaction conditions here explored (the absence of other peaks demonstrate that no other crystalline impurities are present). In addition, for the sample produced at 430 °C, all the XRD peaks are symmetrical and narrow, demonstrating that the sample is made of crystalline particles in the micron size range; this material will be referred to as microcrystalline Sn3N4 in the following text. A Rietveld fit to this XRD pattern (Rwp = 5.0%, Rp = 3.4%) yielded a lattice parameter of 9.0549(2) Å and an average crystallite size of 310(40) nm (ESI, Fig. S2 and Table S1†). TEM micrographs corroborate this crystallite size (Fig. 2a).
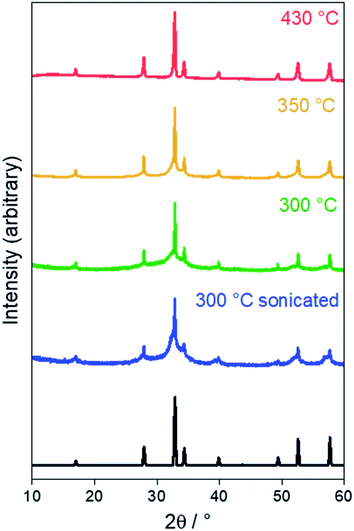 | ||
| Fig. 1 Powder XRD patterns for the products of solvothermal synthesis at various temperatures. The black pattern denotes the literature Sn3N4 reflection positions and intensities.75 | ||
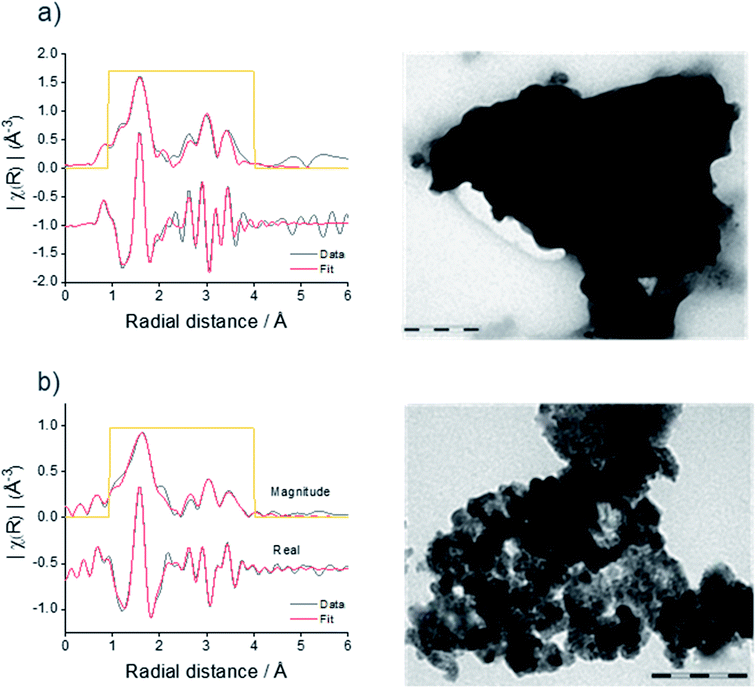
In the XRD data for the sample prepared at 300 °C, broad asymmetric peaks are present at similar positions to small sharp peaks, the latter resembling the microcrystalline sample obtained at 430 °C. The asymmetric broadening feature is due to the fact that the sample is made of a mixture of nano-sized and larger crystallites. The presence of nano-size crystallites could be increased by sonicating the sample in HCl, the associated XRD pattern shows that the asymmetric broadening of the peaks is accentuated. The material obtained by heating at 300 °C followed by sonication will be referred to as nanocrystalline Sn3N4 in all that follows. A two-phase Rietveld fit (Rwp = 9.4%, Rp = 7.4%) confirmed the presence of two distinct phases, both fitting well as Sn3N4 (ESI, Fig. S2 and Table S1†). The lattice parameters of the two phases were 9.0514(4) and 9.139(2) Å, with average crystallite sizes of 137(13) nm (13.2(4)% of the material present) and 5.950(9) nm (86.8(2)%), respectively. TEM shows crystallites around both of these sizes, with a greater number of nanocrystalline particles present (Fig. 2b).
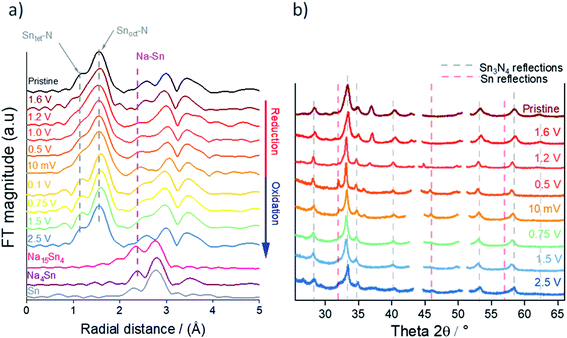
The microcrystalline and nanocrystalline Sn3N4 samples were also characterised by XANES and EXAFS collected at the Sn K-edge. Fig. 2 shows the magnitudes of the Fourier transforms of the K3-weighted EXAFS data. A peak doublet at ∼1.5 Å radial distance is present in both samples and corresponds to the distances between N sites and tetrahedral tin site (Sntet–N) and octahedral tin site (Snoct–N) at 2.05 and 2.20 Å, as expected for the spinel Sn3N4 structure and in agreement with previous studies.59 Peaks between 2.5 and 4 Å are attributed to other Sn–Sn interactions within the structure.59 While XRD is suitable to characterise the composition of the microcrystalline sample, the nanocrystalline sample gives broad diffraction peaks. However, EXAFS shows that both samples have a very similar set of correlations with similar intensities (see results of the fit in the ESI, Table S2†), confirming structural similarities of Sn3N4 in both samples. In addition, the analysis of the Sn K-edge XANES data enables the evaluation of the Sn oxidation state (see more details below), which were found to be 3.7 and 3.3 for the Sn3N4 micro and nanocrystalline samples, respectively.
The estimation of the nitrogen content of the Sn3N4 samples by combustion analysis gives values (10.1% and 8.2% for the microcrystalline and nanocrystalline samples) that are lower than the expected for pure, stoichiometric Sn3N4 (13.6%). This can be ascribed, in part, to the presence of nitrogen vacancies, which is supported by the fact that the Sn K-edge XANES analysis provides values of the oxidation state of tin lower than 4. The elemental analysis also shows that the samples also contain carbon and hydrogen (12.4% C and 2.0% H for the microcrystalline sample and 1.0% C and 2.0% H for the nanocrystalline sample). The lower content of carbon in the nanocrystalline sample is expected, since less decomposition of the solvent (benzene) will take place at the lower temperature used for the solvothermal synthesis method.68,69 Taking into account the presence of carbon and hydrogen residues and the nitrogen vacancies (calculated from the tin oxidation number), the expected values of the nitrogen content are 10.9% and 11.1% for the microcrystalline and nanocrystalline samples. The experimental values of the nitrogen content are somewhat lower (10.1% and 8.2% for the microcrystalline and nanocrystalline samples). The process of washing the samples in an HCl solution after synthesis can produce a hydrolysis reaction producing a partial oxygen substitution of nitrogen sites at particle surfaces, forming a tin oxy-nitride, and this effect will be more severe for the nanocrystalline sample since it has a higher surface area. The XRD and EXAFS results show that the spinel structure is preserved after the oxygen-nitrogen substitution. Incomplete combustion of the samples, as observed in other metal nitride studies,76 could also contribute to the lower than expected nitrogen content obtained from the elemental analysis.
Electrochemistry of Sn3N4 in sodium half cells
Sn3N4 exhibits good stability in deionised water, hence water processable binders can be employed in electrode preparation, avoiding toxic organic solvents. In our previous study, Sn3N4 electrodes prepared with sodium alginate as a binder demonstrated the best electrochemical stability during cycling and so we continued using sodium alginate for this work.36 The binder is comparatively more rigid than the commonly used PVDF, a property that increases the electrode's ability to withstand large volume changes during cycling.77–79 Na half-cells were constructed with 1 mol dm−3 NaPF6 in EC/DEC with 5 wt% FEC electrolyte, again following previous work.36 FEC was used as an additive that improves the electrochemical performance of tin-based electrodes.80–83Galvanostatic cycling of microcrystalline Sn3N4 in Na half-cells was investigated at 50 and 200 mA g−1 (Fig. 3). At 200 mA g−1, 671 mA h g−1 of capacity was passed on first reduction (discharge, negative current) to 10 mV, of which 214 mA h g−1 was recovered on the first oxidation (charge, positive current) to 2.5 V. This large initial capacity loss (32%) is tentatively attributed to irreversible processes such as the decomposition of the electrolyte and formation of an SEI.20,36,84,85 Subsequent cycles demonstrated good cycling stability with a capacity fade of 7% between the 10th (268 mA h g−1) and 50th (250 mA h g−1) oxidations. The coulombic efficiency was 98% at the 50th cycle, indicating a stable, reversible electrochemical process. Greater capacities were achieved at a more modest current of 50 mA g−1, with 520 mA h g−1 of capacity passed after the 50th oxidation, with a coulombic efficiency of 97%. Capacity fade between the 10th (546 mA h g−1) and 50th (521 mA h g−1) oxidation was just 4%.
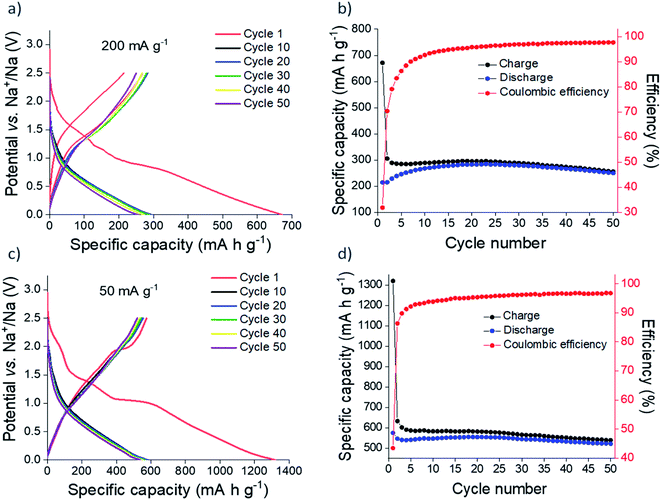 | ||
| Fig. 3 Galvanostatic cycling (a and c) and plot of specific capacity vs. cycle number (b and d) of microcrystalline Sn3N4 in Na half-cells at 200 mA g−1 (a and b) and 50 mA g−1 (c and d). | ||
Galvanostatic cycling of nanocrystalline Sn3N4 in Na half-cells (Fig. 4) shows greater capacities compared to the microcrystalline sample. At 200 mA g−1, after the initial irreversible capacity loss, a reversible (oxidation) capacity of 420 mA h g−1 was achieved. Capacity fade from the 10th (421 mA h g−1) to the 50th (416 mA h g−1) oxidation was only ∼1%. In addition, the coulombic efficiency rose to 98%, demonstrating the favourable reversibility of the charge/discharge reactions on cycling. As expected, more capacity was achieved at the lower current of 50 mA g−1. Reversible capacities of ∼850 mA h g−1 were obtained during cycling. The coulombic efficiency at the 50th cycle was 94%.
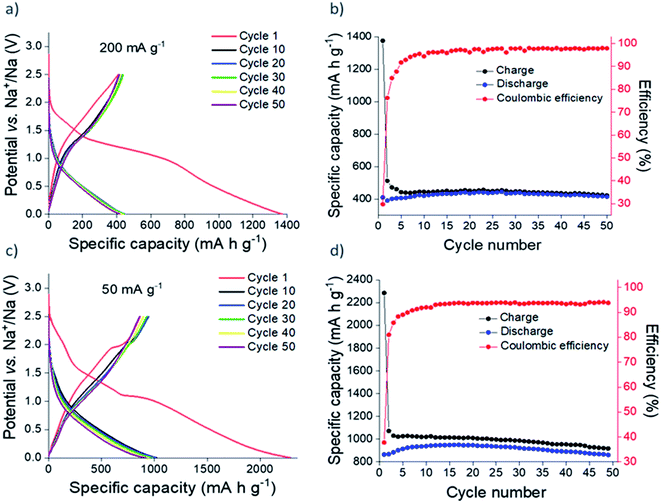 | ||
| Fig. 4 Galvanostatic cycling (a and c) and plot of specific capacity vs. cycle number (b and d) of nanocrystalline Sn3N4 in Na half-cells at 200 mA g−1 (a and b) and 50 mA g−1 (c and d). | ||
The capacity of these Sn3N4 electrodes is remarkable considering that other high capacity tin-based materials all incorporate a carbon architecture material such as graphene sheets, hollow spheres or nanotubes (see Table 1). In other Sn-based conversion systems without a secondary support, capacity fading over multiple cycles is a problem. Wang et al. cycled SnO2 at 50 mA g−1 with a capacity of 200 mA h g−1 achieved after 50 cycles.86 Ma et al. compared Sn4P3/hollow C core–shell composites (Table 1) with unsupported Sn4P3, and cycling the unsupported material delivered a capacity of just 104 mA h g−1 after the 20th cycle at 100 mA g−1.31 The cycling of unsupported SnS electrodes was reported by Yu et al. with ∼200 mA h g−1 achieved after 50 cycles at 100 mA g−1.87 In addition, further improvements could be achieved in full cell studies, since the reactivity of the sodium metal counter electrode has been shown to compromise cycling stability in studies in Na half-cells.88,89
Similar to other conversion anode materials,26–31 the first cycle coulombic efficiency of the Sn3N4 samples studied here (30–45%) is not suitable for commercial applications, but further improvements could be achieved by material development. For example, the use of a yolk–shell design, where the active material nanoparticles are sealed inside a carbon shell, has produced major performance improvements for other conversion materials, which has been attributed to the fact that the yolk–shell design enables the volumetric expansion associated with the electrochemical reactions while avoiding the direct contact of the active material with the electrolyte.20,90 The investigation of alternative electrolytes is another highly promising route for improving performance and coulombic efficiency.91
DFT study of the charge storage mechanism
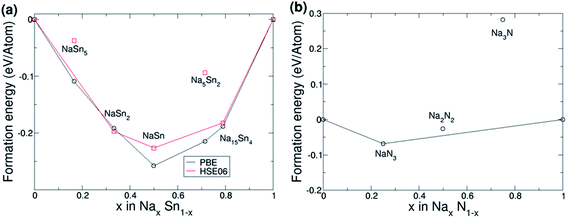
Previously, it was suggested that Sn3N4 electrodes could undergo complete conversion to Sn metal and Na3N with subsequent alloying of Sn with Na to Na15Sn4.36 Here, we exploit ab initio calculations to identify the candidate compounds involved in the reaction mechanism of sodiation of Sn3N4; this is later analysed in view of the XRD, XANES and EXAFS results.In order to construct the possible reaction pathways, we first investigated the stability of the various phases of NaxSny and NaxNy compounds. We applied a similar approach to AIRRS,45 except that for any stoichiometry where a known experimental structure exists, we only consider that structure. The PBE functional was used for an initial search, and we then studied the most stable candidates with the HSE06 functional. The HSE06 functional is necessary for considering nitrogen-based structures due to the difference in the N2 molecule's binding energy in PBE and HSE06 (the binding energy of N2 in HSE06 is 9.54 eV, whereas in PBE it is 8.44 eV and the experimental value is 9.79 eV).92 After calculation of the formation energies of the different compounds, using eqn (3) and (4), the lines connecting the compounds of lower formation energy (known as convex hull) were calculated. When a candidate compound lies above the convex hull, it is concluded that the compound is not thermodynamically stable.
The results of the calculations of the formation energies of Sn–Na compounds are shown in Fig. 5a. The calculations made with the PBE functional agree with the results reported by Stratford et al.45 To ensure chemical accuracy, additional calculations were made with the HSE06 functional. Whilst the formation energies are generally slightly smaller, the general trend in the convex hull is in good agreement with the previous PBE results. Our HSE06 calculations also show that all phases are metallic as expected. Our first principles simulations combined Bader charge analysis which shows that Sn atoms are charge neutral (0.0|e|) in the β phase due to charge being evenly distributed. As the fraction of Na increases, the Sn atoms become increasingly negatively charged with the Na15Sn4 phase Sn atoms possessing Bader charges of −3.7|e|.
The calculation of formation energies of Na–N compounds is shown in Fig. 5b. Due to the significant error in binding energies of the N2 molecule in PBE, only HSE06 results are discussed. Fig. 5b shows that NaN3 is the only candidate compound that lies on the convex hull, which means that the other candidate compounds are not thermodynamically stable. For example, Na3N produces a positive energy of formation per atom (Ef = 0.29 eV in HSE06), which means that formation of Na3N from bulk Na and N2 gas is not thermodynamically favourable. These findings agree with the experimental enthalpy of formation of Na3N obtained by differential thermal analysis: 64 kJ mol−1 (or 0.66 eV),48 which would correspond to a formation energy per atom of 0.66 eV/4 = 0.17 eV. However, the fact that Na3N is metastable does not mean that it cannot be formed and remain stable: Na3N has been successfully synthesised by atomic co-deposition and the reaction of sodium with active nitrogen,47–49 and it was stated that Na3N remained stable for weeks unless it was heated to ∼100 °C.48 At high pressures Na3N was also found to remain stable.93 Our results of the metastability of Na3N are also in agreement with previous theoretical calculations.46,50,53,94
For the elucidation of the energy storage mechanism of Sn3N4 in sodium-ion cells, we studied the reaction of formation of Na interstitials and substitutional sites in bulk and surface Sn3N4 (see ESI, Tables S3 and S4†). For the study of surface reactions, slabs of material with [001] surface terminations were generated. The plane of cleavage was chosen based on the consideration that both surfaces must be (a) symmetric, (b) charge neutral and (c) stoichiometric. From these criteria four surfaces were created and relaxed. The most stable of these (see ESI, Fig. S3†) was then considered for the surface reaction calculations. We considered slab systems with various thicknesses ranging from 0.3 to 2 nm to converge the energy calculations.
Three different mechanisms for the bulk sodiation of Sn3N4 were considered: (a) the addition of interstitial Na ions into Sn3N4 (with an associated reduction of the Sn oxidation state, reaction (7)), (b) the substitution of Na onto Sn sites (with an associated formation of Sn metal, reaction (8)), (c) or the substitution of Na onto N sites (with an associated formation of N2, reaction (9)).
| Na interstitial formation: Sn3N4 + xNa → NaxSn3N4 | (7) |
| Substitution of Sn sites: Sn3N4 + yNa → NaySn3−yN4 + ySn | (8) |
| Substitution of N sites: Sn3N4 + zNa → NazSn3N4−z + z/2N2 | (9) |
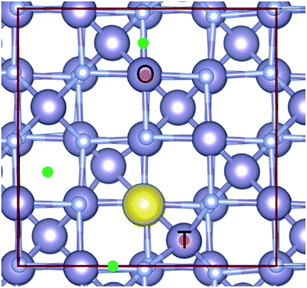
The associated reaction energies, per Na atom, are given in Table S3, ESI.† We found that, unsurprisingly, the least energetically favourable of these was Na substituting into the N site (reaction (9)). For the addition of Na interstitial sites (reaction (7)), we considered various sites for interstitial Na as shown in Fig. 6. The lowest energy configuration (shown in yellow: 16c interstitial forming a pseudo-octahedral Na site face linking to two SnN4 tetrahedra and edge linking to four SnN6 octahedra) was then considered in a larger supercell, corresponding to Na0.0625Sn3N4. This structure was found to be energetically favourable with a formation energy of −0.426 eV per Na atom. Apart from the formation of this energetically favourable Na interstitial, other Na interstitial sites considered (see Fig. 6 and ESI, Table S3†) were found to have a positive formation energy, meaning that they were not thermodynamically stable with respect to bulk Sn3N4 and Na. The energy of formation of Na interstitials ranged between 1.68 and 3.8 eV using PBE, and the values obtained with HSE06 were 0.3 eV lower. However, it is worth noting that the formation energy for inserting two Na interstitials into the structure was 1.28 eV (per Na atom) (compared to 1.68–3.8 eV for the first interstitial considered here), indicating that the expansion of the structure to accommodate the first Na atom results in a lower formation energy for subsequent Na intercalations. The third reaction pathway considered was Na substituting onto the Sn site (reaction (8)), which was also found to be energetically unfavourable. Substituting the Sn tetrahedra (Sntet) had a formation energy of 4.33 eV in PBE, and substitution at the Sn octahedral site (Snoct) was slightly less favourable at 4.47 eV in PBE (see sites in Fig. 6).
In summary, ab initio calculations were applied to evaluate the energy of formation of bulk NaxSnyNz compounds, of which only Na0.0625Sn3N4 was found to be stable. Therefore, it can be proposed that the electrochemical sodiation of Sn3N4 will produce the bulk formation Na0.0625Sn3N4. However, the capacity associated with such a process is very small: the theoretical capacity is only 4 mA h g−1. Previous studies have also identified NaSnN as a stable compound, this phase contains Na ions intercalated in between two-dimensional layers of [SnN]−.54,55 The sodiation of Sn3N4 to form bulk NaSnN has an associated theoretical capacity of 65 mA h g−1. However, the bulk conversion of the Sn3N4 material into NaSnN is not supported by our experimental data: XRD data of the electrodes discharged to different potentials in Na half-cells (see discussion below, Fig. 9b) show that the diffraction pattern of the Sn3N4 spinel structure is still clearly visible even after polarization to 10 mV vs. Na+/Na, thus demonstrating that the core of Sn3N4 particles undergoes little structural change. The absence of transformation of bulk Sn3N4 into bulk NaSnN could be attributed to kinetic limitations. On the other hand, the sodiation of Sn3N4 to form Na0.0625Sn3N4 involves little structural rearrangement, so it is expected to be facile and the observed XRD patterns of the sodiated (i.e. reduced) electrodes are also consistent with Na0.0625Sn3N4. Thus, we conclude that sodiation of Sn3N4 starts with the facile insertion of a small of amount of sodium in the Sn3N4 structure, forming the identified stable compound Na0.0625Sn3N4. On the other hand, the surface of Sn3N4 particles undergoes significant reactions during cycling in Na half cells. To study the surface reactions, additional calculations were performed to evaluate the energy of formation of surface compounds.
By performing ab initio calculations with the PBE functional, we found that the insertion of Na into the Sn3N4 surface (reaction (7)) was generally energetically favourable, resulting in a significant energy gain (at the surface the formation energy is −3.5 eV for the adsorption of 1 Na atom). Further below the surface, this energy decreases but remains favourable for all the slabs we have considered (up to 2 nm thick). This indicates that, near the surface, the energetic cost of expansion and strain on Sn3N4 associated with sodiation reactions is less than the energy gained from adsorbing Na. Furthermore, on the top surface layers of Sn3N4, the substitution of a Na into a Sn site, forming NaySn3−yN4 + ySn (reaction (8)) becomes favourable, with formation energies of −1.9 eV for surface substitutions and −0.6 eV for subsurface (1 monolayer below) substitutions (both tin tetrahedral sites). As these represent the first steps of conversion of the Sn3N4 structure, this suggests a potential ∼1.9 V vs. Na+/Na for the surface process. However, we treat this with caution as it is heavily dependent on surface reconstructions and terminations. These findings suggest that the electrochemical reaction of sodiation of Sn3N4 is likely initiated by the insertion of Na on the surface followed by the substitution of Sn by Na at the Sn3N4 surface, resulting in the formation of a Sn metal coating on top of the Sn3N4 nanoparticle. Then, Sn metal could react further with Na forming different NaxSny alloys, with Na15Sn4 as the final product, as shown in previous studies of the sodiation of Sn in Na-ion cells.39–42,45 It is reasonable to assume that the products of these surface reactions will grow as a shell around a core with NaySn3N4 structure (possibly made of Na0.0625Sn3N4, according to our calculations). These findings can explain the increase in the capacity values observed with the nanocrystalline tin nitride electrode, as the material will have a larger surface area compared with the microcrystalline material. Unfortunately, the larger surface also increases the electrolyte breakdown occurring in the first charge cycle, which can explain the larger irreversible capacity loss witnessed on the initial cycle of the nanocrystalline material.95
Structural and chemical change during cycling
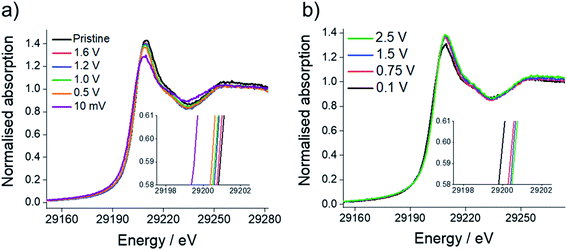
In order to elucidate the reactions undergone by Sn3N4 materials in Na half-cells, electrodes were extracted from the cell at potentials chosen from features observed in the potential profile (Fig. 7, also see differential capacity plots in the ESI, Fig. S4†). These were 1.6, 1.2, 1.0, 0.5 and 0.01 V vs. Na/Na+ during reduction and 0.1, 0.75, 1.5 and 2.5 V vs. Na/Na+ during oxidation. Samples were then characterised by XRD, XANES and EXAFS. These experiments utilised the microcrystalline Sn3N4 in order to obtain more useful diffraction data, although it is recognised that the nanocrystalline material has the larger capacity. On first reduction, there is a sloping plateau over 1.6 V (Fig. 7) followed by a small plateau at 1 V. We attribute this process to the insertion of Na ions into the Sn3N4 structure via surface reactions such as the substitution of Na to Sn sites which produces Sn metal coatings. These reactions were found to be energetically favourable (negative formation energies) at the Sn3N4 surface by DFT calculations. At lower potentials the formation of NaxSny phases is expected, which likely requires some Sn to have already formed. A large, sloping plateau is observed at 0.5 V, that could be ascribed to the alloying reaction (Sn → NaxSn). This alloying process continues to 10 mV, as described in SnO2 and Sn4P3 systems.96–98 Since the sodiation of Sn produces a series of NaxSny compounds at potentials in between 0.5 V and 0 V vs. Na+/Na, these last processes have been assigned to the Sn alloying reactions (Sn → NaxSny).39–42,45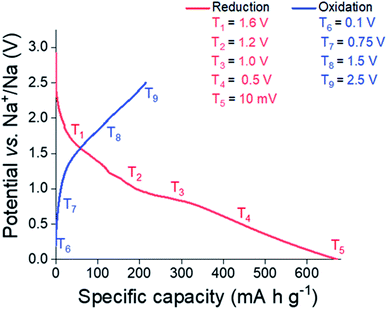 | ||
| Fig. 7 Initial galvanostatic cycle of microcrystalline Sn3N4 depicting where samples were taken for the ex situ XRD, XANES and EXAFS studies. | ||
Sn K-edge XANES analysis was performed to probe changes in the oxidation state of Sn in the cycled electrodes. For that purpose, prior to the measurements, Sn–K edges were calibrated against Sn standards with defined oxidation states (Sn, SnO2, SnO and Na4Sn with oxidation states of 0, +4, +2 and −4, respectively, see ESI, Fig. S5†). The XANES spectra (Fig. 8) show the edge energy shifting to lower energy values during the first reduction and a decrease in the intensity of the white line position at the fully reduced state (10 mV vs. Na+/Na), corresponding to an average oxidation state of −0.1 (ESI, Table S5†). Whilst a negative oxidation state implies that Na–Sn alloying has taken place, it also suggests incomplete conversion of Sn3N4 to Na–Sn alloys, as we would expect a much lower oxidation state (−1.25) for the fully sodiated Na15Sn4 phase. Fig. 8 also shows an increase in the edge energy shift and intensity of the white line position in the XANES spectra during the first oxidation of the Sn3N4 electrode. The average oxidation state of Sn was 3.5 in the fully charged state (2.5 V vs. Na+/Na), very close to the average oxidation state of the pristine sample (3.7). This provides strong evidence that reformation of Sn3N4 occurs.
Fig. 9b shows the ex situ XRD data of Sn3N4 electrodes cycled to the same set of potentials as in the XANES measurements in Fig. 8. It is observed that the reflections corresponding to Sn3N4 become sharper on reduction of the electrode, this suggests that the smaller crystallites are reacting more readily and hence the average crystallite size increases. At 0.5 V, clear reflections for Sn metal appear in the pattern. This is in agreement with the findings from the DFT calculations, which predict that sodiation would induce the insertion of Na into the surfaces of the Sn3N4 particles, thus ejecting Sn metal, followed by the growth of a Na–Sn alloy shell around the Sn3N4 particles. Formation of Na–Sn alloys is not clearly visible in the XRD data, indicating poor crystallinity or small particle size of the Na–Sn alloys. During the initial stages of the re-oxidation, the intensity of the Sn metal reflections diminishes but small Sn diffraction peaks are still visible at the end of charge (2.5 V), suggesting incomplete reversibility of the conversion process. At the end of oxidation, the Sn3N4 peaks become broader, similar to the pristine samples, indicating that the electrochemical reactions are reversible and the small crystallites reoxidise recovering the spinel Sn3N4 structure. The pristine electrode exhibits a reflection at 37.5° that disappears upon reduction and it is not recovered after oxidation. This peak appears due to the use of a homogeniser for the electrode preparation: Fig. S1 in the ESI† shows that electrodes prepared without homogenization do not have this peak and exhibit the same changes in the XRD pattern induced by the electrochemical reactions. Unfortunately, the assignment of this peak is unclear: NiO and CrO2 show reflections close to that position, but at higher angles, and they show other reflections that are not observed in the experimental patterns (see ESI, Fig. S6†). The pattern of the electrode at the end of oxidation (2.5 V) shows a very small peak at 26.2°, which could be ascribed to the formation of small amounts of SnO2, but again, the position of the peak is not exactly as expected for SnO2 and other reflections of SnO2 are not observed (ESI, Fig. S7†).
The EXAFS spectra during the first cycle (Fig. 9a) show a peak doublet at 1.5 Å radial distance corresponding to Sn–N bonds. The intensity of the lower radial distance peak within the doublet, corresponding to the tetrahedral Sntet–N bond distance, decreases greatly during reduction compared to the octahedral Snoct–N site (Fig. 9a and expanded in ESI, Fig. S8†) suggesting that Na substitution has taken place preferentially on the tetrahedral Sn sites. This is in agreement with the first principle calculations that showed substitution of Na onto tetrahedral Sn sites to be slightly more favourable than on octahedral sites (ESI, Table S3†). It is worth mentioning that the decrease in the intensity of the peak related to the tetrahedral Sntet–N bond distance starts at very high potentials (1.6 V), supporting our interpretation of the electrochemical data that the first sloping plateau centred at 1.6 V is due to sodiation surface reactions of substitution of a Sn tetrahedral site by Na. Then, as the potential is further reduced, a new environment starts to emerge from 1 V to 10 mV which could be assigned to the formation of Na–Sn alloys. The intensity of the tetrahedral Sntet–N peak increases in the EXAFS spectra during the subsequent reoxidation of the electrode suggesting that the spinel Sn3N4 is reforming. This is in agreement with the increased oxidation state calculated from the XANES analysis (ESI, Table S5†).
Discussion of reaction mechanism
Previously we proposed that the electrochemical reactions of Sn3N4 in Na-ion cells could proceed via a conversion and alloying mechanism:36| Conversion: Sn3N4 + 12Na+ + 12e− → 4Na3N + 3Sn | (10) |
| Alloying of Sn: 4Sn + 15Na+ + 15e− → Na15Sn4 | (11) |
Combination of reactions (10) and (11) has an associated theoretical capacity of 1512 mA h g−1. This reaction mechanism is, thus, consistent with the observed reversible capacities of up to 850 mA h g−1. The fact that the experimental capacity is lower than the theoretical capacity could be ascribed to incomplete conversion of Sn3N4 and alloying to produce Na15Sn4. Indeed, many battery materials undergoing conversion reactions do not reach the full theoretical capacity. Nanostructuring of the material (that is, decreasing the particle size) often results in significant improvements in the practical capacity, due to a better utilisation of the whole material. This is also observed in the present work by comparing the reversible capacities of the microcrystalline and nanocrystalline samples. Furthermore, the XRD characterisation evidences the presence of unreacted Sn3N4 throughout the whole discharge and charge process for the lower capacity microcrystalline sample.
The analysis of XANES to quantify the variation of the Sn oxidation state following reduction and oxidation is also consistent with reactions (10) and (11). The Sn oxidation state in microcrystalline Sn3N4 is found to become negative (ca. −0.1) after reduction, which demonstrates the formation of Sn–Na alloys. While the expected Sn oxidation state in Na15Sn4 is more negative, the XANES data provides an average measurement for the whole sample, and some unreacted or partially reacted Sn3N4 at the end of discharge is demonstrated by XRD. On charge, the Sn oxidation state increases to +3.5, which suggests that the original Sn3N4 material is recovered after charge, and further support is obtained from the XRD characterisation, which shows the re-growth of broad Sn3N4 reflections upon oxidation.
However, reaction (10) involves the formation of Na3N which is metastable and decomposes at around 100 °C. We then considered the possibility that reaction (10) was not reversible due to decomposition of Na3N and the associated loss of N2, if that was the case, the electrochemical reactions would only involve the Sn–Na alloying reaction (reaction (11)), except for the first discharge (reduction) of the cell which would also include reaction (10). However, reaction (11) of Na alloying of Sn to Na15Sn4 has a theoretical capacity of 732 mA h g−1 when referred to the mass of the initial Sn3N4 material. This capacity value is lower than the observed values of the reversible capacities and it is also inconsistent with the high Sn oxidation state obtained by XANES at the end of oxidation (ca. 3.5) and the recovery of Sn3N4 observed in XRD measurements. All these measurements suggest that the electrochemical reactions on oxidation largely recover the original compound, Sn3N4. That would not be possible if N2 was lost in the form of gas. Insertion of additional Na beyond Na15Sn4 has been suggested from the analysis of operando NMR measurements of Sn reactions in Na-ion cells,45 but such additional Na insertion on the Na–Sn alloy is insufficient to explain the experimental capacities observed in this work. The discharge profile of Sn3N4 in Na-half cells is also distinct from that observed for Sn, which again supports the hypothesis that the electrochemical reactions are not simply Na–Sn alloying (reaction (11)).14
The results of DFT calculations concur that Na3N is not stable against decomposition to Na and N2, in agreement with experimental observations. On the other hand, NaN3 and Na2N2 are stable or potentially stable. Considering the formation of NaN3 or Na2N2 in the first conversion reaction, the following possible reaction mechanisms can be proposed:
| Conversion with NaN3 formation: 3Sn3N4 + 4Na+ + 4e− → 4NaN3 + 9Sn | (12) |
| Overall with NaN3 formation: 12Sn3N4 + 151Na+ + 151e− → 16NaN3 + 9Na15Sn4 | (13) |
| Conversion with Na2N2 formation: Sn3N4 + 4Na+ + 4e− → 2Na2N2 + 3Sn | (14) |
| Overall with Na2N2 formation: 4Sn3N4 + 61Na+ + 61e− → 8Na2N2 + 3Na15Sn4 | (15) |
The theoretical capacity of conversion and alloying is 818 mA h g−1 with azide formation (reaction (13)) and 992 mA h g−1 with azenide (reaction (15)). Of the phases considered the highest reversible capacity of ∼850 mA h g−1 after 50 cycles can only be explained by the azenide (Na2N2, reaction (15)). The Raman spectrum of fully sodiated Sn3N4 electrodes does not show evidence of formation of NaN3 or Na2N2, although this could be ascribed to the poor sensitivity of Raman measurements to detect small amounts of these compounds (ESI, Fig. S9†).
Conclusions
Microcrystalline and nanocrystalline Sn3N4 were prepared using solvothermal conditions at 430 °C, or at 300 °C followed by ultrasound treatment in aqueous HCl. Sn3N4 electrodes of both materials were cycled in Na half-cells, with the nanocrystalline electrode providing a higher capacity and good cycling stability over 50 cycles. Indeed, the capacity exceeds those reported for other tin-based materials, and good cycling stability with other tin-based materials has only been achieved with carbon supports or composite structures. The results presented here bring a deeper understanding of the Sn3N4 reaction mechanism in Na-ion cells. They provide evidence for the formation of Na–Sn alloys at the end of discharge and of reformation of Sn3N4 at the end of charge. DFT calculations combined with ex situ X-ray diffraction and X-ray absorption spectroscopy indicate that the N from Sn3N4 remains in the electrode in the form of some sort of Na–N compound. Na insertion into the Sn3N4 nanoparticles, ejecting some Sn which forms SnxNay phases on the surface, has been shown to be energetically feasible from DFT calculations and is also consistent with the observed changes in the Sn–N and Na–Sn bond distances obtained from EXAFS spectra and with the change in the oxidation state obtained from XANES. The new solvothermal synthesis here developed is a simple and low cost synthesis route that enables an unprecedented control of the Sn3N4 particle size, which is critical to achieve full utilization of Sn3N4 and thus high capacity.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors thank EPSRC for funding an early career fellowship to NGA (EP/N024303/1) and the Smartlab diffractometer (EP/K00509X/1 and EP/K009877/1). Thanks also to Diamond for beam time at B18 under the Energy Materials block allocation grant administered by Prof. Alan Chadwick (SP14239), and to Prof. Andrea Russell for access to the Raman spectrometer. We acknowledge the use of the EPSRC-funded National Chemical Database service hosted by the Royal Society of Chemistry.References
- C. Vaalma, D. Buchholz, M. Weil and S. Passerini, Nat. Rev. Mater., 2018, 3, 18013 CrossRef.
- M. Lao, Y. Zhang, W. Luo, Q. Yan, W. Sun and S. X. Dou, Adv. Mater., 2017, 29, 1700622 CrossRef PubMed.
- H. Zhang, I. Hasa and S. Passerini, Adv. Energy Mater., 2018, 8, 1870082 CrossRef.
- S. Roberts and E. Kendrick, Nanotechnol., Sci. Appl., 2018, 11, 23–33 CrossRef CAS PubMed.
- Y. Lei, X. Li, L. Liu and G. Ceder, Chem. Mater., 2014, 26, 5288–5296 CrossRef CAS.
- Y. H. Jung, A. S. Christiansen, R. E. Johnsen, P. Norby and D. K. Kim, Adv. Funct. Mater., 2015, 25, 3227–3237 CrossRef CAS.
- P.-F. Wang, Y. You, Y.-X. Yin and Y.-G. Guo, Adv. Energy Mater., 2018, 8, 1701912 CrossRef.
- B. Senthilkumar, C. Murugesan, L. Sharma, S. Lochab and P. Barpanda, Small Methods, 2019, 3, 1800253 CrossRef CAS.
- S. Baskar, R. Angalakuthi, C. Murugesan, S. B. Krupanidhi and P. Barpanda, ECS Trans., 2018, 85, 227–234 CrossRef CAS.
- N. Sun, H. Liu and B. Xu, J. Mater. Chem. A, 2015, 3, 20560–20566 RSC.
- V. Simone, A. Boulineau, A. de Geyer, D. Rouchon, L. Simonin and S. Martinet, J. Energy Chem., 2016, 25, 761–768 CrossRef.
- H. Hou, X. Qiu, W. Wei, Y. Zhang and X. Ji, Adv. Energy Mater., 2017, 7, 1602898 CrossRef.
- H. Ying and W.-Q. Han, Adv. Sci., 2017, 4, 1700298 CrossRef PubMed.
- Z. Li, J. Ding and D. Mitlin, Acc. Chem. Res., 2015, 48, 1657–1665 CrossRef CAS PubMed.
- A. Jahel, C. M. Ghimbeu, A. Darwiche, L. Vidal, S. Hajjar-Garreau, C. Vix-Guterl and L. Monconduit, J. Mater. Chem. A, 2015, 3, 11960–11969 RSC.
- J. Qin, N. Zhao, C. Shi, E. Liu, F. He, L. Ma, Q. Li, J. Li and C. He, J. Mater. Chem. A, 2017, 5, 10946–10956 RSC.
- Y. Ching Lu, C. Ma, J. Alvarado, N. Dimov, Y. Shirley Meng and S. Okada, J. Mater. Chem. A, 2015, 3, 16971–16977 RSC.
- C. Xia, F. Zhang, H. Liang and H. N. Alshareef, Nano Res., 2017, 10, 4368–4377 CrossRef CAS.
- Y. Kim, Y. Kim, A. Choi, S. Woo, D. Mok, N.-S. Choi, Y. S. Jung, J. H. Ryu, S. M. Oh and K. T. Lee, Adv. Mater., 2014, 26, 4139–4144 CrossRef CAS PubMed.
- J. Liu, P. Kopold, C. Wu, P. A. van Aken, J. Maier and Y. Yu, Energy Environ. Sci., 2015, 8, 3531–3538 RSC.
- Y. Liu, X. Fang, M. Ge, J. Rong, C. Shen, A. Zhang, H. A. Enaya and C. Zhou, Nano Energy, 2015, 16, 399–407 CrossRef CAS.
- Y. Wei, Z. Wang, H. Ye, J. Mou, D. Lei, Y. Liu, W. Lv, B. Li, F. Kang and Y.-B. He, ChemistrySelect, 2017, 2, 11365–11369 CrossRef CAS.
- M. Gu, A. Kushima, Y. Shao, J.-G. Zhang, J. Liu, N. D. Browning, J. Li and C. Wang, Nano Lett., 2013, 13, 5203–5211 CrossRef CAS PubMed.
- J. Yue, W. Wang, N. Wang, X. Yang, J. Feng, J. Yang and Y. Qian, J. Mater. Chem. A, 2015, 3, 23194–23200 RSC.
- Y. Cheng, J. Huang, J. Li, Z. Xu, L. Cao and H. Qi, J. Power Sources, 2016, 324, 447–454 CrossRef CAS.
- M. K. Datta, R. Epur, P. Saha, K. Kadakia, S. K. Park and P. N. Kumta, J. Power Sources, 2013, 225, 316–322 CrossRef CAS.
- Q. Wu, Q. Shao, Q. Li, Q. Duan, Y. Li and H. Wang, ACS Appl. Mater. Interfaces, 2018, 10, 15642–15651 CrossRef CAS PubMed.
- J. Cui, Z.-L. Xu, S. Yao, J. Huang, J.-Q. Huang, S. Abouali, M. A. Garakani, X. Ning and J.-K. Kim, J. Mater. Chem. A, 2016, 4, 10964–10973 RSC.
- L. Wu, H. Lu, L. Xiao, J. Qian, X. Ai, H. Yang and Y. Cao, J. Mater. Chem. A, 2014, 2, 16424–16428 RSC.
- Q. Li, Z. Li, Z. Zhang, C. Li, J. Ma, C. Wang, X. Ge, S. Dong and L. Yin, Adv. Energy Mater., 2016, 6, 1600376 CrossRef.
- L. Ma, P. Yan, S. Wu, G. Zhu and Y. Shen, J. Mater. Chem. A, 2017, 5, 16994–17000 RSC.
- J. S. C. Kearney, M. Graužinytė, D. Smith, D. Sneed, C. Childs, J. Hinton, C. Park, J. S. Smith, E. Kim, S. D. S. Fitch, A. L. Hector, C. J. Pickard, J. A. Flores-Livas and A. Salamat, Angew. Chem., Int. Ed., 2018, 57, 11623–11628 CrossRef CAS PubMed.
- T. Lindgren, M. Larsson and S.-E. Lindquist, Sol. Energy Mater. Sol. Cells, 2002, 73, 377–389 CrossRef CAS.
- F. Qu, Y. Yuan and M. Yang, Chem. Mater., 2017, 29, 969–974 CrossRef CAS.
- L. Baggetto, N. A. M. Verhaegh, R. A. H. Niessen, F. Roozeboom, J.-C. Jumas and P. H. L. Notten, J. Electrochem. Soc., 2010, 157, A340 CrossRef CAS.
- X. Li, A. L. Hector, J. R. Owen and S. I. U. Shah, J. Mater. Chem. A, 2016, 4, 5081–5087 RSC.
- C. J. Pickard and R. J. Needs, Phys. Rev. Lett., 2006, 97, 045504 CrossRef PubMed.
- G. Trimarchi, A. J. Freeman and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 092101 CrossRef.
- V. L. Chevrier and G. Ceder, J. Electrochem. Soc., 2011, 158, A1011–A1014 CrossRef CAS.
- L. D. Ellis, T. D. Hatchard and M. N. Obrovac, J. Electrochem. Soc., 2012, 159, A1801–A1805 CrossRef CAS.
- S. Komaba, Y. Matsuura, T. Ishikawa, N. Yabuuchi, W. Murata and S. Kuze, Electrochem. Commun., 2012, 21, 65–68 CrossRef CAS.
- J. W. Wang, X. H. Liu, S. X. Mao and J. Y. Huang, Nano Lett., 2012, 12, 5897–5902 CrossRef CAS PubMed.
- L. Baggetto, P. Ganesh, R. P. Meisner, R. R. Unocic, J.-C. Jumas, C. A. Bridges and G. M. Veith, J. Power Sources, 2013, 234, 48–59 CrossRef CAS.
- L. Baggetto, C. A. Bridges, J.-C. Jumas, D. R. Mullins, K. J. Carroll, R. A. Meisner, E. J. Crumlin, X. Liu, W. Yang and G. M. Veith, J. Mater. Chem. A, 2014, 2, 18959–18973 RSC.
- J. M. Stratford, M. Mayo, P. K. Allan, O. Pecher, O. J. Borkiewicz, K. M. Wiaderek, K. W. Chapman, C. J. Pickard, A. J. Morris and C. P. Grey, J. Am. Chem. Soc., 2017, 139, 7273–7286 CrossRef CAS PubMed.
- M. Jansen and J. C. Schön, Z. Anorg. Allg. Chem., 1998, 624, 533–540 CrossRef CAS.
- D. Fischer and M. Jansen, Angew. Chem., Int. Ed. Engl., 2002, 41, 1755–1756 CrossRef CAS PubMed.
- G. V. Vajenine, Inorg. Chem., 2007, 46, 5146–5148 CrossRef CAS PubMed.
- G. V. Vajenine, Solid State Sci., 2008, 10, 450–454 CrossRef CAS.
- J. C. Schön, M. A. C. Wevers and M. Jansen, Solid State Sci., 2000, 2, 449–456 CrossRef.
- M. Corazza, S. Trincone and A. Virgili, Am. J. Clin. Dermatol., 2004, 5, 295–300 CrossRef PubMed.
- T. Pham, T. L. Palmieri and D. G. Greenhalgh, J. Burn Care Rehabil., 2001, 22, 246–248 CrossRef CAS PubMed.
- X. Zhang, A. Zunger and G. Trimarchi, J. Chem. Phys., 2010, 133, 194504 CrossRef PubMed.
- W. Sun, C. J. Bartel, E. Arca, S. R. Bauers, B. Matthews, B. Orvañanos, B.-R. Chen, M. F. Toney, L. T. Schelhas, W. Tumas, J. Tate, A. Zakutayev, S. Lany, A. M. Holder and G. Ceder, Nat. Mater., 2019, 18, 732–739 CrossRef CAS PubMed.
- N. S. P. Watney, Z. A. Gál, M. D. S. Webster and S. J. Clarke, Chem. Commun., 2005, 4190–4192 RSC.
- A. C. Larson and R. B. Von Dreele, Generalized Structure Analysis System (GSAS), Los Alamos National Laboratory Report LAUR, 2004, pp. 86–748 CrossRef CAS; B. H. Toby, J. Appl. Crystallogr., 2001, 34, 210–213 CrossRef CAS.
- R. B. Von Dreele and A. C. Larson, GSAS manual, LANSCE MSH805, Los Alamos National Laboratory, NM87545, 2000 Search PubMed.
- F. Guérin and D. Richeson, J. Chem. Soc., Chem. Commun., 1994, 2213–2214 RSC.
- D. Lützenkirchen-Hecht, N. Scotti, H. Jacobs and R. Frahm, J. Synchrotron Radiat., 2001, 8, 698–700 CrossRef PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- O. A. Vydrov, J. Heyd, A. V. Krukau and G. E. Scuseria, J. Chem. Phys., 2006, 125, 074106 CrossRef PubMed.
- M. Yu and D. R. Trinkle, J. Chem. Phys., 2011, 134, 064111 CrossRef PubMed.
- M. K. Aydinol, A. F. Kohan, G. Ceder, K. Cho and J. Joannopoulos, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 1354–1365 CrossRef CAS.
- P. Chirico, A. L. Hector and B. Mazumder, Dalton Trans., 2010, 39, 6092–6097 RSC.
- J. Choi and E. G. Gillan, J. Mater. Chem., 2006, 16, 3774–3784 RSC.
- P. Xi, Z. Xu, D. Gao, F. Chen, D. Xue, C.-L. Tao and Z.-N. Chen, RSC Adv., 2014, 4, 14206–14209 RSC.
- B. Mazumder, P. Chirico and A. L. Hector, Inorg. Chem., 2008, 47, 9684–9690 CrossRef CAS PubMed.
- B. Mazumder and A. L. Hector, J. Mater. Chem., 2008, 18, 1392–1398 RSC.
- S. I. U. Shah, A. L. Hector, X. Li and J. R. Owen, J. Mater. Chem. A, 2015, 3, 3612–3619 RSC.
- J. Choi and E. G. Gillan, Inorg. Chem., 2005, 44, 7385–7393 CrossRef CAS PubMed.
- L. Lei, W. Yin, X. Jiang, S. Lin and D. He, Inorg. Chem., 2013, 52, 13356–13362 CrossRef CAS PubMed.
- Y. Gu, F. Guo, Y. Qian, H. Zheng and Z. Yang, Mater. Lett., 2003, 57, 1679–1682 CrossRef CAS.
- P. Maneechakr, S. Karnjanakom and J. Samerjit, RSC Adv., 2016, 6, 73947–73952 RSC.
- N. Scotti, W. Kockelmann, J. Senker, S. Traßel and H. Jacobs, Z. Anorg. Allg. Chem., 1999, 625, 1435–1439 CrossRef CAS.
- I. AlShibane, J. S. J. Hargreaves, A. L. Hector, W. Levason and A. McFarlane, Dalton Trans., 2017, 46, 8782–8787 RSC.
- P. Kumar Dutta, U. Kumar Sen and S. Mitra, RSC Adv., 2014, 4, 43155–43159 RSC.
- I. Kovalenko, B. Zdyrko, A. Magasinski, B. Hertzberg, Z. Milicev, R. Burtovyy, I. Luzinov and G. Yushin, Science, 2011, 334, 75–79 CrossRef CAS PubMed.
- L. Ling, Y. Bai, Z. Wang, Q. Ni, G. Chen, Z. Zhou and C. Wu, ACS Appl. Mater. Interfaces, 2018, 10, 5560–5568 CrossRef CAS PubMed.
- Z. Yang, A. A. Gewirth and L. Trahey, ACS Appl. Mater. Interfaces, 2015, 7, 6557–6566 CrossRef CAS PubMed.
- H. Kim, J. Kim, H. Kim, Y. Kim, J. H. Ryu, S. M. Oh and S. Yoon, J. Electroanal. Chem., 2018, 808, 137–140 CrossRef CAS.
- C. Bommier and X. Ji, Small, 2018, 14, 1703576 CrossRef PubMed.
- L. Ji, M. Gu, Y. Shao, X. Li, M. H. Engelhard, B. W. Arey, W. Wang, Z. Nie, J. Xiao, C. Wang, J.-G. Zhang and J. Liu, Adv. Mater., 2014, 26, 2901–2908 CrossRef CAS PubMed.
- R. Mogensen, D. Brandell and R. Younesi, ACS Energy Lett., 2016, 1, 1173–1178 CrossRef CAS.
- E. M. Lotfabad, P. Kalisvaart, A. Kohandehghan, D. Karpuzov and D. Mitlin, J. Mater. Chem. A, 2014, 2, 19685–19695 RSC.
- Y. Wang, Y. Jin, C. Zhao, Y. Duan, X. He and M. Jia, Mater. Lett., 2017, 191, 169–172 CrossRef CAS.
- S.-H. Yu, A. Jin, X. Huang, Y. Yang, R. Huang, J. D. Brock, Y.-E. Sung and H. D. Abruña, RSC Adv., 2018, 8, 23847–23853 RSC.
- C. Bommier, D. Leonard, Z. Jian, W. F. Stickle, P. A. Greaney and X. Ji, Adv. Mater. Interfaces, 2016, 3, 1600449 CrossRef.
- D. I. Iermakova, R. Dugas, M. R. Palacín and A. Ponrouch, J. Electrochem. Soc., 2015, 162, A7060 CrossRef CAS.
- N. Liu, H. Wu, M. T. McDowell, Y. Yao, C. Wang and Y. Cui, Nano Lett., 2012, 12, 3315–3321 CrossRef CAS PubMed.
- J. Zhang, D.-W. Wang, W. Lv, S. Zhang, Q. Liang, D. Zheng, F. Kang and Q.-H. Yang, Energy Environ. Sci., 2017, 10, 370–376 RSC.
- C. Kittel, Introduction to Solid State Physics, John Wiley & Sons, New York, 8th edn, 2005 Search PubMed.
- G. V. Vajenine, X. Wang, I. Efthimiopoulos, S. Karmakar, K. Syassen and M. Hanfland, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 224107 CrossRef.
- M. Jansen, C. R. Chim., 2018, 21, 958–968 CrossRef CAS.
- A. Manthiram, A. V. Murugan, A. Sarkar and T. Muraliganth, Energy Environ. Sci., 2008, 1, 621–638 RSC.
- D. Ma, Y. Li, H. Mi, S. Luo, P. Zhang, Z. Lin, J. Li and H. Zhang, Angew. Chem., Int. Ed., 2018, 57, 8901–8905 CrossRef CAS PubMed.
- J. Qian, Y. Xiong, Y. Cao, X. Ai and H. Yang, Nano Lett., 2014, 14, 1865–1869 CrossRef CAS PubMed.
- Y. Cheng, A. Nie, L.-Y. Gan, Q. Zhang and U. Schwingenschlögl, J. Mater. Chem. A, 2015, 3, 19483–19489 RSC.
- S. Fitch, G. Cibin, S. Hepplestone, N. Garcia-Araez and A. Hector, 2020, DOI:10.5258/SOTON/D1482.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ta04034g |
| This journal is © The Royal Society of Chemistry 2020 |