A new metric for relating macroscopic chromatograms to microscopic surface dynamics: the distribution function ratio (DFR)†
Logan D. C.
Bishop
 a,
Anastasiia
Misiura
a,
Anastasiia
Misiura
 a and
Christy F.
Landes
a and
Christy F.
Landes
 *abcd
*abcd
aDepartment of Chemistry, Rice University, Houston, Texas 77251, USA. E-mail: cflandes@rice.edu
bDepartment of Electrical and Computer Engineering, Rice University, Houston, Texas 77251, USA
cDepartment of Chemical and Biomolecular Engineering, Rice University, Houston, Texas 77251, USA
dSmalley-Curl Institute, Rice University, Houston, Texas 77251, USA
First published on 2nd June 2021
Abstract
Heterogeneous stationary phase chemistry causes chromatographic tailing that lowers separation efficiency and complicates optimizing mobile phase conditions. Model-free metrics are attractive for assessing optimal separation conditions due to the low quantity of information required, but often do not reveal underlying mechanisms that cause tailing, for example, heterogeneous retention modes. We report a new metric, which we call the Distribution Function Ratio (DFR), based on a graphical comparison between the chromatogram and Gaussian cumulative distribution functions, achieving correspondence to ground truth surface dynamics with a single chromatogram. Using a Monte Carlo framework, we show that the DFR can predict the prevalence of heterogeneous retention modes with high precision when the relative desorption rate between modes is known, as in during surface dynamics experiments. Ground truth comparisons reveal that the DFR outperforms both the asymmetry factor and skewness by yielding a one-to-one correspondence with heterogeneous retention mode prevalence over a broad range of experimentally realistic values. Perhaps of more value, we illustrate that the DFR, when combined with the asymmetry factor and skewness, can estimate microscopic surface dynamics, providing valuable insights into surface chemistry using existing chromatographic instrumentation. Connecting ensemble results to microscopic quantities through the lens of simulation establishes a new chemistry-driven route to measuring and advancing separations.
1. Introduction
Understanding the microscopic surface mechanisms underlying chromatographic separations is crucial for moving drug production from quality by testing1 to quality by design.2 Doing so would help reduce the purification and separation cost of new protein pharmaceuticals as well as alleviate the energy burden induced by industrial separations.3–5 Recent efforts to move towards separations-by-design include novel column designs, continuous flow systems, new single-analyte measurements, advanced statistical analysis, and mechanistic simulations and theory.1,6–10,12–19,42 It is thus possible to correlate microscopic phenomena to ensemble observables such as chromatographic elution curves. Most discussions of tailing address column overloading,19–21 but tailing can also occur due to rare, heterogeneous interactions with the stationary phase surface. Surface heterogeneity can be introduced by surface defects7,9 or result from specific versus non-specific binding,11 an effect often seen in chiral separations.22 Ideally, we also need new methods to extract mechanistic details from macroscopic separation observables.Detailed chemical information is captured in the lineshape of a chromatogram. Lineshape analysis can infer the number of adsorption events in the column,23 varied adsorption kinetics,24 non-linear column contributions,25 and flow effects.26,27 Other methods rely on analytical models that approximate the curve using variables without physical meaning,27,28 fitting peaks based on analytical series,29 or need ancillary equipment during data collection.30,31 Conversely, model-less metrics using only the chromatogram have been utilized to interpret microscale phenomena and are common metrics for separation optimization32,33 but rarely can relate changes in chromatogram shape to changes in stationary phase surface chemistry. Here, a disconnect forms between relating the results of an ensemble separation performed in a column measured in millimeters to microscopic details measured over micrometers of stationary phase surface, such as those captured in single-molecule studies.34–36 Recently, we demonstrated that the most popular graphical metric, the asymmetry factor (As), is not suitable for microscale studies of surfaces due to non-linear relationships with respect to rare retention mode statistics and underestimation of the amount of analyte lost in the tail.37 Development of a graphical metric that infers surface chemical effects from ensemble chromatograms would translate decades of opaque experimental optimization into powerful observations of chemical phenomena occurring on the stationary phase surface.
The Distribution Function Method (DFM)38–40 detects peak variations by comparing two distributions in a parametric plot, providing qualitative proof of minute deviation, but lacking correlation to an underlying mechanism. Repurposing the DFM to create trackable phenomena can correlate chromatogram lineshape to ground truth physical chemistry at the surface, like mixed-mode adsorption41 and stationary phase hopping,42 from ensemble data alone. Pivoting to include mobile phase simulations could extend correlations to mobile phase artifacts from flow43,44 and column structure,45–49 extra column components and injection methods,50–52 and diffusion within pores.53–56 Correlation of simulated effects with chromatogram lineshape provides a necessary bridge between macroscale and microscale measurements.57,58
In this work, we expand the DFM as a ratio of the chromatographic cumulative distribution function (CDF) and a Gaussian CDF, a method we call the Distribution Function Ratio (DFR), to calculate microscopic surface dynamics from a single chromatogram. Comparisons to a Gaussian lineshape improve upon Rix's original method by eliminating the need for ancillary peaks to characterize the chromatogram.39 Further, chromatogram lineshape is shown to correlate pseudo-linearly to mixed-mode adsorption dynamics, capturing important surface statistics using only the ensemble chromatogram. Mixed-mode adsorption dynamics, a model for kinetic tailing in low dilution and topic of interest for pharmaceutical separations,59,60 is used to simulate chromatograms from ground truth statistics and demonstrate the utility and precision of the DFR. Here, we show that the DFR outperforms As and statistical skewness over a wide range of relative prevalence and relative desorption rate of rare, high energy, slow desorbing retention modes on the stationary phase surface. Use of the DFR with microscale surface information provides high precision estimates of surface retention modes. However, in absence of microscale surface insight, As and skewness can be used in combination with the DFR to estimate surface dynamics from the ensemble peak alone. The DFR is used to analyze a separation of a model protein, lysozyme, capturing valuable statistics about surface retention modes. Combining the DFR with ground truth simulations generates calibration curves that connect peak shape to surface physicochemistry, creating an optimizable metric that interrogates stationary phase surface dynamics while reporting on the quality of separation. Using the DFR quantifies rare surface defects and specific adsorption using only ensemble chromatography.
2. Experimental section
2.1. Theory
Tracing the source of mixed-mode kinetic tailing requires knowledge of the prevalence and desorption statistics of retention modes on the stationary phase surface. We examine tailing in mixed-mode chromatography where a protein alternates between flowing in the mobile phase and surface adsorption through two different retention modes, the first mode fast desorbing and prevalent, the other slower desorbing and increasingly rare. Each retention mode has a distinct rate of desorption (kj) and expected desorption time (〈τj〉) that describes an exponential distribution of singular desorption times (τj), where higher energy retention modes have longer expected desorption times.61 Stationary phases with two retention modes (m = 2) induce tailing and broadening in chromatography,60,62,63 though a proliferation of retention modes (m > 2) can exist depending on surface microstructure and functionalization.64–67 The number of retention modes on the surface and their desorption rates can be gathered experimentally using microscale, surface measurements.13,42 However, direct observations of surface dynamics are limited spatially, on the order of micrometers, while column lengths are on the millimeter scale. Capturing the desorption time differences between common and rare modes and correlating their prevalence to column-wide experimental parameters is critical for reducing chromatographic tailing and can only be achieved through simulation and theory.Modeling the tailing effects of mixed-mode adsorption requires knowledge of molecular elution histories. Kinetic chromatographic tailing occurs when a small population of molecules forms a broad distribution of elution times due to interactions with a rare, high energy retention mode, even in dilute conditions where column overload does not occur.24,63 The stochastic theory of chromatography captures rare interactions by describing molecular elution as a molecule undergoing a random walk between moments of mobility and stationarity. The elution history of each molecule is then a series of connected adsorption events sampled from available retention modes.68 A master equation for the retention time of a single molecule (T) that incorporates interactions for every adsorption event across all retention modes is then eqn (1):
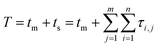 | (1) |
The molecular histories produced by the Monte Carlo simulations are random samples of the “frequency functions” described by Dondi.73,74 Analytically, each frequency function is the sum of all nth fold convolutions of the distribution of the retention mode desorption times over n adsorption/desorption steps for 0 ≤ n ≤ ∞. For the homogeneous case, the stationary phase time, cs(t):
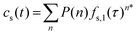 | (2) |
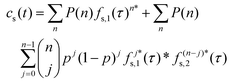 | (3) |
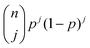 is the Bernoulli coefficient for j interactions with the common retention mode with relative prevalence p out of n total adsorption/desorption steps and fs,2(τ) is the distribution of desorption times for the rare retention mode. Monte Carlo simulations avoid convolutions by directly calculating the sum of random variables over n adsorption/desorption steps, constructing the distributions in cs(t) through random sampling. As such, we define cs(t) non-analytically as a mixture model75 of our Monte Carlo calculated molecular history distributions where each distribution is differentiated by the number of interactions with a rare retention mode (eqn (4)):
is the Bernoulli coefficient for j interactions with the common retention mode with relative prevalence p out of n total adsorption/desorption steps and fs,2(τ) is the distribution of desorption times for the rare retention mode. Monte Carlo simulations avoid convolutions by directly calculating the sum of random variables over n adsorption/desorption steps, constructing the distributions in cs(t) through random sampling. As such, we define cs(t) non-analytically as a mixture model75 of our Monte Carlo calculated molecular history distributions where each distribution is differentiated by the number of interactions with a rare retention mode (eqn (4)): | (4) |
 . Quantifying deviations from the Gaussian distribution is then an avenue to measure statistics of the tailing distributions in the chromatogram lineshape without specifying an analytical model for each distribution fi(t).
. Quantifying deviations from the Gaussian distribution is then an avenue to measure statistics of the tailing distributions in the chromatogram lineshape without specifying an analytical model for each distribution fi(t).
2.2. Metric definition
Methods developed from the DFM38,39 can detect small deviations in the lineshape of two distributions while remaining tolerant to excessive experimental noise.38 Briefly, the DFM qualitatively differentiates two distributions (Fig. 1A) by comparing the shape of each chromatogram's CDF (Fig. 1A, inset) normalized to the time interval (0,1) through the function θ(t) (see ESI†), and abbreviated as θ when used as a variable. Our modification of the DFM always compares to a Gaussian CDF, adopting the Gaussian as the ‘ideal’ chromatogram through the posing of eqn (4). Further, taking the ratio of both CDFs generates trackable peak phenomena, providing quantitative tracking of underlying physical chemistry rather than qualitative acknowledgment of the difference of two chromatograms, as in Rix's original work. Mathematically, the DFR for any chromatogram/Gaussian pair (c(θ), g(θ)) is then the ratio of their CDFs (see ESI†) over the normalized time interval θ (eqn (5)):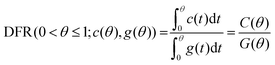 | (5) |
 | ||
| Fig. 1 Utilizing CDFs to detect differences between chromatograms and the Gaussian lineshape. (A) A simulated chromatogram overlaid with a Gaussian curve. (Inset) CDFs of each curve graphed in normalized time. (B) The DFR comparing both curves with the quantity of interest, DFR peak position (θ*), annotated. (Inset) Rix's parametric DFM comparison for both curves.38 | ||
The result of eqn (5) is a unique, characteristic curve for every chromatogram (Fig. 1B) with a critical value in the form of peak position (θ*). Generating quantitative, optimizable peak phenomena differentiates the DFR from the original DFM result (Fig. 1B, inset), which only qualitatively assesses if two distributions are different through deviations along the diagonal. As such, two separate chromatograms are needed to quantify chemical effects in a single experiment. The DFR retains the benefits of Rix's original method in only utilizing the chromatogram lineshape without fitting to a model but extracts chemical information through comparison to the Gaussian curve normalized in time and concentration, avoiding the need for a second chromatogram. Normalization also minimizes the contribution of broadening by the mobile phase (Fig. S2†), further isolating the stationary phase contributions. Because deviations from a Gaussian represent contributions due to heterogeneous surface interactions, per eqn (4), information about the tailing distributions is captured in the DFR lineshape. Ground truth simulations correlate the energy and prevalence of rare retention modes to the chromatogram lineshape and validate that the DFR can capture statistics of tailing distributions. The DFR provides an estimate of the relative column prevalence of a retention mode identified through microscale surface measurements, bridging the spatial difference between surface dynamics measurements (μm scale) and the full-length column (mm scale). Further, estimating microscopic surface dynamics from the ensemble chromatogram alone provides a no-cost evaluation of the need for more complex, micrometer resolution experiments.
2.3. Computational details
Chromatographic simulations were performed using a Monte Carlo framework programmed in Python 3 programming language84 (Python Software Foundation, https://www.python.org/) using Numpy85 and Scipy.86 The simulation framework is based on the work of Dondi14 and Cavazzini,13 and detailed in our previous publications.38,42 The benefits of the Monte Carlo framework is that it is agnostic towards retention mechanisms when the mathematics are properly posed and is the only route for modeling non-linear chromatography.87,88 Surface crowding is not included in the simulations, meaning that all chromatographic artifacts are the product of kinetic tailing rather than thermodynamic column overloading. Therefore, changes measured with the DFR only relate to surface kinetic effects, a connection unachievable experimentally and only partially realized in microscale surface experiments without simulation. The simulations treat time and distance as abstract, unitless quantities that are adaptable to any column length or surface chemistry. Time is measured in the unitless value δt, which adapts to the units of the kinetic rate for the retention mode.89 Our Monte Carlo simulation framework treats each molecular elution as a random walk down a connected series of column ‘slices’, where the slice width is the expected travel distance between transitions in the mobile-stationary phase interface. Elution speed is set such that each molecule takes 1δt to traverse a column slice. For the simulations in this work, the simulated column has 1000 column slices with a constant mobile phase time tm = 1000δt. The number of slices correlates to the difference in linear distance between a wide-field microscope field of view (∼32 μm) and a real column (∼30 mm).Adsorption events are simulated using statistical sampling parameterized by the probability of interaction with the stationary phase surface, the probability of encountering a specific retention mode (pj), and the expected desorption time of that retention mode (〈τj〉). A schematic for the random walk a molecule undergoes in each slice is shown in Fig. 2. Here, we assume each molecule has a probability (pa = 0.5) of undergoing adsorption exactly once within each slice. The probability of interaction with the surface is arbitrarily chosen but operates as a tunable parameter adjusted to fit available surface dynamics data. The original stochastic theory assumes that an average probability is satisfactory if a molecule fluctuates through the range of adsorption probabilities many times between adsorptions.68 Further, Hlushkou et al. have described the probability of adsorption upon interaction with the surface as a constant based upon geometrical and energetic consideration for the adsorption process.89,90 However, we note that our probability is conditioned on the phase ratio of the column and could be expanded to include local heterogeneity of the stationary phase surface. Including local fluctuations in probability in the model framework is a natural extension as more experimental information becomes available.
 | ||
| Fig. 2 A graphical depiction of a simulated column ‘slice’ showing the probabilistic decision branches to simulate interactions with the stationary phase. A protein encounters the surface, undergoes adsorption with some probability (pa), and adsorbs to the surface through one of j retention modes with a likelihood of selection pj. Each mode has a distinct rate of desorption kj. Figure modified with permission from ref. 37. Copyright Elsevier 2020. | ||
Each slice can be considered a column feature, such as a bead, similar to the description provided by Horvath et al.91 The ‘surface’ of each slice has m retention modes, each with some probability of selection (pj). In the case of our simulations, the probability of interacting with the low energy, faster desorbing retention mode is higher than interaction with high energy, slower desorbing retention mode (p1 ≫ p2). After retention mode selection, a desorption time (Δτ) is sampled from an exponential distribution parameterized on the desorption rate constant (kj) of the retention mode (e−τkj) with expected desorption time of 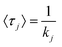 .23,61 Simulating many molecules down the column and aggregating the elution histories together generates a chromatogram.
.23,61 Simulating many molecules down the column and aggregating the elution histories together generates a chromatogram.
2.4. Experimental methods
The chromatographic experiments were carried out using a home-built Fast Protein Liquid Chromatography (FPLC) system. Protein solutions of 8.3 μM Lysozyme from chicken egg white (>98%; Sigma) in the presence of 1 M sodium chloride (NaCl) were prepared in 10 mM HEPES buffer (Sigma, pH 7.2). All the solutions were injected into the FPLC using a 1 mL syringe (Becton Dickinson) with an injection volume of 300 μL. A constant flow of 2 ml min−1 was controlled using a peristaltic pump (Watson-Marlow, 120 Series). Absorbance from the analyte was monitored at 280 nm using a UV detector (Spectrum Chromatography). The signal then was converted from current to voltage by a digital recorder (Hantek, 365E) controlled by Hantek 365 software that registered the output signal. The syringe hydrophilic filters with polyvinylidene fluoride (PVDF) membranes (hydrophilic 0.45 μm pore size, 25 mm diameter) and hydrophobic filters with PVDF membranes (hydrophobic 0.45 μm pore size, 25 mm diameter) used as chromatographic media were purchased from Cole-Parmer and Sigma Aldrich, respectively. A series of three connected PVDF syringe filters were assembled and integrated with the setup. All components of the FPLC system were connected using silicone tubing (MED-X.D., 0.063′′ internal diameter).2.5. Computational details
A two-mode system was simulated using four different ratios of desorption rates over a range of strong retention mode prevalence. The common, low energy retention mode has an expected desorption time of 〈τ1〉 = 4δt, equivalent to four times as long as necessary to traverse the column slice. Expected desorption times of the rare, high energy retention mode are then a factor longer than the expected desorption times of the common, low energy retention mode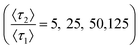 over a range of relative prevalence (10–5 ≤ p2 ≤ 10–2) covering several orders of magnitude. Relative prevalence is defined with respect to the number of slices in the column. Here, the relative prevalence relates to the absolute number of times a molecule interacts with a rare site (0.01 ≤ (im=2) ≤10). Each simulation consisted of 300
over a range of relative prevalence (10–5 ≤ p2 ≤ 10–2) covering several orders of magnitude. Relative prevalence is defined with respect to the number of slices in the column. Here, the relative prevalence relates to the absolute number of times a molecule interacts with a rare site (0.01 ≤ (im=2) ≤10). Each simulation consisted of 300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 simulated molecules, which was shown to be sufficient for stabilization of the curve shape (Fig. S3†). The distribution of adsorption events per molecule (n) forms a Gaussian about 〈n〉 = 500 given a 50% chance of adsorbing to the surface in a 1000 slice column. The average number of adsorption–desorption events as well as the chance of adsorbing to the stationary phase can be validated through peak analysis of ensemble data.13,23 Adjusting the probability of adsorption (pa) and the number of slices will change the value of n and therefore the shape of the chromatogram. However, previous studies with similar theories and models have extracted useful information from a small number of interactions and discussed methods for scaling the profile in terms of the average number of adsorption events.13,14,73,92 Simulated molecule histograms are smoothed with a Savitzky–Golay filter before cubic splining, producing the final chromatographic curve used for analysis (Fig. S4†).93,94
000 simulated molecules, which was shown to be sufficient for stabilization of the curve shape (Fig. S3†). The distribution of adsorption events per molecule (n) forms a Gaussian about 〈n〉 = 500 given a 50% chance of adsorbing to the surface in a 1000 slice column. The average number of adsorption–desorption events as well as the chance of adsorbing to the stationary phase can be validated through peak analysis of ensemble data.13,23 Adjusting the probability of adsorption (pa) and the number of slices will change the value of n and therefore the shape of the chromatogram. However, previous studies with similar theories and models have extracted useful information from a small number of interactions and discussed methods for scaling the profile in terms of the average number of adsorption events.13,14,73,92 Simulated molecule histograms are smoothed with a Savitzky–Golay filter before cubic splining, producing the final chromatographic curve used for analysis (Fig. S4†).93,94
Functions that are used in the DFR must be normalized in time and concentration. The time domain is normalized using the function θ(t) beginning/ending when the signal passes above/below a defined percent of the peak height. The recovered mass within those bounds is normalized to one  . The bounds chosen for each sample are 1% of the max height of cs(t). The shape of cs(t) is compared to a Gaussian distribution in θ with the mean at θ = 0.5. Normalization of time and mass generates the same Gaussian curve for any chromatographic peak making any form of peak fitting unnecessary. Bounds for the Gaussian CDF
. The bounds chosen for each sample are 1% of the max height of cs(t). The shape of cs(t) is compared to a Gaussian distribution in θ with the mean at θ = 0.5. Normalization of time and mass generates the same Gaussian curve for any chromatographic peak making any form of peak fitting unnecessary. Bounds for the Gaussian CDF 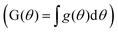 is set to 1.5% the max height of the representative Gaussian. How bound selection changes the shape of G(θ) (Fig. S5A†) and the percent of the curve that falls outside the bounds (Fig. S5B†) are shown in the ESI. DFR peak position (θ*) is found using the first derivative test.
is set to 1.5% the max height of the representative Gaussian. How bound selection changes the shape of G(θ) (Fig. S5A†) and the percent of the curve that falls outside the bounds (Fig. S5B†) are shown in the ESI. DFR peak position (θ*) is found using the first derivative test.
4. Results and discussion
4.1. Extracting relative desorption rate and high energy retention mode prevalence using the DFR
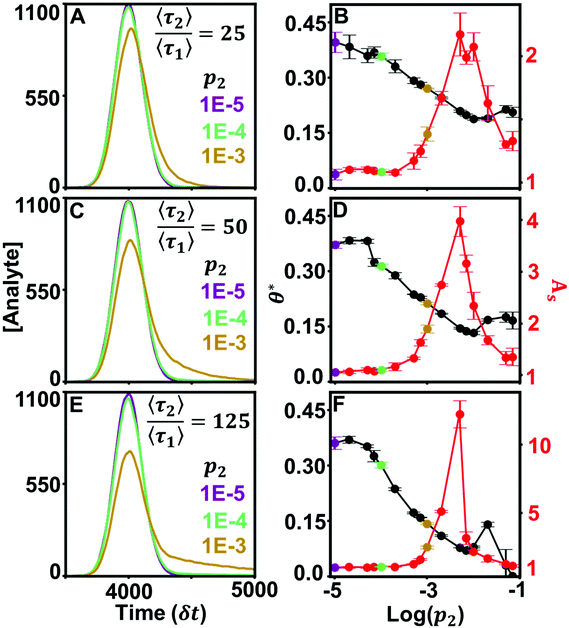
Curvature changes in the chromatographic lineshape encode information about the relative prevalence of stronger retention modes at the stationary phase surface and are extractable by tracking the DFR peak position (θ*). Fig. 3 compares the sensitivity of θ* and As to changes in the prevalence of the high energy retention mode (p2) at several relative desorption rates . At minor differences in desorption rates, low enough that chromatographic peaks are visually similar (Fig. 3A), θ* still detects surface heterogeneity at low levels of prevalence and can differentiate between prevalence with high precision (Fig. 3B). As does not share the traits of sensitivity or differentiability, reporting homogeneity at low prevalence and losing predictive power through lack of one-to-one correspondence at higher prevalence. Higher desorption rate ratios
. At minor differences in desorption rates, low enough that chromatographic peaks are visually similar (Fig. 3A), θ* still detects surface heterogeneity at low levels of prevalence and can differentiate between prevalence with high precision (Fig. 3B). As does not share the traits of sensitivity or differentiability, reporting homogeneity at low prevalence and losing predictive power through lack of one-to-one correspondence at higher prevalence. Higher desorption rate ratios  of 50 (Fig. 3C/D) and 125 (Fig. 3E/F) do not diminish the precision or differentiability of the DFR or improve the results of As. Using As cannot provide an accurate assessment of surface homogeneity, even when chromatograms visually tail. Tracking θ* provides a pseudo-linear, one-to-one correspondence over a wide range of prevalence with high precision at a variety of different retention mode energies with a single chromatogram when the ratio of desorption rates is known.
of 50 (Fig. 3C/D) and 125 (Fig. 3E/F) do not diminish the precision or differentiability of the DFR or improve the results of As. Using As cannot provide an accurate assessment of surface homogeneity, even when chromatograms visually tail. Tracking θ* provides a pseudo-linear, one-to-one correspondence over a wide range of prevalence with high precision at a variety of different retention mode energies with a single chromatogram when the ratio of desorption rates is known.
The DFR can still differentiate surface effects when the difference between retention mode desorption rates nears homogeneity. Fig. S6† examines a kinetic scenario where the ratio of expected desorption times between the low and high energy retention modes is a factor of 5. Small differences in kinetics produce chromatograms that appear symmetric and are indifferentiable by eye (Fig. S6A†). θ* tracks the prevalence of the slow retention mode while As is incapable of differentiating between the peaks (Fig. S6B†). Development of custom-designed columns and stationary phases95,96 could be advanced by a metric that can interrogate surface heterogeneity at a wide range of experimental conditions, especially near-homogeneous conditions that approximate, but do not reach, the ideal Gaussian lineshape. Implementing the DFR in tandem with surface dynamics measurements to direct the selection of macroscopic experimental parameters achieves chemistry-driven design of stationary phases.
4.2. Tracking θ* identifies surface dynamics when other graphical metrics fail
Values of θ* are unique for each prevalence within a desorption rate trendline but are not unique between relative desorption rates. Fig. 4 graphs all four simulated chromatogram sets for three metrics: As (Fig. 4A), skewness (Fig. 4B), and θ* (Fig. 4C). Identifying surface dynamics from the ensemble measurement requires a one-to-one correspondence trend across a wide range of possible prevalence values for the relative desorption rate. Here, both As and skewness either lose sensitivity over a range of values or provide two possible prevalence even when the relative desorption rate between modes is known. Knowledge of the surface dynamics does not provide the means to correctly assess the prevalence of a retention mode in the full column. Conversely, θ* provides a near one-to-one correspondence over several orders of magnitude, providing an optimizable metric when the relative desorption rate has been measured. Therefore, spatially limited microscale measurements of surface dynamics can extrapolate the rare retention mode prevalence across the length of the macroscale column. Complications arise when the relative desorption rates (〈τ1〉, 〈τ2〉) are unavailable to direct selection of a θ* trend line, such as when surface dynamics measurements have not been performed. Here, the one-to-one correspondence of θ* no longer holds when other relative desorption rates are considered (Fig. 4C). Microscopy measurements are necessary to achieve a high precision estimate of surface dynamics, either in identifying relative desorption rate or relative prevalence of retention modes. However, aggregating several ensemble accessible metrics can educate the selection of relative desorption rate and mode prevalence. | ||
| Fig. 4 Comparison of the graphical metrics of As (A), skewness (B), and θ* (C) for all simulated chromatograms used in Fig. 3 and S4†. | ||
4.3. Estimating mixed-mode prevalence and desorption rate without surface dynamics measurements
Combining θ* with ancillary graphical metrics can estimate p2 or 〈τ2〉 when information about surface dynamics is unavailable. Fig. 5 presents a workflow for estimating surface heterogeneity from ensemble information alone. As an example, we consider two chromatograms with kinetics that do not lie along trendlines presented previously (Fig. 5A). To direct selection of a θ* trendline, other graphical information can be incorporated. Fig. 5B is a parametric plot of Asversus skewness that can be used in the same manner as a phase diagram. Calculating both As and skewness can help estimate the value of 〈τ2〉 from simulated data by identifying a range of valid relative desorption ratios. The values for the chromatograms in Fig. 5A are marked with crosses and correctly estimate the relative desorption rate between retention modes for both simulations. Fig. 5C illustrates possible solutions for 〈τ2〉 and p2 for the simulated chromatograms given the values of θ*. Using information provided by the parametric plot in Fig. 5B, the set of possible solutions (dotted line, Fig. 5C) is reduced to a smaller estimate set with stricter bounds (solid line, Fig. 5C). Here, we have successfully estimated the microscale surface values of 〈τ2〉 and p2 from the ensemble chromatogram alone, bridging the knowledge gap through simulations. | ||
Fig. 5 Estimating surface heterogeneity from ensemble information. (A) Simulated chromatograms with kinetic rates  and 95 with p2 = 0.001. (B) A parametric plot of As and skewness from Fig. 4C trendlines. Chromatograms in panel A are denoted with crosses (C) All θ* trends with possible (dotted) and estimated (solid) solutions for simulated chromatograms from panel A. and 95 with p2 = 0.001. (B) A parametric plot of As and skewness from Fig. 4C trendlines. Chromatograms in panel A are denoted with crosses (C) All θ* trends with possible (dotted) and estimated (solid) solutions for simulated chromatograms from panel A. | ||
4.4. Using θ* to guide assessment of experimental chromatograms
Evaluating θ* in ensemble separations connects experimental results to simulated chromatograms, enabling analysis of plausible surface chemistry. The effectiveness of profile shape analysis has been illustrated experimentally using a library of standard control curves.97 Here, we replicate that process using simulated two-retention mode curves to estimate surface dynamics in two ensemble separations. Fig. 6 shows two real separations of lysozyme over hydrophobic and hydrophilic PVDF membranes and DFR analysis used to detect possible heterogeneity on the stationary phase surface. Fig. 6A overlays the chromatograms for lysozyme flowed over hydrophobic and hydrophilic membranes. We begin our analysis with the assumption that the chromatogram can be best explained using a two-retention mode system, a kinetic scenario well studied in theory and commonly seen experimentally on otherwise homogeneous surfaces.9,61,65,92,98,99 Subsequent, rarer, stronger retention modes are possible but negligibly contribute to profile shape (Fig. S1†).Fig. 6B/C present DFR analysis for the hydrophobic and hydrophilic separation, respectively, overlaying the experimental data with a simulated chromatogram that matches in θ*. In both cases, a simulated peak was found that showed good agreement with the raw data. Peak position/height were matched to reduce differences in tm and normalize for concentration, respectively. The time-domain was normalized to account for differences between the time resolution of the FPLC detector (0.6 ms) versus the simulated unit of time (δt).88 Possible solutions for the surface kinetics are extrapolated from simulated chromatograms that closely match the experimental curve shape and the experimental value of θ* (Tables S1 and S2†). The subset of the simulations used to extrapolate the surface kinetics are co-plotted with the experimental data in Fig. S7 and S8.†
The matching simulated chromatograms indicate that the surfaces could be described using a two-retention mode system where the rare, long binding mode has a relative desorption time of 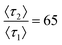 and relative prevalence p2 = 0.007 on the hydrophobic membrane and
and relative prevalence p2 = 0.007 on the hydrophobic membrane and 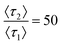 and p2 = 0.01 on the hydrophilic membrane. Previous work in the group suggests that the transition from hydrophobic to hydrophilic character decreases the hopping behavior of lysozyme on the stationary phase surface.100 Increased hopping motion, also called continuous-time random walks, can lead to changes in peak shape.42 The increase in the prevalence of long interactions on the hydrophilic membrane could also be caused by the increased unfolding of lysozyme on the hydrophilic surface, where the change in surface character introduces a new mode of interaction.101 Both possibilities represent starting points for imaging of the stationary phase surface to understand the possible chemical moieties that lead to rare surface interactions.
and p2 = 0.01 on the hydrophilic membrane. Previous work in the group suggests that the transition from hydrophobic to hydrophilic character decreases the hopping behavior of lysozyme on the stationary phase surface.100 Increased hopping motion, also called continuous-time random walks, can lead to changes in peak shape.42 The increase in the prevalence of long interactions on the hydrophilic membrane could also be caused by the increased unfolding of lysozyme on the hydrophilic surface, where the change in surface character introduces a new mode of interaction.101 Both possibilities represent starting points for imaging of the stationary phase surface to understand the possible chemical moieties that lead to rare surface interactions.
Peak analysis of the hydrophilic surface homogeneous population was performed by removing the contribution of interactions with the rare retention mode, a benefit of using simulations. Using methods described by Felinger,23 we estimate that 〈τ1〉 = 40 ms if 〈n〉 = 645 (Fig. S9†). Both values could be scaled to adjust for varied values of 〈n〉. We can conclude that θ* would be suitable as a guide for automatically matching experimental chromatograms to simulated data as the analysis only relies on the profile shape, not the chemical identity of the separatory mode or analyte. Simulation/measurement of mobile phase effects would improve the match between peaks as well as refine estimates of 〈τ1〉 and 〈n〉, but lies outside the scope of this work.
5. Conclusions
Surface defects and rare chemistries can be detected and estimated using only the ensemble chromatogram. Using the DFR to translate a macroscale chromatogram in terms of microscale surface dynamics offers a route to quality by design rather than quality by testing. Mechanistic insights into the surface allow θ* to estimate rare retention mode prevalence with higher precision than other commonly used metrics. In absence of microscale surface measurements, θ* can be supplemented by As and skewness to refine the range of possible prevalence/relative desorption time estimates, achieving accurate measurements of surface dynamics using only macroscale data. Using the DFR, experimentally measured ensemble chromatograms can be analyzed to verify if direct observations of retention modes adequately capture qualities of the stationary phase across the whole column. The modular nature of the framework can extend our simulation to include other column effects. Future extensions could include modeling the effects of column construction such as slurry concentration, extra-column broadening effects, and patterned stationary phases. Connecting macroscale chromatograms and microscale surface dynamics directs parameter tuning using surface chemistry rather than phenomenological observations, achieving chemistry-driven design.Author contributions
Logan D. C. Bishop: Conceptualization, methodology, software, formal analysis, investigation, writing – original draft, writing review & editing. Anastasiia Misiura: Conceptualization, methodology, investigation, validation, resources, writing – original draft. Christy F. Landes: Conceptualization, methodology, visualization, writing – review & editing, supervision, project administration, funding acquisition.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
C. F. L. and A. M. acknowledge the Welch Foundation (Grant C-1787) for support of this work. L. D. C. B. acknowledges that this material is based upon work supported by the National Science Foundation Graduate Research Fellowship Program (Grant 1842494).References
- D. G. Sauer, M. Melcher, M. Mosor, N. Walch, M. Berkemeyer, T. Scharl-Hirsch, F. Leisch, A. Jungbauer and A. Dürauer, Real-time monitoring and model-based prediction of purity and quantity during a chromatographic capture of fibroblast growth factor 2, Biotechnol. Bioeng., 2019, 116(8), 1999–2009 CrossRef CAS PubMed.
- A. S. Rathore, Quality by Design (QbD)-Based Process Development for Purification of a Biotherapeutic, Trends Biotechnol., 2016, 34(5), 358–370 CrossRef CAS PubMed.
- National Academies of Science, Engineering and Medicine, A Research Agenda for Transforming Separation Science, The National Academies Press, Washington, DC, 2019 Search PubMed.
- J. Avorn, The $2.6 Billion Pill - Methodologic and Policy Considerations, N. Engl. J. Med., 2015, 372(20), 1877–1879 CrossRef CAS PubMed.
- M. Beccaria and D. Cabooter, Current developments in LC-MS for pharmaceutical analysis, Analyst, 2020, 145(4), 1129–1157 RSC.
- R. Kiesswetter, F. Brandl, N. Kastner-Pustet and A. Mannschreck, Chiroptical detection during liquid chromatography: Deconvolution of overlapping peaks of enantiomers and its applications, Chirality, 2003, 15, S40–S49 CrossRef CAS PubMed.
- J. N. Mabry, M. J. Skaug and D. K. Schwartz, Single-Molecule Insights into Retention at a Reversed-Phase Chromatographic Interface, Anal. Chem., 2014, 86(19), 9451–9458 CrossRef CAS PubMed.
- M. J. Skaug, J. N. Mabry and D. K. Schwartz, Single-Molecule Tracking of Polymer Surface Diffusion, J. Am. Chem. Soc., 2014, 136(4), 1327–1332 CrossRef CAS PubMed.
- M. J. Wirth and M. A. Legg, Single-molecule probing of adsorption and diffusion on silica surfaces, Annu. Rev. Phys. Chem., 2007, 58, 489–510 CrossRef CAS PubMed.
- M. J. Wirth and D. J. Swinton, Single-molecule study of an adsorbed oligonucleotide undergoing both lateral diffusion and strong adsorption, J. Phys. Chem. B, 2001, 105(7), 1472–1477 CrossRef CAS.
- L. Kisley, J. X. Chen, A. P. Mansur, B. Shuang, K. Kourentzi, M. V. Poongavanam, W. H. Chen, S. Dhamane, R. C. Willson and C. F. Landes, Unified superresolution experiments and stochastic theory provide mechanistic insight into protein ion-exchange adsorptive separations, Proc. Natl. Acad. Sci. U. S. A., 2014, 111(6), 2075–2080 CrossRef CAS PubMed.
- L. Kisley, J. X. Chen, A. P. Mansur, S. Dominguez-Medina, E. Kulla, M. K. Kang, B. Shuang, K. Kourentzi, M. V. Poongavanam, S. Dhamane, R. C. Willson and C. F. Landes, High ionic strength narrows the population of sites participating in protein ion-exchange adsorption: A single-molecule study, J. Chromatogr. A, 2014, 1343, 135–142 CrossRef CAS PubMed.
- A. Cavazzini, F. Dondi, A. Jaulmes, C. Vidal-Madjar and A. Felinger, Monte Carlo model of nonlinear chromatography: correspondence between the microscopic stochastic model and the macroscopic Thomas kinetic model, Anal. Chem., 2002, 74(24), 6269–6278 CrossRef CAS PubMed.
- F. Dondi, P. Munari, M. Remelli and A. Cavazzini, Monte Carlo model of nonlinear chromatography, Anal. Chem., 2000, 72(18), 4353–4362 CrossRef CAS PubMed.
- W. Calabrase, L. D. C. Bishop, C. Dutta, A. Misiura, C. F. Landes and L. Kisley, Transforming Separation Science with Single-Molecule Methods, Anal. Chem., 2020, 92(20), 13622–13629 CrossRef CAS PubMed.
- N. Pamme, Continuous flow separations in microfluidic devices, Lab Chip, 2007, 7(12), 1644–1659 RSC.
- M. Catani, O. H. Ismail, F. Gasparrini, M. Antonelli, L. Pasti, N. Marchetti, S. Felletti and A. Cavazzini, Recent advancements and future directions of superficially porous chiral stationary phases for ultrafast high-performance enantioseparations, Analyst, 2017, 142(4), 555–566 RSC.
- U. J. Wünsch and J. A. Hawkes, Mathematical chromatography deciphers the molecular fingerprints of dissolved organic matter, Analyst, 2020, 145(5), 1789–1800 RSC.
- M. Leśko, J. Samuelsson, E. Glenne, K. Kaczmarski and T. Fornstedt, Predictions of overloaded concentration profiles in supercritical fluid chromatography, J. Chromatogr. A, 2021, 1639, 461926–461937 CrossRef PubMed.
- P. Vajda and G. Guiochon, The modeling of overloaded elution band profiles in supercritical fluid chromatography, J. Chromatogr. A, 2014, 1333, 116–123 CrossRef CAS PubMed.
- F. Gritti, A. Felinger and G. Guiochon, Overloaded gradient elution chromatography on heterogeneous adsorbents in reversed-phase liquid chromatography, J. Chromatogr. A, 2003, 1017(1–2), 45–61 CrossRef CAS PubMed.
- T. Fornstedt, G. M. Zhong and G. Guiochon, Peak tailing and mass transfer kinetics in linear chromatography, J. Chromatogr. A, 1996, 741(1), 1–12 CrossRef CAS.
- A. Felinger, Molecular movement in an HPLC column: A stochastic analysis, LCGC North Am., 2004, 22(7), 642–647 CAS.
- J. C. Giddings, Kinetic Origin of Tailing in Chromatography, Anal. Chem., 1963, 35(13), 1999–2002 CrossRef CAS.
- J. L. Excoffier, A. Jaulmes, C. Vidalmadjar and G. Guiochon, Characterization of Small Variations in Profiles of Chromatographic Elution Peaks and Effect of Nonlinearity of Sorption Isotherm, Anal. Chem., 1982, 54(12), 1941–1947 CrossRef CAS.
- B. A. Rogers, Z. Wu, B. C. Wei, X. M. Zhang, X. Cao, O. Alabi and M. J. Wirth, Submicrometer Particles and Slip Flow in Liquid Chromatography, Anal. Chem., 2015, 87(5), 2520–2526 CrossRef CAS PubMed.
- A. Felinger, Data analysis and signal processing in chromatography, Elsevier, 1998, vol. 21 Search PubMed.
- Ł. Komsta, Y. Heyden and J. Sherma, Chemometrics in Chromatography, CRC Press, Boca Raton, 2018 Search PubMed.
- F. Dondi, Approximation Properties of the Edgeworth Cramer Series and Determination of Peak Parameters of Chromatographic Peaks, Anal. Chem., 1982, 54(3), 473–477 CrossRef CAS.
- A. Gergely, P. Horvath and B. Noszal, Deconvolution of composite chromatographic peaks by simultaneous dual detections, J. Chromatogr. Sci., 2000, 38(10), 425–429 CAS.
- O. Trapp, Chromatographic peak deconvolution of constitutional isomers by multiple-reaction-monitoring mass spectrometry, J. Chromatogr. A, 2010, 1217(7), 1010–1016 CrossRef CAS PubMed.
- J. J. Baeza-Baeza, M. J. Ruiz-Angel, M. C. Garcia-Alvarez-Coque and S. Carda-Broch, Half-width plots, a simple tool to predict peak shape, reveal column kinetics and characterise chromatographic columns in liquid chromatography: state of the art and new results, J. Chromatogr. A, 2013, 1314, 142–153 CrossRef CAS PubMed.
- M. F. Wahab, D. C. Patel and D. W. Armstrong, Peak Shapes and Their Measurements: The Need and the Concept Behind Total Peak Shape Analysis, LC GC Eur., 2017, 30(12), 670–678 Search PubMed.
- L. Mockl and W. E. Moerner, Super-resolution Microscopy with Single Molecules in Biology and Beyond-Essentials, Current Trends, and Future Challenges, J. Am. Chem. Soc., 2020, 142(42), 17828–17844 CrossRef CAS PubMed.
- H. H. Chen, X. H. Xie and T. Y. Chen, Single-molecule microscopy for in-cell quantification of protein oligomeric stoichiometry, Curr. Opin. Struct. Biol., 2021, 66, 112–118 CrossRef CAS PubMed.
- M. Pan, Y. Zhang, G. Yan and T.-Y. Chen, Dissection of Interaction Kinetics through Single-Molecule Interaction Simulation, Anal. Chem., 2020, 92(17), 11582–11589 CrossRef CAS PubMed.
- L. D. C. Bishop, A. Misiura, N. A. Moringo and C. F. Landes, Unraveling peak asymmetry in chromatography through stochastic theory powered Monte Carlo simulations, J. Chromatogr. A, 2020, 1625, 461323–461331 CrossRef CAS PubMed.
- H. Rix, Detection of Small Variations in Shape Between Two Chromatographic Peaks, J. Chromatogr., 1981, 204(JAN), 163–165 CrossRef CAS.
- H. Rix and J. P. Malenge, Detecting Small Variations in Shape, IEEE Trans. Syst. Man Cybern., 1980, 10(2), 90–96 Search PubMed.
- J. Roles and G. Guiochon, Precision and accuracy of the gas solid adsorption-isotherms derived by the elution-by-characteristic-points method, J. Chromatogr., 1992, 591(1–2), 245–265 CrossRef CAS.
- L. Pasti, A. Cavazzini, A. Felinger, M. Martin and F. Dondi, Single-molecule observation and chromatography unified by levy process representation, Anal. Chem., 2005, 77(8), 2524–2535 CrossRef CAS PubMed.
- N. A. Moringo, L. D. C. Bishop, H. Shen, A. Misiura, N. C. Carrejo, R. Baiyasi, W. Wang, F. Ye, J. T. Robinson and C. F. Landes, A mechanistic examination of salting out in protein–polymer membrane interactions, Proc. Natl. Acad. Sci. U. S. A., 2019, 116(46), 22938–22945 CrossRef CAS PubMed.
- K. H. Jensen, A. Valente and H. A. Stone, Flow rate through microfilters: Influence of the pore size distribution, hydrodynamic interactions, wall slip, and inertia, Phys. Fluids, 2014, 26(5), 13 Search PubMed.
- Z. Wu, B. C. Wei, X. M. Zhang and M. J. Wirth, Efficient Separations of Intact Proteins Using Slip-Flow with Nano-Liquid Chromatography-Mass Spectrometry, Anal. Chem., 2014, 86(3), 1592–1598 CrossRef CAS PubMed.
- J. M. Vanson, A. Boutin, M. Klotz and F. X. Coudert, Transport and adsorption under liquid flow: the role of pore geometry, Soft Matter, 2017, 13(4), 875–885 RSC.
- F. Gritti, J. Hochstrasser, A. Svidrytski, D. Hlushkou and U. Tallarek, Morphology-transport relationships in liquid chromatography: Application to method development in size exclusion chromatography, J. Chromatogr. A, 2020, 1620, 460991–461007 CrossRef CAS PubMed.
- C. Salmean and S. Dimartino, 3D-Printed Stationary Phases with Ordered Morphology: State of the Art and Future Development in Liquid Chromatography, Chromatographia, 2019, 82(1), 443–463 CrossRef CAS.
- U. Tallarek, D. Hlushkou, J. Rybka and A. Holtzel, Multiscale Simulation of Diffusion in Porous Media: From Interfacial Dynamics to Hierarchical Porosity, J. Phys. Chem. C, 2019, 123(24), 15099–15112 CrossRef CAS.
- U. Tallarek, J. Hochstrasser, F. Ziegler, X. H. Huang, C. Kubel and M. R. Buchmeiser, Olefin Ring-closing Metathesis under Spatial Confinement: Morphology-transport Relationships, ChemCatChem, 2021, 13(1), 281–292 CrossRef CAS.
- Y. Vanderheyden, K. Vanderlinden, K. Broeckhoven and G. Desmet, Problems involving the determination of the column-only band broadening in columns producing narrow and tailed peaks, J. Chromatogr. A, 2016, 1440, 74–84 CrossRef CAS PubMed.
- F. Gritti, D. Brousmiche, M. Gilar, T. H. Water and K. Wyndham, Kinetic mechanism of water dewetting from hydrophobic stationary phases utilized in liquid chromatography, J. Chromatogr. A, 2019, 1596, 41–53 CrossRef CAS PubMed.
- M. Grabarics, M. Lettow, A. T. Kirk, G. Von Helden, T. J. Causon and K. Pagel, Plate-height model of ion mobility-mass spectrometry, Analyst, 2020, 145(19), 6313–6333 RSC.
- R. Kumarasinghe, T. Ito and D. A. Higgins, Nanoconfinement and Mass Transport in Silica Mesopores: the Role of Charge at the Single Molecule and Single Pore Levels, Anal. Chem., 2020, 92(1), 1416–1423 CrossRef CAS PubMed.
- G. Ghimire, R. Espinoza, H. Xu, S. Nasaka, N. Kameta, M. Masuda, D. A. Higgins and T. Ito, Diffusion Behavior of Differently Charged Molecules in Self-Assembled Organic Nanotubes Studied Using Imaging Fluorescence Correlation Spectroscopy, Langmuir, 2019, 35(24), 7783–7790 CrossRef CAS PubMed.
- H. Xu, S. Nagasaka, N. Kameta, M. Masuda, T. Ito and D. A. Higgins, Spectroscopic imaging studies of nanoscale polarity and mass transport phenomena in self-assembled organic nanotubes, Phys. Chem. Chem. Phys., 2017, 19(30), 20040–20048 RSC.
- J. Rybka, A. Höltzel, A. Steinhoff and U. Tallarek, Molecular Dynamics Study of the Relation between Analyte Retention and Surface Diffusion in Reversed-Phase Liquid Chromatography, J. Phys. Chem. C, 2019, 123, 3672–3681 CrossRef CAS.
- L. D. C. Bishop and C. F. Landes, From a Protein's Perspective: Elution at the Single-Molecule Level, Acc. Chem. Res., 2018, 51(9), 2247–2254 CrossRef CAS.
- N. A. Moringo, H. Shen, L. D. C. Bishop, W. Wang and C. F. Landes, Enhancing Analytical Separations Using Super-Resolution Microscopy, Annu. Rev. Phys. Chem., 2018, 69(1), 353–375 CrossRef CAS PubMed.
- H. B. Liu, J. Jeong, Y. H. Kao and Y. T. Zhang, Characterization of free thiol variants of an IgG1 by reversed phase ultra high pressure liquid chromatography coupled with mass spectrometry, J. Pharm. Biomed. Anal., 2015, 109, 142–149 CrossRef CAS PubMed.
- A. Cavazzini, M. Remelli and F. Dondi, Stochastic theory of two-site adsorption chromatography by the characteristic function method, J. Microcolumn Sep., 1997, 9(4), 295–302 CrossRef CAS.
- A. Felinger, Determination of rate constants for heterogeneous mass transfer kinetics in liquid chromatography, J. Chromatogr. A, 2006, 1126(1–2), 120–128 CrossRef CAS PubMed.
- J. C. Giddings, Kinetic Model for Chromatographic Dispersion and Electrodiffusion, J. Chem. Phys., 1957, 26(6), 1755–1756 CrossRef CAS.
- J. C. Giddings, Stochastic Considerations on Chromatographic Dispersion, J. Chem. Phys., 1957, 26(1), 169–173 CrossRef CAS.
- K. V. Kumar, S. Gadipelli, B. Wood, K. A. Ramisetty, A. A. Stewart, C. A. Howard, D. J. L. Brett and F. Rodriguez-Reinoso, Characterization of the adsorption site energies and heterogeneous surfaces of porous materials, J. Mater. Chem. A, 2019, 7(17), 10104–10137 RSC.
- M. J. Wirth and D. J. Swinton, Single-molecule probing of mixed-mode adsorption at a chromatographic interface, Anal. Chem., 1998, 70(24), 5264–5271 CrossRef CAS.
- L. Kisley, U. Patil, S. Dhamane, K. Kourentzi, L. J. Tauzin, R. C. Willson and C. F. Landes, Competitive multicomponent anion exchange adsorption of proteins at the single molecule level, Analyst, 2017, 142(17), 3127–3131 RSC.
- J. J. Zhou, M. Q. Wang, B. L. Zhang and Q. Y. Zhang, Metal coordination assisted thermo-sensitive magnetic imprinted microspheres for selective adsorption and efficient elution of proteins, Colloids Surf., A, 2021, 612, 125981–125990 CrossRef CAS.
- J. C. Giddings and H. Eyring, A Molecular Dynamic Theory of Chromatography, J. Phys. Chem., 1955, 59(5), 416–421 CrossRef CAS.
- D. A. Mcquarrie, On Stochastic Theory of Chromatography, J. Chem. Phys., 1963, 38(2), 437–445 CrossRef CAS.
- A. Felinger, L. Pasti and F. Dondi, Fourier-Analysis of Multicomponent Chromatograms - Theory and Models, Anal. Chem., 1990, 62(17), 1846–1853 CrossRef CAS.
- G. Desmet, A finite parallel zone model to interpret and extend Giddings’ coupling theory for the eddy-dispersion in porous chromatographic media, J. Chromatogr. A, 2013, 1314, 124–137 CrossRef CAS.
- M. J. Wirth, M. D. Ludes and D. J. Swinton, Spectroscopic observation of adsorption to active silanols, Anal. Chem., 1999, 71(18), 3911–3917 CrossRef CAS.
- F. Dondi, A. Cavazzini, M. Martin, E. Grushka and S. Lunte, Correspondence between chromatography, single-molecule dynamics, and equilibrium: A stochastic approach, in Advances in Chromatography, ed. P. R. Brown, Marcel Dekker, New York, 2005, vol. 43, pp. 179–230 Search PubMed.
- F. Dondi and G. Guiochon, in Theoretical Advancement in Chromatography and Related Separation Techniques, Springer Netherlands, 1st edn, 1992 Search PubMed.
- G. J. Mclachlan, S. X. Lee and S. I. Rathnayake, Finite Mixture Models, Annu. Rev. Stat. Appl., 2019, 6(1), 355–378 CrossRef.
- D. Hlushkou, A. Svidrytski and U. Tallarek, Tracer-Size-Dependent Pore Space Accessibility and Long-Time Diffusion Coefficient in Amorphous, Mesoporous Silica, J. Phys. Chem. C, 2017, 121(15), 8416–8426 CrossRef CAS.
- S. Schweiger, S. Hinterberger and A. Jungbauer, Column-to-column packing variation of disposable pre-packed columns for protein chromatography, J. Chromatogr. A, 2017, 1527, 70–79 CrossRef CAS PubMed.
- G. Desmet and K. Broeckhoven, Extra-column band broadening effects in contemporary liquid chromatography: Causes and solutions, TrAC, Trends Anal. Chem., 2019, 119, 115619–115633 CrossRef CAS.
- A. E. Reising, S. Schlabach, V. Baranau, D. Stoeckel and U. Tallarek, Analysis of packing microstructure and wall effects in a narrow-bore ultrahigh pressure liquid chromatography column using focused ion-beam scanning electron microscopy, J. Chromatogr. A, 2017, 1513, 172–182 CrossRef CAS PubMed.
- F. Dondi and M. Remelli, The characteristic function method in the stochastic theory of chromatography, J. Phys. Chem., 1986, 90(9), 1885–1891 CrossRef CAS.
- Z. Papai and T. L. Pap, Analysis of peak asymmetry in chromatography, J. Chromatogr. A, 2002, 953(1–2), 31–38 CrossRef CAS PubMed.
- M. F. Wahab, D. C. Patel and D. W. Armstrong, Total peak shape analysis: detection and quantitation of concurrent fronting, tailing, and their effect on asymmetry measurements, J. Chromatogr. A, 2017, 1509, 163–170 CrossRef CAS PubMed.
- M. F. Wahab, T. C. O'Haver, F. Gritti, G. Hellinghausen and D. W. Armstrong, Increasing chromatographic resolution of analytical signals using derivative enhancement approach, Talanta, 2019, 192, 492–499 CrossRef CAS PubMed.
- K. J. Millman and M. Aivazis, Python for Scientists and Engineers, Comput. Sci. Eng., 2011, 13(2), 9–12 Search PubMed.
- S. van der Walt, S. C. Colbert and G. Varoquaux, The NumPy Array: A Structure for Efficient Numerical Computation, Comput. Sci. Eng., 2011, 13(2), 22–30 Search PubMed.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, I. Polat, Y. Feng, E. W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. N. H. Ribeiro, F. Pedregosa, P. van Mulbregt and C. SciPy, SciPy 1.0: fundamental algorithms for scientific computing in Python, Nat. Methods, 2020, 17(3), 261–272 CrossRef CAS PubMed.
- A. Felinger, L. Pasti, F. Dondi, M. van Hulst, P. J. Schoenmakers and M. Martin, Stochastic theory of size exclusion chromatography: Peak shape analysis on single columns, Anal. Chem., 2005, 77(10), 3138–3148 CrossRef CAS PubMed.
- A. Felinger, Molecular dynamic theories in chromatography, J. Chromatogr. A, 2008, 1184(1–2), 20–41 CrossRef CAS PubMed.
- D. Hlushkou, F. Gritti, A. Daneyko, G. Guiochon and U. Tallarek, How Microscopic Characteristics of the Adsorption Kinetics Impact Macroscale Transport in Chromatographic Beds, J. Phys. Chem. C, 2013, 117(44), 22974–22985 CrossRef CAS.
- D. Hlushkou, F. Gritti, G. Guiochon, A. Seidel-Morgenstern and U. Tallarek, Effect of Adsorption on Solute Dispersion: A Microscopic Stochastic Approach, Anal. Chem., 2014, 86(9), 4463–4470 CrossRef CAS PubMed.
- K. Horvath, M. Olajos, A. Felinger and P. Hajos, Retention controlling and peak shape simulation in anion chromatography using multiple equilibrium model and stochastic theory, J. Chromatogr. A, 2008, 1189(1–2), 42–51 CrossRef CAS PubMed.
- A. Cavazzini, M. Remelli, F. Dondi and A. Felinger, Stochastic theory of multiple-site linear adsorption chromatography, Anal. Chem., 1999, 71(16), 3453–3462 CrossRef CAS.
- A. Savitzky and M. J. E. Golay, Smoothing+differentiation of data by simplified least squares procedures, Anal. Chem., 1964, 36(8), 1627–1639 CrossRef CAS.
- F. E. Lytle and R. K. Julian, Automatic Processing of Chromatograms in a High-Throughput Environment, Clin. Chem., 2016, 62(1), 144–153 CrossRef CAS PubMed.
- K. Broeckhoven, S. Eeltink, W. De Malsche, F. Matheuse, G. Desmet and D. Cabooter, Current and Future Chromatographic Columns: Is One Column Enough to Rule Them All?, LCGC North Am., 2018, 36(6), 9–17 CAS.
- G. Desmet, D. Cabooter and K. Broeckhoven, Graphical Data Representation Methods To Assess the Quality of LC Columns, Anal. Chem., 2015, 87(17), 8593–8602 CrossRef CAS PubMed.
- A. F. Kadjo, P. K. Dasgupta and K. Srinivasan, Shape-Based Peak Identity Confirmation in Liquid Chromatography, Anal. Chem., 2021, 93(8), 3848–3856 CrossRef CAS PubMed.
- J. T. Cooper and J. M. Harris, Imaging Fluorescence-Correlation Spectroscopy for Measuring Fast Surface Diffusion at Liquid/Solid Interfaces, Anal. Chem., 2014, 86(15), 7618–7626 CrossRef CAS PubMed.
- J. T. Cooper, E. M. Peterson and J. M. Harris, Fluorescence Imaging of Single-Molecule Retention Trajectories in Reversed-Phase Chromatographic Particles, Anal. Chem., 2013, 85(19), 9363–9370 CrossRef CAS PubMed.
- N. A. Moringo, H. Shen, L. J. Tauzin, W. X. Wang, L. D. C. Bishop and C. F. Landes, Variable Lysozyme Transport Dynamics on Oxidatively Functionalized Polystyrene Films, Langmuir, 2017, 33(41), 10818–10828 CrossRef CAS PubMed.
- J. Hansen, K. Ely, D. Horsley, J. Herron, V. Hlady and J. D. Andrade, The adsorption of lysozymes: A model system. Makromolekulare Chemie, Macromol. Symp., 1988, 17(1), 135–154 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1an00370d |
| This journal is © The Royal Society of Chemistry 2021 |