Machine learning and chemometrics for electrochemical sensors: moving forward to the future of analytical chemistry
Pumidech
Puthongkham
 *abc,
Supacha
Wirojsaengthong
a and
Akkapol
Suea-Ngam
d
*abc,
Supacha
Wirojsaengthong
a and
Akkapol
Suea-Ngam
d
aDepartment of Chemistry, Faculty of Science, Chulalongkorn University, Bangkok 10330, Thailand. E-mail: Pumidech.P@chula.ac.th
bElectrochemistry and Optical Spectroscopy Center of Excellence (EOSCE), Chulalongkorn University, Bangkok 10330, Thailand
cCenter of Excellence in Responsive Wearable Materials, Chulalongkorn University, Bangkok 10330, Thailand
dDepartment of Materials, Department of Bioengineering, and Institute of Biomedical Engineering, Imperial College London, London, SW7 2AZ, UK
First published on 7th September 2021
Abstract
Electrochemical sensors and biosensors have been successfully used in a wide range of applications, but systematic optimization and nonlinear relationships have been compromised for electrode fabrication and data analysis. Machine learning and experimental designs are chemometric tools that have been proved to be useful in method development and data analysis. This minireview summarizes recent applications of machine learning and experimental designs in electroanalytical chemistry. First, experimental designs, e.g., full factorial, central composite, and Box–Behnken are discussed as systematic approaches to optimize electrode fabrication to consider the effects from individual variables and their interactions. Then, the principles of machine learning algorithms, including linear and logistic regressions, neural network, and support vector machine, are introduced. These machine learning models have been implemented to extract complex relationships between chemical structures and their electrochemical properties and to analyze complicated electrochemical data to improve calibration and analyte classification, such as in electronic tongues. Lastly, the future of machine learning and experimental designs in electrochemical sensors is outlined. These chemometric strategies will accelerate the development and enhance the performance of electrochemical devices for point-of-care diagnostics and commercialization.
1. Introduction
Electrochemical sensors have been widely developed and settled into a period of sustained growth with diverse applications across environmental, food, and biomedical fields.1,2 The optimization of electrode materials and detection conditions is essential to maximize sensor performance. However, most studies typically optimize one variable at a time,3 which is straightforward but problematic, especially if two or more variables interact with each other.4 The conditions determined to prepare and operate the sensor might not be the true optimum, preventing the ultimate applications of the electrochemical sensors in the field or point-of-care diagnostics. A chemometric tool named experimental design or design of experiment (DoE) has been invented for systematically and statistically valid parameter optimization.4 However, electrochemists may still be reluctant to utilize this advantageous method to fabricate and optimize their sensors.Recently, machine learning (ML) has become a popular method to analyze complex relationships in experimental data.5 It has been found to be a crucial tool to predict quantitative structure–activity relationship of drugs and biologically active molecules effectively.6 Deep learning, one of the most popular ML algorithms, has the potential to analyze data from continuous sensing for anomaly detection, instrumental failure,7 or Internet of Things.8 For analytical chemistry, there are emerging opportunities for ML,9 such as integration in the lab-on-a-chip device to quantify and classify molecules and biological moieties.10,11 Furthermore, ML has been utilized in several electrochemical applications. The electrochemical impedance spectra (EIS) of Li-ion batteries were analyzed by ML to predict their remaining battery capacity.12 ML was also combined with density functional theory (DFT) calculation to predict the energy levels and redox potentials of organic battery electrodes.13 For organic electrosynthesis, the cyclic voltammogram (CV) of organic compounds were correlated with the reaction yield to optimize a synthetic route.14 Text mining and natural language processing were also implemented to extract the experimental data from published articles to find the best battery and electrolyte composition.15 Nevertheless, ML applications in electroanalytical chemistry are still limited,9 since the data are complicated and not always straightforward to build an expansive database.
This article summarizes the recent applications of DoE and ML in developing electrochemical sensors and analyzing their data. The basic concepts and the roles of common DoE in planning and optimizing parameters in electrochemical sensors and detection will be first discussed. Then, the brief fundamentals of ML algorithms and their applications to reveal the hidden knowledge in electrochemistry and to interpret and extract qualitative and quantitative information from electrochemical data will be examined. Finally, the future of DoE and ML in analytical electrochemistry will be forecasted. Indeed, DoE and ML are beneficial for all analytical techniques, but electrochemistry research is currently underutilizing them. Using DoE for optimizing electrochemical sensors and ML in data analysis will maximize their potential for complicated sample analysis and point-of-care applications. We hope that this review will encourage the readers in electrochemical science to appreciate the potential benefits of these emerging methods and to apply them in future research. Implementing DoE and ML for sensor fabrication and data analysis will improve their performance for real samples and will aid the digitization of chemical experiments16 to meet the future demand.
2. Experimental design for optimizing electrochemical sensors
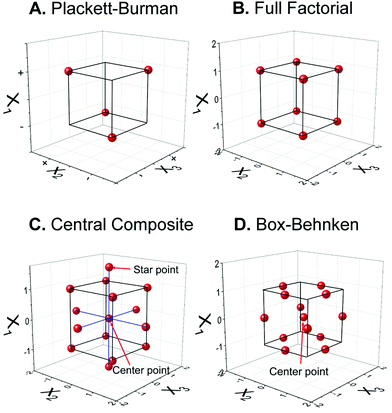
2.1. Common experimental designs
Optimization of the sensor fabrication and detection parameters is the key step to maximize the analytical performance of electrochemical sensors. Traditionally, one-factor-at-a-time (OFAT) is the experimental design that has been leveraged and mounted as the standard optimization in analytical chemistry by varying one parameter at a time while fixing others.17 This dominating design assumes that each factor is not influenced by others, thus the optimum value of each factor can be determined separately then combined together later. This approach is simple, but it has many obvious drawbacks—OFAT requires a lot of experiments.3 For example, investigating an experiment with parameters including five pH values and five concentrations with five replicates for each condition requires 125 runs. Performing these many experiments exploits unnecessary time and cost, generates unnecessary waste, and is unsustainable. Another limitation is that OFAT does not consider the cooperative effect from the interaction between factors, leading to the lack of promise for obtaining the true optimal.17 These problems are critical for developing biosensors with complicated mechanisms and instrumentation, especially for point-of-care diagnostics in resource-limited areas.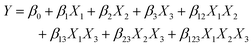 | (1) |
The magnitude of each β coefficient illustrates the impact or significance of each factor and interaction. Kechagias et al. reported the three-level FFD to model the machinability prediction in turning of a Ti-6Al-4V alloy, which has three parameters, thus 27 runs were performed.19 Nevertheless, although the FFD can solve the OFAT lacking of interaction consideration, the number of FFD runs is still large. One way to reduce the number of experiments is to use Fractional Factorial Design (FrFD), which keeps only half or quarter of the points from FFD to eliminate its redundancy between the runs.17 Nevertheless, FFD does not consider higher-order terms such as quadratic behavior, so it may prevent some undesired phenomena such as nonlinear noise to be accounted for.
2.2. Method optimization from the response surface methodology
The next step after performing experiments according to the chosen DoE is to determine the optimum point. Response surface methodology (RSM) visualizes the relationship between a pair of variables by plotting the response surface.24 With the surface, more understanding of the whole experimental system is achieved and leads to improved optimization.24 For example, the effect of pH on the measurement of glucosamine using a gold nanoparticle (AuNP)/polyaniline-modified electrode was illustrated as a stack of response surfaces (Fig. 2A), which clearly displayed that lower pH increases the signal.25 From it, a contour plot of the chosen pH can be constructed from the surface to find the optimum amount of AuNPs and polyaniline (Fig. 2B).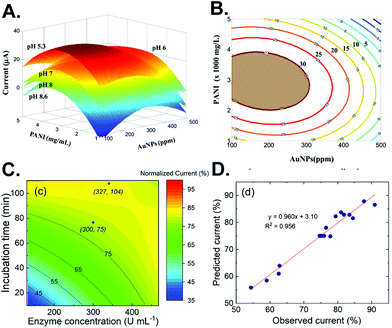 | ||
| Fig. 2 Example of RSM for electrochemical sensor optimization. (A) Surfaces from different pH combined with the effect of gold nanoparticles and polyaniline on glucosamine detection. (B) A contour plot of the chosen pH from (A). Reprinted from ref. 25 with permission from Elsevier. (C) A surface contour plot of the enzyme concentration and incubation time for enzymatic biosensor optimization. (D) Correlation between the observed and predicted response. Adapted with permission from ref. 26. Copyright 2019 American Chemical Society. | ||
Another advantage of RSM is to evaluate the effect on the response if the variables are shifted, as sometimes the mathematically derived optimal condition is not convenient to perform. If the slope of the surface is not too large, then slightly shifting the value from the optimal may ease the experimental setting while preserving the nearly optimized condition. Alternatively, a surface contour plot of the electrochemical signal with gradual color mapping can visualize the difference between the mathematically derived optimum point (red) and the chosen point (blue), as implemented in enzymatic sensor optimization (Fig. 2C).26 Subsequently, the predicted and observed experimental results from using such different conditions can be statistically compared to evaluate the model (Fig. 2D).25–27
2.3. Experimental design for optimizing electrochemical sensors and waveforms
DoE with RSM has gained popularity for electrochemical sensor optimization with more than one independent variable. Ören Varol et al. utilized FFD to perform 17 runs to optimize the amount of two modifiers, pH, and scan rate for graphene/azobenzene-perylene diimide derivative-modified carbon paste electrode for dopamine detection.28 RSMs between each pair of variables were plotted to determine the optimum point, and the optimized sensor has a detection limit (LoD) of 0.26 μM. Brahma et al. used BBD to optimize functionalized multiwalled carbon nanotubes (fMWCNT), ethylenedioxythiophene (EDOT), and o-phenylenediamine (o-PD) to modified a glassy carbon electrode for p-chlorometaxylenol detection.29 The chosen DoE and RSM allows the optimization of fMWCNT electrodeposition and EDOT and o-PD electropolymerization to maximize the response from the analyte from their electrocatalytic properties without the diminishing effect from the polymer thickness. Hendawy et al. also utilized FrFD to screen the significant factors in the fabrication of the graphene oxide/MWCNT/carbon paste electrode and the square wave voltammetry (SWV) waveform for the simultaneous voltammetric determination of paracetamol, guaifenesin, and ascorbic acid.30Multiple DoEs can be subsequently implemented to screen important variables and to optimize the electrode preparation. A non-enzymatic lactose sensor based on a molecular imprinted polymer on a graphite paper electrode was optimized.31 PBD was utilized to screen seven factors including lactose template concentration, pyrrole monomer concentration, electropolymerization cycle, lactose extraction, electropolymerization pH, lactose rebinding time, and rebinding pH. Only three of these factors were significant and subsequently optimized by CCD, improving the LoD of the sensor to 0.88 nM. For more complicated biosensors, Rizi et al. prepared an electrochemical DNA biosensor to detect Mycobacterium tuberculosis based on complementary target hybridization.32 Again, 11 variables from the electrode fabrication (probe concentration and immobilization time) and detection (such as electrochemical parameters, pH, and temperature) were screened by PBD. CCD was subsequently optimized for the most significant variables: buffer molarity, probe concentration, and differential pulse voltammetry (DPV) scan rate. The optimized biosensor had a LOD of 0.141 nM with a wide linear range. These studies showed that performing thorough optimization by CCD with only significant parameters screened by PBD is a useful strategy.
3. Machine learning for developing electrochemical sensors and analyzing electrochemical data
3.1. Classification of electrochemical data
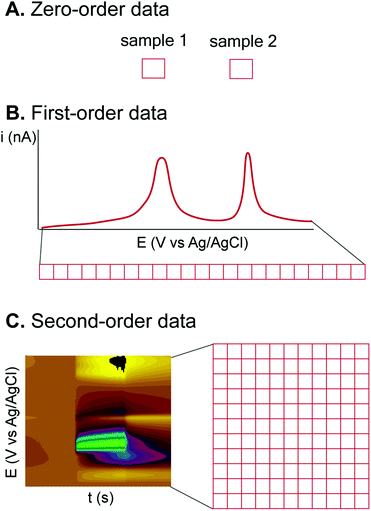
Electrochemical techniques are diverse and thus provide data with different dimensionality or orders (Fig. 3), which are compatible with different ML algorithms.33 Zero-order (or zero-dimensional) data are obtained from an electrochemical measurement that gives a single value (Fig. 3A). For example, a pH meter or a potentiometric ion-selective electrode gives a single pH or p-ion value from each sample or measurement.34 Zero-dimensional data can be treated by univariate analysis, such as simple linear regression between ion-selective electrode potential and p-ion.First-order (or one-dimensional) data are given from a technique which measures the value of a dependent variable from a varied independent variable and can be treated as a vector (Fig. 3B). Many electrochemical experiments fall into this category, such as chronoamperometry (current from a single applied potential vs. time) and voltammetry (current vs. applied potential). One-dimensional data can be treated by multivariate data analysis if the whole vector of data is utilized. For example, DPV of a mixture can be analyzed by principal component analysis (PCA) and regression (PCR) to identify the compounds and their concentrations.35 However, from the same technique, a single data point can be chosen to be analyzed, e.g., current at a selected potential, to reduce the problem to the zero-order, and the more simple univariate analysis can be applied.
Second-order (or two-dimensional) data are obtained from a technique with two independent variables varied together, so the data can be plotted as a matrix (Fig. 3C). Spectroelectrochemistry is one technique that gives second-order data from one dependent variable (absorbance) and two independent variables (wavelength and applied potential).36 Fast-scan cyclic voltammetry (FSCV), a dominating electrochemical technique for in vivo detection of neurotransmitters, also gives two-dimensional data of the current from the varied potential (triangular waveform) and time.37 Treatment of second-order electrochemical data is complicated because of the extra dimension. Reducing the data to first-order by PCA or manually choosing a single applied potential to analyze the data for visualization is possible, but huge amounts of information is eliminated by this approach. One feasible strategy to deal with second-order data is to plot the data matrix as an image, and the problem can be reduced to image recognition, with numerous ML and processing algorithms available.38,39 Higher-order data are also possible for techniques which vary more than two variables simultaneously.
3.2. Common machine learning algorithms
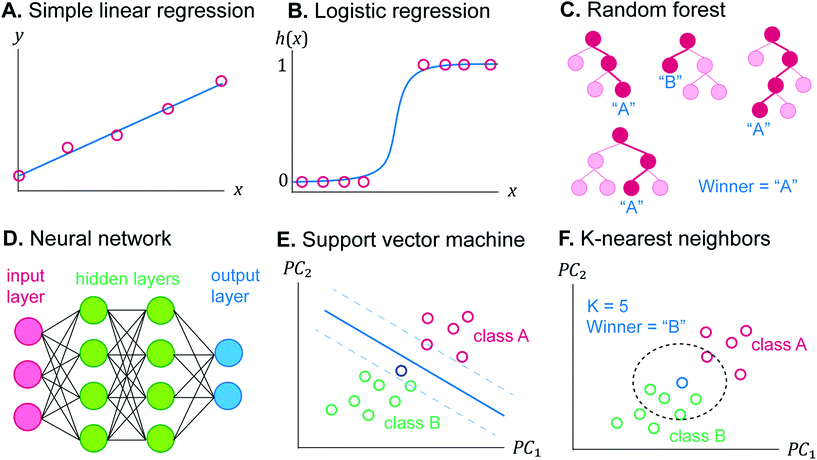
ML is an automated method for data analysis to make a decision without any explicit instruction. The algorithms “learn” the decision rule from the given data, which is called “training set”. One distinct property of ML is that its performance is improved when it is trained with more data, therefore a large set of experiments must be performed to build the training set to maximize the performance of ML.5 In general, ML problems can be classified into supervised and unsupervised learning.9 Supervised learning analyzes the relationship between the independent variables (“features”), and the dependent variables (“label”), and it uses the discovered relationship to predict the label of new data from their features. Supervised learning can be categorized into regression and classification.40 The problem of quantifying the unknown concentration is regression, while identifying the chemical species is classification. In contrast, unsupervised learning deals with the unlabeled data to find the inherent structure to cluster the data into groups. To the best of our knowledge, unsupervised ML has not been utilized for electrochemical sensors, but it was utilized to group unknown biological tissues from their mass spectra for omics applications to discover the similarity or network between their biological activities.41There are many ML algorithms or models. The following list includes only supervised learning models and is not exhaustive. Further mathematical details on the algorithm, cost function, and decision rule updating can be found elsewhere.9,40,42
| y = β0 + β1x | (2) |
The most familiar method to find the best coefficients is the least squares method, which is to minimize the average of the squared difference between the predicted and the true label.40
Multiple linear regression deals with more than one independent variable. For instance, analyzing complicated samples may require the whole voltammogram to determine the analyte concentration.9 Polynomial regression can be also treated similar to the multiple linear regression.3 For example, the function y = β0 + β1x + β2x2 + β3x3 can be viewed as the multiple linear regression involving three independent variables. In this case, the linear function can be written in the vectorized form as
| y = βTx | (3) |
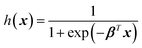 | (4) |
The graph of h(x) resembles the sigmoid curve (Fig. 4B), and the shape allows the binary classification into positive (h(x) = 1) or negative (h(x) = 0). Notice that the logistic function fitting is done by finding the best β, similar to (2) or (3). The model can be evaluated on their accuracy by determining h(x) of the test set and comparing with their true labels. Logistic regression can also classify more than two classes. Each class has different hi(x), and the class of each training example can be determined from the class giving the highest hi(x).44
3.3. Machine learning implementation
There are many steps in implementing ML.39 First, the data are collected, preprocessed, and split into training, cross validation, and test sets. Then, the ML algorithm must be chosen based on the nature of the problem (classification or regression, linear or nonlinear, zero, first, or second-order). Next, the algorithm learns from the training set to find the best decision rule. In general, coefficients and weights in the first learning iteration are randomized and predict the output of the training set, and the difference between the predicted output and the true output is evaluated as a “cost” or “loss”, such as mean squared error as in the simple linear regression. Subsequently, the cost is used to update the coefficients and weights in the right gradient and direction by a method such as gradient descent, and the updated parameters are used in the next iteration. These steps are iterated until the prediction accuracy of the training set is satisfactory.The selected ML model requires optimization of the architecture as well, such as the highest degree in polynomial regression or the K in KNN. These internal parameters are called hyperparameters.47 Hyperparameters are optimized by evaluating the prediction accuracy of the cross validation set by the models optimized from the training set with different hyperparameters. Finally, the best ML model and architecture are evaluated by the prediction accuracy and other performance parameters with the test set, which can be compared with those of other models to find the best ML algorithm to be implemented in the future.
3.4. Machine learning for the investigation of electrochemistry and electrode materials
Currently, ML algorithms have been implemented to identify the electrode reaction mechanism from electrochemical data, since this step typically needs human decision and is prone to human errors. For example, SVM was utilized to identify the equivalent circuit of the electrode reaction from the EIS Nyquist plots.45 SVM was trained from the database consisting of over 500 published spectra classified into five circuit models, and it performed better than other models such as decision tree and random forest. For CV, the Bond group sought an alternative approach to classify the experimental and simulated voltammograms into different electrode reaction mechanisms (E, EE, and EC).55 Because the CV shape depends on such mechanisms, the voltammograms were treated as images instead of numerical data, and the problem became image recognition, which was solved by the convolutional neural network (CNN) (Fig. 5A). The algorithm correctly identified the mechanism with 89% accuracy, the misclassification was similar to human's decisions, and the effect of noise, resistance, and scan rate on the accuracy was also extensively studied. Whether these ML models can also determine other electrode reaction parameters directly from the data should be explored in the future.
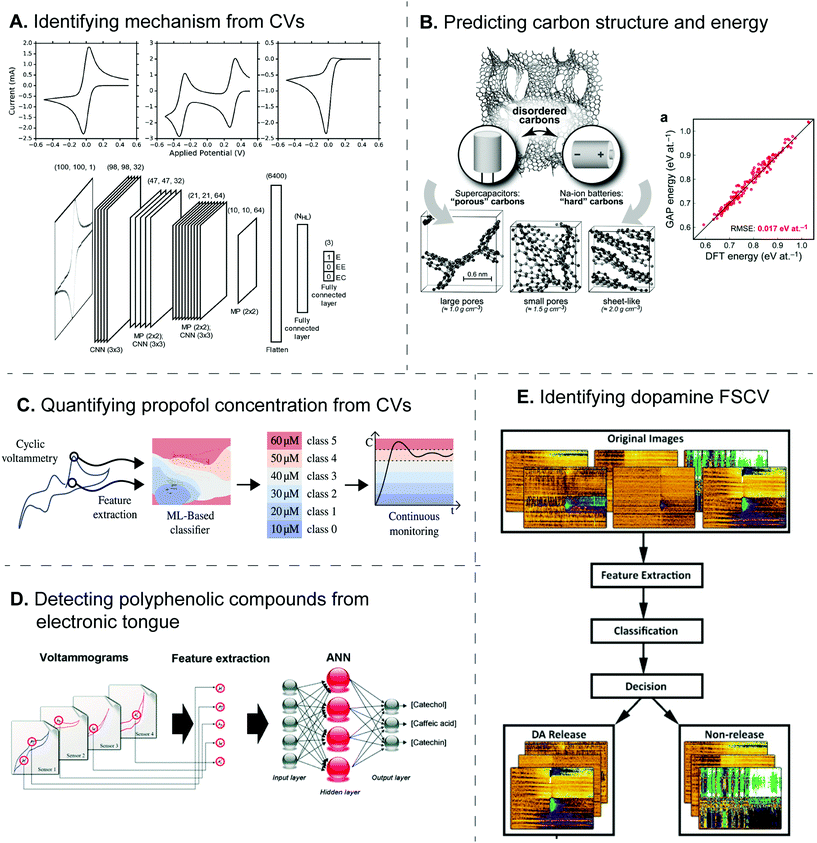 | ||
| Fig. 5 Examples of machine learning applications for electrochemical sensors. (A) Deep CNN identifies the electrode reaction mechanism from CVs. Adapted with permission from ref. 55. Copyright 2019 American Chemical Society. (B) GAP-based ML predicted the structure of amorphous carbons and their energies. Adapted with permission from ref. 60. Published by The Royal Society of Chemistry. (C) SVM classified the CV of propofol into a level of concentration to aid the continuous monitoring. Adapted from ref. 52 with permission from Elsevier (Copyright 2021). (D) Neural network combined the CVs from electronic tongue to identify and quantify amounts of polyphenolic compounds. Adapted from ref. 62 with permission from The Royal Society of Chemistry. (E) Neural network detects dopamine FSCV from the false color plot. Adapted from ref. 48 with permission from Elsevier (Copyright 2020). | ||
3.5. Machine learning for the analysis of signals from electrochemical sensors
There are some studies that utilize neural networks for quantitative analysis. The Wen group trained a neural network by feeding the peak current–concentration pairs as a training set before using the model to predict the unknown concentration from the electrochemical data. This method was used to determine the amount of amaranth at the MWCNT/N-doped graphene/PEDOT:PSS electrode64 and maleic hydrazide at PEDOT–COOH modified with copper nanoparticles by DPV.50 In both studies, the nonlinear relationship between the concentration and peak current was obtained, so the prediction accuracy was improved. More condition variations such as pH changes, fouling compounds, or more real samples could be included to test the robustness of the prediction.
ML models were also applied to analyze electrochemical signals from cyclic square wave voltammetry (CSWV), which combines selectivity from CV with sensitivity enhancement from SWV.49 Dean et al. compared the performance of different ML algorithms in classifying heavy metals and explosives in seawater from CSWV analysis.49 Evaluated by the F1 score, CNN and long-short term memory (LSTM) performed better than simple dimensionality reduction techniques such as SVM and PCA. While CNN is widely accepted for image recognition problems, it is interesting that LSTM, which is commonly used for time-series data analysis, also exhibited superior performance. Furthermore, the combination of CNN and LSTM also enhanced the classification performance, and it was also used with a multilayer epitaxial graphene electrode for metal ions and pesticide contaminant detection in seawater by the same research group.67
Furthermore, electronic tongues possess the potential to identify the geographical-dependent products and their authenticity. For example, ML was used to identify wine with different polyphenolic compounds from CVs obtained from four enzyme-modified electrodes.62 DoE feature selection was performed to choose 23 significant potential points from the voltammogram for neural network regression with three output nodes, corresponding to the amount of three polyphenolic antioxidants giving the electrochemical signals (Fig. 5D). Wang et al. also developed nanocomposite-modified glassy carbon electrodes to distinguish Chinese rice wines from different geographical origins by a deep learning algorithm trained from 200 PCA-transformed CV and SWV,71 where the electrochemical signal was produced from electroactive components including 5′-GMP, Tyr, and GA in the rice wines. While the classification accuracy was over 95%, the neural network needed 50 hidden layers, which may require a long training duration.
Temporal information from electrochemical measurements can also provide better differentiation for electronic tongues. Analyzing temporal patterns require a time-series algorithm, and automation is essential for continuous measurement such as in environmental or wearable sensors. For example, an electronic nose for malodor detection was constructed from ten commercial electrochemical gas sensors for H2S, NH3, and SO2 detection.72 The smoothed temporal responses with their features (amplitude, average, and variance) were trained by different learning models to distinguish odor. Different ML models were suitable for different tasks, e.g., to determine whether the odor is offensive or to differentiate offensive odors. The same scheme of time-series analysis could be applied in other continuous measurements such as pollution control or smart home devices.
Nevertheless, CNN could be applied to other electrochemical techniques giving second-order data, such as three-dimensional or multiple step chronoamperometry. This technique applies a series of different potentials to collect a set of chronoamperograms to obtain the electrochemical properties of different electroactive species.75 Previously, classical methods such as parallel factor analysis and multivariate curve resolution alternating least squares were applied to such data to differentiate the electrochemical signal from similar compounds.76 ML indeed has the potential to improve the analysis of the three-dimensional surface obtained from the technique.
4. Moving forward to the future of electrochemical sensors and biosensors by machine learning and experimental design
4.1. Reducing chemicals, time, and waste in developing electrochemical sensors
One of the major goals of DoE is to reduce the number of optimizing experiments by strategically choosing the values of independent variables to test.17 Decreasing the number of experiments also decreases the chemical and reagent usages, improves the working efficiency, and reduces the generated waste from the experiment. Therefore, implementing DoE in developing sensors meets the scope of green chemistry, which investigates the practice of carefully designed chemical processes to improve their efficiency and sustainability.77 Although systematic DoEs have been available for many decades, they were not widely adapted to optimize electrochemical sensors, with the OFAT approach still dominating the field. OFAT, however, is not useless—it should be used when studying or discovering new materials or systems. When obtaining their capabilities, the systematic DoE should be then performed to optimize the sensor fabrication. ML can also be a useful tool to find the appropriate chemical structure and composition for the best electrochemical sensor.As DoE should be a common method to optimize any system, including DoE in sensor research should not be the focus of the work per se. Emphasizing DoE without regarding the chemical aspect of the work blurs the actual novelty and discourages the discussion on how the sensor component improves its analytical performance. Instead, DoE should be a tool for understanding the effect of each sensor component, detection condition, and their synergistic effects. DoE indeed will be an important tool to develop point-of-care diagnostics while achieving the goal of green chemistry and sustainability simultaneously.
4.2. Pushing the analytical performance of electrochemical sensors
An ideal electrochemical sensor must possess high selectivity, high sensitivity, and low LoD, as well as high reproducibility and repeatability. The traditional, chemical approach to improve a sensor to meet those criteria is to increase the signal-to-noise ratio by fabricating electrocatalytic materials, conducting polymers, and selective recognition elements on the sensor.78,79 Ratiometric sensors have been also proposed to correct the sensitivity being altered from the baseline change.80 ML and DoE are useful to investigate and optimize the best sensor composition. However, with the availability of signal processing tools such as Fourier transform and digital filters, these methods have been successfully complemented to the chemical approach to improve the sensor.38,81,82 Accordingly, the question now is how signal processing and analysis by ML can improve the figures of merit of electrochemical sensors. Recently, Cho et al. implemented ML to detect H2 below the chemical LoD using a metal resistive gas sensor.83 With a deep neural network structure for anomaly detection, H2 with ultralow concentration (<10 ppm) can be detected from the temporal resistivity profile. Furthermore, more theoretical work could be done to formalize how to evaluate the quantitative parameters such as sensitivity and LoD for ML regression, as in the work by Chiappini et al., suggesting to estimate the sensitivity of the neural network from the uncertainty of the output and input.84 Being able to quantify the figures of merit with low LoD will accelerate applications of electrochemical sensors where the clinically relevant concentration is extremely low, such as SARS-CoV-2 diagnosis.854.3. Validating electrochemical sensors for point-of-care diagnostics and commercialization
Novel biosensors for point-of-care diagnostics are currently being treated as devices for screening purposes only. Their reliability issues from the performance-portability tradeoff impede them from making the final decision. Commercialized and wearable sensors are also subjected to similar problems as they are affected by varied temperature and noise.86 ML can help the developed sensors to overcome this agenda by learning the fingerprint of the chemicals and biomarkers from a wide range of training sets and experimental conditions.87 This objective has been accomplished in nonspecific detection such as artificial nose and tongue that realize for a group of similar chemical species. For instance, Kim et al. reported a surface-enhanced Raman scattering nose from a nanostructured gold surface modified with different surface functional groups (amine, hydroxyl, carboxyl, and methyl) to distinguish lipid, nucleic acid, and proteins by linear discriminant analysis.88 Thus, combining the selectivity from ML and recognition elements of the electrochemical sensor will greatly enhance the reliability and will push the application for the real settings.One key important issue is the limited heterogeneity of the database to train the ML algorithm. ML generally performs well with the data similar to or generated from the same environment as the training set, but testing it with the data from a new system or country frequently results in the failure.89 Training the ML algorithms with a wide range of possible detection conditions will help it recognize the pattern and chemical fingerprint, which will improve the performance and reliability of electrochemical sensors. This task requires an expansive database of electrochemical data to train and test the ML algorithm. In the foreseen future, automated robot experimenters might be invented and used to generate exhaustive data to save human time and energy.90 Another concern regarding electrochemical data is their sensitivity to the instrumentation, thus their identity might need to be included. Nevertheless, compared to other gold-standard methods, electrochemical sensors are truly portable and can be affordable and efficient household devices. Accordingly, ML will be a crucial key for point-of-care diagnostics devices and commercialized sensors for biomedical, food, and environmental monitoring with reliable results.
4.4. Training chemists to approach the future
There are two approaches to encourage the applications of ML and DoE in electrochemical sensors. One approach is that chemists can collaborate with outside experts or statisticians to initiate the project and solve the problem when applying these unfamiliar methods in their analytical chemistry work. Without conceptual understanding, chemists may treat these ML and DoE methods as a black box, preventing them from choosing and optimizing the algorithm, while those experts may not understand the chemical problems that chemists try to solve. Another approach that is more sustainable is to train current and future chemists on DoE and ML. Traditionally, chemistry students may be required to take a course in statistics, but it is apparently inadequate for today and tomorrow. A course or short training on DoE, programming, and ML will be useful for the future chemists to understand the nature of these tools and appropriately apply them in their research. Combining these tools with chemical insights will enhance their creativity to propose novel solutions for significant scientific problems, including how to make a better electrochemical sensor to improve quality of life.5. Conclusions
In this article, we summarize and discuss the progress and thoughts in DoE and ML applications to optimize electrochemical sensors and to analyze complicated electrochemical data that are emerging and turning the field of analytical chemistry. Choosing appropriate DoE instead of the OFAT design enables simultaneous optimization of parameters related to electrode fabrication. DoE also considers interactions between factors, while saving the time and cost from non-essential experiments, and RSM is a useful methodology to optimize such effects on the response to aid the optimization of the electrochemical sensor. To investigate how electrode chemical structures affect their electrochemical properties, ML has proved itself to be a versatile tool for both regression and classification. Utilizing ML algorithms such as a neural network and SVM is superior to analyze potentiometric, voltammetric, and impedimetric data from electrochemical sensors and electronic tongues, as they are advantageous over classical univariate methods. The successful implementation of DoE and ML will contribute to chemical sustainability, enhance the sensor performance, and accelerate the applications of complex electrochemical sensors in the broadest sense.Conflicts of interest
There is no conflict of interest to declare.Acknowledgements
Research in the Puthongkham Lab is currently supported by the Grant for Development of New Faculty Staff, Ratchadaphiseksomphot Endowment Fund, Chulalongkorn University (DNS 64_038_23_003_1), and the National Research Council of Thailand (NRCT) (N41A640073).References
- C. Zhu, G. Yang, H. Li, D. Du and Y. Lin, Anal. Chem., 2015, 87, 230–249 CrossRef CAS PubMed.
- A. Suea-Ngam, L. Bezinge, B. Mateescu, P. D. Howes, A. J. DeMello and D. A. Richards, ACS Sens., 2020, 5, 2701–2723 CrossRef CAS PubMed.
- M. D. Peris-Díaz and A. Krężel, TrAC, Trends Anal. Chem., 2021, 135, 116157 CrossRef.
- S. Tortorella and S. Cinti, Anal. Chem., 2021, 93, 2713–2722 CrossRef CAS PubMed.
- M. I. Jordan and T. M. Mitchell, Science, 2015, 349, 255–260 CrossRef CAS PubMed.
- W. P. Walters and R. Barzilay, Acc. Chem. Res., 2021, 54, 263–270 CrossRef CAS PubMed.
- S. Namuduri, B. N. Narayanan, V. S. P. Davuluru, L. Burton and S. Bhansali, J. Electrochem. Soc., 2020, 167, 037552 CrossRef CAS.
- M. Mayer and A. J. Baeumner, Chem. Rev., 2019, 119, 7996–8027 CrossRef CAS PubMed.
- L. B. Ayres, F. J. V. Gomez, J. R. Linton, M. F. Silva and C. D. Garcia, Anal. Chim. Acta, 2021, 1161, 338403 CrossRef CAS PubMed.
- A. Isozaki, J. Harmon, Y. Zhou, S. Li, Y. Nakagawa, M. Hayashi, H. Mikami, C. Lei and K. Goda, Lab Chip, 2020, 20, 3074–3090 RSC.
- A. Suea-Ngam, P. D. Howes, M. Srisa-Art and A. J. DeMello, Chem. Commun., 2019, 55, 9895–9903 RSC.
- Y. Zhang, Q. Tang, Y. Zhang, J. Wang, U. Stimming and A. A. Lee, Nat. Commun., 2020, 11, 6–11 CrossRef PubMed.
- O. Allam, R. Kuramshin, Z. Stoichev, B. W. Cho, S. W. Lee and S. S. Jang, Mater. Today Energy, 2020, 17, 100482 CrossRef.
- Y. Chen, B. Tian, Z. Cheng, X. Li, M. Huang, Y. Sun, S. Liu, X. Cheng, S. Li and M. Ding, Angew. Chem., 2021, 60, 4199–4207 CrossRef CAS PubMed.
- R. Mahbub, K. Huang, Z. Jensen, Z. D. Hood, J. L. M. Rupp and E. A. Olivetti, Electrochem. Commun., 2020, 121, 106860 CrossRef CAS.
- L. Wilbraham, S. H. M. Mehr and L. Cronin, Acc. Chem. Res., 2021, 54, 253–262 CrossRef CAS PubMed.
- R. G. Brereton, Applied Chemometrics for Scientists, John Wiley & Sons, Ltd, Chichester, UK, 2007 Search PubMed.
- A. V. Filgueiras, J. Gago, I. García, V. M. León and L. Viñas, Mar. Pollut. Bull., 2021, 162, 111841 CrossRef CAS PubMed.
- J. D. Kechagias, K.-E. Aslani, N. A. Fountas, N. M. Vaxevanidis and D. E. Manolakos, Measurement, 2020, 151, 107213 CrossRef.
- K. Chindaphan, K. Wongravee, T. Nhujak, T. Dissayabutra and M. Srisa-Art, J. Sep. Sci., 2019, 42, 2867–2874 CrossRef CAS PubMed.
- S. Wirojsaengthong, D. Aryuwananon, W. Aeungmaitrepirom, B. Pulpoka and T. Tuntulani, Talanta, 2021, 231, 122371 CrossRef CAS PubMed.
- C. García-Gómez, P. Drogui, F. Zaviska, B. Seyhi, P. Gortáres-Moroyoqui, G. Buelna, C. Neira-Sáenz, M. Estrada-alvarado and R. G. Ulloa-Mercado, J. Electroanal. Chem., 2014, 732, 1–10 CrossRef.
- M. Ahmadi and F. Ghanbari, Environ. Sci. Pollut. Res., 2016, 23, 19350–19361 CrossRef CAS PubMed.
- M. A. Bezerra, R. E. Santelli, E. P. Oliveira, L. S. Villar and L. A. Escaleira, Talanta, 2008, 76, 965–977 CrossRef CAS PubMed.
- A. Suea-Ngam, P. Rattanarat, K. Wongravee, O. Chailapakul and M. Srisa-Art, Talanta, 2016, 158, 134–141 CrossRef CAS PubMed.
- A. Suea-Ngam, P. D. Howes, C. E. Stanley and A. J. DeMello, ACS Sens., 2019, 4, 1560–1568 CrossRef CAS PubMed.
- A. Suea-Ngam, L.-T. Deck, P. D. Howes and A. J. DeMello, Anal. Chim. Acta, 2020, 1135, 29–37 CrossRef CAS PubMed.
- T. Ören Varol, B. Perk, O. Avci, O. Akpolat, Ö. Hakli, C. Xue, Q. Li and Ü. Anik, Measurement, 2019, 147, 14–19 CrossRef.
- B. Brahma, S. Sen, P. Sarkar and U. Sarkar, Anal. Chim. Acta, 2021, 1168, 338595 CrossRef CAS PubMed.
- H. A. M. Hendawy, A. M. Ibrahim, W. S. Hassan, A. Shalaby and H. M. El-sayed, Microchem. J., 2019, 145, 428–434 CrossRef CAS.
- J. L. da Silva, E. Buffon, M. A. Beluomini, L. A. Pradela-Filho, D. A. Gouveia Araújo, A. L. Santos, R. M. Takeuchi and N. R. Stradiotto, Anal. Chim. Acta, 2021, 1143, 53–64 CrossRef CAS PubMed.
- K. S. Rizi, B. Hatamluyi, M. Rezayi, Z. Meshkat, M. Sankian, K. Ghazvini, H. Farsiani and E. Aryan, Talanta, 2021, 226, 122099 CrossRef CAS PubMed.
- J. M. Díaz-Cruz, M. Esteban and C. Ariño, Chemometrics in Electroanalysis, Springer International Publishing, Cham, 2019 Search PubMed.
- E. Zdrachek and E. Bakker, Anal. Chem., 2021, 93, 72–102 CrossRef CAS PubMed.
- G. Moro, H. Barich, K. Driesen, N. Felipe Montiel, L. Neven, C. Domingues Mendonça, S. Thiruvottriyur Shanmugam, E. Daems and K. De Wael, Anal. Bioanal. Chem., 2020, 412, 5955–5968 CrossRef CAS PubMed.
- J. J. A. Lozeman, P. Führer, W. Olthuis and M. Odijk, Analyst, 2020, 145, 2482–2509 RSC.
- P. Puthongkham and B. J. Venton, Analyst, 2020, 145, 1087–1102 RSC.
- P. Puthongkham, J. Rocha, J. R. Borgus, M. Ganesana, Y. Wang, Y. Chang, A. Gahlmann and B. J. Venton, Anal. Chem., 2020, 92, 10485–10494 CrossRef CAS PubMed.
- F. Cui, Y. Yue, Y. Zhang, Z. Zhang and H. S. Zhou, ACS Sens., 2020, 5, 3346–3364 CrossRef CAS PubMed.
- T. Hastie, R. Tibshirani and J. Friedman, The Elements of Statistical Learning, Springer New York, New York, NY, 2009 Search PubMed.
- M. Tuck, L. Blanc, R. Touti, N. H. Patterson, S. Van Nuffel, S. Villette, J. C. Taveau, A. Römpp, A. Brunelle, S. Lecomte and N. Desbenoit, Anal. Chem., 2021, 93, 445–477 CrossRef CAS PubMed.
- K. P. Murphy, Machine Learning: A Probabilistic Perspective, The MIT Press, 2012 Search PubMed.
- R. B. Keithley, R. Mark Wightman and M. L. Heien, TrAC, Trends Anal. Chem., 2009, 28, 1127–1136 CrossRef CAS PubMed.
- A. Barati Farimani, M. Heiranian and N. R. Aluru, npj 2D Mater. Appl., 2018, 2, 14 CrossRef.
- S. Zhu, X. Sun, X. Gao, J. Wang, N. Zhao and J. Sha, J. Electroanal. Chem., 2019, 855, 113627 CrossRef CAS.
- E. C. Rivera, J. J. Swerdlow, R. L. Summerscales, P. P. T. Uppala, R. M. Filho, M. R. C. Neto and H. J. Kwon, Sensors, 2020, 20, 625 CrossRef PubMed.
- K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Nature, 2018, 559, 547–555 CrossRef CAS PubMed.
- G. H. G. Matsushita, A. H. Sugi, Y. M. G. Costa, A. Gomez-A, C. Da Cunha and L. S. Oliveira, Comput. Biol. Med., 2019, 114, 103466 CrossRef CAS PubMed.
- S. N. Dean, L. C. Shriver-Lake, D. A. Stenger, J. S. Erickson, J. P. Golden and S. A. Trammell, Sensors, 2019, 19, 2392 CrossRef PubMed.
- Y. Sheng, W. Qian, J. Huang, B. Wu, J. Yang, T. Xue, Y. Ge and Y. Wen, Microchim. Acta, 2019, 186, 543 CrossRef PubMed.
- M. Wesoły and P. Ciosek-Skibińska, Sens. Actuators, B, 2018, 267, 570–580 CrossRef.
- S. Aiassa, I. Ny Hanitra, G. Sandri, T. Totu, F. Grassi, F. Criscuolo, G. De Micheli, S. Carrara and D. Demarchi, Biosens. Bioelectron., 2021, 171, 112666 CrossRef CAS PubMed.
- L. Gundry, S. X. Guo, G. Kennedy, J. Keith, M. Robinson, D. Gavaghan, A. M. Bond and J. Zhang, Chem. Commun., 2021, 57, 1855–1870 RSC.
- R. A. DePalma and S. P. Perone, Anal. Chem., 1979, 51, 829–832 CrossRef CAS.
- G. F. Kennedy, J. Zhang and A. M. Bond, Anal. Chem., 2019, 91, 12220–12227 CrossRef CAS PubMed.
- Q. Cao, P. Puthongkham and B. J. Venton, Anal. Methods, 2019, 11, 247–261 RSC.
- P. Puthongkham and B. J. Venton, ACS Sens., 2019, 4, 2403–2411 CrossRef CAS PubMed.
- P. Puthongkham, C. Yang and B. J. Venton, Electroanalysis, 2018, 30, 1073–1081 CrossRef CAS PubMed.
- M. A. Caro, G. Csányi, T. Laurila and V. L. Deringer, Phys. Rev. B, 2020, 102, 174201 CrossRef CAS.
- V. L. Deringer, C. Merlet, Y. Hu, T. H. Lee, J. A. Kattirtzi, O. Pecher, G. Csányi, S. R. Elliott and C. P. Grey, Chem. Commun., 2018, 54, 5988–5991 RSC.
- B. Rohr, H. S. Stein, D. Guevarra, Y. Wang, J. A. Haber, M. Aykol, S. K. Suram and J. M. Gregoire, Chem. Sci., 2020, 11, 2696–2706 RSC.
- X. Cetó, F. Céspedes, M. I. Pividori, J. M. Gutiérrez and M. Del Valle, Analyst, 2012, 137, 349–356 RSC.
- Y. Rong, A. V. Padron, K. J. Hagerty, N. Nelson, S. Chi, N. O. Keyhani, J. Katz, S. P. A. Datta, C. Gomes and E. S. McLamore, Analyst, 2018, 143, 2066–2075 RSC.
- T. Xue, P. Liu, J. Zhang, J. Xu, G. Zhang, P. Zhou, Y. Li, Y. Zhu, X. Lu and Y. Wen, ACS Omega, 2020, 5, 28452–28462 CrossRef CAS PubMed.
- M. Bonet-San-Emeterio, A. González-Calabuig and M. del Valle, Electroanalysis, 2019, 31, 390–397 CrossRef CAS.
- J. J. Ye, C. H. Lin and X. J. Huang, J. Electroanal. Chem., 2020, 872, 113934 CrossRef CAS.
- L. C. Shriver-Lake, R. L. Myers-Ward, S. N. Dean, J. S. Erickson, D. A. Stenger and S. A. Trammell, Sensors, 2020, 20, 1–9 CrossRef PubMed.
- E. A. Baldwin, J. Bai, A. Plotto and S. Dea, Sensors, 2011, 11, 4744–4766 CrossRef PubMed.
- W. Hu, L. Wan, Y. Jian, C. Ren, K. Jin, X. Su, X. Bai, H. Haick, M. Yao and W. Wu, Adv. Mater. Technol., 2019, 4, 1–38 Search PubMed.
- A. González-Calabuig, D. Guerrero, N. Serrano and M. del Valle, Electroanalysis, 2016, 28, 663–670 CrossRef.
- J. Wang, L. Zhu, W. Zhang and Z. Wei, Anal. Chim. Acta, 2019, 1050, 60–70 CrossRef CAS PubMed.
- J. Zhou, C. M. Welling, M. M. Vasquez, S. Grego and K. Chakrabarty, IEEE Trans. Biomed. Circuits Syst., 2020, 14, 705–714 Search PubMed.
- B. J. Venton and Q. Cao, Analyst, 2020, 145, 1158–1168 RSC.
- Z. Zhang and A. Z. Kouzani, Neural Comput. Appl., 2021 DOI:10.1007/s00521-021-06113-4.
- N. Papadopoulos, C. Hasiotis, G. Kokkinidis and G. Papanastasiou, Electroanalysis, 1993, 5, 99–102 CrossRef CAS.
- S. G. Lemos and J. Gonzalez-Rodriguez, Anal. Chim. Acta, 2020, 1132, 36–46 CrossRef CAS PubMed.
- P. Anastas and N. Eghbali, Chem. Soc. Rev., 2010, 39, 301–312 RSC.
- M. M. Barsan, M. E. Ghica and C. M. A. Brett, Anal. Chim. Acta, 2015, 881, 1–23 CrossRef CAS PubMed.
- R. Pilolli, L. Monaci and A. Visconti, TrAC, Trends Anal. Chem., 2013, 47, 12–26 CrossRef CAS.
- J. Zhou, L. Zhang and Y. Tian, Anal. Chem., 2016, 88, 2113–2118 CrossRef CAS PubMed.
- S. Balaji Ramachandran and K. D. Gillis, J. Neurosci. Methods, 2018, 293, 338–346 CrossRef PubMed.
- M. Kang, E. Kim, S. Chen, W. E. Bentley, D. L. Kelly and G. F. Payne, Biosens. Bioelectron., 2018, 112, 127–135 CrossRef CAS PubMed.
- S. Y. Cho, Y. Lee, S. Lee, H. Kang, J. Kim, J. Choi, J. Ryu, H. Joo, H. T. Jung and J. Kim, Anal. Chem., 2020, 92, 6529–6537 CrossRef CAS PubMed.
- F. A. Chiappini, F. Allegrini, H. C. Goicoechea and A. C. Olivieri, Anal. Chem., 2020, 92, 12265–12272 CrossRef CAS PubMed.
- B. D. Kevadiya, J. Machhi, J. Herskovitz, M. D. Oleynikov, W. R. Blomberg, N. Bajwa, D. Soni, S. Das, M. Hasan, M. Patel, A. M. Senan, S. Gorantla, J. E. McMillan, B. Edagwa, R. Eisenberg, C. B. Gurumurthy, S. P. M. Reid, C. Punyadeera, L. Chang and H. E. Gendelman, Nat. Mater., 2021, 20, 593–605 CrossRef CAS PubMed.
- N. Promphet, S. Ummartyotin, W. Ngeontae, P. Puthongkham and N. Rodthongkum, Anal. Chim. Acta, 2021, 1179, 338643 CrossRef CAS PubMed.
- N. Artrith, K. T. Butler, F.-X. Coudert, S. Han, O. Isayev, A. Jain and A. Walsh, Nat. Chem., 2021, 13, 505–508 CrossRef CAS PubMed.
- N. Kim, M. R. Thomas, M. S. Bergholt, I. J. Pence, H. Seong, P. Charchar, N. Todorova, A. Nagelkerke, A. Belessiotis-Richards, D. J. Payne, A. Gelmi, I. Yarovsky and M. M. Stevens, Nat. Commun., 2020, 11, 207 CrossRef CAS PubMed.
- M. Roberts, D. Driggs, M. Thorpe, J. Gilbey, M. Yeung, S. Ursprung, A. I. Aviles-Rivero, C. Etmann, C. McCague, L. Beer, J. R. Weir-McCall, Z. Teng, E. Gkrania-Klotsas, J. H. F. Rudd, E. Sala and C.-B. Schönlieb, Nat. Mach. Intell., 2021, 3, 199–217 CrossRef.
- Y. Shi, P. L. Prieto, T. Zepel, S. Grunert and J. E. Hein, Acc. Chem. Res., 2021, 54, 546–555 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2021 |