Open Access Article
Open Access ArticleIdentification of synthesisable crystalline phases of water – a prototype for the challenges of computational materials design
Edgar A.
Engel
 *
*
TCM Group, Cavendish Laboratory, University of Cambridge, J. J. Thomson Avenue, Cambridge CB3 0HE, UK. E-mail: eae32@cam.ac.uk
First published on 28th September 2020
Abstract
We discuss the identification of experimentally realisable crystalline phases of water to outline and contextualise some of the diverse building blocks of a computational materials design process. The example of water ice allows us to highlight important challenges and to discuss recent steps towards their resolution. Starting with an extensive database-driven computational search for (meta-)stable crystalline phases, we use dimensionality-reduction techniques to visualise and rationalise the configuration space of ice, screen for promising candidates for thermodynamic stability, and, finally, touch upon accurate, predictive determination of relative stabilities. We conclude by highlighting some of the open problems in practical computational materials design.
I. Introduction
The following discusses and contextualises work published over the recent years. In particular, it highlights and synthesises the work published in refs. 55, 87, 115 and 137. It does not contain any novel work. Since the first calculations in statistical physics,1 computer simulations have cemented themselves as an integral part of the physical sciences. In materials science the field of computational materials design (CMD) has profited particularly from Moore's law and computing architectures tailored towards big data applications. CMD promises to accelerate the discovery and design of novel, technologically interesting materials. With materials as the catalyst for incisive technological (and societal) developments, CMD promises to actively change the world we live in.In the following, we set aside computationally aided but experimentally driven materials discovery despite its unquestionable value: whether it is the computational identification of the atomic structure of an experimentally discovered phase, or materials design by means of tweaking an established class of structure in terms of dopants/composition/stress/etc.
With this caveat the potential of CMD has arguably not been realised yet. Its greatest value – the ability to characterise structures and materials at a rate that exceeds that of experiment by orders of magnitude – is also its greatest weakness, since CMD easily overwhelms experimental capacities for syntheses and validating predictions. The variable predictive power of CMD studies and a preference for comparatively simple and/or well established materials compound this issue. The remainder of this highlight article will be a prime example.
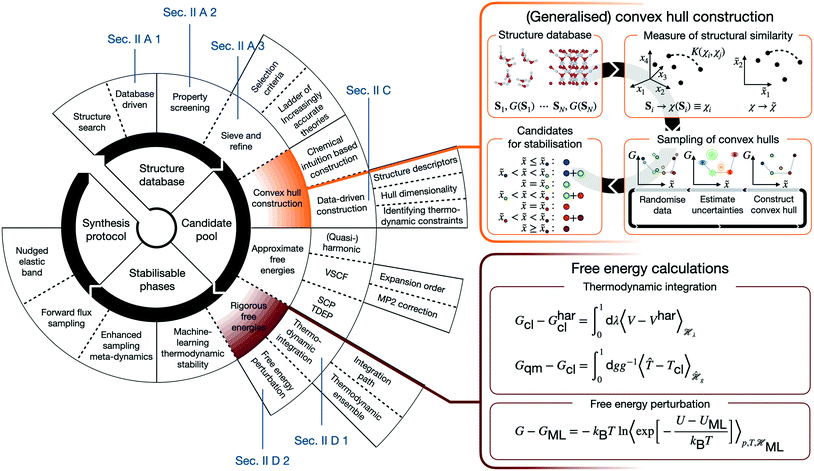
Numerous studies such as ref. 2–8 demonstrate the efficient computational generation of novel structures by combining atomistic calculations with structure searching techniques,9–15 but the fewest result in the synthesis of a novel material. In order to understand the reasons for this inefficiency, it is worth outlining the canonical CMD workflow. CMD starts with a search of the space of possible (meta-)stable structures. Their number inevitably requires distilling promising candidates, before predictive assessments of thermodynamic stability and properties can identify structures, for which is worthwhile to establish possible synthesis pathways. Real CMD workflows are substantially less streamlined and may be constructed from a variety of building blocks, as schematically illustrated in Fig. 1. This renders CMD complex, material-specific, and labour- and expertise-intensive, making the integration of the above building blocks into a unified, accessible framework the key to computationally driven discovery of technologically relevant materials.
In view of this complexity, it is worthwhile juxtaposing an outline of the “canonical” workflow with that described in the following. The arguably most widespread workflow involves generating atomic or molecular configurations from scratch (or by chemical substitution), and subsequently determining their configurational energies using molecular force fields or density functional theory (DFT). Structures are then screened according to their properties and/or configurational energies. In contrast, in the following we describe a database-driven approach to generating ice structures, which are then geometry optimised using DFT and globally screened for thermodynamic stability using a generalised convex hull construction. Crucially, extensive and rigorous free energy calculations put our understanding of thermodynamic stability on a firm footing. Both canonical approaches and the subsequently described one are usually followed by further characterisation of the most promising candidates.
Using the example of identifying crystalline phases of water with the thus outlined workflow, we illustrate some of the more recent developments in (i) screening of structure data and (ii) free energy methods for high-throughput applications, we review the process of identifying crystalline phases of water. Much of the computational detail is brushed under the carpet in order to leave a clearer view of how methodological developments may be married together in a CMD workflow.
II. Water ice as a case study
Despite its apparent simplicity water exhibits phenomena, which are characteristic of multiple classes of materials. Proton (dis-)order is an instance of configurational disorder, otherwise observed in materials such as doped semi-conductors16–18 and high-entropy alloys,19 while the molecular nature of ice leads to features that are characteristic of molecular systems in general: anomalous behaviour relating to thermal expansion20 and isotopic substitution21,22 reveals the importance of nuclear quantum effects (NQE). Polymorphism and hydrogen bonding and dispersion interactions play important roles, just like in pharmaceuticals23–26 and layered materials, such as graphene–hBN superlattices.27 Properties and thermodynamic stability can be tuned by isotopic substitution,28–30 reminiscent of e.g. other molecular crystals.31–33 Last but not least, the phase-diagram of water prominently highlights the importance of meta-stability: seven of 18 experimentally characterised crystalline phases34 are metastable.35Water and ice are some of the most extensively studied systems in the physical sciences, and have been investigated across a wide range of temperatures and pressures. For the purpose of this exercise, we will assume our knowledge to be limited to (i) the liquid form and (ii) its propensity for forming four-connected, tetrahedral networks following the “Bernal–Fowler ice rules”.36 We set aside all further understanding of the phase-diagram to highlight to which extend decades of experimental and theoretical work could be reproduced in a single, state-of-the-art, computational exploration of the phase-space of water.
A. Survey of locally-stable crystal structures
Searching for (meta-)stable phases implies exploring phase-space, for instance using molecular dynamics (MD), nested sampling,37 or other algorithms. MD approaches range from plain (path-integral) MD to minimum hopping,11 (temperature) replica-exchange MD, multithermal-multibaric ensembles,38 and enhanced sampling meta-dynamics.39,40 While such approaches can directly provide thermodynamic stabilities, they do not lend themselves to high-throughput applications. Consequently, extensive structure searches typically explore configuration-space and only assess local stability in terms of their potential energy. A history of crystal structure predictions highlights the potential of diverse searching techniques.9,10,13,15,41–49 The possibly simplest and most elegant approach is to generate many different random arrangements of atoms and performing a local potential energy minimisation with respect to the atomic positions (and lattice parameters for periodic configurations) using a first-principles electronic-structure method such as DFT.9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 731 structures† with unit cell volumes up to 800 Å3‡ are supplemented with the energetically favourable, low density structures from the IZA database59 of experimentally synthesised aluminosilicates, for which energies and densities correlate with their ice counterparts.51
731 structures† with unit cell volumes up to 800 Å3‡ are supplemented with the energetically favourable, low density structures from the IZA database59 of experimentally synthesised aluminosilicates, for which energies and densities correlate with their ice counterparts.51
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 963 structures using the ReaxFF force field,60 removal of duplicates and high-energy configurations,§ the remaining 15
963 structures using the ReaxFF force field,60 removal of duplicates and high-energy configurations,§ the remaining 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 882 distinct structures are then refined using DFT variable-cell geometry optimisations with the PBE62 functional.
882 distinct structures are then refined using DFT variable-cell geometry optimisations with the PBE62 functional.
The size of this dataset reflects a key challenge of CMD: the number of locally-stable structures inevitably renders the identification of distinct, synthesisable structures a needle-in-a-haystack problem. Setting aside kinetic effects, a rigorous analysis of experimental relevance requires exploring the phase-diagram not just as a function of temperature and pressure, but also electric fields,63 doping,64 isotopic substitution,28–30 presence of guest molecules,65–68 and other thermodynamic constraints. Since this is not computationally viable for large numbers of structures, it becomes crucial to (i) rationalise the space of locally-stable structures, and (ii) distill structures whose favorable energetics and/or particular structural features provide leverage for stabilisation at conditions different from those of the search.
B. Rationalising configuration space
A two-dimensional representation of the similarity of the structures (see Fig. 2) provides a human-readable visualisation of structure space and an aid in developing an intuitive understanding of structural relationships, such as proton-(dis-)order, stacking faults, and two- and three-dimensional periodicity.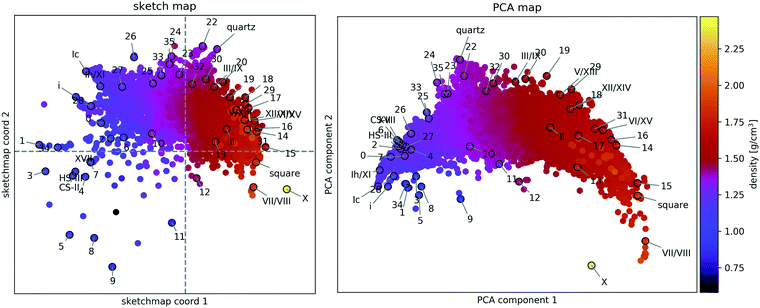 | ||
Fig. 2 Structural similarity of 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 882 distinct PBE-DFT geometry-optimised ice structures. The sketch-map coordinates (left panel) and PCA (right panel) principal components (PC) are abstract measures of structural features. Hence their numerical value is not indicated. The mass density of each structure is encoded by the colour of the respective point and the known phases of ice and the 34 candidates from ref. 55 are labelled according to the original scheme. 882 distinct PBE-DFT geometry-optimised ice structures. The sketch-map coordinates (left panel) and PCA (right panel) principal components (PC) are abstract measures of structural features. Hence their numerical value is not indicated. The mass density of each structure is encoded by the colour of the respective point and the known phases of ice and the 34 candidates from ref. 55 are labelled according to the original scheme. | ||
Any such representation depends on the underlying measure of structural similarity. The field of properties regression for atomistic systems has gifted us with a variety of ways of encoding atomic positions (and unit cells) Si of structure i in feature vectors/descriptors X(Si), whose components are individual features χ. Descriptors that remain invariant under changes of representation of the same periodic structure (e.g. due to changes in particle labelling or a different choice of unit cell) and under translations and rigid rotations of the structure¶ are particularly suited to structure comparisons in terms of a kernel measure of similarity,|| such as:
K(Si,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sj) = (X(Si)·X(Sj))ξ Sj) = (X(Si)·X(Sj))ξ | (1) |
Given a similarity measure, a variety of dimensionality reduction algorithms can be employed to extract a two-dimensional representation aimed at optimally reproducing the distances between pairs of structures. Both linear projections, such as principal components analysis (PCA),78 and non-linear embeddings, such as kernel PCA,79 UMAP,80 t-SNE,81 and sketch-map82 have their merits.
A sketch-map of the 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 882 ice structures is shown in the lefthand panel of Fig. 2, while the righthand panel shows a PCA projection of the same data. Reassuringly, the overall distribution of structures is consistent with the search strategy. The upper sector, corresponding to tetrahedral ices and silica-like networks is densely sampled, while the lower sector, corresponding to very dense (right) and very open structures (left), is sparse. At high density, this sparsity is due to geometric constraints limiting the number of pure phases and the absence of (phase-separated) mixtures, for which interfacial regions lead to reduced density. Meanwhile, at low density this sparsity arises from the preselection strategy, making the latter the biggest limitation to the comprehensiveness of the survey.
882 ice structures is shown in the lefthand panel of Fig. 2, while the righthand panel shows a PCA projection of the same data. Reassuringly, the overall distribution of structures is consistent with the search strategy. The upper sector, corresponding to tetrahedral ices and silica-like networks is densely sampled, while the lower sector, corresponding to very dense (right) and very open structures (left), is sparse. At high density, this sparsity is due to geometric constraints limiting the number of pure phases and the absence of (phase-separated) mixtures, for which interfacial regions lead to reduced density. Meanwhile, at low density this sparsity arises from the preselection strategy, making the latter the biggest limitation to the comprehensiveness of the survey.
The observation that Fig. 2 is consistent with our understanding of the structure data** validates the underlying similarity measure and its use in evaluating a data-driven indicator of thermodynamic stability.
C. Screening for stabilisable structures
Stabilising structures, which are un-/meta-stable at the conditions of the survey, relies on exploiting structural features to manipulate the relative stability of structures. For instance, by increasing pressure one can stabilise more dense structures with respect to less dense ones, while by pumping guest molecules such as H2, methane, or carbon-dioxide into ice networks one can achieve the opposite effect.Assuming that the Gibbs free energy G depends linearly on a structural feature χ such as molar volume.
| G = G0 + Φχ | (2) |
In the macroscopic limit, where interfacial energy costs become negligible, all other phases are unstable to decomposition into phase-separated mixtures of “vertex structures” at fixed χ. The CH construction generalises to more than one feature, considering G(X) instead of G(χ), and is routinely performed for concentrations of multiple chemical species.83 In practice kinetic effects may suppress decomposition almost indefinitely,84 but (as we will argue in section II D) thermodynamic stability is still the key indicator for synthesisability.
Conventionally, CH are constructed almost exclusively on composition and atomic/molar volume.2–8
Choosing which feature(s) to construct a CH on effectively amounts to choosing a stabilisation mechanism and specifying which experimental boundary condition Φ shall be adjusted to stabilise different vertices. In general, this limits which stabilisable structures are identified. For instance, an molar-volume based CH identifies various pressure-stabilised ice structures (and clathrate hydrates, whose stability is subject to the presence of guest molecules66–68), but does not reveal phases whose synthesis requires electro-freezing,63 geometric constraints,85,86etc.
A generalised convex hull (GCH) construction follows a data-driven approach to feature selection.87 Here it is constructed on the same features as the map in the righthand panel of Fig. 2, where the features are linearly decorrelated using a PCA projection,
X → ![[X with combining tilde]](https://www.rsc.org/images/entities/b_char_0058_0303.gif) = UX = UX | (3) |
G(A) = αG(B) + (1 − α)G(C)![[X with combining tilde]](https://www.rsc.org/images/entities/b_char_0058_0303.gif) (A) = α (A) = α![[X with combining tilde]](https://www.rsc.org/images/entities/b_char_0058_0303.gif) (B) + (1 − α) (B) + (1 − α)![[X with combining tilde]](https://www.rsc.org/images/entities/b_char_0058_0303.gif) (C), (C), | (4) |
![[X with combining tilde]](https://www.rsc.org/images/entities/b_char_0058_0303.gif) that retain the variance of the dataset,†† the resultant pool of candidates still reflects the full diversity of locally-stable structures.
that retain the variance of the dataset,†† the resultant pool of candidates still reflects the full diversity of locally-stable structures.
This inclusiveness comes at a price: the abstract nature of the principal components ![[X with combining tilde]](https://www.rsc.org/images/entities/b_char_0058_0303.gif) requires correlating them with more intuitive properties such as density and composition to understand if/which experimentally realisable conditions may be leveraged to stabilise different vertices (or “candidates”). Fortunately, the pool of vertices is typically orders of magnitude smaller than the underlying structure database, greatly simplifying such analyses.
requires correlating them with more intuitive properties such as density and composition to understand if/which experimentally realisable conditions may be leveraged to stabilise different vertices (or “candidates”). Fortunately, the pool of vertices is typically orders of magnitude smaller than the underlying structure database, greatly simplifying such analyses.
In principle, the (G)CH construction assumes not only assumes eqn (2) but also the availability of exact Gibbs free energies, G. In practice, neither G(![[X with combining tilde]](https://www.rsc.org/images/entities/b_char_0058_0303.gif) ) nor lattice parameters and atomic positions are known exactly, rendering the (G)CH probabilistic in nature. While this is neglected in ref. 55, there are practical benefits to a rigorous, probabilistic treatment of the (G)CH.
) nor lattice parameters and atomic positions are known exactly, rendering the (G)CH probabilistic in nature. While this is neglected in ref. 55, there are practical benefits to a rigorous, probabilistic treatment of the (G)CH.
Since the uncertainties in lattice parameters and atomic positions propagate to the (G)CH in a non-trivial way due to the mapping to features ![[X with combining tilde]](https://www.rsc.org/images/entities/b_char_0058_0303.gif) , it is convenient to Monte-Carlo sample CHs based on free energies and geometries, which are repeatedly randomised according to their respective uncertainties.
, it is convenient to Monte-Carlo sample CHs based on free energies and geometries, which are repeatedly randomised according to their respective uncertainties.
Importantly, very similar structures (for example owing to stacking faults or partial disorder) compete for stability and acquire small individual probabilities of constituting a vertex. This renders it possible to reduce them to a single representative structure for further analysis, by iteratively eliminating the N lowest probability candidates with a cumulative probability less than one (which guarantees that no cluster is eliminated entirely in one step) from the dataset and resampling the GCH for the thus reduced dataset.
The probabilistic approach also significantly reduces the sensitivity to errors in input energies compared to conventional deterministic CH constructions.87
D. Thermodynamic stability
Given the evident role of kinetics in experimental syntheses,84 it is worthwhile justifying the subsequent focus on thermodynamic stability. Database analysis shows that experimentally observed metastable phases other than explosives are typically less than 200 meV per atom away from thermodynamic stability,89 begging the question whether experimentally observed metastability is a remnant of thermodynamic stability at some other thermodynamic conditions89 – a hypothesis which is supported by the observation that many of the meta-stable/stabilisable structures identified in section II C match the (experimentally) known ice phases and clathrate hydrates. It has further been argued that the chances of synthesising a structure increase with the associated phase-space volume.90 Free energy is thus still deemed the central indicator of synthesisability.Within the Born–Oppenheimer (BO) approximation91 reliable, quantitative predictions of free energies require an accurate description of the electronic structure and resultant BO potential energy surface (PES), and the rigorous treatment of the statistical mechanics of anharmonic quantum nuclear fluctuations. While the PES can arguably be calculated routinely and accurately by first-principles methods for any conventional atomic configuration,92–101 the computational cost of extensive sampling of the nuclear degrees of freedom with first-principles methods has promoted affordable, approximate descriptions of nuclear fluctuations. Indeed, water and ice have been studied invoking a variety of approximations to both electronic structure and nuclear fluctuations, including simple electrostatic dipole models for the energetics of proton-ordering,102 force-field (PI)MD studies,20,103–106 and first-principles quasi-harmonic (QHA)20,107 and vibrational self-consistent field (VSCF)61 studies. These have greatly advanced our understanding of the nature of water and ice. In particular, they have helped to (qualitatively) disentangle the roles of NQE, proton-disorder, and vibrational anharmonicity, and to understand the associated energy scales. They further show that predicting the thermodynamic stability of general ice polymorphs requires sub-meV per molecule accuracy,61 which unfortunately cannot be guaranteed with common approximate free energy methods,108 but require rigorous PI-based approaches, such as thermodynamic integration (TI).109–113
Their computational cost has previously rendered the required first-principles PI calculations impractical for any but the smallest systems, but sophisticated and affordable surrogate ML potentials have started facilitating extensive PI simulations with first-principles accuracy for more complicated systems, including water and ice.106,114,115
The ML potential of choice is a Behler–Parrinello type, artificial neural network potential (NNP),73,129,130 trained on reference data for 1593 diverse, 64-molecule structures of liquid water.115 It is first used to determine the classical free energy difference between ice Ih and Ic for the surrogate PES, ΔGIh→Iccl,NNP, by means of TI from a Debye crystal to classical ice at 25 K in the NVT ensemble and a transitions to the NPT ensemble to evaluate the temperature dependence of ΔGIh→Iccl,NNP between 25 K and 300 K.131 NQEs are then taken into account by integrating the quantum centroid virial kinetic energy 〈TCV〉 with respect to the fictitious “atomic” mass from the classical to the quantum-mechanical limit.106,114,132,133
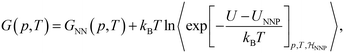 | (5) |
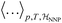 denotes the ensemble average at temperature T and pressure p using the surrogate NNP Hamiltonian
denotes the ensemble average at temperature T and pressure p using the surrogate NNP Hamiltonian 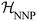 . During FEP U is explicitly calculated using the first-principles reference method, but, with a sufficiently accurate NNP, orders of magnitude fewer reference calculations are required than would be required during direct statistical sampling of the nuclear degrees of freedom.
. During FEP U is explicitly calculated using the first-principles reference method, but, with a sufficiently accurate NNP, orders of magnitude fewer reference calculations are required than would be required during direct statistical sampling of the nuclear degrees of freedom.
Starting from different proton arrangements consistent with the Bernal–Fowler ice rules is crucial, because (i) the proton order is effectively “frozen in” at the timescales available to simulation,134 even at temperature where ice I is proton-disordered, and (ii) differences in ΔGNN between such arrangements can be as large as several meV per molecule.61,121,135 Hence, different representative configurations (with zero net polarisation) were generated for each polymorph using the hydrogen-disordered ice generator136 to calculate ΔGIh→Iccl,NNP and ΔGIh→Ic. Similarly, G(p, T) − GNN(p, T) was determined as the average over multiple 64-molecule realisations of each polymorph.
Fig. 4 shows that ΔGIh→Iccl is negative, while the quantum-mechanical ΔGIh→Ic is close to zero at 200–250 K and increases to 0.2 ± 0.2 meV per H2O at 300 K, confirming the conclusion of ref. 61 that NQE are crucial in stabilizing the hexagonal form.
 | ||
| Fig. 4 ΔGIh→Ic(T) with error bars at ambient pressure. The errors associated with the classical (cl) and quantum-mechanical (qm) revPBE0-D3 values arise predominantly from differences in ΔGNN between proton-orderings. The smaller errors in ΔGIh→Iccl,NNP(T) are due to the larger simulation cell used to obtain it. The data was taken from ref. 115. | ||
In more general terms, the above highlights the intricacies of determining relative stabilities of ice polymorphs and the value of surrogate ML potentials for predictive simulations of thermodynamic properties.
Of course, large scale application to the candidates from a (G)CH demands fairly universal applicability. The universality of the above hinges on that of the NNP, which in turn hinges on the decomposition of atomic configurations into local environments.
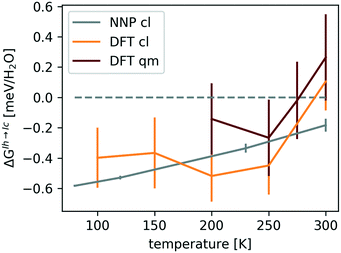
Indeed, the above NNP proves reasonably accurate for the 53 candidate structures from section II C.¶¶ To demonstrate this, the 53 candidates were geometry optimised at the revPBE0-D3 reference level of theory and harmonic vibrational calculations were performed as a simple measure of (nuclear) dynamics. Performing analogous calculations with the NNP shows that it accurately reproduces the reference configurational energies, densities, and vibrational density of states for the 53 ice phases137 (see Fig. 5 and 6).
 | ||
| Fig. 5 Correlation between NNP and revPBE0-D3 energies (top) and densities (bottom) for the 53 ice polymorphs from section II C. The data was taken from ref. 137. | ||
 | ||
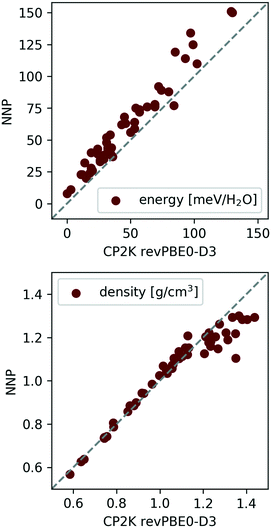
| Fig. 6 Comparison between the NNP and revPBE0-D3 Γ-point phonon density of states (DOS) for proton-ordered realisations of ices VI and Ih, and a low-density hypothetical phase. The discrepancies in the low frequencies are attributed to the importance of long-range interactions for long wavelength vibrational modes. The case of Ih is of particular interest, since the NNP has proven to be an excellent surrogate potential for revPBE0-D3 level free energy calculations for ice Ih. The data was taken from ref. 137. | ||
To rationalise this universality the atomic structure of the 53 candidates is compared to that of 1000 structurally diverse snapshots of 64-molecule liquid water, which constitute part of the training data of the NNP. The latter are farthest-point-sampled138 from simulations of bulk liquid water at high temperatures and densities between 0.7 and 1.2 gram per ml and subsequently relaxed to the corresponding local PES minima.
The comparison is again based on a SOAP description. A meaningful comparison of entire structures and local environments is rendered possible by a linear PCA projection, combined with constructing features of structures (global descriptors) as averages over those of the constituent atomic environments (local descriptors). The PCA map in the lefthand panel of Fig. 7 shows that the presence and absence of long-range order clearly distinguishes the 53 ice phases from the 1000 snapshots of liquid water, while the two righthand panels of Fig. 7 shows that the local atomic environments found in liquid water prototype all atomic environments pertinent to the 53 ice phases.||||
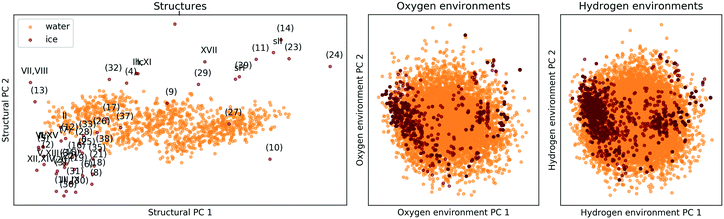 | ||
| Fig. 7 PCA maps comparing the 53 ice polymorphs from section II C to 1000 snapshots of liquid water. The ice structure are labelled according to the scheme in Fig. 2. The left panel compares extended structures (i.e. the complete unit cells), while in the central and right panels oxygen or hydrogen-centered local environments are compared. The data was taken from ref. 137. | ||
Like most common ML potentials, the above NNP exploits the notion of “nearsightedness”, which implies that the energy and forces associated with any atom are largely determined by its neighbours, while long-range interactions can be approximated in a mean-field manner.139,140 The energetics and dynamics of extended systems are reconstructed from atom-centered energy contributions and forces, which only depend on local atomic environments. Consequently, the understanding of local properties encoded in the liquid water training data suffices for free energy calculations for general ice phases.
Notably, if such universal applicability cannot be achieved, assessing the uncertainty in the ML predictions allows implementing either an active learning strategy124 or a baselining procedure,141 to ensure universally meaningful energy and force predictions.
With an understanding of thermodynamic stability, one may now consider establishing possible synthesis pathways, using approaches such as forward flux sampling,142 or via the identification of suitable collective variables.143,144
III. Conclusions and open problems
Ref. 55 probably constitutes the most extensive survey of (meta-)stable, crystalline phases of ice to date. Yet, the recent discoveries of stable low-density forms48,67,68,145 suggest that our understanding of the p–T phase-diagram is probably still incomplete. The general phase diagram, including thermodynamic and geometric constraints such as electric fields or substrates, is even less well established. Furthermore, the observed properties of ice are not fully determined by its ideal, pure, crystalline forms, but reflect the extensive presence of defects, ranging from point-defects like hydrogen bonding/Bjerrum defects146 and atomic substitutions,64 to extended defects like stacking-disorder147–149 and grain boundaries150 and surfaces.151 Their nature and extent pertains to the stability of and transitions between phases and thus our understanding of the space of crystalline phases of water, but has been studied much more sparsely (at least in computational science).The above outlines how data-driven approaches facilitate the extensive survey of synthesisable crystalline phases of water. In the process it highlights three important challenges, in particular, and suggests transferable strategies for their resolution. The first concerns the (potentially extensive) space of candidate structures generated at the outset of a CMD workflow. Given that the number of candidates is typically far too large to permit developing an understanding by visual inspection of individual candidates, the above proposes using suitable measures of structural similarity coupled to dimensionality reduction algorithms to extract the key distinguishing structural features, thereby rendering large numbers of candidates comparable. The second challenge is that of screening the thus rationalised structure space for candidates with an appreciable chance of being experimentally realisable. A generalised convex hull construction is thus used to gauge stability at general thermodynamic conditions. The final challenge lies in putting the resultant understanding of thermodynamic stability for a potentially still appreciable number of candidates on a more solid footing. The above highlights that the use of ML surrogate potentials renders it feasible to perform accurate and extensive free energy calculations for significant numbers of candidates to more rigorously assess phase behaviour. It moreover highlights that suitable constructed ML models provide a sufficiently transferable basis for doing so.
While the above tricks of the trade can in principle be applied to “design” new materials by uncovering phases with novel and/or valuable properties, it is worth emphasising that it does not yet constitute a universal CMD framework. First and foremost, the identification of stabilisation mechanisms has barely been touched upon and the characterisation of properties and possible synthesis pathways has been set aside entirely. Second, there are obvious caveats to its universality. For instance, stabilisable structures which are unstable at the conditions of the initial structure search will escape identification, as will structures that are dynamically/entropically stabilised. The latter constitute an important and promising class of materials.152 Moreover, the above approach relies on the availability of (i) an accurate description of electronic structure of the system of interest and (ii) the accuracy of surrogate potentials, which treat long-range interactions in a mean-field manner in return for the ability to generalise across different polymorphs/conformations.
Last but not least, the availability of a usable, integrated package is the key to CMD fulfilling its potential. This has not been addressed, although atomic structure-, workflow-, and data-management tools/platforms such as ASE,153 AiiDa154,155 and the Materials Cloud156 provide an excellent basis.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
EAE acknowledges financial support from Trinity College, Cambridge. The original work was performed with support of the Engineering and Physical Sciences Research Council of the UK [EP/J017639/1], the European Research Council under the European Union’s Horizon 2020 research and innovation programme [677013-HBMAP], and the NCCR MARVEL, funded by the Swiss National Science Foundation (SNSF).Notes and references
- N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth and A. H. Teller, J. Chem. Phys., 1953, 21, 1087 CrossRef CAS.
- C. J. Pickard, M. Martinez-Canales and R. J. Needs, Phys. Rev. B, 2012, 85, 214114 CrossRef.
- S. Azadi, B. Monserrat, W. M. Foulkes and R. J. Needs, Phys. Rev. Lett., 2014, 112, 165501 CrossRef.
- N. D. Drummond, B. Monserrat, J. H. Lloyd-Williams, P. López Ríos, C. J. Pickard and R. J. Needs, Nat. Commun., 2015, 6, 7794 CrossRef CAS.
- I. Errea, M. Calandra, C. J. Pickard, J. R. Nelson, R. J. Needs, Y. Li, H. Liu, Y. Zhang, Y. Ma and F. Mauri, Phys. Rev. Lett., 2015, 114, 157004 CrossRef.
- A. P. Drozdov, M. I. Eremets, I. A. Troyan, V. Ksenofontov and S. I. Shylin, Nature, 2015, 525, 73 CrossRef CAS.
- M. Mayo, K. J. Griffith, C. J. Pickard and A. J. Morris, Chem. Mater., 2016, 28, 2011 CrossRef CAS.
- B. Monserrat, R. J. Needs, E. Gregoryanz and C. J. Pickard, Phys. Rev. B, 2016, 94, 134101 CrossRef.
- C. J. Pickard and R. J. Needs, Phys. Rev. Lett., 2006, 97, 045504 CrossRef.
- C. W. Glass, A. R. Oganov and N. Hansen, Comput. Phys. Commun., 2006, 175, 713 CrossRef CAS.
- M. Amsler and S. Goedecker, J. Chem. Phys., 2010, 133, 224104 CrossRef.
- T.-Q. Yu and M. E. Tuckerman, Phys. Rev. Lett., 2011, 107, 015701 CrossRef.
- Q. Zhu, A. R. Oganov, C. W. Glass and H. T. Stokes, Acta Crystallogr., Sect. B: Struct. Sci., 2012, 68, 215 CrossRef CAS.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314 CrossRef CAS.
- A. M. Reilly, et al. , Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 439 CrossRef CAS.
- T. H. Nguyen and S. K. O’Leary, J. Appl. Phys., 2000, 88, 3479 CrossRef CAS.
- E. M. Thomas, B. C. Popere, H. Fang, M. L. Chabinyc and R. A. Segalman, Chem. Mater., 2018, 30, 2965 CrossRef CAS.
- F. S. A. Fediai, A. Emering and W. Wenzel, Phys. Chem. Chem. Phys., 2020, 22, 10256 RSC.
- E. P. George, D. Raabe and R. O. Ritchie, Nat. Rev. Mater., 2019, 4, 515 CrossRef CAS.
- B. Pamuk, J. M. Soler, R. Ramírez, C. P. Herrero, P. W. Stephens, P. B. Allen and M. V. Fernandez-Serra, Phys. Rev. Lett., 2012, 108, 193003 CrossRef CAS.
- P. Bridgman, J. Chem. Phys., 1935, 3, 597 CrossRef CAS.
- K. Röttger, A. Endriss, J. Ihringer, S. Doyle and W. F. Kuhs, Acta Crystallogr., Sect. B: Struct. Sci., 1994, 50, 644 CrossRef.
- A. Tkatchenko, R. A. Di Stasio, R. Car and M. Scheffler, Phys. Rev. Lett., 2012, 108, 236402 CrossRef.
- R. A. DiStasio Jr., O. A. von Lilienfeld and A. Tkatchenko, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 14791 CrossRef.
- N. Marom, R. A. DiStasio Jr., V. Atalla, S. Levchenko, A. M. Reilly, J. R. Chelikowsky, L. Leiserowitz and A. Tkatchenko, Am. Ethnol., 2013, 52, 6629 CAS.
- J. Hermann, R. A. DiStasio Jr. and A. Tkatchenko, Chem. Rev., 2017, 117, 4714 CrossRef CAS.
- A. Geim and I. Grigorieva, Nature, 2013, 499, 419 CrossRef CAS.
- L. del Rosso, M. Celli, F. Grazzi, M. Catti, T. C. Hansen, A. D. Fortes and L. Ulivi, Nat. Mater., 2020, 19, 663 CrossRef CAS.
- K. Komatsu, S. Machida, F. Noritake, T. Hattori, A. Sano-Furukawa, R. Yamane, K. Yamashita and H. Kagi, Nat. Commun., 2020, 11, 464 CrossRef CAS.
- C. G. Salzmann and B. J. Murray, Nat. Mater., 2020, 19, 581 CrossRef.
- R. Blinc, J. Phys. Chem. Solids, 1960, 13, 204 CrossRef CAS.
- S. Crawford, Angew. Chem., Int. Ed., 2009, 48, 755 CrossRef CAS.
- T. D. Nguyen, et al. , Nat. Mater., 2010, 9, 345 CrossRef CAS.
- P. V. Hobbs, Ice physics, Oxford University Press, Oxford, 2010 Search PubMed.
- V. F. Petrenko and R. W. Whitworth, Physics of Ice, Oxford University Press, Oxford, 1999 Search PubMed.
- J. D. Bernal and R. H. Fowler, J. Chem. Phys., 1933, 1, 515 CrossRef CAS.
- R. J. N. Baldock, N. Bernstein, K. M. Salerno, L. B. Pártay and G. Csányi, Phys. Rev. E, 2017, 96, 043311 CrossRef.
- P. M. Piaggi and M. Parrinello, J. Chem. Phys., 2019, 150, 244119 CrossRef.
- D. Quigley and P. M. Rodger, Mol. Simul., 2009, 35, 613 CrossRef CAS.
- F. Giberti, et al. , IUCrJ, 2015, 2, 256 CrossRef CAS.
- S. Curtarolo, G. L. W. Hart, M. B. Nardelli, N. Mingo, S. Sanvito and O. Levy, Nat. Mater., 2013, 12, 191 CrossRef CAS.
- A. R. Oganov, C. J. Pickard and Q. Zhu, et al. , Nat. Rev. Mater., 2019, 4, 331 CrossRef.
- C. J. Pickard, M. Martinez-Canales and R. J. Needs, Phys. Rev. Lett., 2013, 110, 245701 CrossRef.
- J. Hama and K. Suito, On metallization of ice under ultra-high pressures, In Physics and chemistry of ice, ed. N. Maeno and T. Hondoh, Hokkaido University Press, Sapporo, 1992 Search PubMed.
- C. J. Pickard, M. Martinez-Canales and R. J. Needs, Phys. Rev. Lett., 2013, 110, 245701 CrossRef.
- J. Russo, F. Romano and H. Tanaka, Nat. Mater., 2014, 13, 733 CrossRef CAS.
- C. J. Fennell and J. D. Gezelter, J. Chem. Theory Comput., 2005, 1, 662 CrossRef CAS.
- Y. Huang, C. Zhu, L. Wang, J. Zhao and X. C. Zeng, Chem. Phys. Lett., 2017, 671, 186 CrossRef CAS.
- T. Matsui, M. Hirata, T. Yagasaki, M. Matsumoto and H. Tanaka, J. Chem. Phys., 2017, 147, 091101 CrossRef.
- I. A. Baburin, D. M. Proserpio, V. A. Saleev and A. V. Shipilova, Phys. Chem. Chem. Phys., 2015, 17, 1332 RSC.
- G. A. Tribello, B. Slater, M. A. Zwijnenburg and R. G. Bell, Phys. Chem. Chem. Phys., 2010, 12, 8597 RSC.
- J. Emmer and M. Wiebcke, J. Chem. Soc., Chem. Commun., 1994, 2079 RSC.
- M. Wiebcke, J. Chem. Soc., Chem. Commun., 1991, 1507 RSC.
- M. Wiebcke, J. Emmer and J. Felsche, J. Chem. Soc., Chem. Commun., 1993, 1604 RSC.
- E. A. Engel, A. Anelli, M. Ceriotti, C. J. Pickard and R. J. Needs, Nat. Commun., 2018, 9, 2173 CrossRef.
- C. Baerlocher, W. M. Meier and D. H. Olson, Atlas of Zeolite Framework Types, Elsevier, Amsterdam, 2007 Search PubMed.
- M. M. J. Treacy, I. Rivin, E. Balkovsky, K. H. Randall and M. D. Foster, Microporous Mesoporous Mater., 2004, 74, 121 CrossRef CAS.
- D. J. Earl and M. W. Deem, Ind. Eng. Chem. Res., 2006, 45, 5449 CrossRef CAS.
- C. Baerlocher and L. McCusker, Database of zeolite structures, http://www.iza-structure.org/databases/, accessed: 28/06/ 2017 Search PubMed.
- A. C. T. van Duin, S. Dasgupta, F. Lorant and W. A. G. III, J. Phys. Chem. A, 2001, 105, 9396 CrossRef CAS.
- E. A. Engel, B. Monserrat and R. J. Needs, Phys. Rev. X, 2015, 5, 021033 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- A. Pulido, L. Chen, T. Kaczorowski, D. Holden, M. A. Little, S. Y. Chong, B. J. Slater, D. P. McMahon, B. Bonillo, C. J. Stackhouse, A. Stephenson, C. M. Kane, R. Clowes, T. Hasell, A. I. Cooper and G. M. Day, Nature, 2017, 657, 543 Search PubMed.
- H. Fukazawa, S. Ikeda and S. Mae, Chem. Phys. Lett., 1998, 282, 215 CrossRef CAS.
- G. A. Tribello and B. Slater, J. Chem. Phys., 2009, 131, 024703 CrossRef.
- A. Falenty, T. C. Hansen and W. F. Kuhs, Nature, 2014, 516, 231 CrossRef CAS.
- L. del Rosso, F. Grazzi, M. Celli, D. Colognesi, V. Garcia-Sakai and L. Ulivi, J. Phys. Chem. C, 2016, 120, 26955 CrossRef CAS.
- L. del Rosso, M. Celli and L. Ulivi, Nat. Commun., 2016, 7, 13394 CrossRef CAS.
- A. Grisafi, D. M. Wilkins, G. Csányi and M. Ceriotti, Phys. Rev. Lett., 2018, 120, 036002 CrossRef CAS.
- M. Rupp, A. Tkatchenko, K.-R. Müller and O. A. von Lilienfeld, Phys. Rev. Lett., 2012, 108, 058301 CrossRef.
- K. Hansen, F. Biegler, R. Ramakrishnan, W. Pronobis, O. A. Von Lilienfeld, K.-R. Müller and A. Tkatchenko, J. Phys. Chem. Lett., 2015, 6, 2326 CrossRef CAS.
- B. Huang and A. von Lilienfeld, 2019, arXiv:1707.04146.
- J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401 CrossRef.
- A. P. Bartók, M. J. Gillan, F. R. Manby and G. Csányi, Phys. Rev. B, 2013, 88, 054104 CrossRef.
- S. De, A. P. Bartók, G. Csányi and M. Ceriotti, Phys. Chem. Chem. Phys., 2016, 18, 13754 RSC.
- M. J. Willatt, F. Musil and M. Ceriotti, J. Chem. Phys., 2019, 150, 154110 CrossRef.
- S. N. Pozdnyakov, M. J. Willatt, A. P. Bartók, C. Ortner, G. Csányi and M. Ceriotti, 2020, arXiv:2001.11696.
- M. E. Tipping and C. M. Bishop, J. R. Stat. Soc. Series B Stat. Methodol., 1999, 61, 611 CrossRef.
- B. Schölkopf, A. J. Smola and K.-R. Müller, in Advances in kernel methods, MIT Press, Cambridge, MA, USA, 1999, p. 327 Search PubMed.
- L. McInnes and J. Healy, 2018, arXiv:1802.03426.
- L. J. P. van der Maaten and G. E. Hinton, J. Mach. Learn. Res., 2008, 9, 2579 Search PubMed.
- M. Ceriotti, G. A. Tribello and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 13023 CrossRef CAS.
- H. Niu, A. R. Oganov, X.-Q. Chen and D. Li, Sci. Rep., 2015, 5, 18347 CrossRef CAS.
- R. Malik, F. Zhou and G. Ceder, Nat. Mater., 2011, 10, 587 CrossRef CAS.
- G. Algara-Siller, O. Lehtinen, F. C. Wang, R. R. Nair, U. Kaiser, H. A. Wu, A. K. Geim and I. V. Grigorieva, Nature, 2015, 519, 443 CrossRef CAS.
- D. Takaiwa, I. Hatano, K. Koga and H. Tanaka, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 39 CrossRef CAS.
- A. Anelli, E. A. Engel, C. J. Pickard and M. Ceriotti, Phys. Rev. Mater., 2018, 2, 103804 CrossRef CAS.
- K. Fukunaga and D. R. Olsen, IEEE Trans. Comput., 1971, 20, 176 Search PubMed.
- W. Sun, et al. , Sci. Adv., 2016, 2, e1600225 CrossRef.
- V. Stevanovic, Phys. Rev. Lett., 2016, 116, 075503 CrossRef.
- M. Born and R. Oppenheimer, Ann. Phys., 1927, 389, 457 CrossRef.
- K. Lejaeghere, G. Bihlmayer, T. Björkman, P. Blaha, S. Blügel, V. Blum, D. Caliste, I. E. Castelli, S. J. Clark, A. D. Corso, S. de Gironcoli, T. Deutsch, J. K. Dewhurst, I. D. Marco, C. Draxl, M. Dułak, O. Eriksson, J. A. Flores-Livas, K. F. Garrity, L. Genovese, P. Giannozzi, M. Giantomassi, S. Goedecker, X. Gonze, O. Grånäs, E. K. U. Gross, A. Gulans, F. Gygi, D. R. Hamann, P. J. Hasnip, N. A. W. Holzwarth, D. Iuşan, D. B. Jochym, F. Jollet, D. Jones, G. Kresse, K. Koepernik, E. Küçükbenli, Y. O. Kvashnin, I. L. M. Locht, S. Lubeck, M. Marsman, N. Marzari, U. Nitzsche, L. Nordström, T. Ozaki, L. Paulatto, C. J. Pickard, W. Poelmans, M. I. J. Probert, K. Refson, M. Richter, G. Rignanese, S. Saha, M. Scheffler, M. Schlipf, K. Schwarz, S. Sharma, F. Tavazza, P. Thunström, A. Tkatchenko, M. Torrent, D. Vanderbilt, M. J. van Setten, V. V. Speybroeck, J. M. Wills, J. R. Yates, G. Zhang and S. Cottenier, Science, 2016, 351, 6280 CrossRef.
- B. M. Austin, D. Y. Zubarev and W. A. Lester, Chem. Rev., 2012, 112, 263 CrossRef CAS.
- G. Onida, L. Reining and A. Rubio, Rev. Mod. Phys., 2002, 74, 601 CrossRef CAS.
- G. Kotliar, S. Y. Savrasov, K. Haule, V. S. Oudovenko, O. Parcollet and C. A. Marianetti, Rev. Mod. Phys., 2006, 78, 865 CrossRef CAS.
- G. Rohringer, H. Hafermann, A. Toschi, A. A. Katanin, A. E. Antipov, M. I. Katsnelson, A. I. Lichtenstein, A. N. Rubtsov and K. Held, Rev. Mod. Phys., 2018, 90, 025003 CrossRef CAS.
- F. Neese, M. Atanasov, G. Bistoni, D. Maganas and S. Ye, J. Am. Chem. Soc., 2019, 141, 2814 CrossRef CAS.
- C. Riplinger, P. Pinski, U. Becker, E. F. Valeev and F. Neese, J. Chem. Phys., 2016, 144, 024109 CrossRef.
- T. Gruber, K. Liao, T. Tsatsoulis, F. Hummel and A. Grüneis, Phys. Rev. X, 2018, 8, 021043 CAS.
- E. Caldeweyher and J. G. Brandenburg, J. Phys.: Condens. Matter, 2018, 30, 213001 CrossRef.
- A. Zen, J. G. Brandenburg, J. Klimeš, A. Tkatchenko, D. Alfè and A. Michaelides, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 1724 CrossRef CAS.
- J. Lekner, Phys. B, 1998, 252, 149 CrossRef CAS.
- S. Habershon, T. E. Markland and D. E. Manolopoulos, J. Chem. Phys., 2009, 131, 024501 CrossRef.
- R. Ramírez and C. P. Herrero, J. Chem. Phys., 2010, 133, 144511 CrossRef.
- R. Ramírez, N. Neuerburg and C. P. Herrero, J. Chem. Phys., 2012, 137, 134503 CrossRef.
- B. Cheng, J. Behler and M. Ceriotti, J. Phys. Chem. Lett., 2016, 7, 2210 CrossRef CAS.
- R. Ramírez, N. Neuerburg, M.-V. Fernández-Serra and C. P. Herrero, J. Chem. Phys., 2012, 137, 044502 CrossRef.
- V. Kapil, E. A. Engel, M. Rossi and M. Ceriotti, J. Chem. Theory Comput., 2019, 15, 5845 CrossRef CAS.
- J. G. Kirkwood, J. Chem. Phys., 1935, 3, 300 CrossRef CAS.
- D. Chandler and P. G. Wolynes, J. Chem. Phys., 1981, 74, 4078 CrossRef CAS.
- M. Parrinello and A. Rahman, J. Chem. Phys., 1984, 80, 860 CrossRef CAS.
- L. M. Ghiringhelli, J. H. Los, E. J. Meijer, A. Fasolino and D. Frenkel, Phys. Rev. Lett., 2005, 94, 145701 CrossRef.
- M. Tuckerman, Statistical Mechanics: Theory and Molecular Simulation, Oxford University Press, Oxford, UK, 2010 Search PubMed.
- B. Cheng and M. Ceriotti, J. Chem. Phys., 2014, 141, 244112 CrossRef.
- B. Cheng, E. A. Engel, J. Behler, C. Dellago and M. Ceriotti, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 1110 CrossRef CAS.
- Y. Zhang and W. Yang, Phys. Rev. Lett., 1998, 80, 890 CrossRef CAS.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158 CrossRef CAS.
- L. Goerigk and S. Grimme, Phys. Chem. Chem. Phys., 2011, 13, 6670 RSC.
- S. Grimme, J. Antony, S. Ehrlich and S. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- O. Marsalek and T. E. Markland, J. Phys. Chem. Lett., 2017, 8, 1545 CrossRef CAS.
- Z. Raza, D. Alfè, C. G. Salzmann, J. Klimeš, A. Michaelides and B. Slater, Phys. Chem. Chem. Phys., 2011, 13, 19788 RSC.
- M. Macher, J. Klimeš, C. Franchini and G. Kresse, J. Chem. Phys., 2014, 140, 084502 CrossRef CAS.
- F. Musil, M. J. Willatt, M. A. Langovoy and M. Ceriotti, J. Chem. Theory Comput., 2019, 15, 906 CrossRef.
- E. V. Podryabinkin and A. V. Shapeev, Comput. Mater. Sci., 2017, 140, 171 CrossRef CAS.
- N. Bernstein, G. Csányi and V. L. Deringer, npj Comput. Mater., 2019, 5, 99 CrossRef.
- R. Tibshirani, J. R. Stat. Soc. Series B Stat. Methodol., 1996, 58, 267 Search PubMed.
- B. D. Conduit, N. G. Jones, H. J. Stone and G. J. Conduit, Mater. Des., 2017, 131, 358 CrossRef CAS.
- P. C. Verpoort, P. MacDonald and G. J. Conduit, Comput. Mater. Sci., 2018, 147, 176 CrossRef CAS.
- J. Behler, Angew. Chem., Int. Ed., 2017, 56, 12828 CrossRef CAS.
- T. Morawietz, A. Singraber, C. Dellago and J. Behler, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 8368 CrossRef CAS.
- B. Cheng and M. Ceriotti, Phys. Rev. B, 2018, 97, 054102 CrossRef CAS.
- M. Ceriotti and T. E. Markland, J. Chem. Phys., 2013, 138, 014112 CrossRef.
- B. Cheng, A. T. Paxton and M. Ceriotti, Phys. Rev. Lett., 2018, 120, 225901 CAS.
- C. Drechsel-Grau and D. Marx, Phys. Rev. Lett., 2014, 112, 148302 CrossRef.
- S. J. Singer and C. Knight, in Advances in Chemical Physics, ed. S. A. Rice and A. R. Dinner, Wiley & Sons, Inc, Hoboken, NJ, USA, 2011, vol. 147 Search PubMed.
- M. Matsumoto, T. Yagasaki and H. Tanaka, J. Comput. Chem., 2018, 39, 61 CrossRef CAS.
- B. Monserrat, J. G. Brandenburg, E. A. Engel and B. Cheng, Nat. Commun., 2020, 11, 5757 CrossRef CAS.
- Y. Eldar, M. Lindenbaum, M. Porat and Y. Y. Zeevi, IEEE Trans. Image Process., 1997, 6, 1305 CAS.
- W. Kohn, Phys. Rev. Lett., 1996, 76, 3168 CrossRef CAS.
- J. Behler, J. Chem. Phys., 2016, 145, 170901 CrossRef.
- G. Imbalzano, Y. Zhuang, V. Kapil, K. Rossi, E. A. Engel, F. Grasselli and M. Ceriotti, 2020, arXiv:2011.08828 [physics.chem-ph].
- R. J. Allen, et al. , J. Chem. Phys., 2006, 124, 024102 CrossRef.
- V. Rizzi, D. Mendels, E. Sicilia and M. Parrinello, J. Chem. Theory Comput., 2019, 15, 4507 CrossRef CAS.
- L. Bonati, V. Rizzi and M. Parrinello, J. Phys. Chem. Lett., 2020, 11, 2998 CrossRef CAS.
- Y. Huang, C. Zhu, L. Wang, X. Cao, Y. Su, X. Jiang, S. Meng, J. Zhao and X. C. Zeng, Sci. Adv., 2016, 2, e1501010 CrossRef.
- P. J. Wooldridge, H. H. Richardson and J. P. Devlin, J. Chem. Phys., 1987, 87, 4126 CAS.
- E. B. Moore and V. Molinero, Phys. Chem. Chem. Phys., 2011, 13, 20008 CAS.
- W. F. Kuhs, C. Sippel, A. Falenty and T. C. Hansen, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 21259 CrossRef CAS.
- T. L. Malkin, B. J. Murray, C. G. Salzmann, V. Molinero, S. J. Pickering and T. F. Whale, Phys. Chem. Chem. Phys., 2015, 17, 60 RSC.
- P. A. F. P. Moreira, R. G. de Aguiar Veiga, I. de Almeida Ribeiro, R. Freitas, J. Helfferich and M. de Koning, Phys. Chem. Chem. Phys., 2018, 20, 13944 RSC.
- M. Watkins, D. Pan, E. G. Wang, A. Michaelides, J. VandeVondele and B. Slater, Nat. Mater., 2011, 10, 794 CrossRef CAS.
- C. Toher, C. Oses, D. Hicks and S. Curtarolo, npj Comput. Mater., 2019, 5, 69 CrossRef.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef.
- G. Pizzi, A. Cepellotti, R. Sabatini, N. Marzari and B. Kozinsky, Comput. Mater. Sci., 2016, 111, 218 CrossRef.
- S. P. Huber, S. Zoupanos, M. U. L. Talirz, L. Kahle, R. Häuselmann, D. Gresch, T. Müller, A. V. Yakutovich, C. W. Andersen, F. F. Ramirez, C. S. Adorf, F. Gargiulo, S. Kumbhar, E. Passaro, C. Johnston, A. Merkys, A. Cepellotti, N. Mounet, N. Marzari, B. Kozinsky and G. Pizzi, Sci. Data, 2020, 7, 300 CrossRef.
- L. Talirz, S. Kumbhar, E. Passaro, A. V. Yakutovich, V. Granata, F. Gargiulo, M. Borelli, M. Uhrin, S. P. Huber, S. Zoupanos, C. S. Adorf, C. W. Andersen, O. Schütt, C. A. Pignedoli, D. Passerone, J. VandeVondele, T. C. Schulthess, B. Smit, G. Pizzi and N. Marzari, Sci. Data, 2020, 7, 299 CrossRef.
Footnotes |
| † This selection contains duplicates since the databases are not mutually exclusive. |
| ‡ And without 3-rings, which would normally induce excessive strain in an ice structure. |
| § In practice, structures with configurational energy exceeding that of an energy-volume convex hull by a multiple of the free energy differences arising from different proton-ordering and NQE of around 10 meV per H2O (ref. 61) were eliminated. |
| ¶ Recent covariantly transforming variants permit predictions of tensorial properties.69 |
| || Which is at this point defined in the high-dimensional space spanned by the components of the feature vector. |
| ** Structures related by proton-disorder (which permits extracting one proton-ordered representative per cluster) and those related by stacking disorder are clustered together. |
| †† The decay of the eigenvalues provides indication of the intrinsic dimensionality of the dataset.88 |
| ‡‡ revPBE0-D3 predicts a difference in lattice energy between the most stable proton-ordered forms of ice Ic and Ih of UIc − UIh = −0.3 meV per H2O, UIc − UIh = −0.3 meV/H2Oin good agreement with results from diffusion Monte Carlo of UIc − UIh = −0.4 ± 2.9 meV per H2O (ref. 121) and the random phase approximation of −0.2 meV per H2O (ref. 121) and 0.7 meV per H2O.122 |
| §§ Notably, uncertainty estimation123 and active learning124,125 have paved the way for the use of ML approaches also in configuration- and phase-space exploration. Beyond regression, dimensionality-reduction techniques have proven useful in rationalising phase-spaces75 and identifying critical structural features,126 and imputation in dealing with inhomogeneous/incomplete datasets.127,128 |
| ¶¶ Three mixed phases and the very high pressure phase X were set aside. |
| |||| The ordered nature of the ice structures is reflected in comparatively few distinct atomic environments. |
| This journal is © The Royal Society of Chemistry 2021 |