Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Crystallographic tomography and molecular modelling of structured organic polycrystalline powders†
Parmesh
Gajjar
 *a,
Thai T. H.
Nguyen
*a,
Thai T. H.
Nguyen
 b,
Jun
Sun
c,
Ioanna D.
Styliari
b,
Jun
Sun
c,
Ioanna D.
Styliari
 d,
Hrishikesh
Bale
e,
Samuel A.
McDonald
a,
Timothy L.
Burnett
d,
Hrishikesh
Bale
e,
Samuel A.
McDonald
a,
Timothy L.
Burnett
 a,
Benjamin
Tordoff
f,
Erik
Lauridsen
a,
Benjamin
Tordoff
f,
Erik
Lauridsen
 c,
Robert B.
Hammond
c,
Robert B.
Hammond
 b,
Darragh
Murnane
b,
Darragh
Murnane
 *d,
Philip J.
Withers
*d,
Philip J.
Withers
 ag and
Kevin J.
Roberts
ag and
Kevin J.
Roberts
 b
b
aHenry Moseley X-ray Imaging Facility, Department of Materials, The University of Manchester, Manchester, M13 9PL, UK. E-mail: parmesh.gajjar@alumni.manchester.ac.uk
bCentre for the Digital Design of Drug Products, School of Chemical and Process Engineering, University of Leeds, Woodhouse Lane, Leeds, LS2 9JT, UK
cXnovo Technology ApS, Theilgaards Alle 9,1th, 4600 Køge, Denmark
dSchool of Life and Medical Sciences, University of Hertfordshire, College Lane, Hatfield, AL10 9AB, UK. E-mail: d.murnane@herts.ac.uk
eCarl Zeiss X-ray Microscopy, 4385 Hopyard Rd #100, Pleasanton, CA 94588, USA
fCarl Zeiss Microscopy GmbH, Carl-Zeiss-Straße 22, 73447 Oberkochen, Germany
gHenry Royce Institute for Advanced Materials, The University of Manchester, Manchester, M13 9PL, UK
First published on 2nd March 2021
Abstract
A fundamental understanding of the behaviour of polycrystalline materials, including pharmaceuticals, is vital for control of their physicochemical and crystalline properties, which in turn has the potential to improve drug product development for example. In this work, attenuation X-ray computed tomography (CT) and diffraction contrast tomography (DCT) are combined with molecular modelling to understand the powder packing behaviour and crystal interactions of the organic cubic compound hexamine (hexamethylenetetramine). It is the first application of DCT to polycrystalline organic materials. The crystal morphology is predicted through synthonic modelling, with fully 3D-resolved confirmation of the crystallography of the external {110} facets, edges and corner directions by DCT. Analysis of the powder-bed reveals agglomerate structures and orientational texture, with its chemical origins energetically predicted to be face-to-face in accordance with the experimental data. Finally, measurements of crystal & crystallite interactions provide evidence for different mechanisms of powder bed agglomeration.
1 Introduction
The structuring and behaviour of dry particles when consolidated into powder beds is a ubiquitous problem in fine chemical industries.1 For example, the fluidization of powders by a carrier gas is an essential requirement for fluid catalytic cracking of hydrocarbons;2 and the flow, mixing, densification and fluidization of powders are common processes in pharmaceutical production.3 To understand the structure and function of crystalline powders, a knowledge of variability across multiple scales of analysis (supramolecular, crystal, inter-particulate) is necessary. The assessment of the micromeritic properties is commonplace.4 However, the supramolecular basis of powder structuring remains largely inferential (e.g. polymorphic form, morphology, surface chemistry and inter-particulate bonding).5,6Powder bed structuring derives from the population balance of particle size and shapes with the respective orientations determining the adjacent surface chemistries responsible for inter-particulate cohesion forces. Molecular modelling of the supramolecular arrangements responsible for crystal chemistry provides a route to design crystalline products. By understanding the spatial supramolecular arrangements and intermolecular forces, it is possible to predict, and control the intermolecular interactions (synthons7) necessary to design crystallisation processes,8,9 and to understand inter-particle interactions.10,11
Cohesive van der Waals and electrostatic inter-particulate forces can be highly anisotropic in nature,12 but can be modelled and manipulated using extrinsic chemical synthon force vectors.13 Furthermore, preferential solvent interaction on particle facets14,15 drives anisotropy of surface adhesion force response for crystals under variable relative humidity.16 Single particle techniques provide effective measurement of anisotropic cohesion forces,16–18 but direct measurement of powders is challenging. There is a clear need for techniques that provide non-destructive granular information for polycrystalline organic powders.
X-ray computed tomography (CT) is a non-destructive X-ray microscopy (XRM) technique19–21 capable of 3D imaging of particle morphology22 and powder micromeritic properties,23 but providing no direct chemical or crystallographic information.24 X-ray diffraction (XRD) methods on the other hand are routinely used to analyze crystal structure and different chemical phases within a sample, but are unable to give any precise characterisation of the spatial orientations and relative positions of micro-particles within a bulk powder bed. Consequently, a number of diffraction tomographies have evolved to enable 3D mapping of crystalline structures.25–28 Diffraction Contrast Tomography (DCT29–31) is one such technique. As the sample is rotated the constituent crystal grains give rise to diffraction spots as they meet the Bragg diffraction condition.29 The three-dimensional crystal grain shapes are then reconstructed on the basis of these spots from a limited number of projections using an algebraic reconstruction technique. Since it involves a similar set up to X-ray CT, it can easily be acquired in parallel to provide 3D crystallographic information such as grain centroids, orientations, shapes and interaction networks. The DCT technique is possible at synchrotron facilities (e.g. ESRF32) using monochromatic X-rays and on laboratory instruments (LabDCT33) using a polychromatic X-ray beam, with example applications including metals,34–36 metalloids,37 and minerals.38,39 Early work has used X-ray CT and XRD together to examine isolated organic crystals,40,41 but DCT of polycrystalline organic powders has not previously been applied in part due to experimental challenges arising from the typically lower absorption cross-section and the lower crystal symmetry typical of such organic crystals.
In this study we have performed 3D crystallographic analysis of a polycrystalline organic powder bed for the compound hexamine, which crystallises in a symmetric body-centred cubic lattice structure that gives rise to a highly-equant dodecahedral morphology. Hexamine has historical significance as the first organic crystal to have its structure determined by X-ray diffraction nearly 100 years ago,42 and so is a prime choice here for the first application of DCT to polycrystalline organic materials. Widely used in organic synthesis43 and coordination polymer production,44 hexamine also shows interesting crystal behaviour such as inter-crystal agglomeration,45 solvent inclusions,46 as well as physical instability to environmental humidity.47 This paper examines how the combination of X-ray CT & DCT with molecular modelling can aid the understanding of the crystallography and granular structure of a hexamine powder bed.
2 Results
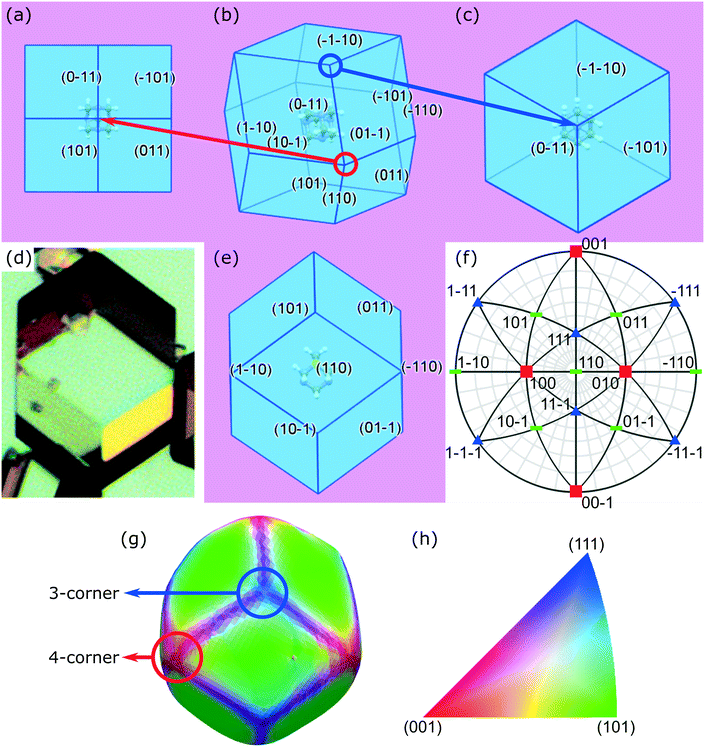
2.1 Crystal morphology assessment
Crystal habit attributes for hexamine crystals predicted from molecular & inter-molecular (synthonic) modelling are given in Table 1. The high multiplicity (number of symmetry-equivalent faces) of the predicted forms is due to the high symmetry of the cubic crystal system of hexamine and indicates that a small number of forms dominates the crystal morphology. The observed morphology is a rhombic dodecahedron comprised of the single {110} form as shown in Fig. 1b.| Crystal surface | Interplannar spacing dhkl (Å) | Multiplicity | # Edges | # Corners | Slice energy Esl (kcal mol−1) | Attachment energy Eatt (kcal mol−1) | Surface area (%) | Surface energy (mJm−2) | |
|---|---|---|---|---|---|---|---|---|---|
| 3-Corner | 4-Corner | ||||||||
| {110} | 4.898 | 12 | 24 | 8 | 6 | −7.84 | −10.34 | 100 | 105.8 |
The typical crystal-habit of hexamine with twelve equivalent {110} faces, has two types of corners: six are termini of the four-fold inversion axes in the <100> directions, and eight are termini of the three-fold rotation axes in the <111> directions. These two types of corner will be hereafter referred to as ‘four-corner’ and ‘three-corner’ respectively. The hexamine crystal-habit also has twenty four edges orientated in <111> directions and the orientation of hexamine molecules on all of the edges is the same.
Crystallographic analysis reveals that there are two main synthons dominating the crystal chemistry and habit of hexamine, as shown in Fig. 2: synthon S1, along the directions <111>, i.e. between the corner and body-centred cubic molecules with interaction strength −1.56 kcal mol−1 and synthon S2, along directions <100> with energy −0.61 kcal mol−1. Synthon analysis shows that both synthons contribute to the attachment energy, and hence growth of the {110} crystal surfaces.
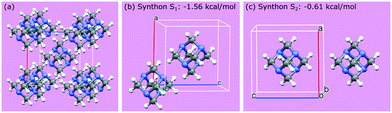 | ||
| Fig. 2 (a) Packing within a hexamine unit cell; (b and c) two strongest intermolecular interactions (synthons S1 and S2) in the crystal structure of hexamine. | ||
The morphological prediction with the single {110} form agrees with previous studies.48,49 In addition, the calculated lattice energy Ecr using the Dreiding potential set converged to −18.18 kcal mol−1, showing good agreement with the experimental lattice energy calculated from the heat of sublimation ΔHsub (ref. 50) (see ESI† data).
The rhombic dodecahedral shape can be observed in the optical microscopy images, as shown in Fig. 1d. The particle displays clean facets, and as hexamine has only {110} facets, it is easy to deduce in this case that each facet must be of a {110} family. This was explicitly confirmed through individual crystal identification within the agglomerated powder bed using DCT (Fig. 1g).
2.2 Powder bed structure
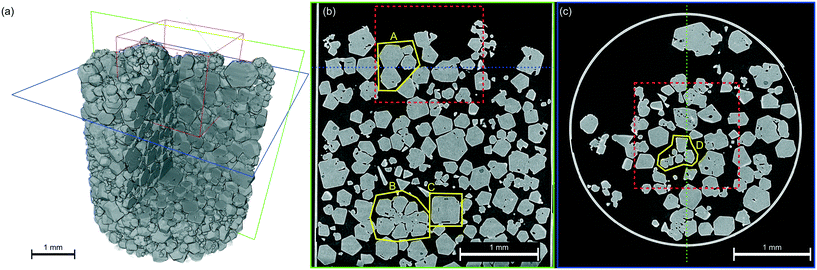
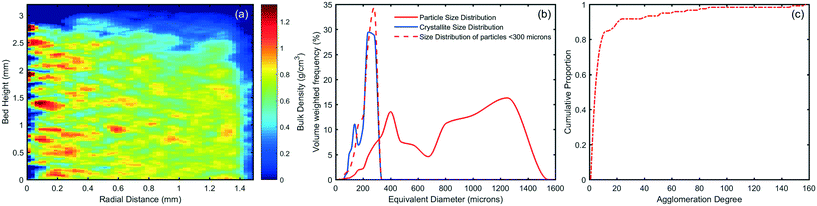
Attenuation X-ray CT provides insight into the overall powder bed structure, as shown in Fig. 3, with the average bulk particle solids fraction in the lower part of the bed quantified as 53% giving an average bulk density of 0.70 g cm−3. Bulk density as a function of radius and height in Fig. 4a reveals structure within the powder bed, with areas closer to the centre of the tube showing a higher bulk density as well as ordering between higher and lower density regions indicative of particle–particle interactions. The particle size-distribution in Fig. 4b and Table S2 (ESI†) shows a wide range of sizes, highlighting the agglomerated nature of the powder bed.Within the powder bed, the rhombic dodecahedron shape of hexamine crystals can be seen in 3D. Moreover, many particles can be seen to be fused as agglomerates, showing the agglomerated nature of the bed. The source of agglomerates within a powder bed could be from crystallisation (surface epitaxial nucleation, collision and cementation1) or through solid bridging during storage. In Fig. 3 particle A shows one fused agglomerate structure, interestingly with air voids resembling 3 spokes separated by 120°, whilst particle B shows a larger ‘cluster’ fused agglomerate formed with 7 particles collecting around a central particle. One hypothesis for the formation of such clusters in hexamine is through dendritic growth,45 and particle D provides evidence for this with a clear bridge between two crystals. Particle C is an example of liquid inclusions identified within crystals, highlighting mother liquor impurities that have been trapped during the crystallisation process51 and representing a particle containing areas of poor crystal perfection.
The size of individual crystals and crystallites within particles identified through DCT provides a benchmark for structures within the virtual X-ray CT powder bed to be classified as single crystals or fused agglomerates, and hence determining the powder bed to be 83 vol% agglomerated. Agglomeration of hexamine can occur both during the crystallisation process, as well as due to hygroscopic interactions during storage. The distribution of the agglomeration degree of each of the fused agglomerates is shown in Fig. 4c, showing 80% of the agglomerates contain up to 10 hexamine crystals.
2.3 Powder crystallographic analysis
Individual crystal particles, and crystallite-containing powder grains were identified within the powder bed of aggregated and agglomerated particles using DCT, with a single cross-section shown in Fig. 5a. A map of the completeness metric is shown in Fig. 5b, which together with examination of the crystal morphology provides an indication of areas of high (E) and low crystal morphological quality (F) across the powder bed. The poor morphological quality of F can seen in Fig. 5d, with a non-rhombic dodecahedral morphology and multiple air inclusions located on one horizontal plane. Particle E shown in Fig. 5c highlights a clearly faceted dodecahedral crystal with two solid-bridges joining it to other particles, and it is possible to see how crystallites combine within fused agglomerates in G & H. These two fused agglomerates also contain air inclusions, except here they are at the boundaries between the individual crystallites of which the particle is composed. These results generated from the bulk powder are consistent with previous microscopy observations of isolated crystals.52,532.4 Crystallographic texture
The crystallographic orientations of each of the crystals and crystallites in the powder bed is shown in Fig. 6, where each crystal/crystallite is coloured according to the orientation of its unit cell with respect to the z axis in the laboratory frame of reference.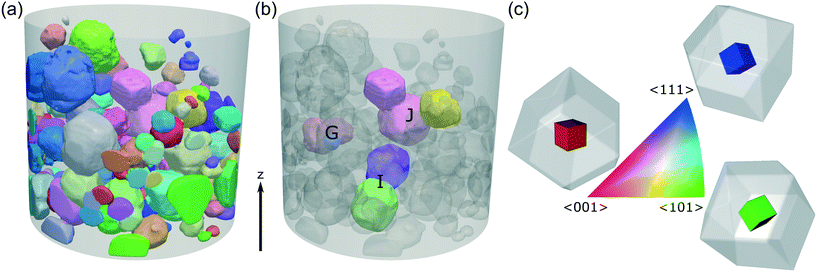 | ||
| Fig. 6 (a) A 3D view of the powder bed, with each crystallite coloured according to the orientation of its unit cell with respect to the vertical z axis in the sample frame of reference. The shaded cylinder (1.2 mm diameter, 1.4 mm height) shows the extent of the DCT analysis region and each crystallite shown has a maximum completeness of at least 0.75. (b) Clusters of crystallites G, I, J selected for analysis of crystallite interactions. (c) The orientation-colour map is given by the inverse pole figure (IPF),54 with 3 sketches showing the <001>, <101> and <111> orientations. The coloured cube shows the orientation of the unit cell, with the surrounding grey rhombic dodecahedron showing the orientation of the hexamine crystal. | ||
Fig. 7 shows pole figures for projections of the unit cell directions <001>, <101> and <111> directions in the upper hemisphere. Only those crystals/crystallites with a maximum completeness of at least 0.75 are shown, with over 200 such crystals/crystallites in the powder bed. The bright spots in these pole figures correspond to 2.5 multiples of a random distribution (mrds)55 and indicate that there is a texture to the powder bed. If the particles were randomly orientated within the bed, the pole figure would be an even colour around 1 mrds.
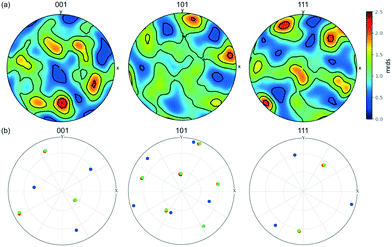 | ||
| Fig. 7 (a) Pole figure showing the stereographic projections of the <001>, <101> and <111> directions of the unit cell of all of the crystallites, projecting the upper hemisphere onto a horizontal plane normal to the vertical z axis in the sample frame of reference. The scale is in terms of ‘multiples of random distribution’ (mrds). (b) Pole figure of the three crystallites G1 (green circles), G2 (blue), G3 (red) within the agglomerate structure G in Fig. 5. | ||
Although the hexamine crystals were simply poured into the polyimide tube, the pole figure shows that the crystals/crystallites are not completely random but display co-operative interactions with each other.
2.5 Surface chemical origins of powder bed structuring
The nature of the co-operative interactions between crystallites were further analysed by examining the interactions between individual particles and the individual crystallites within the agglomerates using a molecular grid search (section 5.4). The results in Table 2 showing that the strongest interaction energy is for a face–face interaction, even after taking differing numbers of molecules within the probes into account. This demonstrates that face to face alignment of crystallites within agglomerates, and of crystal particles within the powder bed is most energetically favourable. Visual examination of the DCT data shows that the majority of crystals/crystallites are in face-to-face contact, with three example clusters of crystals/crystallites shown in Fig. 6b and 9.| Interaction | Face–face | Face–edge | Face–3-corner | Face–4-corner |
|---|---|---|---|---|
| Greatest total interaction energy (kcal mol−1) | −27.0 | −15.2 | −6.9 | −6.67 |
| Interaction energies normalised with number of probe molecules (kcal mol−1) | −5.4 | −3.8 | −1.7 | −1.3 |
Bringing together the model of the crystal morphology and the crystallographic orientation and position provided by DCT in Table S3 (ESI†), it is possible to construct models of the above crystal/crystallite interactions. Starting from a list of the vertex co-ordinates in a reference crystal/crystallite co-ordinate system, these can be scaled according to the measured equivalent diameter before a rigid body transformation to rotate and translate each crystal/crystallite with respect to the reference crystal/crystallite. These model interactions are shown in Fig. 9b, d and f and clearly demonstrate face-to-face contact.
The interactions in Fig. 9 also reveal the relative crystallographic alignments of the unit-cells. Fig. 9a shows the cluster of crystallites (G1, G2 and G3) that makes up agglomerate G from Fig. 5; crystallites G1 and G3 have very close alignment, which is confirmed through the pole figure in Fig. 7b where G1 (green) and G3 (red) have exactly the same crystallographic orientation, i.e. these two crystals are essentially epitaxially aligned and have formed as a single unit during crystallisation. Solid-bridged crystals J1 & J2 are also interesting as they reveal an inter-crystal twin-boundary, i.e. the unit cell of J1 is rotated through 60° about <111> compared to the unit cell of J2. These pairs of crystals suggest ordered alignments, whereas the alignment between particles I1 & I2 suggests a more random alignment.
2.6 Agglomerate structure
A 3D visualisation of cluster agglomerate B from Fig. 3 is shown in Fig. 10a, showing the individual crystals to be crystallographically very well aligned, highlighting a rather a beautiful and well-ordered structure. A 2D slice cut through the cluster perpendicular to the <111> direction is shown in Fig. 10b, strongly suggesting an epitaxial arrangement. It is also interesting that voids appear to be positioned between the individual crystals. A mechanism for the formation of such a structure is being explored in a separate parallel study.3 Discussion
In order to understand the crystallographic origins of powder bed structuring, two important questions are: 1) can the 3D crystal morphology be identified within a powder bed? 2) How does the crystallographic orientation direct crystal–crystal interactions in a powder? In this work, the combination of attenuation X-ray CT and diffraction contrast tomography (DCT) coupled with molecular modelling allowed us to provide insight on these questions for a polycrystalline hexamine powder bed. X-ray CT and DCT provided experimental assessment of the crystal morphology, powder bed structure, and the crystallography. By exploiting the measured crystal & crystallite orientations along with the crystallographic texture data, we have been able to analyse the chemical force vectors for interactions between individual hexamine crystals using molecular modelling.Experimental measurements of the crystal morphology (Fig. 1) enabled the type and direction of predicted facets, edges and corners to be verified for hexamine crystals. These measurements of a powder bed were carried out in situ which not only allowed the 3D morphology of multiple crystals to be seen but also information concerning their mutual orientation with one another. This is in contrast to previous microscopy studies that analysed isolated hexamine crystals in 2D.53,56 Processing is known to affect morphology,57 and often commercially available materials are different from those crystals grown under specific conditions.58 This work opens the door to quantifying the overall quality of the crystals within a powder bed notably conferring the crystal-to-crystal ability to assess variability in their surface properties defined by the predicted morphology.59,60 As an example, consider particles E and F (Fig. 5), with the former close to an ideal rhombic dodecahedron but the latter markedly different. The completeness DCT metric by itself is insufficient to highlight areas of poor crystal quality, since it is affected by the strength and position of spots, altered crystallinity and weaker signals from edges of particles amongst other factors. However, taken together with attenuation X-ray CT data, it can indicate particles of poor crystal quality. Particle F has many random air voids, and one hypothesis is that it was formed from many small crystallites rapidly nucleating together. These crystallites would give weak and overlapping diffraction spots, hence the locally lower completeness. Clearly, identifying such poor quality crystals within the entire bed is a step in the right direction, and it may be possible to develop a more robust metric for assessment of crystal morphological quality.
The question of how hexamine crystals interact within the powder bed was answered using a combination of molecular modelling and X-ray CT–DCT, with the observed crystallographic texture (Fig. 7) understood on a chemical-force basis in terms of preferred face–face interactions between the hexamine crystals (Fig. 8). Furthermore it was possible to create models of observed (i.e. non simulated) particle–particle interactions (Fig. 9). These physical chemical force vectors provide a missing but vital link between knowledge of the crystal morphology48 and crystal–crystal interactions at a condensed matter scale.61,62 This should lead to better predictive models of hexamine behaviour, which would be useful for example in optimising industrial scale processes.56
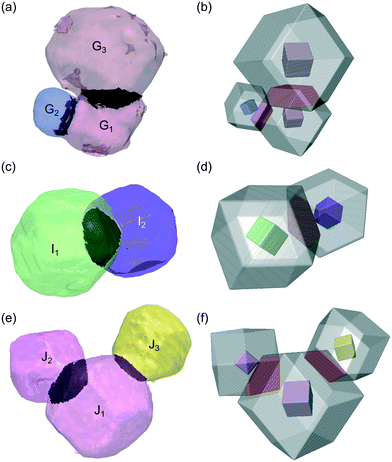 | ||
| Fig. 9 Three different clusters of particles isolated from the powder bed that display crystal face-to-face interactions, with the experimental data shown in (a, c and e) and models of the same crystal interactions constructed from the experimental data in (b, d and f). The interactions between G1–G2–G3 are shown in (a and b), between I1–I2 in (c and d), and J1–J2–J3 in (e and f). In the experimental data, each crystal/crystallite has the same colour as in Fig. 6 with some transparency and the darker shading indicating the contact area. The model interactions show a transparent crystallite morphology with the unit cell inside coloured according to its orientation, and the overlapping volume coloured red. The legend for the colours is given by the inverse pole figure in Fig. 6d. | ||
In the present study, the fraction (83 vol%) of the hexamine powder bed that is agglomerated is high, but there are a number of different mechanisms for fused agglomerate formation.1 For example, crystals may fuse during the crystallisation process due to crystal–crystal interactions. Growth solvents such as water can aid this process by acting as a capillary liquid film between the crystals, encouraging their joining together. Agglomerates can also nucleate on the surfaces of existing crystals. Hexamine is known to be hygroscopic, and modelling of a water probe molecule with the faces, edges and corners of a hexamine crystal shows that interaction energy in all cases is ∼−4.85 ± 0.1 kcal mol−1, i.e. less than the interaction energy of hexamine face-to-face, but more than hexamine face-to-edge. Crystallographic orientation of hexamine particles within the powder may therefore direct anisotropic capillary layer formation, and the subsequent creation of anisotropic crystalline bridges resulting in cohesive agglomerates. For example, it could be conjectured that particles B or F (Fig. 3 and 5) have formed during the crystallisation process, whereas crystal E (Fig. 5) shows some evidence of bridges with other crystals through the action of environmental moisture sorption processes.
Although this work investigated hexamine as an initial test substance for X-ray CT–DCT analysis of a polycrystalline organic compound, it nevertheless demonstrates the multiple aspects of relevance to other polycrystalline substances. Agglomerates formed during crystallisation or storage may have different alignments between the crystal unit cells,1 and the molecular scale modelling of particle collision and cementation processes underlying this agglomeration mechanism have been previously analysed.63 Ordered alignments (e.g. twin-boundaries) are more likely during crystallisation, whilst random alignments more likely during storage. Some interactions such as crystallites G1 & G3 in Fig. 7b, 9a and b or the highly aligned cluster agglomerate B (Fig. 10) are consistent with the former case, whereas others such as crystals I1 & I2 in Fig. 9c and d appear more consistent with the latter case, giving further evidence that multiple agglomerate formation mechanisms can be identified within a powder bed using a combined X-ray CT–DCT approach.
 | ||
| Fig. 10 (a) A 3D rendering of cluster agglomerate structure B from Fig. 3 showing hexamine crystals arranged in a ring around a central crystal; (b) a cross-sectional slice through the same agglomerate in the <111> direction suggesting an epitaxial relationship between the crystals. | ||
It was not possible to differentiate between agglomeration during crystallisation compared to hygroscopic powder ageing in the current study due to the delay between sample preparation and scanning. However it is promising that crystallographic and morphological study could be undertaken on such a challenging polycrystalline powder bed, even after significant powder ageing. Physical observations of the sample showed that it was free-flowing when loading into the Kapton tube, but not free-flowing by the time of scanning, indicating an agglomeration mechanism at work during this time. The non-destructive nature of X-ray CT–DCT analysis opens the door for future studies using time-resolved measurements35,64 of the crystallographic texture to study the evolution of crystal growth/crystal fusion and its effect on storage or during processing of organic compounds. Understanding the physicochemical basis for agglomeration during and post-crystallisation process will ultimately allow processes to be engineered to avoid poorer quality crystals dominating the powder structure.
There is clearly promise in combined X-ray CT–DCT as a 3D crystallographic analysis technique for organic powders that synergises with molecular modelling, but further work is needed before it is widely applicable. The volume of the crystallographic measurements from DCT reported here was limited to a cylinder of height 1.2 mm and diameter 1.2 mm, whereas the X-ray CT data corresponds to a cylinder of height 3.4 mm and diameter 3.3 mm (Fig. 6). While the DCT volume contains over 500 indexed crystals or crystallites, with over 200 of high completeness that is sufficient to give a texture pole figure (Fig. 7), it does not include complex structures such as the ‘cluster’ fused agglomerate particle B (Fig. 10) and hence is not able to provide crystallographic insight into how these structures form. For example, cluster agglomerates may form during the crystallisation process, or due to solid bridging of individual crystal particles during powder storage. Furthermore, 2× pixel binning was employed for the X-ray CT and DCT measurements (Table 3), reducing the resolution, but also the overall scan time. Given that individual crystals & crystallites were ∼250 μm in size, this is acceptable but it does mean that some smaller crystallites (e.g. at the top of particle G) remained undetected. Compromises between scan area and resolution are necessary with laboratory X-ray sources (i.e. used here in LabDCT) to prevent excessively long scan times, but DCT using synchrotron sources with much higher X-ray flux would allow both larger scan area and high resolution in shorter scan times.
| Mode | Voltage (V) | Power (W) | Magnification optic | Detector binning | No. projections | Exposure time per projection (s) | Total scan time (h) |
|---|---|---|---|---|---|---|---|
| Attenuation X-ray CT | 80 | 7 | 4× | 2× | 1601 | 0.75 | ∼1 |
| LabDCT | 110 | 10 | 4× | 2× | 201 | 120 | ∼7 |
Hexamine can be considered to be atypical with its cubic unit cell; the majority of organic compounds (inc. pharmaceuticals) being dominated by more asymmetric orthorhombic, monoclinic and triclinic forms.65 Such compounds provide a greater challenge for resolving 3D crystallographic information since the diffraction patterns are more complex, with a higher likelihood of overlapping spots. Further, crystal imperfection and strain can also weaken the diffraction spots making DCT more difficult. Work is currently underway to analyse DCT data for lactose monohydrate, a common pharmaceutical excipient used in tabletting and inhalation medicine, which has a monoclinic crystal structure.
4 Conclusions
Organic polycrystalline materials are a vital part of the fine chemicals industries and a firm understanding of the chemical basis behind powder bed structuring is of utmost importance to address processes of fluidization, flow and densification during production. X-ray CT–DCT studies combined with molecular modelling on polycrystalline hexamine have been used to understand the surface chemistry and particle–particle adhesion forces that dominate the powder structuring of hexamine. The predicted morphology ({110} facets, edges and different corners) was experimentally verified, along with identification of good and poor morphological quality across the bed and observation of inclusions. The chemical origins of crystallographic texture were seen to be preferential face to face alignments of crystals. Finally, the interactions between individual crystallites within fused agglomerates provided evidence for the different mechanisms of powder bed agglomeration.5 Experimental methodology
5.1 Materials and preparation
Hexamine (![[greater than or equal, slant]](https://www.rsc.org/images/entities/char_2a7e.gif) 98%) and anhydrous ethanol were purchased from Sigma-Aldrich. A suspension containing 0.0486 g g−1 of hexamine in ethanol was prepared in a 100 mL glass reactor AutoMATE multi-reactor system (HEL group). The hexamine suspension in ethanol was continuously stirred at a rate of ∼500 rpm. The solution was heated from room temperature (25 °C) to 50 °C at a heating rate of 1 °C min−1 and held at 50 °C for 15 minutes to ensure complete dissolution. The solution was then cooled to 5 °C at a slow cooling rate of 0.1 °C min−1 and kept constant at 5 °C until the onset of nucleation. Around one day after nucleation, the product crystals were isolated from the mother liquors using a vacuum pump VacMaster 10 system, the filtered samples were dried at room temperature under a fume hood.
98%) and anhydrous ethanol were purchased from Sigma-Aldrich. A suspension containing 0.0486 g g−1 of hexamine in ethanol was prepared in a 100 mL glass reactor AutoMATE multi-reactor system (HEL group). The hexamine suspension in ethanol was continuously stirred at a rate of ∼500 rpm. The solution was heated from room temperature (25 °C) to 50 °C at a heating rate of 1 °C min−1 and held at 50 °C for 15 minutes to ensure complete dissolution. The solution was then cooled to 5 °C at a slow cooling rate of 0.1 °C min−1 and kept constant at 5 °C until the onset of nucleation. Around one day after nucleation, the product crystals were isolated from the mother liquors using a vacuum pump VacMaster 10 system, the filtered samples were dried at room temperature under a fume hood.
The crystal structure HXMTAM10 from the Cambridge Structural Database66 was to represent this material because it was solved using neutron diffraction at low temperature.67 The unit cell parameters are a = b = c = 6.9274 Å and α = β = γ = 90°.
5.2 Optical microscopy
Suspended hexamine particles were harvested from the growth solution using a plastic pipette and dispersed onto a glass slide. Each slide was imaged using an Olympus BX51 light microscope with a UMPlanFl 5× objective lens to characterize the shapes of there crystallised hexamine crystals.5.3 X-ray CT & laboratory diffraction contrast tomography
The hexamine crystals were prepared for DCT analysis by placing them inside a sample mount68 made from a 2 cm length of 3 mm diameter polyimide tubing, as shown in Fig. S2a (ESI†). There was a delay of 2 years between the sample being prepared (i.e. preparation of hexamine crystals and loading into the sample mount) and scanned. During this time, the sample was stored at room temperature and uncontrolled ambient humidity.Scans were performed on a Zeiss Xradia Versa 520 X-ray microscope fitted with a LabDCT module. First, an attenuation X-ray CT scan was acquired at the top of the powder bed using the settings in Table 3, with one projection shown in Fig. S2b (ESI†). The data were reconstructed through a filtered back-projection algorithm21 implemented within the Zeiss XMReconstructor software to form a virtual 3D representation of the powder bed. The reconstructed voxel side length was 3.38 μm, and two cross-sectional slices through the virtual bed are shown in Fig. 3. The hexamine was separated from the air through an automated greyscale thresholding, and the particle solids fractions calculated following Turner et al.24
For the LabDCT characterisation, three diffraction datasets were acquired at the top of powder bed using the settings in Table 3, with ∼80 μm overlap of the illuminated part of the sample between each dataset. A 250 μm by 750 μm letterbox aperture was used to limit the number of diffraction spots, and a 2.5 mm by 2.5 mm beamstop was used to prevent transmitted X-rays being recorded on the detector. For all of the absorption and diffraction scans, the source to sample distance was 14.4 mm and the sample to detector distance was also 14.4 mm to obey the Laue focusing condition. Obeying the Laue condition focuses the diffracted beam onto the detector in line-shaped spots, increases the signal to noise ratio and substantially reduces overlap between different diffraction spots. One diffraction projection is shown in Fig. S2c (ESI†).
Finally, the LabDCT reconstructions were performed using each individual diffraction dataset together with the sub-volume of the reconstructed absorption data corresponding to the illuminated part of the powder-bed for that diffraction data. The reconstructions were performed using the proprietary GrainMapper3D™ software version 2.2 (Xnovo Technology ApS) with a reconstructed voxel side length of 6 μm, giving 3 DCT volumes with voxels of each identified crystal assigned a separate integer value. The reconstruction also gives metrics for each crystal such as the crystallographic orientation, and completeness which quantifies the confidence in the identified crystals. The completeness metric is calculated as the ratio of observed diffraction spots in the actual diffraction data to expected spots.33 Finally, the 3 individual DCT volumes were stitched together to form one DCT volume, with the total sub-volume of the powder bed analysed by LabDCT shown in Fig. 3.
Image analysis and visualisation was performed using a combination of the commercial software packages MATLAB® (Mathworks, USA) with the MTEX toolbox,54 Dream3D (BlueQuartz Software, USA) and Dragonfly Pro (Object Research Systems, Canada).
5.4 Computational modelling methodology
The intermolecular interaction energies in the hexamine crystal lattice were calculated and ranked by strength using the software package HABIT98 (University of Leeds, UK).69 A summation of these energy terms was used to calculate the lattice energy (Ecr) which was compared to the experimental sublimation enthalpy (ΔHsub) to ascertain whether the force field selected accurately estimated the intermolecular strengths between the molecules.For each of the morphologically important crystal surfaces (hkl), the lattice energy (Ecr) was partitioned, respecting the growth process on each surface, into contributions to the slice energy (Eslice) and attachment energy (Eatt) as indicated in eqn (1)
| Ecr = Ehklatt + Ehklslice. | (1) |
The attachment energies were scaled to determine relative growth rates at each surface and used to construct a Wulff plot to generate a prediction of the crystal habit according to the attachment energy model. This allows a prediction of the growth rates for the crystal surfaces Rhkl which are proportional to the attachment energy (eqn (2)).
| Rhkl ∼ Ehklatt | (2) |
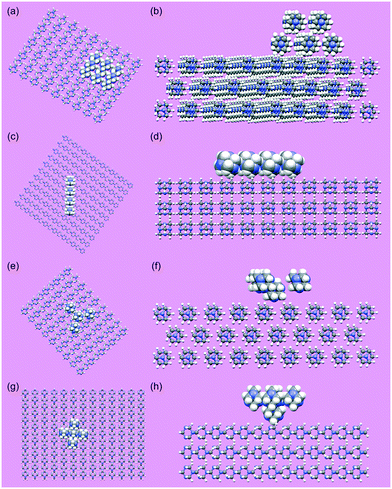
An approach employing grid-based, systematic searching was applied for molecular scale modelling of the distribution of interaction energies between a hexamine (110) crystal surface and (i) a (110) surface, (ii) a <111> edge, and (iii) corners (3-corner and 4-corner) of a second hexamine crystal. The modelling approach is based on scanning a cluster of molecules, which are representative of a surface, edge or corner of a crystal and, collectively, act as a probe, over a slab of molecules which represents the crystal surface of interest. In principle, the surface and probe may represent the same material, as was the case here, or different materials. Systematic grid-based searching has been applied to investigate solvent wetting of crystal surfaces in which a single molecule is used as the probe.15 Similarly, in a separate approach, a method has been developed to investigate molecule–molecule interaction energies between two crystal surfaces and produce energy maps.70
The method adopted here first requires the construction of the molecular probe that represents a crystal surface, edge or corner. A set of cartesian coordinates, describing the positions of the atoms in the cluster of molecules which becomes the probe, is generated from the crystal structure of hexamine. To represent the (110) surface, the probe consists of nine molecules having centres of coordinates located within, or at the corners, of a bounding box with a size defined by a single reticule of the (110) surface, and a perpendicular height which equals the inter-planar spacing d110. A common centre of coordinates is defined for the molecules of the probe cluster. This common centre of coordinates is employed to position the probe on the translation grid for the systematic search. One rigid-body rotation is allowed as a further degree of freedom in the search. The axis of rotation passes through the common centre of coordinates and is parallel to the reciprocal lattice plane normal for the (110) surface of hexamine. To represent an edge for form {110} of hexamine, the cartesian coordinates of four molecules were extracted. This was achieved by packing the interior of a polyhedron, representing the hexamine crystal habit, with molecules. After packing with molecules, an edge of the polyhedron was aligned parallel to the (110) surface slab and four molecules within the polyhedron most proximal to the surface slab were selected to create the cluster representing an edge. Similarly, to generate a molecular cluster representing a corner of a hexamine crystal, the polyhedron was placed with a corner terminating the lattice row [111] positioned closest to the (110) surface slab, and the direction [111] aligned parallel to the reciprocal lattice plane normal for surface (110). The four molecules most proximal to the surface slab were selected to represent the corner. Systematic searching of the interactions of these molecular-clusters, acting as probes, with the (110) surface of hexamine was performed and the interactions were ranked on energy.
Conflicts of interest
Some of the funding for the INFORM2020 project was provided by Carl Zeiss Microscopy, where two of the authors are employed. Xnovo Technology is a private corporation owned and financially supported by its shareholders. Some or all of the authors with Xnovo Technology affiliations may have a financial interest in the company.Acknowledgements
We kindly acknowledge James Carr and Berzah Yavuzyegit for technical assistance with LabDCT. This work is part of the INFORM2020 consortium, which is funded through EPSRC grant EP/N025075/1 “Molecules to manufacture: Processing and Formulation Engineering of Inhalable Nanoaggregates and Micro-particles”. Additional funding for INFORM2020 was provided by Carl Zeiss Microscopy. This work also builds upon research on morphological modelling supported by EPSRC grant EP/I028293/1 “HABIT – Crystal morphology from crystallographic and growth environment factors” and the Synthonic Engineering programme supported by Pfizer, Boeringer-Ingellheim, Novartis and Syngenta. PG acknowledges support from EP/M010619/1. Beamtime was kindly provided by the Henry Moseley X-ray Imaging Facility (HMXIF), which was established through EPSRC grants EP/F007906/1, EP/I02249X/1 and EP/F028431/1, and is now part of the National Research facility in X-ray CT funded through EPSRC grant EP/T02593X/1. HMXIF is also a part of the Henry Royce Institute for Advanced Materials, established through EPSRC grants EP/R00661X/1, EP/P025498/1 and EP/P025021/1.References
- A. G. Jones, Anal. Proc., 1993, 30, 456–457 RSC.
- E. T. C. Vogt and B. M. Weckhuysen, Chem. Soc. Rev., 2015, 44(20), 7342–7370 RSC.
- P. D. Jager, T. Bramante and P. E. Luner, J. Pharm. Sci., 2015, 104(11), 3804–3813 CrossRef CAS PubMed.
- Y. Zhou and J. Zhu, Chem. Eng. Sci., 2019, 207, 653–662 CrossRef CAS.
- M. Leane, et al. , Pharm. Dev. Technol., 2015, 20(1), 12–21 CrossRef CAS PubMed.
- S. Chattoraj and C. C. Sun, J. Pharm. Sci., 2018, 107(4), 968–974 CrossRef CAS PubMed.
- G. R. Desiraju, Angew. Chem., Int. Ed. Engl., 1995, 34, 2311–2327 CrossRef CAS.
- J. Pickering, R. B. Hammond, V. Ramachandran, M. Soufian and K. J. Roberts, in Engineering Crystallography: From Molecule to Crystal to Functional Form, Springer Netherlands, Dordrecht, 2017, pp. 155–176 Search PubMed.
- M. Bryant, I. Rosbottom, I. J. Bruno, R. Docherty, C. M. Edge, R. B. Hammond, R. Peeling, J. Pickering, K. J. Roberts and A. G. P. Maloney, Cryst. Growth Des., 2019, 19, 5258–5266 CrossRef CAS.
- R. B. Hammond, K. Pencheva and K. J. Roberts, Cryst. Growth Des., 2007, 7, 875–884 CrossRef CAS.
- R. B. Hammond, S. Jeck, C. Y. Ma, K. Pencheva, K. J. Roberts and T. Auffret, J. Pharm. Sci., 2009, 98, 4589–4602 CrossRef CAS PubMed.
- J. Y. Y. Heng, A. Bismarck and D. R. Williams, AAPS PharmSciTech, 2006, 7, E12–E20 CrossRef PubMed.
- T. T. H. Nguyen, R. B. Hammond, I. D. Styliari, D. Murnane and K. J. Roberts, CrystEngComm, 2020, 22, 3347–3360 RSC.
- S. R. Modi, A. K. R. Dantuluri, S. R. Perumalla, C. C. Sun and A. K. Bansal, Cryst. Growth Des., 2014, 14, 5283–5292 CrossRef CAS.
- I. Rosbottom, J. H. Pickering, B. Etbon, R. B. Hammond and K. J. Roberts, Phys. Chem. Chem. Phys., 2018, 20, 11622–11633 RSC.
- K. C. Pingali, T. Shinbrot, A. Cuitino, F. J. Muzzio, E. Garfunkel, Y. Lifshitz and A. B. Mann, Int. J. Pharm., 2012, 438, 184–190 CrossRef CAS PubMed.
- J. C. Hooton, M. D. Jones and R. Price, J. Pharm. Sci., 2006, 95, 1288–1297 CrossRef CAS PubMed.
- T. Mandal and M. D. Ward, J. Am. Chem. Soc., 2013, 135, 5525–5528 CrossRef CAS PubMed.
- S. R. Stock, Int. Mater. Rev., 1999, 44, 141–164 CrossRef CAS.
- S. R. Stock, Int. Mater. Rev., 2008, 53, 129–181 CrossRef CAS.
- L. A. Feldkamp, L. C. Davis and J. W. Kress, J. Opt. Soc. Am. A, 1984, 1, 612–619 CrossRef.
- F. J. S. Doerr and A. J. Florence, Int. J. Pharm.: X, 2020, 100041 CAS.
- P. Gajjar, I. D. Styliari, T. T. H. Nguyen, J. Carr, X. Chen, J. A. Elliott, R. B. Hammond, T. L. Burnett, K. Roberts, P. J. Withers and D. Murnane, Eur. J. Pharm. Biopharm., 2020, 151, 32–44 CrossRef CAS PubMed.
- T. D. Turner, P. Gajjar, I. S. Fragkopoulos, J. Carr, T. T. H. Nguyen, D. Hooper, F. Clarke, N. Dawson, P. J. Withers and K. J. Roberts, Cryst. Growth Des., 2020, 20, 4252–4263 CrossRef CAS.
- H. F. Poulsen, S. F. Nielsen, E. M. Lauridsen, S. Schmidt, R. M. Suter, U. Lienert, L. Margulies, T. Lorentzen and D. J. Jensen, J. Appl. Crystallogr., 2001, 34, 751–756 CrossRef CAS.
- B. C. Larson, W. Yang, G. E. Ice, J. D. Budai and J. Z. Tischler, Nature, 2002, 415, 887–890 CrossRef CAS PubMed.
- S. D. M. Jacques, K. Pile, P. Barnes, X. Lai, K. J. Roberts and R. A. Williams, Cryst. Growth Des., 2005, 5, 395–397 CrossRef CAS.
- K. Pile, X. Lai, S. D. M. Jacques, K. J. Roberts and P. Barnes, J. Cryst. Growth, 2006, 294, 41–45 CrossRef CAS.
- W. Ludwig, S. Schmidt, E. M. Lauridsen and H. F. Poulsen, J. Appl. Crystallogr., 2008, 41, 302–309 CrossRef CAS.
- G. Johnson, A. King, M. G. Honnicke, J. Marrow and W. Ludwig, J. Appl. Crystallogr., 2008, 41, 310–318 CrossRef CAS.
- W. Ludwig, P. Reischig, A. King, M. Herbig, E. M. Lauridsen, G. Johnson, T. J. Marrow and J. Y. Buffière, Rev. Sci. Instrum., 2009, 80, 033905 CrossRef CAS PubMed.
- P. Reischig, A. King, L. Nervo, N. Viganó, Y. Guilhem, W. J. Palenstijn, K. J. Batenburg, M. Preuss and W. Ludwig, J. Appl. Crystallogr., 2013, 46, 297–311 CrossRef CAS.
- F. Bachmann, H. Bale, N. Gueninchault, C. Holzner and E. M. Lauridsen, J. Appl. Crystallogr., 2019, 52, 643–651 CrossRef CAS PubMed.
- N. Viganò, A. Tanguy, S. Hallais, A. Dimanov, M. Bornert, K. J. Batenburg and W. Ludwig, Sci. Rep., 2016, 6, 20618 CrossRef PubMed.
- S. A. McDonald, C. Holzner, E. M. Lauridsen, P. Reischig, A. P. Merkle and P. J. Withers, Sci. Rep., 2017, 7, 5251 CrossRef CAS PubMed.
- J. Sun, Y. Zhang, A. Lyckegaard, F. Bachmann, E. M. Lauridsen and D. Juul Jensen, Scr. Mater., 2019, 163, 77–81 CrossRef CAS.
- R. Keinan, H. Bale, N. Gueninchault, E. M. Lauridsen and A. J. Shahani, Acta Mater., 2018, 148, 225–234 CrossRef CAS.
- M. J. Pankhurst, N. Gueninchault, M. Andrew and E. Hill, Mineral. Mag., 2019, 83, 705–711 CrossRef CAS.
- A. A. Shiryaev, F. V. Kaminsky, W. Ludwig, D. A. Zolotov, A. V. Buzmakov and S. V. Titkov, Geochem. Int., 2019, 57, 1015–1023 CrossRef CAS.
- D. R. Merrifield, V. Ramachandran, K. J. Roberts, W. Armour, D. Axford, M. Basham, T. Connolley, G. Evans, K. E. McAuley, R. L. Owen and J. Sandy, Meas. Sci. Technol., 2011, 22, 115703 CrossRef.
- S. N. Yusop, PhD thesis, The University of Leeds, 2014 Search PubMed.
- R. G. Dickinson and A. L. Raymond, J. Am. Chem. Soc., 1923, 45, 22–29 CrossRef CAS.
- N. Blažzević, D. Kolbah, B. Belin, V. Šunjić and F. Kajfež, Synthesis, 1979, 1979, 161–176 CrossRef.
- A. M. Kirillov, Coord. Chem. Rev., 2011, 255, 1603–1622 CrossRef CAS.
- R. J. Davey and A. Rütti, J. Cryst. Growth, 1976, 32, 221–226 CrossRef CAS.
- K. G. Denbigh and E. T. White, Chem. Eng. Sci., 1966, 21, 739–753 CrossRef CAS.
- R. J. Trepanier and M. A. Whitehead, Z. Naturforsch., A: Phys., Phys. Chem., Kosmophys., 1986, 41, 392–395 Search PubMed.
- R. Docherty, G. Clydesdale, K. J. Roberts and P. Bennema, J. Phys. D: Appl. Phys., 1991, 24, 89–99 CrossRef CAS.
- J. A. Dirksen and T. A. Ring, Chem. Eng. Sci., 1991, 46, 2389–2427 CrossRef CAS.
- S. Tsuzuki, H. Orita, K. Honda and M. Mikami, J. Phys. Chem. B, 2010, 114, 6799–6805 CrossRef CAS PubMed.
- S. J. Urwin, G. Levilain, I. Marziano, J. M. Merritt, I. Houson and J. H. Ter Horst, Org. Process Res. Dev., 2020, 24, 1443–1456 CrossRef CAS PubMed.
- E. T. White, PhD thesis, Imperial College London, 1964 Search PubMed.
- R. A. Duckett and A. R. Lang, J. Cryst. Growth, 1973, 18, 135–142 CrossRef CAS.
- G. Nolze and R. Hielscher, J. Appl. Crystallogr., 2016, 49, 1786–1802 CrossRef CAS.
- O. Engler and V. Randle, Introduction to Texture Analysis: Macrotexture, Microtexture, and Orientation Mapping, CRC Press, 2009 Search PubMed.
- A. Alamdari and F. Tabkhi, Chem. Eng. Process.: Process Intesif., 2004, 43, 803–810 CrossRef CAS.
- V. Chikhalia, R. T. Forbes, R. A. Storey and M. Ticehurst, Eur. J. Pharm. Sci., 2006, 27, 19–26 CrossRef CAS PubMed.
- W. Kaialy, A. Alhalaweh, S. P. Velaga and A. Nokhodchi, Int. J. Pharm., 2011, 421, 12–23 CrossRef CAS PubMed.
- G. Clydesdale, R. B. Hammond, V. Ramachandran, K. J. Roberts and P. Mougin, Mol. Cryst. Liq. Cryst., 2005, 440, 235–257 CrossRef CAS.
- R. J. Davey, S. L. M. Schroeder and J. H. Ter Horst, Angew. Chem., Int. Ed., 2013, 52, 2166–2179 CrossRef CAS PubMed.
- C. Ramírez-Aragón, J. Ordieres-Meré, F. Alba-Elías and A. González-Marcos, Materials, 2018, 11, 2341 CrossRef PubMed.
- B. El-Kassem, N. Salloum, T. Brinz, Y. Heider and B. Markert, Comput. Part. Mech., 2021, 8, 87–111 CrossRef.
- M. Brunsteiner, A. G. Jones, F. Pratola, S. L. Price and S. J. R. Simons, Cryst. Growth Des., 2005, 5, 3–16 CrossRef CAS.
- J. Sun, C. Holzner, H. Bale, M. Tomita, N. Gueninchault, F. Bachmann, E. Lauridsen, T. Inaguma and M. Kimura, ISIJ Int., 2020, 60, 528–533 CrossRef CAS.
- S. Datta and D. J. W. Grant, Nat. Rev. Drug Discovery, 2004, 3, 42–57 CrossRef CAS PubMed.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179 CrossRef CAS PubMed.
- S. P. Kampermann, T. M. Sabine, B. M. Craven and R. K. McMullan, Acta Crystallogr., Sect. A: Found. Crystallogr., 1995, 51, 489–497 CrossRef PubMed.
- P. Gajjar, I. D. Styliari, T. L. Burnett, X. Chen, J. A. Elliott, W. J. Ganley, R. Hammond, H. Nguyen, R. Price, K. Roberts, P. J. Withers and D. Murnane, Respiratory Drug Delivery Europe, 2019, vol. 2019, pp. 155–168 Search PubMed.
- G. Clydesdale, K. J. Roberts and R. Docherty, J. Cryst. Growth, 1996, 166, 78–83 CrossRef CAS.
- A. Moldovan, Interfacial Interactions of Faceted Organic Crystals - An in-silico study with Atomic Force Microscopy, PhD thesis, The University of Leeds, 2020 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ce01712d |
| This journal is © The Royal Society of Chemistry 2021 |