Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Impact of polymorphism on mechanical properties of molecular crystals: a study of p-amino and p-nitro benzoic acid with nanoindentation†
Benjamin P. A.
Gabriele
a,
Craig J.
Williams
b,
Matthias E.
Lauer
c,
Brian
Derby
 b and
Aurora J.
Cruz-Cabeza
b and
Aurora J.
Cruz-Cabeza
 *a
*a
aDepartment of Chemical Engineering and Analytical Science, University of Manchester, UK. E-mail: aurora.cruzcabeza@manchester.ac
bDepartment of Materials, University of Manchester, UK
cRoche Innovation Center Basel, Basel, Switzerland
First published on 4th March 2021
Abstract
We report on nanoindentation data for two pairs of polymorphic compounds of p-aminobenzoic acid (pABA) and p-nitrobenzoic acid (pNBA). Variations of 60% or higher are observed in both stiffness and hardness data between the two forms of each pair. We interpret these observations through variations of periodic bond chains (PBCs), i.e. variations in continuous intermolecular interactions strength and nature. Aided with hardness data of polymorphs from the literature, we then further assess how PBCs can be used to assess and compare mechanical properties of polymorphs. We define a new parameter, s-PBC, which quantifies the strongest PBC interaction that needs breaking so as to allow a switch of the PBC network from 3D to 2D/1D. We found that higher values of s-PBCs, normalised by the mean molecular volumes, usually led to higher values of mechanical properties. Although not infallible, this trend seemed to hold well when comparing polymorphs of a given compound, but not so much when comparing across different compounds.
Mechanical properties impact the manufacturing routes of molecular materials since they strongly determine the processing steps required.1–3 The mechanical properties of solids are intimately related to their constituent molecules and chemistry as well as their short and long-range arrangements in the solid state. Notably, the ability of many molecules to crystallise into different crystal structures, known as polymorphs,4 is well known as well as the consequences of polymorphism in a material's physicochemical properties5–7 and intellectual property (IP).8 Due to the strong economic impact of polymorphism on IP, as well as the fact that variations of physical properties across polymorphic forms can hinder or enable manufacturing (potentially leading to substantial money and time loss or gained), increasing efforts have been directed in the past decades towards developing computational crystal structure and polymorph prediction methods.9,10 Beyond the prediction of structure, much work has been focused in recent years on achieving a qualitative prediction of the mechanical behaviour of crystalline molecular crystals such as shearing, bending or brittleness11 – sometimes between polymorphs.12 Further work is needed, however, on quantitative predictions of mechanical properties. To achieve this, we still need to accurately measure stiffness and hardness of a significant number of molecular crystals and their polymorphs so as to provide a significant dataset against which theoretical models can be compared. Recent developments in the area of nanoindentation13,14 offer opportunities to remedy this.
Following a first study of nanoindentation of a series of p-derivatives of benzoic acid crystals,15 we investigate here the impact of polymorphism on mechanical properties of p-nitrobenzoic acid (pNBA) and p-aminobenzoic acid (pABA). Both compounds crystallise into various polymorphs, including forms I (CSD refcode: NBZOAC03 (ref. 16)) and II (NBZOAC14 (ref. 17)) for pNBA and forms α (AMBNAC06 (ref. 18)) and β (AMBNAC04 (ref. 19)) for pABA. Both pairs of polymorphs are related enantiotropically with transition temperatures of 51 °C (ref. 20) for pNBA (pNBA-I being the low temperature form) and 13.8 °C for pABA (β-pABA being the low temperature form).21,22pNBA crystallises readily into its form I at room temperature and into its form II at temperatures above 51 °C.20 Both polymorphs of pABA and pNBA, once crystallised and removed from their crystallisation solution, are also reported to not convert to another form at room temperature over time.20,23pABA crystallises into its α-form from all temperatures and most solvents24 except for water at low supersaturation levels from which β-pABA is crystallised. Using mechanical data derived from nanoindentation experiments on these two pairs of polymorphs, we rationalise the observed variations in stiffness and hardness between polymorphs from observed differences in intermolecular interactions and crystal packing, and we compare the observed variations with those reported for other polymorphic systems.
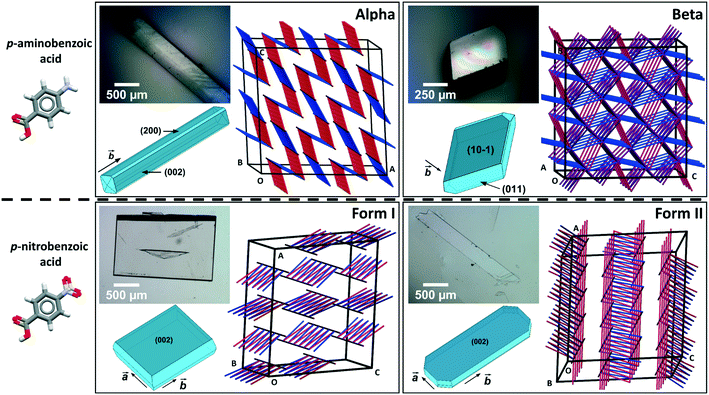
Comparing mechanical data across different polymorphs can be challenging because mechanical properties of single crystals are highly anisotropic thus they depend on the crystal orientation (the hkl values of the faces indented).25 In our previous study of mechanical properties of benzoic acid derivatives measured by nanoindentation, we were able to compare stiffness and hardness data across different compounds because they all crystallised with common crystal packing features (consisting of hydrogen bonded dimers and infinite aromatic stacks) and they were indented along equivalent crystal directions.15 Since crystal structure and packing change in different polymorphs, it is not obvious which crystal orientations, if any, could enable the most relevant comparison of mechanical properties between different forms. In pABA, for example, the α-form consists of continuous aromatic stacking interactions along the b-axis and discrete, 0D R22(8) hydrogen bonded carboxylic acid dimers. Instead, the β-form is dominated by continuous hydrogen bonds between carboxylic and amine groups and 0D inverted aromatic stacked dimers. In pNBA, forms I and II have some similarities, including discrete R22(8) carboxylic acid dimers and continuous aromatic stacking. Furthermore, the dominant crystal face for both pNBA forms I and II renders the aromatic stacking interactions orthogonal to the indentation direction (i.e. parallel to the indenter stage). pNBA forms I and II in fact share a common layer of molecules whereby the carboxylic acid dimers and aromatic stacks are arranged identically (presented in ESI†). These layers, however, pack in different ways by means of different symmetry operations (form I crystallises in A2/a whilst form I P21/c). Micrographs of single crystals of pABA and pNBA polymorphs with their respective face indexing are shown in Fig. 1 (data for α-pABA and pNBA-I were retrieved from a previous study).15 We note that two faces are highlighted for α-pABA in Fig. 1, (200) and (002), because they are crystallographically and structurally identical and thus they cannot be differentiated. Thus, on indenting different crystals of α-pABA, some would have been indented on the (200) face and others on the (002) but no differences are observed in the mechanical behaviour because of the structural identity between these faces.
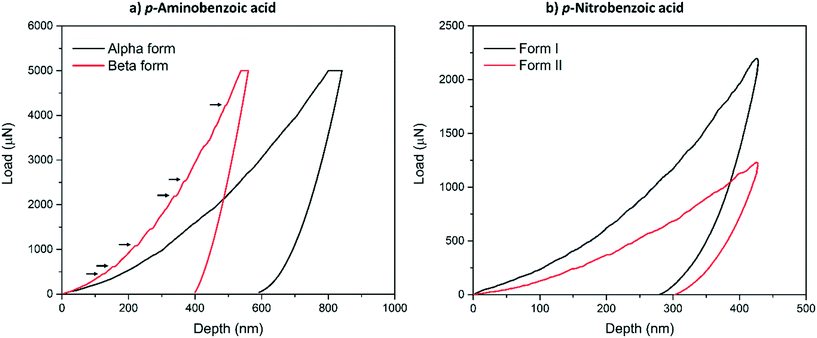
Typical load-depth (P–d) curves measured with nanoindentation for the α-pABA and β-pABA are presented in Fig. 2a and for pNBA-I and pNBA-II in Fig. 2b. For pABA, the experiments were done in load-controlled mode. At maximum load (for both forms, PMAX = 5000 μN), the final depth of penetration reached for β-pABA was just 400 nm whilst it was 600 nm for α-pABA. Many sudden bursts (pop-ins) occurred in the loading section of the P–d curve on β-pABA (Fig. 2a, red curve, black arrows) whilst those were hardly distinguishable in α-pABA (only very light discontinuities were observed on loading). For pNBA, the experiments were done in displacement-controlled mode. At maximum depth of penetration, hMAX, the maximum load required for form I was twice higher than that of form II. As in α-pABA, the loading section of form I pNBA has very light discontinuities but cannot be designated as real “bursts”. In form II pNBA, however, both very small pop-ins and some discontinuities are observed. Of particular interest, the unloading sections of all curves in Fig. 2 are “pop-out” free. “Pop-out” events are sudden burst towards lower penetration depth upon indentation pressure release and are characteristic of pressure-induced polymorphic transformation.26,27 Here, their absence are suggesting that no polymorphic transformation occurred upon pressure released, which may suggest that no polymorphic transformation occurred at all upon indentation and that E and H values extracted correspond to the true values of the polymorphs.
Table 1 shows the derived elastic modulus (using a Poisson ratio of 0.3 for pABA and pNBA, reported as a typical value for molecular single crystals25) and hardness data obtained from indenting the polymorphs of these two systems together with other data on polymorphs retrieved from the literature. In pABA, the elastic modulus E and the hardness H are ca. 60% and 130% higher respectively for β-pABA than for α-pABA. In pNBA, E and H are ca. 60% and 80% higher respectively for form I than for form II. The periodic bond chains (PBCs) networks for these crystal structures are shown Fig. 1. PBCs illustrate the network structure of the intermolecular interactions in the crystals. Using a PBC cut-off value of −13.1 kJ mol−1, pNBA-I has a 1D PBC network, pNBA-II and α-pABA have 2D PBC networks whilst β-pABA has a 3D PBC network. The crystal structure of β-pABA is dominated by an infinite head to tail (between the carboxylic acid and the amino group) hydrogen bonds (HBs) which further assemble into a 3D-HB PBC network. In β-pABA, each molecule is involved in 4 HBs. The 3D PBCs network based on strong HBs (−19 kJ mol−1 is the weakest interaction in the β-pABA 3D network) leads to higher mechanical properties for β-pABA compared to the other systems. We notice that the loading section of the load-depth trace for β-pABA has marked pop-ins in the load-depth curve. These pop-ins could be associated with possible fracturing, although none was observed at the surface of β-pABA single crystals upon indentation, as shown on AFM images in Fig. 3. Images of indents on the four systems revealed crack-free indents (see ESI†). In summary for pABA, β-pABA with 3D PBCs is stiffer and harder than α-pABA with 2D PBCs. For pNBA, form I with 1D PBCs is stiffer and harder than form II, however with 2D PBCs.
| Systema | SG | Indent. face | CSD refcode | PBC dim. | s-PBC (kJ mol−1) | Nature of s-PBC | (hkl) 2D layer, rugosity (Å) | Easiest shear directionb | E (±stdv) (GPa) | H (±stdv) (MPa) | E ratioc | H ratioc |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a STZ = sulfathiazole; CCM = curcumin; FlA = fluorinated amide; FAM = famotidine; FEB = febuxostat; FEL = felodipine. b This was estimated visually. Since many of the 2D layers are corrugated, shear along the direction of the ridges would be easier than against the ridges (see Bryant, Maloney and Sykes). The symmetry operation applied upon shear of one molecular position along this direction is also given. The symmetry relationships are: t = translation, I = inversion, g = glide plane, s = screw and z′ = no symmetry due to Z′ > 1. c Highest over lowest. d This work. | ||||||||||||
| pABA-α | P21/n | (200) | AMBNAC06 | 2D | 13.8 | NH⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C |
1D, −0.4 | b-axis [t] | 7.17 ± 0.25 | 221 ± 17 | 1.6 | 2.3 |
| pABA-βd | P21/n | (10−1) | AMBNAC04 | 3D | 19.8 | NH⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) =C =C |
(010), −1.0 | a-axis [t] | 11.38 ± 0.32 | 512 ± 25 | ||
| pNBA-Id | A2/a | (002) | NBZOAC03 | 1D | 9.8 | Other | (001), 0.0 | b-axis [t] | 9.19 ± 0.48 | 322 ± 22 | 1.6 | 1.8 |
| pNBA-II | P21/c | (002) | NBZOAC14 | 2D | 9.8 | Other | (001), 0.4 | a-axis [t] | 5.88 ± 0.25 | 182 ± 10 | ||
| STZ-I28 | P21/n | (100) | SUTHAZ28 | 3D | 22.8 | NH⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S S |
(001), −2.9 | a-axis [i] | 10.01 | 356 | 2.0 | 3.0 |
| STZ-II28 | P21/c | (100) | SUTHAZ24 | 3D | 31.0 | NH⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S S |
(100), 0.2 | b-axis [t] | 20.44 | 1080 | ||
| STZ-III28 | P21/c | (100) | SUTHAZ25 | 3D | 30.4 | NH⋯N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
(100), 0.2 | b-axis [z′] | 16.42 | 704 | ||
| STZ-IV28 | P21/n | (10−1) | SUTHAZ26 | 3D | 17.5 | NH⋯N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
(10−1), 0.1 | b-axis [s] | 17.31 | 881 | ||
| CCM-I28 | P2/n | (001) | BINMEQ02 | 3D | 26.1 | Other | (101), −0.2 | b-axis [i] | 11.15 | 432 | 2.0 | 1.3 |
| CCM-II28 | Pca21 | (100) | BINMEQ08 | 3D | 22.0 | OH⋯–O– | (100), −3.8 | b-axis [z′t] | 5.68 | 341 | ||
| CCM-III28 | Pbca | (001) | BINMEQ07 | 3D | 21.8 | OH⋯–O– | (001), −3.5 | b-axis [g] | 5.60 | 330 | ||
| FlA-I29 | P21 | (001) | VAPMEH | 2D | 7.0 | Aromatic | (001), 0.6 | b-axis [t] | 8.36 | 347 | 1.4 | 2.0 |
| FlA-II29 |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
(001) | VAPMEH01 | 2D | 6.1 | Aromatic | (001), 0.5 | a-axis [t] | 6.17 | 172 | ||
| FAM-A30 | P21/c | (100) | FOGVIG04 | 3D | 27.1 | NH⋯N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
(001), −1.9 | b-axis [t] | 22.6 | 1580 | 1.2 | 1.9 |
| (001) | 20.1 | 1330 | ||||||||||
| FAM-B30 | P21/n | (−101) | FOGVIG05 | 3D | 16.9 | Other | (−101), −0.2 | b-axis [t] | 19.5 | 840 | ||
| FEB-Q31 | P21/c | NR | HIQQAB | 3D | 24.9 | Other | (010), −2.2 | a-axis [t] | 2.5 | 214 | 1.8 | 1.4 |
| FEB-H1 (ref. 31) |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
NR | HIQQAB02 | 3D | 20.8 | Other | (010), −0.6 | a-axis [z′] | 4.5 | 310 | ||
| FEL-I32 | P21/c | (100) | DONTIJ | 3D | 32.7 | NH⋯O | 1D, −0.5 | a-axis [t] | 12.8 | 553 | 2.1 | 2.2 |
| FEL-II32 | C2/c | (100) | DONTIJ04 | 3D | 26.8 | Other | (001), −0.4 | b-axis [i] | 6.2 | 260 | ||
| FEL-III32 | P21/n | (10−1) | DONTIJ02 | 3D | 26.0 | Other | (101), −1.1 | b-axis [t] | 10.5 | 451 | ||
 | ||
| Fig. 3 Height images (8 μm scan size) of indents made on a single crystal of a) α-pABA and b) β-pABA, acquired using atomic force microscopy (AFM) in PeakForce QNM mode in air. | ||
Table 1 collects E and H data for our polymorphs of pABA and pNBA as well as for sulfathiazole28 (STZ), curcumin28 (CCM), a fluorinated amide29 (FIA), famotidine30 (FAM), febuxostat31 (FEB) and felodipine32 (FEL) polymorphs reported by other groups (all measured by nanoindentation with a Berkovich tip). Table 1 also summarises on the PBC dimensionality of all those crystal structures (using a cut-off value of −13.1 kJ mol−1) as well as the PBC value switching the networks from 3D to 2D/1D (s-PBC), the nature of the s-PBC interaction, the (hkl) of the strongest 2D plane with its rugosity, and the direction of easiest shear for all those systems. We note that the s-PBC is the PBC interaction that needs breaking so as to allow a switch of the PBC network from 3D to 2D or 1D network. The value is given as positive since the interaction needs breaking. We explore this value here since once this s-PBC is broken this would allow for some slip systems. Thus, less stabilising s-PBCs will be easier to break and give rise to slip planes, thus this may be related to softer material responses. Additionally, the strongest 2D layer remaining after breaking the s-PBC is identified with its (hkl) value and its rugosity calculated using the Bryant, Maloney and Sykes method.33
Two main observations can be drawn from the data in Table 1. First, there is a tendency for hard materials to have 3D PBCs and higher absolute values of s-PBCs. A molecular level identification of these s-PBC (Table 1) shows that PBCs involving hydrogen bond interactions are usually stronger in nature than s-PBC involving other type of van der Waals dominated interactions or aromatic interactions. However, when molecules are larger (i.e. FEL), other type of interactions may become as important as hydrogen bonds. Usually, across a family of polymorphs, s-PBC tend to be of a similar nature though not always. Second, although we observed this trend for most of the compounds in the table, still some polymorphs may not obey this trend, such as FEB or STZ-IV. These correlations are complex since there are many plausible mechanisms of plastic deformation which would affect the resulting hardness of the material (i.e. anisotropy, plasticity due to impurity or imperfection profile, or plastic deformation initiated from the smoothest plane instead of the weakest).
Whilst some trends in stiffness and hardness may be derived across isomechanical groups of crystals with similar packings and interactions (for example between E and melting points15,34 or lattice energies per unit of volume and hardness35), such correlations may be harder to achieve for polymorphic structures since the crystal packings can be very different. In previous studies of nanoindentation on polymorphs (including those in Table 1), it has been shown that there is a large variation in mechanical properties between polymorphs. The ratio of E and H in polymorphs can lie somewhere between 1.2–2.0 for E and 1.3–3.0 for H. These large variations cannot match the small differences in melting points or lattice energies (see ESI†) since these are both very similar in polymorphs. First principle simulations, however, have been promisingly used for the direct computation of stiffness matrices for various polymorphic systems.36–38 Prediction of hardness is a much more complex exercise.
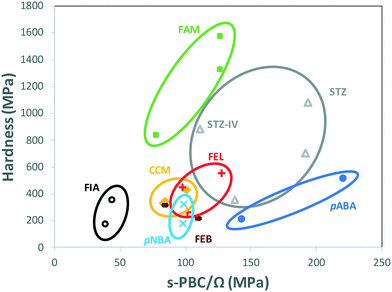
When comparing data of polymorphs within individual systems in Table 1, rather than comparing all data altogether, a clear trend appears. Fig. 4 shows the hardness of every system in Table 1 as a function of their s-PBC normalised by their mean molecular volume Ω. Values for polymorphs of different compounds are circled separately. For all systems but one (FEB) and mostly all polymorphs except for STZ-IV, there is a clear tendency for higher values of nanoindentation hardness to lead to higher values of s-PBC density. This is somewhat expected because higher values of s-PBC mean stronger 3D-networks with no easy slip-system and thus harder materials. The s-PBC model, however, is a very simple model based on PBCs also known as energy frameworks.39 The novelty here is that the identification of the s-PBC allows for a quantification of the slip resistance. We note that for systems where correlations fail, the 2D layers may have different degrees of corrugation or the shear direction may require of different symmetry operations. The easiest shear direction was assumed as the direction of propagation of ridges for corrugated layers. Thus, a highly corrugated layer may be hard to shear against the corrugation but can be easily sheared along the propagation of ridges and valleys.33 Here, the symmetry is important. Shear along a direction related by translation may result in the breaking and reforming of interactions as the molecules shear (slip). Shear along a direction related by other symmetry operations, however, may result in molecules occupying a lattice site with the wrong orientation which in turn may cause strains and repulsions and perhaps even cracks or brittle behaviour. We note that the systems that tend to fail the correlations (FEB and STZ-IV) do have differing layer rugosities and differing symmetry operations along the easiest shear directions.
This finding is encouraging since the calculation of s-PBC is straight forward thus would provide a qualitative assessment of which polymorph would be expected to be harder. Deriving a quantitative tool, however, is much more challenging. The data spreads differently in Fig. 4 for different systems. For example, values of hardness for FIA and pABA range from 172 to 512 MPa and are found respectively at the lowest and the highest values of s-PBC/Ω. These observations should be taken carefully since there is still a lack of data available in the literature of single-component polymorphs to establish high quality, qualitative (and quantitative) predictions of mechanical properties of polymorphs.
In conclusion, we have reported here on mechanical properties measured by nanoindentation on two polymorphic compounds, pABA and pNBA. We observed strong variations in E and H between polymorphic forms, in particular for pABA which sees an increase of a factor of 2.3 between the hardness of its α and β forms. This particular variation can be quickly assessed by means of variations between s-PBCs of the forms. Using these new data together with previous literature data on hardness of polymorphs, we attempted to establish trends among mechanical properties. We found that hardness data can be, in some of these cases, qualitatively estimated for polymorphs of individual compounds using s-PBC/Ω. This is encouraging since this simple method can be used for the qualitative prediction of relative hardness of polymorphs in, say, a computer-generated polymorphic landscape. However, there is a limited amount of data available on polymorphs of molecular compounds thus further experimental and computational studies are required to validate these trends. The roots of this model lie in the well-studied energy frameworks39 which has been used by others to understand mechanical properties of different crystals forms39 and also polymorphs:40 s-PBC is just the interaction limit that turns the energy framework from 3D to 2D/1D. This is indeed a very simple model and many aspects of the system are not taken into consideration including molecular flexibility41 and its impact in mechanical behaviour, impact of temperature42,43 (calculations are done at 0 K) or interlocking of the plausible slip planes.33 We see this model as a qualitative utility which should be of course taken with caution since the origin of the hardness of materials is indeed very complex.
Experimental section
Single crystals of pNBA (>98%, Fluka Analytical) forms I and II were produced by the slow evaporation of a saturated isopropanol (puriss. >99.5%, Merck) solution at RT and an acetonitrile (>99.9%, HPLC grade, Fisher Chemical) solution at 70 °C respectively. Crystals of α-pABA were grown from slow cooling crystallisation experiments of supersaturated acetonitrile solutions (50 to 25 °C, −1 °C h−1, supersaturation ratio S = 1.6). Large crystals of β-pABA were obtained by seeding a slightly saturated aqueous solution with ∼100 μm β-pABA seeds. The solution was left to evaporate for 5–10 days for the seeds to grow and reach a size of ca. 0.5–1 mm. Crystals were viewed under crossed polarised light (Axioplan 2 microscope, Zeiss, Jena, Germany) and only single crystals were retained whilst twinned crystals were discarded. Representative single crystals were mounted on a goniometer on a single crystal X-ray diffractometer (XCalibur-2, Rigaku Oxford Diffraction, Tokyo, Japan) with a MoKα X-ray source (λ = 0.71073 Å), and 360 successive images were taken of the crystals while rotating it. X-ray diffraction measurements were carried out, and using the software CrysAlisPro44 (version 171.40.14d, Rigaku Oxford Diffraction), the unit cell parameters were verified to match those in the crystals' respective CSD refcode (see introduction) and face indexing was carried out, attributing their respective Miller indices to the different faces of the crystals studied.Nanoindentation experiments were carried out on 7 to 10 single crystals per polymorph studied. Crystals were mounted only if their crystal habit clearly matched that assessed via face indexing and indented only if their surface tilt was lower than 3%. On each crystal, 9 indents were carried out using a Hysitron Ti950 Triboindenter (Bruker Nanomechanical Test Instruments, Minneapolis, USA) with a diamond Berkovich tip at a constant temperature of 23.1 ± 0.5 °C. Reduced elastic modulus and hardness data were extracted using the unloading section of the load-depth curves as described in ISO 14577.45 Indents were first carried out at various loads or depths of penetration to determine the minimum load or depths at which minimal variation in the data was observed, as described in a previous study.14 Indents on pNBA crystals (both forms) were carried out in displacement-control mode, with a 5 second loading, a 2 second holding at hMAX = 425 nm, and a 5 second unloading LF sections. For pABA, indents were carried out in load-control mode, with 5 seconds used for loading, holding and unloading, with PMAX = 5 mN. The distance between indents was 40 μm.
Periodic bond chains (PBCs) were computed from the crystal structures retrieved from the CSD using Material Studio 2019 (ref. 46) (Dassault Systèmes, BIOVIA) with the COMPASSII forcefield (and its atomic charges). The cut-off value of the PBC was increased progressively until the structure went from a 3D to a 2D/1D structure. This reveals the s-PBC value. Crystal structures were geometry optimised by relaxing all atomic positions in the unit cell while allowing for unit cell parameters to optimise prior to PBC calculations.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank the University of Manchester and Hoffmann-La Roche for financial support. This work was supported by the Henry Royce Institute for Advanced Materials, funded through EPSRC grants EP/S009493/1, EP/R00661X/1, EP/P025021/1, and EP/P025498/1.References
- C. C. Sun and H. Hou, Improving Mechanical Properties of Caffeine and Methyl Gallate Crystals by Cocrystallization, Cryst. Growth Des., 2008, 8, 1575–1579 CrossRef CAS.
- S. Karki, T. Friščić, L. Fábián, P. R. Laity, G. M. Day and W. Jones, Improving Mechanical Properties of Crystalline Solids by Cocrystal Formation: New Compressible Forms of Paracetamol, Adv. Mater., 2009, 21, 3905–3909 CrossRef CAS.
- P. P. Bag, M. Chen, C. C. Sun and C. M. Reddy, Direct Correlation among Crystal Structure, Mechanical Behaviour and Tabletability in a Trimorphic Molecular Compound, CrystEngComm, 2012, 14, 3865–3867 RSC.
- J. Haleblian and W. McCrone, Pharmaceutical Applications of Polymorphism, J. Pharm. Sci., 1969, 911–929 CrossRef CAS PubMed.
- R. J. Roberts and R. C. Rowe, Influence of Polymorphism on the Young's Modulus and Yield Stress of Carbmazepine Sulfathiazole and Sulfanilamide, Int. J. Pharm., 1996, 129, 79–94 CrossRef CAS.
- D. Hasa, M. Pastore, M. Arhangelskis, B. Gabriele, A. J. Cruz-Cabeza, G. S. Rauber, A. D. Bond and W. Jones, On the Kinetics of Solvate Formation through Mechanochemistry, CrystEngComm, 2019, 21, 2097–2104 RSC.
- Y. Liu, B. Gabriele, R. J. Davey and A. J. Cruz-Cabeza, Concerning Elusive Crystal Forms: The Case of Paracetamol, J. Am. Chem. Soc., 2020, 142, 6682–6689 CrossRef CAS PubMed.
- J. Bernstein, Polymorphism - A Perspective, Cryst. Growth Des., 2011, 11, 632–650 CrossRef CAS.
- S. L. Price, D. E. Braun and S. M. Reutzel-Edens, Can Computed Crystal Energy Landscapes Help Understand Pharmaceutical Solids?, Chem. Commun., 2016, 7065–7077 RSC.
- M. R. Ward, S. Younis, A. J. Cruz-Cabeza, C. L. Bull, N. P. Funnell and I. D. H. Oswald, Discovery and Recovery of Delta P-Aminobenzoic Acid, CrystEngComm, 2019, 21, 2058–2066 RSC.
- C. M. Reddy, G. Rama Krishna and S. Ghosh, Mechanical Properties of Molecular Crystals - Applications to Crystal Engineering, CrystEngComm, 2010, 12, 2296–2314 RSC.
- S. Saha and G. R. Desiraju, Trimorphs of 4-Bromophenyl 4-Bromobenzoate. Elastic, Brittle, Plastic, Chem. Commun., 2018, 54, 6348–6351 RSC.
- U. Ramamurty and J. I. Jang, Nanoindentation for Probing the Mechanical Behavior of Molecular Crystals-a Review of the Technique and How to Use It, CrystEngComm, 2014, 16, 12–23 RSC.
- B. P. A. Gabriele, C. J. Williams, M. E. Lauer, B. Derby and A. J. Cruz-Cabeza, Nanoindentation of Molecular Crystals: Lessons Learned from Aspirin, Cryst. Growth Des., 2020, 20, 5956–5966 CrossRef CAS PubMed.
- B. P. A. Gabriele, C. J. Williams, M. E. Lauer, B. Derby and A. J. Cruz-Cabeza, Isomechanical Groups in Molecular Crystals and Role of Aromatic Interactions, Cryst. Growth Des., 2020, 20, 7516–7525 CrossRef CAS.
- M. Colapietro and A. Domenicano, Structural Studies of Benzene Derivatives. II. Refinement of the Crystal Structure of p-Nitrobenzoic Acid, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1977, 33, 2240–2243 CrossRef.
- M. E. Light, CCDC 1476879. CSD Commun., 2016.
- S. Athimoolam and S. Natarajan, 4-Carboxy-Anilinium (2R,3R)-Tartrate and a Redetermination of the α-Polymorph of 4-Amino-Benzoic Acid, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2007, 63, 514–517 CrossRef PubMed.
- S. Gracin and A. Fischer, Redetermination of the β-Polymorph of p-Aminobenzoic Acid, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2005, 61, o1242–o1244 CrossRef CAS.
- Binti, S. of L. S. and N. in B. A. D. S. and S. Sachithananthan, Studies of Local Structure and Nucleation in Benzoic Acid Derivative Systems, 2017 Search PubMed.
- H. Hao, M. Barrett, Y. Hu, W. Su, S. Ferguson, B. Wood and B. Glennon, The Use of in Situ Tools to Monitor the Enantiotropic Transformation of P-Aminobenzoic Acid Polymorphs, Org. Process Res. Dev., 2012, 16, 35–41 CrossRef CAS.
- R. A. Sullivan, R. J. Davey, G. Sadiq, G. Dent, K. R. Back, J. H. Ter Horst, D. Toroz and R. B. Hammond, Revealing the Roles of Desolvation and Molecular Self-Assembly in Crystal Nucleation from Solution: Benzoic and p -Aminobenzoic Acids, Cryst. Growth Des., 2014, 14, 2689–2696 CrossRef CAS.
- A. J. Cruz-Cabeza, R. J. Davey, I. D. H. Oswald, M. R. Ward and I. J. Sugden, Polymorphism in P-Aminobenzoic Acid, CrystEngComm, 2019, 21, 2034–2042 RSC.
- S. Gracin and Å. C. Rasmuson, Polymorphism and Crystallization of P-Aminobenzoic Acid, Cryst. Growth Des., 2004, 4, 1013–1023 CrossRef CAS.
- I. Lubomirsky, I. Azuri, E. Meirzadeh, D. Ehre, S. R. Cohen, A. M. Rappe, M. Lahav and L. Kronik, Unusually Large Young's Moduli of Amino Acid Molecular Crystals, Angew. Chem., Int. Ed., 2015, 54, 13566–13570 CrossRef PubMed.
- H. Park, H. Nie, A. Dhiman, V. Tomar and Q. T. Zhou, Understanding Dynamics of Polymorphic Conversion during the Tableting Process Using In Situ Mechanical Raman Spectroscopy, Mol. Pharmaceutics, 2020, 17(8), 3043–3052 CrossRef CAS PubMed.
- A. Fischer-Cripps, Nanoindentation Testing, in Nanoindentation, 2011, pp. 21–38 Search PubMed.
- M. K. Mishra, P. Sanphui, U. Ramamurty and G. R. Desiraju, Solubility-Hardness Correlation in Molecular Crystals: Curcumin and Sulfathiazole Polymorphs, Cryst. Growth Des., 2014, 14, 3054–3061 CrossRef CAS.
- P. K. Mondal, M. S. R. N. Kiran, U. Ramamurty and D. Chopra, Quantitative Investigation of the Structural, Thermal, and Mechanical Properties of Polymorphs of a Fluorinated Amide, Chem. – Eur. J., 2017, 23, 1023–1027 CrossRef CAS PubMed.
- M. Egart, B. Janković, N. Lah, I. Ilić and S. Srčič, Nanomechanical Properties of Selected Single Pharmaceutical Crystals as a Predictor of Their Bulk Behaviour, Pharm. Res., 2015, 32, 469–481 CrossRef CAS PubMed.
- J. A. Yadav, K. S. Khomane, S. R. Modi, B. Ugale, R. N. Yadav, C. M. Nagaraja, N. Kumar and A. K. Bansal, Correlating Single Crystal Structure, Nanomechanical, and Bulk Compaction Behavior of Febuxostat Polymorphs, Mol. Pharmaceutics, 2017, 14, 866–874 CrossRef CAS PubMed.
- M. K. Mishra, G. R. Desiraju, U. Ramamurty and A. D. Bond, Studying Microstructure in Molecular Crystals with Nanoindentation: Intergrowth Polymorphism in Felodipine, Angew. Chem., Int. Ed., 2014, 53, 13102–13105 CrossRef CAS PubMed.
- M. J. Bryant, A. G. P. Maloney and R. A. Sykes, Predicting Mechanical Properties of Crystalline Materials through Topological Analysis, CrystEngComm, 2018, 20, 2698–2704 RSC.
- M. K. Mishra, S. Varughese, U. Ramamurty and G. R. Desiraju, Odd-Even Effect in the Elastic Modulii of α,ω- Alkanedicarboxylic Acids, J. Am. Chem. Soc., 2013, 135, 8121–8124 CrossRef CAS PubMed.
- H. J. Frost and M. F. Ashby, Scaling Laws and Isomechanical Groups, in Deformation-mechanism Maps: The Plasticity and Creep of Metals and Ceramics, 1982, pp. 133–140 Search PubMed.
- R. J. Roberts, R. S. Payne and R. C. Rowe, Mechanical Property Predictions for Polymorphs of Sulphathiazole and Carbamazepine, Eur. J. Pharm. Sci., 2000, 9, 277–283 CrossRef CAS PubMed.
- T. Beyer, G. M. Day and S. L. Price, The Prediction, Morphology, and Mechanical Properties of the Polymorphs of Paracetamol, J. Am. Chem. Soc., 2001, 123, 5086–5094 CrossRef CAS PubMed.
- A. M. Reilly and A. Tkatchenko, Role of Dispersion Interactions in the Polymorphism and Entropic Stabilization of the Aspirin Crystal, Phys. Rev. Lett., 2014, 113, 1–5 CrossRef.
- M. J. Turner, S. P. Thomas, M. W. Shi, D. Jayatilaka and M. A. Spackman, Energy Frameworks: Insights into Interaction Anisotropy and the Mechanical Properties of Molecular Crystals, Chem. Commun., 2015, 51, 3735–3738 RSC.
- C. Wang and C. Sun, Identifying Slip Planes in Organic Polymorphs by Combined Energy Framework Calculations and Topological Analysis, Cryst. Growth Des., 2018, 18(3), 1909–1916 CrossRef CAS.
- B. P. A. Gabriele, C. J. Williams, M. E. Lauer, B. Derby and A. J. Cruz-Cabeza, Probing Anisotropic Mechanical Behaviour in Carbamazepine Form III, CrystEngComm, 2021 10.1039/D0CE01659D.
- R. M. Mohamed, M. K. Mishra, L. M. Al-Harbi, M. S. Al-Ghamdi, A. M. Asiri, C. M. Reddy and U. Ramamurty, Temperature Dependence of Mechanical Properties in Molecular Crystals, Cryst. Growth Des., 2015, 15, 2474–2479 CrossRef CAS.
- R. M. Mohamed, M. K. Mishra, L. M. Al-Harbi, M. S. Al-Ghamdi and U. Ramamurty, Anisotropy in the Mechanical Properties of Organic Crystals: Temperature Dependence, RSC Adv., 2015, 5, 64156–64162 RSC.
- CrysAlis PRO, Version 171.40.14d, Oxford Diffraction /Agilent Technologies UK Ltd, Yarnton, England, 2018 Search PubMed.
- ISO 14577, Metallic Materials — Instrumented Indentation Test for Hardness and Materials Parameters, Int. Organ. Stand., Geneva, Switz, 2015 Search PubMed.
- Dassault Systèmes BIOVIA, Materials Studio, Release 2019, Dassault Systèmes, San Diego, 2019 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ce00041a |
| This journal is © The Royal Society of Chemistry 2021 |