Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Reducing crystal structure overprediction of ibuprofen with large scale molecular dynamics simulations†
Nicholas F.
Francia
 a,
Louise S.
Price
a,
Louise S.
Price
 b and
Matteo
Salvalaglio
b and
Matteo
Salvalaglio
 *a
*a
aThomas Young Centre and Department of Chemical Engineering, University College London, London WC1E 7JE, UK. E-mail: m.salvalaglio@ucl.ac.uk
bDepartment of Chemistry, University College London, 20 Gordon Street, London WC1H 0AJ, UK
First published on 19th July 2021
Abstract
The control of the crystal form is a central issue in the pharmaceutical industry. The identification of putative polymorphs through Crystal Structure Prediction (CSP) methods is based on lattice energy calculations, which are known to significantly over-predict the number of plausible crystal structures. A valuable tool to reduce overprediction is to employ physics-based, dynamic simulations to coalesce lattice energy minima separated by small barriers into a smaller number of more stable geometries once thermal effects are introduced. Molecular dynamics simulations and enhanced sampling methods can be employed in this context to simulate crystal structures at finite temperature and pressure. Here we demonstrate the applicability of approaches based on molecular dynamics to systematically process realistic CSP datasets containing several hundreds of crystal structures. The system investigated is ibuprofen, a conformationally flexible active pharmaceutical ingredient that crystallises both in enantiopure forms and as a racemic mixture. By introducing a hierarchical approach in the analysis of finite-temperature supercell configurations, we can post-process a dataset of 555 crystal structures, identifying 65% of the initial structures as labile, while maintaining all the experimentally known crystal structures in the final, reduced set. Moreover, the extensive nature of the initial dataset allows one to gain quantitative insight into the persistence and the propensity to transform of crystal structures containing common hydrogen-bonded intermolecular interaction motifs.
Introduction
Computational crystal structure prediction (CSP) methods rely on lattice energy calculations to identify and rank putative polymorphic structures. In the final stages of state-of-the-art CSP workflows, lattice energy rankings are refined by performing expensive calculations involving high quality, periodic electronic structure calculations and introducing entropic effects through free energy calculations.1–5 While the quality of the methods employed in the final refinement and ranking stage is constantly improving, their computational cost is typically prohibitive and approaches to achieve a rational reduction of the number of putative structures predicted by lattice-energy based methods (CSP_0) are needed.4,6 Both in industry and academia, CSP methods are becoming increasingly popular given their success in predicting experimental crystal forms starting from only the molecule geometry.4,6–10 For the vast majority of these methods, the different crystal packings are generated ignoring thermal motion and assuming that the lattice energies are a reasonable approximation of the thermodynamic stability of experimental forms. These approaches, identified as CSP_0,11 have been widely used in the 6th CCDC CSP blind test,12 successfully reproducing the experimental forms. A limitation in using local minima of the lattice energy landscape as candidate polymorph structures is that the lattice energy landscape is rugged, and its local minima grossly outnumber the experimentally known polymorphs. This limitation makes it impossible to distinguish possible new polymorphs from artefacts of the CSP_0 static models. In fact, those states characterised by small barriers should coalesce to significantly more stable structures or melt at finite temperature and pressure.1,11,13 Furthermore, it has been shown that the ensemble of configurations accessible corresponding to a single polymorph at ambient temperature can correspond to multiple lattice energy minima.14By introducing finite temperature and pressure effects, we have recently proposed a workflow able to reduce the number of putative polymorphs drastically. The procedure described in ref. 15, applied to the cases of urea and succinic acid, consists of:
• Molecular dynamics (MD) simulations to equilibrate all structures at 300 K and 1 bar.
• Automatically identify those states that are unstable or cluster those that belong to the same dynamic ensembles using structural probabilistic fingerprints.
• Perform enhanced sampling simulations on the cluster centres to overcome MD limits and assess their stability.
In this work, we apply the approach introduced in ref. 15 to a dataset of 555 crystal structures of ibuprofen: an application of the size and complexity typical of modern CSP studies. Ibuprofen is a conformationally flexible, chiral molecule possessing two enantiomers with different pharmacological properties. S-Ibuprofen is the biologically active one while R-ibuprofen needs to be transformed in the body to its S-counterpart.16,17 This popular pain-relieving API is commonly available in its racemic form I.18 A more expensive enantiopure form, here labelled form E, contains only the S-ibuprofen.19,20 More recently, a second less-stable racemic form II was observed in a differential scanning calorimetry experiment.21–23
Here, in addition to demonstrating the method's applicability to a dataset one order of magnitude larger than previously attempted, we describe new tools implemented in the analysis to handle sets of more than 500 CSP_0-generated structures. In particular, we introduced a fast molecule-dependent classification to reduce the time needed to compare crystal structures and cluster equivalent geometries. This improvement results in a rapid clustering analysis, which was repeatedly deployed at regular steps during biased simulations to systematically detect structural transitions without following molecular trajectories one at a time, an impractical task when dealing with several hundreds of finite-temperature dynamic simulations. Moreover, the application of the simulation workflow to a large dataset of mostly hydrogen-bonded CSP_0 crystal packings has allowed us to quantitatively analyse the emergence of conformational and orientational disorder at finite temperature, and to assess the persistence of H-bond interaction motifs. Finally, we investigate the dependence of the unsupervised clustering used to identify analogous structures on the choice of collective descriptors at the basis of the probabilistic fingerprints used to define a dissimilarity metric between finite temperature crystal supercells. With the improvements in efficiency introduced in this work, the reduction workflow introduced in ref. 15 can be deployed efficiently to reduce CSP_0 sets of the size and complexity approaching those of real-world applications.
Methods
CSP_0 lattice energy landscape
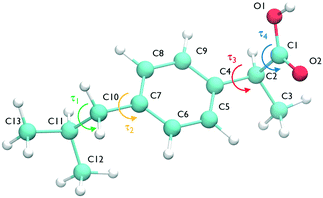
The ibuprofen search was carried out using CrystalPredictor1.9,24 which allows the molecule to assume different conformations. In particular, we considered the two torsional groups of angles (τ1, τ2) and (τ3, τ4), shown in Fig. 1, that were separately varied from 0 to 360 degrees in 20 degree steps. The anti conformation of the carboxylic acid group25–28 was not considered in the search, as the known experimental structures of ibuprofen do not contain it. A recent study of carboxyl groups25 showed that the neutral carboxyl group is only observed in anti configurations in about 12% of crystal structures, but of these, intramolecular hydrogen bonds (which are not available in ibuprofen) dominate. Of intermolecular hydrogen bond interactions of the carboxyl group, just 3% contain the anti configuration.25 With the workflow adopted in this work, it is highly unlikely that any structures could change to the anti conformation during the CSP_0 stage. However, as discussed in the following sections, MD-based simulations are free to explore the entire configuration space of individual molecules.The search used molecular fragments taken from the ab initio optimised molecule at the PBE0/6-31G(d,p) level of theory. The fixed point charges used in this initial step are obtained using the larger basis set aug-cc-pVDZ. The parameters from the FIT potential29 with polar hydrogens30 were used for the repulsion–dispersion contributions to the energy.
The search was performed in 59 space groups with one molecule in the asymmetric unit cell. After removing the duplicates, the structures are labelled as their rank order at this stage, using the prefix R for racemic and E for enantiopure depending on their symmetry.
The resulting unique structures were then optimised with DFTB3-D3 (ref. 31) to relax atomic positions and remove the possible unfeasible geometries derived from the use of rigid fragments of the molecule. The accurate evaluation of the lattice energies was performed with a single step DMACRYS32 calculation, using distributed multipoles obtained from the PBE0/aug-cc-pVDZ charge density with GDMA2.2 (ref. 33) and the repulsion–dispersion potential described in the previous paragraph.29,30
After rescaling the lattice energies by Z, the 555 crystal structures within 10 kJ mol−1 of the global minimum are finally optimised with CrystalOptimizer2.4.7.1.34 The choice of this energy cutoff was motivated by the study in ref. 2 which identifies 97% of the relative energies between conformational polymorphs being below 10 kJ mol−1 and the fact that all ibuprofen experimental forms are within this range in our search. Both the crystal structure and molecular conformation are optimised in a two-level method, with the intramolecular energies and hessian evaluated at the PBE0/6-31G(d,p) level of theory and the intermolecular energy calculated from the distributed multipoles (extracted from the charge density at the PBE0/aug-cc-pVDZ level of theory) and the repulsion–dispersion parameters described above. The smaller 6-31G(d,p) basis set was found to accurately assess the conformation of the molecule, but it was not sufficient to model the electrostatic forces of molecules in the experimentally observed crystal structures, thus justifying the use of the augmented basis set. This set of refined structures comprises the CSP_0 landscape shown in Fig. 4A.
Structure preparation and atom typing
The General Amber Force Field35 has been used to describe the ibuprofen molecule. Atom types are assigned with the AmberTools suite36 while point charges are assigned with the AM1-BCC model.37 Simulations are performed with the Gromacs MD package.38,39 This requires atomic coordinate files to be written in the order specified by the reference forcefield topology. Hence, all atoms in crystal cells must be rearranged to match the forcefield index. This is done by transforming molecules in graphs and applying the VF2 graph match algorithms40 available in the Python library NetworkX.41 Finally, in order to see possible transitions or formation of orientational disorder in a relatively small computational time, for each crystal we generated a supercell of at least 200 molecules. The simulation boxes are chosen to have a nearly cubic shape with each cell edge around 4.5 nm.Energy minimisation
We optimised the atoms' positions using the steepest descent algorithm. The neighbour lists are updated every 10 steps using the Verlet cutoff scheme. Electrostatic and van der Waals interactions are calculated using a cutoff of 1.0 nm while long-range interactions are treated with the smooth particle mesh Ewald (PME)42 and Lennard-Jones PME. After a first atoms' position optimisation, we used LAMMPS to relax the cell parameters (feature not available in Gromacs), using InterMol43 to convert the molecular forcefield. A second energy minimisation with Gromacs is performed to take into account differences between the two packages.43 Finally, the GAFF lattice energies are estimated with the equation: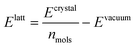 | (1) |
Equilibration at finite temperature and pressure
We performed a 3 ns simulation in the canonical ensemble at 300 K, followed by 4 ns in the isothermal–isobaric ensemble at 300 K and 1 bar. We used the velocity Verlet integrator with a 1 fs timestep. We controlled the temperature with the Bussi–Donadio–Parrinello thermostat44 and equilibrated the systems at 1 bar for the first 1 ns using the Berendsen anisotropic barostat45 and then switched to the Parrinello–Rahman barostat46 for the following 3 ns.Probabilistic fingerprints
Effective descriptors of the different geometries generated should be able to handle the displacement of atomic positions from equilibrium in finite-temperature simulations and efficiently capture the differences between crystal packings. In this context, we previously proposed15 a set of system-dependent probability densities that describes the relative position, relative orientation and possible conformations,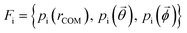 , as the fingerprint of each crystal when dealing with flexible molecules. PLUMED 2 (ref. 47) has been extensively used to analyse trajectories and generate distributions. An example of the inputs used to generate the components of the structural fingerprints described here are available on PLUMED-NEST, the public repository of the PLUMED consortium,48 as plumID:21.019.
, as the fingerprint of each crystal when dealing with flexible molecules. PLUMED 2 (ref. 47) has been extensively used to analyse trajectories and generate distributions. An example of the inputs used to generate the components of the structural fingerprints described here are available on PLUMED-NEST, the public repository of the PLUMED consortium,48 as plumID:21.019.
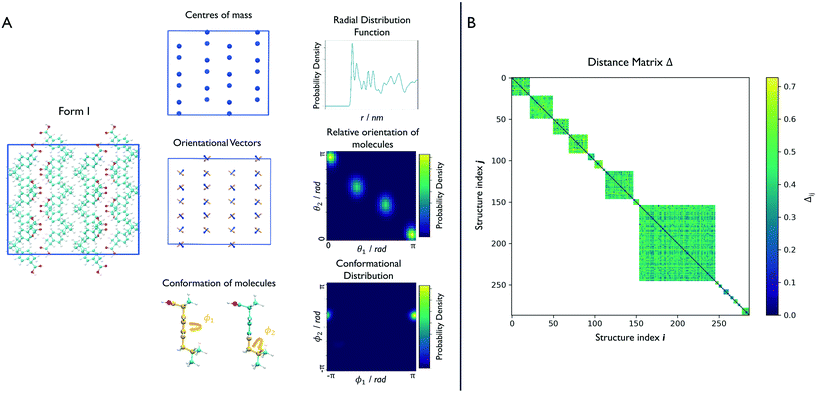
In the case of ibuprofen, the term pi(rCOM) represents the radial distribution function of centres of mass of molecules in the ith crystal structure. The relative orientation of molecules in the ith crystal structure is described by the 2D probability density distribution 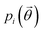 , a function of the intermolecular angles θ1 and θ2, obtained from two orthogonal vectors connecting the atoms C6–C8 and C7–C4 of the aromatic ring of the molecule, as shown in Fig. 2A. Finally the conformational contribution to Fi,
, a function of the intermolecular angles θ1 and θ2, obtained from two orthogonal vectors connecting the atoms C6–C8 and C7–C4 of the aromatic ring of the molecule, as shown in Fig. 2A. Finally the conformational contribution to Fi, 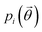 , was defined following the conformational analysis reported in ref. 49, which employs the 2D distribution of the global (ϕ1) and local (ϕ2) torsional angles shown in Fig. 2A. The former represents the relative orientation of the two substituents of the aromatic ring while the latter captures the relative position of the methyl groups. In this approximation, molecules can adopt six possible conformational states. In order to assess the generality of the choice of relatively coarse conformational descriptors, we compared it with an alternative, more fine-grained representation, making use of two 2D distributions (pi(τ1, τ2) and pi(τ3, τ4), Fig. 1). The two different approaches, despite the difference in level of detail, and of the associated computational cost, lead to similar results. Within the conformational fingerprints we did not include descriptors of the syn/anti periplanar conformational isomerism of the carboxylic acid group. We have a posteriori validated this choice by analysing all trajectories, and observing that out of the 555 crystal structures analysed we observed only once the spontaneous transition of a few molecules to the anti conformation, in correspondence to the onset of disorder in a high energy structure. This confirms that the spontaneous occurrence of anti conformers observed in disordered ibuprofen systems27,28 is unlikely in crystalline packings. Finally, the probabilistic fingerprints are complemented by an additional parameter used to classify structures based on their chirality.
, was defined following the conformational analysis reported in ref. 49, which employs the 2D distribution of the global (ϕ1) and local (ϕ2) torsional angles shown in Fig. 2A. The former represents the relative orientation of the two substituents of the aromatic ring while the latter captures the relative position of the methyl groups. In this approximation, molecules can adopt six possible conformational states. In order to assess the generality of the choice of relatively coarse conformational descriptors, we compared it with an alternative, more fine-grained representation, making use of two 2D distributions (pi(τ1, τ2) and pi(τ3, τ4), Fig. 1). The two different approaches, despite the difference in level of detail, and of the associated computational cost, lead to similar results. Within the conformational fingerprints we did not include descriptors of the syn/anti periplanar conformational isomerism of the carboxylic acid group. We have a posteriori validated this choice by analysing all trajectories, and observing that out of the 555 crystal structures analysed we observed only once the spontaneous transition of a few molecules to the anti conformation, in correspondence to the onset of disorder in a high energy structure. This confirms that the spontaneous occurrence of anti conformers observed in disordered ibuprofen systems27,28 is unlikely in crystalline packings. Finally, the probabilistic fingerprints are complemented by an additional parameter used to classify structures based on their chirality.
Structural (dis)similarity and clustering
The similarity between two fingerprints, Fi and Fj, is quantitatively determined by computing the Hellinger distance, Hij, between each equivalent distribution, defined as: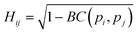 | (2) |
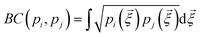 is the Bhattacharyya coefficient and ξ is the vector variable used. The distance between structures i and j, Δij, is finally defined as the norm of the vector of Hellinger distances:
is the Bhattacharyya coefficient and ξ is the vector variable used. The distance between structures i and j, Δij, is finally defined as the norm of the vector of Hellinger distances: 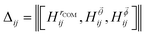 .
.
However, prior to the clustering analysis, we want to remove those structures that are unstable at finite temperature and pressure and melt or develop into a disordered packing. Two strategies have been adopted in this context in order to take into account the emergence of both orientational and conformational disorder. Firstly, orientational disorder is considered by comparing the distribution of the intermolecular torsional angle, p(θ1), of the structures with an uniform distribution typical of the liquid state, pU(θ) = 1/2π, hence:
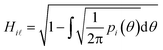 | (3) |
We can now group together the finite-temperature putative polymorphs that coalesce to the same geometry. In order to reduce the number of comparisons needed, we can exploit two properties that we have already determined for each structure, namely the chirality and the conformations the molecules adopt in the crystal. Δij is therefore calculated only between structures that share the same chirality and conformer composition, drastically reducing the number of comparisons necessary to perform a full clustering of the trajectories, and resulting in the distance matrix in Fig. 2B. To each of the resulting subgroups, corresponding to square sub-regions of the dissimilarity matrix Δ in which the value Δij is defined (see Fig. 2B), we applied the fast search and find of density peaks (FSFDP) clustering algorithm.50 The structure with the lowest potential energy in each cluster is taken for the next step.
Metadynamics
In order to overcome MD timescale limitations and sample possible slow transitions, we performed well tempered metadynamics (WTmetaD) simulations51 on the cluster centres. In WTmetaD, an adaptive bias potential acts on a limited number of degrees of freedom, called collective variables (CVs), pushing the system to explore more efficiently its configuration space. The choice of CVs is motivated by the need to enhance structural fluctuations without specifically leading the transformation along a specific pathway. To this aim we used density and potential energy, a choice that has the advantage of being general and computationally efficient and therefore suitable for large sets of structures. Given their generality, these CVs can be applied to every crystal but are expected to enhance transitions only between similar structures and have a reduced accuracy in computing the free energy differences between two specific crystal structures. The bias potential is updated every 1 ps with Gaussians characterised by an initial height of 2 kJ mol−1 and a width of 10 kg m−3 for the density and 2 kJ mol−1 for the potential energy. These simulations are performed using Gromacs patched with PLUMED 2.47 The work performed on the system through the introduction of a bias potential at a time t is represented by the reweighting factor, C(t),52 defined as: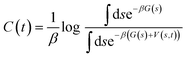 | (4) |
Results
The CSP_0 analysis identified the global minimum, structure R227, as the experimental Form I with an RMSD30 of 0.014 Å between the CSP_0 structure and the experimental structure minimised with the same computational method. The search was performed considering Z′ = 1. Hence the enantiopure form E, which has Z′ = 2, cannot be found. The high-energy structure R5596 approximately reproduces the geometry of form II with an RMSD15 of 0.66 Å. However, the packing similarity analysis revealed a poor overlap between the two structures. We included in the finite-temperature analysis also the experimental structures IBPRAC16 (ref. 18) (form I), JEKNOC12 (ref. 19) (form E) and IBPRAC04 (ref. 22) (form II) available in the Cambridge Structural Database (CSD)53 in order to monitor their evolution and predicted persistence throughout the different steps of the reduction process. From a lattice energy perspective, the difference in stability of the experimentally known polymorphs predicted at the CSP_0 stage is significant. Form E is found to be at +5.02 kJ mol−1 from form I, while form II is at +16.87 kJ mol−1. The large scale set of crystal structures simulated at finite temperature and pressure displays a significant variability attested by the 14 different hydrogen-bonding motifs identified in the CSP_0 dataset. The motifs search was carried out using the CSD-Material module in Mercury.54 The ring R22(8) motif55 is the dominant intermolecular interaction motif, recorded in more than half of the structures, including all the experimental ones. H-Bonded chains also account for a significant proportion of the structures in the initial dataset, with 151 unit cells displaying the C11(4) motif and 41 unit cells stabilised by the C11(2) one.Lattice energies are very sensitive to the method used, so when comparing the CSP_0 energies to GAFF, differences are expected. In general, GAFF tends to overestimate the lattice energy differences. Despite this, form I is found to be among the most stable structures, 4th in the ranking. Form II was confirmed to be very high in energy, at +28.15 kJ mol−1 from the global minimum. Form E is located between them at +8.77 kJ mol−1, confirming the relative ranking obtained at the level of theory deployed in the CSP_0 step.
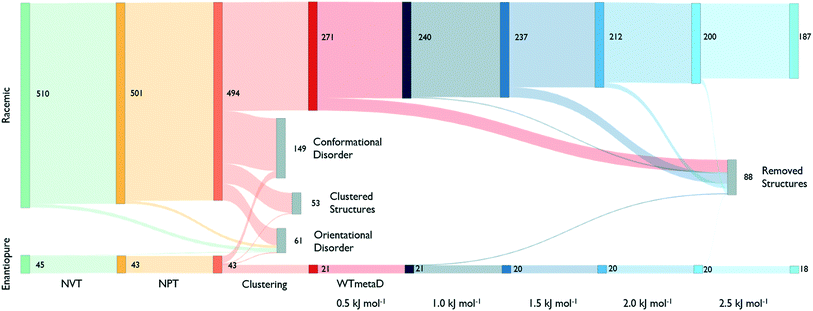
The reduction process starts by equilibrating all structures at 300 K and 1 bar. Fig. 3, shows that around 40% of the structures melt or present disorder after 4 ns of dynamic simulation in the NPT ensemble. The remaining structures are then clustered based on their chirality and molecule conformations.
In the largest group of racemic structures, molecules show conformational flexibility along the local torsional angle (see Fig. 2), producing two peaks in the conformational component of the structural fingerprint. Experimental form II is among these with less than 10% of the molecules in the supercell assuming a distorted conformation. In this step, molecules are free to rearrange and adopt the anti conformation of the carboxylic acid group. However, only one high-energy disordered structure ends up having some molecules in this conformation.
The clustering analysis shows that only a few states coalesce into common finite-temperature crystal structures while most of them preserve their geometry. The stable form I is one of the few systems that produce a cluster, and it is among the most populated ones. On the other hand, form II formed a small cluster with the CSP_0 structure that best matches its geometry while no structure transformed to a configuration compatible with form E.
Cluster centres are then subject to WTmetaD simulations. In order to automatically analyse trajectories and detecting transitions as a function of the work performed by the WTmetaD bias, fingerprints are generated at every increment of 0.5 kJ mol−1 of C(t) or by looking at the last frames of those trajectories stopped due to large fluctuations of the DRMSD (see the methods section). Every time fingerprints are generated, clustering is performed, identifying structures that convert and are thus removed from the count of independent, persistent structures.
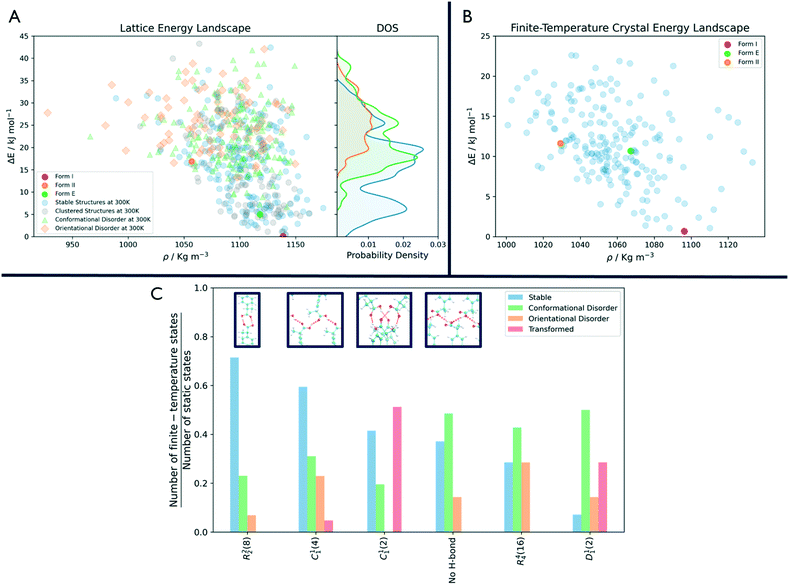
As shown in Fig. 3, the number of persistent putative polymorphs decreases throughout the workflow. By the end of the analysis, from the initial set of 555 CSP_0 lattice energy minima, we retain 205 persistent structures, corresponding to a 65% of reduction. All experimental structures came out as thermodynamically stable, preserving their geometry during finite-temperature biased simulations. In Fig. 4A, we show the lattice energy landscape at 0 K and depict them based on their behaviour at 300 K.
Orientationally disordered structures at finite-temperature are on average, located at higher energies in the 0 K landscape than the structures exhibiting conformational disorder. Persistent crystal structures at 300 K span over the entire lattice energy range. The overlap in lattice energy between the distributions of labile and persistent crystal structures highlights how a reduction of the lattice energy landscape based solely on lattice energy is insufficient and would actually miss high energy experimental structures like form II. The resulting finite-temperature crystal energy landscape, in Fig. 4B, shows a general decrease in the potential energy difference for those structures that survive.
Among the dominant hydrogen-bonding motifs, the ring motif R22(8) and the chain motif C11(4) were shown to be more persistent than the average, with a decrease in number of structures of 29% and 41%, considering all stable structures. While being present in the final set, the chain motif C11(2) tended to convert to the more stabilising C11(4). Looking at the rare motifs, 9 of them disappear during the analysis. Motifs D33(10), R33(12), R33(6), R44(8), R66(12) and R66(24) all result in melted structures while motifs C22(6), R22(6) and R44(12) transform to other motifs.
Discussion
Through an MD-based reduction of the lattice energy landscape we drastically reduced the number of putative polymorphs of Ibuprofen. Form I, the most stable experimentally known polymorph came out as second in the final ranking with structure R4124 being the global minimum (see the ESI† for a complete list of crystal structures, energies and labels). However, many structures converted to the experimental form, suggesting that form I could act as kinetic trap for labile states. Form I and the enantiopure form E were able to preserve their CSP_0 geometry with little variation due to the molecular motion. In form II, a few molecules dynamically change conformation during biased and unbiased simulations, showing the possibility of dynamic disorder in the crystal at standard conditions. This is evidenced also by the presence of two conformationally disordered structures, R2315 and R6595, that resemble form II. Structure R5596, which presents geometrical similarities with form II at 0 K, effectively converts to the experimental one at 300 K.The R22(8) motif is the most frequent intermolecular interaction motif in the final set being present in 119 structures and is dominant among the low-energy structures. From Fig. 4C, we can see that structures associated with this motif, are most likely to preserve their H-bonds. However, other motifs seem to be favoured at 300 K compared to their initial number in the CSP_0 set. In particular, the chain motif C11(4) has a similar persistence to R22(8) and is present in 10 of the 18 enantiopure structures, including the most stable one (E6134). This could indicate that the hydrogen-bonded carboxylic acid dimer of the R22(8) pattern is favoured during the nucleation or growth process. The rotation of the carboxyl group is associated with the inter-conversion between motifs C11(2) and C11(4) with the balance shifted towards the latter. Interestingly, 12 structures are shown to be persistent at finite-temperature and pressure despite the lack of H-bonding motifs and their high potential energy. The use of highly polar solvents that preclude H-bonding interactions could favour the formation of these structures.56
In Fig. 4A, the states that are effectively persistent at finite temperature and pressure are shown as blue dots. From the probability density on the right of the same figure, we can see that some of these are high energy structures. This implies that the use of energy cutoff, although often necessary, can lead to the removal of relevant geometries from the analysis. In this case, the ibuprofen form II could have been ignored being higher in energy than the typical energy cutoffs used, usually in the range 5–15 kJ mol−1.
Conclusions
In this work, we have tackled the systematic reduction of a large-scale dataset of CSP_0 crystal structures, including 555 putative crystal structures of ibuprofen by systematically applying MD simulations.15 To scale up one order of magnitude in the number of crystal structures considered, compared to previous studies, we implemented new strategies to further increase the efficiency of the clustering and analysis protocols, drastically reducing the need for manual inspection of the trajectories in different steps. In particular, through a systematic conformational analysis, we could automatically detect disorder formation in the simulation box. Moreover, partitioning a priori the distance matrix in subsets based on the number and type of conformers present in the crystal structure, small and fast to manage, allowed us to efficiently repeat the clustering analysis at regular intervals during the metadynamics simulations. This procedure allowed us to detect transitions under progressively enhanced fluctuations of the supercells' density and lattice energy. The systematic setup and analysis of 555 trajectories, which altogether amounts to 8 μs across multiple MD protocols, is made possible by an ad hoc Python library, available at https://github.com/mme-ucl/pypol.Applying this approach to a set of 555 CSP_0-generated structures of ibuprofen resulted in a 65% reduction of the number of predicted structures, leading to a group of 205 persistent lattice structures. All the experimentally known structures persisted throughout the analysis with minor variations from their original geometry. In this work we have decided to probe the persistence of crystal structures associated to energy perturbations of the order of 2.5 kJ mol−1. Sampling larger energy scales is likely to yield further reductions in the number of crystal structures. Interestingly, despite the significant variability in the intermolecular interaction motifs present in the initial dataset (14), we find that the motifs R22(8) and C11(4) are dominant in the final set.
The approach that we propose in this work will enable a rational reduction of crystal energy landscapes by identifying and removing crystal structures that are short lived at finite-temperature from further analysis, typically performed with computationally expensive electronic structure methods. We envisage the application of the proposed approach as a physics-based alternative to a straightforward application of an energy-cutoff.
In fact, as shown in Fig. 4A, labile and persistent structures' distributions in energy are overlapped, and a cut-off based reduction of the initial set would be prone to removing from further analysis interesting, long-lived putative polymorphs.
By taking advantage of the implementation discussed and tested in this work, we can now study CSP_0 crystal energy landscapes of scale and complexity approaching those of real-world applications.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Professor Sarah L. Price for fruitful discussions. Professors Claire Adjiman & Costas Pantelides at Imperial College London are acknowledged for sharing with us the CrystalPredictor and CrystalOptimizer programs. The CSP computational software is developed under EPSRC grant EP/K039229/1. Calculations were performed on University College London's Myriad and Kathleen High Performance Computing Facilities. NFF acknowledges Eli Lilly Digital Design for support through a PhD scholarship. LSP and MS are also partially funded by Eli Lilly Digital Design.References
- S. L. Price, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2013, 69, 313–328 CrossRef CAS PubMed.
- A. J. Cruz-Cabeza, S. M. Reutzel-Edens and J. Bernstein, Chem. Soc. Rev., 2015, 44, 8619–8635 RSC.
- J. Nyman and G. M. Day, CrystEngComm, 2015, 17, 5154–5165 RSC.
- G. Sun, X. Liu, Y. A. Abramov, S. O. Nilsson Lill, C. Chang, V. Burger and A. Broo, Cryst. Growth Des., 2021, 21, 1972–1983 CrossRef CAS.
- E. Schneider, L. Vogt and M. E. Tuckerman, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 542–550 CrossRef CAS PubMed.
- M. Yang, E. Dybeck, G. Sun, C. Peng, B. Samas, V. M. Burger, Q. Zeng, Y. Jin, M. A. Bellucci, Y. Liu, P. Zhang, J. Ma, Y. A. Jiang, B. C. Hancock, S. Wen and G. P. Wood, Cryst. Growth Des., 2020, 20, 5211–5224 CrossRef CAS.
- Y. A. Abramov, Org. Process Res. Dev., 2013, 17, 472–485 CrossRef CAS.
- S. L. Price, D. E. Braun and S. M. Reutzel-Edens, Chem. Commun., 2016, 52, 7065–7077 RSC.
- J. Nyman, O. S. Pundyke and G. M. Day, Phys. Chem. Chem. Phys., 2016, 18, 15828–15837 RSC.
- J. Hoja, H. Y. Ko, M. A. Neumann, R. Car, R. A. DiStasio and A. Tkatchenko, Sci. Adv., 2019, 5, 3338–3347 CrossRef PubMed.
- S. L. Price, Faraday Discuss., 2018, 211, 9–30 RSC.
- A. M. Reilly, R. I. Cooper, C. S. Adjiman, S. Bhattacharya, A. D. Boese, J. G. Brandenburg, P. J. Bygrave, R. Bylsma, J. E. Campbell, R. Car, D. H. Case, R. Chadha, J. C. Cole, K. Cosburn, H. M. Cuppen, F. Curtis, G. M. Day, R. A. DiStasio, A. Dzyabchenko, B. P. Van Eijck, D. M. Elking, J. A. Van Den Ende, J. C. Facelli, M. B. Ferraro, L. Fusti-Molnar, C. A. Gatsiou, T. S. Gee, R. De Gelder, L. M. Ghiringhelli, H. Goto, S. Grimme, R. Guo, D. W. Hofmann, J. Hoja, R. K. Hylton, L. Iuzzolino, W. Jankiewicz, D. T. De Jong, J. Kendrick, N. J. De Klerk, H. Y. Ko, L. N. Kuleshova, X. Li, S. Lohani, F. J. Leusen, A. M. Lund, J. Lv, Y. Ma, N. Marom, A. E. Masunov, P. McCabe, D. P. McMahon, H. Meekes, M. P. Metz, A. J. Misquitta, S. Mohamed, B. Monserrat, R. J. Needs, M. A. Neumann, J. Nyman, S. Obata, H. Oberhofer, A. R. Oganov, A. M. Orendt, G. I. Pagola, C. C. Pantelides, C. J. Pickard, R. Podeszwa, L. S. Price, S. L. Price, A. Pulido, M. G. Read, K. Reuter, E. Schneider, C. Schober, G. P. Shields, P. Singh, I. J. Sugden, K. Szalewicz, C. R. Taylor, A. Tkatchenko, M. E. Tuckerman, F. Vacarro, M. Vasileiadis, A. Vazquez-Mayagoitia, L. Vogt, Y. Wang, R. E. Watson, G. A. De Wijs, J. Yang, Q. Zhu and C. R. Groom, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 439–459 CrossRef CAS PubMed.
- C. S. Adjiman, J. G. Brandenburg, D. E. Braun, J. Cole, C. Collins, A. I. Cooper, A. J. Cruz-Cabeza, G. M. Day, M. Dudek, A. Hare, L. Iuzzolino, D. McKay, J. B. Mitchell, S. Mohamed, S. Neelamraju, M. Neumann, S. Nilsson Lill, J. Nyman, A. R. Oganov, S. L. Price, A. Pulido, S. Reutzel-Edens, I. Rietveld, M. T. Ruggiero, J. C. Schön, S. Tsuzuki, J. van den Ende, G. Woollam and Q. Zhu, Faraday Discuss., 2018, 211, 493–539 RSC.
- E. C. Dybeck, D. P. McMahon, G. M. Day and M. R. Shirts, Cryst. Growth Des., 2019, 19, 5568–5580 CrossRef CAS.
- N. F. Francia, L. S. Price, J. Nyman, S. L. Price and M. Salvalaglio, Cryst. Growth Des., 2020, 20, 6847–6862 CrossRef CAS.
- A. M. Evans, Clin. Rheumatol., 2001, 20, 9–14 CrossRef PubMed.
- G. Geisslinger, K. P. Stock, G. L. Bach, D. Loew and K. Brune, Agents Actions, 1989, 27, 455–457 CrossRef CAS PubMed.
- K. Ostrowska, M. Kropidowska and A. Katrusiak, Cryst. Growth Des., 2015, 15, 1512–1517 CrossRef CAS.
- M. D. King, W. D. Buchanan and T. M. Korter, J. Pharm. Sci., 2011, 100, 1116–1129 CrossRef CAS PubMed.
- A. A. Freer, J. M. Bunyan, N. Shankland and D. B. Sheen, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1993, 49, 1378–1380 CrossRef.
- E. Dudognon, F. Danède, M. Descamps and N. T. Correia, Pharm. Res., 2008, 25, 2853–2858 CrossRef CAS PubMed.
- P. Derollez, E. Dudognon, F. Affouard, F. Danède, N. T. Correia and M. Descamps, Acta Crystallogr., Sect. B: Struct. Sci., 2010, 66, 76–80 CrossRef CAS PubMed.
- P. A. Williams, C. E. Hughes and K. D. Harris, Cryst. Growth Des., 2012, 12, 5839–5845 CrossRef CAS.
- P. G. Karamertzanis and C. C. Pantelides, Mol. Phys., 2007, 105, 273–291 CrossRef CAS.
- L. D'Ascenzo and P. Auffinger, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2015, 71, 164–175 CrossRef PubMed.
- L. Leiserowitz, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1976, 32, 775–802 CrossRef.
- M. T. O. Abe, M. T. Viciosa, N. T. Correia and F. Affouard, Phys. Chem. Chem. Phys., 2018, 20, 29528–29538 RSC.
- K. Adrjanowicz, K. Kaminski, M. Dulski, P. Wlodarczyk, G. Bartkowiak, L. Popenda, S. Jurga, J. Kujawski, J. Kruk, M. K. Bernard and M. Paluch, J. Chem. Phys., 2013, 139, 111103 CrossRef CAS PubMed.
- D. E. Williams and S. R. Cox, Acta Crystallogr., Sect. B: Struct. Sci., 1984, 40, 404–417 CrossRef.
- D. S. Coombes, S. L. Price, D. J. Willock and M. Leslie, J. Phys. Chem., 1996, 100, 7352–7360 CrossRef CAS.
- L. Iuzzolino, P. McCabe, S. L. Price, J. G. Brandenburg and J. Gerit Brandenburg, Faraday Discuss., 2018, 211, 275 RSC.
- S. L. Price, M. Leslie, G. W. Welch, M. Habgood, L. S. Price, P. G. Karamertzanis and G. M. Day, Phys. Chem. Chem. Phys., 2010, 12, 8478–8490 RSC.
- A. J. Stone, J. Chem. Theory Comput., 2005, 1, 1128–1132 CrossRef CAS PubMed.
- E. N. Pistikopoulos, M. C. Georgiadis, V. Dua, C. S. Adjiman and A. Galindo, Process Systems Engineering, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2011, vol. 6, p. 317 Search PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- D. H. Case, J. E. Campbell, P. J. Bygrave and G. M. Day, J. Chem. Theory Comput., 2016, 12, 910–924 CrossRef CAS PubMed.
- A. Jakalian, B. L. Bush, D. B. Jack and C. I. Bayly, J. Comput. Chem., 2000, 21, 132–146 CrossRef CAS.
- E. Lindahl, M. J. Abraham, B. Hess and D. van der Spoel, GROMACS 2021 Manual, 2021, DOI:10.5281/zenodo.4457591.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- L. P. Cordella, P. Foggia, C. Sansone and M. Vento, IEEE Trans. Pattern Anal. Mach. Intell., 2004, 26, 1367–1372 CrossRef PubMed.
- A. A. Hagberg, D. A. Schult and P. J. Swart, 7th Python Sci. Conf., (SciPy 2008), 2008, pp. 11–15 Search PubMed.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- M. R. Shirts, C. Klein, J. M. Swails, J. Yin, M. K. Gilson, D. L. Mobley, D. A. Case and E. D. Zhong, J. Comput.-Aided Mol. Des., 2017, 31, 147–161 CrossRef CAS PubMed.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- M. Parrinello and A. Rahman, Phys. Rev. Lett., 1980, 45, 1196–1199 CrossRef CAS.
- G. A. Tribello, M. Bonomi, D. Branduardi, C. Camilloni and G. Bussi, Comput. Phys. Commun., 2014, 185, 604–613 CrossRef CAS.
- M. Bonomi, G. Bussi, C. Camilloni, G. A. Tribello, P. Banáš, A. Barducci, M. Bernetti, P. G. Bolhuis, S. Bottaro, D. Branduardi, R. Capelli, P. Carloni, M. Ceriotti, A. Cesari, H. Chen, W. Chen, F. Colizzi, S. De, M. De La Pierre, D. Donadio, V. Drobot, B. Ensing, A. L. Ferguson, M. Filizola, J. S. Fraser, H. Fu, P. Gasparotto, F. L. Gervasio, F. Giberti, A. Gil-Ley, T. Giorgino, G. T. Heller, G. M. Hocky, M. Iannuzzi, M. Invernizzi, K. E. Jelfs, A. Jussupow, E. Kirilin, A. Laio, V. Limongelli, K. Lindorff-Larsen, T. Löhr, F. Marinelli, L. Martin-Samos, M. Masetti, R. Meyer, A. Michaelides, C. Molteni, T. Morishita, M. Nava, C. Paissoni, E. Papaleo, M. Parrinello, J. Pfaendtner, P. Piaggi, G. M. Piccini, A. Pietropaolo, F. Pietrucci, S. Pipolo, D. Provasi, D. Quigley, P. Raiteri, S. Raniolo, J. Rydzewski, M. Salvalaglio, G. C. Sosso, V. Spiwok, J. Šponer, D. W. Swenson, P. Tiwary, O. Valsson, M. Vendruscolo, G. A. Voth and A. White, Nat. Methods, 2019, 16, 670–673 CrossRef PubMed.
- V. Marinova, G. P. Wood, I. Marziano and M. Salvalaglio, J. Chem. Theory Comput., 2018, 14, 6484–6494 CrossRef CAS PubMed.
- A. Rodriguez and A. Laio, Science, 2014, 344, 1492–1496 CrossRef CAS PubMed.
- A. Barducci, G. Bussi and M. Parrinello, Phys. Rev. Lett., 2008, 100, 020603 CrossRef PubMed.
- P. Tiwary and M. Parrinello, J. Phys. Chem. B, 2015, 119, 736–742 CrossRef CAS PubMed.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot, S. C. Ward and IUCr, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179 CrossRef CAS PubMed.
- C. F. MacRae, I. Sovago, S. J. Cottrell, P. T. Galek, P. McCabe, E. Pidcock, M. Platings, G. P. Shields, J. S. Stevens, M. Towler and P. A. Wood, J. Appl. Crystallogr., 2020, 53, 226–235 CrossRef CAS PubMed.
- J. Bernstein, R. E. Davis, L. Shimoni and N. Chang, Angew. Chem., Int. Ed. Engl., 1995, 34, 1555–1573 CrossRef CAS.
- R. Bobrovs, L. Drunka, A. A. Auzins, K. Jaudzems and M. Salvalaglio, Cryst. Growth Des., 2021, 21, 436–448 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Tables of the potential energies of structures at different steps. See DOI: 10.1039/d1ce00616a |
| This journal is © The Royal Society of Chemistry 2021 |